Entangled Harmonic Oscillators and Space-Time Entanglement

Abstract

The mathematical basis for the Gaussian entanglement is discussed in detail, as well as its implications in the internal space-time structure of relativistic extended particles. It is shown that the Gaussian entanglement shares the same set of mathematical formulas with the harmonic oscillator in the Lorentz-covariant world. It is thus possible to transfer the concept of entanglement to the Lorentz-covariant picture of the bound state, which requires both space and time separations between two constituent particles. These space and time variables become entangled as the bound state moves with a relativistic speed. It is shown also that our inability to measure the time-separation variable leads to an entanglement entropy together with a rise in the temperature of the bound state. As was noted by Paul A. M. Dirac in 1963, the system of two oscillators contains the symmetries of the $O(3,2)$ de Sitter group containing two $O(3,1)$ Lorentz groups as its subgroups. Dirac noted also that the system contains the symmetry of the $Sp\left(4\right)$ group, which serves as the basic language for two-mode squeezed states. Since the $Sp\left(4\right)$ symmetry contains both rotations and squeezes, one interesting case is the combination of rotation and squeeze, resulting in a shear. While the current literature is mostly on the entanglement based on squeeze along the normal coordinates, the shear transformation is an interesting future possibility. The mathematical issues on this problem are clarified.

1. Introduction

Entanglement problems deal with fundamental issues in physics. Among them, the Gaussian entanglement is of current interest not only in quantum optics [1,2,3,4], but also in other dynamical systems [3,5,6,7,8]. The underlying mathematical language for this form of entanglement is that of harmonic oscillators. In this paper, we present first the mathematical tools that are and may be useful in this branch of physics.

The entangled Gaussian state is based on the formula:

$$\frac{1}{cosh\eta }\sum _k{(tanh\eta )}^k{\chi }_k\left(x\right){\chi }_k\left(y\right)$$

(1)

where ${\chi }_n\left(x\right)$ is the $n^{th}$ excited-state oscillator wave function.

In Chapter 16 of their book [9], Walls and Milburn discussed in detail the role of this formula in the theory of quantum information. Earlier, this formula played the pivotal role for Yuen to formulate his two-photon coherent states or two-mode squeezed states [10]. The same formula was used by Yurke and Patasek in 1987 [11] and by Ekert and Knight [12] for the two-mode squeezed state where one of the photons is not observed. The effect of entanglement is to be seen from the beam splitter experiments [13,14].

In this paper, we point out first that the series of Equation (1) can also be written as a squeezed Gaussian form:

$$\frac{1}{\sqrt{\pi }}exp\left\{-\frac{1}{4}\left[e^{-2\eta }{(x+y)}^2+e^{2\eta }{(x-y)}^2\right]\right\}$$

(2)

which becomes:

$$\frac{1}{\sqrt{\pi }}exp\left\{-\frac{1}{2}\left(x^2+y^2\right)\right\}$$

(3)

when $\eta =0$.

We can obtain the squeezed form of Equation (2) by replacing x and y by $x^{\prime }$ and $y^{\prime }$, respectively, where:

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}cosh\eta & -sinh\eta \\ -sinh\eta & cosh\eta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$$

(4)

If x and y are replaced by z and t, Equation (4) becomes the formula for the Lorentz boost along the z direction. Indeed, the Lorentz boost is a squeeze transformation [3,15].

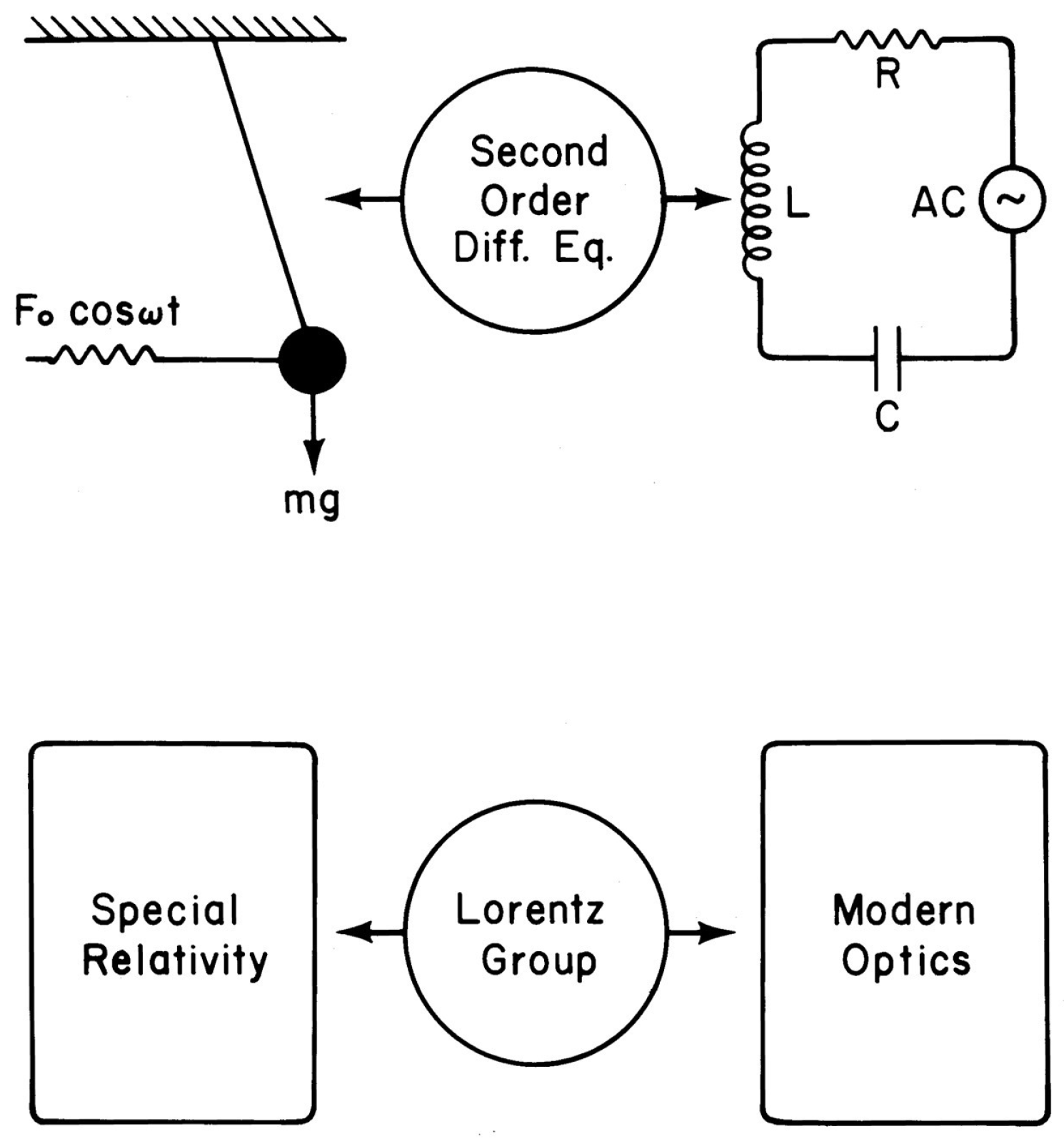
The squeezed Gaussian form of Equation (2) plays the key role in studying boosted bound states in the Lorentz-covariant world [16,17,18,19,20], where z and t are the space and time separations between two constituent particles. Since the mathematics of this physical system is the same as the series given in Equation (1), the physical concept of entanglement can be transferred to the Lorentz-covariant bound state, as illustrated in Figure 1.

We can approach this problem from the system of two harmonic oscillators. In 1963, Paul A. M. Dirac studied the symmetry of this two-oscillator system and discussed all possible transformations applicable to this oscillator [21]. He concluded that there are ten possible generators of transformations satisfying a closed set of commutation relations. He then noted that this closed set corresponds to the Lie algebra of the $O(3,2)$ de Sitter group, which is the Lorentz group applicable to three space-like and two time-like dimensions. This $O(3,2)$ group has two $O(3,1)$ Lorentz groups as its subgroups.

We note that the Lorentz group is the language of special relativity, while the harmonic oscillator is one of the major tools for interpreting bound states. Therefore, Dirac’s two-oscillator system can serve as a mathematical framework for understanding quantum bound systems in the Lorentz-covariant world.

Within this formalism, the series given in Equation (1) can be produced from the ten-generator Dirac system. In discussing the oscillator system, the standard procedure is to use the normal coordinates defined as:

$$u=\frac{x+y}{\sqrt{2}},\mathrm{and}v=\frac{x-y}{\sqrt{2}}$$

(5)

In terms of these variables, the transformation given in Equation (4) takes the form:

$$\left(\begin{array}{c}{u}^{\prime }\\ v^{\prime }\end{array}\right)=\left(\begin{array}{cc}{e}^{-\eta }& 0\\ 0& e^{\eta }\end{array}\right)\left(\begin{array}{c}u\\ v\end{array}\right)$$

(6)

where this is a squeeze transformation along the normal coordinates. While the normal-coordinate transformation is a standard procedure, it is interesting to note that it also serves as a Lorentz boost [18].

With these preparations, we shall study in Section 2 the system of two oscillators and coordinate transformations of current interest. It is pointed out in Section 3 that there are ten different generators for transformations, including those discussed in Section 2. It is noted that Dirac derived ten generators of transformations applicable to these oscillators, and they satisfy the closed set of commutation relations, which is the same as the Lie algebra of the $O(3,2)$ de Sitter group containing two Lorentz groups among its subgroups. In Section 4, Dirac’s ten-generator symmetry is studied in the Wigner phase-space picture, and it is shown that Dirac’s symmetry contains both canonical and Lorentz transformations.

While the Gaussian entanglement starts from the oscillator wave function in its ground state, we study in Section 5 the entanglements of excited oscillator states. We give a detailed explanation of how the series of Equation (1) can be derived from the squeezed Gaussian function of Equation (2).

In Section 6, we study in detail how the sheared state can be derived from a squeezed state. It appears to be a rotated squeezed state, but this is not the case. In Section 7, we study what happens when one of the two entangled variables is not observed within the framework of Feynman’s rest of the universe [22,23].

In Section 8, we note that most of the mathematical formulas in this paper have been used earlier for understanding relativistic extended particles in the Lorentz-covariant harmonic oscillator formalism [20,24,25,26,27,28]. These formulas allow us to transport the concept of entanglement from the current problem of physics to quantum bound states in the Lorentz-covariant world. The time separation between the constituent particles is not observable and is not known in the present form of quantum mechanics. However, this variable effects the real world by entangling itself with the longitudinal variable.

2. Two-Dimensional Harmonic Oscillators

The Gaussian form:

$${\left[\frac{1}{\sqrt{\pi }}\right]}^{1/4}exp\left(-\frac{x^2}{2}\right)$$

(7)

is used for many branches of science. For instance, we can construct this function by throwing dice.

In physics, this is the wave function for the one-dimensional harmonic oscillator in the ground state. This function is also used for the vacuum state in quantum field theory, as well as the zero-photon state in quantum optics. For excited oscillator states, the wave function takes the form:

$${\chi }_n\left(x\right)={\left[\frac{1}{\sqrt{\pi }{2}^{n}n!}\right]}^{1/2}{H}_n\left(x\right)exp\left(\frac{-x^2}{2}\right)$$

(8)

where $H_n\left(x\right)$ is the Hermite polynomial of the $n^{th}$ degree. The properties of this wave function are well known, and it becomes the Gaussian form of Equation (7) when $n=0$.

We can now consider the two-dimensional space with the orthogonal coordinate variables x and y and the same wave function with the y variable:

$${\chi }_m\left(y\right)={\left[\frac{1}{\sqrt{\pi }{2}^{m}m!}\right]}^{1/2}{H}_m\left(y\right)exp\left(\frac{-y^2}{2}\right)$$

(9)

and construct the function:

$${\psi }^{n,m}(x,y)=\left[{\chi }_n\left(x\right)\right]\left[{\chi }_m\left(y\right)\right]$$

(10)

This form is clearly separable in the x and y variables. If n and m are zero, the wave function becomes:

$${\psi }^{0,0}(x,y)=\frac{1}{\sqrt{\pi }}exp\left\{-\frac{1}{2}\left(x^2+y^2\right)\right\}$$

(11)

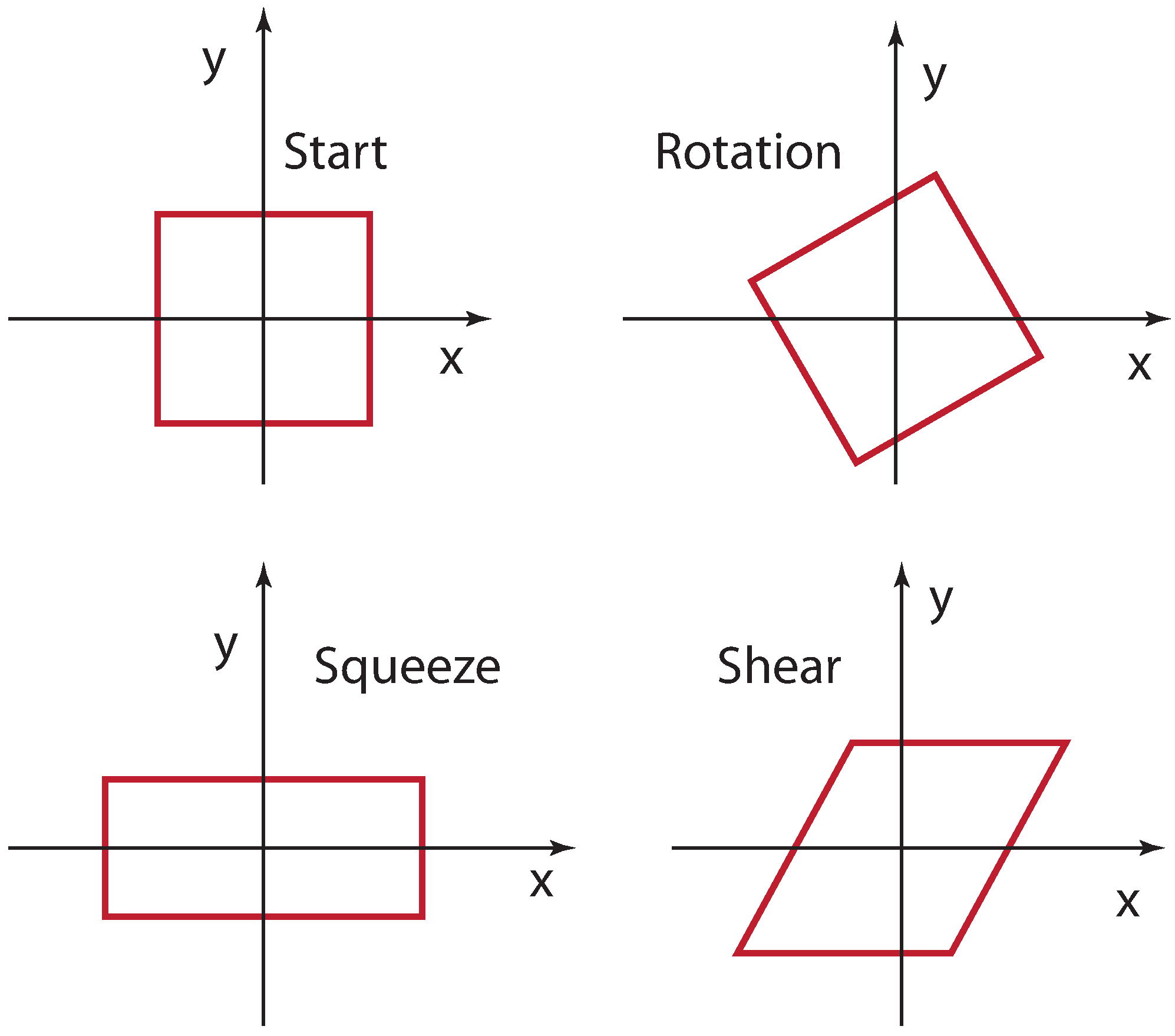
Under the coordinate rotation:

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$$

(12)

this function remains separable. This rotation is illustrated in Figure 2. This is a transformation very familiar to us.

We can next consider the scale transformation of the form:

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}{e}^{\eta }& 0\\ 0& e^{-\eta }\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$$

(13)

This scale transformation is also illustrated in Figure 2. This area-preserving transformation is known as the squeeze. Under this transformation, the Gaussian function is still separable.

If the direction of the squeeze is rotated by 45${}^{\circ }$, the transformation becomes the diagonal transformation of Equation (6). Indeed, this is a squeeze in the normal coordinate system. This form of squeeze is most commonly used for squeezed states of light, as well as the subject of entanglements. It is important to note that, in terms of the x and y variables, this transformation can be written as Equation (4) [18]. In 1905, Einstein used this form of squeeze transformation for the longitudinal and time-like variables. This is known as the Lorentz boost.

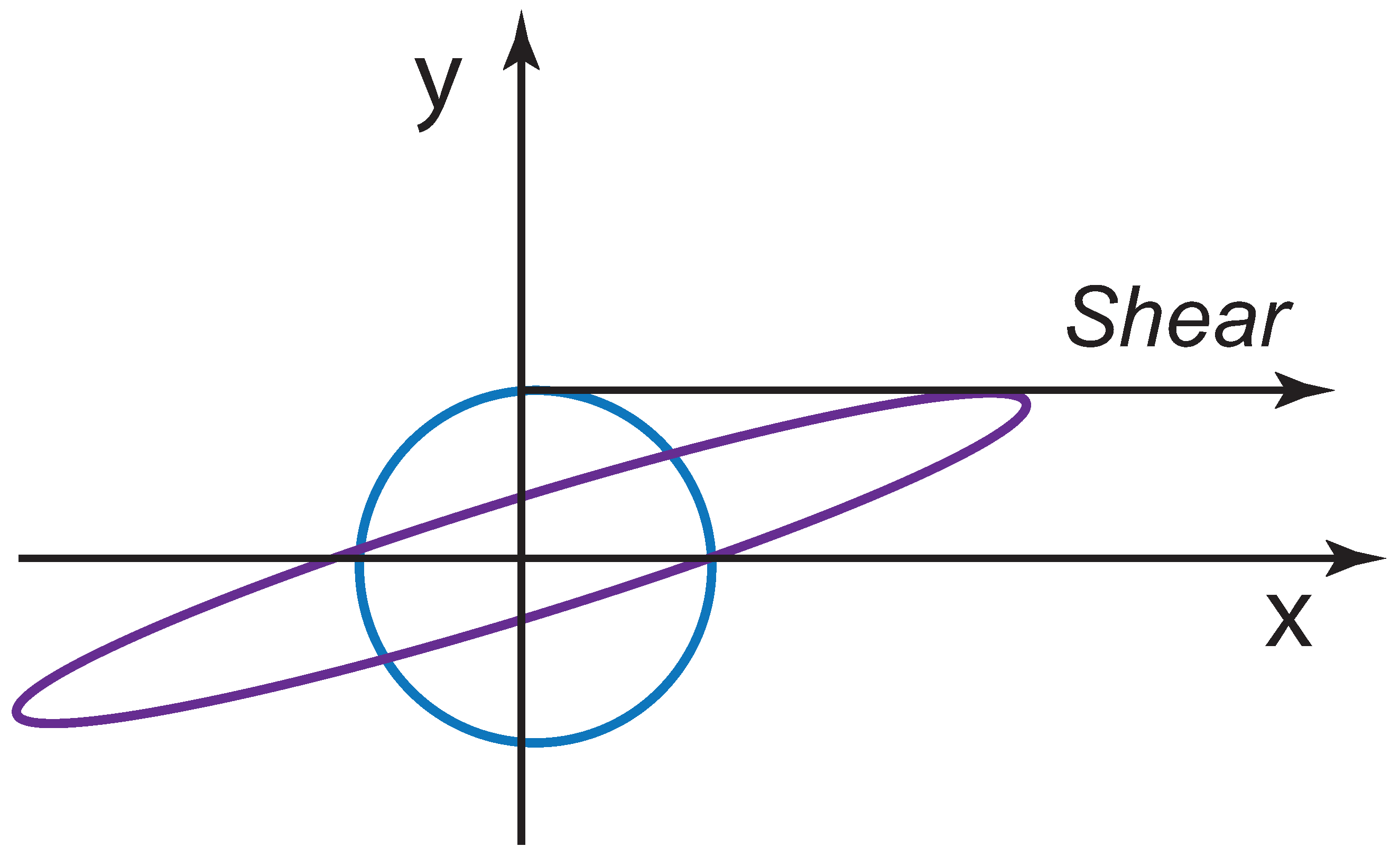
In addition, we can consider the transformation of the form:

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& 2\alpha \\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$$

(14)

This transformation shears the system as is shown in Figure 2.

After the squeeze or shear transformation, the wave function of Equation (10) becomes non-separable, but it can still be written as a series expansion in terms of the oscillator wave functions. It can take the form:

$$\psi (x,y)=\sum _{n,m}{A}_{n,m}{\chi }_n\left(x\right){\chi }_m\left(y\right)$$

(15)

with:

$$\sum _{n,m}{\left|A_{n,m}\right|}^2=1$$

if $\psi (x,y)$ is normalized, as was the case for the Gaussian function of Equation (11).

2.1. Squeezed Gaussian Function

Under the squeeze along the normal coordinate, the Gaussian form of Equation (11) becomes:

$${\psi }_{\eta }(x,y)=\frac{1}{\sqrt{\pi }}exp\left\{-\frac{1}{4}\left[e^{-2\eta }{(x+y)}^2+e^{2\eta }{(x-y)}^2\right]\right\}$$

(16)

which was given in Equation (2). This function is not separable in the x and y variables. These variables are now entangled. We obtain this form by replacing, in the Gaussian function of Equation (11), the x and y variables by $x^{\prime }$ and $y^{\prime }$, respectively, where:

$$x^{\prime }=(cosh\eta )x-(sinh\eta )y,\mathrm{and}{y}^{\prime }=(cosh\eta )y-(sinh\eta )x$$

(17)

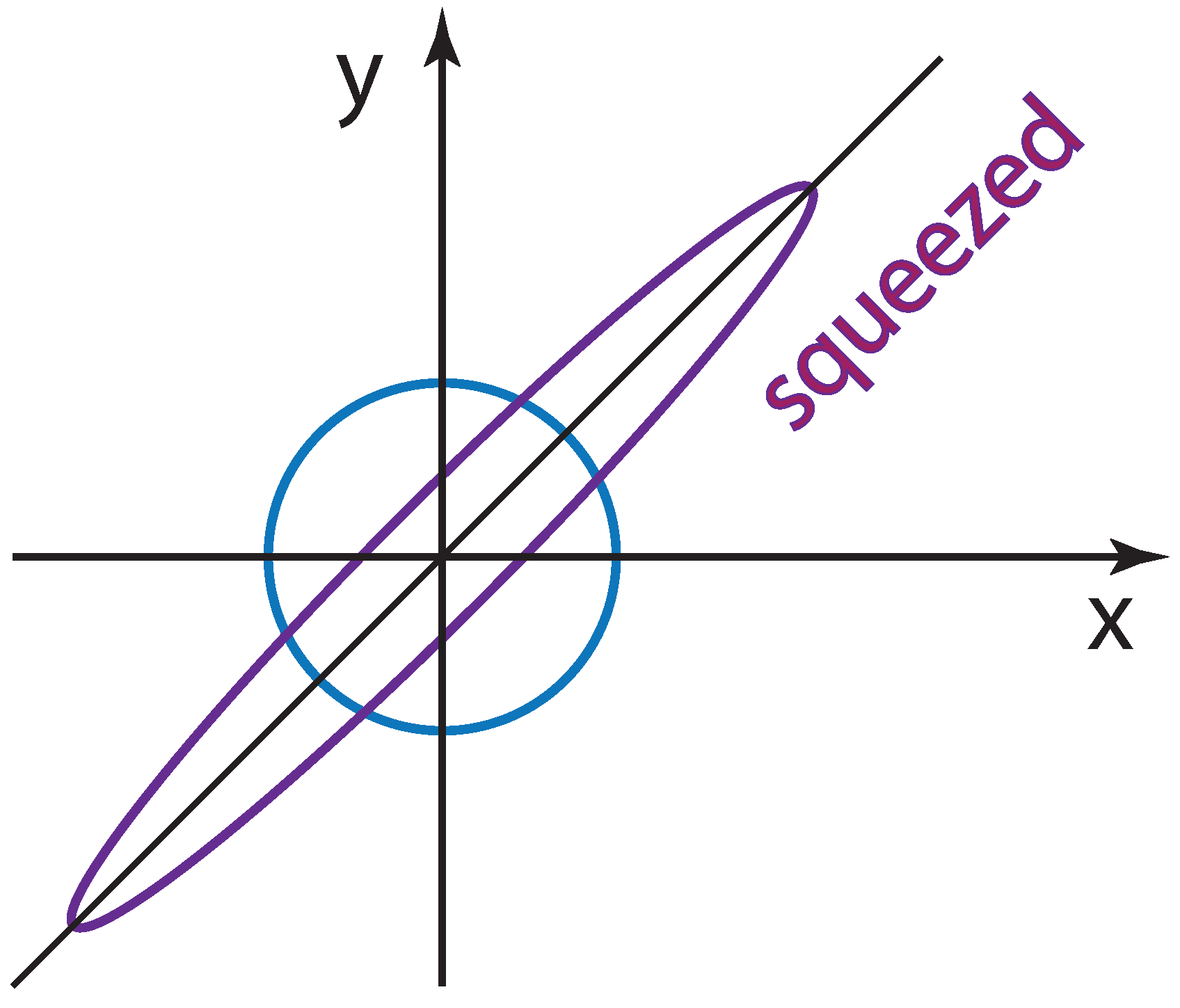
This form of squeeze is illustrated in Figure 3, and the expansion of this squeezed Gaussian function becomes the series given in Equation (1) [20,26]. This aspect will be discussed in detail in Section 5.

In 1976 [10], Yuen discussed two-photon coherent states, often called squeezed states of light. This series expansion served as the starting point for two-mode squeezed states. More recently, in 2003, Giedke et al. [1] used this formula to formulate the concept of the Gaussian entanglement.

There is another way to derive the series. For the harmonic oscillator wave functions, there are step-down and step-up operators [17]. These are defined as:

$$a=\frac{1}{\sqrt{2}}\left(x+\frac{\partial }{\partial x}\right),\mathrm{and}{a}^{†}=\frac{1}{\sqrt{2}}\left(x-\frac{\partial }{\partial x}\right)$$

(18)

If they are applied to the oscillator wave function, we have:

$$a{\chi }_n\left(x\right)=\sqrt{n}{\chi }_{n-1}\left(x\right),\mathrm{and}{a}^{†}{\chi }_n\left(x\right)=\sqrt{n+1}{\chi }_{n+1}\left(x\right)$$

(19)

Likewise, we can introduce b and $b^{†}$ operators applicable to ${\chi }_n\left(y\right)$:

$$b=\frac{1}{\sqrt{2}}\left(y+\frac{\partial }{\partial y}\right),\mathrm{and}{b}^{†}=\frac{1}{\sqrt{2}}\left(y-\frac{\partial }{\partial y}\right)$$

(20)

Thus

$$\begin{array}{c}{\left(a^{†}\right)}^n{\psi }^0\left(x\right)=\sqrt{n!}{\chi }_n\left(x\right)\hfill \\ {\left(b^{†}\right)}^n{\psi }^0\left(y\right)=\sqrt{n!}{\chi }_n\left(y\right)\hfill \end{array}$$

(21)

and:

$$a{\chi }_0\left(x\right)=b{\chi }_0\left(y\right)=0$$

(22)

In terms of these variables, the transformation leading the Gaussian function of Equation (11) to its squeezed form of Equation (16) can be written as:

$$exp\left\{\frac{\eta }{2}\left(a^{†}{b}^{†}-ab\right)\right\}$$

(23)

which can also be written as:

$$exp\left\{-\eta \left(x\frac{\partial }{\partial y}+y\frac{\partial }{\partial x}\right)\right\}$$

(24)

Next, we can consider the exponential form:

$$exp\left\{(tanh\eta )a^{†}{b}^{†})\right\}$$

(25)

which can be expanded as:

$$\sum _n\frac{1}{n!}{(tanh\eta )}^n{\left(a^{†}{b}^{†}\right)}^n$$

(26)

If this operator is applied to the ground state of Equation (11), the result is:

$$\sum _n{(tanh\eta )}^n{\chi }_n\left(x\right){\chi }_n\left(y\right)$$

(27)

This form is not normalized, while the series of Equation (1) is. What is the origin of this difference?

There is a similar problem with the one-photon coherent state [29,30]. There, the series comes from the expansion of the exponential form:

$$exp\left\{\alpha a^{†}\right\}$$

(28)

which can be expanded to:

$$\sum _n\frac{1}{n!}{\alpha }^n{\left(a^{†}\right)}^n$$

(29)

However, this operator is not unitary. In order to make this series unitary, we consider the exponential form:

$$exp\left(\alpha a^{†}-{\alpha }^{*}a\right)$$

(30)

which is unitary. This expression can then be written as:

$$e^{-\alpha {\alpha }^{*}/2}\left[exp\left(\alpha a^{†}\right)\right]\left[exp\left({\alpha }^{*}a\right)\right]$$

(31)

according to the Baker–Campbell–Hausdorff (BCH) relation [31,32]. If this is applied to the ground state, the last bracket can be dropped, and the result is:

$$e^{-\alpha {\alpha }^{*}/2}exp\left[\alpha a^{†}\right]$$

(32)

which is the unitary operator with the normalization constant:

$$e^{-\alpha {\alpha }^{*}/2}$$

Likewise, we can conclude that the series of Equation (27) is different from that of Equation (1) due to the difference between the unitary operator of Equation (23) and the non-unitary operator of Equation (25). It may be possible to derive the normalization factor using the BCH formula, but it seems to be intractable at this time. The best way to resolve this problem is to present the exact calculation of the unitary operator leading to the normalized series of Equation (11). We shall return to this problem in Section 5, where squeezed excited states are studied.

2.2. Sheared Gaussian Function

In addition, there is a transformation called “shear,” where only one of the two coordinates is translated, as shown in Figure 2. This transformation takes the form:

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& 2\alpha \\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$$

(33)

which leads to:

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{c}x+2\alpha y\\ y\end{array}\right)$$

(34)

This shear is one of the basic transformations in engineering sciences. In physics, this transformation plays the key role in understanding the internal space-time symmetry of massless particles [33,34,35]. This matrix plays the pivotal role during the transition from the oscillator mode to the damping mode in classical damped harmonic oscillators [36,37].

Under this transformation, the Gaussian form becomes:

$${\psi }_{shr}(x,y)=\frac{1}{\sqrt{\pi }}exp\left\{-\frac{1}{2}\left[{(x-2\alpha y)}^2+y^2\right]\right\}$$

(35)

It is possible to expand this into a series of the form of Equation (15) [38].

The transformation applicable to the Gaussian form of Equation (11) is:

$$exp\left(-2\alpha y\frac{\partial }{\partial x}\right)$$

(36)

and the generator is:

$$-iy\frac{\partial }{\partial x}$$

(37)

It is of interest to see where this generator stands among the ten generators of Dirac.

However, the most pressing problem is whether the sheared Gaussian form can be regarded as a rotated squeezed state. The basic mathematical issue is that the shear matrix of Equation (33) is triangular and cannot be diagonalized. Therefore, it cannot be a squeezed state. Yet, the Gaussian form of Equation (35) appears to be a rotated squeezed state, while not along the normal coordinates. We shall look at this problem in detail in Section 6.

3. Dirac’s Entangled Oscillators

Paul A. M. Dirac devoted much of his life-long efforts to the task of making quantum mechanics compatible with special relativity. Harmonic oscillators serve as an instrument for illustrating quantum mechanics, while special relativity is the physics of the Lorentz group. Thus, Dirac attempted to construct a representation of the Lorentz group using harmonic oscillator wave functions [17,21].

In his 1963 paper [21], Dirac started from the two-dimensional oscillator whose wave function takes the Gaussian form given in Equation (11). He then considered unitary transformations applicable to this ground-state wave function. He noted that they can be generated by the following ten Hermitian operators:

$$\begin{array}{c}{L}_1=\frac{1}{2}\left(a^{†}b+b^{†}a\right),L_2=\frac{1}{2i}\left(a^{†}b-b^{†}a\right)\hfill \\ L_3=\frac{1}{2}\left(a^{†}a-b^{†}b\right),S_3=\frac{1}{2}\left(a^{†}a+b{b}^{†}\right)\hfill \\ K_1=-\frac{1}{4}\left(a^{†}{a}^{†}+aa-b^{†}{b}^{†}-bb\right)\hfill \\ K_2=\frac{i}{4}\left(a^{†}{a}^{†}-aa+b^{†}{b}^{†}-bb\right)\hfill \\ K_3=\frac{1}{2}\left(a^{†}{b}^{†}+ab\right)\hfill \\ Q_1=-\frac{i}{4}\left(a^{†}{a}^{†}-aa-b^{†}{b}^{†}+bb\right)\hfill \\ Q_2=-\frac{1}{4}\left(a^{†}{a}^{†}+aa+b^{†}{b}^{†}+bb\right)\hfill \\ Q_3=\frac{i}{2}\left(a^{†}{b}^{†}-ab\right)\hfill \end{array}$$

(38)

He then noted that these operators satisfy the following set of commutation relations.

$$\begin{array}{c}[L_i,L_j]=i{ϵ}_{ijk}{L}_k,[L_i,K_j]=i{ϵ}_{ijk}{K}_k,[L_i,Q_j]=i{ϵ}_{ijk}{Q}_k\hfill \\ [K_i,K_j]=[Q_i,Q_j]=-i{ϵ}_{ijk}{L}_k,[L_i,S_3]=0\hfill \\ [K_i,Q_j]=-i{\delta }_{ij}{S}_3,[K_i,S_3]=-i{Q}_i,[Q_i,S_3]=i{K}_i\hfill \end{array}$$

(39)

Dirac then determined that these commutation relations constitute the Lie algebra for the $O(3,2)$ de Sitter group with ten generators. This de Sitter group is the Lorentz group applicable to three space coordinates and two time coordinates. Let us use the notation $(x,y,z,t,s)$, with $(x,y,z)$ as the space coordinates and $(t,s)$ as two time coordinates. Then, the rotation around the z axis is generated by:

$$L_3=\left(\begin{array}{ccccc}0& -i& 0& 0& 0\\ i& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)$$

(40)

The generators $L_1$ and $L_2$ can also be constructed. The $K_3$ and $Q_3$ generators will take the form:

$$K_3=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& i& 0\\ 0& 0& i& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right),Q_3=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& i\\ 0& 0& 0& 0& 0\\ 0& 0& i& 0& 0\end{array}\right)$$

(41)

From these two matrices, the generators $K_1,K_2,Q_1,Q_2$ can be constructed. The generator $S_3$ can be written as:

$$S_3=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& -i\\ 0& 0& 0& i& 0\end{array}\right)$$

(42)

The last five-by-five matrix generates rotations in the two-dimensional space of $(t,s)$. If we introduce these two time variables, the $O(3,2)$ group leads to two coupled Lorentz groups. The particle mass is invariant under Lorentz transformations. Thus, one Lorentz group cannot change the particle mass. However, with two coupled Lorentz groups, we can describe the world with variable masses, such as the neutrino oscillations.

In Section 2, we used the operators $Q_3$ and $K_3$ as the generators for the squeezed Gaussian function. For the unitary transformation of Equation (23), we used:

$$exp\left(-i\eta Q_3\right)$$

(43)

However, the exponential form of Equation (25) can be written as:

$$exp\left\{-i(tanh\eta )\left(Q_3+i{K}_3\right)\right\}$$

(44)

which is not unitary, as was seen before.

From the space-time point of view, both $K_3$ and $Q_3$ generate Lorentz boosts along the z direction, with the time variables t and s, respectively. The fact that the squeeze and Lorentz transformations share the same mathematical formula is well known. However, the non-unitary operator $i{K}_3$ does not seem to have a space-time interpretation.

As for the sheared state, the generator can be written as:

$$Q_3-L_2$$

(45)

leading to the expression given in Equation (37). This is a Hermitian operator leading to the unitary transformation of Equation (36).

4. Entangled Oscillators in the Phase-Space Picture

Also in his 1963 paper, Dirac states that the Lie algebra of Equation (39) can serve as the four-dimensional symplectic group $Sp\left(4\right)$. This group allows us to study squeezed or entangled states in terms of the four-dimensional phase space consisting of two position and two momentum variables [15,39,40].

In order to study the $Sp\left(4\right)$ contents of the coupled oscillator system, let us introduce the Wigner function defined as [41]:

$$\begin{array}{c}W(x,y;p,q)={\left(\frac{1}{\pi }\right)}^2\int exp\left\{-2i(p{x}^{\prime }+q{y}^{\prime })\right\}\hfill \\ \times {\psi }^{*}(x+x^{\prime },y+y^{\prime })\psi (x-x^{\prime },y-y^{\prime })d{x}^{\prime }d{y}^{\prime }\hfill \end{array}$$

(46)

If the wave function $\psi (x,y)$ is the Gaussian form of Equation (11), the Wigner function becomes:

$$W(x,y:p,q)={\left(\frac{1}{\pi }\right)}^{2}exp\left\{-\left(x^2+p^2+y^2+q^2\right)\right\}$$

(47)

The Wigner function is defined over the four-dimensional phase space of $(x,p,y,q)$ just as in the case of classical mechanics. The unitary transformations generated by the operators of Equation (38) are translated into Wigner transformations [39,40,42]. As in the case of Dirac’s oscillators, there are ten corresponding generators applicable to the Wigner function. They are:

$$\begin{array}{ccc}\hfill L_1& =& +\frac{i}{2}\left\{\left(x\frac{\partial }{\partial q}-q\frac{\partial }{\partial x}\right)+\left(y\frac{\partial }{\partial p}-p\frac{\partial }{\partial y}\right)\right\}\hfill \\ \hfill L_2& =& -\frac{i}{2}\left\{\left(x\frac{\partial }{\partial y}-y\frac{\partial }{\partial x}\right)+\left(p\frac{\partial }{\partial q}-q\frac{\partial }{\partial p}\right)\right\}\hfill \\ \hfill L_3& =& +\frac{i}{2}\left\{\left(x\frac{\partial }{\partial p}-p\frac{\partial }{\partial x}\right)-\left(y\frac{\partial }{\partial q}-q\frac{\partial }{\partial y}\right)\right\}\hfill \\ \hfill S_3& =& -\frac{i}{2}\left\{\left(x\frac{\partial }{\partial p}-p\frac{\partial }{\partial x}\right)+\left(y\frac{\partial }{\partial q}-q\frac{\partial }{\partial y}\right)\right\}\hfill \end{array}$$

(48)

and:

$$\begin{array}{ccc}\hfill K_1& =& -\frac{i}{2}\left\{\left(x\frac{\partial }{\partial p}+p\frac{\partial }{\partial x}\right)-\left(y\frac{\partial }{\partial q}+q\frac{\partial }{\partial y}\right)\right\}\hfill \\ \hfill K_2& =& -\frac{i}{2}\left\{\left(x\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}\right)-\left(p\frac{\partial }{\partial p}+q\frac{\partial }{\partial q}\right)\right\}\hfill \\ \hfill K_3& =& +\frac{i}{2}\left\{\left(x\frac{\partial }{\partial q}+q\frac{\partial }{\partial x}\right)+\left(y\frac{\partial }{\partial p}+p\frac{\partial }{\partial y}\right)\right\}\hfill \\ \hfill Q_1& =& +\frac{i}{2}\left\{\left(x\frac{\partial }{\partial x}+q\frac{\partial }{\partial q}\right)-\left(y\frac{\partial }{\partial y}+p\frac{\partial }{\partial p}\right)\right\}\hfill \\ \hfill Q_2& =& -\frac{i}{2}\left\{\left(x\frac{\partial }{\partial p}+p\frac{\partial }{\partial x}\right)+\left(y\frac{\partial }{\partial q}+q\frac{\partial }{\partial y}\right)\right\}\hfill \\ \hfill Q_3& =& -\frac{i}{2}\left\{\left(y\frac{\partial }{\partial x}+x\frac{\partial }{\partial y}\right)-\left(q\frac{\partial }{\partial p}+p\frac{\partial }{\partial q}\right)\right\}\hfill \end{array}$$

(49)

These generators also satisfy the Lie algebra given in Equations (38) and (39). Transformations generated by these generators have been discussed in the literature [15,40,42].

As in the case of Section 3, we are interested in the generators $Q_3$ and $K_3$. The transformation generated by $Q_3$ takes the form:

$$\left[exp\left\{\eta \left(x\frac{\partial }{\partial y}+y\frac{\partial }{\partial x}\right)\right\}\right]\left[exp\left\{-\eta \left(p\frac{\partial }{\partial q}+q\frac{\partial }{\partial p}\right)\right\}\right]$$

(50)

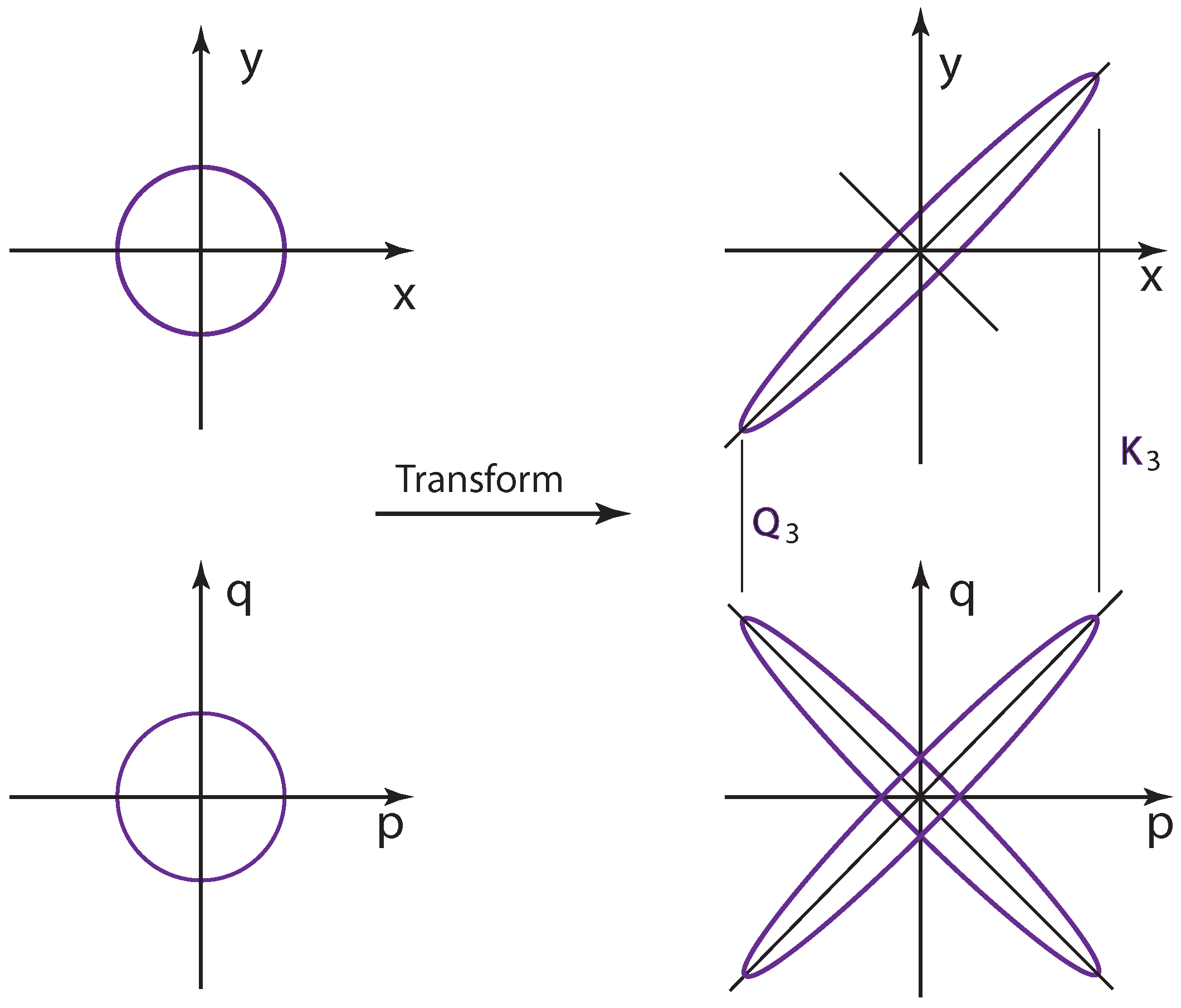
This exponential form squeezes the Wigner function of Equation (47) in the $xy$ space, as well as in their corresponding momentum space. However, in the momentum space, the squeeze is in the opposite direction, as illustrated in Figure 4. This is what we expect from canonical transformation in classical mechanics. Indeed, this corresponds to the unitary transformation, which played the major role in Section 2.

Even though shown insignificant in Section 2, $K_3$ had a definite physical interpretation in Section 3. The transformation generated by $K_3$ takes the form:

$$\left[exp\left\{\eta \left(x\frac{\partial }{\partial q}+q\frac{\partial }{\partial x}\right)\right\}\right]\left[exp\left\{\eta \left(y\frac{\partial }{\partial p}+p\frac{\partial }{\partial y}\right)\right\}\right]$$

(51)

This performs the squeeze in the $xq$ and $yp$ spaces. In this case, the squeezes have the same sign, and the rate of increase is the same in all directions. We can thus have the same picture of squeeze for both $xy$ and $pq$ spaces, as illustrated in Figure 4. This parallel transformation corresponds to the Lorentz squeeze [20,25].

As for the sheared state, the combination:

$$Q_3-L_2=-i\left(y\frac{\partial }{\partial x}+q\frac{\partial }{\partial p}\right)$$

(52)

generates the same shear in the $pq$ space.

5. Entangled Excited States

In Section 2, we discussed the entangled ground state and noted that the entangled state of Equation (1) is a series expansion of the squeezed Gaussian function. In this section, we are interested in what happens when we squeeze an excited oscillator state starting from:

$${\chi }_n\left(x\right){\chi }_m\left(y\right)$$

(53)

In order to entangle this state, we should replace x and y, respectively, by $x^{\prime }$ and $y^{\prime }$ given in Equation (17).

The question is how the oscillator wave function is squeezed after this operation. Let us note first that the wave function of Equation (53) satisfies the equation:

$$\frac{1}{2}\left\{\left(x^2-\frac{{\partial }^2}{\partial x^2}\right)-\left(y^2-\frac{{\partial }^2}{\partial y^2}\right)\right\}{\chi }_n\left(x\right){\chi }_m\left(y\right)=(n-m){\chi }_n\left(x\right){\chi }_m\left(y\right)$$

(54)

This equation is invariant under the squeeze transformation of Equation (17), and thus, the eigenvalue $(n-m)$ remains invariant. Unlike the usual two-oscillator system, the x component and the y component have opposite signs. This is the reason why the overall equation is squeeze-invariant [3,25,43].

We then have to write this squeezed oscillator in the series form of Equation (15). The most interesting case is of course for $m=n=0$, which leads to the Gaussian entangled state given in Equation (16). Another interesting case is for $m=0$, while n is allowed to take all integer values. This single-excitation system has applications in the covariant oscillator formalism where no time-like excitations are allowed. The Gaussian entangled state is a special case of this single-excited oscillator system.

The most general case is for nonzero integers for both n and m. The calculation for this case is available in the literature [20,44]. Seeing no immediate physical applications of this case, we shall not reproduce this calculation in this section.

For the single-excitation system, we write the starting wave function as:

$${\chi }_n\left(x\right){\chi }_0\left(y\right)={\left[\frac{1}{\pi 2^{n}n!}\right]}^{1/2}{H}_n\left(x\right)exp\left\{-\left(\frac{x^2+y^2}{2}\right)\right\}$$

(55)

There are no excitations along the y coordinate. In order to squeeze this function, our plan is to replace x and y by $x^{\prime }$ and $y^{\prime }$, respectively, and write ${\chi }_n\left(x^{\prime }\right){\chi }_0\left(y^{\prime }\right)$ as a series in the form:

$${\chi }_n\left(x^{\prime }\right){\chi }_0\left(y^{\prime }\right)=\sum _{k^{\prime },k}{A}_{k^{\prime },k}\left(n\right){\chi }_{k^{\prime }}\left(x\right){\chi }_k\left(y\right)$$

(56)

Since $k^{\prime }-k=n$ or $k^{\prime }=n+k$, according to the eigenvalue of the differential equation given in Equation (54), we write this series as:

$${\chi }_n\left(x^{\prime }\right){\chi }_0\left(y^{\prime }\right)=\sum _{k^{\prime },k}{A}_k\left(n\right){\chi }_{(k+n)}\left(x\right){\chi }_k\left(y\right)$$

(57)

with:

$$\sum _k{\left|A_k\left(n\right)\right|}^2=1$$

(58)

This coefficient is:

$$A_k\left(n\right)=\int {\chi }_{k+n}\left(x\right){\chi }_k\left(y\right){\chi }_n\left(x^{\prime }\right){\chi }_0\left(y^{\prime }\right)dxdy$$

(59)

This calculation was given in the literature in a fragmentary way in connection with a Lorentz-covariant description of extended particles starting from Ruiz’s 1974 paper [45], subsequently by Kim et al. in 1979 [26] and by Rotbart in 1981 [44]. In view of the recent developments of physics, it seems necessary to give one coherent calculation of the coefficient of Equation (59).

We are now interested in the squeezed oscillator function:

$$\begin{array}{c}{A}_k\left(n\right)={\left[\frac{1}{{\pi }^2{2}^{n}n!{(k+n)}^2(n+k)!k^{2}k!}\right]}^{1/2}\hfill \\ \times \int H_{n+k}\left(x\right)H_k\left(y\right)H_n\left(x^{\prime }\right)exp\left\{-\left(\frac{x^2+y^2+x^{\prime 2}+y^{\prime 2}}{2}\right)\right\}dxdy\hfill \end{array}$$

(60)

As was noted by Ruiz [45], the key to the evaluation of this integral is to introduce the generating function for the Hermite polynomials [46,47]:

$$G(r,z)=exp\left(-r^2+2rz\right)=\sum _m\frac{r^m}{m!}{H}_m\left(z\right)$$

(61)

and evaluate the integral:

$$I=\int G(r,x)G(s,y)G(r^{\prime },x^{\prime })exp\left\{-\left(\frac{x^2+y^2+x^{\prime 2}+y^{\prime 2}}{2}\right)\right\}dxdy$$

(62)

The integrand becomes one exponential function, and its exponent is quadratic in x and y. This quadratic form can be diagonalized, and the integral can be evaluated [20,26]. The result is:

$$I=\left[\frac{\pi }{cosh\eta }\right]exp(2rstanh\eta )exp\left(\frac{2r{r}^{\prime }}{cosh\eta }\right)$$

(63)

We can now expand this expression and choose the coefficients of $r^{n+k},s^k,r^{\prime n}$ for $H_{(n+k)}\left(x\right),H_n\left(y\right)$ and $H_n\left(z^{\prime }\right)$, respectively. The result is:

$$A_{n;k}={\left(\frac{1}{cosh\eta }\right)}^{(n+1)}{\left[\frac{(n+k)!}{n!k!}\right]}^{1/2}{(tanh\eta )}^k$$

(64)

Thus, the series becomes:

$${\chi }_n\left(x^{\prime }\right){\chi }_0\left(y^{\prime }\right)={\left(\frac{1}{cosh\eta }\right)}^{(n+1)}\sum _k{\left[\frac{(n+k)!}{n!k!}\right]}^{1/2}{(tanh\eta )}^k{\chi }_{k+n}\left(x\right){\chi }_k\left(y\right)$$

(65)

If $n=0$, it is the squeezed ground state, and this expression becomes the entangled state of Equation (16).

6. E(2)-Sheared States

Let us next consider the effect of shear on the Gaussian form. From Figure 3 and Figure 5, it is clear that the sheared state is a rotated squeezed state.

In order to understand this transformation, let us note that the squeeze and rotation are generated by the two-by-two matrices:

$$K=\left(\begin{array}{cc}0& i\\ i& 0\end{array}\right),J=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right)$$

(66)

which generate the squeeze and rotation matrices of the form:

$$\begin{array}{c}exp\left(-i\eta K\right)=\left(\begin{array}{cc}cosh\eta & sinh\eta \\ sinh\eta & cosh\eta \end{array}\right)\hfill \\ exp\left(-i\theta J\right)=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)\hfill \end{array}$$

(67)

respectively. We can then consider:

$$S=K-J=\left(\begin{array}{cc}0& 2i\\ 0& 0\end{array}\right)$$

(68)

This matrix has the property that $S^2=0$. Thus, the transformation matrix becomes:

$$exp(-i\alpha S)=\left(\begin{array}{cc}1& 2\alpha \\ 0& 1\end{array}\right)$$

(69)

Since $S^2=0$, the Taylor expansion truncates, and the transformation matrix becomes the triangular matrix of Equation (34), leading to the transformation:

$$\left(\begin{array}{c}x\\ y\end{array}\right)\to \left(\begin{array}{c}x+2\alpha y\\ y\end{array}\right)$$

(70)

The shear generator S of Equation (68) indicates that the infinitesimal transformation is a rotation followed by a squeeze. Since both rotation and squeeze are area-preserving transformations, the shear should also be an area-preserving transformations.

In view of Figure 5, we should ask whether the triangular matrix of Equation (69) can be obtained from one squeeze matrix followed by one rotation matrix. This is not possible mathematically. It can however, be written as a squeezed rotation matrix of the form:

$$\left(\begin{array}{cc}{e}^{\lambda /2}& 0\\ 0& e^{-\lambda /2}\end{array}\right)\left(\begin{array}{cc}cos\omega & sin\omega \\ -sin\omega & cos\omega \end{array}\right)\left(\begin{array}{cc}{e}^{-\lambda /2}& 0\\ 0& e^{\lambda /2}\end{array}\right)$$

(71)

resulting in:

$$\left(\begin{array}{cc}cos\omega & e^{\lambda }sin\omega \\ -e^{-\lambda }sin\omega & cos\omega \end{array}\right)$$

(72)

If we let:

$$(sin\omega )=2\alpha e^{-\lambda }$$

(73)

Then:

$$\left(\begin{array}{cc}cos\omega & 2\alpha \\ -2\alpha e^{-2\lambda }& cos\omega \end{array}\right)$$

(74)

If λ becomes infinite, the angle ω becomes zero, and this matrix becomes the triangular matrix of Equation (69). This is a singular process where the parameter λ goes to infinity.

If this transformation is applied to the Gaussian form of Equation (11), it becomes:

$$\psi (x,y)=\frac{1}{\sqrt{\pi }}exp\left\{-\frac{1}{2}\left[{(x-2\alpha y)}^2+y^2\right]\right\}$$

(75)

The question is whether the exponential portion of this expression can be written as:

$$exp\left\{-\frac{1}{2}\left[e^{-2\eta }{(xcos\theta +ysin\theta )}^2+e^{2\eta }{(xsin\theta -ycos\theta )}^2\right]\right\}$$

(76)

The answer is yes. This is possible if:

$$\begin{array}{c}tan\left(2\theta \right)=\frac{1}{\alpha }\hfill \\ e^{2\eta }=1+2{\alpha }^2+2\alpha \sqrt{{\alpha }^2+1}\hfill \\ e^{-2\eta }=1+2{\alpha }^2-2\alpha \sqrt{{\alpha }^2+1}\hfill \end{array}$$

(77)

In Equation (74), we needed a limiting case of λ becoming infinite. This is necessarily a singular transformation. On the other hand, the derivation of the Gaussian form of Equation (75) appears to be analytic. How is this possible? In order to achieve the transformation from the Gaussian form of Equations (11) to (75), we need the linear transformation:

$$\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)\left(\begin{array}{cc}{e}^{\eta }& 0\\ 0& e^{-\eta }\end{array}\right)$$

(78)

If the initial form is invariant under rotations as in the case of the Gaussian function of Equation (11), we can add another rotation matrix on the right-hand side. We choose that rotation matrix to be:

$$\left(\begin{array}{cc}cos(\theta -\pi /2)& -sin(\theta -\pi /2)\\ sin(\theta -\pi /2)& cos(\theta -\pi /2)\end{array}\right)$$

(79)

write the three matrices as:

$$\left(\begin{array}{cc}cos{\theta }^{\prime }& -sin{\theta }^{\prime }\\ sin{\theta }^{\prime }& cos{\theta }^{\prime }\end{array}\right)\left(\begin{array}{cc}cosh\eta & sinh\eta \\ sinh\eta & cosh\eta \end{array}\right)\left(\begin{array}{cc}cos{\theta }^{\prime }& -sin{\theta }^{\prime }\\ sin{\theta }^{\prime }& cos{\theta }^{\prime }\end{array}\right)$$

(80)

with:

$${\theta }^{\prime }=\theta -\frac{\pi }{4}$$

The multiplication of these three matrices leads to:

$$\left(\begin{array}{cc}(cosh\eta )sin\left(2\theta \right)& sinh\eta +(cosh\eta )cos\left(2\theta \right)\\ sinh\eta -(cosh\eta )cos\left(2\theta \right)& (cosh\eta )sin\left(2\theta \right)\end{array}\right)$$

(81)

The lower-left element can become zero when $sinh\eta =cosh\left(\eta \right)cos\left(2\theta \right)$, and consequently, this matrix becomes:

$$\left(\begin{array}{cc}1& 2sinh\eta \\ 0& 1\end{array}\right)$$

(82)

Furthermore, this matrix can be written in the form of a squeezed rotation matrix given in Equation (72), with:

$$\begin{array}{c}cos\omega =(cosh\eta )sin\left(2\theta \right)\hfill \\ e^{-2\lambda }=\frac{cos\left(2\theta \right)-tanh\eta }{cos\left(2\theta \right)+tanh\eta }\hfill \end{array}$$

(83)

The matrices of the form of Equations (72) and (81) are known as the Wigner and Bargmann decompositions, respectively [33,36,48,49,50].

7. Feynman’s Rest of the Universe

We need the concept of entanglement in quantum systems of two variables. The issue is how the measurement of one variable affects the other variable. The simplest case is what happens to the first variable while no measurements are taken on the second variable. This problem has a long history since von Neumann introduced the concept of the density matrix in 1932 [51]. While there are many books and review articles on this subject, Feynman stated this problem in his own colorful way. In his book on statistical mechanics [22], Feynman makes the following statement about the density matrix.

When we solve a quantum-mechanical problem, what we really do is divide the universe into two parts—the system in which we are interested and the rest of the universe. We then usually act as if the system in which we are interested comprised the entire universe. To motivate the use of density matrices, let us see what happens when we include the part of the universe outside the system.

Indeed, Yurke and Potasek [11] and also Ekert and Knight [12] studied this problem in the two-mode squeezed state using the entanglement formula given in Equation (16). Later in 1999, Han et al. studied this problem with two coupled oscillators where one oscillator is observed while the other is not and, thus, is in the rest of the universe as defined by Feynman [23].

Somewhat earlier in 1990 [27], Kim and Wigner observed that there is a time separation wherever there is a space separation in the Lorentz-covariant world. The Bohr radius is a space separation. If the system is Lorentz-boosted, the time-separation becomes entangled with the space separation. However, in the present form of quantum mechanics, this time-separation variable is not measured and not understood.

This variable was mentioned in the paper of Feynman et al. in 1971 [43], but the authors say they would drop this variable because they do not know what to do with it. While what Feynman et al. did was not quite respectable from the scientific point of view, they made a contribution by pointing out the existence of the problem. In 1990, Kim and Wigner [27] noted that the time-separation variable belongs to Feynman’s rest of the universe and studied its consequences in the observable world.

In this section, we first reproduce the work of Kim and Wigner using the x and y variables and then study the consequences. Let us introduce the notation ${\psi }_{\eta }^n(x,y)$ for the squeezed oscillator wave function given in Equation (65):

$${\psi }_{\eta }^n(x,y)={\chi }_n\left(x^{\prime }\right){\chi }_0\left(y^{\prime }\right)$$

(84)

with no excitations along the y direction. For $\eta =0$, this expression becomes ${\chi }_n\left(x\right){\chi }_0\left(y\right).$

From this wave function, we can construct the pure-state density matrix as:

$${\rho }_{\eta }^n(x,y;r,s)={\psi }_{\eta }^n(x,y){\psi }_{\eta }^n(r,s)$$

(85)

which satisfies the condition ${\rho }^2=\rho$, which means:

$${\rho }_{\eta }^n(x,y;r,s)=\int {\rho }_{\eta }^n(x,y;u,v){\rho }_{\eta }^n(u,v;r,s)dudv$$

(86)

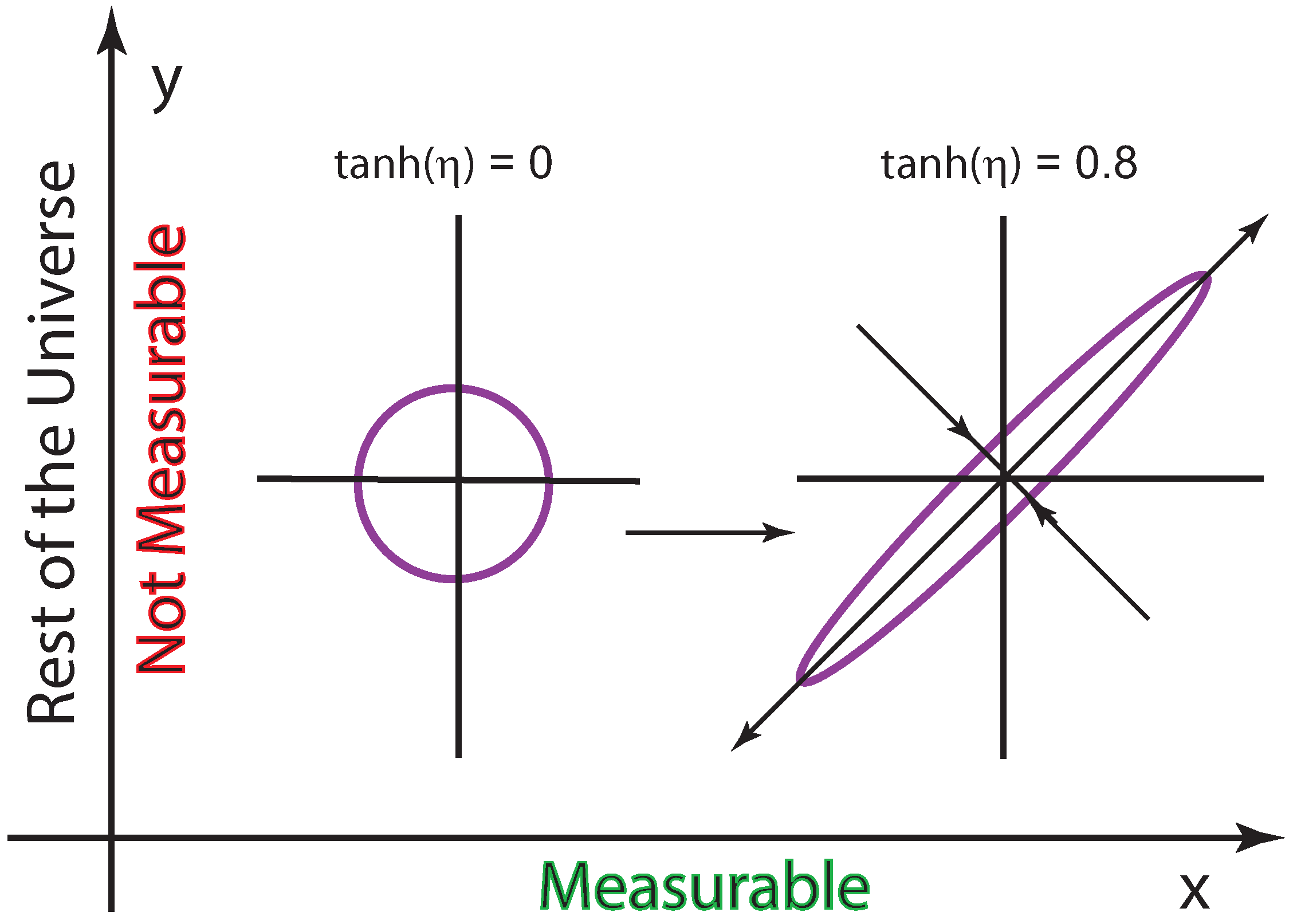
As illustrated in Figure 6, it is not possible to make measurements on the variable $y.$ We thus have to take the trace of this density matrix along the y axis, resulting in:

$$\begin{array}{c}{\rho }_{\eta }^n(x,r)=\int {\psi }_{\eta }^n(x,y){\psi }_{\eta }^n(r,y)dy\hfill \\ ={\left(\frac{1}{cosh\eta }\right)}^{2(n+1)}\sum _k\frac{(n+k)!}{n!k!}{(tanh\eta )}^{2k}{\chi }_{n+k}\left(x\right){\chi }_{k+n}\left(r\right)\hfill \end{array}$$

(87)

The trace of this density matrix is one, but the trace of ${\rho }^2$ is:

$$\begin{array}{c}Tr\left({\rho }^2\right)=\int {\rho }_{\eta }^n(x,r){\rho }_{\eta }^n(r,x)drdx\hfill \\ ={\left(\frac{1}{cosh\eta }\right)}^{4(n+1)}\sum _k{\left[\frac{(n+k)!}{n!k!}\right]}^2{(tanh\eta )}^{4k}\hfill \end{array}$$

(88)

which is less than one. This is due to the fact that we are not observing the y variable. Our knowledge is less than complete.

The standard way to measure this incompleteness is to calculate the entropy defined as [51,52,53]:

$$S=-Tr\left(\rho (x,r)ln\left[\rho \right(x,r\left)\right]\right)$$

(89)

which leads to:

$$\begin{array}{c}S=2(n+1)[{(cosh\eta )}^{2}ln(cosh\eta )-{(sinh\eta )}^{2}ln(sinh\eta )]\hfill \\ -{\left(\frac{1}{cosh\eta }\right)}^{2(n+1)}\sum _k\frac{(n+k)!}{n!k!}ln\left[\frac{(n+k)!}{n!k!}\right]{(tanh\eta )}^{2k}\hfill \end{array}$$

(90)

Let us go back to the wave function given in Equation (84). As is illustrated in Figure 6, its localization property is dictated by its Gaussian factor, which corresponds to the ground-state wave function. For this reason, we expect that much of the behavior of the density matrix or the entropy for the $n^{th}$ excited state will be the same as that for the ground state with n = 0. For this state, the density matrix is:

$${\rho }_{\eta }(x,r)={\left(\frac{1}{\pi cosh\left(2\eta \right)}\right)}^{1/2}exp\left\{-\frac{1}{4}\left[\frac{{(x+r)}^2}{cosh\left(2\eta \right)}+{(x-r)}^{2}cosh\left(2\eta \right)\right]\right\}$$

(91)

and the entropy is:

$$S_{\eta }=2\left[{(cosh\eta )}^{2}ln(cosh\eta )-{(sinh\eta )}^{2}ln(sinh\eta )\right]$$

(92)

The density distribution ${\rho }_{\eta }(x,x)$ becomes:

$${\rho }_{\eta }(x,x)={\left(\frac{1}{\pi cosh\left(2\eta \right)}\right)}^{1/2}exp\left(\frac{-x^2}{cosh\left(2\eta \right)}\right)$$

(93)

The width of the distribution becomes $\sqrt{cosh\left(2\eta \right)}$, and the distribution becomes wide-spread as η becomes larger. Likewise, the momentum distribution becomes wide-spread as can be seen in Figure 4. This simultaneous increase in the momentum and position distribution widths is due to our inability to measure the y variable hidden in Feynman’s rest of the universe [22].

In their paper of 1990 [27], Kim and Wigner used the x and y variables as the longitudinal and time-like variables respectively in the Lorentz-covariant world. In the quantum world, it is a widely-accepted view that there are no time-like excitations. Thus, it is fully justified to restrict the y component to its ground state, as we did in Section 5.

8. Space-Time Entanglement

The series given in Equation (1) plays the central role in the concept of the Gaussian or continuous-variable entanglement, where the measurement on one variable affects the quantum mechanics of the other variable. If one of the variables is not observed, it belongs to Feynman’s rest of the universe.

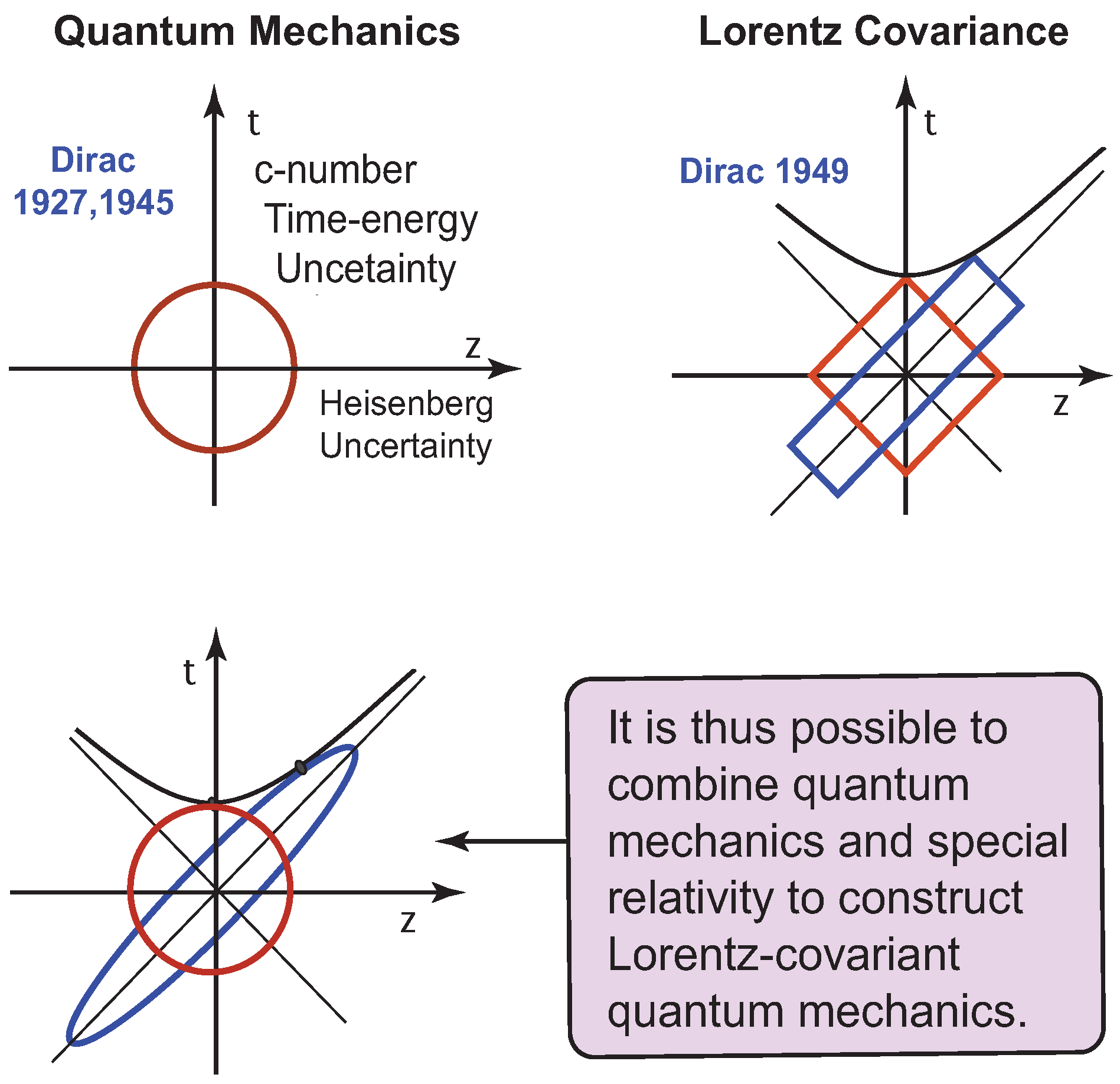
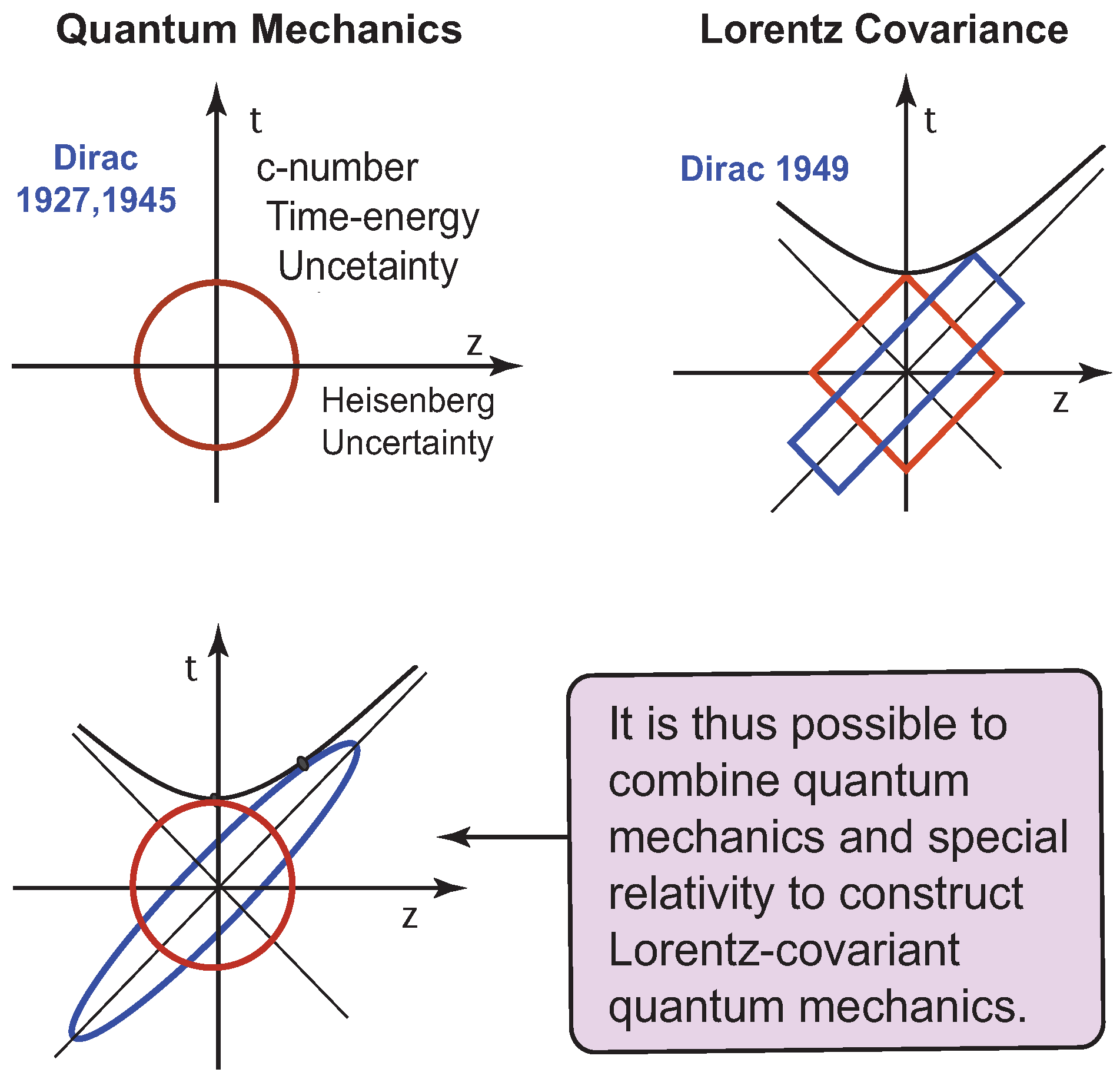
The series of the form of Equation (1) was developed earlier for studying harmonic oscillators in moving frames [20,24,25,26,27,28]. Here, z and t are the space-like and time-like separations between the two constituent particles bound together by a harmonic oscillator potential. There are excitations along the longitudinal direction. However, no excitations are allowed along the time-like direction. Dirac described this as the “c-number” time-energy uncertainty relation [16]. Dirac in 1927 was talking about the system without special relativity. In 1945 [17], Dirac attempted to construct space-time wave functions using harmonic oscillators. In 1949 [18], Dirac introduced his light-cone coordinate system for Lorentz boosts, demonstrating that the boost is a squeeze transformation. It is now possible to combine Dirac’s three observations to construct the Lorentz covariant picture of quantum bound states, as illustrated in Figure 7.

If the system is at rest, we use the wave function:

$${\psi }_0^n(z,t)={\chi }_n\left(z\right){\chi }_0\left(t\right)$$

(94)

which allows excitations along the z axis, but no excitations along the t axis, according to Dirac’s c-number time-energy uncertainty relation.

If the system is boosted, the z and t variables are replaced by $z^{\prime }$ and $t^{\prime }$ where:

$$z^{\prime }=(cosh\eta )z-(sinh\eta )t,\mathrm{and}{t}^{\prime }=-(sinh\eta )z+(cosh\eta )t$$

(95)

This is a squeeze transformation as in the case of Equation (17). In terms of these space-time variables, the wave function of Equation (84), can be written as:

$${\psi }_{\eta }^n(z,t)={\chi }_n\left(z^{\prime }\right){\chi }_0\left(t^{\prime }\right)$$

(96)

and the series of Equation (65) then becomes:

$${\psi }_{\eta }^n(z,t)={\left(\frac{1}{cosh\eta }\right)}^{(n+1)}\sum _k{\left[\frac{(n+k)!}{n!k!}\right]}^{1/2}{(tanh\eta )}^k{\chi }_{k+n}\left(z\right){\chi }_k\left(t\right)$$

(97)

Since the Lorentz-covariant oscillator formalism shares the same set of formulas with the Gaussian entangled states, it is possible to explain some aspects of space-time physics using the concepts and terminologies developed in quantum optics, as illustrated in Figure 1.

The time-separation variable is a case in point. The Bohr radius is a well-defined spatial separation between the proton and electron in the hydrogen atom. However, if the atom is boosted, this radius picks up a time-like separation. This time-separation variable does not exist in the Schrödinger picture of quantum mechanics. However, this variable plays the pivotal role in the covariant harmonic oscillator formalism. It is gratifying to note that this “hidden or forgotten” variable plays a role in the real world while being entangled with the observable longitudinal variable. With this point in mind, let us study some of the consequences of this space-time entanglement.

First of all, does the wave function of Equation (96) carry a probability interpretation in the Lorentz-covariant world? Since $dzdt=d{z}^{\prime }d{t}^{\prime }$, the normalization:

$$\int |{\psi }_{\eta }^n{(z,t)|}^{2}dtdz=1$$

(98)

This is a Lorentz-invariant normalization. If the system is at rest, the z and t variables are completely dis-entangled, and the spatial component of the wave function satisfies the Schrödinger equation without the time-separation variable.

However, in the Lorentz-covariant world, we have to consider the inner product:

$$\left({\psi }_{\eta }^n(z,t),{\psi }_{{\eta }^{\prime }}^m(z,t)\right)=\int \left[{\psi }_{\eta }^n{(z,t)]}^{*}{\psi }_{{\eta }^{\prime }}^m(z,t)\right)dzdt$$

(99)

The evaluation of this integral was carried out by Michael Ruiz in 1974 [45], and the result was:

$${\left(\frac{1}{|cosh(\eta -{\eta }^{\prime }\left)\right|}\right)}^{n+1}{\delta }_{nm}$$

(100)

In order to see the physical implications of this result, let us assume that one of the oscillators is at rest with ${\eta }^{\prime }=0$ and the other is moving with the velocity $\beta =tanh\left(\eta \right)$. Then, the result is:

$$\left({\psi }_{\eta }^n(z,t),{\psi }_0^m(z,t)\right)={\left(\sqrt{1-{\beta }^2}\right)}^{n+1}{\delta }_{nm}$$

(101)

Indeed, the wave functions are orthonormal if they are in the same Lorentz frame. If one of them is boosted, the inner product shows the effect of Lorentz contraction. We are familiar with the contraction $\sqrt{1-{\beta }^2}$ for the rigid rod. The ground state of the oscillator wave function is contracted like a rigid rod.

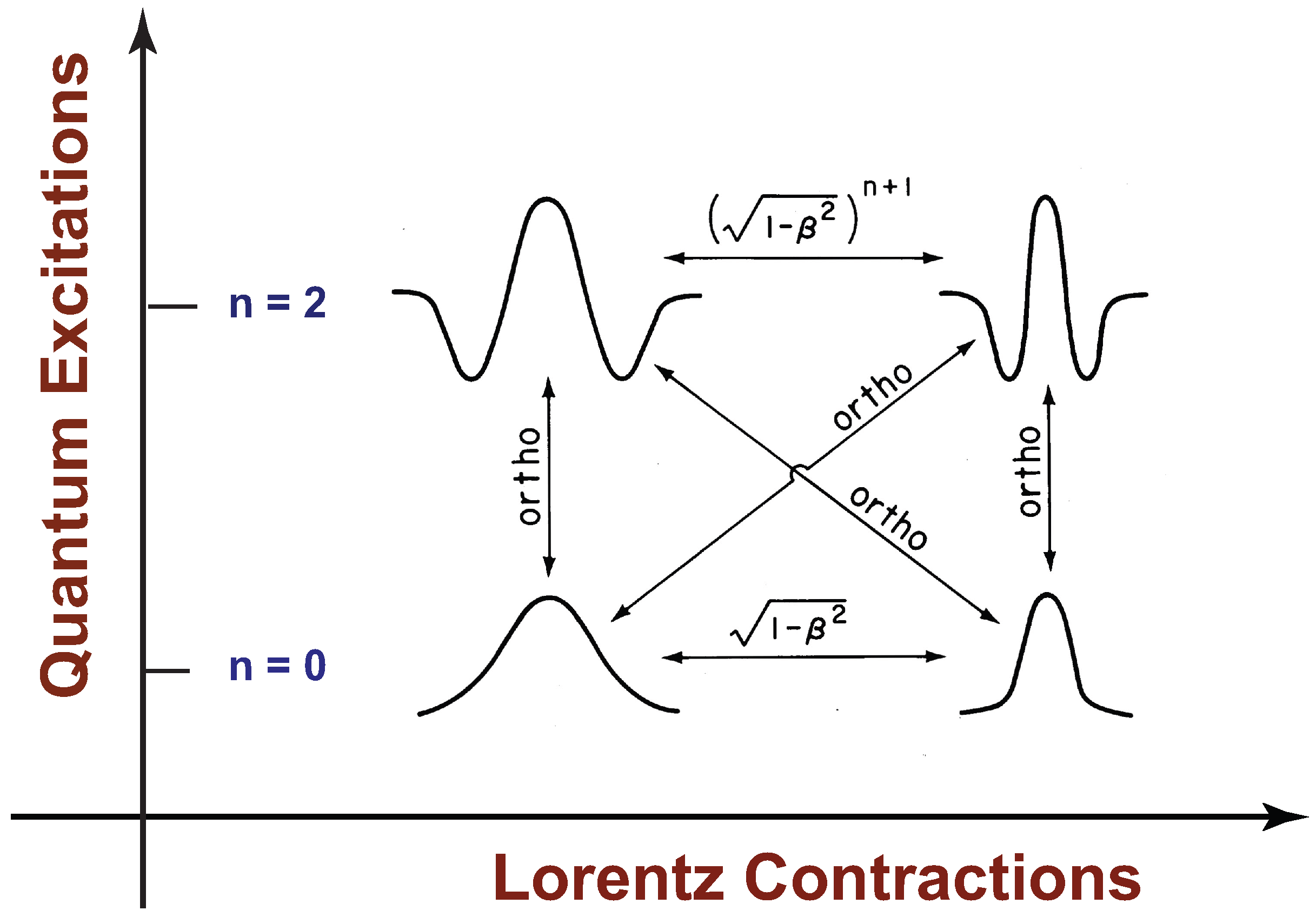
The probability density $|{\psi }_{\eta }^0{\left(z\right)|}^2$ is for the oscillator in the ground sate, and it has one hump. For the $n^{th}$ excited state, there are $(n+1)$ humps. If each hump is contracted like $\sqrt{1-{\beta }^2}$, the net contraction factor is ${\left(\sqrt{1-{\beta }^2}\right)}^{n+1}$ for the $n^{th}$ excited state. This result is illustrated in Figure 8.

With this understanding, let us go back to the entanglement problem. The ground state wave function takes the Gaussian form given in Equation (11):

$${\psi }_0(z,t)=\frac{1}{\sqrt{\pi }}exp\left\{-\frac{1}{2}\left(z^2+t^2\right)\right\}$$

(102)

where the x and y variables are replaced by z and t, respectively. If Lorentz-boosted, this Gaussian function becomes squeezed to [20,24,25]:

$${\psi }_{\eta }^0(z,t)=\frac{1}{\sqrt{\pi }}exp\left\{-\frac{1}{4}\left[e^{-2\eta }{(z+t)}^2+e^{2\eta }{(z-t)}^2\right]\right\}$$

(103)

leading to the series:

$$\frac{1}{cosh\eta }\sum _k{(tanh\eta )}^k{\chi }_k\left(z\right){\chi }_k\left(t\right)$$

(104)

According to this formula, the z and t variables are entangled in the same way as the x and y variables are entangled.

Here, the z and t variables are space and time separations between two particles bound together by the oscillator force. The concept of the space separation is well defined, as in the case of the Bohr radius. On the other hand, the time separation is still hidden or forgotten in the present form of quantum mechanics. In the Lorentz-covariant world, this variable affects what we observe in the real world by entangling itself with the longitudinal spatial separation.

In Chapter 16 of their book [9], Walls and Milburn wrote down the series of Equation (1) and discussed what would happen when the η parameter becomes infinitely large. We note that the series given in Equation (104) shares the same expression as the form given by Walls and Milburn, as well as other papers dealing with the Gaussian entanglement. As in the case of Wall and Milburn, we are interested in what happens when η becomes very large.

As we emphasized throughout the present paper, it is possible to study the entanglement series using the squeezed Gaussian function given in Equation (103). It is then possible to study this problem using the ellipse. Indeed, we can carry out the mathematics of entanglement using the ellipse shown Figure 9. This figure is the same as that of Figure 6, but it illustrates the entanglement of the space and time separations, instead of the x and y variables. If the particle is at rest with $\eta =0$, the Gaussian form corresponds to the circle in Figure 9. When the particle gains speed, this Gaussian function becomes squeezed into an ellipse. This ellipse becomes concentrated along the light cone with $t=z$, as η becomes very large.

The point is that we are able to observe this effect in the real world. These days, the velocity of protons from high-energy accelerators is very close to that of light. According to Gell-Mann [54], the proton is a bound state of three quarks. Since quarks are confined in the proton, they have never been observed, and the binding force must be like that of the harmonic oscillator. Furthermore, the observed mass spectra of the hadrons exhibit the degeneracy of the three-dimensional harmonic oscillator [43]. We use the word “hadron” for the bound state of the quarks. The simplest hadron is thus the bound state of two quarks.

In 1969 [55], Feynman observed that the same proton, when moving with a velocity close to that of light, can be regarded as a collection of partons, with the following peculiar properties.

• The parton picture is valid only for protons moving with velocity close to that of light.
• The interaction time between the quarks becomes dilated, and partons are like free particles.
• The momentum distribution becomes wide-spread as the proton moves faster. Its width is proportional to the proton momentum.
• The number of partons is not conserved, while the proton starts with a finite number of quarks.

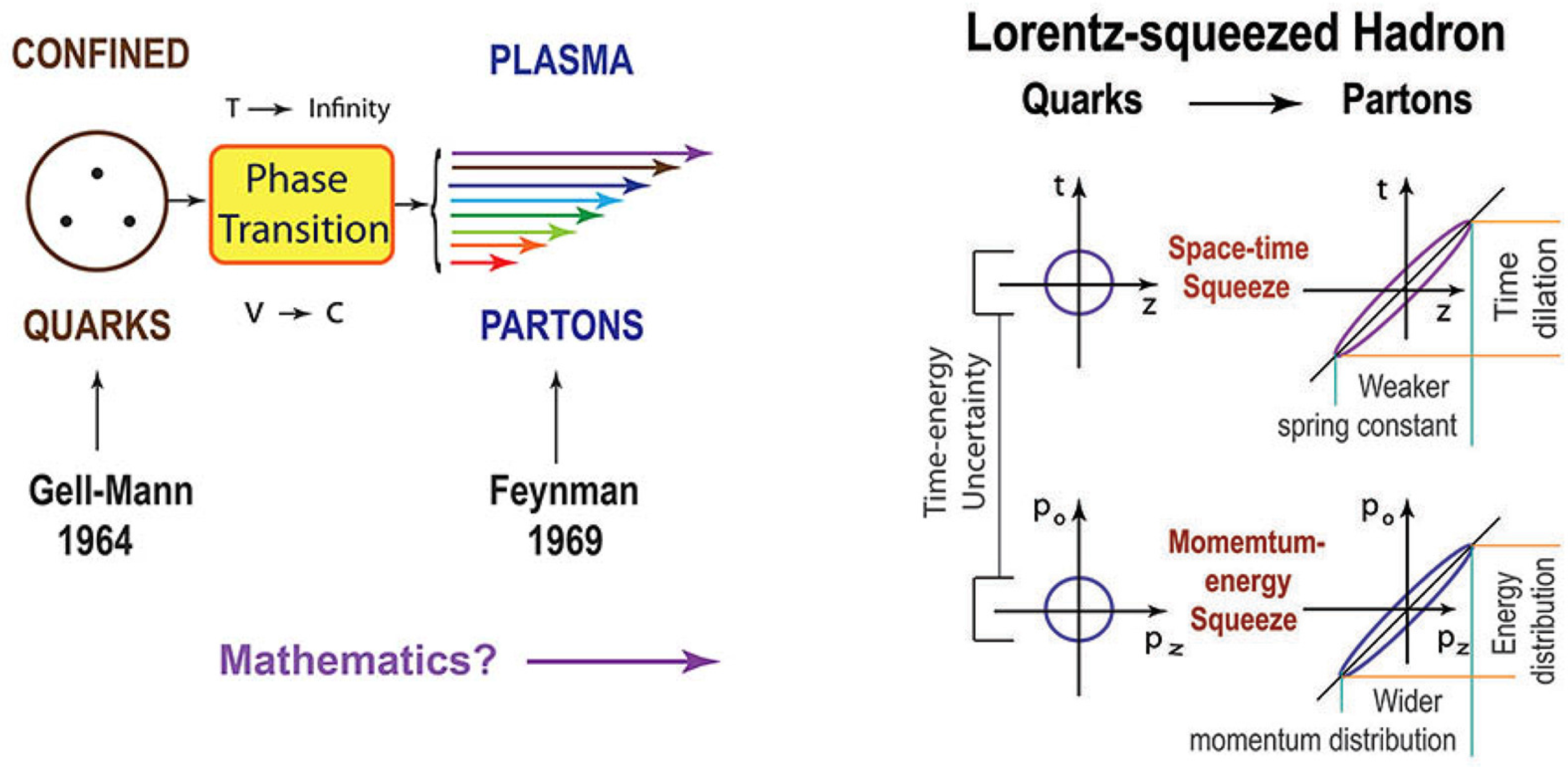
Indeed, Figure 10 tells why the quark and parton models are two limiting cases of one Lorentz-covariant entity. In the oscillator regime, the three-particle system can be reduced to two independent two-particle systems [43]. Also in the oscillator regime, the momentum-energy wave function takes the same form as the space-time wave function, thus with the same squeeze or entanglement property as illustrated in this figure. This leads to the wide-spread momentum distribution [20,56,57].

Also in Figure 10, the time-separation between the quarks becomes large as η becomes large, leading to a weaker spring constant. This is why the partons behave like free particles [20,56,57].

As η becomes very large, all of the particles are confined into a narrow strip around the light cone. The number of particles is not constant for massless particles as in the case of black-body radiation [20,56,57].

Indeed, the oscillator model explains the basic features of the hadronic spectra [43]. Does the oscillator model tell the basic feature of the parton distribution observed in high-energy laboratories? The answer is yes. In his 1982 paper [58], Paul Hussar compared the parton distribution observed in a high-energy laboratory with the Lorentz-boosted Gaussian distribution. They are close enough to justify that the quark and parton models are two limiting cases of one Lorentz-covariant entity.

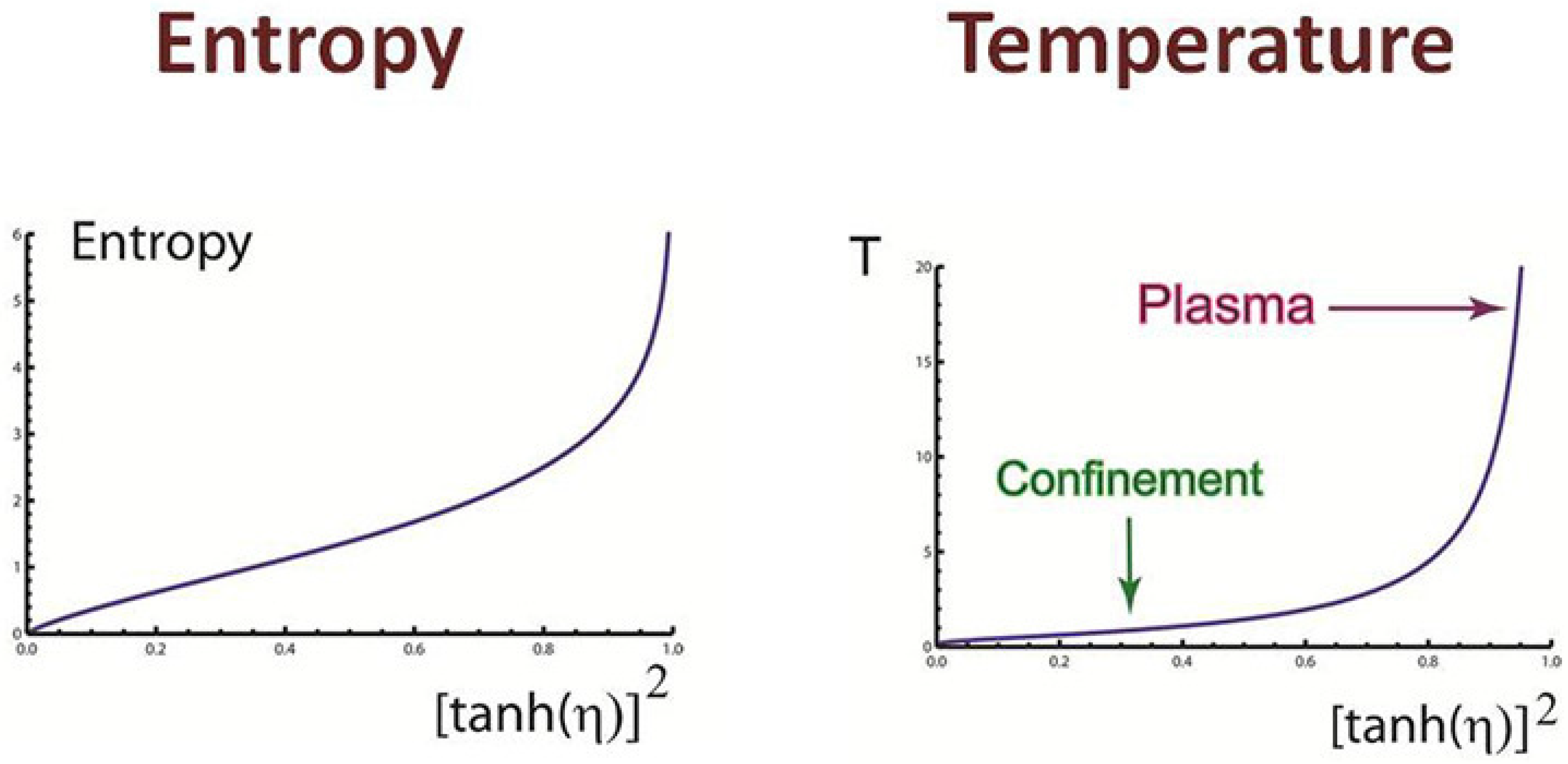
To summarize, the proton makes a phase transition from the bound state into a plasma state as it moves faster, as illustrated in Figure 10. The unobserved time-separation variable becomes more prominent as η becomes larger. We can now go back to the form of this entropy given in Equation (92) and calculate it numerically. It is plotted against ${(tanh\eta )}^2={\beta }^2$ in Figure 11. The entropy is zero when the hadron is at rest, and it becomes infinite as the hadronic speed reaches the speed of light.

Let us go back to the expression given in Equation (87). For this ground state, the density matrix becomes:

$${\rho }_{\eta }(z,z^{\prime })={\left(\frac{1}{cosh\eta }\right)}^2\sum _k{(tanh\eta )}^{2k}{\chi }_k\left(z\right){\chi }_k\left(z^{\prime }\right)$$

(105)

We can now compare this expression with the density matrix for the thermally-excited oscillator state [22]:

$${\rho }_{\eta }(z,z^{\prime })=\left(1-e^{-1/T}\right)\sum _k{\left[e^{-1/T}\right]}^k{\chi }_k\left(z\right){\chi }_k\left(z^{\prime }\right)$$

(106)

By comparing these two expressions, we arrive at:

$${[tanh\left(\eta \right)]}^2=e^{-1/T}$$

(107)

and thus:

$$T=\frac{-1}{ln\left[{(tanh\eta )}^2\right]}$$

(108)

This temperature is also plotted against ${(tanh\eta )}^2$ in Figure 11. The temperature is zero if the hadron is at rest, but it becomes infinite when the hadronic speed becomes close to that of light. The slope of the curvature changes suddenly around ${(tanh\eta )}^2=0.8$, indicating a phase transition from the bound state to the plasma state.

In this section, we have shown how useful the concept of entanglement is in understanding the role of the time-separation in high energy hadronic physics including Gell–Mann’s quark model and Feynman’s parton model as two limiting cases of one Lorentz-covariant entity.

9. Concluding Remarks

The main point of this paper is the mathematical identity:

$$\frac{1}{\sqrt{\pi }}exp\left\{-\frac{1}{4}\left[e^{-2\eta }{(x+y)}^2+e^{2\eta }{(x-y)}^2\right]\right\}=\frac{1}{cosh\eta }\sum _k{(tanh\eta )}^k{\chi }_k\left(x\right){\chi }_k\left(y\right)$$

(109)

which says that the series of Equation (1) is an expansion of the Gaussian form given in Equation (2).

The first derivation of this series was published in 1979 [26] as a formula from the Lorentz group. Since this identity is not well known, we explained in Section 5 how this formula can be derived from the generating function of the Hermite polynomials.

While the series serves useful purposes in understanding the physics of entanglement, the Gaussian form can be used to transfer this idea to high-energy hadronic physics. The hadron, such as the proton, is a quantum bound state. As was pointed out in Section 8, the squeezed Gaussian function of Equation (109) plays the pivotal role for hadrons moving with relativistic speeds.

The Bohr radius is a very important quantity in physics. It is a spatial separation between the proton and electron in the the hydrogen atom. Likewise, there is a space-like separation between constituent particles in a bound state at rest. When the bound state moves, it picks up a time-like component. However, in the present form of quantum mechanics, this time-like separation is not recognized. Indeed, this variable is hidden in Feynman’s rest of the universe. When the system is Lorentz-boosted, this variable entangles itself with the measurable longitudinal variable. Our failure to measure this entangled variable appears in the form of entropy and temperature in the real world.

While harmonic oscillators are applicable to many aspects of quantum mechanics, Paul A. M. Dirac observed in 1963 [21] that the system of two oscillators contains also the symmetries of the Lorentz group. We discussed in this paper one concrete case of Dirac’s symmetry. There are different languages for harmonic oscillators, such as the Schrödinger wave function, step-up and step-down operators and the Wigner phase-space distribution function. In this paper, we used extensively a pictorial language with circles and ellipses.

Let us go back to Equation (109); this mathematical identity was published in 1979 as textbook material in the American Journal of Physics [26], and the same formula was later included in a textbook on the Lorentz group [20]. It is gratifying to note that the same formula serves as a useful tool for the current literature in quantum information theory [59,60].