Abstract
Nowadays, several wireless location systems have been developed in the research world. The goal of these systems has always been to find the greatest accuracy as possible. However, if every node takes data from the environment, we can gather a lot of information, which may help us understand what is happening around our network in a cooperative way. In order to develop this cooperative location and tracking system, we have implemented a sensor network to capture data from user devices. From this captured data we have observed a symmetry behavior in people’s movements at a specific site. By using these data and the symmetry feature, we have developed a statistical cooperative approach to predict the new user’s location. The system has been tested in a real environment, evaluating the next location predicted by the system and comparing it with the next location in the real track, thus getting satisfactory results. Better results have been obtained when the stochastic cooperative approach uses the transition matrix with symmetry.
1. Introduction
Currently, wireless networks can be used in many scenarios [1]. One of them is location systems, particularly in indoor spaces because in outdoor environments the most useful location system is GPS [2]. At this time, there are many indoor wireless location systems that identify where we are [3,4].
Inside the wireless indoor location systems (ILSs), we have to differentiate between infrastructure-based ILS and infrastructure-free ILS. Each system has its advantages and disadvantages. Infrastructure-free ILS does not require any type of additional devices other than the final devices, but they require collection of data from several sensors like wireless connection, compass, tour and direction, etc. [5]. Some of them need a connection to another big system—like a cloud—to send the information, and this outsider system calculates the location of the end device [6]. Others estimate their position by multilateration using their neighbors [7]. Instead, infrastructure-based ILS uses the deployed wireless network to have devices as a reference from end devices, because they let us extract information to locate someone. In this case, the processing can be done by the final devices or in a server. This depends on the final system implemented. We are going to focus on the infrastructure-based ILS, because the system presented in this paper follows its features.
Infrastructure-based ILS uses different location techniques and algorithms, which are based on the received signal strength (RSS) [8]. According to [9], we can divide these device location techniques into three general categories: proximity, triangulation, and scene analysis.
- Proximity detection or connectivity-based is one of the simplest positioning methods to implement. It provides symbolic relative location information.
- Triangulation uses the geometric properties of triangles to determine the target location [10]. There are two kinds of techniques: (1) techniques based on the measurement of the propagation-time system and RSS-based and received signal phase methods; and (2) techniques based on the angle of arrival of that the mobile signal is coming from.
- Scene analysis is based on the theory of pattern recognition [11], which combines an electronic map with location information to obtain the real position.
Some papers provide a comparison between these three methods [12]. As [9] concludes, the best ILS will be the one which joins several technologies and methods to estimate the position. Moreover, it will need cooperative localization, which will help mobile nodes to determine locations. Thus, we should introduce the concept of cooperation in our system.
Cooperation is the strategy of a group of entities working together to achieve a common goal [13]. The cooperation concept could be important because it allows joining data from several devices in order to take a better decision. Nowadays, cooperation in wireless networks can be approached from different angles, and in fact, it has different meanings and connotations. An example is the cooperation between wireless nodes as a way to improve the coverage of our wireless networks. For instance, some authors use cooperation techniques to add several antennas in a device to improve the level of signal-noise ratio (SNR) [14] and/or coverage [15]. Another important issue is their communication, which includes several techniques exploiting the joint collaborative efforts of some entities in the system. Algorithms interact with the data collected from the devices in order to enhance the performance of the system.
Human behavior has a symmetric feature. There is symmetry in the movement of our locomotor system [16] until the device is mobile [17]. This last study shows that human mobility is symmetric on a macroscopic level. It explores the spatial behavior of human mobility through a variety of mobility traces collected from different network environments, and the authors conclude that the number of users that move from point A to point B approximates the number of users that go in the opposite direction. On that basis, we have developed a statistical cooperative approach to estimate a user’s location. This location system is based on Bayes’ theorem, where several cooperative data and the symmetry of human mobility are taken into account. The system has been tested in a real environment. Since we are interested in modelling the localization behaviour of an individual user, we studied recorded tracks. We propose a statistical model able to estimate the next location of a track. Previous works, like [17], have shown how human mobility presents as symmetrical behavior. This can be easily verified when observing the transition matrix. We have used this fact to quickly estimate it using the statistical model. Our experiments show that the best results have been obtained when the stochastic cooperative approach uses this symmetry as a premise.
The rest of this paper is organized as follows. Section 2 presents some papers about indoor location systems and cooperative networks. Section 3 briefly explains the main features of our wireless location system and the nodes used. We present a symmetry study of the mobility of the users in our wireless system in Section 4. Next, in Section 5, we propose a statistical approach to estimate a user’s location in a cooperative way. Section 6 explains the test bench used in our study to predict the new location of a user by knowing the actual location and other external factors, like temporal information of our cooperative location system. Finally, we show the main contributions, our conclusion, and the future work in Section 7.
2. Related Work
In this section, we must first state that we have not found any paper directly related to the study of the symmetrical behavior of people using cooperative location systems. For this reason, we have focused this section on discussing some works related to indoor wireless location systems and cooperative networks, as well as the existence of some works related with cooperative location.
Firstly, we analyze some works where the authors have proposed location systems for indoor environments using wireless local networks. For instance, in [3] the authors give a comprehensive survey of numerous indoor positioning systems (IPSs), which include both commercial products and research-oriented solutions. Evaluation criteria are proposed for assessing these systems, namely security and privacy, cost, performance, robustness, complexity, user preferences, commercial availability, and limitations. They compare the existing IPSs and outline the trade-offs among these systems from the viewpoint of a user in a personal network. Z. Deng et al. present the latest research on indoor positioning in [18]. The authors compare positioning accuracy and the cost of typical local and wide area indoor positioning systems. They conclude that the development tendency of an indoor positioning system—which aimed at high-accuracy indoor positioning in a wide area—includes three aspects: seamless Location Based Services (LBS) architecture based on heterogeneous network; key technologies in indoor positioning for decimeter-accuracy; and seamless outdoor and indoor GIS.
The same authors of this paper present a hybrid stochastic approach for self-location of wireless nodes in indoor environments in [19]. This paper proposes a new stochastic approach which is based on a combination of deductive and inductive methods. Our goal in this work is to reduce the training phase in an indoor environment without the loss of precision. Another example is [20]. In this case, the authors propose an accurate RSS-based indoor positioning system using compressive sensing. Their location estimator consists of a coarse localizer—where the RSS is compared to a number of clusters to detect in which cluster the node is located—followed by a fine localization step, using the theory of compressive sensing, to further refine the location estimation. Experimental results improve the localization accuracy and complexity over the traditional RSS-based methods.
The authors of [21] propose a scheme for indoor positioning by fusing floor map, Wi-Fi and smartphone sensor data to provide meter-level positioning without additional infrastructure. Their algorithm combines the complementary advantages of all three techniques using a particle filter (PF) model. The experimental test results indicate that the integration of these techniques can not only avoid the “cross-wall” phenomenon but also the gross-error effects inherent to Wi-Fi and P-O measurements. Finally, another paper related with indoor location systems is [22]. This paper presents an experimental study of the feasibility of using multiple wireless technologies simultaneously for location estimation. They have collected signal strength information from both IEEE 802.11 and Bluetooth wireless network technologies. They developed and applied algorithms for determining location using data for each wireless technology, and then used a simple algorithm for fusing the location estimation from both technologies in order to try enhancing the accuracy of the location estimation.
All previous works [18,19,20,21,22] are focused on the location process. In other words, they try to have the smallest error in positioning renders. Moreover, these works do not use any cooperative feature to estimate the location of the end user. Therefore, we need to look for some cooperative location systems. When we talk about cooperation in networks, it is difficult to associate this feature with network, broadly speaking. For example, the same authors of this paper present a solution to increase the lifetime of the sensor nodes in [23]. In this work, they show how organizing sensors in cooperative groups can reduce the global energy consumption of the whole Wireless Sensor Network (WSN). They also show that a cooperative group-based network reduces the number of the messages transmitted inside the WSNs, which implies a reduction of energy consumed by the whole network, and, consequently, an increase of the network lifetime. An application of cooperative networks is presented in [24]. This paper shows an application for environmental monitoring from a cooperative group-based wireless sensor network. It is based on the use of different alarm levels to define the level of danger or importance of an event.
In [25], authors presented the first paper that used cooperation with location systems. This article was intended to emphasize the basic statistical signal processing background necessary to understand the state-of-the-art of device location systems and to make progress in the sensor network localization research. In cooperative localization, sensors work together in a peer-to-peer manner to make measurements and then form a map of the network. Another paper, where the authors introduce the notion of network experimentation and propose an experimentation methodology particularly suited for cooperative localization wireless networks, is [26]. This study enables the performance evaluation of various network localization algorithms under a common setting. They developed an experimentation methodology for the characterization of cooperative wireless networks in realistic environments, established a database with range and waveform measurements for cooperative wireless channels, and characterized range errors and evaluated network localization algorithms for several conditions.
In [27], authors investigated a 2D experimental cooperative location system for wireless sensor networks which was based on the RSS indicator measures. The cooperative localization algorithm is based on the weighted least squares method, where the weights are calculated according to the quality of the range and position estimation. Experimental results showed that the performance of the cooperative localization algorithm is better than the one obtained by a non-cooperative algorithm. Finally, in [28], authors proposed a novel cooperative localization scheme based on user mobility for indoor environments. The main idea is to exploit user mobility information as given by the inertial measurement data from smartphones, to further narrow down the constraint area of the Linear Matrix Inequality (LMI) based scheme, thus increasing the localization accuracy. To better take advantage of a user’s direction of movement and velocity information, the authors proposed the application of Kalman filter to improve the estimated positions. According to the simulations, this system reduces the mean error and variance for indoor localization.
Works [25,26,27,28] are connected with this work because the cooperation between nodes inside a wireless location system are crucial to achieve the goal of reducing the error for indoor location. The main difference with our work is that these systems do not try to study the people’s behavior and whether or not their mobility follows a pattern.
3. Wireless Indoor Location System
3.1. Wireless Infrastructure
In this section we to explain our wireless location system. It is based on several nodes, which are located in strategic points in order to take relevant data from people.
In this first step we have placed eight nodes around the most important buildings in Gandia’s campus at Universitat Politècnica de Valencia (see Figure 1). Node 1 is located at the secretariat, where many people go to check their documents. Node 2 is at the canteen. Nodes 3 and 4 are at the library, with node 3 at the entrance where people can take books to consult at home, and node 4 at the study room. Node 5 is placed at the entry of the computer science building and node 6 is at the entry of the natural science building. Finally, we have nodes 7 and 8 at the classroom’s building. Node 7 is placed very near to the classrooms—where there are many students—and node 8 is at the main entrance of this building. This system has been placed in a real environment, so it means that the nodes are influenced by interferences of other devices that are not included in the wireless location system. But, this is a typical feature of any environment where there are wireless devices like smartphones, access points, laptops, etc. This is a positive feature because we can say that our system works properly in real environments with other wireless interferences.
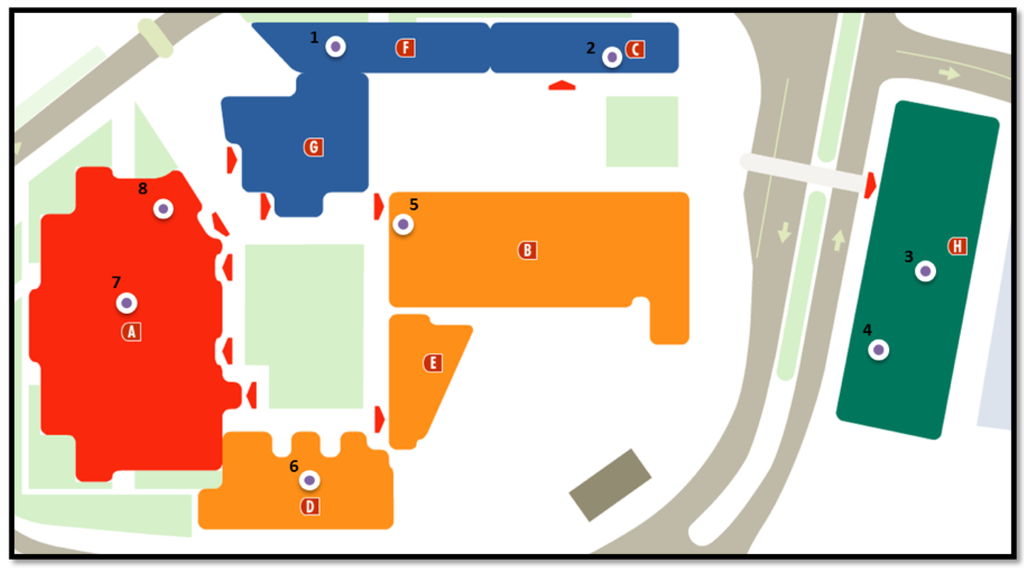
Figure 1.
Wireless Location System developed in Gandia’s Campus.
Our nodes have been programmed to save what is around it, and how much time a device is inside its coverage. The data related to the node’s identity is obfuscated using a one-way operation. In this way we keep the privacy of the users’ devices. Every node has 2 network interfaces. One is a Bluetooth interface in order to know how many devices are near each node, and the other one is a Wi-Fi interface, which is used to send all data to a server. This server is responsible for running our cooperative data processing and executing our cooperative decision-making algorithm.
3.2. Node Description
For this project we selected a device with embedded Linux (kernel Android JB 4.1.1). In order to make the design process simpler, we used a commercially available board (Android MiniPC UG007 II). This allowed us to have a highly configurable device, with very good characteristics and many communication options with a price tag less than 50€. It has a RK3066 1.6GHz Cortex A9 Dual Core processor, an internal flash memory of 8GB (enough space to store all the data collected for this project) and a miniSD card reader. The electronic device can be observed in Figure 2.

Figure 2.
Electronic device used.
The two available network interfaces are IEEE 802.11b/g/n and Bluetooth 2.1. The latter has been used as the basis of studying the mobility patterns of the users. We have replaced the patch antenna with a pigtail, so we can add an external antenna with higher gain. In order to test the fact that the external antenna has bigger coverage radius, we performed some measurements of coverage of the sensor device with the patch antenna and with a monopole antenna with 5 dBi of gain. In Figure 3 we can appreciate that the sensor device with the patch antenna only has a coverage radius of 8 m, and with the external antenna we can get up to 20 m.
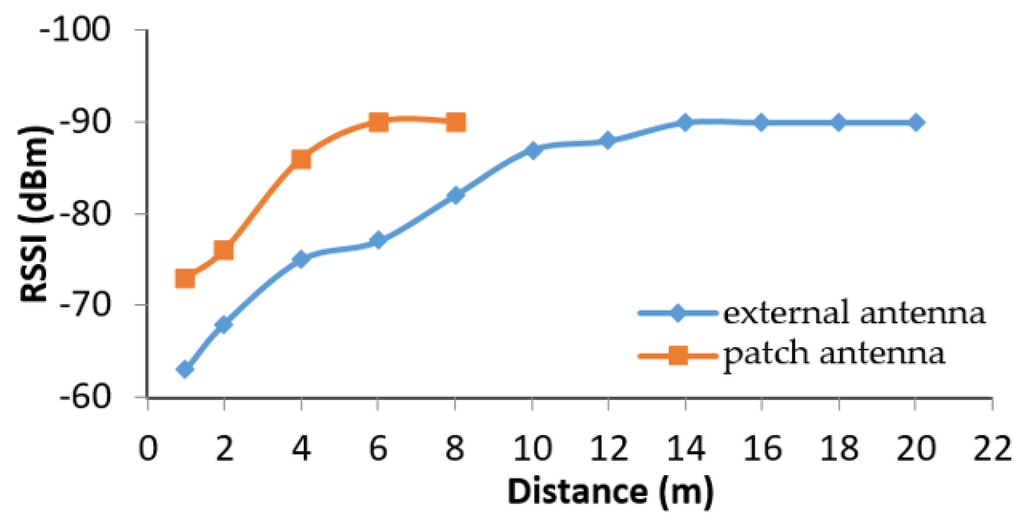
Figure 3.
Coverage of the sensor device.
4. Studying the Transition Symmetry
We performed a symmetry study of the mobility of the users in the work [17]. The main focus of in this study is the transition matrix (TM), which is a matrix of L x L elements where L is the number of locations (l). Every element, aij, denotes the number of transitions observed from location li to lj. It is not possible to have a transition from li to li, thus the values of the main diagonal are zero.
A transition matrix is considered symmetric when aij ≈ aji ∀ij ∈ {1...L}. Figure 4 shows a graphical representation of the TM obtained in our experiment. This TM considers transitions within six weeks and aggregates all users. The TM shows a clear symmetry in relation to the main diagonal.
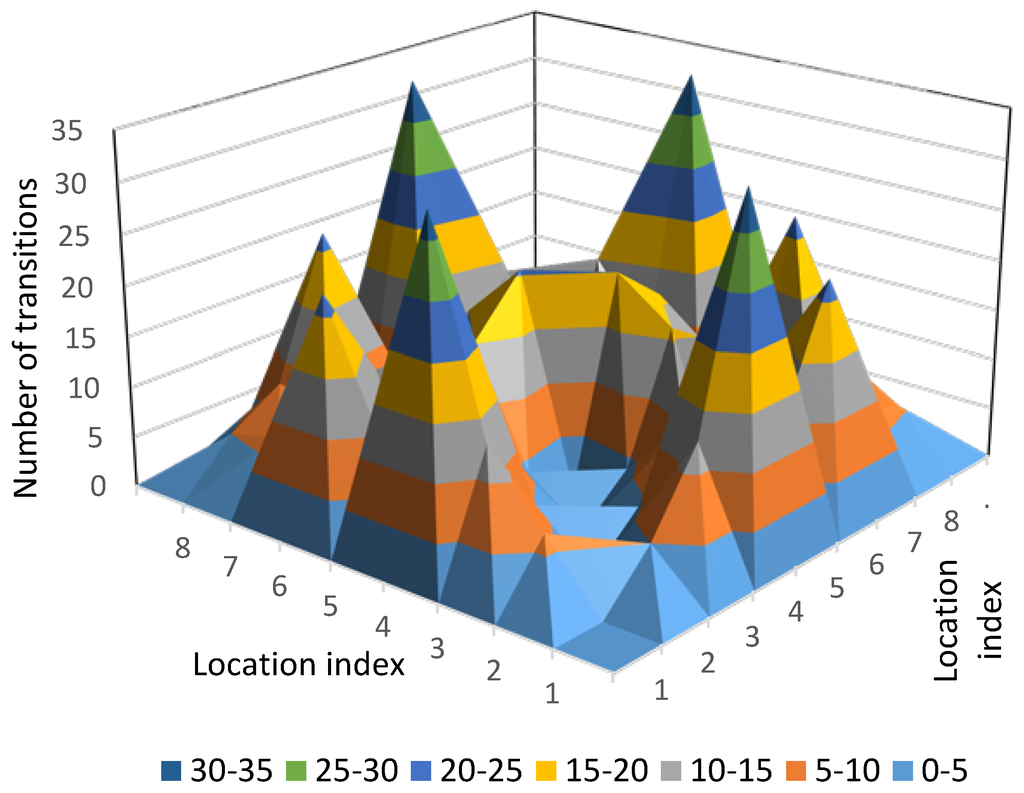
Figure 4.
Transition matrix between the eight locations.
In the traces of the Wireless Local Area Network (WLAN), the symmetric behavior could be a consequence of the ping-pong effect, as it has been reported in [11]. However, this effect was disregarded in our experiments, as the sensors’ locations rendered them without overlapping areas.
In order to quantify symmetry as we observe user mobility, a metric called coefficient of symmetry, α, can be used:
where T is the total number of transitions in the TM. The values of α are contained in the [0,1] range. The lower the α value, the higher symmetry it presents. We can compute α for all users or for a number of users, n. The relation between the number of users taken into account and the coefficient of symmetry is shown in Figure 5. It can be observed that as the number of users increases, the symmetry increases as well.
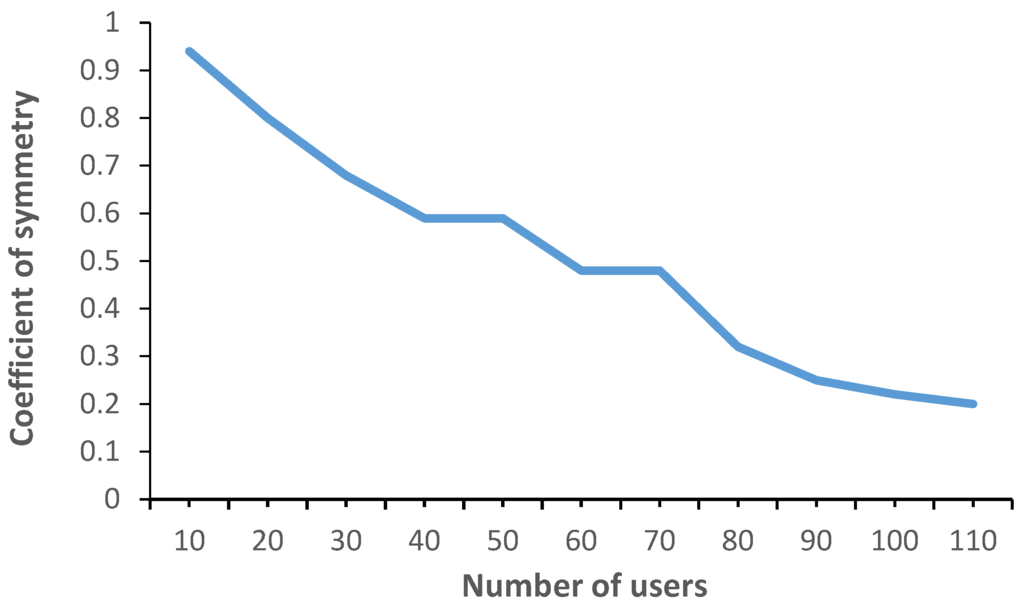
Figure 5.
Coefficient of symmetry as a function of the number of user.
5. Stochastic Approach for Cooperative Location Estimation
5.1. Introduction
A cooperative decision-making problem describes a situation involving several opinions or information—in our case it is data from nodes—which can obtain benefits by cooperating with one another. The problems they face are who will cooperate with whom, and how the corresponding benefits will be divided. Obviously, a node shares its information when taking part in a coalition. However, the extent of cooperation depends on the benefits that the cooperation has to offer, so a coalition is only likely to be formed if all members of this coalition agree on a specific distribution of the benefits. Finding such an agreement, however, could be troublesome when these members have mutually conflicting interests.
In order to analyze this situation, we used a general mathematical framework [29] that demonstrates cooperative decision-making problems. Assume represents a finite set of nodes. The benefit of cooperation will be explained by , which is a topological space representation of outcome space. Its representation depends on the decision making problem that is under consideration. Moreover, this outcome space is the benefit made by each coalition . It can be represented by a subset . An outcome then produces the cost to node i. In order to evaluate several outcomes, each node has a preference relation over outcome space . So, node i is only interested in what it receives; it does not take into account any other data. After that, given any two outcomes , we assume if node i finds the outcome y at least as good as the outcome . On the one hand, if node i finds the outcome y strictly better than the outcome we say . On the other hand, if node i is indifferent between the outcomes y and we can write . To sum up, a cooperative decision making model can be described by a tuple .
5.2. Stochastic Approach
In this section we explain mathematical assumptions used in our proposal. We analyzed methods for collaborative location estimation from a statistical point of view. Table 1 shows the variables used in the analysis.

Table 1.
Mathematical variables used in the model.
The location estimation problem can be statistically stated as follows. For simplicity, the true distribution Pr(X = x) and Pr(X = x|Y = y) are denoted as Pr(x) and Pr(x|y). The model parameters are denoted by p().
Let l be the location of a person. In our problem, we considered only a finite number of possible locations. For example, in Figure 1 there are only eight possible locations, l1, …, l8. We are interested in the study of movement from one location to another. Thus, we denote as l’ the previous location from where the user is coming.
We are interested in modeling the location behavior of an individual user. We identified a user using the network connection of personal devices (typically mobile phones, tablets, or wearable devices). These kinds of devices use Medium Access Control (MAC) address that is identified in the network. MAC address does not change (unless the user intentionally hacks it). Since, generally, a user carries the same device, we can assume with minimal error that a MAC address identifies a user. We use the approximation that a user has only one personal device and that it is always connected.
Finally, in our model, we have also taken temporal information into account. Specifically, the hour of the day (h) and the day of the week (d). We assume that the location depends only on these four variables, as defined in Equation (2):
Once this function is estimated, the problem can be formulated to find the location l that maximizes the probability Pr(l|l’, u, h, d) for a given observation l’, u, h and d. Using Bayes’ theorem, we can write:
The denominator in Equation (3) does not depend on the location variable l. Therefore, the location estimation problem can be presented as:
where Pr(l) is the prior probability of the location l, knowing the observation. This probability can be used to incorporate information so that more training locations [30] or tracking [31] can be used in our statistical model. In order to estimate the prior probability, we can use the uniform distribution.
In Equation (3), Pr(l’, u, h, d|l) is the so called likelihood function. It estimates the probability of one observation given a location. For estimating this probability, we can assume that the variables l’, u, h, and d are independent. Thus, we can write:
Depending on the number of data available for training, other assumptions can be made. For example, if we have no information about a certain user, we can remove p(u|l) from the equation:
Or if we have a lot of temporal information, we can estimate h and d jointly:
In Section 4 we have verified that our transition matrix is symmetric. That is, the number of transitions observed from location li to lj is very similar to transitions from lj to li; therefore, p(l’|l) ≈ p(l|l’). We can use this fact to better estimate p(l’|l). We assume that p(l’|l) = p(l|l’), and define p(l’, l) as the probability to go from l’ to l or go from l to l’. Using this assumption, Equation (4) can be reformulated as:
5.3. Inductive Training
We use an inductive approach that estimates the likelihood function using past observations. That is, several measurements are taken for each training place; then, the function Pr(l’, u, h, d |l) is estimated. The main drawback of this approach is the time consuming training phase. We denote as T the set of training data, formed by t observations with their respective locations. Each piece of training data, Ti, is represented as (li, l’i, ui, hi, di), where i can be from 1 to t. Several alternatives have been proposed in the literature to estimate p(l’, u, h, d |l) from T: the histogram method [32,33], the Bayesian method [34], or the kernel method [32,35]. The Bayesian method is used in this paper.
6. Experimental Results
In order to perform the experimental study, our system logged data for six weeks, in April and May. The only data collected was from users with open Bluetooth devices. A total of 861 different users were logged. As it is shown in Figure 1, the data was logged from eight different locations.
The set of data obtained has been divided into two sets: for the training corpus we used the first five weeks and for the test corpus we use the last week.
6.1. Time Spent in Each Location
As we have seen in the previous point, our wireless location system is more focused on finding out how much time a device is near to a reference node than its exact position. For this reason, we have not paid special attention to the accuracy of our wireless location system. Otherwise, we are going to use the cooperation between collected data to make a decision about the behavior of the system.
According to our location system, which we have explained before, there are some places where people spend more time than others. Usually, these places are classrooms, study rooms or the canteen. Places where people only pass through or perform a brief task, which requires less time, can be called passing places. In Figure 6a, we can see the collected data from every node on our network. Each user can have a very different temporal pattern. To demonstrate this affirmation, in this figure we have represented 10 users for a morning. We can affirm our nodes placed on points 3, 5 and 8 are entirely passing places, so we cannot conclude a lot from data obtained from these places. On the other hand, points 2, 4, 6 and 8 are interesting because people expend more time in these places. Point 1 is placed in an extraordinary location, the secretariat, where students manage a lot of matters related to their degree. People spend a lot time here, but only at the beginning or at the end of each course. As this data was obtained in April, there are few users. In Figure 6b, we can see the collected data for different time slots. In Figure 6b we can see that the time spent in each location is the same as the average and independent of the observation time.
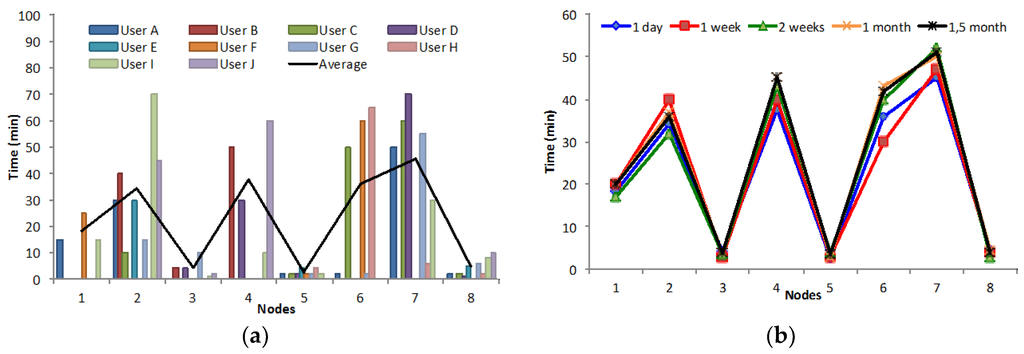
Figure 6.
Spending time average in each location. (a) Comparison for 10 users for a morning; (b) As a function of the studied time.
6.2. Evaluation of the Location Estimation
In Section 5 we proposed a statistical model that is able to predict the new location of a user by using the current location and other external factors such as time information. In order to evaluate this model, we prepared another experiment. We used the training corpus (five weeks) to estimate the statistical model, and the test corpus (one week) to evaluate it. For each location in the test corpus, we obtained the next location predicted by the system and compared it with the next location in the real track. Then, we measured the percentage of correct predictions. Figure 7 shows the results. We have used an increasing number of training samples, from 20.000 to 160.000. We evaluated three alternative models: (a) uses the initial equation proposed in Equation (5); (b) when a user had more than 10 training samples, we use Equation (5), in other cases, we use Equation (6), where p(u|l) is removed; (c) uses Equation (7), with variables h and d jointly estimated; (d) uses Equation (8) that assumes TM is symmetric ((b) considerations are also used).
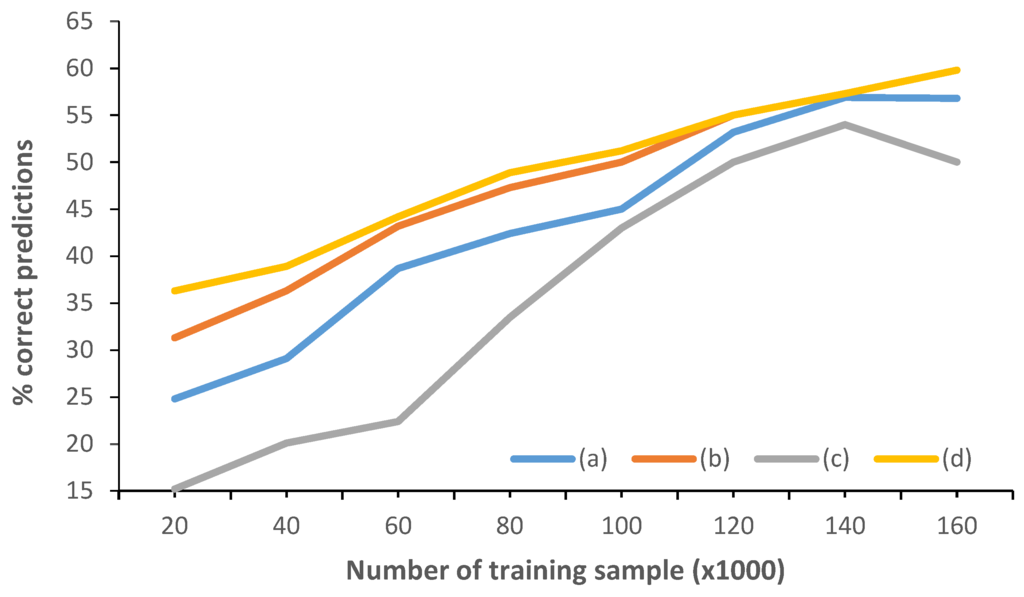
Figure 7.
Percentage of correct predictions (a) using the initial Equation (5); (b) using Equation (6); (c) using Equation (7); (d) using Equation (8).
From Figure 7 we can observe that (b) obtains better results than (a), especially with only a few training samples. To use Equation (7), graph (c), is not a not a good idea, probably because the number of training samples is not sufficient for a joint estimation. In (d), Equation (8) is used; we assumed that p(l’|l) = p(l|l’), and replaced these by p(l’, l). With this approach we obtained the best results. However, with a big enough training data sample, the upgrade stops being significant in respect to (b).
7. Conclusions
This paper analyzed the mobility traces of personal devices using wireless networks. First, we described the design of a cooperative sensor network. Then we showed the development of our experiment and the data collected. Using these data we have performed a symmetry study on the mobility of the users. Our results show a clear symmetry, that is to say, the number of users that move from li to lj approximates the number of users that go from lj to li.
Our interest has been focused on modeling the location behavior of an individual user. We proposed a statistical model which is able to predict the next step in a trace. This model can be trained from the traces collected. We want to use the observed symmetry to improve our statistical model, so we propose a new model that takes symmetry into account. The new model achieves better results when the number of training samples is limited.
In future works we will use this system in other types of places such as rural areas and water environments. Moreover, we will use the developed system to predict people’s behavior in order to provide more technical or human resources when these requirements are predicted.
Acknowledgments
This work is supported by the “Universitat Politècnica de Valencia” through “PAID-05-12”.
Author Contributions
Miguel García-Pineda and Jesús Tomás conceived and designed the experiments; Miguel García-Pineda performed the experiments; Jesús Tomás and Jaime Lloret analyzed the data; Alejandro Canovas contributed reagents/materials/analysis tools; Jesús Tomás, Miguel García-Pineda and Jaime Lloret wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chandra, P.; Dobkin, D.M.; Bensky, D.; Olexa, R.; Lide, D.; Dowla, F. Wireless Networking: Know It All; Newnes Know It All Series; Newnes: Oxford, UK, 2007. [Google Scholar]
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS: Principles and Applications; Artech House Publishers: Norwood, MA, USA, 2006. [Google Scholar]
- Gu, Y.; Lo, A.; Niemegeers, I. A survey of indoor positioning systems for wireless personal networks. IEEE Commun. Surv. Tutor. 2009, 11, 13–32. [Google Scholar] [CrossRef]
- Maghdid, H.S.; Lami, I.A.; Ghafoor, K.Z.; Lloret, J. Seamless Outdoors-Indoors Localization Solutions on Smartphones: Implementation and Challenges. ACM Comput. Surv. 2016, 48. [Google Scholar] [CrossRef]
- Li, F.; Zhao, C.; Ding, G.; Gong, J.; Liu, C.; Zhao, F. A reliable and accurate indoor localization method using phone inertial sensors. In Proceedings of the 2012 ACM Conference on Ubiquitous Computing (UbiComp ‘12), New York, NY, USA, 5–8 September 2012; pp. 421–430. [CrossRef]
- Zheng, Y.; Shen, G.; Li, L.; Zhao, C.; Li, M.; Zhao, F. Travi-Navi: Self-deployable indoor navigation system. In Proceedings of the 20th Annual International Conference on Mobile Computing and Networking (MobiCom ‘14), Maui, HI, USA, 7–11 September 2014; pp. 471–482. [CrossRef]
- Pineda-Briseño, A.; Menchaca-Mendez, R.; Chavez, E.; Guzman, G.; Menchaca-Mendez, R.; Quintero, R.; Torres, M.; Moreno, M.; Diaz-De-Leon, J.L. A Probabilistic Approach to Location Estimation in MANETs. Ad Hoc Sens. Wirel. Netw. 2015, 28, 97–114. [Google Scholar]
- Sendra, S.; Lloret, J.; Turro, C.; Aguiar, J. IEEE 802.11a/b/g/n Short Scale Indoor Wireless Sensor Placement. Int. J. Ad Hoc Ubiquitous Comput. (IJAHUC) 2014, 15, 68–82. [Google Scholar] [CrossRef]
- Farid, Z.; Nordin, R.; Ismail, M. Recent Advances in Wireless Indoor Localization Techniques and System. J. Comput. Netw. Commun. 2013, Article ID 185138. [Google Scholar] [CrossRef]
- Elbes, M.; Al-Fuqaha, A.; Anan, M. A Precise Indoor Localization Approach based on Particle Filter and Dynamic Exclusion Techniques. Netw. Protocols Algorithms 2015, 26, 50–71. [Google Scholar]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Garcia, M.; Boronat, F.; Tomas, J.; Lloret, J. The Development of Two Systems for Indoor Wireless Sensors Self-location. Ad Hoc Sen. Wirel. Netw. 2009, 8, 235–258. [Google Scholar]
- Fitzek, F.H.; Katz, M.D. Cooperation in Wireless Networks: Principles and Applications. Real Egoistic Behavior Is to Cooperate! Springer: Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Nosratinia, A.; Hunter, T.E.; Hedayat, A. Cooperative communication in wireless networks. IEEE Commun. Mag. 2004, 42, 74–80. [Google Scholar] [CrossRef]
- Mulligan, R.; Ammari, H.M. Coverage in Wireless Sensor Networks: A Survey. Netw. Protocols Algorithms 2010, 2, 27–53. [Google Scholar] [CrossRef]
- Hsiao-Wecksler, E.T.; Polk, J.D.; Rosengren, K.S.; Sosnoff, J.J.; Hong, S. A Review of New Analytic Techniques for Quantifying Symmetry in Locomotion. Symmetry 2010, 2, 1135–1155. [Google Scholar] [CrossRef]
- Nunes, B.A.A.; Obraczka, K. On the symmetry of user mobility in wireless networks. In Proceedings of the 2011 IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Lucca, Tuscany, Italy, 21 November 2011; pp. 1–6. [CrossRef]
- Deng, Z.; Yu, Y.; Yuan, X.; Wan, N.; Yang, L. Situation and development tendency of indoor positioning. China Commun. 2013, 10, 42–55. [Google Scholar] [CrossRef]
- Lloret, J.; Tomas, J.; Garcia, M.; Canovas, A. A Hybrid Stochastic Approach for Self-Location of Wireless Sensors in Indoor Environments. Sensors 2009, 9, 3695–3712. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Au, W.S.A.; Valaee, S.; Tan, Z. Received-Signal-Strength-Based Indoor Positioning Using Compressive Sensing. IEEE Trans. Mob. Comput. 2012, 11, 1983–1993. [Google Scholar] [CrossRef]
- Wang, J.; Hu, A.; Liu, C.; Li, X. A Floor-Map-Aided WiFi/Pseudo-Odometry Integration Algorithm for an Indoor Positioning System. Sensors 2015, 15, 7096–7124. [Google Scholar] [CrossRef] [PubMed]
- Pandya, D.; Jain, R.; Lupu, E. Indoor location estimation using multiple wireless technologies. In Proceedings of the 14th IEEE Proceedings on Personal, Indoor and Mobile Radio Communications, Beijing, China, 7–9 September 2003; pp. 2208–2212. [CrossRef]
- Garcia, M.; Sendra, S.; Lloret, J.; Canovas, A. Saving energy and improving communications using cooperative group-based wireless sensor networks. Telecommun. Syst. 2013, 52, 2489–2502. [Google Scholar] [CrossRef]
- Garcia, M.; Lloret, J. A cooperative group-based sensor network for environmental monitoring. In Cooperative Design, Visualization, and Engineering; Springer Berlin Heidelberg: Luxembourg, Luxembourg, 2009; pp. 276–279. [Google Scholar] [CrossRef]
- Patwari, N.; Ash, J.N.; Kyperountas, S.; Hero, A.O., III; Moses, R.L.; Correal, N.S. Locating the nodes: Cooperative localization in wireless sensor networks. IEEE Signal Proc. Mag. 2005, 22, 54–69. [Google Scholar] [CrossRef]
- Conti, A.; Guerra, M.; Dardari, D.; Decarli, N.; Win, M.Z. Network Experimentation for Cooperative Localization. IEEE J. Sel. Areas Commun. 2012, 30, 467–475. [Google Scholar] [CrossRef]
- Maali, A.; Zeroukhi, L.; Guerfi, A.D.; Baudoin, G.; Mimoun, H. Experimental validation of the cooperative localization algorithm in wireless sensor network. In Proceedings of the European Microwave Conference (EuMC 2013), Nuremberg, Germany, 6–11 October 2013; pp. 334–337.
- Wang, X.; Zhou, H.; Mao, S.; Pandey, S.; Agrawal, P.; Bevly, D.M. Mobility improves LMI-based cooperative indoor localization. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC 2015), New Orleans, LA, USA, 9–12 March 2015; pp. 2215–2220. [CrossRef]
- Suijs, J.P.M. Cooperative Decision Making in a Stochastic Environment (No. urn: nbn: nl: ui: 12-76799). Tilburg University, 1998. Available online: http://EconPapers.repec.org/RePEc:tiu:tiutis:a84d779a-d5a9-48e9-bfe7-46dea6f1de69 (accessed on 1 July 2016).
- Krishnan, P.; Krishnakumar, A.S.; Ju, W.H.; Mallows, C.; Gamt, S.N. A system for LEASE: Location estimation assisted by stationary emitters for indoor RF wireless networks. In Proceedings of the Twenty-third Annual Joint Conference of the IEEE Computer and Communications Societies, INFOCOM 2004, Hong Kong, China, 7–10 March 2004; Volume 2, pp. 1001–1011. [CrossRef]
- Wang, H.; Jia, F. A Hybrid Modeling for WLAN Positioning System. In Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing, 2007 (WiCom 2007), Shanghai, China, 21–25 September 2007; pp. 2152–2155. [CrossRef]
- Roos, T.; Myllymäki, P.; Tirri, H.; Misikangas, P.; Sievänen, J. A probabilistic approach to WLAN user location estimation. Int. J. Wirel. Inf. Netw. 2002, 9, 155–164. [Google Scholar] [CrossRef]
- Xie, H.; Tanin, E.; Kulik, L. Distributed Histograms for Processing Aggregate Data from Moving Objects. In Proceedings of the 2007 International Conference on Mobile Data Management, Mannheim, Germany, 7–11 May 2007; pp. 152–157. [CrossRef]
- Krishnamachari, B.; Iyengar, S. Distributed Bayesian algorithms for fault-tolerant event region detection in wireless sensor networks. IEEE Trans. Comput. 2004, 53, 241–250. [Google Scholar] [CrossRef]
- Nguyen, X.; Jordan, M.; Sinopoli, B. A kernel-based learning approach to ad hoc sensor network localization. ACM Trans. Sens. Netw. 2005, 1, 134–152. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).