On the Boundedness and Symmetry Properties of the Fractal Sets Generated from Alternated Complex Map

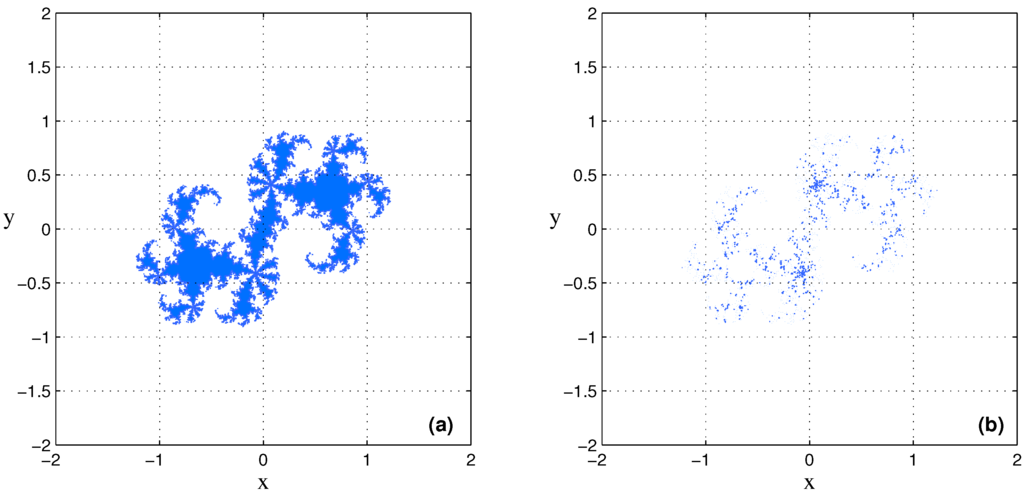
Abstract

A complex map can give rise to two kinds of fractal sets: the Julia sets and the parameters sets (or the connectivity loci) which represent different connectivity properties of the corresponding Julia sets. In the significative results of (Int. J. Bifurc. Chaos, 2009, 19:2123–2129) and (Nonlinear. Dyn. 2013, 73:1155–1163), the authors presented the two kinds of fractal sets of a class of alternated complex map and left some visually observations to be proved about the boundedness and symmetry properties of these fractal sets. In this paper, we improve the previous results by giving the strictly mathematical proofs of the two properties. Some simulations that verify the theoretical proofs are also included.

1. Introduction

Julia set [1], one of the most attractive fractal sets, is proposed by Gaston Julia when he studied the following complex quadratic polynomial

$$P_c:z_{n+1}=z_n^{\alpha }+cc\in \mathbb{C},\alpha =2$$

(1)

Since it was proposed, Julia set has attracted significant interests in the topics of property analysis [2,3,4,5], superior iteration [6,7,8], time-delay [9], control [10,11] and so forth. Due to its good explanation for lots of complicated phenomena, Julia set has also been widely applied in the fields of physics [12], biology [13], image cryptography [14] and so on.

As mentioned in the research of [15,16], it may not be quite accurate to depict the evolution of the natural process mentioned above just by employing a unique system. In some cases, the alternated iterations can be used to have a better understanding of the natural process. In particular, for system (1), Danca et al. [17,18] proposed its alternated version as follows:

$$P_{c_1,c_2}:z_{n+1}=\left\{\begin{array}{c}{z}_n^2+c_1,\mathrm{if}n\mathrm{is}\mathrm{even},\hfill \\ z_n^2+c_2,\mathrm{if}n\mathrm{is}\mathrm{odd},\hfill \end{array}\right.$$

(2)

where $z_n,c_1=p+iq,c_2=r+is\in \mathbb{C}$, $C={(c_1,c_2)}^T\left(T\mathrm{means}\mathrm{transposition}\right)$.

Based on the Fatou–Julia theorem [19] (see Theorem 2), the Julia set (see Definition 1) generated from $P_{c_1,c_2}$, which is denoted as $J\left(P_{c_1,c_2}\right)$, can be connected, disconnected and totally disconnected via choosing different parameters $c_1,c_2$ [17]. To test numerically which values of the parameters $c_1,c_2$ give rise to connected, disconnected, or totally disconnected $J\left(P_{c_1,c_2}\right)$, the auxiliary complex quadratic polynomial $Q_{c_1,c_2}$ was proposed in [17]:

$$Q_{c_1,c_2}:w_{n+1}={(w_n^2+c_1)}^2+c_2,$$

(3)

where $w_n=x_n+i{y}_n$. Furthermore, they proved that the Julia sets generated from $P_{c_1,c_2}$ and $Q_{c_1,c_2}$ are the same with given $c_1,c_2$. Thus the connectivity of $J\left(P_{c_1,c_2}\right)$ relies on the critical orbits of system (3). In [18], the graphical results of the connectivity loci which represent the three connectivity states of the corresponding $J\left(P_{c_1,c_2}\right)$ were unveiled by analyzing the critical orbits of (3). In concrete terms, the fractal sets which represent the connected, disconnected, totally disconnected Julia sets were respectively denoted as the Connectedness–Locus, Disconnectedness–Locus and Totally connectedness–Locus [17,18]. Based on these graphical results, some observations about the boundedness and symmetry properties of these connectivity loci were summarized in Section 4 of [18]. These unproved properties are just the original purpose and the starting point of this article.

Actually, there has been some research on the boundedness and symmetry properties for the fractal sets of complex maps which have only one critical point (see the classical M-J sets [2,20,21] and the generalized M-J sets [4,22,23]). For the systems like (3) which have more than one critical point, the results mainly focused on the properties of their Julia sets (see the Julia sets of cubic polynomials [3] and the superior Julia set [6]). To our knowledge, few research papers have addressed the problems about the boundedness and symmetry properties of their connectivity loci (or Mandelbrot set) since all the critical orbits should be considered.

Thus, as a supplementary research of [17,18], the purpose and achievement of this paper are no other than giving the mathematical proof about the two properties of the Connectedness–Locus and the Julia sets generated from (2) via analyzing all the critical orbits of system (3).

The remainder of this paper is outlined as follows. Section 2 recalls some definitions and theorems about the alternated complex map. In Section 3, the boundedness properties of the alternated Julia sets and the Connectedness–Locus are proposed and proved. In Section 4, the symmetry properties of the 3-D slice of Connectedness–Locus and the alternated Julia sets are analyzed in two theorems. Simulations are given to support the validity of the results. Finally, Section 5 concludes the paper.

2. The Fractal Sets Generated from Alternated Complex Map

In this section, some necessary definitions and theorems are recalled and given.

Definition 1. 

[17] The filled Julia set of the system (2), denoted as $K\left(P_{c_1,c_2}\right)$, is the set of all the values of initial conditions $z_0$ such that

$$\underset{n\to \infty }{lim}|P^n(z_0,c_1,c_2)|\nrightarrow \infty ,$$

(4)

where $P^n(·)$ represents the n-th iteration of the initial point $z_0$. The Julia set of $P_{c_1,c_2}$ which is the boundary of the filled Julia set is denoted as

$$J\left(P_{c_1,c_2}\right)=\partial \left(K\left(P_{c_1,c_2}\right)\right).$$

(5)

Theorem 1. 

[17,18] $J\left(P_{c_1,c_2}\right)$ and $J\left(Q_{c_1,c_2}\right)$ are the same for given $c_1$ and $c_2$ parameter values.

Theorem 2. 

[19] The connectivity properties of the Julia set for a complex polynomial of degree $d>2$ can be identified based on the following cases:

• The Julia set is connected if and only if all the critical orbits are bounded.
• The Julia set is totally disconnected, a cantor set, if (but not only if) all the critical orbits are unbounded.
• For a polynomial with at least one critical orbit unbounded, the Julia set is totally disconnected if and only if all the bounded critical orbits are aperiodic.

Then from Theorem 1 and Theorem 2, the connectivity of the $J\left(P_{c_1,c_2}\right)$ or $K\left(P_{c_1,c_2}\right)$ (J and K have the same connectivity properties [18]) relies on the boundedness of the three critical points of $Q_{c_1,c_2}$: $0,\pm \sqrt{-c_1}$. The following definition is given.

Definition 2. 

[18] The Connectedness-Locus of the alternated complex map (2), denoted as $M_e\left(P_{c_1,c_2}\right)$, is composed by all the initial constant $c_1,c_2$ such that the orbits of 0 and $\sqrt{-c_1}$ are bounded (since $\pm \sqrt{-c_1}$ behave the same boundedness properties).

In [17,18], $M_e\left(P_{c_1,c_2}\right)$ is named as “Connectedness–Locus” or “Connected zone”. The reason we denote it as $M_e\left(P_{c_1,c_2}\right)$ in this paper is that it has the same efficacy with the classical Mandelbrot set [20] which gives rise to the connectedness property. Thus, in this paper, we could also call $M_e\left(P_{c_1,c_2}\right)$ the Mandelbrot-efficacy set.

As shown in Definition 2, $M_e\left(P_{c_1,c_2}\right)$ is formed by the initial constants $c_1,c_2$, which illustrates that it belongs to a four-dimensional space $(p,q,r,s)$. By fixing $q_0=0$, the 3-D slice of $M_e\left(P_{c_1,c_2}\right)$ is shown in Figure 1a (also see the red part of Figure 1 in [18]). The internal slice of $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0}$ with $p_0=0$ is revealed in Figure 1b. The partial enlarged views of Figure 1b are successively shown in Figure 1c,d which fully display the beautiful and complex fractal structure of $M_e\left(P_{c_1,c_2}\right)$.

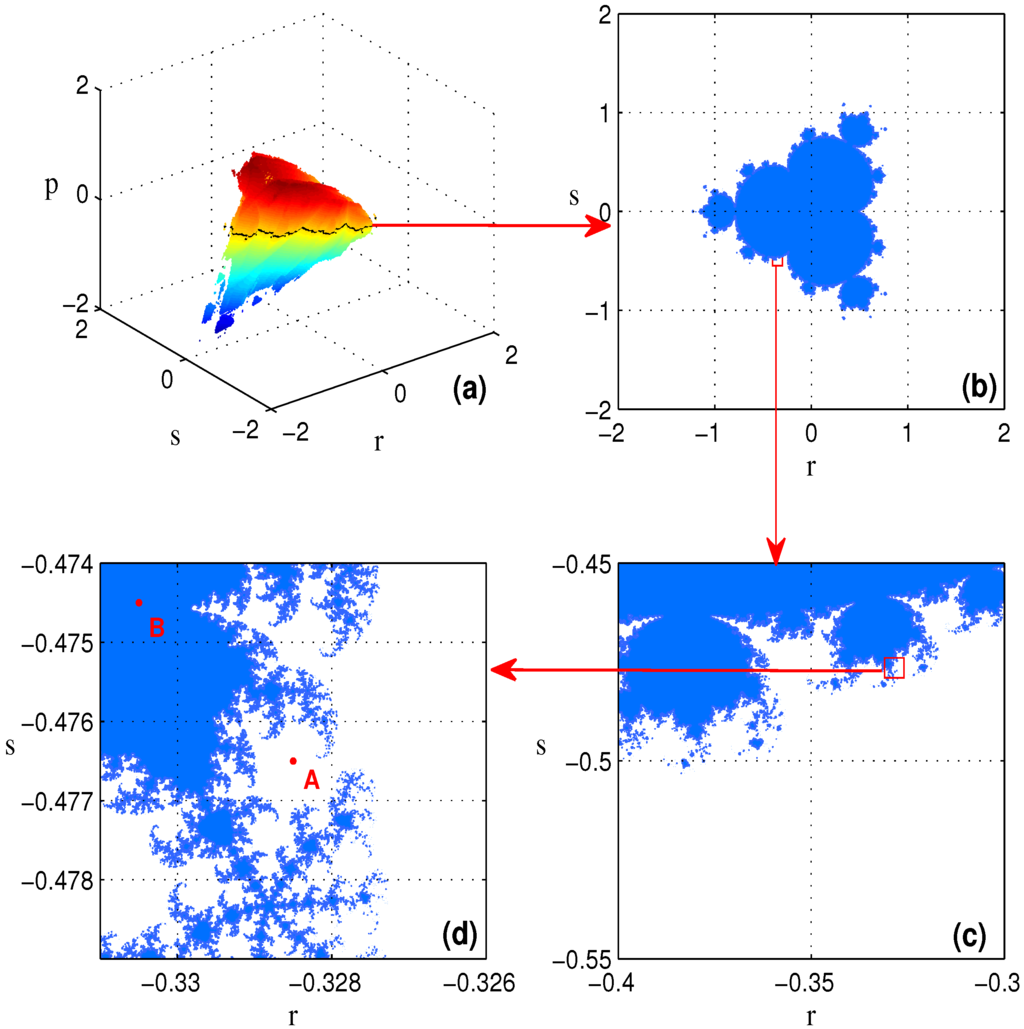
Figure 1. (a) The 3-D slice of Mandelbrot-efficacy set: $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0}$; (b) The 2-D slice of $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0}$ with $p_0=0$; (c,d) The partial enlarged views of $M_e{\left(P_{c_1,c_2}\right)}_{p_0=0,q_0=0}$.

The Julia sets $J\left(P_{c_1,c_2}\right)$ with different parameters A and B which are located in Figure 1d are shown in Figure 2. It can be seen that $J\left(P_{c_1,c_2}\right)$ is connected with $c_2=-0.3305-0.4745i$ but disconnected with $c_2=-0.3285-0.4765i$.

Figure 2. (a) $K\left(P_{c_1,c_2}\right)$ with $c_1=0,c_2=-0.3305-0.4745i$ (A in Figure 1d); (b) $K\left(P_{c_1,c_2}\right)$ with $c_1=0,c_2=-0.3285-0.4765i$ (B in Figure 1d).

3. Boundedness of the Fractal Sets Generated from Alternated Complex Map

In this section, by analysing the orbits of the three critical points of system (3), the boundedness properties of $J\left(P_{c_1,c_2}\right)$ and $M_e\left(P_{c_1,c_2}\right)$ are given in the next two theorems.

Theorem 3. 

$J\left(P_{c_1,c_2}\right)\subset \{z_0\left|\right|z_0|\le \max \{|c_1|,|c_2|,R\}\},$ where R is the real root of the complex equation ${\lambda }^3-2{\lambda }^2-\lambda -2=0$. $i.e.s$ $T\approx 2.659$ (Solution of R is based on the Cardan’s formula [24]).

Proof. 

If $\exists w_0$ such that $|w_0|>\max \{|c_1|,|c_2|,R\}$, one can get

$$\begin{array}{cc}|w_1|\hfill & =|w_0^4+2w_0^2{c}_1+c_1^2+c_2|\hfill \\ & >|w_0{|}^4-2|w_0{|}^2|c_1|-|c_1{|}^2-\left|c_2\right|\hfill \\ & >|w_0{|}^4-2|w_0{|}^3-|w_0{|}^2-\left|w_0\right|\hfill \\ & =|w_0\left|\right(|w_0{|}^3-2|w_0{|}^2-|w_0|-1).\hfill \end{array}$$

Since $|w_0{|}^3-2|w_0{|}^2-\left|w_0\right|>2$ when $|w_0|>R$, there exists a $ϵ>0$ such that

$$|w_1|>(1+ϵ)|w_0|.$$

Then, $|w_1|>|w_0|>\max \{|c_1|,|c_2|,R\}$, one gets

$$\begin{array}{cc}|w_2|\hfill & =|w_1^4+2w_1^2{c}_1+c_1^2+c_2|\hfill \\ & >|w_1\left|\right(|w_1{|}^3-2|w_1{|}^2-|w_1|-1).\hfill \\ & >|w_1\left|\right(|w_0{|}^3-2|w_0{|}^2-|w_0|-1).\hfill \\ & >(1+ϵ)|w_1|.\hfill \end{array}$$

Finally, one can get $|w_n{|>(1+ϵ)}^n\left|w_0\right|\to \infty$ when $n\to \infty$. Then from Definition 1, one knows that $J\left(Q_{c_1,c_2}\right)\subset \{w_0\left|\right|w_0|\le \max \{|c_1|,|c_2|,R\}\}.$ As $J\left(Q_{c_1,c_2}\right)=J\left(P_{c_1,c_2}\right)$, the theorem is obtained.  ☐

Theorem 4. 

$M_e\left(P_{c_1,c_2}\right)\subset \{(c_1,c_2)\left|\right|c_1|\le R,|c_2|\le R\},$ where R is the same as Theorem 3.

Proof. 

Derive the $max\left\{\right|c_1|,|c_2|,R\}$ in Theorem 3 into three cases as follows:

$$\left\{\begin{array}{ccc}& \max \left\{\right|c_1|,|c_2\left|\right\}\hfill & >R:\left\{\begin{array}{c}\mathrm{①}:|c_1|>\max \{|c_2|,R\}\\ \mathrm{②}:|c_2|>\max \{|c_1|,R\}.\end{array}\right.\hfill \\ \mathrm{③}:\hfill & \max \left\{\right|c_1|,|c_2\left|\right\}\hfill & \le R.\hfill \end{array}\right.$$

(①): For case ①, one knows that $|c_1|>|c_2|$ and $|c_1|>T$, the orbit of the critical value 0 satisfies that

$$\begin{array}{cc}\left|Q\right(0\left)\right|\hfill & =|c_1^2+c_2|\ge |c_1{|}^2-\left|c_2\right|\hfill \\ & >|c_1{|}^2-|c_1|>|c_1|(R-1)\hfill \\ & >|c_1|.\hfill \end{array}$$

Then, $\left|Q\right(0\left)\right|$ satisfies the condition of Theorem 3, it is clear that the orbit of 0 is diverging.

(②): For case ②, one knows that $|c_2|>|c_1|$ and $|c_2|>R$, the orbit of the critical value $\sqrt{-c_1}$ satisfies that:

$$\begin{array}{cc}|Q^2\left(\sqrt{-c_1}\right)|\hfill & =|c_2^4+2c_2^2{c}_1+c_1^2+c_2|\hfill \\ & \ge |c_2{|}^4-|2c_2{|}^2|c_1|-|c_1{|}^2-\left|c_2\right|\hfill \\ & >|c_2{|}^4-|2c_2{|}^3-|c_2{|}^2-\left|c_2\right|\hfill \\ & >|c_2|(R^3-2R^2-R-1)\hfill \\ & >|c_2|.\hfill \end{array}$$

Thus, $|Q^2\left(\sqrt{-c_1}\right)|$ satisfies the condition of Theorem 3, one can know that the orbit of $\sqrt{-c_1}$ is diverging.

Taken together, for all the three critical values, their orbits are bounded only when $max\left\{\right|c_1|,|c_2\left|\right\}\le R.$ (case ③). From Definition 2, one gets: $M_e\left(P_{c_1,c_2}\right)\subset \{(c_1,c_2)\left|\right|c_1|\le R,|c_2|\le R\}.$  ☐

Remark 1. 

When $c_1=c_2=c$, system (2) becomes the classical map (1). The complex equation ${\lambda }^3-2{\lambda }^2-\lambda -2=0$ in Theorem 3 becomes $\lambda -2=0$.

• Then Theorem 3 becomes: $J\left(P_c\right)\subset \left\{z\right|\left|z\right|\le max\left\{\right|c|,2\}\}.$
• Theorem 4 becomes: $M\left(P_c\right)\subset \left\{c\right|\left|c\right|\le 2\}.$

$J\left(P_c\right)$ and $M\left(P_c\right)$ mean the Julia set and Mandelbrot set of $P_c$. The conclusions in this remark are consistent with the classical results [20].

4. Symmetry of the Fractal Sets Generated from Alternated Complex Map

Symmetry [2,4,23] is an important property of fractal sets. This section focuses on the symmetry properties of the Julia set $J\left(P_{c_1,c_2}\right)$ and the 3-D slice of the Mandelbrot-efficacy set $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0}$. The following two theorems are given and proved.

Theorem 5. 

The Mandelbrot-efficacy set $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0}$ is symmetric around the $pr$-plane.

Proof. 

For the critical points $0,\pm \sqrt{-c_1}$, we give them a unitary expression $w_0^{\prime }$. Then by choosing any two parameters values

$${(c_1,c_2)}^T={(p_0,0,r_0,s_0)}^T,{(c_1,\overline{c_2})}^T={(p_0,0,r_0,-s_0)}^T,$$

the orbits of all the three critical points $w_0^{\prime }$ preserve complex conjugacy when $n>1$. That is:

$$({w_n^{\prime }}^2+c_1{)}^2+c_2=w_{n+1}^{\prime },$$

$${({w_n^{\prime }}^2+c_1)}^2+\overline{c_2}=\overline{w_{n+1}^{\prime }}.$$

Thus, the critical orbits $w_n^{\prime }$ behave the same boundedness property by choosing any two parameters which are symmetric around the $pr$-plane. Then, based on Definition 2, the two parts of $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0}$ divided by the $pr$-plane are symmetric.  ☐

It is illustrated in Figure 3 that the 2-D slices $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0,s_0}$ have the same morphological structure with $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0,-s_0}$. The simulations verify the validity of the Theorem 5.

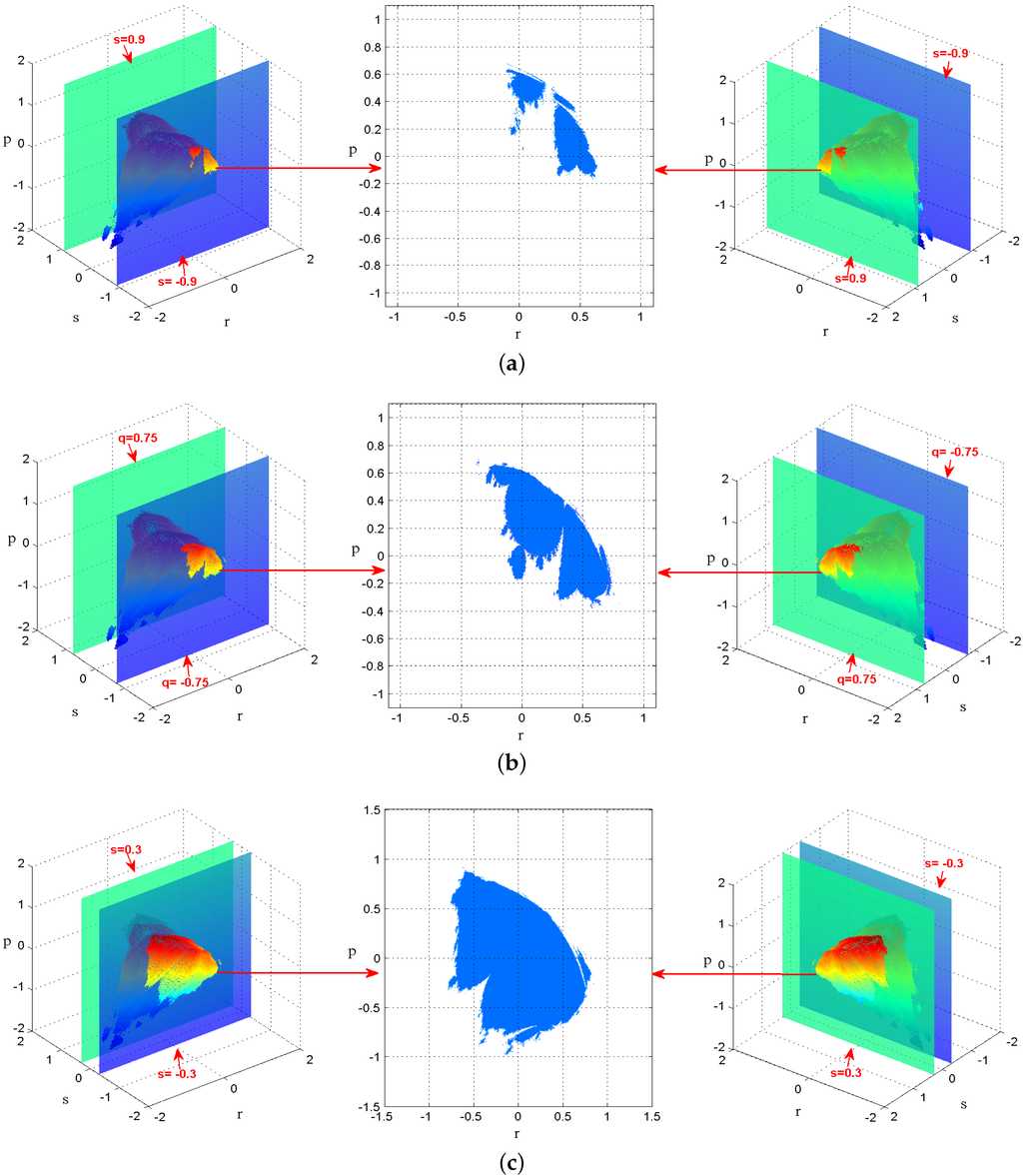
Figure 3. (a) $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0,s_0=-0.9}$ and $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0,s_0=0.9};$ (b) $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0,s_0=-0.75}$ and $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0,s_0=0.75};$ (c) $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0,s_0=-0.3}$ and $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0,s_0=0.3.}$

Theorem 6. 

The Julia set $J\left(P_{c_1,c_2}\right)$ is centrally symmetric around the origin.

Proof. 

When $c_1,c_2$ are given, one gets a corresponding Julia set. For any two initial points $w_0$ and $-w_0$, they map to the same $w_1={(w_0^2+c_1)}^2+c_2$.

Thus for any two points which are centrally symmetric around the origin, their orbits behave the same boundedness properties. From Definition 1, one knows that $J\left(P_{c_1,c_2}\right)$ is centrally symmetric around the origin.  ☐

With the help of the graphical method proposed in [18], we supplement the Disconnectedness-Locus (gray zone) and the Totally disconnectedness-Locus (white zone) to $M_e{\left(P_{c_1,c_2}\right)}_{q_0=0,s_0=-0.75}$. Then three different points are picked out and their corresponding filled Julia sets are shown in Figure 4.

The simulations of both Figure 4 and Figure 2 verify the correctness of Theorem 6.

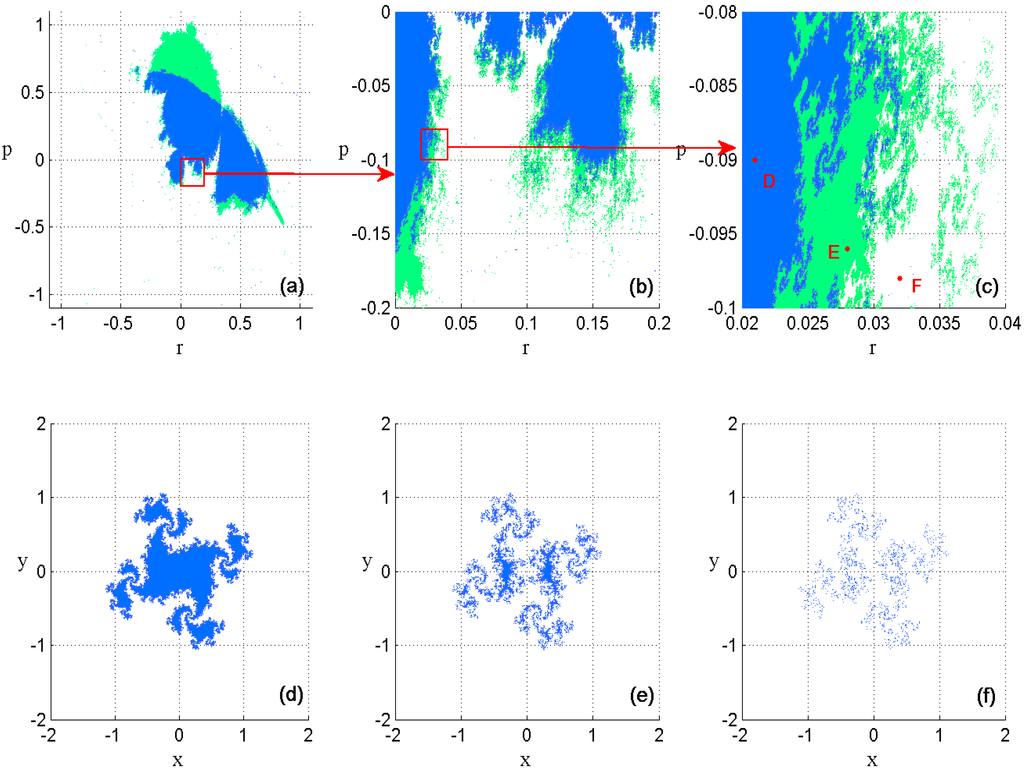
Figure 4. (a–c) The connectivity loci of system (2) and its partial enlarged views; (d) Connected $K\left(P_{c_1,c_2}\right)$ with $c_1=-$0.09, $c_2=0.021-0.75i$ (D point in (c)); (e) Disconnected $K\left(P_{c_1,c_2}\right)$ with $c_1=-$0.096, $c_2=0.028-0.75i$ (E point); (f) Totally disconnected $K\left(P_{c_1,c_2}\right)$ with $c_1=-$0.098, $c_2=0.032-0.75i$ (F point).

5. Conclusions

Fractals is one of the hottest topics in the fields of nonlinear dynamics. The properties of fractal sets are necessary to be investigated and favorable for the practical applications. This work focus on the boundedness and symmetry properties of the fractal sets generated from a class of alternated complex map. This is an important supplementary theoretical research for the existing related research and could represent a guide for the future research on the properties analysis about the complex maps with higher order or more complicated alternate rules.