Smartphone User Identity Verification Using Gait Characteristics
Abstract
:1. Introduction
2. Materials and Methods
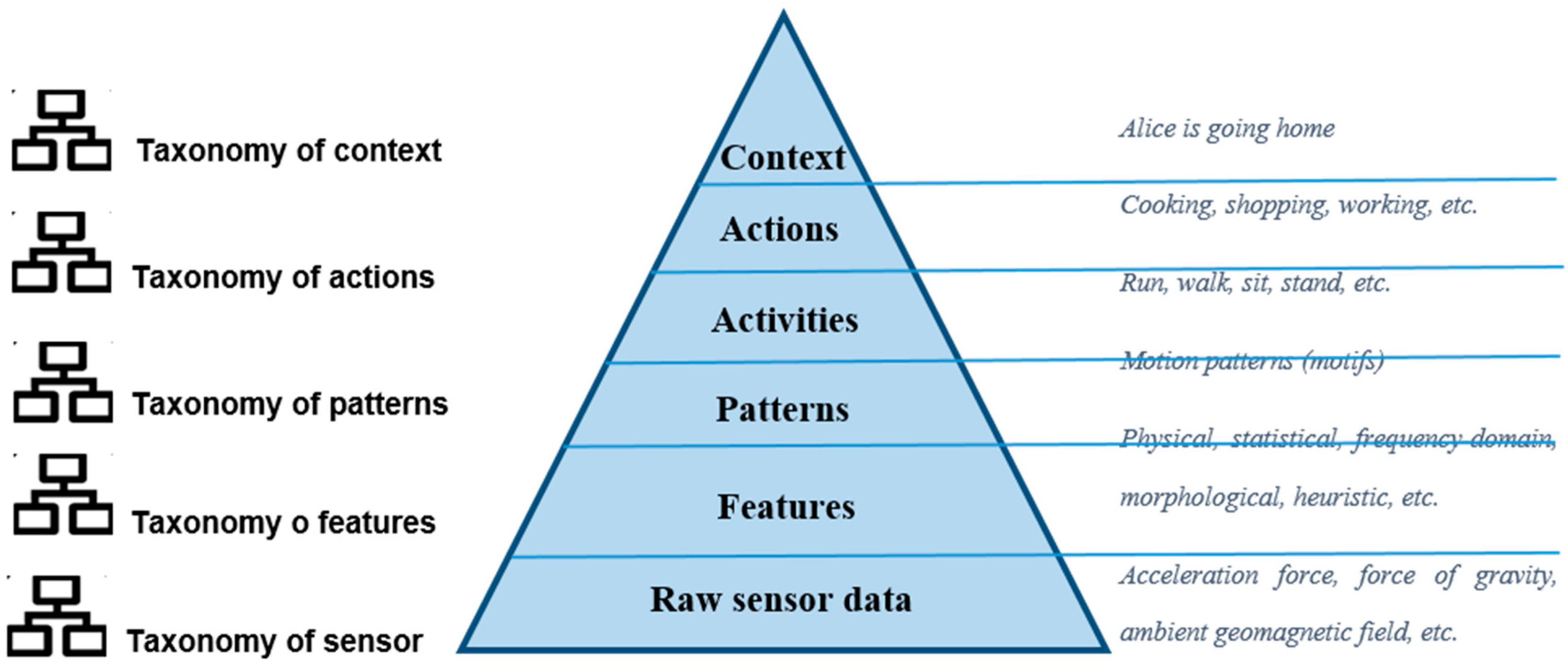
2.1. Background
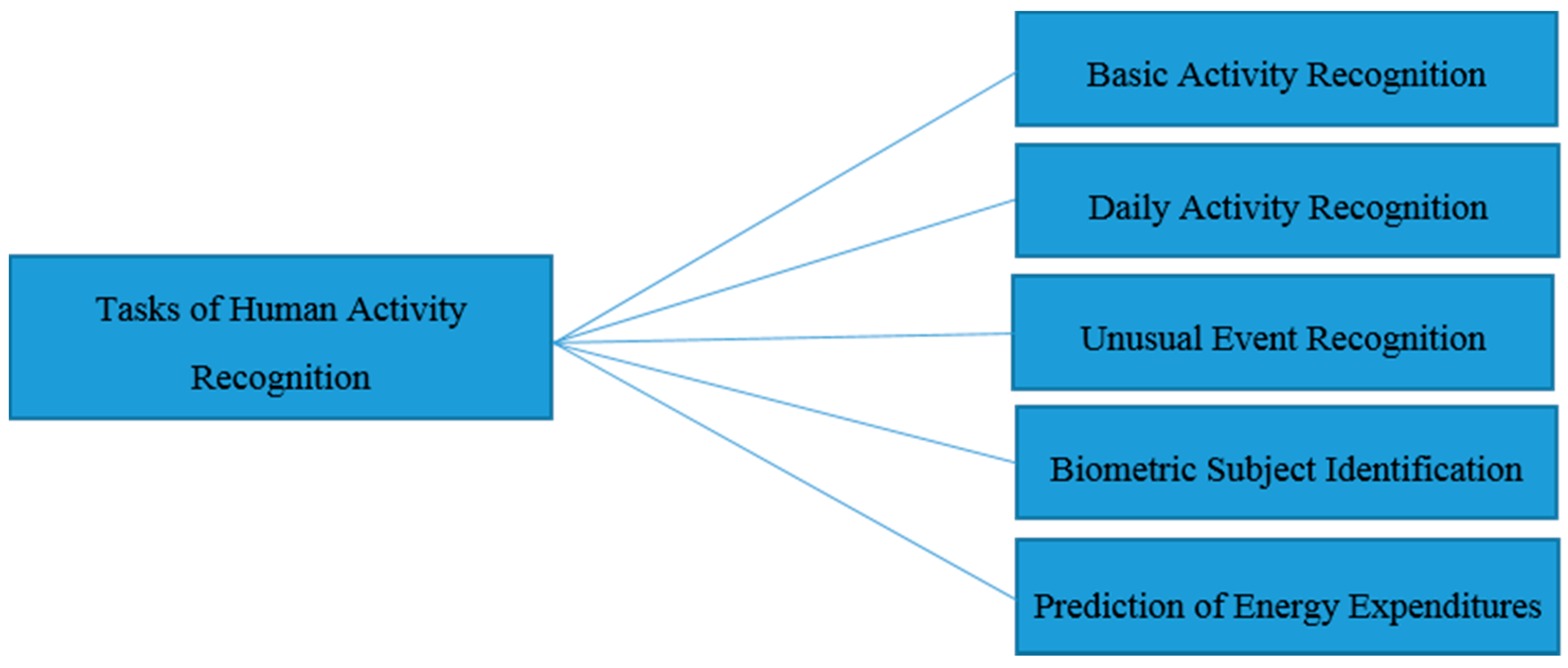
2.2. Tasks of HAR
- Sudden events can be defined as an abrupt, unintentional and unexpected change in the human body position that happens during a short period of observation, has not been observed before (i.e., was not present in the training dataset) and is unpredictable [33]. In the case of a home care assistance system, a sudden event refers specifically to a sudden fall by a patient or elderly person that requires immediate response. Detection and tracking of the position and movement of human body and parts thereof are useful features for early indication of a sudden fall event.
- Abnormal events are actions that are performed at an unusual location and at an unusual time [34]. This type of events can be characterized as temporal or spatial outliers, which deviate from normal events as represented in the training dataset or learned motion patterns and require a longer observation for identifying it.
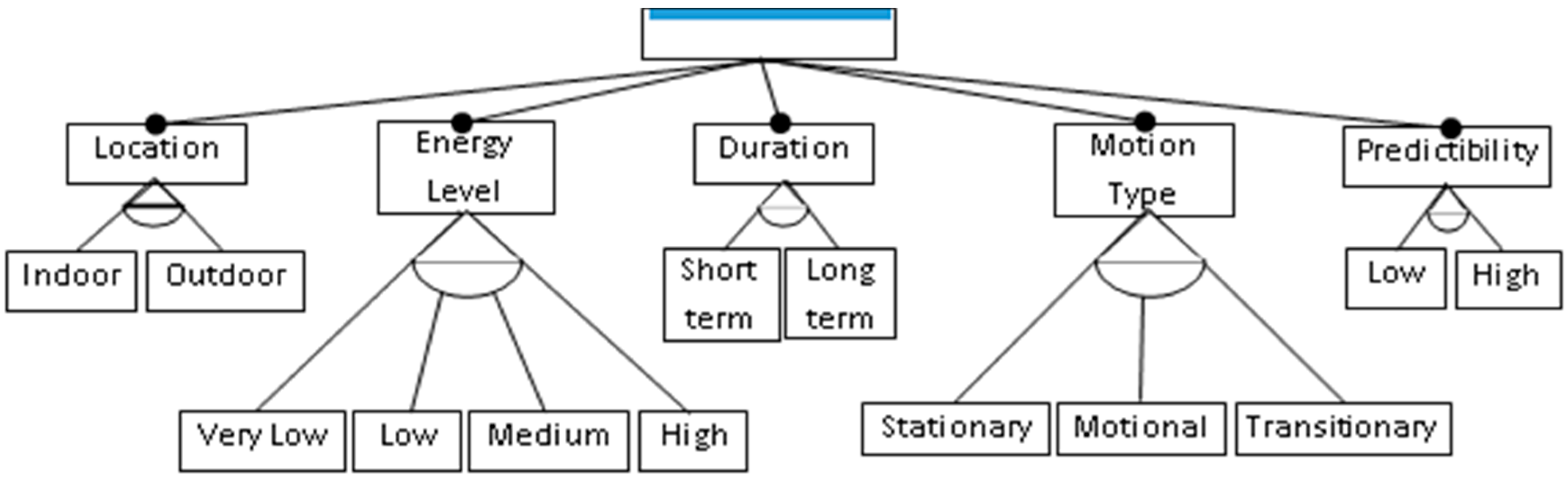
2.3. Taxonomy of Human Activities
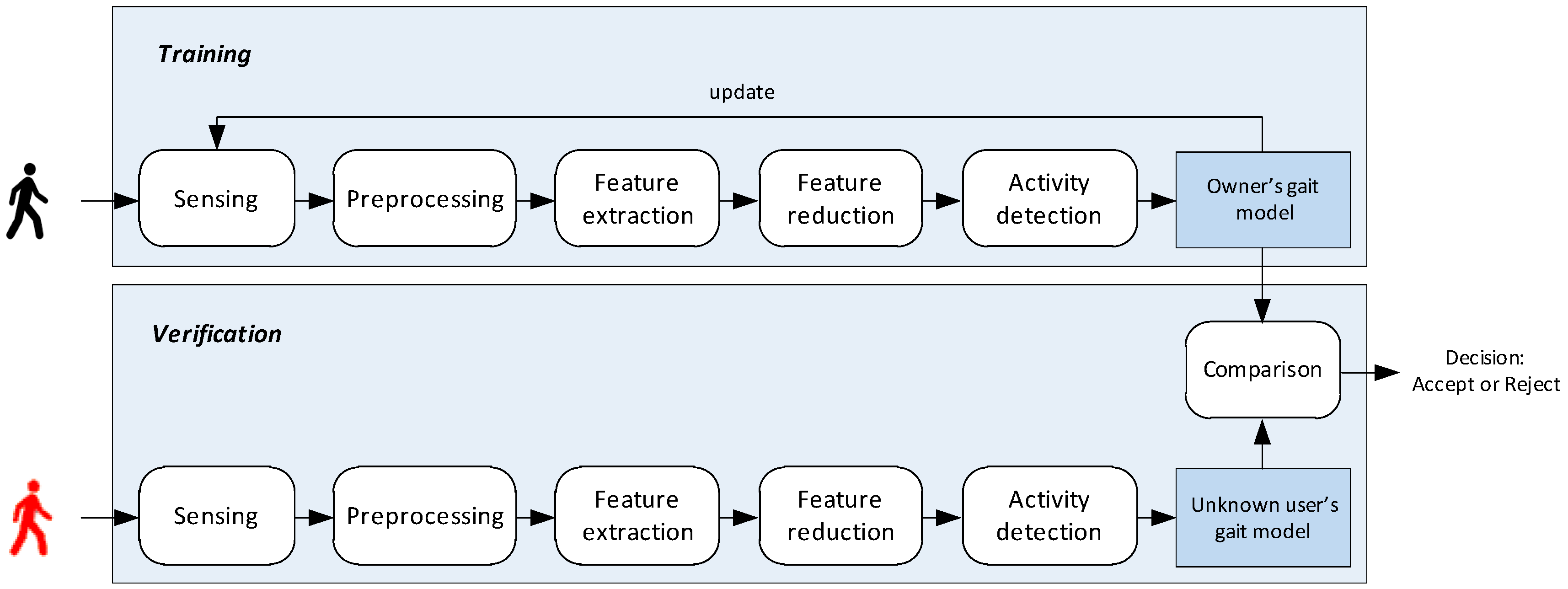
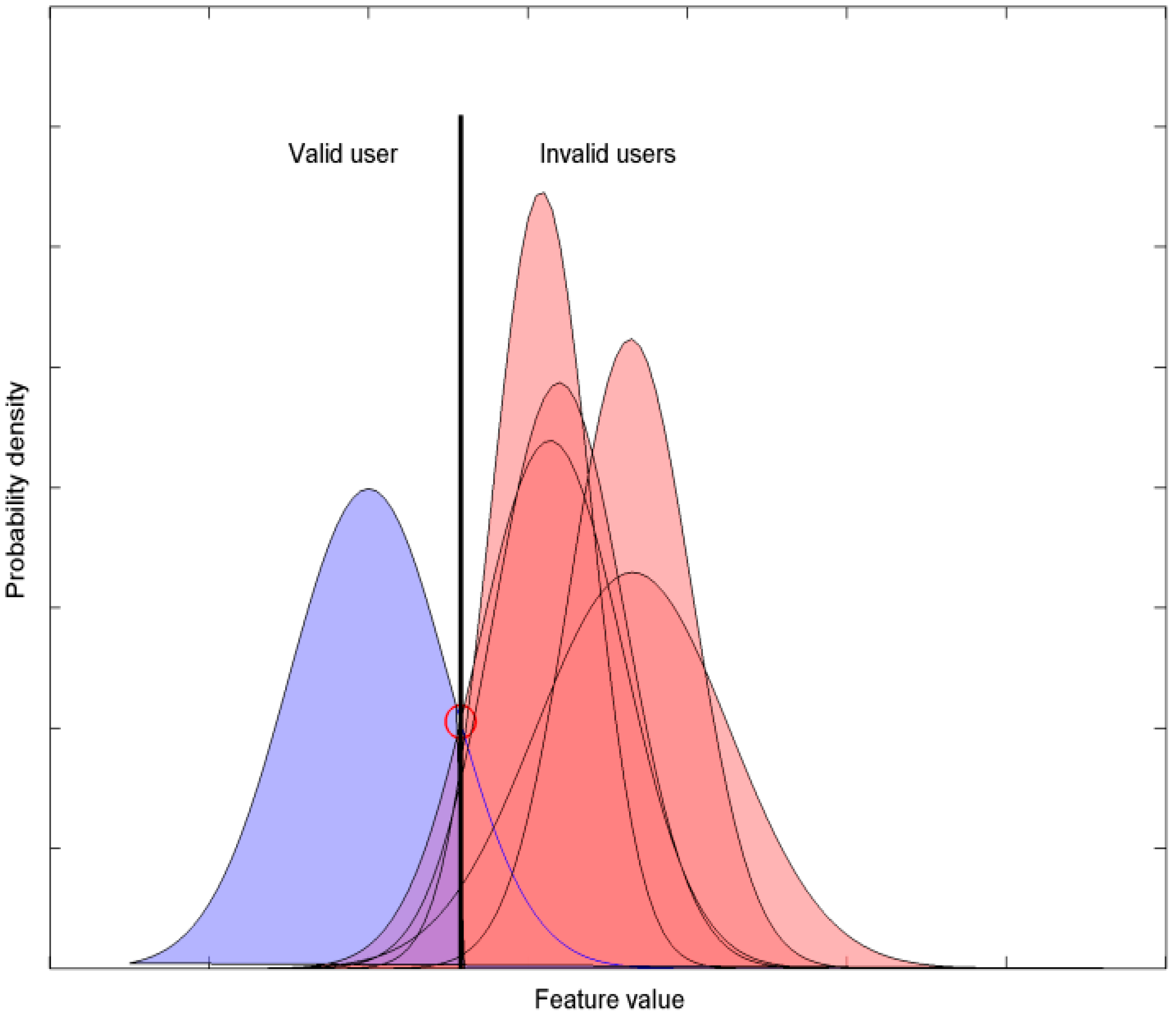
2.4. General Scheme of Gait-Based User Identity Verification
2.5. Description of the Method
3. Results
3.1. Dataset
3.2. Features
3.3. Evaluation Metrics
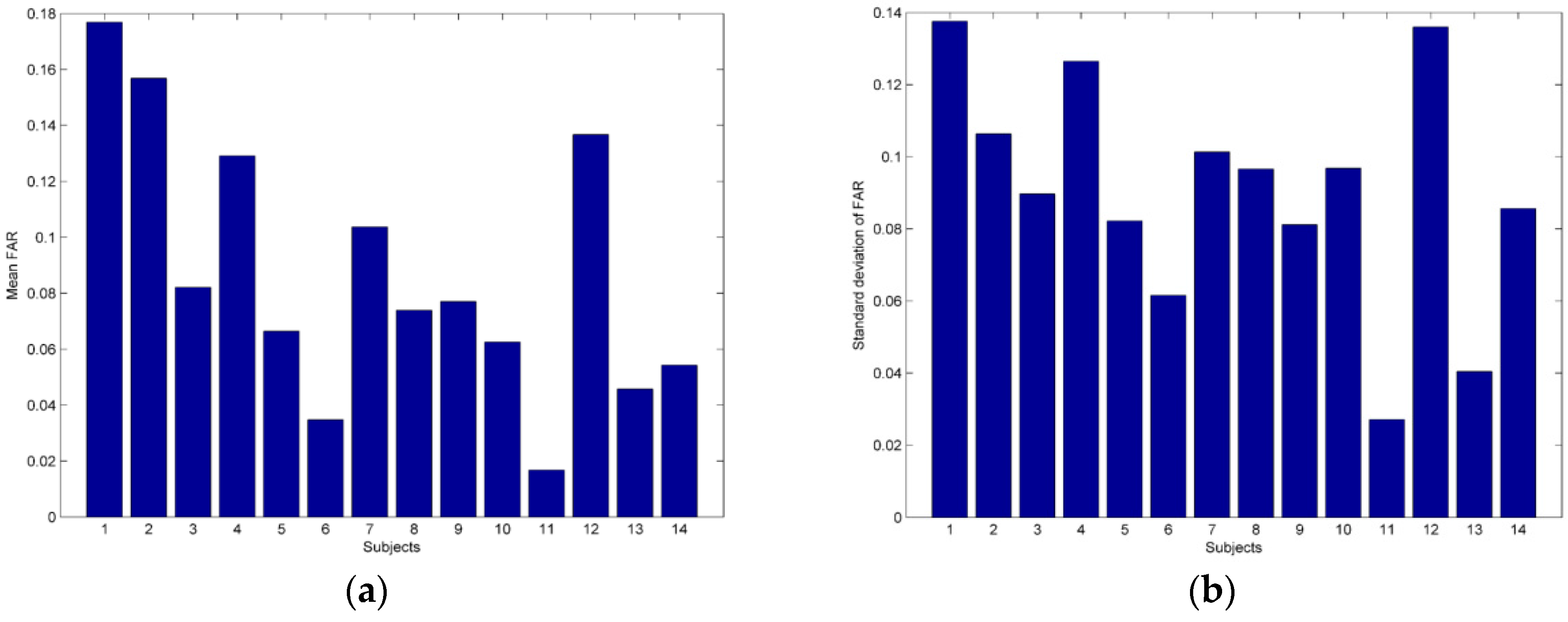
- False Accept Rate (FAR) is the probability (or a portion of recognition attempts) that the identity verification system incorrectly identifies the hijacker (impostor) as the genuine user. For a user, the FAR is a measure of system security.
- False Reject Rate (FRR) is the probability (or a portion of recognition attempts) that the identity verification system incorrectly rejects the genuine user. For a user, the FRR measures the user inconvenience level.
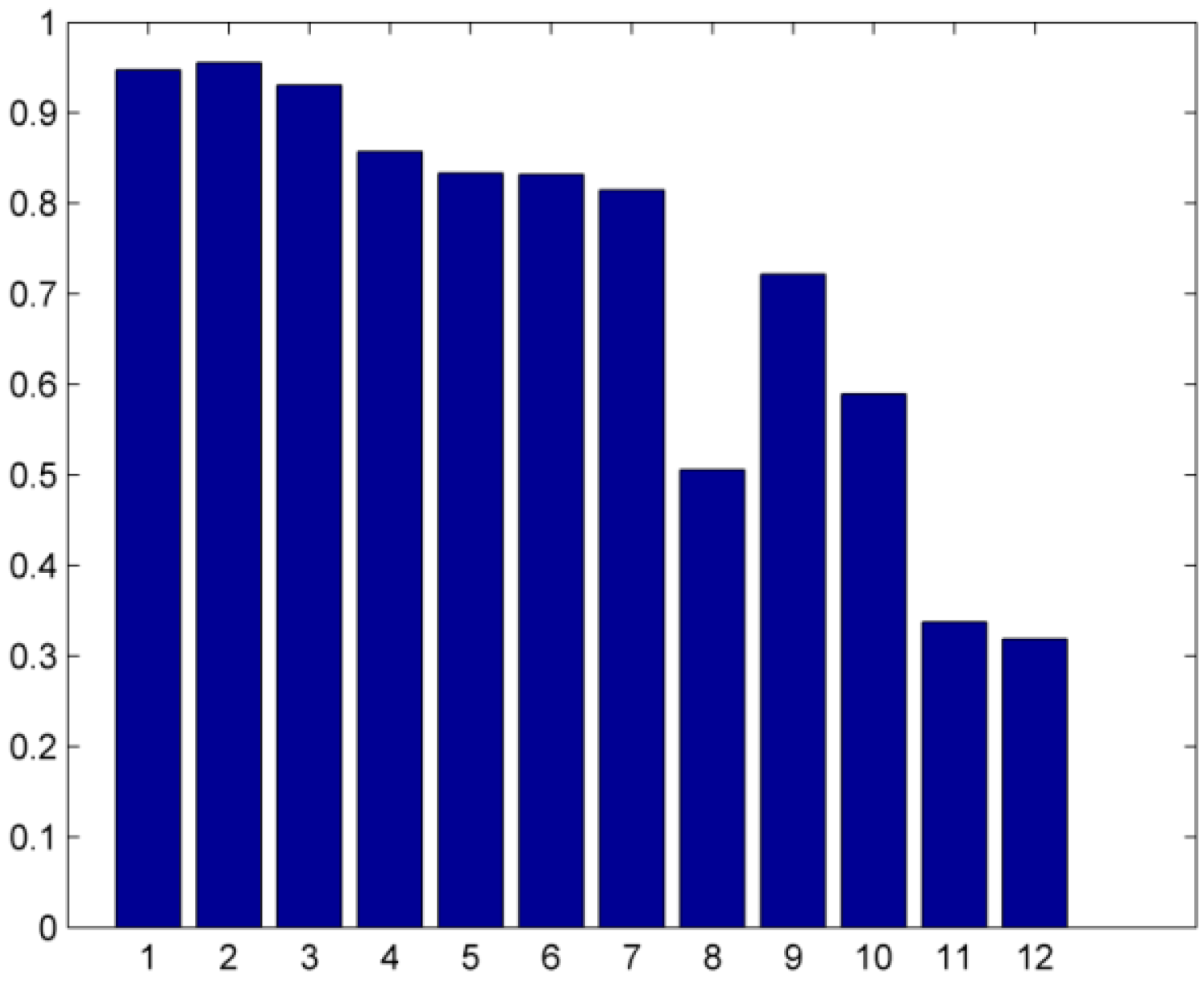
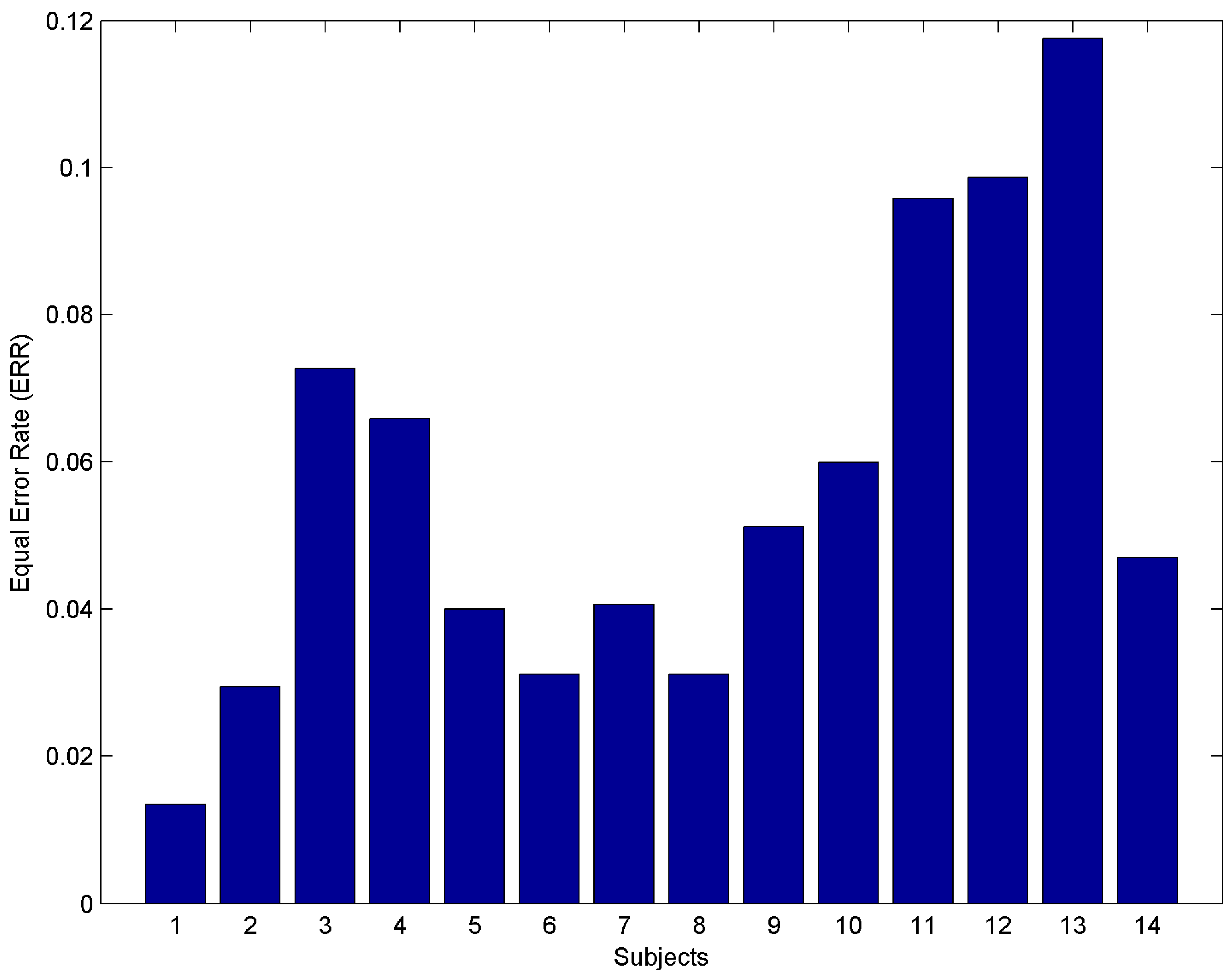
- Equal Error Rate (EER) is the rate at which both FAR and FRR are equal. The lower the value of ERR is, the higher is the accuracy of the biometric system.
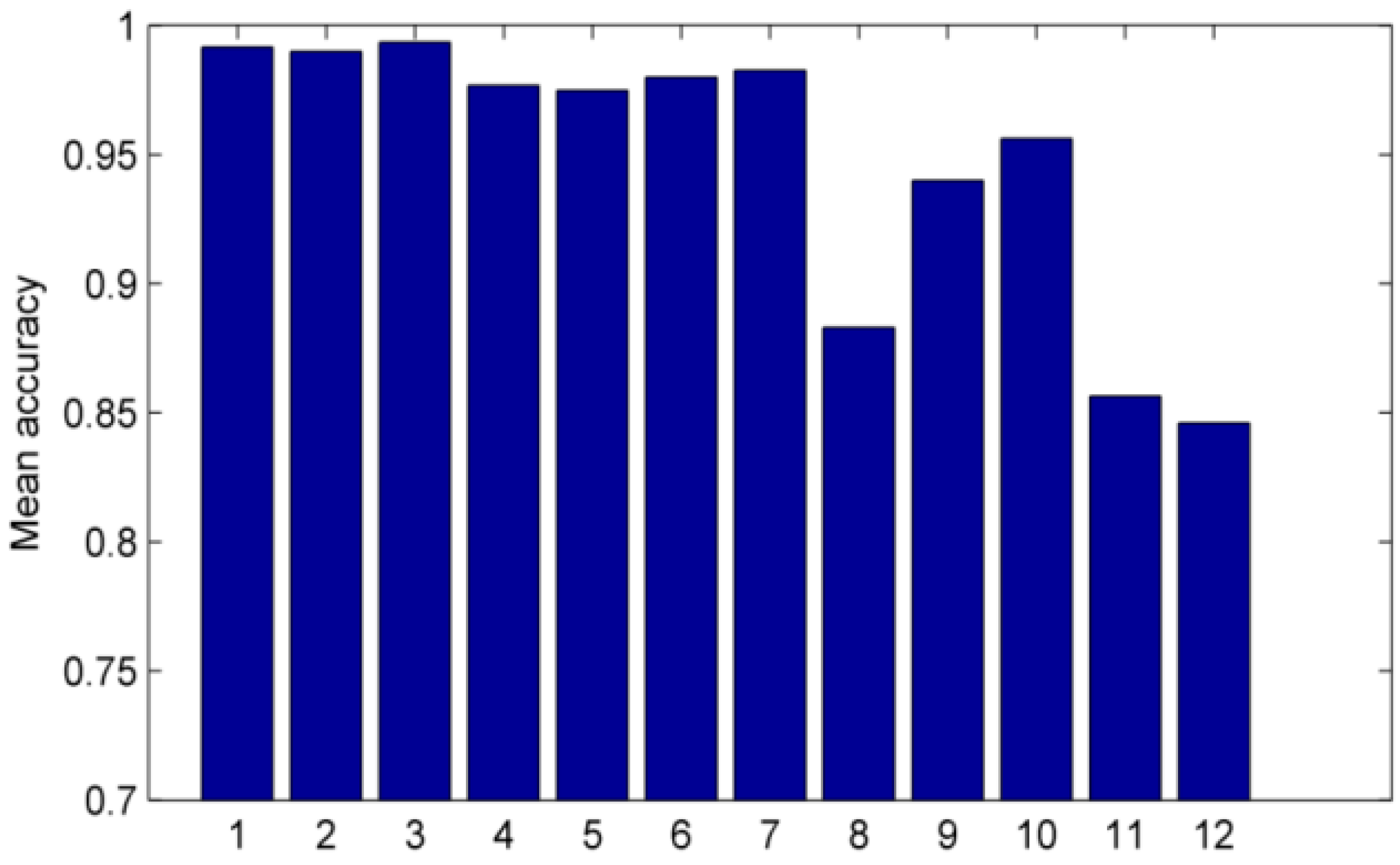
- Accuracy (or a true positive rate, TPR) is a proportion of all recognition attempts where subjects were identified correctly.
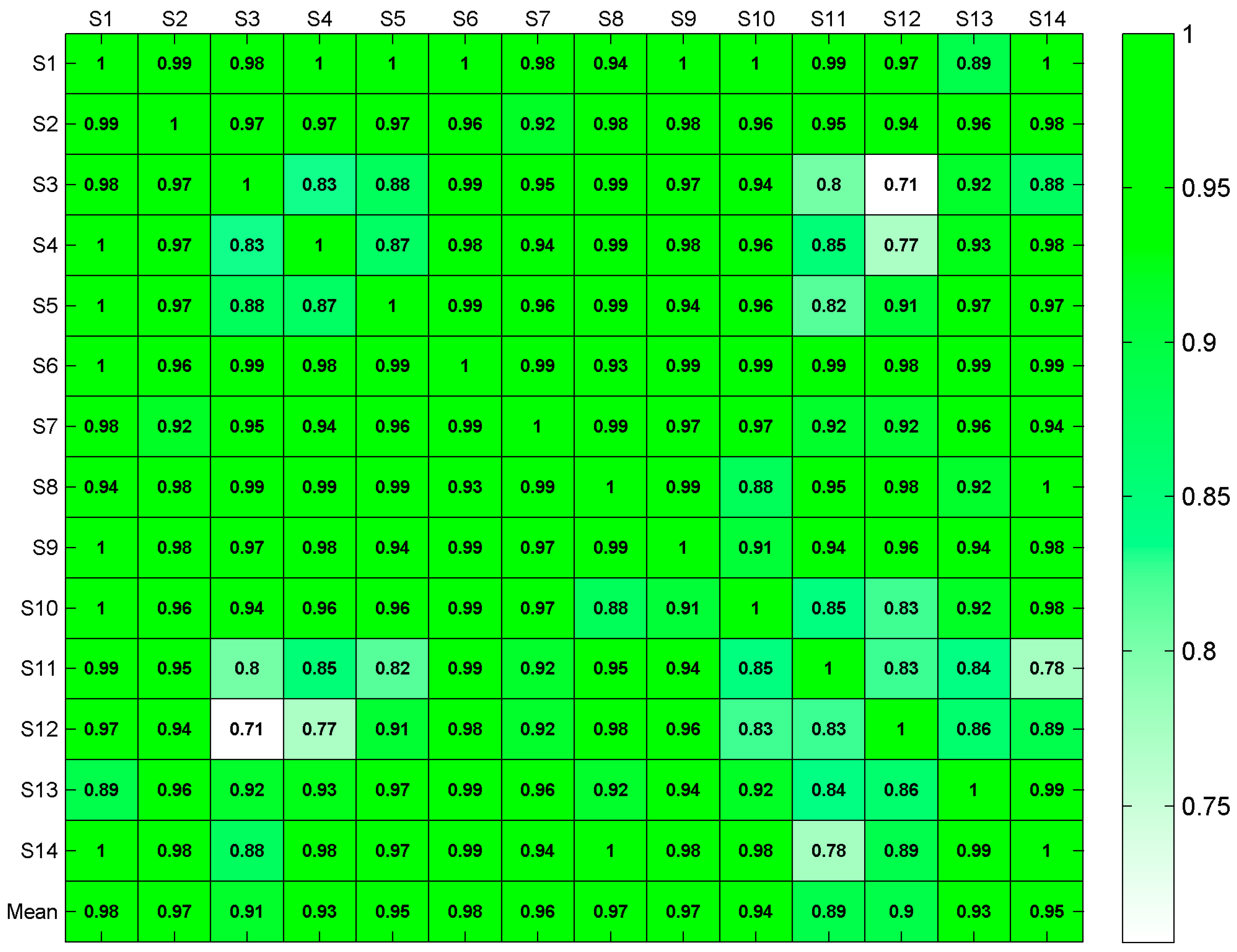
3.4. Results
4. Evaluation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Phone Theft in America. Available online: https://transition.fcc.gov/cgb/events/Lookout-phone-theft-in-america.pdf/ (accessed on 17 June 2016).
- Clarke, N.L.; Furnell, S.M. Authentication of users on mobile telephones—A survey of attitudes and practices. Comput. Secur. 2005, 24, 519–527. [Google Scholar] [CrossRef]
- Breitinger, F.; Nickel, C. User survey on phone security and usage. In Proceedings of the Special Interest Group on Biometrics and Electronic Signatures, Darmstadt, Germany, 9–10 September 2010; pp. 139–144.
- Wayman, J.; Jain, A.; Maltoni, D.; Maio, D. An introduction to biometric authentication systems. In Biometric Systems; Springer: London, UK, 2005; pp. 1–20. [Google Scholar]
- Sprager, S.; Juric, M.B. Inertial sensor-based gait recognition: A review. Sensors 2015, 15, 22089–22127. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K.; Flynn, P.J.; Ross, A.A. (Eds.) Handbook of Biometrics; Springer: Berlin/Heidelberg, Germany, 2008.
- Kwapisz, J.R.; Weiss, G.M.; Moore, S.A. Cell phone-based biometric identification. In Proceedings of the Fourth IEEE International Conference on Biometrics: Theory Applications and Systems (BTAS), Washington, DC, USA, 27–29 September 2010; pp. 1–7.
- Nickel, C.; Zhou, X.; Busch, C. Template Protection for Biometric Gait Data. In Proceedings of the Special Interest Group on Biometrics and Electronic Signatures, Darmstadt, Germany, 9–10 September 2010; pp. 77–83.
- Wang, L.; Tan, T.; Hu, W.; Ning, H. Automatic gait recognition based on statistical shape analysis. IEEE Trans. Image Process. 2003, 12, 1120–1131. [Google Scholar] [CrossRef] [PubMed]
- Ailisto, H.; Lindholm, M.; Mantyjarvi, J.; Vildjounaite, E.; Makela, S.M. Identifying people from gait pattern with accelerometers. In Proceedings of the Biometric Technology for Human Identification II, Orlando, FL, USA, 28 March 2005; pp. 7–14.
- Thang, H.M.; Viet, V.Q.; Thuc, N.D.; Choi, D. Gait identification using accelerometer on mobile phone. In Proceedings of the International Conference on Control, Automation and Information Sciences (ICCAIS), Ho Chi Minh, Vietnam, 26–29 November 2012; pp. 344–348.
- Liu, R.; Zhou, J.Z.; Liu, M.; Hou, X.F. A wearable acceleration sensor system for gait recognition. In Proceedings of the 2nd IEEE Conference on Industrial Electronics and Applications (ICIEA), Harbin, China, 23–25 May 2007; pp. 2654–2659.
- Pan, G.; Zhang, Y.; Wu, Z. Accelerometer-based gait recognition via voting by signature points. Electron. Lett. 2009, 45, 1116–1118. [Google Scholar] [CrossRef]
- Sprager, S. A Cumulant-based method for gait identification using accelerometer data with principal component analysis and support vector machine. In Proceedings of the 2nd WSEAS International Conference on Sensors, Signals, Visualization, Imaging, Simulation and Materials, Baltimore, MD, USA, 7–9 November 2009; pp. 94–99.
- Bachlin, M.; Schumm, J.; Roggen, D.; Toster, G. Quantifying gait similarity: User authentication and real-world challenge. In Advances in Biometrics; Tistarelli, M., Nixon, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5558, pp. 1040–1049. [Google Scholar]
- Trivino, G.; Alvarez-Alvarez, A.; Bailador, G. Application of the computational theory of perceptions to human gait pattern recognition. Pattern Recogn. 2010, 43, 2572–2581. [Google Scholar] [CrossRef]
- Frank, J.; Mannor, S.; Precup, D. Activity and gait recognition with time-delay embeddings. In Proceedings of the 24th AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; pp. 1581–1586.
- Nickel, C.; Brandt, H.; Busch, C. Classification of Acceleration Data for Biometric Gait Recognition on Mobile Devices. In Proceedings of the Special Interest Group on Biometrics and Electronic Signatures, Darmstadt, Germany, 8–9 September 2011; Volume 191, pp. 57–66.
- Kobayashi, T.; Hasida, K.; Otsu, N. Rotation invariant feature extraction from 3-D acceleration signals. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 3684–3687.
- Juefei-Xu, F.; Bhagavatula, C.; Jaech, A.; Prasad, U.; Savvides, M. Gait-id on the move: Pace independent human identification using cell phone accelerometer dynamics. In Proceedings of the IEEE Fifth International Conference on Biometrics: Theory, Applications and Systems (BTAS), Arlington, VA, USA, 23–27 September 2012; pp. 8–15.
- Hoang, T.; Nguyen, T.D.; Luong, C.; Do, S.; Choi, D. Adaptive Cross-Device Gait Recognition Using a Mobile Accelerometer. J. Inf. Proc. Syst. 2013, 9, 333. [Google Scholar] [CrossRef]
- Derawi, M.; Bours, P. Gait and activity recognition using commercial phones. Comput. Secur. 2013, 39, 137–144. [Google Scholar] [CrossRef]
- Wolff, M. Behavioral biometric identification on mobile devices. In Foundations of Augmented Cognition; Springer: Berlin/Heidelberg, Germany, 2013; pp. 783–791. [Google Scholar]
- Lu, H.; Huang, J.; Saha, T.; Nachman, L. Unobtrusive gait verification for mobile phones. In Proceedings of the 2014 ACM International Symposium on Wearable Computers, Seattle, WA, USA, 13–17 September 2014; pp. 91–98.
- Lin, B.-S.; Liu, Y.-T.; Yu, C.; Jan, G.E.; Hsiao, B.-T. Gait Recognition and Walking Exercise Intensity Estimation. Int. J. Environ. Res. Public Health 2014, 11, 3822–3844. [Google Scholar] [CrossRef] [PubMed]
- Johnston, A.H.; Weiss, G.M. Smartwatch-based biometric gait recognition. In Proceedings of the IEEE 7th International Conference on Biometrics Theory, Applications and Systems, Arlington, VA, USA, 8–11 September 2015; pp. 1–6.
- Attal, F.; Mohammed, S.; Dedabrishvili, M.; Chamroukhi, F.; Oukhellou, L.; Amirat, Y. Physical human activity recognition using wearable sensors. Sensors 2015, 15, 31314–31338. [Google Scholar] [CrossRef] [PubMed]
- Abidine, M.B.; Fergani, B. News Schemes for Activity Recognition Systems Using PCA-WSVM, ICA-WSVM, and LDA-WSVM. Information 2015, 6, 505–521. [Google Scholar] [CrossRef]
- Pei, L.; Guinness, R.; Chen, R.; Liu, J.; Kuusniemi, H.; Chen, Y.; Chen, L.; Kaistinen, J. Human behavior cognition using smartphone sensors. Sensors 2013, 13, 1402–1424. [Google Scholar] [CrossRef] [PubMed]
- Huynh, D.T.G. Human Activity Recognition with Wearable Sensors. Ph.D. Thesis, Technische University of Darmstadt, Darmstadt, Germany, August 2008. [Google Scholar]
- Bobick, A. Movement, activity, and action: The role of knowledge in the perception of motion. Philos. Trans. R. Soc. Lond. B 1997, 352, 1257–1265. [Google Scholar] [CrossRef] [PubMed]
- Govindaraju, V. A Generative Framework to Investigate the Underlying Patterns in Human Activities. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Barcelona, Spain, 6–13 November 2011; pp. 1472–1479.
- Suriani, N.S.; Hussain, A.; Zulkifley, M.A. Sudden event recognition: A survey. Sensors 2013, 13, 9966–9998. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K.; Ross, A.; Prabhakar, S. An introduction to biometric recognition. IEEE Trans. Circuits Syst. Video Technol. 2004, 14, 4–20. [Google Scholar] [CrossRef]
- Yampolskiy, R.V.; Govindaraju, V. Behavioural biometrics: A survey and classification. Int. J. Biom. 2008, 1, 81–113. [Google Scholar] [CrossRef]
- Drosou, A.; Ioannidis, D.; Moustakas, K.; Tzovaras, D. Spatiotemporal analysis of human activities for biometric authentication. Comput. Vis. Image Underst. 2012, 116, 411–421. [Google Scholar] [CrossRef]
- Lustrek, M.; Cvetkovic, B.; Kozina, S. Energy expenditure estimation with wearable accelerometers. In Proceedings of the 2012 IEEE International Symposium on Circuits and Systems ISCAS, Seoul, Korea, 20–23 May 2012; pp. 5–8.
- Ainsworth, B.E.; Haskell, W.L.; Herrmann, S.D.; Meckes, N.; Bassett, D.R., Jr.; Tudor-Locke, C.; Greer, J.L.; Vezina, J.; Whitt-Glover, M.C.; Leon, A.S. Compendium of physical activities: A second update of codes and MET values. Med. Sci. Sports Exerc. 2011, 43, 1575–1581. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Sheng, W. Motion- and location-based online human daily activity recognition. Pervasive Mob. Comput. 2011, 7, 256–269. [Google Scholar] [CrossRef]
- Incel, O.D.; Kose, M.; Ersoy, C. A review and taxonomy of activity recognition on mobile phones. BioNanoScience 2013, 3, 145–171. [Google Scholar] [CrossRef]
- Lara, O.D.; Labrador, M.A. A survey on human activity recognition using wearable sensors. IEEE Commun. Surv. Tutor. 2013, 15, 1192–1209. [Google Scholar] [CrossRef]
- Fleury, A.; Noury, N.; Vacher, M. Improving supervised classification of activities of daily living using prior knowledge. Int. J. E-Health Med. Commun. 2011, 2, 17–34. [Google Scholar] [CrossRef]
- Capela, N.A.; Lemaire, E.D.; Baddour, N. Feature selection for wearable smartphone-based human activity recognition with able bodied, elderly, and stroke patients. PLoS ONE 2015, 10, e0124414. [Google Scholar] [CrossRef] [PubMed]
- Atallah, L.; Lo, B.; King, R.; Yang, G.-Z. Sensor positioning for activity recognition using wearable accelerometers. IEEE Trans. Biomed. Circ. Syst. 2011, 5, 320–329. [Google Scholar] [CrossRef] [PubMed]
- Könönen, V.; Mäntyjärvi, J.; Similä, H.; Pärkkä, J.; Ermes, M. Automatic feature selection for context recognition in mobile devices. Pervasive Mob. Comput. 2010, 6, 181–197. [Google Scholar]
- Choujaa, D.; Dulay, N. Tracme: Temporal activity recognition using mobile phone data. In Proceedings of the IEEE/IFIP International Conference on Embedded and Ubiquitous Computing EUC’08, Shanghai, China, 17–20 December 2008; pp. 119–126.
- Kang, K.C. FODA: Twenty years of perspective on feature modeling. In Proceedings of the 4th International Workshop on Variability Modelling of Software-Intensive Systems, Linz, Austria, 27–29 January 2010; pp. 1–9.
- Damaševičius, R.; Štuikys, V.; Toldinas, J. Domain ontology-based generative component design using feature diagrams and meta-programming technique. In Proceedings of the 2nd European Conference on Software Architecture ECSA, Paphos, Cyprus, 29 September–1 October 2008; pp. 338–341.
- Achlioptas, D. Database-friendly random projections. In Proceedings of the ACM Symposium on the Principles of Database Systems, Santa Barbara, CA, USA, 31 May–3 June 2001; pp. 274–281.
- Johnson, W.B.; Lindenstrauss, J. Extensions of Lipshitz mapping into Hilbert space. Contemp. Math. 1984, 26, 189–206. [Google Scholar]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065. [Google Scholar] [CrossRef]
- Zhang, M.; Sawchuk, A.A. USC-HAD: A daily activity dataset for ubiquitous activity recognition using wearable sensors. In Proceedings of the 2012 ACM Conference on Ubiquitous Computing, New York, NY, USA, 1–4 December 2012; pp. 1036–1043.
- Mathie, M.; Celler, B.G.; Lovell, N.H.; Coster, A. Classification of basic daily movements using a triaxial accelerometer. Med. Biol. Eng. Comput. 2004, 42, 679–687. [Google Scholar] [CrossRef] [PubMed]
- Damaševičius, R.; Vasiljevas, M.; Šalkevičius, J.; Woźniak, M. Human activity recognition in AAL environments using random projections. Comput. Math. Methods Med. 2016, 2016. [Google Scholar] [CrossRef] [PubMed]



| Ref. | Features | Methods | Subjects | Results |
|---|---|---|---|---|
| Wang et al. [9] | Domain specific (e.g., relative time in cycle or slope of straight line between two endpoints) | Maximum-based cycle extraction, Dynamic Time Warping (DTW) distance | 24 | 5% (EER) |
| Ailisto et al. [10] | Averaged x (forward), and z (vertical) acceleration signals | Template matching, cross-correlation | 36 | 6.4% (EER) |
| Thang et al. [11] | Time and frequency domain features | Gait templates, Dynamic Time Warping (DTW), Support Vector Machine (SVM) | 11 | DTW: 79.1%; SVM: 92.7% (accuracy) |
| Rong et al. [12] | Acceleration | Zerocrossing-based cycle extraction, DTW | 21 | 5.6% (EER) |
| Pan et al. [13] | Extrema in acceleration data space | Difference-of-Gaussian filtering, Nearest Neighbors | 30 | 96.7% (accuracy) |
| Sprager [14] | Order 1–4 cumulants of acceleration data | Support Vector Machine (SVM) | 6 | 92.9% (accuracy) |
| Bachlin et al. [15] | FFT coefficients | FFT, one-way Analysis of Variance (ANOVA) | 5 | 2.8%–21.3% (EER) |
| Trivino et al. [16] | Vertical acceleration, lateral acceleration, and acceleration in the progress direction. | Fuzzy Finite State Machine (FFSM), linguistic model | 11 | 3% (EER) |
| Frank et al. [17] | acceleration data | time-delay embedding models, k Nearest Neighbors | 25 | Perfect classification |
| Nickel et al. [18] | Mel- and Bark-frequency cepstral coefficients (MFCC, BFCC) | SVM classifier | 48 | 5.9% (FMR); 6.3% (FNMR) |
| Kwapisz [7] | Average, average acceleration value, standard deviation, average absolute difference, average resultant acceleration, time between peaks, binned distribution | J48 and Neural Net classifiers | 36 | 82.1%–92.9% (positive authentication rate) |
| Kobayashi et al. [19] | Cross-correlations of Fourier transform coefficients | Multi-class classification by nearest means in Fisher discriminant space and majority voting | 58 | 45%–50% (accuracy) |
| Juefei-Xu et al. [20] | Accelerometer and gyroscope data | SVM, a time frequency spectrogram model and a cyclo-stationary model | 36 | 96.8%–99.4% (accuracy) |
| Hoang et al. [21] | Magnitude of the acceleration forces acting on three directions (x, y and z) | Gait template matching | 38 | 3.5% (EER) |
| Derawi and Bours [22] | Magnitude of the acceleration | Weighted moving average (WMA) filter, cycle detection, Manhattan distance metric, LibSVM | 10 | 99.6%—same subject, 87.6%—cross-subject (accuracy) |
| Wolff [23] | Variance in acceleration and orientation across the three dimensions (x, y, and z) | Gaussian distribution model | 83% (accuracy) | |
| Lu et al. [24] | Mean, variance, skewness, kurtosis, energy, mean crossing rate, energy ratio between vertical & horizontal components, spectrum peak, spectral entropy, ratio between low and high frequency band energy, compressed sub-band cepstral coefficients, compressed sub-band cepstral coefficients of autocorrelation | Gaussian Mixture Model—Universal Background Model (GMM-UBM) | 47 | 14% (EER) |
| Lin et al. [25] | Spectral energy diagrams of pitch, roll, acceleration X, acceleration Y, and acceleration Z | αβ filtering, Empirical Mode Decomposition (EMD), Fourier Transform, Linear Discriminant Analysis (LDA) | 10 | 90% (recognition rate) |
| Johnston et al. [26] | Average sensor value, standard deviation, average absolute difference between the 200 values and the mean of these values, time between peaks (each axis), binned distribution, average resultant acceleration | Multilayer Perceptron (MLP), Random Forest, Rotation Forest, and Naive Bayes | 59 | 2.6%–8.1% (EER) |
| Rank | Feature | Description |
|---|---|---|
| 1 | Moving variance of 100 samples of gyroscope data along z-axis | , here |
| 2 | Moving variance of 100 samples of acceleration intensity data | , here |
| 3 | First eigenvalue of moving covariance of difference between acceleration and gyroscope data | |
| 4 | Moving energy of gyroscope data along z-axis | , here |
| 5 | Moving energy of difference between acceleration and gyroscope data along z-axis | , here , |
| 6 | Moving variance of 100 samples of acceleration data along x-axis | , here |
| 7 | First eigenvalue of moving covariance between acceleration data | |
| 8 | First eigenvalue of moving covariance between gyroscope data | |
| 9 | Moving energy of orientation vector of acceleration data | , here |
| 10 | Movement intensity of gyroscope data |
| According to Jain et al. [4] | According to Wayman et al. [2] |
|---|---|
|
|
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Damaševičius, R.; Maskeliūnas, R.; Venčkauskas, A.; Woźniak, M. Smartphone User Identity Verification Using Gait Characteristics. Symmetry 2016, 8, 100. https://doi.org/10.3390/sym8100100
Damaševičius R, Maskeliūnas R, Venčkauskas A, Woźniak M. Smartphone User Identity Verification Using Gait Characteristics. Symmetry. 2016; 8(10):100. https://doi.org/10.3390/sym8100100
Chicago/Turabian StyleDamaševičius, Robertas, Rytis Maskeliūnas, Algimantas Venčkauskas, and Marcin Woźniak. 2016. "Smartphone User Identity Verification Using Gait Characteristics" Symmetry 8, no. 10: 100. https://doi.org/10.3390/sym8100100
APA StyleDamaševičius, R., Maskeliūnas, R., Venčkauskas, A., & Woźniak, M. (2016). Smartphone User Identity Verification Using Gait Characteristics. Symmetry, 8(10), 100. https://doi.org/10.3390/sym8100100






