1. Introduction
Let
G be a simple graph on the vertex set
. Denote by
the adjacency matrix of
G, and
the eigenvalues of
in the non-increasing order. The normalized Laplacian matrix of
G is defined as
, where
is the unit
matrix, and
is the diagonal matrix of vertex degrees. Here, if the degree
of vertex
is zero, we set
by convention. The eigenvalues of
are referred to as the normalized Laplacian eigenvalues of graph
G, denoted by
. The basic properties and applications of the eigenvalues and the normalized Laplacian eigenvalues can be found in the monographs [
1,
2].
The Estrada index of graph
G is defined in [
3] as
which was introduced earlier as a molecular structure-descriptor by the Cuban–Spanish scholar Ernesto Estrada [
4]. The Estrada index as a graph-spectrum-based invariant has found its widespread applicability in chemistry (such as the degree of folding of long-chain polymeric molecules [
4,
5], extended atomic branching [
6], and the Shannon entropy descriptor [
7,
8,
9]) and complex networks, see e.g., [
10,
11,
12,
13,
14]. Various quantitative estimates of the Estrada index have been reported, see e.g., [
15,
16,
17,
18,
19,
20]. In a similar manner, the normalized Laplacian Estrada index of graph
G, or the
-Estrada index, is introduced in [
21] as
Some tight bounds for
are established analogously therein.
It is natural to ask how good these bounds are for typical graphs, or random graphs. In [
22] it is shown that the Estrada index for Erdös-Rényi random graph model is much better than some universal bounds. Specifically, for almost all random graphs
with
being a constant, it holds that [
22]
where
is a quantity goes to 0 as
n goes to infinity.
In this paper, we consider a more general setting, the edge-independent random graph
, where two vertices
and
are adjacent independently with probability
. Here,
are not assumed to be equal. Graphs with heterogeneous node degrees and structure features, to which most real networks belong, can be constructed by tuning the connection probability
in the edge-independent model. For example, both scale-free networks and small-world networks can be readily modeled by
. In this regard, Erdös-Rényi random graph model having Poisson degree distributions is apparently too simple to delineate real-life complex networks connected through a disordered pattern of many different interactions [
23].
Using the recent spectra results developed in [
24], we obtain bounds for
and recover the relation Equation (
3) as a special case. In particular, we are able to identify that
. Noting that
goes to infinity as
n tends to infinity [
22], the estimate of
favorably informs us the precise behavior of
for a typical graph
G. We also study a close relative of
, where each vertex may have a self-loop. Such graphs are of great importance in theoretical chemistry since they represent conjugated molecules. In addition, we obtain tight bounds for
, which improve some existing bounds in [
21].
2. Estrada Index of Random Graphs
We begin with the definition of edge-independent random graphs. For , let be the edge-independent random graphs with vertex set V in which two vertices and are adjacent independently with probability . Since edges are undirected, we have . Hence, is symmetric, and its eigenvalues can be arranged in the non-increasing order as usual. We say that a graph property holds in almost surely (a.s.) if the probability that a random graph has the property converges to 1 as n approaches infinity.
Denote by Δ and δ, respectively, the maximum and minimum degrees of an edge-independent random graph . For two functions and taking real values, we say , or , if . Also, , if there exists a constant C such that for all large enough x, and , if both and hold. We have the following useful result regarding the spectrum of edge-independent random graphs.
Lemma 1. [
24]
Consider a random graph .
If ,
thenfor every .
Using the definition Equation (
1), we then obtain our first result.
Theorem 1. If ,
then Proof. It follows from Lemma 1 that
for each
. Taking exponentials and summarizing over all
k readily yield the conclusion.
Two remarks are in order. First, if all
are bounded away from zero,
i.e.,
for
, then
a.s. [
25]. Thus, it follows from Theorem 1 that
Second, if for and for , we reproduce the Erdös-Rényi random graph . As mentioned before, we are also interested in graphs with possible self-loops, which will be denoted by . Specifically, is obtained by setting all in .
Theorem 2. Consider a random graph with .
We have Proof. Recalling the definition of
, we have now
, where
is the matrix whose all entries equal 1. By the Chernoff bound, it holds that
a.s. Since the eigenvalues of
are
,
, Theorem 1 immediately implies that
which concludes the proof. ☐
Note that Theorem 2 easily yields the estimate of Equation (
3). Our proof here is more direct than that in [
22], where Weyl’s inequality was heavily relied on. Since
in the case of
, the following corollary is immediate.
Corollary 1. Consider a random graph with .
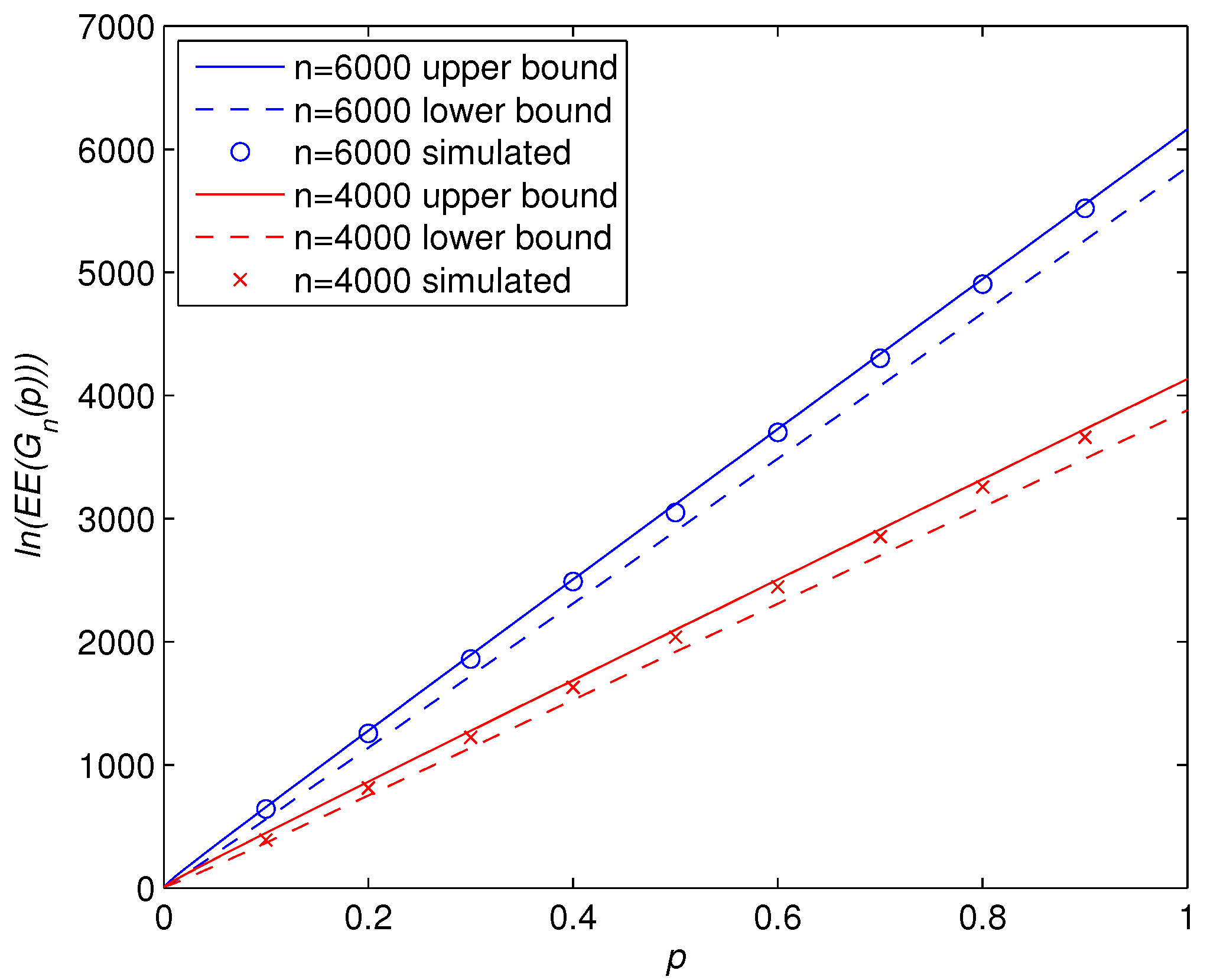
We have To illustrate the effectiveness of our theoretical bounds, we display in
Figure 1 the variations of
with the connection probability
p. We observe that the numerical value of
lies between the two bounds in line with our theoretical prediction in Theorem 2. Moreover, it turns out that the upper bound is prominently sharper than the lower bound. Therefore, it would be desirable to obtain less conservative lower bounds for random graph
.
Figure 1.
Logarithmic Estrada index versus connection probability p for two different graph sizes of 4000 and 6000. Theoretical bounds (solid and dashed curves) are from Theorem 2. Simulated results (circles and crosses) are obtained by means of an ensemble averaging of 100 randomly generated graphs yielding a statistically ample enough sampling.
Figure 1.
Logarithmic Estrada index versus connection probability p for two different graph sizes of 4000 and 6000. Theoretical bounds (solid and dashed curves) are from Theorem 2. Simulated results (circles and crosses) are obtained by means of an ensemble averaging of 100 randomly generated graphs yielding a statistically ample enough sampling.
3. 𝓛-Estrada Index of Random Graphs
In this section, we study the normalized Laplacian Estrada index of edge-independent random graphs.
Let be a diagonal matrix with its -element given by . Given a matrix M, denote its rank by . We have the following result.
Lemma 2. [
24]
Consider a random graph .
If and ,
thenfor every .
For brevity, define
. Recalling the definition Equation (
2), we then have the following result regarding
-Estrada index.
Theorem 3. If and ,
then Proof. Thanks to Lemma 2, we have
for each
. Taking exponentials and summarizing over all
k readily yield the conclusion.
Note that, if
for
, then
a.s. [
25]. Hence, if
, then Theorem 3 implies that
Concerning the homogeneous random graph model , we have the following result.
Theorem 4. Consider a random graph with .
We have Before presenting the proof, we give some remarks here. First, for the loopless random graph version
, we have
. Since
, Theorem 3 is no longer applicable in this case. Second, it is shown in ([
21],Thm 3.5) that, for a graph
G on the vertex set
V with
,
with the equality holds if and only if
G is a complete bipartite regular graph. We have
as
. Therefore, our upper bound is better than that in Equation (
4).
Proof of Theorem 4. First note that
a.s. by the Chernoff bound. Since
, we have
. Noting that
, the eigenvalues of
are
and
. From Theorem 3, we readily conclude that
as desired. ☐
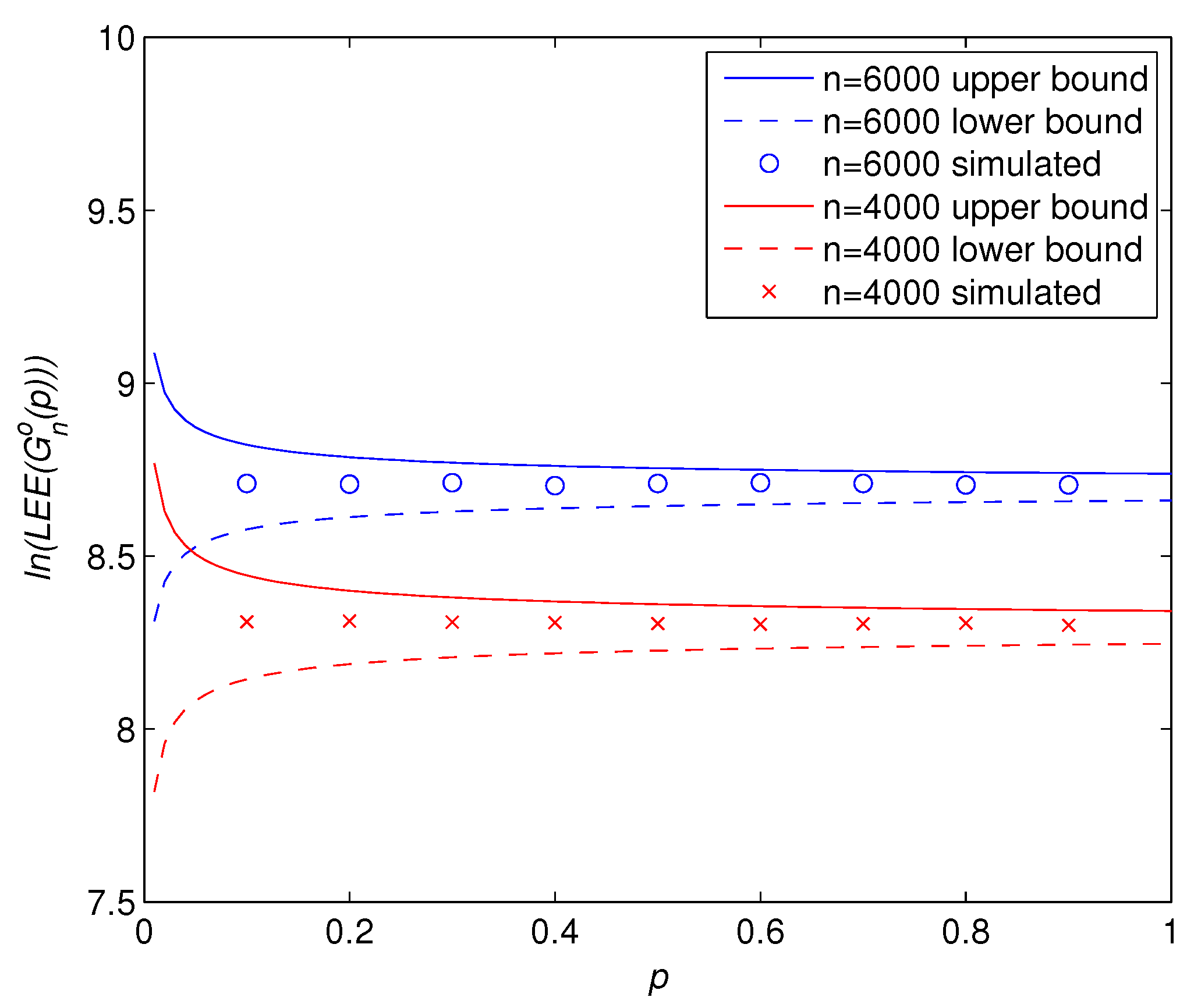
Figure 2 shows the variations of
with the connection probability
p. The numerical value of
lies between the two bounds in line with our theoretical prediction in Theorem 4. An interesting observation is that the normalized Laplacian Estrada index of a random graph
remain almost unchanged with respect to graph density,
i.e.,
p, in spite of different monotonicity of the two derived bounds.
Figure 2.
Logarithmic -Estrada index versus connection probability p for two different graph sizes of 4000 and 6000. Theoretical bounds (solid and dashed curves) are from Theorem 4. Simulated results (circles and crosses) are obtained by means of an ensemble averaging of 100 randomly generated graphs yielding a statistically ample enough sampling.
Figure 2.
Logarithmic -Estrada index versus connection probability p for two different graph sizes of 4000 and 6000. Theoretical bounds (solid and dashed curves) are from Theorem 4. Simulated results (circles and crosses) are obtained by means of an ensemble averaging of 100 randomly generated graphs yielding a statistically ample enough sampling.