Abstract
The paper presents the group theory of optimally-localized and symmetry-adapted Wannier functions in a crystal of any given space group G or magnetic group M. Provided that the calculated band structure of the considered material is given and that the symmetry of the Bloch functions at all of the points of symmetry in the Brillouin zone is known, the paper details whether or not the Bloch functions of particular energy bands can be unitarily transformed into optimally-localized Wannier functions symmetry-adapted to the space group G, to the magnetic group M or to a subgroup of G or M. In this context, the paper considers usual, as well as spin-dependent Wannier functions, the latter representing the most general definition of Wannier functions. The presented group theory is a review of the theory published by one of the authors (Ekkehard Krüger) in several former papers and is independent of any physical model of magnetism or superconductivity. However, it is suggested to interpret the special symmetry of the optimally-localized Wannier functions in the framework of a nonadiabatic extension of the Heisenberg model, the nonadiabatic Heisenberg model. On the basis of the symmetry of the Wannier functions, this model of strongly-correlated localized electrons makes clear predictions of whether or not the system can possess superconducting or magnetic eigenstates.1. Introduction
The picture of strongly-correlated localized or nearly-localized electrons is the basis of a successful theoretical description of both high-temperature superconductivity and magnetism (see, e.g., [1–3] and the citations given there). The appertaining localized electron states are often represented by atomic orbitals that define, for instance, partially filled s-, d- or p- bands.
Another option is to represent the localized electron states by optimally-localized and symmetry-adapted Wannier functions. In contrast to atomic functions, Wannier functions situated at adjacent atoms are orthogonal and form a complete set of basis functions within the considered narrow, partially filled band. Consequently, Wannier functions contain all of the physical information about this energy band. At first, however, the use of Wannier functions within the theory of superconductivity and magnetism appears to be hampered by the well-known fact that we need a closed complex of energy bands (Definition 1) for the construction of optimally-localized Wannier functions. Such closed complexes, however, do not exist in the band structures of the metals where all of the bands are connected to each other by band degeneracies.
In the literature, there have been proposed several procedures to tackle this problem; see, e.g., the review article [4]. The present paper, however, and all of the papers of the authors published previously (and cited below) solve this problem in another way, by constructing Wannier functions with the reduced symmetry of a magnetic group or by constructing spin-dependent Wannier functions. In both cases, interfering band degeneracies are sometimes removed in the band structure with the reduced symmetry. The physical power of this natural method of producing closed complexes of energy bands in suitable band structures is corroborated by two observations:
Materials possessing a magnetic structure with the magnetic group M also possess a closed, narrow and roughly half-filled complex of energy bands in their band structure whose Bloch functions can be unitarily transformed into optimally-localized Wannier functions that are symmetry-adapted to the magnetic group M. These energy bands form a “magnetic band”; see Definition 16.
Both normal and high-temperature superconductors (and only superconductors) possess a closed, narrow and roughly half-filled complex of energy bands in their band structure whose Bloch spinors can be unitarily transformed into optimally-localized spin-dependent Wannier functions that are symmetry-adapted to the (full) space group G of the material. These energy bands form a “superconducting band”; see Definition 22.
The first observation (i) was made at the band structures of Cr [5], Fe [6], La2CuO4 [7], YBa2Cu3O6 [8], undoped LaFeAsO [9] and BaFe2As2 [10]; the second observation (ii) at the band structures of numerous elemental superconductors [11] and of the (high-temperature) superconductors La2CuO4 [7], YBa2Cu3O7 [12], MgB2 [12] and doped LaFeAsO [13]. It is particularly important that partly filled superconducting bands cannot be found in those elemental metals (such as Li, Na, K, Rb, Cs, Ca, Cu, Ag and Au) that do not become superconducting [11]. An investigation into the band structures of the transition metals in terms of superconducting bands straightforwardly leads to the Matthias rule [14].
These two observations can be interpreted in a clear way within a nonadiabatic extension of the Heisenberg model, the nonadiabatic Heisenberg model [12,15]. This model of strongly-correlated localized electrons is determined by three new postulates and defines a nonadiabatic mechanism stabilizing the hopping motion in narrow bands. On the basis of the symmetry of the Wannier functions, the nonadiabatic model makes clear predictions of whether or not the related nonadiabatic Hamiltonian Hn can possess superconducting or magnetic eigenstates [5,10,11,16]. In this context, the nonadiabatic Heisenberg model no longer uses terms like s-, p- or d-bands, but only speaks of superconducting or magnetic bands.
In some materials, the nonadiabatic Heisenberg model predicts that a small distortion of the lattice or a doping is required for the stability of the superconducting or magnetic state. Thus, in undoped LaFeAsO [9] and in BaFe2As2 [10], the antiferromagnetic state must be stabilized by an experimentally well-established distortion [17,18], while in YBa2Cu3O6 [8], it is stable in the undistorted crystal. Superconductivity in LaFeAsO [9] requires the experimentally-confirmed doping [18–21]. Furthermore, the superconducting state in LiFeAs [22] should be accompanied by a small distortion of the lattice, which, to our knowledge, is experimentally not yet confirmed. Superconductivity in YBa2Cu3O7 [12], MgB2 [12], as well as in the transition elements [11] (such as in Nb [16]), on the other hand, does not require any distortion or doping.
In the case of (conventional and high-Tc [23]) superconductivity, the nonadiabatic Heisenberg model provides a new mechanism of Cooper pair formation, which may be described in terms of constraining forces [16] and spring-mounted Cooper pairs [24].
Any application of the nonadiabatic Heisenberg model starts with an examination of whether or not there exist closed band complexes with optimally-localized symmetry-adapted usual or spin-dependent Wannier functions in the band structure of the material under consideration. In the following (in Sections 2–7), we shall summarize and update the group theory of Wannier functions as published in former papers and give a detailed description of how to determine the symmetry of optimally-localized Wannier functions if they exist in the given band structure. In Sections 2–6, we shall consider usual (i.e., spin-independent) Wannier functions as defined in the first subsection of Section 2. In the following subsections of Section 2 and in Sections 3–5, the spatial symmetry of the Wannier functions will be specified. The central theorem to determine the spatial symmetry of optimally-localized symmetry-adapted Wannier functions will be Theorem 5. Then, in Section 6, we shall consider magnetic groups by adding the time-inversion symmetry. Finally, in Section 7, we shall define and specify spin-dependent Wannier functions.
Since we use the most general definition of Wannier functions, they are identical with the maximally-localized Wannier functions calculated from first principles [25] by minimizing their total spread [26] so long as the latter are symmetry-adapted, too. The methods complement each other, because by group theory, we cannot provide any procedure to calculate the Wannier functions. The present paper only examines the existence of optimally-localized symmetry-adapted Wannier functions.
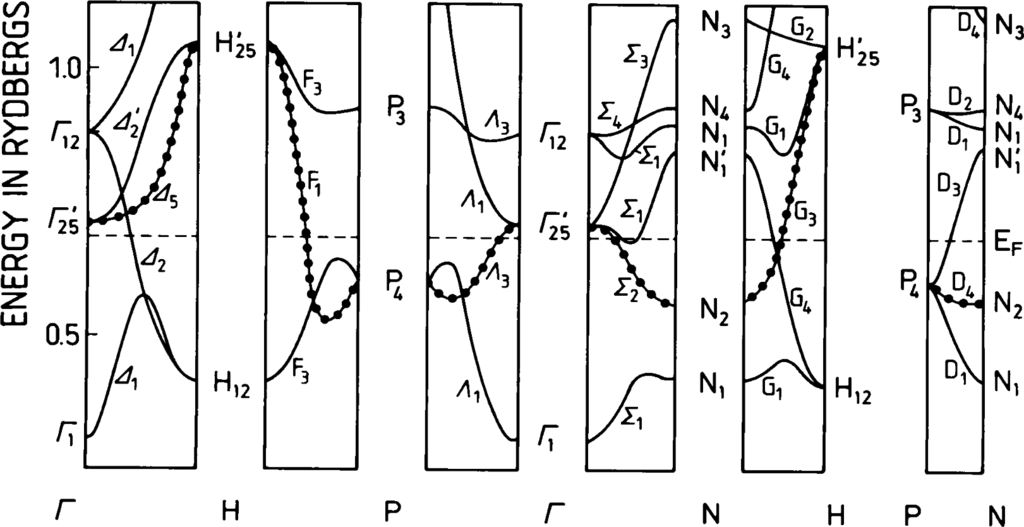
The closed complexes of energy bands used in this paper, however, differ from the optimal subspaces, as defined by Souza et al. [27]: for instance, the subspace method allows the construction of well-localized Wannier-like functions even for the conduction bands of copper. With our methods, on the other hand, we cannot construct optimally-localized symmetry-adapted Wannier functions close to the Fermi energy in copper, which are centered at the atomic positions. In other words, copper neither possesses a magnetic nor a superconducting band with the physical consequence that copper neither is magnetic nor superconducting. Moreover, our closed complexes of energy bands never comprise all of the partially filled bands near the Fermi level; see, e.g., the superconducting band of niobium depicted in Figure 1 or the numerous magnetic and superconducting bands presented in the papers cited above. The energy bands belonging to our closed complexes are determined by the symmetry of the Bloch functions. Nevertheless, we believe that the subspace method used by Souza et al. might be combined with the symmetry method used in this paper.
Though we shall also define the two terms “magnetic” and “superconducting” band (Definitions 16 and 22, respectively), which are related to the nonadiabatic Heisenberg model, the presented group theory is independent of any physical model of magnetism or superconductivity.
2. Usual (Spin-Independent) Wannier Functions
2.1. Definition
Consider a closed complex of μ energy bands in the band structure of a metal or a semiconductor.
Definition 1 (closed). A complex of energy bands is called closed if the bands are not connected by degeneracies to bands not belonging to the complex.
Definition 2 (closed band). In the following, a closed complex of μ energy bands is referred to as a single closed band consisting of μ branches.
The metals do not possess closed bands in their band structures. However, closed bands may arise after the activation of a perturbation, reducing the symmetry in such a way that interfering band degeneracies are removed. Such a reduction of the symmetry may be caused by a magnetic structure or by a (slight) distortion of the crystal.
Hence, we assume that the Hamiltonian of a single electron in the considered material consists of a part with the unperturbed space group G and a perturbation with the space group H,
In general, the considered closed energy band of μ branches was not closed before the perturbation was activated.
Assume the Bloch functions (labeled by the wave vector and the branch index q) as the solutions of the Schrödinger equation of to be completely calculated in the first domain of the Brillouin zone.
Definition 3 (first domain). Let h be the order of the point group H0 of H. Then, the Brillouin zone is divided by the planes of symmetry into h domains. An arbitrarily chosen domain we call the first domain. This first domain shall comprise the bounding planes, lines and points of symmetry, too.
As in [28], in the rest of the Brillouin zone, the Bloch functions shall be determined by the equation:
Definition 4 (symmetry operator). P (a) denotes the symmetry operator assigned to the space group operation consisting of a point group operation α and the associated translation, acting on a wave function according to:
The Bloch functions of the closed band under observation can be unitarily transformed into Wannier functions:
Definition 5 (optimally-localized). The Wannier functions are called optimally-localized if the coefficients may be chosen in such a way that the generalized Bloch functions move, for fixed, continuously through to whole space [28].
As was already shown in [29], the Bloch functions as the eigenfunctions of the Hamiltonian may be chosen in such a way that they vary continuously as functions of through the first domain and, in particular, approach continuously the boundaries of the first domain. From Equations (3) and (4), however, we cannot conclude that they also cross continuously the boundaries of the domains within the Brillouin zone or at the surface of the Brillouin zone. Fortunately, this problem is solvable by group-theoretical methods [28,30]. Theorem 5 shall define the condition for optimally-localized and symmetry-adapted (Definition (7)) Wannier functions.
2.2. Symmetry-Adapted Wannier Functions
In [28], we demanded that symmetry-adapted Wannier functions satisfy the equation:
Equation (10) defines the symmetry of Wannier functions in general terms; in particular, they may be centered at a variety of positions being different from the positions of the atoms. However, in the context of superconducting and magnetic bands, we may restrict ourselves to Wannier functions centered at the positions of the atoms.
Thus, we assume:
that the positions of the Wannier functions in Equation (6) are the positions of atoms,
that only atoms of the same sort are considered (although, of course, other atoms may exist) and
that there is one Wannier function at each atom.
Under these assumptions [15],
– the Wannier functions may be labeled by the positions of the atoms,
where– the matrix representatives D(α) of the representation D in Equation (10) have one non-vanishing element Dij(α) with:
in each row and each column and– Equation (10) may be written in the considerably simplified form:
whereand the subscripts i and j denote the number of the atoms at position and , respectively.
Definition 6 (number of the atom). The subscript i of the vector in Equation (13) defines the number of the atom at position.
Definition 7 (symmetry-adapted). We call the Wannier functions symmetry-adapted to H if they satisfy Equation (15).
Theorem 1. The third assumption (iii) shows immediately that the number μ of the branches of the band under observation equals the number of the considered atoms in the unit cell.
Equations (15) and (16) define the non-vanishing elements, and hence, we may write Equation (14) more precisely,
Definition 8 (the representation defining the Wannier functions). In what follows, the representation D of H0 with the matrix representatives
Definition 9 (unitary generalized permutation matrices). Since the matrices D(α) defining the Wannier functions have one non-vanishing element obeying Equation (17) in each row and each column, they are so-called unitary generalized permutation matrices.
3. Determination of the Representations D Defining the Wannier Functions
In the following Section 4, we shall give a simple condition (Theorem 5) for optimally-localized and symmetry-adapted Wannier functions yielding the representations of the Bloch functions at all of the points of symmetry in the Brillouin zone. However, in Theorem 5, the representations D defining the Wannier functions must be known. Hence, first of all, we have to determine in this section all of the possible representations that may define the Wannier functions. In this context, we assume first that all of the atoms are connected by symmetry. This restricting assumption shall not be abandoned until Section 3.4.
Definition 10 (connected by symmetry). Two atoms at positions and are connected by symmetry if there exists at least one element in the space group H satisfying the equation:
3.1. General Properties of the Representatives D(α) of D
First consider the diagonal elements:
Definition 11 (group of position). The group of the position is defined by:
Hence, the non-vanishing diagonal elements di(α) of the matrices D(α) form a one-dimensional representation di of the point group of . The Wannier functions transform according to:
In constructing the representation D defining the Wannier functions, we cannot arbitrarily choose the one-dimensional representations di of , because they must be chosen in such a way that the matrix representatives D(α) form a representation of the point group H0, i.e., they must obey the multiplication rule:
In what follows, we assume that all of the groups are normal subgroups of H. In fact, in all of the crystal structures that we examined in the past, was a normal subgroup, be it because it was a subgroup of Index 2 or be it because it was the intersection of two subgroups of Index 2. Both cases are sufficient for a normal subgroup. We believe that in all physically-relevant crystal structures, is a normal subgroup of H. If not, the present formalism must be extended for these structures.
When the groups are normal subgroups of H, each of the groups contains only complete classes of H,
Let be a space group operation of H moving ρi into ρj,
On the other hand, Equation (26) shows that c is an element of , too. When a runs through all of the elements of , then also c runs through all of the elements of . Consequently, all of the groups , as well as all of the related point groups contain the same elements.
Thus, we may omit the index i and define:
Definition 12 (group of position). The group Gp and the related point group G0p of the positions of the atoms are defined by:
3.2. Necessary condition for of the representatives D(α) of D
The one-dimensional representations di of G0p must be chosen in such a way that the matrices D(α) defining the Wannier functions form a representation D of the complete point group H0. A necessary condition is given by the evident Theorem 2.
Theorem 2. If the matrices D(α) cannot be completely reduced into the irreducible representations of H0, then they do not form a representation of the point group H0.
This theorem is necessary, but not sufficient: even if the matrices D(α) can be completely reduced into the irreducible representations of H0, then they need not form a representation of the point group H0 [31]. The complete decomposition of a reducible representation is described, e.g., in [31,32]; in particular, see Equation (1.3.18) of [32]. Theorem 2 leads to three important cases:
– Case (i): If all of the representations di are subduced from one-dimensional representations of H0, then all of the representations di are equal,
The representation d may be equal to any one-dimensional representation of G0p subduced from a one-dimensional representation of H0.– Case (ii): If all of the representations di are subduced from two-dimensional representations of H0, then one half of the representations di is equal to dA, and the other half is equal to dB,
where dA and dB are subduced from the same two-dimensional representation of H0. In special cases, the two representations dA and dB may be equal; see below.– Case (iii): “Mixed” representations D consisting of both representations di subduced from one-and two-dimensional representations of H0 do not exist.
These results, (i)–(iii), follow from the very fact that Equation (15) describes an interchange of the Wannier functions at different positions . Such an interchange, however, does not alter the symmetry of the Wannier functions.
3.3. Sufficient Condition for of the Representatives D(α) of D
For α ∈ G0p the matrices D(α) defining the Wannier functions are diagonal, while the remaining matrices D(α) (for α ∈ H0 − G0p) do not possess any diagonal element. Theorem 2 only gives information about the diagonal matrices D(α). Hence, this theorem indeed cannot be sufficient, because we do not know whether or not the remaining matrices obey the multiplication rule (25).
In this section, we assume that the matrices D(α) already satisfy Theorem 2 and examine the conditions under which they actually form a (generally reducible) representation of H0. In doing so, we consider separately the two cases, (i) and (ii), of the preceding Section 3.2.
3.3.1. Case (i) of Section 3.2
No further problems arises when Case (i) of Section 3.2 is realized. In this case, Theorem 2 is necessary and sufficient. To justify this assertion, we write down explicitly the non-diagonal elements of the matrices D(α).
Let δ be any one-dimensional representation of H0 subducing the representation d in Equation (30). If we put all of the non-vanishing elements of the matrices D(α) equal to the elements δ(α) of δ,
3.3.2. Case (ii) of Section 3.2
The situation is a little more complicated when Case (ii) of Section 3.2 is realized. Now, the representations dA and dB in Equation (31) may be distributed across the positions in such a way that the matrices D(α) form a representation of H0 or do not. Though we always find a special distribution of the dA and dB yielding matrices D(α) actually forming a representation of H0, we have to rule out those distributions not leading to a representation of H0, because in the following (in Equations (38), (66) and (111)), we need the matrices D(α) explicitly.
Let Δ be (with the matrix representatives Δ (α)) a two-dimensional representation of H0 subducing the two representations dA and dB of G0p. The matrix representatives Δ(α) may be determined, e.g., from Table 5.1 of [32].
As a first step, Δ must be unitarily transformed (by a matrix Q) in such a way that the matrices Δ(α) are diagonal for α ∈ G0p,
Now, consider a certain distribution of the representations dA and dB across the positions . Then, we may determine the elements of the matrices D(α), if they exist, be means of the formula:
It turns out that in each case, the matrices determined by Equation (34) satisfy the multiplication rule in Equation (25) if Equation (34) produces for each space group operation a ∈ H a unitary generalized permutation matrix D(α). This may be understood because Equation (34) defines the complex numbers Dji(α) in such a way that the Wannier functions transform in Equation (15) in an unequivocal manner like the basis functions for . With “like” the basis functions, we want to express that by application of any space group operator , they are multiplied in Equation (15) by the same complex number as the basis functions for . The Wannier functions would indeed be basis functions for if they would not be moved from one position to another by some space group operations. Hence, we may expect that the matrices D(α) satisfy the multiplication rule in Equation (25) just as the matrices do. Nevertheless, the multiplication rule should be verified numerically in any case.
When using this Equation (34), a little complication arises if the group of position G0p contains so few elements that the two one-dimensional representations dA and dB subduced from are equal. Thus, in this case, we have no problem with the distribution of dA and dB across the positions . Theorem 2 is necessary and sufficient, and we may directly solve Equation (38) of Theorem 5.
However, when in Section 6 or in Section 7.3 we will consider magnetic groups, we need all of the representatives D(α) of the representation D explicitly. Fortunately, also when the representations dA and dB are equal, Equation (34) is applicable: in this case, their exists at least one diagonal matrix representative of with vanishing trace and . We may define pairs:
Finally, it should be mentioned that the elements of the non-diagonal matrices D(α) are not fully fixed (as already remarked in [30]): In Equation (32), we may use the elements δ(α) of any one-dimensional representation δ subducing the representation d. We receive in each case the same diagonal, but different non-diagonal matrices nevertheless satisfying the multiplication rule (25). Analogously, in Equation (34), we may determine the matrices D(α) by means of any two-dimensional representation subducing dA and dB.
In the following Theorem 3, we summarize our results in the present Section 3.3.
Theorem 3. The Wannier function at the position is basis function for a one-dimensional representation di of the “point group of position” G0p ⊂ H0 (Definition 12); cf. Equation (24). The representations di fix the (generally reducible) representation D of H0 defining the Wannier functions (Definition 8). The matrix representatives D(α) of D are unitary generalized permutation matrices. We distinguish between two cases, (i) and (ii).
Case (i): If the representations di are subduced from one-dimensional representations of the point group H0, then all of the Wannier functions of the band under observation are basis functions for the same representation d, which may be any one-dimensional representation of G0p subduced from a one-dimensional representation of H0. The representation D exists always; its matrix representatives D(α) may be calculated by Equation (32).
Case (ii): If the representations di are subduced from two-dimensional representations of the point group H0, then the Wannier functions are basis functions for the two one-dimensional representations dA and dB of G0p subduced from the same two-dimensional representation of H0. One half of the Wannier functions is the basis function for dA and the other half for dB. In special cases, the representations dA and dB may be equal; see above. The representation D exists for a given distribution of the representations dA and dB across the positions if Equation (34) yields unitary generalized permutation matrices D(α) satisfying the multiplication rule in Equation (25).
A third case with representations di subduced from one-dimensional, as well as from two-dimensional representations of H0 does not exist.
3.4. Not All of the Atoms Are Connected by Symmetry
If not all of the atoms at the positions are connected by symmetry (Definition 10), the representation D defining the Wannier functions consists of representatives D(α), which may be written in block-diagonal form:
We may summarize as follows.
Theorem 4. Each block Dq in Equation (37) forms its own representation of H0 and, hence, must comply separately and independently with the criteria given in Theorem 3.
The groups of position Gp belonging to different blocks may (but need not) be different. However, we assume that the sum in Equation (37) consists only of blocks with coinciding groups of position. If this is not true in special cases, the number µ of the atoms in Equation (7) must be reduced until the groups of position coincide in the sum in Equation (37). Briefly speaking, in such a (probably rare) case, atoms of the same sort must be treated like different atoms.
4. Condition for Optimally-Localized Symmetry-Adapted Wannier Functions
Remember that we consider a closed energy band of µ branches and let a representation D defining the Wannier functions be given, which was determined according to Theorems 3 and 4. Then, we may give a simple condition for optimally-localized symmetry-adapted Wannier functions based on the theory of Wannier functions published in [28,30].
Theorem 5. Let be a point of symmetry in the first domain of the Brillouin zone for the considered material, and let be the little group of in Herrings sense. That means, is the finite group denoted in [32] by (and listed for all of the space groups in Table 5.7 ibidem). Furthermore, let be the µ-dimensional representation of whose basis functions are the µ Bloch functions with wave vector and (with ) the character of either is irreducible or the direct sum over small irreducible representations of.
We may choose the coefficients giq( ) in Equation (7) in such a way that the Wannier functions are optimally-localized (Definition 1) and symmetry-adapted to H (Definition 7) if the character of satisfies at each point of symmetry in the first domain of the Brillouin zone the equation:
Definition 13 (point of symmetry). The term point of symmetry we use as defined in [32]: is a point of symmetry if there exists a neighborhood of in which no point except has the symmetry group.
Thus, a point of symmetry has a higher symmetry than all surrounding points.
We add a few comments on Theorem 5.
– In Equation (39), we write ni(a), rather than ni(α), because the group G0p depends on .
– The representation D defining the Wannier functions is equivalent to the representation , i.e., to the representation for ; see Equation (50).
– In the majority of cases, all of the representations di in Equation (39) are equal. The only exceptions arises when:
not all of the positions are connected by symmetry or
the one-dimensional representations di of G0p are subduced from a higher-dimensional representation of H0.
– a basic form of Theorem 5 was published first in Equation (23) of [7] and used in several former papers; Equation (23) of [7] yields the same results as Theorem 5
if all of the are connected by symmetry and
if all of the representations di of G0p are subduced from one-dimensional representations of H0.
– The irreducible representations of the Bloch functions of the considered band at the points ~k of symmetry may be determined from the representations as follows:
Theorem 6. Let possess r irreducible representations with the characters (1 ≤ m ≤ r), and assume that contains the m-th irreducible representation, say, cm times. Then, the numbers cm may be calculated by means of Equation (1.3.18) of [32],
5. Proof of Theorem 5
The existence of the optimally-localized symmetry-adapted Wannier functions is defined in Satz 4 of [28]: such Wannier functions exist in a given closed energy band of µ branches if Equations (4.28) and (4.17) of [28] are satisfied. We show in this section that the fundamental Theorem 5 complies with these two equations if the Wannier functions meet Assumptions (i)–(iii) in Section 2.2.
5.1. Equation (4.28) of [28]
As the first step, consider Equation (4.28) of [28] stating that optimally-localized and symmetry-adapted Wannier functions may exist only if two representations and are equivalent,
The representation as defined in Theorem 5 is the direct sum of the representations of the Bloch functions of the considered band at point . The character of the representation is simply given by:
The matrix representatives of are defined in Equation (4.26) of [28],
The traces of the matrices can be determined by transforming Equation (43) with the complex conjugate of the matrix M defined by Equation (2.1) of [30],
Definition 14 (horizontal bar). In line with [30], we denote matrices transformed with M (or M*) by a horizontal bar to indicate that these matrices belong to the diagonal matrices.
As shown in [30] (see Equations (2.18) and (2.19) of [30]), the second factor:
Thus, the matrices:
Strictly speaking, in [28], we have proven that the condition (41) must be satisfied for the points of symmetry lying in the first domain on the surface of the Brillouin zone. Equation (38) demands that in addition, the representation is equivalent to the representation D, which is evidently true; see Equation (50).
5.2. Equation (4.17) of [28]
As the second step, we show that Equation (4.17) of [28] does not reduce the validity of Theorem 5, but this equation is satisfied whenever Assumptions (i)–(iii) in Section 2.2 are valid. Taking the complex conjugate of Equation (4.17) of [28] and transforming this equation with the matrix M∗ already used in Equation (45), we receive the equation:
Just as the matrix:
6. Magnetic Groups
Assume a magnetic structure to be given in the considered material„ and let:
We demand that the equation:
Still, we assume that there is exactly one Wannier function at each position , i.e., the three assumptions, (i)–(iii), of Section 2.2 remain valid. Thus, [15], Equation (60) may be written in the more compact form:
Definition 15 (symmetry-adapted to a magnetic group). We call the Wannier functions symmetry-adapted to the magnetic group M if, in addition to Equation (15), Equation (62) is satisfied.
Again (cf. Section 2.2), Equation (62) defines the non-vanishing elements of the matrix N. Hence, also, N has one non-vanishing element in each row and each column,
As already expressed by Equation (60), we only consider bands of µ branches, which are not connected to other bands, also after the introduction of the new anti-unitary operation . That means that the considered band consists of µ branches, as well, after, as before the introduction of . Hence, the matrix N must satisfy the equations:
Assume Theorem 5 to be satisfied in the considered energy band and remember that then, the coefficients in Equation (7) can be chosen in such a way that the Wannier functions of this band are optimally-localized and symmetry-adapted to H. In [33], we have shown that the Wannier functions may even be chosen symmetry-adapted to the magnetic group M if Equation (7.1) of [33],
Transforming Equation (67) with the matrix M* already used in Equation (45) and using:
We summarize the results of the present Section 6 in:
Theorem 7. The coefficients in Equations (7) may be chosen in such a way that the Wannier functions are optimally-localized (Definition 5) and even symmetry-adapted to the magnetic group M in Equation (57) (Definition 15) if, according to Theorem 5, they may be chosen symmetry-adapted to H and if, in addition, there exists a µ-dimensional matrix N satisfying Equations (64)–(66).
The representation D in Equations (65) and (66) is the representation defining the Wannier functions as used in Theorem 5.
In most cases, we may set the non-vanishing elements of N equal to one.
Definition 16 (magnetic band). If, according to Theorem 7, the unitary transformation in Equation (6) may be chosen in such a way that the Wannier functions are optimally-localized and symmetry-adapted to the magnetic group M in Equation (57), we call the band under consideration (as defined by the representations in Equation (38)) a “magnetic band related to the magnetic group M ”.
Within the nonadiabatic Heisenberg model, the existence of a narrow, roughly half-filled magnetic band in the band structure of a material is a precondition for the stability of a magnetic structure with the magnetic group M in this material. However, the magnetic group M must be “allowed” in order that the time-inversion symmetry does not interfere with the stability of the magnetic state [10].
7. Spin-Dependent Wannier Functions
7.1. Definition
Assume the Hamiltonian of a single electron in the considered material to be given, and assume to consist of a spin-independent part and a spin-dependent perturbation ,
Consider again a closed energy band of µ branches that, in general, was not closed before the perturbation was activated. Now, each branch is doubled, which means that it consists of two bands related to the two different spin directions. Just as in Section 2.1, we assume that the Bloch spinors are chosen in such a way that they vary continuously through the first domain and approach continuously the boundaries of the first domain. In the rest of the Brillouin zone and in the remaining space, they shall be given again by Equations (3) and (4) [33], where, however, P(a) acts now on both and t; see Equation (85).
We define “spin-dependent Wannier functions” by replacing the Bloch functions in Equation (7) by linear combinations:
The matrices:
Within the nonadiabatic Heisenberg model, we strictly consider the limiting case of vanishing spin-orbit coupling,
If :
– was the basis function for a non-degenerate representation already before the spin-dependent perturbation s was activated or
– was the basis function for a degenerate representation before s was activated and this degeneracy is not removed by s (see Section 7.4.2),
where the functions us(t) denote Pauli’s spin functions:with the spin quantum number and the spin coordinate . Equation (80) applies to the vast majority of points in the Brillouin zone.If, at a special point , the Bloch function were the basis function for a degenerate single-valued representation before the perturbation s was activated and if this degeneracy were removed by s, then Equation (80) is unusable for the sole reason that we do not know which of the basis functions of the degenerate representation we should avail ourselves of in this equation. In fact, in this case, the Bloch spinors are well-defined linear combinations of the functions comprising all of the basis functions of the degenerate single-valued representation (as given, e.g., in Table 6.12 of [32]). These specific linear combinations are not, considered because, at this stage, they are of no importance within the nonadiabatic Heisenberg model.
In the framework of the approximation defined by Equation (80), the two functions in Equation (72) are usual Bloch functions with the spins lying in the ±z direction if:
7.2. Symmetry-Adapted Spin-Dependent Wannier Functions
We demand that symmetry-adapted spin-dependent Wannier functions satisfy, in analogy to Equation (15), the equation:
The vectors and are still given by Equations (13) and (16), respectively. The matrices D(α) = [Dij(α)] in Equation (83) are again unitary generalized permutation matrices, and the subscripts i and j denote the number of the atoms at position and , respectively; see Definition 6.
The operators P (a) now act additionally on the spin coordinate t of a function ,
We have to take into consideration that the double-valued representations of a group g are not really representations of g, but of the abstract “double group” gd of order 2|g|, while the single-valued representations are representations of both g and gd [32].
Definition 17 (double-valued). Though we use the familiar expression “double-valued” representation of a group g, we consider the double-valued representations as ordinary single-valued representations of the related abstract double group gd, denoted by a superscript “d”.
Since the index m of the spin-dependent Wannier functions is interpreted as spin quantum number, we demand that the term:
Definition 18 (symmetry-adapted). We call the spin-dependent Wannier functions “symmetry-adapted to the double group Hd related to space group H” if they satisfy Equation (83) for a ∈ Hd, where the matrices [dmm′ (α)] are the representatives of the two-dimensional double-valued representation d1/2 of O(3).
Consequently, symmetry-adapted spin-dependent Wannier functions are basis functions for the double-valued representation:
Definition 19 (representation defining spin-dependent Wannier functions). The single-valued representation D of H0 defined by Equation (83) shall be referred to in short as “the representation defining the spin-dependent Wannier functions” and its matrix: representatives
While usual (spin-independent) Wannier functions are basis functions for the representation D defining the Wannier functions, spin-dependent Wannier functions are basis functions for the double-valued representation:
Furthermore, the representation D defining the spin-dependent Wannier functions has to meet the conditions given in Section 3, as shall be summarized in:
Theorem 8. The two spin-dependent Wannier function and at the position are basis functions for the two-dimensional representation:
In addition, Theorem 4 must be noted.
Theorem 5 does not distinguish between usual and spin-dependent Wannier functions, but uses only the special representations of the Bloch functions or Bloch spinors, respectively, at the points of symmetry. Thus, Theorem 5 applies to both usual and spin-dependent Wannier functions, if in the case of spin-dependent Wannier functions, we replace the little groups by the double groups . Just as the groups , the groups are finite groups in Herrings sense, as denoted in [32] by , and, fortunately, are explicitly given in Table 6.13 ibidem.
When we consider single-valued representations, then the sum on the right-hand side of Equation (38) runs over the µ diagonal elements of the matrices in Equation (51). When we consider double-valued representations, on the other hand, this sum runs over 2µ diagonal elements of the corresponding matrices:
We need not to solve Equation (38) directly, but we may determine the representations complying with Equation (38) in a quicker way. Equation (93) shows that we may write the matrices simply as Kronecker products,
Now, assume that we have already determined according to Theorem 5 the single-valued representations in the closed band under consideration. Then, the representations and are equivalent (see Equation (41)), and consequently, also the representations:
Definition 20 (affiliated single-valued band). In this context, we call the band defined by the double-valued representations in Equation (96) the “double-valued band” and the band defined by the single-valued representations an “affiliated single-valued band”.
While a double-valued band may possess several affiliated single-valued bands, any single-valued band is affiliated with exactly one double-valued band.
The affiliated single-valued band is a closed band that, generally, does not exist in the band structure of the considered material. That means that the Bloch functions of the closed band under consideration band generally do not form a basis for the representations, even if Equation (80) is valid; see, e.g., the single-valued band affiliated with the superconducting band (Definition 22) of niobium as given in Equation (150).
We may summarize the result of this section in:
Theorem 9. Remember that we consider a closed energy band of µ branches, and let a representation D be given defining the spin-dependent Wannier functions, which was determined according to Theorem 8. The band may only be closed after the spin-dependent perturbation s was activated.
Let be a point of symmetry in the first domain of the Brillouin zone for the considered material, and let be the little double group of in Herrings sense. That means, is the finite group denoted in [32] by and explicitly given in Table 6.13 ibidem. Furthermore, let be the 2µ-dimensional representation of whose basis functions are the 2µ Bloch spinors with wave vector. either is irreducible or the direct sum over double-valued irreducible representations of. The representations follow Equation (96),
We may choose the coefficients and in Equations (73) and (72), respectively, in such a way that the spin-dependent Wannier functions are optimally-localized (Definition 5) and symmetry-adapted to the double group Hd (Definition 18) if the characters of the single-valued representations satisfy Equation (38).
The complex numbers di(α) in Equation (39) stand for the elements of the one-dimensional representations di of fixing the given representation D defining the spin-dependent Wannier functions (according to Definition 19).
7.3. Time Inversion
7.3.1. Time-Inversion Symmetry of the Spin-Dependent Wannier Functions
Within the nonadiabatic Heisenberg model, we are not interested in spin-dependent Wannier functions that are symmetry-adapted to a general magnetic group, as given in Equation (57), but we only demand that they are adapted to the “grey” [32] magnetic group:
The index m of the spin-dependent Wannier functions we still interpret as the quantum number of the crystal spin. Consequently, we demand that K acts on m in the same way as it act on s,
Definition 21 (symmetry-adapted to a magnetic group). We call the spin-dependent Wannier functions “symmetry-adapted to the magnetic group Md” as given in Equation (98) if they are symmetry-adapted to Hd (Definition 18), and if, in addition, Equation (100) is satisfied.
In analogy to Equation (83), Equation (100) may be written as:
Equation (101) shows that the 2µ-dimensional matrix:
The first Equation (106) is true because:
In the third Equation (108), the diagonal matrix has the form:
We summarize our results in this Section 7.3.1 in:
Theorem 10. The coefficients and in Equations (73) and (72), respectively, may be chosen in such a way that the spin-dependent Wannier functions are optimally-localized (Definition 5) and even symmetry-adapted to the magnetic group Md in Equation (98) (Definition 21) if, according to Theorem 9, they may be chosen symmetry-adapted to Hd and if, in addition, the representation D defining the spin-dependent Wannier functions used in Theorem 9 is real.
Definition 22 (superconducting band). If, according to Theorem 10, the unitary transformation in Equation (74) may be chosen in such a way that the spin-dependent Wannier functions are optimally-localized and symmetry-adapted to the magnetic group Md in Equation (98), we call the band under consideration (as defined by the double-valued representations in Equation (97)) a superconducting band.
Within the nonadiabatic Heisenberg model, the existence of a narrow, roughly half-filled superconducting band in the band structure of a material is a precondition for the stability of a superconducting state in this material.
7.3.2. Time-Inversion Symmetry of the Matrices
In this section, we derive the time-inversion symmetry of the matrices defined in Equation (72) and shall give the result in Theorem 11. Though evidence for this important theorem was already provided in [11] and later papers [16,35], we repeat the proof with the notations used in the present paper.
Combining Equations (73) and (74), we may write the spin-dependent Wannier functions as:
By application of the operator K of time-inversion on Equation (115), we receive:
Equation (100), on the other hand, may be written as:
Comparing Equation (118) with Equation (116), we receive the two equations:
Equation (72) yields the two equations:
Theorem 11. Substituting Equations (122) and (123) into Equation (121), we obtain the fundamental condition:
Within the nonadiabatic Heisenberg model, the validity of this condition is the cause of the formation of symmetrized Cooper pairs in superconducting bands [16,35,36].
This Equation (125) may evidently be written in the more compact form:
7.4. -Dependence of the Matrices
Only those bands are of physical relevance in the theory of superconductivity which are closed not before the spin-dependent perturbation s is activated. In this section, we derive the essential property of such bands and shall give the result in Theorem 12.
Let be a point lying on the surface of the first domain in the Brillouin zone for the space group H, and let be the little group of . In this section, need not be a point of symmetry (according to Definition 13), but also may lie in a line or a plane of symmetry. However, we only consider wave vectors for which Equation (80) is valid. Hence, in general, the Bloch functions are basis functions for a one-dimensional (single-valued) representation of . Nevertheless, in very rare cases, the Bloch function can be a basis function for a degenerate (single-valued) representation. Both cases shall be examined separately.
Just as in Equation (3.1) of [28] we arrange the 2µ Bloch spinors in Equation (80) as a column vector:
Then, the analogous column vector consisting of the Bloch spinors in Equation (73) may be written as:
The matrices and are defined by Equations (75) and (76) and still follow Equations (8) and (77), respectively, and:
The matrices must satisfy Equations (4.8) and (4.29) of [28] in order that the Wannier functions are symmetry-adapted and optimally-localized. (We shall consider only Equation (4.29) of [28], because this equation comprises Equation (4.8) ibidem).
Using the notations of the present paper, Equation (4.29) of [28] may be written as:
7.4.1. The Bloch Functions Are Basis Functions for a Non-Degenerate Representation
In this subsection, we assume that the Bloch states are basis functions for a one-dimensional (single-valued) representation of .
The representations are the direct sum over the double-valued representations of the Bloch spinors in the considered band, as arranged in the column vector given in Equation (127). Hence, the matrices on the left-hand side of Equation (133) may be written as:
The matrices on the right-hand side of Equation (133) may be written as:
Equation (137) shows that also the matrices between the square brackets form a representation being the direct sum over double-valued representations, and hence, Equation (133) splits into the µ equations:
We now distinguish between two possibilities:
– If the considered energy band was already closed before the spin-dependent perturbation Hs was activated, then the affiliated single-valued band actually exists as a closed band in the band structure of the material under consideration, and thus, the representations and are equal,
Hence, all of the µ equations (138) are solved by:with the consequence that the Wannier functions are, in fact, not spin-dependent, but are usual Wannier functions, as defined in Equation (6).– If the considered energy band was not closed before the spin-dependent perturbation Hs was activated, then not all of the representations are equal to . Evidently, the q-th equation is not solved by when , and consequently, the Wannier function actually are spin-dependent.
We summarize this result in Theorem 12.
Theorem 12. If the considered energy band were not closed before the spin-dependent perturbation Hs was activated, the matrices in Equation (72) cannot be chosen independent of.
In the Section 7.5, the matrix shall by determined for some points in the Brillouin zone of niobium.
7.4.2. The Bloch Functions Are Basis Functions for a Degenerate Representation
In rare cases, it can happen that at a special point , some of the Bloch states are basis functions for a degenerate (single-valued) representation and that this degeneracy is not removed by the perturbation . For example, each of the two superconducting bands in the space group (129) listed in Table 3(b) of [13] consist of two branches degenerate at points M and A. The single-valued Bands 1 and 2 in Table 3(a) of [13] are affiliated with the superconducting Band 1 in Table 3(b) ibidem; Bands 3 and 4 in Table 3(a) are affiliated with Band 2 in Table 3(b).
It is crucial for the localization of the spin-dependent Wannier functions that also in this case, Equation (133) is solvable. We reveal the solubility of this equation for the example of the bands listed in Table 3 of [13].
At point M in each of these bands, Equation (138) may be written as:
Though and again are equivalent, it is not immediately evident that Equation (141) is solvable, because is not a general 4 × 4 matrix. However, also, the representations and have a very special form, since they may be written simply as Kronecker products. Equation (141) indeed is solvable, since it expresses the most general unitary transformation between these special representations.
For instance, consider the point M of one of the bands in Table 3b of [13], and let be given by the calculated band structure of the material under consideration. In addition, let us choose Band 1 in Table 3a of [13] as the affiliated single-valued band. Thus, we have , and Equation (141) is solved by:
Though both Band 1 and Band 2 in Table 3b of [13] are mathematically correct superconducting bands, they cannot be occupied in undoped LaFeAsO [13], which, consequently, is not superconducting.
7.4.3. Additions
In this subsection, we show that neither Equation (120) nor Equation (126) is inconsistent with Equation (133). Remember that in this section, we only consider points for which Equation (80) is valid.
First, taking the complex conjugate of Equation (134), we receive with and the condition:
Secondly, transforming the complex conjugate of Equation (138) with the matrix n in Equation (103) and using and
7.5. Example: Band Structure of Niobium
Consider the superconducting band (Definition 22) of niobium in Figure 1, as denoted by the dotted line. At the four points of symmetry Γ, H, N and P in the Brillouin zone for the space group of niobium, this band is characterized by the representations:
Hence, at the points Γ, H, P and N, the Bloch spinors can be transformed in such a way that at each of the four points Γ, H, N and P, two spinors form basis functions for the double-valued representations:
The representations in Equation (150) define (the only) single-valued band affiliated with the superconducting band defined by the representations in Equation (149) (Definition 20). The representation D defining the spin-dependent Wannier functions (Definition 19) is equal to
The Bloch functions of the superconducting band cannot be unitarily transformed into usual Wannier functions, which are optimally-localized and symmetry-adapted to , since it was not closed before the spin-dependent perturbation s was activated. Thus (Theorem 12), we cannot choose the matrix in Equation (72) (with q = 1, since we only have one branch in the superconducting band of Nb) independent of when we demand that the Wannier functions are optimally-localized and symmetry-adapted. This important statement shall be demonstrated by an example:
Consider the point N with the wave vector in the first domain of the Brillouin zone for . The representations , and in Equation (138) are given by Equations (150) and (148),
In the same way, we find:
Equations (155) and (156) demonstrate that cannot be chosen independent of in the superconducting band of niobium.
8. Conclusions
In the present paper, we gave the group theory of optimally-localized and symmetry-adapted Wannier functions with the expectation that it will be helpful to determine the symmetry of the Wannier functions in the band structure of any given material. The paper is written in such a way that it should be possible to create a computer program automating the determination of the symmetry of the Wannier functions.
In this paper, we restricted ourselves to Wannier functions that define magnetic or superconducting bands. That means that we considered only Wannier functions centered at the atomic positions. When other physical phenomena shall be explored, as, e.g., the metallic bond, other Wannier functions may be needed, which are centered at other positions, e.g., between the atoms. It should be noted that [28,30,33] define optimally-localized and symmetry-adapted Wannier functions in general terms, which may be centered at a variety of positions being different from the positions of the atoms.
Acknowledgments
We are very indebted to Guido Schmitz for his support of our work.
Author Contributions
Ekkehard Krüger wrote the group theory in Sections 2–7; Horst P. Strunk initiated this paper and wrote parts of Section 1, the Introduction.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Scalapino, D.J. The Case for dx2 − y2 Pairing in the Cuprate Superconductors. Phys. Rep. 1995, 250, 329–365. [Google Scholar]
- Lechermann, F.; Boehnke, L.; Grieger, D.; Piefke, C. Electron correlation and magnetism at the LaAlO3/SrTiO3 interface: A DFT+DMFT investigation. Phys. Rev. B. 2014, 90. [Google Scholar] [CrossRef]
- Eberlein, A.; Metzner, W. Superconductivity in the two-dimensional t-t′–Hubbard model. Phys. Rev. B. 2014, 89. [Google Scholar] [CrossRef]
- Marzari, N.; Mostofi, A.A.; Yates, J.R.; Souza, I.; Vanderbilt, D. Maximally localized Wannier functions: Theory and applications. Rev. Mod. Phys. 2012, 84, 1419–1475. [Google Scholar]
- Krüger, E. Stability and symmetry of the spin–density–wave–state in chromium. Phys. Rev. B. 1989, 40, 11090–11103. [Google Scholar]
- Krüger, E. Energy band with Wannier functions of ferromagnetic symmetry as the cause of ferromagnetism in iron. Phys. Rev. B. 1999, 59, 13795–13805. [Google Scholar]
- Krüger, E. Antiferromagnetic, Neutral, and Superconducting Band in La2CuO4. J. Supercond. 2005, 18, 433–454. [Google Scholar]
- Krüger, E. Theoretical investigation of the magnetic structure in YBa2Cu3O6. Phys. Rev. B. 2007, 75. [Google Scholar] [CrossRef]
- Krüger, E.; Strunk, H.P. Theoretical investigation of the magnetic structure in YBa2Cu3O6. J. Supercond. 2011, 24, 2103–2117. [Google Scholar]
- Krüger, E.; Strunk, H.P. Structural Distortion in Antiferromagnetic BaFe2As2 as a Result of Time-Inversion Symmetry. J. Supercond. 2014, 27, 601–612. [Google Scholar]
- Krüger, E. Superconductivity Originating from Quasi-Orbital Electrons II. The Superconducting Ground State of Quasi-Orbital Conduction Electrons. Phys. Status Solidi B. 1978, 85, 493–503. [Google Scholar]
- Krüger, E. Superconducting Bands Stabilizing Superconductivity in YBa2Cu3O7 and MgB2. J. Supercond. 2010, 23, 213–223. [Google Scholar]
- Krüger, E. The Reason why Doping Causes Superconductivity in LaFeAsO. J. Supercond. 2012, 25, 989–999. [Google Scholar]
- Krüger, E. Modified BCS Mechanism of Cooper Pair Formation in Narrow Energy Bands of Special Symmetry II. Matthias Rule Reconsidered. J. Supercond. 2001, 14, 551–561. [Google Scholar]
- Krüger, E. Nonadiabatic extension of the Heisenberg model. Phys. Rev. B. 2001, 63. [Google Scholar] [CrossRef]
- Krüger, E. Modified BCS Mechanism of Cooper Pair Formation in Narrow Energy Bands of Special Symmetry I. Band Structure of Niobium. J. Supercond. 2001, 14, 469–489. [Google Scholar]
- Huang, Q.; Qiu, Y.; Bao, W.; Green, M.A.; Lynn, J.W.; Gasparovic, Y.C.; Wu, T.; Wu, G.; Chen, X.H. Neutron-Diffraction Measurements of Magnetic Order and a Structural Transition in the Parent BaFe2As2 Compound of FeAs-Based High-Temperature Superconductors. Phys. Rev. Lett. 2008, 101. [Google Scholar] [CrossRef]
- De la Cruz, C.; Huang, Q.; Lynn, J.W.; Li, J.; Ratcliff, W., II; Zarestky, J.L.; Mook, H.A.; Chen, G.F.; Luo, J.L.; Wang, N.L.; et al. Magnetic order close to superconductivity in the iron-based layered LaO1−x Fx FeAs systems. Nature 2008, 453, 899–902. [Google Scholar]
- Nomura, T.; Kim, S.W.; Kamihara, Y.; Hirano, M.; Sushko, P.V.; Kato, K.; Takata, M.; Shluger, A.L.; Hosono, H. Crystallographic phase transition and high-Tc superconductivity in LaFeAsO. Supercond. Sci. Technol. 2008, 21, 125028–125036. [Google Scholar]
- Kitao, S.; Kobayashi, Y.; Higashitaniguchi, S.; Saito, M.; Kamihara, Y.; Hirano, M.; Mitsui, T.; Hosono, H.; Seto, M. Spin Ordering in LaFeAsO and Its Suppression in Superconductor LaFeAsO0.89F0.11 Probed by Mössbauer Spectroscopy. J. Phys. Soc. Jpn. 2008, 77. [Google Scholar] [CrossRef]
- Nakai, Y.; Ishida, K.; Kamihara, Y.; Hirano, M.; Hosono, H. Evolution from Itinerant Antiferromagnet to Unconventional Superconductor with Fluorine Doping in LaFeAs(O1−x Fx) Revealed by 75As and 139La Nuclear Magnetic Resonance. J. Phys. Soc. Jpn. 2008, 77. [Google Scholar] [CrossRef]
- Krüger, E.; Strunk, H.P. Structural Distortion as Prerequisite for Superconductivity in LiFeAs. J. Supercond. 2012, 25, 1743–1745. [Google Scholar]
- Krüger, E. One- and Two-Dimensional Sublattices as Preconditions for High–Tc Superconductivity. Phys. Status Solidi B. 1989, 156, 345–354. [Google Scholar]
- Krüger, E. Modified BCS Mechanism of Cooper Pair Formation in Narrow Energy Bands of Special Symmetry III. Physical Interpretation. J. Supercond. 2002, 15, 105–108. [Google Scholar]
- Ibañez-Azpiroz, J.; Eiguren, A.; Bergara, A.; Pettini, G.; Modugno, M. Self-consistent tight-binding description of Dirac points moving and merging in two-dimensional optical lattices. Phys. Rev. A. 2013, 88. [Google Scholar] [CrossRef]
- Marzari, N.; Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B. 1997, 56. [Google Scholar] [CrossRef]
- Souza, I.; Marzari, N.; Vanderbilt, D. Maximally localized Wannier functions for entangled energy bands. Phys. Rev. B. 2001, 65, 035109:1–035109:13. [Google Scholar]
- Krüger, E. Symmetrische verallgemeinerte Wannierfunktionen I. Definition und Grundlagen. Phys. Status Solidi B. 1972, 52, 215–230. [Google Scholar]
- Bouckaert, L.P.; Smoluchowski, R.; Wigner, E. Theory of Brillouin Zones and Symmetry Properties of Wave Functions in Crystals. Phys. Rev. 1936, 50, 58–67. [Google Scholar]
- Krüger, E. Symmetrische verallgemeinerte Wannierfunktionen II. Eigenschaften and Beispiele-Bandstruktur des Germaniums. Phys. Status Solidi B. 1972, 52, 519–531. [Google Scholar]
- Streitwolf, H.W. Gruppentheorie in der Festkörperphysik; Akademische Verlagsgesellschaft Geest & Portig KG: Leipzig, Germany, 1967; In German. [Google Scholar]
- Bradley, C.; Cracknell, A.P. The Mathematical Theory of Symmetry in Solids; Claredon: Oxford, UK, 1972. [Google Scholar]
- Krüger, E. Spinabhängige und optimal lokalisierte Funktionen geringer Energieunschärfe in Metallen. Phys. Status Solidi B. 1974, 61, 193–206. [Google Scholar]
- Krüger, E. Superconductivity Originating from Quasi-Orbital Electrons III. Quasi-Orbital Conduction Electrons in Non-Adiabatic Systems. Phys. Status Solidi B. 1978, 90, 719–731. [Google Scholar]
- Krüger, E. Spin-phonon interaction as possible necessity for superconductivity. Phys. Rev. B. 1984, 30, 2621–2633. [Google Scholar]
- Krüger, E. Superconductivity Originating from Quasi-Orbital Electrons I. The Model of Quasi-Orbital Conduction Electrons. Phys. Status Solidi B. 1978, 85, 261–270. [Google Scholar]
- Mattheis, L.F. Electronic Structure of Niobium and Tantalum. Phys. Rev. B. 1969, 1, 373–381. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).