Supersymmetric Displaced Number States
Abstract
: We introduce, generate and study a family of supersymmetric displaced number states (SDNS) that can be considered generalized coherent states of the supersymmetric harmonic oscillator. The family is created from the seminal supersymmetric boson-fermion entangling annihilation operator introduced by Aragone and Zypman and later expanded by Kornbluth and Zypman. Using the momentum representation, the states are obtained analytically in compact form as displaced supersymmetric number states. We study their position-momentum uncertainties, and their bunchiness by classifying them according to their Mandel Q-parameter in phase space. We were also able to find closed form analytical representations in the space and number basis.1. Introduction
In search for quantum states of the harmonic oscillator Hamiltonian, which, while being fully quantum are as classical as possible, Schrödinger found in 1926 minimum uncertainty states (MUS) that do not spread and with centers that follow a classical trajectory [1]. Later, these states found applications in Quantum Optics, and in 1963 Glauber, Sudarshan and Klauder proved the equivalence of MUS, vacuum displaced states, and eigenstates of the annihilation operator [2,3]. In the 1970s, quantum squeezing [4] was introduced as two-photon coherent states [5,6].
In the context of Supersymmetry, the supersymmetric coherent states (SCS) where discovered in 1986 [7,8] as eigenstates of the supersymmetric annihilation operator:
Here, we extend the study of uncertainties in states of the supersymmetric harmonic oscillator to include supersymmetric displaced number states (SDNS) that can be considered generalized coherent states of the supersymmetric harmonic oscillator. In addition, we perform a quantitative study of the Mandel Q-number, which classifies the states according to their quantum-classical content.
Unlike what happens in the standard quantum harmonic oscillator, in the supersymmetric case, the eigenstates of Equation (1) and the displaced ground state give rise to different states. Moreover, the SDNS are displaced supersymmetric number states, both ground and excited. Thus, while there is no expectation that the SDNS are simply related to the eigenstates of Equation (1), it is still interesting to enquire into the likely interesting properties of these novel supersymmetric states of the harmonic oscillator.
In Section 2, the SDNS are defined and an explicit representation obtained in the space introduced above. Section 3 presents results on for the SDNS. Section 4 classifies the statistical properties of the SDNS according to whether they are sub- or super-Poissonian. Section 5 is for the conclusions.
2. Supersymmetric Displaced Number States
The displaced number states of the quantum harmonic oscillator were first used in quantum electrodynamics, to generalize the Jaynes-Cummings model to include atom-electromagnetic field interactions for strong fields [9,10]. These of course were not supersymmetric, but since it is natural to treat the quantized electromagnetic field as a coherent state (for example to study stimulated emission of radiation in atom-field system [11]), and since Jaynes-Cummings has been considered extensively in supersymmetry (see for example [12]), the supersymmetric displaced number states introduced and explored here, are interesting candidates to represent quantized fields in the context of supersymmetric Jaynes-Cummings. The base formed by the external product of these states representing the electromagnetic field, and the momentum representation of the atomic states, are exact eigenstates in the limit in which the atomic transitions are small compared with the frequency of the field. In addition, when this limit is violated, still the basis affords an economical convergence of perturbation theory when compared with a plain number state base. The translation operator is defined in that context (Equation (13) in [9]) as
To find the SDNS, we need to displace the supersymmetric number states under the action of . We recall [8] that the supersymmetric number states with energy are
To consolidate notation we describe the number states as
Thus our problem reduces to find the states
Here we emphasize that the displaced states are , not just as is standard practice when studying coherent states. Thus, these states do not need to agree with supersymmetric coherent states on two counts. First, because, as explained above, the displaced ground state and the eigenstates of the annihilation operator are not the same in supersymmetry. Second, because in regular quantum mechanics, the eigenstates of the annihilation operator agree with the displaced ground state, while here we are displacing all number states. In addition, in what follows, n is understood as the label of the state being displaced.
To make progress we work in the momentum representation of the number states,
The exponential in Equation (3) is now readily found,
Using Equations (5) and (7a),
To emphasize, n remains a parameter in the SDNS because all number states have been displaced, not only the ground states as is the common case when finding regular coherent states. To simplify notation in what follows we will use the expression valid for . All results apply also to setting θ to zero.
As mentioned above, the translation operator is unitary as can be readily seen from Equation (7a). Indeed, since
3. Uncertainties
Here we compute the uncertainties Δp·Δx in the state . The intermediate integrals can be obtained analytically in closed form,
The integrals above are understood as follows. Take and operator O,
Then,
Using Equation (9a–d)
It is interesting to compare these uncertainties with those of the number states of the standard quantum harmonic oscillator. In that case and the same result is valid for the displaced states by Equation (2). Then supersymmetry, by means of the degeneracy in energy given by θ, affords to reduce the uncertainty albeit by a small amount. The uncertainty reaches its minimum possible only for (and necessarily ), and for and .
4. Probability Distribution of the SDNS Light
The Poisson probability density is normally associated in natural phenomena with the probability of an event happening during a given time interval. It is characteristic of the Poisson distribution that the variance is equal to the mean. The regular coherent states follow a Poisson distribution while, in comparison, thermal radiation has a super-Poissonian distribution characterized by bunching of photon arrival at the detector, and a variance larger than the mean. In contrast, it was first experimentally found that some fluorescence resonant light antibunches, that is, it arrives at the detector at more regular intervals than the Poissonian light. This can be found theoretically in sub-Poissionian distributions for which the variance is smaller than the mean, and it is a signature of non-classical light displaying irreducible quantum effects [13]. Mandel introduced the Q-parameter
In the supersymmetric case, the proper number operator is [7],
Using the states Equations (8) and (12) in Equation (11),
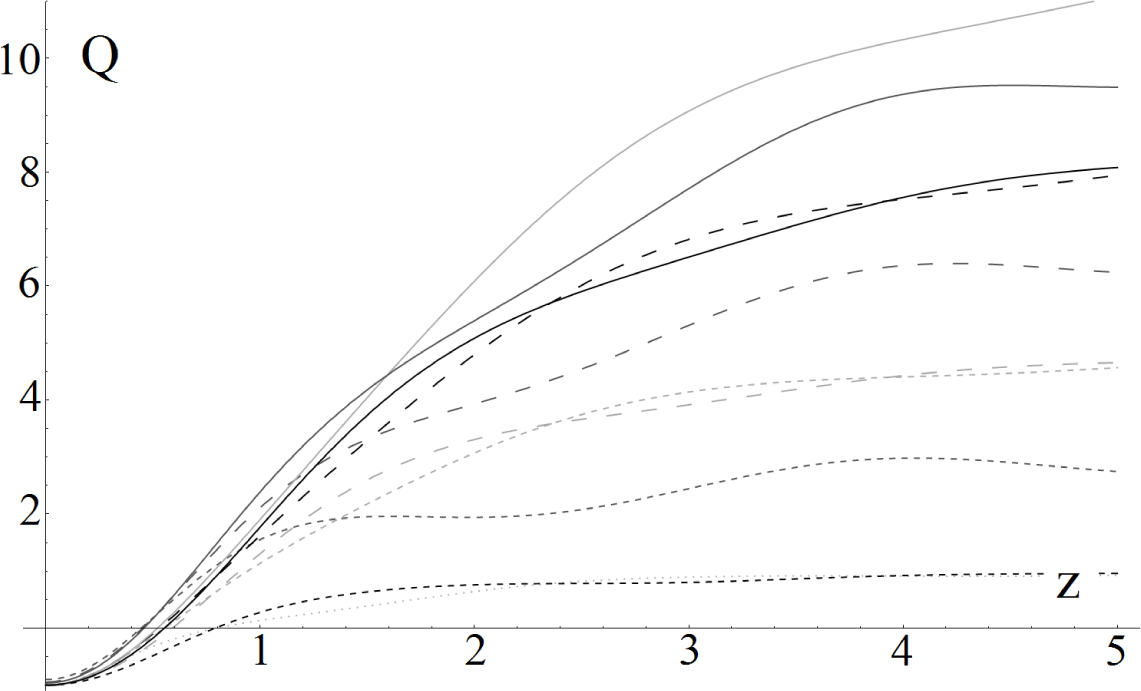
To clarify, since Q is a complicated function of several variables, we recall that z is the index that labels the SDNS, n indexes the original state that was displaced with T (Equation (3)), and θ is an angle variable in that spans the two-dimensional space of energy .
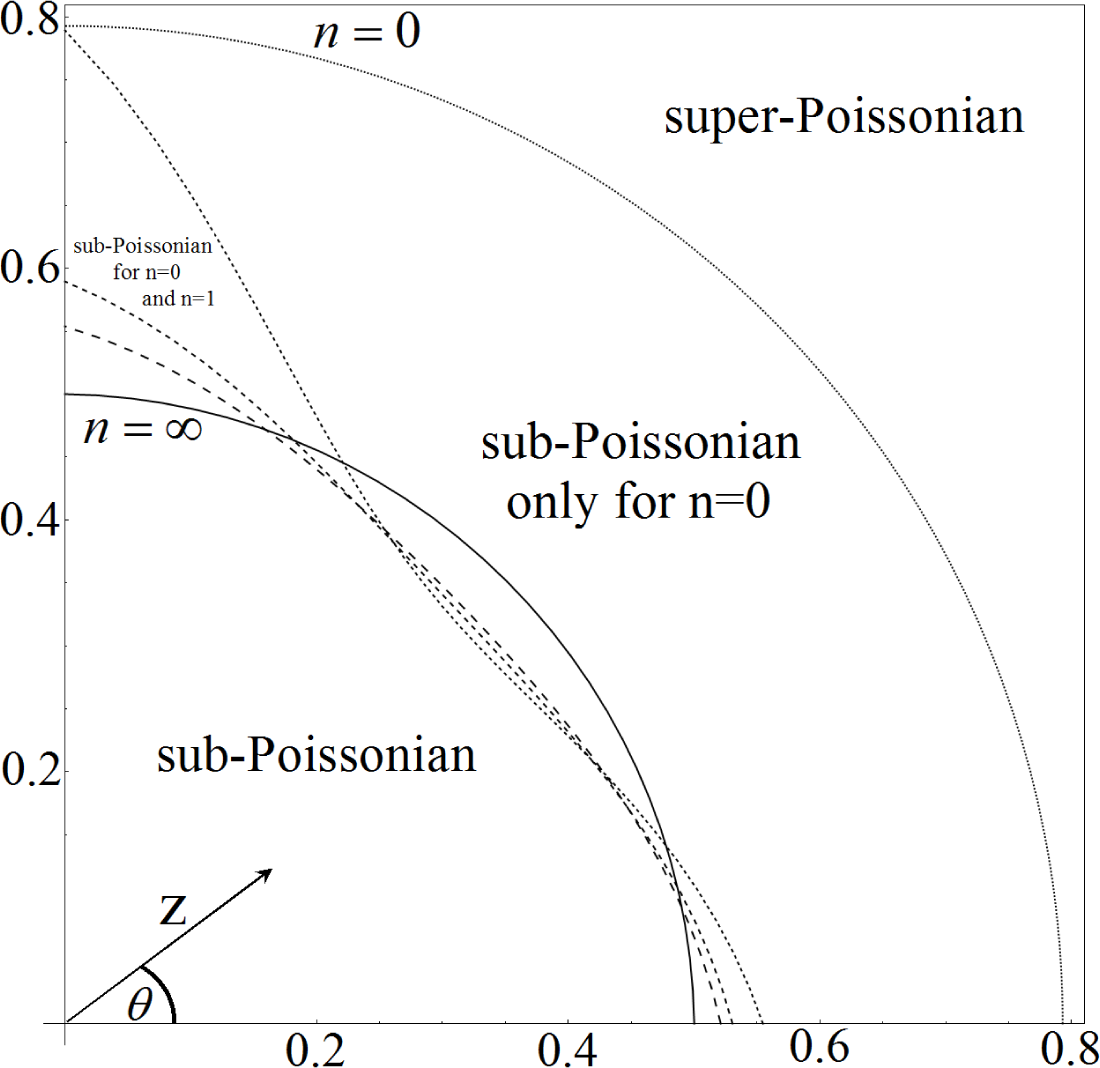
Figure 1 shows graphs of Q vs. z for various and θ. There it is shown the interesting region for and , for all and θ. That means that the states are strongly non-classical in that region. On the other hand, for the states become more thermal-like in character. We want to classify the states more precisely and find their phase diagram in (n, z, θ) space. To do that, we notice that the boundaries between sub-Poissonian and super-Poissonian are the Poissonian regions corresponding to . Thus, we set to zero the numerator in Equation (15),
Whenever then is positive, and the corresponding SDNS are super-Poissonian, that is thermal-like states, which are more bunched than Poissonian ones. For values of less than , the SDNS staes are sub-Poissonian, and show purely quantum properties such as antibunching. In the region the character of the states depends on .
5. Further Properties of SDNS
In this section we consider the normalization, representation in the number base, and representation in the position base of the .
5.1. Normalization
We begin from the identity [15]
When one recovers the normalization condition of the standard eigenfunctions in Equation (6). Of particular interest here is the case s = 1. Indeed, by setting that value, and also and m = 1, Equations (6) and (17) give,
Moreover, according to Equation (17) values of other than 0 or 1 will give vanishing integrals for m = 0 or 1. This property will come handy in what follows.
From Equation (8) and using the closure of the momentum states ,
Since
Thus, we see that the states are normalized (z' = z), but are not generally orthogonal to each other.
5.2. Number Representation
Equation (8) can be written in the explicit equivalent form
Using the number base, Equation (4c), and taking the state of energy ,
Then,
Using Equation (6),
Now we Taylor expand the exponential of imaginary argument,
Using Equation (17), for given n and m, only the single term for contributes to the sum and the integral is explicitly known,
Using Equation (27) in Equation (23b),
5.3. Position Representation
Call, as usual, the position. Then, using the closure of the states,
Looking at Equation (8), the last integral in Equation (29) involves four integrals of the type
6. Conclusions
We have defined and obtained an explicit representation of the Supersymmetric Displaced Number States (SDNS) in the momentum representation. In addition, we have studied their uncertainties and their probability distributions. Both cases were amenable of explicit analytical close from solutions, making them useful to gain insight into this new problem, and in the future to test numerical solutions of cases that must be handled numerically. The uncertainties of these new SDNS happen to be similar, but slightly smaller, than those of ordinary generalized coherent states. Reference [16] reviews displaced states of the standard quantum harmonic oscillator introduced in the 1950s by displacing not only the ground state (as is the case for the seminal Schrödinger coherent states) but also any excited number state. As for the probability distributions of the SDNS, we classified them according to their Mandel Q-parameter in (n, z, θ) phase space and found a region of finite volume where their sub-Poissonian behavior makes them states with strong quantum characteristics. In the section before the conclusions, we provide explicit representation of the SDNS both in the space and the number basis. Future works calls for similar studies using more general Supersymmetric annihilation operators, as those introduced recently [8]. In those cases, the momentum representation is not a natural basis. We have not yet found analytical answers in those cases.
Acknowledgments
The author likes to thank the Gamson fund for supporting this project.
Conflicts of Interest
The author declares no conflict of interest.
References
- Schrödinger, E. Der stetige Übergang von der Mikro-zur Makromechanik. Naturwissenschaften 1926, 14, 664–666, In German. [Google Scholar]
- Zhang, W.M.; Feng, D.H.; Gilmore, R. Coherent states: Theory and some applications. Rev. Mod. Phys. 1990, 62, 867–927. [Google Scholar]
- Perelomov, A.M. Generalized Coherent States and Their Applications; Springer: Berlin, Germany, 1986. [Google Scholar]
- Scully, M.O.; Zubairy, M.S. Quantum Optics, 3rd ed; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Yuen, H.P. Two-photon coherent states of the radiation field. Phys. Rev. A. 1976, 13, 2226–2243. [Google Scholar]
- Dodonov, V.V. Nonclassical’ states in quantum optics: A “squeezed” review of the first 75 years. J. Opt. B. 2002, 4, R1–R33. [Google Scholar]
- Aragone, C.; Zypman, F.R. Supercoherent States. J. Phys. A. 1986, 90, 2267–2279. [Google Scholar]
- Kornbluth, M.; Zypman, F.R. Uncertainties of coherent states for a generalized supersymmetric annihilation operator. J. Math. Phys. 2013, 54. [Google Scholar] [CrossRef]
- Crisp, M.D. Application of the Displaced Oscillator Basis in Quantum Optics. Phys. Rev. A. 1992, 46, 4138–4149. [Google Scholar]
- Daoud, M.; Hussin, V. General sets of coherent states and the Jaynes-Cummings model. J. Phys. A. 2002, 35, 7381–7402. [Google Scholar]
- Cummings, F.W. Stimulated emission of radiation in a single mode. Phys. Rev. 1965, 140, A1051–A1056. [Google Scholar]
- Panahi, H.; Jahangiri, L. Generalized Jaynes-Cummings Model and Shape Invariant Potentials: Master Function Approach. Int. J. Theor. Phys. 2014. [Google Scholar] [CrossRef]
- Gerry, C.C.; Knight, P.L. Introductory Quantum Optics; Cambridge University Press: Cambridge, UK, 2008; pp. 154–196. [Google Scholar]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995; p. 737. [Google Scholar]
- Arfken, G. Mathematical Methods for Physicists; Academic Press: New York, NY, USA, 1970; p. 615, Problem 13.1.12. [Google Scholar]
- Philbin, T.G. Generalized Coherent States. Am. J. Phys. 2014, 82, 742–748. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zypman, F.R. Supersymmetric Displaced Number States. Symmetry 2015, 7, 1017-1027. https://doi.org/10.3390/sym7021017
Zypman FR. Supersymmetric Displaced Number States. Symmetry. 2015; 7(2):1017-1027. https://doi.org/10.3390/sym7021017
Chicago/Turabian StyleZypman, Fredy R. 2015. "Supersymmetric Displaced Number States" Symmetry 7, no. 2: 1017-1027. https://doi.org/10.3390/sym7021017
APA StyleZypman, F. R. (2015). Supersymmetric Displaced Number States. Symmetry, 7(2), 1017-1027. https://doi.org/10.3390/sym7021017




