Topology and the Visualization of Space
Abstract
: Overlapping patterns provide the diagrammatics for four-dimensional space. If these patterns are three-dimensional lattices, and if one imagines them extended in three-dimensional space, then the diagram makes a model of physical space.1. Introduction
As Scott Carter has explained to me [1], to braid threads one must go over and under the one-dimensional threads—passing through two more dimensions than the threads themselves. To braid sheets, not ribbons but sheets, one needs access to four spatial dimensions, to go over and under the infinite two-dimensional sheets. In my painting, five fat sheets, each with a different color and a different internal structure, are shown braided together, slipping over and under each other in higher-dimensional space.
2. The Five Sheets
In the painting reproduced as Figure 1, the five sheets are:
Figure 2 is a quasicrystal lattice in 5-fold orientation where the acute angles are 72° and 36°; it is a slice through a quasicrystal cloud that was made with the deBruijn algorithm [2] and see Appendix, where whole cells are taken. (Centers of the cells are computed, and when centers are within certain parameters, whole cells are kept. Software of my design.) This lattice is yellow in the painting.
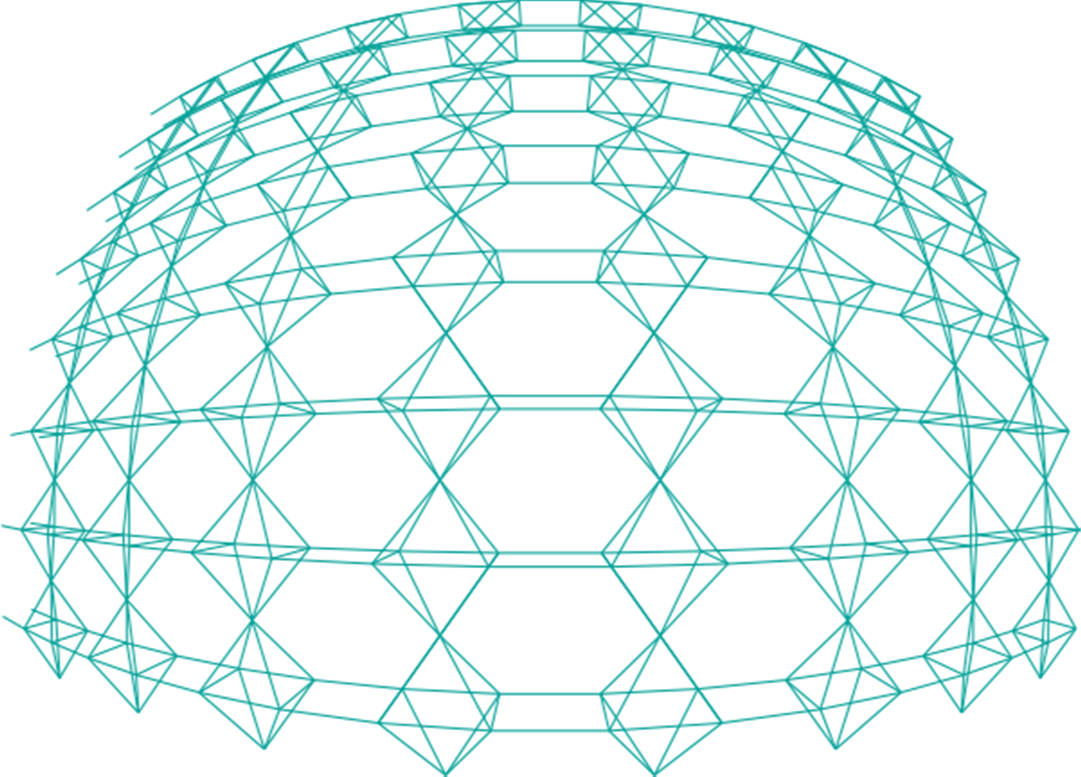
I call the pattern in Figure 3 Persian Dome. The two fundamental tessellation elements are an elongated octagon, and a four-pointed star, which also has eight sides. The octagons are tessellated along two perpendicular axes, and are slightly separated forming small four-pointed stars as negative shapes. The larger four-pointed stars are tessellated point to point. The pattern was taken from Islamic architecture, and “domed” by me using Formian software (see note at end of essay) from the University of Surrey in Guilford. In the painting, this pattern is light green.
Also created and curved with Formian is the lattice that I call Nose (Figure 4). Octahedra are tessellated vertex to vertex in the north-south axis, but they are separated by line segments in the east-west axis. The curvature is on the order of a nosecone, but whether or not it is exactly parabolic is hidden in the Formian software. In the painting, this lattice is light blue.
Dodecahedra flat (Figure 5), is a disconnected lattice; such lattices are anathema to topologists (how would one count the holes?), but the disconnected lattice suits my purpose, which is to define a slab of space without cluttering the field of view. Formian generated this field of dodecahedra, drawn in perspective, and oriented flat (or almost flat) to the picture plane. The dodecahedra are a delicate white.
In the painting 2ZHP (Figure 6), is a field of rhombic dodecahedra, which are the simplest sub-assemblies in a three-dimensional quasicrystal. There are three such sub-assemblies, often called zonohedra [3]. Shown above is the complete hypar projection, but only a section of this is used in the artwork. The disconnected vermillion figures dance around, twisting and flexing, as the zonohedra are shown projected to a doubly-curved surface and drawn in perspective.
3. Overlap, Braiding and the Artifacts of Projection
Elements in each of the five patterns (let us also call the lattices and disconnected fields patterns) are filled in with color, which are sometimes transparent and sometimes opaque. These filled plates define the braiding at that point. For example the vermillion rhombic dodecahedron in the upper left has three plates filled with either red, orange, or yellow. Here, the rhombic dodecahedra pattern is clearly on top of the light yellow 5-fold, but elsewhere in the painting it is behind the 5-fold. Small pentagons that are color-filled plates of the dodecahedra pattern are behind the yellow 5-fold at some locations, yet on top of the 5-fold at other places. There are two complications to the overlapping: objects can be close to the viewer in the third dimension and far away in the fourth, and projection from four to three (and again to a picture plane) can induce apparent, paradoxical intersections.
To accept the first complication, imagine that you are only your eyes looking out a picture window. The mountains are the same distance from the floor as you are—the same Y component. Although close in the Y direction, the mountains are far away in the Z direction. Likewise, a pattern can remain on top, be consistently close in the third dimension, while parts of it slip far behind in the fourth dimension. Secondly, whereas infinite patterns may slip over and under each other in the n + 2 dimension, there are apparent self-intersections as artifacts of the projection when these overlappings are projected to an n − 1 dimension.
Sorting out all these complications is not the point. My paintings are not equations, and it is not possible to read a mathematical resolution in them. Rather they revel in the richness and paradox of higher-dimensional visual phenomena. With a knowing nod to the mathematical possibilities, the paintings encourage an acceptance of such spatial complexity. Further, they encourage a taste for, and even a giddy joy, in spatial complexity.
There is a 100 year history of artists being influenced by the “fourth dimension”, either the four-dimensional geometry of the platonic solids in dimension 4, or a mysticism rationalized by the fourth dimension, or by considering time as the fourth dimension. This increasingly well-known history is best studied in the many works of Linda Henderson, beginning with The Fourth Dimension and Non-Euclidean Geometry in Modern Art [4]. I know of no artist other than myself, however, who has studied and taken inspiration from higher-dimensional topology.
4. Fat Sheets, Fatter and Fatter
In 1952, Albert Einstein added a fifth appendix to his popular 1916 book Relativity: The Special and the General Theory. The following quote, which I read forty years ago, is one of the most important sources for my art, of which I count only three or four.
“When a smaller box s is situated, relatively at rest, inside the hollow space of the larger box S, then the hollow space of s is a part of the hollow space of S, and the same “space”, which contains both of them, belongs to each of the boxes. When s is in motion with respect to S, however, the concept is less simple. One is then inclined to think that s encloses always the same space, but a variable part of the space S. It then becomes necessary to apportion to each box its particular space, not thought of as bounded, and to assume that these two spaces are in motion with respect to each other.
Before one has become aware of this complication, space appears as an unbounded medium or container in which material objects swim around. But it must now be remembered that there is an infinite number of spaces, which are in motion with respect to each other” [5], pp. 138–139, emphasis added.
At the end of the paragraph, Einstein adds that this notion of “spaces” is “far from having played a considerable role even in scientific thought”.
My abbreviated paraphrase of the Einstein quote, many spaces in the same space, became my shorthand for a more complicated view of both the objective space of relativity physics and the subjective space of my experience. I played different roles: simultaneously a son and a father. I worked in or was influenced by different traditions: Persian miniatures and Abstract Expressionism; nineteenth century French painting and computer art. I lived in and was formed in different places: Japan and Iran; New England and Europe.
This “spaces” view of special relativity allows us to notice that the multiple separate boxes s, even when expanded, are projected into the single larger space S. Elsewhere [6,7], I have written of the importance of this observation: the different special relativity formalisms of Henri Poincaré, Hermann Minkowski, and Roger Penrose are necessarily mathematically equivalent, and they can all be seen to be projective systems, most obviously in Penrose’s formulation of the Lorentz transformations as projective transformations on the Riemann sphere. Since much of quantum mechanics takes place in a projective space, and since projective space seems necessary for quantum information theory’s depiction of non-local phenomenon, here perhaps is a major clue to understanding reality: it is a projective phenomenon. A light ray has a direction, but no fixed length depending on the motion of the observer; it could even be a dimensionless point in its own frame of reference, in its own box traveling at the velocity of light. The light ray is best described as a projective point, rather than a line in space.
We tend to think with the calculus slicing model of space: all of space at T1, then T2, then T3, etc. It might actually be more productive to think with the seemingly paradoxical projective model: all of the spaces in the same space at the same time. I have acquired this opinion by looking at my paintings, and perhaps others could too.
5. Symbols, Pictures, and Diagrammatics
When a Catholic sees a sketch, even a crude sketch, of a woman holding a baby and wearing a blue shawl, there is a rush of feeling: compassion, gratitude, humility, and so on. For that woman is surely the Virgin Mary and the child is the Christ. Someone from a different religion might just see a woman and a baby. An artist would be required to go beyond the symbolism and provide the experience of the holy: by imbuing the scene with a golden light or expressing a great tenderness between mother and child. To be effective on its own, symbolism requires that the viewer be learned in the symbols. The apogee of symbolism is the algebraic equation, which—although it embodies a picture of the world—is nevertheless so coded that only those schooled in its methods can experience this. An artist working with the same vision as, say, those who understand the Lorentz transformation equations, causes even the innocent to experience the vertiginous yet lyrical qualities of that space. Diagrammatics, it seems to me, is somewhere in the middle between the symbolic and the pictorial: although it is not the purpose of mathematicians to dwell on the emotive, the hope is to communicate more fully and to reach more than just the initiate, as diagrammatics engages the visual mind and evokes visual intuitions.
6. Conclusions
There are visionary physicists who believe that everything that is and that happens is so and does so because of a property of space. Einstein believed that gravity exists because space can be curved. Penrose believes that fundamental, massless particles exist because space can be accurately described by projective geometry. David Bohm believed that non-local, quantum reality exists because space can be infinitely smeared over itself. We honor their vision and join this group when we imagine empty space to be rich and fecund.
Conflicts of Interest
The author declares no conflict of interest.
Appendix
In the case of the three-dimensional quasicrystal, deBruijn’s algorithm starts with a pattern, a tessellation of six-dimensional hypercubes. Each six-dimensional hypercube is composed of five-dimensional hypercubes, each of which is composed of four-dimensional hypercubes, each of which, in turn, is composed of regular cubes, set in six-dimensional space. A single one of these regular, right-angle cubes is selected from this dense tessellation and then multiplied by a projection matrix to deliver one of two differently skewed cubes, oriented, and placed in three-dimensional space. With repeated applications of the algorithm, a three-dimensional quasicrystal will be made. The algorithm, then, has two procedures: selection and projection, and the order in which these procedures are employed is irrelevant to the outcome. The projection matrix is a given in the algorithm; it is the collection of rays normal to the faces of a dodecahedron, often called a star of vectors. Think of these rays as the origin of our starting six-dimensional regular tessellation (all mutually perpendicular) now bent by projection into three-dimensional space. What were 90 degree angles are now angles of the irrational number arccosine one over the square root of five, about 63.44 degrees. The devil is in the selection procedure, which is too complicated to discuss in detail here. Nevertheless, I can hint at the selection procedures used.
If one wished to select first then project, a test is devised to first project to a field perpendicular to the final field to see if the component would pass through a spatial gate. If so, keep it and then proceed to project it to its final position. If not, discard. The testing gate is a triacontahedron whose dimensions are a given in the program. (One Japanese mathematician, whose name I have unfortunately lost, poetically called the triacontrahedron gate a crystal ball one peered into to see the future go/no go of the tested element.) In effect, the result of the test is a thin slice of the six-dimensional cubic lattice. This method is sometimes called the Direct Projection Method or the Slice and Project Method. Alternatively, if one wishes to project (in a given way) the entire six-dimensional hypercubic lattice to three-dimensional space first, then the problem is to choose which skewed cubes tessellate that three-dimensional space, and reject all others of the very many cells that interlace with that tessellation. In a process that I correctly programmed, yet that still amazes and mystifies me, one can cycle through the combinations of projected axes, three at a time, and construct one of only two skewed cubes, in the proper orientation, and placed at the correct location in three-dimensional space. This second method, sometimes called the Grand Dual Method, is superior to the Slice and Project Method in that it can render the zonohederal subgroupings that are nested in the quasicrystal.
A note on Formian: Formian was developed by the Engineering Department at the University of Surrey in Guilford. It was created to generate geometry for architectural spaceframes. It not easy to use, and there is no available manual. Nevertheless, it has functions that are very useful for topologists and artists. It generates patterns by reflecting, rotating, and translating simple elements; it has many procedures for curving patterns and lattices; and it allows one to work in an arbitrary number of dimensions. Extra dimensions can be added or subtracted as the patterns are being generated: it is not necessary to specify data structures in advance.
References and Notes
- Many thanks to Scott Carter for conversations, emails, and books since 1999
- De Brujn, N.G. The Algebraic Theory of Penrose’s Non-Periodic Tiling of the Plane. Indag. Math 1981, 84, 39–66. [Google Scholar]
- The other zonohedra are the rhombic icosahedron made of five fat cells and five skinny cells, and the rhombic triacontrahedron, made of ten cells of each kind. Sometimes the single fat cell is also called one of the zonohedra.
- Henderson, L.D. The Fourth Dimension and Non-Euclidean Geometry in Modern Art; Princeton University Press: Princeton, NJ, USA, 1983. [Google Scholar]
- Einstein, A. Relativity and the Problem of Space. In Relativity: The Special and the General Theory, 15th ed.; Crown Publishers: New York, NY, USA, 1952. [Google Scholar]
- Robbin, T. Shadows of Reality, the Fourth Dimension in Relativity, Cubism, and Modern Thought; Yale University Press: New Haven, CT, USA, 2006. [Google Scholar]
- Robbin, T.; David, Bohm; Roger, Penrose. the Search for Non-local Causality, Available online: http://www.interaliamag.org/articles/david-bohm-roger-penrose-and-the-search-for-non-local-causality/ accessed on 22 December 2014.





© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robbin, T. Topology and the Visualization of Space. Symmetry 2015, 7, 32-39. https://doi.org/10.3390/sym7010032
Robbin T. Topology and the Visualization of Space. Symmetry. 2015; 7(1):32-39. https://doi.org/10.3390/sym7010032
Chicago/Turabian StyleRobbin, Tony. 2015. "Topology and the Visualization of Space" Symmetry 7, no. 1: 32-39. https://doi.org/10.3390/sym7010032
APA StyleRobbin, T. (2015). Topology and the Visualization of Space. Symmetry, 7(1), 32-39. https://doi.org/10.3390/sym7010032




