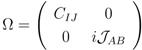Supersymmetric Extensions of Non-Relativistic Scaling Algebras
1. Introduction
 like
like 
 measures the anisotropy in the time direction t. When
measures the anisotropy in the time direction t. When  = 1, this is the usual scaling symmetry in relativistic field theories. The case with
= 1, this is the usual scaling symmetry in relativistic field theories. The case with  ≠ 1 does not respect the Lorentz symmetry any more and the system has to be realized in a non-relativistic manner. The invariance under the anisotropic scaling (1) is a key ingredient to construct the spacetime metrics of the gravity duals [6,7,8]. Then the spacetimes described by these metrics are homogeneous and are represented by cosets [9]. Thus it is of importance to consider symmetry algebras with an isotropic scaling invariance like conformal symmetries in conformal field theories. (For example, the Schrödinger symmetry [10,11] fixes the behavior of two-point functions [12,13].) The scaling symmetry provides us a first clue in looking for the holographic description as in the usual study of AdS/CFT.
≠ 1 does not respect the Lorentz symmetry any more and the system has to be realized in a non-relativistic manner. The invariance under the anisotropic scaling (1) is a key ingredient to construct the spacetime metrics of the gravity duals [6,7,8]. Then the spacetimes described by these metrics are homogeneous and are represented by cosets [9]. Thus it is of importance to consider symmetry algebras with an isotropic scaling invariance like conformal symmetries in conformal field theories. (For example, the Schrödinger symmetry [10,11] fixes the behavior of two-point functions [12,13].) The scaling symmetry provides us a first clue in looking for the holographic description as in the usual study of AdS/CFT. ≠ 1. The former is the Schrödinger algebra [10,11] and the latter is the Lifshitz algebra (For the explicit algebra, e.g., see [6,7,9,13]). The Schrödinger algebra comprises the centrally extended Galilean (Bargmann) algebra and the dilatation with
≠ 1. The former is the Schrödinger algebra [10,11] and the latter is the Lifshitz algebra (For the explicit algebra, e.g., see [6,7,9,13]). The Schrödinger algebra comprises the centrally extended Galilean (Bargmann) algebra and the dilatation with  ≠ 1 . (Rigorously speaking, the
≠ 1 . (Rigorously speaking, the  = 2 case is called the Schrödinger algebra and then the generator of special conformal transformation is contained. However, for convenience, we will call the algebra with
= 2 case is called the Schrödinger algebra and then the generator of special conformal transformation is contained. However, for convenience, we will call the algebra with  ≠ 1 the Schrödinger algebra with
≠ 1 the Schrödinger algebra with  loosely as in most of the recent works.) The Lifshitz algebra consists of time and spatial translations, spatial rotations and the dilatation with
loosely as in most of the recent works.) The Lifshitz algebra consists of time and spatial translations, spatial rotations and the dilatation with  ≠ 1 (in particular, no Galilean boost). It is well known that the two algebras can be realized as subalgebras of relativistic conformal algebras (
≠ 1 (in particular, no Galilean boost). It is well known that the two algebras can be realized as subalgebras of relativistic conformal algebras (  = 1) and it would be helpful to see a schematic sequence of the algebras like
= 1) and it would be helpful to see a schematic sequence of the algebras like 
 case and a new result on supersymmetric Lifshitz algebras.
case and a new result on supersymmetric Lifshitz algebras.2. General Prescriptions

 = 1) and Kµ describes special conformal transformations. For a generator T, the dimension d(T) is measured as
= 1) and Kµ describes special conformal transformations. For a generator T, the dimension d(T) is measured as 



 . Indeed, the Schrödinger and Lifshitz algebras are obtained from a relativistic conformal algebra by shifting the relativistic dilatation D(
. Indeed, the Schrödinger and Lifshitz algebras are obtained from a relativistic conformal algebra by shifting the relativistic dilatation D(  = 1) with a certain U(1) generator V like
= 1) with a certain U(1) generator V like 
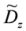 plays a central role in our discussions.
plays a central role in our discussions.

3. Non-Relativistic Superalgebras from psu(2,2|4)

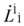 , which are the Cartan generators of the two su(2)s. By taking a linear combination of the two generators, a couple of new u(1) generators are defined as
, which are the Cartan generators of the two su(2)s. By taking a linear combination of the two generators, a couple of new u(1) generators are defined as 


(1) Schrödinger algebra with an arbitrary ![Symmetry 04 00517 i134]() and 24 supercharges (d-υ ≥ 0)
and 24 supercharges (d-υ ≥ 0)
 ≠ 2. As we explain in detail as the next example, the
≠ 2. As we explain in detail as the next example, the  = 2case is a bit special.
= 2case is a bit special.

 , the dynamical critical exponent also becomes
, the dynamical critical exponent also becomes  .
.
 ,
, 






(2) Schrödinger algebra with ![Symmetry 04 00517 i134]() = 2 and 24 supercharges (d - υ ≥ 0)
= 2 and 24 supercharges (d - υ ≥ 0)
 = 2 is a bit special because V does not appear in the right-hand side of the (anti-)commutation relations. It implies that the algebra may be closed without V.
= 2 is a bit special because V does not appear in the right-hand side of the (anti-)commutation relations. It implies that the algebra may be closed without V.

(3) Schrödinger algebra with an arbitrary ![Symmetry 04 00517 i134]() and 16 supercharges (d - υ ≥ 0 and d ≥ 0)
and 16 supercharges (d - υ ≥ 0 and d ≥ 0)

 in the literature. This subalgebra is specified by imposing an additional condition d ≥ 0as well as d - υ ≥ 0. The condition comes from the prescription to eliminate negative dimension generators as explained in Section 2.
in the literature. This subalgebra is specified by imposing an additional condition d ≥ 0as well as d - υ ≥ 0. The condition comes from the prescription to eliminate negative dimension generators as explained in Section 2. (4) Lifshitz algebra with an arbitrary ![Symmetry 04 00517 i134]() and 16 supercharges (d - υ ≥ 0 and d + υ ≥ 0)
and 16 supercharges (d - υ ≥ 0 and d + υ ≥ 0)

 ≠ 2. The case with
≠ 2. The case with  = 2is a bit special as we will explain in the next example. It also contains 16 supercharges and thus the resulting algebra should be referred to as the super Lifshitz algebra. This subalgebra can be pictorially understood by imposing an additional Lifshitz condition d + υ ≥ 0 as well as the Schrödinger condition d - υ ≥ 0 .
= 2is a bit special as we will explain in the next example. It also contains 16 supercharges and thus the resulting algebra should be referred to as the super Lifshitz algebra. This subalgebra can be pictorially understood by imposing an additional Lifshitz condition d + υ ≥ 0 as well as the Schrödinger condition d - υ ≥ 0 . (5) Lifshitz algebra with ![Symmetry 04 00517 i134]() = 2 and 16 supercharges (d - υ ≥ 0 and d + υ ≥ 0)
= 2 and 16 supercharges (d - υ ≥ 0 and d + υ ≥ 0)

 = 2 because d2(H) = 2 . The (anti-)commutation relations are given by (5) with
= 2 because d2(H) = 2 . The (anti-)commutation relations are given by (5) with  = 2, (6), (9), (12) and (40). This is the Lifshitz algebra with 16 supercharges and center M. In the bosonic case M does not appear in the right-hand side of commutators and hence it can be eliminated to give the usual Lifshitz algebra. However, in the supersymmetric case, the anti-commutator of
= 2, (6), (9), (12) and (40). This is the Lifshitz algebra with 16 supercharges and center M. In the bosonic case M does not appear in the right-hand side of commutators and hence it can be eliminated to give the usual Lifshitz algebra. However, in the supersymmetric case, the anti-commutator of 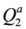 and
and  gives rise to M. Thus, by restricting to representations with zero central charge M, or by dropping
gives rise to M. Thus, by restricting to representations with zero central charge M, or by dropping 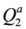 and
and  , the generator M can also be removed. In the latter case, the resulting 8 super Lifshitz algebra is generated by
, the generator M can also be removed. In the latter case, the resulting 8 super Lifshitz algebra is generated by 
 = 2 starts from a Schrödinger spacetime with
= 2 starts from a Schrödinger spacetime with  = 0 [27,28]. This construction can be explained algebraically by identifying the dilatation D0 in the Schrödinger spacetime with
= 0 [27,28]. This construction can be explained algebraically by identifying the dilatation D0 in the Schrödinger spacetime with  = 0with the generator M in the Lifshitz spacetime with
= 0with the generator M in the Lifshitz spacetime with  = 2. That is, the Lifshitz algebra with
= 2. That is, the Lifshitz algebra with  = 2 can also be obtained as a subalgebra of Schrödinger algebra with
= 2 can also be obtained as a subalgebra of Schrödinger algebra with  = 0.
= 0.
4. Non-Relativistic Superalgebras from osp(8|4)



(1) Schrödinger algebra with an arbitrary ![Symmetry 04 00517 i134]() and 24 supercharges (d - υ ≥ 0)
and 24 supercharges (d - υ ≥ 0)

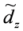 and υ of the generators are summarized in the list,
and υ of the generators are summarized in the list,
 because dz(H) =
because dz(H) =  . The commutation relations of the bosonic subalgebra are given by
. The commutation relations of the bosonic subalgebra are given by




(2) Schrödinger algebra with ![Symmetry 04 00517 i134]() = 2 and 24 super charges (d -υ ≥ 0)
= 2 and 24 super charges (d -υ ≥ 0)
 = 2 case is a bit special and the generator V does not appear in the right-hand side of the (anti-)commutation relations. This implies that V may be omitted. After eliminating V, the resulting algebra generated by
= 2 case is a bit special and the generator V does not appear in the right-hand side of the (anti-)commutation relations. This implies that V may be omitted. After eliminating V, the resulting algebra generated by 
(3) Schrödinger algebra with an arbitrary ![Symmetry 04 00517 i134]() and 16 supercharges (d - υ ≥ 0 and d ≥ 0)
and 16 supercharges (d - υ ≥ 0 and d ≥ 0)

(4) Lifshitz algebra with an arbitrary ![Symmetry 04 00517 i134]() and 16 supercharges (d - υ ≥ 0 and d + υ ≥ 0)
and 16 supercharges (d - υ ≥ 0 and d + υ ≥ 0)

 = 2 , the generator M becomes a center but it appears in the anti-commutator of QI2’s. However, by restricting to representations with zero central charge M, or by removing supercharges QI2, the exact Lifshitz algebra is reproduced.
= 2 , the generator M becomes a center but it appears in the anti-commutator of QI2’s. However, by restricting to representations with zero central charge M, or by removing supercharges QI2, the exact Lifshitz algebra is reproduced.5. Non-Relativistic Superalgebras from osp(8*|4)



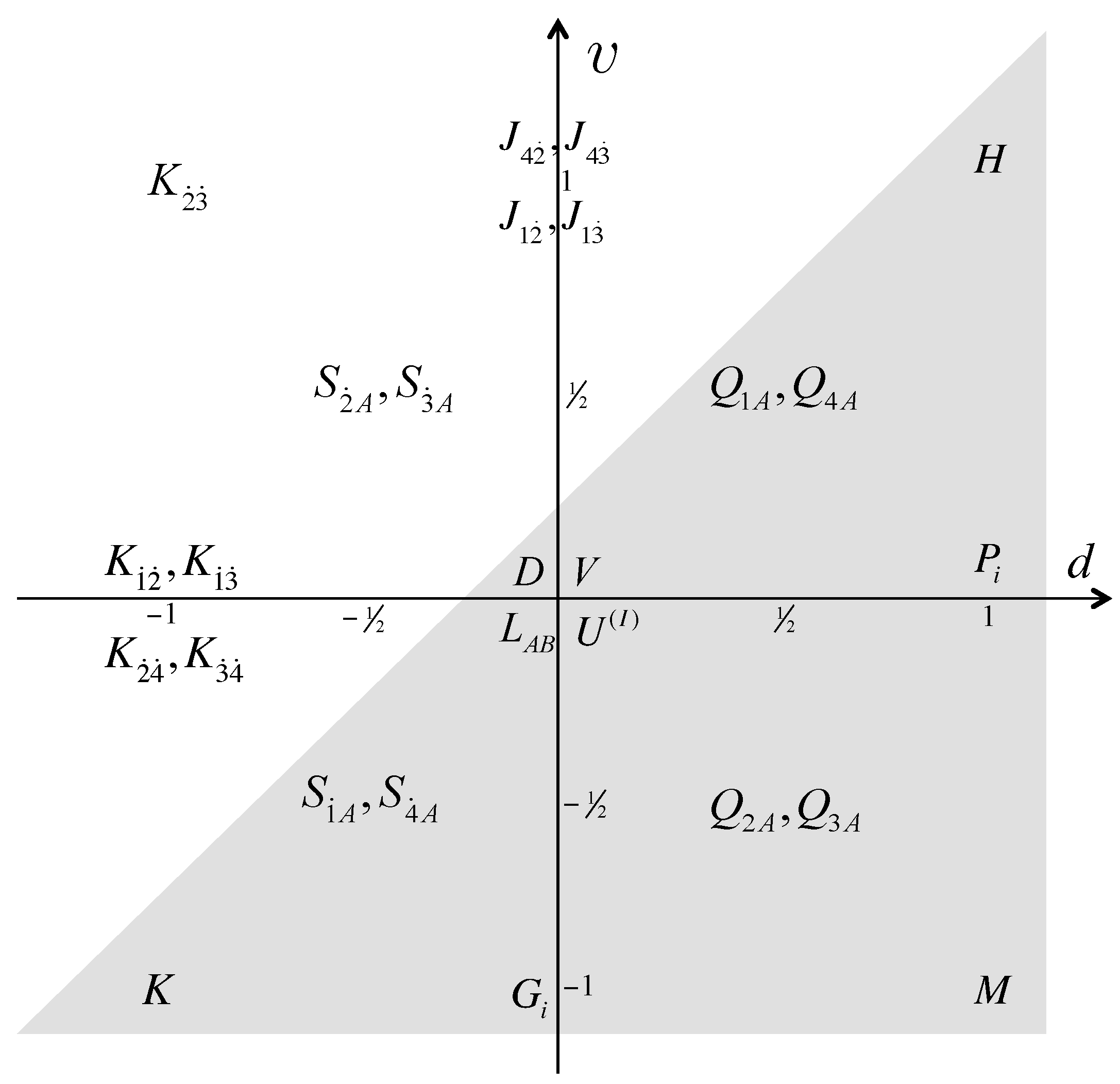


(1) Schrödinger algebra with an arbitrary ![Symmetry 04 00517 i134]() and 24 supercharges (d - υ ≥ 0)
and 24 supercharges (d - υ ≥ 0)


 because dz(H) =
because dz(H) =  . The commutation relations of bosonic subalgebra are
. The commutation relations of bosonic subalgebra are 





(2) Schrödinger algebra with ![Symmetry 04 00517 i134]() = 2 and 24 supercharges (d - υ ≥ 0)
= 2 and 24 supercharges (d - υ ≥ 0)
 = 2 is a bit special again. Then V does not appear in the right-hand side of commutators. It implies that V may be eliminated when
= 2 is a bit special again. Then V does not appear in the right-hand side of commutators. It implies that V may be eliminated when  = 2 . The reduced algebra is generated by the set of the generators,
= 2 . The reduced algebra is generated by the set of the generators, 
(3) Schrödinger algebra with an arbitrary ![Symmetry 04 00517 i134]() and 16 supercharges (d - υ ≥ 0 and d ≥ 0)
and 16 supercharges (d - υ ≥ 0 and d ≥ 0)

(4) Lifshitz algebra with an arbitrary ![Symmetry 04 00517 i134]() and 16 supercharges (d - υ ≥ 0 and d + υ ≥ 0)
and 16 supercharges (d - υ ≥ 0 and d + υ ≥ 0)

 = 2 , by restricting to representations with zero central charge M or by removing half of supersymmetries.
= 2 , by restricting to representations with zero central charge M or by removing half of supersymmetries.6. Summary
 . We hope that our result would be useful in constructing gravity solutions preserving superalgebras including the anisotropic scaling and in discussing the relation to the field-theory side.
. We hope that our result would be useful in constructing gravity solutions preserving superalgebras including the anisotropic scaling and in discussing the relation to the field-theory side.A. psu(2,2|4)


 and
and 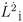







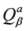 (its conjugate
(its conjugate 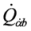 )
) 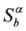 (its conjugate
(its conjugate 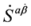 )
) 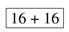

 and special conformal transformation
and special conformal transformation 

B. osp(p|2q)













Example: osp(8|4)

 ,
, , and
, and  is the symplectic form.
is the symplectic form. ) with
) with  = 1, 2 . Then the related quantities are rewritten as
= 1, 2 . Then the related quantities are rewritten as 
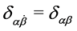 Note that
Note that 
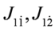 and
and 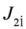 are regarded as independent generators. It is straightforward to rewrite the (anti-)commutation relations of osp(8|4) in terms of these generators.
are regarded as independent generators. It is straightforward to rewrite the (anti-)commutation relations of osp(8|4) in terms of these generators. 

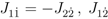 and
and 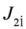 )
) 



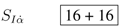



C. osp(8*|4)


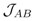 is the symplectic form. The anti-symmetric matrix RIJ generates so(2,6) . The symmetric matrix LAB generates usp(4).
is the symplectic form. The anti-symmetric matrix RIJ generates so(2,6) . The symmetric matrix LAB generates usp(4).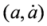 with a = 1,…4 and
with a = 1,…4 and 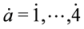 . Then the related quantities are rewritten as [37].
. Then the related quantities are rewritten as [37]. 

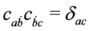 and
and 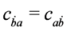 .
.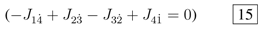









7. Acknowledgments
References and Notes
- Maldacena, J.M. The large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge theory correlators from non-critical string theory. Phys. Lett. B 1998, 428, 105–114. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar]
- Hartnoll, S.A. Lectures on holographic methods for condensed matter physics. Class. Quant. Grav. 2009, 26, 224002:1–224002:61. [Google Scholar]
- Sachdev, S. Condensed matter and AdS/CFT. Lect. Notes Phys. 2011, 828, 273–311. [Google Scholar] [CrossRef]
- Son, D.T. Toward an AdS/cold atoms correspondence: A Geometric realization of the Schrodinger symmetry. Phys. Rev. D 2008, 78, 046003:1–046003:7. [Google Scholar]
- Balasubramanian, K.; McGreevy, J. Gravity duals for non-relativistic CFTs. Phys. Rev. Lett. 2008, 101, 061601:1–061601:4. [Google Scholar]
- Kachru, S.; Liu, X.; Mulligan, M. Gravity Duals of Lifshitz-like Fixed Points. Phys. Rev. D 2008, 78, 106005:1–106005:8. [Google Scholar]
- Schafer-Nameki, S.; Yamazaki, M.; Yoshida, K. Coset Construction for Duals of Non-relativistic CFTs. J. High Energy Phys. 2009. [Google Scholar]
- Hagen, C.R. Scale and conformal transformations in galilean-covariant field theory. Phys. Rev. D 1972, 5, 377–388. [Google Scholar]
- Niederer, U. The maximal kinematical invariance group of the free Schrodinger equation. Helv. Phys. Acta 1972, 45, 802–810. [Google Scholar]
- Henkel, M. Schrodinger invariance in strongly anisotropic critical systems. J. Statist. Phys. 1994, 75, 1023–1061. [Google Scholar] [CrossRef]
- Nishida, Y.; Son, D.T. Nonrelativistic conformal field theories. Phys. Rev. D 2007, 76, 086004:1–086004:14. [Google Scholar]
- Duval, C.; Horvathy, P.A. On Schrodinger superalgebras. J. Math. Phys. 1994, 35, 2516–2538. [Google Scholar] [CrossRef]
- Henkel, M.; Unterberger, J. Supersymmetric extensions of Schrödinger invariance. Nucl. Phys. B 2006, 746, 155–201. [Google Scholar] [CrossRef]
- Sakaguchi, M.; Yoshida, K. Super Schrödinger algebra in AdS/CFT. J. Math. Phys. 2008, 49, 102302:1–102302:13. [Google Scholar]
- Sakaguchi, M.; Yoshida, K. More super Schrodinger algebras from psu(2,2|4). J. High Energy Phys. 2008. [Google Scholar]
- Maldacena, J.M.; Martelli, D.; Tachikawa, Y. Comments on string theory backgrounds with non-relativistic conformal symmetry. J. High Energy Phys. 2008.
- Hartnoll, S.A.; Yoshida, K. Families of IIB duals for nonrelativistic CFTs. J. High Energy Phys. 2008. [Google Scholar]
- Donos, A.; Gauntlett, J.P. Supersymmetric solutions for non-relativistic holography. J. High Energy Phys. 2009. [Google Scholar]
- Donos, A.; Gauntlett, J.P. Solutions of type IIB and D=11 supergravity with Schrodinger(z) symmetry. J. High Energy Phys. 2009. [Google Scholar]
- Ooguri, H.; Park, C.-S. Supersymmetric non-relativistic geometries in M-theory. Nucl. Phys. B 2010, 824, 136–153. [Google Scholar] [CrossRef]
- Donos, A.; Gauntlett, J.P. Schrodinger invariant solutions of type IIB with enhanced supersymmetry. J. High Energy Phys. 2009. [Google Scholar]
- Bobev, N.; Kundu, A. Deformations of Holographic Duals to Non-Relativistic CFTs. J. High Energy Phys. 2009. [Google Scholar]
- Bobev, N.; Kundu, A.; Pilch, K. Supersymmetric IIB Solutions with Schrodinger Symmetry. J. High Energy Phys. 2009. [Google Scholar]
- Liu, H.-S.; Lu, H. Supersymmetry of the Schrodinger and PP wave solutions in Einstein-Weyl supergravities. 2012. arXiv:1206.4371.. [Google Scholar]
- Balasubramanian, K.; Narayan, K. Lifshitz spacetimes from AdS null and cosmological solutions. J. High Energy Phys. 2010. arXiv:1005.3291v3.. [Google Scholar]
- Donos, A.; Gauntlett, J.P. Lifshitz Solutions of D = 10 and D = 11 supergravity. J. High Energy Phys. 2010. [Google Scholar]
- Gregory, R.; Parameswaran, S.L.; Tasinato, G.; Zavala, I. Lifshitz solutions in supergravity and string theory. J. High Energy Phys. 2010. [Google Scholar]
- Cassani, D.; Faedo, A.F. Constructing Lifshitz solutions from AdS. J. High Energy Phys. 2011. [Google Scholar]
- Halmagyi, N.; Petrini, M.; Zaffaroni, A. Non-Relativistic Solutions of N = 2 Gauged Supergravity. J. High Energy Phys. 2011. [Google Scholar]
- Narayan, K. Lifshitz-like systems and AdS null deformations. Phys. Rev. D 2011, 84, 086001:1–086001:10. [Google Scholar]
- Chemissany, W.; Hartong, J. From D3-Branes to Lifshitz Space-Times. Class. Quant. Grav. 2011, 28, 195011:1–195011:13. [Google Scholar]
- Beisert, N. The dilatation operator of N = 4 super Yang-Mills theory and integrability. Phys. Rept. 2005; 405, 1–202. [Google Scholar]
- The triality of SO(8) and hence of SO*(8) makes this possible. Concretely, we take
- Claus, P.; Kallosh, R.; Van Proeyen, A. M 5-brane and superconformal (0,2) tensor multiplet in 6 dimensions. Nucl. Phys. B 1998, 518, 117–150. [Google Scholar]
- A chiral spinor of SO(2,6) is decomposed into
under
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sakaguchi, M.; Yoshida, K. Supersymmetric Extensions of Non-Relativistic Scaling Algebras. Symmetry 2012, 4, 517-536. https://doi.org/10.3390/sym4030517
Sakaguchi M, Yoshida K. Supersymmetric Extensions of Non-Relativistic Scaling Algebras. Symmetry. 2012; 4(3):517-536. https://doi.org/10.3390/sym4030517
Chicago/Turabian StyleSakaguchi, Makoto, and Kentaroh Yoshida. 2012. "Supersymmetric Extensions of Non-Relativistic Scaling Algebras" Symmetry 4, no. 3: 517-536. https://doi.org/10.3390/sym4030517
APA StyleSakaguchi, M., & Yoshida, K. (2012). Supersymmetric Extensions of Non-Relativistic Scaling Algebras. Symmetry, 4(3), 517-536. https://doi.org/10.3390/sym4030517