Abstract
In order to investigate why crystal symmetry lowers with increasing temperature by phase transition of TII–III (=369 K) in Cs3H(SeO4)2, in spite of the fact that crystal symmetry in the high-temperature phase of many ionic conductors becomes higher by the phase transition, we have studied the relation between the change in crystal symmetry and the appearance of proton motion. It was found from the analysis of domains based on crystal structure that the number of possible geometrical arrangement of hydrogen bond in phase II becomes two times larger than that in phase III, derived from the lowering of crystal symmetry with increasing temperature. These results indicate that the lowering of crystal symmetry in phase II appears by the increase of the number of geometrical arrangements and by the enhancement of the flexibility of hydrogen bond. Considering that the enhancement of the flexibility of hydrogen bond yields mobile proton in phase II, it is deduced that mobile proton in phase II appears in exchange for the lowering of crystal symmetry at II–III phase transition.
1. Introduction
It is known that M3H(XO4)2 compounds (M = K, Rb, Cs; X = S, Se) exhibit a superprotonic conductivity and becomes the electrolyte of the fuel cell [1,2,3,4,5,6,7,8,9,10,11]. The Cs3H(SeO4)2 crystal, which is one of M3H(XO4)2 superprotonic conductors, exhibits a superprotonic conductivity above 456 K (=TI–II). At room temperature, the Cs3H(SeO4)2 crystal shows a ferroelasticity and becomes insulator [12,13]. Moreover, Cs3H(SeO4)2 shows the interesting feature that the phase transition from the low-temperature monoclinic-C2/m phase (phase III) to high-temperature monoclinic-A2/a phase (phase II) exists at 369 K (=TII–III) [14,15,16,17,18]. In conjunction with the phase transition at TII–III, some interesting phenomena are observed [18]. For example: (1) Mobile proton appears above TII–III, as shown in the motional narrowing of NMR line width in Figure 1a; and (2) the increase of the electrical conductivity is observed above TII–III as a precursor effect of superprotonic conductivity (Figure 1b) [18]. Furthermore, the spatial symmetry C2/m in phase III is higher than the symmetry of A2/a in phase II. That is, in Cs3H(SeO4)2, the crystal symmetry decreases by TII–III with the increase of temperature, in spite of the fact that crystal symmetry in a lot of materials becomes higher with increasing temperature. In this way, the phase transition at TII–III includes useful information needed to understand the relation between proton conductivity and the change in crystal symmetry. Therefore the investigation of the phase transition of TII–III will lead to the key factor needed for the appearance of flexibility of proton migration which determines proton conductivity. In the present study, we have examined possible proton sites before and after II–III phase transition from the geometrical arrangement of hydrogen bond, and have investigated why the lowering of crystal symmetry at TII–III is realized.
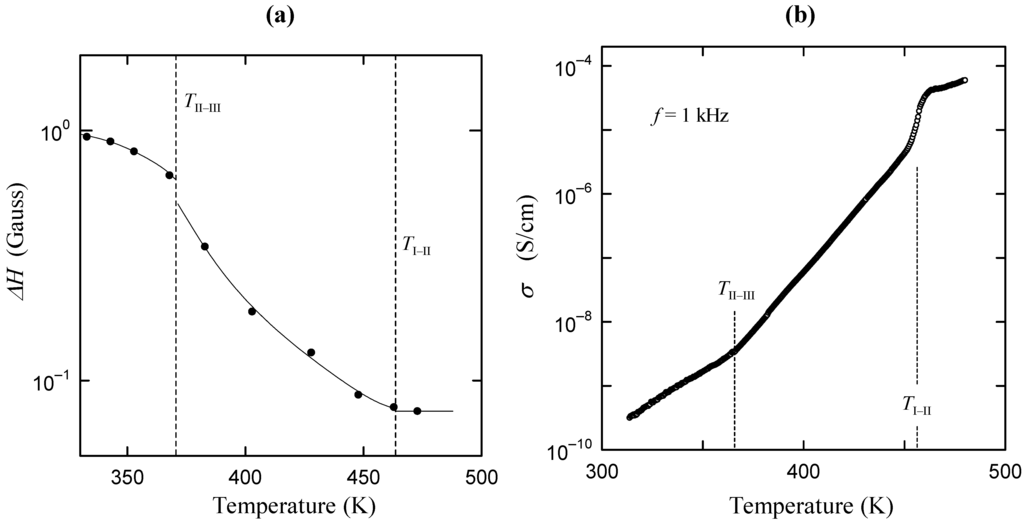
Figure 1.
(a) Temperature dependence of the line width ΔH in the 1H-NMR absorption line; (b) Temperature dependence of electrical conductivity along the b axis.
2. Experimental Procedure and Crystal Structure
2.1. Experimental Procedure
Cs3H(SeO4)2 single crystals were grown by the slow evaporation method from an aqueous solution of Cs2SeO4 and H2SeO4 with a molar ratio of Cs2SeO4/H2SeO4 = 3:1 at 35 °C. Optical observations were carried out using the polarizing microscope. The specimens used in the optical observations were approximately 0.1 to 0.2 mm in thickness.
2.2. Crystal Structure
In order to obtain the possible geometrical arrangement of hydrogen bond from the change in ferroelastic domain structure, it is necessary to use the crystal structure. Therefore, in this subsection, we show the crystal structure in phases III, II and I. Figure 2a–c show the crystal structures in phases III, II and I, respectively, based on the results reported by Merinov et al. [13,14,15]. In phase III, the Cs3H(SeO4)2 crystal belongs to a monoclinic system with the space group C2/m. The lattice parameters are aIII = 10.903(3) Å, bIII = 6.3904(8) Å, cIII = 8.452(2) Å, βIII = 112.46(1)° and Z = 2 at room temperature [16]. As shown in Figure 2a, it is evident that in phase III the hydrogen bonds are composed between SeO4 tetrahedrons along the direction parallel to the a-axis. In phase II, the crystal shows the monoclinic-A2/a symmetry. The lattice parameters are aII = 11.037(1) Å, bII = 6.415(1) Å, cII = 16.042(4) Å, βII = 102.69(1)° and Z = 4 at 400 K [14]. Moreover, in phase II, the hydrogen bonds are formed between SeO4 tetrahedrons along the approximately [310] or 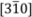 direction, as shown in Figure 2b. In phase I, the Cs3H(SeO4)2 crystal belongs to a trigonal system with the space group
direction, as shown in Figure 2b. In phase I, the Cs3H(SeO4)2 crystal belongs to a trigonal system with the space group 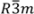 . The lattice constants become aI = 6.4260(6) Å, cI = 23.447(2) Å, Z = 3 at 470 K [15]. As shown in Figure 2c, the distance between neighboring O(2) atoms is same in time-averaged structure. Considering that hydrogen bond is composed between O(2) atoms, three equivalent positions for a proton appear in phase I, and proton conductivity is realized in phase I. In this way, from the crystal structure, we can clearly see that the phase transitions of TII–III and TI–II are structural phase transition. Especially, it is interesting property that the orientation of the hydrogen bond by the phase transition of TII–III mainly changes. This result implies that the difference in the geometrical arrangement of hydrogen bond observed in phases III and II includes the information for the flexibility of proton motion and the lowering of crystal symmetry at TII–III phase transition.
. The lattice constants become aI = 6.4260(6) Å, cI = 23.447(2) Å, Z = 3 at 470 K [15]. As shown in Figure 2c, the distance between neighboring O(2) atoms is same in time-averaged structure. Considering that hydrogen bond is composed between O(2) atoms, three equivalent positions for a proton appear in phase I, and proton conductivity is realized in phase I. In this way, from the crystal structure, we can clearly see that the phase transitions of TII–III and TI–II are structural phase transition. Especially, it is interesting property that the orientation of the hydrogen bond by the phase transition of TII–III mainly changes. This result implies that the difference in the geometrical arrangement of hydrogen bond observed in phases III and II includes the information for the flexibility of proton motion and the lowering of crystal symmetry at TII–III phase transition.
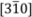 direction, as shown in Figure 2b. In phase I, the Cs3H(SeO4)2 crystal belongs to a trigonal system with the space group
direction, as shown in Figure 2b. In phase I, the Cs3H(SeO4)2 crystal belongs to a trigonal system with the space group 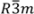 . The lattice constants become aI = 6.4260(6) Å, cI = 23.447(2) Å, Z = 3 at 470 K [15]. As shown in Figure 2c, the distance between neighboring O(2) atoms is same in time-averaged structure. Considering that hydrogen bond is composed between O(2) atoms, three equivalent positions for a proton appear in phase I, and proton conductivity is realized in phase I. In this way, from the crystal structure, we can clearly see that the phase transitions of TII–III and TI–II are structural phase transition. Especially, it is interesting property that the orientation of the hydrogen bond by the phase transition of TII–III mainly changes. This result implies that the difference in the geometrical arrangement of hydrogen bond observed in phases III and II includes the information for the flexibility of proton motion and the lowering of crystal symmetry at TII–III phase transition.
. The lattice constants become aI = 6.4260(6) Å, cI = 23.447(2) Å, Z = 3 at 470 K [15]. As shown in Figure 2c, the distance between neighboring O(2) atoms is same in time-averaged structure. Considering that hydrogen bond is composed between O(2) atoms, three equivalent positions for a proton appear in phase I, and proton conductivity is realized in phase I. In this way, from the crystal structure, we can clearly see that the phase transitions of TII–III and TI–II are structural phase transition. Especially, it is interesting property that the orientation of the hydrogen bond by the phase transition of TII–III mainly changes. This result implies that the difference in the geometrical arrangement of hydrogen bond observed in phases III and II includes the information for the flexibility of proton motion and the lowering of crystal symmetry at TII–III phase transition. 3. Results and Discussion
Figure 3a–c show domain structures viewed along the direction perpendicular to the (001) plane in phases III, II and I in Cs3H(SeO4)2, respectively. It is evident that domain structure changes at the phase transition of TII–III and TI–II. As shown in Figure 3a, optical observation by means of polarizing microscope indicate that the Cs3H(SeO4)2 crystal in phase III is optically biaxial with an interrelationship between the crystallographic axes (aIII, bIII in phase III) and the indicatrix axes (X, Y): aIII//X, bIII//Y in phase III. In phase III, domains consist of polydomains with the two types of domain boundaries. In the present paper, the observed three kinds of domains in phase III (or phase II) are called as domains D1, D2 and D3, and two types of domain boundaries are named as W- and W'-domain boundaries. The W- and W'-domain boundaries were classified as the planes of {311} and {11n} respectively, where, n is determined by the strain compatibility condition. Moreover, the adjacent domains separated by the W- or W'-domain boundary are related to the mirror symmetry on the W-domain boundary or the twofold rotational symmetry on the W'-domain boundary, respectively. We can also see that the orientation of any domain Di is different by almost 120° from that of its adjacent domain Dj (i, j = 1, 2 and 3).
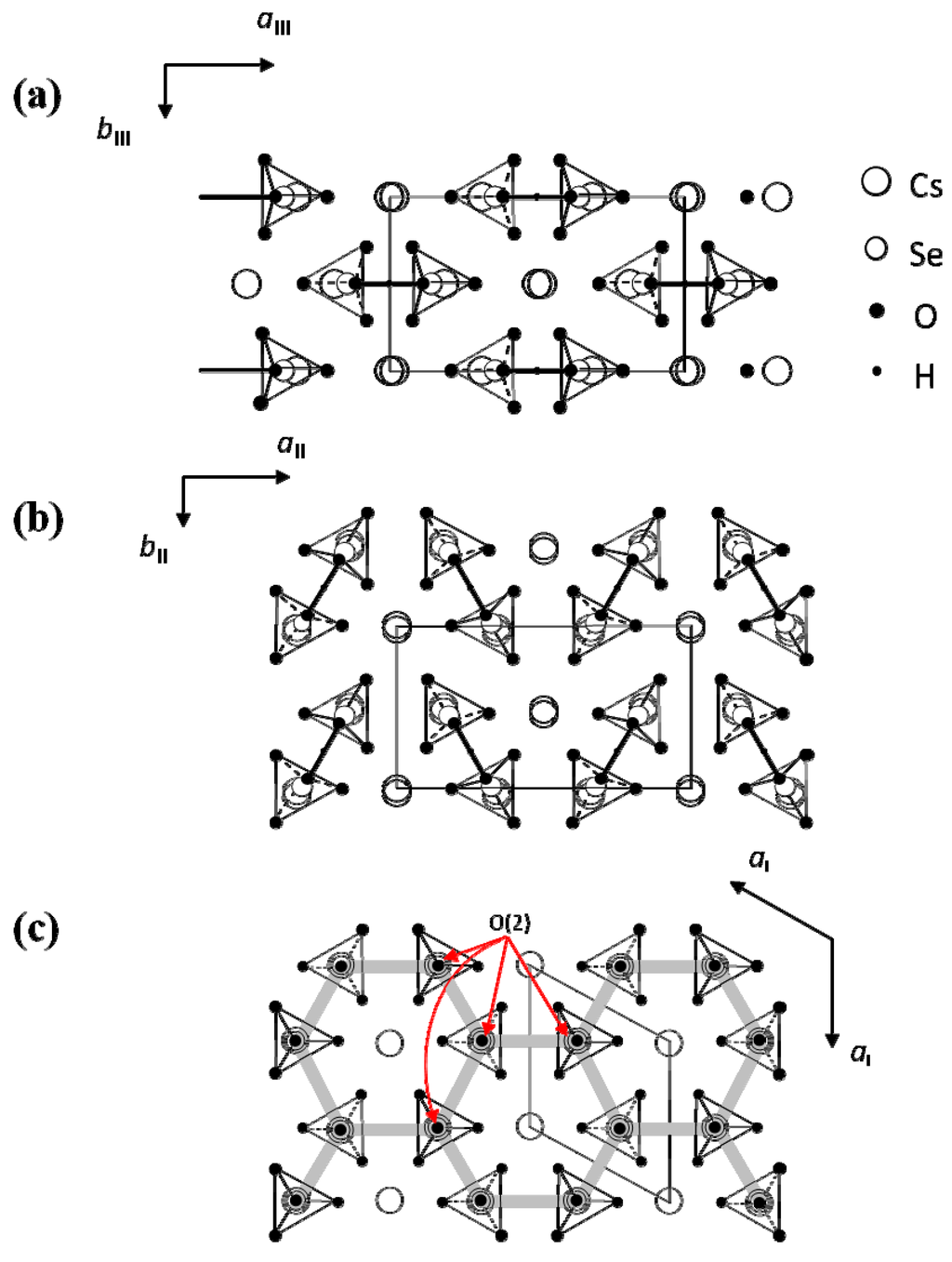
Figure 2.
Crystal structure in the a–b plane (a) in phase III; (b) in phase II and (c) in phase I. Tetrahedrons shown by the dashed and solid lines are shown in downward and upward SeO4 tetrahedrons, respectively. Bold gray lines in (c) show the possible hydrogen bonds.
The angles θ between the aIII (or bIII) axes of neighboring two domains are observed as θ = 119.0° for the W-domain boundary and θ = 121.0° for the W'-domain boundary. The angle between the aIII (or bIII) axes of neighboring two domains are calculated from the lattice constants using the equations, θ = 2 tan -1 (aIII/bIII) in the W-domain boundary and θ = π − 2 tan -1 (aIII/3bIII) in the W'-domain boundary. The observed angles agree satisfactorily with the calculated values θ = 119.25° in the W-domain boundary and θ = 120.74° in the W'-domain boundary. In phase II, domain structure changes from that observed in phase III by the phase transition of TII–III, as shown in Figure 3b. From this result, we can confirm that crystal symmetry changes at TII–III. The crystal in phase II is also optically biaxial with a relation between the crystallographic axes (aII, bII in phase II) and the indicatrix axes (X, Y): aII//X, bII//Y in phase II, respectively. Moreover, it is noted that the kinds of domain and domain boundary in phase II are the same as those in phase III, although the domain pattern changes at II–III phase transition. The angles θ between the aII (or bII) axes of neighboring two domains are observed as θ = 119.5° for the W-domain boundary and θ = 120.5° for the W'-domain boundary. These values are in good agreement with the values θ = 119.67° and θ = 120.33° calculated from the values of aII and bII in phase II. In this way, these angles in phase II are almost the same as those observed in phase III. These facts imply that the change in crystal structure is slight at II–III phase transition.
Figure 3.
Domain structure (a) in phase III; (b) in phase II and (c) in phase I. Symbol of cross denotes the directions of crystal axes.
According to Sapriel [19], the orientation of domain boundaries generated by the ferroelastic phase transition from to A2/a is the same as those from to C2/m, because the orientation of the domain boundaries is determined by the change in the point group. This is consistent with our results. On the other hand, as shown in Figure 3c, in phase I, we can see clearly that the domain boundaries disappear just above TI–II, and the crystal becomes optically uniaxial. The result in the present study is also consistent with the fact that the phase transition at TI–II is the ferroelastic-paraelastic phase transition and that the space group in the phase I becomes  . Considering that in the phase transition at TI–II domain boundaries vanish, the averaged structure of the crystal structure in all domains in phase II becomes crystal structure in phase I. That is, the crystal structure in phase I is obtained by averaging and superposing the crystal structure in all domains with the symmetry of domain boundary.
. Considering that in the phase transition at TI–II domain boundaries vanish, the averaged structure of the crystal structure in all domains in phase II becomes crystal structure in phase I. That is, the crystal structure in phase I is obtained by averaging and superposing the crystal structure in all domains with the symmetry of domain boundary.
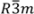 . Considering that in the phase transition at TI–II domain boundaries vanish, the averaged structure of the crystal structure in all domains in phase II becomes crystal structure in phase I. That is, the crystal structure in phase I is obtained by averaging and superposing the crystal structure in all domains with the symmetry of domain boundary.
. Considering that in the phase transition at TI–II domain boundaries vanish, the averaged structure of the crystal structure in all domains in phase II becomes crystal structure in phase I. That is, the crystal structure in phase I is obtained by averaging and superposing the crystal structure in all domains with the symmetry of domain boundary. Figure 4 shows the superposed structure obtained by the superposition of the crystal structure in all domains with the symmetries of W- and W'-domain boundaries. The averaged structure for atomic position in crystal structure of Figure 4 satisfactorily agrees with that obtained from X-ray study in phase I (Figure 2c). In this way, the averaged structure of the crystal structure in all ferroelastic domains gives the structure in high-temperature phase of ferroelastic materials. Moreover, we note that the superposed structure in Figure 4 displays the possible situation of the disordering of atoms. That is, we can obtain the information of the disordering of atom, especially the possible geometrical arrangement of hydrogen bond, from the superposed crystal structure by the ferroelastic domains.
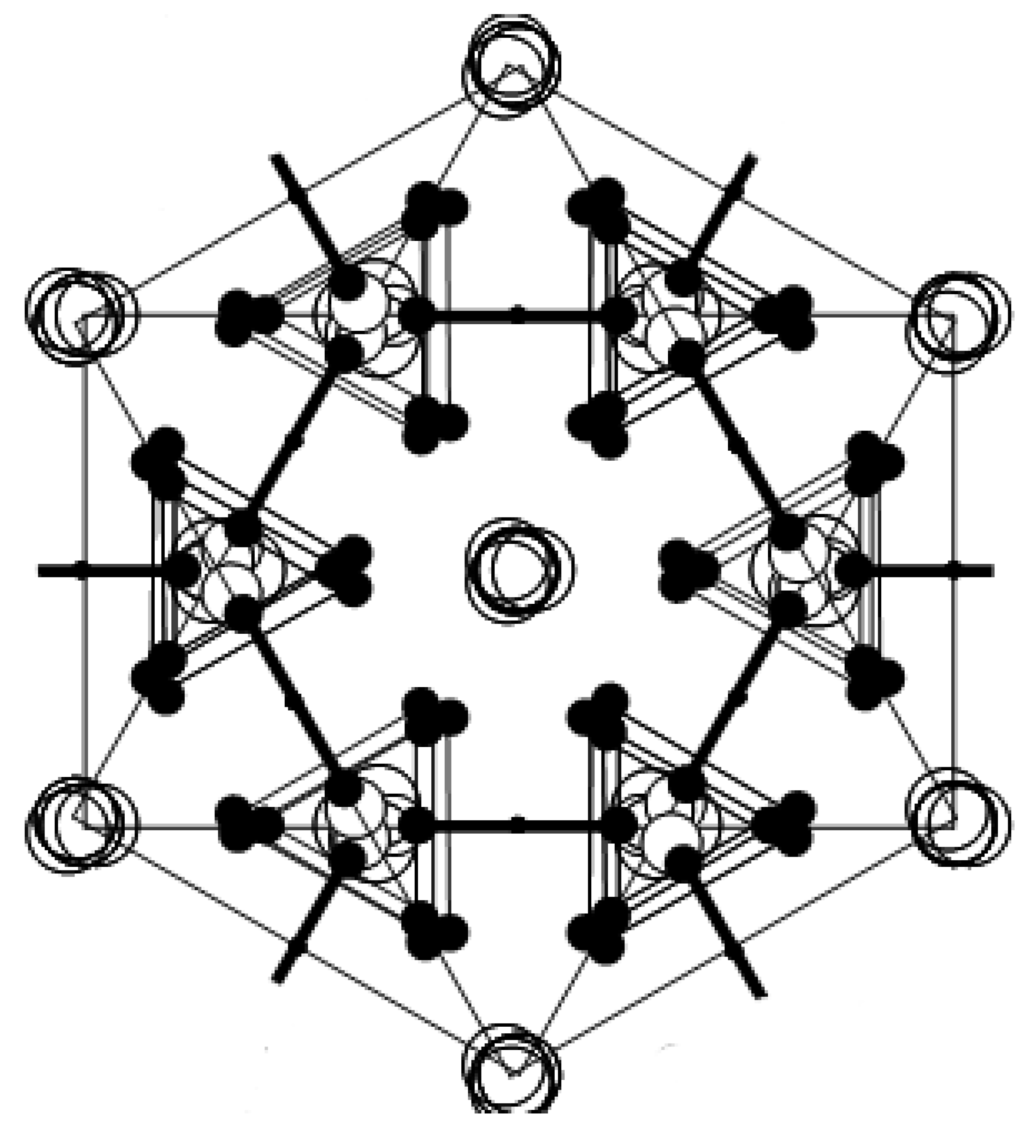
Figure 4.
Superposition of all domains in phase II. Symbol of cross denotes the directions of crystal axes.
In order to investigate the possible geometrical arrangement of hydrogen bond in phases III and II, we have carried out the superposition of crystal structure in domains in phases III and II. Figure 5a,b show the crystal structures in phases III and II including three domains D1, D2 and D3, respectively. In Figure 5a,b, three domains D1, D2 and D3 separated by the W-boundary in phases III and II are shown as an example. It is evident that the main difference in phases III and II is the hydrogen-bond arrangement. As described above, the possible hydrogen-bond arrangement is observed from the superposition of all domains. Figure 5c shows the possible hydrogen-bond arrangement obtained by the superposition of crystal structure of D1 and D3 in phase III, as an example. The hydrogen bonds in Figure 5c are realized by the break and recombination of hydrogen bond in the case of the existence of mobile proton with the position between two hydrogen bonds of phase III kept. Therefore, as shown in Figure 5c, if proton at i-site moves to k-site, j-site proton must be needed to move to l-site, in order to realize the crystal symmetry in phase III. In this way, in phase III, the recombination of two hydrogen bonds is simultaneously needed for one proton transport. That is, when proton is fixed in hydrogen bond, the hydrogen-bond arrangement in phase III is stable. Actually, in phase III, proton migration cannot be observed.
On the other hand, it is known that proton in phase II begins to move as a precursor motion of superprotonic motion, as shown in Figure 1. As described above, when proton moves from one hydrogen bond to another hydrogen bond, the geometrical arrangement of hydrogen bond in phase III is not appropriate. That is, when proton moves between the hydrogen bonds, the recombination of hydrogen bond is difficult in the crystal structure of phase III, because the simultaneous transport of two protons is needed in the crystal structure in phase III. This fact means that the hydrogen-bond pattern should be rearranged by II–III phase transition, as the recombination of hydrogen bond by proton transport is easily realized in phase II. Figure 5d shows the equivalent position obtained from the superposition of domain 1 and domain 3 in phase II, as an example. Considering that protons in phase II move from one hydrogen bond to another hydrogen bond as the precursor motion of superprotonic motion, proton at j'-site can easily move to k'-site without depending on the transport of proton at i'-site by the crystal structure in phase II. This result indicates that proton can easily move with the crystal structure in phase II. That is, the crystal structure in phase II is flexible for proton motion, because proton migration is not suppressed by another hydrogen bond. From these results, it is deduced that the flexibility of hydrogen bond increases in phase II in exchange for the lowering of crystal symmetry. In addition, these results imply that, in order to obtain higher proton conductivity in solid acid electrolyte, it is necessary to design a crystal structure with the flexibility of hydrogen bond. We are now planning to prepare new proton conductors, in which Cs ions are replaced by Tl and Pb ions. These results will appear in future issues.
Figure 5.
Schematic diagram of crystal structure (a) in phase III and (b) in phase II, including three kinds of domains. Domains D1, D2 and D3 are shown by the black, red and blue colors, respectively. Averaged structure composed by the superposition of domains D1 and D3 (c) in phase III and (d) in phase II.
4. Conclusions
In order to investigate the origin of the lowering of crystal symmetry, we investigated the change in possible hydrogen bond patterns by phase transition of TII–III on the basis of the crystal and domain structures. From the analyses of the hydrogen-bond network around TII–III, we found that the number of the network patterns of hydrogen bonds in phase II is two times larger than that in phase III. These results indicate that the increase of the proton activity in phase II is caused by the increase in the number of possible geometrical arrangements of hydrogen bonds. From the analysis of the possible geometrical arrangement of hydrogen bonds, when the proton is fixed in the hydrogen bond, the hydrogen-bond arrangement in phase III is stable. On the other hand, in phase II, the proton can easily move, because the crystal structure in phase II has the flexibility for proton motion and proton migration is not suppressed. From these results, it is deduced that mobile protons in phase II appear in exchange for the lowering of crystal symmetry at II–III phase transition.
References
- Gesi, K. Dielectric properties and phase transitions in X3H(SO4)2 and X3D(SO4)2 crystals (X: K, Rb). J. Phys. Soc. Jpn. 1980, 48, 886–889. [Google Scholar] [CrossRef]
- Baranov, A.I. Crystals with disordered hydrogen-bond networks and superprotonic conductivity: Review. Crystallogr. Rep. 2003, 48, 1012–1037. [Google Scholar] [CrossRef]
- Pawlowski, A.; Pawlaczyk, C.; Hilzcer, B. Electric conductivity in crystal group Me3H(SeO4)2 (Me: NH+4, Rb+, Cs+). Solid State Ionics 1990, 44, 17–19. [Google Scholar] [CrossRef]
- Kamimura, H.; Watanabe, S. A novel approach to the mechanism of ionic conductivity below and at the ferroelastic phase transition in the zero-dimensional hydrogen-bonded crystal M3H(XO4)2 with M = Rb or Cs; X = S or Se. Phil. Mag. 2001, B81, 1011–1019. [Google Scholar] [CrossRef]
- Matsuo, Y.; Takahashi, K.; Ikehata, S. Evidence for proton conduction below superionic transition on Rb3H(SeO4)2. Solid State Commun. 2001, 119, 79–81. [Google Scholar] [CrossRef]
- Matsuo, Y.; Hatori, J.; Nakajima, Y.; Ikehata, S. Superprotonic and ferroelastic phase transition in K3H(SO4)2. Solid State Commun. 2004, 130, 269–274. [Google Scholar] [CrossRef]
- Kamimura, H.; Matsuo, Y.; Ikehata, S.; Ito, T.; Komukae, M.; Osaka, T. On the mechanism of superionic conduction in the zero-dimensional hydrogen-bonded crystals M3H(XO4)2 with M = K, Rb, Cs and X = S, Se. Phys. Status Solidi B 2004, 241, 61–68. [Google Scholar] [CrossRef]
- Matsuo, Y.; Hatori, J.; Yoshida, Y.; Saito, K.; Ikehata, S. Proton conductivity and spontaneous strain below superprotonic phase transition in Rb3H(SeO4)2. Solid State Ionics 2005, 176, 2461–2465. [Google Scholar] [CrossRef]
- Hatori, J.; Matsuo, Y.; Ikehata, S. The relation between elasticity and the superprotonic phase transition temperature for M3H(XO4)2. Solid State Commun. 2006, 140, 452–454. [Google Scholar] [CrossRef]
- Ishii, T. Superprotonic phase transition in M3H(XO4)2. Solid State Ionics 2007, 178, 667–670. [Google Scholar] [CrossRef]
- Matsuo, Y.; Tanaka, Y.; Hatori, J.; Ikehata, S. Effect of uniaxial stress in superprotonic phase transition in Cs3H(SeO4)2. Solid State Ionics 2008, 179, 1125–1127. [Google Scholar] [CrossRef]
- Komukae, M.; Osaka, T.; Kaneko, T.; Makita, Y. Dielectric study of phase transitions in Cs3H(SeO4)2 and its isotope effect. J. Phys. Soc. Jpn. 1985, 54, 3401–3405. [Google Scholar] [CrossRef]
- Baranov, A.I.; Tregubchenko, A.V.; Shuvalov, L.A.; Shchagina, N.M. Structural phase transitions and proton conductivity of Cs3H(SeO4)2 and (NH4)3H(SeO4)2 crystals. Sov. Solid State Phys. 1987, 29, 1448–1449. [Google Scholar]
- Merinov, B.V.; Baranov, A.I.; Shuvalov, L.A. Crystal structure of ferroelastic phase II of Cs3H(SeO4)2. Sov. Phys. Crystallogr. 1991, 36, 639–642. [Google Scholar]
- Merinov, B.V.; Baranov, A.I.; Shuvalov, L.A. Crystal structure and mechanism of protonic conductivity of the superionic phase of Cs3H(SeO4)2. Sov. Phys. Crystallogr. 1990, 35, 200. [Google Scholar]
- Merinov, B.V.; Bolotina, N.B.; Baranov, A.I.; Shuvalov, L.A. Crystal structure of Cs3H(SeO4)2 (T = 295 K) and its changes at the phase transitions. Sov. Phys. Crystallogr. 1988, 33, 824–827. [Google Scholar]
- Komukae, M.; Sakata, K.; Osaka, T.; Makita, Y. Optical and x-ray studies in ferroelastic Cs3H(SeO4)2. J. Phys. Soc. Jpn. 1994, 63, 1009–1017. [Google Scholar] [CrossRef]
- Matsuo, Y.; Tanaka, Y.; Hatori, J.; Ikehata, S. Proton activity and spontaneous strain of Cs3H(SeO4)2 in the phase transition at 369 K. Solid State Commun. 2005, 134, 361–365. [Google Scholar]
- Sapriel, J. Domain-wall orientation in ferroelastic. Phys. Rev. B 1975, 12, 5128–5140. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).