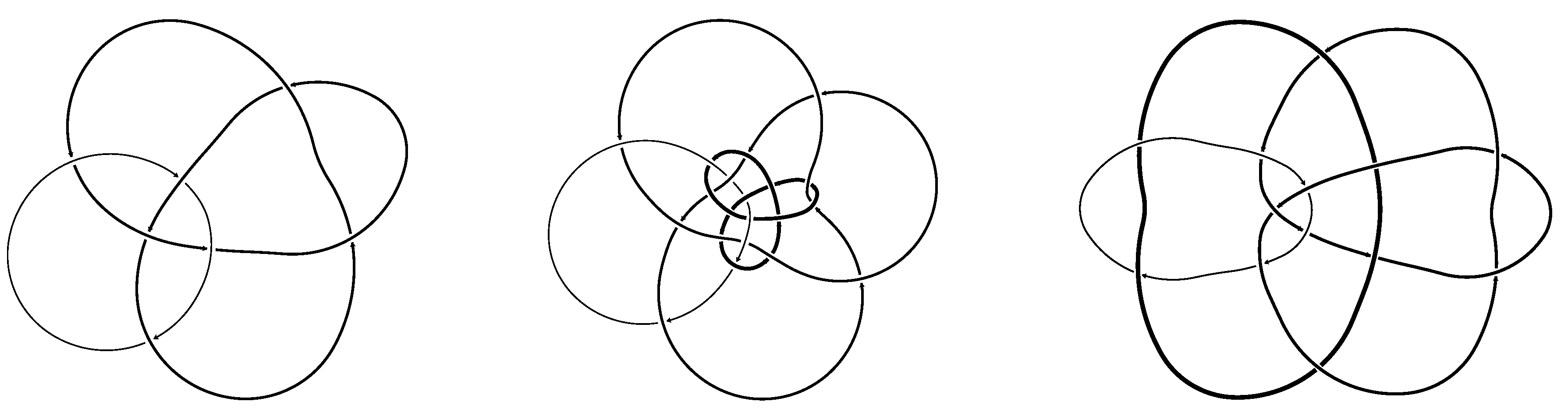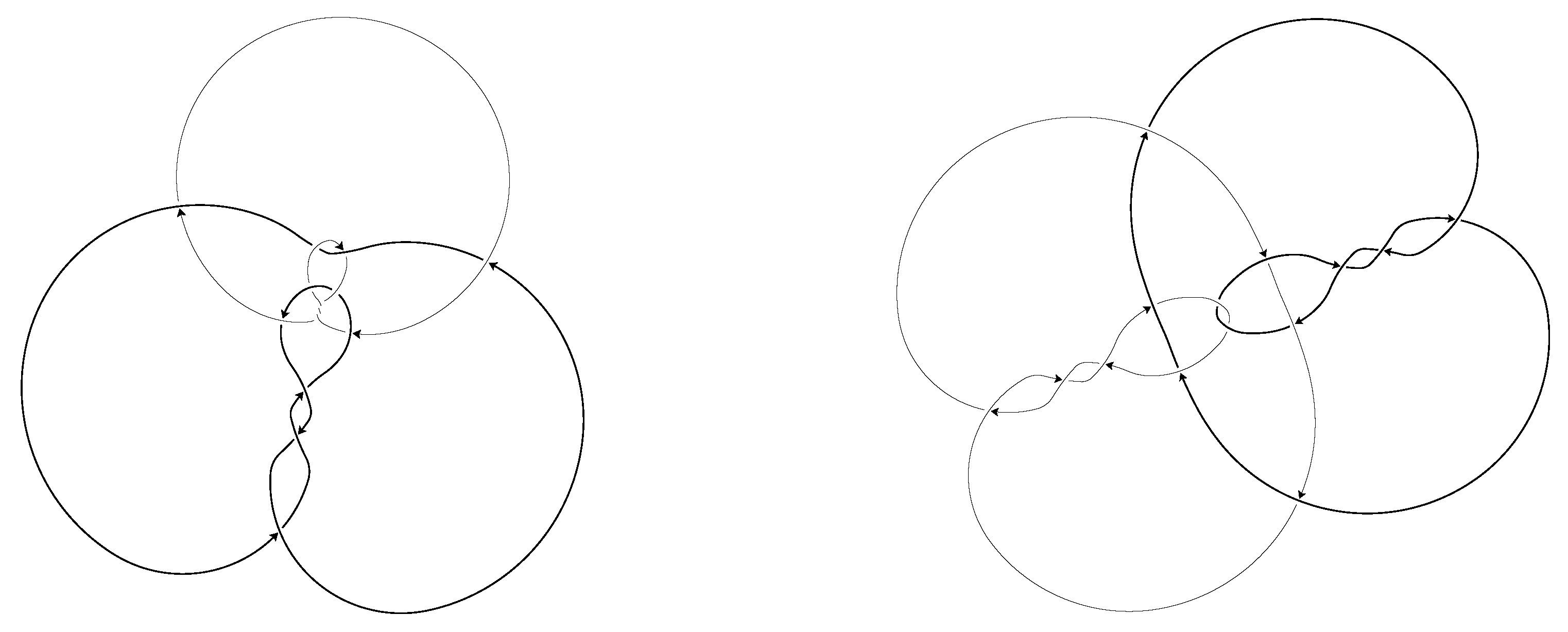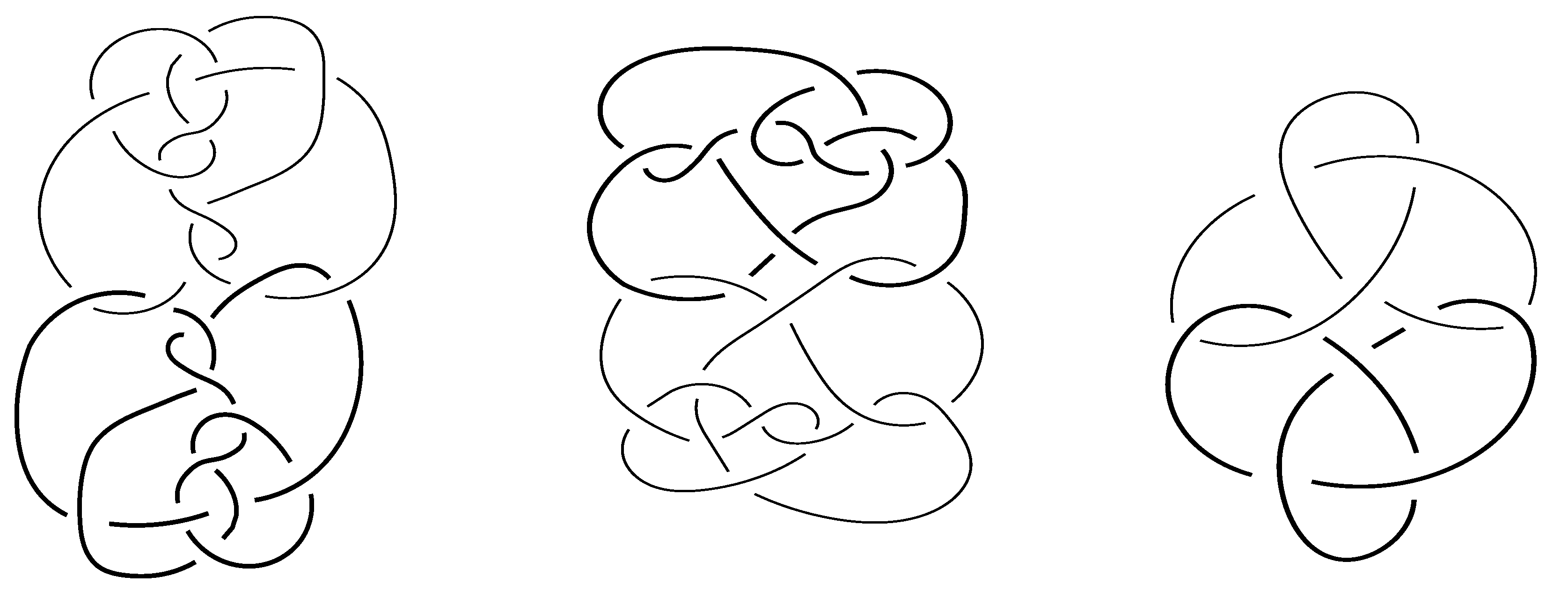1. Introduction
The symmetry group of a link
L is a well-studied object in knot theory. It is defined to be the mapping class group of the pair
and is frequently denoted
. A variety of approaches exist for computing symmetry groups for prime knots and links; see for instance [
1,
2,
3,
4].
This paper considers a different but related group of link symmetries. The image of the group homomorphism
represents what we call
intrinsic link symmetries, where we focus upon the action on
L itself and only record the orientation of the ambient
.
Without using the language of mapping class groups Whitten [
5], following ideas of Fox, defined the group structure of
in 1969. They denoted this group as either
or
, where
is the number of components of
L . This group (cf. Definition 2.1) can be described as a semidirect product of
groups recording the orientation of each component of the link
L with the permutation group
representing component exchanges, crossed with another
recording the orientation of
:
An element
in
acts on
L to produce a new link
. If
, then
and
L are the same as sets; however the components of
L have been renumbered and reoriented. If
, the new link
is the mirror image of
L , again with renumbering and reorientation. We can then define the intrinsic symmetry group
by
We refer to our paper [
6] for a thorough description of the history, construction, and applications of intrinsic symmetry groups. In that paper, we find the intrinsic symmetry groups for all 48 prime links of eight or fewer crossings.
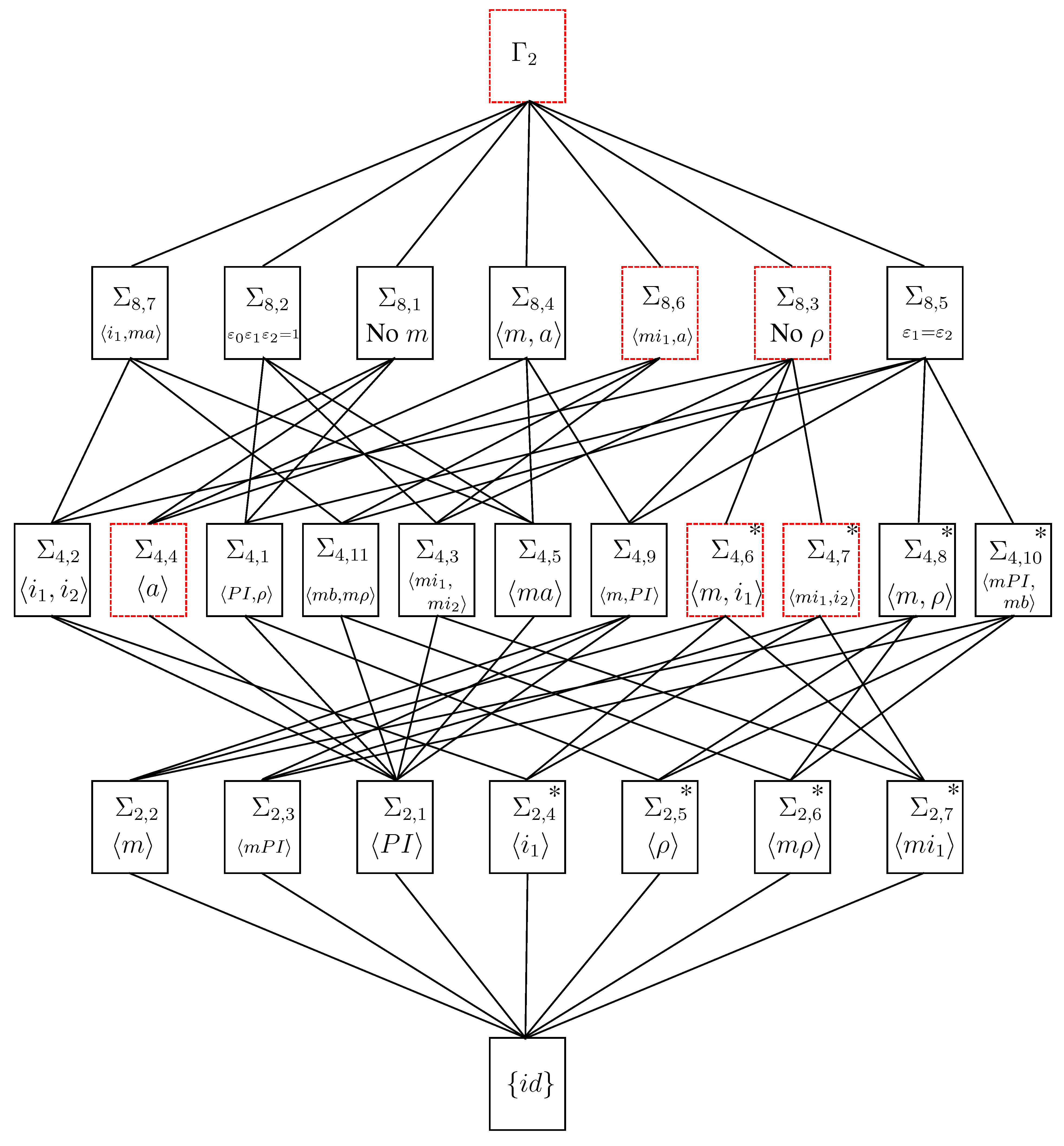
The goal of this paper is to describe how frequently the various possible intrinsic symmetry groups of two-component links occur in examples. There are 27 possible symmetry groups, representing the different subgroups of
up to conjugacy. The subgroups are only considered up to conjugacy as conjugation corresponds to merely relabeling and reorienting the components of the link; see
Section 2.3.
Figure 1 displays the subgroup lattice of
. In
Table 1, we present prime, nonsplit examples for 21 of these groups; some examples are already known, some are new. Many new examples were found using the software
SnapPea; see
Section 3 for details. We present in
Table 2 a report on how frequently each symmetry group occurs among the 77,036 two-component hyperbolic links with 14 or fewer crossings. In
Section 5, we restrict to the case of alternating, nonsplit two-component links, for which only 12 of the 27 symmetry groups are possible. In particular, no alternating link with an even number of components may have full symmetry. We realize alternating, prime examples for 11 of these 12 groups.
2. The Whitten Group
We begin by giving the details of our construction of the Whitten group
and the symmetry group
. Consider operations on an oriented, labeled link
L with
components. We may reverse the orientation of any of the components of
L or permute the components of
L by any element of the permutation group
. However, these operations must interact with each other as well: if we reverse component 3 and exchange components 3 and 5, we must decide whether the orientation is reversed before or after the permutation. Further, we can reverse the orientation on the ambient
as well, a process which is clearly unaffected by the permutation. To formalize our choices, we follow [
5] to introduce the Whitten group of a
-component link.
Definition 2.1 Consider the homomorphism given bywhere is defined asFor and , we define the Whitten group
as the semidirect product with the group operation 2.1. Intrinsic Symmetries of a Link
Given a link
L consisting of
oriented knots in
, we may order the knots so that
Consider the following operations on
L :
Let
be a combination of any of the moves (1), (2), or (3). We think of
as an element of the set
in the following way. Let
and
Lastly, let
be the permutation of the
associated to
. To be explicitly clear, permutation
p permutes the labels of the components; the component originally labeled
i will be labeled
after the action of
.
For each element,
in
, we define
where
is
with orientation reversed and
is the mirror image of
. We note that the
appears above either for all component knots or for none; it appears if
, meaning the entire link
L is mirrored,
i.e., we reverse the ambient orientation on
. Note that the
i th component of
is
the possibly reversed or mirrored
th component of
L . Since we are applying
instead of
to
we are taking the convention of first permuting and then reversing the appropriate components.
We can now define the subgroup of which corresponds to the symmetries of the link L.
Definition 2.2 Given a link, L and , we say that L admits
when there exists an isotopy taking each component of L to the corresponding component of which respects the orientations of the components. We define the intrinsic symmetry group
(also called the Whitten symmetry group
) of L to be The intrinsic symmetry group is a subgroup of , and its left cosets represent the different isotopy classes of links among all symmetries . By counting the number of cosets, we determine the number of (labeled, oriented) isotopy classes of a particular prime link.
Next, we provide a few examples of symmetry subgroups. Recall that the first Whitten group has order four and that is a non-Abelian 16 element group.
Example 2.3 Let , a trefoil knot. It is well known that and , but , so we have . This means that the two cosets of are and , and there are two isotopy classes of knots. A trefoil knot is thus invertible. ⋄
Example 2.4 Let , whose components are an unknot and a trefoil . Since the components and are of different knot types, we conclude that no symmetry in can contain the permutation . As we describe in [6], certain symmetries are impossible for alternating links with nonzero self-writhe, such as . In particular, such a link never admits a symmetry that reverses the ambient orientation, i.e., one with . These two obstructions rule out 12 of the 16 elements in , so we may conclude that has order four or less. It is not difficult to find isotopies that show that L is purely invertible
, meaning isotopic to , and individually invertible
in the first component, meaning isotopic to . (Section 2.2 describes our notation in further detail.) Thus, both and are included in the Whitten group for L. Hence, is the four element group . There are four cosets of this four element group in the 16 element group , so there are four (labeled, oriented) isotopy classes of links. ⋄
2.2. Notation
We introduce some notations and names for commonly occurring symmetries. Let describe a mirror of the link and denote a pure exchange symmetry. Individually inverting component k is denoted by where and (for ). Let ; observe that these elements have order 4. A link has pure invertible symmetry if . Finally, let . We shall sometimes use this notation in a product form, e.g., .
Note that we use Thistlethwaite notation to specify links unless the link has twelve or more crossings, in which case we use DT (Dowker–Thistlethwaite) codes. Henceforth, “symmetry group” will always refer to the intrinsic symmetry group
. We use the notation from [
6] for symmetry groups:
is the
jth subgroup of order
k in our subgroup lattice for
.
2.3. Subgroups of
In order to classify the possible symmetry groups of two-component links, we must find the subgroups of . For any , the symmetry groups and are conjugate via . Therefore if a link L has symmetry group , which is conjugate to group , then there exists some such that has symmetry group ; link is merely a relabeled and reoriented copy of L . Thus, the truly different symmetry groups are represented by the conjugacy classes of subgroups.
Proposition 2.5 There are 35 subgroups of and 27 mutually nonconjugate subgroups. A maximal set of nonconjugate subgroups consists of 7 subgroups of order two denoted through , 11 subgroups of order four denoted through and seven subgroups of order eight denoted through , as well as the trivial subgroup and the full group. Generators for these groups and the lattice structure of the subgroups appear in Figure 1. We note that this proposition corrects a mistake in the literature [
7], in which it is reported that 28 possible symmetry groups exist. All 12 groups explicitly listed therein are distinct.
Proof: From the semidirect product structure we can see that all but four of the 15 non-identity elements of are order two. The exceptions are , , , and , each of which has order four. Thus, there are 11 subgroups of of order two. Via computations in , we proceed to find 15 subgroups of order four and 7 subgroups of order eight. Combined with the trivial subgroup and all of , we arrive at a total of 35 subgroups.
However, some of these subgroups occur in conjugate pairs. For example, the subgroups and are conjugate four-element subgroups, since , , and .
There are four conjugate pairs of two-element subgroups and four conjugate pairs of four-element subgroups. Therefore precisely 27 mutually nonconjugate subgroups of
exist. Our calculations (by hand) of these
subgroups and the corresponding lattice structure given in
Figure 1 have been verified using the software
Magma. □
3. Computational Examples
For a hyperbolic link L , we may compute its symmetry group using the software SnapPea. This software can calculate the mapping class group of the link complement. The elements of which extend through the boundary tori to automorphisms of all of form a copy of inside . We can detect such maps using the following standard lemma.
Lemma 3.1 A map in extends to all of if and only if it sends meridians of the boundary tori to meridians. Moreover, any two such extensions are isotopic.
We utilize the
Python front end
SnapPy for
SnapPea written by Marc Culler and Nathan Dunfield. To each map on the boundary tori of the link complement,
SnapPy assigns a collection of
matrices along with a permutation element which records how the components of the link were permuted. Each matrix is
and records the images of the meridians and longitudes of the appropriate component, along with the orientation of the ambient space. The effect of the map on the orientation
of the given component and the orientation
of
is given by the rules below. Note that if the matrix for one boundary torus indicates that the orientation on
is reversed, then so will the matrices for all other boundary tori, since these matrices result from restricting a single map on
.
Using these rules, it is easy to extract
from
SnapPy. We computed the symmetry group for all 77,036 two-component hyperbolic links of 14 and fewer crossings in
SnapPy’s database.
Table 2 shows the census of symmetry groups of hyperbolic links found using
SnapPy. The data file containing the Whitten group elements for these links is included in the
Arxiv data repository and it is a future project to incorporate our computational techniques into
SnapPy.
There are 293 non-hyperbolic two-component links with up to 14 crossings in Thistlethwaite’s link table. For these links, we were unable to compute the symmetry groups using SnapPea. We were able to get partial information about the symmetry groups using the
Mathematica package
KnotTheory [
8]. For each link
L and each Whitten group element
, we computed a number of invariants of
L and
in an attempt to rule out
as an element of
. To rule out “exchange” symmetries, we applied two tests. First, we computed the Jones polynomials of each component of
L to try to rule out exchanges between components of different knot types. If that failed, we turned to the “satellite lemma”, which we use often in [
6].
Lemma 3.2 Suppose that is a satellite of L constructed by replacing component i with a knot or link K. Then L cannot have a pure exchange symmetry exchanging components i and j unless and are isotopic.
Proof: Such a pure exchange would carry an oriented solid tube around to a corresponding oriented solid tube around . If we imagine K embedded in this tube, this generates an isotopy between and . □
The point of this lemma is that we can often distinguish
and
using classical invariants which are insensitive to the original labeling of the link. In our computations, we replaced component
i of
L and
with a
torus link (for
) and compared the Jones polynomials of the resulting links. An example is shown in
Figure 2.
Ruling out elements of the Whitten group using these methods gave us a subgroup of
guaranteed to contain
. We found 9 links with
, 89 links with
, 194 links with
and 1 link with
. Consulting the subgroup lattice of
along with
Table 2, we saw that only this last link, the 194th 14-crossing two component non-hyperbolic link in Thistlethwaite’s table, might have had a new symmetry group which was not already represented by a hyperbolic link. The potential group was
. However, rearranging the diagram as in
Figure 3 ruled out
by revealing a pure exchange symmetry.
Having obtained supergroups of the groups for these non-hyperbolic links, we turned to obtaining subgroups of . To do so, we viewed each diagram as a polyhedral decomposition of the 2-sphere and enumerated the combinatorial symmetries of each polyhedron using Mathematica. Those symmetries which extended to symmetries of the link after crossing information was taken into account were classified according to the Whitten element they represented. We called these diagrammatic symmetries of each link. Of course, different diagrams are expected to reveal additional symmetries, so the diagrammatic symmetry group of a diagram of a link is only a subgroup of . In most cases, we still have a number of potential symmetries which may or may not be present for the link. However, we found 70 cases where the diagrammatic symmetry groups represented all of since they agreed with the “supergroups” computed earlier: 6 links with , 4 links with , and 60 links with .
4. Examples of Links with Particular Symmetry Groups
Table 1 lists examples of prime, nonsplit links by their intrinsic symmetry groups. We present examples for 21 of the 27 different symmetry groups.
The example links for the groups
and
were originally found by Hillman [
7]. He listed examples for many of the 12 subgroups that do not include
or
in that paper as well. The examples for the groups
,
,
,
, and
were generally known; for example, proofs that these links exhibit the given symmetry groups are found in [
6].
The examples for
,
and
are found in
Figure 4 and are new to the literature; we prove that these symmetry groups are correct below. All other examples have been found using
SnapPea and are new to the literature.
Theorem 4.1 The three links in Figure 4 possess the symmetry groups , and , respectively. Proof: The link on the far left in
Figure 4 is comprised of two components of
, while the link in the center is comprised of knots
and
. The knot
has no symmetry, therefore the only possible nontrivial symmetries for these links are
and
respectively. These two links achieve said symmetries through a 180 degree rotation about a line perpendicular to the page.
The two components of the link 10n59 in the far right in
Figure 4 are a left- and a right-handed trefoil (
and
). Since the trefoil is not mirrorable, we cannot mirror link 10n59 without permuting components, and vice versa. Therefore its symmetry group is a subgroup of
. The link exhibits the
symmetry through a 180 degree rotation about a line perpendicular to the page;
Figure 5 shows it also admits the symmetry
. Thus,
. □
5. Intrinsic Symmetry Groups of Alternating Links
Alternating, nonsplit two-component links only have 12 possible intrinsic symmetry groups; 15 groups will never occur when the link is alternating. To understand why, we will utilize a property of Conway polynomials [
9]. Though this result is classically known, we provide a proof here for completeness.
Lemma 5.1 Let L be a link with c components. Consider a symmetry that reverses the orientation of either all or no components of L. Then, the Conway polynomial of L changes sign according to the formula .
Proof: We shall proceed by induction on the number of components. For knots (
), this is well known. Let
be defined as above. Let
K be one of the components of
L . Resolve each of the
n overcrossings that
K has with the other components of
L according to the skein relation of the Conway polynomial; similarly, resolve the corresponding
n undercrossings in
. As this will turn every crossing
K has with
L or
into over or under crossings, we eventually get down to split links
and
. We obtain
and
where
or 1 if the
jth over crossing of
K in
L was a
crossing or a
crossing, respectively.
As and are split, . Moreover, every crossing we resolved was an intercomponent crossing, so is a link with components for every j ; therefore by the inductive hypothesis, .
This lemma rules out four possible symmetries for nonsplit, alternating two-component links L. Recall that the Conway polynomial does not vanish for nonsplit, alternating links. Thus such a link L cannot admit a symmetry of the form . Only 12 subgroups of fail to contain one of the four elements of this form; the other 15 groups cannot be symmetry groups for an alternating two-component link, which proves the following proposition.
Proposition 5.2 Only 12 intrinsic symmetry groups are possible for alternating, nonsplit two-component links. These 12 groups may be viewed as a subdiagram of Figure 1: they form the order ideal generated by two groups, and , i.e., these two groups and all of their subgroups. Alternating examples appear in
Table 1 for all but one of these 12 groups; the exception is
, where no example, alternating or not, is known.
6. Future Directions
We have found prime, nontrivial examples for 21 of the 27 possible intrinsic symmetry groups of two-component links. Do examples exist for the 6 remaining subgroups? In considering links of 14 or fewer crossings, our exhaustive approach has not captured the full complexity of possible link structures. It seems possible that some of the missing groups, especially the smaller ones, will appear among links of 20 or fewer crossings. For instance, examples for three groups () appeared first for 14-crossing links; perhaps examples of links with the three missing groups of order four will appear “soon” in the tables. In particular, we conjecture that there is an alternating link with symmetry group , which would complete the set of examples for alternating, nonsplit two-component links.
More interesting is the search for nonsplit links with full symmetry. The unlink with components possesses full symmetry; to date no nonsplit examples are known. A two-component link L with symmetry group must have linking number zero and be nonalternating; its two knot components must be of the same knot type, which itself must possess full symmetry. We are compelled to put forth the following conjecture.
Conjecture 6.1 There does not exist a prime, nonsplit two-component link with full symmetry.
Another project is to extend our catalog of the relative frequencies of different intrinsic symmetry groups. To date, we have only approached hyperbolic two-component links of 14 or fewer crossings; raising the number of components is an obvious next step. However, searching for the intrinsic symmetry groups of links with more components becomes more daunting, as the number of such groups rises considerably; see
Table 3. Few examples of intrinsic symmetry groups are known for
-component links for
; we found a handful in [
6]. However, using
SnapPy, searching for examples and developing a catalog of frequencies seems like an approachable problem.