Polyominoes and Polyiamonds as Fundamental Domains of Isohedral Tilings with Rotational Symmetry
Abstract
:1. Introduction
2. p4
2.1. Creating Polyominoes as Fundamental Domains for p4 Symmetry Groups
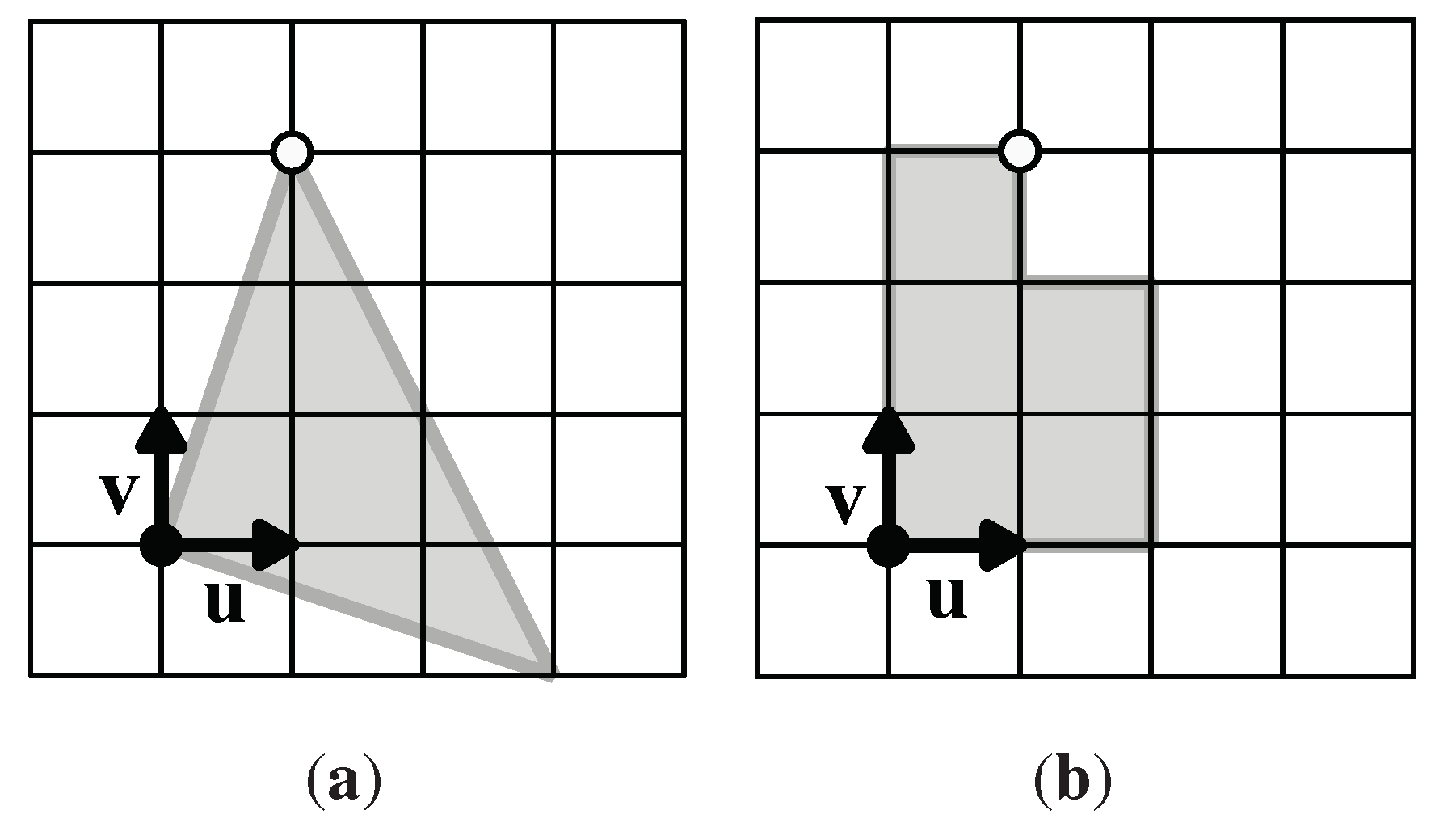
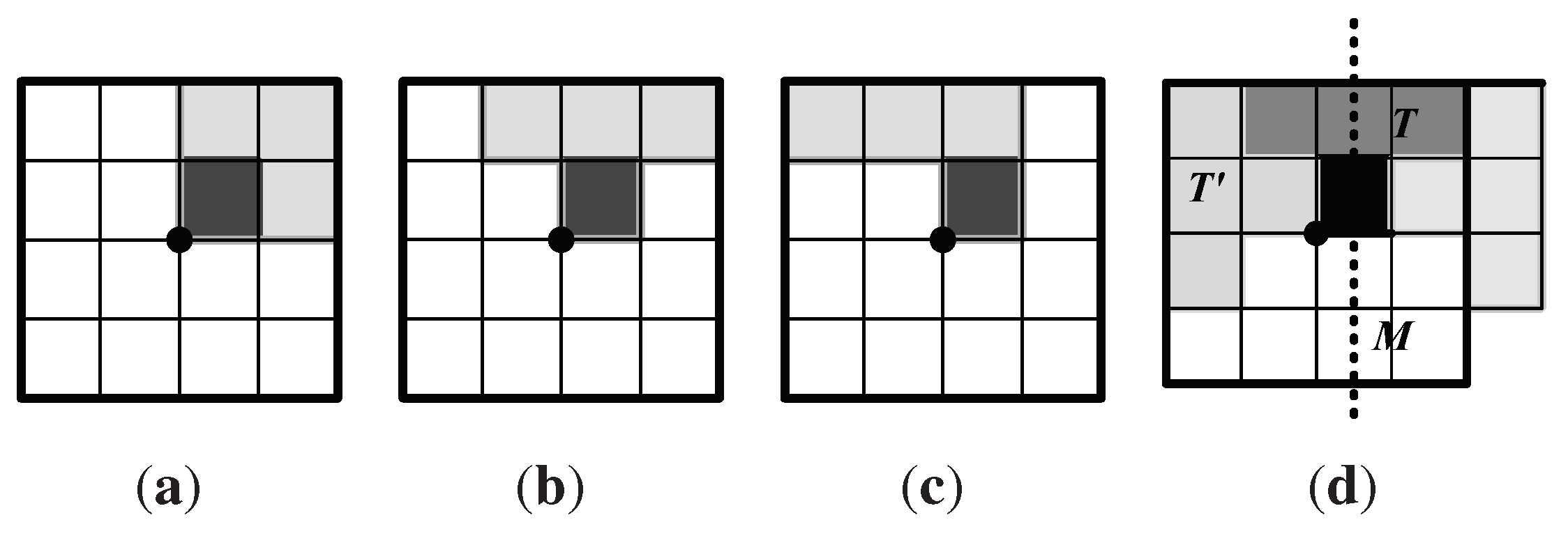
- T is a set of unit squares; is a set of unit squares that are edge-adjacent to the squares in T; is a set of n-ominoes.
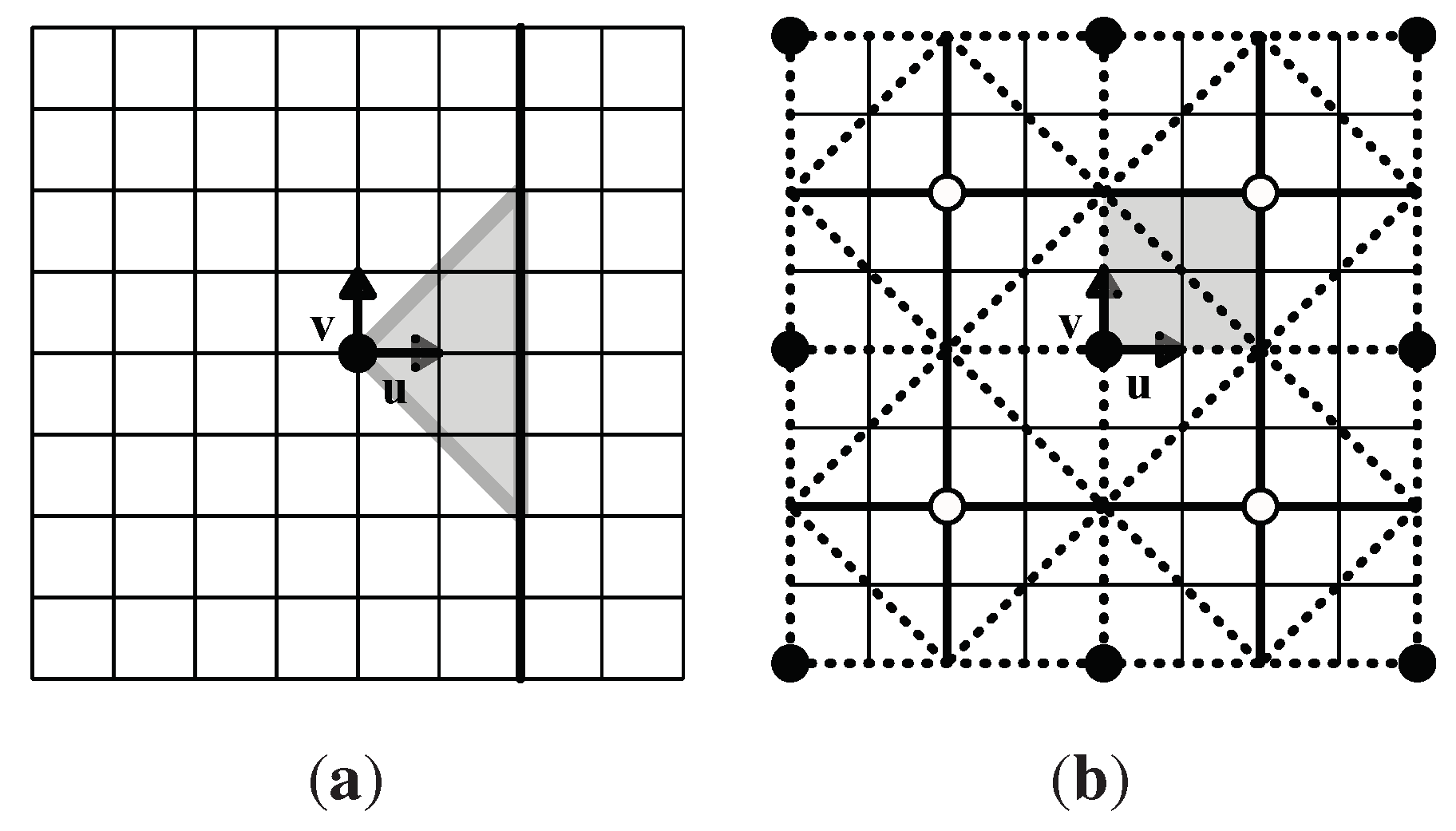
- When T is the empty set, we define as the set of four squares around the origin (the four unit squares at the lower left in Figure 1.)
- We define , the Boolean function of T, which is true if and a white circle is on the boundary of T. Otherwise is false.
- . This is the set of all unit squares that are edge-adjacent to those in T, but not equivalent to any unit squares in T.
- Fix n (from the list in (2) above). Begin with empty.
- Make T empty. Make . Make . Make .
- For in , if , choose an element e (a unit square) of . Remove e from and save the pair in .
- Increase k by 1. Add e (from step 3) to T to create a new -omino T, and let for the new T. Add the new pair to .
- If and , quit the procedure.
- If is true, an n-omino tile is completed and add T to provided there is no equivalent tile in . We regard two n-ominoes equivalent if conditions (a) and (b) below are satisfied.
- (a)
- The tiles are congruent (including mirror reflection).
- (b)
- When the tiles are superimposed, the positions of m-fold rotational centers on the boundaries of the tiles are the same. If there are several m-fold rotation centers for the same m, they can be permuted appropriately before comparison.
- If , decrease k by 1.
- Go back to step 3.
2.2. Symmetries of Tiles
- Select a polyomino that has rotation and/or reflection symmetry, and examine its tiling generated by G.
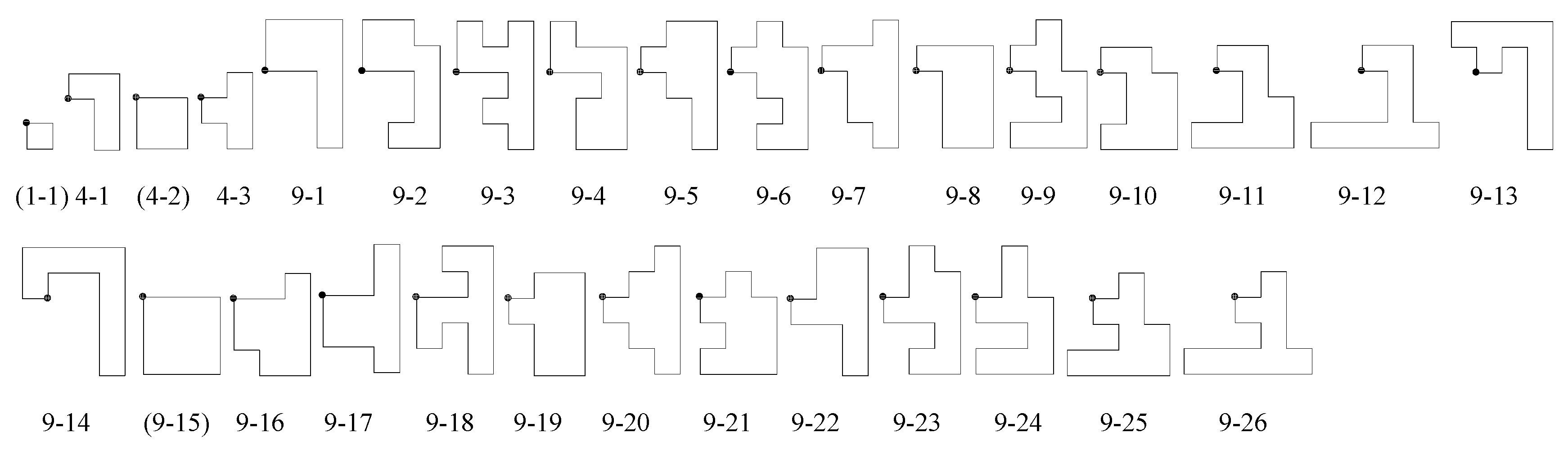
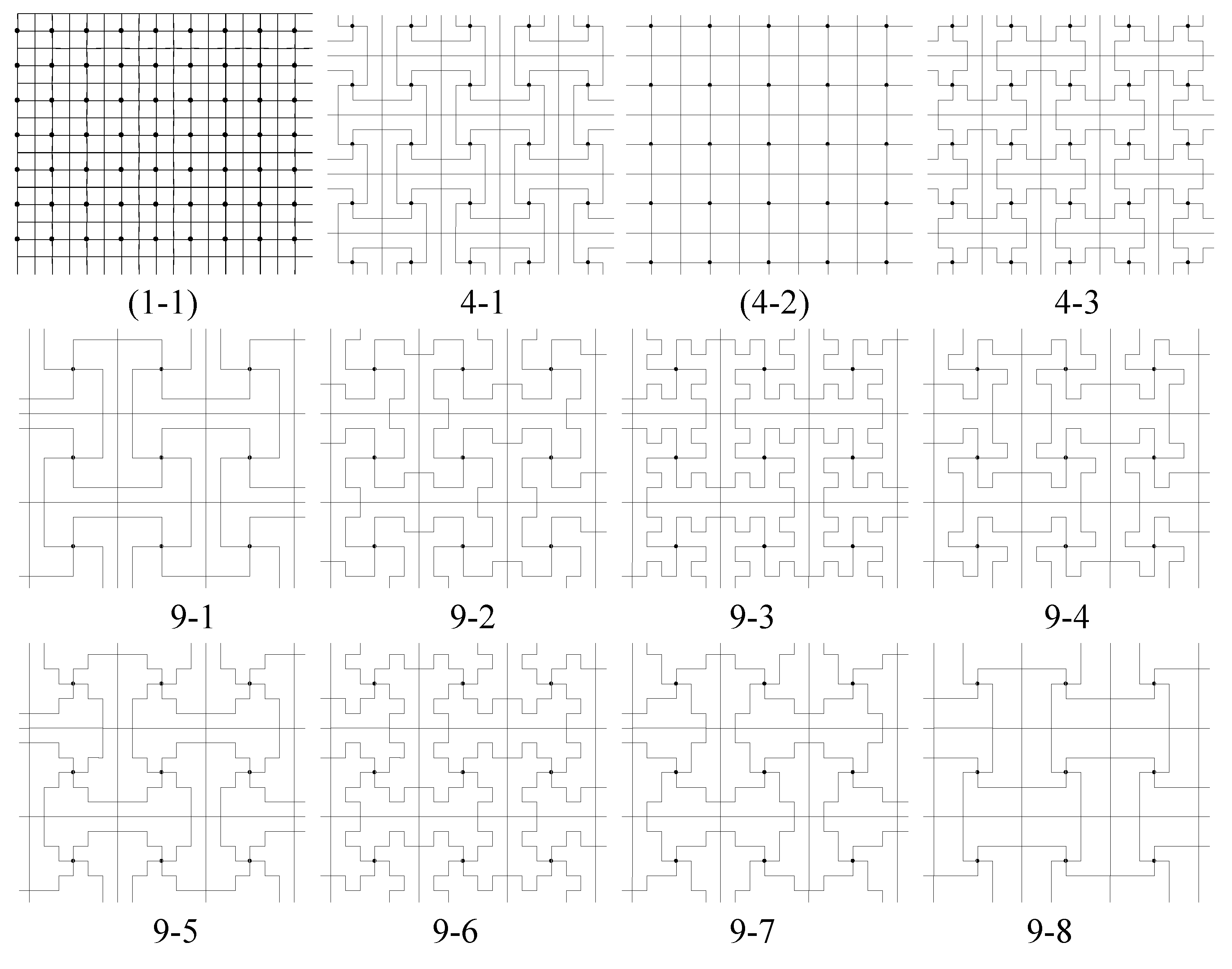
- Look at all vertices and centers of unit squares in a polyomino in except for the original 4-fold centers we have chosen (black and white centers), and determine whether or not is invariant under a 4-fold rotation about such a point. If so, then it is a new 4-fold center for , and this symmetry is not in G. For example, in Figure 3, tilings (5-2) and (5-2-2), while generated differently, are the same tiling and have 4-fold centers at every vertex where 4 tiles meet. Tiling (5-3) has 4-fold rotation centers at the centers of the “cross” tiles and at every vertex where 4 tiles meet. These tilings have full symmetry groups of type p4, with G as a proper subgroup.
- Other new symmetry elements of can be sought by using Chart 2 in [6]. If the line joining the black and white 4-fold centers we placed is an axis of mirror reflection for , then is type p4m. For example, in Figure 3, tilings (1-1) and (4-3) are type p4m. If this line is not a mirror reflection axis, but the line connecting two adjacent (nearest) 2-fold centers for is a mirror reflection axis for , then is type p4g. For example, in Figure 3, tiling (2-1) is type p4g.
3. p4g
3.1. Creating Polyominoes as Fundamental Domains for p4g Symmetry Groups
3.2. Symmetries of Tiles
4. p4m
5. p3
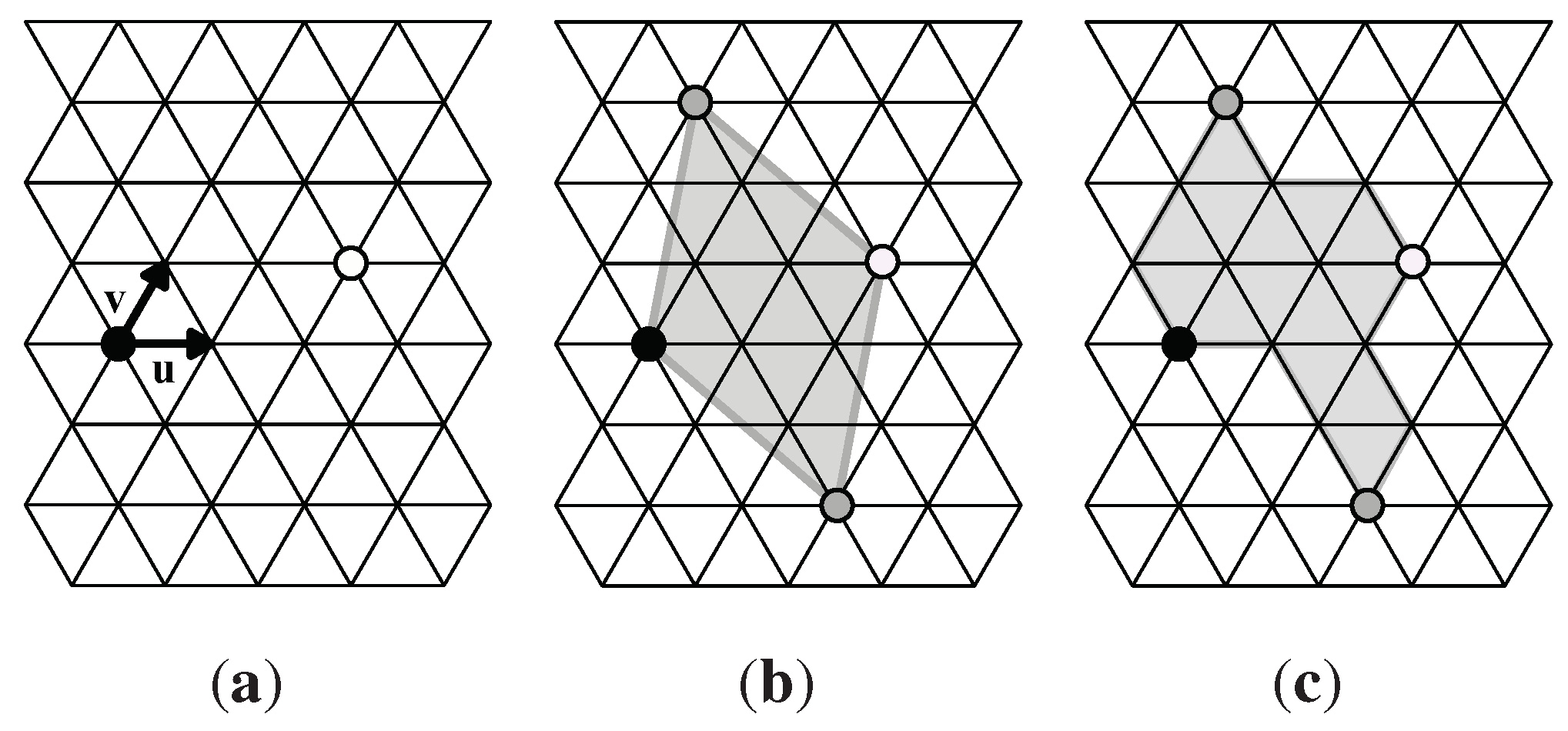
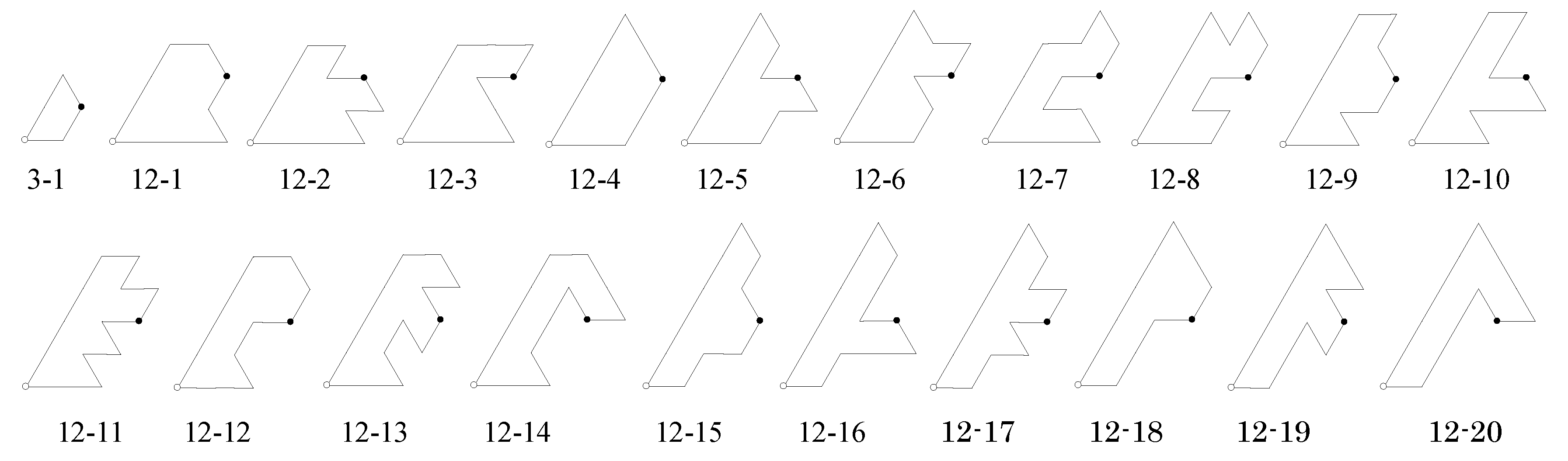
5.1. Creating Polyiamonds as Fundamental Domains for p3 Symmetry Groups
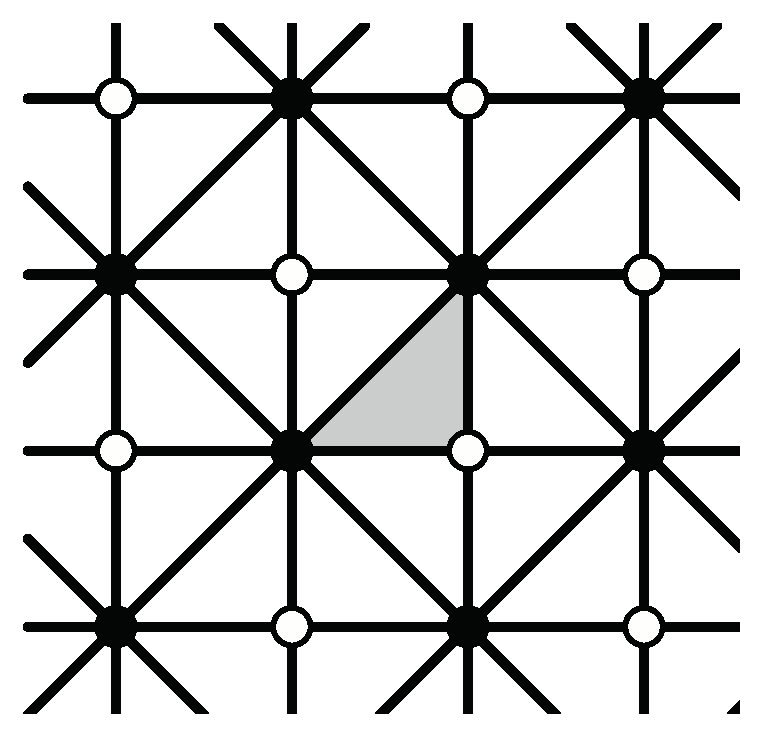
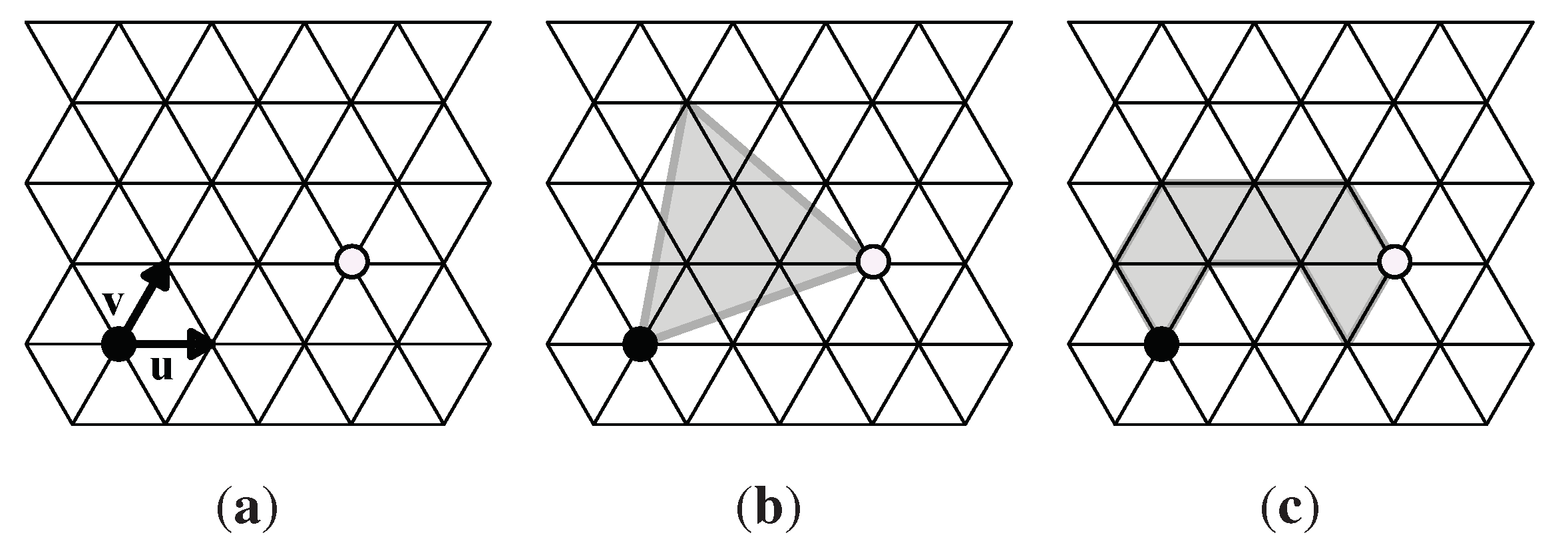
- T is a set of unit triangles; is a set of unit triangles that are edge-adjacent to the triangles in T; is a set of n-iamonds.
- When T is the empty set, we define as the set of six triangles around the origin in Figure 9(a).
- We define , the Boolean function of T, which is true if and a white circle is on the boundary of T . Otherwise is false.
- . This is the set of all unit triangles that are edge-adjacent to those in T, but not equivalent to any unit triangles in T.
5.2. Symmetries of Tiles
- Select a polyiamond T that has rotation and/or reflection symmetry, and examine its tiling generated by G.
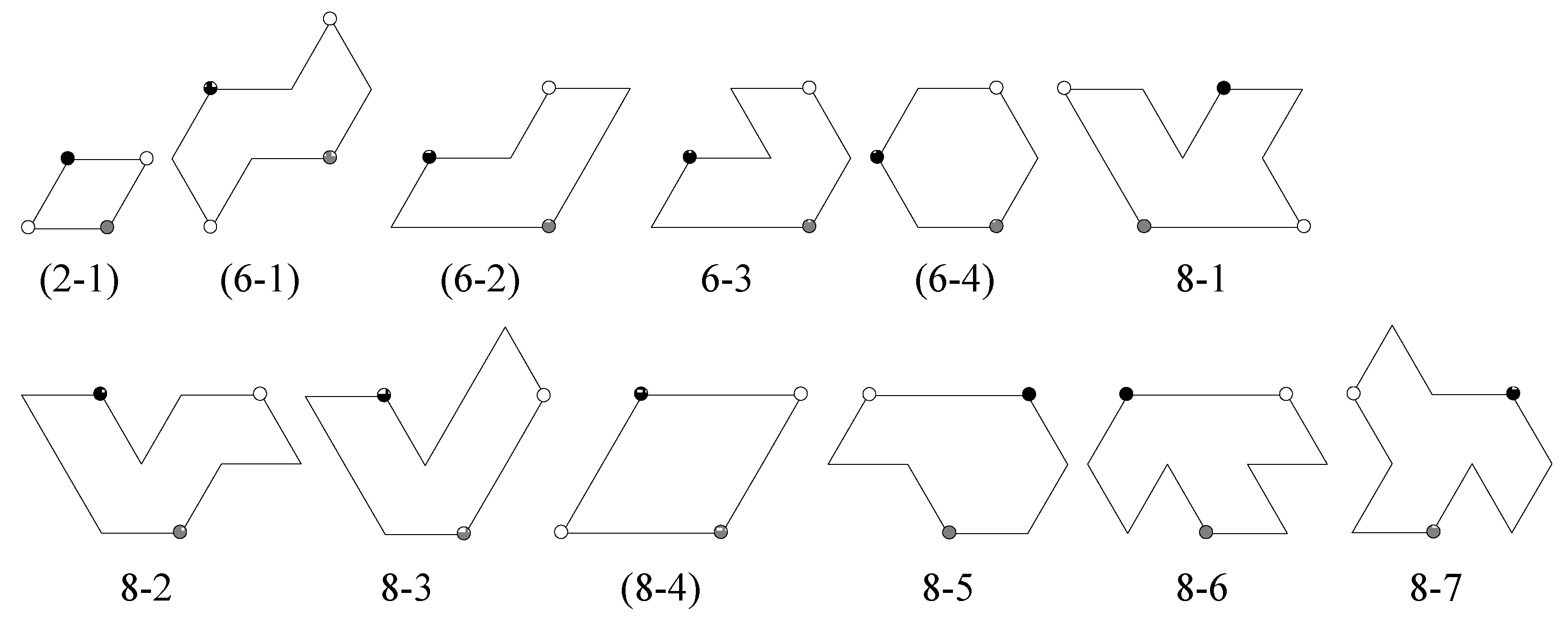
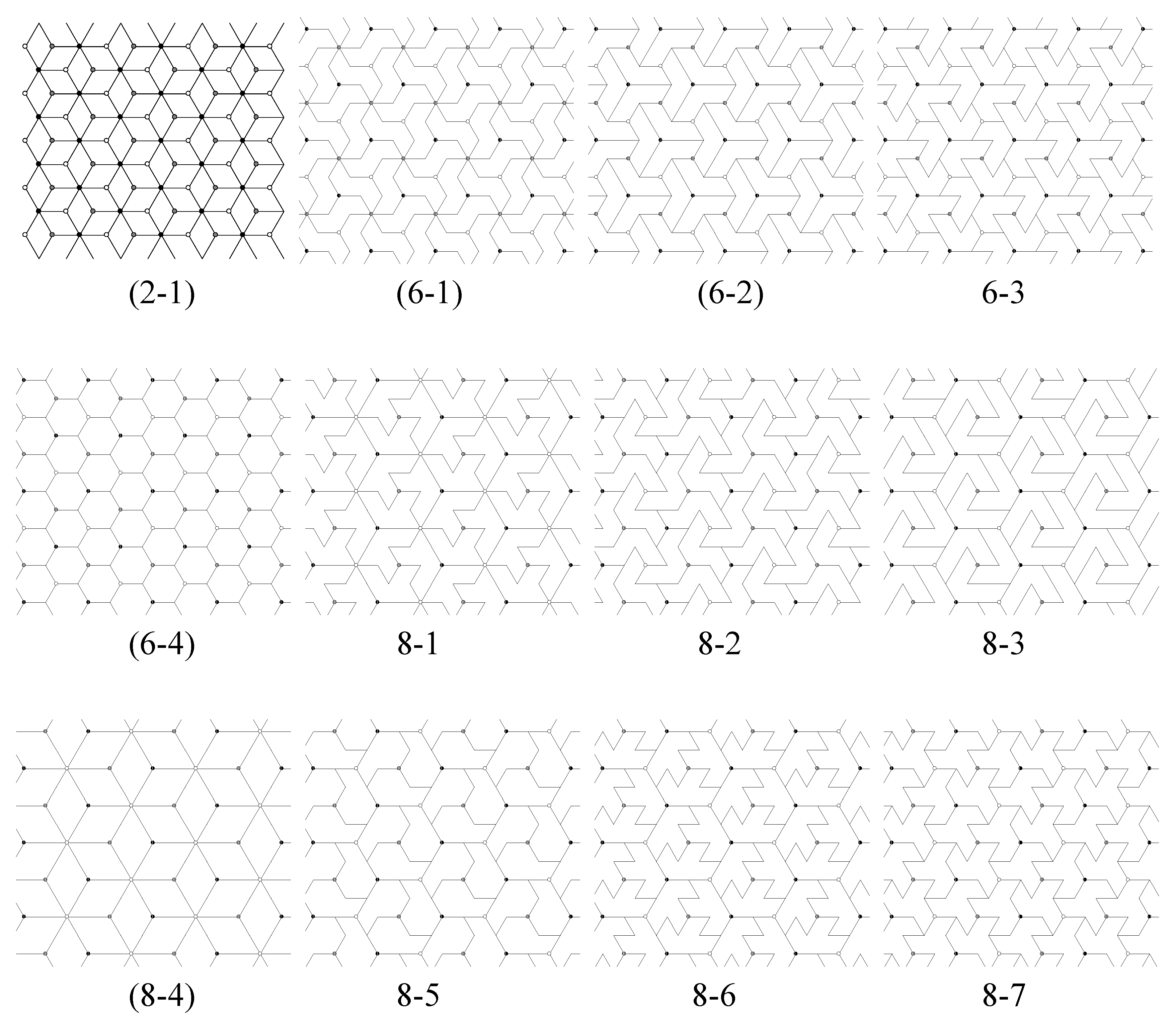
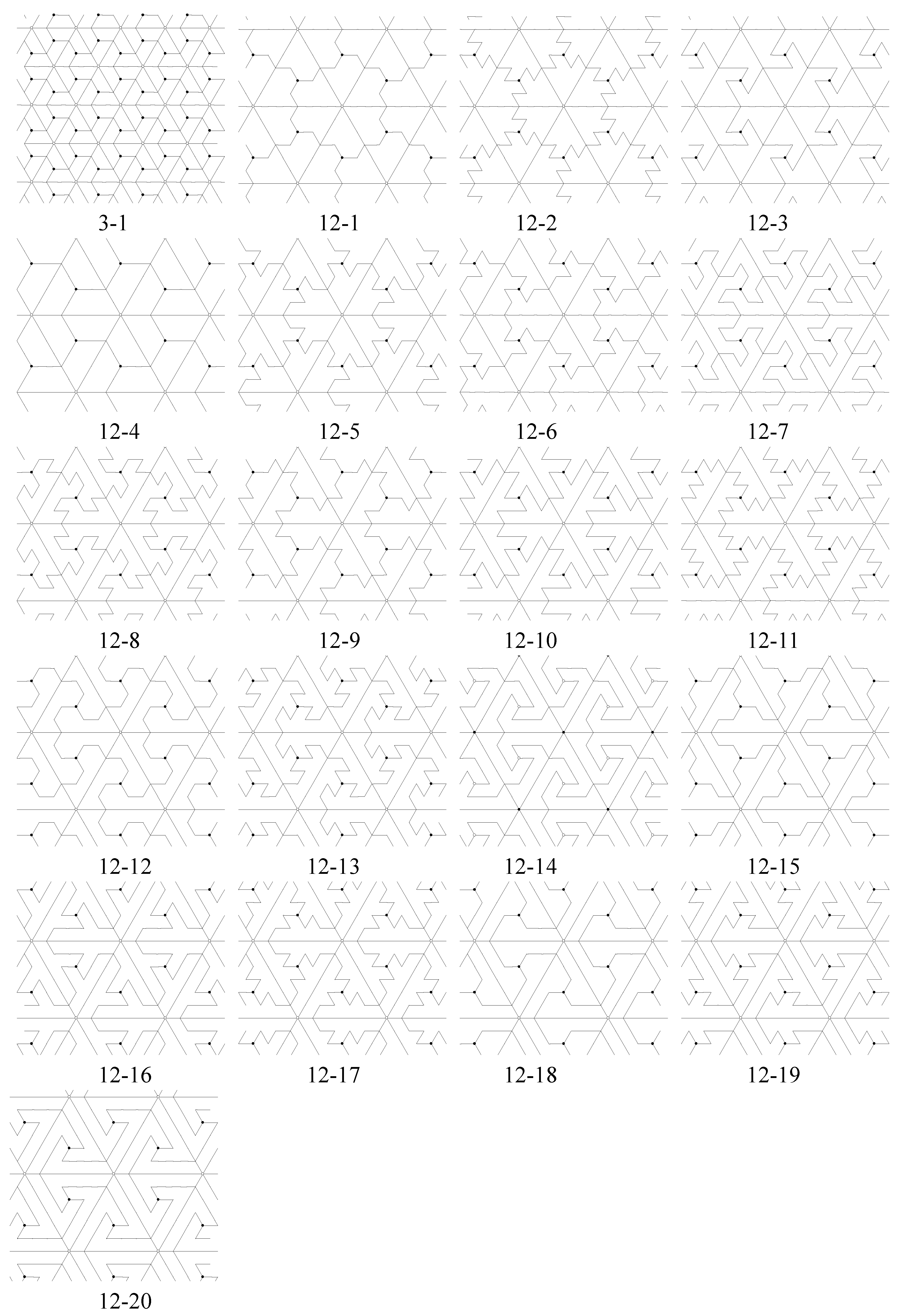
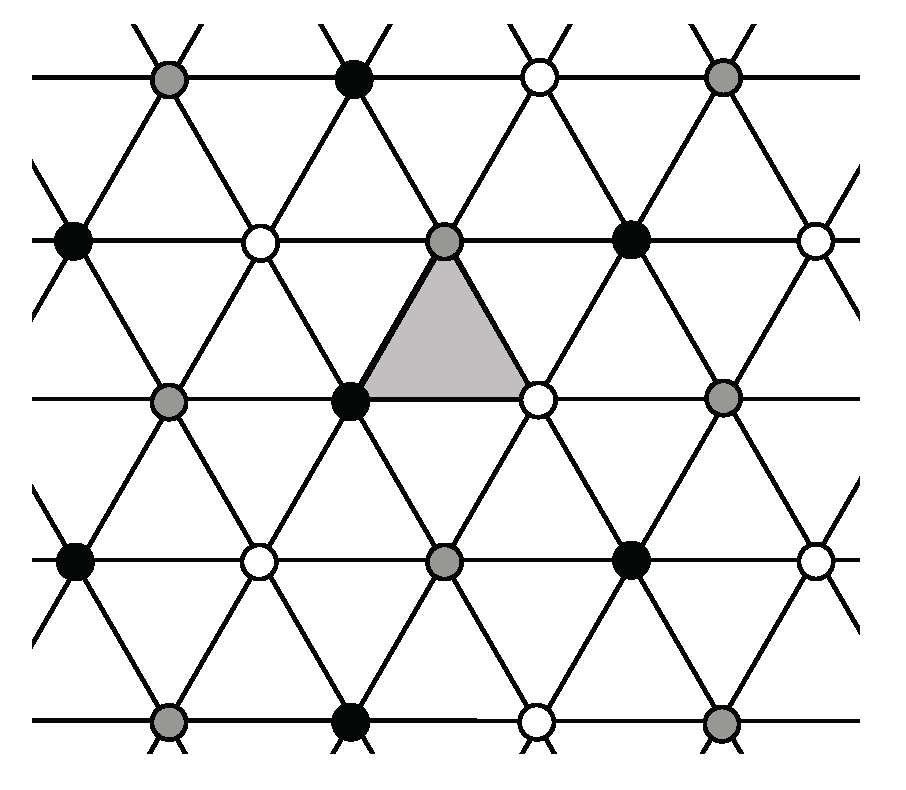
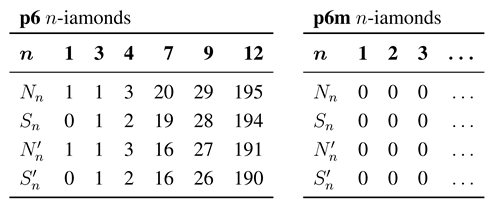
- Look at all vertices and centers of unit triangles in T except for those centers of rotation in G (black, white and gray centers), and determine whether or not any can be new 3-fold centers for . If a new 3-fold center is found, then the full symmetry group of contains G as a proper subgroup and T is not a fundamental domain for . If a new 3-fold center is a 6-fold center, is type p6m if there is a reflection axis joining it to any nearest 3-fold center; otherwise, is type p6. Tiling (6-4) in Figure 11 is type p6m, and has a 6-fold center at the center of the hexagonal 6-iamond. If there are new 3-fold centers but none are 6-fold centers, then is type p3.
- If the tiling contains only 3-fold centers for G, we seek new symmetry elements by using Chart 2 in [6].
- If some 3-fold center for G is a 6-fold center, the tiling will have p6m symmetry if the line joining a 6-fold center to a nearest 3-fold center is a reflection axis for , otherwise it will have p6 symmetry. In Figure 11, tilings (2-1) and (8-4) have p6m symmetry, and tiling (6-1) has p6 symmetry.
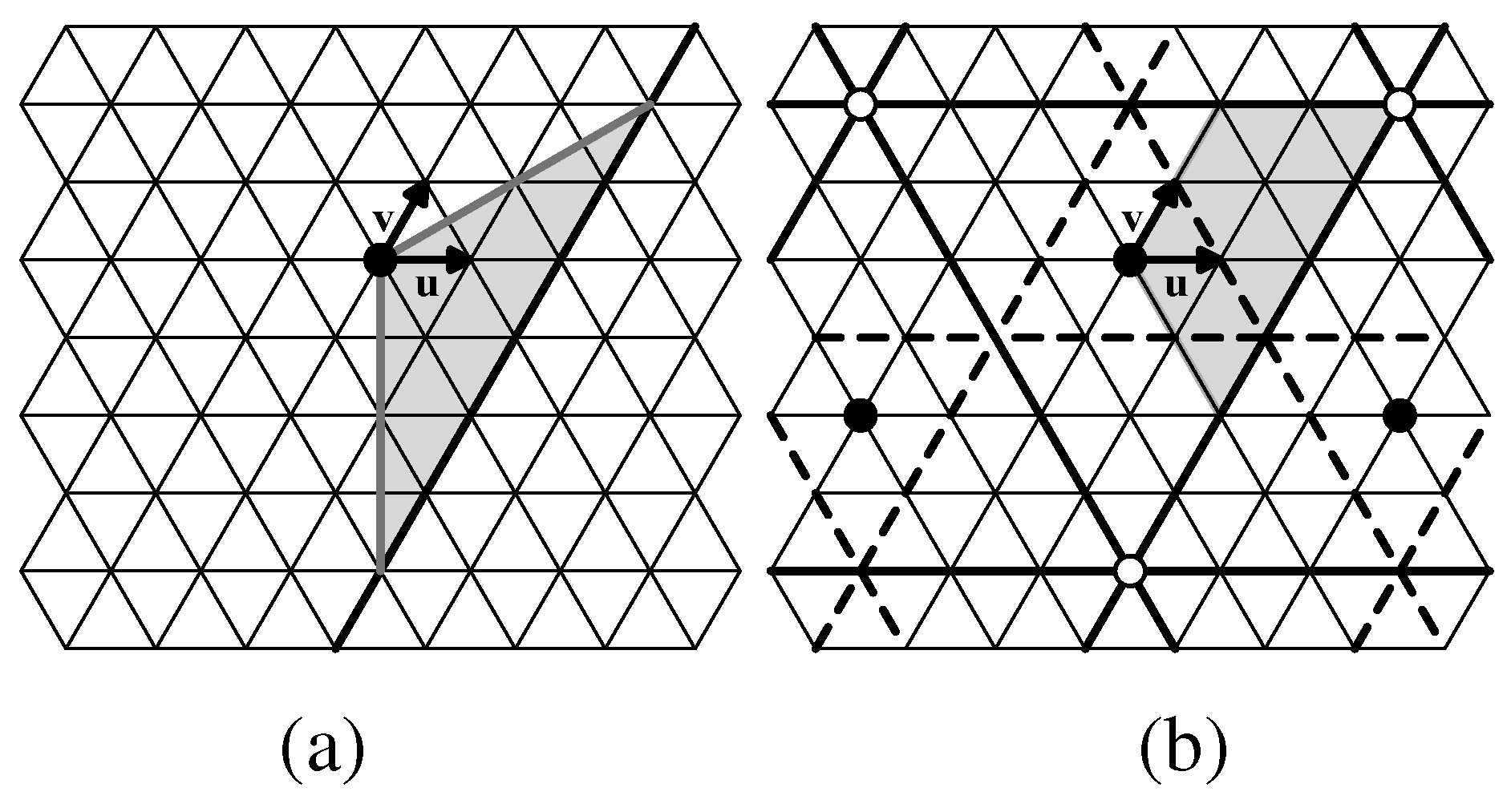
6. p31m
6.1. Creating Polyiamonds as Fundamental Domains for p31m Symmetry Groups
6.2. Symmetries of Tiles
7. p3m1
8. p6
8.1. Creating Polyiamonds as Fundamental Domains for p6 Symmetry Groups
8.2. Symmetries of Tiles
- Select a polyiamond that has rotation and/or reflection symmetry, and examine its tiling generated by G.
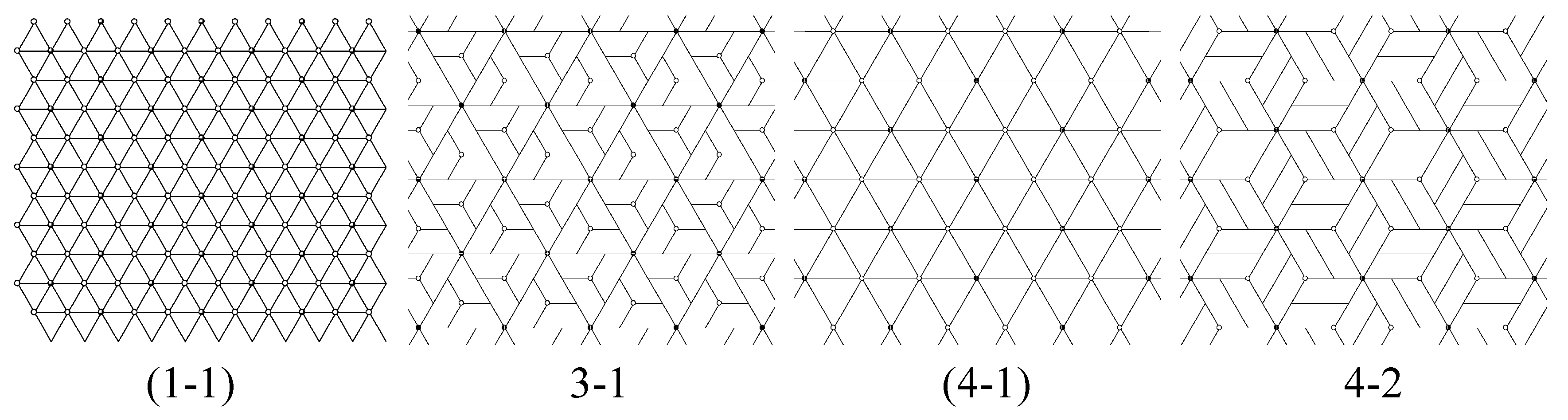
- If the line connecting adjacent 6-fold and 3-fold centers (black to white) is a reflection axis for , the tiling has p6m symmetry. Tilings (1-1) and (4-1) in Figure 18 have p6m symmetry. These tilings also have 3-fold centers for the tiling at the centers of the polyiamond tiles.
- Otherwise, look at all vertices and centers of unit triangles in a polyiamond in except for those black and white rotation centers in the p6 group we have generated and determine whether or not they can be new 3-fold centers for . If new 3-fold centers are found, the full symmetry group of the tiling contains G as a proper subgroup. Tiling (7-1) in Figure 18 has a larger p6 symmetry group than G since there are 3-fold rotation centers for at the centers of the rotor-like polyiamond tiles. Note that the same tiles appear in tiling 7-1-2, but in this tiling, the centers of the tiles are not 3-fold centers of rotation for .
9. p6m
10. Enumeration Tables
11. Summary
Acknowledgement
References
- Fukuda, H.; Mutoh, N.; Nakamura, G.; Schattschneider, D. A method to generate polyominoes and polyiamonds for tilings with rotational symmetry. Graphs Comb. 2007, 23, 259–267. [Google Scholar] [CrossRef]
- Fukuda, H.; Mutoh, N.; Nakamura, G.; Schattschneider, D. Enumeration of Polyominoes, Polyiamonds and Polyhexes for Isohedral Tilings with Rotational Symmetry. In Computational Geometry and Graph Theory; Springer: Berlin/Heidelberg, Germany, 2008; Volume 4535, pp. 68–78. [Google Scholar]
- Fukuda, H.; Kanomata, C.; Mutoh, N.; Nakamura, G.; Schattschneider, D. Polyominoes and polyiamonds as fundamental domains for isohedral tilings of crystal class D2. Symmetry 2011, 3, 325–364. [Google Scholar] [CrossRef]
- Rhoads, G.C. Tilings by polyomoinoes, polyhexes, and polyiamonds. J. Comput. Appl. Math. 2005, 174, 329–353. [Google Scholar] [CrossRef]
- Keating, K.; Vince, A. Isohedral polyomino tiling of the plane. Discret. Comput. Geom. 1999, 21, 615–630. [Google Scholar] [CrossRef]
- Schattschneider, D. The plane symmetry groups: Their recognition and notation. Am. Math. Mon. 1978, 85, 439–450. [Google Scholar] [CrossRef]


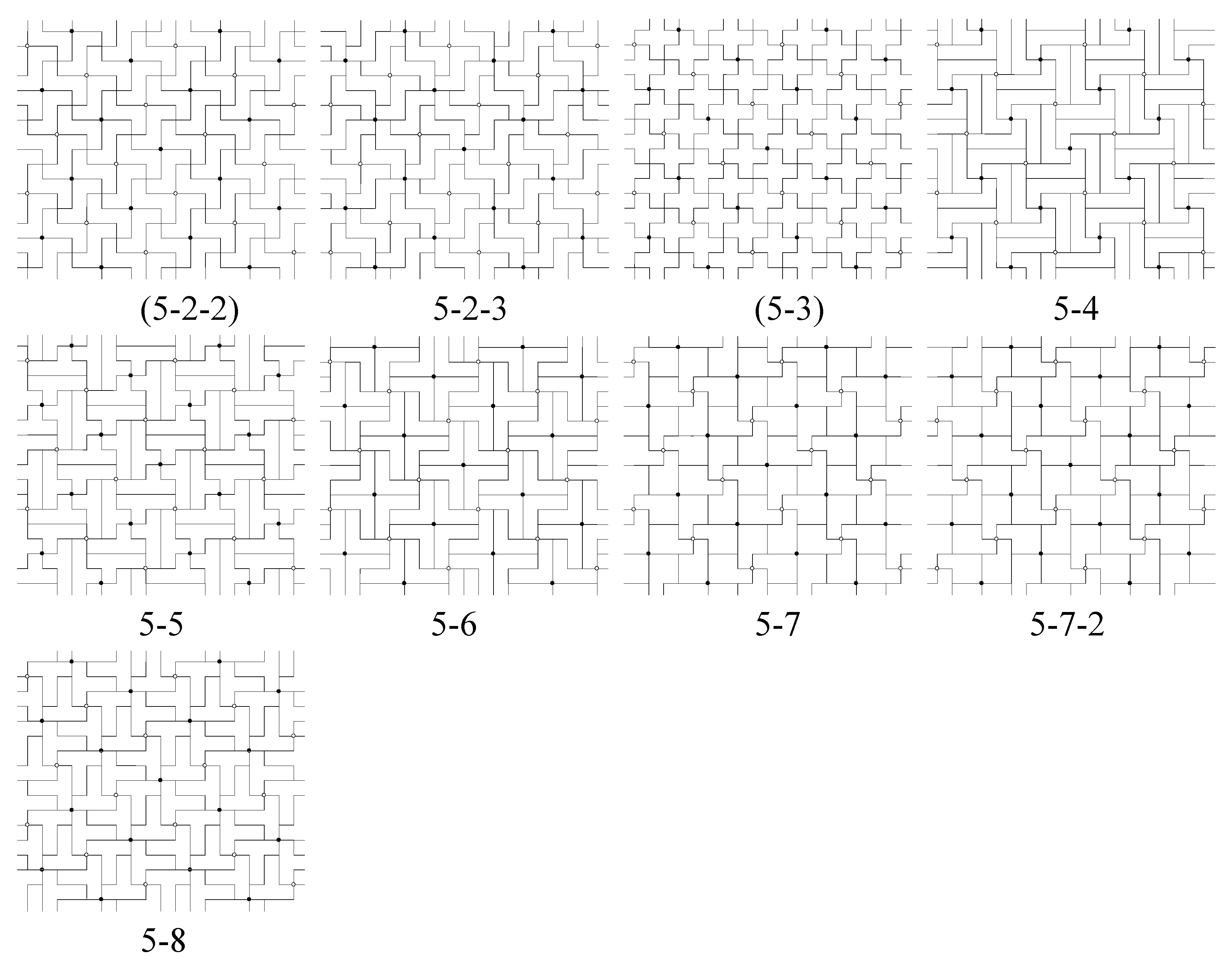
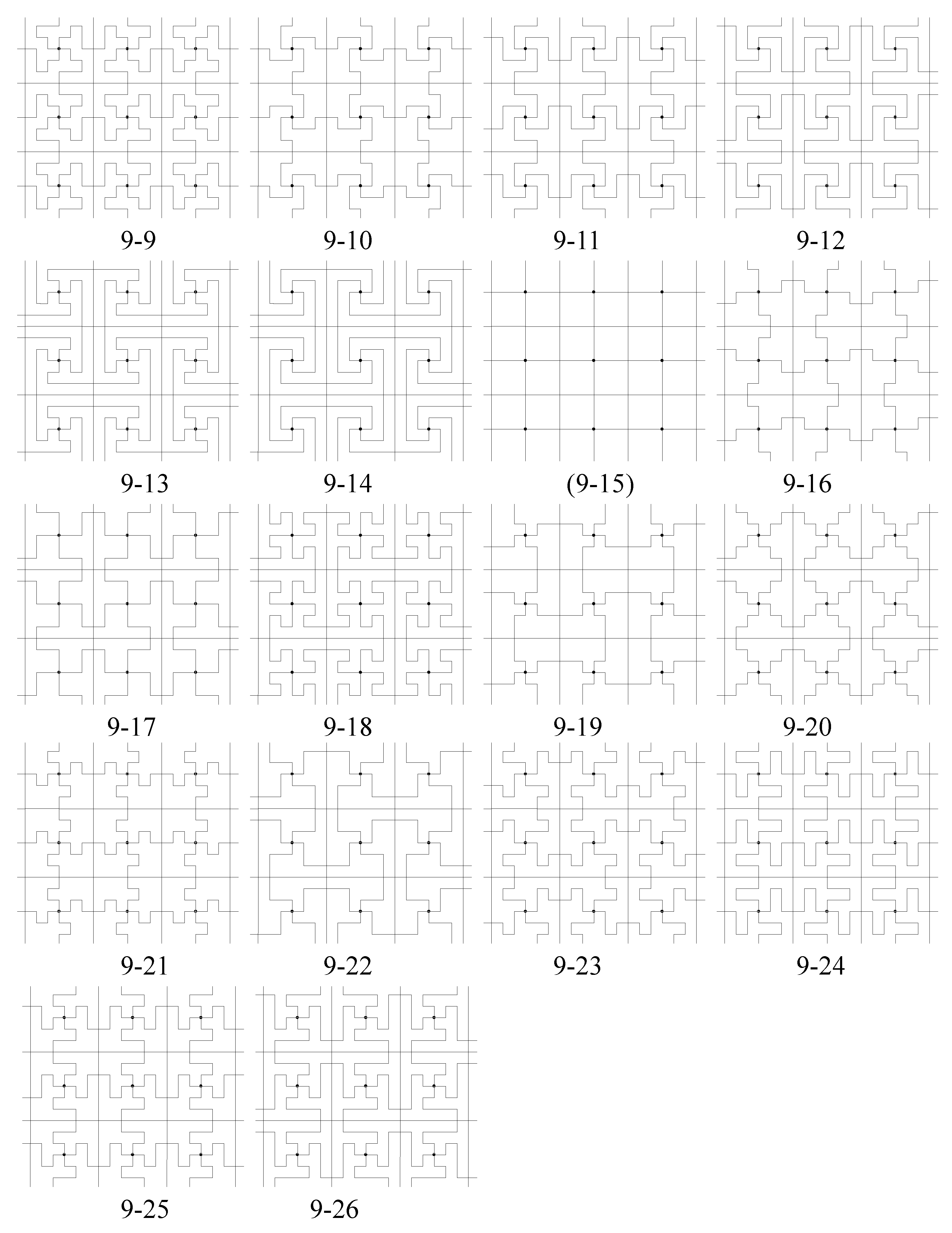





© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Fukuda, H.; Kanomata, C.; Mutoh, N.; Nakamura, G.; Schattschneider, D. Polyominoes and Polyiamonds as Fundamental Domains of Isohedral Tilings with Rotational Symmetry. Symmetry 2011, 3, 828-851. https://doi.org/10.3390/sym3040828
Fukuda H, Kanomata C, Mutoh N, Nakamura G, Schattschneider D. Polyominoes and Polyiamonds as Fundamental Domains of Isohedral Tilings with Rotational Symmetry. Symmetry. 2011; 3(4):828-851. https://doi.org/10.3390/sym3040828
Chicago/Turabian StyleFukuda, Hiroshi, Chiaki Kanomata, Nobuaki Mutoh, Gisaku Nakamura, and Doris Schattschneider. 2011. "Polyominoes and Polyiamonds as Fundamental Domains of Isohedral Tilings with Rotational Symmetry" Symmetry 3, no. 4: 828-851. https://doi.org/10.3390/sym3040828
APA StyleFukuda, H., Kanomata, C., Mutoh, N., Nakamura, G., & Schattschneider, D. (2011). Polyominoes and Polyiamonds as Fundamental Domains of Isohedral Tilings with Rotational Symmetry. Symmetry, 3(4), 828-851. https://doi.org/10.3390/sym3040828




