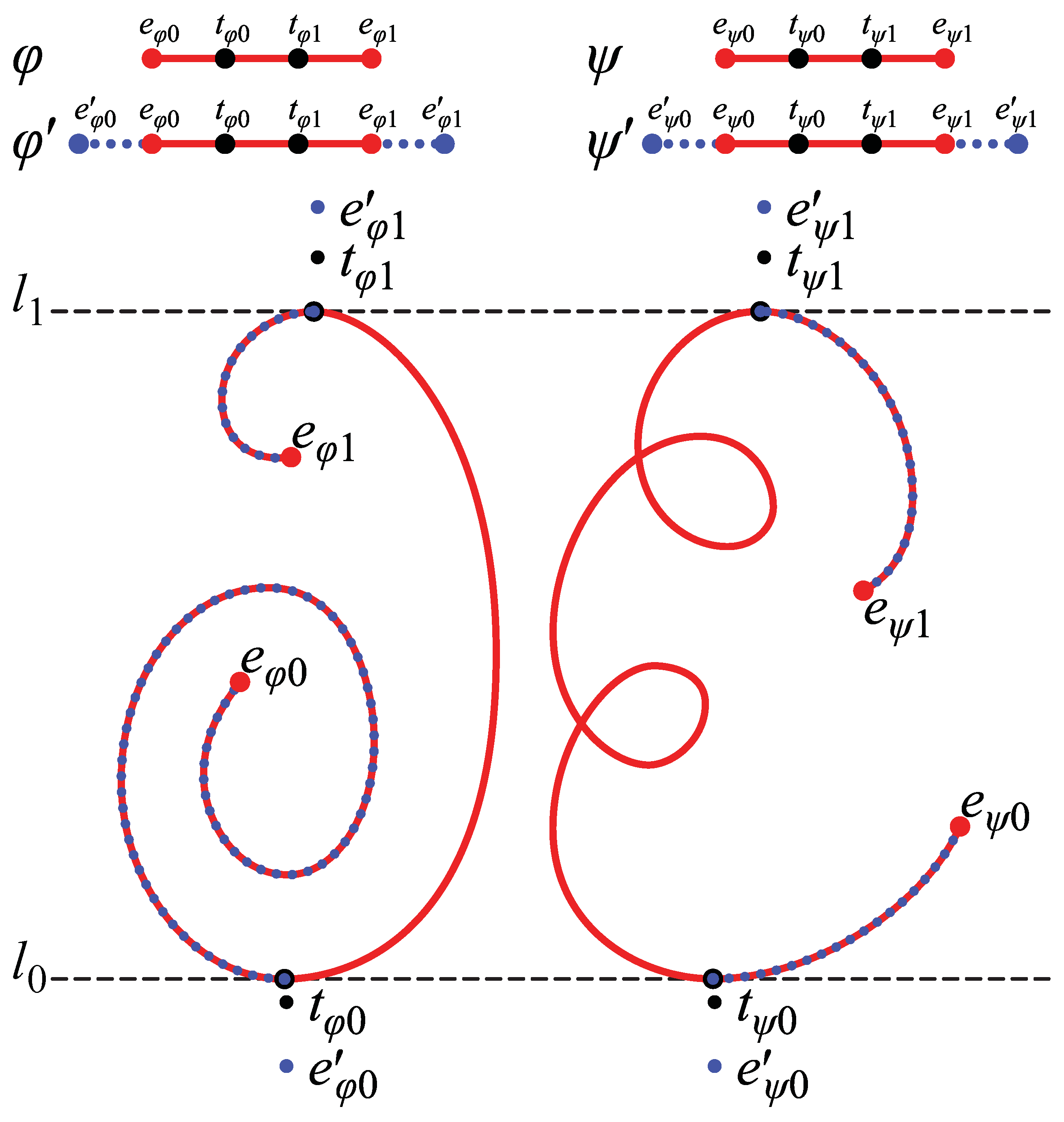We begin with notation. Consider two curves Φ and Ψ in a 3D space and their 2D images φ and ψ. Let Φ and Ψ be symmetric with respect to a plane Πs, whose normal is ns(nx, ny, nz). Let Pi(xΦi, yΦi, zΦi), be a point on Φ and Qi(xΨi, yΨi, zΨi) be its symmetric counterpart on Ψ. Symmetry line segments, which are line segments connecting pairs of corresponding points on Φ and Ψ are parallel to the normal of Πs in the 3D space. Perspective images of these lines intersect at the vanishing point v on the image plane. The 3D orientation of Πs is specified by its slant σs and tilt τs. Without restricting generality, assume τs = 0. Note that when τs is not zero, we can always rotate the 3D coordinate system around the z-axis by τs. Under this assumption, the normal to the symmetry plane is ns(nx, 0, nz). The slant of the symmetry plane is σs = atan(nx/nz).
2.1. A Pair of 2D Curves with Unique Correspondences—The Case of a Perspective Projection
We first consider the case of a perspective projection. The equivalent theorem for an orthographic projection will be proved as a special case of a perspective projection. Theorem 1 states that for any pair of curves in the 2D image, there exists a pair of 3D curves that are symmetric with respect to a plane. The gist of the proof is as follows. Given a pair of 2D curves, the vanishing point of a perspective projection is computed from the endpoints of the curves. The vanishing point determines unique point correspondences between the two curves. It also determines the symmetry plane uniquely for a given position of the center of perspective projection F. Given the plane of symmetry, for any pair of 2D points it is always possible to find a pair of 3D points that are mirror symmetric with respect to this plane.
Theorem 1: Let
φ and
ψ be curves in a 2D image that are tame. Let the endpoints of
φ be
eφ0 and
eφ1, and the endpoints of
ψ be
eψ0 and
eψ1. Assume that the lines
eφ0eψ0 and
eφ1eψ1 intersect at a point
v that (i) is not on
φ or
ψ and (ii) is not between
eφ0 and
eψ0 or between
eφ1 and
eψ1. Additionally, assume that each half line that emanates from
v and intersects
φ has a unique intersection with
ψ and
vice versa (see
Figure 3). Then, for a given center of projection
F there exists a pair of continuous curves
Φ and
Ψ and a plane
Πs in a 3D space such that
Φ and
Ψ are mirror-symmetric with respect to
Πs and that
φ is a perspective projection of
Φ and
ψ is a perspective projection of
Ψ.
Proof:
Figure 3.
F = [0, 0, zf] is the center of perspective projection and ΠI (z = 0) is the image plane. φ and ψ are two given curves on the image plane. eφ0 and eφ1 are the endpoints of φ, and eψ0 and eψ1 are the end points of ψ. The lines eφ0eψ0 and eφ1eψ1 intersect at point v on the x-axis. A line that is emanating from v and intersects with φ has a unique intersection with ψ and vice versa.
Figure 3.
F = [0, 0, zf] is the center of perspective projection and ΠI (z = 0) is the image plane. φ and ψ are two given curves on the image plane. eφ0 and eφ1 are the endpoints of φ, and eψ0 and eψ1 are the end points of ψ. The lines eφ0eψ0 and eφ1eψ1 intersect at point v on the x-axis. A line that is emanating from v and intersects with φ has a unique intersection with ψ and vice versa.
In order to prove this theorem, we have to show that for any pair of corresponding points on φ and ψ, we can find their backprojections in the 3D space, such that these backprojected points are mirror-symmetric with respect to the same plane Πs. That is, the line segment connecting the backprojected points is bisected by Πs and parallel to the normal of Πs. It will be also shown that the backprojected points form a pair of continuous curves.
Let’s set the direction of
x-axis so that the vanishing point
v is on the
x-axis,
v = [
xv, 0, 0]. We express
φ and
ψ in a polar coordinate system (
r,
α), where
r is the distance from the vanishing point
v and
α is the angle measured relative to the direction of the
x-axis. Then, the point
pi = [
xφi,
yφi, 0] = [
xv + rφ(
αi)cos
αi,
rφ(
αi)sin
αi, 0] on
φ and the point
qi = [
xψi,
yψi, 0] = [
xv + rψ(
αi)cos
αi,
rψ(
αi)sin
αi, 0] on
ψ are corresponding. Note that both
rφ(
α) and
rψ(
α) are continuous functions and they are always positive (
rφ(
α),
rψ(
α) > 0). Let the equation of the symmetry plane
Πs be:
![Symmetry 03 00365 i001]() Pi
Pi and
Qi, the 3D inverse perspective projections of
pi and
qi, are symmetric with respect to
Πs if and only if they satisfy the following two requirements: the line segment connecting
Pi and
Qi is parallel to the normal of
Πs and is bisected by
Πs.
The following equation represents the fact that the line segment connecting
Pi and
Qi is parallel to the normal of the plane
Πs:
![Symmetry 03 00365 i002]()
Note that in an inverse perspective projection, an image point [
x,
y, 0] projects to a 3D point [
x(
zf –
z)/
zf,
y(
zf –
z)/
zf,
z]. Hence,
Pi = [(
zf –
zΦi)(
xv + rφ(
αi)cos
αi)/
zf, (
zf –
zΦi)
rφ(
αi)sin
αi/
zf,
zΦi] and
Qi = [(
zf –
zΨi)(
xv + rψ(
αi)cos
αi)/
zf, (
zf –
zΨi)
rψ(
αi)sin
αi/
zf,
zΨi]. Then, combining (1) and (2), we obtain:
![Symmetry 03 00365 i003]()
From Equation (3), we obtain the following three facts. First, –
d/
c is an intersection of the symmetry plane
Πs and the
z-axis; it specifies the position of
Πs. Second, the normal to this plane is [–
xv/
zf, 0, 1], which is parallel to a vector [
xv, 0, –
zf] connecting the center of perspective projection with the vanishing point. This immediately follows from the fact that
v is the vanishing point corresponding to the lines connecting the pairs of 3D symmetric points, which are all normal to the symmetry plane. Third, a vanishing line (horizon)
h of
Πs is parallel to the y-axis on the image plane
ΠI. The line
h intersects
x-axis at:
![Symmetry 03 00365 i004]()
The next equation represents the fact that the line segments connecting pairs of 3D symmetric points are bisected by the symmetry plane. Let
Mi be the midpoint between
Pi and
Qi –the midpoint lies on the symmetry plane
Πs:
![Symmetry 03 00365 i005]()
From Equations (2) and (5), a perspective projection of
Mi to the image plane
ΠI can be written as follows:
![Symmetry 03 00365 i006]()
Equation (6) shows that
mi is on a 2D line segment
piqi and is determined only by 2D image features on
ΠI. It does not depend on the position of the center of projection
F. Recall that both
rφ(
α) and
rψ(
α) are continuous functions and they are always positive (
rφ(
α),
rψ(
α) > 0). It follows that the midpoints of the corresponding pairs of points on
φ and
ψ form a 2D continuous curve between
φ and
ψ on
ΠI. From Equations 2–6, we have:
![Symmetry 03 00365 i007]()
![Symmetry 03 00365 i008]()
It is obvious that (7) and (8) represent continuous functions unless
mi is on
h:
xmi = xh. Using Equations (6) and (4), we can rewrite
xmi = xh as follows:
![Symmetry 03 00365 i009]()
Note that the left-hand side of Equation (9) is a cross-ratio [
xv + rφ(
αi)cos
αi,
xv + rψ(
αi)cos
αi;
xv,
xh] = [
xφi,
xψi;
xv,
xh]. If
xmi = xh,
zΦi and
zΨi diverge to ±∞ and
Φ and
Ψ are not continuous. This is because a projecting line emanating from
F and going through
mi does not intersect
Πs. As a result,
Mi, which should be a midpoint between
Pi and
Qi, cannot be determined. Recall that 2D projections of midpoints of 3D symmetric pairs of points form a 2D continuous curve on
ΠI. Hence, this curve must not have any intersection or tangent point with
h. The whole curve must be either to the left or right of
h. It follows that the denominators in (7) and (8) must be always positive or always negative for given
φ and
ψ. If this criterion is not satisfied, the 3D curves will not be continuous. Note that if the position of the center of projection
F is a free parameter (this happens when the camera is uncalibrated), it is always possible to set
F and thus
h so that the criterion for continuity will be satisfied because the curve connecting the midpoints does not depend on
F.
Note that
d/
c is the only free parameter in Equations (7) and (8), once the vanishing point and the center of projection are fixed. Specifically, Equations (7) and (8) show that the left-hand sides are linear functions of
d/
c. Recall that in an inverse perspective projection, an image point [
x,
y, 0] projects to a 3D point [
x(
zf –
z)/
zf,
y(
zf –
z)/
zf,
z]. Assume that
d/
c ≠ –
zf —otherwise, the 3D interpretation will be degenerate with all the 3D points coinciding with the center of perspective projection
F (Except for the case when the symmetry plane coincides with the YOZ plane. This can happen when the image curves are themselves symmetric). It can be seen that
d/
c determines the size, but not the shape of the 3D curves
Φ and
Ψ;
zf +
d/
c is a scale factor with respect to
F as a center of scaling. Recall that the denominators in (7) and (8) must be always positive or always negative. From Equations (7) and (8),
d/
c can be adjusted so that
Φ and
Ψ are in front of the center of projection
F and the image plane
ΠI. The symmetric pair of 3D curves produced from the curves in
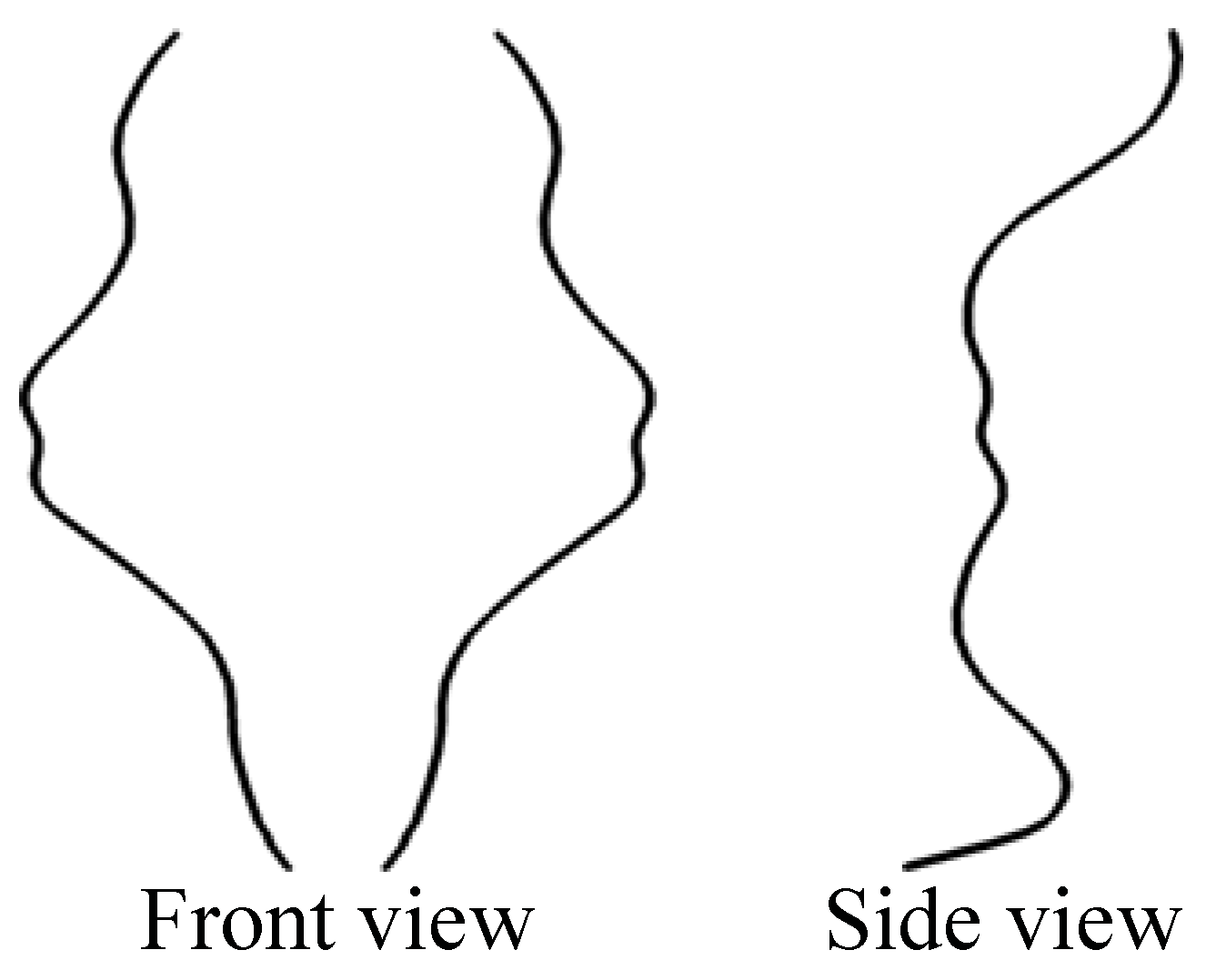
Figure 3 using Equations (7) and (8) is shown in
Figure 4.
In this proof, it was assumed that the position of the vanishing point
v is known or can be computed from the given 2D image. If the position of the vanishing point on the image plane is not known or is uncertain in the 2D image, the shape of the 3D symmetric interpretation is defined up to two free parameters [
19]. These two unknown parameters correspond to the slant and tilt of the symmetry plane
Πs.
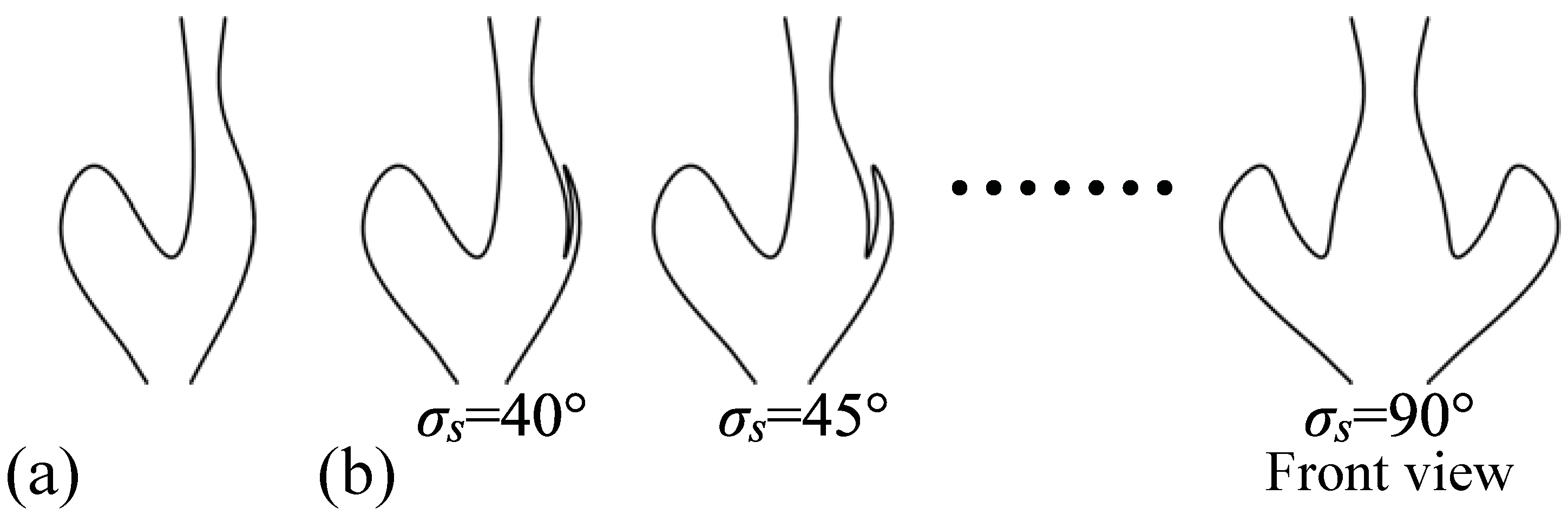
2.2. A Pair of 2D Curves with Unique Symmetric Correspondences—the Case of an Orthographic Projection
An orthographic projection is produced from a perspective projection by moving the center of perspective projection to infinity. As a result, the vanishing point corresponding to the symmetry line segments is also moved to infinity regardless of the slant of the symmetry plane. This implies that the 3D symmetric interpretation is always possible regardless of the position of the 2D curves on the image plane. In other words, the criteria for deciding whether the 3D curves are behind or in front of the camera are irrelevant in the case of an orthographic projection. We begin with modifying Equations (7) and (8) so that the position of the vanishing point is expressed as a function of the focal length of the camera. It will then be easy to transform the equations representing a perspective projection to equations representing an orthographic projection.
Under a perspective projection, the projected symmetry line segments in
ΠI intersect at a vanishing point
v. Since
v is an intersection of
ΠI and a line which emanates from
F and is parallel to
ns, the position of
v is [
xv, 0, 0] = [–
zf tan
σs, 0, 0]. The sine and cosine of the slant
σs of the symmetry plane
Πs can be expressed as follows:
![Symmetry 03 00365 i010]()
where
L is the distance between the vanishing point
v and the center of projection
F:
![Symmetry 03 00365 i011]()
Let
Pi = [
xΦi,
yΦi,
zΦi], be a point on
Φ and
Qi = [
xΨi,
yΨi,
zΨi] be its symmetric counterpart on
Ψ. Recall that the symmetry line segments are parallel to the normal
ns of the symmetry plane
Πs and
ns = [sin
σs, 0, cos
σs]. Hence,
yΦi =
yΨi. Let,
pi = [
xφi,
yφi, 0] be a perspective image of
Pi and
qi = [
xψi,
yψi, 0] be a perspective image of
Qi in
ΠI. A line segment connecting
Pi and
Qi is a symmetry line segment and a line segment connecting
pi and
qi is a projected symmetry line segment; recall that a projected symmetry line segment intersects the x-axis at
v. The
pi and
qi were represented in a polar coordinate system and written as
pi = [
xφi,
yφi, 0] = [
xv +
rφicos
αi,
rφisin
αi, 0] and
qi = [
xψi,
yψi, 0] = [
xv +
rψicos
αi,
rψisin
αi, 0], where
rφi and
rψi are the distances of
pi and
qi from
v when
α =
αi. Note that the 3D points
Pi and
Qi and their 2D projections
pi and
qi satisfy Equations (7) and (8). From Equations (7), (10) and (11), we obtain
zΦi (an analogous formula can be written for
zΨi):
![Symmetry 03 00365 i012]()
Recall that an orthographic projection is produced from a perspective projection by moving the center of projection
F to infinity:
zf → +∞. As
zf goes to infinity,
L goes to positive infinity, as well. From Equation (12), the limit of
zΦi as
zf goes to infinity is:
![Symmetry 03 00365 i013]()
The limit of
zΨi is obtained in an analogous way:
![Symmetry 03 00365 i014]()
Recall that in an inverse perspective projection, an image point [
x,
y,0] projects to a 3D point [
x(
zf –
z)/
zf,
y(
zf –
z)/
zf,
z]. As
zf goes to infinity, the limit of [
x(
zf –
z)/
zf,
y(
zf –
z)/
zf,
z] is [
x,
y,
z], which is an inverse orthographic projection of [
x,
y, 0].
Note that
xv goes to negative infinity as
zf goes to infinity; it follows that all
αi become zero. This means that the projected symmetry line segments become parallel to one another and to the
x-axis, and the vanishing point
v goes to infinity. Hence, the slant
σs of the symmetry plane cannot be computed from the 2D image; instead,
σs becomes a free parameter in the 3D interpretation under an orthographic projection. It follows that there are infinitely many 3D symmetric curves that are consistent with a pair of 2D curves
φ and
ψ. In other words, the 3D curves form a one-parameter family characterized by
σs;
σs changes the aspect ratio and the orientation of the 3D shapes of the curves
Φ and
Ψ [
10]. Note that if sin2
σs = 0 (
σs is 0 or 90°),
zΦi and
zΨi diverge to ±∞. Hence,
σs should not be 0 or 90°. These two cases correspond to degenerate views of
Φ and
Ψ. When
σs is 0°, the symmetry plane is parallel to the image plane;
φ and
ψ will then coincide with each other in the 2D image. In such a case, the 3D recovery of a pair of symmetric 3D curves becomes trivial: one produces any
Φ from
ϕ and then
Ψ is obtained as a mirror reflection of
Φ. When
σs is 90°, the symmetry plane is perpendicular to the image plane. In such a case,
φ and
ψ, themselves, must be mirror symmetric in the 2D image in order for the 3D symmetric interpretation to exist. But then, the 2D curves themselves represent one possible 3D symmetric interpretation. The ratio
d/
c is another free parameter, but it only changes the position of
Φ and
Ψ along the z-axis and does not change their 3D shapes or orientations. From these results, Theorem 1 for a perspective projection generalizes to Theorem 2 for an orthographic projection.
Theorem 2: Let
φ and
ψ be curves that are tame in a single 2D image. Let the endpoints of
φ be
eφ0 and
eφ1, and the endpoints of
ψ be
eψ0 and
eψ1. Assume that
φ and
ψ have the following properties: (i)
eφ0eψ0||
eφ1eψ1 and (ii) a line that is parallel to
eφ0eψ0 and intersects with
φ has a unique intersection with
ψ and
vice versa (see
Figure 5). Then, there exist infinitely many pairs of continuous curves
Φ and
Ψ and a plane
Πs in a 3D space, such that
Φ and
Ψ are mirror-symmetric with respect to
Πs and that
φ is an orthographic projection of
Φ and
ψ is an orthographic projection of
Ψ.
Proof:
Figure 5.
φ and ψ are two 2D curves. eφ0 and eφ1 are the endpoints of φ, and eψ0 and eψ1 are the end points of ψ. The lines eφ0eψ0 and eφ1eψ1 are parallel to the x-axis and do not have any intersection with φ and ψ. A line that is parallel to eφ0eψ0 and intersects with φ has a unique intersection with ψ and vice versa.
Figure 5.
φ and ψ are two 2D curves. eφ0 and eφ1 are the endpoints of φ, and eψ0 and eψ1 are the end points of ψ. The lines eφ0eψ0 and eφ1eψ1 are parallel to the x-axis and do not have any intersection with φ and ψ. A line that is parallel to eφ0eψ0 and intersects with φ has a unique intersection with ψ and vice versa.
Let the orientations of the line segments
eφ0eψ0 and
eφ1eψ1 be horizontal. This does not restrict the generality: if these line segments are not horizontal, we rotate the image so that they become horizontal. For any point
pi = [
xφi,
yφi] on
φ, we find its counterpart on
ψ as
qi = [
xψi,
yψi]. Note that
qi is found as an intersection of
ψ and a horizontal line
y =
yφi. Hence,
yφi =
yψi. We assume that this intersection is unique. Then, both
φ and
ψ can be represented as functions of
y:
xφi =
xφ(
yφi) and
xψi =
xψ(
yφi). From Equations (13) and (14), the 3D symmetric curves
Φ and
Ψ are produced by computing the positions of all points
Pi and
Qi as follows:
![Symmetry 03 00365 i015]()
![Symmetry 03 00365 i016]()
where
σs is a slant of the symmetry plane. The tilt
τs of the symmetry plane is zero. Equations (15) and (16) allow one to compute a pair of 3D symmetric curves
Φ and
Ψ from a pair of 2D curves
φ and
ψ under an orthographic projection. It is obvious from these equations that
Φ and
Ψ are continuous when
φ and
ψ are continuous. Recall that slant
σs is a free parameter; it can be arbitrary, except for sin2
σs = 0. So, the 3D symmetric curves form a one-parameter family characterized by
σs. Equations (15–16) show that a relation between the pair of 2D curves
φ and
ψ and the pair of 3D curves
Φ and
Ψ becomes computationally simple when
σs is 45° (or – 45°) and
d/
c is 0; the absolute value of the
z-coordinate of
Qi is equal to the x-coordinate of
Pi and the absolute value of the z-coordinate of P
i is equal to the
x-coordinate of Q
i. The symmetric pair of 3D curves produced using Equations (15) and (16) and consistent with
φ and
ψ in
Figure 5 is shown in
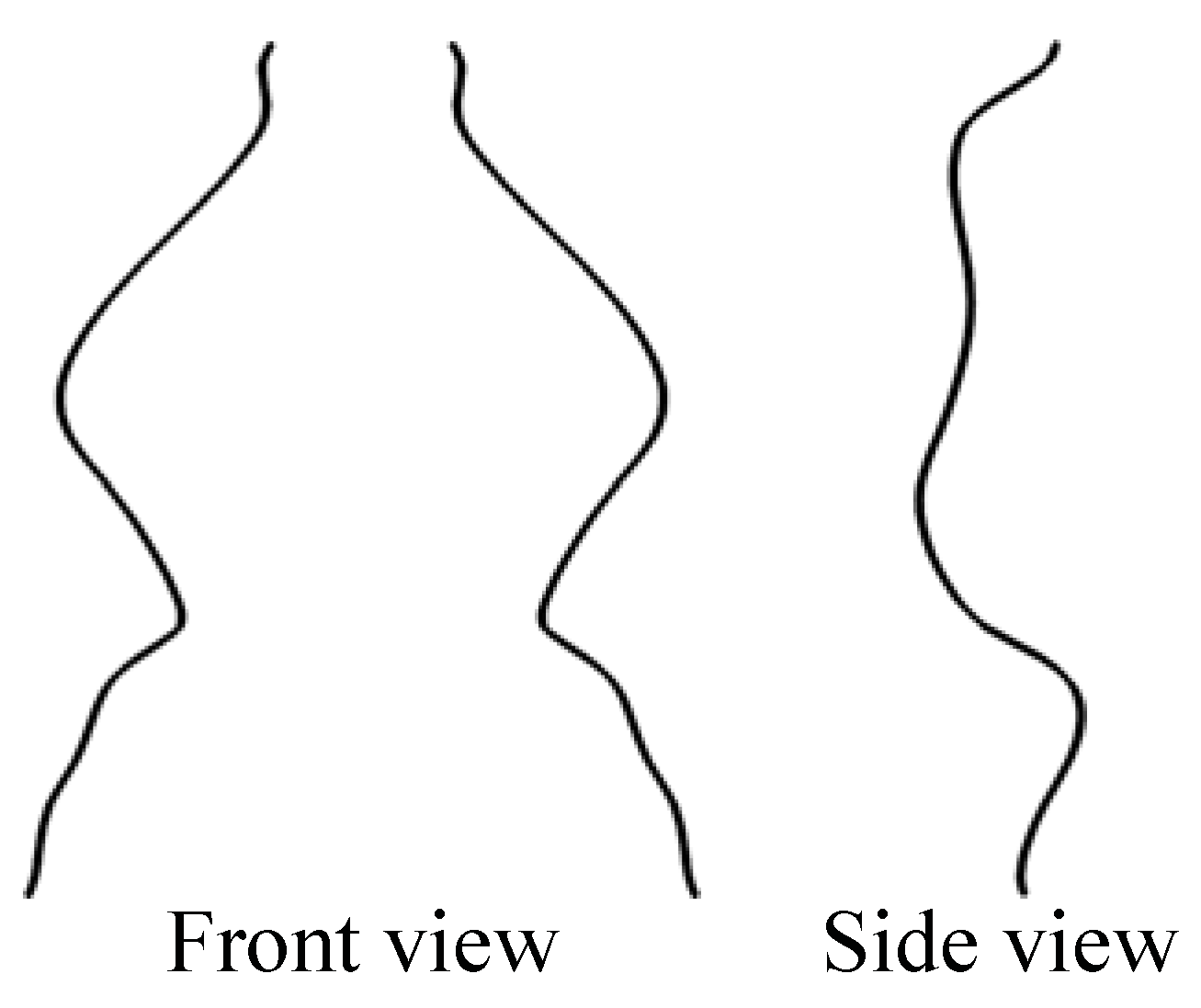
Figure 6.
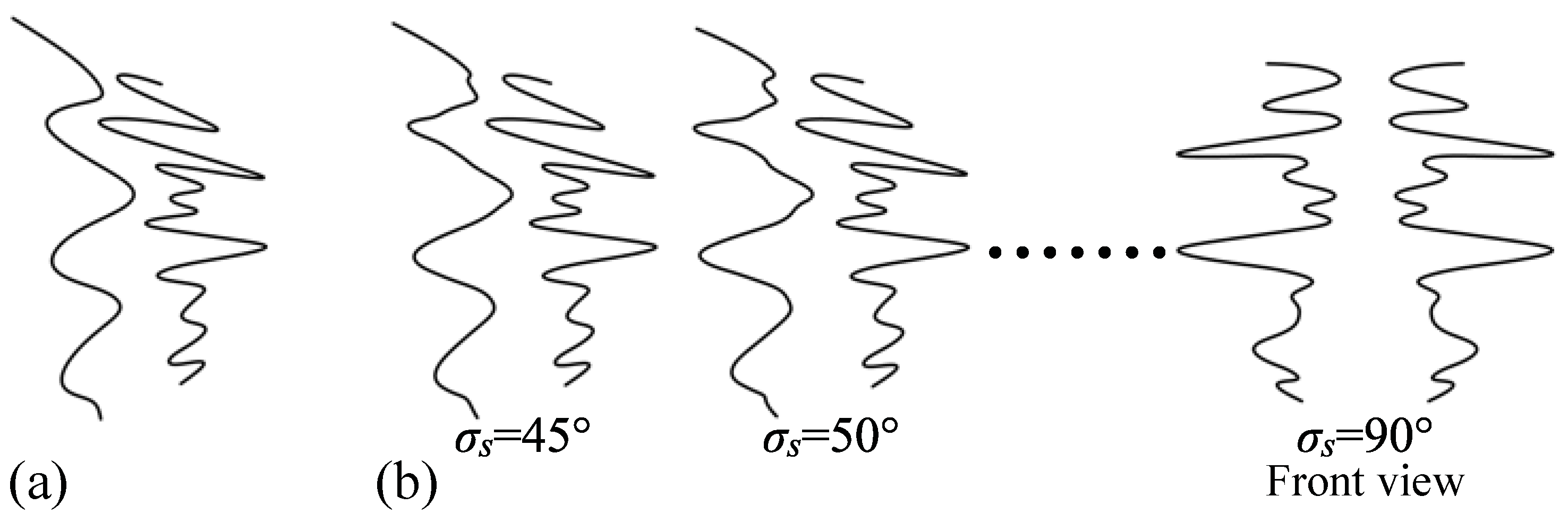
If the direction of the lines connecting the corresponding points on φ and ψ is not known or is uncertain, the family of 3D interpretations is characterized by two parameters: slant and tilt of the symmetry plane.
2.3. A Pair of 2D Curves with Multiple Symmetric Correspondences
In the two theorems above, it was assumed that correspondences between points of
φ and
ψ are unique. We generalize these theorems to the case of non-unique correspondences. A point on
φ can have multiple corresponding points on
ψ (and
vice versa). In such a case, the 3D interpretation of
φ will have segments whose 2D projections perfectly overlap one another in the 2D image (
Figure 7). In other words, the 3D symmetry will be hidden in the depth direction, and thus, the 3D view will be degenerate (see Discussion). First, we consider the case of an orthographic projection. This case will then be generalized to a perspective projection.
Figure 7.
An asymmetric pair of 2D curves with multiple symmetric correspondences and its 3D symmetric interpretation. (
a) An asymmetric pair of 2D curves. Some points of the right curve correspond to three points of the left curve. These curves can be still interpreted as a 2D orthographic projection of a symmetric pair of 3D curves. The slant
σs of the symmetry plane was set to 35°; (
b) Three different views of the 3D symmetric interpretation produced from the pair of the 2D curves in (
a). The numbers in the bottom are the values of the slant
σs of the symmetry plane of the symmetric pair of the 3D curves. For
σs equal to 35°, the image is identical to that in (
a). When
σs is 90°, its 2D projection itself becomes symmetric. See Demo 5 in supplemental material for an interactive illustration of the 3D symmetric curves [
2].
Figure 7.
An asymmetric pair of 2D curves with multiple symmetric correspondences and its 3D symmetric interpretation. (
a) An asymmetric pair of 2D curves. Some points of the right curve correspond to three points of the left curve. These curves can be still interpreted as a 2D orthographic projection of a symmetric pair of 3D curves. The slant
σs of the symmetry plane was set to 35°; (
b) Three different views of the 3D symmetric interpretation produced from the pair of the 2D curves in (
a). The numbers in the bottom are the values of the slant
σs of the symmetry plane of the symmetric pair of the 3D curves. For
σs equal to 35°, the image is identical to that in (
a). When
σs is 90°, its 2D projection itself becomes symmetric. See Demo 5 in supplemental material for an interactive illustration of the 3D symmetric curves [
2].
Theorem 3: Let
φ and
ψ be curves that are tame in a 2D image. Let the endpoints of
φ be
eφ0 and
eφ1, the endpoints of
ψ be
eψ0 and
eψ1. Let a line connecting
eφ0 and
eψ0 be
l0 and that connecting
eφ1 and
eψ1 be
l1. Assume that
φ and
ψ have the following properties: (i)
l0||
l1, (ii)
l0 and
l1 do not have any intersection with
φ and
ψ and (iii) a line that is parallel to
l0 and intersects
φ has one or a finite number of intersections with
ψ and
vice versa (see
Figure 8). Then, there exist infinitely many pairs of
continuous curves
Φ and
Ψ and a plane
Πs in a 3D space, such that
Φ and
Ψ are mirror-symmetric with respect to
Πs and that
φ is an orthographic projection of
Φ and
ψ is an orthographic projection of
Ψ.
Proof:
Figure 8.
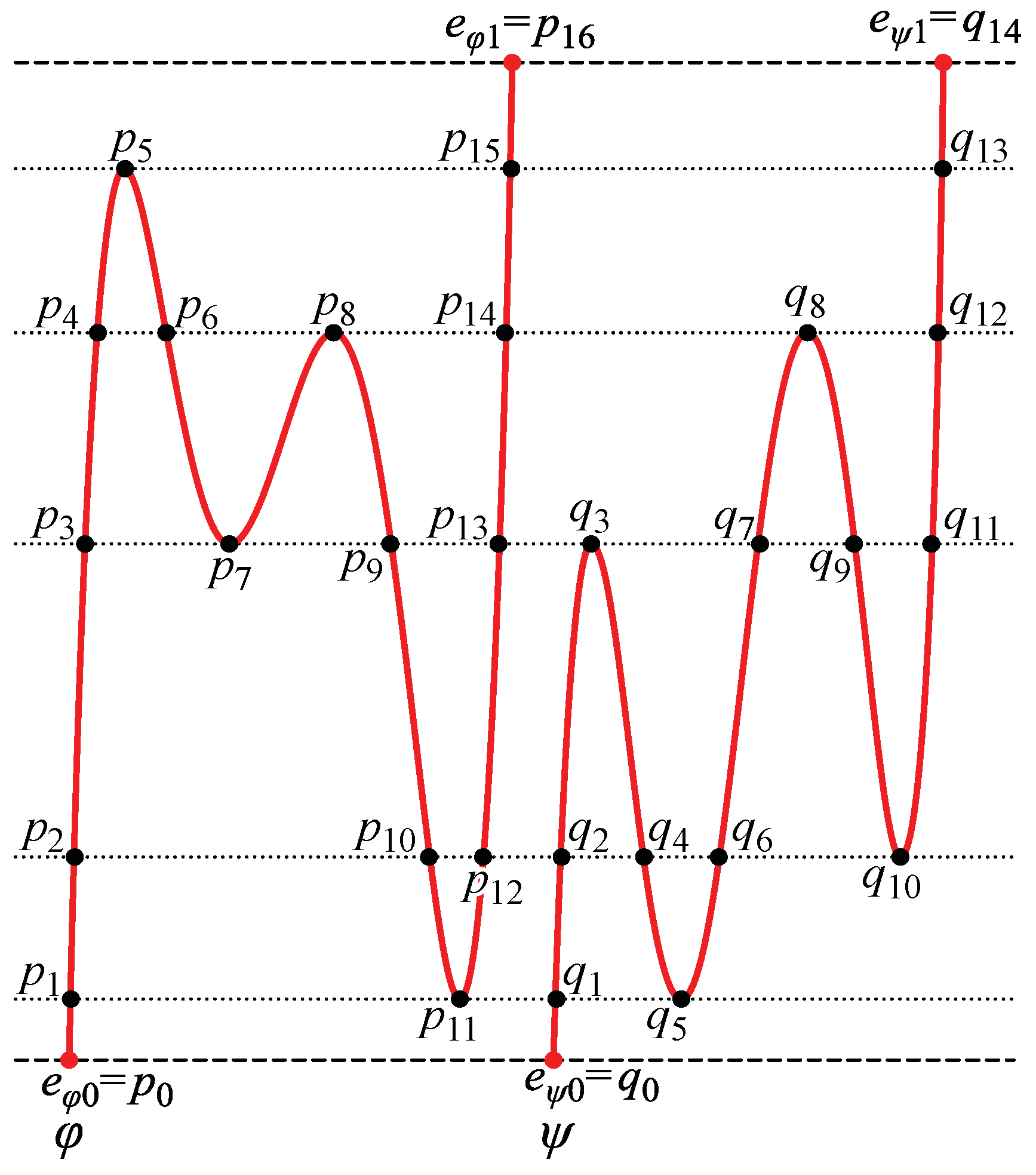
φ and ψ are 2D curves. eφ0 and eφ1 are the endpoints of φ, and eψ0 and eψ1 are the end points of ψ. l0 is a line connecting eφ0 and eψ0, and l1 is a line connecting eφ1 and eψ1. l0 and l1 are parallel to the x-axis and do not have any intersection with φ and ψ. A line that is parallel to l0 and intersects with φ has one or more intersections with ψ and vice versa.
Figure 8.
φ and ψ are 2D curves. eφ0 and eφ1 are the endpoints of φ, and eψ0 and eψ1 are the end points of ψ. l0 is a line connecting eφ0 and eψ0, and l1 is a line connecting eφ1 and eψ1. l0 and l1 are parallel to the x-axis and do not have any intersection with φ and ψ. A line that is parallel to l0 and intersects with φ has one or more intersections with ψ and vice versa.
In order to prove this theorem, we first divide a pair of φ and ψ into multiple pairs of fragments, such that each pair satisfies the assumptions of Theorem 2. Then, we find their backprojections that are mirror-symmetric pairs of continuous curves in the 3D space. Next, we will show that these multiple pairs of 3D curves can share a common symmetry plane Πs and produce a symmetric pair of continuous curves.
As before we assume that the orientations of the line segments
eφ0eψ0 and
eφ1eψ1 are horizontal. In this case,
eφ0,
eφ1,
eψ0 and
eψ1 are either global maxima or minima of
φ and
ψ along a vertical axis on the 2D image. Consider horizontal lines that are tangent to the curves at their local extrema (
Figure 8). Intersections and tangent points of these horizontal lines with
φ and
ψ are labeled by numbers sequentially along each curve;
p1, …,
pm on
φ and
q1, …,
qn on
ψ (in
Figure 8,
n = 15, and
m = 13). Both
φ and
ψ are divided into segments
p1p2,
p2p3 etc. Let the endpoints
eφ0,
eφ1,
eψ0 and
eψ1 on
φ and
ψ be
p0,
pm+1,
q0 and
qn+1, respectively. Let
cφi be a segment of
ϕ connecting
pi and its successor
pi+1. Then,
cφi is a curve that is monotonic and continuous between
pi and
pi+1 and these two points are the endpoints of
cφi. Similarly, let
cψj be a segment of
ψ connecting
qj and its successor
qj+1. A segment
cφi of
φ has, at least, one corresponding segment of
ψ; the endpoints of these segments of
ϕ and
ψ form parallel line segments. From Theorem 2, a pair of
cφi and each of the corresponding segments of
ψ are consistent with an infinite number of 3D symmetric interpretations under an orthographic projection; the one-parameter family of symmetric pairs of 3D curves is characterized by the slant of a symmetry plane. The tilt of the symmetry plane is zero and its depth along the z-axis is arbitrary. It follows that, among all corresponding pairs of 2D segments of these curves, their possible 3D symmetric interpretations can share a common symmetry plane
Πs with some slant
σs and depth. Hence,
φ and
ψ are consistent with a one parameter family of symmetric pairs of the 3D fragmented curves that are backprojections of the 2D segments of the 2D curves. In order to prove Theorem 3, we show that,
for each member of the family, the symmetric pairs of the 3D fragmented curves produce a symmetric pair of 3D continuous curves whose endpoints are backprojections of the endpoints of φ and ψ. An orthographic projection of such a symmetric pair of the 3D continuous curves will be
φ and
ψ.
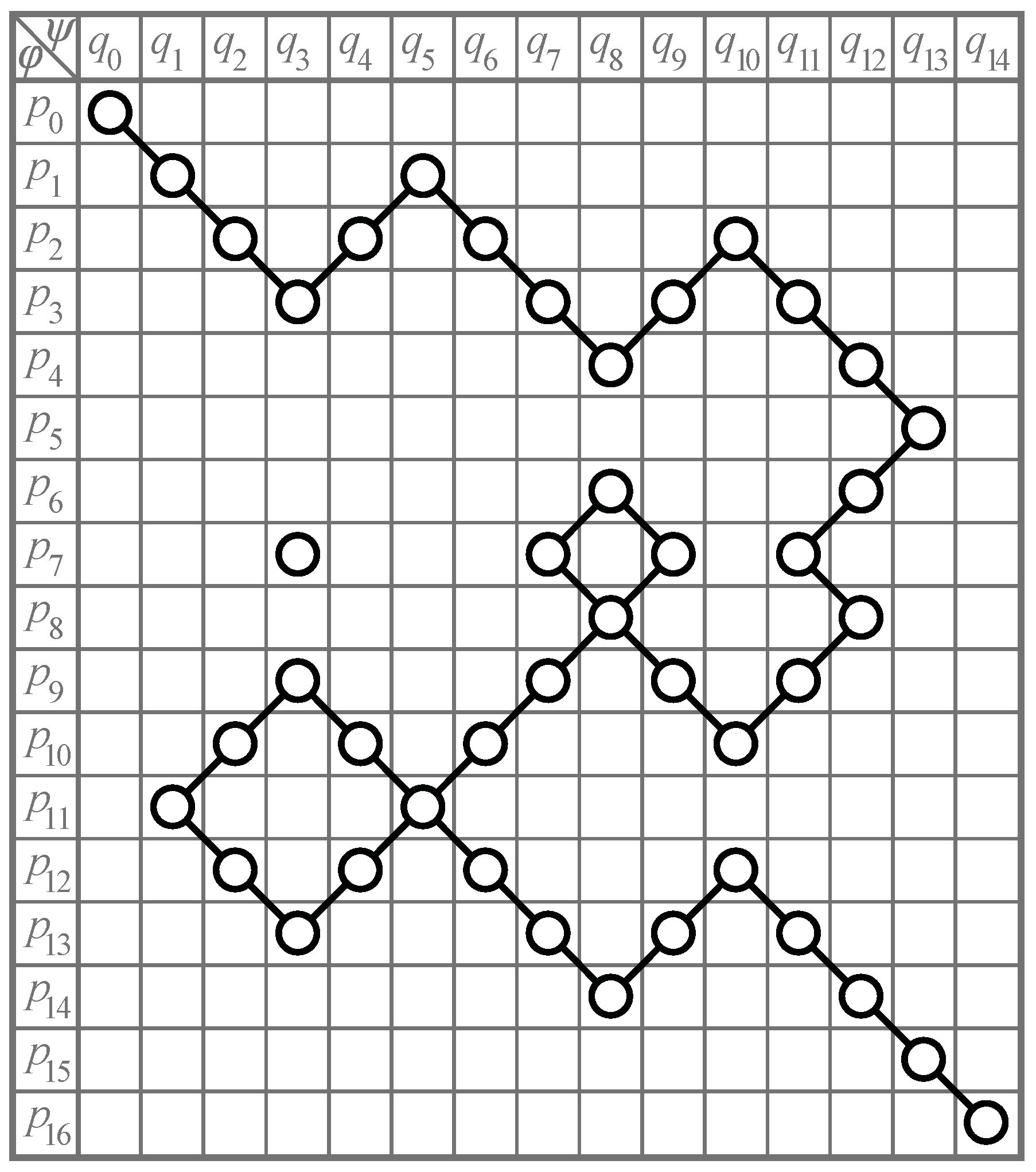
A table representing pairs of the segments of
φ and
ψ and their endpoints is shown in
Figure 9. The rows of the table represent the points
p0, …,
pm+1 on
φ. The columns represent the points
q0, …,
qn+1 on
ψ. A circle at (
pi,
qj) represents a corresponding pair of points
pi and
qj in
Figure 8. These circles are nodes in a graph representing the possible correspondences among pairs of points in
Figure 8. Let an edge in this graph connecting (
pi,
qj) and (
pk,
ql) be labeled (
pi,
qj)-(
pk,
ql). Note that the edge (
pi,
qj)-(
pk,
ql) is the same as (
pk,
ql)-(
pi,
qj). The edge (
pk,
ql)-(
pi,
qj) represents a pair of segments of
ϕ and
ψ, such that
cφ min(i,k) connects
pi and
pk and
cψ min(j,l) connects
qj and
ql. Recall that the endpoints of each segment on
ϕ and
ψ are two neighboring points of
φ or
ψ; |
I −
k| = 1 and |
j −
l| = 1. Hence, an edge in the graph shown in
Figure 9 can only connect two nodes that are diagonally next to each other in the table and a node can be connected to, at most, four nodes by four edges. A pair of nodes can be connected to each other only by a single edge. The end nodes of (
pi,
qj)-(
pk,
ql) are either the maxima or minima of these segments and their endpoints form horizontal line segments. Hence, from the Theorem 2, a pair of segments of
ϕ and
ψ represented by each edge in the graph is consistent with a one-parameter family of pairs of 3D curves that is symmetric with respect to the common symmetry plane
Πs.
Consider two edges (
pi,
qj)-(
pk,
ql) and (
pi,
qj)-(
pg,
qh) connected to a common node (
pi,
qj). These edges represent two pairs of segments of the 2D curves; a pair
cφmin(i,k) and
cψmin(j,l) and a pair
cφmin(i,g) and
cψmin(j,h). The two segments
cφmin(i,k) and
cφmin(i,g) are connected to each other at their common endpoint
pi (see
Figure 8). In the same way,
cψmin(j,l) and
cψmin(j,h) are connected to each other at their common endpoint
qj. Hence, these two pairs of 2D curves can be regarded as a pair of 2D curves whose endpoints are represented by (
pk,
ql) and (
pg,
qh) that are the end nodes of the path formed by the edges. Note that each (
pi,
qj)-(
pk,
ql) and (
pi,
qj)-(
pg,
qh) is consistent with infinitely many pairs of 3D continuous curves. Assume that they are symmetric with respect to the common symmetry plane
Πs whose slant and depth are given. Then, two symmetric pairs of 3D continuous curves are uniquely determined; these 3D curves are backprojections of
cφmin(i,k),
cφmin(i,g),
cψmin(j,l) and
cψmin(j,h), respectively. The 3D curves that are backprojections of
cφmin(i,k) and
cφmin(i,g) are connected to each other at their common endpoint that is a backprojection of
pi; these two 3D curves can be regarded as a single 3D curve. The same way, the 3D curves that are backprojections of
cψmin(j,l) and
cψmin(j,h) can be regarded as a single 3D curve. It follows that the two symmetric pairs of 3D curves produced from
cφmin(i,k),
cφmin(i,g),
cψmin(j,l) and
cψmin(j,h) can be regarded as a single symmetric pair of 3D continuous curves. Their endpoints are backprojections of the 2D points represented by the end nodes (
pk,
ql) and (
pg,
qh) of the continuous path. This can be generalized to all segments of
ϕ and
ψ as follows. A continuous path of the edges in the table in
Figure 9 represents a pair of 2D continuous curves; the 2D curves are composed of the 2D segments of
φ and
ψ and their endpoints are represented by the end nodes of the path. The 2D curves are consistent with an infinite number of symmetric pairs of 3D continuous curves. The endpoints of the 3D curves are backprojections of the points represented by the end nodes of the path. So, if there is a continuous path connecting (
p0,
q0) and (
pm+1,
qn+1) in the graph in
Figure 9, then this path represents a pair of 2D continuous curves
φ and
ψ and this pair of the 2D curves is consistent with a one-parameter family of symmetric pairs of 3D continuous curves.
The existence of a continuous path of edges connecting (
p0,
q0) and (
pm+1,
qn+1) in the graph will now be proved by using concepts from a graph theory. A graph is called connected if there is a continuous path of edges between every pair of nodes in the graph. If (
p0,
q0) and (
pm+1,
qn+1) belong to a connected graph, there is a path connecting (
p0,
q0) and (
pm+1,
qn+1). A connected graph has even number of nodes of odd degree, where degree of a node refers to number of edges connected to the node [
20]. If (
p0,
q0) and (
pm+1,
qn+1) are the only nodes of odd degree in the graph, they must belong to the same connected graph and there must be a continuous path connecting (
p0,
q0) and (
pm+1,
qn+1). Next, we provide a classification of possible nodes in the graph and show that there are only four types: of degree zero, one, two or four. This will conclude the proof.
Consider
p1, …,
pm on
φ and
q1, …,
qn on
ψ. If a node (
pi,
qj) exists in the table,
pi and
qj form a horizontal line segment in
Figure 8. Note that (
pi,
qj) can be connected to, at most, four nodes in the graph that are diagonally next to (
pi,
qj): (
pi−1,
qj−1), (
pi−1,
qj+1), (
pi+1,
qj−1) and (
pi+1,
qj+1). Hence, the maximum degree of each node in the table is four. These four neighboring nodes represent possible pairs of neighboring points of
pi along
φ and
qj along
ψ. Consider a pair of the neighboring points
pi+1 and
qj + 1. The node (
pi+1,
qj+1) exists if and only if
pi+1 and
qj+1 are a corresponding pair; they form a horizontal line segment in
Figure 8. Note that
pi + 1 and
pi are connected by
cφi and
qj+1 and
qj are connected by
cψj. If both (
pi+1,
qj+1) and (
pi,
qj) exist in the graph, they are connected by (
pi+1,
qj+1)-(
pi,
qj) representing a pair of segments
cφi and
cψj. Therefore, the number of edges in the graph connected to (
pi,
qj) can be computed by verifying the existence of the four neighboring nodes.
In order to compute the number of edges connected to each node, points and corresponding pairs of points represented by the nodes in the graph are classified. Consider points
p1, …,
pm and
q1, …,
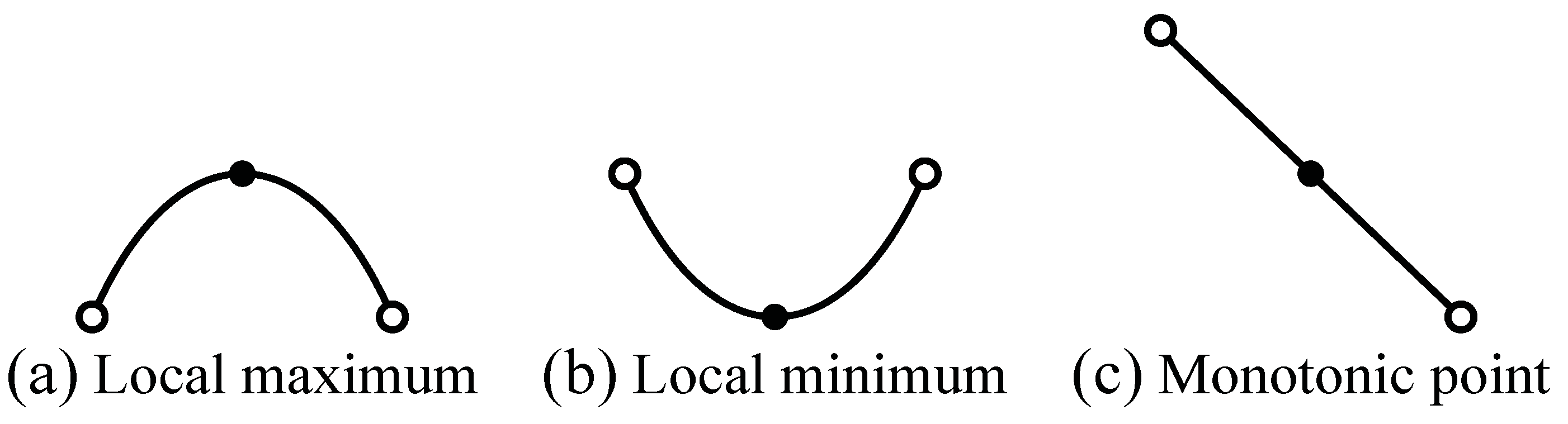
qn. First, these points can be classified into three types: local maxima, local minima and points at which the curve is monotonic (
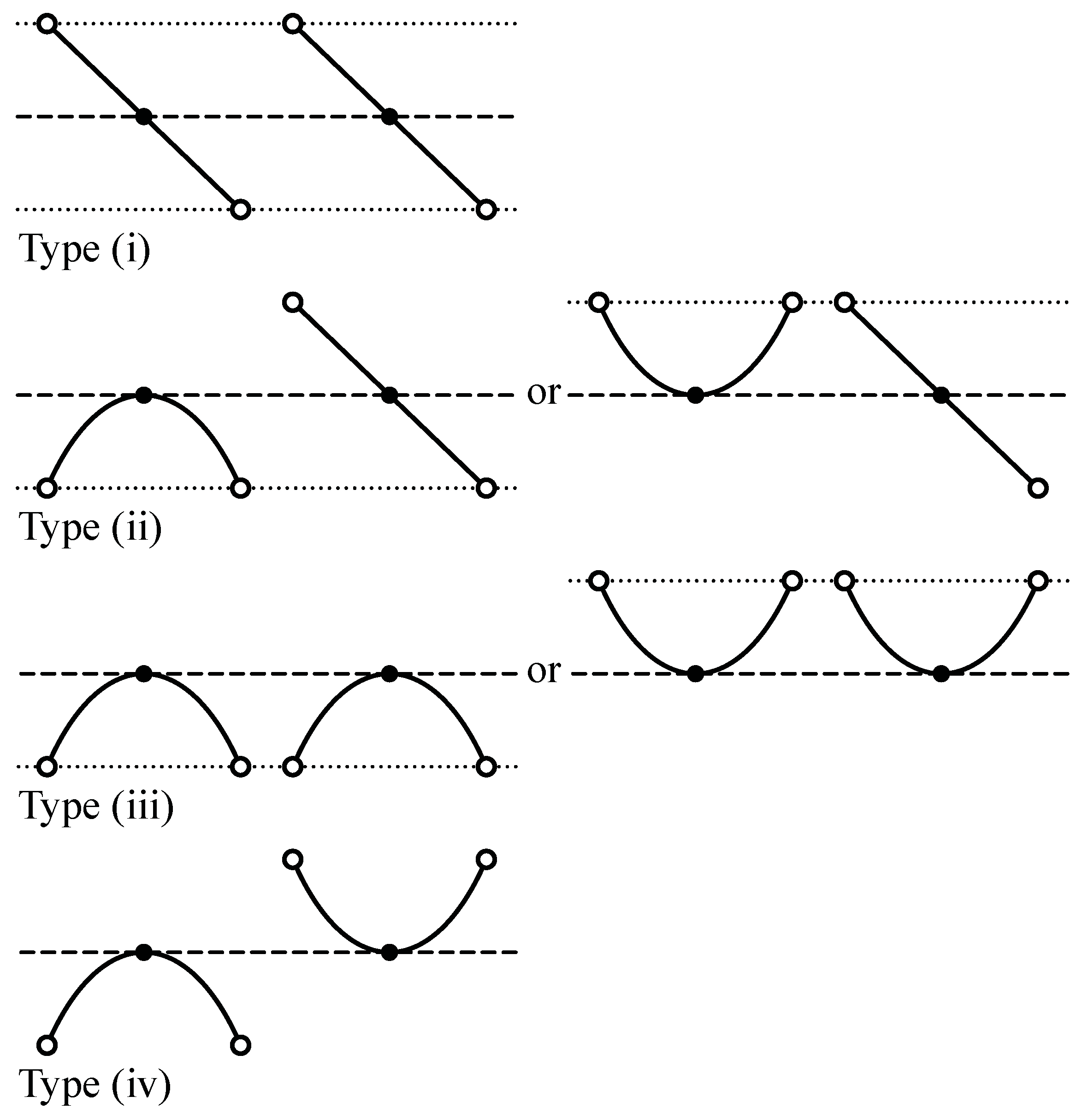
Figure 10). If a point is a local maximum, its neighboring points are lower than the local maximum. If a point is a local minimum, its neighboring points are higher than the local minimum. If a point is a “monotonic point”, one of its neighboring points is higher and the other is lower. Next, based on the classification of the points, the corresponding pairs of the points can be classified into three types (
Figure 11). Type (i): if two monotonic points are corresponding, a node representing this pair of points is connected to two nodes by two edges. Hence, the degree of this node is two; Type (ii): if a monotonic point and a local maximum/minimum are corresponding, the degree of a node representing this pair is also two; Type (iii): if two local maxima/minima are corresponding, the degree of a node representing this pair is four; Type (iv): if a local maximum and a local minimum are corresponding, the degree of a node representing this pair is zero. From these facts, the degree of any node which does not represent the endpoints of the two curves is always even (0, 2 or 4).
Next, consider pairs of endpoints of
φ and
ψ: (
p0,
q0) and (
pm + 1,
qn+1). Recall that
p0 =
eφ0,
pm+1 =
eφ1,
q0 =
eψ0 and
qn+1 =
eψ1; so, the line segments
p0q0 and
pm+1qn+1 are horizontal in
Figure 8. Hence, these pairs of the endpoints are corresponding pairs and the nodes representing these pairs exist in the graph. Note that these endpoints are global maxima and minima of
φ and
ψ; the global maxima form a corresponding pair and the global minima form a corresponding pair. Recall that if two local maxima or two local minima form a corresponding pair, there are four corresponding pairs of their neighboring points. However, each endpoint has only one neighboring point. Hence, there is one corresponding pair of the neighboring points for each pair of the endpoints. Therefore, each (
p0,
q0) and (
pm+1,
qn+1) is connected to a single node and their degrees are one, which is an odd number.
Note that the case where
φ or
ψ has a local extremum at which a horizontal line connecting
eφ0 and
eψ0 or
eφ1 and
eψ1 is tangent to the curve of the extremum, is analogous to Type (ii) in
Figure 11. The extremum of the curve corresponds to an endpoint of the other curve that is on the horizontal tangent line. Unlike Type (ii), the endpoint has only one neighboring point that forms a corresponding pair with the neighboring points of the local extremum. Hence, the degree of a node representing the pair of the local extremum and the endpoint is also two, which is an even number.
From these facts, there are two nodes (
p0,
q0) and (
pm+1,
qn+1) whose degrees are odd (1) and the degrees of all other nodes are even (0, 2 or 4). Hence, (
p0,
q0) and (
pm+1,
qn+1) must belong to the same connected graph and these two nodes are connected by a continuous path of edges. This continuous path in the graph represents the correspondences between 3D continuous curves of a symmetric pair whose orthographic projections are the 2D curves
φ and
ψ, respectively. Once the correspondences are formed, the pair of the 3D curves can be produced using Equations (15) and (16). Note that the slant of the symmetry plane
Πs is a free parameter of the 3D symmetric interpretation of
φ and
ψ under an orthographic projection. A symmetric pair of 3D curves produced from the pair of 2D curves in
Figure 8 is shown in Demo 6 in supplemental material [
2].
This proof of Theorem 3 for an orthographic projection can be easily generalized to the case of a perspective projection:
Theorem 4: Let φ and ψ be curves that are tame in a single 2D image. Let the endpoints of φ be eφ0 and eφ1, and the endpoints of ψ be eψ0 and eψ1. Let a line connecting eφ0 and eψ0 be l0 and that connecting eφ1 and eψ1 be l1. Assume that φ and ψ have the following properties: (i) l0 and l1 intersect at a point v that is not on φ or ψ; (ii) l0 and l1 do not have any intersection with φ and ψ; (iii) v is not between eφ0 and eψ0 or between eφ1 and eψ1; and (iv) a half line that emanates from v and intersects with φ has one or a finite number of intersections with ψ and vice versa. Then, there exists a pair of continuous curves Φ and Ψ and a plane Πs in a 3D space for a given center of projection F, such that Φ and Ψ are mirror-symmetric with respect to Πs and that φ is a perspective projection of Φ and ψ is a perspective projection of Ψ.
Proof: In the proof of Theorem 3 for the case of an orthographic projection, the 2D curves φ and ψ were divided by lines which were parallel to eφ0eψ0 and were tangent to either of the 2D curves. In the case of a perspective projection, φ and ψ are divided by lines which emanate from the vanishing point v and are tangent to either of the 2D curves. The rest of this proof is identical to that of Theorem 3. The only difference is that in the case of a perspective projection the 3D interpretation is unique—the slant of the symmetry plane is not a free parameter.
In the four theorems above it was assumed that an endpoint of one curve corresponds to an endpoint of the other curve. Next, we generalize Theorems 3 and 4 to the case where an endpoint of a curve may or may not correspond to an endpoint of the other curve. This can happen, for example, in the presence of occlusion. We begin with the case of an orthographic projection.
Theorem 5: Let
φ and
ψ be curves that are tame in a 2D image. Assume that there exist two lines
l0 and
l1 which satisfy the following properties: (i)
l0 and/or
l1 is either tangent to both
φ and
ψ or passes through their endpoints, (ii)
l0||
l1, (iii)
l0 and
l1 do not have any intersection with
φ and
ψ and (iv) a line that is parallel to
l0 and intersects
φ has one or a finite number of intersections with
ψ and
vice versa (see
Figure 12). Then, there exist infinitely many pairs of
continuous curves
Φ and
Ψ and a plane
Πs in a 3D space, such that
Φ and
Ψ are mirror-symmetric with respect to
Πs and that
φ is an orthographic projection of
Φ and
ψ is an orthographic projection of
Ψ.
In order to prove this theorem, we first extend φ and ψ and obtain a pair of 2D curves φ′ and ψ′ that perfectly overlap φ and ψ in the 2D image and satisfy the assumptions of Theorem 3. Then, we find the backprojections of φ′ and ψ′ in the 3D space, such that these backprojected curves are mirror-symmetric with respect to a plane Πs. Their orthographic projections in the 2D image coincide with φ′ and ψ′, as well as with φ and ψ.
Let the orientations of l0 and l1 be horizontal. In this case, tangent points of φ and ψ to l0 or l1 are either global maxima or minima of φ and ψ along a vertical axis on the 2D image. Assume that the endpoints of these curves are not global extrema—the case when they are global extrema has been considered in the previous theorems. Let the tangent points of φ to l0 and l1 be tφ0 and tφ1. Let an endpoint of φ, which is closer (as measured by the arc length along the curve) to tφ0 be eφ0, and that, which is closer to tφ1 be eφ1. The same way, let the tangent points of ψ to l0 or l1 be tψ0 and tψ1, and the endpoints ψ be eψ0 and eψ1.
We extend the 2D curves
φ and
ψ by adding arcs that start from
eφ0,
eφ1,
eψ0 and
eψ1, which are endpoints of
φ and
ψ. The extension starting from
eφ0 is identical to the segment of
φ between
eφ0 and
tφ0. Similarly, the extension starting from
eφ1 is identical to the segment of
φ between
eφ1 and
tφ1. Let this new curve be
φ′. Let the endpoints of
φ′ be
e′
φ0 and
e′
φ1, so that the positions of
e′
φ0 and
e′
φ1 are respectively the same as those of
tφ0 and
tφ1 in the 2D image. The same way, let the extended curve produced from
ψ be
ψ′ and the endpoints of
ψ′ be
e′
ψ0 and
e′
ψ1. The positions of
e′
ψ0 and
e′
ψ1 are respectively the same as those of
tψ0 and
tψ1 in the 2D image. The curves
φ′ and
ψ′ perfectly overlap
φ and
ψ in the 2D image (
Figure 12). Therefore, the 3D interpretations of
φ′ and
ψ′ are also consistent with the 3D interpretations of
φ and
ψ. It is easy to see that
φ′ and
ψ′ satisfy the assumptions of Theorem 3. Therefore, it follows from the proof of Theorem 3 that there exists a one-parameter family of symmetric pairs of continuous 3D curves
Φ′ and
Ψ′, such that
φ′ is an orthographic projection of
Φ′ and
ψ′ is an orthographic projection of
Ψ′. This, in turn, implies that
φ and
ψ are also orthographic projection of
Φ′ and
Ψ′. A symmetric pair of 3D curves produced from the pair of 2D curves in
Figure 12 is shown in Demo 7 in supplemental material [
2] (It looks like each of the 3D curves in Demo 6 has four endpoints, rather than two, as would be expected from Theorem 3. It also looks like each of the 3D curves has two bifurcations. All of the four points that look like endpoints are actually 180° turns of the 3D curve. The real endpoints of the 3D curve are at the bifurcations).
Proof:
Figure 12.
φ and
ψ (red solid curves) are 2D curves.
eφ0 and
eφ1 are the endpoints of
φ, and
eψ0 and
eψ1 are the end points of
ψ.
l0 is tangent to both
φ and
ψ at
tφ0 and
tψ0, and
l1 is tangent to both
φ and
ψ at
tφ1 and
tψ1.
l0 and
l1 are parallel to the
x-axis and do not have any intersection with
φ and
ψ. The two curves,
φ and
ψ are extended by adding arcs (blue dotted curves) that start from
eφ0,
eφ1,
eψ0 and
eψ1. The additional arcs are identical to the segments of
φ and
ψ (note that the blue dotted curves are perfectly overlapping the red solid curves in the image). They end at
e′
φ0,
e′
φ1,
e′
ψ0 and
e′
ψ1 whose positions are respectively the same as those of
tφ0,
tφ1,
tψ0 and
tψ1. See Demo 7 in supplemental material for an interactive illustration of the 3D symmetric curves produced from
φ and
ψ [
2].
Figure 12.
φ and
ψ (red solid curves) are 2D curves.
eφ0 and
eφ1 are the endpoints of
φ, and
eψ0 and
eψ1 are the end points of
ψ.
l0 is tangent to both
φ and
ψ at
tφ0 and
tψ0, and
l1 is tangent to both
φ and
ψ at
tφ1 and
tψ1.
l0 and
l1 are parallel to the
x-axis and do not have any intersection with
φ and
ψ. The two curves,
φ and
ψ are extended by adding arcs (blue dotted curves) that start from
eφ0,
eφ1,
eψ0 and
eψ1. The additional arcs are identical to the segments of
φ and
ψ (note that the blue dotted curves are perfectly overlapping the red solid curves in the image). They end at
e′
φ0,
e′
φ1,
e′
ψ0 and
e′
ψ1 whose positions are respectively the same as those of
tφ0,
tφ1,
tψ0 and
tψ1. See Demo 7 in supplemental material for an interactive illustration of the 3D symmetric curves produced from
φ and
ψ [
2].
This proof of Theorem 5 for an orthographic projection can be easily generalized to the case of a perspective projection, the same way as the proof of Theorem 3 was generalized to the case of perspective projection:
Theorem 6: Let φ and ψ be curves that are tame in a 2D image. Assume that there exist two lines l0 and l1 which satisfy the following properties: (i) l0 and/or l1 is either tangent to both φ and ψ or passes through their endpoints; (ii) l0 and l1 intersect at a point v that is not on φ or ψ; (iii) l0 and l1 do not have any other intersections with φ and ψ; (iv) v is not between eφ0 and eψ0 or between eφ1 and eψ1, and (v) a half line that emanates from v and intersects with φ has one or a finite number of intersections with ψ and vice versa. Then, there exists a pair of continuous curves Φ and Ψ and a plane Πs in a 3D space for a given center of projection F, such that Φ and Ψ are mirror-symmetric with respect to Πs and that φ is a perspective projection of Φ and ψ is a perspective projection of Ψ.

 Pi and Qi, the 3D inverse perspective projections of pi and qi, are symmetric with respect to Πs if and only if they satisfy the following two requirements: the line segment connecting Pi and Qi is parallel to the normal of Πs and is bisected by Πs.
Pi and Qi, the 3D inverse perspective projections of pi and qi, are symmetric with respect to Πs if and only if they satisfy the following two requirements: the line segment connecting Pi and Qi is parallel to the normal of Πs and is bisected by Πs. Note that in an inverse perspective projection, an image point [x, y, 0] projects to a 3D point [x(zf – z)/zf, y(zf – z)/zf, z]. Hence, Pi = [(zf – zΦi)(xv + rφ(αi)cosαi)/zf, (zf – zΦi)rφ(αi)sinαi/zf, zΦi] and Qi = [(zf – zΨi)(xv + rψ(αi)cosαi)/zf, (zf – zΨi)rψ(αi)sinαi/zf, zΨi]. Then, combining (1) and (2), we obtain:
Note that in an inverse perspective projection, an image point [x, y, 0] projects to a 3D point [x(zf – z)/zf, y(zf – z)/zf, z]. Hence, Pi = [(zf – zΦi)(xv + rφ(αi)cosαi)/zf, (zf – zΦi)rφ(αi)sinαi/zf, zΦi] and Qi = [(zf – zΨi)(xv + rψ(αi)cosαi)/zf, (zf – zΨi)rψ(αi)sinαi/zf, zΨi]. Then, combining (1) and (2), we obtain:
 From Equation (3), we obtain the following three facts. First, –d/c is an intersection of the symmetry plane Πs and the z-axis; it specifies the position of Πs. Second, the normal to this plane is [– xv/zf, 0, 1], which is parallel to a vector [xv, 0, – zf] connecting the center of perspective projection with the vanishing point. This immediately follows from the fact that v is the vanishing point corresponding to the lines connecting the pairs of 3D symmetric points, which are all normal to the symmetry plane. Third, a vanishing line (horizon) h of Πs is parallel to the y-axis on the image plane ΠI. The line h intersects x-axis at:
From Equation (3), we obtain the following three facts. First, –d/c is an intersection of the symmetry plane Πs and the z-axis; it specifies the position of Πs. Second, the normal to this plane is [– xv/zf, 0, 1], which is parallel to a vector [xv, 0, – zf] connecting the center of perspective projection with the vanishing point. This immediately follows from the fact that v is the vanishing point corresponding to the lines connecting the pairs of 3D symmetric points, which are all normal to the symmetry plane. Third, a vanishing line (horizon) h of Πs is parallel to the y-axis on the image plane ΠI. The line h intersects x-axis at:
 The next equation represents the fact that the line segments connecting pairs of 3D symmetric points are bisected by the symmetry plane. Let Mi be the midpoint between Pi and Qi –the midpoint lies on the symmetry plane Πs:
The next equation represents the fact that the line segments connecting pairs of 3D symmetric points are bisected by the symmetry plane. Let Mi be the midpoint between Pi and Qi –the midpoint lies on the symmetry plane Πs:
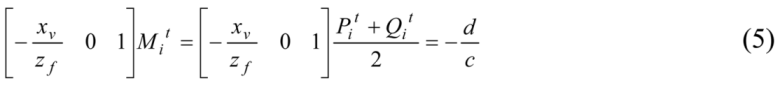 From Equations (2) and (5), a perspective projection of Mi to the image plane ΠI can be written as follows:
From Equations (2) and (5), a perspective projection of Mi to the image plane ΠI can be written as follows:
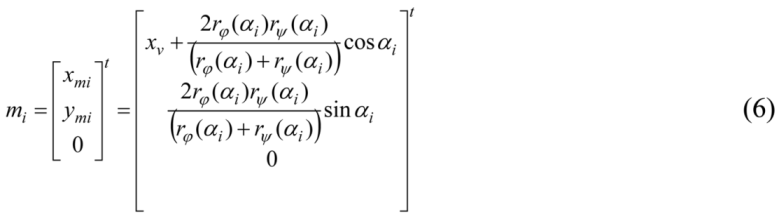 Equation (6) shows that mi is on a 2D line segment piqi and is determined only by 2D image features on ΠI. It does not depend on the position of the center of projection F. Recall that both rφ(α) and rψ(α) are continuous functions and they are always positive (rφ(α), rψ(α) > 0). It follows that the midpoints of the corresponding pairs of points on φ and ψ form a 2D continuous curve between φ and ψ on ΠI. From Equations 2–6, we have:
Equation (6) shows that mi is on a 2D line segment piqi and is determined only by 2D image features on ΠI. It does not depend on the position of the center of projection F. Recall that both rφ(α) and rψ(α) are continuous functions and they are always positive (rφ(α), rψ(α) > 0). It follows that the midpoints of the corresponding pairs of points on φ and ψ form a 2D continuous curve between φ and ψ on ΠI. From Equations 2–6, we have:
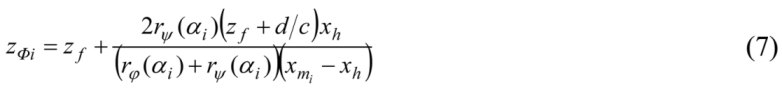
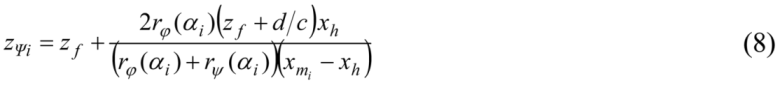 It is obvious that (7) and (8) represent continuous functions unless mi is on h: xmi = xh. Using Equations (6) and (4), we can rewrite xmi = xh as follows:
It is obvious that (7) and (8) represent continuous functions unless mi is on h: xmi = xh. Using Equations (6) and (4), we can rewrite xmi = xh as follows:
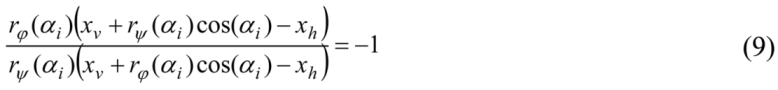 Note that the left-hand side of Equation (9) is a cross-ratio [xv + rφ(αi)cosαi, xv + rψ(αi)cosαi; xv, xh] = [xφi, xψi; xv, xh]. If xmi = xh, zΦi and zΨi diverge to ±∞ and Φ and Ψ are not continuous. This is because a projecting line emanating from F and going through mi does not intersect Πs. As a result, Mi, which should be a midpoint between Pi and Qi, cannot be determined. Recall that 2D projections of midpoints of 3D symmetric pairs of points form a 2D continuous curve on ΠI. Hence, this curve must not have any intersection or tangent point with h. The whole curve must be either to the left or right of h. It follows that the denominators in (7) and (8) must be always positive or always negative for given φ and ψ. If this criterion is not satisfied, the 3D curves will not be continuous. Note that if the position of the center of projection F is a free parameter (this happens when the camera is uncalibrated), it is always possible to set F and thus h so that the criterion for continuity will be satisfied because the curve connecting the midpoints does not depend on F.
Note that the left-hand side of Equation (9) is a cross-ratio [xv + rφ(αi)cosαi, xv + rψ(αi)cosαi; xv, xh] = [xφi, xψi; xv, xh]. If xmi = xh, zΦi and zΨi diverge to ±∞ and Φ and Ψ are not continuous. This is because a projecting line emanating from F and going through mi does not intersect Πs. As a result, Mi, which should be a midpoint between Pi and Qi, cannot be determined. Recall that 2D projections of midpoints of 3D symmetric pairs of points form a 2D continuous curve on ΠI. Hence, this curve must not have any intersection or tangent point with h. The whole curve must be either to the left or right of h. It follows that the denominators in (7) and (8) must be always positive or always negative for given φ and ψ. If this criterion is not satisfied, the 3D curves will not be continuous. Note that if the position of the center of projection F is a free parameter (this happens when the camera is uncalibrated), it is always possible to set F and thus h so that the criterion for continuity will be satisfied because the curve connecting the midpoints does not depend on F. where L is the distance between the vanishing point v and the center of projection F:
where L is the distance between the vanishing point v and the center of projection F:
 Let Pi = [xΦi, yΦi, zΦi], be a point on Φ and Qi = [xΨi, yΨi, zΨi] be its symmetric counterpart on Ψ. Recall that the symmetry line segments are parallel to the normal ns of the symmetry plane Πs and ns = [sinσs, 0, cosσs]. Hence, yΦi = yΨi. Let, pi = [xφi, yφi, 0] be a perspective image of Pi and qi = [xψi, yψi, 0] be a perspective image of Qi in ΠI. A line segment connecting Pi and Qi is a symmetry line segment and a line segment connecting pi and qi is a projected symmetry line segment; recall that a projected symmetry line segment intersects the x-axis at v. The pi and qi were represented in a polar coordinate system and written as pi = [xφi, yφi, 0] = [xv + rφicosαi, rφisinαi, 0] and qi = [xψi, yψi, 0] = [xv + rψicosαi, rψisinαi, 0], where rφi and rψi are the distances of pi and qi from v when α = αi. Note that the 3D points Pi and Qi and their 2D projections pi and qi satisfy Equations (7) and (8). From Equations (7), (10) and (11), we obtain zΦi (an analogous formula can be written for zΨi):
Let Pi = [xΦi, yΦi, zΦi], be a point on Φ and Qi = [xΨi, yΨi, zΨi] be its symmetric counterpart on Ψ. Recall that the symmetry line segments are parallel to the normal ns of the symmetry plane Πs and ns = [sinσs, 0, cosσs]. Hence, yΦi = yΨi. Let, pi = [xφi, yφi, 0] be a perspective image of Pi and qi = [xψi, yψi, 0] be a perspective image of Qi in ΠI. A line segment connecting Pi and Qi is a symmetry line segment and a line segment connecting pi and qi is a projected symmetry line segment; recall that a projected symmetry line segment intersects the x-axis at v. The pi and qi were represented in a polar coordinate system and written as pi = [xφi, yφi, 0] = [xv + rφicosαi, rφisinαi, 0] and qi = [xψi, yψi, 0] = [xv + rψicosαi, rψisinαi, 0], where rφi and rψi are the distances of pi and qi from v when α = αi. Note that the 3D points Pi and Qi and their 2D projections pi and qi satisfy Equations (7) and (8). From Equations (7), (10) and (11), we obtain zΦi (an analogous formula can be written for zΨi):
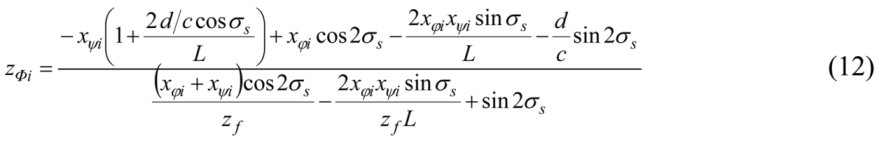 Recall that an orthographic projection is produced from a perspective projection by moving the center of projection F to infinity: zf → +∞. As zf goes to infinity, L goes to positive infinity, as well. From Equation (12), the limit of zΦi as zf goes to infinity is:
Recall that an orthographic projection is produced from a perspective projection by moving the center of projection F to infinity: zf → +∞. As zf goes to infinity, L goes to positive infinity, as well. From Equation (12), the limit of zΦi as zf goes to infinity is:
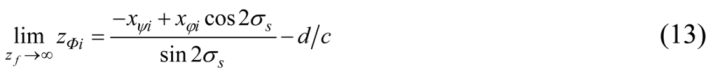 The limit of zΨi is obtained in an analogous way:
The limit of zΨi is obtained in an analogous way:
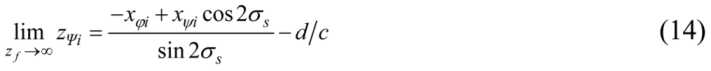 Recall that in an inverse perspective projection, an image point [x, y,0] projects to a 3D point [x(zf – z)/zf, y(zf – z)/zf, z]. As zf goes to infinity, the limit of [x(zf – z)/zf, y(zf – z)/zf, z] is [x, y, z], which is an inverse orthographic projection of [x, y, 0].
Recall that in an inverse perspective projection, an image point [x, y,0] projects to a 3D point [x(zf – z)/zf, y(zf – z)/zf, z]. As zf goes to infinity, the limit of [x(zf – z)/zf, y(zf – z)/zf, z] is [x, y, z], which is an inverse orthographic projection of [x, y, 0].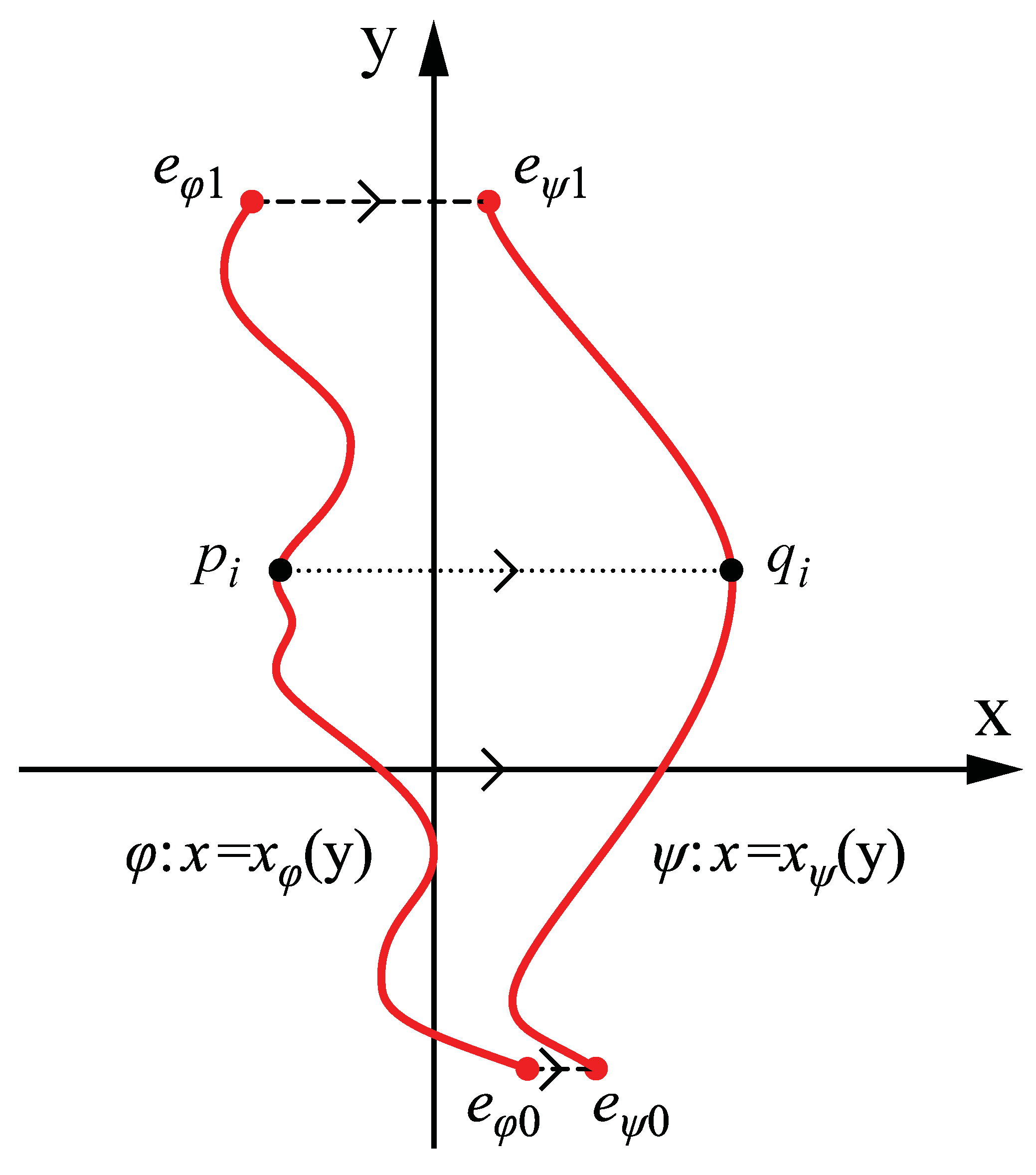
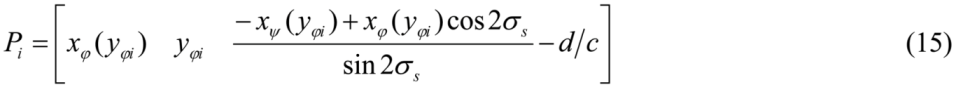
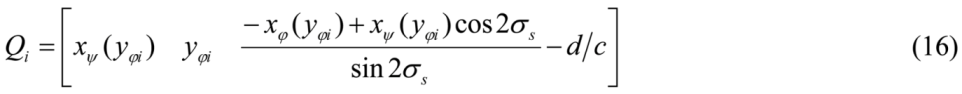 where σs is a slant of the symmetry plane. The tilt τs of the symmetry plane is zero. Equations (15) and (16) allow one to compute a pair of 3D symmetric curves Φ and Ψ from a pair of 2D curves φ and ψ under an orthographic projection. It is obvious from these equations that Φ and Ψ are continuous when φ and ψ are continuous. Recall that slant σs is a free parameter; it can be arbitrary, except for sin2σs = 0. So, the 3D symmetric curves form a one-parameter family characterized by σs. Equations (15–16) show that a relation between the pair of 2D curves φ and ψ and the pair of 3D curves Φ and Ψ becomes computationally simple when σs is 45° (or – 45°) and d/c is 0; the absolute value of the z-coordinate of Qi is equal to the x-coordinate of Pi and the absolute value of the z-coordinate of Pi is equal to the x-coordinate of Qi. The symmetric pair of 3D curves produced using Equations (15) and (16) and consistent with φ and ψ in Figure 5 is shown in Figure 6.
where σs is a slant of the symmetry plane. The tilt τs of the symmetry plane is zero. Equations (15) and (16) allow one to compute a pair of 3D symmetric curves Φ and Ψ from a pair of 2D curves φ and ψ under an orthographic projection. It is obvious from these equations that Φ and Ψ are continuous when φ and ψ are continuous. Recall that slant σs is a free parameter; it can be arbitrary, except for sin2σs = 0. So, the 3D symmetric curves form a one-parameter family characterized by σs. Equations (15–16) show that a relation between the pair of 2D curves φ and ψ and the pair of 3D curves Φ and Ψ becomes computationally simple when σs is 45° (or – 45°) and d/c is 0; the absolute value of the z-coordinate of Qi is equal to the x-coordinate of Pi and the absolute value of the z-coordinate of Pi is equal to the x-coordinate of Qi. The symmetric pair of 3D curves produced using Equations (15) and (16) and consistent with φ and ψ in Figure 5 is shown in Figure 6.