Polyominoes and Polyiamonds as Fundamental Domains for Isohedral Tilings of Crystal Class D₂

Abstract

We describe computer algorithms that produce the complete set of isohedral tilings by n-omino or n-iamond tiles in which the tiles are fundamental domains and the tilings have pmm, pmg, pgg or cmm symmetry [1]. These symmetry groups are members of the crystal class $D_2$ among the 17 two-dimensional symmetry groups [2]. We display the algorithms’ output and give enumeration tables for small values of n. This work is a continuation of our earlier works for the symmetry groups p3, p31m, p3m1, p4, p4g, p4m, p6, and p6m [3,4,5].

1. Introduction

Polyominoes and polyiamonds and their tiling properties have been the subject of research and recreation for more than 50 years [6,7,8,9,10]. Several investigators have asked how many different n-ominoes and n-iamonds exist for each n, and how many of these can tile the plane, and in how many different ways. In this article, we continue our investigations of a different question: how many different n-ominoes and n-iamonds can serve as fundamental domains for isohedral tilings of the plane with respect to a given plane symmetry group? In our earlier work [3,4,5] we addressed this question for symmetry groups with 3-, 4-, or 6-fold rotational symmetries. In this article, we address the question for symmetry groups of types pmm, pmg, pgg, and cmm, which are all in the crystal class $D_2$ among the 17 two-dimensional symmetry groups [1,2]. We describe algorithms that construct the polyomino and polyiamond tiles and produce the isohedral tilings for which the tiles are fundamental domains.

A polyomino (or n-omino) is a tile homeomorphic to a disk, made up of n unit squares that are connected at their edges; that is, the intersection of two unit squares in the polyomino is either empty or an edge of both squares. Similarly a polyiamond (or n-iamond) is a tile homeomorphic to a disk, made up of n unit equilateral triangles that are connected at their edges; the intersection of two unit triangles in the polyiamond is either empty or an edge of both triangles.

An isohedral tiling of the plane is a tiling by congruent tiles in which the symmetry group of the tiling acts transitively on the tiles. A fundamental domain for an isohedral tiling is a region of least area that generates the whole tiling when acted on by the symmetry group of the tiling [7,11].

Sometimes an isohedral tiling $\mathcal{T}$ produced here will be generated by a symmetry group G acting on a tile T and G is a proper subgroup of the full symmetry group of $\mathcal{T}$. We make the following definition: a tile T is a fundamental domain for G if elements of G acting on T produce the tiling $\mathcal{T}$, and T is a region of minimal area for which G can generate the tiling $\mathcal{T}$.

The following theorem will be important in this study.

Theorem 1.

Let G be one of the 17 two-dimensional symmetry groups and $\mathcal{T}$ an isohedral tiling generated by G acting on a tile T that is a fundamental domain for G. Let $G^{\prime }$ be the full symmetry group of $\mathcal{T}$. If G is a proper subgroup of $G^{\prime }$, there is element of $G^{\prime }$ (other than the identity) that leaves T invariant. In this case, a fundamental domain for $G^{\prime }$ has area smaller than T.

Proof. 

Since T is a fundamental domain for G, the only element of G that leaves T invariant is the identity. Let $g^{\prime }$ be an element of $G^{\prime }$ that is not in G. The tile $g^{\prime }T$ is in $\mathcal{T}$, and since G acts transitively on the tiles of $\mathcal{T}$, there is an element g in G such that $gT=g^{\prime }T$. But then $g^{-1}{g}^{\prime }T=T$, and $g^{-1}{g}^{\prime }$ is not the identity. The element $g^{-1}{g}^{\prime }$ is a rotation or reflection in $G^{\prime }$ that divides T into two or more congruent parts that are permuted under the action of $g^{-1}{g}^{\prime }$. Thus a fundamental domain for $G^{\prime }$ is contained in (or equal to) one of these parts, and has area smaller than T. ☐

Remark. 

It is possible for a fundamental domain D for the full symmetry group of an isohedral tiling to be symmetric, but in that case, the isometry that leaves D invariant is not an element of the symmetry group of the tiling.

A fundamental domain for an isohedral tiling cannot contain two points that are identical under the action of the symmetry group of the tiling. This leads immediately to the following observation:

Observation 1

In an isohedral tiling in which each tile is fundamental domain, no tile can contain a rotation center or axis of reflection for the whole tiling except on its boundary.

2. pmm

Figure 1 shows the symmetry elements of a pmm group G.

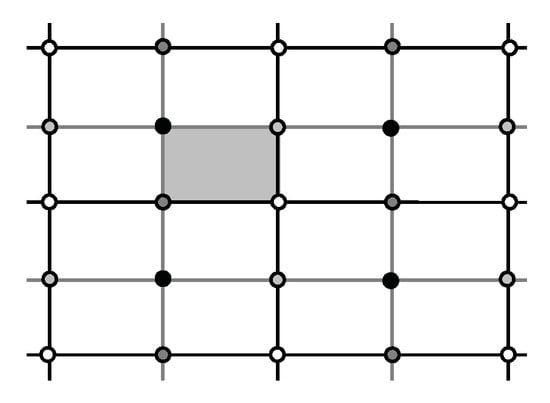
Figure 1. The symmetry elements of a pmm symmetry group G. Black, white, gray, and dark gray circles mark the four inequivalent 2-fold rotation centers; black and gray horizontal lines and black and gray vertical lines are the four inequivalent mirror reflection axes. The shaded area is a fundamental domain for G.

Horizontal and vertical lines are mirror reflection axes; and where these intersect, circles mark the 2-fold rotation centers. The rectangular shaded area T is a fundamental domain for G. Since this area is bounded by reflection axes, this is the only tile having the area of a fundamental domain (observation 1 in Section 1).

However, the full symmetry group of the tiling $\mathcal{T}$ generated by G acting on the shaded rectangle has additional reflection and 2-fold rotation symmetries induced by the $D_2$ symmetry of T, and so G is a proper subgroup of the full symmetry group of $\mathcal{T}$. Thus by Theorem 1, T is not a fundamental domain for the full symmetry group of the tiling. It is impossible for any polyiamond tile to be a rectangle. Hence we have the following theorem.

Theorem 2.

There are no pmm isohedral tilings having polyominoes as fundamental domains. However, if the symmetry of tiles is ignored or is destroyed by asymmetric markings, then there are pmm isohedral tilings having rectangular $kl$-ominoes as fundamental domains, where k and l are positive integers. There are no pmm isohedral tilings by polyiamonds.

3. Displacement Points, Fault Lines and the Slide Operation

3.1. Definitions and Observations

In an isohedral tiling $\mathcal{T}$ by polyomino (or polyiamond) tiles, there can be vertices p of the tiling at which the vertex of one tile T meets the edge of another tile $T^{\prime }$ at a point that is not a corner of a unit square (or unit triangle) in $T^{\prime }$. When this is the case, if we look at the underlying tiling $\mathcal{U}$ by units that make up the polyomino or polyiamond tiles, we will see that in the case of polyomino tiles, such a point p is a vertex of degree 3 in $\mathcal{U}$, and in the case of polyimaond tiles, such a point p is a vertex of degree 4 in $\mathcal{U}$. We will call such vertices displacement points of the tiling $\mathcal{T}$. The two tilings in Figure 2 have displacement points; in each, one displacement point has been labeled p.

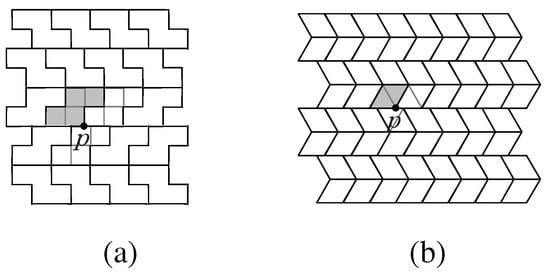
Figure 2. The point p is a displacement point for an isohedral tiling by (a) a 4-omino T and (b) a 2-iamond T, shown shaded. Heavy lines are edges of the tiles; thin lines show the units that make up the tiles to which p belongs. In (a), note that the tile T has $C_2$ symmetry, but the rotation that leaves T invariant does not leave the whole tiling invariant (see Remark, page 326).

By definition of displacement point and the examples in Figure 2, it is clear that a tiling with displacement points cannot be constructed on a single lattice of unit squares (or triangles). The following theorem shows that the displacement points of such a tiling must lie on lines that fracture the regular lattice of unit squares or triangles.

Theorem 3.

If p is a displacement point in an isohedral tiling $\mathcal{T}$ by polyominoes or polyiamonds then p is on a line that is the union of edges of tiles, and every vertex of a tile edge on this line is a displacement point in $\mathcal{T}$. Moreover, all such lines in $\mathcal{T}$ are parallel.

Proof. 

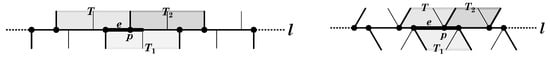
If a displacement point p exists in a tiling $\mathcal{T}$ as described, then it is the vertex of a tile T in the tiling, and hence a vertex of a unit square (or triangle) that meets the interior of an edge e of another unit square (or triangle) in an adjacent tile $T_1$, as illustrated in Figure 2 and Figure 3. Let l be the line on which e lies. Since the unit squares (triangles) in the polyomino (polyiamond) tiles meet edge-to-edge, e is part of an edge of T and also part of an edge of two other adjacent tiles $T_1$ and $T_2$; edges of all three tiles must lie on l. The vertices of T, $T_1$, and $T_2$ on l must also be displacement points. Repeating the argument for tiles adjacent to T, $T_1$, and $T_2$ and so on, it follows that the line l contains an infinite number of displacement points, and l is the union of edges of tiles whose vertices are these displacement points. Further, these successive displacement points along l forbid other displacement points on lines in $\mathcal{T}$ that are not parallel to the line l. Thus all lines containing displacement points must be parallel. ☐

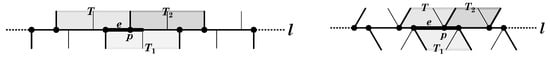
Figure 3. Enlargement of the region near the displacement point p for the tilings in Figure 2. Here the shaded polyomino (polyiamond) tiles T, $T_1$, $T_2$ are only partially shown, edges of unit squares or triangles that are not edges of tiles are thin lines, vertices of tiles are black dots, and the edge e of the unit square (triangle) that contains p in its interior is a thick black segment.

In an isohedral tiling that has displacement points, we will call the lines that contain them fault lines. Theorem 3 indicates that fault lines in a tiling partition the tiling into infinite parallel strips that are bounded by the fault lines.

By Theorem 3, since fault lines cannot intersect we obtain the following corollary.

Corollary 1.

Isohedral tilings by polyominoes or polyiamonds that have 3-, 4-, or 6-fold rotation centers do not have any displacement points.

3.2. Types of Tilings and the Slide Operation for pmg and pgg Groups

Each symmetry group G of type pmg or pgg has as its rotation symmetry elements a rectangular lattice of 2-fold centers (these are centers for ${180}^{\circ }$ rotations in G); an example of such a lattice is shown in Figure 4. In these groups, adjacent 2-fold centers in a horizontal row are not equivalent.

Figure 4. A rectangular lattice of 2-fold centers for a pmg or pgg symmetry group.

Throughout this section, a polyomino or polyiamond tile T will be a fundamental domain for an isohedral tiling $\mathcal{T}$ generated by a pmg or pgg group G. In our construction of these tiles T in the following two sections, the boundary of T will contain two adjacent inequivalent 2-fold centers for $\mathcal{T}$. Rotations of ${180}^{\circ }$ about these two centers and a reflection (in the case of pmg) or a glide reflection (in the case of pgg) generates G, and acting on T, generate $\mathcal{T}$. We classify these tilings $\mathcal{T}$ into two distinct types.

Type 1: A line through a (horizontal) row of 2-fold centers in the tiling $\mathcal{T}$ is not the union of edges of tiles T.

When $\mathcal{T}$ is type 1, we will call its polyomino or polyiamond tile T a type 1 tile.

Type 2: A line through a (horizontal) row of 2-fold centers in the tiling $\mathcal{T}$ is the union of edges of tiles T.

When a tiling $\mathcal{T}$ is type 2, we will call its polyomino or polyiamond tile T a type 2 tile. The 2-fold centers on the boundary of a type 2 tile T will lie on a single (straight) edge of T and the composition of ${180}^{\circ }$ rotations about those centers translates that edge to fill out a line L that contains translated copies of those 2-fold centers. L will contain all 2-fold centers in row in the full lattice of 2-fold centers for G. We will call the line L a slide line, and the vertices on L of the translated copies of T will be called slide points.

In a type 2 tiling $\mathcal{T}$ by tile T, the structure of the lattice of 2-fold centers for $\mathcal{T}$ implies that slide lines are equispaced (see Figure 4), and so partition the tiling into parallel regions of equal height, bounded by the slide lines. These regions are tiled with copies of T and will be called slide regions. Alternate slide regions will be translated copies of one another by a vertical translation that is the composition of two ${180}^{\circ }$ rotations about two 2-fold centers, one immediately above the other in the lattice. This translation separates slide regions into two classes A and $A^{*}$ that are stacked alternately $A{A}^{*}A{A}^{*}\dots$ as shown in Figure 5.

Figure 5. Slide regions for the tiling $\mathcal{T}$. Bounding lines for these regions are slide lines. Regions with the same label are congruent by a vertical translation.

We define an ε-slide operation on the tiling $\mathcal{T}$ as an operation that moves all slide regions A in the same direction parallel to the slide lines by an amount $\epsilon >0$, while holding the $A^{*}$ regions fixed. Sliding the tiles in alternate strips moves the tiles and the slide points by a distance of $\epsilon$ along the slide lines.

Theorem 4.

Let $\mathcal{T}$ be a type 2 isohedral tiling by a polyomino or polyiamond T. An ε-slide operation on $\mathcal{T}$ produces a new isohedral tiling ${\mathcal{T}}^{\prime }$ by T. The operation translates every 2-fold center of $\mathcal{T}$ by a distance of $\epsilon /2$ in a direction parallel to the slide lines, and so the shifted lattice of 2-fold centers is congruent to the original lattice and is equal to or contained in the lattice of 2-fold centers for the tiling ${\mathcal{T}}^{\prime }$.

Proof. 

The $\epsilon$-slide operation moves all tiles in alternate strips in the same direction parallel to the slide lines by a distance of $\epsilon$ and leaves the tiles in the other strips fixed. This operation moves 2-fold centers for the tiling $\mathcal{T}$ a distance of $\epsilon /2$ since every 2-fold center for $\mathcal{T}$ is on a slide line and is located midway between adjacent slide points on those lines. (In the case $\mathcal{T}$ has 2-fold centers at slide points, the distance between such a 2-fold center and the slide point that coincides with it is 0, and so we may consider such a 2-fold center to be “midway between” the coinciding vertices of two edge-adjacent tiles on opposite sides of the slide line.) Thus the new tiling ${\mathcal{T}}^{\prime }$ has 2-fold centers in a lattice congruent to that of $\mathcal{T}$. These 2-fold centers map the tiles T to adjacent tiles, so the tiling ${\mathcal{T}}^{\prime }$ is isohedral. ☐

When $\mathcal{T}$ is as in Theorem 4, we denote by ${\epsilon }_0$ the least distance between a slide point q and a corner v of a unit square (or unit triangle) on the slide line containing q (see Figure 6 for an illustration). Then $0\le {\epsilon }_0\le s/2$, where s is the length of an edge of a unit square (or triangle) in T. The tiling $\mathcal{T}$ has no displacement points if and only if ${\epsilon }_0=0$. An ${\epsilon }_0$-slide operation on $\mathcal{T}$ that moves q to v will align all unit squares (or unit triangles) that meet the slide line, and the resulting tiling will have no displacement points. In fact, for every integer k, and $\epsilon ={\epsilon }_0+ks$, an $\epsilon$-slide will produce a tiling with no displacement points, and these are the only values of $\epsilon$ for which this is possible. (When k is negative, the slide will be in the direction from v to q.) So except for a countable number of values of $\epsilon$, an $\epsilon$-slide operation will move displacement points in $\mathcal{T}$ to new displacement points in ${\mathcal{T}}^{\prime }$.

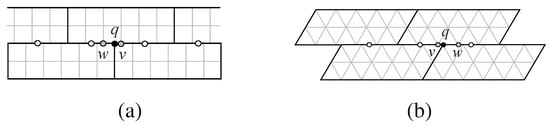
Figure 6. (a) A tiling by $2\times 6$ polyomino rectangles; (b) A tiling by 20-iamond parallelograms. White circles mark 2-fold centers along a slide line for the tilings. The point q is a slide point, v and w are neighboring vertices of unit squares or unit triangles on the slide line. Here ${\epsilon }_0$ is the distance from q to v and is less than $s/2$, so these tilings are in general position.

We will say that a type 2 tiling $\mathcal{T}$ is in general position whenever $0<{\epsilon }_0<s/2$. Every tiling in general position in the family defined by $\epsilon$-slide operations on $\mathcal{T}$ will have displacement points. When $\mathcal{T}$ has no displacement points (${\epsilon }_0=0$), an $\epsilon$-slide operation with $\epsilon \ne ks/2$, k an integer, will transform $\mathcal{T}$ to a new tiling ${\mathcal{T}}^{\prime }$ in general position. We summarize our observations in the next theorem.

Theorem 5.

Let $\mathcal{T}$ be a type 2 isohedral tiling by a polyomino or polyiamond T. Then an ε-slide operation on T produces a new isohedral tiling ${\mathcal{T}}^{\prime }$ by T.

(a) 

If $\mathcal{T}$ has displacement points, then ${\mathcal{T}}^{\prime }$ has no displacement points if $\epsilon ={\epsilon }_0+ks$, k any integer, and ${\mathcal{T}}^{\prime }$ has displacement points for all $\epsilon \ne {\epsilon }_0+ks$;

(b) 

If $\mathcal{T}$ has no displacement points, then ${\mathcal{T}}^{\prime }$ has no displacement points if $\epsilon =ks$, k any integer, and ${\mathcal{T}}^{\prime }$ has displacement points for all $\epsilon \ne ks$;

(c) 

There is an uncountably infinite family of tilings in general position that are obtained from $\mathcal{T}$ by ε-slide operations on $\mathcal{T}$.

We will call a rectangular polyomino tile a brick. Figure 7 gives illustrations of brick tilings for various values of ${\epsilon }_0$.

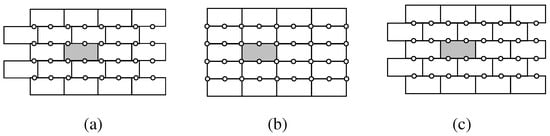
Figure 7. Type 2 isohedral tilings by bricks that are m unit squares high and n unit squares wide. One brick (shaded) is a fundamental domain for the group G generated by 2-fold centers marked by white circles. The tilings are related by an $\epsilon$-slide operation. (a) One tiling in an uncountably infinite family of tilings in general position; all are the same topological type and have pmg symmetry group; (b) 2-fold centers coincide with vertices and midpoints of edges of the bricks; ${\epsilon }_0=0$. The tiling has pmm symmetry group unless $m=n$, when it is type p4m; (c) 2-fold centers and slide points are equispaced along the slide lines. When n is even, ${\epsilon }_0=0$; when n is odd ${\epsilon }_0=s/2$. The symmetry group is type cmm.

4. pmg

4.1. pmg Tilings and Slide Lines

The lattice of symmetries of a pmg group G consists of equispaced parallel reflection axes (horizontal in Figure 8) and midway between them, rows of equispaced 2-fold centers. Glide-reflection axes are perpendicular to the reflection axes, and contain columns of 2-fold centers.

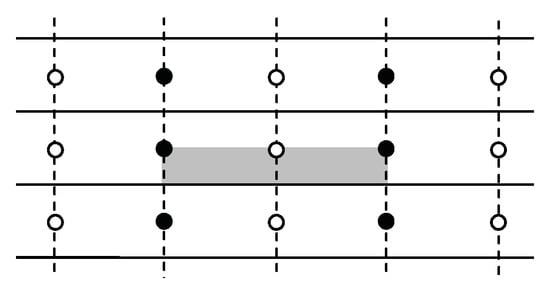
Figure 8. The lattice of symmetries of a pmg group G. Reflection axes are solid lines, glide-reflection axes are dotted, and the black and white circles mark inequivalent 2-fold centers. The shaded region is a fundamental domain for G. G is generated by a reflection in one axis and ${180}^{\circ }$ rotations about two adjacent black and white centers nearest that axis and on the same side of the axis.

Because we want to produce tiles T that are fundamental domains for this pmg group G, two inequivalent 2-fold centers for G must be located on the boundary of such T, and in the tiling $\mathcal{T}$ generated by G, edges of T must lie on reflection axes for $\mathcal{T}$ (observation 1 in Section 1). We will distinguish between tilings of type 1 and type 2 as defined in Section 3. Figure 9 and Figure 10 show isohedral tilings of types 1 and 2, respectively, by polyominoes and polyiamonds in which the tiles are fundamental domains for the group G.

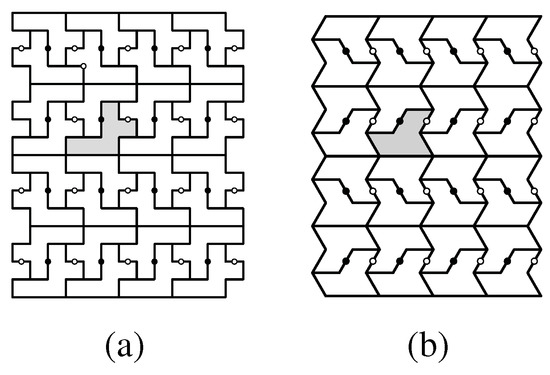
Figure 9. Isohedral tilings of type 1 by (a) a 6-omino T and (b) a 6-iamond T; in each, T is a fundamental domain for the pmg group G. Black and white circles mark inequivalent 2-fold centers for the tilings.

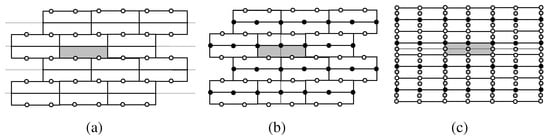
Figure 10. Type 2 isohedral tilings $\mathcal{T}$ by a brick polyomino tile T (shaded) that is k unit squares high and n unit squares wide; the tilings are related by $\epsilon$-slide operations. T is a fundamental domain for the pmg group G whose lattice of 2-fold centers (white circles) and reflection axes (thin lines) are shown in (a), where $\mathcal{T}$ is in general position; In (b), new black 2-fold centers for $\mathcal{T}$ are at intersections of reflection axes of G with new vertical reflection axes (one is shown as a thin line). When n is even, ${\epsilon }_0=0$, and when n is odd, ${\epsilon }_0=s/2$. $\mathcal{T}$ has a cmm symmetry group; In (c), $\mathcal{T}$ is edge-to-edge; the $D_2$ symmetry of T induces additional new gray 2-fold centers and new horizontal reflection axes for $\mathcal{T}$ (one is shown as a thin line). Here ${\epsilon }_0=0$ and $\mathcal{T}$ has a pmm symmetry group unless $k=n$, when it has a p4m symmetry group.

When the tiling $\mathcal{T}$ is type 2, $\mathcal{T}$ will have alternate slide regions that are translated copies of one another by a vertical translation that is the composition of two ${180}^{\circ }$ rotations about adjacent 2-fold centers on a glide-reflection axis. By Theorems 4 and 5, $\epsilon$-slide operations on $\mathcal{T}$ produce an infinite family of new tilings ${\mathcal{T}}^{\prime }$ that all contain a lattice of 2-fold centers congruent to the lattice of 2-fold centers of $\mathcal{T}$. Clearly this operation slides the reflection axes of $\mathcal{T}$ along themselves, so these are also reflection axes for ${\mathcal{T}}^{\prime }$. The glide-reflection symmetries in a pmg tiling are compositions of its 2-fold rotation and reflection symmetries, so we have the following theorem.

Theorem 6.

When $\mathcal{T}$ is a type 2 isohedral tiling generated by the pmg group G acting on a polyomino or polyiamond fundamental domain, an ε-slide operation on $\mathcal{T}$ will produce a new isohedral tiling ${\mathcal{T}}^{\prime }$ whose symmetry group $G^{\prime }$ contains a copy of G, that is, the lattice of symmetries of $G^{\prime }$ contains a lattice of symmetries congruent to the lattice of symmetries of G.

The following theorem gives another important fact for the pmg tilings we consider.

Theorem 7.

Let $\mathcal{T}$ be an isohedral tiling having a polyomino or polyiamond as fundamental domain for a pmg group G. If $\mathcal{T}$ has a fault line l, then l must be a slide line parallel to a reflection axis, and every slide line in $\mathcal{T}$ is a fault line. The fault lines in $\mathcal{T}$ are equispaced, with the distance between two adjacent fault lines equal to the distance between two adjacent reflection axes.

Proof. 

Let $\mathcal{T}$ be a tiling as described. In the lattice of symmetry elements for G, let M be a reflection axis. Then M cannot be a fault line in the tiling, since the reflection in M of tiles whose edges lie on M will keep those edges and their vertices fixed. Denote by c a 2-fold center for G nearest to M, $l_c$ the line through c parallel to M, and $R_c$ the region bounded by M and $l_c$, including these bounding lines. The line $l_c$ must contain all the 2-fold centers for G nearest M and on the same side of M as c (see Figure 8). One of these 2-fold centers, $c^{\prime }$, is on the boundary of a tile T containing c. The tiling $\mathcal{T}$ is generated by the actions on $R_c$ of reflections in M and ${180}^{\circ }$ rotations about c and $c^{\prime }$. These symmetries will map fault lines in $\mathcal{T}$ to other fault lines in $\mathcal{T}$, so if $\mathcal{T}$ has a fault line, there must be a fault line l in the interior of $R_c$ or l is the boundary line $l_c$. Suppose l is in the interior of $R_c$. By Theorem 3, since l is a fault line, edges of tiles make up the line l, and tiles must lie on both sides of l. But then the tiles between M and l cannot contain any 2-fold centers, since l is in the interior of $R_c$ and the 2-fold center c was chosen to be nearest M. This contradicts the fact that every tile must contain two 2-fold centers on its boundary. Therefore, $l=l_c$. Since l is the union of edges of tiles (Theorem 3) and the tile T contains the 2-fold centers c and $c^{\prime }$, the edge of T must lie on l, and hence l is a slide line. Since there can be no other fault lines in $R_c$, all other fault lines in $\mathcal{T}$ will be images of $l_c$ by symmetries in G. These are all the slide lines in $\mathcal{T}$, and the distance between adjacent lines in this array is the same as the distance between adjacent mirror lines (see Figure 8). ☐

Corollary 2.

Let $\mathcal{T}$ be an isohedral tiling having a polyomino or polyiamond tile T as fundamental domain for a pmg group G. If $\mathcal{T}$ has a fault line, then $\mathcal{T}$ must be a type 2 tiling.

Another fact that will be useful is the following:

Theorem 8.

Let $\mathcal{T}$ be an isohedral tiling having a polyomino or polyiamond tile T as fundamental domain for a given pmg group G and let $G^{\prime }$ be the full symmetry group of $\mathcal{T}$. Let c and $c^{\prime }$ be the 2-fold centers for G on the boundary of T and denote by $t_{c{c}^{\prime }}$ the translation that is the composition of ${180}^{\circ }$ rotations about c and $c^{\prime }$.

(1) 

If $\mathcal{T}$ is a type 1 tiling, let $T^{\prime }$ be the image of T by a ${180}^{\circ }$ rotation about c. If M and $M^{\prime }$ are reflection axes for G closest to c, then $t_{c{c}^{\prime }}$ translates T and $T^{\prime }$ to tile the region R bounded by M and $M^{\prime }$. If b is a 2-fold center for $G^{\prime }$ and b is not a 2-fold center for G, then T has $C_2$ or $D_2$ symmetry or b lies on a reflection axis for G.

(2) 

If $\mathcal{T}$ is a type 2 tiling, let M be a reflection axis for G closest to the slide line L through c and $c^{\prime }$. Then $t_{c{c}^{\prime }}$ translates T to tile the region R bounded by M and L. If b is a 2-fold center for $G^{\prime }$ and b is not a 2-fold center for G, then b cannot lie on a slide line for the group G.

Proof. 

(1) Let N be the line through c parallel to M and $M^{\prime }$; then N contains $c^{\prime }$ and all 2-fold centers for G between M and $M^{\prime }$ since M and $M^{\prime }$ are the reflection axes in G closest to c. Since T rotates about c onto $T^{\prime }$, the edges of $T^{\prime }$ contain c and an image $c^{″}$ of $c^{\prime }$. This implies that translations generated by $t_{c{c}^{\prime }}$ translate T and $T^{\prime }$ to tiles that contain images of c and $c^{\prime }$. Since every 2-fold center on N is the image of c or $c^{\prime }$ by these translations, every 2-fold center on N is contained in a translated copy of T and $T^{\prime }$. N contains all the 2-fold centers in the region R bounded by M and $M^{\prime }$, so R is tiled by translated copies of T and $T^{\prime }$. Now suppose that b is a 2-fold center for $G^{\prime }$ and b is not a 2-fold center for G. We may assume that b is in R since every point in $\mathcal{T}$ is equivalent (by the action of G) to a point in R; we may also assume that T contains b since copies of T tile R. Since b is a 2-fold center for $G^{\prime }$, either a ${180}^{\circ }$ rotation about b leaves T invariant (T has $C_2$ or $D_2$ symmetry) or maps T to an adjacent tile $T_1$ in $\mathcal{T}$. If this rotation does not leave T invariant, then b must be on the boundary of T, and since b is not a 2-fold center for G, b is distinct from c and $c^{\prime }$ and so $T_1$ is not in R. This implies that b must lie on M or $M^{\prime }$.

(2) Since $\mathcal{T}$ is a type 2 tiling, the slide line through c and $c^{\prime }$ is the union of edges of copies of T. So we may assume that T lies between L and M. As noted in Section 3, the translation $t_{c{c}^{\prime }}$ moves T along L, filling out a strip contained in R, the region bounded by M and L. The length of the vector for $t_{c{c}^{\prime }}$ must equal the length of an edge of T on L. There can be no tiles in R other than these translates of T since if there were, they would have to contain on their edges 2-fold centers for G, and there are no such 2-fold centers between L and M. Now suppose that b is a 2-fold center for $G^{\prime }$ and b is not a 2-fold center for G and that b lies on L. Then b is distinct from all 2-fold centers on L and translations of b by $t_{c{c}^{\prime }}$ would place a copy of b between c and $c^{\prime }$. But then the composition of a ${180}^{\circ }$ rotation about b with a ${180}^{\circ }$ rotation about c would be a translation symmetry of $\mathcal{T}$ whose vector is parallel to, but shorter than, that of $t_{c{c}^{\prime }}$. This is impossible, since that translation would overlap the copies of T in R. ☐

Corollary 3.

All notation is as in Theorem 8. (1) When $\mathcal{T}$ is a type 1 tile, the double tile $T\cup T^{\prime }$ has two parallel and congruent straight edges that lie on M and $M^{\prime }$. In addition, the other two edges of this double tile are translated images of each other, so are congruent and parallel. (2) When $\mathcal{T}$ is a type 2 tile, T must have two parallel and congruent straight edges, with one of these edges lying on the slide line L for G that contains c and $c^{\prime }$, and the other lying on M. In addition, the other two edges of T are translated images of each other, so are congruent and parallel.

4.2. Creating Polyominoes as Fundamental Domains of pmg Symmetry Groups

We can now describe how to produce polyomino tiles that are fundamental domains for a given pmg group G. At first we create tiles whose isohedral tilings generated by the group G will not have any displacement points. These tilings will have a single underlying lattice of unit squares, and symmetries in G will keep this lattice invariant.

To build our desired n-omino tiles, we begin with a lattice of unit squares. Our pmg group G can be generated by a reflection and two inequivalent 2-fold rotations whose centers lie on a line parallel to the reflection axis, and are nearest the reflection axis. By observation 1 in Section 1 and the symmetries of the lattice of unit squares, the 2-fold centers must be located at vertices or midpoints of edges of unit squares, and reflection axes must be located on edges of unit squares.

So we place a black circle as a 2-fold center on a lattice of unit squares and call this the origin, then place orthogonal unit vectors $\mathbf{u}$ and $\mathbf{v}$ at the origin, as shown in Figure 11.

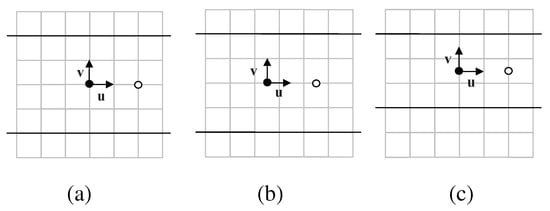
Figure 11. The square lattice for a pmg group G. The black and white circles are inequivalent 2-fold centers, and black lines are reflection axes; these symmetry elements generate G. (a)–(c) illustrate the three essentially different locations for the origin relative to the lattice of unit squares. The positive integers x and y that determine the placement of the white center and the reflection axes are restricted as follows. In (a) and (b), y must be even, and in (c) x must be even and y must be odd. For these examples, (a) $x=4$, $y=4$; (b) $x=4$, $y=4$; (c) $x=4$, $y=3$.

Next, we place a white 2-fold center at a point $x\mathbf{u}/2$ where x is a positive integer. This white center will be a nearest 2-fold center that is inequivalent to the black 2-fold center. Finally, we place two horizontal lines along edges of squares in the lattice; these will be reflection axes nearest the origin. The axes are at $\pm y\mathbf{v}/2$, where y is a positive integer. G is the pmg symmetry group generated by ${180}^{\circ }$ rotations about the black and white 2-fold centers and reflections in one of the two reflections axes we have placed. Figure 11 shows the three essentially different locations for the origin relative to the lattice of unit squares and gives restrictions on x and y for each case.

The area S of a fundamental domain for G is given by

$$S=xy/2$$

(1)

where the area of a unit square is 1. Since we want our n-omino to be a fundamental domain, $n=S$ and S must be an integer. Therefore,

$$n=1,2,3,\dots .$$

(2)

Actions by the group G on the unit squares classify the unit squares into n equivalence classes. We denote the equivalence class of a unit square e as $C(e)$.

For each integer $n>0$, we construct an n-omino tile $T_n$ that is a fundamental domain for the group G by the following procedure.

Begin by choosing a unit square that contains the origin (the black circle in Figure 11), then build up the polyomino tile by placing unit squares, one at a time, edge-to-edge with squares of a partially-built tile. At each stage the unit square added is not equivalent (under the action of G) to any of the squares already in the partially-built tile. The tile $T_n$ is complete when it contains exactly one unit square from each of the equivalence classes $C(e)$ and contains the white 2-fold center in Figure 11. The completed tile $T_n$ is compared to all n-ominos previously constructed by the procedure and if it is not equivalent to any of these, it is added to the collection of all n-omino tiles constructed by the procedure. Tiles are equivalent only if they are congruent and when marked with an asymmetric motif, generate the same tiling by the action of the group G (or for type 2 tiles, generate the same infinite family of tilings). The algorithm uses backtracking to ensure that no two tiles produced are made up of exactly the same set of unit squares. Details of this process, called Procedure 1 in [5], can be found there; it is used here with slightly modified notation, noted below.

• For $0<k\le n$, $T_k$ is a set of unit squares that form a k-omino, $B(T_k)$ the set of unit squares that are edge-adjacent to those in $T_k$, and ${\mathcal{T}}_n$ a set of inequivalent n-omino tiles. In the set $T_k$, all squares are taken from the region between the two reflection axes placed at the outset of the process (see Figure 11). (In [5], $T_k$ is denoted by T.)
• For the empty set ∅ we define $B(\varnothing )$ to be the set of unit squares that contain the origin.
• We define $E(T_k)$, the Boolean function of $T_k$, which is true if $k=n$ and the white 2-fold center is on the boundary of $T_k$. Otherwise $E(T_k)$ is false.

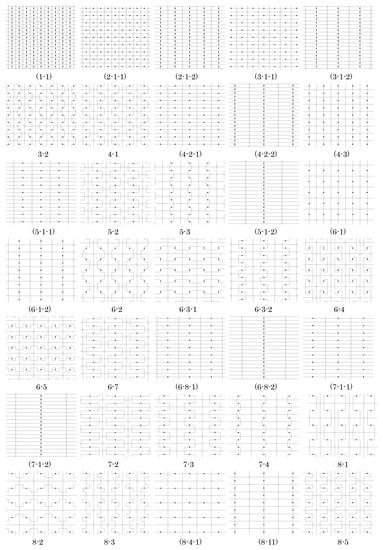
Figure 12 shows the complete set ${\mathcal{T}}_n$ of n-omino tiles constructed by this procedure for $n\le 6$. In Figure 12, and in all subsequent displays of tiles, each tile has a label n-k-m, where n is the number of units (squares or triangles) that make up the tile, k is the tile number (two tiles are congruent if and only if their labels begin with the same n-k), and m counts the number of inequivalent tiles for each tile number.

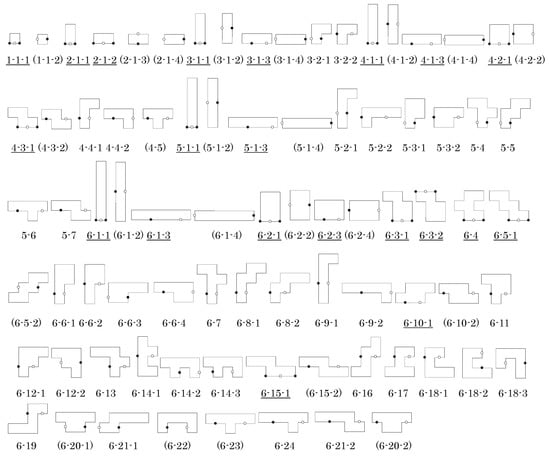
Figure 12. List of n-ominoes for $n\le 6$ produced by the procedure in Section 4.2; these are fundamental domains for the pmg groups G used to generate their corresponding isohedral tilings in Figure 13. Labels indicate n followed by the tile number for that n. Parentheses indicate that the corresponding tiling has symmetry group larger than G. Underline indicates that the corresponding tiling is type 2 and so has slide lines; there is an infinite family of tilings by that tile having the same slide lines.

Rotations of ${180}^{\circ }$ about the black and white 2-fold centers on the edges of a polyomino tile T in ${\mathcal{T}}_n$ fills out a strip tiled by copies of T and bounded by the two reflection axes placed at the outset. Repeated reflections of this strip in the reflection axes on its boundary produces an isohedral tiling $\mathcal{T}$ having T as a fundamental domain for the pmg group G. For each tile T in Figure 12 and $n\le 5$, Figure 13 shows the corresponding tiling by T generated in this manner, or in the case when T is a type 2 tile, a representative of an infinite family of tilings. When T is a type 2 tile, the black 2-fold center can be at any point between a vertex and midpoint of the edge on which it lies; Figure 12 shows only a representative tile T with 2-fold centers in the original positions placed at the beginning of the process (as in Figure 11). More details on these tilings and their symmetries are in the next section.

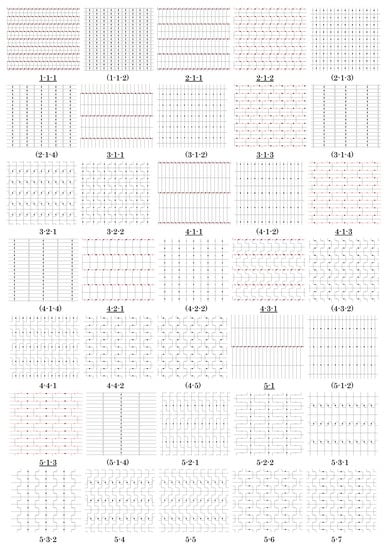
Figure 13. List of isohedral tilings by the n-ominoes in Figure 12 for $n\le 5$; the n-ominoes are fundamental domains for the pmg groups G that generate the tilings. Labels correspond to those in Figure 12. Tilings with underlined labels are in general position and represent an infinite family of tilings. Red lines indicate slide lines.

4.3. Symmetries of the Polyomino Tilings

Our procedure described in the previous section produces polyomino tiles T that are fundamental domains for a given pmg group G that generates an isohedral tiling $\mathcal{T}$. However, it is possible that $\mathcal{T}$ has additional symmetries, that is, G is a proper subgroup of the full symmetry group $G^{\prime }$ of $\mathcal{T}$ and T is not a fundamental domain for $G^{\prime }$ (Theorem 1). The pmg group G can be a proper subgroup of a symmetry group of any of these types: pmm, cmm, p4m, p4g, or pmg.

If $\mathcal{T}$ has symmetries that are not in G, then by Theorem 1, there is an element h in $G^{\prime }$ that leaves T invariant (and h is not in G). If h or $h^2$ is not a ${180}^{\circ }$ rotation, then h is a reflection whose axis must be parallel or perpendicular to the reflection axes for G. In either case, the composition of h with a reflection in G or a glide reflection in G will produce a 2-fold rotation not in G. Thus to determine if $\mathcal{T}$ has symmetries that are not in G, we only need to look for 2-fold centers for $G^{\prime }$ that are not 2-fold centers for G. We consider two cases separately.

4.3.1. $\mathcal{T}$ Is a Type 1 Tiling

In order to seek 2-fold centers not in G, we look at all vertices, midpoints of edges and centers of unit squares in a polyomino T in the tiling $\mathcal{T}$ except for those equivalent to the original 2-fold centers we have chosen (black and white centers in Figure 11), and investigate whether or not they can be new 2-fold centers of $\mathcal{T}$. If a new 2-fold center is found, we indicate that G is not the full symmetry group of $\mathcal{T}$ by putting parentheses around the labels of the tile T in Figure 12 and its corresponding tiling $\mathcal{T}$ in Figure 13.

By Theorem 8, either the new 2-fold center is a symmetry for T (and T has either $C_2$ or $D_2$ symmetry) or it lies on a reflection axis for G. When T has only $C_2$ symmetry, the tiling $\mathcal{T}$ will have a pmg symmetry group larger than G (e.g., tiling 4-3-2 in Figure 13). When T has only $D_1$ symmetry and the 2-fold centers on T are symmetric with respect to the mirror axis for T, $\mathcal{T}$ will have cmm symmetry (e.g., tiling 4-5 in Figure 13). When T has $D_2$ symmetry, T is a brick. All type 1 tilings by bricks have pmm symmetry (e.g., tilings 2-1-3, 2-1-4 in Figure 13) unless the brick is square, and in that case, the tiling has p4m symmetry (e.g., tilings 1-1-2, 4-2-2 in Figure 13).

4.3.2. $\mathcal{T}$ Is a Type 2 Tiling

In this case, by Theorem 6, every $\epsilon$-slide operation on $\mathcal{T}$ produces a new tiling ${\mathcal{T}}_1$ whose symmetry group $G_1$ contains a copy of G, that is, the lattice of symmetries of $G_1$ contains a lattice of symmetries congruent to the lattice of symmetries of G. To determine whether or not $G_1$ is the full symmetry group of $\mathcal{T}$, we look for 2-fold rotation symmetries of $\mathcal{T}$ that are not in $G_1$. If the polyomino T is a brick, then the tiling may have additional 2-fold rotation symmetries that are not in $G_1$. Figure 10 illustrates this.

The next theorem says that the special brick tilings in Figure 10b,c are the only instances in which the full symmetry group of $\mathcal{T}$ is not a copy of the generating group G.

Theorem 9.

Let $\mathcal{T}$ be a type 2 isohedral tiling with a polyomino fundamental domain T such that for some ε, an ε-slide operation on $\mathcal{T}$ can produce a tiling ${\mathcal{T}}^{\prime }$ that has pmg symmetry group G. If T is not a brick, then every new tiling ${\mathcal{T}}_1$ obtained from $\mathcal{T}$ by an ε-slide operation is also a pmg isohedral tiling whose symmetry group $G_1$ is a copy of G. If T is a brick, then the special tilings in Figure 10b,c are the only tilings ${\mathcal{T}}_1$ obtained from $\mathcal{T}$ by an ε-slide operation that have symmetry group $G_1$ not a copy of G.

Proof. 

To make notation easier, we may assume that our isohedral tiling $\mathcal{T}$ with fundamental domain T has a pmg symmetry group G. Let ${\mathcal{T}}^{\prime }$ be obtained from $\mathcal{T}$ by an $\epsilon$-slide operation and let $G^{\prime }$ be the full symmetry group of ${\mathcal{T}}^{\prime }$. Then by Theorem 6, $G^{\prime }$ contains a subgroup $G_1$ that is a copy of G, so $G_1$ is a pmg symmetry group with fundamental domain T. Suppose c is a 2-fold center for $G^{\prime }$ and c is not a 2-fold center for $G_1$. Then c must lie in a region R bounded by a reflection axis M for $G_1$ and a slide line L for $G_1$ nearest M. By Theorem 8, c cannot lie on L, so c must lie on M or lie in the interior of R. Also by Theorem 8 and its corollary, opposite edges of T lie on L and M and the other two edges of T must be parallel.

If c is on M, then a ${180}^{\circ }$ rotation about c will map M to M, preserving all vertices on M, and so c must be at a vertex v or midpoint m of an edge of a tile T on M. We claim that the only possibility in this case is for T to be a brick.

To see this, refer to Figure 14, where E represents an edge of T that contains c but does not lie on L or M. E reflects across M to an edge $E_1$ of an adjacent tile $T^{\prime }$, and E also rotates ${180}^{\circ }$ about c to an edge $E_2$ of an adjacent tile. $E_1$ and $E_2$ must either coincide or be parallel. But this is only possible if E is a straight edge of T perpendicular to M and L. Thus T is a brick, and c must be a black 2-fold center in Figure 10b,c.

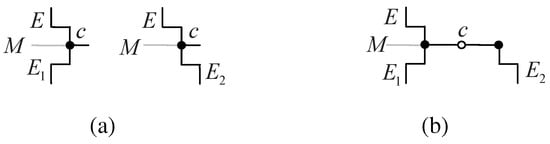
Figure 14. The 2-fold center c is on M, and E represents an edge of tile T. E reflects in M onto edge $E_1$ and E rotates ${180}^{\circ }$ about c onto edge $E_2$. In $\mathcal{T}$, $E_1$ and $E_2$ must be parallel or coincide. (a) c at a vertex on M; (b) c at the midpoint of an edge of T on M.

If c is in the interior of R, then c is contained in a tile T and a ${180}^{\circ }$ rotation about c must leave T invariant or send T to an adjacent tile in R. Thus c must be on a line midway between L and M. Let $L^{\prime }$ be the slide line for $G_1$ such that M is midway between L and $L^{\prime }$, and $R^{\prime }$ the region between M and $L^{\prime }$. Let $c^{\prime }$ be a 2-fold center on L that is nearest c. The translation $t^{\prime }$ that is the composition of ${180}^{\circ }$ rotations about c and $c^{\prime }$ will map R to $R^{\prime }$ or $R^{\prime }$ to R. But the tiles in R and $R^{\prime }$ have opposite orientations, so $t^{\prime }$ is not a symmetry of ${\mathcal{T}}^{\prime }$ unless the edges of tiles are are straight and perpendicular to L and M, that is, T is a brick. In this case, c is a gray 2-fold center in Figure 10c. ☐

When the polyomino T is a type 2 tile, the tiling $\mathcal{T}$ that it generates may not be in general position. In this case, we can perform an $\epsilon$-slide operation to obtain a tiling in general position. In Figure 13, we display only one tiling in general position to represent the whole infinite family of tilings corresponding to T. By Theorem 9, when T is not a brick, every tiling in the family will have a pmg symmetry group $G_1$ which is identical to G, only differing in the placement of the 2-fold centers on the slide lines (and on the edges of tiles on those slide lines). In addition, T will be a fundamental domain for each of these tilings. We underline the label of each of these tiles in Figure 12 and the label for one corresponding representative tiling in general position in Figure 13.

4.4. Creating Polyiamonds as Fundamental Domains for pmg Symmetry Groups

In this section we describe a procedure for how to produce polyiamond tiles that are fundamental domains for a given pmg group G; the procedure is similar to that in Section 4.2. At first we create tiles whose isohedral tilings generated by the group G will not have any displacement points. These tilings will have a single underlying lattice of unit triangles, and symmetries in G will keep this lattice invariant.

Our pmg group G can be generated by a reflection and two inequivalent 2-fold rotations whose centers lie on a line parallel to the reflection axis, and are nearest the reflection axis. By observation 1 in Section 1 and the symmetries of the lattice of unit triangles, the 2-fold centers must be located at vertices or midpoints of edges of unit triangles, and reflection axes must be located on edges of triangles.

First we place a black circle as a 2-fold center on a lattice of unit triangles and call this the origin, then place vectors $\mathbf{u}$ and $\mathbf{v}$ at the origin along (or parallel to) the edges of unit triangles, as shown in Figure 15. Then we place a white 2-fold center at a point $x\mathbf{u}/2$ where x is any positive integer. This white center will be a nearest 2-fold center that is inequivalent to the black 2-fold center. Finally, we place two horizontal lines along edges of triangles in the lattice; in the symmetry group G, these will be reflection axes nearest the origin. The placements of the axes are at $\pm y\mathbf{v}/2$, where y is a positive integer. G is the pmg symmetry group generated by ${180}^{\circ }$ rotations about the black and white 2-fold centers and reflections in one of the two reflections axes we have placed. Figure 15 shows the three essentially different locations for the origin relative to the lattice of unit triangles, and gives restrictions on x and y for each case.

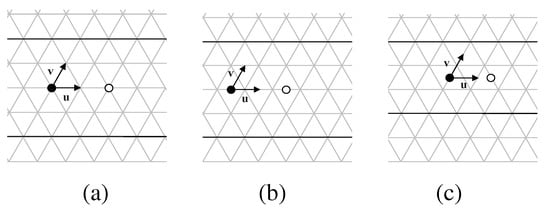
Figure 15. The triangular lattice for a pmg group G. The black and white circles are inequivalent 2-fold centers, and black lines are reflection axes; these symmetry elements generate G. (a)–(c) illustrate the three essentially different locations of the origin relative to the lattice of unit triangles. The positive integers x and y that determine the placement of the white center and the reflection axes are restricted as follows. In (a) and (b), y must be even, and in (c) y must be odd. For these examples, (a) $x=4$, $y=4$; (b) $x=4$, $y=4$; (c) $x=3$, $y=3$.

The area S of a fundamental domain for G is given by

$$S=xy$$

(3)

where the area of a unit triangle is 1. Note that $n=S$ and S must be an integer. Therefore,

$$n=1,2,3,\dots .$$

(4)

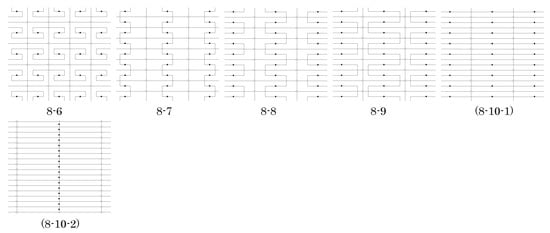
Actions by the group G on the unit triangles classify the unit triangles into n equivalence classes; we denote the equivalence class of a unit triangle e as $C(e)$. For each integer $n>0$, we construct an n-iamond tile $T_n$ that is a fundamental domain for the group G by the procedure described in Section 4.2, where our units are now unit triangles rather than unit squares, and reference is to Figure 15.

Figure 16 shows the complete set ${\mathcal{T}}_n$ of n-iamond tiles constructed by this procedure for $n\le 8$. Rotations of ${180}^{\circ }$ about the black and white 2-fold centers on the edges of a polyiamond tile T in ${\mathcal{T}}_n$ fill out a strip tiled by copies of T and bounded by the two reflection axes placed at the outset. Repeated reflections of this strip in the reflection axes on its boundary produces an isohedral tiling $\mathcal{T}$ having T as a fundamental domain for the pmg group G.

Figure 16. List of n-iamonds for $n\le 8$ produced by the procedure in Section 4.4; these are fundamental domains for the pmg groups G used to generate their corresponding isohedral tilings in Figure 17. Labels indicate n followed by the tile number for that n. Parentheses indicate that the corresponding tiling has symmetry group larger than G. Underlines indicate that the corresponding tiling has slide lines, so there is an infinite family of tilings by that tile having the same slide lines and same pmg symmetry group.

For each tile T in Figure 16 and $n\le 6$, Figure 17 shows the corresponding tiling by T generated in this manner, or in the case when T is a type 2 tile, a representative of an infinite family of tilings. When T is a type 2 tile, Figure 16 shows only a representative tile T with 2-fold centers in the original positions placed at the outset. More details on these tilings and their symmetries are in the next section.

Figure 17. List of isohedral tilings by the n-iamonds in Figure 16 for $n\le 6$; the n-iamonds are fundamental domains for the pmg groups G that generate the tilings. Labels correspond to those in Figure 16. Tilings with underlined labels are in general position and represent an infinite family of tilings. Red lines indicate slide lines.

4.5. Symmetries of the Polyiamond Tilings

Our procedure described in the previous section produces polyiamond tiles T that are fundamental domains for a given pmg group G that generates an isohedral tiling $\mathcal{T}$. As noted in Section 4.3, the pmg group G can be a proper subgroup of the full symmetry group $G^{\prime }$ of $\mathcal{T}$. For polyiamond tiles T, $G^{\prime }$ might be a cmm, p6m, or pmg symmetry group. Also, as pointed out in Section 4.3, in order to determine whether $\mathcal{T}$ has symmetries that are not in G, we only need to look for 2-fold centers that are not symmetry elements in G. We consider two cases separately.

4.5.1. $\mathcal{T}$ Is a Type 1 Tiling

In order to seek 2-fold centers not in G, we look at all vertices, midpoints of edges and centers of unit triangles in a polyiamond T in the tiling $\mathcal{T}$ except for those equivalent to the original 2-fold centers we have chosen (black and white centers in Figure 15), and investigate whether or not they can be new 2-fold centers of $\mathcal{T}$. If a new 2-fold center is found, we indicate that G is not the full symmetry group of $\mathcal{T}$ by putting parentheses around the labels of the tile T in Figure 16 and its corresponding tiling $\mathcal{T}$ in Figure 17.

By Theorem 8, either the new 2-fold center is a symmetry for T (and T has either $C_2$ or $D_2$ symmetry) or it lies on a reflection axis for G. When T has only $C_2$ symmetry, the tiling $\mathcal{T}$ will have pmg symmetry group $G^{\prime }$ larger than G (e.g., tilings 4-1-3 and 6-3-2 in Figure 17); in particular, every type 1 tiling $\mathcal{T}$ by a parallelogram tile T will have symmetry group $G^{\prime }$ of type pmg. When T has mirror symmetry and the 2-fold centers on T are symmetric to a mirror axis for T, $\mathcal{T}$ will have p6m symmetry (e.g., tiling 4-3 in Figure 17) or cmm symmetry (see Figure 18; tiles 8–23 and 8–25 in Figure 16 will also produce cmm tilings).

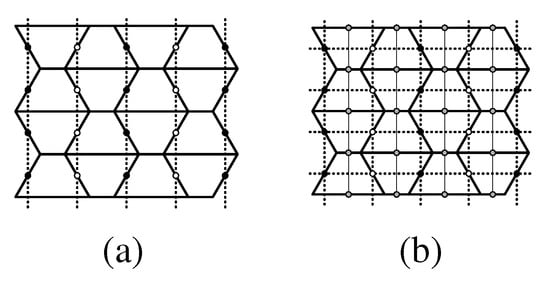
Figure 18. (a) A type 1 isohedral tiling $\mathcal{T}$ by polyiamond tile 8-7-2 in Figure 16; this tile is a fundamental domain for the pmg group G generated by the 2-fold centers marked by black and white circles and the horizontal black reflection axes; glide-reflection axes for G are vertical dotted lines; (b) The full symmetry group $G^{\prime }$ of $\mathcal{T}$ is type cmm, with additional vertical reflection axes (thin lines), 2-fold centers (gray circles), and horizontal glide-reflection axes.

4.5.2. $\mathcal{T}$ Is a Type 2 Tiling

By Theorem 6, the full symmetry group $G^{\prime }$ of $\mathcal{T}$ contains a subgroup $G_1$ that is a copy of G, so $G_1$ is a pmg symmetry group with fundamental domain T. If $G_1$ is not the full symmetry group of $\mathcal{T}$, then as with type 1 tilings, we look for 2-fold rotation symmetries of $\mathcal{T}$ that are not in G. The argument in Theorem 9 is valid for a type 2 tiling with polyiamond fundamental domain T, and polyiamonds cannot be bricks.

Theorem 10.

Let $\mathcal{T}$ be a type 2 isohedral tiling with a polyiamond fundamental domain T such that for some ε, an ε-slide operation on $\mathcal{T}$ can produce a tiling ${\mathcal{T}}^{\prime }$ that has pmg symmetry group G. Then every new tiling ${\mathcal{T}}_1$ obtained from $\mathcal{T}$ by an ε-slide operation is also a pmg isohedral tiling whose symmetry group $G_1$ is a copy of G.

5. pgg

5.1. pgg Tilings, Fault Lines, and Slide Lines

The lattice of symmetries of a pgg group G consists of two sets of equispaced parallel glide-reflection axes, one set perpendicular to the other (vertical and horizontal in Figure 19) and midway between them, rows of equispaced 2-fold centers. The generating glide vectors are defined by the (horizontal and vertical) distances between two adjacent 2-fold centers; these are also equal to the distances between two adjacent parallel glide-reflection axes.

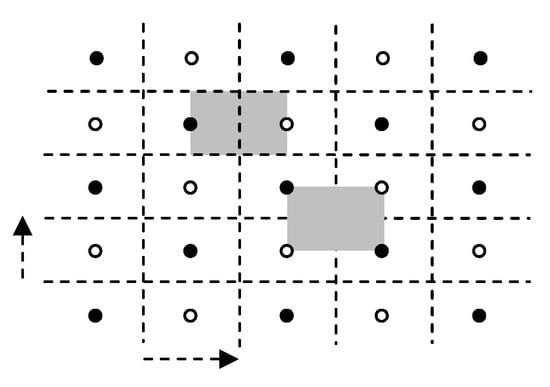
Figure 19. The lattice of symmetries of a pgg group G. Glide-reflection axes are dotted lines and their minimal glide vectors are shown as dotted vectors. Black and white circles mark inequivalent 2-fold centers. Each shaded region is a fundamental domain for G. G is generated by a ${180}^{\circ }$ rotation about a 2-fold center and a glide reflection whose glide-reflection axis is closest to that 2-fold center.

In a pgg isohedral tiling $\mathcal{T}$ having a polyomino or polyiamond tile T as fundamental domain, fault lines can occur in two distinct ways. The first is along slide lines. For type 2 tilings, $\epsilon$-slides along slide lines can produce an uncountably infinite family of tilings having slide lines as fault lines (Theorem 5). Also, by Theorem 4, an $\epsilon$-slide operation merely shifts the 2-fold centers a distance of $\epsilon /2$ in the direction of the slide, and the lattice of 2-fold centers of the new tiling ${\mathcal{T}}^{\prime }$ contains this shifted copy of the lattice of 2-fold centers of $\mathcal{T}$. Glide-reflection axes parallel to the slide lines are midway between slide lines and so are preserved by the slide, and so are their glide vectors, since these are determined by the lattice of 2-fold centers. A glide reflection g whose axis is perpendicular to slide lines is the composition of a ${180}^{\circ }$ rotation about a 2-fold center and a glide reflection whose glide-reflection axis is parallel to a slide line, so the glide vector for g is preserved, but its glide reflection axis is shifted by $\epsilon /2$. We state these observations in the following theorem.

Theorem 11.

Let $\mathcal{T}$ be a type 2 isohedral tiling having a polyomino or polyiamond as fundamental domain for a pgg group G. Then an ε-slide operation on $\mathcal{T}$ will produce a new isohedral tiling ${\mathcal{T}}^{\prime }$ whose symmetry group $G^{\prime }$ contains a copy of G, that is, the lattice of symmetries of $G^{\prime }$ contains a lattice of symmetries congruent to the lattice of symmetries of G.

For both type 1 and type 2 tilings, other fault lines can occur along glide-reflection axes that are made up of edges of tiles. If a glide-reflection axis is a fault line, we will denote it by $L_g$. For a fault line $L_g$, the minimal glide vector will have length $ks/2$, with k odd, and s the edge-length of a unit square. The displacement points along $L_g$ will be at a midpoints of edges of unit squares (or triangles) that make up $L_g$. If one such fault line $L_g$ occurs in the tiling $\mathcal{T}$, then every glide-reflection axis parallel to $L_g$ will be a fault line, since all of these are images of $L_g$ by ${180}^{\circ }$ rotations and translations. This set of fault lines that are glide-reflection axes partitions $\mathcal{T}$ into parallel strips of equal width.

However, $\epsilon$-slide operations for these strips are not possible, since sliding alternate strips bounded by the glide-reflection axes by a directed distance of $\epsilon$ would not preserve the lattice of 2-fold centers for $\mathcal{T}$, and we only permit slide operations that preserve the lattice of pgg symmetries. Thus midpoints of edges of unit squares (or triangles) are the only positions possible for displacement points along $L_g$ fault lines. Theorem 12 states that slide lines and $L_g$ glide-reflection axes are the only possibilities for fault lines in $\mathcal{T}$.

Theorem 12.

Let $\mathcal{T}$ be an isohedral tiling having a polyomino or polyiamond as fundamental domain for a pgg group G. If $\mathcal{T}$ has a fault line l, then l is (1) a glide-reflection axis or (2) a slide line parallel to a glide-reflection axis. In case (1), every glide reflection axis in $\mathcal{T}$ parallel to l is a fault line, and in case (2) every slide line in $\mathcal{T}$ is a fault line. The fault lines in $\mathcal{T}$ are equispaced.

Proof. 

Let l be a fault line for $\mathcal{T}$. If l is not a glide-reflection axis or a slide line, then l lies strictly between a glide-reflection axis M for $\mathcal{T}$ and a nearest row of 2-fold centers for $\mathcal{T}$ parallel to M. A glide reflection in M takes l to another fault line $l^{\prime }$, and $l^{\prime }$ also is strictly between M and a nearest row of 2-fold centers on the opposite side of M. So there are no 2-fold centers between l and $l^{\prime }$. But this is impossible since edges of tiles make up the lines l and $l^{\prime }$ (Theorem 3) and the tiles between l and $l^{\prime }$ must contain 2-fold centers. ☐

Figure 20 gives examples to illustrate the three possibilities for fault lines in a pgg isohedral tiling $\mathcal{T}$ having a polyomino or polyiamond tile T as fundamental domain.

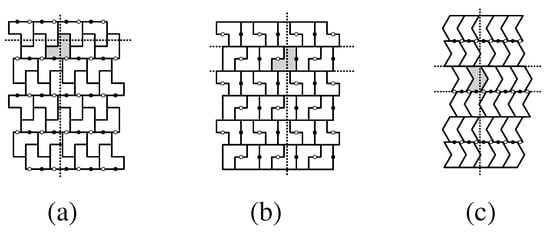
Figure 20. Three different possibilities for fault lines in a pgg isohedral tiling $\mathcal{T}$ having a polyomino or polyimond tile T as fundamental domain. Dotted glide-reflection axes in relation to one tile are shown. (a) $\mathcal{T}$ is type 2, T is a 3-omino; slide lines are fault lines. (b) $\mathcal{T}$ is type 1, T is a 3-omino; glide-reflection axes are fault lines. (c) $\mathcal{T}$ is type 2, T is a 4-iamond; both slide lines and glide-reflection axes are fault lines.

All the examples in Figure 20 show pgg tilings in which the edges of tiles make up lines that partition the tiling into horizontal strips, and in each of these cases, the boundaries of the strips are fault lines. Slide lines for type 2 tilings will always partition the tiling into parallel strips. However, in pgg tilings, glide-reflection axes can be boundaries of parallel strips that partition the tiling even when these axes are not fault lines. In many of the pgg tilings we consider, the tiling is not composed of strips of tiles bounded by lines that are unions of edges of tiles. This feature is most prevalent in tilings in which the glide-reflection axes are at a ${45}^{\circ }$ angle to the horizontal. Most of these tilings have a pronounced diagonal pattern.

5.2. Creating Polyominoes as Fundamental Domains for pgg Symmetry Groups

We now describe how to produce polyomino tiles that are fundamental domains for a given pgg group G. At first we create tiles whose isohedral tilings generated by the group G will not have any displacement points on slide lines. Displacement points for these tilings can only occur on glide-reflection axes, at midpoints of edges of unit squares.

Our pgg group G can be generated by a glide reflection and two adjacent inequivalent 2-fold rotations whose centers lie on a line parallel to the glide-reflection axis and are nearest to that axis. By observation 1 in Section 1 and the symmetries of the lattice of unit squares, the 2-fold centers must be located at vertices or midpoints of edges of unit squares. Glide-reflection axes must be located on (1) lines in the lattice of unit squares, or (2) lines through midpoints of two edges of a unit square, or (3) lines through opposite vertices of unit squares.

We first place a black circle as a 2-fold center on a lattice of unit squares and call this the origin, then place orthogonal unit vectors $\mathbf{u}$ and $\mathbf{v}$ at the origin. Next we place the two parallel glide-reflection axes nearest to the origin. These can be parallel to $\mathbf{u}$ or parallel to $\mathbf{u}+\mathbf{v}$ and go through the points $\pm y\mathbf{v}/2$, where y is a positive integer. Finally we place a white 2-fold center. This is at a point $x\mathbf{u}/2$ when the glide-reflection axes are parallel to $\mathbf{u}$, and at a point $x(\mathbf{u}+\mathbf{v})/2$ when the glide-reflection axes are parallel to $\mathbf{u}+\mathbf{v}$, where x is a positive integer. This white center will be a nearest 2-fold center that is inequivalent to the black 2-fold center. The placement of this 2-fold center determines the length of the minimal glide vector for the glide-reflection axes we placed.

Figure 21 shows four essentially different locations of the 2-fold centers relative to the lattice of unit squares and placement of glide-reflection axes, and gives restrictions on x and y for each case.

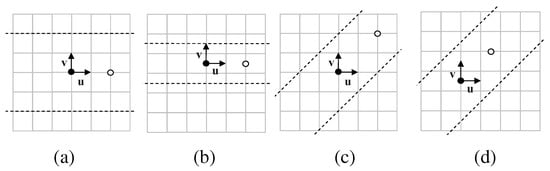
Figure 21. The square lattice for a pgg group G. The black and white circles are inequivalent 2-fold centers, and dotted black lines are glide-reflection axes; these symmetry elements generate G. (a)–(d) illustrate the four different locations of the 2-fold centers relative to the lattice of unit squares and placement of glide-reflection axes. Restrictions on positive integers x and y used to place the white centers and glide-reflection axes are as follows. In (a), when x is odd, y must be even; In (b), x must be even; In (c), both x and y must be even; In (d), x and y must have opposite parities. In the examples shown, (a) x = 4, y = 4; (b) x = 4, y = 2; (c) x = 4, y = 4; (d) x = 3, y = 4.

G is the pgg symmetry group generated by ${180}^{\circ }$ rotations about the black and white 2-fold centers and glide reflections in one of the two glide-reflection axes we have placed. The area S of a fundamental domain for G is given by

$$S=xy/2$$

(5)

where the area of a unit square is 1. Note that $n=S$ and S must be an integer. Therefore,

$$n=1,2,3,\dots .$$

(6)

Actions by the group G on the unit squares classify the unit squares into n equivalence classes; the equivalence class of a unit square e is denoted $C(e)$.

For each integer $n>0$, we construct an n-omino tile $T_n$ that is a fundamental domain for the group G by the procedure described in Section 4.2 and reference is to Figure 21. Figure 22 shows the complete set ${\mathcal{T}}_n$ of n-omino tiles constructed by this procedure for $n\le 5$.

Figure 22. List of n-ominoes for $n\le 5$ produced by the procedure in Section 5.2; these are fundamental domains for the pgg groups G used to generate their corresponding isohedral tilings in Figure 23. Labels indicate n followed by the tile number for that n. Parentheses indicate that the corresponding tiling has symmetry group larger than G. Underlines indicate that the corresponding tiling is type 2 and so has slide lines; there is an infinite family of tilings by that tile having the same slide lines.

Rotations of ${180}^{\circ }$ about the black and white 2-fold centers on the edges of a polyomino tile T in ${\mathcal{T}}_n$ fills out a band tiled by copies of T, then repeated glide reflections of this band in the two glide-reflection axes placed at the outset produces an isohedral tiling $\mathcal{T}$ having T as a fundamental domain for the pgg group G.

We note that in building a polyomino, when unit squares are taken from the region between the two glide-reflection axes shown in Figure 21a and x is odd and y is even, the tiling will have displacement points along horizontal glide-reflection axes (see Figure 20b). For each tile T in Figure 22 and $n\le 4$, Figure 23 shows the corresponding tiling by T generated in this manner, or in the case when T is a type 2 tile, a representative of an infinite family of tilings. When T is a type 2 tile, the black 2-fold center can be at any point between a vertex and midpoint of the edge on which it lies; Figure 22 shows only a representative tile T with 2-fold centers in the original positions placed at the outset. We underline the labels of type 2 tilings and the type 2 tiles that generate them in our listings. More details on these tilings and their symmetries are in the next section.

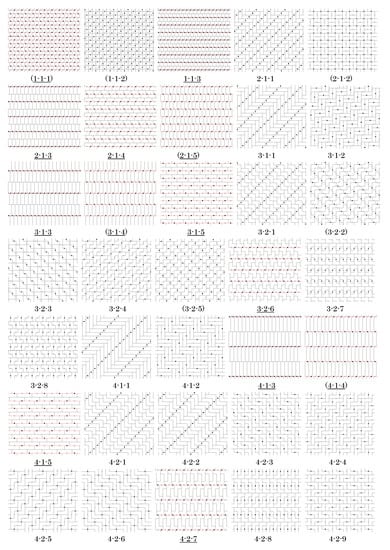
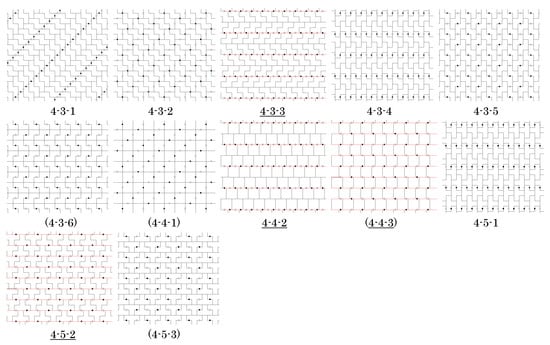
Figure 23. List of isohedral tilings by the n-ominoes in Figure 22 for $n\le 4$; the n-ominoes are fundamental domains for the pgg groups G that generate the tilings. Labels correspond to those in Figure 22. Tilings with underlined labels are in general position and represent an infinite family of tilings. Red lines indicate slide lines.

5.3. Symmetries of the Polyomino Tilings

Our procedure described in the previous section produces polyomino tiles T that are fundamental domains for a given pgg group G that generates an isohedral tiling $\mathcal{T}$. However, it is possible that $\mathcal{T}$ has additional symmetries, that is, G is a proper subgroup of the full symmetry group $G^{\prime }$ of $\mathcal{T}$ and T is not a fundamental domain for $G^{\prime }$ (Theorem 1). The pgg group G can be a proper subgroup of a symmetry group of any of these types: pgg, pmm, cmm, p4m, p4g, or pmg. As argued in Section 4.3, to determine if $\mathcal{T}$ has symmetries that are not in G, we only need to look for 2-fold centers for $G^{\prime }$ that are not 2-fold centers for G. In order to seek 2-fold centers not in G, we look at all vertices, midpoints of edges and centers of unit squares in a polyomino T in the tiling $\mathcal{T}$ except for those equivalent to the original 2-fold centers we have chosen (black and white centers in Figure 21), and investigate whether or not they can be new 2-fold centers of $\mathcal{T}$. If a new 2-fold center is found, we indicate that G is not the full symmetry group of $\mathcal{T}$ by putting parentheses around the labels of the tile T in Figure 22 and its corresponding tiling $\mathcal{T}$ in Figure 23. In the case of a type 2 tiling, although there may be a finite number of $\epsilon$-slides of the tiling that produce a tiling with larger symmetry group than G, we put parentheses only around the labels of those type 2 tilings for which every tiling in the infinite family has a symmetry group larger than G.

For brick tiles T, if the inequivalent 2-fold centers on T are located on one edge of T or on opposite edges of T so that a line through them is perpendicular to those edges, we will not distinguish between type 1 and type 2 tilings, since the type 1 case occurs as a special case of a type 2 tiling. The tilings generated by G for these brick tiles will always have slide lines, and depending on the rectangular shape and the position of the 2-fold centers and glide-reflection axes, the pmg, pmm, and cmm tilings in Figure 7 can be generated by G, as well as p4m tilings. Brick tilings unique to this pgg group G are those of “herringbone” type in which the 2-fold centers on a brick tile are on adjacent edges (e.g., tiles and tilings 2-1-1, 3-1-1 in Figure 22 and Figure 23); a square brick of this type generates a p4m tiling (e.g., tiles and tilings 1-1-2 and 4-4-1 in Figure 22 and Figure 23). Other brick tilings have the inequivalent 2-fold centers on a brick tile on opposite edges, where a line through them makes a ${45}^{\circ }$ angle with those edges (e.g., tiling 2-1-2 which has p4g symmetry, and 4-1-2 in Figure 23).

For tiles that are not bricks, we consider two cases separately. The observations that follow are true for both polyominoes and polyiamonds.

5.3.1. $\mathcal{T}$ Is a Type 1 Tiling

When T has only $C_2$ symmetry and translated images of T fill out parallel strips in $\mathcal{T}$ bounded by adjacent glide-reflection axes, $G^{\prime }$ will be type pmg (e.g., tiling 4-3-6 in Figure 23). Figure 24a shows the situation for an arbitrary $C_2$ tile T: the 2-fold center for T is a 2-fold center for $G^{\prime }$ and produces new glide-reflection axes in $G^{\prime }$; horizontal glide-reflection axes in G are reflection axes in $G^{\prime }$.

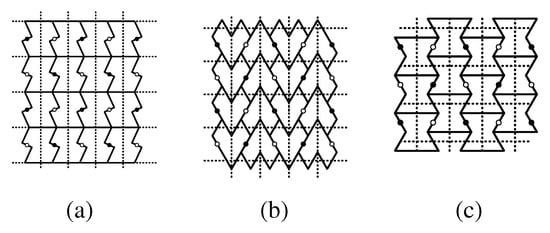
Figure 24. Three type 1 tilings $\mathcal{T}$ generated by a pgg group G whose lattice of symmetry elements is shown. The full symmetry group $G^{\prime }$ of each tiling is larger than G. (a) A general tile with $C_2$ symmetry; $G^{\prime }$ is type pmg; (b) A tile with $D_1$ symmetry; $G^{\prime }$ is type pmg; (c) A tile with $D_2$ symmetry; $G^{\prime }$ is type cmm.

When T has $D_1$ symmetry, and its mirror line is on a glide-reflection axis in $\mathcal{T}$, then $G^{\prime }$ will be type pmg (e.g., tilings 3-2-2 and 4-5-3 in Figure 23). Figure 24b illustrates the situation for a 6-iamond chevron: the mirror symmetry of T produces new 2-fold centers on the horizontal glide reflection axes of $\mathcal{T}$ and new glide-reflection axes through the original 2-fold centers in the full symmetry group $G^{\prime }$, and vertical glide-reflection axes in G are reflection axes in $G^{\prime }$.

When T has $D_2$ symmetry, and one of its mirror lines is a glide-reflection axis in $\mathcal{T}$, then $G^{\prime }$ will be type cmm. Figure 24c illustrates the situation for a 6-iamond bow tie: the additional symmetries of T produce new 2-fold centers and new glide-reflection axes through the original 2-fold centers, and reflection axes for T are reflection axes in $G^{\prime }$.

5.3.2. $\mathcal{T}$ Is a Type 2 Tiling

Type 2 tilings will have slide lines, and unlike the case for a pmg group, there can be 2-fold centers on slide lines that are not in the group G. This happens only when the original 2-fold centers for a tile T (placed at the outset) are at slide points of the tiling $\mathcal{T}$, and the new 2-fold center is midway between these. Moreover, the existence of the new 2-fold centers requires that T have a mirror line on the glide-reflection axis for $\mathcal{T}$ parallel to the slide line and that the edges of T not on the slide line are parallel. (The composition of the new 2-fold rotation with a glide reflection in an axis perpendicular to the slide line produces a reflection in the glide-reflection axis parallel to the slide line; the composition of an original 2-fold rotation with the new 2-fold rotation produces a translation that must carry T to an adjacent tile.) For such tilings $\mathcal{T}$ in which T is not a brick, $\mathcal{T}$ will have pmg symmetry.

When a tile T for a type 2 tiling $\mathcal{T}$ has mirror symmetry and its mirror line is perpendicular to a slide line, then for some $\epsilon$-slides the mirror line for T may coincide with a glide-reflection axis for $\mathcal{T}$ and become a reflection axis for $\mathcal{T}$. If this happens, the tiling may have pmg, cmm, or in the case T is a polyiamond, p6m symmetry (e.g., tiling 4-5-2 in Figure 23; also see Figure 25). Except for these special positions, the tilings will have pgg symmetry group G.

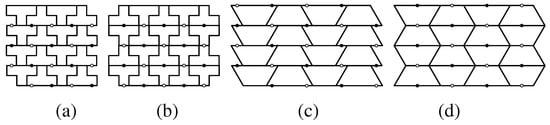
Figure 25. Four special positions of type 2 tilings generated by a pgg group whose lattice of 2-fold centers is shown. (a) and (b) are tilings in the family 4-5-2 of Figure 23; (a) is type pmg; (b) is type cmm; (c) and (d) are tilings by a trapezoidal 3-iamond; (c) is type pmg; (d) is type cmm.

5.4. Creating Polyiamonds as Fundamental Domains for pgg Symmetry Groups

To produce polyiamond tiles that are fundamental domains for a given pgg group G, we follow a pattern similar to that in Section 5.2 and create tiles whose isohedral tilings generated by the group G will have either no displacement points or displacement points only on glide-reflection axes $L_g$. As before, the 2-fold centers must be located at vertices or midpoints of edges of unit triangles. Glide-reflection axes must be located on (1) lines in the lattice of unit triangles, or (2) lines through midpoints of two edges of a unit triangle, or (3) lines that join a vertex and midpoint of an opposite edge of a unit triangle, or (4) lines through adjacent midpoints of two joined triangles. Since glide reflections in axes of types (1) or (2) combine with 2-fold rotations to produce glide reflections in axes of types (3) or (4), we only need to consider the first two types.

To begin, we place a black circle as a 2-fold center on a lattice of unit triangles and call this the origin, then place vectors $\mathbf{u}$ and $\mathbf{v}$ at the origin along (or parallel to) edges of unit triangles, as shown in Figure 26. Next we place two horizontal glide-reflection axes nearest to the origin. These go through the points $\pm y\mathbf{v}/2$, where y is a positive integer. Finally we place a white 2-fold center at a point $x\mathbf{u}/2$, where x is a positive integer. This white center will be a nearest 2-fold center that is inequivalent to the black 2-fold center. The placement of this 2-fold center determines the length of the minimal glide vector for the glide-reflection axes placed.

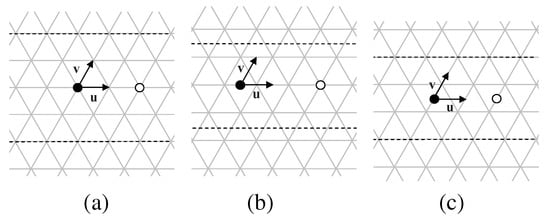
Figure 26. The triangular lattice for a pgg group G. The black and white circles are inequivalent 2-fold centers, and dotted black lines are glide-reflection axes; these symmetry elements generate G. (a)–(c) illustrate the three different locations of the black 2-fold centers relative to the lattice of unit triangles and placement of glide-reflection axes. Restrictions on positive integers x and y that determine the placement of the white center and glide-reflection axes are as follows. In (a) and (b), x even and y odd is excluded, and in (c), x and y both even is excluded. In these examples, (a) $x=4$, $y=4$; (b) $x=5$, $y=3$; (c) $x=4$, $y=3$.

G is the pgg symmetry group generated by ${180}^{\circ }$ rotations about the black and white 2-fold centers and glide reflections in one of the two glide-reflection axes we have placed. The area S of a fundamental domain for G is given by

$$S=xy$$

(7)

where the area of a unit triangle is 1. Note that $n=S$ and S must be an integer. Therefore,

$$n=1,2,3,\dots .$$

(8)

Actions by the group G on the unit triangles classify the unit triangles into n equivalence classes; the equivalence class of a unit triangle e is denoted $C(e)$. For each integer $n>0$, we construct an n-iamond tile $T_n$ that is a fundamental domain for the group G by the procedure described in Section 4.2, with unit triangles instead of unit squares, and reference to Figure 26.

We note that for the origin placed as in Figure 26a,b, when x is odd and y is even, and in Figure 26c, when both x and y are odd, the glide reflection in the horizontal axis will cause a displacement, and so in building the polyiamond tile, unit triangles must be chosen between the two glide-reflection axes placed at the outset. These glide-reflection axes will be fault lines $L_g$ in the tiling. Figure 27 shows the complete set ${\mathcal{T}}_n$ of n-iamond tiles constructed by this procedure for $n\le 6$.

Figure 27. List of n-iamonds for $n\le 6$ produced by the procedure in Section 5.4; these are fundamental domains for the pgg groups G used to generate their corresponding isohedral tilings in Figure 28. Labels indicate n followed by the tile number for that n. Parentheses indicate that the corresponding tiling has symmetry group larger than G. Underline indicates that the corresponding tiling is type 2 and so has slide lines; there is an infinite family of tilings by that tile having the same slide lines.

Rotations of ${180}^{\circ }$ about the black and white 2-fold centers on the edges of a polyiamond tile T in ${\mathcal{T}}_n$ fill out a band tiled by copies of T, then repeated glide reflections of this band in the two glide-reflection axes placed at the outset produce an isohedral tiling $\mathcal{T}$ having T as a fundamental domain for the pgg group G. Figure 28 shows, for each tile T in Figure 27 and $n\le 5$, the corresponding tiling by T generated in this manner, or in the case when T is a type 2 tile, a representative of an infinite family of tilings. When T is a type 2 tile, the black 2-fold center can be at any point between a vertex and midpoint of the edge on which it lies; Figure 27 shows only a representative tile T with 2-fold centers in the original positions placed at the outset. More details on these tilings and their symmetries are in the next section.

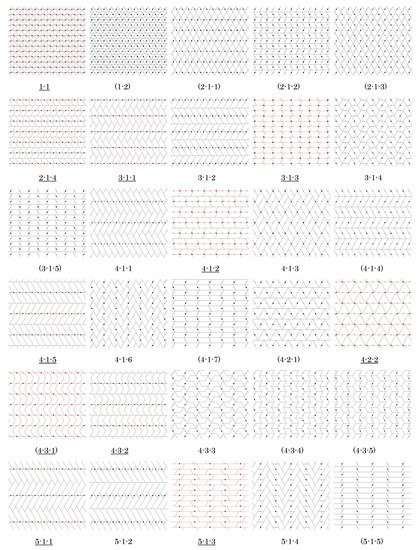
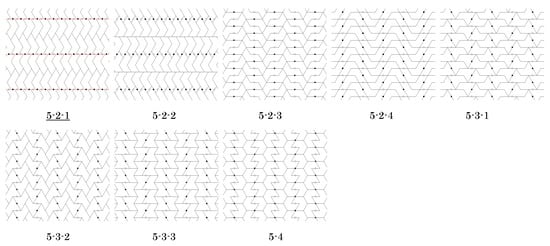
Figure 28. List of isohedral tilings by the n-iamonds in Figure 27 for $n\le 5$; the n-iamonds are fundamental domains for the pgg groups G that generate the tilings. Labels correspond to those in Figure 27. Tilings with underlined labels are in general position and represent an infinite family of tilings. Red lines indicate slide lines.

5.5. Symmetries of the Polyiamond Tilings

Our procedure described in the previous section produces polyiamond tiles T that are fundamental domains for a given pgg group G that generates an isohedral tiling $\mathcal{T}$. However, it is possible that G is a proper subgroup of the full symmetry group $G^{\prime }$ of $\mathcal{T}$ and T is not a fundamental domain for $G^{\prime }$ (Theorem 1). The pgg group G can be a proper subgroup of a symmetry group of any of these types: pgg, cmm, pmg, or p6m. In Section 5.3, we described additional symmetries possible for the full symmetry group $G^{\prime }$ for both polyomino and polyiamond tiles having symmetry. Tilings 2-1-2, 4-1-4, and 4-1-7 in Figure 28 have tiles with $C_2$ symmetry and have pmg symmetry group. In particular, all tilings by polyiamond parallelogram tiles that fill out parallel strips bounded by adjacent glide-reflection axes will have pmg symmetry group. Tilings 3-1-5, 4-2-1, and 4-3-5 in Figure 28 have tiles with $D_1$ symmetry and have pmg symmetry group. Tiling 2-1-1 in Figure 28 has a tile with $D_2$ symmetry and has cmm symmetry group.

6. cmm

6.1. cmm Tilings

The lattice of symmetries of a cmm group G consists of two sets of equispaced parallel reflection axes, one set perpendicular to the other (vertical and horizontal in Figure 29) and midway between them, glide-reflection axes. Perpendicular reflection axes are inequivalent, and perpendicular glide-reflection axes are inequivalent. Every 2-fold center is at the intersection of two reflection axes or the intersection of two glide-reflection axes. The generating glide vectors are defined by the (horizontal and vertical) distances between two adjacent parallel reflection axes or parallel glide-reflection axes.

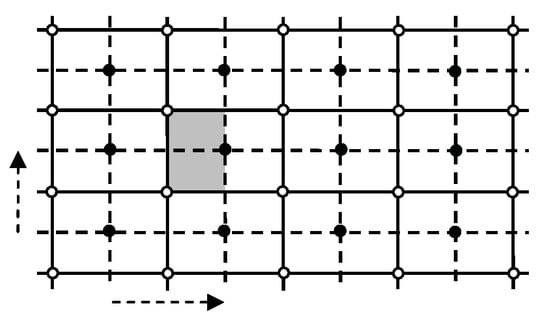
Figure 29. The lattice of symmetries of a cmm group G. Reflection axes are solid lines, glide-reflection axes are dotted lines and their minimal glide vectors are shown as dotted vectors. Black and white circles mark inequivalent 2-fold centers. The shaded region is a fundamental domain for G. G is generated by a ${180}^{\circ }$ rotation about a black 2-fold center and reflections in perpendicular reflection axes nearest that center.

Because we want to produce tiles T that are fundamental domains for this cmm group G, two inequivalent 2-fold centers for G must be located on the boundary of such T, and in the tiling, edges of T must lie on reflection axes (observation 1 in Section 1). Thus the grid of perpendicular reflection axes in the cmm lattice in Figure 29 must lie on lattice lines in the underlying lattice of unit squares (for polyomino tilings) or unit triangles (for polyiamond tilings). This is impossible for the triangle lattice.

Theorem 13.

There is no cmm isohedral tiling having a polyiamond as fundamental domain.

When T is a polyomino tile that is a fundamental domain for the cmm group G, a ${180}^{\circ }$ rotation about the 2-fold center on T that is not on a reflection axis will fill out a rectangle bounded by four reflection axes that lie on lattice lines in the underlying lattice of unit squares. This rotation preserves the underlying lattice of unit squares within this rectangle, and reflections in the axes that bound it will also preserve the full underlying lattice of unit squares.

Theorem 14.

There are no displacement points in any cmm isohedral tiling having a polyomino as fundamental domain.

6.2. Creating Polyominoes as Fundamental Domains for cmm Symmetry Groups

We now describe how to produce polyomino tiles that are fundamental domains for a given cmm group G. G can be generated by a 2-fold rotation about a center not on a reflection axis and reflections in two perpendicular axes nearest that 2-fold center. As before, the 2-fold centers for G must be located at vertices or midpoints of edges of unit squares, and the reflection axes must be along edges of unit squares.

We begin by placing a black circle as a 2-fold center on a lattice of unit squares and call this the origin, then place orthogonal unit vectors $\mathbf{u}$ and $\mathbf{v}$ at the origin. There are two distinct positions, as shown in Figure 30. Next we place the two horizontal and vertical reflection axes nearest to the origin. The vertical axes go through $\pm x\mathbf{u}$, where x is a positive integer. The horizontal axes go through $\pm yv/2$, with the following restrictions. When the origin is at a vertex of a unit square as in Figure 30a, y must be an even positive integer and when the origin is at the midpoint of an edge of a unit square as in Figure 30b, y must be an odd positive integer. The white 2-fold centers are at intersections of reflection axes placed reflection axes. The black and white 2-fold centers are inequivalent.

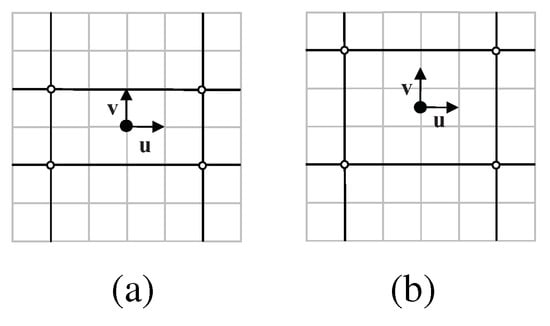
Figure 30. The square lattice for a cmm group G. The black circle is a 2-fold center, and black lines are reflection axes; these symmetry elements generate G. (a) and (b) illustrate the two different locations of the 2-fold centers relative to the lattice of unit squares. In (a) and (b) x is any positive integer, but in (a) y must be an even positive integer, and in (b) y must be an odd positive integer. In these two examples (a) $x=2$, $y=2$; (b) $x=2$ and $y=3$.

G is the cmm symmetry group generated by ${180}^{\circ }$ rotations about the black 2-fold center and reflections in two perpendicular reflection axes we have placed. The area S of a fundamental domain for G is given by

$$S=xy$$

(9)

where the area of a unit square is 1. Note that $n=S$ and S must be an integer. Therefore,

$$n=1,2,3,\dots .$$

(10)

As before, actions of G on the unit squares partitions the unit squares into n equivalence classes; the equivalence class of a unit square e is denoted $C(e)$. For each integer $n>0$, we construct an n-omino tile $T_n$ that is a fundamental domain for the group G by the procedure described in Section 4.2, with reference to Figure 30. Here the unit squares must be taken from the region enclosed by the reflection axes shown in Figure 30. Figure 31 shows the complete set ${\mathcal{T}}_n$ of n-omino tiles constructed by this procedure for $n\le 10$.

Figure 31. List of n-ominoes for $n\le 10$ produced by the procedure in Section 6.2; these are fundamental domains for the cmm groups G used to generate their corresponding isohedral tilings in Figure 32. Labels indicate n followed by the tile number for that n. Parentheses indicate that the corresponding tiling has symmetry group larger than G.

A ${180}^{\circ }$ rotation of a polyomino tile T in ${\mathcal{T}}_n$ about the black 2-fold center on T fills out the rectangle bounded by the reflection axes placed at the outset, and repeated reflections of this rectangle in those axes produce an isohedral tiling $\mathcal{T}$ having T as a fundamental domain for the cmm group G. Figure 32 shows the set of tilings generated in this manner, corresponding to the tiles in Figure 31 for $n\le 8$. More details on these tilings and their symmetries are in the next section.

Figure 32. List of isohedral tilings by the n-ominoes in Figure 31 for $n\le 8$; the n-ominoes are fundamental domains for the cmm groups G that generate the tilings. Labels correspond to those in Figure 31.

6.3. Symmetries of the Polyomino Tilings

The polyomino tiles T produced by our procedure in Section 6.2 are fundamental domains for a cmm group G that generates an isohedral tiling $\mathcal{T}$. When G is a proper subgroup of the full symmetry group $G^{\prime }$ of $\mathcal{T}$, the tile T must have symmetry, and this symmetry is an element of $G^{\prime }$ (Theorem 1). Since our tiles are polyominoes, the cmm group G can be a proper subgroup of a group of any of these types: pmm, cmm, p4g, p4m.

Our construction of a polyomino fundamental domain for the cmm group G produces a tile T bounded by reflection axes on three sides, with its fourth side a rectilinear edge having 2-fold symmetry (see Figure 33).

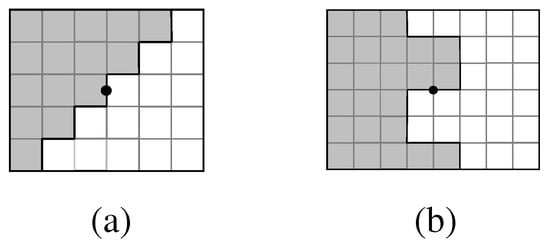
Figure 33. Two polyomino fundamental domains (shaded) for a cmm group G. The black circle is a 2-fold center, and the edges of the bounding rectangle are reflection axes. Although the shaded fundamental domain on the left has mirror symmetry, the mirror is not compatible with the cmm reflection axes.

The only such tiles T that have symmetry compatible with the cmm lattice are those in which the fourth side is a straight edge, that is, T is a brick. When T is a brick, a ${180}^{\circ }$ rotation about the 2-fold center on its edge places a copy of T edge-to-edge with T, and reflections in the bounding reflection axes produce an isohedral edge-to-edge tiling.

Theorem 15.

Let $\mathcal{T}$ be an isohedral tiling having a polyomino tile T as fundamental domain for a cmm group G. If T is not a brick, then G is the full symmetry group of $\mathcal{T}$. If T is a brick, then T has pmm symmetry, unless T is a square, in which case $\mathcal{T}$ has p4m symmetry.

7. Enumeration Tables

Table 1 gives the number of isohedral tilings of types pmg, pgg and cmm having n-ominoes or n-iamonds as fundamental domains for small values of n.

Table 1. The number of isohedral tilings of types pmg, pgg and cmm having n-ominoes or n-iamonds as fundamental domains.

In Table 1, $N_n$ is the number of tiles $T_n$ in ${\mathcal{T}}_n$ for a given pmg, pgg, or cmm symmetry group G that generates an isohedral tiling having $T_n$ as a fundamental domain. Recall that we defined tiles $T_n$ to be equivalent only if they generate the same tiling by the action of the group G when each tile is marked with an asymmetric motif. So $N_n$ is also the number of isohedral tilings having G as full symmetry group and having n-omino or n-iamond tiles as fundamental domain, when each tile is marked with an asymmetric motif. Here the infinite family of type 2 tilings for a single $T_n$ is counted as one tiling.

For example, the tiles 4-3-1 and 4-3-2 in Figure 12 are congruent and their corresponding tilings are the same, but the placement of their 2-fold centers is different, and so if the tiles are marked with an asymmetric motif, they generate different isohedral tilings. Thus they are not equivalent. Moreover in this case, the tiling generated by tile 4-3-1 has slide lines, so there are an infinite number of type 2 tilings related to this tile.

$S_n$ is the corresponding number for the $N_n$ tilings when the asymmetric motif of each tile is removed. That is, $S_n$ is the number of isohedral tilings having full symmetry group G and having (unmarked) nominoes or n-iamonds as fundamental domains. In our figures that depict the isohedral tilings for small values of n, these tilings do not have parentheses around their labels. The numbers $S_n$ are the most important “counting” results in this article. We note that often for a type 2 tile $T_n$ and the corresponding type 2 tiling $\mathcal{T}$ it generates, there may be a small finite number of values of $\epsilon \ge 0$ for which an $\epsilon$-slide of $\mathcal{T}$ produces a tiling for which G is not the full symmetry group, but the remaining infinite number of tilings in the family of type 2 tilings corresponding to $T_n$ have G as their full symmetry group. The labels for these type 2 tiles and their tilings have not been marked with parentheses and the tilings for a single tile are counted as one in the number $S_n$.

$N_n^{\prime }$ is the number of non-congruent tiles in the $N_n$ tilings, counted by ignoring rotation centers attached to tiles; similarly, $S_n^{\prime }$ is the number of non-congruent tiles in the $S_n$ tilings. These are counts of different tile numbers k in the labels n-k-m of tiles counted by $N_n$ and $S_n$.

For example, for a pgg symmetry group having 4-iamonds as fundamental domains, there are 14 tiles in Figure 27 whose label begins with 4, so $N_4=14$. But 6 of the corresponding tilings in Figure 28 have additional symmetry (namely 4-1-4, 4-1-7, 4-2-1, 4-3-1, 4-3-4, and 4-3-5) indicated by parentheses around their labels, so $S_4=14-6=8$. Also in Figure 27 we can see that among the 4-iamonds tiles, there are only 3 distinct shapes, indicated by the tile numbers: a parallelogram (tiles 4-1), an equilateral triangle (tile 4-2), and a chevron (tiles 4-3). Thus $N_4^{\prime }=3$. Similarly, among the eight 4-iamonds counted by $S_4$ (tiles 4-1-1, 4-1-2, 4-1-3, 4-1-5, 4-1-6, 4-2-2, 4-3-2, and 4-3-3), there are also these three distinct shapes, so $S_4^{\prime }=3$.

8. Summary

We have described computer algorithms that can enumerate and display isohedral tilings by n-omino or n-iamond tiles for given n in which the tiles are fundamental domains and the tilings have pmm, pmg, pgg and cmm symmetry. These symmetry groups belong to crystal class $D_2$ among the 17 two-dimensional symmetry groups.

We have shown that there are no isohedral tilings with symmetry group pmm that have polyominoes or polyiamonds as fundamental domains. For symmetry groups of types pmg, pgg and cmm we used the backtracking procedure described in Section 4.2 to obtain the set ${\mathcal{T}}_n$ of n-omino or n-iamond tiles where each tile produced one isohedral tiling, generated by a given symmetry group of one of these three types. If we let G denote the symmetry group we can denote ${\mathcal{T}}_n(G)$ as the set ${\mathcal{T}}_n$ for that symmetry group, and ${\mathcal{T}}_n^{*}(G)$ the corresponding set of isohedral tilings. Note that if some tiling in ${\mathcal{T}}_n^{*}(G)$ is type 2, it belongs to an infinite family in ${\mathcal{T}}_n^{*}(G)$.

We investigated the symmetries of tilings in the set ${\mathcal{T}}_n^{*}(G)$ including infinite families of type 2 tilings and noted those tilings that satisfy the following conditions: (1) the full symmetry group of the tiling is G, and (2) the tiles are fundamental domains for G. We denote ${\mathcal{S}}_n^{*}(G)$ as the subset of ${\mathcal{T}}_n^{*}(G)$ that satisfies conditions (1) and (2), and the corresponding set of tiles as ${\mathcal{S}}_n(G)$. For small values of n, these tiles and their tilings were displayed in our figures and given labels without parentheses; where a tiling was type 2, a representative in general position was shown, and its label underlined.

We emphasize that the set ${\mathcal{S}}_n^{*}(G)$ is the complete set of all isohedral tilings having G as symmetry group and having n-omino or n-iamond tiles as fundamental domains. The enumeration of ${\mathcal{S}}_n^{*}(G)$ is the main counting result of this article. We have given details of how to obtain the set ${\mathcal{S}}_n^{*}(G)$ from ${\mathcal{T}}_n(G)$ through ${\mathcal{T}}_n^{*}(G)$. Table 1 in Section 7 gives the number of elements $N_n$ and $S_n$ in the set ${\mathcal{T}}_n^{*}(G)$ and ${\mathcal{S}}_n^{*}(G)$, respectively, where the infinite family of a type 2 tiling is counted as one tiling.