Enriching the Symmetry of Maxwell Equations through Unprecedented Magnetic Responses of Artificial Metamaterials and Their Revolutionary Applications
Abstract
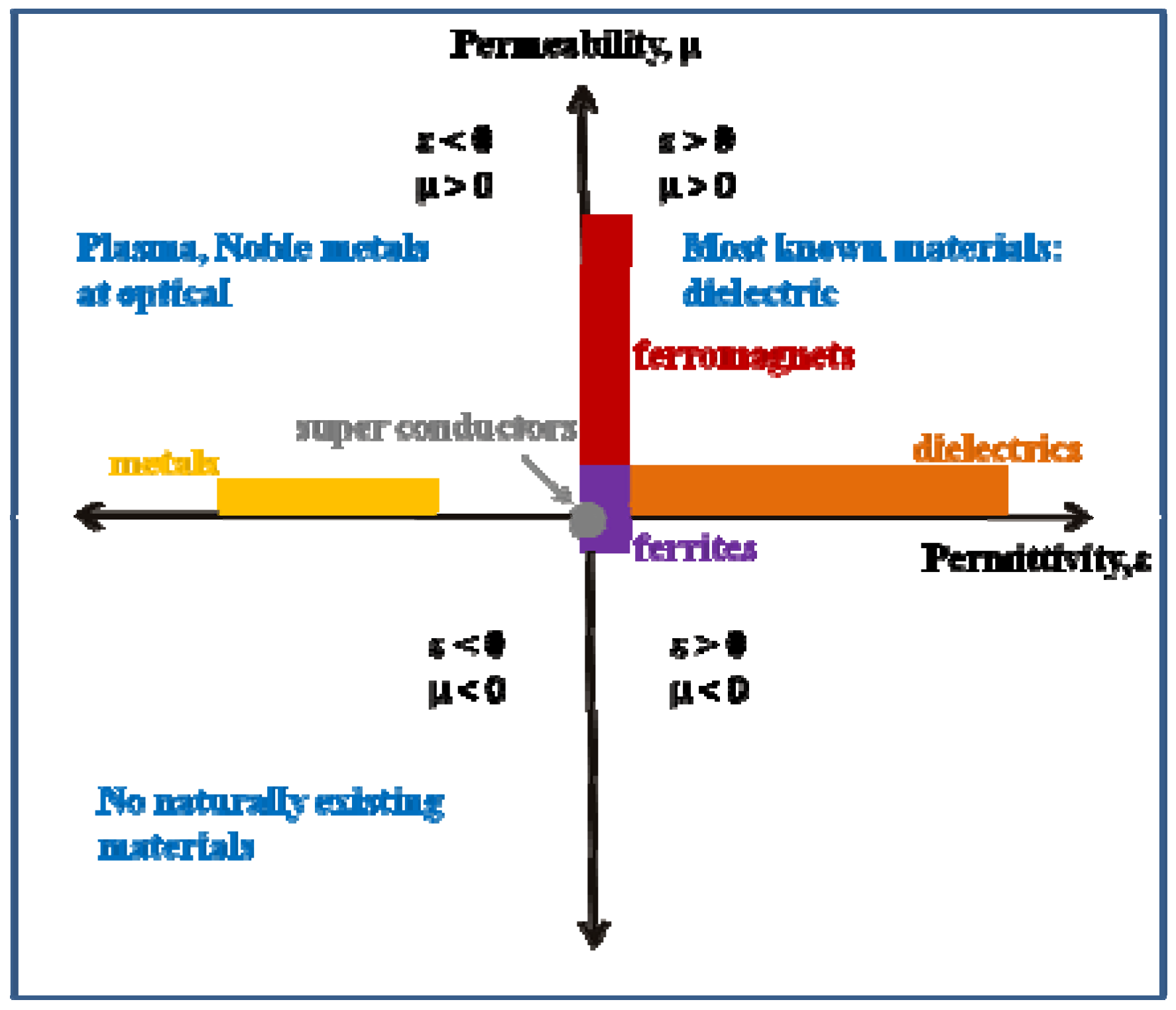
:1. Introduction and Background
2. Enriching Magnetic Responses by Artificial Magnetic Metamaterials
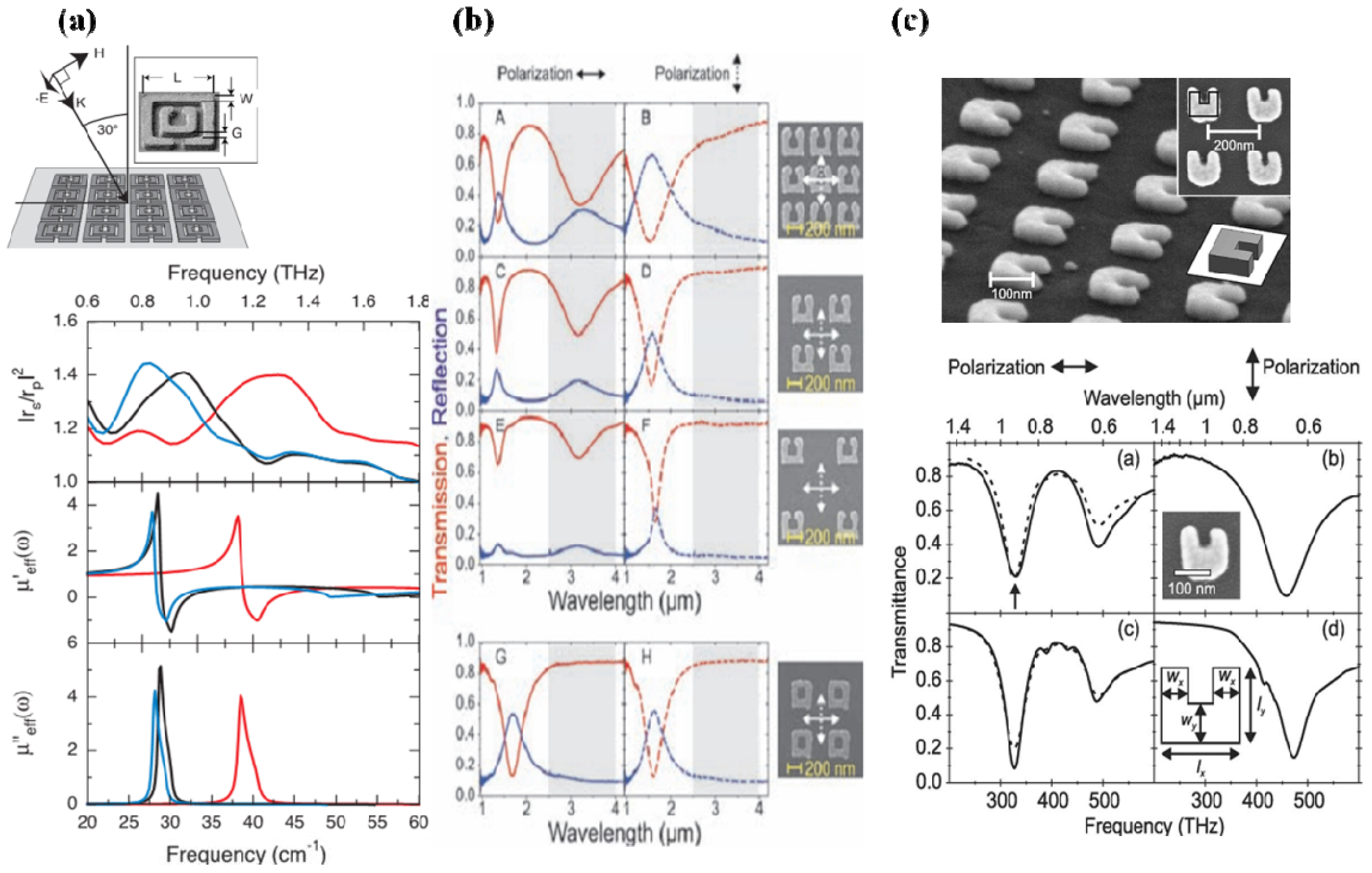
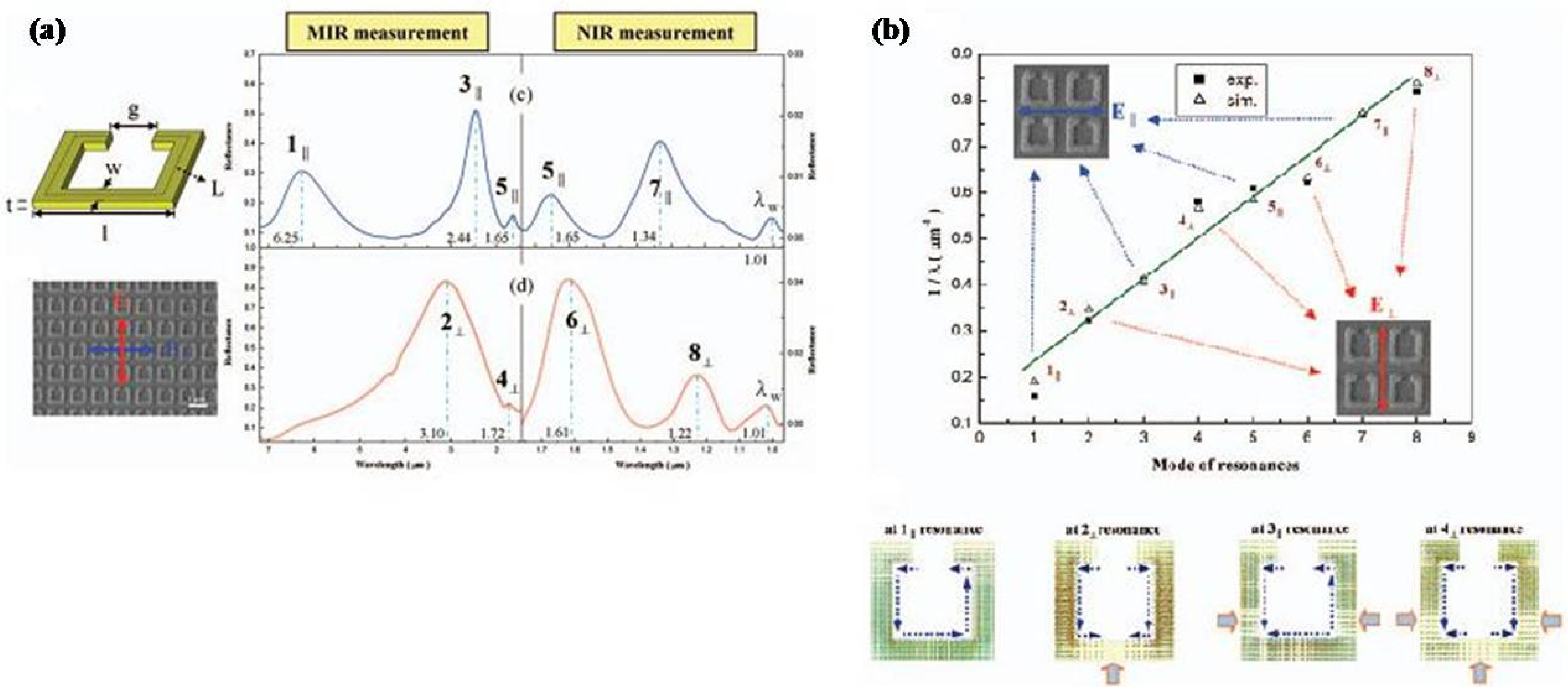
2.1. Split-Ring Resonators
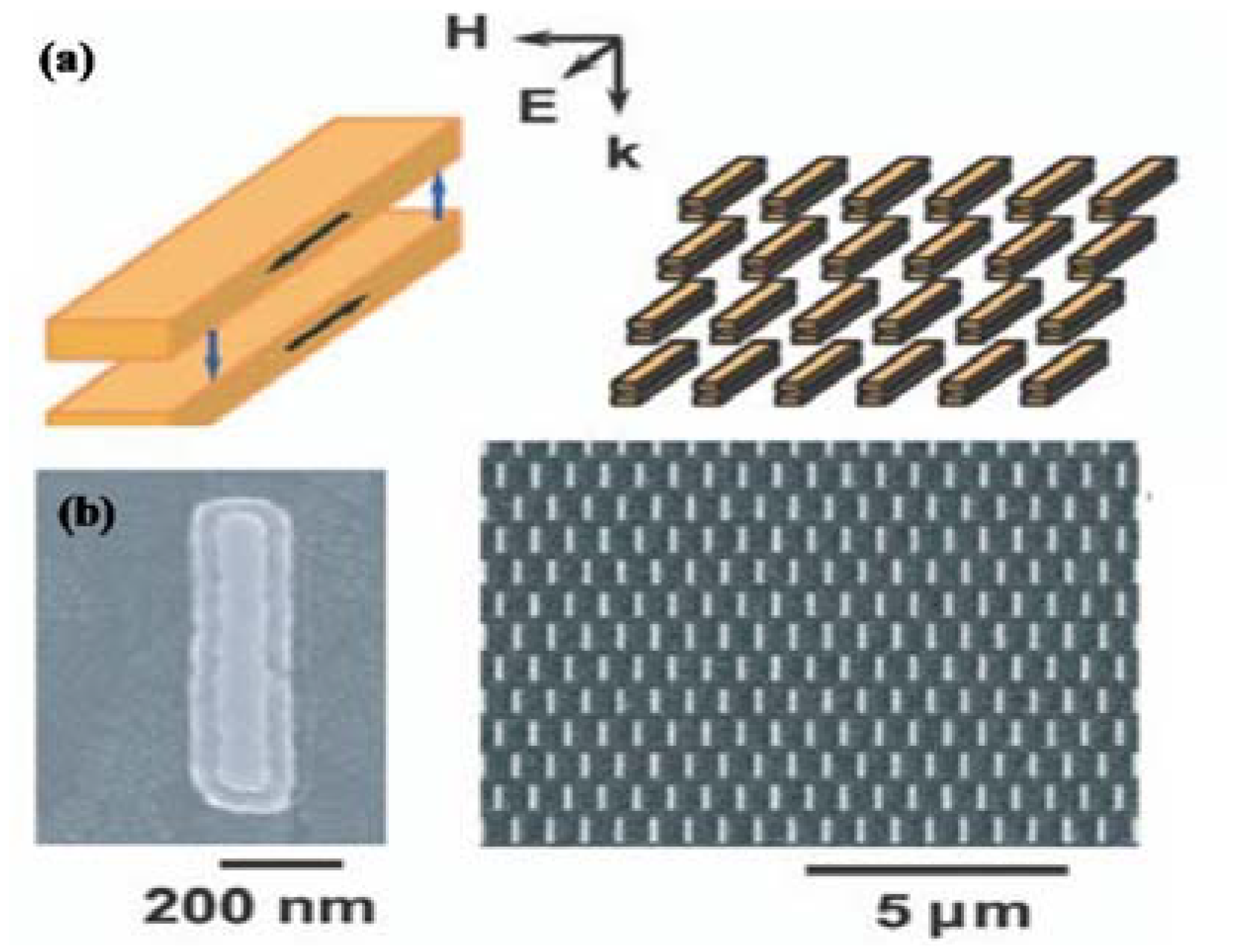
2.2. Sandwich Structures (Fishnet Structures)
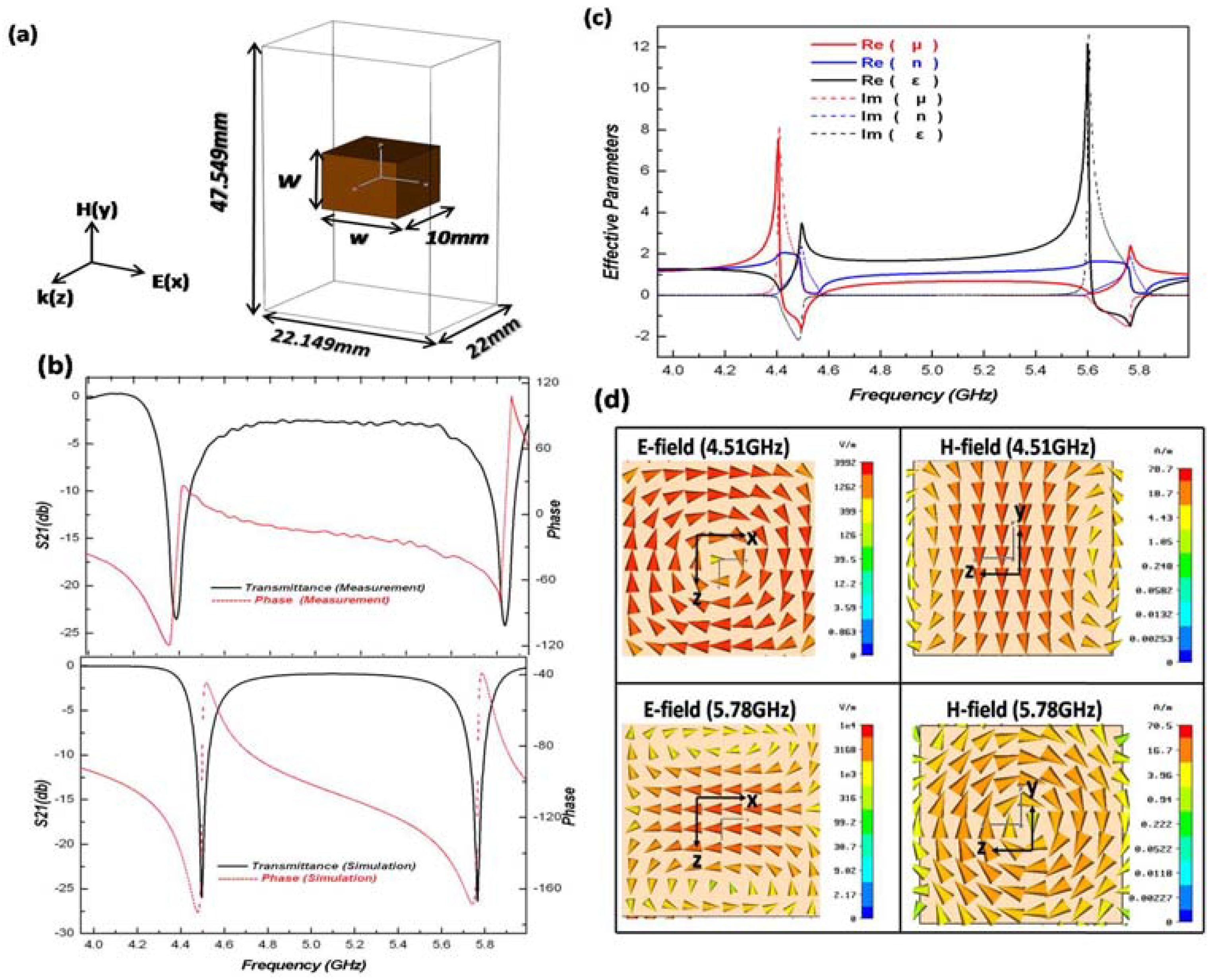
2.3. High-Permittivity Dielectric Composites
3. Extended Applications
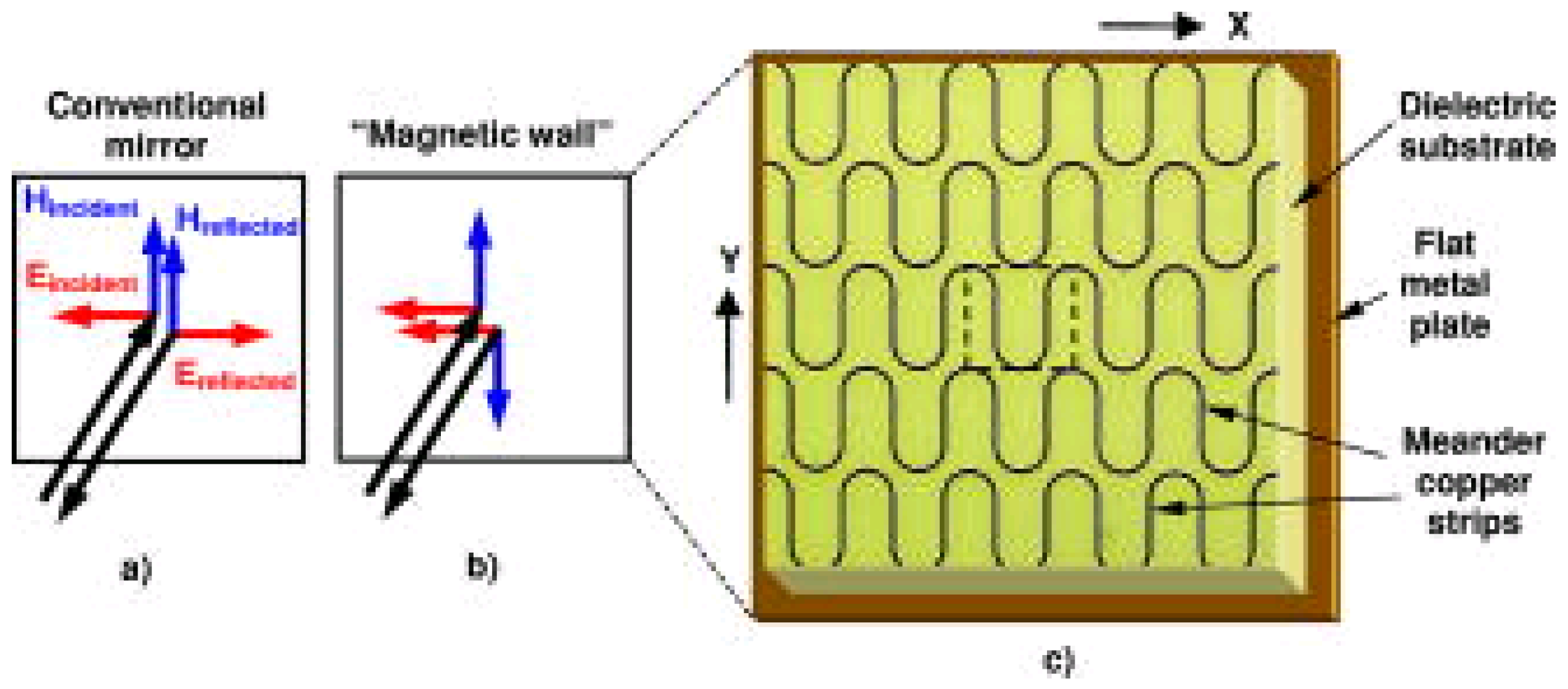
3.1. Magnetic Walls
3.2. Magnetic Surface Plasmon Resonance
3.3. Invisibility Cloaking
3.4. Artificial Electromagnetically Induced Transparency
3.5. Slow-Light Effect by NRIM
4. Conclusions
Acknowledgments
References
- Pimenov, A.; Loidl, A.; Gehrke, K.; Moshnyaga, V.; Samwer, K. Negative refraction observed in a metallic ferromagnet in the gigahertz frequency range. Phys. Rev. Lett. 2007, 98, 197401. [Google Scholar] [CrossRef] [PubMed]
- Rachford, F.J.; Armstead, D.; Harris, V.; Vittoria, C. Simulations of ferrite-dielectric-wire composite negative index materials. Phys. Rev. Lett. 2007, 99, 057202. [Google Scholar] [CrossRef] [PubMed]
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental verification of a negative index of refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B. A chiral route to negative refraction. Science 2004, 306, 1353–1355. [Google Scholar] [CrossRef] [PubMed]
- Seddon, N.; Bearpark, T. Observation of the inverse Doppler effect. Science 2003, 302, 1537–1540. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Grzegorczyk, T.; Zhang, Y.; Pacheco, J., Jr.; Wu, B.I.; Kong, J.; Chen, M. Cerenkov radiation in materials with negative permittivity and permeability. Opt. Express 2003, 11, 723–724. [Google Scholar] [CrossRef] [PubMed]
- Taubner, T.; Korobkin, D.; Urzhumov, Y.; Shvets, G.; Hillenbrand, R. Near-field microscopy through a SiC superlens. Science 2006, 313, 1595. [Google Scholar] [CrossRef] [PubMed]
- Merlin, R. Analytical solution of the almost-perfect lens problem. Appl. Phys. Lett. 2004, 84, 1290–1292. [Google Scholar] [CrossRef]
- Grbic, A.; Eleftheriades, G.V. Overcoming the diffraction limit with a planar left-handed transmission-line lens. Phys. Rev. Lett. 2004, 92, 117403. [Google Scholar] [CrossRef]
- Narimanov, E.E.; Shalaev, V.M. Optics: Beyond diffraction. Nature 2007, 447, 266–267. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.T.; Padilla, W.J.; Zide, J.M.O.; Gossard, A.C.; Taylor, A.J.; Averitt, R.D. Active terahertz metamaterials devices. Nature 2006, 444, 597–600. [Google Scholar] [CrossRef] [PubMed]
- Tsakmakidis, K.L.; Boardman, A.D.; Hess, O. Trapped rainbow storage of light in metamaterials. Nature 2007, 450, 397–401. [Google Scholar] [CrossRef] [PubMed]
- Veselago, G. The electrodynamics of substances with simultaneously negative values of ε and μ. Sov. Phys. Usp. 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- Reynet, O.; Acher, O. Voltage controlled metamaterials. Appl. Phys. Lett. 2004, 84, 1198–2000. [Google Scholar] [CrossRef]
- Wiltshire, M.C.K.; Pendry, J.B.; Young, I.R.; Larkman, D.J.; Gilderdale, D.J.; Hajnal, J.V. Microstructured magnetic materials for RF flux guides in magnetic resonance imaging. Science 2001, 291, 849–851. [Google Scholar] [CrossRef]
- Zhang, S.; Fan, W.; Panoiu, N.C.; Malloy, K.J.; Osgood, R.M.; Brueck, S.R. Experimental demonstration of near-infrared negative-index metamaterials. Phys. Rev. Lett. 2005, 95, 137404. [Google Scholar] [CrossRef]
- Alici, K.B.; Ozbay, E. A planar metamaterial: Polarization independent fishnet structure. Photonics Nanostruct. 2008, 6, 102–107. [Google Scholar] [CrossRef]
- Lai, Y.J.; Chen, C.K.; Yen, T.J. Creating negative refractive identity via single-dielectric resonators. Opt. Express 2009, 17, 12960–12970. [Google Scholar] [CrossRef] [PubMed]
- Lomakin, V.; Fainman, Y.; Urzhumov, Y.; Shvets, G. Doubly negative metamaterials in the near infrared and visible regimes based on thin film nanocomposites. Opt. Express 2006, 14, 11164–11177. [Google Scholar] [CrossRef] [PubMed]
- Chiang, Y.J.; Yen, T.J. A highly symmetric two-handed metamaterial spontaneously matching the wave impedance. Opt. Express 2008, 16, 12764–12770. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.R.; Schultz, S.; Markoš, P.; Soukoulis, C.M. Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients. Phys. Rev. B 2002, 65, 195104. [Google Scholar] [CrossRef]
- Chen, X.; Grzegorczyk, T.M.; Wu, B.I.; Pacheco, J., Jr.; Kong, J.A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E 2004, 70, 016608. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef] [PubMed]
- Dolling, G.; Enkrich, C.; Wegener, M.; Zhou, J.F.; Soukoulis, C.M.; Linden, S. Cut-wire pairs and plate pairs as magnetic atoms for optical metamaterials. Opt. Lett. 2006, 30, 3198–3200. [Google Scholar] [CrossRef]
- Gay-Balmaz, P.; Martin, O.J.F. Efficient isotropic magnetic resonators. Appl. Phys. Lett. 2002, 81, 939–941. [Google Scholar] [CrossRef]
- Mills, D.L.; Burstein, E. Polaritons: The electromagnetic modes of media. Rep. Prog. Phys. 1974, 37, 817–926. [Google Scholar] [CrossRef]
- Smith, D.R.; Padilla, W.J.; Vier, D.C.; Nemat-Nasser, S.C.; Schultz, S. Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 2000, 84, 4184. [Google Scholar] [CrossRef]
- Weiland, T.; Schuhmann, R. Ab initio numerical simulation of left-handed metamaterials: Comparison of calculations and experiments. J. Appl. Phys. 2001, 90, 5419. [Google Scholar] [CrossRef]
- Shelby, R.A.; Smith, D.; Nemat-Nasser, S.; Schultz, S. Microwave transmission through a two-dimensional, isotropic, left-handed metamaterials. Appl. Phys. Lett. 2001, 78, 489–491. [Google Scholar] [CrossRef]
- Marqués, R.; Martel, J.; Mesa, F.; Medina, F. A new 2D isotropic left-handed metamaterial design: theory and experiment. Microw. Opt. Technol. Lett. 2002, 36, 405. [Google Scholar]
- Markoš, P.; Soukoulis, C.M. Numerical studies of left-handed materials and arrays of split ring resonators. Phys. Rev. E 2002, 65, 036622. [Google Scholar] [CrossRef] [PubMed]
- Rockstuhl, C.; Zentgraf, T.; Guo, H.; Liu, N.; Etrich, C.; Loa, I.; Syassen, K.; Kuhl, J.; Lederer, F.; Giessen, H. Resonances of split-ring resonator metamaterials in the near infrared. Appl. Phys. B 2006, 84, 219–227. [Google Scholar] [CrossRef]
- Falcone, F.; Lopetegi, T.; Laso, M.A.; Baena, J.D.; Bonache, J.; Beruete, M.; Marqués, R.; Martín, F.; Sorolla, M. Babinet principle applied to the design of metasurfaces and metamaterials. Phys. Rev. Lett. 2004, 93, 197401. [Google Scholar] [CrossRef] [PubMed]
- Marqués, R.; Medina, F.; Rafii-El-Idrissi, R. Role of bianisotropy in negative permeability and left-handed metamaterials. Phys. Rev. B 2002, 65, 144440. [Google Scholar] [CrossRef]
- Katsarakis, N.; Koschny, T.; Kafesaki, M. Electric coupling to the magnetic resonance of split ring resonators. Appl. Phys. Lett. 2004, 84, 2943–2945. [Google Scholar] [CrossRef]
- Kafesaki, M.; Koschny, T.; Penciu, R.S.; Gundogdu, T.F.; Economou, E.N.; Soukoulis, C.M. Left-handed metamaterials: detailed numerical studies of the transmission properties. J. Opt. A: Pure Appl. Opt. 2005, 7, S12–S22. [Google Scholar] [CrossRef]
- Yen, T.J.; Padilla, W.J.; Fang, N.; Vier, D.C.; Smith, D.R.; Pendry, J.B.; Basov, D.N.; Zhang, X. Terahertz magnetic response from artificial materials. Science 2004, 303, 1494–1496. [Google Scholar] [CrossRef]
- Linden, S.; Enkrich, C.; Wegener, M.; Zhou, J.; Koschny, T.; Soukoulis, C.M. Magnetic response of metamaterials at 100 terahertz. Science 2004, 306, 1351–1353. [Google Scholar] [CrossRef] [PubMed]
- Klein, M.W.; Enkrich, C.; Wegener, M.; Soukoulis, C.M.; Linden, S. Single-slit split-ring resonators at optical frequencies: Limits of size scaling. Opt. Lett. 2006, 31, 1259–1261. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Koschny, T.; Kafesaki, M.; Economou, E.N.; Pendry, J.B.; Soukoulis, C.M. Saturation of the magnetic response of split-ring resonators at optical frequencies. Phys. Rev. Lett. 2005, 95, 223902. [Google Scholar] [CrossRef] [PubMed]
- Soukoulis, C.M. Magnetic response of split ring resonators at terahertz frequencies. Phys. Status Solidi B 2007, 244, 1181–1187. [Google Scholar] [CrossRef]
- Rockstuhl, C. On the reinterpretation of resonances in split-ring-resonators at normal incidence. Opt. Express 2006, 14, 8827–8836. [Google Scholar] [CrossRef] [PubMed]
- Sheridan, A.K.; Clark, A.W.; Glidle, A.; Cooper, J.M.; Cumming, D.R.S. Multiple plasmon resonances from gold nanostructures. Appl. Phys. Lett. 2007, 90, 143105. [Google Scholar] [CrossRef]
- Chen, C.Y.; Wu, S.C.; Yen, T.J. Experimental verification of standing-wave plasmonic resonances in split-ring resonators. Appl. Phys. Lett. 2008, 93, 034110. [Google Scholar] [CrossRef]
- Pdilla, W.J.; Taylor, A.J.; Highstrete, C.; Lee, M.; Averitt, R.D. Dynamical electric and magnetic metamaterial response at terahertz frequencies. Phys. Rev. Lett. 2006, 96, 107401. [Google Scholar] [CrossRef]
- Chen, H.T.; O’Hara, J.F.; Azad, A.K.; Taylor, A.J.; Averitt, R.D.; Shrekenhamer, D.B.; Padilla, W.J. Experimental demonstration of frequency-agile terahertz metamaterials. Nat. Photon. 2008, 2, 295. [Google Scholar] [CrossRef]
- Degiron, A.; Mock, J.J.; Smith, D.R. Modulating and tuning the response of metamaterials at the unit cell level. Opt. Express 2007, 15, 1115–1127. [Google Scholar] [CrossRef]
- Shadrivov, I.V.; Morrison, S.K.; Kivshar, Y.S. Tunable split-ring resonators for nonlinear negative-index metamaterials. Opt. Express 2006, 14, 9344–9349. [Google Scholar] [CrossRef] [PubMed]
- Tao, H.; Strikwerda, A.C.; Fan, K.; Padilla, W.J.; Zhang, X.; Averitt, R.D. Reconfigurable terahertz metamaterials. Phys. Rev. Lett. 2009, 103, 147401. [Google Scholar] [CrossRef] [PubMed]
- Driscoll, T.; Andreev, G.O.; Basov, D.N.; Palit, S.; Cho, S.Y.; Jokerst, N.M.; Smith, D.R. Tuned permeability in terahertz split-ring resonators for devices and sensors. Appl. Phys. Lett. 2007, 91, 062511. [Google Scholar] [CrossRef]
- Debus, C.; Bolivar, P.H. Frequency selective surfaces for high sensitivity terahertz sensing. Appl. Phys. Lett. 2007, 91, 184102. [Google Scholar] [CrossRef]
- Lahiri, B.; Khokhar, A.; De La Rue, R.; McMeekin, S.G.; Johnson, N. Asymmetric split ring resonators for optical sensing of organic materials. Opt. Express 2009, 17, 1107–1115. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C.K. Metamaterials and negative refractive index. Science 2004, 305, 788. [Google Scholar] [CrossRef] [PubMed]
- Soukoulis, C.M.; Linden, S.; Wegener, M. Negative refractive index at optical wavelengths. Science 2007, 315, 47. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X. Metamaterials: A new frontier of science and technology. Chem. Soc. Rev. 2011, 40, 2494–2507. [Google Scholar] [CrossRef]
- Shalaev, V.M.; Cai, W.; Chettiar, U.K.; Yuan, H.K.; Sarychev, A.K.; Drachev, V.P.; Kildishev, A.V. Negative index of refraction in optical metamaterials. Opt. Lett. 2005, 30, 3356–3358. [Google Scholar] [CrossRef]
- Cai, W.; Chettiar, U.K.; Yuan, H.K.; de Silva, V.C.; Kildishev, A.V.; Drachev, V.P.; Shalaev, V.M. Metamagnetics with rainbow colors. Opt. Express 2007, 15, 3333–3341. [Google Scholar] [CrossRef]
- Dolling, G.; Enkrich, C.; Wegener, M.; Soukoulis, C.M.; Linden, S. Low-loss negative-index metamaterial at telecommunication wavelengths. Opt. Lett. 2006, 31, 1800–1802. [Google Scholar] [CrossRef]
- Dolling, G.; Enkrich, C.; Wegener, M.; Soukoulis, C.M.; Linden, S. Simultaneous negative phase and group velocity of light in a metamaterial. Science 2006, 312, 892–894. [Google Scholar] [CrossRef] [PubMed]
- Dolling, G.; Enkrich, C.; Wegener, M.; Soukoulis, C.M.; Linden, S. Negative-index metamaterial at 780 nm wavelength. Opt. Lett. 2007, 32, 53–55. [Google Scholar] [CrossRef]
- Valentine, J.; Zhang, S.; Zentgraf, T.; Ulin-Avila, E.; Genov, D.A.; Bartal, G.; Zhang, X. Three-dimensional optical metamaterial with a negative refractive index. Nature 2008, 455, 376–379. [Google Scholar] [CrossRef]
- Zhang, S.; Fan, W.; Malloy, K.J.; Brueck, S.R.; Panoiu, N.C.; Osgood, R.M. Near-infrared double negative metamaterials. Opt. Express 2005, 13, 4922–4930. [Google Scholar] [CrossRef] [PubMed]
- Lezec, H.J.; Dionne, J.A.; Atwater, H.A. Negative refraction at visible frequencies. Science 2007, 316, 430–432. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Liu, Z.; Liu, Y.; Wang, Y.; Sun, C.; Bartal, G.; Stacy, A.M.; Zhang, X. Optical negative refraction in bulk metamaterials of nanowires. Science 2008, 321, 930. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, S.; Pendry, J.B. Photonic band-gap effects and magnetic activity in dielectric composites. J. Phys. Condens. Matter. 2002, 14, 4035–4044. [Google Scholar] [CrossRef]
- Merlin, R. Metamaterials and the Landau-Lifshitz permeability argument: Large permittivity begets high-frequency magnetism. Proc. Natl. Acad. Sci.USA 2009, 106, 1693–1698. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler. Metallösungen. Ann. Phys. 1908, 25, 377–445. [Google Scholar]
- Wheeler, M.S.; Aitchison, J.S.; Mojahedi, M. Three-dimensional array of dielectric spheres with an isotropic negative permeability at infrared frequencies. Phys. Rev. B 2005, 72, 193103. [Google Scholar] [CrossRef]
- Shvets, G.; Urzhumov, Y.A. Engineering the electromagnetic properties of periodic nanostructures using electrostatic resonances. Phys. Rev. Lett. 2004, 93, 243902. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley and Sons Inc.: New York, NY, USA, 1999. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 7th ed.; John Wiley and Sons Inc.: New York, NY, USA, 1996. [Google Scholar]
- Felbacq, D.; Bouchitté, G. Theory of mesoscopic magnetism in photonic crystals. Phys. Rev. Lett. 2005, 94, 183902. [Google Scholar] [CrossRef] [PubMed]
- Peng, L.; Ran, L.; Chen, H.; Zhang, H.; Kong, J.A.; Grzegorczyk, T.M. Experimental observation of left-handed behavior in an array of standard dielectric resonators. Phys. Rev. Lett. 2007, 98, 157403. [Google Scholar] [CrossRef]
- Schuller, J.A.; Zia, R.; Taubner, T.; Brongersma, M.L. Dielectric metamaterials based on electric and magnetic resonances of silicon carbide particles. Phys. Rev. Lett. 2007, 99, 107401. [Google Scholar] [CrossRef]
- Ahmadi, A.; Mosallaei, H. Physical configuration and performance modeling of all-dielectric metamaterials. Phys. Rev. B 2008, 77, 045104. [Google Scholar] [CrossRef]
- Ma, Y.G.; Zhao, L.; Wang, P.; Ong, C.K. Fabrication of negative index materials using dielectric and metallic composite route. Appl. Phys. Lett. 2008, 93, 184103. [Google Scholar] [CrossRef]
- Vendik, O.G.; Gashinova, M.S. Artificial double negative (DNG) media composed by two different dielectric sphere lattices embedded in a dielectric matrix. Proc. Eur. Microw. Conf. 2004, 34, 1209–1212. [Google Scholar]
- Lepetit, T.; Akmansoy, E.; Ganne, J.P. Experimental measurement of negative index in an all-dielectric metamaterial. Appl. Phys. Lett. 2009, 95, 121101. [Google Scholar] [CrossRef]
- Vendik, I.; Odit, M.; Kozlov, D. 3D metamaterials based on a regular array of resonant dielectric inclusions. Radioengineering 2009, 18, 111–116. [Google Scholar]
- Zhao, Q.; Kang, L.; Du, B.; Zhao, H.; Xie, Q.; Huang, X.; Li, B.; Zhou, J.; Li, L. Experimental demonstration of isotropic negative permeability in a three-dimensional dielectric composite. Phys. Rev. Lett. 2008, 101, 027402. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Du, B.; Kang, L.; Zhao, H.J.; Xie, Q.; Li, B.; Zhang, X.; Zhou, J.; Li, L.T.; Meng, Y.G. Tunable negative permeability in an isotropic dielectric composite. Appl. Phys. Lett. 2008, 92, 051106. [Google Scholar] [CrossRef]
- Vynck, K.; Felbacq, D.; Centeno, E.; Căbuz, A.I.; Cassagne, D.; Guizal, B. All-dielectric rod-type metamaterials at optical frequencies. Phys. Rev. Lett. 2009, 102, 133901. [Google Scholar] [CrossRef] [PubMed]
- Gaillot, D.P.; Croënne, C.; Lippens, D. An all-dielectric route for terahertz cloaking. Opt. Express 2008, 16, 3986–3992. [Google Scholar] [CrossRef] [PubMed]
- Fedotov, V.A.; Mladyonov, P.L.; Prosvirnin, S.L.; Zheludev, N.I. Planar electromagnetic metamaterial with a fish scale structure. Phys. Rev. E 2005, 72, 036603. [Google Scholar] [CrossRef] [PubMed]
- Fedotov, V.A.; Rogacheva, A.V.; Prosvirnin, S.L.; Mladyonov, P.L.; Zheludev, N.I. Mirror that does not change the phase of reflected waves. Appl. Phys. Lett. 2006, 88, 091119. [Google Scholar] [CrossRef]
- Powell, C.J.; Swan, J.B. Effect of oxidation on the characteristic loss spectra of aluminium and magnesium. Phys. Rev. 1960, 118640, 643. [Google Scholar]
- Sanders, R.W.; Belanger, R.M.; Motokawa, M.; Jaccarino, V.; Rezende, S.M. Far-infrared laser study of magnetic polaritons in FeF2 and Mn impurity mode in FeF2:Mn. Phys. Rev. B 1981, 23, 1190. [Google Scholar] [CrossRef]
- Remer, L.; Lüthi, B.; Sauer, H.; Geick, R.; Camley, R.E. Nonreciprocal optical reflection of the uniaxial antiferromagnet MnF2. Phys. Rev. Lett. 1986, 56, 2752. [Google Scholar] [CrossRef]
- Liu, H.; Genov, D.A.; Wu, D.M.; Liu, Y.M.; Steele, J.M.; Sun, C.; Zhu, S.N.; Zhang, X. Magnetic plasmon propagation along a chain of connected subwavelength resonators at infrared frequencies. Phys. Rev. Lett. 2007, 97, 243902. [Google Scholar] [CrossRef]
- Linden, S.; Decker, M.; Wegener, M. Model system for a one-dimensional magnetic photonic crystal. Phys. Rev. Lett. 2006, 97, 083902. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.M.; Li, T.; Liu, H.; Wang, F.M.; Zhu, S.N.; Zhang, X. Magnetic plasmon modes in periodic chains of nanosandwiches. Opt. Express 2008, 16, 3560. [Google Scholar] [CrossRef] [PubMed]
- Gollub, J.N.; Smith, D.R.; Vier, D.C.; Perram, T.; Mock, J.J. Experimental characterization of magnetic surface plasmons on metamaterials with negative permeability. Phys. Rev. B 2005, 71, 195402. [Google Scholar] [CrossRef]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Ji, C.; Mock, J.J.; Chin, J.Y.; Cui, T.J.; Smith, D.R. Broadband ground-plane cloak. Science 2009, 323, 366–369. [Google Scholar] [CrossRef] [PubMed]
- Ergin, T.; Stenger, N.; Brenner, P.; Pendry, J.B.; Wegener, M. Three-dimensional invisibility cloak at optical wavelengths. Science 2010, 328, 337–339. [Google Scholar] [CrossRef]
- Lai, Y.; Chen, H.Y.; Zhang, Z.Q.; Chan, C.T. Complementary media invisibility cloak that cloaks objects at a distance outside the cloaking shell. Phys. Rev. Lett. 2009, 102, 093091. [Google Scholar] [CrossRef]
- Lai, Y.; Ng, J.; Chen, H.Y.; Han, D.Z.; Xiao, J.J.; Zhang, Z.Q.; Chan, C.T. Illusion optics: The optical transformation of an object into another object. Phys. Rev. Lett. 2009, 102, 253902. [Google Scholar] [CrossRef]
- Lukin, M.D.; Imamoglu, A. Controlling photons using electromagnetically induced transparency. Nature 2001, 413, 273–276. [Google Scholar] [CrossRef]
- Zhao, X.P.; Luo, W.; Huang, J.X.; Fu, Q.H.; Song, K.; Cheng, X.C.; Luo, C.R. Trapped rainbow effect in visible light left-handed heterostructures. Appl. Phys. Lett. 2009, 95, 071111–071113. [Google Scholar] [CrossRef]
- Zhang, S.; Genov, D.A.; Wang, Y.; Liu, M.; Zhang, X. Plasmon-induced transparency in metamaterials. Phys. Rev. Lett. 2008, 101, 047401. [Google Scholar] [CrossRef]
- Liu, N.; Langguth, L.; Weiss, T.; Kästel, J.; Fleischhauer, M.; Pfau, T.; Giessen, H. Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit. Nat. Mater. 2009, 8, 758–762. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Weiss, T.; Mesch, M.; Langguth, L.; Eigenthaler, U.; Hirscher, M.; Sönnichsen, C.; Giessen, H. Plasmonic metamaterial analogue of electromagnetically induced transparency for plasmonic sensing. Nano Lett. 2010, 10, 1103–1107. [Google Scholar] [CrossRef] [PubMed]
- Tsakmakidis, K.L.; Hermann, C.; Klaedtke, A.; Jamois, C.; Hess, O. Surface plasmon polaritons in generalized slab heterostructures with negative permittivity and permeability. Phys. Rev. B 2006, 73, 085104. [Google Scholar] [CrossRef]
- Lu, W.T.; Savo, S.; Casse, B.D.F.; Sridhar, S. Slow microwave waveguide made of negative permeability metamaterials. Microw. Opt. Tech. Lett. 2009, 51, 2705–2709. [Google Scholar] [CrossRef]
- Tsakmakidis, K.L.; Klaedtke, A.; Aryal, D.P.; Jamois, C.; Hess, O. Single-mode operation in the slow-light regime using oscillatory waves in generalized left-handed heterostructures. Appl. Phys. Lett. 2006, 89, 201103. [Google Scholar] [CrossRef]
- Rawal, S.; Sinha, R.K.; De La Rue, R.M. Slow light miniature devices with ultra-flattened dispersion in silicon-on-insulator photonic crystal. Opt. Express 2009, 17, 13315–13325. [Google Scholar] [CrossRef]
- Oskooi, A.F.; Joannopoulos, J.D.; Johnson, S.G. Zero-group-velocity modes in chalcogenide holey photonic-crystal fibers. Opt. Express 2009, 17, 10082–10090. [Google Scholar] [CrossRef]
- Vukovic, S.M.; Aleksic, N.B.; Timotijevic, D.V. Guided modes in left-handed waveguides. Opt. Commun. 2008, 281, 1500–1509. [Google Scholar] [CrossRef]
- Lai, H.M.; Kwok, C.W.; Loo, Y.W.; Xu, B.Y. Energy-flux pattern in the Goos-Hanchen effect. Phys. Rev. E 2000, 62, 7330–7339. [Google Scholar] [CrossRef]
- Berman, P.R. Goos-Hanchen shift in negatively refractive media. Phys. Rev. E 2002, 66, 3. [Google Scholar] [CrossRef] [PubMed]
- Gan, Q.Q.; Ding, Y.J.; Bartoli, F.J. “Rainbow” trapping and releasing at telecommunication wavelengths. Phys. Rev. Lett. 2009, 102, 4. [Google Scholar] [CrossRef] [PubMed]



© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lai, Y.-C.; Chen, C.-K.; Huang, T.-Y.; Un, I.-W.; Yang, Y.-H.; Yen, T.-J. Enriching the Symmetry of Maxwell Equations through Unprecedented Magnetic Responses of Artificial Metamaterials and Their Revolutionary Applications. Symmetry 2011, 3, 283-304. https://doi.org/10.3390/sym3020283
Lai Y-C, Chen C-K, Huang T-Y, Un I-W, Yang Y-H, Yen T-J. Enriching the Symmetry of Maxwell Equations through Unprecedented Magnetic Responses of Artificial Metamaterials and Their Revolutionary Applications. Symmetry. 2011; 3(2):283-304. https://doi.org/10.3390/sym3020283
Chicago/Turabian StyleLai, Yueh-Chun, Cheng-Kuang Chen, Tsung-Yu Huang, Ieng-Wai Un, Yu-Hang Yang, and Ta-Jen Yen. 2011. "Enriching the Symmetry of Maxwell Equations through Unprecedented Magnetic Responses of Artificial Metamaterials and Their Revolutionary Applications" Symmetry 3, no. 2: 283-304. https://doi.org/10.3390/sym3020283
APA StyleLai, Y.-C., Chen, C.-K., Huang, T.-Y., Un, I.-W., Yang, Y.-H., & Yen, T.-J. (2011). Enriching the Symmetry of Maxwell Equations through Unprecedented Magnetic Responses of Artificial Metamaterials and Their Revolutionary Applications. Symmetry, 3(2), 283-304. https://doi.org/10.3390/sym3020283



