The Influence of Perception on the Distribution of Multiple Symmetries in Nature and Art
Abstract
:1. Introduction
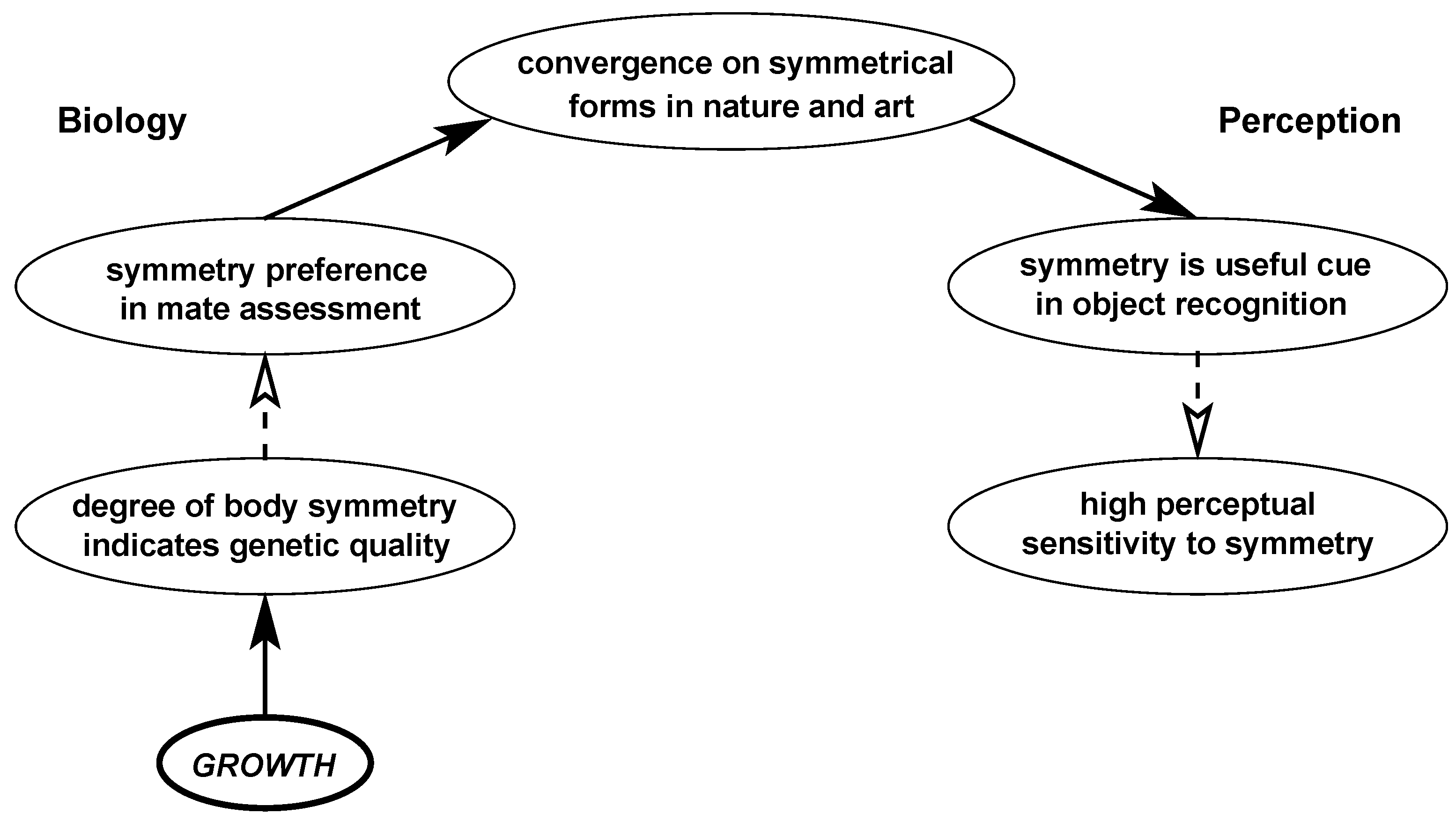
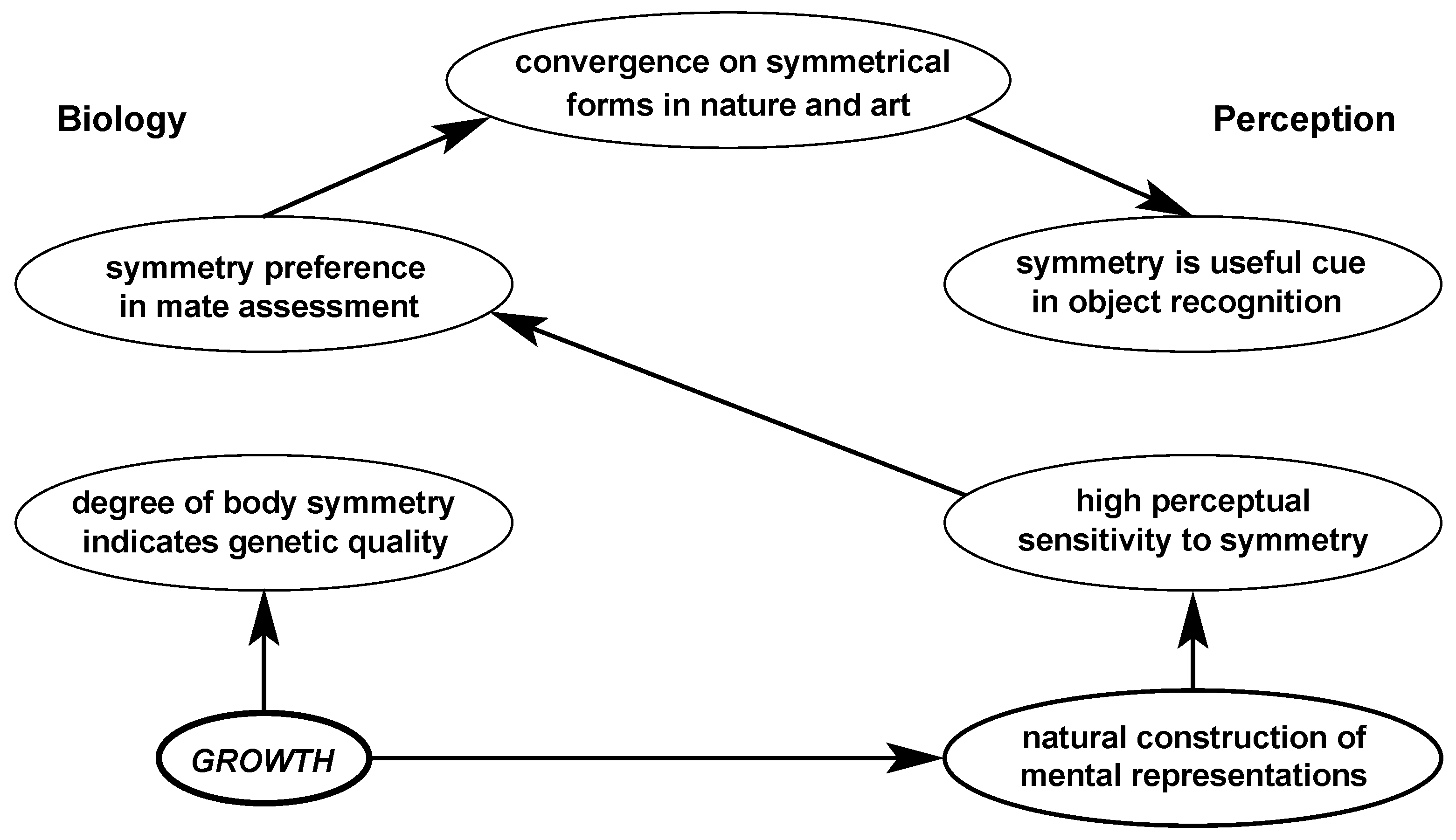
2. Evolutionary Considerations
3. Multiple Symmetry in Nature and Art
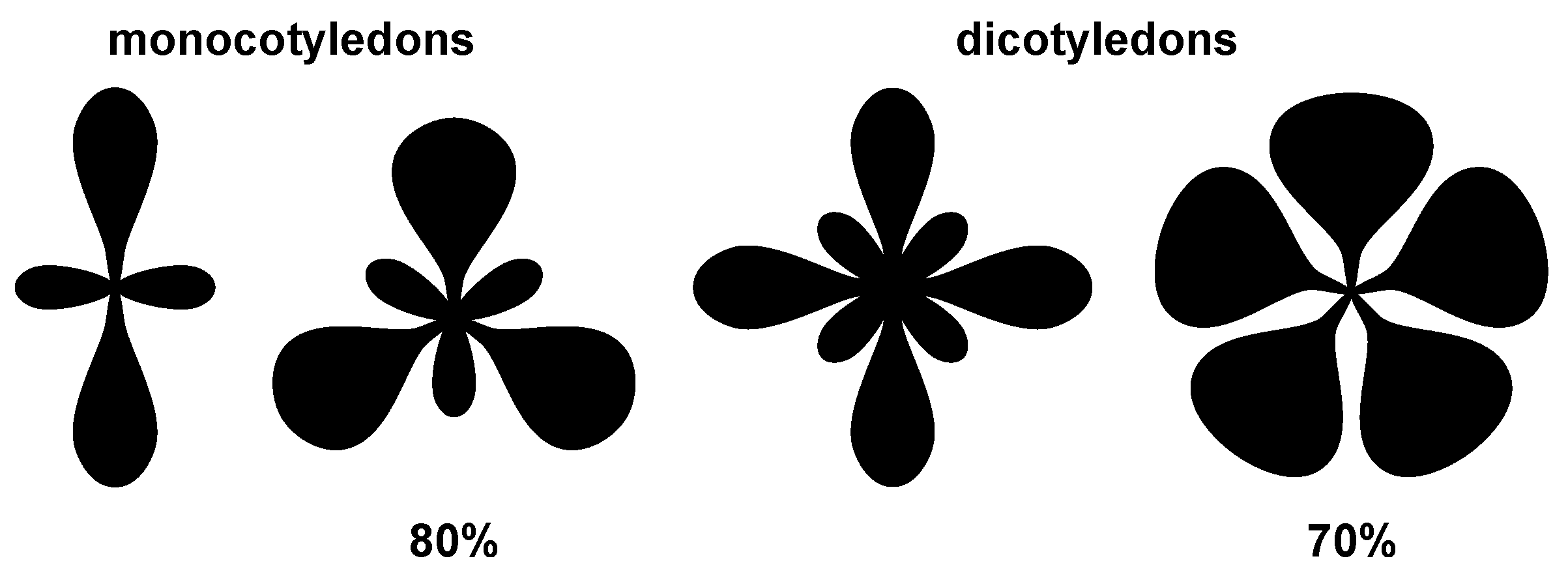
3.1. Flowers
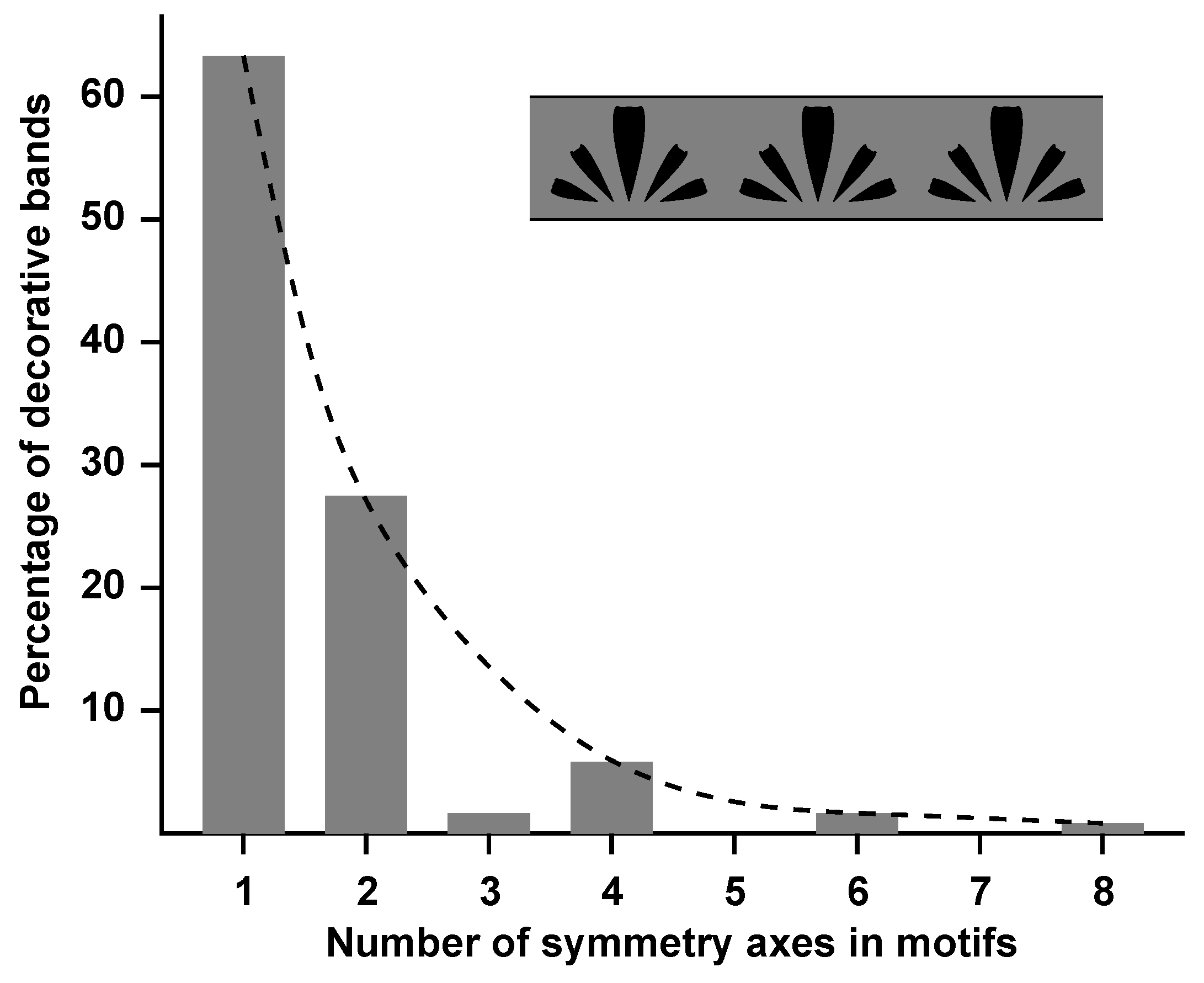
3.2. Human Designs
4. Models of Human Symmetry Perception
4.1. The Transformational Approach
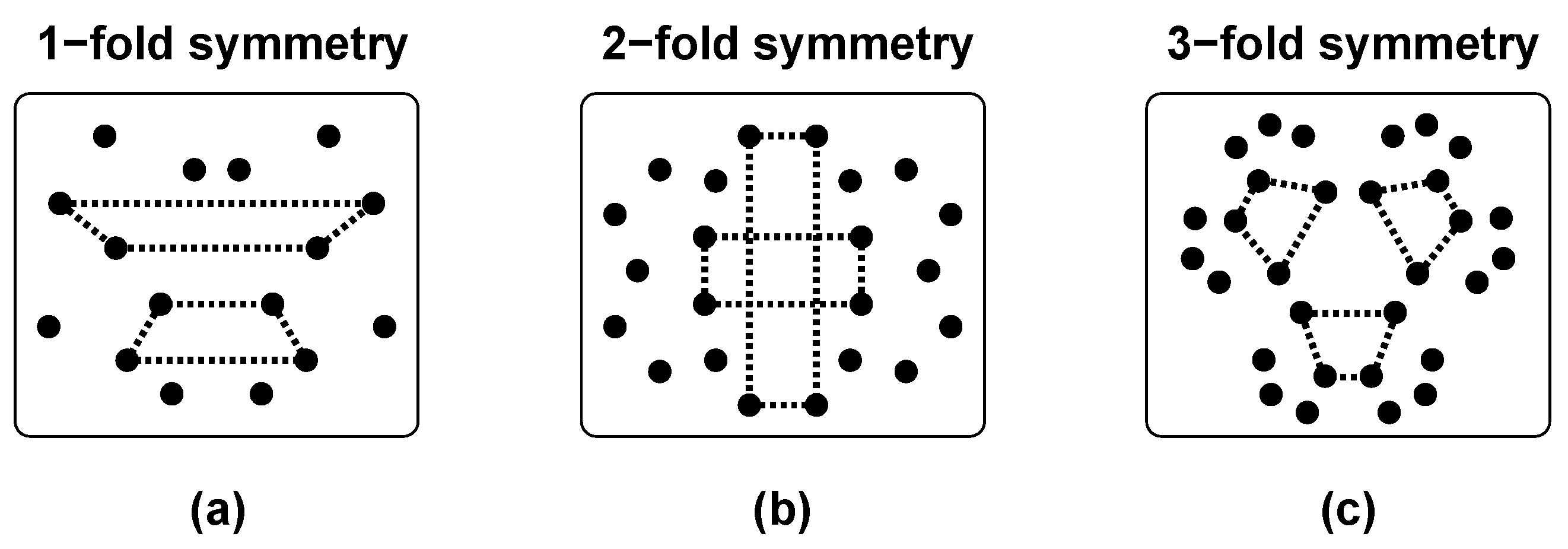
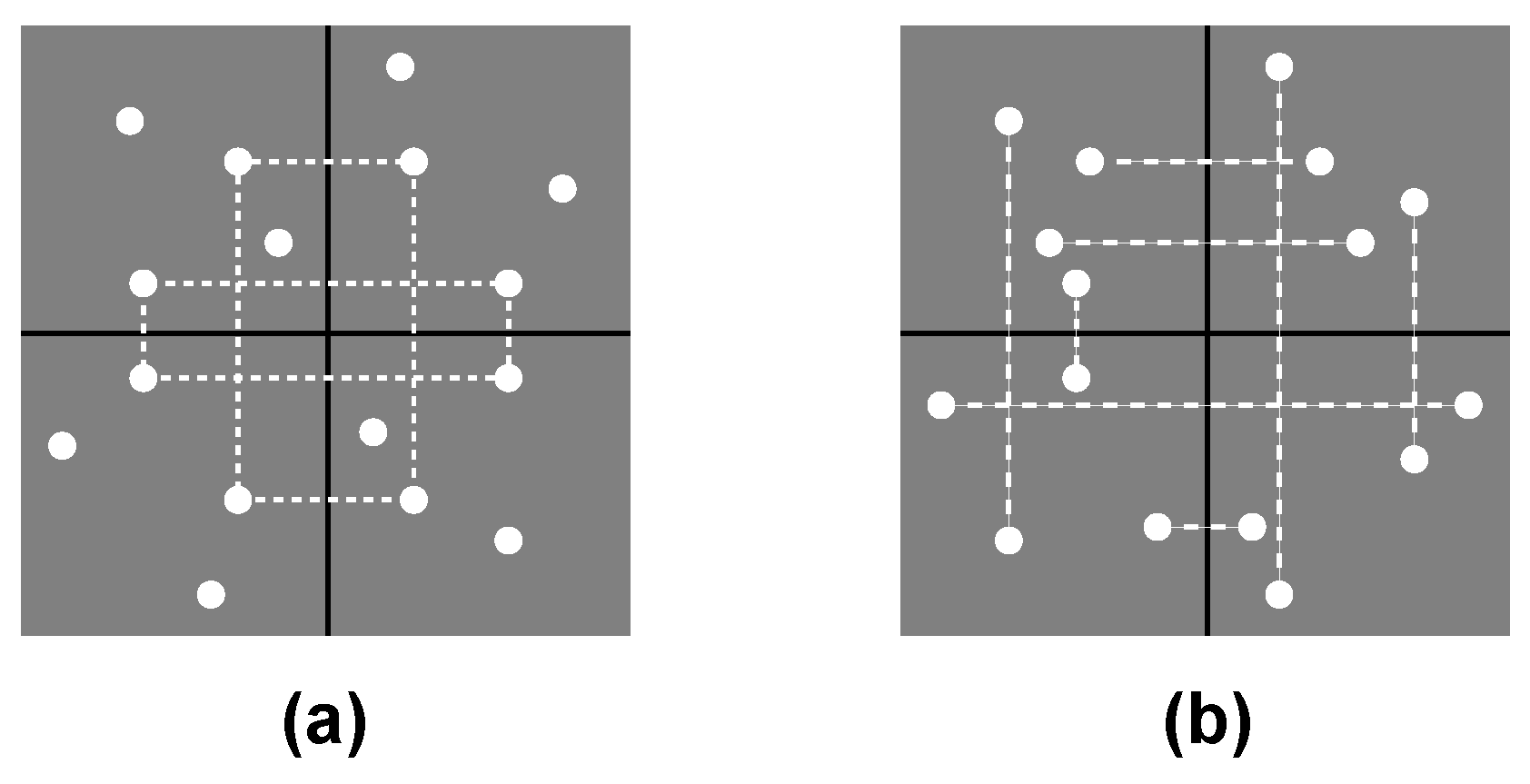
4.2. The Bootstrap Model
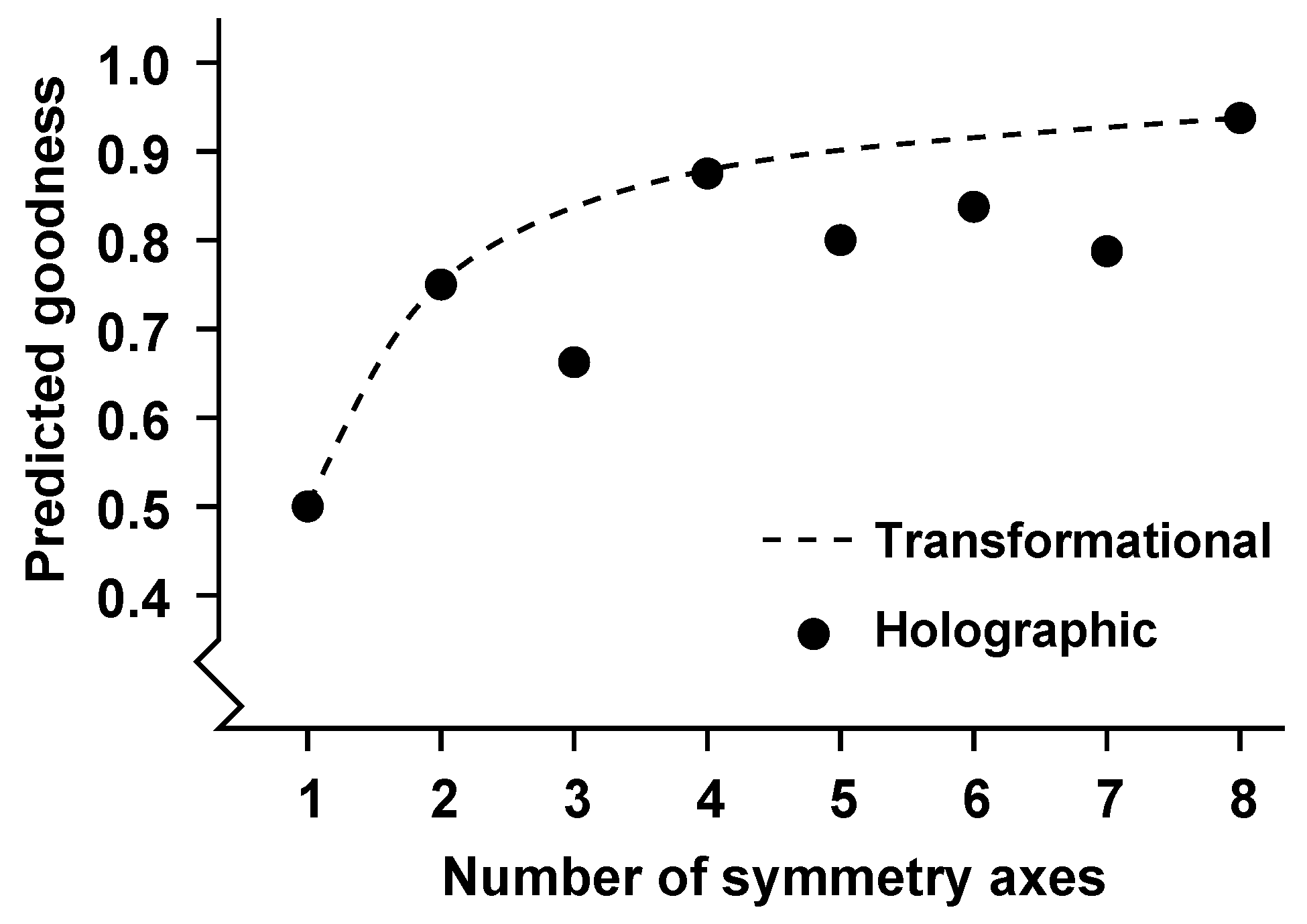
4.3. The Holographic Approach
5. Multiple Symmetry Perception
6. Discussion and Conclusions
References
- Allen, G. The origin of the sense of symmetry. Mind 1879, 4, 301–316. [Google Scholar] [CrossRef]
- Hargittai, I. Symmetry: Unifying Human Understanding; Pergamon: New York, NY, USA, 1986. [Google Scholar]
- Shubnikov, A.V.; Koptsik, V.A. Symmetry in Science and Art; Plenum: New York, NY, USA, 1974. [Google Scholar]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Grammer, K.; Thornhill, R. Human (Homo sapiens) facial attractiveness and sexual selection: The role of symmetry and averageness. J. Comp. Psychol. 1994, 108, 233–242. [Google Scholar] [CrossRef] [PubMed]
- Johnstone, R.A. Female preferences for symmetrical males as a by-product of selection for mate recognition. Nature 1994, 372, 172–175. [Google Scholar] [CrossRef] [PubMed]
- Møller, A.P. Female swallow preference for symmetrical male sexual ornaments. Nature 1992, 357, 238–240. [Google Scholar] [CrossRef] [PubMed]
- Møller, A.P. Bumblebee preference for symmetrical flowers. Proc. Natl. Acad. Sci. USA 1995, 92, 2288–2292. [Google Scholar] [CrossRef] [PubMed]
- Swaddle, J.; Cuthill, I.C. Preference for symmetric males by female zebra finches. Nature 1993, 367, 165–166. [Google Scholar] [CrossRef]
- Thornhill, R.; Gangestad, S.W. Human fluctuating asymmetry and sexual behavior. Psychol. Sci. 1994, 5, 297–302. [Google Scholar] [CrossRef]
- Watson, P.J.; Thornhill, R. Fluctuating asymmetry and sexual selection. Trend. in Ecol. Evolut. 1994, 9, 21–25. [Google Scholar] [CrossRef]
- Pashler, H. Coordinate frame for symmetry detection and object recognition. J. Exp. Psychol. Hum. Percept. Perform. 1990, 16, 150–163. [Google Scholar] [CrossRef]
- Vetter, T.; Poggio, T. Symmetric 3D objects are an easy case for 2D object recognition. Spatial Vision 1994, 8, 443–453. [Google Scholar]
- Driver, J.; Baylis, G.C.; Rafal, R.D. Preserved figure-ground segregation and symmetry perception in visual neglect. Nature 1992, 360, 73–75. [Google Scholar] [CrossRef] [PubMed]
- Leeuwenberg, E.L.J.; Buffart, H.F.J.M. The perception of foreground and background as derived from structural information theory. Acta Psychol. 1984, 55, 249–272. [Google Scholar] [CrossRef]
- Machilsen, B.; Pauwels, M.; Wagemans, J. The role of vertical mirror symmetry in visual shape detection. J. Vision 2009, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Kanizsa, G. Seeing and thinking. Acta Psychol. 1985, 59, 23–33. [Google Scholar] [CrossRef]
- van Lier, R.J.; van der Helm, P.A.; Leeuwenberg, E.L.J. Competing global and local completions in visual occlusion. J. Exp. Psychol. Hum. Percept. Perform. 1995, 21, 571–583. [Google Scholar] [CrossRef] [PubMed]
- Treder, M.S. Behind the looking-glass: A review on human symmetry perception. Symmetry 2010, 2, 1510–1543. [Google Scholar] [CrossRef]
- Tyler, C.W. Human Symmetry Perception and Its Computational Analysis; Tyler, C.W., Ed.; VSP: Zeist, The Netherlands, 1996; pp. 3–22. [Google Scholar]
- van der Helm, P.A.; Leeuwenberg, E.L.J. Goodness of visual regularities: A nontransformational approach. Psychol. Rev. 1996, 103, 429–456. [Google Scholar] [CrossRef]
- Wagemans, J. Characteristics and models of human symmetry detection. Trends Cogn. Sci. 1997, 1, 346–352. [Google Scholar] [CrossRef]
- Barlow, H.B.; Reeves, B.C. The versatility and absolute efficiency of detecting mirror symmetry in random dot displays. Vision Res. 1979, 19, 783–793. [Google Scholar] [CrossRef]
- Giurfa, M.; Eichmann, B.; Menzel, R. Symmetry perception in an insect. Nature 1996, 382, 458–461. [Google Scholar] [CrossRef]
- Horridge, G.A. The honeybee (Apis mellifera) detects bilateral symmetry and discriminates its axis. J. Insect Physiol. 1996, 42, 755–764. [Google Scholar] [CrossRef]
- van der Helm, P.A. Weber-Fechner behaviour in symmetry perception? Atten. Percept. Psychophys. 2010, 72, 1854–1864. [Google Scholar] [CrossRef] [PubMed]
- Møller, A.P. Fluctuating asymmetry in male sexual ornaments may reliably reveal male quality. Anim. Behav. 1990, 40, 1185–1187. [Google Scholar] [CrossRef]
- Thompson, D.W. On Growth and Form; University Press: Cambridge, UK, 1942; (Original work published 1917). [Google Scholar]
- Enquist, M.; Arak, A. Symmetry, beauty and evolution. Nature 1994, 372, 169–172. [Google Scholar] [CrossRef] [PubMed]
- Heywood, V.H. Flowering Plants of the World; Batsford: London, UK, 1993. [Google Scholar]
- Endress, P.K. Floral phyllotaxis and floral evolution. Bot. Jahrb. 1987, 108, 417–438. [Google Scholar]
- Giurfa, M.; Dafni, A.; Neal, P.R. Floral symmetry and its role in plant-pollinator systems. Int. J. Plant Sci. 1999, 160, S41–S50. [Google Scholar] [CrossRef] [PubMed]
- Neal, P.R.; Dafni, A.; Giurfa, M. Floral symmetry and its role in plant-pollinator systems: Terminology, Distribution, and Hypotheses. Annu. Rev. Ecol. Syst. 1998, 29, 345–373. [Google Scholar] [CrossRef]
- Horridge, G.A. Visual discrimination of radial cues by the honeybee (Apis mellifera). J. Insect Physiol. 2000, 46, 629–645. [Google Scholar] [CrossRef]
- Washburn, D.K.; Crowe, D.W. Symmetries of Culture: Theory and Practice of Plane Pattern Analysis; University of Washington Press: Seattle, WA, USA, 1988. [Google Scholar]
- Wynn, T. Archaeology and cognitive evolution. Behav. Brain Sci. 2002, 25, 389–402, 432–438. [Google Scholar] [CrossRef]
- Hardonk, M. Cross-cultural Universals of Aesthetic Appreciation in Decorative Band Patterns. Ph.D. Thesis, Radboud University, Nijmegen, The Netherlands, 1999. [Google Scholar]
- Forstner, D. Die Welt der Symbole; Tyriola Verlag: Innsbruck, 1961. [Google Scholar]
- Labat, R. Manuel D’épigraphie Akkadienne: Signes, Syllabaire, Idéogrammes, 6th ed.; Imprimerie Nationale: Paris, France, 1988. [Google Scholar]
- Boselie, F. The golden section and the shape of objects. Empir. Stud. Arts. 1997, 15, 131–141. [Google Scholar] [CrossRef]
- Garner, W.R. The Processing of Information and Structure; Erlbaum: Potomac, MD, USA, 1974. [Google Scholar]
- Palmer, S.E. Human and Machine Vision; Beck, J., Hope, B., Rosenfeld, A., Eds.; Academic Press: New York, NY, USA, 1983; pp. 269–339. [Google Scholar]
- Palmer, S.E.; Hemenway, K. Orientation and symmetry: Effects of multiple, rotational, and near symmetries. J. Exp. Psychol. Hum. Percept. Perform. 1978, 4, 691–702. [Google Scholar] [CrossRef] [PubMed]
- Royer, F.L. Detection of symmetry. J. Exp. Psychol. Hum. Percept. Perform. 1981, 7, 1186–1210. [Google Scholar] [CrossRef] [PubMed]
- Wagemans, J.; van Gool, L.; Swinnen, V.; van Horebeek, J. Higher-order structure in regularity detection. Vision Res. 1993, 33, 1067–1088. [Google Scholar] [CrossRef]
- Viola, C.M. Grundzüge der Kristallographie; W. Engelman: Leipzig, Germany, 1904. [Google Scholar]
- Jenkins, B. Component processes in the perception of bilaterally symmetric dot textures. Percept. Psychophys. 1983, 34, 433–440. [Google Scholar] [CrossRef] [PubMed]
- Wagemans, J.; van Gool, L.; d’Ydewalle, G. Detection of symmetry in tachistoscopically presented dot patterns: Effects of multiple axes and skewing. Percept. Psychophys. 1991, 50, 413–427. [Google Scholar] [CrossRef] [PubMed]
- van der Helm, P.A.; Leeuwenberg, E.L.J. A better approach to goodness: Reply to Wagemans (1999). Psychol. Rev. 1999, 106, 622–630. [Google Scholar] [CrossRef]
- Treder, M.S.; van der Vloed, G.; van der Helm, P.A. Interactions between constituent single symmetries in multiple symmetry. Atten. Percept. Psychophys. 2011. In Press. [Google Scholar] [CrossRef]
- van der Helm, P.A.; Leeuwenberg, E.L.J. Holographic goodness is not that bad: Reply to Olivers, Chater, and Watson (2004). Psychol. Rev. 2004, 111, 261–273. [Google Scholar] [CrossRef]
- van der Vloed, G.; Csathó, Á.; van der Helm, P.A. Symmetry and repetition in perspective. Acta Psychol. 2005, 120, 74–92. [Google Scholar] [CrossRef]
- van der Helm, P.A.; Leeuwenberg, E.L.J. Accessibility, a criterion for regularity and hierarchy in visual pattern codes. J. Math. Psychol. 1991, 35, 151–213. [Google Scholar] [CrossRef]
- van der Helm, P.A.; Treder, M.S. Detection of (anti)symmetry and (anti)repetition: Perceptual mechanisms versus cognitive strategies. Vision Res. 2009, 49, 2754–2763. [Google Scholar] [CrossRef] [PubMed]
- Treder, M.S.; van der Helm, P.A. Symmetry versus repetition in cyclopean vision: A microgenetic analysis. Vision Res. 2007, 47, 2956–2967. [Google Scholar] [CrossRef] [PubMed]
- Csathó, Á.; van der Vloed, G.; van der Helm, P.A. Blobs strengthen repetition but weaken symmetry. Vision Res. 2003, 43, 993–1007. [Google Scholar] [CrossRef]
- Csathó, Á.; van der Vloed, G.; van der Helm, P.A. The force of symmetry revisited: Symmetry-to-noise ratios regulate (a)symmetry effects. Acta Psychol. 2004, 117, 233–250. [Google Scholar] [CrossRef] [PubMed]
- Attneave, F. Some informational aspects of visual perception. Psychol. Rev. 1954, 61, 183–193. [Google Scholar] [CrossRef] [PubMed]
- Attneave, F. Symmetry, information, and memory for patterns. Am. J. Psychol. 1955, 68, 209–222. [Google Scholar] [CrossRef] [PubMed]
- Barlow, H.B. Current Problems in Animal Behaviour; Thorpe, W.H., Zangwill, O.L., Eds.; Cambridge University Press: Cambridge, UK, 1961; pp. 331–360. [Google Scholar]
- Barlow, H. The exploitation of regularities in the environment by the brain. Behav. Brain. Sci. 2001, 24, 602–607, 652–671. [Google Scholar] [CrossRef]
- Leeuwenberg, E.L.J. Quantitative specification of information in sequential patterns. Psychol. Rev. 1969, 76, 216–220. [Google Scholar] [CrossRef]
- Leeuwenberg, E.L.J. A perceptual coding language for visual and auditory patterns. Amer. J. Psychol. 1971, 84, 307–349. [Google Scholar] [CrossRef]
- Nucci, M.; Wagemans, J. Goodness of regularity in dot patterns: global symmetry, local symmetry, and their interactions. Perception 2007, 36, 1305–1319. [Google Scholar] [CrossRef]
- Hamada, J.; Ishihara, T. Complexity and goodness of dot patterns varying in symmetry. Psychol. Res. 1988, 50, 155–161. [Google Scholar] [CrossRef] [PubMed]
- Wenderoth, P.; Welsh, S. Effects of pattern orientation and number of symmetry axes on the detection of mirror symmetry in dot and solid patterns. Perception 1998, 27, 965–976. [Google Scholar] [CrossRef] [PubMed]
- van der Vloed, G. The Structure of Visual Regularities. Ph.D. Thesis, Radboud University, Nijmegen, The Netherlands, 2005. [Google Scholar]
- Beh, H.C.; Latimer, C.R. Symmetry detection and orientation perception: Electrocortical responses to stimuli with real and implicit axes of orientation. Aust. J. Psychol. 1997, 49, 128–133. [Google Scholar] [CrossRef]
- Gurnsey, R.; Herbert, A.M.; Kenemy, J. Bilateral symmetry embedded in noise is detected accurately only at fixation. Vision Res. 1998, 38, 3795–3803. [Google Scholar] [CrossRef]
- Lee, T.S.; Mumford, D.; Romero, R.; Lamme, V.A.F. The role of the primary visual cortex in higher level vision. Vision Res. 1998, 38, 2429–2454. [Google Scholar] [CrossRef]
- Sally, S.; Gurnsey, R. Symmetry detection across the visual field. Spatial Vision 2001, 14, 217–234. [Google Scholar] [PubMed]
- Joung, W.; Latimer, C. Tilt aftereffects generated by symmetrical dot patterns with two or four axes of symmetry. Spatial Vision 2003, 16, 155–182. [Google Scholar] [CrossRef]
- Joung, W.; van der Zwan, R.; Latimer, C.R. Tilt aftereffects generated by bilaterally symmetrical patterns. Spatial Vision 2000, 13, 107–128. [Google Scholar]
- van der Zwan, R.; Leo, E.; Joung, W.; Latimer, C.; Wenderoth, P. Evidence that both area V1 and extrastriate visual cortex contribute to symmetry perception. Curr. Biol. 1998, 8, 889–892. [Google Scholar] [CrossRef]
- Koffka, K. Principles of Gestalt Psychology; Routledge & Kegan Paul: London, UK, 1935. [Google Scholar]
- van der Helm, P.A. Simplicity versus likelihood in visual perception: From surprisals to precisals. Psychol. Bull. 2000, 126, 770–800. [Google Scholar] [CrossRef]
- Birkhoff, G.D. Aesthetic Measure; Harvard University Press: Cambridge, MA, UK, 1933. [Google Scholar]
- Boselie, F.; Leeuwenberg, E.L.J. Birkhoff revisited: Beauty as a function of effect and means. Amer. J. Psychol. 1985, 98, 1–39. [Google Scholar] [CrossRef] [PubMed]
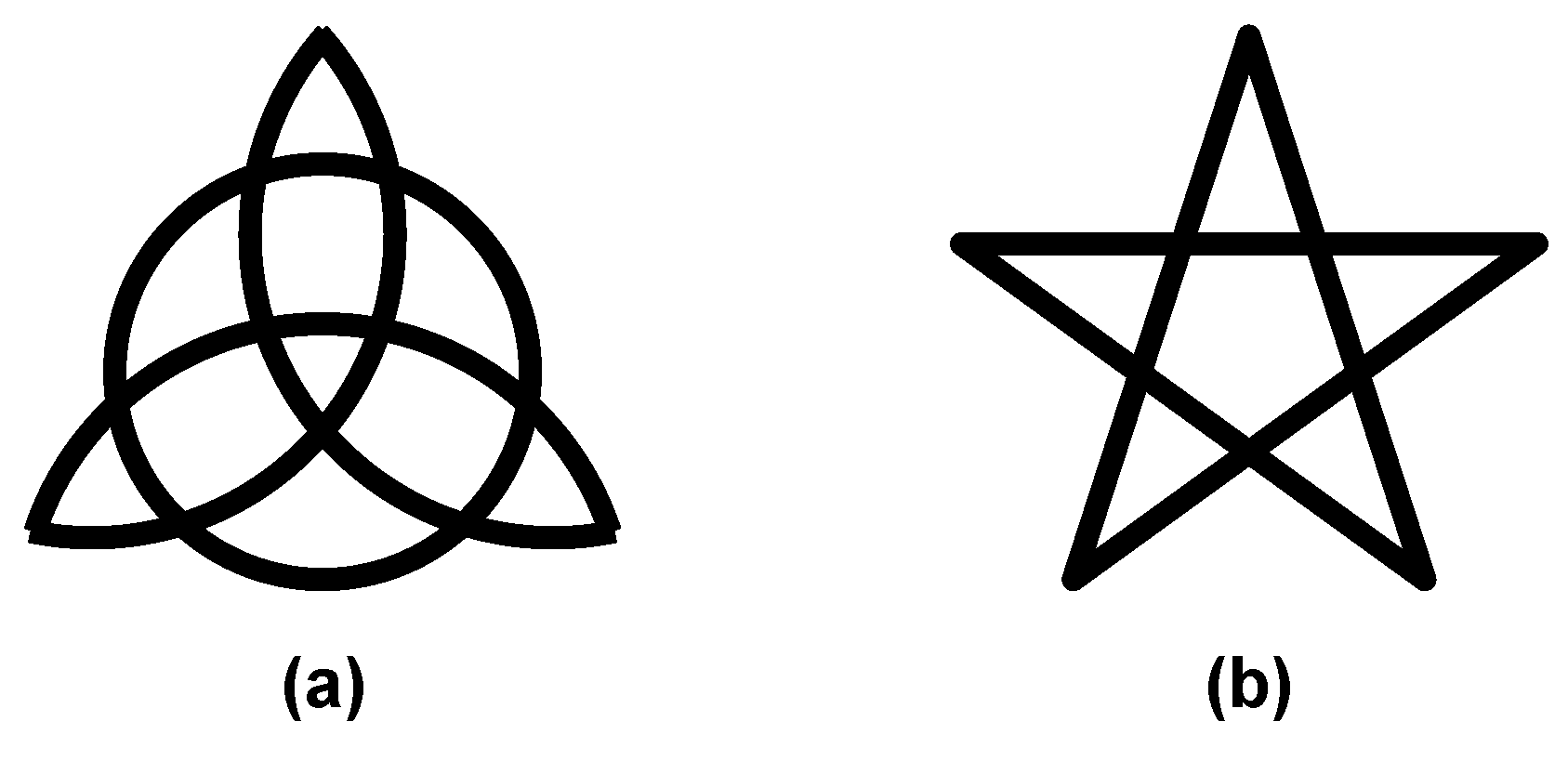




© 2011 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Van der Helm, P.A. The Influence of Perception on the Distribution of Multiple Symmetries in Nature and Art. Symmetry 2011, 3, 54-71. https://doi.org/10.3390/sym3010054
Van der Helm PA. The Influence of Perception on the Distribution of Multiple Symmetries in Nature and Art. Symmetry. 2011; 3(1):54-71. https://doi.org/10.3390/sym3010054
Chicago/Turabian StyleVan der Helm, Peter A. 2011. "The Influence of Perception on the Distribution of Multiple Symmetries in Nature and Art" Symmetry 3, no. 1: 54-71. https://doi.org/10.3390/sym3010054
APA StyleVan der Helm, P. A. (2011). The Influence of Perception on the Distribution of Multiple Symmetries in Nature and Art. Symmetry, 3(1), 54-71. https://doi.org/10.3390/sym3010054



