Symmetry and Asymmetry in Bouncing Gaits
Abstract
:1. Introduction
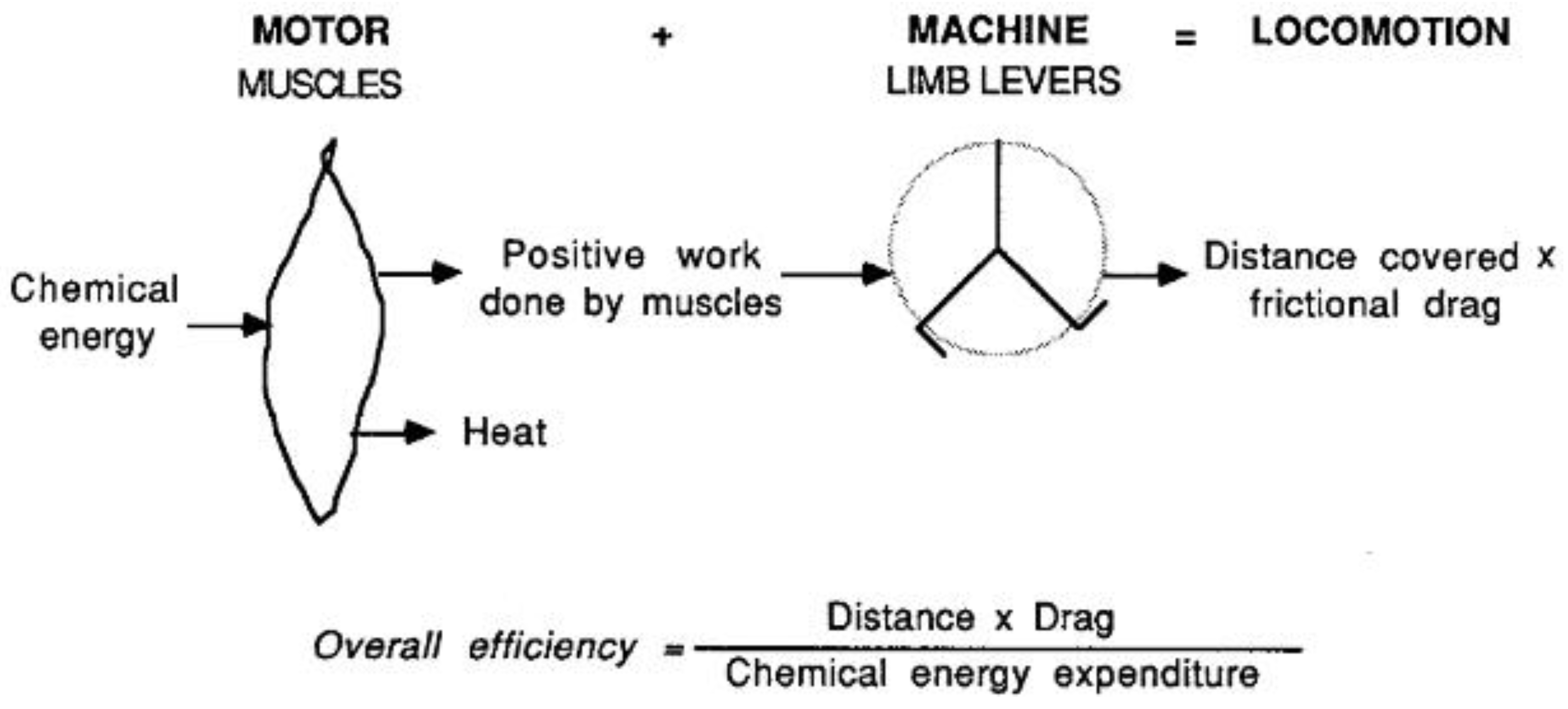
1.1. The Motor and the Machine
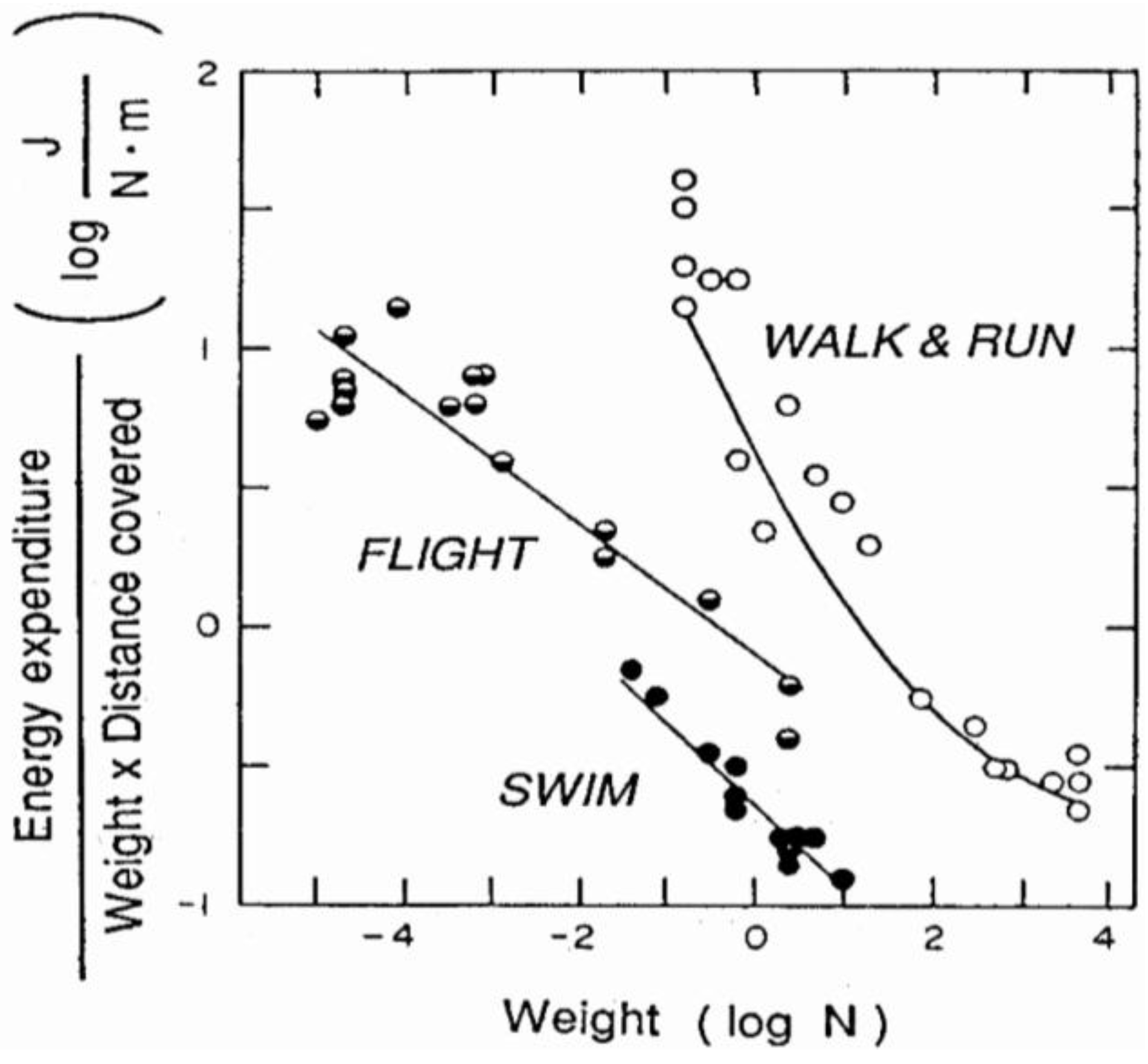
1.2. The Problem of Terrestrial Locomotion
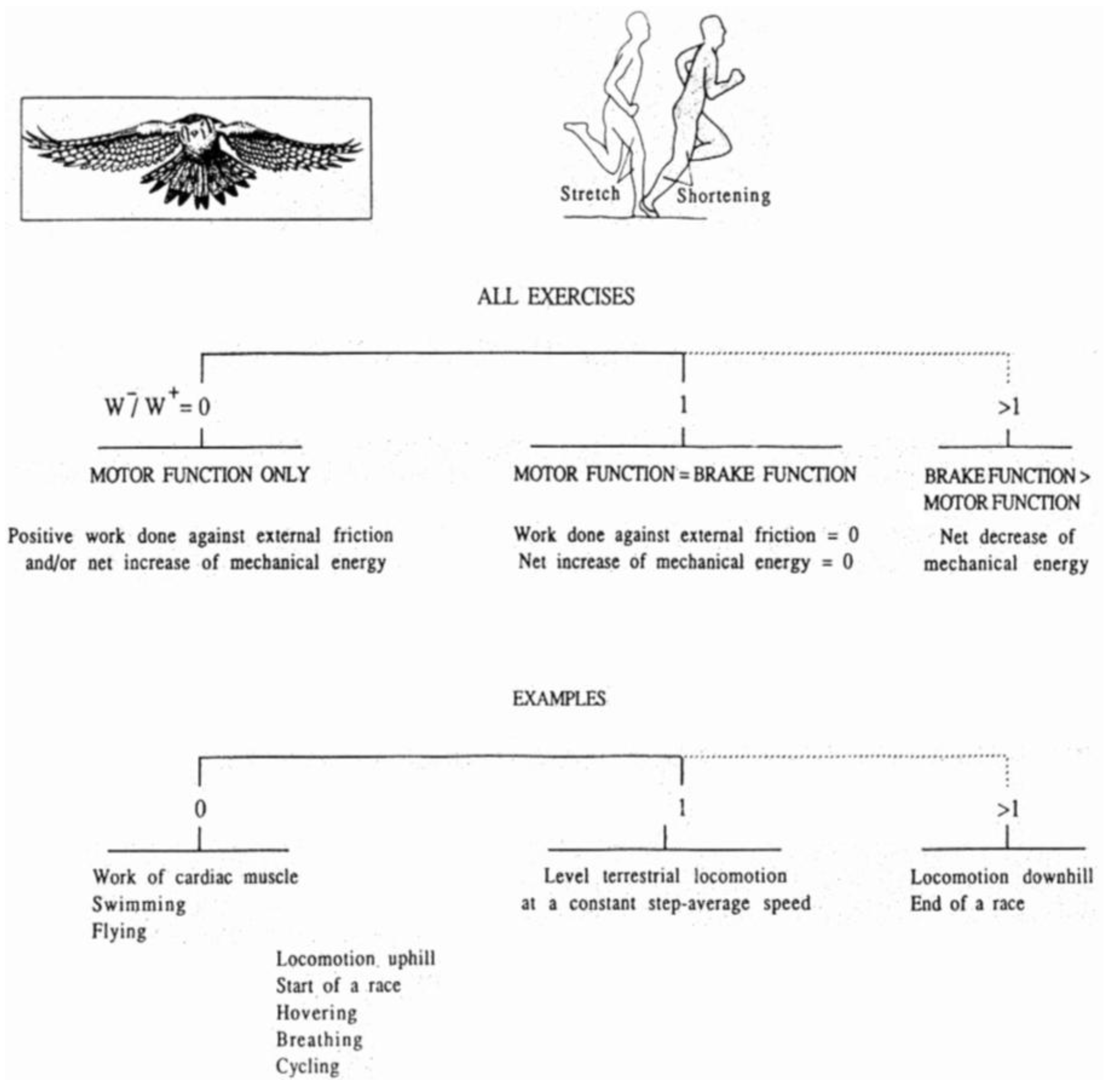
1.3. Positive and Negative Muscular Work
1.4. Two Partial Solutions: Pendular Exchange in Walking and Storage-Release of ‘Elastic’ Energy in Bouncing Gaits
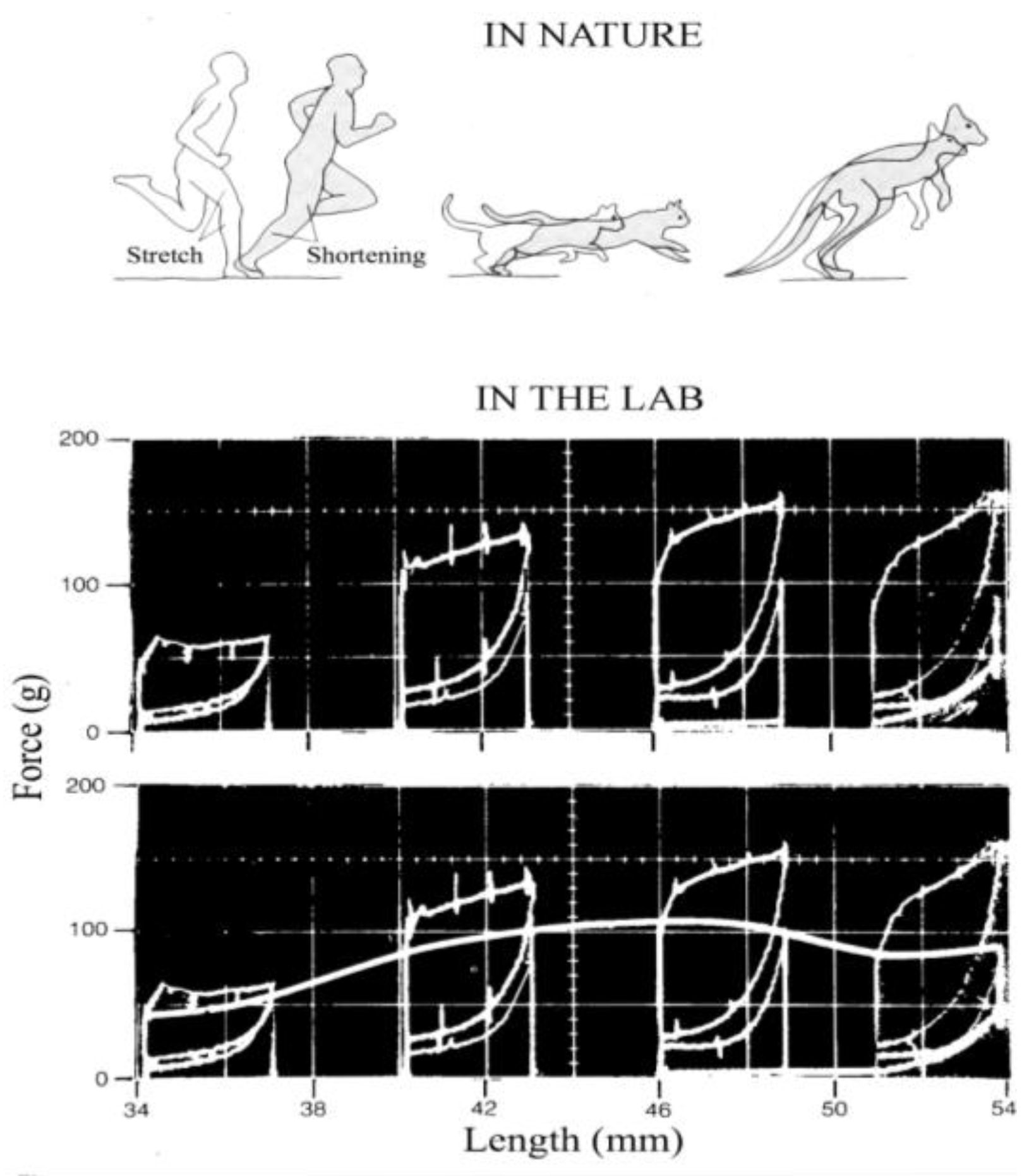
1.5. The Stretch-Shorten Cycle of Muscle-Tendon Units
2. Experimental Section
2.1. External Work
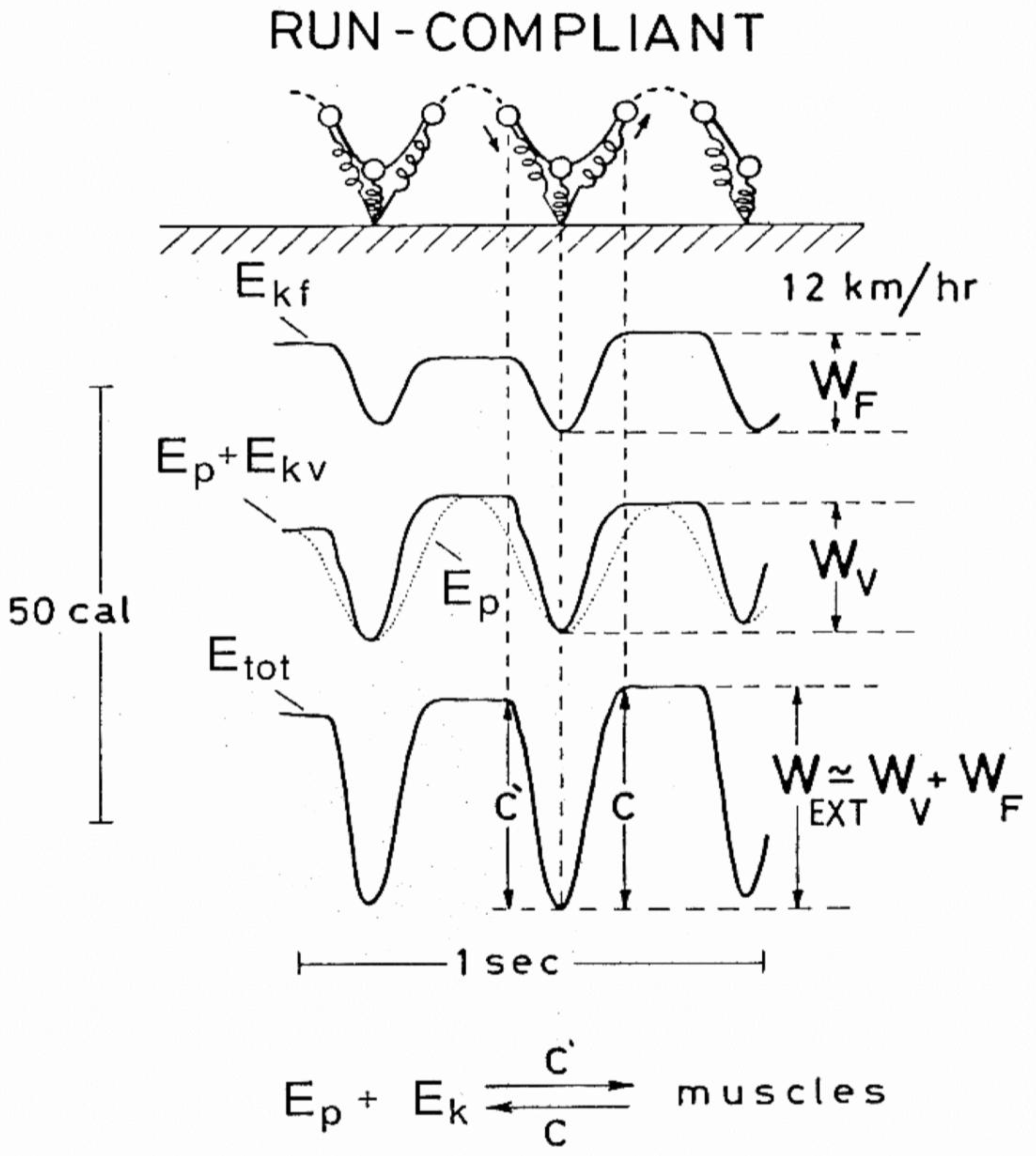
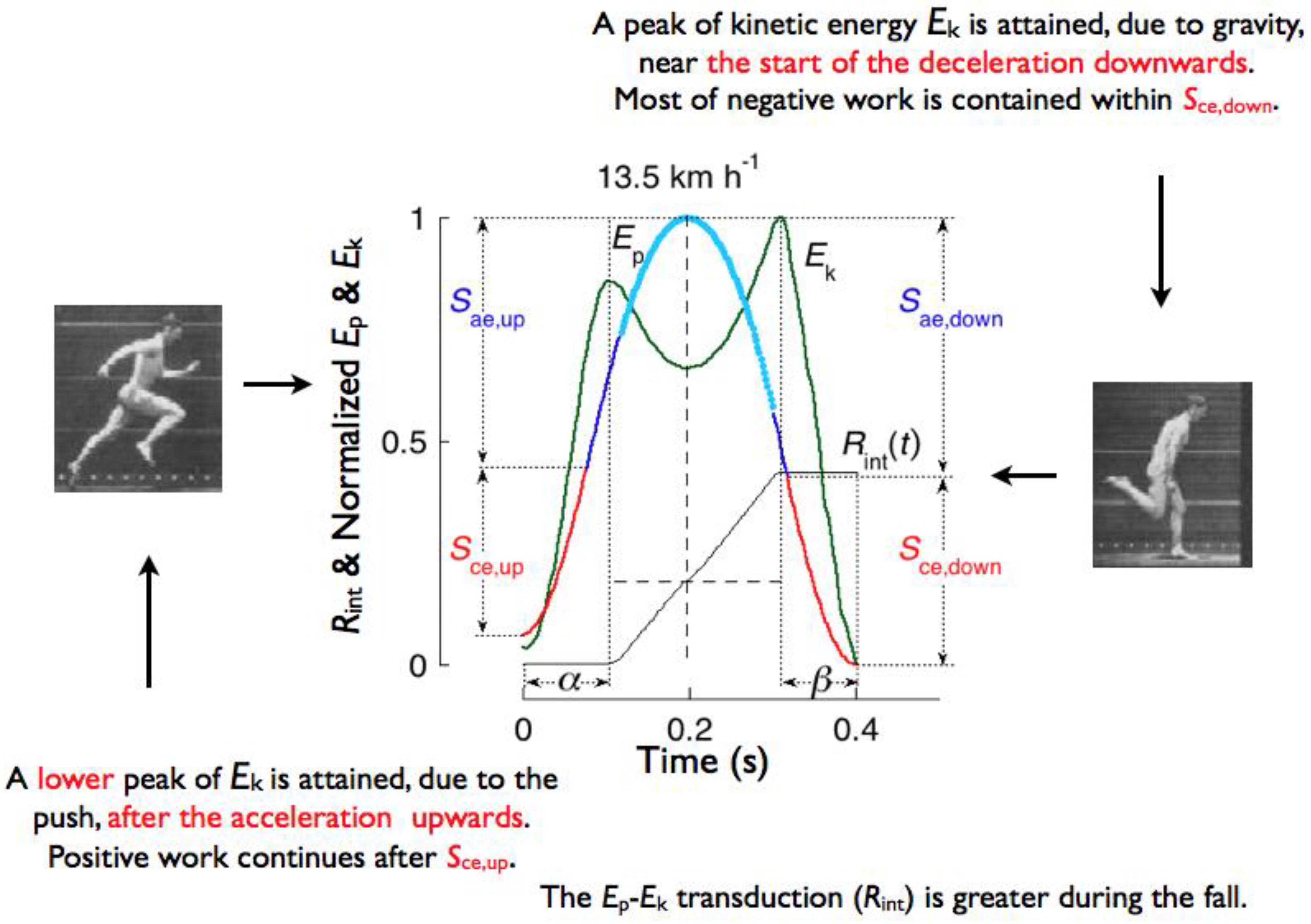
2.2. Within-Step Analysis of the Potential-Kinetic Energy Transduction
2.3. Internal Work
2.4. Total Work
3. The on-Off-Ground Asymmetry
3.1. The Spring-Mass Model
3.2. The Symmetric Rebound
3.3. The on-off-ground Asymmetric Rebound
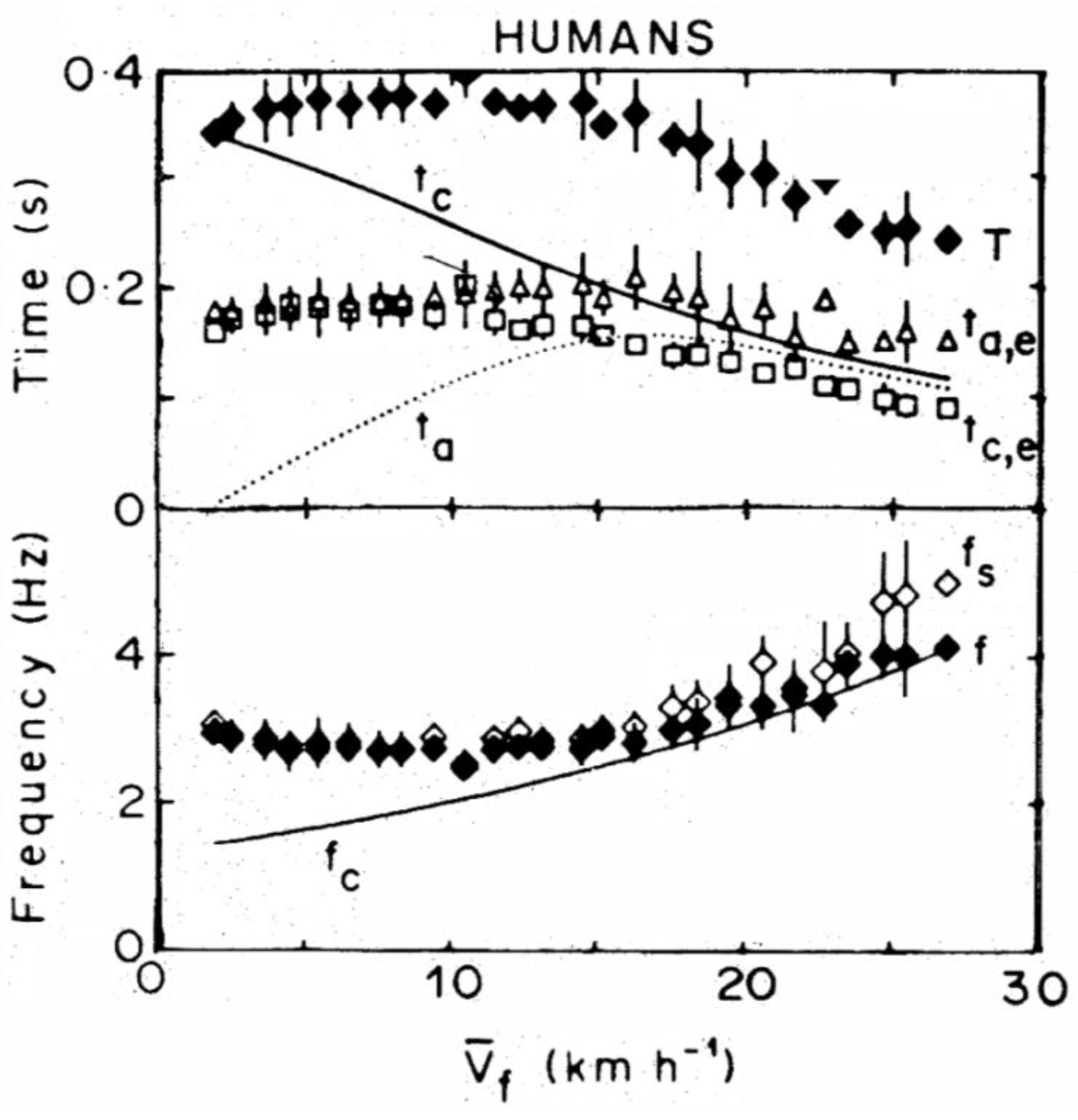
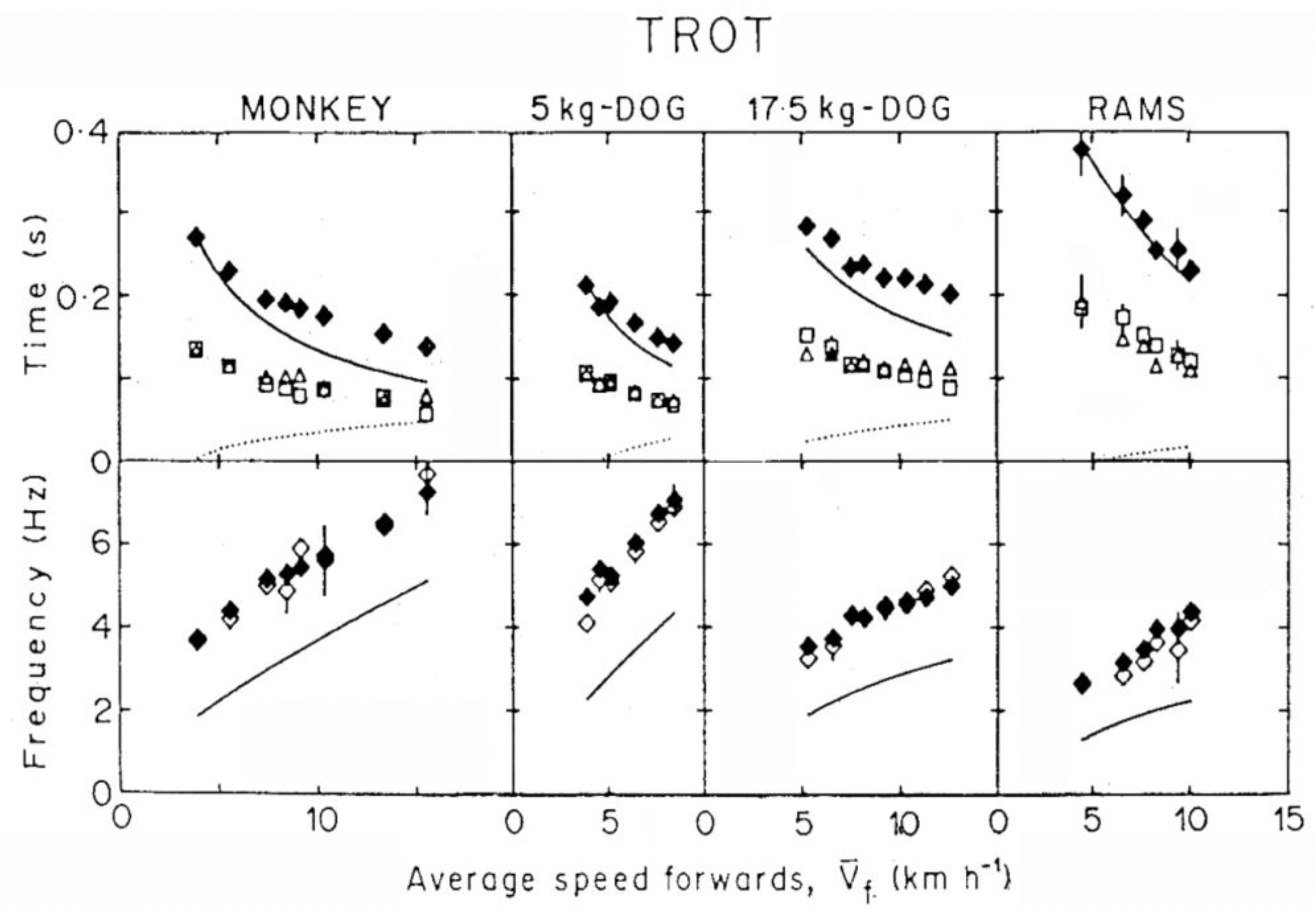
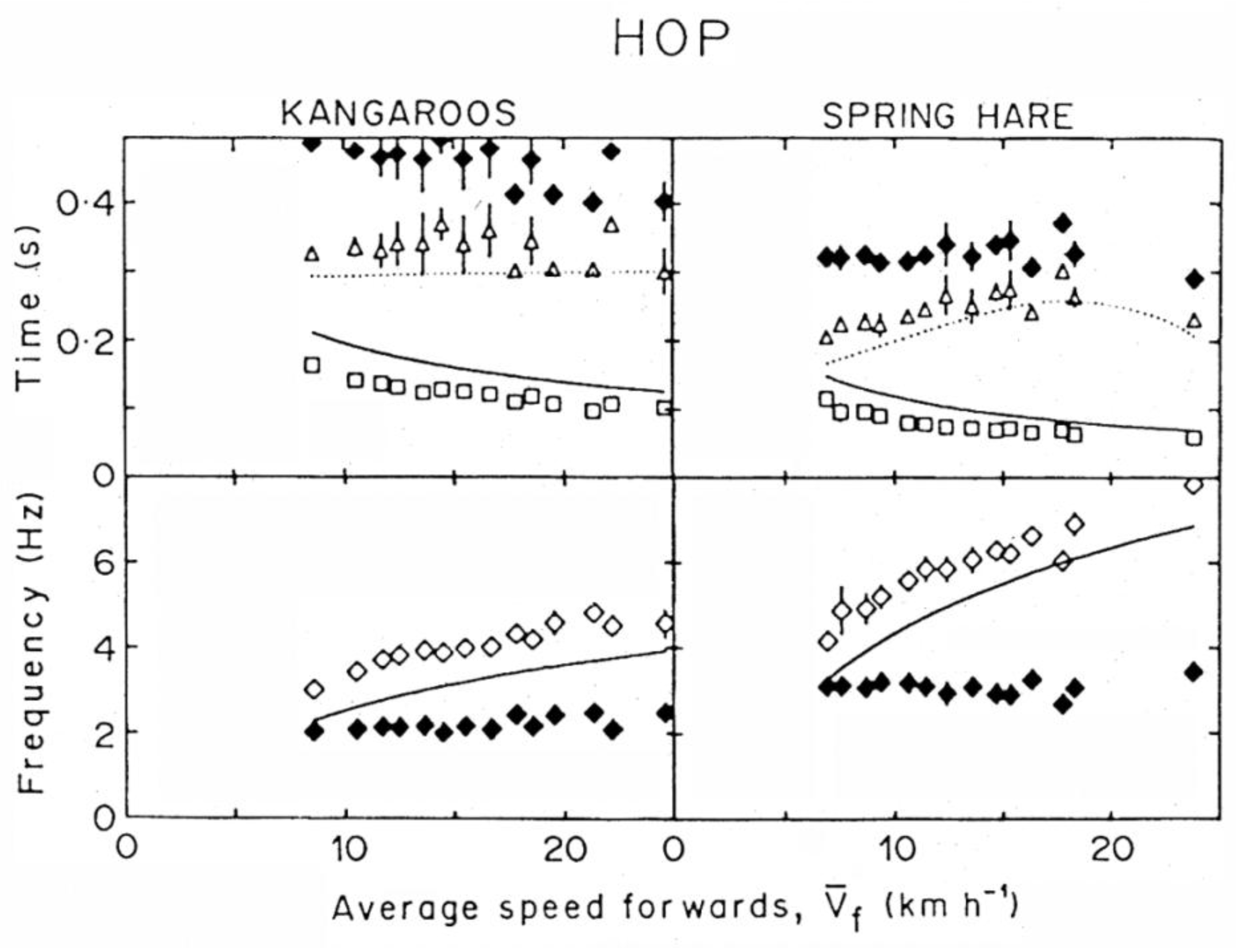
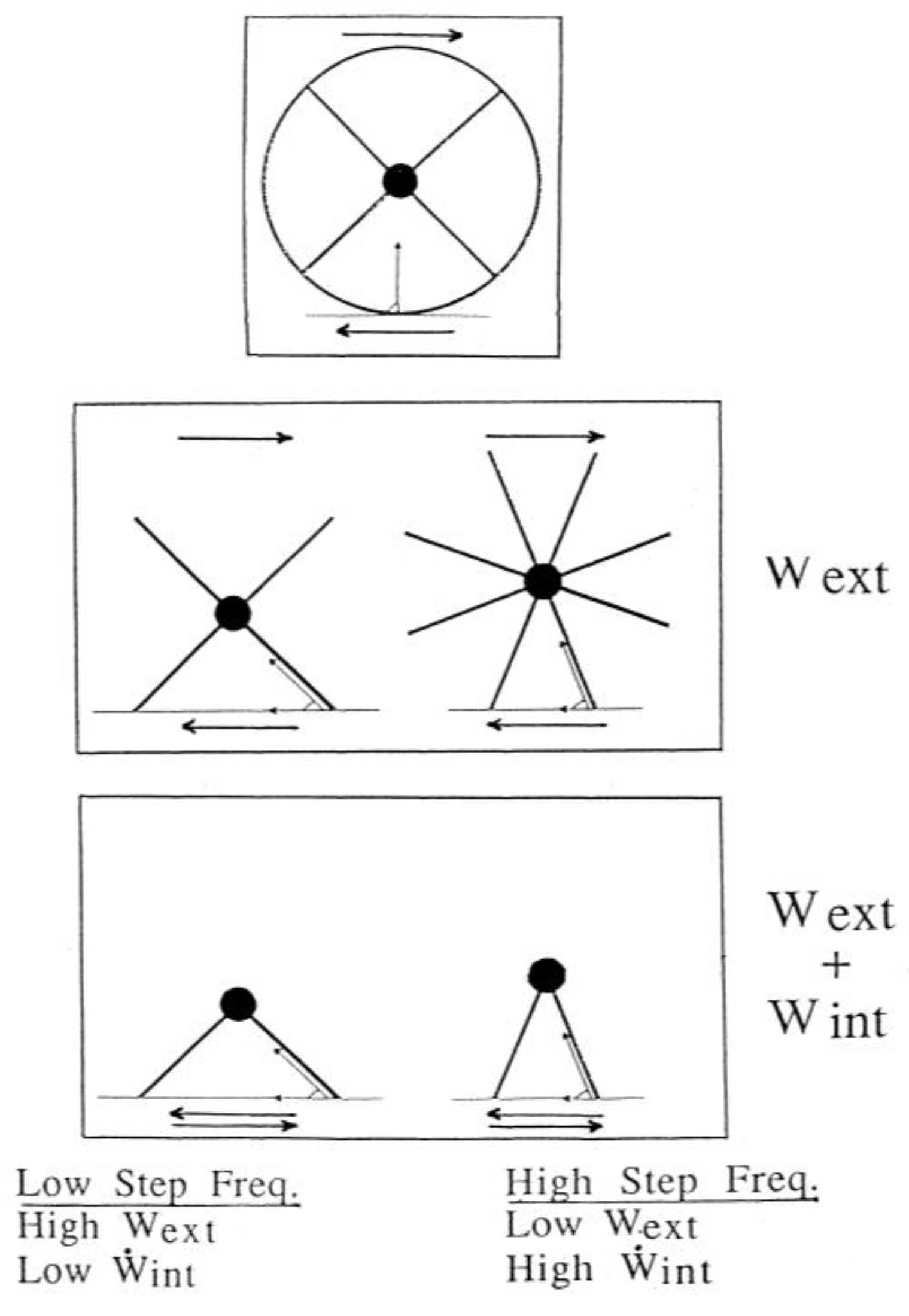
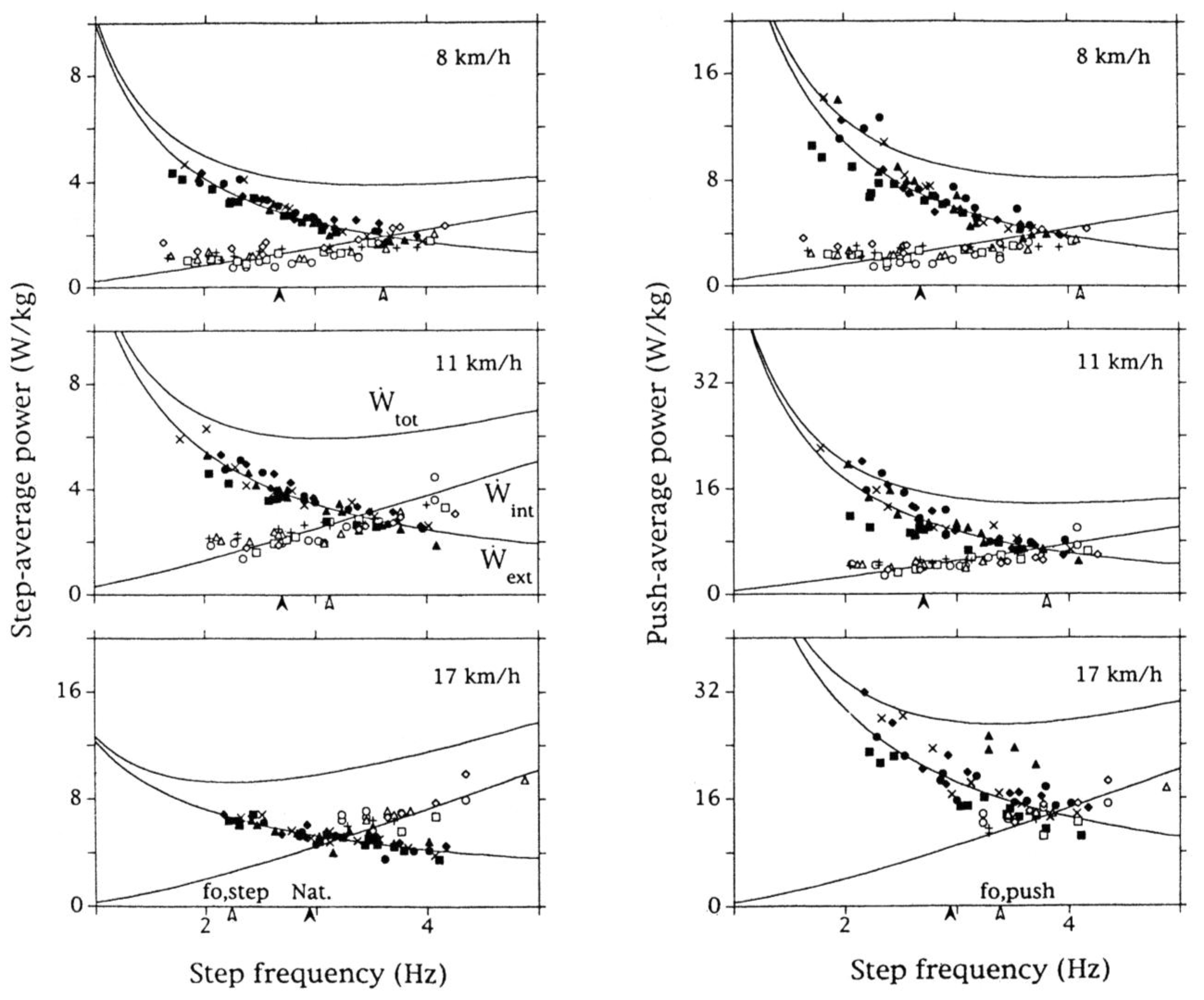
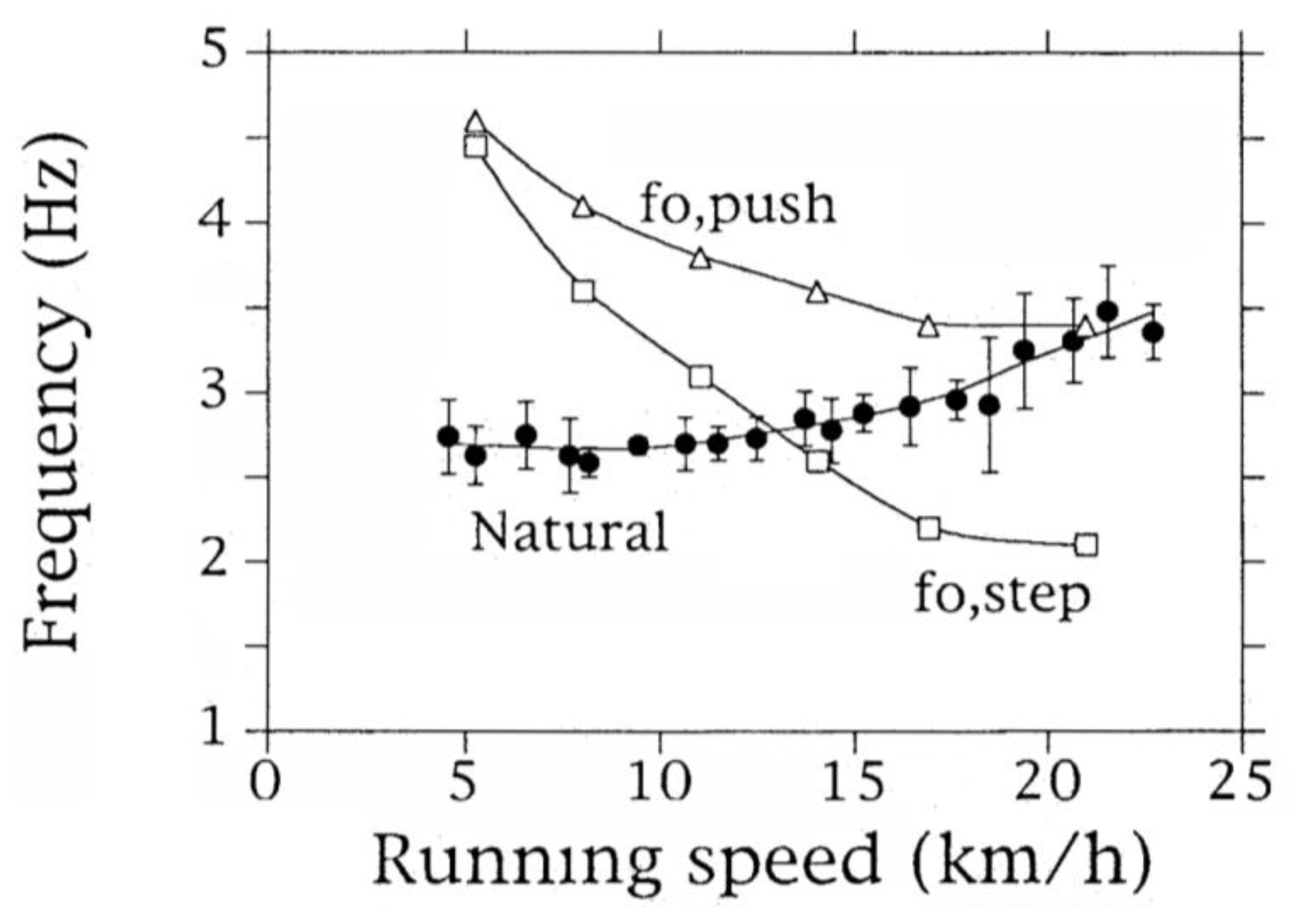
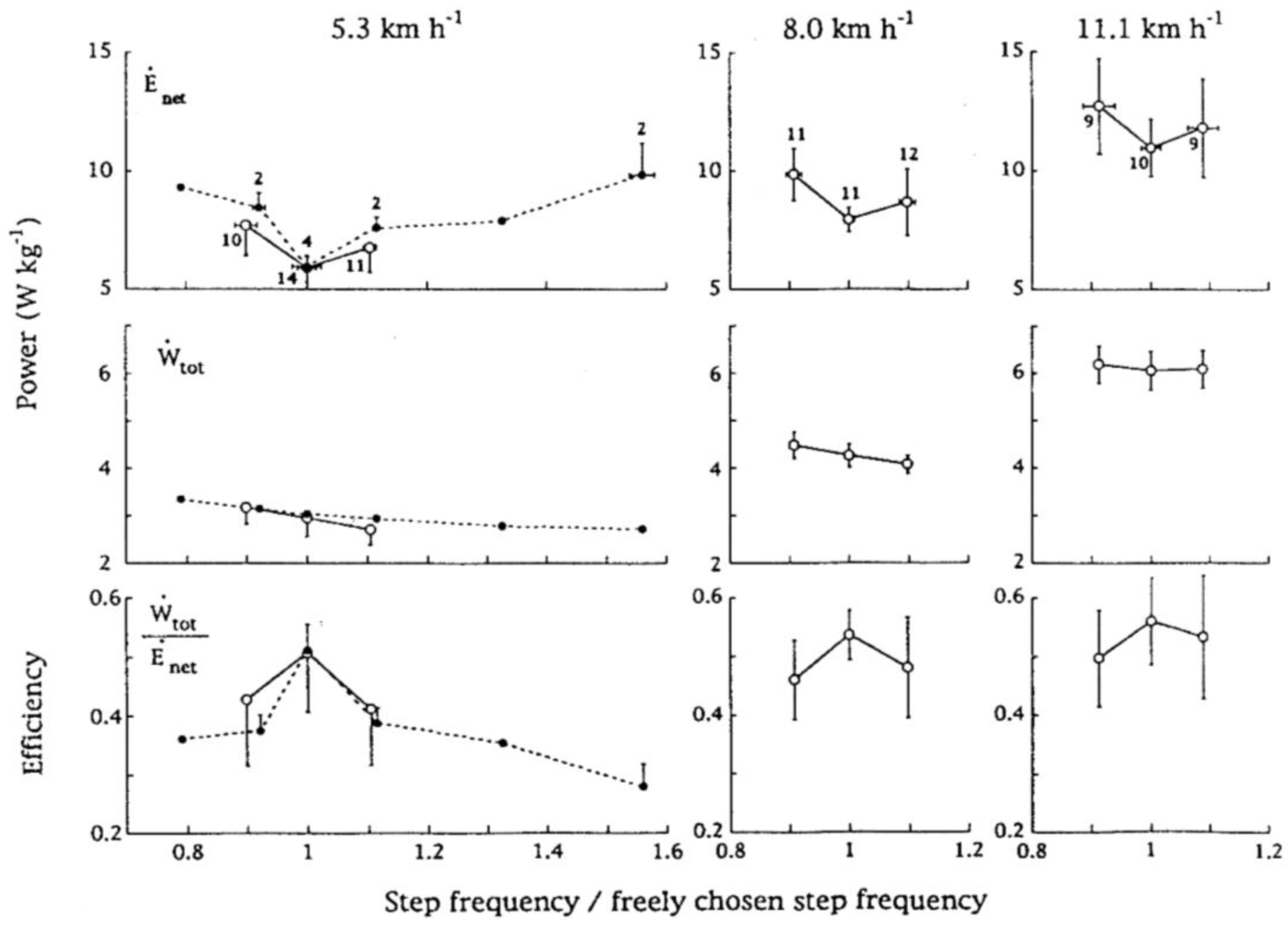
3.4. Effect of Step Frequency on Mechanical Power Output
3.5. Difference between Frequency Minimizing Mechanical Power Output and Freely Chosen Step Frequency
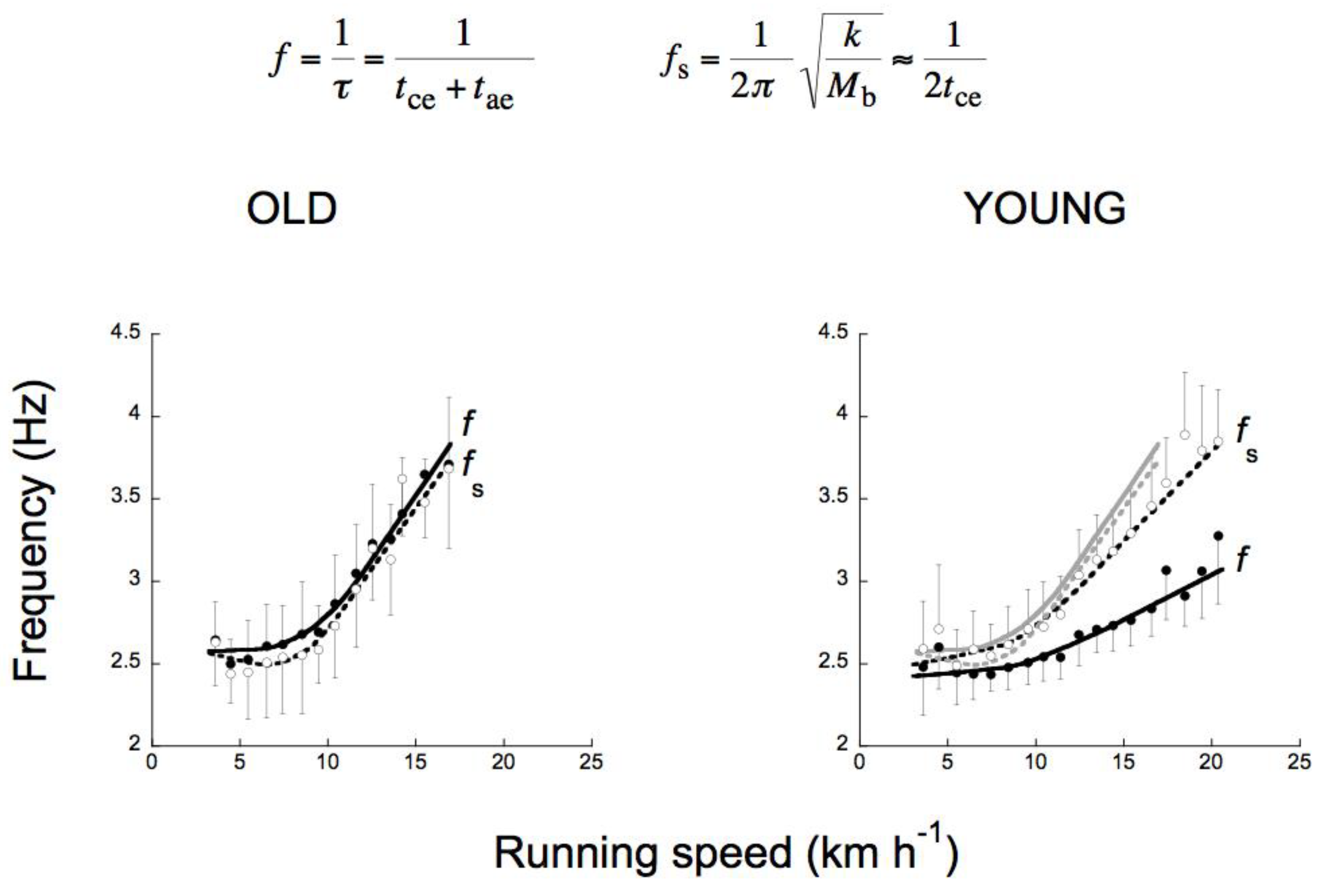
3.6. Tuning Step Frequency to the Resonant Frequency of the Bouncing System in Human Running
3.7. The Two Power Limits Conditioning Step Frequency at High Running Speeds
4. The Landing-Takeoff Asymmetry
4.1. Height of the Center of Mass at Touch Down and Takeoff
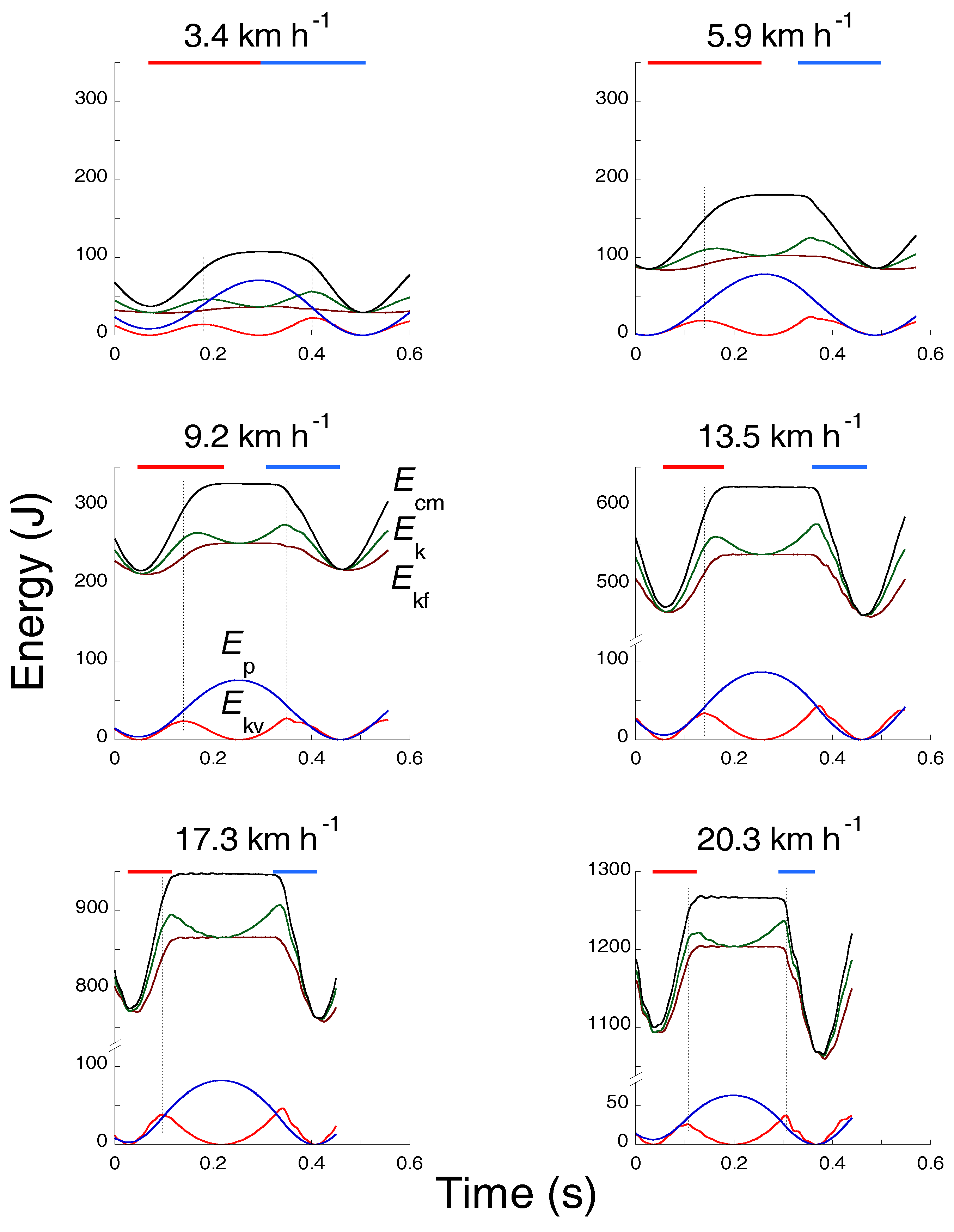
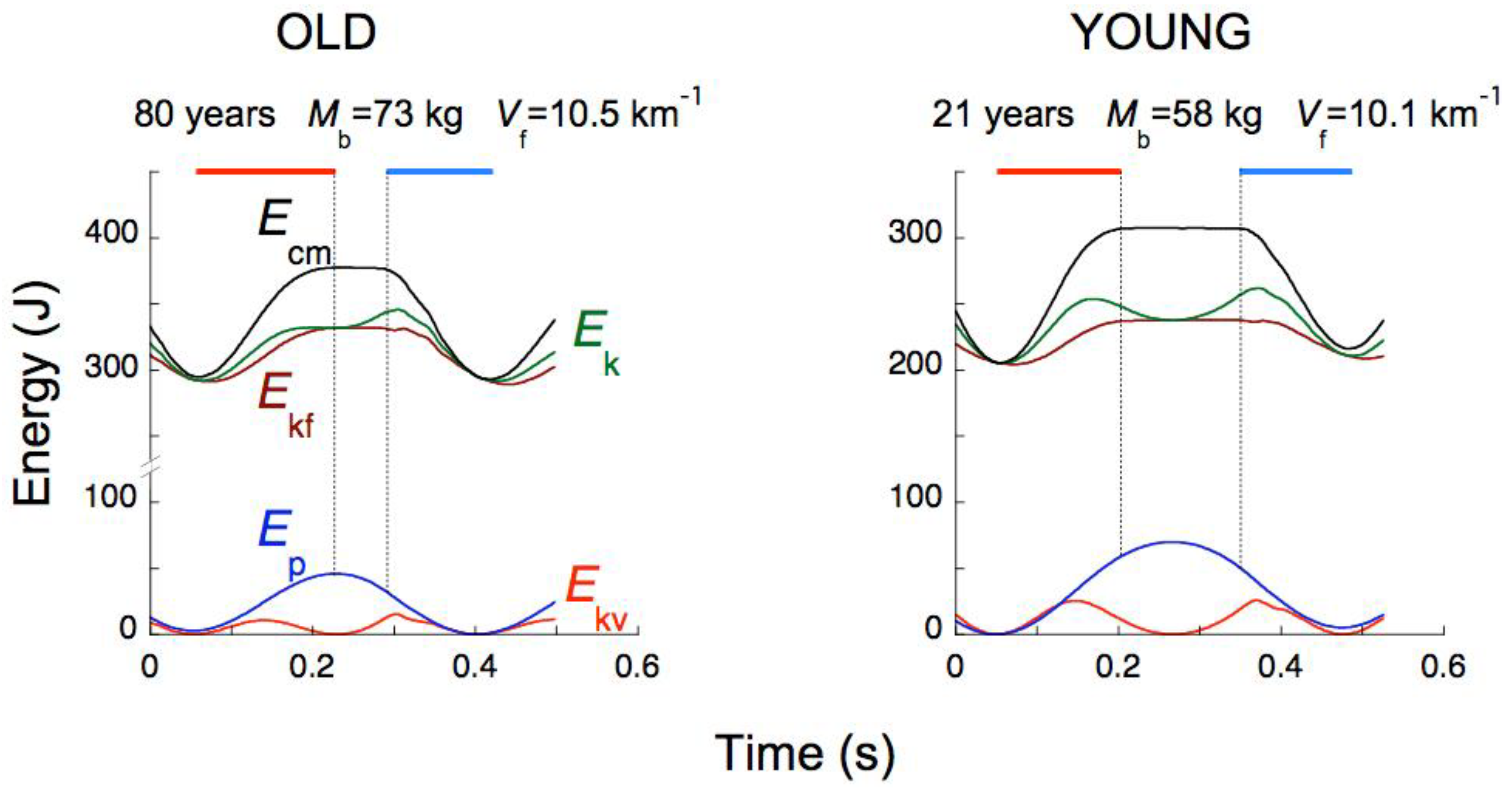
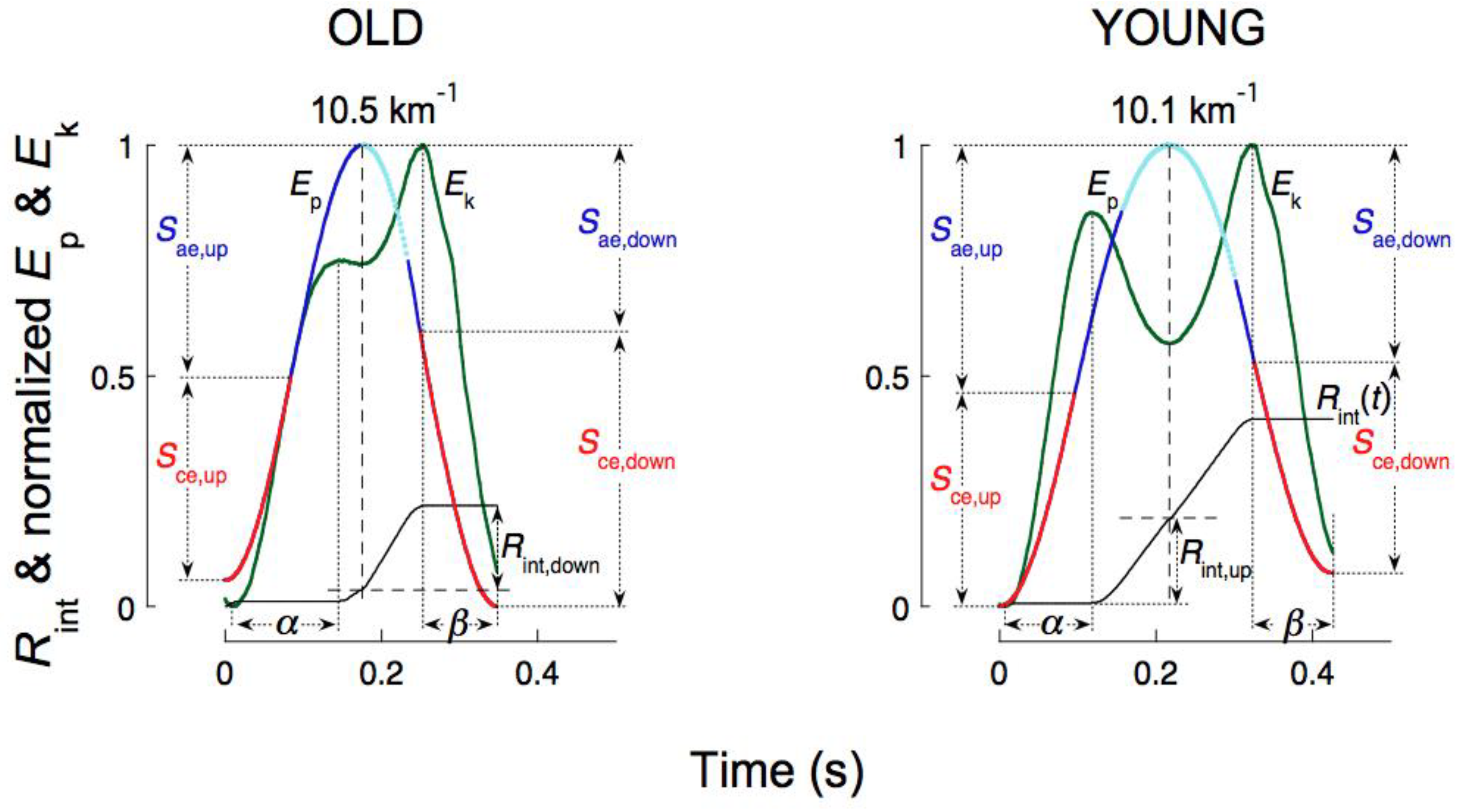
4.2. The Four Phases of the Bounce and the Transduction of Mechanical Energy during the Running Step
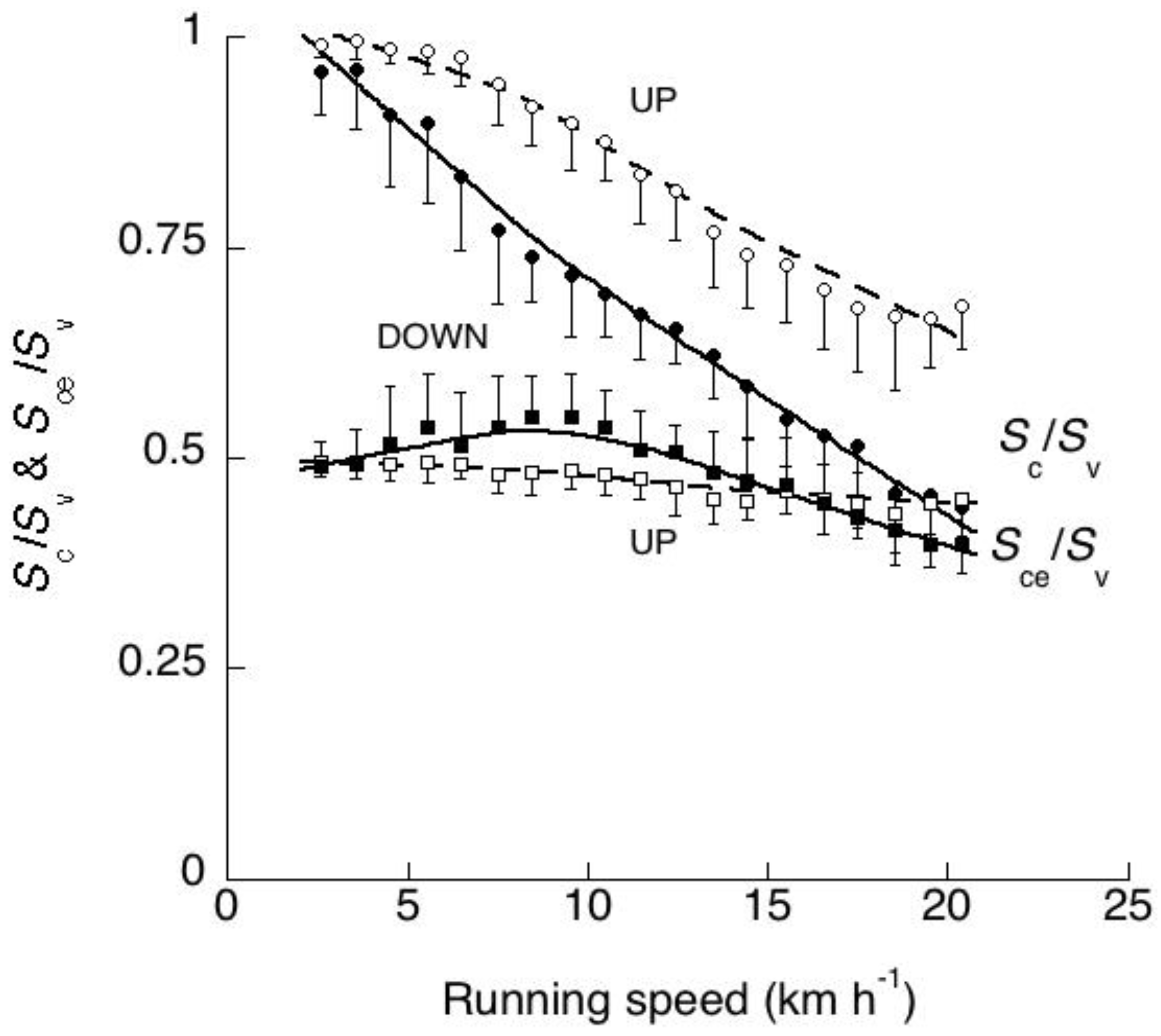
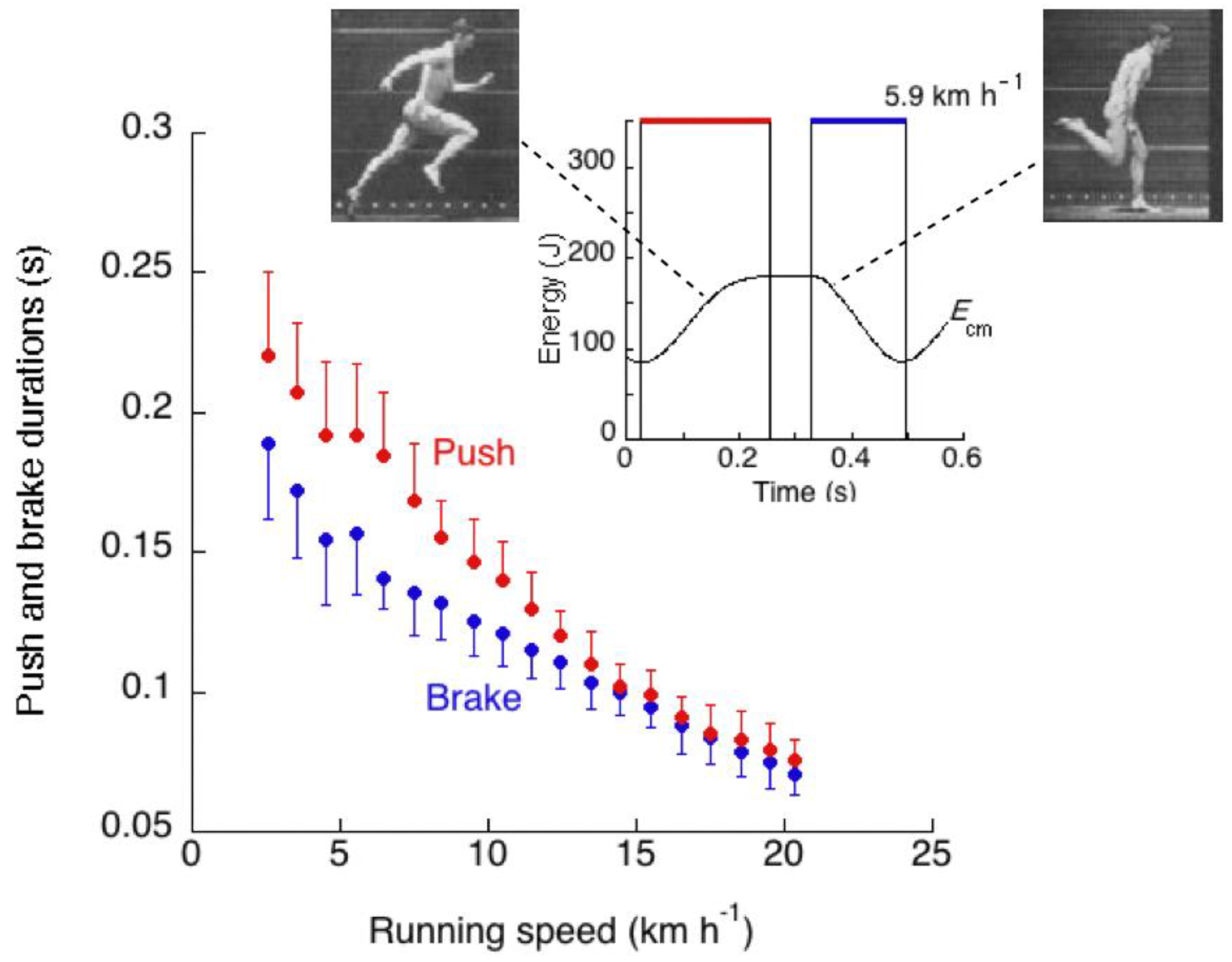
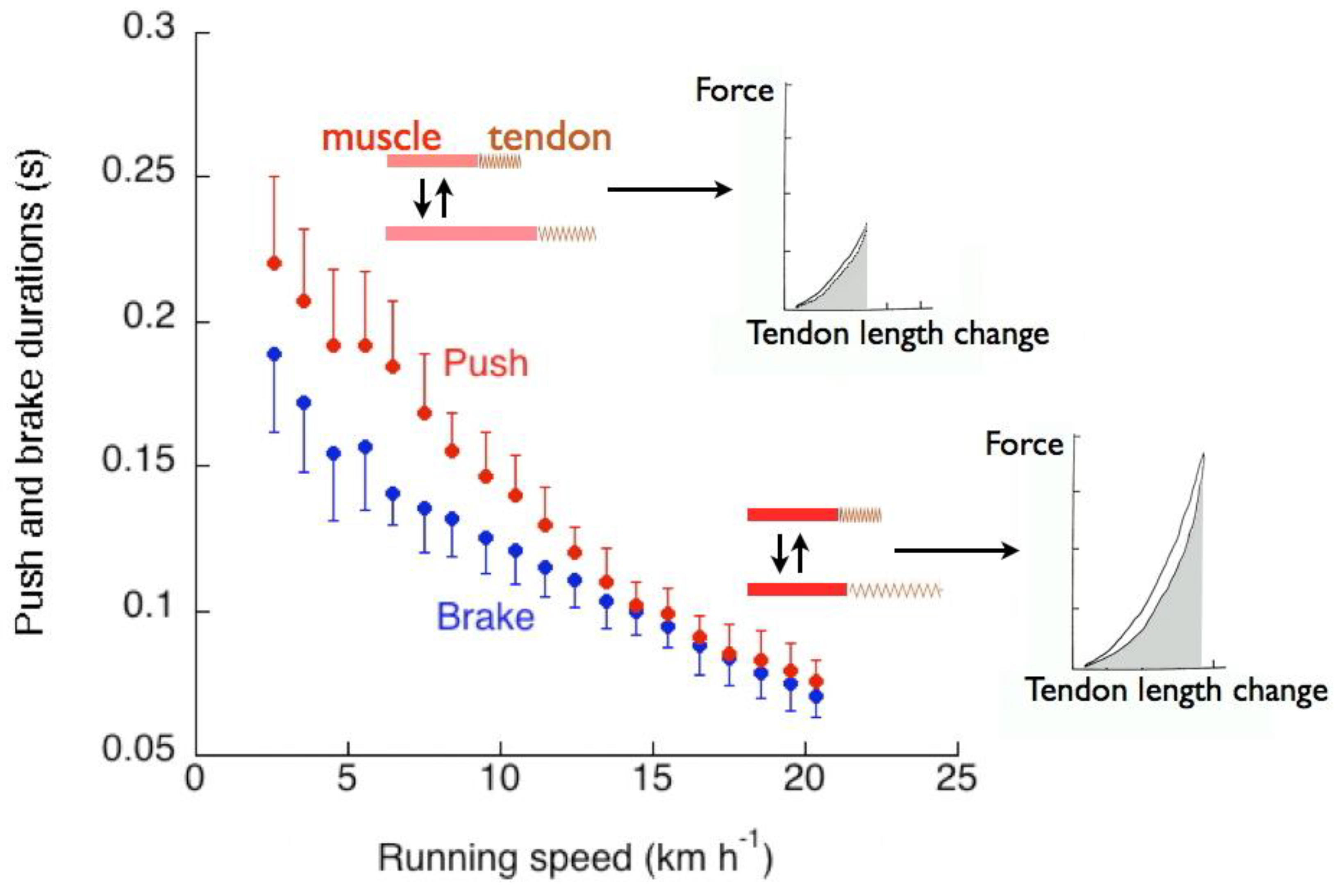
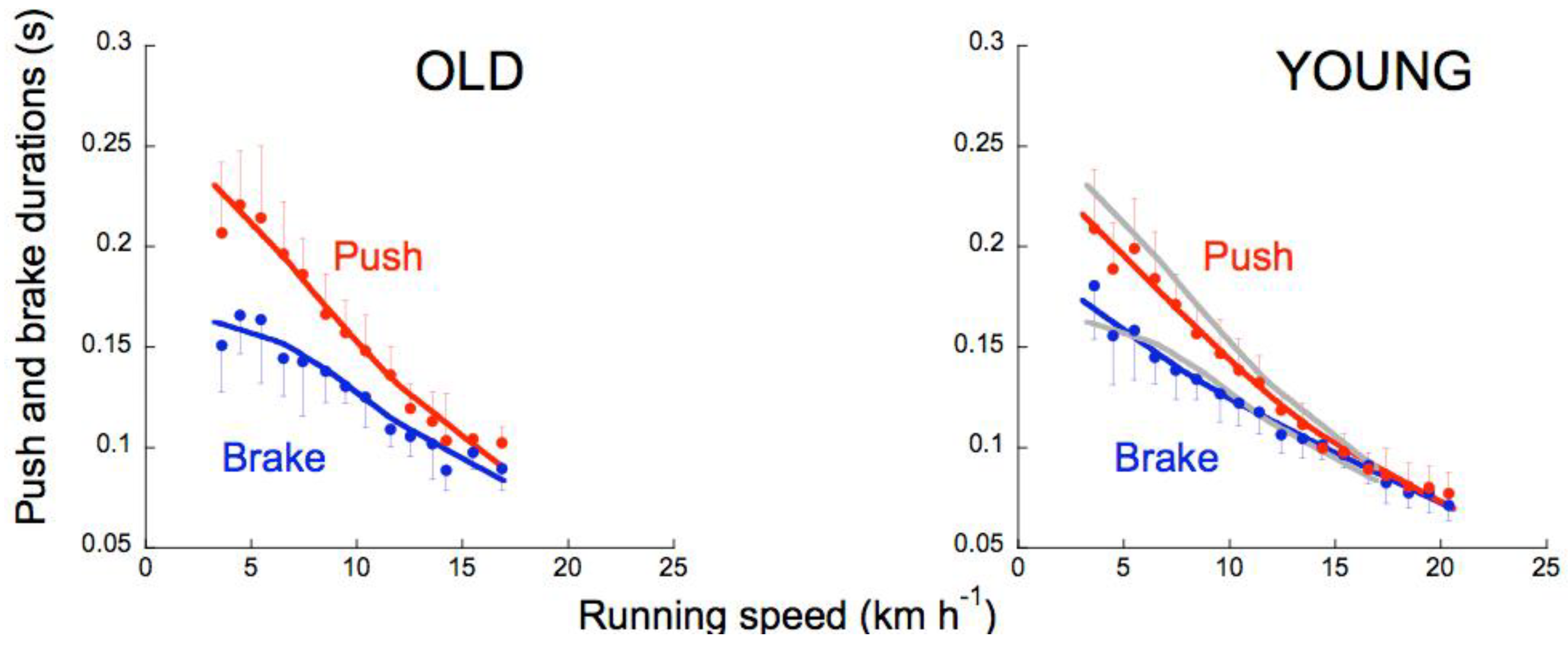
4.3. Positive and Negative Work Durations and Muscle-Tendon Units Response during Stretching and Shortening
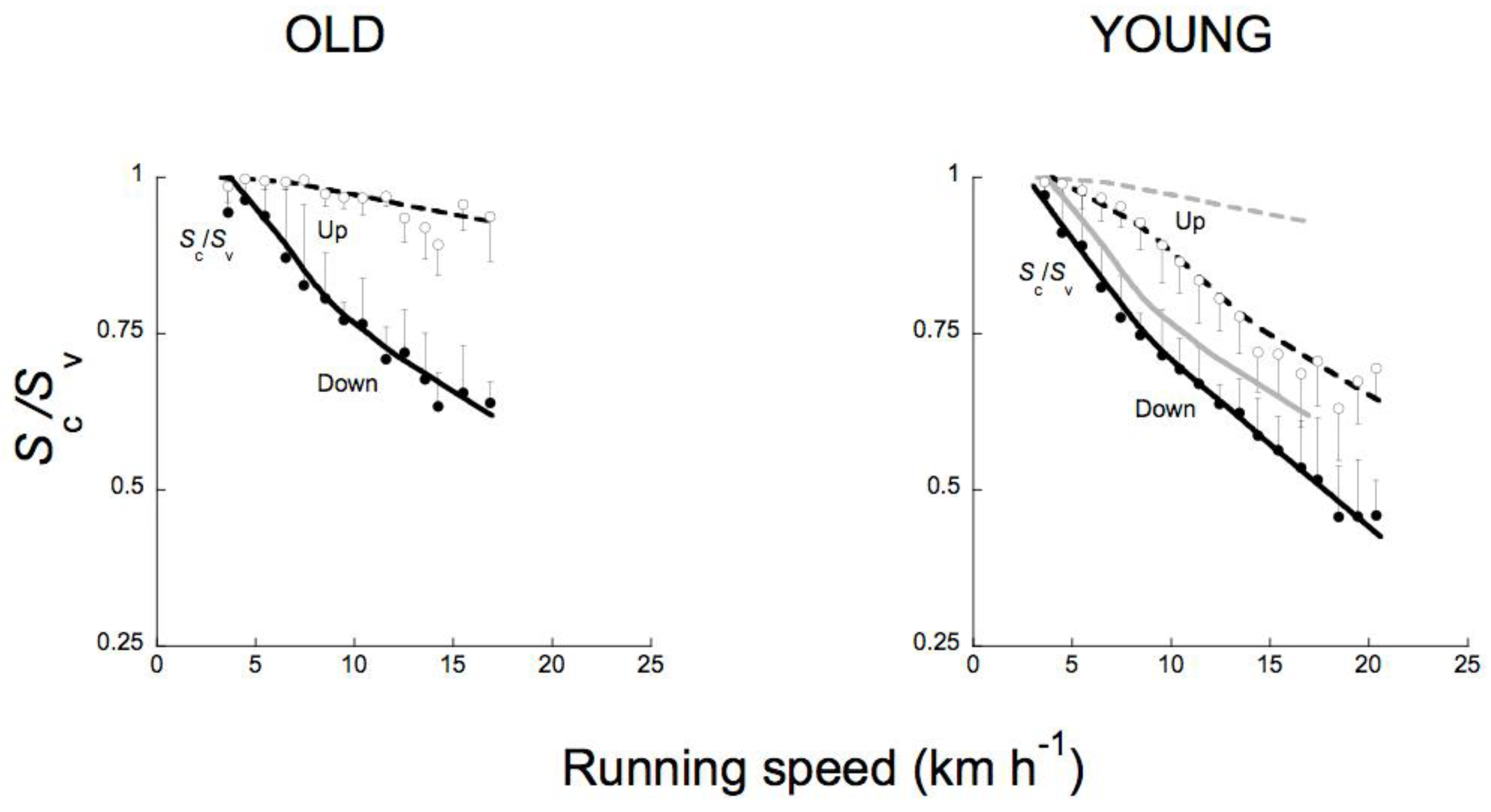
4.4. Effect of Running Speed on Landing-Takeoff Asymmetry in Adult Humans
4.5. The Landing-Takeoff Asymmetry in Old Humans
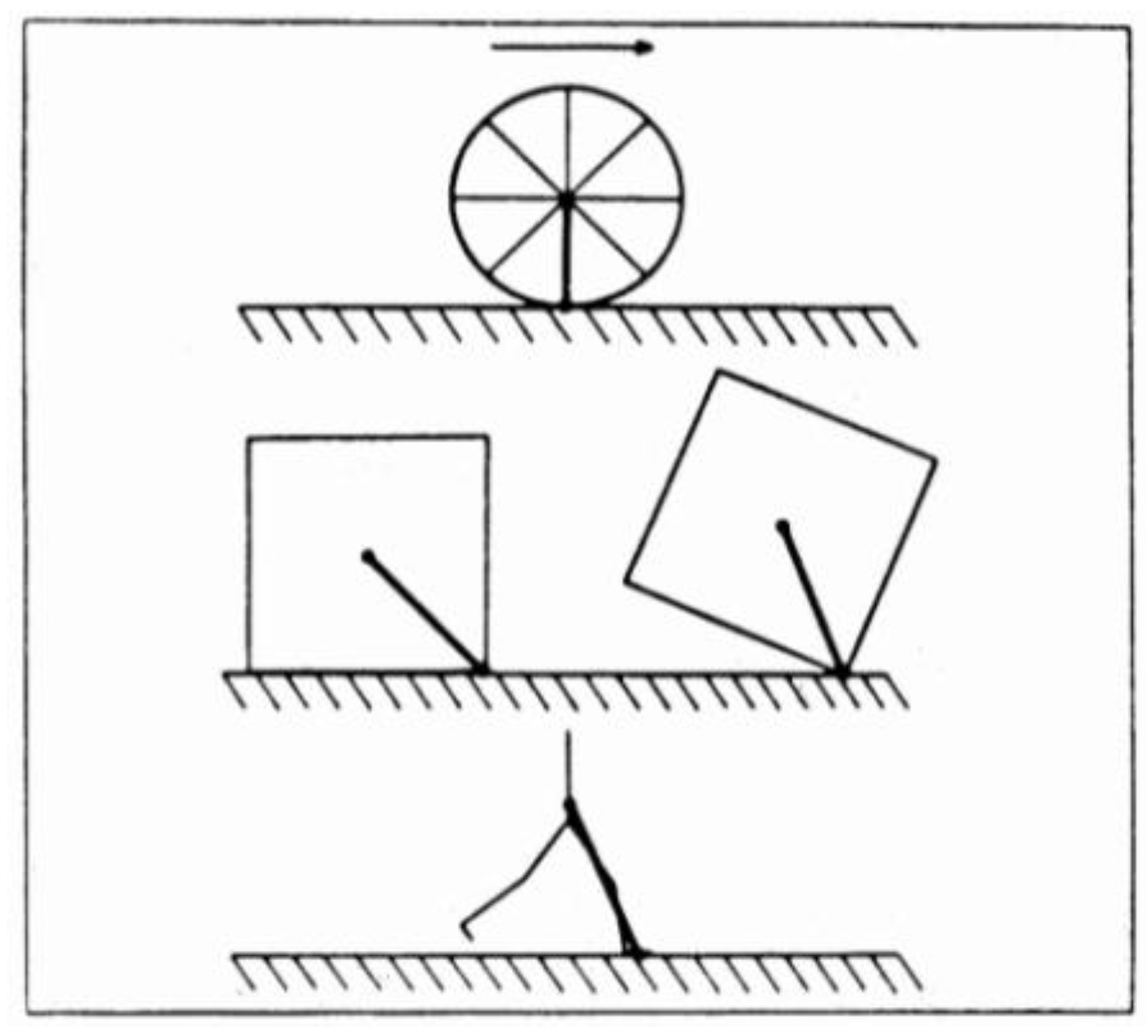
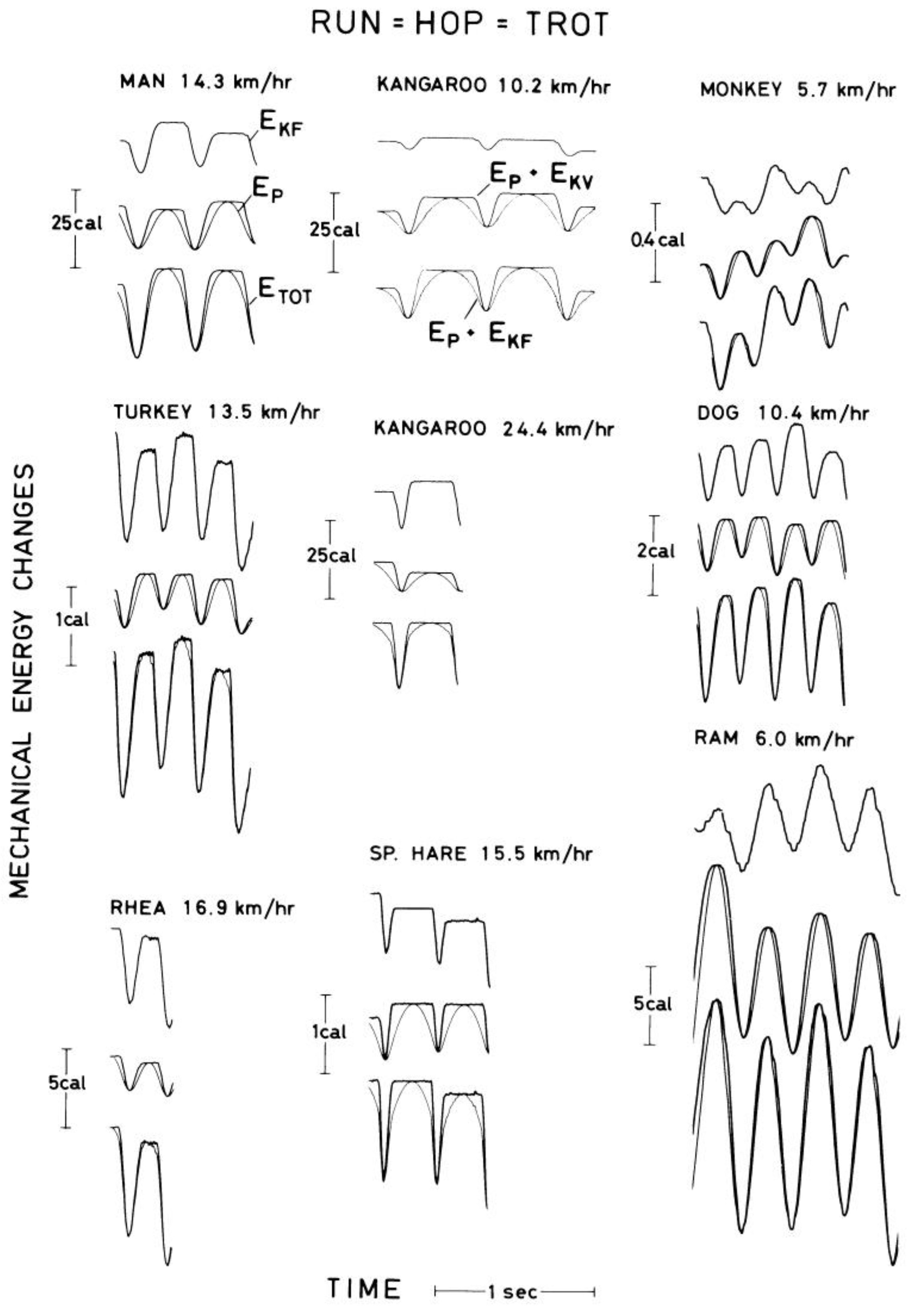
4.6. Asymmetric Motor or Asymmetric Machine?
4.7. Different Machines with the Same Motor
4.8. Factors Affecting the Elastic Storage Mechanism
5. Concluding Remarks
5.1. Muscular Work Requirements
5.2. Tools at Disposal
5.3. Strategies Used
Acknowledgements
List of Symbols
| α β | step phases during which Ep and Ek increase (α) or decrease (β) simultaneously. |
| τ | step period, i.e., period of repeating change in the mechanical energy of the center of mass. |
| Ek | kinetic energy of the center of mass in the sagittal plane. |
| Ekf | kinetic energy of forward motion of the center of mass. |
| Ekv | kinetic energy of vertical motion of the center of mass. |
| Ep | gravitational potential energy of the center of mass. |
| Ecm | mechanical energy of the center of mass. |
| average force during negative external work. | |
| average force during positive external work. | |
| Fv | vertical force. |
| g | acceleration of gravity. |
| H | height of the center of mass of the whole body. |
| Mb | body mass. |
| r(t) | instantaneous recovery of mechanical energy calculated from the absolute value of the changes, both increments and decrements, in Ep, Ek and Ecm during each time interval in the step period. |
| Rint | cumulative energy recovery attained at the end of the step due to Ek - Ep transduction. |
| Rint,down | fraction of Rint attained during the downward displacement of the center of mass. |
| Rint,up | fraction of Rint attained during the lift of the center of mass. |
| Sae,up | upward displacement of the center of mass taking place during its upward deceleration. |
| Sae,down | downward displacement of the center of mass taking place during its downward acceleration. |
| Sc,down | downward vertical displacement of the center of mass during contact. |
| Sce,down | downward displacement of the center of mass from the equilibrium position where Fv = Mb g to the lowest point of its trajectory. |
| Sce,up | upward displacement of the center of mass from the lowest point of its trajectory to the equilibrium position where Fv = Mb g. |
| Sc,up | upward vertical displacement of the center of mass during contact. |
| Sv,down | downward vertical displacement of the center of mass. |
| Sc | vertical displacement of the center of mass during contact: Sc = (Sc,up + Sc,down)/2. |
| Sv,up | upward vertical displacement of the center of mass. |
| Sv | vertical displacement of the center of mass: Sv = (Sv,up + Sv,down)/2. |
| tbrake | duration of negative external work production. |
| tpush | duration of positive external work production. |
| W+kf | Positive work done at each step to increase the forward speed of the center of mass. |
| W+v | Positive work done at each step to sustain the gravitational potential energy changes of the center of mass. |
| W+ext | Positive work done at each step to increase the mechanical energy of the center of mass. |
References
- Tucker, V.A. Aerial and terrestrial locomotion: a comparison of energetics. In Comparative Physiology; Bolis, L., Schmidt-Nielsen, K., Maddrell, H.P., Eds.; North Holland: Amsterdam, The Netherlands, 1973; pp. 63–76. [Google Scholar]
- Williams, T.M. The evolution of cost efficient swimming in marine mammals: limits to energetic optimization. Phil. Trans. R. Soc. Lond. 1999, 354, 192–201. [Google Scholar] [CrossRef]
- Margaria, R. Sulla fisiologia e specialmente sul consumo energetico della marcia e della corsa a varie velocità ed inclinazioni del terreno. Atti Reale Accad. Naz. Lincei (Memorie) 1938, 7, 299–368. [Google Scholar]
- Wilkie, D.R. Thermodynamics and the interpretation of biological heat measurements. Prog. Biophys. Mol. Biol. 1960, 10, 259–298. [Google Scholar] [CrossRef]
- Dickinson, S. The efficiency of bicycle-pedalling, as affected by speed and load. J. Physiol. 1929, 67, 242–255. [Google Scholar] [CrossRef]
- Hill, A.V. The air-resistance to a runner. Proc. R. Soc. Lond. Ser. B 1928, 102, 380–385. [Google Scholar] [CrossRef]
- Pugh, L.G.C.E. The influence of wind resistance in running and walking and the mechanical efficiency of work against horizontal or vertical forces. J. Physiol. 1971, 213, 255–276. [Google Scholar] [CrossRef] [PubMed]
- Lejeune, T.M.; Willems, P.A.; Heglund, N.C. Mechanics and energetics of human locomotion on sand. J. Exp. Biol. 1998, 201, 2071–2080. [Google Scholar] [PubMed]
- Hill, A.V. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. Ser. B 1938, 126, 136–195. [Google Scholar]
- Katz, B. The relation between force and speed in muscular contraction. J. Physiol. 1939, 96, 45–64. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.C.; Aubert, X.M. The force exerted by active striated muscle during and after change of length. J. Physiol. 1952, 117, 77–86. [Google Scholar] [PubMed]
- Edman, K.A.P.; Elzinga, G.; Noble, M.I.M. Enhancement of mechanical performance by stretch during titanic contractions of vertebrate skeletal muscle fibers. J. Physiol. 1978, 281, 139–155. [Google Scholar] [CrossRef] [PubMed]
- Lombardi, V.; Piazzesi, G. The contractile response during steady lengthening of stimulated frog muscle fibers. J. Physiol. 1990, 431, 141–171. [Google Scholar] [CrossRef] [PubMed]
- Minetti, A.E.; Ardigò, L.P.; Saibene, F. Mechanical determinants of gradient walking energetics in man. J. Physiol. 1993, 472, 725–735. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A.; Komarek, L.; Mazzoleni, S. The mechanics of sprint running. J. Physiol. 1971, 217, 709–721. [Google Scholar] [CrossRef] [PubMed]
- Campbell, E.J.M.; Agostoni, E.; Newsom Davis, J. The Respiratory Muscles: Mechanics and Neural Control; Lloyd-Luke: London, UK, 1970; pp. 115–137. [Google Scholar]
- Kaneko, M.; Yamazaki, T. Internal mechanical work due to velocity changes of the limb in working on a bicycle ergometer. In Biomechanics VI, Proceedings of the Sixth International Congress of Biomechanics, Copenhagen, Denmark; University Park Press: Baltimore, MD, USA, 1978; Volume 1, pp. 86–92. [Google Scholar]
- Minetti, A.E.; Ardigò, L.P.; Susta, D.; Cotelli, F. Using leg muscles as shock absorbers: theoretical predictions and experimental results of drop landing performance. Ergonomics 1998, 41, 1771–1791. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A.; Saibene, F.P.; Margaria, R. Mechanical work in running. J. Appl. Physiol. 1964, 19, 249–256. [Google Scholar] [CrossRef] [PubMed]
- Alexander, R.M.; Vernon, A. The mechanics of hopping by kangaroos (Macropodidae). J. Zool. 1975, 177, 265–303. [Google Scholar] [CrossRef]
- Biewener, A.A.; Konieczynski, D.D.; Baudinette, R.V. In vivo muscle force-length behavior during steady-speed hopping in tammar wallabies. J. Exp. Biol. 1998, 201, 1681–1694. [Google Scholar] [PubMed]
- Cavagna, G.A.; Heglund, N.C.; Taylor, C.R. Mechanical work in terrestrial locomotion: two basic mechanisms for minimizing energy expenditure. Am. J. Physiol. 1977, 233, R243–R261. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A.; Dusman, B.; Margaria, R. Positive work done by a previously stretched muscle. J. Appl. Physiol. 1968, 24, 21–32. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A.; Citterio, G. Effect of stretching on the elastic characteristics and the contractile component of frog striated muscle. J. Physiol. 1974, 239, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Heglund, N.C.; Cavagna, G.A. Mechanical work, oxygen consumption, and efficiency in isolated frog and rat muscle. Am. J. Physiol. 1987, 253, C22–C29. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A.; Heglund, N.C.; Harry, J.D.; Mantovani, M. Storage and release of mechanical energy by contracting frog muscle fibers. J. Physiol. 1994, 481, 689–708. [Google Scholar] [CrossRef] [PubMed]
- Mantovani, M.; Heglund, N.C.; Cavagna, G.A. Energy transfer during stress relaxation of contracting frog muscle fibers. J. Physiol. 2001, 537, 923–939. [Google Scholar] [CrossRef] [PubMed]
- Levin, A.; Wyman, J. The Viscous Elastic Properties of Muscle. Proc. R. Soc. Lond. B 1927, 101, 218–243. [Google Scholar] [CrossRef]
- Fenn, W.O. Frictional and kinetic factors in the work of sprint running. Am. J. Physiol. 1930, 92, 583–611. [Google Scholar] [CrossRef]
- Fenn, W.O. Work against gravity and work due to velocity changes in running: movements of the Center of Gravity Within the Body and Foot Pressure on the Ground. Am. J. Physiol. 1930, 93, 433–462. [Google Scholar] [CrossRef]
- Cavagna, G.A.; Saibene, F.P.; Margaria, R. External work in walking. J. Appl. Physiol. 1963, 18, 1–9. [Google Scholar] [CrossRef]
- Blickhan, R. The spring-mass model for running and hopping. J. Biomech. 1989, 22, 1217–1227. [Google Scholar] [CrossRef]
- Cavagna, G.A.; Thys, H.; Zamboni, A. The sources of external work in level walking and running. J. Physiol. 1976, 262, 639–657. [Google Scholar] [CrossRef]
- Cavagna, G.A. Force platforms as ergometers. J. Appl. Physiol. 1975, 39, 174–179. [Google Scholar] [CrossRef]
- Cavagna, G.A.; Franzetti, P.; Fuchimoto, T. The mechanics of walking in children. J. Physiol. 1983, 343, 323–339. [Google Scholar] [CrossRef]
- Cavagna, G.A.; Legramandi, M.A.; Peyré-Tartaruga, L.A. The landing-take-off asymmetry of human running is enhanced in old age. J. Exp. Biol. 2008, 211, 1571–1578. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A.; Willems, P.A.; Legramandi, M.A.; Heglund, N.C. Pendular energy transduction within the step in human walking. J. Exp. Biol. 2002, 205, 3413–3422. [Google Scholar] [PubMed]
- Cavagna, G.A.; Kaneko, M. Mechanical work and efficiency in level walking and running. J. Physiol. 1977, 268, 467–481. [Google Scholar] [CrossRef]
- Willems, P.A.; Cavagna, G.A.; Heglund, N.C. External, internal and total work in human locomotion. J. Exp. Biol. 1995, 198, 379–393. [Google Scholar]
- Cavagna, G.A.; Willems, P.A.; Franzetti, P.; Detrembleur, C. The two power limits conditioning step frequency in human running. J. Physiol. 1991, 437, 95–108. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A.; Mantovani, M.; Willems, P.A.; Musch, G. The resonant step frequency in human running. Pflugers Arch. 1997, 434, 678–684. [Google Scholar] [CrossRef]
- Heglund, N.C.; Fedak, M.A.; Taylor, C.R.; Cavagna, G.A. Energetics and mechanics of terrestrial locomotion. IV. Total mechanical energy changes as a function of speed and body size in birds and mammals. J. Exp. Biol. 1982, 97, 57–66. [Google Scholar] [PubMed]
- Cavagna, G.A.; Franzetti, P. The determinants of the step frequency in walking in humans. J. Physiol. 1986, 373, 235–242. [Google Scholar] [CrossRef]
- Alexander, R.M. Optimization and gaits in the locomotion of vertebrates. Physiol. Rev. 1989, 69, 1199–1227. [Google Scholar] [CrossRef] [PubMed]
- Aleshinsky, S.Y. An energy ‘sources’ and ‘fractions’ approach to the mechanical energy expenditure problem, I–V. J. Biomech. 1986, 19, 287–315. [Google Scholar] [CrossRef]
- Williams, K.R.; Cavanagh, P.R. A model for the calculation of mechanical power during distance running. J. Biomech. 1983, 16, 115–128. [Google Scholar] [CrossRef]
- Caldwell, G.E.; Forrester, L.W. Estimates of mechanical work and energy transfers: demonstration of a rigid body power model of the recovery leg in gait. Med. Sci. Sports Ex. 1992, 24, 1396–1412. [Google Scholar] [CrossRef]
- McMahon, T.A.; Cheng, G.C. The mechanics of running: how does stiffness couple with speed? J. Biomech. 1990, 23, 65–78. [Google Scholar] [CrossRef]
- Ferris, D.P.; Farley, C.T. Interaction of leg stiffness and surface stiffness during human hopping. J. Appl. Physiol. 1997, 82, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Ferris, D.P.; Liang, K.; Farley, C.T. Runners adjust leg stiffness for their first step on new running surface. J. Biomech. 1999, 32, 787–794. [Google Scholar] [CrossRef]
- Kerdok, A.E.; Biewener, A.A.; McMahon, T.A.; Weyand, P.G.; Herr, H.M. Energetics and mechanics of human running on surfaces of different stiffnesses. J. Appl. Physiol. 2002, 92, 469–478. [Google Scholar] [CrossRef] [PubMed]
- McMahon, T.A.; Valiant, G.; Frederick, E.C. Groucho running. J. Appl. Physiol. 1987, 62, 2326–2337. [Google Scholar] [CrossRef]
- Cavagna, G.A.; Franzetti, P.; Heglund, N.C.; Willems, P.A. The determinants of the step frequency in running, trotting and hopping in man and other vertebrates. J. Physiol. 1988, 399, 81–92. [Google Scholar] [CrossRef]
- Schepens, B.; Willems, P.A.; Cavagna, G.A. The mechanics of running in children. J. Physiol. 1998, 509, 927–940. [Google Scholar] [CrossRef] [PubMed]
- Farley, C.T.; Glasheen, J.; McMahon, T.A. Running springs: speed and animal size. J. Exp. Biol. 1993, 185, 71–86. [Google Scholar] [PubMed]
- Margaria, R. Biomechanics and Energetics of Muscular Exercise; Clarendon Press: Oxford, UK, 1976. [Google Scholar]
- Cavagna, G.A.; Legramandi, M.A.; Peyré-Tartaruga, L.A. Old men running: mechanical work and elastic bounce. Proc. R. Soc. B-Biol. Sci. 2008, 275, 411–418. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A. The landing-take-off asymmetry in human running. J. Exp. Biol. 2006, 209, 4051–4060. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A. The two asymmetries of the bouncing step. Eur. J. Appl. Physiol. 2009, 107, 739–742. [Google Scholar] [CrossRef] [PubMed]
- Muybridge, E. The Human Figure in Motion; Dover Publications Inc.: New York, NY, USA, 1955. [Google Scholar]
- Morgan, D.L. Separation of active and passive components of short-range stiffness of muscle. Am. J. Physiol. 1977, 232, C45–C49. [Google Scholar] [CrossRef] [PubMed]
- Roberts, T.J.; Marsh, R.L.; Weyand, P.G.; Taylor, C.R. Muscular force in running turkeys: the economy of minimizing work. Science 1997, 275, 1113–1115. [Google Scholar] [CrossRef]
- Ker, R.F.; Bennett, M.B.; Bibby, S.R.; Kester, R.C.; Alexander, R.M. The spring in the arch of the human foot. Nature 1987, 325, 147–149. [Google Scholar] [CrossRef]
- McMahon, T.A. The spring in the human foot. Nature 1987, 325, 108–109. [Google Scholar] [CrossRef]
- Alexander, R.M. Tendon elasticity and muscle function. Comp. Biochem. Physiol. 2002, 133A, 1001–1011. [Google Scholar] [CrossRef]
- Biewener, A.A. Muscle–tendon stresses and elastic energy storage during locomotion in the horse. Comp. Biochem. Physiol. 1998, 120B, 73–87. [Google Scholar] [CrossRef]
- Fukunaga, T.; Kawakami, Y.; Kuno, S.; Funato, K.; Fukashiro, S. Muscle architecture and function in humans. J. Biomechanics 1997, 5, 457–463. [Google Scholar] [CrossRef]
- Kubo, K.; Kanehisa, H.; Kawakami, Y.; Fukunaga, T. Elasticity of tendon structures of the lower limbs in sprinters. Acta Physiol. Scand. 2000, 168, 327–335. [Google Scholar] [CrossRef] [PubMed]
- Kubo, K.; Kanehisa, H.; Takeshita, D.; Kawakami, Y.; Fukashiro, S.; Fukunaga, T. In vivo dynamics of human medial gastrocnemius muscle-tendon complex during stretch-shortening cycle exercise. Acta Physiol. Scand. 2000, 170, 127–135. [Google Scholar] [CrossRef]
- Kurokawa, S.; Fukunaga, T.; Fukashiro, S. Behavior of fascicles and tendinous structures of human gastrocnemius during vertical jumping. J. Appl. Physiol. 2001, 90, 1349–1358. [Google Scholar] [CrossRef] [PubMed]
- Kawakami, Y.; Muraoka, T.; Ito, H.; Kanehisa, H.; Fukunaga, T. In vivo muscle fiber behavior during counter-movement exercise in humans reveals a significant role for tendon elasticity. J. Physiol. 2002, 540, 635–646. [Google Scholar] [CrossRef]
- Karamanidis, K.; Arampatzis, A. Mechanical and morphological properties of different muscle-tendon units in the lower extremity and running mechanics: effect of aging and physical activity. J. Exp. Biol. 2005, 208, 3907–3923. [Google Scholar] [CrossRef] [PubMed]
- Kawakami, Y.; Fukunaga, T. New insights into in vivo human skeletal muscle function. Exerc. Sport Sci. Rev. 2006, 34, 16–21. [Google Scholar] [CrossRef] [PubMed]
- McGuigan, M.P.; Yoo, E.; Lee, D.V.; Biewener, A.A. Dynamics of goat distal hind limb muscle-tendon function in response to locomotor grade. J. Exp. Biol. 2009, 212, 2092–2104. [Google Scholar] [CrossRef] [PubMed]
- Kram, R.; Taylor, C.R. Energetics of running: a new perspective. Nature 1990, 346, 265–267. [Google Scholar] [CrossRef] [PubMed]
- Alexander, R.M.; Ker, R.F. Running is priced by the step. Nature 1990, 346, 220–221. [Google Scholar] [CrossRef] [PubMed]
- Farley, C.T.; Blickhan, R.; Saito, J.; Taylor, C.R. Hopping frequency in humans: a test of how springs set stride frequency in bouncing gaits. J. Appl. Physiol. 1991, 71, 2127–2132. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, A.M.; Herr, H.M. Leg exoskeleton reduces the metabolic cost of human hopping. J. Appl. Physiol. 2009, 107, 670–678. [Google Scholar] [CrossRef] [PubMed]
- Moritz, C.T. A spring in your step: some is good, more is not always better. J. Appl. Physiol. 2009, 107, 643–644. [Google Scholar] [CrossRef] [PubMed]
- Phillips, S.K.; Bruce, S.A.; Woledge, R.C. In mice, the muscle weakness due to age is absent during stretching. J. Physiol. 1991, 437, 63–70. [Google Scholar] [CrossRef] [PubMed]
- Ochala, J.; Dorer, D.J.; Frontera, W.R.; Krivickas, L.S. Single skeletal muscle fiber behavior after a quick stretch in young and older men: a possible explanation of the relative preservation of eccentric force in old age. Pflugers Arch. 2006, 452, 464–470. [Google Scholar] [CrossRef] [PubMed]
- Vandervoort, A.A.; Kramer, J.F.; Wharram, E.R. Eccentric knee strength of elderly females. J. Gerontol. 1990, 45, B125–B128. [Google Scholar] [CrossRef] [PubMed]
- Porter, M.M.; Vandervoort, A.A.; Kramer, J.F. Eccentric peak torque of the plantar and dorsiflexors is maintained in older women. J. Gerontol. A Biol. Sci. Med. Sci. 1997, 52, B125–B131. [Google Scholar] [CrossRef]
- Pousson, M.; Lepers, R.; Van Hoecke, J. Changes in isokinetic torque and muscular activity of elbow flexors muscles with age. Exp. Gerontol. 2001, 36, 1687–1698. [Google Scholar] [CrossRef]
- Klass, M.; Baudry, S.; Duchateau, J. Aging does not affect voluntary activation of the ankle dorsiflexors during isometric, concentric and eccentric contractions. J. Appl. Physiol. 2005, 99, 31–38. [Google Scholar] [CrossRef] [PubMed]
- Vogel, H.G. Influence of maturation and age on mechanical and biochemical parameters of connective tissue of various organs in the rat. Connec. Tissue Res. 1978, 6, 161–166. [Google Scholar] [CrossRef]
- Carrier, D.R.; Heglund, N.C.; Earls, K.D. Variable gearing during locomotion in the human musculoskeletal system. Science 1994, 265, 651–653. [Google Scholar] [CrossRef] [PubMed]
- Bullimore, S.R.; Burn, J.F. Consequences of forward translation of the point of force application for the mechanics of running. J. Theor. Biol. 2006, 238, 211–219. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A.; Legramandi, M.A. The bounce of the body in hopping, running and trotting: different machines with the same motor. Proc. R. Soc. B-Biol. Sci. 2009, 276, 4279–4285. [Google Scholar] [CrossRef] [PubMed]
- McGowan, C.P.; Baudinette, R.V.; Biewener, A.A. Differential design for hopping in two species of wallabies. Comp. Biochem. Physiol. 2008, 150A, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Herr, H.; Popovic, M. Angular momentum in human walking. J. Exp. Biol. 2008, 211, 467–481. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A.; Mazzanti, M.; Heglund, N.C.; Citterio, G. Mechanical transients initiated by ramp stretch and release to Po in frog muscle fibers. Am. J. Physiol. 1986, 251, C571–C579. [Google Scholar] [CrossRef] [PubMed]
- Biewener, A.A.; Alexander, R.M.; Heglund, N.C. Elastic energy storage in the hopping of kangaroo rats (Dipodomys spectabilis). J. Zool. 1981, 195, 369–383. [Google Scholar] [CrossRef]
- Bennett, M.B.; Taylor, G.C. Scaling of elastic strain energy in kangaroos and the benefits of being big. Nature 1995, 378, 56–59. [Google Scholar] [CrossRef] [PubMed]
- Alexander, R.M.; Jayes, A.S.; Maloiy, G.M.O.; Wathuta, E.M. Allometry of the leg muscles of mammals. J. Zool. 1981, 194, 539–552. [Google Scholar] [CrossRef]
- Pollock, C.M.; Shadwick, R.E. Allometry of muscle, tendon, and elastic energy storage capacity in mammals. Am. J. Physiol. 1994, 266, R1022–R1031. [Google Scholar] [CrossRef] [PubMed]

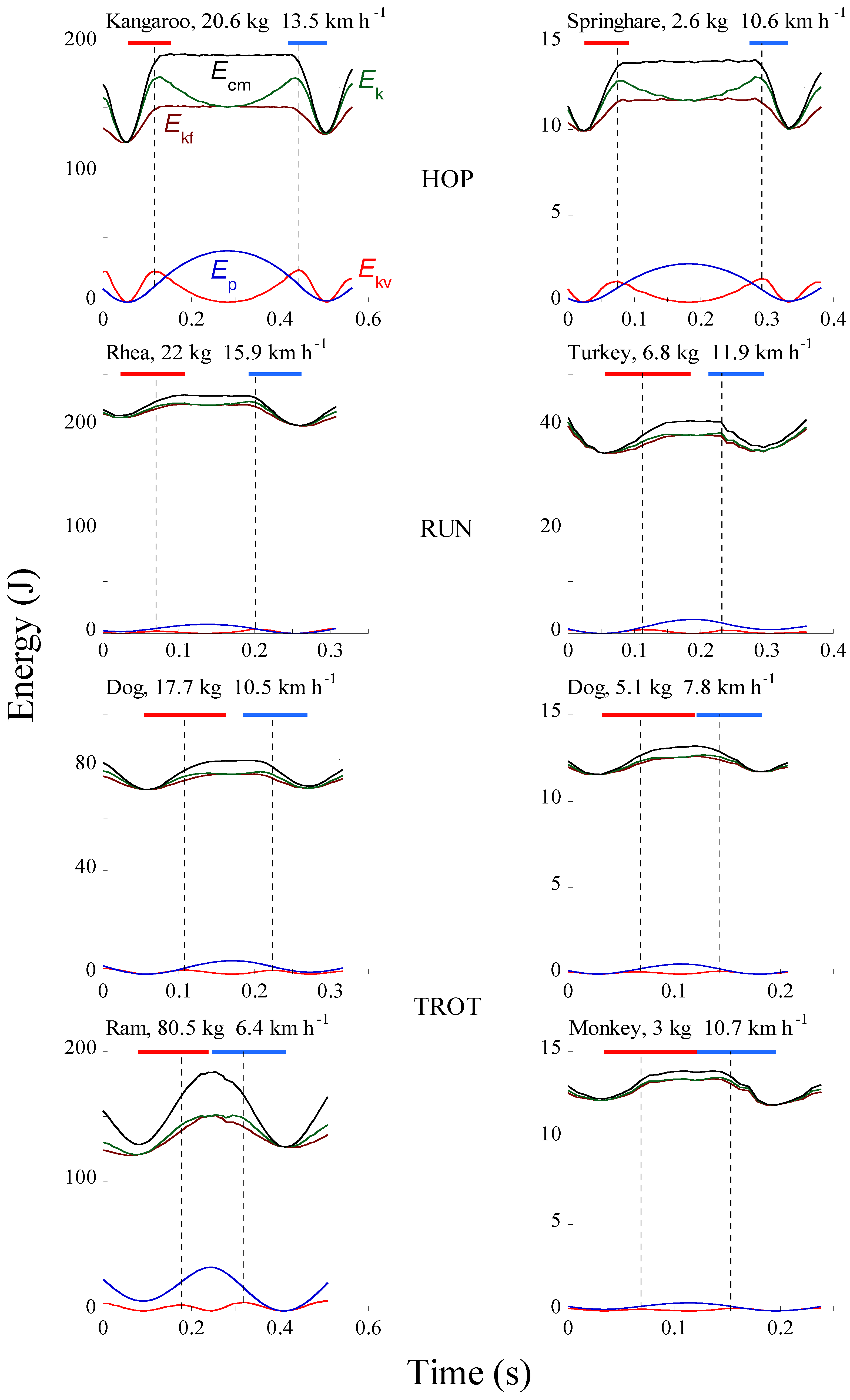
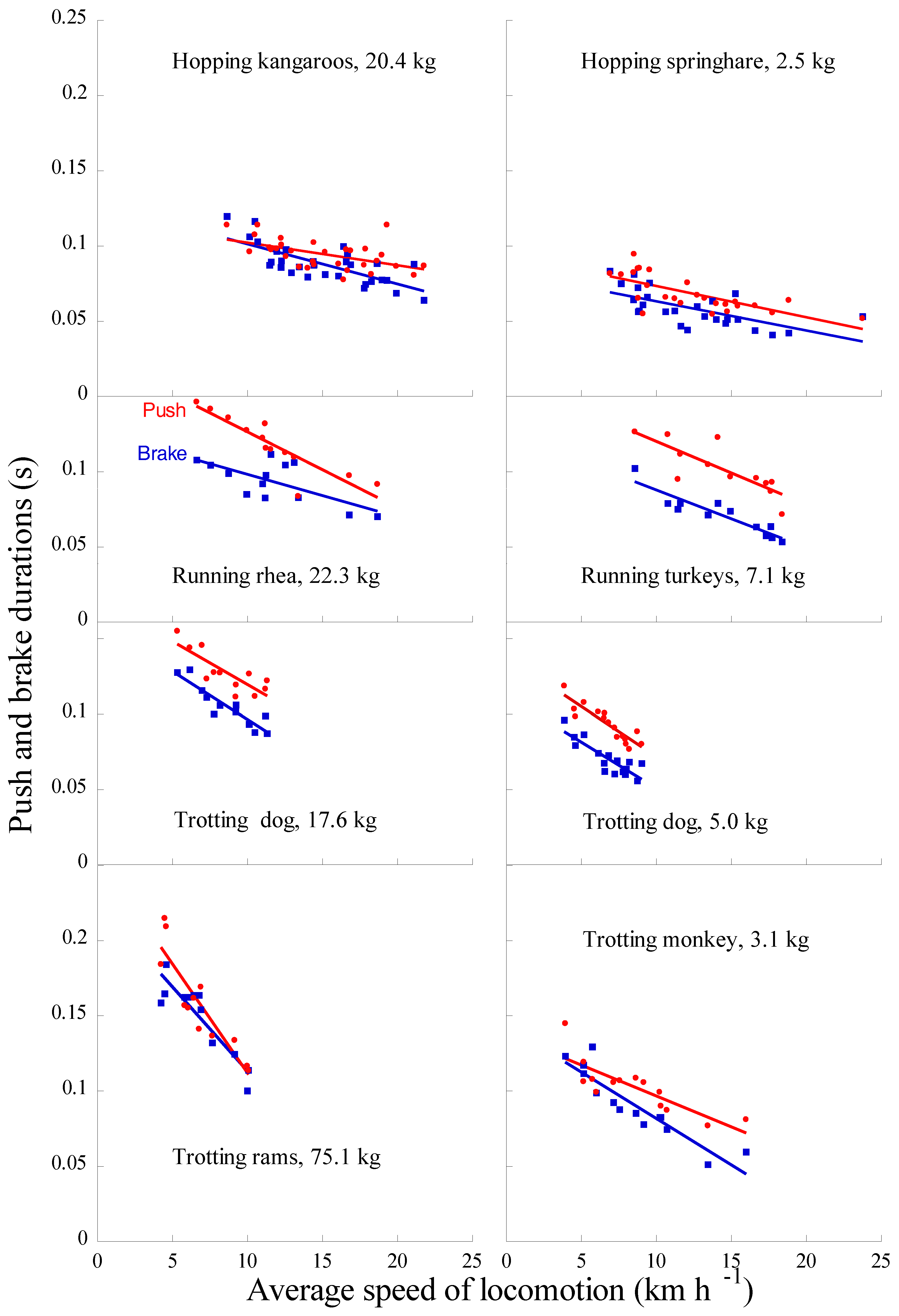
| a | ||||
| HOP | RUN | |||
| Kangaroos n = 31 | Springhare n = 26 | Rhea n = 13 | Turkeys n = 12 | |
| Mass (kg) | 20.4 ± 0.5 | 2.5 ± 0.1 | 22.4 ± 0.4 | 7.2 ± 0.3 |
| tpush (s) | 0.095 ± 0.010 | 0.069 ± 0.012 | 0.118 ± 0.019 | 0.102 ± 0.017 |
| tbrake (s) | 0.088 ± 0.013 | 0.059 ± 0.012 | 0.094 ± 0.014 | 0.071 ± 0.014 |
| tpush/tbrake | 1.091 ± 0.151 | 1.190 ± 0.196 | 1.272 ± 0.189 | 1.443 ± 0.140 |
| k/Mb (s−2) | 644.9 ± 170.5 | 1411.3 ± 492.0 | 596.7 ± 270.0 | 886.7 ± 252.7 |
| fs (Hz) | 4.01 ± 0.52 | 5.90 ± 1.02 | 3.82 ± 0.77 | 4.70 ± 0.65 |
| fstep (Hz) | 2.19 ± 0.19 | 3.04 ± 0.20 | 3.63 ± 0.43 | 4.44 ± 0.43 |
| Av,mx,up (ms−2) | 39.45 ± 4.72 | 42.30 ± 10.85 | 12.53 ± 2.64 | 13.40 ± 2.58 |
| W ext/Wmetab | 0.501 | 0.207 | 0.147 | 0.124 |
| b | ||||
| TROT | ||||
| Large dog n = 12 | Small dog n = 16 | Rams n = 12 | Monkey n = 14 | |
| Mass (kg) | 17.6 ± 0.2 | 5.0 ± 0.2 | 76.2 ± 11.4 | 3.1 ± 0.2 |
| tpush (s) | 0.128 ± 0.014 | 0.093 ± 0.012 | 0.158 ± 0.033 | 0.103 ± 0.017 |
| tbrake (s) | 0.105 ± 0.014 | 0.071 ± 0.011 | 0.149 ± 0.025 | 0.091 ± 0.023 |
| tpush/tbrake | 1.217 ± 0.099 | 1.334 ± 0.145 | 1.062 ± 0.119 | 1.166 ± 0.182 |
| k/Mb (s−2) | 762.1 ± 182.0 | 1547.4 ± 378.2 | 397.2 ± 183.3 | 1193.0 ± 444.4 |
| fs (Hz) | 4.36 ± 0.55 | 6.21 ± 0.80 | 3.10 ± 0.68 | 5.41 ± 1.00 |
| fstep (Hz) | 4.31 ± 0.41 | 6.18 ± 0.69 | 3.31 ± 0.64 | 5.21 ± 0.87 |
| Av,mx,up (ms-2) | 10.44 ± 1.61 | 8.99 ± 1.10 | 6.19 ± 2.41 | 9.66 ± 2.59 |
| Wext/ Wmetab | 0.262 | — | — | 0.153 |
© 2010 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavagna, G.A. Symmetry and Asymmetry in Bouncing Gaits. Symmetry 2010, 2, 1270-1321. https://doi.org/10.3390/sym2031270
Cavagna GA. Symmetry and Asymmetry in Bouncing Gaits. Symmetry. 2010; 2(3):1270-1321. https://doi.org/10.3390/sym2031270
Chicago/Turabian StyleCavagna, Giovanni A. 2010. "Symmetry and Asymmetry in Bouncing Gaits" Symmetry 2, no. 3: 1270-1321. https://doi.org/10.3390/sym2031270
APA StyleCavagna, G. A. (2010). Symmetry and Asymmetry in Bouncing Gaits. Symmetry, 2(3), 1270-1321. https://doi.org/10.3390/sym2031270





