Symmetry in Boolean Satisfiability
Abstract
:1. Introduction
2. Boolean Satisfiability

3. Symmetry Definitions and Notations

4. Graph Automorphism
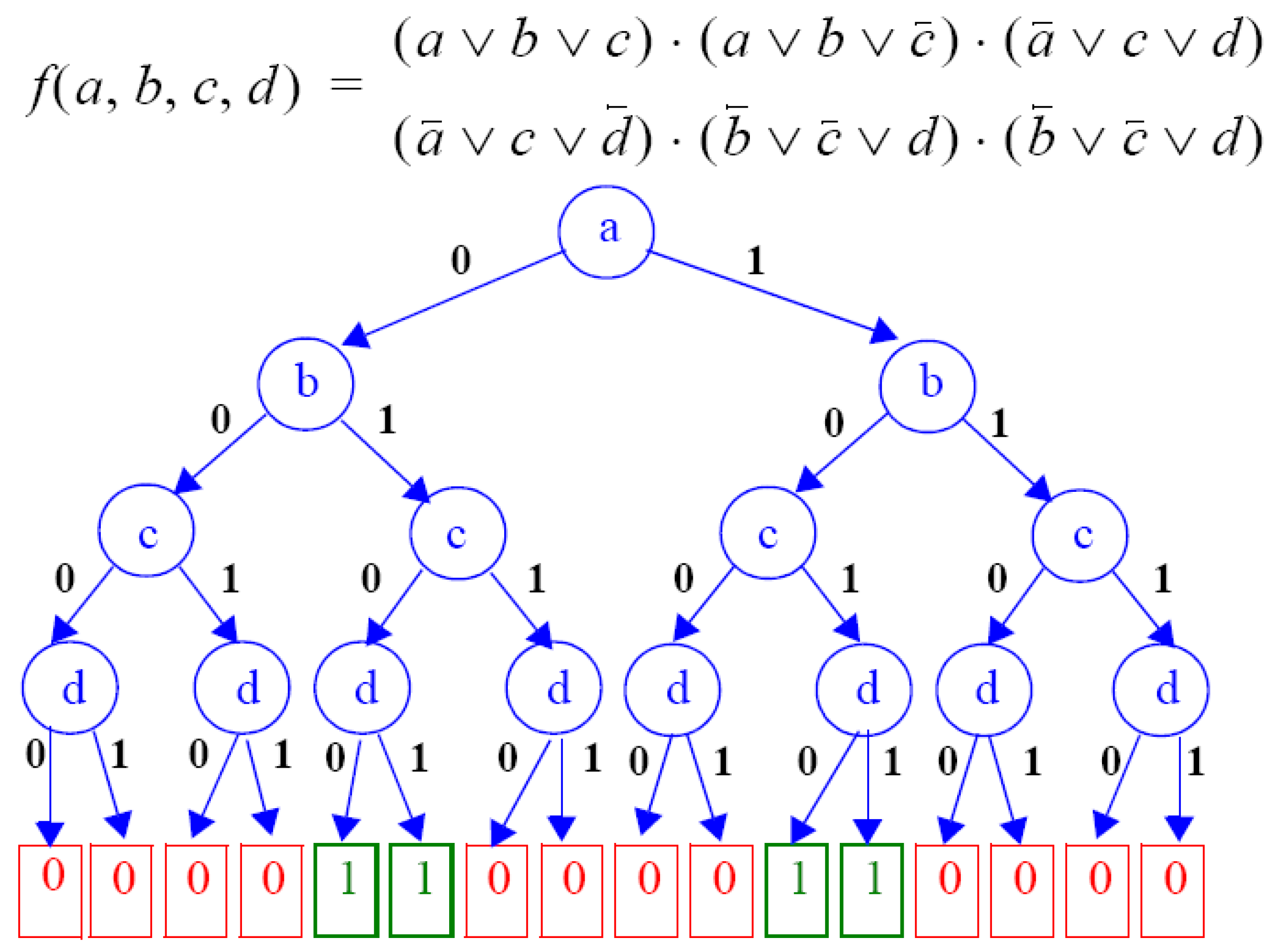
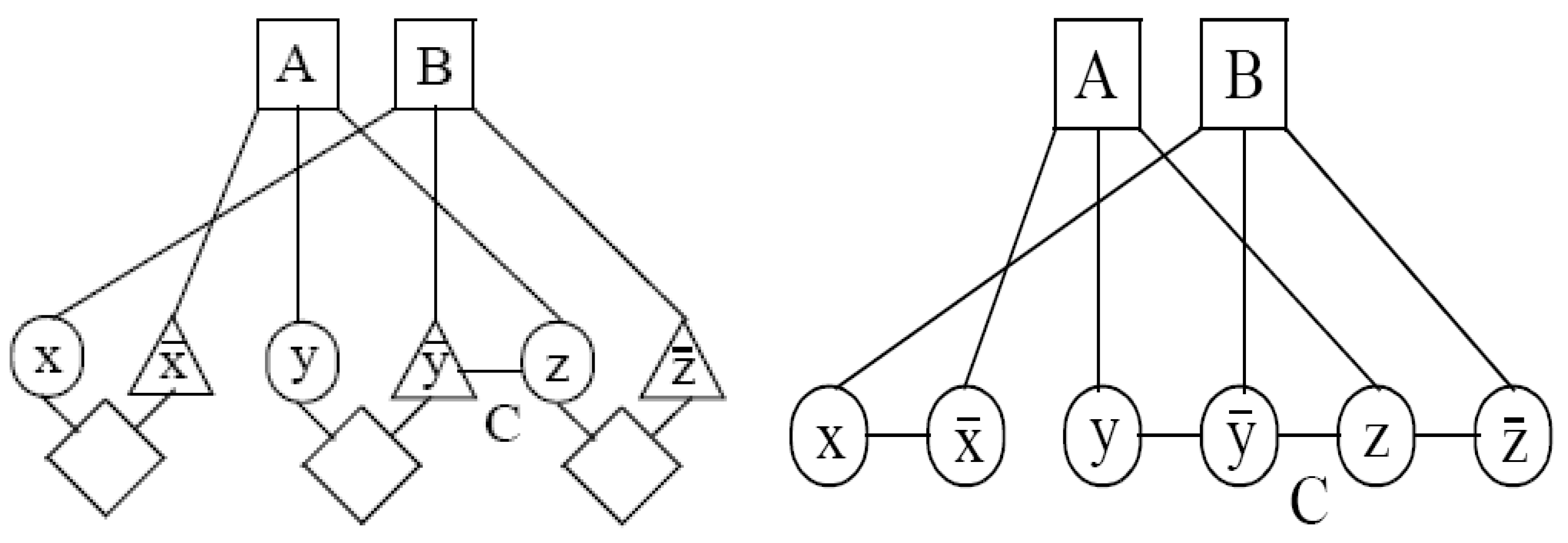
5. Detecting Symmetries in CNF Formulas
- A single vertex is created for each clause in Cx.
- Two vertices are created for each variable, representing its positive and negative literals.
- Edges are added connecting a clause vertex to its respective literal vertices.
- A single vertex is created for each clause in Cx.
- Two vertices are created for each variable, representing its positive and negative literals.
- Edges are added connecting a clause vertex to its respective literal vertices.
6. Breaking Symmetries in CNF Formulas
- An outer conjunction over all permutations in the group of symmetries.
- An inner conjunction over all variables in the permutation.



7. Experimental Results
8. Conclusions
References
- Biere, A.; Cimatti, A.; Clarke, E.; Fujita, M.; Zhu, Y. Symbolic model checking using SAT procedures instead of BDDs. In Proceedings of the Design Automation Conference (DAC), New Orleans, LA, USA, June 1999; pp. 317–320. [Google Scholar]
- Nam, G.; Aloul, F.; Sakallah, K.; Rutenbar, R.A. Comparative study of two boolean formulations of FPGA detailed routing constraints. IEEE Trans. Comput. 2004, 53, 688–696. [Google Scholar] [CrossRef]
- Sagahyroon, A.; Aloul, F. Using SAT-based techniques in power estimation. Microelectronics J. 2007, 38, 706–715. [Google Scholar] [CrossRef]
- Aloul, F.; Kandasamy, N. Sensor Deployment for Failure Diagnosis in Networked Aerial Robots: A Satisfiability-Based Approach. In Lecture Notes on Computer Science; Marques-Silva, J., Sakallah, K.A., Eds.; Springer-Verlag: Berlin, Germany, 2007; Volume 4501, pp. 369–376. [Google Scholar]
- Aloul, F.; Al-Rawi, B.; Aboelaze, M. Routing in optical and non-optical networks using boolean satisfiability. J. Commun. 2007, 2, 49–56. [Google Scholar] [CrossRef]
- Aloul, F.; Tarhuni, M. PN Code acquisition using boolean satisfiability techniques. In Proceedings of the IEEE Wireless Communications & Networking Conference, Budapest, Hungary, 5–8 April 2009; pp. 632–637. [Google Scholar]
- Aloul, F.; Al-Rawi, B.; Al-Farra, A.; Al-Roh, B. Solving employee timetabling problems using boolean satisfiability. In Proceedings of the IEEE Innovations in Information Technology Conference, Dubai, UAE, November 2006; pp. 1–5. [Google Scholar]
- Cook, S. The Complexity of Theorem Proving Procedures. In Proceedings of the Annual ACM Symposium on the Theory of Computing, Shaker Heights, OH, USA, 1971; pp. 151–158. [Google Scholar]
- Prasad, M.; Chong, P.; Keutzer, K. Why is ATPG easy? In Proceedings of the Design Automation Conference (DAC), New Orleans, LA, USA, June 1999; pp. 22–28. [Google Scholar]
- Marques-Silva, J.; Sakallah, K. GRASP: A Search Algorithm for Propositional Satisfiability. IEEE Trans. Comput. 1999, 48, 506–521. [Google Scholar] [CrossRef]
- Moskewicz, M.; Madigan, C.; Zhao, Y.; Zhang, L.; Malik, S. Chaff: Engineering an Efficient SAT Solver. In Proceedings of the Design Automation Conference (DAC), Las Vegas, NV, USA, June 2001; pp. 530–535. [Google Scholar]
- Goldberg, E.; Novikov, Y. BerkMin: A Fast and Robust SAT-solver. In Proceedings of the Design Automation and Test Conference in Europe (DATE), Paris, France, March 2002; pp. 142–149. [Google Scholar]
- Een, N.; Sorensson, N. An Extensible SAT-solver. In Proceedings of the International Conference on Theory and Applications of Satisfiability Testing (SAT), Santa Margherita Ligure, Italy, May 2003; pp. 502–508. [Google Scholar]
- Davis, M.; Longman, G.; Loveland, D. A Machine Program for Theorem Proving. J. ACM 1962, 5, 394–397. [Google Scholar] [CrossRef]
- Marques-Silva, J.; Glass, T. Combinational Equivalence Checking Using Satisfiability and Recursive Learning. In Proceedings of the Design Automation and Test Conference in Europe (DATE), Munich, Germany, March 1999; pp. 145–149. [Google Scholar]
- Bjesse, P.; Claessen, K. SAT-based Verification without State Space Traversal. In Proceedings of the Formal Methods in Computer-Aided Design (FMCAD), Austin, TX, USA, November 2000; pp. 372–389. [Google Scholar]
- Mneimneh, M.; Aloul, F.; Weaver, C.; Chatterjee, S.; Sakallah, K.; Austin, T. Scalable Hybrid Verification of Complex Microprocessors. In Proceedings of the Design Automation Conference (DAC), Las Vegas, NV, USA, June 2001; pp. 41–46. [Google Scholar]
- Fallah, F.; Devadas, S.; Keutzer, K. Functional Vector Generation for HDL Models Using Linear Programming and 3-Satisfiability. In Proceedings of the Design Automation Conference (DAC), San Francisco, CA, USA, June 1998; pp. 528–533. [Google Scholar]
- Marques-Silva, J.; Sakallah, K. Robust Search Algorithms for Test Pattern Generation. In Proceedings of the International Symposium on Fault Tolerant Computing (FTCS), Seattle, WA, USA, June 1997; pp. 151–161. [Google Scholar]
- Chen, C.; Gupta, S. A Satisfiability-Based Test Generator for Path Delay Faults in Combinational Circuits. In Proceedings of the Design Automation Conference (DAC), Las Vegas, NV, USA, June 1996; pp. 209–214. [Google Scholar]
- Aloul, F.; Ramani, A.; Markov, I.L.; Sakallah, K. Generic ILP versus Specialized 0-1 ILP. In Proceedings of the International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, November 2002; pp. 450–457. [Google Scholar]
- Memik, S.; Fallah, F. Accelerated Boolean Satisfiability-Based Scheduling of Control Data Flow Graphs for High-Level Synthesis. In Proceedings of the International Conference on Computer Design (ICCD), Freiberg, Germany, September 2002; pp. 395–401. [Google Scholar]
- Chen, P.; Keutzer, K. Towards True Crosstalk Noise Analysis. In Proceedings of the International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, November 1999; pp. 132–138. [Google Scholar]
- Aloul, F.; Hassoun, S.; Sakallah, K.; Blaauw, D. Robust SAT-Based Search Algorithm for Leakage Power Reduction. In Lecture Notes on Computer Science; Youm, H.Y., Yung, M., Eds.; Springer-Verlag: Berlin, Germany, 2002; Volume 2451, pp. 167–177. [Google Scholar]
- Creignou, N.; Kanna, S.; Sudan, M. Complexity Classifications of Boolean Constraint Satisfaction Problems; Society for Industrial Mathematics: Philadelphia, PA, USA, 2001. [Google Scholar]
- Hungerford, T. Algebra. In Graduate Texts in Mathematics; Springer: New York, NY, USA, 1973. [Google Scholar]
- McKay, B. Practical Graph Isomorphism. Congressus Numerantium 1981, 30, 45–87. [Google Scholar] [CrossRef]
- Babai, L. Automorphism Groups, Isomorphism, Reconstruction. In Handbook of Combinatorics; MIT Press: Cambridge, MA, USA, 1996; Volume 2, Chapter 27; pp. 1447–1541. [Google Scholar]
- Darga, P.; Sakallah, K.; Markov, I. Faster Symmetry Discovery using Sparsity of Symmetries. In Proceedings of the Design Automation Conference (DAC), Anaheim, CA, USA, June 2008; pp. 149–154. [Google Scholar]
- Crawford, J. A Theoretical Analysis of Reasoning by Symmetry in First-Order Logic. In Proceedings of the AAAI Workshop on Tractable Reasoning, San Jose, CA, USA, July 1992; pp. 17–22. [Google Scholar]
- Crawford, J.; Ginsberg, M.; Luks, E.; Roy, A. Symmetry-Breaking Predicates for Search Problems. In Proceedings of the International Conference Principles of Knowledge Representation and Reasoning, Cambridge, MA, USA, November 1996; pp. 148–159. [Google Scholar]
- Aloul, F.; Ramani, A.; Markov, I.L.; Sakallah, K. Solving Difficult Instances of Boolean Satisfiability in the Presence of Symmetries. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2003, 22, 1117–1137. [Google Scholar] [CrossRef]
- Aloul, F.; Sakallah, K.; Markov, I.L. Efficient Symmetry-Breaking for Boolean Satisfiability. IEEE Trans. Comput. 2006, 55, 549–558. [Google Scholar] [CrossRef]
- DIMACS Challenge Benchmarks. Available online: ftp://Dimacs.rutgers.EDU/pub/challenge/sat/benchmarks/cnf (accessed on 11 June 2010).
- Urquhart, A. Hard Examples for Resolution. J. ACM 1987, 34, 209–219. [Google Scholar] [CrossRef]
- SAT 2002 Competition. Available online: http://www.satlive.org/SATCompetition/submittedbenchs.html (accessed on 11 June 2010).
- Pipatsrisawat, K.; Darwiche, A. A New Clause Learning Scheme for Efficient Unsatisfiability Proofs. In Proceedings of the Conference on Artificial Intelligence, Chicago, IL, USA, July 2008; pp. 1481–1484. [Google Scholar]
- The International SAT Competition. Available online: http://www.satcompetition.org/ (accessed on 11 June 2010).
| Permutation | CNF Formula |
|---|---|
 |  |
| SBP | Clauses |
|---|---|
 |  |
| Instance | S/U | # of Symmetries | # of Generators |
|---|---|---|---|
| chnl10_11 | UNS | 4.19631E + 28 | 39 |
| chnl10_12 | UNS | 6.04269E + 30 | 41 |
| chnl10_13 | UNS | 1.02121E + 33 | 43 |
| chnl11_12 | UNS | 7.31165E + 32 | 43 |
| chnl11_13 | UNS | 1.23567E + 35 | 45 |
| chnl11_14 | UNS | 2.42191E + 37 | 47 |
| fpga12_10_sat | SAT | 5.41777E + 16 | 28 |
| fpga12_11_sat | SAT | 1.78786E + 18 | 29 |
| fpga12_9_sat | SAT | 5.41777E + 14 | 25 |
| fpga13_10_sat | SAT | 1.89622E + 17 | 28 |
| fpga13_11_sat | SAT | 1.2515E + 19 | 30 |
| fpga13_12_sat | SAT | 9.01083E + 20 | 32 |
| hole10 | UNS | 1.4485E + 14 | 19 |
| hole11 | UNS | 1.91202E + 16 | 21 |
| hole12 | UNS | 2.98275E + 18 | 23 |
| hole13 | UNS | 5.42861E + 20 | 25 |
| hole8 | UNS | 14631321600 | 15 |
| hole9 | UNS | 1.31682E + 12 | 17 |
| s3-3-3-10 | SAT | 34828517376 | 28 |
| s3-3-3-1 | SAT | 8707129344 | 26 |
| s3-3-3-3 | SAT | 69657034752 | 29 |
| s3-3-3-4 | SAT | 26121388032 | 27 |
| s3-3-3-8 | SAT | 34828517376 | 28 |
| Urq3_5 | UNS | 536870912 | 29 |
| Urq4_5 | UNS | 8.79609E + 12 | 43 |
| Urq5_5 | UNS | 4.72237E + 21 | 72 |
| x1_16 | UNS | 131072 | 17 |
| x1_24 | UNS | 16777216 | 24 |
| x1_32 | UNS | 4294967296 | 32 |
| x1_36 | UNS | 68719476736 | 36 |
| TOTAL | 2.43444E + 37 | 941 | |
| Instance | S/U | Saucy Time (Sec) | RSAT Time (Sec) | MiniSAT Time (Sec) | ||||
|---|---|---|---|---|---|---|---|---|
| Orig | w/SBP | Speedup | Orig | w/SBP | Speedup | |||
| chnl10_11 | UNS | 0.04 | >1000 | 0.01 | >100000 | 67.92 | 0.01 | 6792 |
| chnl10_12 | UNS | 0.05 | >1000 | 0.01 | >100000 | 115.26 | 0.01 | 11526 |
| chnl10_13 | UNS | 0.07 | >1000 | 0.01 | >100000 | 108.97 | 0.01 | 10897 |
| chnl11_12 | UNS | 0.07 | >1000 | 0.01 | >100000 | 520.44 | 0.01 | 52044 |
| chnl11_13 | UNS | 0.08 | >1000 | 0.01 | >100000 | >1000 | 0.01 | >100000 |
| chnl11_14 | UNS | 0.09 | >1000 | 0.01 | >100000 | >1000 | 0.01 | >100000 |
| fpga12_10_sat | SAT | 0.04 | 0.01 | 0.001 | 10 | 0.01 | 0.01 | 1 |
| fpga12_11_sat | SAT | 0.05 | 0.01 | 0.001 | 10 | >1000 | 0.01 | >100000 |
| fpga12_9_sat | SAT | 0.03 | 0.04 | 0.01 | 4 | 0.01 | 0.01 | 1 |
| fpga13_10_sat | SAT | 0.05 | 0.05 | 0.001 | 50 | 0.01 | 0.01 | 1 |
| fpga13_11_sat | SAT | 0.06 | 0.08 | 0.001 | 80 | 0.01 | 0.01 | 1 |
| fpga13_12_sat | SAT | 0.07 | 0.01 | 0.01 | 1 | 0.01 | 0.01 | 1 |
| hole10 | UNS | 0.01 | 348.65 | 0.001 | 348650 | 65.85 | 0.01 | 6585.0 |
| hole11 | UNS | 0.01 | >1000 | 0.001 | >1000000 | >1000 | 0.01 | >100000 |
| hole12 | UNS | 0.01 | >1000 | 0.001 | >1000000 | >1000 | 0.01 | >100000 |
| hole13 | UNS | 0.03 | >1000 | 0.001 | >1000000 | >1000 | 0.01 | >100000 |
| hole8 | UNS | 0 | 0.18 | 0.001 | 180 | 0.49 | 0.01 | 49.0 |
| hole9 | UNS | 0 | 51.14 | 0.001 | 51140 | 3.24 | 0.01 | 324.0 |
| s3-3-3-10 | SAT | 0.42 | 2.25 | 0.09 | 25 | 0.69 | 0.26 | 2.7 |
| s3-3-3-1 | SAT | 0.24 | 0.08 | 0.75 | 0.1 | 1.44 | 0.12 | 12 |
| s3-3-3-3 | SAT | 0.4 | 0.07 | 0.16 | 0.4 | 0.31 | 0.19 | 1.6 |
| s3-3-3-4 | SAT | 0.37 | 0.79 | 0.36 | 2.2 | 0.21 | 0.14 | 1.5 |
| s3-3-3-8 | SAT | 0.35 | 0.4 | 0.27 | 1.5 | 0.16 | 0.17 | 0.9 |
| Urq3_5 | UNS | 0.03 | 369.57 | 0.1 | 3695 | 84.44 | 0.19 | 444.4 |
| Urq4_5 | UNS | 0.08 | >1000 | 135.54 | >7.4 | >1000 | 27.25 | 36.7 |
| Urq5_5 | UNS | 0.37 | >1000 | >1000 | 1 | >1000 | 780.4 | 1.3 |
| x1_16 | UNS | 0 | 0.01 | 0.01 | 1 | 0.02 | 0.001 | 20 |
| x1_24 | UNS | 0.01 | 34.04 | 0.01 | 3404 | 2.77 | 0.03 | 92.3 |
| x1_32 | UNS | 0.01 | 1.33 | 0.01 | 133 | 13.84 | 0.01 | 1384 |
| x1_36 | UNS | 0.03 | 188.77 | 0.29 | 650.9 | 42.85 | 0.16 | 267.8 |
| TOTAL | 3 | 11997 | 1138 | 9029 | 809 | |||
© 2010 by the author; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Aloul, F.A. Symmetry in Boolean Satisfiability. Symmetry 2010, 2, 1121-1134. https://doi.org/10.3390/sym2021121
Aloul FA. Symmetry in Boolean Satisfiability. Symmetry. 2010; 2(2):1121-1134. https://doi.org/10.3390/sym2021121
Chicago/Turabian StyleAloul, Fadi A. 2010. "Symmetry in Boolean Satisfiability" Symmetry 2, no. 2: 1121-1134. https://doi.org/10.3390/sym2021121
APA StyleAloul, F. A. (2010). Symmetry in Boolean Satisfiability. Symmetry, 2(2), 1121-1134. https://doi.org/10.3390/sym2021121





