Hartee Fock Symmetry Breaking Effects in La₂CuO₄: Hints for connecting the Mott and Slater Pictures and Pseudogap Prediction

Abstract

This work expands the results and derivations presented in a recent letter. It is argued that symmetry breaking Hartree-Fock (HF) solutions of a simple model of the Cu-O planes in La${}_2$CuO${}_4$, are able to describe the insulator and antiferromagnetic characters of this material. Then, this classical primer of a Mott insulator is alternatively obtained here as an exact Slater insulator within the simplest of the $firstprinciples$ schemes. Moreover, pseudogap HF states are also predicted. The maximal energy gap of $100meV$ over the Fermi surface of this wavefunction, reasonably well matches the ARPES upper pseudogap measurements for La${}_2$CuO${}_4$ in the zero doping limit. These surprising results followed after eliminating spin and crystal symmetry constraints usually imposed on the HF orbitals. The discussion helps to clarify the role of the antiferromagnetism and pseudogaps in the physics of the HTSC materials and indicates a promising way to start conciliating the Mott and Slater pictures for the description of the transition metal oxides.

1. Introduction

The Hubbard type of models in the theory of strongly correlated electron systems are notably successful [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. In particular, it is remarkable the way they reproduce the properties of Mott insulators, such as metal-transitions oxides and copper-oxygen layered HTc compounds [11]. However, the efforts for developing approaches having more basic foundations has not ceased, due to the expectation that they could open the way for obtaining more exact and specific results [8,9,21]. In this sense, methods that are grouped into the so-called Band Theory approach are also known in the literature as first principles schemes. They are procedures for electronic structure calculations that begin with the interactions among electrons or atoms in vacuum. The study of the band structure they predict is expected to offer a road toward the effective and precise determination of the physical properties of each material [21,22]. Some of them are: the Configurations Interaction scheme (CI); the Local Density Approximations method (LDA)[23], the Local Spin Density Approximations procedure (LSDA) and the Hartree-Fock method (HF). However, the above mentioned potentialities of those first principles approaches have failed in describing many of the so-called strongly correlated electron systems [11]. For example, the LSDA, a sophisticated generalization of the LDA procedure, was devised to describe local spin structures [21]. However, although the method has given satisfactory descriptions of the physical properties in few materials, this success has not been universal, and it also wrongly predicted the properties of some compounds, for example, the here considered La${}_2$CuO${}_4$ [21].

The motivation for this work and its previous letter version (See Ref. [24]), arose from a primary suspicion that perhaps the self-consistent Hartree Fock (HF) method could have been underestimated in its possibilities for helping in the above described searches [2,25,33]. In this sense, the criterium is widespread that for obtaining behaviors such as the Mott insulator character, the presence of short range correlations among electrons with spin quantized in different directions becomes necessary. For example, paraphrasing one type of Mott’s argument for specific systems:"... two electrons with spin resting on contrary directions are forbidden to occupy the same Wannier orbital... ". Moreover, the orthodox HF approaches do not take into account the correlations among electrons of different spins. Therefore, two electrons with opposite spins do not disturb each other and consequently both of them can occupy the same Wannier orbital. Therefore, the usual HF approach generally appeared as not viable for investigating a system in which the Mott’s argument is appropriate. However, the physical sources of the validity of the cited Mott’s statements in some systems are not completely clear. For example: what is the physical origin of these short range correlations assumed in it? Even the proper concept of correlations, roughly described as: ”everything missing in the single-particle HF state for to be the real many body ground state”, renders their origin unclear. Resulting from the study presented here, we believe that numerous and important correlation effects can be effectively described even in the framework of the HF scheme, after removing certain symmetry restrictions, which obstruct the finding of the best HF solutions. Such constraints are usually imposed on the space formed by the single particle orbitals, which are employed to construct the determinant like states among which the Hartree-Fock one shows minimal energy. For example, if after solving the HF problem, it occurs that the resulting self-consistent potential breaks the symmetry of the original crystalline lattice, it could create a gap and thus produce a Mott kind of insulating solution. This effect was originally discovered by Slater in Ref. [2]. This symmetry breaking effect has also been underlined and deepened more recently in Ref. [42,43]. However, the removal of this kind of symmetry restrictions alone have not been able to describe the insulator properties of a large class of materials [11,21]. One of the central results of the present investigation, as will be described in what follows, is the identification of another important kind of symmetry restrictions, whose relevance had been seemingly overlooked up to now.

The present work considers the Hartree-Fock self-consistent problem as applied to a simple one band model of La${}_2$CuO${}_4$ [34], by following a particular approach. In order to leave freedom to obtain paramagnetic, ferromagnetic and antiferromagnetic solutions in the same context, we look for single particle orbitals being non separable in their spacial and spinor dependences, i.e., they will have the structure $\varphi (x,s)\ne \varphi \left(x\right)\psi \left(s\right)$. In other words, in those states there is no absolute common quantization direction for the electron spin. Thus, in each position the spin is quantized in a specific direction, and the equations of motion to be used will reflect this fact. Note that to proceed in this way is nothing other than to apply the Dirac’s unrestricted formulation of the HF procedure [25], or its more recent implementation in the so-called "non-collinear magnetism" schemes [26,27,28,29,30]. In this approach, either within the density functional or in the context of Hartree-Fock calculations, in each case single particle states are allowed to show spatial spin orientations varying from point to point. A review of the allowed spontaneous breaking symmetry magnetic lattice structures that can arise within the extended Hartree-Fock crystal calculations can be found in Ref. [31].

In our view, the restriction to $\alpha$ and $\beta$ types of orbitals, usually employed in HF electronic band and quantum chemistry calculations, prohibits from the start the prediction of possible spontaneously symmetry breaking effects [33,44]. Such a particular structure excessively reduces the space of functions to be examined and consequently eliminates possibilities of obtaining exotic solutions, which could perhaps be able to describe currently classified as purely strong correlation effects. We believe that in the context of the band theory, or more precisely, under the HF approach, it could be yet possible to reproduce the main characteristics of a wide class of Mott insulator kind of materials. The results of the simple model investigated here, as it will be seen, support this possibility for an important compound such as La${}_2$CuO${}_4$, which under certain doping levels turns into a high temperature superconductor [34]. The present work is headed in that direction, with the aim of further evidencing the potential of implementing the above considerations in self-consistent HF calculations for describing electronic bands in transition metal oxides and in studying the mechanism of HTc superconductivity. It seems worth to remark that the symmetry breaking effects in the context of Hartree-Fock scheme can be frequently accompanied by a symmetry-restoration transition to a symmetric state. This state turns to be a linear combination of degenerate symmetry breaking solutions, which are not representable as mean field configurations [41,42]. Such symmetrized states are always necessary in the case of finite (mesoscopic) systems [42]. For infinitely extended crystals, in particular for the bulk HTc ones, the resonating valence bond (RVB) state for high-Tc materials is an example of a symmetry-restored configuration [32]. However, the experimental observations of the antiferromagnetic structure in the La${}_2$CuO${}_4$ indicates that the RVB state is not the preferred one for the half filling case considered here. However, the result might vary upon doping. The generalization of the current analysis to include the hole doping is expected to be considered elsewhere.

The paper has the following structure. In Section 2 we describe the details of the HF self-consistent method employed in next sections. Specifically, the imposition of restrictions on the space of single particle states in which the solutions is searched are discussed. In Section 3, the effective model we are going to solve is explained. The symmetry restrictions assumed and the corresponding tight-binding Bloch basis are defined. Section 4 is devoted to deriving the HF equations associated with the set of interacting electrons. Their free hamiltonian is given by a specially constructed effective tight binding model. The tight binding Bloch basis associated with the model is chosen in this section to have the maximal symmetry given by the group of translations leaving invariant the copper-oxygen plane in La${}_2$CuO${}_4$. Considering the previously mentioned paramagnetic solution in a generic form, the free parameters of the effective hamiltonian are adjusted to reproduce the form of the single half filled band in the Matheiss calculation of the band structure of La${}_2$CuO${}_4$ [22]. After defining the free hamiltonian of the model, the antiferromagnetic and pseudogap paramagnetic HF solutions are obtained. Both solutions are also compared in this section. Their physical properties are commented on in corresponding subsections. For the AF solution, it is underlined how it gives a primer of a material conventionally classified as a Mott insulator, which here is obtained as an exact Slater insulator one, by means of the simplest of the first principles methods, the HF one. As for the pseudogap state, it is described how it predicts a reasonable estimate for the measures of the upper pseudogap in underdoped La${}_2$CuO${}_4$. The physical properties of this solution gives indications that generalize about the here considered HF scheme, to include temperature and doping, has opportunity to describe the phase diagram of the material, including the superconducting transition. Appendix A presents notations, algebraic developments, constants and definitions used throughout the text. In the final section, the main conclusions of the work are reviewed and various tasks for its extension are commented.

2. Rotational Invariant Hartree-Fock Method

In Quantum Mechanics, the state of a system of N particles is described by a function depending on each one particle’s spinor and spacial coordinates $f_n(x_1;s_1,\dots ,x_N;s_N)$, where n represents the corresponding set of quantum numbers [45]. The HF approximation consists in supposing that the above mentioned state can be expressed as a linear combination of N-products of orthonormalized orbitals ${\varphi }_{k_i}(x_i,s_i)$ with $i=1,\dots ,N$. Each orbital is interpreted as a single particle state, because it defines amplitude and probability distributions depending on a single particle coordinates. As usual, in what follows the word coordinates will mean the spacial as well as the spinor ones. If the particles are fermions, the previously mentioned linear combination is called Slater determinant [33,44,45]. Let

$$\widehat{h}(x_1,\dots x_N)=\sum _i{\widehat{h}}_0\left(x_i\right)+\frac{1}{2}\sum _{j\ne i}V(x_i,x_j),$$

(1)

be the N-electrons system hamiltonian, including kinetic plus interaction with the environment hamiltonian ${\widehat{h}}_0$, as well as Coulomb interaction among pairs of electrons V. The HF equations of motion for this system, leading the dynamic of the single particle states in a self-consistent way, are

$$\begin{array}{cc}\hfill [{\widehat{h}}_0\left(x\right)+\sum _{{\eta }_1}\sum _{s^{\prime }}\int d^2{x}^{\prime }{\varphi }_{{\eta }_1}^{*}(x^{\prime },s^{\prime })V(x,x^{\prime }){\varphi }_{{\eta }_1}(x^{\prime },s^{\prime })]{\varphi }_{\eta }(x,s)& \\ \hfill -\sum _{{\eta }_1}[\sum _{s^{\prime }}\int d^2{x}^{\prime }{\varphi }_{{\eta }_1}^{*}(x^{\prime },s^{\prime })V(x,x^{\prime }){\varphi }_{\eta }(x^{\prime },s^{\prime })]{\varphi }_{{\eta }_1}(x,s)& ={\epsilon }_{\eta }{\varphi }_{\eta }(x,s),\end{array}$$

(2)

where $\eta =k_1,\dots ,k_N$ is a label in the basis formed by the solutions. That is, each HF electron state is influenced by the presence of the others. The self-consistent Hamiltonian has two components, the Coulomb like type of mean potential which the electrons create: the direct potential and the contribution reflecting the fact that two electrons cannot occupy the same state: the exchange potential [25].

The HF energy of the N electrons system and the interaction energy of an electron in the $\eta$ state with the remaining ones are given by

$$\begin{array}{ccc}\hfill E_{HF}& =& \sum _{\eta }\langle \eta |{\widehat{h}}_0|\eta \rangle +\frac{1}{2}\sum _{\eta ,{\eta }_1}\langle \eta ,{\eta }_1|V|{\eta }_1,\eta \rangle -\frac{1}{2}\sum _{\eta ,{\eta }_1}\langle \eta ,{\eta }_1|V|\eta ,{\eta }_1\rangle ,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill a_{\eta }& =& \frac{1}{2}\sum _{{\eta }_1}\langle \eta ,{\eta }_1|V|{\eta }_1,\eta \rangle -\frac{1}{2}\sum _{{\eta }_1}\langle \eta ,{\eta }_1|V|\eta ,{\eta }_1\rangle .\hfill \end{array}$$

(4)

The definition of the brackets in the above equation is given in Appendix A., Subsection A.1. It can be noted that the system of equations (2) is rotational invariant because it is written without imposing a spatially absolute direction for the spin quantization of the single electron orbitals. This rotational invariant formulation of the self-consistent HF procedure was firstly introduced by Dirac in [25].

2.1. $\alpha$, $\beta$ and symmetry restrictions

It is a complicated task to solve (2) because it is a system of coupled integro-differential equations. The iterative method is one of the most frequently employed for solving this kind of systems and it is usually complemented by the imposition of symmetry restrictions that simplify the space of states to be investigated. However, the use of such constraints could avoid the obtention of special solutions non obeying the added symmetry conditions. Although in some cases they could retain the minimal energy one, the method can hide the existence of interesting excited states and even could wrongly predict the excitation features in some cases, as it will be seen in what follows. A very common symmetry restriction usually employed in band theory and quantum chemistry calculations is to consider that single particle solutions of (2) have spin quantized in a given direction in every point of the space [22,44]. That is

$$\begin{array}{c}\hfill {\varphi }_{\mathbf{k}}(x,s)=\left\{\begin{array}{cc}{\varphi }_{\mathbf{k}}^{\alpha }\left(x\right)u_{\uparrow }\left(s\right)\hfill & \alpha \mathrm{state},\hfill \\ {\varphi }_{\mathbf{k}}^{\beta }\left(x\right)u_{\downarrow }\left(s\right)\hfill & \beta \mathrm{state},\hfill \end{array}\right.\end{array}$$

(5)

where $u_{\uparrow \downarrow }$ represent the Pauli spinors with spin up and down in a certain direction respectively. If the spacial functions ${\varphi }_{\mathbf{k}}^{\alpha }$ and ${\varphi }_{\mathbf{k}}^{\beta }$ are the same, the HF calculation is called a restricted one, if they are different, the procedure is called unrestricted [44]. It is interesting to investigate the consequences of considering the possible existence of non separable single particle states being solutions of the HF problem. A positive answer to this question can open a natural context for obtaining solutions exhibiting magnetic properties and to allow their comparison with paramagnetic ones.

Another important kind of restrictions posed on the first principles band theory evaluations is the a priori impositions of crystal symmetries. To impose a symmetry on a solution to be searched has the risk of hiding a possible spontaneous breaking of that invariance. This could occurs due to the reduction of the space orbitals in which we are searching. In that case it can turn out that the obtained solutions will not be an absolute extremal of the energy functional, but a conditional one, due to the fixed symmetry constraint. For instance, let us consider the functional space formed by the allowed orbitals and the maximal subset of orbitals U which is invariant under a certain group of transformations T. Consider also the maximal subset U${}_s$ being invariant under the group of transformations T${}_s$, which is a subgroup of T. Then, the set U${}_s$ obtained from imposing less symmetry restrictions a priori, should contain the set U. Therefore, after finding the extremes of the same functional in U and U${}_s$, it could be possible to obtain different results. In this case, the solution in U${}_s$, in general, shall be the most stable of both. However, it could be also the case that looking for a solution in U${}_s$, an extremal function also pertaining to U arises as a solution. In such a situation, such a configuration could be found from the beginning by finding the extreme of the functional in U; that is: by imposing more symmetry restrictions. In terms of the HF scheme, this could mean that the states corresponding to both solutions have identical occupied single-particle states, but they curiously might show different sets of excited ones. Therefore, depending on the particular features of the material, removing a priori imposed symmetry restrictions on the set of allowed orbitals of the HF procedure can predict new properties for the excited single particle states of the system. Such one could be for instance the gap appearance. This effect can have physical relevance after noting that at finite temperatures the more stable state will be preferred by the system and then the state showing a gap should be expected to be selected at non zero temperature.

3. Tight Binding Electron Model: "Removing Symmetries"

In this section, the basis of the effective band model used to describe the dynamic of the less bounded La${}_2$CuO${}_4$ electrons will be presented. The main considerations for defining the model and the determination of its characteristic parameters are given. In Subsection 3.1 the simplified electronic model for the copper-oxygen planes, as well as the main definitions in its structure are introduced. Subsection 3.2 and Subsection 3.3 are devoted to define the symmetry transformation group defining the tight binding Bloch basis.

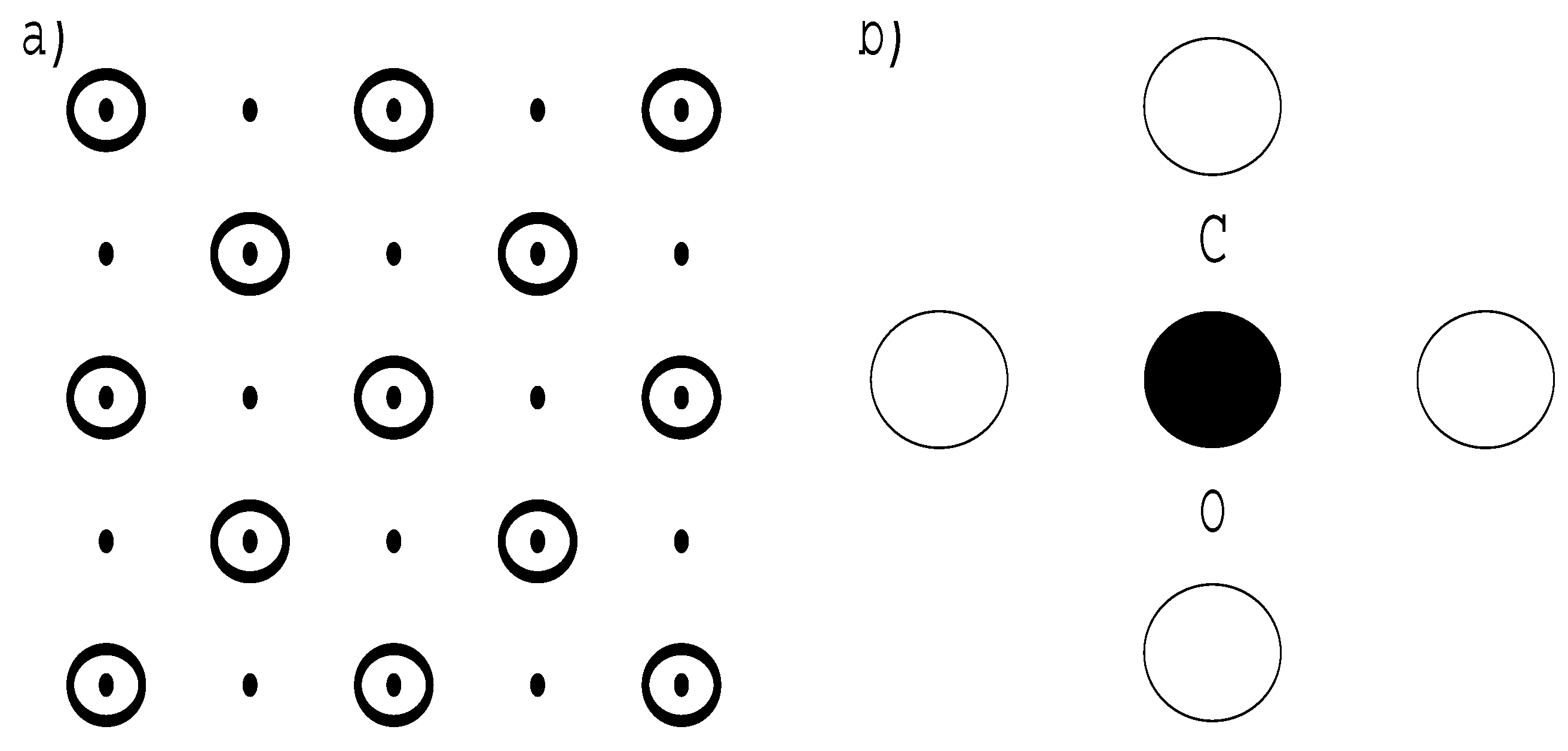
3.1. Model for the Cu-O planes

It is known that at low temperature, La${}_2$CuO${}_4$ is an antiferromagnetic-insulator [34]. However, evidence contradicting the experiments using the Linear Augmented Plane Waves (LAPW) method [22] predicts a metal and paramagnetic zero temperature properties for this material. Nevertheless, such band calculation results show that the conduction electrons are strongly coupled to the Bravais lattice centers of the copper oxygen planes. Clearly this tight-binding behavior is determined by the interaction of the electrons with their surrounding effective environment. This defines the initial hypothesis of our model.

The less bounded electron in the La${}_2$CuO${}_4$ molecule is the non-paired one of Cu${}^{2+}$. That is, differently from O${}^{2-}$ ions, the Cu ones do not have their last shell (3d) closed. Those copper 3d electrons fill the last band of La${}_2$CuO${}_4$ solid. In what follows, they shall be referred to as the electron gas. It seems appropriate to consider those electrons as strongly linked to CuO${}_2$ cells and, moreover, given the above mentioned arguments, with special preference for the Cu centers [5]. Thus, our Bravais lattice is going to be the squared net coincident with the array of copper sites (see Figure 1). The presence of electrons pertaining to the various fully filled bands in the material plus the nuclear charges, plays a double role in the model. Firstly, it will act as an effective polarizable environment, which screens the field created by electron charges constituting the electron gas in the half filled band. Consequently, we will introduce a dielectric constant $ϵ$, which will screen the Coulomb interaction. Secondly, as suggested by its spatial distribution and magnitude, the mean field created by the environment will be assumed to act as a periodic potential W${}_{\gamma }$ being responsible for tight-binding confinment of the electron to the Cu centers.

It is also primordial in the model to take into consideration the interaction F${}_b$ among the electron gas and the ”jellium” neutralizing its charges. This background will be modeled here as a Gaussian distribution of positive charges

$$\begin{array}{c}\hfill {\rho }_b\left(\mathbf{y}\right)=\frac{1}{\pi b^2}exp(-\frac{{\mathbf{y}}^2}{b^2}),\end{array}$$

(6)

surrounding each lattice point and with characteristic radius b.

In resume, the free hamiltonian of the model takes the form

$$\begin{array}{ccc}\hfill {\widehat{h}}_0(\mathbf{x})& =& \sum _{i=1}^N\frac{{\widehat{\mathbf{p}}}_i^2}{2m}+W_{\gamma }(\mathbf{x})+F_b(\mathbf{x}),\hfill \\ \hfill W_{\gamma }(\mathbf{x})& =& W_{\gamma }(\mathbf{x}+\mathbf{R}),\hfill \\ \hfill F_b(\mathbf{x})& =& \frac{e^2}{4\pi ϵ{ϵ}_0}\sum _{\mathbf{R}}\int d^{2}y\frac{{\rho }_b(\mathbf{y}-\mathbf{R})}{|\mathbf{x}-\mathbf{y}|},b\ll p,\hfill \end{array}$$

(7)

where ${\widehat{\mathbf{p}}}_i^2$ is the i-th electron’s squared momentum operator; m is the electron mass; ${ϵ}_0$ is the vacuum permittivity and

$$\begin{array}{ccc}\hfill \mathbf{R}& =& \left\{\begin{array}{c}{n}_{x_1}p{\widehat{\mathbf{e}}}_{x_1}+n_{x_2}p{\widehat{\mathbf{e}}}_{x_2},\hfill \\ \mathrm{with}{n}_{x_1}\mathrm{and}{n}_{x_2}\in \mathbb{Z},\hfill \end{array}\right.\hfill \end{array}$$

(8)

moves on Bravais lattice. The versors ${\widehat{\mathbf{e}}}_{x_1}$ and ${\widehat{\mathbf{e}}}_{x_2}$ are resting on the direction defined by the lattice’s nearest neighbours, see Figure 1 a). It is known that the distance among Cu nearest neighbours is p$\approx$ 3.8 Å [34]. We also consider the interaction among pairs of electrons in the form

$$\begin{array}{c}\hfill V(\mathbf{x},\mathbf{y})=\frac{e^2}{4\pi ϵ{ϵ}_0}\frac{1}{|\mathbf{x}-\mathbf{y}|},\end{array}$$

(9)

which, as remarked above, includes a dielectric constant associated to the presence of the effective environment.

We are looking here for HF solutions with orbitals having a non separable spin and orbit structures. Thus, it was considered that the spin can show a different projection for the different Wannier wavepackets to be added in defining those orbitals. The spin for each of them will be either $\alpha$ or $\beta$ type, if they are linked either to one or the other of the two sublattices shown in Figure 1 a). Thus, the single particle eigenstates will be chosen to be invariant, only under the reduced group of translations which transform each of those sublattices on to itself.

It is important to employ a procedure leaving the characteristics of the electron states in each one of the sublattices independently identified. That will allow us to analyze solutions with dissimilar qualities in a same framework, that is: antiferromagnetic AFM, paramagnetic PM and ferromagnetic FM ones. For this purpose, let us define the points of the two sublattices with indices r = 1, 2, as follows

$$\begin{array}{ccc}\hfill {\mathbf{R}}^{(r)}& =& \sqrt{2}{n}_{1}p{\widehat{\mathbf{q}}}_1+\sqrt{2}{n}_{2}p{\widehat{\mathbf{q}}}_2+{\mathbf{q}}^{(r)}\hfill \\ \hfill & \hfill & \mathrm{with}{n}_1\mathrm{and}{n}_2\in \mathbb{Z},\hfill \\ \hfill {\mathbf{q}}^{(r)}& =& \left\{\begin{array}{cc}\mathbf{0},\hfill & \mathrm{if}\mathrm{r}=1,\hfill \\ p{\widehat{\mathbf{e}}}_{x_1},\hfill & \mathrm{if}\mathrm{r}=2,\hfill \end{array}\right.\hfill \end{array}$$

(10)

where ${\widehat{\mathbf{q}}}_1$ and ${\widehat{\mathbf{q}}}_2$ form the basis versors on each one of them.

3.2. Translations on the sublattices

The solutions we are looking for, will be eigenfunctions of the operators ${\widehat{T}}_{{\mathbf{R}}^{(r)}}$ belonging to the reduced discrete translation group which transforms a given sublattice on itself:

$$\begin{array}{ccc}\hfill {\widehat{T}}_{{\mathbf{R}}^{(r)}}{\varphi }_{\mathbf{k},l}& =& exp(i\mathbf{k}·{\mathbf{R}}^{(r)}){\varphi }_{\mathbf{k},l}.\hfill \end{array}$$

(11)

If the Bravais lattice were infinite, the Brillouin’s zone (B.Z.) associated to ${\widehat{T}}_{{\mathbf{R}}^{(r)}}$ would be the shadowed one on figure 2 a). Note that the continent square in this figure represents the B.Z. associated to the group of translations which leaves invariant the absolute lattice (the lattice formed by the Cu atoms in the CuO planes). However, given the impossibility of considering an infinite lattice for numerically solving the HF problem, it is also not allowed to consider its associated B.Z. as continuous. Therefore we will impose periodic boundary conditions on the ${\varphi }_{\mathbf{k},l}$ in the absolute lattice’s boundaries x${}_1$= -L p y L p, x${}_2$= -L p y L p (see figure 2 b)). This condition determines the allowed set of k values

$$\begin{array}{ccc}\hfill \mathbf{k}& =& \left\{\begin{array}{c}\frac{2\pi }{Lp}(n_1{\widehat{\mathbf{e}}}_{x_1}+n_2{\widehat{\mathbf{e}}}_{x_2}),\hfill \\ \mathrm{with}{n}_1,n_2\in \mathbb{Z}\hfill \\ \mathrm{and}-\frac{L}{2}\le n_1\pm n_2<\frac{L}{2}.\hfill \end{array}\right.\hfill \end{array}$$

(12)

Therefore, after recalling the discussion given in the introduction, note that we are now demanding a lower amount of crystal symmetry on the single particle states that we are looking for, since a lower number of constraints are being imposed on the space of single particle states in which the solutions are searched.

3.3. Tight-Binding basis

The tight binding Bloch functions that we are going to use are the following

$$\begin{array}{ccc}\hfill {\phi }_{\mathbf{k}}^{(r,{\sigma }_z)}(\mathbf{x},s)& =& \sqrt{\frac{2}{N}}{u}^{{\sigma }_z}(s)\sum _{{\mathbf{R}}^{(r)}}exp(i\mathbf{k}·{\mathbf{R}}^{(r)}){\phi }_{{\mathbf{R}}^{(r)}}(\mathbf{x}),\hfill \\ \hfill {\widehat{\sigma }}_z{u}^{{\sigma }_z}& =& {\sigma }_z{u}^{{\sigma }_z},\hfill \\ \hfill {\phi }_{{\mathbf{R}}^{(r)}}(\mathbf{x})& =& \frac{1}{\sqrt{\pi a^2}}exp(-\frac{{(\mathbf{x}-{\mathbf{R}}^{(r)})}^2}{2a^2}),a\ll p,\hfill \end{array}$$

(13)

where N is the number of electrons in the electron gas, ${\widehat{\sigma }}_z$ is the spin z projection operator, where z is the orthogonal direction to the copper oxygen CuO${}_2$ planes; ${\sigma }_z=$ -1, 1, are the eigenvalues of the previously mentioned operator, and r = 1, 2, is the label which indicates each sublattice. As we are going to work on a half filling condition, then N coincides with the number of cells in the crystal with fixed periodic boundary conditions $N_c$. Note that due to the tiny overlapping among nearest neighbors approximation, the exact orthogonal character is only weakly lost between elements corresponding to different sublattices and having the same spin quantization. That occurs because nearest neighbors belong to different arrays. However, the orthogonality between different elements corresponding to the same sublattice is rigourously maintained. This is so because they are constructed as Bloch states in their corresponding sublattices. The Wannier orbitals ${\phi }_0(\mathbf{x}-{\mathbf{R}}^{(r)})$ represent the probability amplitude of finding one electron in the vicinity of the site ${\mathbf{R}}^{(r)}$, that is on the given cell CuO${}_2$.

Let us now describe some simplifications that will be adopted in order to solve the HF problem. The central aim of this work is not to make an exact study of the problem, instead we seek for approximate solutions reflecting qualitatively well the physical properties of La${}_2$CuO${}_4$ and other compounds. Following this principle we take for the Wannier orbitals the explicit form given in (13). Physically, this means that we will consider that the effective potential created by the environment on each electron of the half filled band, is a quadratic function having minima on the copper sites and strongly confining the electrons to them. This last consideration is similar to the one made on the t-J one band model.

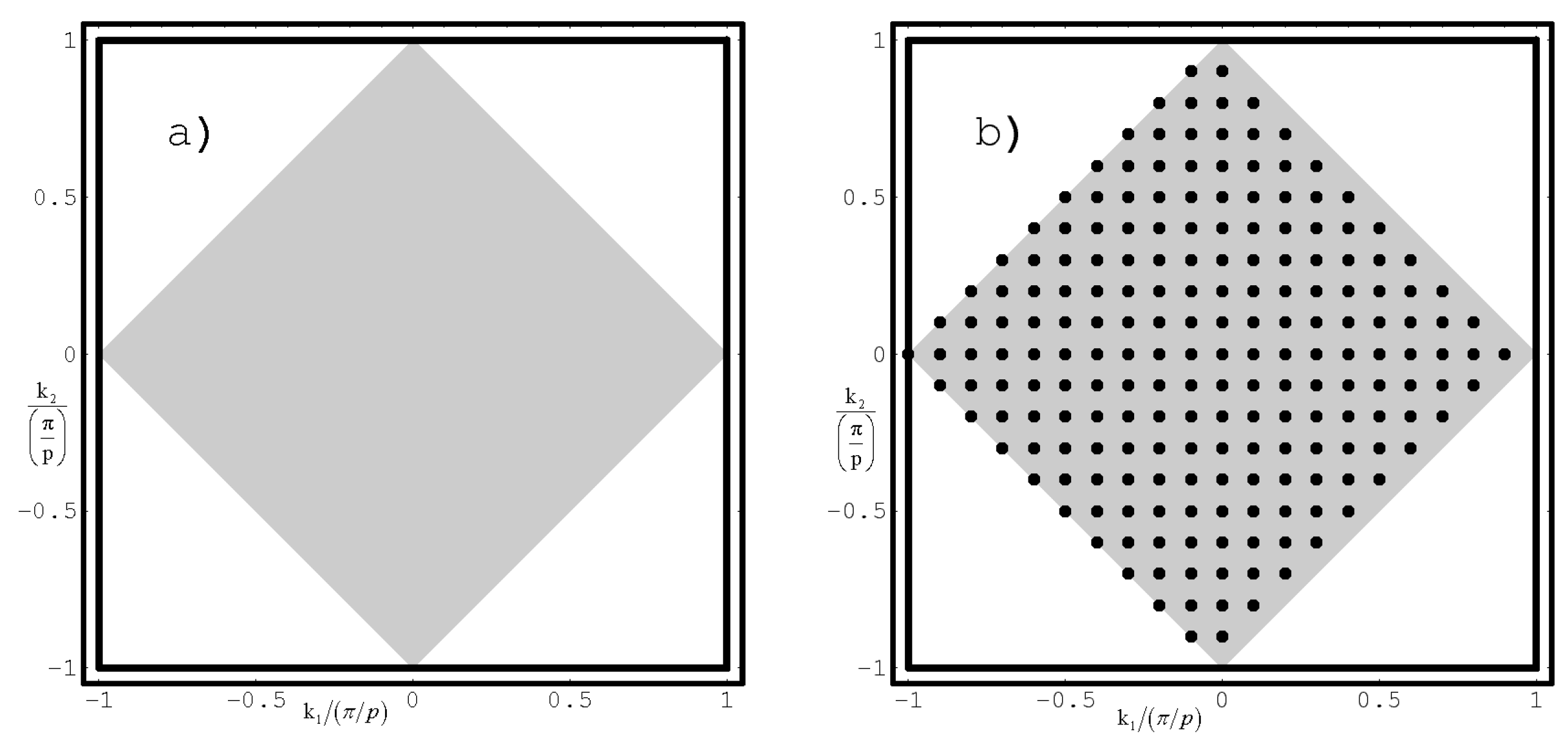
4. Matrix Problem and Solutions

In this section the main results of this work and their discussion are presented. In Subsection 4.1 the equivalent matrix problem, resulting from projecting the HF system of equations (2) on the tight binding Bloch basis (13) defined in the previous section is presented. Subsection 4.2 shows how the model, after imposing the maximal translational symmetry and an $\alpha$ and $\beta$ spin nature on the orbitals, is able to reproduce the dispersion relation of the La${}_2$CuO${}_4$ half filled band, appearing in the precise band structure calculations given in Ref. [22]. The solutions presented in subsection 4.3 and subsection 4.4, illustrate the consequences of releasing symmetry restrictions on the space in which HF solutions are searched. The first one corresponds to a Mott’s insulator-antiferromagnetic ground state. That is, the state corresponds to an insulator even though it has one electron per cell, precisely in the same way as La${}_2$CuO${}_4$ behaves. The second solution obtained corresponds to a paramagnetic state showing a pseudogap, and exactly the same HF energy and set of occupied single particle states of the previously obtained metal-paramagnetic state [22]. It is important to mention that all the band diagrams shown in this section are plotted on the same energy scale and the zero energy point coincides with the Fermi level of the antiferromagnetic ground state (IAF) presented in Subsection 4.3.

4.1. Tight-Binding representation

Let the searched single particle states be represented in the explicitly nonseparable form

$$\begin{array}{ccc}\hfill {\varphi }_{\mathbf{k},l}(\mathbf{x},s)& =& \sum _{r,{\sigma }_z}{B}_{r,{\sigma }_z}^{\mathbf{k},l}{\phi }_{\mathbf{k}}^{(r,{\sigma }_z)}(\mathbf{x},s),\hfill \end{array}$$

(14)

where l is the additional quantum number needed for indexing the stationary state on question, which we are going to define precisely later. After substituting (14), (7) and (9), in (2); followed by projecting the obtained result on the basis ${\phi }_{{\mathbf{k}}^{\prime }}^{(\mathbf{t},{\alpha }_z)}$ and an extensive algebraic work, it is possible to arrive to the following self-consistent matrix problem for the coefficients appearing in expansion (14):

$$\begin{array}{c}\hfill [{\mathrm{E}}_{\mathbf{k}}^0+\tilde{\chi }({\mathrm{G}}_{\mathbf{k}}^{dir}-{\mathrm{G}}_{\mathbf{k}}^{ind}-{\mathrm{F}}_{\mathbf{k}})].{\mathrm{B}}^{\mathbf{k},l}={\tilde{\epsilon }}_l(\mathbf{k}){\mathrm{I}}_{\mathbf{k}}.{\mathrm{B}}^{\mathbf{k},l},\end{array}$$

(15)

where each of the quantities

$$\begin{array}{ccc}\hfill {\mathrm{B}}^{\mathbf{k},l}& =& ∥B_{(r,{\sigma }_z)}^{\mathbf{k},l}∥,\hfill \end{array}$$

(16)

represents a vector having four components given by the four possible pairs $(r,{\sigma }_z)$. The constants

$$\begin{array}{c}\hfill \tilde{\chi }\equiv \frac{m{e}^2}{4\pi {\hslash }^2ϵ{ϵ}_0}\frac{a^2}{p},\\ \hfill {\tilde{\epsilon }}_l(\mathbf{k})\equiv \frac{m{a}^2}{{\hslash }^2}{\epsilon }_l(\mathbf{k}),\end{array}$$

(17)

are dimensionless. In them, e represents the vacuum charge of the electron; ℏ is the reduced Planck constant; a is the characteristic radius of the Wannier orbitals ${\phi }_0$, and p is the nearest neighbors separation. It is clear now that we can define l = 1, 2, 3, 4, as a label indicating each of the four solutions to be obtained for every value of quasi-momentum k. All the implicit parameters in the following 4×4 matrices are also dimensionless

$$\begin{array}{ccc}\hfill {\mathrm{E}}_{\mathbf{k}}^0& =& ∥E_{\mathbf{k},(t,{\alpha }_z);(r,{\sigma }_z)}^0∥,\hfill \\ \hfill {\mathrm{G}}_{\mathbf{k}}^{dir}& =& ∥G_{\mathbf{k},(t,{\alpha }_z);(r,{\sigma }_z)}^{dir}∥,\hfill \\ \hfill {\mathrm{G}}_{\mathbf{k}}^{ind}& =& ∥G_{\mathbf{k},(t,{\alpha }_z);(r,{\sigma }_z)}^{ind}∥,\hfill \\ \hfill {\mathrm{F}}_{\mathbf{k}}& =& ∥F_{\mathbf{k},(t,{\alpha }_z);(r,{\sigma }_z)}∥,\hfill \\ \hfill {\mathrm{I}}_{\mathbf{k}}& =& ∥I_{\mathbf{k},(t,{\alpha }_z);(r,{\sigma }_z)}∥.\hfill \end{array}$$

(18)

The set of quantities (18) constitutes the matrix representations of the periodic potential created by the mean field W${}_{\gamma }$, the direct and exchange terms in (2), the interaction potential with the neutralizing ”jellium” of charges F${}_b$ defined in (7), and the overlapping matrix among nearest neighbors, respectively. Each one of the four pairs $(t,{\alpha }_z)$ and $(r,{\sigma }_z)$ defines a row and a column of the matrix in question, respectively. The explicit forms of the matrix elements are given in Appendix A.

In this new representation the normalization condition for the HF single particle states and the HF energy of the system take the forms

$$\begin{array}{ccc}\hfill 1& =& {\mathrm{B}}^{\mathbf{k},l^{*}}.{\mathrm{I}}_{\mathbf{k}}.{\mathrm{B}}^{\mathbf{k},l},\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill E_{\mathbf{k},l}^{HF}& =& \sum _{\mathbf{k},l}\mathsf{\Theta }({\tilde{\epsilon }}_F-{\tilde{\epsilon }}_l(\mathbf{k}))[{\tilde{\epsilon }}_l(\mathbf{k})-\frac{\tilde{\chi }}{2}{\mathrm{B}}^{\mathbf{k},l^{*}}.({\mathrm{G}}_{\mathbf{k}}^{dir}-{\mathrm{G}}_{\mathbf{k}}^{ind}).{\mathrm{B}}^{\mathbf{k},l}],\hfill \end{array}$$

(20)

where $\mathsf{\Theta }$ is the Heaviside function.

The system (15) is non linear on the variables $B_{r,{\sigma }_z}^{\mathbf{k},l}$, which are the four components of each vector ${\mathrm{B}}^{\mathbf{k},l}$. They can be interpreted as a measure of the probability amplitude of finding an electron in the state (k, l), in the sublattice r, with spin z-projection ${\sigma }_z$. In order to solve the equations numerically by the method of iterations, it is convenient to pre-multiply them by ${\mathrm{I}}_{\mathbf{k}}$ for each k. Note that for each k four eigenvalues (l = 1, 2, 3, 4.) will be obtained, or, equivalently, four bands on the Z.B. (Eq. 23). From Eq. (15), it can be observed that in the representation (13), the HF potentials and in general the total hamiltonian of the system, become block diagonal with respect the sets of states indexed by k. This fact is a consequence of the commutation of each of them with every element of the reduced group of discrete translations; that is: the group of translations which leaves invariant a sublattice.

4.2. Maximally translational symmetric solutions

In this subsection we will search for HF solutions having their orbitals on the space of Bloch functions being eigenfunction of the maximal group of translations leaving invariant the absolute lattice. In other words, we demand the maximum possible symmetry under translations. It will follow that our model is capable of acceptably reproducing the profile of the conduction band dispersion calculated in Ref. [22] for the La${}_2$CuO${}_4$. We will fit the free parameters of the model in order to reproduce in the best way the band dispersion reported in Ref. [22]. The parameters are: the dielectric constant of the effective environment $ϵ$; the characteristic radius of the gaussian Wannier orbitals $\tilde{a}$; the jumping probability between nearest sites for an electron $\tilde{\gamma }$ (it is fixed by the effective environment) and the radius in which the Gaussian orbitals associated to the neutralizing ”jellium” of charges decays $\tilde{b}$ (see Section 3.1).

In what follows the wavy hats will mean dimensionless, see Appendix A.(33). Let us define the Bloch basis for the space of orbitals in which the solution will be searched as

$$\begin{array}{ccc}\hfill {\overline{\phi }}_{\mathbf{Q}}^{{\sigma }_z}(\mathbf{x},s)& =& \sqrt{\frac{1}{N}}{u}^{{\sigma }_z}(s)\sum _{\mathbf{R}}{\phi }_0^{\mathbf{Q}}(\mathbf{x}-\mathbf{R})\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill {\phi }_0^{\mathbf{Q}}(\mathbf{x})& =& exp(i\mathbf{Q}·\mathbf{R}){\phi }_0(\mathbf{x}),\hfill \end{array}$$

(22)

where

$$\begin{array}{ccc}\hfill \mathbf{Q}& =& \left\{\begin{array}{c}\frac{2\pi }{Lp}(n_{x_1}{\widehat{\mathbf{e}}}_{x_1}+n_{x_2}{\widehat{\mathbf{e}}}_{x_2}),\hfill \\ \mathrm{with}{n}_{x_1},n_{x_2}\in \mathbb{Z},\hfill \\ \mathrm{and}-\frac{L}{2}\le n_{x_1},n_{x_2}<\frac{L}{2},\hfill \end{array}\right.\hfill \end{array}$$

(23)

are the quasimomenta of the single particle Bloch states which are eigenfunctions of the maximal group of translations. It is also important to define $N=L\times L$, and R, which are the amount of cells in the absolute lattice and the corresponding parametrization (8), respectively. The functions ${\phi }_0(\mathbf{x})$ are the Gaussian orbitals defined in Section 3.3. The searched HF orbitals will have the form

$$\begin{array}{ccc}\hfill {\overline{\varphi }}_{\mathbf{Q},l}(\mathbf{x},s)& =& \sum _{{\sigma }_z}{\overline{B}}_{{\sigma }_z}^{\mathbf{Q},l}{\overline{\phi }}_{\mathbf{Q}}^{{\sigma }_z}(\mathbf{x},s),\hfill \end{array}$$

(24)

as expressed on the above mentioned basis. This time, the equivalent matrix problem for the ”vector” ${\overline{B}}^{\mathbf{Q},l}$ is of second order for each value of ($\mathbf{Q}$,l). That is, its solutions will be two component vectors. Consequently, l will take the values 1 or 2 now. Thus, in analogy to (15) the new set of equations to be solved results in the form

$$\begin{array}{c}\hfill [{\overline{\mathrm{E}}}_{\mathbf{Q}}^0+\tilde{\chi }({\overline{\mathrm{G}}}_{\mathbf{Q}}^{dir}-{\overline{\mathrm{G}}}_{\mathbf{Q}}^{ind}-{\overline{\mathrm{F}}}_{\mathbf{Q}})].{\overline{\mathrm{B}}}^{\mathbf{Q},l}={\tilde{\epsilon }}_l(\mathbf{Q}){\overline{\mathrm{I}}}_{\mathbf{Q}}.{\overline{\mathrm{B}}}^{\mathbf{Q},l}.\end{array}$$

(25)

Let $\overline{\mathsf{{\rm Y}}}$ and $\mathsf{{\rm Y}}$ anyone of the 2x2 matrices in (25) and its 4x4 equivalent on (15) respectively, the relationship between these matrix elements is the following one

$$\begin{array}{c}\hfill {\overline{\mathsf{{\rm Y}}}}_{({\alpha }_z,{\sigma }_z)}=\frac{1}{2}\sum _{t,r}{\mathsf{{\rm Y}}}_{(t,{\alpha }_z);(r,{\sigma }_z)}.\end{array}$$

(26)

The relationships between the 2x2 and 4x4 matrices for the direct and exchange potentials become slightly more complicated. Besides also satisfying the above mentioned relation, each vector components in their "4x4" definitions must be removed from the sublattice label dependence and multiplied by $\frac{1}{\sqrt{2}}$ (those new quantities are the vector components of the 2x2 problem). For instance: making reference to the definitions given in Appendix A.

$$\begin{array}{ccc}\hfill {\overline{I}}_{\mathbf{Q},({\alpha }_z,{\sigma }_z)}& =& {\delta }_{{\alpha }_z,{\sigma }_z}\left[I_{00}+2I_{01}(cos{Q}_{1}p+cos{Q}_{2}p)\right].\hfill \end{array}$$

Analogously to the ones showed in the previous section, in this representation, the normalization condition for the single particle states and the HF energy of the system take the forms

$$\begin{array}{ccc}\hfill 1& =& {\overline{\mathrm{B}}}^{\mathbf{Q},l^{*}}.{\overline{\mathrm{I}}}_{\mathbf{Q}}.{\overline{\mathrm{B}}}^{\mathbf{Q},l},\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill {\overline{E}}_{\mathbf{Q},l}^{HF}& =& \sum _{\mathbf{Q},l}{\mathsf{\Theta }}_{({\tilde{\epsilon }}_F-{\tilde{\epsilon }}_l(\mathbf{Q}))}[{\tilde{\epsilon }}_l(\mathbf{Q})-\frac{\tilde{\chi }}{2}{\overline{\mathrm{B}}}^{\mathbf{Q},l^{*}}.({\overline{\mathrm{G}}}_{\mathbf{Q}}^{dir}-{\overline{\mathrm{G}}}_{\mathbf{Q}}^{ind}).{\overline{\mathrm{B}}}^{\mathbf{Q},l}].\hfill \end{array}$$

(28)

The method employed for solving all the self-consistent matrix problems considered in this work was an iterative one which started from a guessed particular state configuration. We used a paramagnetic state to begin the iterations in the case examined in this section. The Figure 3 shows the paramagnetic, metallic and doubly degenerate band obtained from the iterative process on (25). A half filling condition has been assumed; that is: a state with one electron per cell is considered. Specifically, for the case of $N=20\times 20$ electrons, the occupied states inside the B.Z. are shown in Figure 3 a) by the points inside the shadowed region. The chosen parameters were: $ϵ$=10, which is a common value for semiconductors, $\tilde{a}$=0.25, $\tilde{b}$=0.05 and $\tilde{\gamma }$=-0.03 (see Appendix A.), by following the criterium of fixing a bandwidth of 3.8 eV [22]. The band obtained here topologically coincides with the conduction band presented in Ref. [22]. In both of them the Fermi level on the Γ-X direction is a square which vertices touch the middle of the B.Z. (of the CuO lattices) sides and also the maximal and minimal energies lay on coinciding points. Therefore, in this subsection the parameters the effective model for the CuO planes employed in this work have been defined.

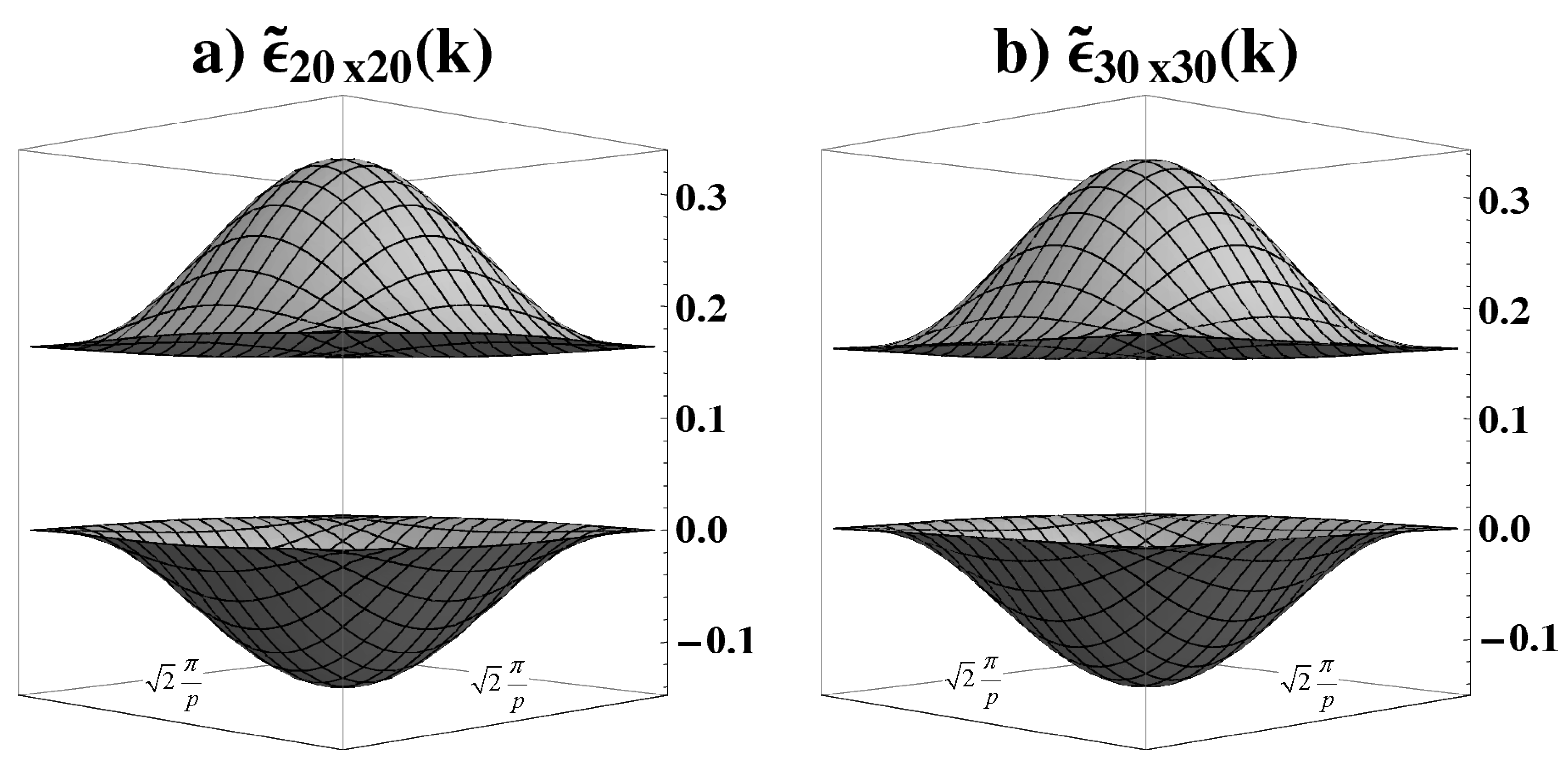
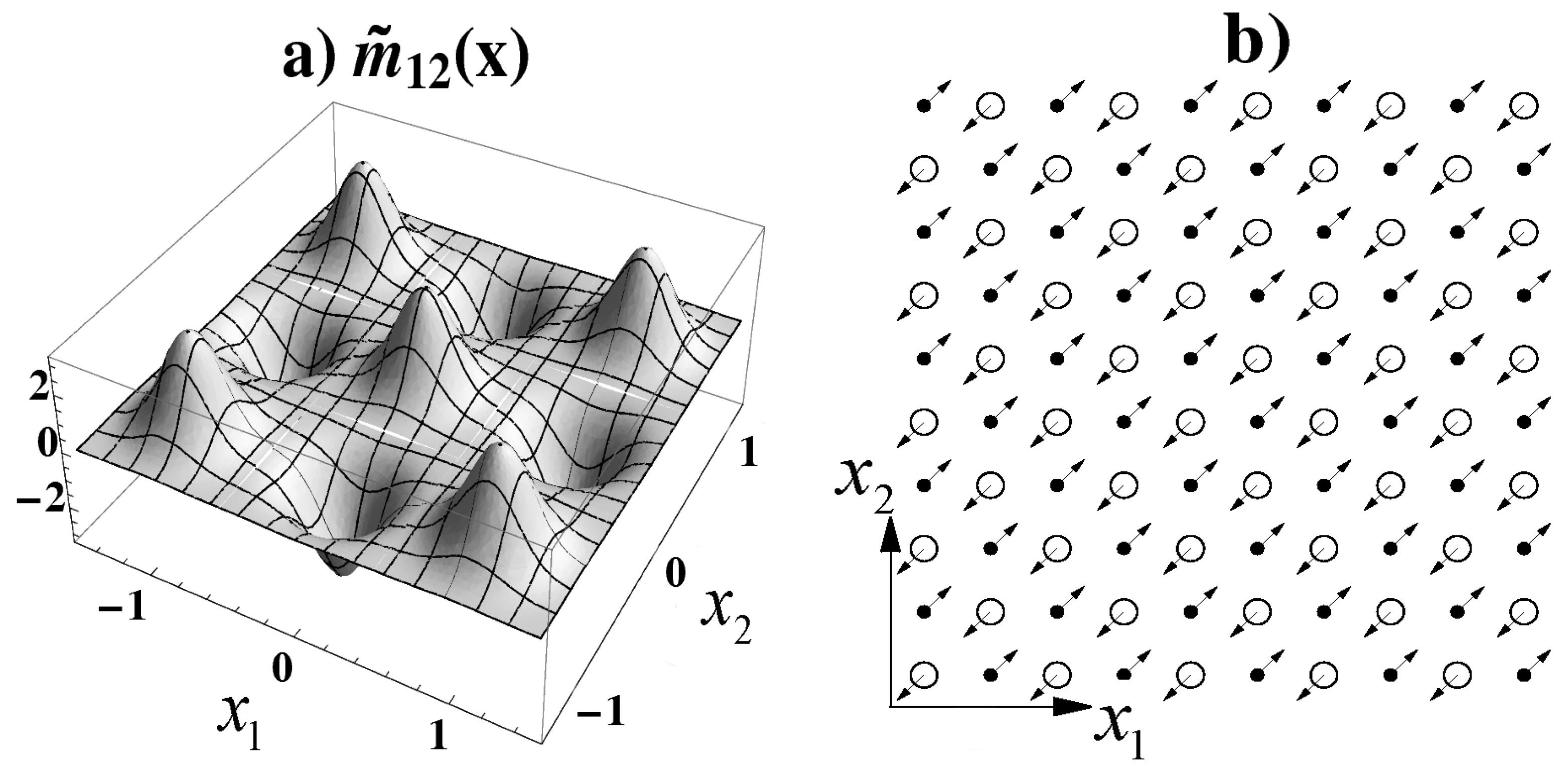
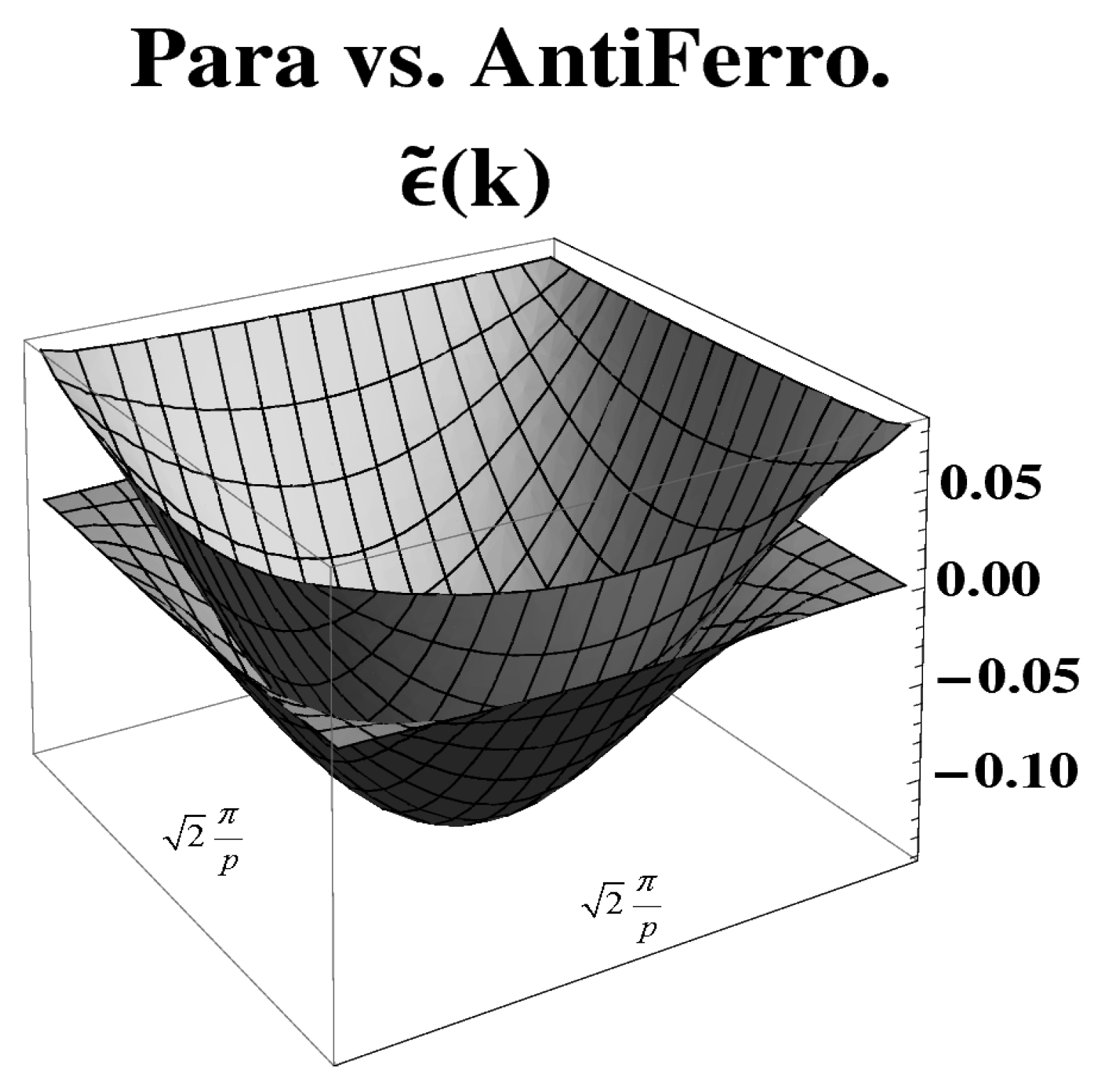
4.3. Insulating and antiferromagnetic solutions

As we have stated before, the solution of the system of equations (15) was performed by the method of successive iterations. The results which presented from now on were found by employing the parameter values $ϵ$, $\tilde{a}$, $\tilde{\gamma }$ and $\tilde{b}$, which were determined in the previous section. It is important to note that $\tilde{a}$, $\tilde{b}$≪1 and also that $\tilde{\gamma }$ must be of the order of the overlapping among nearest neighbors factor. It was necessary to start the iteration process from a particular state having an antiferromagnetic character from the beginning, in order to achieve convergence toward the solution presented in this subsection. In the Figure 4 two sets of results for a half filling band are shown. They correspond to two lattices of 20x20 and 30x30 cells. The bands are depicted on the same scale of energies. The difference between them is of order 10${}^{-5}$ dimensionless units of energy $\frac{{\hslash }^2}{m{a}^2}$= 8.3 eV. Evidently, they are bands corresponding to insulating states. The close similarity of both results indicates that the thermodynamical limit has being satisfactorily achieved for the considered sizes of the periodic system. The HF energy of this HF solution was the lowest among all those found. In coincidence with the experimental evidence, they are states with local magnetic moment resting on the direction of the sublattice x${}_{12}$ (see Figure 5). However, it should be noticed that the result for the orientation of the AF order should be simply considered as an artifact resulting from the initial state chosen for starting the iterative procedure of solution of the HF equations. This is so, because the absence of spin-orbit interaction in the model assures that any spatially rotated HF state will also be a new HF solution, but with the spin polarization also rotated. In the next section we will show the difference between the HF energy of this state and those corresponding to the other determined HF solutions and we shall comment on this respect.

One important quantity which has been experimentally measured is the magnetization. It is therefore motivating to inspect the prediction of the obtained HF state for this magnitude. Its definition is given by the expression

$$\begin{array}{c}\hfill \mathbf{m}(\mathbf{x})=\sum _{{\mathbf{k}}^{\prime },\mathbf{l}}\sum _{s,s^{\prime }}{\varphi }_{{\mathbf{k}}^{\prime },\mathbf{l}}^{*}(\mathbf{x},s)\sigma (s,s^{\prime }){\varphi }_{{\mathbf{k}}^{\prime },\mathbf{l}}(\mathbf{x},s^{\prime }),\end{array}$$

(29)

where

$$\begin{array}{c}\hfill \sigma (s,s^{\prime })={\sigma }_{x_1}(s,s^{\prime }){\widehat{\mathbf{e}}}_{x_1}+{\sigma }_{x_2}(s,s^{\prime }){\widehat{\mathbf{e}}}_{x_2}+{\sigma }_z(s,s^{\prime }){\widehat{\mathbf{e}}}_z,\end{array}$$

and ${\sigma }_{x_1}$= $\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$, ${\sigma }_{x_2}$=$\left(\begin{array}{cc}0& i\\ -i& 0\end{array}\right)$ and ${\sigma }_z$=$\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$ are the Pauli matrices.

In Figure 5 a) the only non vanishing component of (29) in this solution is plotted. An interesting result is that it has been experimentally observed that the 3D solid CuO has a magnetic moment of 0.68 ${\mu }_B$ per Cu site. The observed moments in La${}_2$CuO${}_4$ are near this value although the measurements show a dispersion [34]. The value obtained from evaluating the above formula for our HF state turns out to be 0.67 ${\mu }_B$. Therefore, it can be concluded that the HF procedure presented here satisfactorily describe the antiferromagnetic structure of La${}_2$CuO${}_4$.

It follows that the corresponding single particle states carry a more intensive antiferromagnetism the closer they are to the Fermi surface. Therefore, this property offers a clear explanation of the gradual loss observed in the antiferromagnetic order under the doping with holes [11]. In Figure 6 the dependence of the angle $\varphi$ between the magnetic moments per cell on each of the sublattice 1 and 2, shown by each of the single particle Bloch states, is plotted. These components are defined as the integrals of the magnetic moment density over all the unit cells of the absolute lattice centered in the sublattice points. Note that the states laying just on the Fermi surface are perfectly antiferromagnetic, and the farther from the boundaries the orbitals are, the less antiferromagnetic they become. Then, this HF solution indicates that when the orbitals are allowed to show spatial dependent spin orientations, the individual electrons prefer to reorient their spin when traveling between contiguous lattice cells. This effect could be interpreted as a clean "correlation" property, if considered within a restricted HF picture.

It also follows that the size of the zone in which the antiferromagnetism is strongest, inversely depends on the dielectric constant. Thus, the less is the Coulomb interaction among the electrons in the half filled electron band, the smaller becomes the antiferromagnetic character of the single particle states and the region in which the antiferromagnetism accumulate. Only the single particle states staying exactly on the Fermi surface retain a perfect antiferromagnetism. In addition, the magnitude of the gap also decreases with the increasing of the dielectric constant. In conclusion, in this subsection we were able to show that La${}_2$CuO${}_4$ ground state at half-filling, which is considered as a classical example of a Mott insulator ([40]), can be alternatively described as a Slater insulator, by means of the simplest of the first principles schemes: the Hartree-Fock method. This effect is determined by the combination of two factors: on one side, the antiferromagnetic structure introduces a translational symmetry breaking with a doubling of the unit cell. In the other hand, strong antiferromagnetic effects associated to the entangled spin and spacial structures of the HF single particle orbitals are able to generate a large isolator gap. Therefore, a reduced Brillouin zone is determined in which a full band becomes filled, defining a Slater insulator. This result constitutes a hint which suggests a way for the possible clarification of the Mott-Salter controversy in the framework of the Physics of transition metals oxides [11,34]. This remaining open problem of Solid State Physics could perhaps be understood after showing that a generalization of the present discussion for the series the transition metal oxides is able to describe the band structures for these materials. The expectation on this possibility is suggested by the similarities between the properties of these oxides with those of La${}_2$CuO${}_4$. The consideration of these problems is expected to be discussed elsewhere.

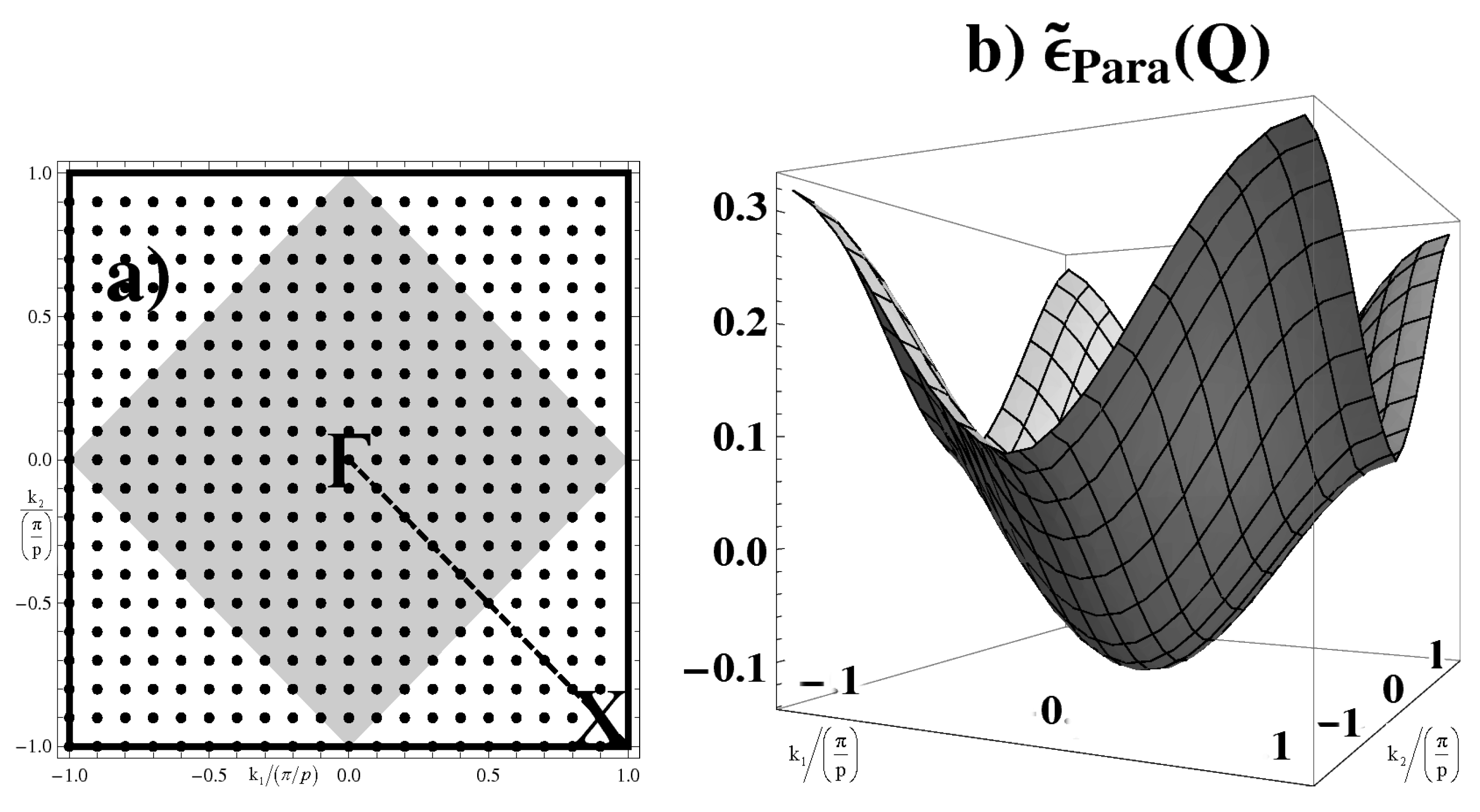
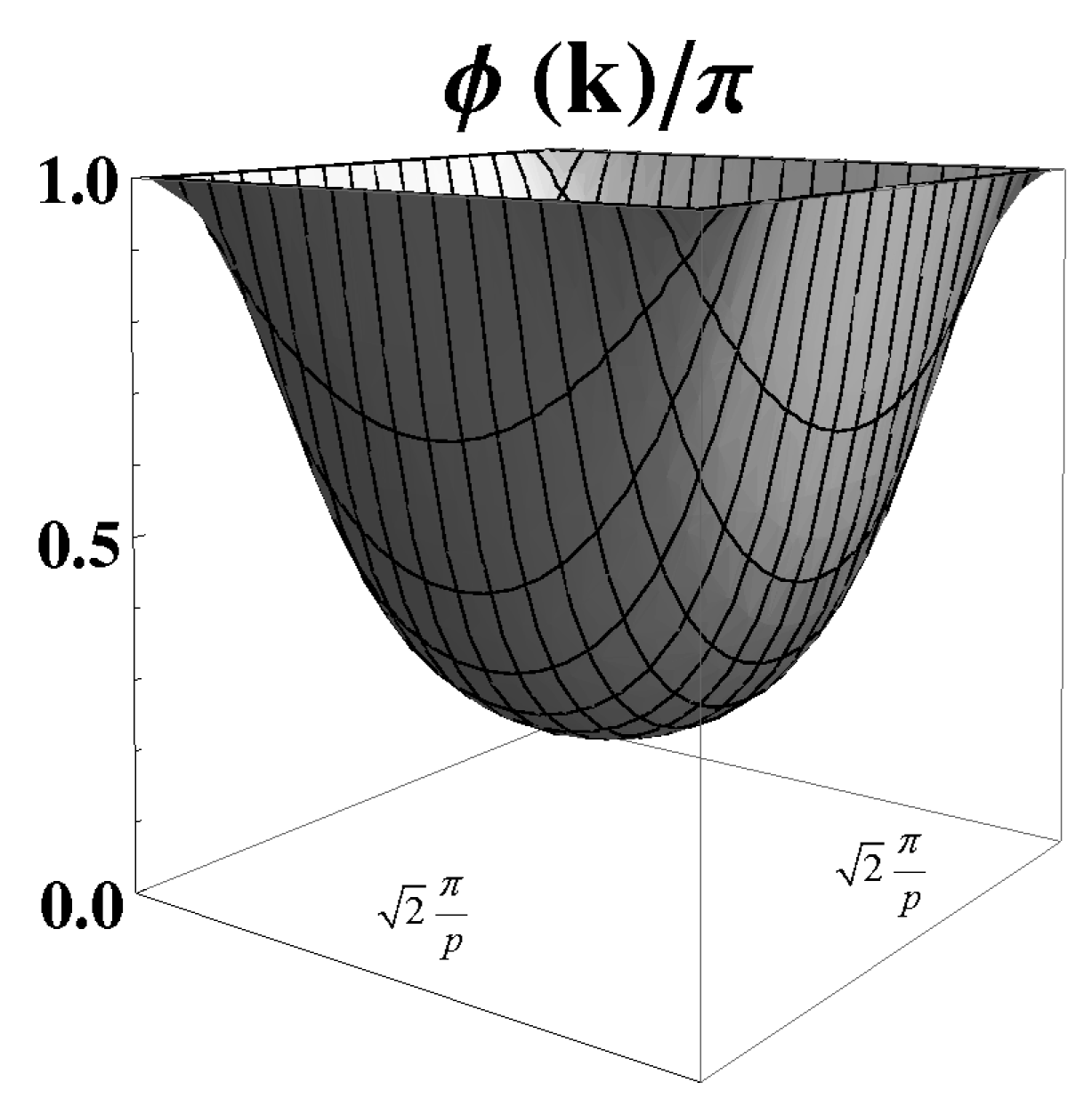
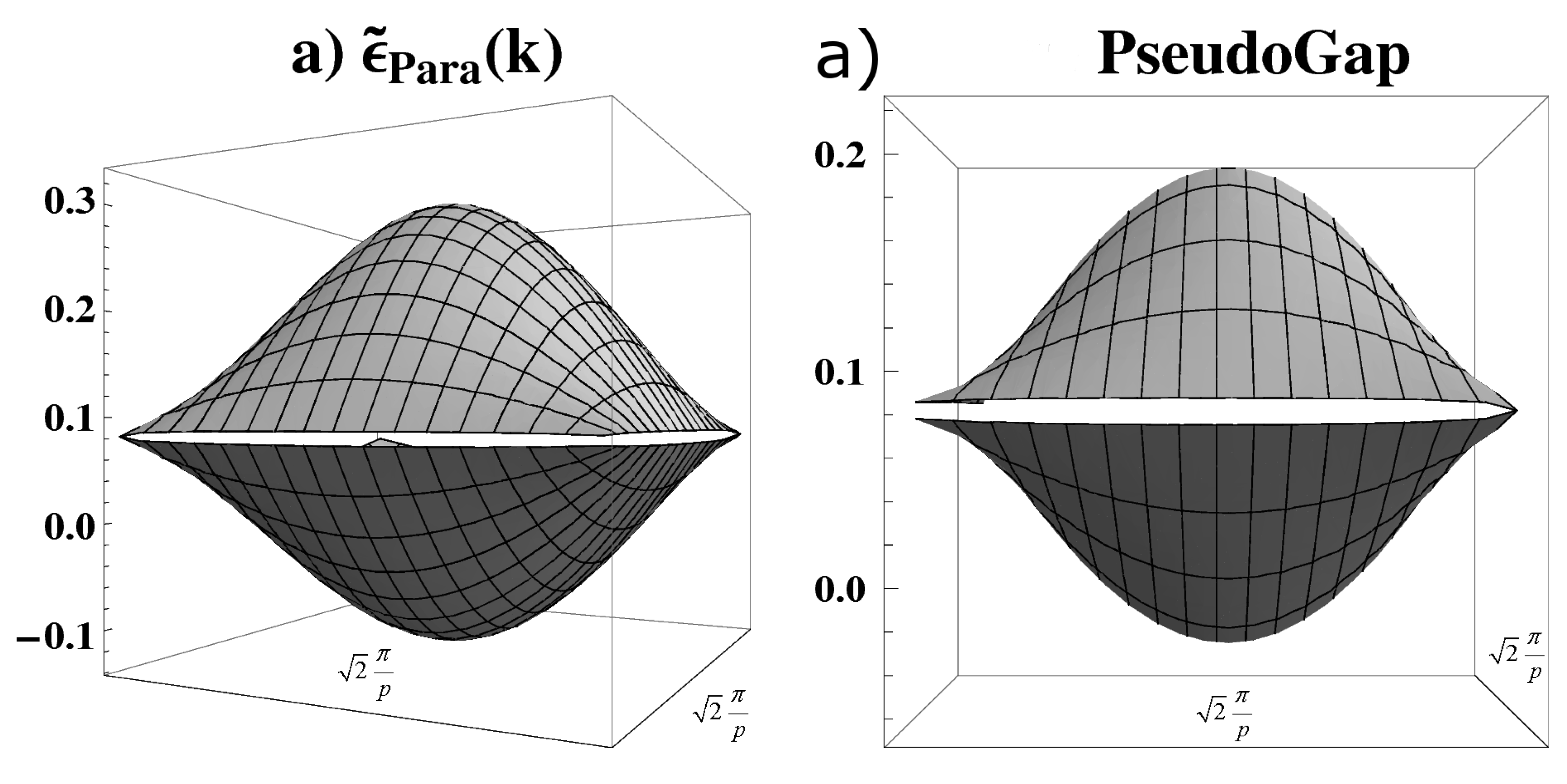
4.4. Paramagnetic solution showing a pseudogap

In Section 1 we had already commented about La${}_2$CuO${}_4$ and its antiferromagnetic and insulator properties at zero hole doping. However, at an intermediate level of doping, this material presents alternative special properties. After the breaking of the antiferromagnetic order and within certain temperature T and doping ranges, the material transits to phases indicating the presence of gaps with strength depending of the position along the Fermi surface (pseudogaps) [15,35]. Two types of such pseudogaps had been already detected by experiments: the $upper$ and the $lower$ ones, indicated by their characteristic temperatures of appearance: $T_o$ and $T^{*}$, respectively. In the La${}_2$CuO${}_4$ and other HTc materials the presence of these properties has been observed in some regions of their paramagnetic PM and superconductor SC phases [14]. It should be noticed that the physical nature of the pseudogap phenomena is yet not fully understood. There exist various proposals for explaining its physical origins [15,38]. In this paper we adopt a definition of the pseudogap as a momentum dependent excitation gap existing along the Fermi surface of the system [15]. The presence of this gap clearly means a depletion of the density of states around the Fermi surface, which is another way to describe the concept [38]. As mentioned above, the experimentally detected pseudogaps are characterized by the fact that the measured gap is higher when the electrons travel parallel to the Cu-O bonds.

Let us illustrate in this subsection how the removal of the translational symmetry restrictions over the HF orbitals (but not the one fixing the spin projection to be $\pm \frac{1}{2}$) allows to obtain another paramagnetic HF state. This solution shows features also exhibited by the above mentioned pseudogap states of HTc superconductor materials in their normal states. In Figure 7 the band spectra corresponding to this HF paramagnetic state obtained from Eq. (15) is shown. Note the existence of a pseudogap which reaches a maximum value of $100meV$ (equivalent to 0.012 dimensionless unit of energy $\frac{{\hslash }^2}{m{a}^2}$ $=8.3eV$). The parameters given in the Subsection 4.2 were employed for this evaluation. Taking into account that this result corresponds to half filling (that is, with the extreme underdoping limit $\delta =0$) the maximal value of the gap at the mid points of the Billouin zone sides, furnishes an estimate of $T_p\simeq 100$ $meV$ for the temperature at which a pseudogap starts to be observed in the experiments. It should be noticed, that the evaluated maximal gap magnitude depends on the effective dielectric constants $ϵ$ and the set of parameters (among them $ϵ$) which were fixed to reproduce the Matheiss single band crossing the Fermi level [22]. Therefore, the result for $T_p$ should not be taken as a precise prediction of any of the two pseudogap temperatures under current consideration. However, the experimental results of ARPES in doped La${}_2$CuO${}_4$ indicated a value of so called $upper$ pseudogap temperature in the region $T_o\approx 100-200meV$, precisely in the here studied extreme underdoped limit [15,35,36,37,38]. Therefore, the PPG Hartree-Fock solution gives a reasonable estimate for the upper pseudogap temperature parameter.

It should be stressed that the HF energy of the PPG wavefunction is exactly coincident with the one corresponding to the paramagnetic and metallic state presented in Subsection 4.2. Moreover, the lowest energy band in both solutions, also are identical, with an upper bound error of ${10}^{-6}$ in dimensionless energy units (that means ${10}^{-5}$ in eV). Thus, the occupied single particle states in both wavefunctions are identical and correspondingly, the momentum dependence of the filled energy band also coincides. Henceforth, the differences between the two paramagnetic solutions obtained only refer to the non occupied orbitals. Those single particle states can not be considered in the band model presented in Subsection 4.2 as a consequence of the crystal symmetry restriction imposed there. For instance, consider the expressions for two states, one occupied an another empty, which are associated to the same quasimomentum value

$$\begin{array}{cc}\hfill {\mathrm{B}}_o^{\mathbf{K}}=\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\\ 0\\ 0\end{array}\right)⟶& {\varphi }_o(\mathbf{x},s)=\sqrt{\frac{1}{N}}{u}_{\uparrow }(s)\sum _{r,{\mathbf{R}}^{(r)}}exp(i\mathbf{K}·{\mathbf{R}}^{(r)}){\phi }_{{\mathbf{R}}^{(r)}}(\mathbf{x}),\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill {\mathrm{B}}_e^{\mathbf{K}}=\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}\\ 0\\ 0\end{array}\right)⟶& {\varphi }_e(\mathbf{x},s)=\sqrt{\frac{1}{N}}{u}_{\uparrow }(s)\sum _{r,{\mathbf{R}}^{(r)}}{(-1)}^{r}exp(i\mathbf{K}·{\mathbf{R}}^{(r)}){\phi }_{{\mathbf{R}}^{(r)}}(\mathbf{x}),\hfill \end{array}$$

(31)

where ${\phi }_{{\mathbf{R}}^{(r)}}$ represents the Gaussian orbitals ${\phi }_0$ centered on ${\mathbf{R}}^{(r)}$.

Comparing with the expression (24), it may be noted that the occupied single particle state (30) can be expanded in the basis (21), and in fact, coincides with the state ${\overline{\varphi }}_o^{\mathbf{K},\uparrow }$ obtained from solving (25). Nevertheless, the excited state (31) was not allowed to pertain to the space of orbitals employed in solving (25). Thus, its reception as a solution is a neat consequence of the removal of the usually imposed crystal symmetry under the maximal group of translations. More precisely: the excited states showing a pseudogap appeared thanks to the allowed independence between the Bloch functions defined in both sublattices, a freedom which was introduced in this work. It should be underlined that the pseudogap state shows no magnetic order, thus the momentum dependent energy gap seems to be a direct consequence of long range Coulomb interaction effects incorporated in the Hartree-Fock solution and absent in the Hubbard model approximations. This circumstance indicates that the experimentally detected pseudogap states in the zero doping limit, could be closely related in their physical origin with charge density waves or excitonic processes, which have their roots in the Coulomb interaction [39]. However, this purely Coulomb nature of the PPG state should be expected only in the zero doping limit, since after adding holes, magnetic correlations are expected to start acting as the energies of the PPG and IAF states approach coincidence.

The HF energies per particle for the paramagnetic-metallic (PM), paramagnetic with pseudogap (PPG) and insulator-antiferromagnetic (IAF) ground states, are shown in

Table 1. Energy per particle differences between the various HF states.

State	IAF	PM	PPG
$\Delta$E (eV)	0.0	+0.076	+0.076

; with the zero energy reference assumed on the last one:

It can be noticed that the energy per particle difference PM (PPG)-IAF and the Néel temperature of this kind of materials are both of the order of various hundreds of Kelvin degrees at the vanishing doping limit under consideration. In figure 8 the PPG (PM) and IAF occupied bands are depicted in a common frame. Note that the main difference in their energies corresponds to the single particle states being closer to the Fermi surface. As we had noted before, the same behavior has the antiferromagnetic character of the single particle states of the IAF solution. Thus, the obtained results suggest the possibility of having success in generalizing the HF discussion considered here to the description of the phase diagram of the La${}_2$CuO${}_4$.

In order to illustrate the last point, let us expose a qualitative picture suggested by the present results. For this purpose, let us assume that a small amount of holes is added to the half filled system considered here. According to figure 8, for both cases, the PPG and IAF, the added holes will tend to bunch near the Fermi surface (curve). Then, the figure indicates that the reduction of the energy in the IAF state will be smaller than the one affecting the PPG state. Assumed that this tendency is maintained, we can expect that the energies of both states will become equal at some critical doping parameter ${\delta }_c.$ Near this value of doping it can be expected that a real solution of the HF problem should show a kind of intermediate nature in which, although AF correlations could yet remain, the long range AF order has already disappeared. This occurrence will lead to an HF description of the disappearance of the AF state when the doping starts increases from zero at vanishing temperature. In addition, the incorporation of the temperature to the HF procedure will also give access to describe the Neel transition for variable doping existing in the low doping region of the La${}_2$CuO${}_4$ phase diagram [34]. After the derivation of the evolution with doping and temperature of the HF energy per particle and the single particle energies, one could expect a decrease with doping of the maximal gap of the single particle energies. This behavior could further describe the decaying with doping of the measured upper pseudogap $T_o$ for La${}_2$CuO${}_4$ [35,36,37]. As for the lower pseudogap, it seems possible that after doping over the disappearance of the AF order, the HF solution could support bounded pairs of holes, glued by the new quasiparticles of this state. Those excitations should be expected to have some degree of magnetic order in their structures. If such is the case and the bounded pairs turn to be sufficiently small in size due to short ranged magnetic interactions, a finite doping threshold could be needed for the bounded pairs to condense in defining a superconducting transition. In this view, the $lower$ pseudogap temperature could related with the preformed pairs gap. We expect to explore these issues in the coming extension of the work.

Let us briefly comment about the relative stability between the PM and PPG states. It can be estimated that, due to the presence of a pseudogap, the PPG ground state should be more stable than the PM at non vanishing temperatures. This might be the case because in order to create excitations on the PPG ground state, temperatures of hundreds of Kelvin degrees are needed, while excitations in the PM ground state can appear in any range of temperatures.

5. Conclusions

The results of this work support the potential of the HF self-consistent method for the description of some secular properties exhibited by transition metals oxides, such as La${}_2$CuO${}_4$. Those are properties usually associated to strong correlation effects, that could be explained by first principle calculations, after being modified to incorporate procedures directed to search for spontaneous symmetry breaking solutions and general ways of exploring the spin structure of the HF obitals. Note that single particle basis of states are not only central in the construction of the HF procedure. They are also essential ingredients of more general schemes as the various types of density functional methods. Thus, the kind of reasoning followed in this work seems to be easily implemented in such discussions. In the present paper we explore those paths in a simplified manner. In order to avoid the intrinsic complexities of La${}_2$CuO${}_4$ material, it was helpful to employ a simple model which was sufficiently flexible for reproducing the dispersion profile of the single half filled band of La${}_2$CuO${}_4$ reported in Ref. [22]. After imposing the maximal symmetry under translations a paramagnetic and metallic ground state (PM) was obtained. Its dispersion properties topologically coincide with the results given in Ref. [22] for the unique band crossing the Fermi level. Then, the free parameters of the effective model were fixed from the requirement of reproducing the bandwidth of the half filled band obtained in [22]. Employing those parameters and removing some symmetry restrictions, solutions were obtained showing new properties. In agreement with the experiment, the insulating-antiferromagnetic (IAF) solution turns to be the most stable among all HF states found. Some of its properties are enumerated below:

• The isolator gap magnitude diminishes with the increasing of the screening constant $ϵ$.
• The antiferromagnetic structure the HF orbitals increases when the states approach the Fermi level. In addition, the size of the outlying region in which antiferromagnetism persists depends on the screening created by the effective environment $ϵ$. That is, by increasing screening, the size of the antiferromagnetic region reduces. Thus, the idea arises that after doping with holes (that is, solving for HF solutions not at half filling condition as it is done here) the antiferromagnetic zone, which is precisely concentrated near the Fermi level could be annihilated, producing in this way a phase transition to a non globally magnetically ordered ground state. This possibility indicates a way to describe the normal state properties of the HTc superconductors through a simple HF study.
• The magnetic moments per cell which are evaluated show a modular value of 0.67 ${\mu }_B$, which is close to the measured moments in La${}_2$CuO${}_4$ and interestingly almost coincide with the measured result of 0.68 ${\mu }_B$ for the Cu sites in the 3D solid CuO [34].

The other HF solution obtained in this work corresponds to a paramagnetic state showing a pseudogap (PPG). Some properties of this excited HF wavefunction are:

• The magnitude of the predicted maximal value of the pseudogap is of the order of 100 $meV$. This result is close to the range 100-200 $meV$ which is experimentally detected through ARPES for the $upper$ pseudogap $T_o$ in the zero doping limit for La${}_2$CuO${}_4$ [15,35,36,37]. The comparison of the filled band spectra of the IAF and PPG states suggests that under a relatively small doping the energy of both states could evolve to coincidence. A decreasing evolution with doping can be expected from future temperature and doping dependent HF pseudogap evaluations. Thus, assuming that the maximal value of the obtained pseudogap describes the experimentally determined $upper$ pseudogap temperature $T_o$, a description of the observed decaying behavior of $T_o$ for increasing doping is suggested. [15].
• Similarly as it happens for the antiferromagnetic character of the IAF ground state, the difference between the one particle energies of IAF and the PPG (PM) solutions is larger for orbitals closer to the Fermi surface. That is, it happens for the electrons with more energy and consequently the first to disappear under doping with holes. Therefore, this outcome further supports the possibility to describe a crossing of the energies of the IAF and PPG states under doping.k
• The pseudogap magnitude diminishes with the increasing of the screening constant $ϵ$. This property, and the fact that the set of parameters were non univocally fixed (to reproduce Matheiss results for the single band crossing the Fermi level in [22]) leads to the opportunity of a better determination of the parameters to match a larger set of observed physical properties of La${}_2$CuO${}_4$.
• At the $T=0$ limit considered here, the states PM and PPG were identical. The difference between them only appears at the excitations of the system. Thus, the removal of some symmetry restrictions defines new properties for unoccupied single particle states. It seems feasible that it could be possible to obtain a gap instead of a pseudogap in other materials, even in the absence of magnetic order. Such an outcome could show the ability of a properly formulated HF description to describe general kinds of Mott insulators, being or not magnetically ordered.

Let us now mention a methodological conclusion of this work. It corresponds to the fact that the results clarifies that the solutions of a general HF problem non necessarily should turn to be a set of single particle orbitals, all having an $\alpha$ or $\beta$ spin structure at all points of the space. This is directly shown by the particular example of the IAF solution in which the HF single particle states have a neatly "entangled" non separable character in their spin and orbital dependence.

The previous comments motivate new objectives for the extension of the work. Two main interests are: on the one hand to perform a closer investigation about the detected potentialities of the first principle calculations. On the other is to look for a description of HTc superconductivity in the context of the simple model examined here. Some specific issues of future searches in connection with these objectives are:

• To generalize the discussion in order to introduce the doping with holes and temperature as new parameters. This will allow to investigate the effects of these parameters on the determined HF states. Of particular interest in a first stage appears the study of the crossing of the energies per particle of the IAF and PPG states under doping. As above remarked, this point could determine the AF destruction phase transition. Furthermore, the mean field study for even larger dopings could shed light on the superconducting phase change.
• To compute the temperature and doping dependent electron Green function of the system, and use it to evaluate the effective polarization of the La${}_2$CuO${}_4$ in the obtained states.
• With the polarization results in hand, it could be possible to attempt solving the Bethe-Salpeter equation for two holes in the HF ground state, to find whether or not it is possible to decide about the existence of preformed Cooper Pairs in the HF model under finite doping and temperature. The possibility for their existence was suggested by the results of Ref. [46], in which it was argued that a strong 2D-screening of the Coulomb interaction is created by a half filled band of tight binding electrons.
• Finally, we intend to follow the hints given by the ideas exposed here to clarify the debate between the Mott and Slater pictures in connection with the electronic structure of transition metal oxides.