Nanotribology of Symmetric and Asymmetric Liquid Lubricants
Abstract
:1. Introduction
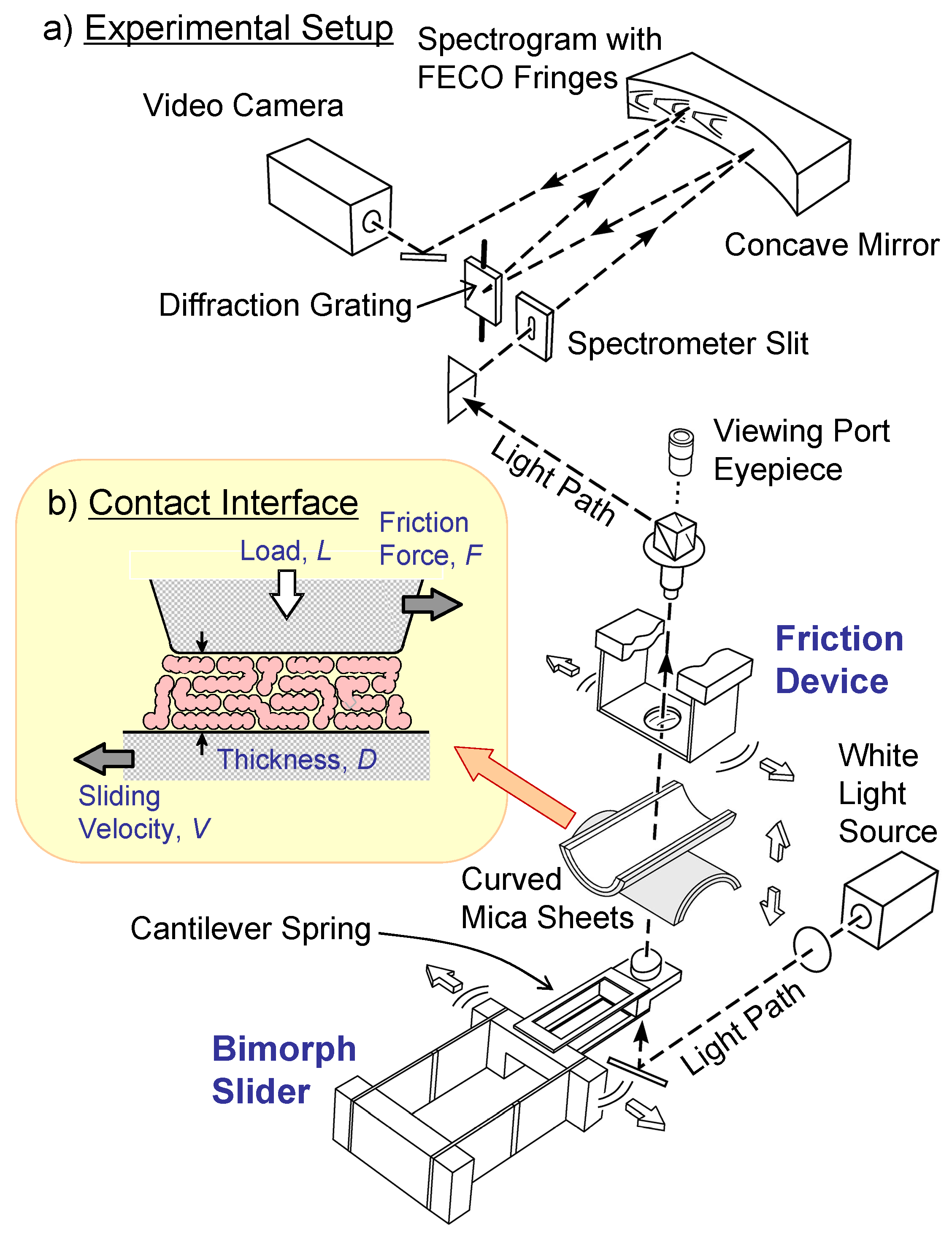
2. The Surface Forces Apparatus (SFA)
2.1. General feature of the SFA
2.2. Tribological measurements
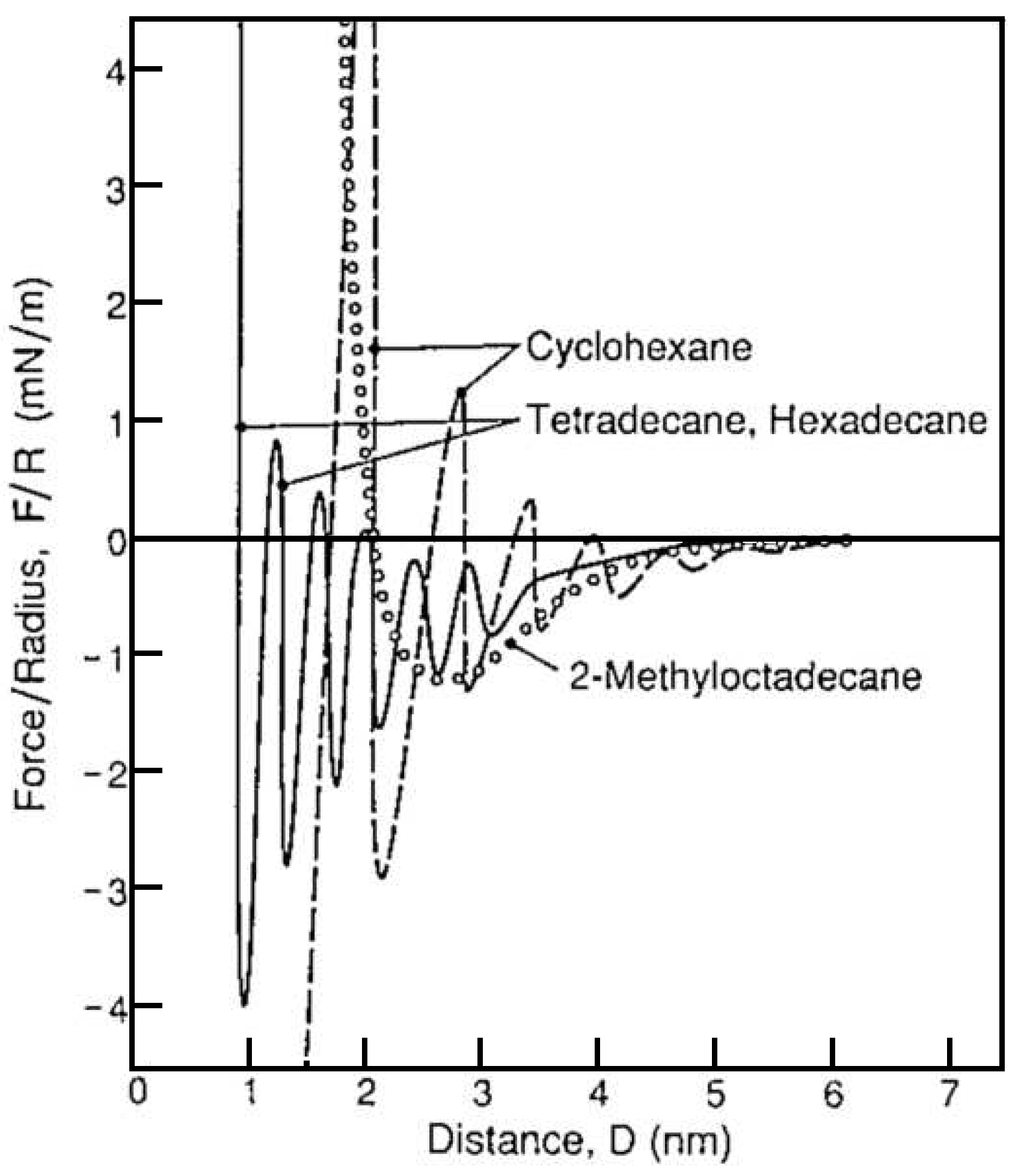
3. Static Structures of Liquid Lubricant Films in Confinement
4. Nanotribological Properties of Molecularly Confined Liquid Lubricants
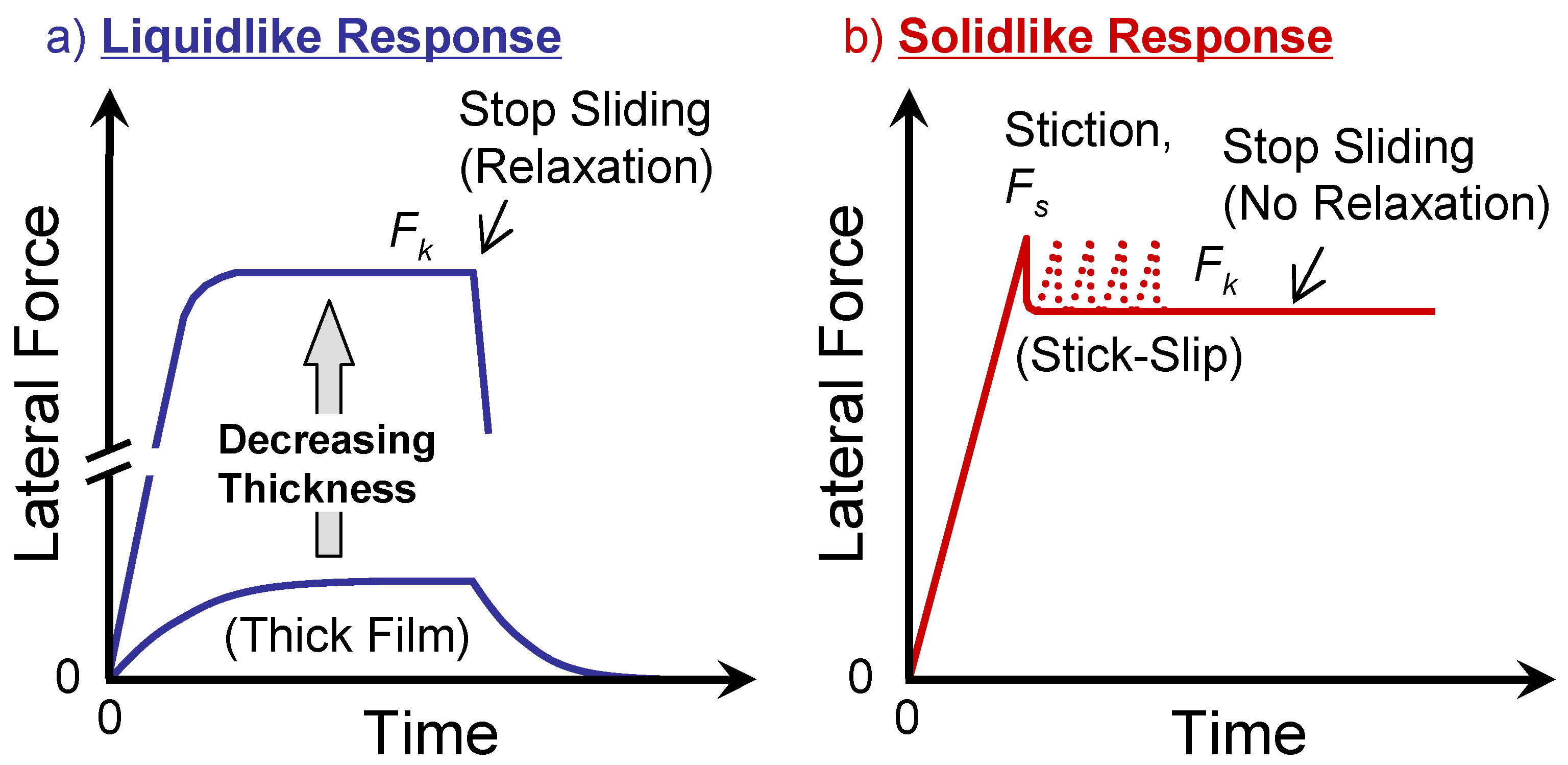
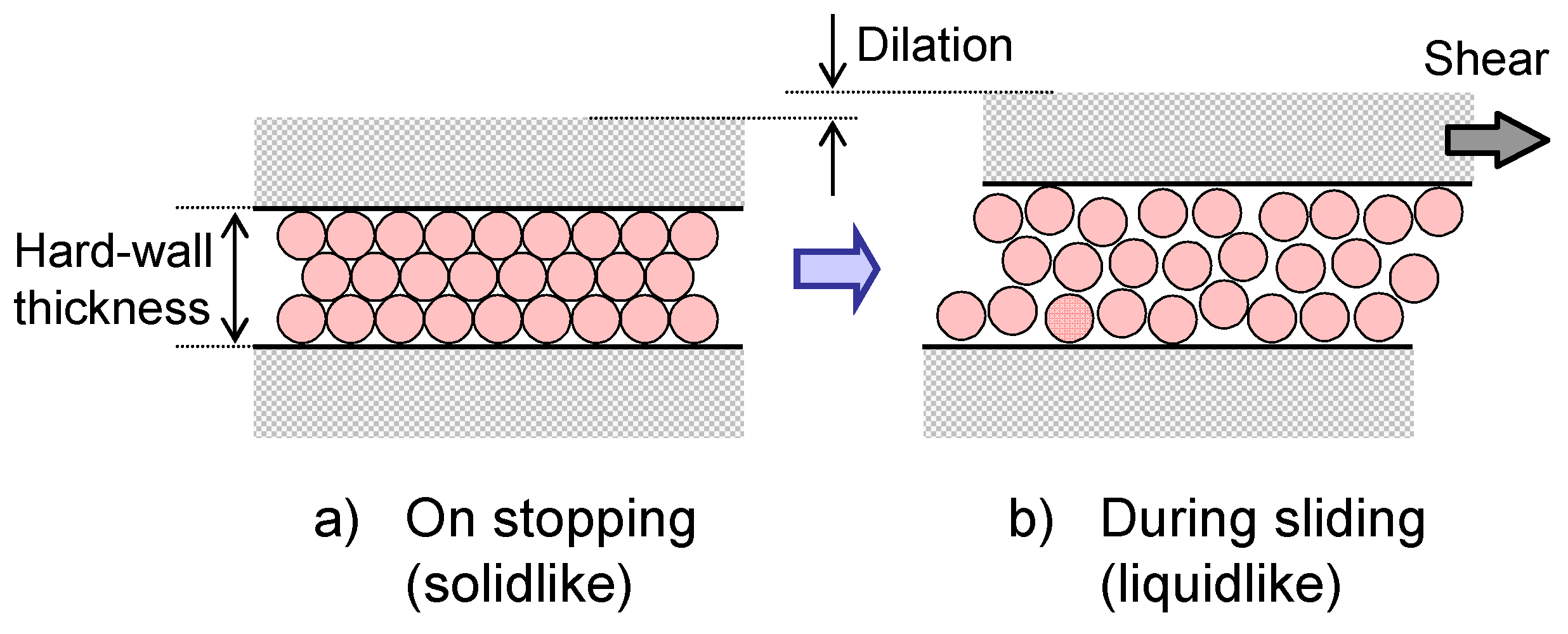
4.1. General Features of the Friction and Lubrication of Confined Liquids
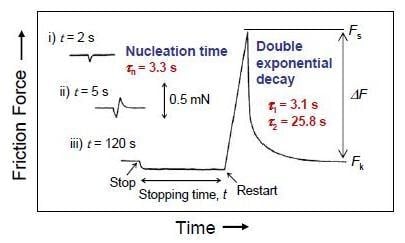
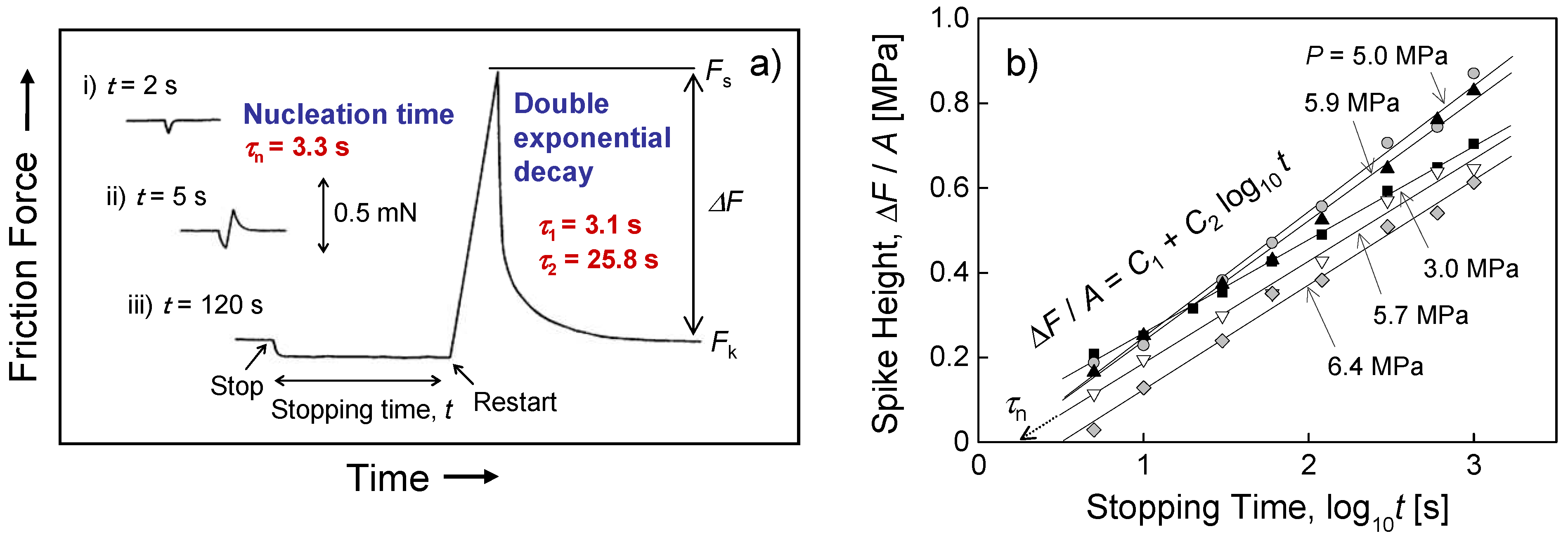
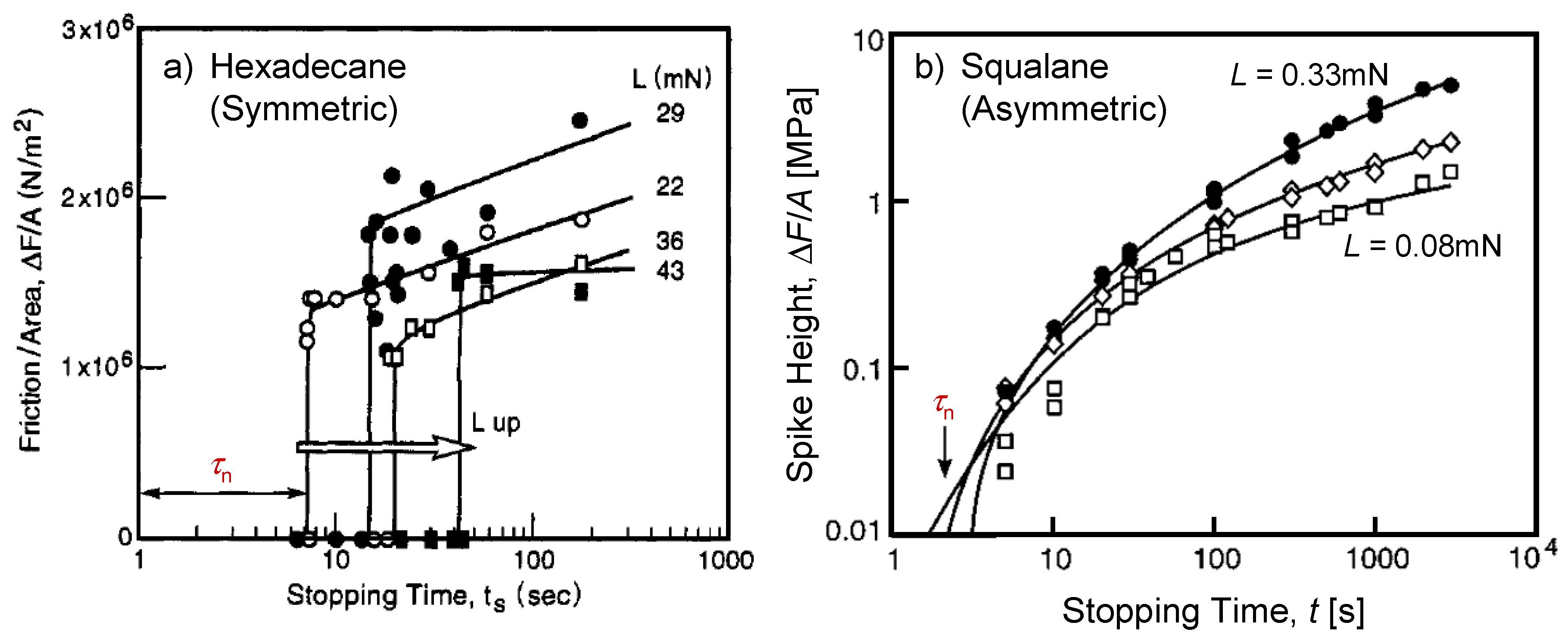
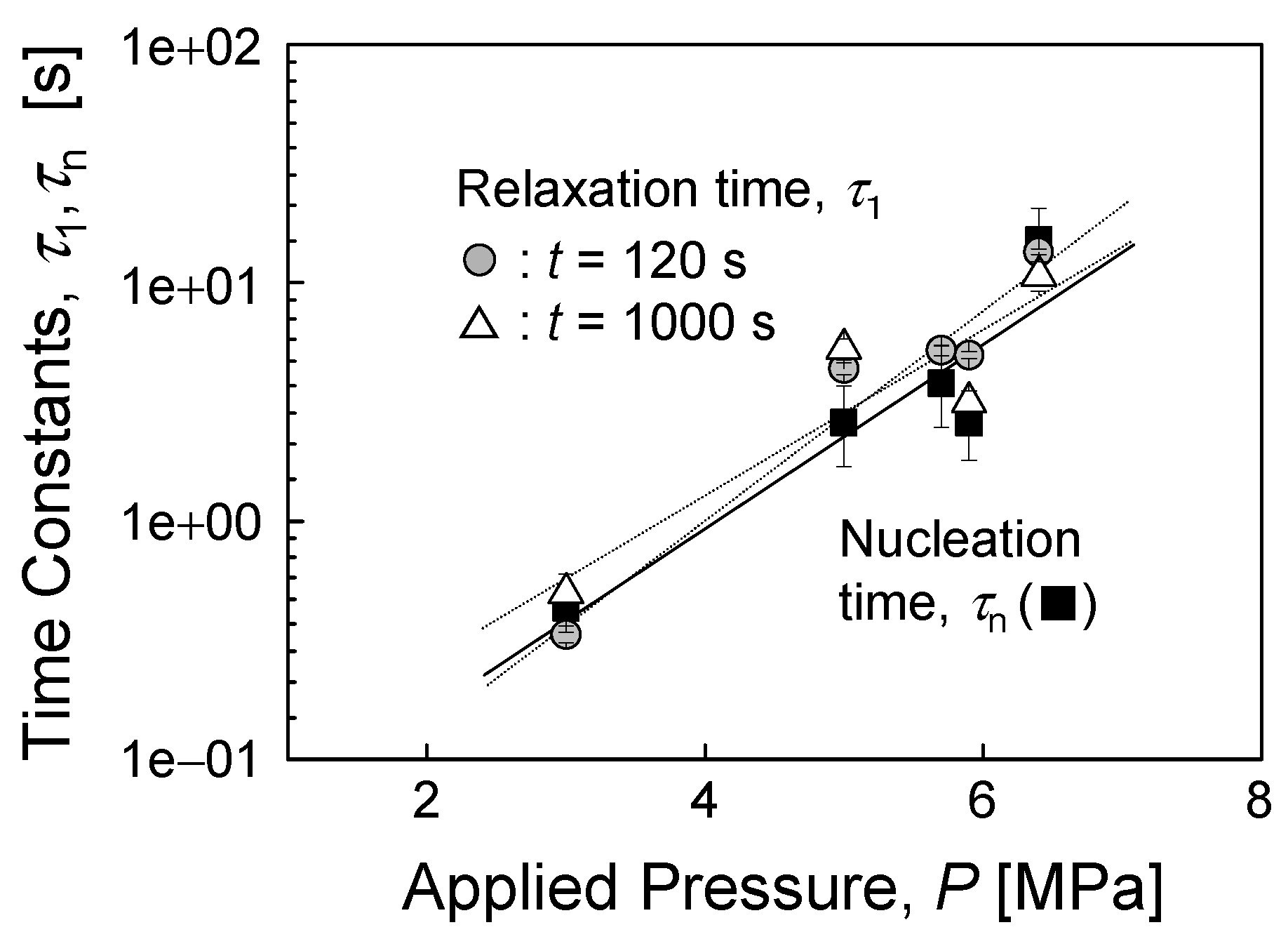
4.2. Static Friction (Stiction) of Confined Liquid Lubricants
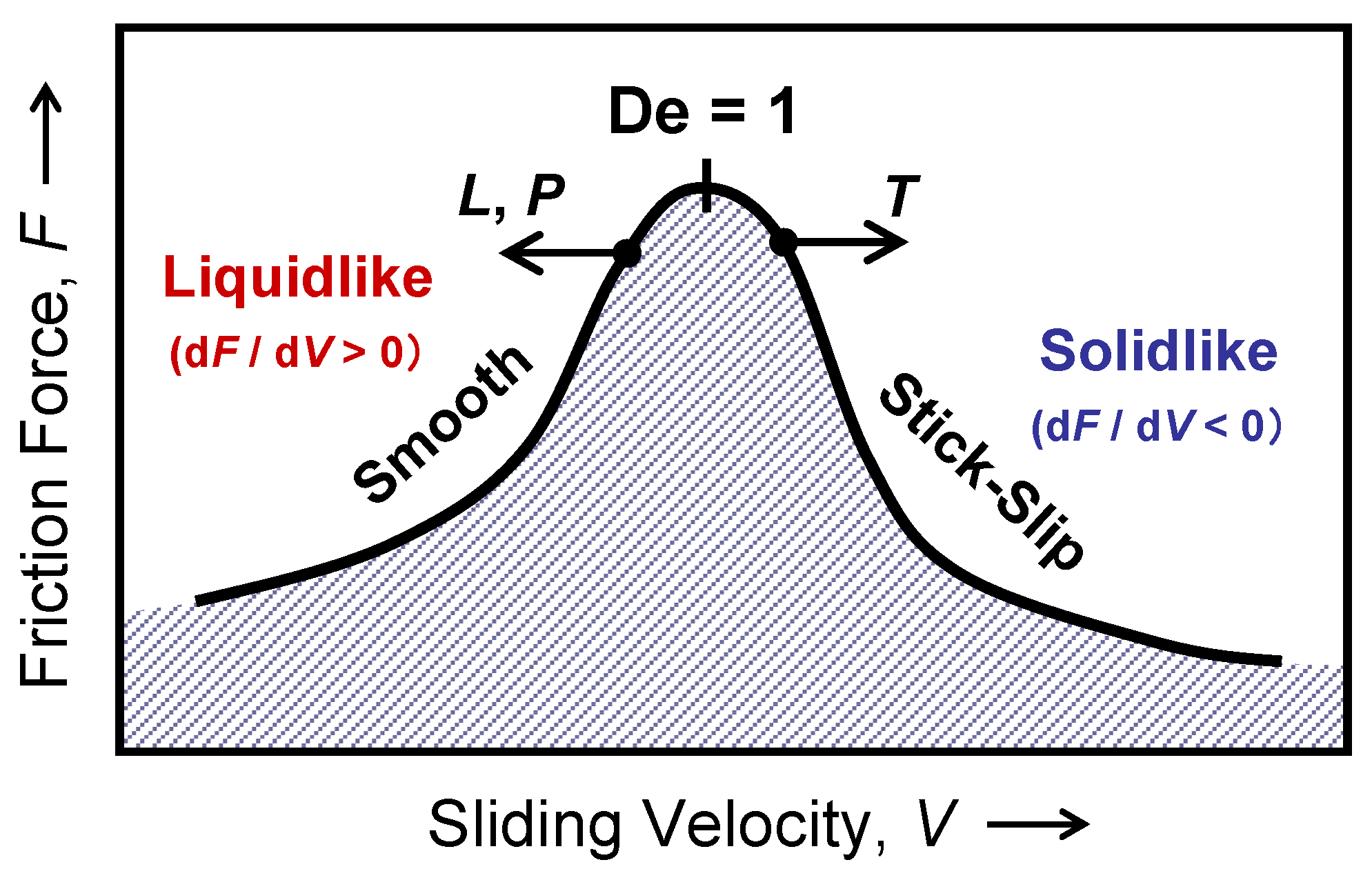
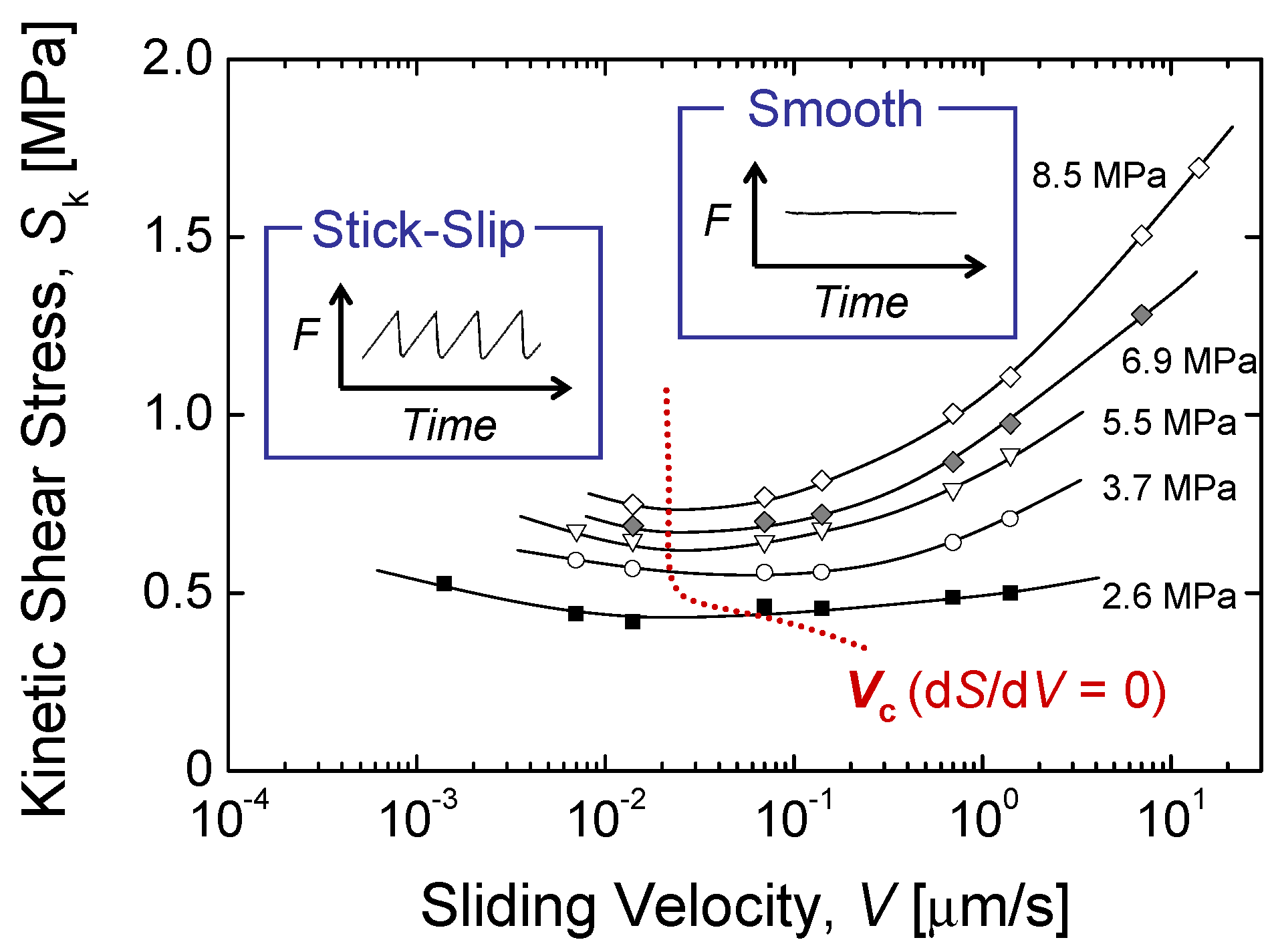
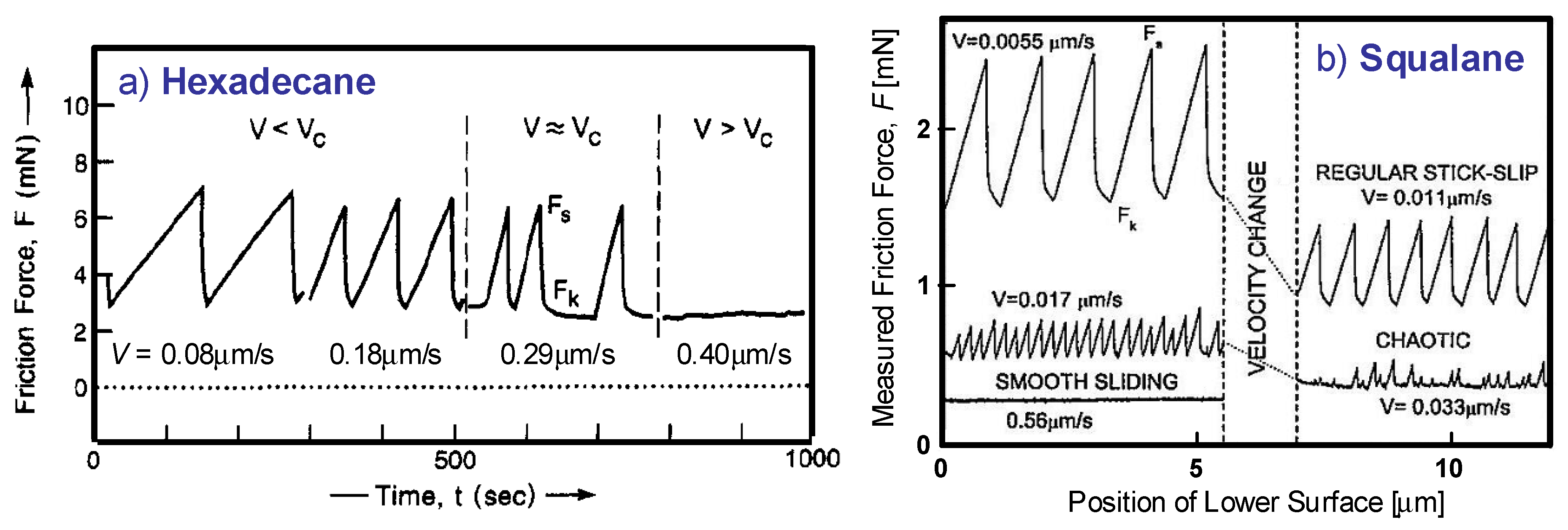
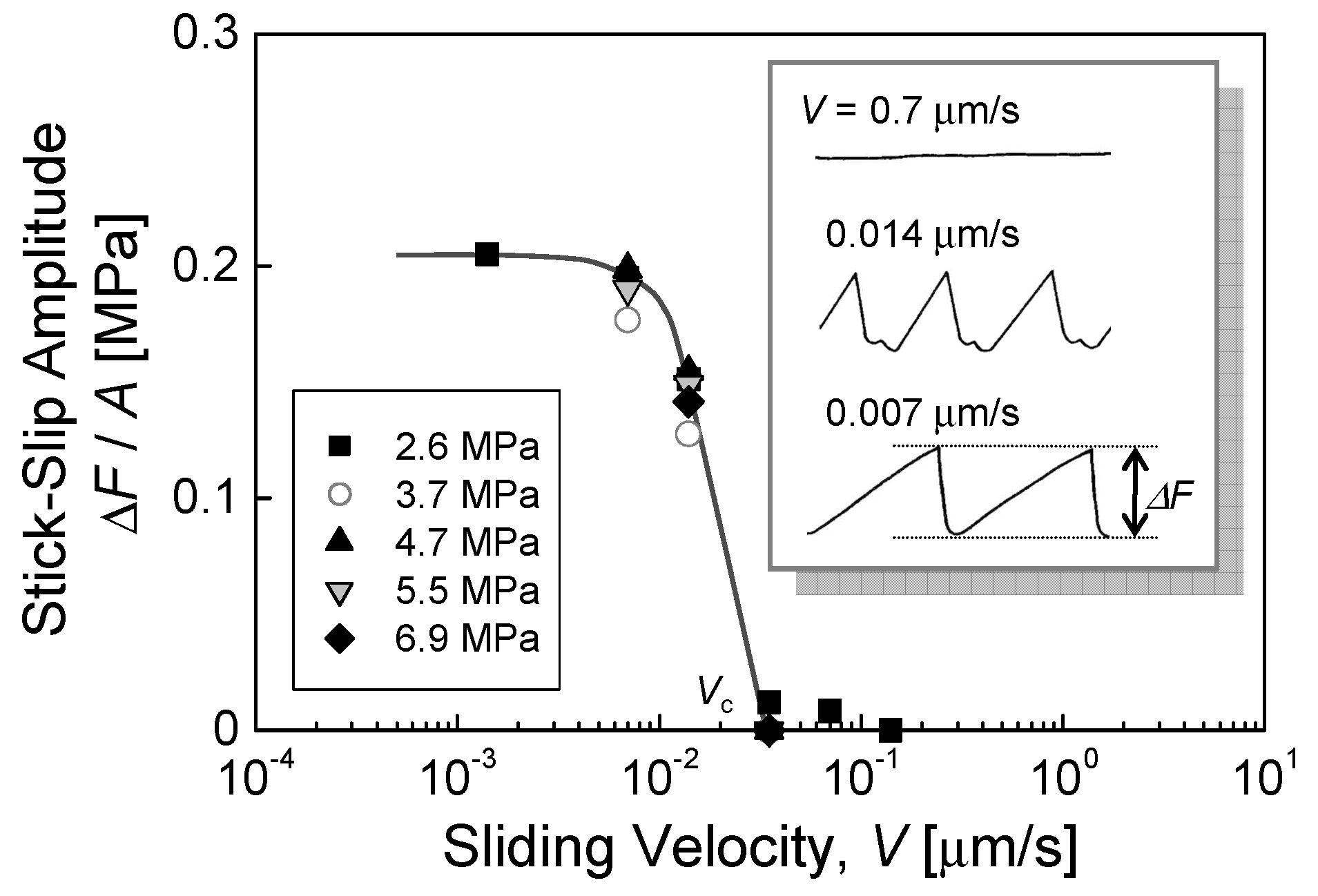
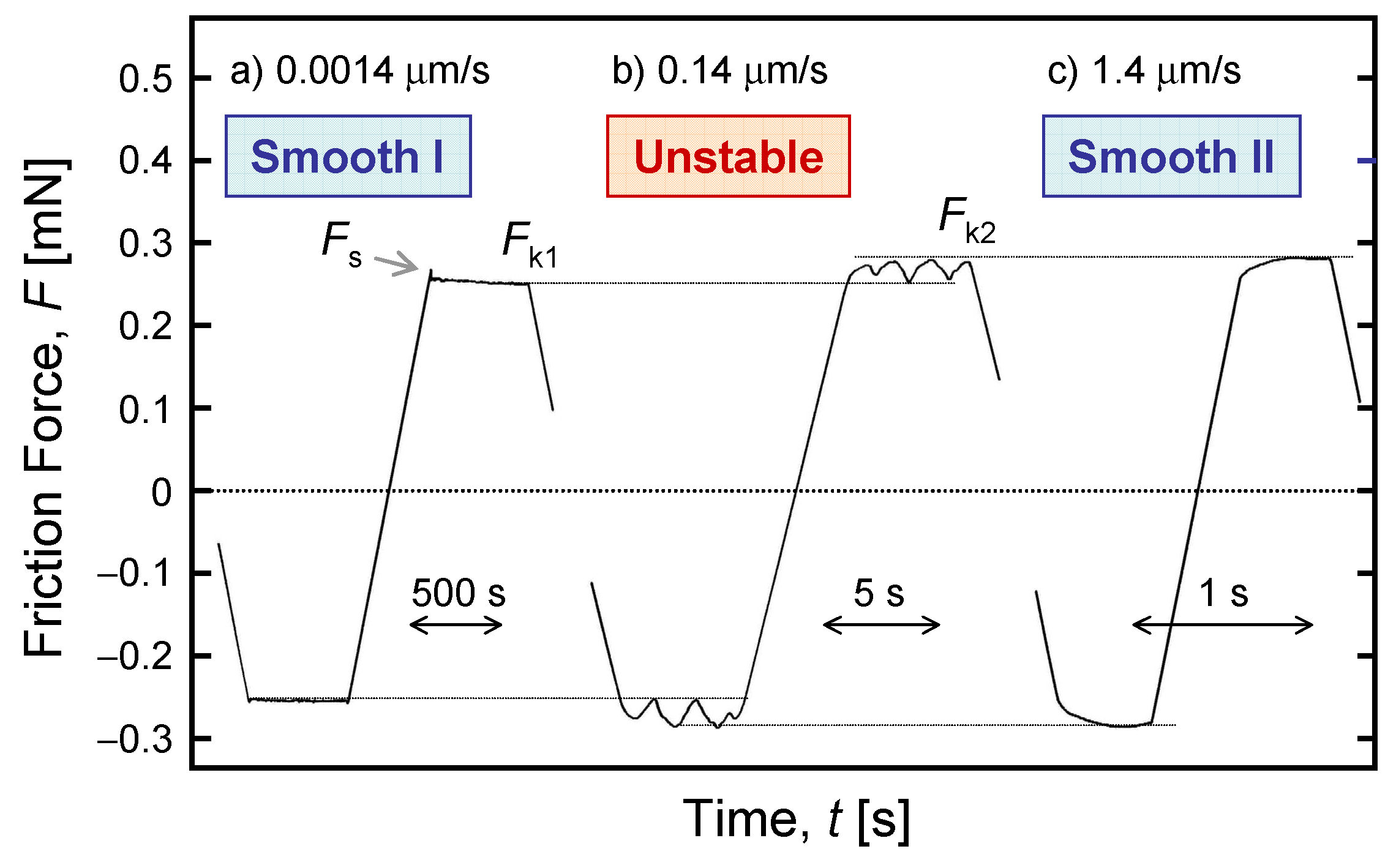
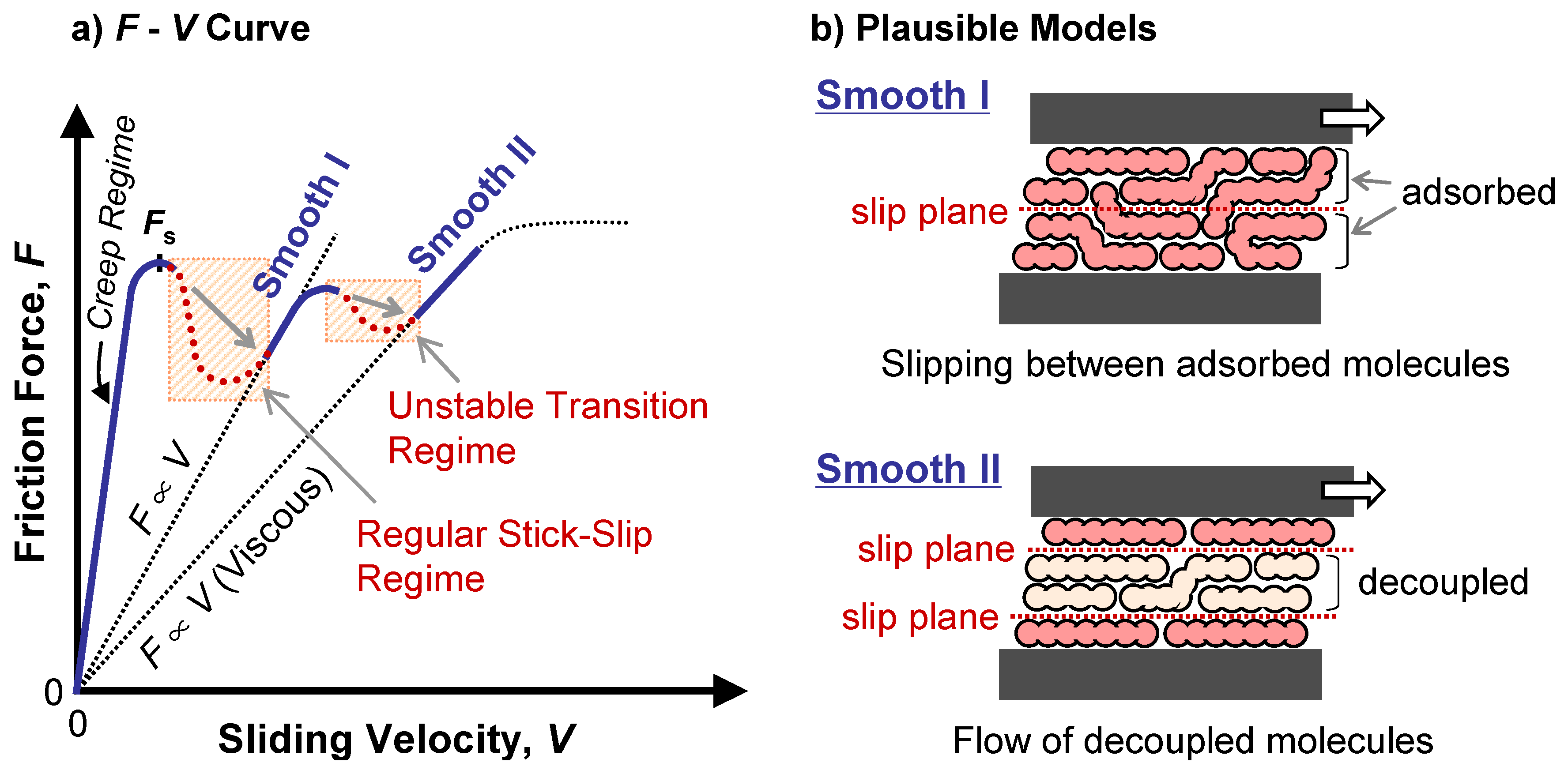
4.3. Kinetic Friction and Stick-Slip Sliding
4.4. Comparison of the Molecular Mechanisms between Stiction and Stick-Slip Friction
4.5. Complex Shear Behaviors of Confined Asymmetric Liquids
4.6. Future Prospects
- i)
- It is difficult to exclude the possibility of the formation of poly-crystalline states for asymmetric liquid systems; we cannot precisely distinguish the two states (poly-crystalline or glasslike) by conventional SFA experiments.
- ii)
- There are publications that report continuous glasslike dynamics for highly-symmetric spherical liquid molecules. Granick et al. examined the nanorheological properties of the molecularly thin films of OMCTS using the SFA and found the continuous increase of relaxation times along with the thickness decrease [38,72]. This is totally incompatible with the abrupt dynamic transitions between solid-like state and liquid-like state for symmetric liquid systems described in this paper. The apparatus and experimental conditions of Granick’s works are slightly different from those of most of the works referred in this paper, but we do not have sufficient explanations for the discrepancy.
- iii)
- Bureau [73] recently reported that the liquid structures in confinement are very dependent on the confinement rate. They studied the molecular layering of a linear alkane n-hexadecane and found that the layering (ordering) is observed when the liquid is confined at an extremely low confinement rate. Increasing confinement rate induces disordered liquid structures even for the symmetric linear liquid. The results included in this paper were obtained under sufficiently low confinement rate; detailed analysis of the rate effect should further improve our understanding on the structuring of liquids in confinement.
- iv)
- The structures and properties in confined liquid films are not uniform in both thickness and in-plain directions. Density distribution of molecules is not uniform in the thickness direction as probed by normal force measurements (see Figure 2) [1]. Also, the contact pressure for Hertzian contact shows a maximum at the center of the contact area, which induces non-uniform molecular density distributions within the contact area [74]. Friction behavior observed by the SFA represents the average properties of the entire film and masks a variety of different local mechanisms of sliding within the film.
5. Summary and Conclusions
Acknowledgments
References and Notes
- Israelachvili, J.N. Intermolecular and Surface Forces, 2nd Ed. ed; Academic Press: London, UK, 1991. [Google Scholar]
- Israelachvili, J.; Berman, A.D. Surface Forces and Microrheology of molecularly thin liquid films. In CRC Handbook of Micro/Nanotribology, 2nd Ed.; Bhushan, B., Ed.; CRC Press: Boca Raton, FL, USA, 1999; Chapter 9; p. 371. [Google Scholar]
- Granick, S. Motions and Relaxations of Confined Liquids. Science 1991, 253, 1374–1379. [Google Scholar] [CrossRef] [PubMed]
- Robbins, M.O.; Muser, M.H. Computer Simulations of Friction, Lubrication and Wear. In Modern Tribology Handbook; Volume One, Bhushan, B., Ed.; CRC Press: Boca Raton, FL, USA, 2001; Chapter 20; p. 717. [Google Scholar]
- Klein, J.; Kumacheva, E. Confinement-Induced Phase Transitions in Simple Liquids. Science 1995, 269, 816–819. [Google Scholar] [CrossRef] [PubMed]
- Heuberger, M.; Zach, M.; Spencer, N.D. Density Fluctuations under Confinement: When is a Fluid Not a Fluid? Science 2001, 292, 905–908. [Google Scholar] [CrossRef] [PubMed]
- Yamada, S. Layering Transitions and Tribology of Molecularly Thin Films of Poly(dimethylsiloxane). Langmuir 2003, 19, 7399–7405. [Google Scholar] [CrossRef]
- Israelachvili, J.; McGuiggan, P.M.; Homola, A.M. Dynamic Properties of Molecularly Thin Liquid Films. Science 1988, 240, 189–191. [Google Scholar] [CrossRef] [PubMed]
- van Alsten, J.; Granick, S. Molecular Tribometry of Ultrathin Liquid Films. Phys. Rev. Lett. 1988, 61, 2570–2573. [Google Scholar] [CrossRef] [PubMed]
- Luengo, G.; Schmitt, F.J.; Hill, R.; Israelachvili, J. Thin Film Rheology and Tribology of Confined Polymer Melts: Contrast with Bulk Properties. Macromolecules 1997, 30, 2482–2494. [Google Scholar] [CrossRef]
- Bhushan, B. Boundary Lubrication Studies Using Atomic Force/Friction Force Microscopy. In CRC Handbook of Micro/Nanotribology, 2nd Ed.; Bhushan, B., Ed.; CRC Press: Boca Raton, FL, USA, 1999; Chapter 8; p. 357. [Google Scholar]
- Bhushan, B.; Israelachvili, J.N.; Landman, U. Nanotribology: Friction, Wear and Lubrication at the Atomic Scale. Nature 1995, 374, 607–616. [Google Scholar] [CrossRef]
- Robbins, M.O.; Baljon, A.R.C. Response of Thin Oligomer Films to Steady and Transient Shear. In Microstructure and Microtribology of Polymer Surfaces; American Chemical Society: Washington, DC, USA, 2000; Chapter 6; p. 91. [Google Scholar]
- Yoshizawa, H.; Israelachvili, J. Fundamental Mechanisms of Interfacial Friction. 2. Stick-Slip Friction of Spherical and Chain Molecules. J. Phys. Chem. 1993, 97, 11300–11313. [Google Scholar]
- Drummond, C.; Israelachvili, J. Dynamic Behavior of Confined Branched Hydrocarbon Lubricant Fluids under Shear. Macromolecules 2000, 33, 4910–4920. [Google Scholar] [CrossRef]
- Drummond, C.; Israelachvili, J. Dynamic Phase Transitions in Confined Lubricant Fluids under Shear. Phys. Rev. E 2001, 63, 041506. [Google Scholar] [CrossRef]
- Gourdon, D.; Israelachvili, J. Transitions between Smooth and Complex Stick-Slip Sliding of Surfaces. Phys. Rev. E 2003, 68, 021602. [Google Scholar] [CrossRef]
- Yamada, S. Nanotribology of Ethers: Effects of Molecular Asymmetry and Fluoroalkyl Chains. Langmuir 2005, 21, 8724–8732. [Google Scholar] [CrossRef]
- Yamada, S. Dynamic Transitions in Molecularly Thin Liquid Films under Frictional Sliding. Langmuir 2008, 24, 1469–1475. [Google Scholar] [CrossRef]
- Yamada, S. Structural Aging and Stiction Dynamics in Confined Liquid Films. J. Chem. Phys. 2009, 131, 184708. [Google Scholar] [CrossRef]
- Golan, Y.; Drummond, C.; Israelachvili, J.; Tenne, R. In Situ Imaging of Shearing Contacts in the Surface Forces Apparatus. Wear 2000, 245, 190–195. [Google Scholar] [CrossRef]
- Israelachvili, J.; McGuiggan, P.M. Adhesion and Short-Range Forces between Surfaces. Part I: New Apparatus for Surface Force Measurements. J. Mater. Res. 1990, 5, 2223–2231. [Google Scholar]
- Israelachvili, J. Thin Film Studies Using Multiple-Beam Interferometry. J. Colloid Interface Sci. 1973, 44, 259–272. [Google Scholar] [CrossRef]
- Heuberger, M.; Luengo, G.; Israelachvili, J. Topographic Information from Multiple Beam Interferometry in the Surface Forces Apparatus. Langmuir 1997, 13, 3839–3848. [Google Scholar] [CrossRef]
- Tadmor, R.; Chen, N.; Israelachvili, J.N. Thickness and Refractive Index Measurements Using Multiple Beam Interference Fringes (FECO). J. Colloid Interface Sci. 2003, 264, 548–553. [Google Scholar] [CrossRef]
- Gee, M.L.; McGuiggan, P.M.; Israelachvili, J.N. Liquid to Solidlike Transitions of Molecularly Thin Films under Shear. J. Chem. Phys. 1990, 93, 1895–1906. [Google Scholar] [CrossRef]
- In-plain ordering of molecules is affected by the surface structure of substrate material. The mica surface used as the standard substrate for SFA experiments has a crystalline (periodic) lattice, which induces the ordering of molecular axis [1]. This effect results in the local alignment of molecules, but there is no preferred orientation within the whole contact area.
- Dhinojwala, A.; Bae, S.C.; Granick, S. Shear-Induced Dilation of Confined Liquid Films. Tribol. Lett. 2000, 9, 55–62. [Google Scholar] [CrossRef]
- Demirel, A.L.; Granick, S. Lubricated Friction and Volume Dilatancy are Coupled. J. Chem. Phys. 2002, 117, 7745–7750. [Google Scholar] [CrossRef]
- Yamada, S.; Israelachvili, J. Friction and Adhesion Hysteresis of Fluorocarbon Surfactant Monolayer-Coated Surfaces Measured with the Surface Forces Apparatus. J. Phys. Chem. B 1998, 102, 234–244. [Google Scholar] [CrossRef]
- Caroli, C.; Baumberger, T.; Bureau, L. Static Aging vs. Dynamic Rejuvenation in Solid Friction. J. Phys. IV France 2002, 12, Pr9-269–273. [Google Scholar]
- Bureau, L.; Baumberger, T.; Caroli, C. Rheological Aging and Rejuvenation in Solid Friction Contacts. Eur. Phys. J. E 2002, 8, 331–337. [Google Scholar] [CrossRef]
- Drummond, C.; Alcantar, N.; Israelachvili, J. Shear Alignment of Confined Hydrocarbon Liquid Films. Phys. Rev. E 2002, 66, 011705. [Google Scholar] [CrossRef]
- Thompson, P.A.; Grest, G.S.; Robbins, M.O. Phase Transitions and Universal Dynamics in Confined Films. Phys. Rev. Lett. 1992, 68, 3448–3451. [Google Scholar] [CrossRef]
- Thompson, P.A.; Robbins, M.O.; Grest, G.S. Structure and Shear Response in Nanometer-Thick Films. Israel J. Chem. 1995, 35, 93–106. [Google Scholar] [CrossRef]
- Rabin, Y.; Hersht, I. Thin Liquid Layers in Shear: Non-Newtonian Effects. Physica A 1993, 200, 708–712. [Google Scholar] [CrossRef]
- Hu, H.W.; Carson, G.A.; Granick, S. Relaxation Time of Confined Liquids under Shear. Phys. Rev. Lett. 1991, 66, 2758–2761. [Google Scholar] [CrossRef]
- Demirel, A.L.; Granick, S. Glasslike Transition of a Confined Simple Fluid. Phys. Rev. Lett. 1996, 77, 2261–2264. [Google Scholar] [CrossRef]
- Granick, S. Soft Matter in a Tight Spot. Phys. Today 1999, 52, 26–31. [Google Scholar] [CrossRef]
- Yamada, S. General Shear-Thinning Dynamics of Confined Fluids. Tribol. Lett. 2002, 13, 167–171. [Google Scholar] [CrossRef]
- Yamada, S.; Nakamura, G.; Hanada, Y.; Amiya, T. Glasslike Transitions in Thin Polymer-Melt Films Due to Thickness Constraint. Tribol. Lett. 2003, 13, 83–89. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd Ed. ed; Wiley: New York, USA, 1980. [Google Scholar]
- Luengo, G.; Israelachvili, J.; Dhinojwala, A.; Granick, S. Generalized Effects in Confined Fluids: New Friction Map for Boundary Lubrication. Wear 1996, 200, 328–335. [Google Scholar] [CrossRef]
- Utz, M.; Debenedetti, P.G.; Stillinger, F.H. Atomistic Simulation of Aging and Rejuvenation in Glasses. Phys. Rev. Lett. 2000, 84, 1471–1474. [Google Scholar] [CrossRef]
- Rottler, R.; Robbins, M.O. Unified Description of Aging and Rate Effects in Yield of Glassly Solids. Phys. Rev. Lett. 2005, 95, 225504. [Google Scholar] [CrossRef]
- Rottler, R.; Robbins, M.O. Macroscopic Friction Laws and Shear Yielding of Glassy Solids. Comput. Phys. Commun. 2005, 169, 177–182. [Google Scholar] [CrossRef]
- Ruina, A. Slip Instability and State Variable Friction Laws. J. Geophys. Res. 1983, 88, 10359–10370. [Google Scholar] [CrossRef]
- Berthoud, P.; Baumberger, T.; G’Sell, C.; Hiver, J.-M. Physical Analysis of the State- and Rate-Dependent Friction Law: Static Friction. Phys. Rev. B 1999, 59, 14313–14327. [Google Scholar] [CrossRef]
- Baumberger, T.; Caroli, C. Solid Friction from Stick-Slip down to Pinning and Aging. Advance in Phys. 2006, 55, 279–348. [Google Scholar] [CrossRef]
- Charrault, E.; Gauthier, C.; Marie, P.; Schirrer, R. Structural Recovery (Physical Ageing) of the Friction Coefficient of Polymers. J. Polymer Sci. B Polymer Phys. 2008, 46, 1337–1347. [Google Scholar] [CrossRef]
- The mechanical time constant of the experimental system is the order of milliseconds.
- Sperling, L.H. Introduction to Physical Polymer Science, 3rd Ed. ed; Wiley Interscience: New York, USA, 2001. [Google Scholar]
- Dowson, D. History of Tribology; Longman: London and New York, 1979. [Google Scholar]
- Yoshizawa, H.; Chen, Y.L.; Israelachvili, J. Fundamental Mechanisms of Interfacial Friction. 1. Relation between Adhesion and Friction. J. Phys. Chem. 1993, 97, 4128–4140. [Google Scholar]
- Yamada, S.; Nakamura, G.; Amiya, T. Shear Properties for Thin Films of Star and Linear Polymer Melts. Langmuir 2001, 17, 1693–1699. [Google Scholar] [CrossRef]
- Israelachvili, J. Tribology of Ideal and Non-Ideal Surfaces and Fluids. In Fundamental of Tribology and Bridging the Gap between the Macro- and Micro/Nanoscales; Bhushan, B., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; p. 631. [Google Scholar]
- Berman, A.D.; Israelachvili, J.N. Control and minimization of friction via surface modification. In Micro/Nanotribology and its Applications, NATO Advanced Science Institute Series; Bhushan, B., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997; p. 317. [Google Scholar]
- Yoshizawa, H.; McGuiggan, P.; Israelachvili, J. Identification of a Second Dynamic State During Stick-Slip Motion. Science 1993, 259, 1305–1308. [Google Scholar] [CrossRef]
- Urbakh, M.; Klafter, J.; Gourdon, D.; Israelachvili, J. The Nonlinear Nature of Friction. Nature 2004, 430, 525–528. [Google Scholar] [CrossRef]
- Berman, A.D.; Ducker, W.A.; Israelachvili, J.N. Origin and characterization of different stick-slip friction mechanisms. Langmuir 1996, 12, 4559–4563. [Google Scholar] [CrossRef]
- Strictly speaking, the lateral velocity at the interface is not exactly zero but mechanical creep at a molecular level is expected [19,43]. This should be of course also expected for the case of stop-start stiction dynamics. This creep deformation is included in Figure 13a.
- Israelachvili, J.N. Adhesion, Friction and Lubrication of Molecularly Smooth Surfaces. In Fundamentals of Friction; Singer, I.L., Pollock, H.M., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992; p. 351. [Google Scholar]
- Thompson, P.A.; Robbins, M.O. Origin of Stick-Slip Motion in Boundary Lubrication. Science 1990, 250, 792–794. [Google Scholar] [CrossRef]
- Akbulut, M.; Chen, N.; Maeda, N.; Israelachvili, J.; Grunewald, T.; Helm, C.A. Crystallization in Thin Liquid Films Induced by Shear. J. Phys. Chem. B 2005, 109, 12509–12514. [Google Scholar] [CrossRef]
- Richetti, P.; Drummond, C.; Israelachvili, J.; In, M.; Zana, R. Inverted Stick-Slip Friction. Europhys. Lett. 2001, 55, 653–659. [Google Scholar] [CrossRef]
- Drummond, C.; Elezgaray, J.; Richetti, P. Behavior of Adhesive Boundary Lubricated Surfaces under Shear: A New Dynamic Transition. Europhys. Lett. 2002, 58, 503–509. [Google Scholar] [CrossRef]
- Drummond, C.; Israelachvili, J.; Richetti, P. Friction between Two Weakly Adhering Boundary Lubricated Surfaces in Water. Phys. Rev. E 2003, 67, 066110. [Google Scholar] [CrossRef]
- Fillippov, A.E.; Klafter, J.; Urbakh, M. Inverted Stick-Slip Friction: What is the Mechanism? J. Chem. Phys. 2002, 116, 6871–6874. [Google Scholar] [CrossRef]
- Qian, L.-M.; Luengo, G.; Perez, E. Thermally Activated Lubrication with Alkanes: The Effect of Chain Length. Europhys. Lett. 2003, 61, 268–274. [Google Scholar] [CrossRef]
- Yamada, S. Nanotribology of Poly(dimethylsiloxane) Melt Confined between Hydrophobic Surfaces. Tribol. Online 2006, 1, 29–33. [Google Scholar] [CrossRef]
- Demirel, A.L.; Granick, S. Friction Fluctuation and Friction Memory in Stick-Slip Motion. Phys. Rev. Lett. 1996, 77, 4330–4333. [Google Scholar] [CrossRef]
- Demirel, A.L.; Granick, S. Origins of Solidification When a Simple Molecular Fluid is Confined between Two Plates. J. Chem. Phys. 2001, 115, 1498–1512. [Google Scholar] [CrossRef]
- Bureau, L. Rate Effects on Layering of a Confined Linear Alkane. Phys. Rev. Lett. 2007, 99, 225503. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Zhao, J.; Bae, S.C.; Granick, S. Contrasting Diffusion and Viscosity in Molecularly-Thin Films. Phys. Rev. Lett. 2002, 89, 136103. [Google Scholar] [CrossRef]
- Heuberger, M. The Extended Surface Forces Apparatus. Part I. Fast Spectral Correlation Interferometry. Rev. Sci. Instr. 2001, 72, 1700–1707. [Google Scholar]
- Dushkin, C.D.; Kurihara, K. Nanotribology of Thin Liquid-Crystal Films Studied by the Shear Force Resonance Method. Colloids Surfaces A: Physicochem. Eng. 1997, 129-130, 131–139. [Google Scholar] [CrossRef]
- Sakuma, H.; Otsuki, K.; Kurihara, K. Viscosity and Lubricity of Aqueous NaCl Solution Confined between Mica Surfaces Studied by Shear Resonance Measurement. Phys. Rev. Lett. 2006, 96, 046104. [Google Scholar] [CrossRef]
- Idziak, S.H.J.; Safinya, C.R.; Hill, R.; Kraiser, K.E.; Ruths, M.; Warriner, H.E.; Steinberg, S.; Liang, K.S.; Israelachvili, J.N. The X-Ray Surface Forces Apparatus: Structure of a Smectic Liquid Crystal under Confinement and Flow. Science 1994, 264, 1915–1918. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Bae, S.C.; Zhao, J.; Granick, S. How Confined Lubricants Diffuse during Shear. Phys. Rev. Lett. 2004, 93, 236105. [Google Scholar] [CrossRef]
- Bae, S.C.; Lee, H.; Lin, Z.; Granick, S. Chemical Imaging in a Surface Forces Apparatus: Confocal Raman Spectroscopy of Confined Poly(dimethylsiloxane). Langmuir 2005, 21, 5685–5688. [Google Scholar] [CrossRef]
- Bae, S.C.; Wong, J.S.; Kim, M.; Jiang, S.; Hong, L.; Granick, S. Using Light to Study Boundary Lubrication: Spectroscopic Study of Confined Fluids. Phil. Trans. R. Soc. A 2008, 366, 1443–1454. [Google Scholar] [CrossRef]
- Jiang, S.; Bae, S.C.; Granick, S. PDMS Melts on Mica Studied by Confocal Raman Scattering. Langmuir 2008, 24, 1489–1494. [Google Scholar] [CrossRef]
| symmetric (e.g., hexadecane [14,58]) | asymmetric (e.g., DBOE [18,20]) | highly asymmetric (e.g., squalane [16,59]) | ||
| stiction behavior | spike height vs. stopping time | immediately increase to its plateau when t exceeds τn (“all or none” behavior) | increase logarithmically with t, long time required to reach to a plateau | |
| possible mechanism | “discontinuous” first-order-like transition (crystallization) | “continuous” glasslike transition | ||
| stick-slip behavior | stick-slip amplitude vs. sliding velocity | insensitive to V (V < Vc), stick-slip abruptly disappears at Vc (“all or none” behavior) | gradually decrease with V, shift to smooth regime at Vc | |
| possible mechanism | “discontinuous” first-order-like transition (crystallization) | “continuous” glasslike transition | ||
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yamada, S. Nanotribology of Symmetric and Asymmetric Liquid Lubricants. Symmetry 2010, 2, 320-345. https://doi.org/10.3390/sym2010320
Yamada S. Nanotribology of Symmetric and Asymmetric Liquid Lubricants. Symmetry. 2010; 2(1):320-345. https://doi.org/10.3390/sym2010320
Chicago/Turabian StyleYamada, Shinji. 2010. "Nanotribology of Symmetric and Asymmetric Liquid Lubricants" Symmetry 2, no. 1: 320-345. https://doi.org/10.3390/sym2010320
APA StyleYamada, S. (2010). Nanotribology of Symmetric and Asymmetric Liquid Lubricants. Symmetry, 2(1), 320-345. https://doi.org/10.3390/sym2010320