Investigation of the Sintering Behavior of Nanoparticulate UN via Molecular Dynamics Simulation
Abstract
1. Introduction
2. MD Simulation of Sintering Process
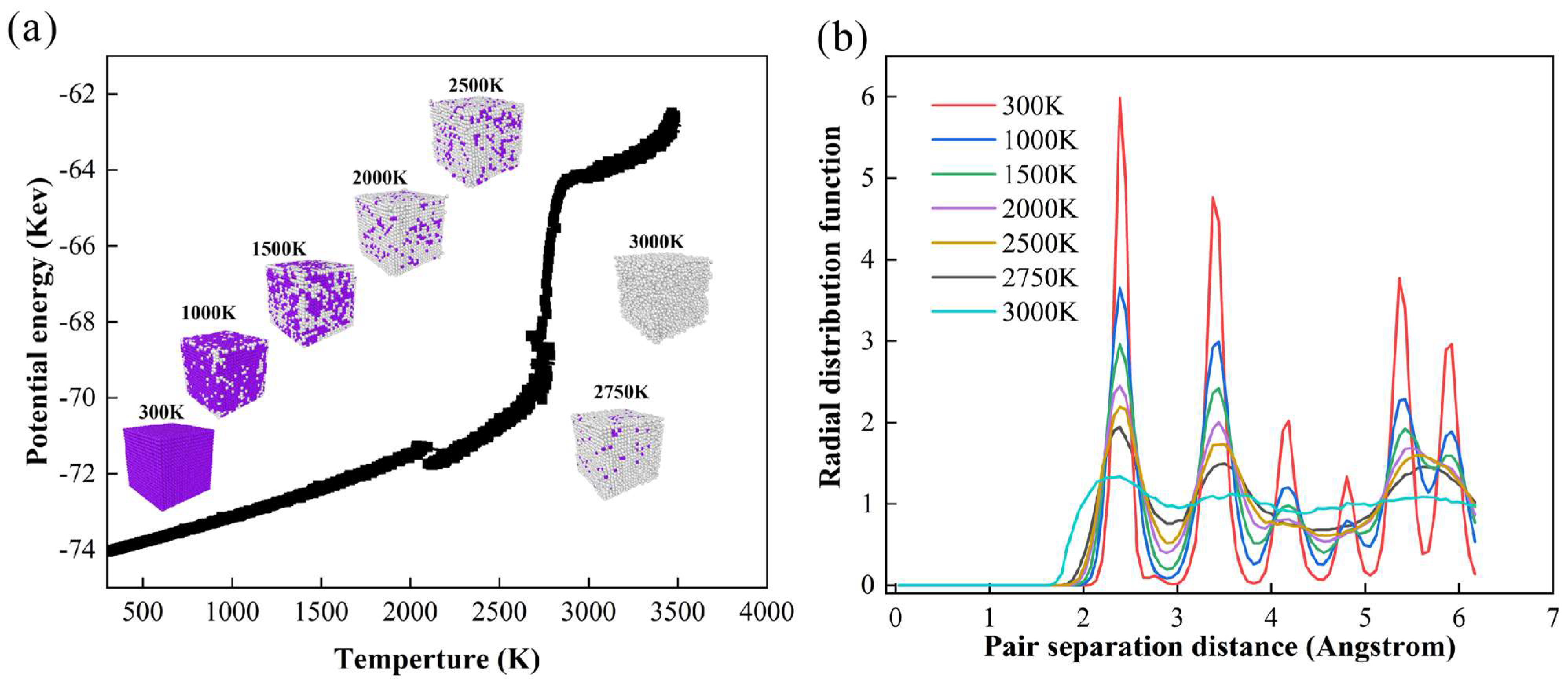
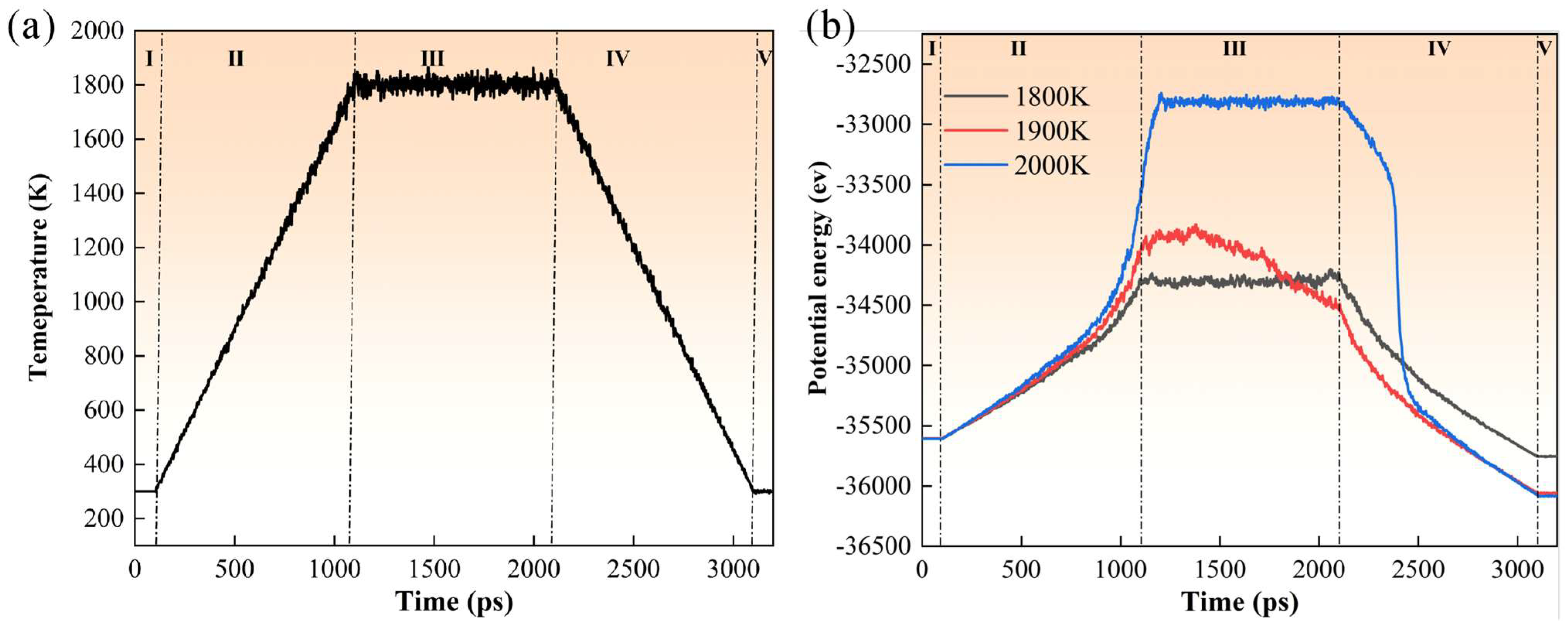
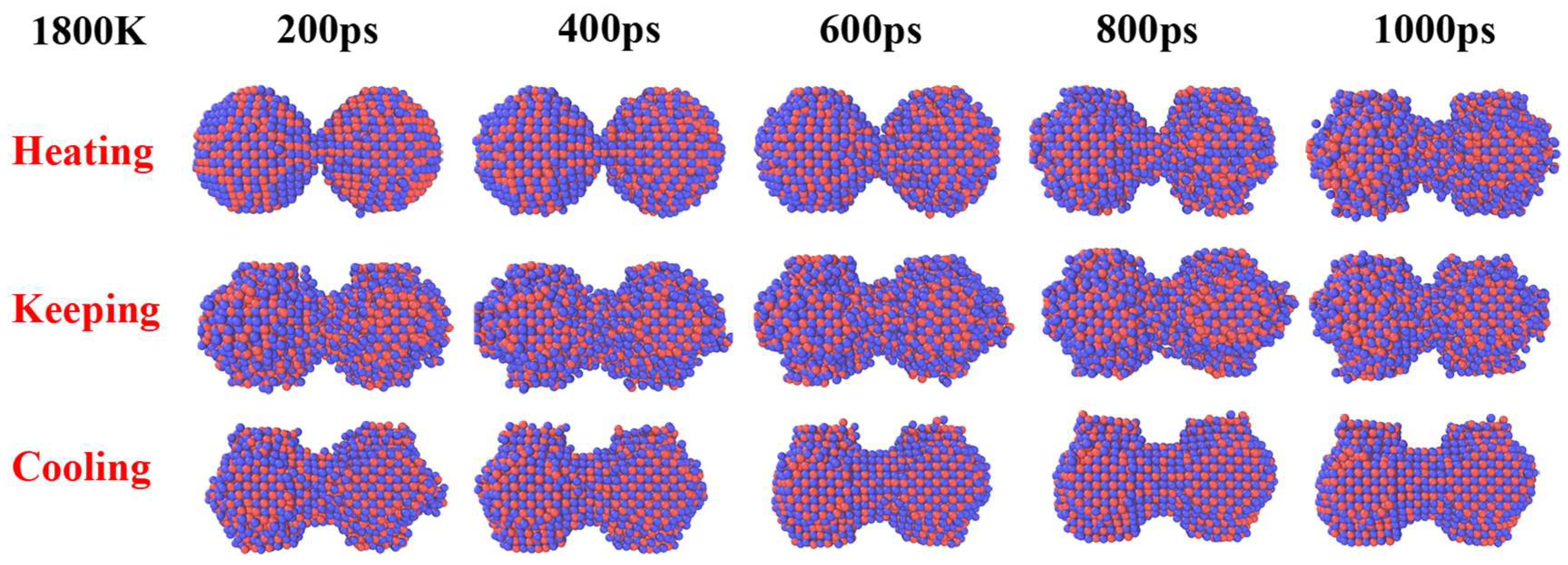
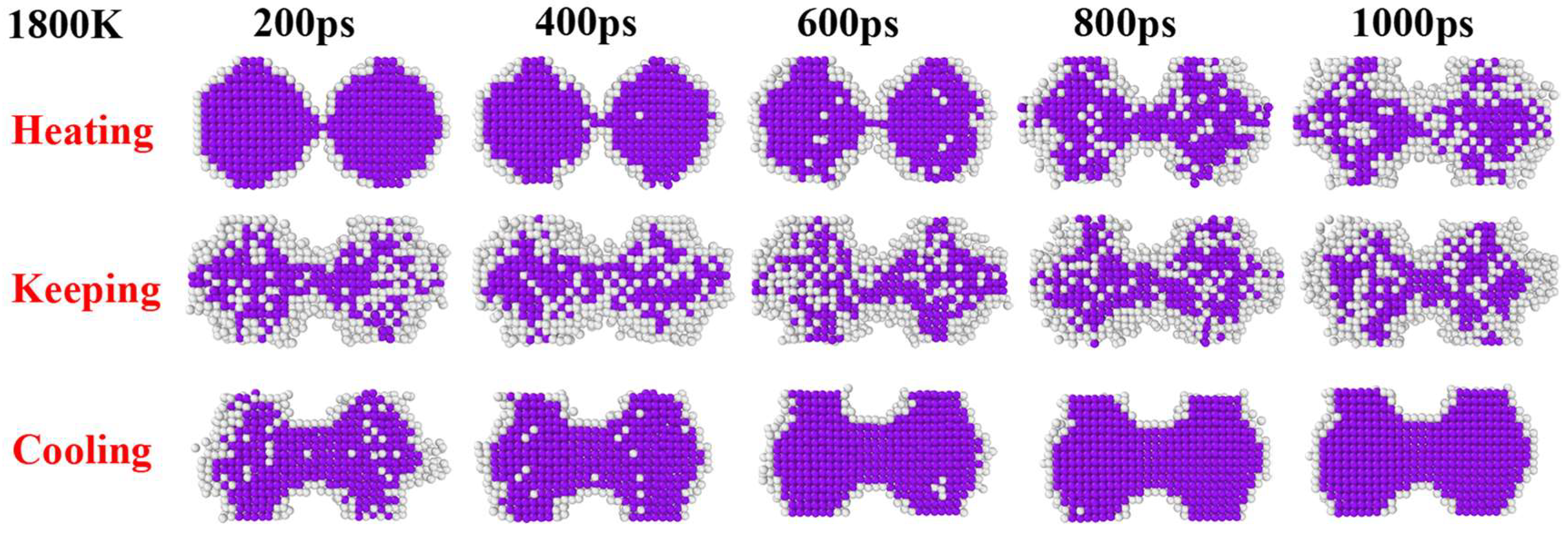
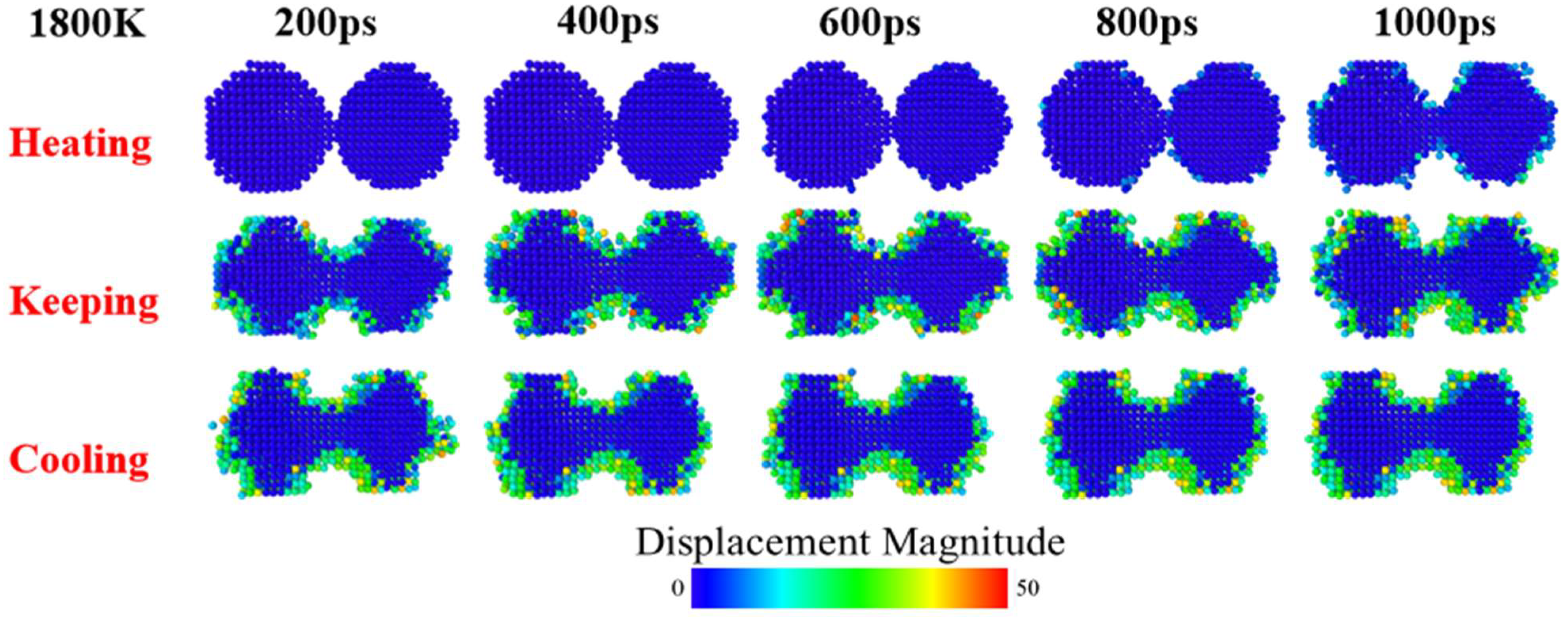
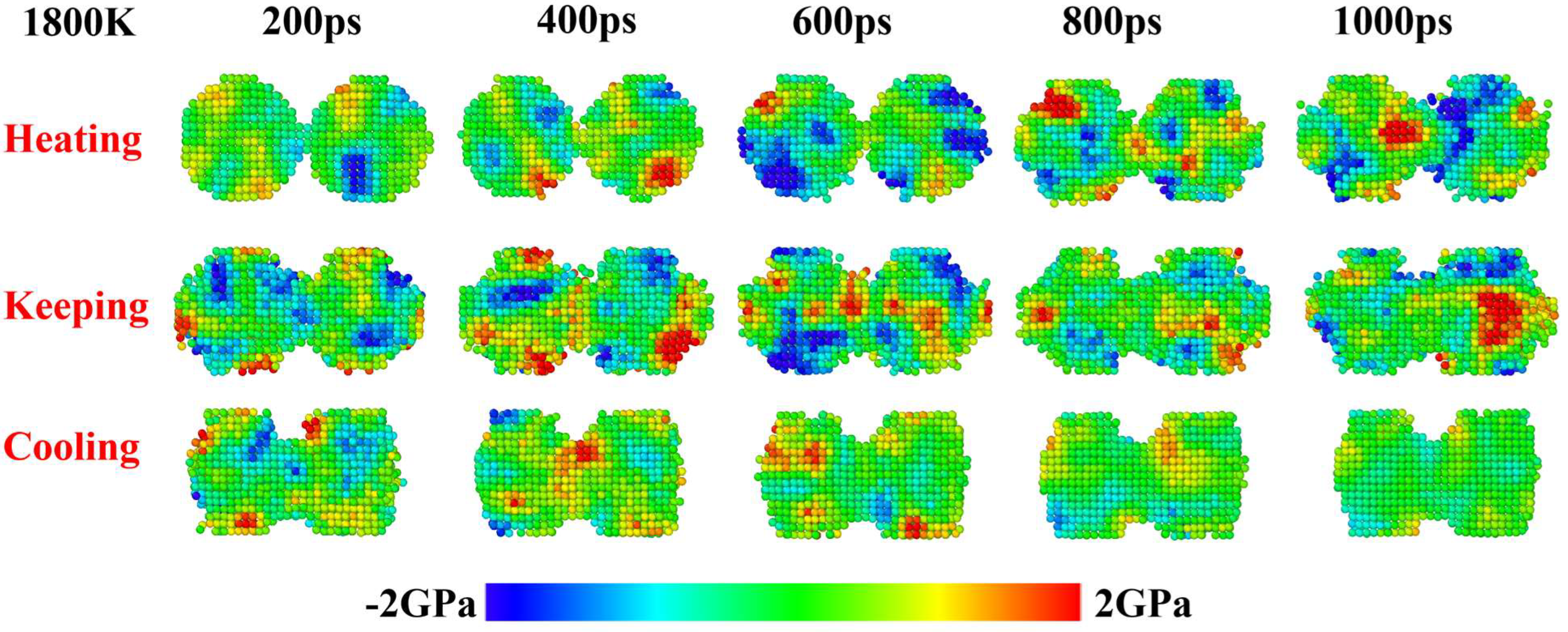
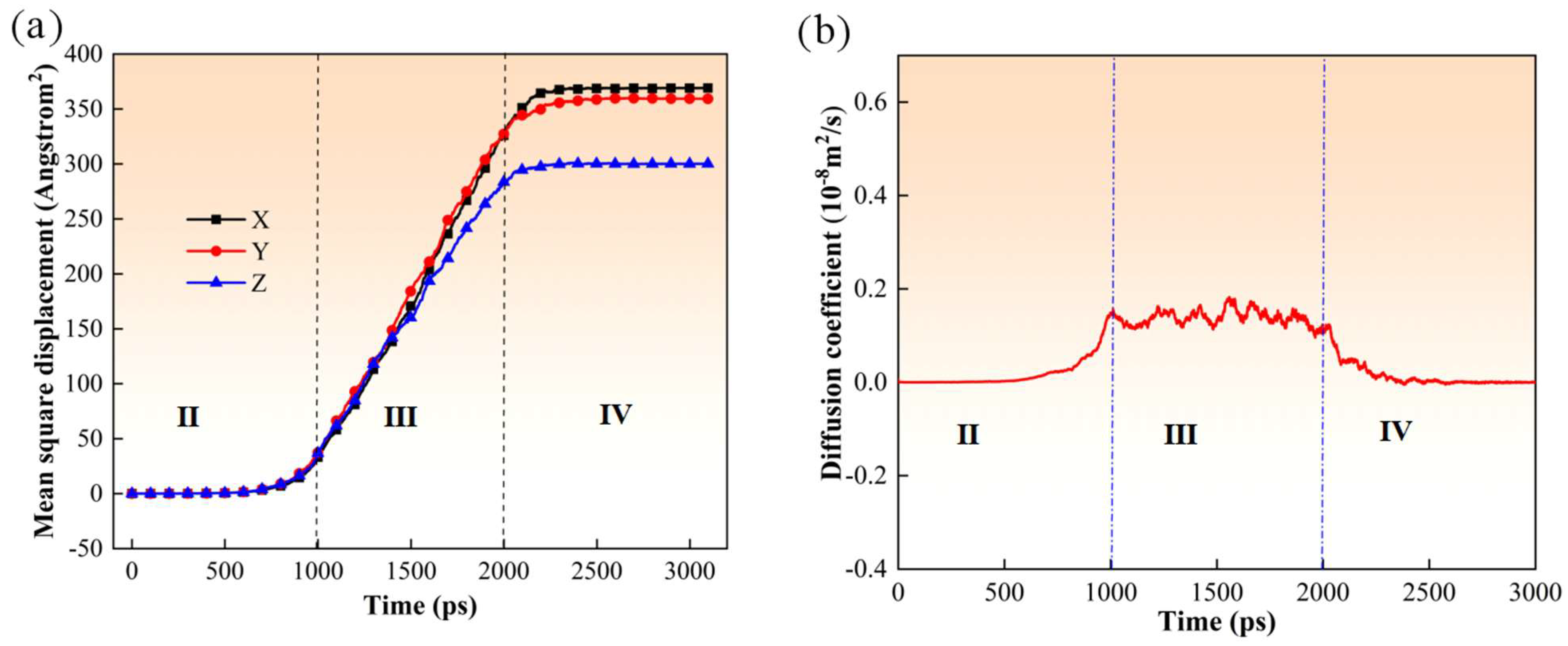
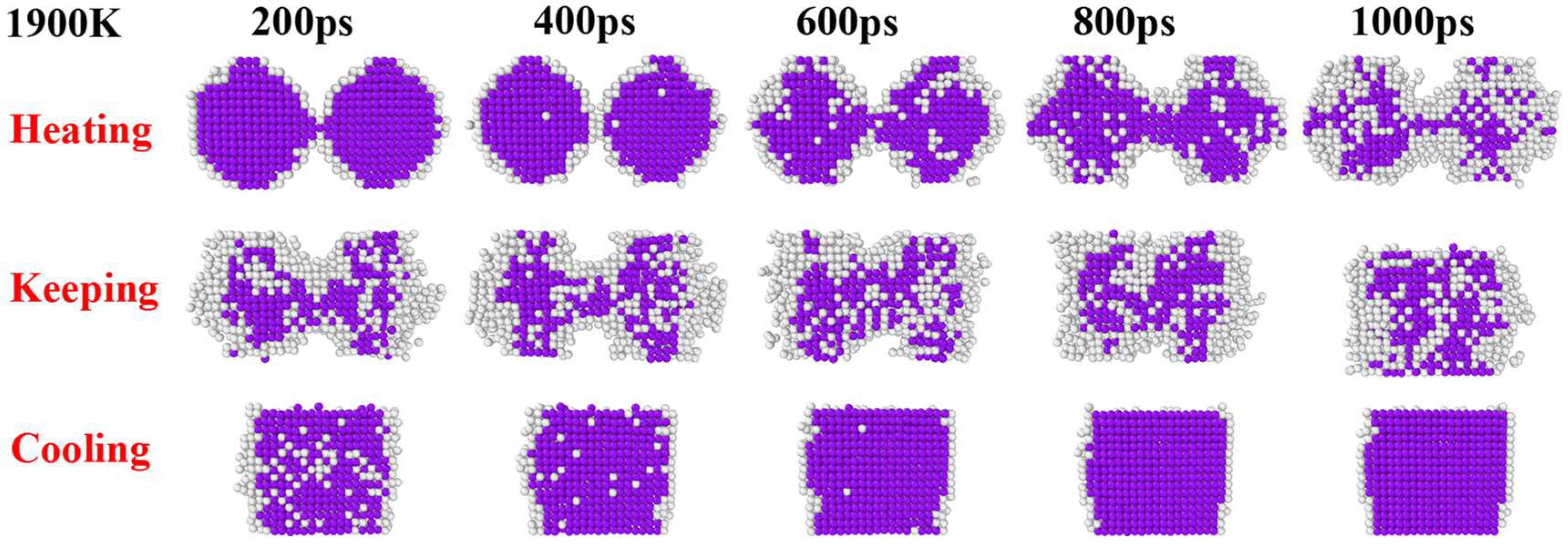
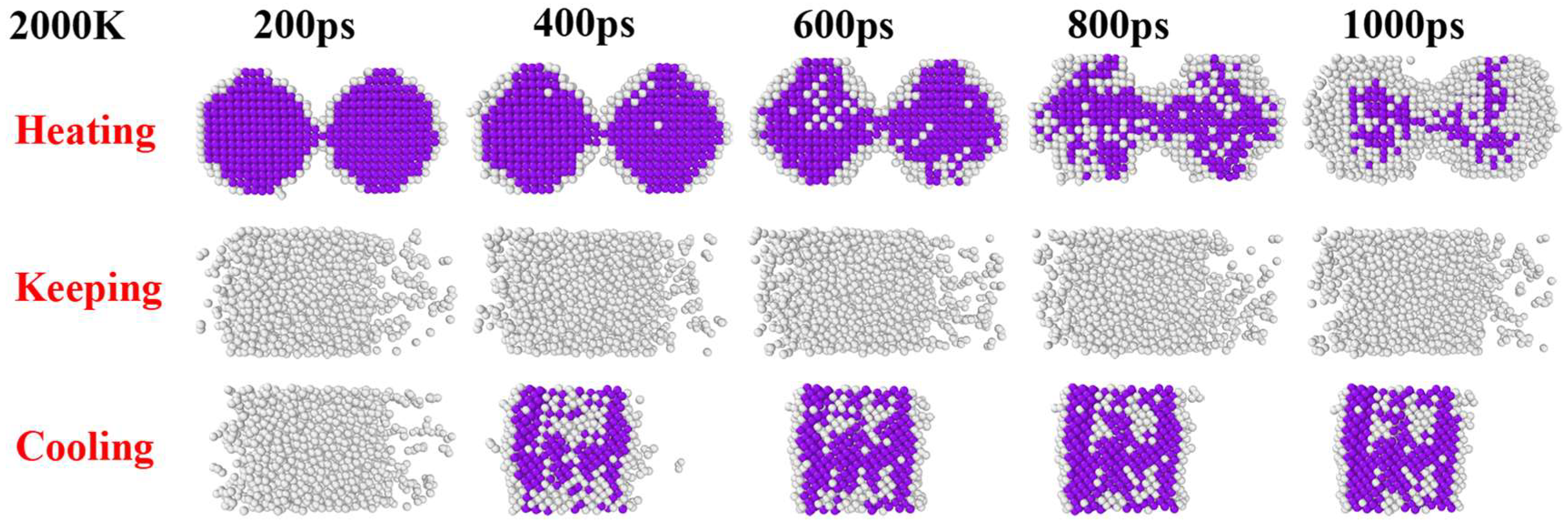
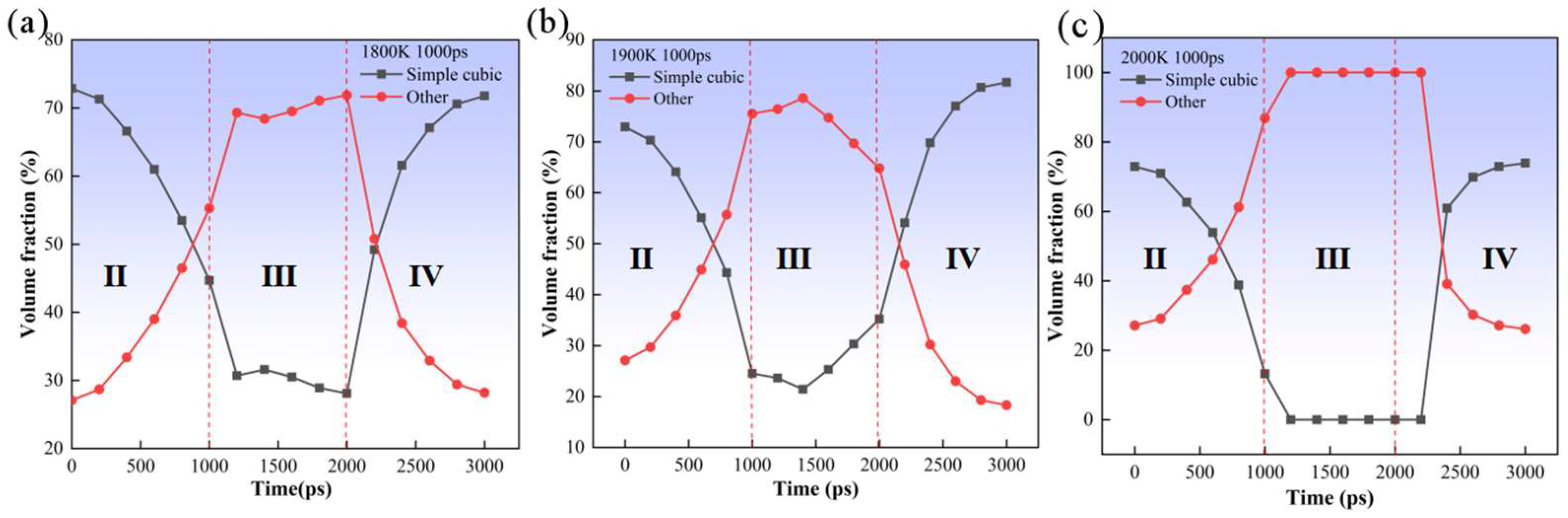
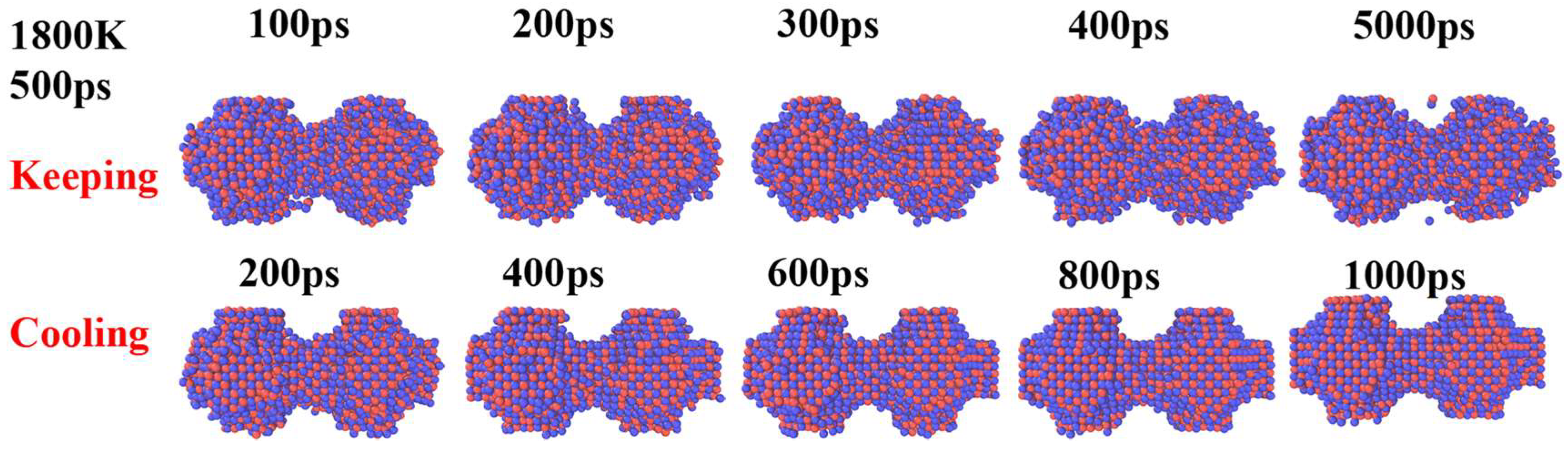
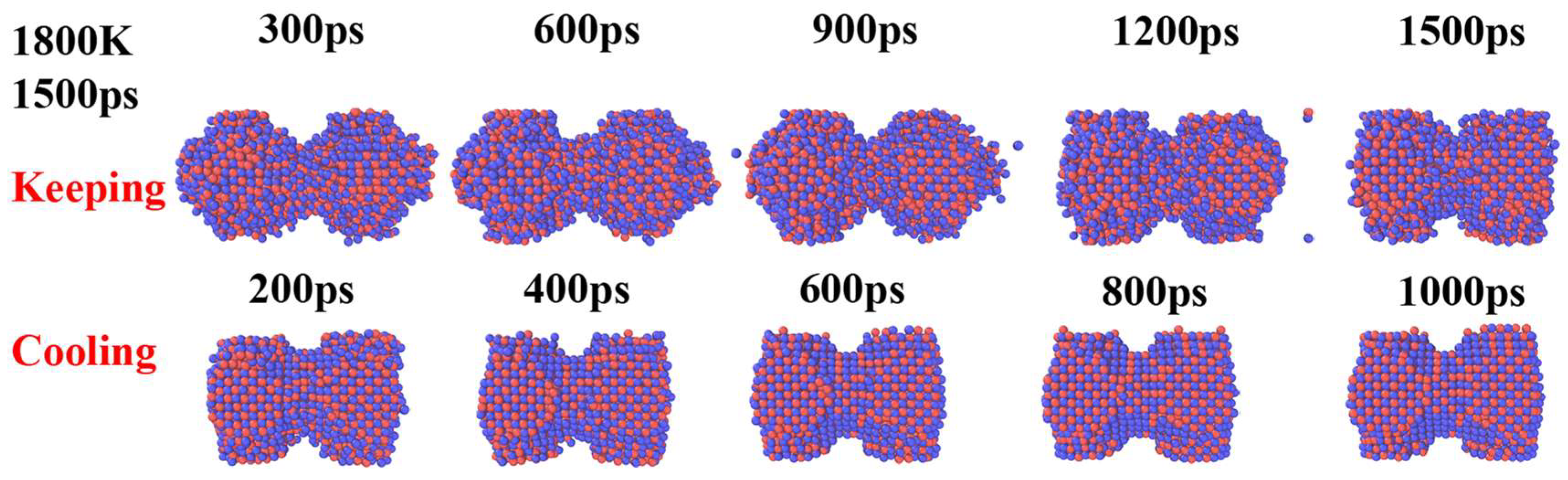
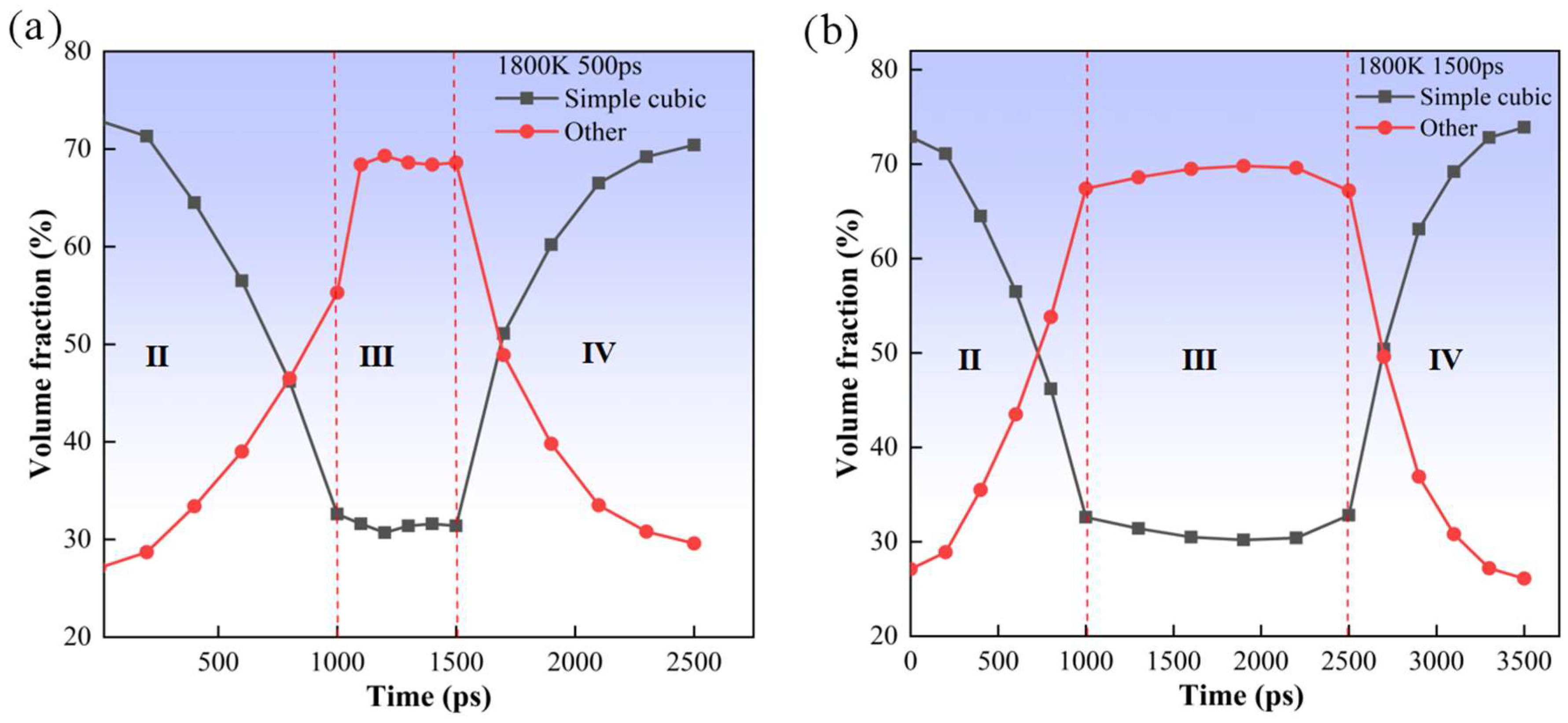
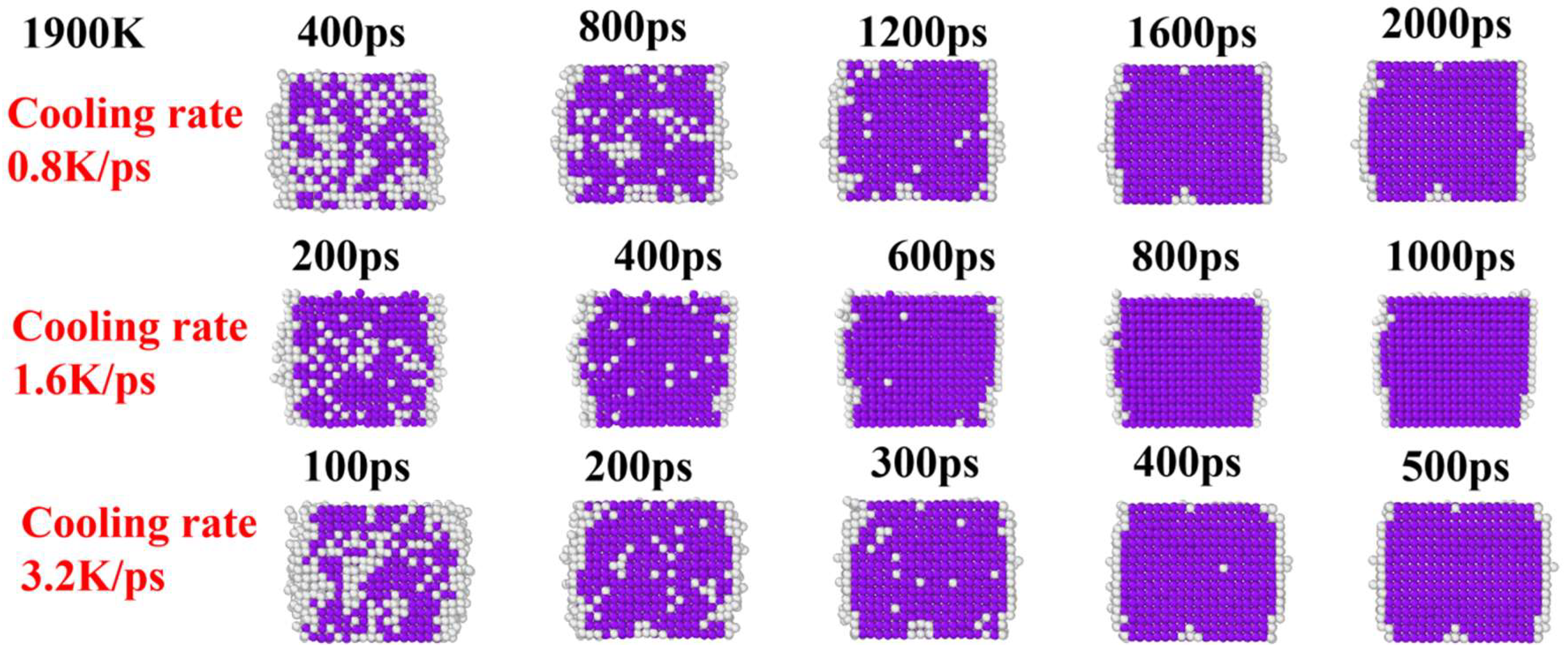
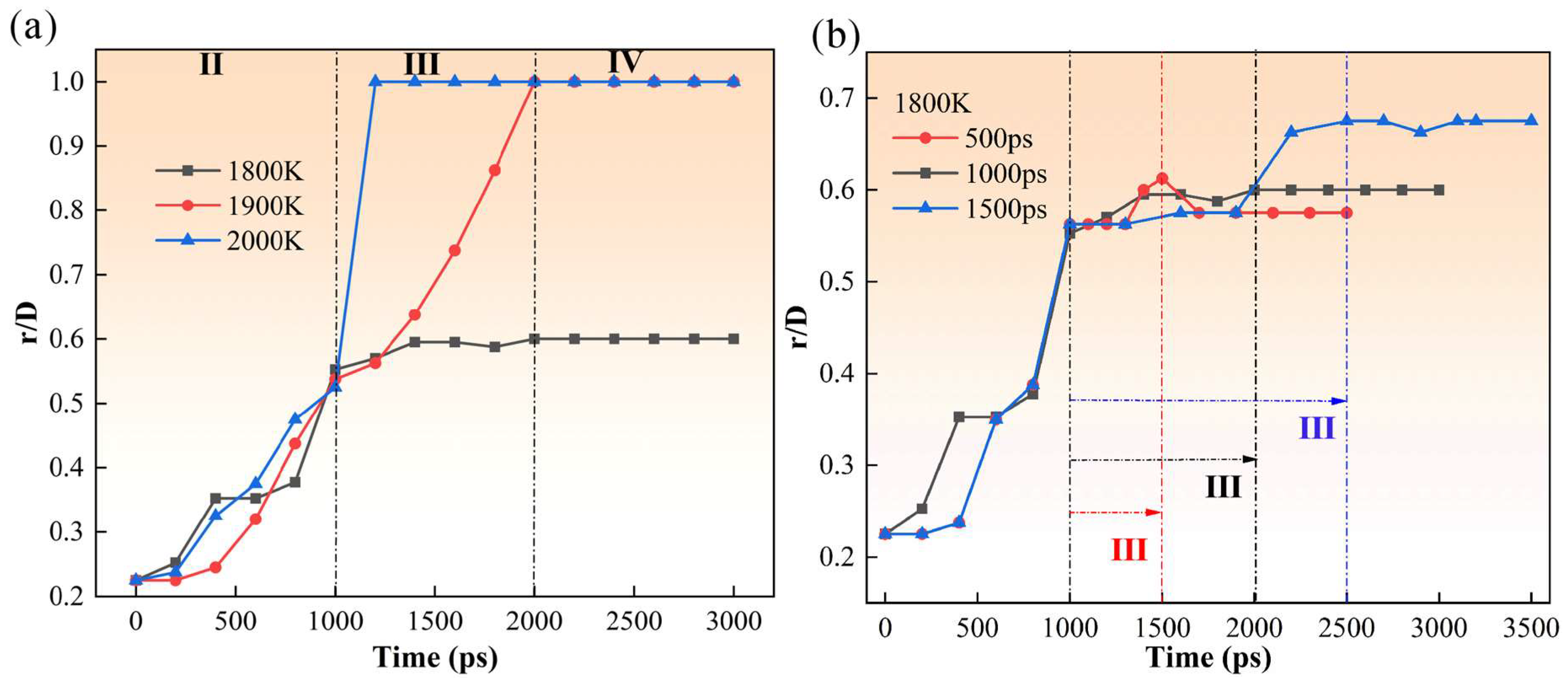
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Taylor, R.; Mathers, G.; Banford, A. The development of future options for aqueous recycling of spent nuclear fuels. Prog. Nucl. Energy 2023, 164, 104837. [Google Scholar] [CrossRef]
- Andersson, D.A.; Stanek, C.R.; Matthews, C.; Uberuaga, B.P. The past, present, and future of nuclear fuel. MRS Bull. 2023, 48, 1154–1162. [Google Scholar] [CrossRef]
- Zanini, A.; Celdran, P.A.; Walter, O.; Carturan, S.M.; Boshoven, J.; Bulgheroni, A.; Biasetto, L.; Manzolaro, M.; Eloirdi, R.; Corradetti, S.; et al. First Structured Uranium-Based Monoliths Produced via Vat Photopolymerization for Nuclear Applications. Adv. Funct. Mater. 2024, 34, 2406916. [Google Scholar] [CrossRef]
- Murphy, G.L.; Gericke, R.; Gilson, S.; Bazarkina, E.F.; Rossberg, A.; Kaden, P.; Thümmler, R.; Klinkenberg, M.; Henkes, M.; Kegler, P.; et al. Deconvoluting Cr states in Cr-doped UO2 nuclear fuels via bulk and single crystal spectroscopic studies. Nat. Commun. 2023, 14, 2455. [Google Scholar] [CrossRef]
- Harrison, R.W.; Morgan, J.; Buckley, J.; Bostanchi, S.; Pearmain, D.; Abram, T.; Goddard, D.; Barron, N. Flash sintering of UO2 pellets for nuclear fuel and wasteform applications. J. Eur. Ceram. Soc. 2025, 45, 116993. [Google Scholar] [CrossRef]
- Gong, B.; Kardoulaki, E.; Yang, K.; Broussard, A.; Zhao, D.; Metzger, K.; White, J.T.; Sivack, M.R.; Mcclellan, K.J.; Lahoda, E.J.; et al. UN and U3Si2 composites densified by spark plasma sintering for accident-tolerant fuels. Ceram. Int. 2022, 48, 10762–10769. [Google Scholar] [CrossRef]
- Yang, J.; Li, J.; Yan, C.; Wang, P.; Yang, H.; Qian, X.; Yang, K.; Xu, S.; Lin, J. Microstructure, thermal properties and irradiation behaviors of uranium nitride (UN) nuclear fuel densified by Spark Plasma Sintering (SPS). J. Nucl. Mater. 2025, 608, 155709. [Google Scholar] [CrossRef]
- Xu, J.; Yang, Z.; Zhong, Y.; Wen, Z.; Duan, L.; He, S.; Xie, L.; Wang, Z.; Wang, Y.; He, H.; et al. Spark plasma sintering of UN: Sintering behaviors, thermal-mechanical properties, and densification mechanism. Ceram. Int. 2025, 51, 60368–60380. [Google Scholar] [CrossRef]
- Yang, K.; Kardoulaki, E.; Zhao, D.; Broussard, A.; Metzger, K.; White, J.T.; Sivack, M.R.; Mcclellan, K.J.; Lahoda, E.J.; Lian, J. Uranium nitride (UN) pellets with controllable microstructure and phase-fabrication by spark plasma sintering and their thermal-mechanical and oxidation properties. J. Nucl. Mater. 2021, 557, 153272. [Google Scholar] [CrossRef]
- Ren, S.; Li, J.; Feng, H.; Liaw, P.K.; Fang, Q. A physically-based constitutive model for the prediction of yield strength in the precipitate-hardened high-entropy alloys. Acta Mech. Sin. 2023, 39, 122393. [Google Scholar] [CrossRef]
- Long, Q.B.; Zhao, H.B.; Qiu, T.S.; Wu, H.; Yan, H.S.; Qiu, S. The effect of leaching agent anions on the desorption behaviours of Al3+ from kaolinite (001) surface: A molecular dynamics simulation. Colloids Surf. A Physicochem. Eng. Asp. 2025, 727, 138247. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Fu, A.; Peng, J. Unraveling the Subsurface Damage and Material Removal Mechanism of Multi-Principal-Element Alloy FeCrNi Coatings During the Scratching Process. Symmetry 2024, 16, 1391. [Google Scholar] [CrossRef]
- Li, J.; Ren, S.; Liu, B.; Liaw, P.K.; Fang, Q. Influence of chemistry and temperature on mechanical behavior and deformation mechanisms of refractory high-entropy alloys: An integrated simulation-modeling analysis. Acta Mech. Sin. 2024, 40, 423122. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, P.; Sun, W. Monitoring micro-structural evolution during aluminum sintering and understanding the sintering mechanism of aluminum nanoparticles: A molecular dynamics study. J. Mater. Sci. Technol. 2020, 57, 92–100. [Google Scholar] [CrossRef]
- Liu, J.; Wang, M.; Liu, P.; Sun, R.; Yang, Y.; Zou, G. Molecular dynamics study of sintering of Al nanoparticles with/without organic coatings. Comput. Mater. Sci. 2021, 190, 110265. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Ye, H.; Liu, X.; Sun, F.; Fan, X.; Zhang, G. Sintering mechanism of Ag nanoparticle-nanoflake: A molecular dynamics simulation. J. Mater. Res. Technol. 2022, 16, 640–655. [Google Scholar] [CrossRef]
- Wang, Z.; Song, Z.; Luo, W.; Shang, T.; Liu, Z.; Yuan, J.; Fan, X.; Zhu, Y. The effect of temperature on the mechanisms of Cu nanoparticle sintering: A molecular dynamic study. Powder Technol. 2024, 440, 119802. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, Q.; Wang, Y.; Li, Y.; Zhang, J. Sintering neck growth mechanism of Fe nanoparticles: A molecular dynamics simulation. Chem. Eng. Sci. 2020, 218, 115583. [Google Scholar] [CrossRef]
- Guo, Q.; Hou, H.; Wang, K.; Li, M.; Liaw, P.K.; Zhao, Y. Coalescence of Al0.3CoCrFeNi polycrystalline high-entropy alloy in hot-pressed sintering: A molecular dynamics and phase-field study. Npj Comput. Mater. 2023, 9, 185. [Google Scholar] [CrossRef]
- Liu, W.; Peng, J.; Liu, J.; Li, J.; Liu, B.; Fang, Q. Investigation of the sintering behavior of nanoparticulate SiC by molecular dynamics simulation. Mater. Today Commun. 2024, 41, 110654. [Google Scholar] [CrossRef]
- Sestito, J.M.; Abdeljawad, F.; Harris, T.A.; Wang, Y.; Roach, A. An atomistic simulation study of nanoscale sintering: The role of grain boundary misorientation. Comput. Mater. Sci. 2019, 165, 180–189. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Tseplyaev, V.I.; Starikov, S.V. The atomistic simulation of pressure-induced phase transition in uranium mononitride. J. Nucl. Mater. 2016, 480, 7–14. [Google Scholar] [CrossRef]
- Brommer, P.; Kiselev, A.; Schopf, D.; Beck, P.; Roth, J.; Trebin, H.R. Classical interaction potentials for diverse materials from ab initio data: A review of potfit. Model. Simul. Mater. Sci. Eng. 2015, 23, 074002. [Google Scholar] [CrossRef]
- Kocevski, V.; Cooper, M.W.; Claisse, A.J.; Andersson, D.A. Development and application of a uranium mononitride (UN) potential: Thermomechanical properties and Xe diffusion. J. Nucl. Mater. 2022, 562, 153553. [Google Scholar] [CrossRef]
- Starikov, S.; Korneva, M. Description of phase transitions through accumulation of point defects: UN, UO2 and UC. J. Nucl. Mater. 2018, 510, 373–381. [Google Scholar] [CrossRef]
- Chen, S.L.; He, X.J.; Yuan, C.X. Recent studies on potential accident-tolerant fuel-cladding systems in light water reactors. Nucl. Sci. Tech. 2020, 31, 32. [Google Scholar] [CrossRef]
- Sahni, S.K.; Bhowmick, S.; Upadhyaya, A. Molecular dynamics simulations of solid-state sintering in Fe35Ni alloy: Understanding the process at the atomic scale. J. Mater. Sci. 2024, 59, 2954–2973. [Google Scholar] [CrossRef]
- Mehrer, H. Diffusion in Solids: Fundamentals, Methods, Materials, Diffusion-Controlled Processes; Springer: Berlin, Heidelberg, 2007. [Google Scholar]
- Nandy, J.; Yedla, N.; Gupta, P.; Sarangi, H.; Sahoo, S. Sintering of AlSi10Mg particles in direct metal laser sintering process: A molecular dynamics simulation study. Mater. Chem. Phys. 2019, 236, 121803. [Google Scholar] [CrossRef]
- Li, X.X.; Yang, C.; Chen, T.; Fu, Z.Q.; Li, Y.Y.; Ivasishin, O.M.; Lavernia, E.J. Effective atomic diffusion coefficient dependence on applied pressure during spark plasma sintering. Materialia 2019, 6, 100334. [Google Scholar] [CrossRef]
- Kuksin, A.Y.; Starikov, S.V.; Smirnova, D.E.; Tseplyaev, V.I. The diffusion of point defects in uranium mononitride: Combination of DFT and atomistic simulation with novel potential. J. Alloys Compd. 2016, 658, 385–394. [Google Scholar] [CrossRef]
- Braginsky, M.; Tikare, V.; Olevsky, E. Numerical simulation of solid state sintering. Int. J. Solids Struct. 2005, 42, 621–636. [Google Scholar] [CrossRef]
- Qi, X.; Liu, W.; He, Z.; Wang, Y.; Yun, D. Phase-Field Simulation of the Densification Process During Sintering of UN Nuclear Fuel. Acta Metall. Sin. 2022, 59, 1513–1522. [Google Scholar]
- Shi, R.; Wood, M.; Heo, T.W.; Wood, B.C.; Ye, J. Towards understanding particle rigid-body motion during solid-state sintering. J. Eur. Ceram. Soc. 2021, 41, 211–231. [Google Scholar] [CrossRef]
- Liu, J.; Lv, W.; Mou, Y.; Chen, C.; Kang, Y. Coalescence behavior of Cu nanoparticles during sintering: Based on atomic scale to macro scale. J. Mater. Res. Technol. 2023, 27, 2490–2507. [Google Scholar] [CrossRef]
- Yi, M.; Wang, W.; Xue, M.; Gong, Q.; Xu, B.X. Modeling and simulation of sintering process across scales. Arch. Comput. Methods Eng. 2023, 30, 3325–3358. [Google Scholar] [CrossRef]
- Wakai, F.; Brakke, K.A. Mechanics of sintering for coupled grain boundary and surface diffusion. Acta Mater. 2011, 59, 5379–5387. [Google Scholar] [CrossRef]
- Singh, R.; Sharma, V. Nano tungsten carbide interactions and mechanical behaviour during sintering: A molecular dynamics study. Comput. Mater. Sci. 2021, 197, 110653. [Google Scholar] [CrossRef]
- Gubicza, J.; Nauyoks, S.; Balogh, L.; Lábár, J.; Zerda, T.W.; Ungár, T. Influence of sintering temperature and pressure on crystallite size and lattice defect structure in nanocrystalline SiC. J. Mater. Res. 2005, 22, 1314–1321. [Google Scholar] [CrossRef]
- Peng, J.; Li, J.; Liu, B.; Fang, Q.; Liaw, P.K. Origin of thermal deformation induced crystallization and microstructure formation in additive manufactured FCC, BCC, HCP metals and its alloys. Int. J. Plast. 2024, 172, 103831. [Google Scholar] [CrossRef]
- Rahimian, M.; Ehsani, N.; Parvin, N.; Baharvandi, H.R. The effect of particle size, sintering temperature and sintering time on the properties of Al-Al2O3 composites, made by powder metallurgy. J. Mater. Process. Technol. 2009, 209, 5387–5393. [Google Scholar] [CrossRef]
- Gürbüz, M.; Şenel, M.C.; Koç, E. The effect of sintering time, temperature, and graphene addition on the hardness and microstructure of aluminum composites. J. Compos. Mater. 2018, 52, 553–563. [Google Scholar] [CrossRef]
- Lu, W.; Chen, Y.; Li, J.; Liaw, P.K.; Fang, Q. Chemical short-range-order induced multiscale strengthening in refractory medium entropy alloys. Acta Mech. Sin. 2024, 40, 223569. [Google Scholar] [CrossRef]
- Tan, F.; Li, L.; Li, J.; Liu, B.; Liaw, P.K.; Fang, Q. Multiscale modelling of irradiation damage behavior in high entropy alloys. Adv. Powder Mater. 2023, 2, 100114. [Google Scholar] [CrossRef]
- Chen, T.; Guo, H.; Zhao, W.; Wei, M.; Wu, M.; Chen, Y.; Liu, B. Fabrication of porous tungsten with tunable pore structures via low-temperature pressureless sintering: Processing and mechanisms. Int. J. Refract. Met. Hard Mater. 2025, 132, 107300. [Google Scholar] [CrossRef]
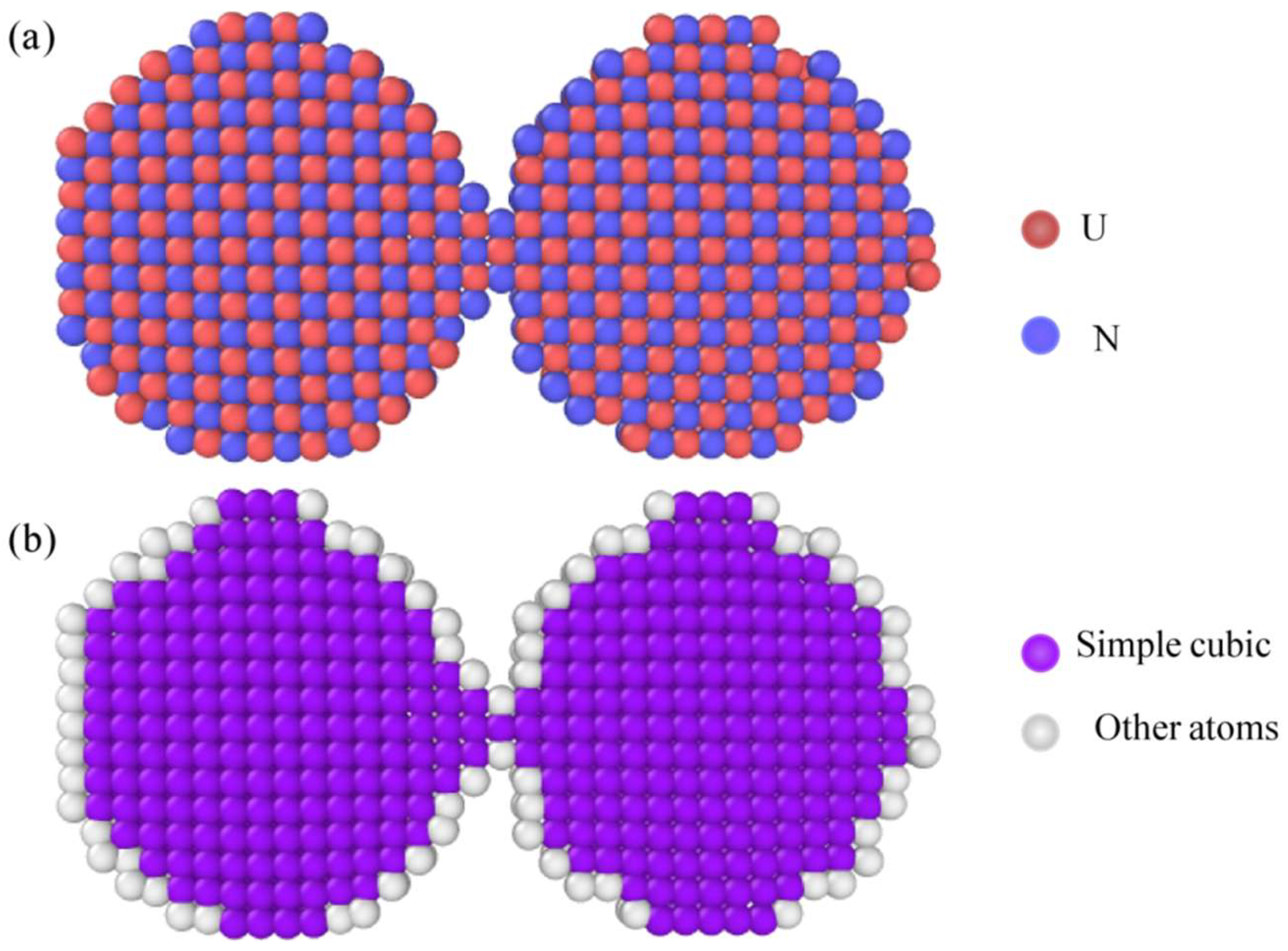
| Material | UN Nanoparticles |
|---|---|
| Box dimensions | 8 nm × 4 nm × 4 nm |
| Particles diameters | 4 nm |
| Number of nanoparticles | 2 |
| Time step | 1 fs |
| Initial temperature | 300 K |
| Boundary condition | p p p |
| Sintering temperature | 1800 K, 1900 K, 2000 K |
| Heating rate | 1.5 K/ps, 1.6 K/ps, 1.7 K/ps |
| Cooling rate | 1.5 K/ps, 1.6 K/ps, 1.7 K/ps |
| Sintering temperature duration | 50 ps, 100 ps, 1500 ps |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Liu, W.; Feng, H.; Liu, B.; Li, J.; Yang, K.; Peng, J.; Fang, Q. Investigation of the Sintering Behavior of Nanoparticulate UN via Molecular Dynamics Simulation. Symmetry 2026, 18, 191. https://doi.org/10.3390/sym18010191
Liu W, Feng H, Liu B, Li J, Yang K, Peng J, Fang Q. Investigation of the Sintering Behavior of Nanoparticulate UN via Molecular Dynamics Simulation. Symmetry. 2026; 18(1):191. https://doi.org/10.3390/sym18010191
Chicago/Turabian StyleLiu, Wentao, Hui Feng, Bin Liu, Jia Li, Kun Yang, Jing Peng, and Qihong Fang. 2026. "Investigation of the Sintering Behavior of Nanoparticulate UN via Molecular Dynamics Simulation" Symmetry 18, no. 1: 191. https://doi.org/10.3390/sym18010191
APA StyleLiu, W., Feng, H., Liu, B., Li, J., Yang, K., Peng, J., & Fang, Q. (2026). Investigation of the Sintering Behavior of Nanoparticulate UN via Molecular Dynamics Simulation. Symmetry, 18(1), 191. https://doi.org/10.3390/sym18010191








