MSGS-SLAM: Monocular Semantic Gaussian Splatting SLAM

Abstract

With the iterative evolution of SLAM (Simultaneous Localization and Mapping) technology in the robotics domain, the SLAM paradigm based on three-dimensional Gaussian distribution models has emerged as the current state-of-the-art technical approach. This research proposes a novel MSGS-SLAM system (Monocular Semantic Gaussian Splatting SLAM), which innovatively integrates monocular vision with three-dimensional Gaussian distribution models within a semantic SLAM framework. Our approach exploits the inherent spherical symmetries of isotropic Gaussian distributions, enabling symmetric optimization processes that maintain computational efficiency while preserving geometric consistency. Current mainstream three-dimensional Gaussian semantic SLAM systems typically rely on depth sensors for map reconstruction and semantic segmentation, which not only significantly increases hardware costs but also limits the deployment potential of systems in diverse scenarios. To overcome this limitation, this research introduces a depth estimation proxy framework based on Metric3D-V2, which effectively addresses the inherent deficiency of monocular vision systems in depth information acquisition. Additionally, our method leverages architectural symmetries in indoor environments to enhance semantic understanding through symmetric feature matching. Through this approach, the system achieves robust and efficient semantic feature integration and optimization without relying on dedicated depth sensors, thereby substantially reducing the dependency of three-dimensional Gaussian semantic SLAM systems on depth sensors and expanding their application scope. Furthermore, this research proposes a keyframe selection algorithm based on semantic guidance and proxy depth collaborative mechanisms, which effectively suppresses pose drift errors accumulated during long-term system operation, thereby achieving robust global loop closure correction. Through systematic evaluation on multiple standard datasets, MSGS-SLAM achieves comparable technical performance to existing three-dimensional Gaussian model-based semantic SLAM systems across multiple key performance metrics including ATE RMSE, PSNR, and mIoU.

1. Introduction

Visual Simultaneous Localization and Mapping (SLAM) [1] serves as a pivotal research topic in the computer vision domain, aiming to achieve three-dimensional map construction of unknown environments while simultaneously tracking camera poses in real-time. Examining recent research developments, traditional SLAM systems [2,3,4] have predominantly focused on map construction as a core problem, which fundamentally influences the design of all processing modules within SLAM systems. However, existing research primarily employs sparse representation methods such as voxels and point clouds, remaining somewhat insufficient in dense map representation. Moreover, these approaches fail to exploit inherent geometric symmetries present in real-world environments, such as bilateral and rotational symmetries, leading to suboptimal utilization of spatial regularity patterns.

Under the impetus of Neural Radiance Fields (NeRF) technology [5], NeRF-based SLAM methods have achieved significant progress in acquiring dense geometric information and constructing high-quality map representations [6]. These methods effectively capture dense photometric information about environments through differentiable rendering techniques, not only generating highly realistic three-dimensional global maps but also demonstrating good robustness against noise and outliers. However, NeRF-SLAM methods employing Multi-Layer Perceptrons (MLPs) [7] as implicit neural representations of scenes exhibit significant limitations [8]. On one hand, they suffer from over-smoothing effects at object boundaries, leading to geometric detail loss. This over-smoothing particularly disrupts preservation of local symmetries crucial for accurate scene understanding, as implicit continuous representation tends to blur symmetric structures. This limitation results in the lack of effective decoupling mechanisms for scene object representation, constraining semantic segmentation and scene editing capabilities. On the other hand, when confronted with extended scenes, they exhibit catastrophic forgetting phenomena, leading to substantial degradation in representation accuracy.

Against this backdrop, our exploration turns toward 3D Gaussian-based semantic SLAM systems [9,10,11,12]. This approach brings multiple significant advantages to SLAM systems: first, its efficient rasterization mechanism substantially improves rendering speed by eliminating view-dependency and adopting simplified spherical Gaussian distributions (rather than complex ellipsoidal forms), achieving real-time dense photometric optimization. Second, this representation possesses linear scaling capabilities, supporting arbitrary increases in map capacity and local editing while maintaining overall rendering quality. Additionally, semantic maps significantly enhance the system’s scene understanding capabilities, while this architectural design facilitates the integration of multimodal semantic information, enabling appearance, geometry, and semantic signals to collaboratively promote camera tracking and scene reconstruction, better meeting the requirements of robotic navigation and mixed reality applications. Moreover, we introduce Metric3D-V2 [13], a state-of-the-art monocular depth estimation model, to provide proxy depth information, further expanding the application scope and research value of this method in the robotics domain. This innovative integration enables real-time rendering of appearance, semantic colors, and proxy depth.

Compared to 3D Gaussian-based semantic RGB-D SLAM systems (such as SGS-SLAM), the system proposed in this research demonstrates comparable performance in key indicators including rendering efficiency, reconstruction quality, and semantic segmentation accuracy. This method significantly enhances the system’s depth reasoning robustness under heterogeneous material surfaces (such as transparent or highly reflective media) and complex lighting conditions, effectively overcoming depth acquisition distortion problems of traditional RGB-D sensors at special optical interfaces, thereby achieving stable scene understanding and reconstruction capabilities in variable environments. Furthermore, the multimodal integration strategy that fuses proxy depth information with explicit spatial representation and semantic features can significantly improve camera pose estimation accuracy and convergence efficiency. More importantly, we combine proxy depth, geometric, and semantic criteria, employing multi-level adjustment methods for keyframe selection, a process based on the identification of previously observed objects in the trajectory. Through extensive experiments in synthetic and real scene benchmarks, we comprehensively compare our method with implicit NeRF-based methods and novel 3D Gaussian-based semantic RGB-D methods, systematically evaluating performance in map construction, tracking, and semantic segmentation.

Overall, our work presents several key contributions, summarized as follows:

‑

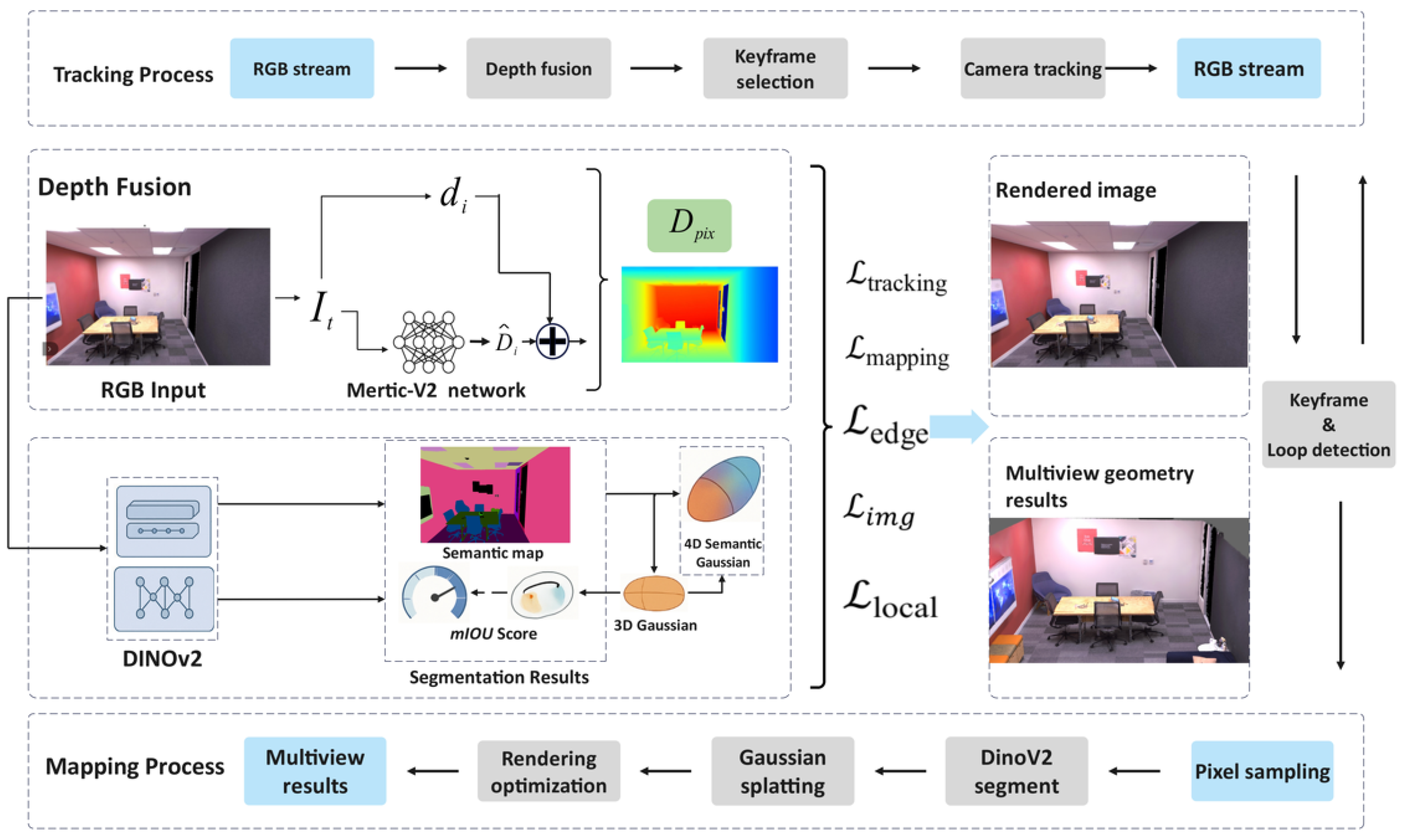
We propose MSGS-SLAM, a monocular semantic SLAM system based on 3D Gaussian splatting. The system integrates Metric3D-V2 [13] for proxy depth estimation to address scale ambiguity, while utilizing four-dimensional semantic Gaussian representation for unified geometric, appearance, and semantic optimization. This approach achieves high-fidelity reconstruction comparable to RGB-D methods while requiring only monocular input.

‑

We develop innovative technical components including uncertainty-aware proxy depth fusion, semantic-guided keyframe selection, and multi-level loop detection mechanisms. The system employs adaptive optimization strategies that leverage appearance, geometric, and semantic information to ensure robust tracking and global consistency correction.

‑

Our monocular approach eliminates the requirement for specialized depth sensors (e.g., LiDAR, structured light sensors) that typically cost $200–2000 compared to standard RGB cameras ($10–100), enabling deployment with ubiquitous consumer devices, existing video datasets, and resource-constrained environments. This fundamental hardware simplification expands applicability to historical data analysis, large-scale urban modeling, and scenarios where RGB-D sensors are impractical due to cost, power, or environmental constraints.

The paper is organized as follows: Section 2 reviews related work in NeRF-based SLAM, 3D Gaussian splatting, and semantic SLAM. Section 3 presents our methodology including proxy depth fusion, semantic Gaussian representation, and loop detection mechanisms. Section 4 provides comprehensive experimental evaluation and ablation studies. Section 5 concludes with discussions and future directions.

2. Related Work

2.1. NeRF-Based SLAM

Neural Radiance Fields (NeRF) have significantly advanced dense SLAM systems through their ability to model complex scenes with implicit neural representations. iNeRF [14] pioneered pose estimation by inverting neural radiance fields, establishing the foundation for NeRF-based SLAM. iMAP [15] introduced the first real-time system using NeRF as the sole map representation, though limited to 2 Hz mapping rates. Despite enabling dense reconstruction, iMAP’s computational bottleneck stemmed from per-frame neural network optimization, severely limiting scalability to larger environments. NICE-SLAM [16] addressed scalability through hierarchical scene representations, introducing multi-resolution voxel grids that improved efficiency but still suffered from memory consumption issues in extended sequences. Co-SLAM [17] improved performance via joint coordinate and sparse parametric encodings. Co-SLAM’s key contribution was decoupling coordinate and color learning, improving convergence speed but not fundamentally addressing over-smoothing at object boundaries. More recent methods include NICER-SLAM [18] for dense RGB SLAM and Point-SLAM [19] utilizing neural point clouds.

Despite these advances, NeRF-based methods face inherent limitations: over-smoothing at object boundaries, catastrophic forgetting in extended scenes, and computational inefficiency due to MLP architectures. The implicit representation’s continuous nature makes it particularly prone to losing fine geometric details at material boundaries, which are crucial for accurate semantic understanding and scene interpretation. These constraints limit real-time applicability in robotics applications.

2.2. 3D Gaussian Splatting SLAM

3D Gaussian Splatting (3DGS) [20] offers superior rendering efficiency through explicit scene representation. The key advantage lies in its differentiable rasterization process, avoiding expensive volumetric sampling required by NeRF methods. MonoGS [21] demonstrated the first monocular 3DGS SLAM, achieving real-time performance at 3 fps with high-fidelity reconstruction. However, MonoGS relied on traditional depth estimation techniques that suffer from significant scale drift in long sequences, limiting practical deployment in extended navigation scenarios. SplaTAM [22] extended this to RGB-D settings, delivering up to 2× performance improvements over existing methods. SplaTAM’s success was attributed to accurate RGB-D depth information, but this hardware requirement significantly increases system cost and limits deployment flexibility. GS-SLAM [23] contributed adaptive expansion strategies and coarse-to-fine tracking. While introducing effective Gaussian densification mechanisms, it lacked semantic awareness, making it unsuitable for applications requiring scene understanding. Recent developments include MM3DGS SLAM [24] for multi-modal fusion and various efficiency-focused variants.

However, existing Gaussian-based SLAM systems lack semantic understanding capabilities, limiting their application in scene interpretation and object-level tasks. This limitation is particularly problematic for robotic applications requiring environment understanding beyond geometric reconstruction, such as navigation planning around specific object categories.

2.3. Semantic SLAM

Traditional semantic SLAM systems [25] integrate semantic information into conventional frameworks. Early approaches like SLAM++ [26] and Kimera [27] focused on object-aware mapping with explicit representations, but suffered from storage limitations and reconstruction quality issues. SLAM++ represented scenes as collections of object models, providing semantic understanding, but also being limited to predefined categories and struggling with novel geometries. Kimera improved with mesh-based reconstruction, yet explicit representation inherently limited scalability and required significant memory resources.

Recent neural implicit methods have shown promise. SNI-SLAM [28] introduced hierarchical semantic representation with cross-attention for multi-modal feature fusion. SNI-SLAM’s contribution was integrating semantic and geometric features through attention mechanisms, enabling robust tracking. However, its NeRF-based implicit representation inherited computational bottlenecks and over-smoothing issues, affecting real-time performance. SGS-SLAM [29] pioneered semantic Gaussian Splatting, incorporating appearance, geometry, and semantic features through multi-channel optimization, achieving state-of-the-art performance in semantic segmentation [30] while maintaining real-time capabilities. SGS-SLAM demonstrated superior boundary preservation compared to implicit methods but remained dependent on RGB-D sensors, limiting applicability in scenarios where depth sensors are unavailable or unreliable.

2.4. Depth Estimation for Monocular SLAM

Monocular SLAM faces the fundamental challenge of scale ambiguity. Traditional solutions rely on bundle adjustment [31] and geometric constraints, while recent learning-based depth estimation methods offer new opportunities. Classical approaches like structure-from-motion require sufficient parallax and texture for reliable depth triangulation, often failing in texture-sparse environments. Recent deep learning methods such as MiDaS [32] produce relative depth maps lacking the metric scale consistency required for accurate SLAM applications. However, most existing approaches either sacrifice accuracy for real-time performance or require complex multi-stage processing. Methods like MonoDepth2 [33] achieve real-time inference but produce inconsistent depth estimates across frames, leading to accumulated drift, while accuracy-focused methods require computationally prohibitive post-processing.

Our MSGS-SLAM addresses these limitations by integrating proxy depth estimation with semantic understanding in a unified 3D Gaussian framework, achieving robust monocular SLAM without compromising real-time performance. Specifically, our approach leverages Metric3D-V2’s metric-scale depth estimates with uncertainty quantification to handle unreliable regions, combining monocular scalability with RGB-D-level reconstruction quality.

3. Method

The overall architecture of the MSGS-SLAM system is shown in Figure 1, comprising four key modules: proxy depth estimation, four-dimensional Gaussian representation, multi-channel tracking and mapping, and semantic-guided loop detection. Unlike traditional RGB-D-based semantic SLAM systems, MSGS-SLAM innovatively integrates monocular vision with four-dimensional Gaussian distribution models, converting monocular camera observations into depth-informed representations through proxy depth estimation, thereby overcoming the inherent scale ambiguity problem of monocular SLAM systems.

3.1. Proxy Depth Fusion

The fundamental challenge faced by monocular visual SLAM systems lies in the inability of monocular cameras to directly provide depth information, resulting in scale ambiguity and geometric vagueness in reconstructed scenes. To address this technical bottleneck, one of the core innovations of MSGS-SLAM is the introduction of a depth estimation proxy framework based on Metric3D-V2 [13]. Compared to traditional RGB-D sensors and other proxy depth frameworks, this architecture demonstrates significant advantages in monocular visual environments: first, the model can achieve completely unsupervised depth estimation without relying on specific depth ground truth data for training; and second, it maintains consistent scale in depth estimation, resolving the inherent scale ambiguity problem of monocular SLAM systems. Additionally, this framework possesses fast execution speed, meeting the requirements of real-time SLAM applications. Furthermore, our depth estimation approach leverages symmetric consistency constraints, exploiting bilateral and reflective symmetries commonly found in architectural structures to enhance depth prediction accuracy and reduce estimation variance in symmetric regions. For each monocular image frame $I_t$, we use the pre-trained Metric3D-V2 model to estimate the depth map ${\widehat{D}}_t$:

$${\widehat{D}}_t=\mathrm{Metric}3\mathrm{D}\text{-}\mathrm{V}2\left(I_t\right)$$

(1)

Unlike depth measurements provided by traditional RGB-D sensors, proxy depth contains inherent uncertainty. To address this, we introduce an uncertainty quantification mechanism $\mathcal{U}\left({\widehat{D}}_t\right)$ to estimate the reliability of depth values:

$$\mathcal{U}\left({\widehat{D}}_t\right)=\exp (-\alpha ·\parallel \nabla {\widehat{D}}_t{\parallel }_2)·\beta ·\mathrm{Conf}\left({\widehat{D}}_t\right)·\gamma ·\theta \left(S_t\right)$$

(2)

where $\parallel \nabla {\widehat{D}}_t{\parallel }_2$ is the depth gradient norm, capturing depth discontinuous regions (typically with higher uncertainty); $\mathrm{Conf}\left({\widehat{D}}_t\right)$ is the confidence map output by Metric3D-V2; $\theta \left(S_t\right)$ is a semantic segmentation accuracy modulation function, defined as:

$$\theta \left(S_t\right)={\displaystyle \frac{1}{1+\exp (-\lambda (\mathrm{mIoU}\left(S_t\right)-\varphi ))}}$$

(3)

The adjustment coefficients $\alpha$, $\beta$, and $\gamma$ are designed to balance different uncertainty sources: $\alpha$ controls sensitivity to geometric discontinuities (recommended range 0.5–1.0), $\beta$ weights the depth estimator’s internal confidence (typically 0.7–0.9), and $\gamma$ incorporates semantic consistency (usually 0.3–0.7). For environments with challenging depth estimation conditions, increasing $\alpha$ and $\gamma$ while reducing $\beta$ provides more robust uncertainty assessment.

This function adopts a sigmoid form, where $\mathrm{mIoU}\left(S_t\right)$ represents the mean Intersection over Union metric of the current frame’s semantic segmentation, $\varphi$ is the threshold parameter, and $\lambda$ controls the function curvature. The parameters $\alpha$, $\beta$, and $\gamma$ are adjustment coefficients that balance the contributions of geometric, appearance, and semantic factors to uncertainty assessment. This uncertainty quantification provides important guidance for subsequent scene reconstruction and optimization.

3.2. Four-Dimensional Semantic Gaussian Representation and Multi-Channel Rendering

Traditional monocular SLAM systems, while advantageous in terms of hardware cost and deployment convenience, are fundamentally limited by their lack of scene understanding and semantic perception capabilities, severely restricting their potential in practical applications such as intelligent navigation, scene interaction, and complex environment adaptation. In MSGS-SLAM, we propose a four-dimensional semantic Gaussian representation model that explicitly represents scenes through a set of three-dimensional Gaussian functions and innovatively integrates semantic information as a fourth-dimensional attribute into the Gaussian representation. Each Gaussian distribution is modeled through an influence function $f(·)$. For computational simplification, we adopt isotropic Gaussian distributions:

$$f^{3D}\left(x\right)=\sigma \exp \left(-{\displaystyle \frac{{\parallel x-\mu \parallel }^2}{2r^2}}\right)$$

(4)

where $\sigma \in [0,1]$ represents opacity, $\mu \in {\mathbb{R}}^3$ represents the center position, and r represents the radius. Each Gaussian distribution also carries RGB color information $c_i={[r_i,g_i,b_i]}^T$ and semantic label information $s_i={[s_i^1,s_i^2,\dots ,s_i^K]}^T$, where K represents the total number of semantic categories. Unlike existing monocular SLAM systems, this multi-channel Gaussian representation allows the system to simultaneously optimize geometric, appearance, and semantic information, achieving more comprehensive scene understanding.

To optimize Gaussian distribution parameters for scene representation, we need to project three-dimensional Gaussians onto the two-dimensional image plane through differentiable rendering. Similar to traditional RGB-D semantic Gaussian SLAM systems (such as SGS-SLAM), we adopt volumetric rendering methods, and additionally incorporate proxy depth channels. The Gaussian distribution’s center $\mu$, radius r, and depth d are projected in the camera coordinate system through standard point rendering formulas:

$${\mu }^{2D}=K{\displaystyle \frac{E_t\mu }{d}},r^{2D}={\displaystyle \frac{lr}{d}},d={\left(E_t\mu \right)}_z$$

(5)

where K is the camera intrinsic matrix, $E_t$ is the camera extrinsic matrix at time t, and l is the focal length.

During rendering, pixel-level rendered color $C_{\mathrm{pix}}$, depth $D_{\mathrm{pix}}$, and semantic information $S_{\mathrm{pix}}$ are computed through front-to-back volumetric rendering:

$$C_{\mathrm{pix}}=\sum _{i=1}^n{c}_i{f}_{i,\mathrm{pix}}^{2D}\prod _{j=1}^{i-1}(1-f_{j,\mathrm{pix}}^{2D})$$

(6)

$$D_{\mathrm{pix}}=\sum _{i=1}^n{d}_i{f}_{i,\mathrm{pix}}^{2D}\prod _{j=1}^{i-1}(1-f_{j,\mathrm{pix}}^{2D}·w_d(d_i,{\widehat{D}}_i))$$

(7)

$$S_{\mathrm{pix}}=\sum _{i=1}^n{s}_i{f}_{i,\mathrm{pix}}^{2D}\prod _{j=1}^{i-1}(1-f_{j,\mathrm{pix}}^{2D})$$

(8)

where $w_d(d_i,{\widehat{D}}_i)=\exp (-\kappa |d_i-{\widehat{D}}_i{|}^2)$ is the depth fusion weight factor, ${\widehat{D}}_i$ is the proxy depth estimate, and $\kappa$ is the balance parameter. This design enables the system to adaptively adjust volumetric rendering weights based on the consistency between proxy depth and rendered depth, improving the accuracy and robustness of depth rendering. Compared to traditional RGB-D systems, this depth fusion mechanism can more flexibly handle depth uncertain regions, achieving precise reconstruction of complex geometric structures.

The introduction of semantic information not only enhances the system’s scene understanding capability but also serves as additional constraints during optimization, promoting accurate reconstruction of geometric and appearance features. During mapping optimization, semantic loss serves as a key component in multi-channel optimization, guiding the system to accurately model critical features such as object boundaries and material changes. Moreover, our approach exploits symmetric correspondences in semantic regions, utilizing bilateral and mirror symmetries commonly present in architectural environments to enforce consistent semantic labeling across symmetric scene elements. This semantic-guided optimization strategy significantly improves the system’s reconstruction quality and segmentation accuracy in complex environments, providing rich environmental representations for downstream tasks such as scene understanding, object interaction, and autonomous navigation. Compared to existing monocular SLAM and NeRF-based systems, MSGS-SLAM achieves more efficient rendering speed and more precise object-level geometric reconstruction through semantic Gaussian representation, effectively overcoming the over-smoothing problems commonly present in neural implicit representations.

By setting $d_i=1$, we can compute the silhouette value ${\mathrm{Sil}}_{\mathrm{pix}}=D_{\mathrm{pix}}(d_i=1)$, which is used to determine pixel visibility in the current view. This is crucial for camera pose estimation and scene reconstruction, especially when dealing with thin objects or complex geometric shapes, where silhouette information can provide additional structural constraints, effectively avoiding geometric degeneracy problems.

3.3. Semantic-Guided System Tracking

In the tracking phase, we propose a keyframe selection algorithm based on semantic guidance and proxy depth collaborative mechanisms. Unlike traditional SLAM systems that rely solely on photometric error or geometric residual minimization tracking methods, which are prone to losing track in scenes with sparse textures, lighting changes, or significant viewpoint variations, MSGS-SLAM innovatively incorporates semantic information as additional constraints, significantly enhancing the system’s robustness in complex environments. Specifically, we utilize high-level semantic representations generated by the DINOv2 visual feature extractor [34], providing the system with scene understanding capabilities that enable the tracking process to focus not only on low-level geometric and appearance features but also to identify and utilize semantic consistency in scenes.

First, the system captures and stores keyframes at fixed time intervals, ensuring temporal consistency of trajectory sampling. Subsequently, keyframes are filtered based on dual geometric and semantic constraints to establish precise associations between current frames and historical observations.

At the geometric constraint level, the system randomly samples pixel points from the current frame, extracts their corresponding three-dimensional Gaussian distributions $G_{\mathrm{sample}}$, and projects them to keyframe viewpoints, generating projected distributions $G_{\mathrm{proj}}$. Based on the geometric visibility of projected distributions, we define an overlap rate evaluation metric:

$$\eta ={\displaystyle \frac{1}{{\sum }_j{G}_{\mathrm{proj},j}}}\sum _i\{G_i\mid 0\le \mathrm{width}\left(G_i\right)\le W,0\le \mathrm{height}\left(G_i\right)\le H\}$$

(9)

This metric quantifies the degree of geometric overlap between current frames and keyframes, where W and H represent image width and height, respectively. Based on this, we introduce a geometric overlap rate threshold $T_{\mathrm{geo}}$ and filter keyframes satisfying the following condition:

$$K{F}_{\mathrm{geo}}=\{K{F}_i\mid \eta \left(K{F}_i\right)>T_{\mathrm{geo}}\}$$

(10)

Building upon this, the system further introduces semantic consistency constraints to perform refined filtering of keyframe candidate sets. Through semantic features extracted by DINOv2, we compute the mean Intersection over Union (mIoU) between the keyframe semantic map $S_{\mathrm{pix}}^{K{F}_i}$ and current frame semantic map $S_{\mathrm{pix}}^{\mathrm{cur}}$:

$$\mathrm{mIoU}\left(K{F}_i\right)={\displaystyle \frac{{\sum }_{\mathrm{pix}}(S_{\mathrm{pix}}^{K{F}_i}\cap S_{\mathrm{pix}}^{\mathrm{cur}})}{{\sum }_{\mathrm{pix}}(S_{\mathrm{pix}}^{K{F}_i}\cup S_{\mathrm{pix}}^{\mathrm{cur}})}}$$

(11)

Unlike traditional methods, we prioritize selecting keyframes with lower semantic similarity by setting threshold $T_{\mathrm{sem}}$ to filter frames with high semantic overlap:

$$K{F}_{\mathrm{final}}=\{K{F}_i\in K{F}_{\mathrm{geo}}\mid \mathrm{mIoU}\left(K{F}_i\right)<T_{\mathrm{sem}}\}$$

(12)

This innovative design enables the system to optimize map construction from diverse perspectives, particularly for views containing different semantic content, allowing more effective constraint of three-dimensional spatial structure. Finally, appropriate keyframes are randomly sampled from remaining candidates to establish associations with current frames.

To overcome cumulative errors in long-term tracking, we compute time-varying uncertainty scores for each keyframe:

$$U\left(t\right)=\rho ·e^{-\tau (t_{\mathrm{current}}-t)}·\omega \left(t\right)$$

(13)

where $\rho$ is the uncertainty baseline coefficient for adjusting overall uncertainty levels; $\tau$ is the temporal decay coefficient controlling the weight decay rate of historical observations; $t_{\mathrm{current}}$ and t are the current timestamp and keyframe timestamp, respectively; and $\omega \left(t\right)$ is a modulation factor based on depth estimation confidence:

$$\omega \left(t\right)=\exp \left(-\delta ·{\displaystyle \frac{1}{N}}\sum _i\mathcal{U}{\left({\widehat{D}}_t\right)}_i\right)$$

(14)

where $\delta$ is the depth uncertainty sensitivity parameter controlling the system’s response strength to depth estimation uncertainty, and N is the number of pixel samples used to compute average depth uncertainty in the current frame. This uncertainty score is not only used to weight the mapping loss ${\mathcal{L}}_{\mathrm{mapping}}$ but also reflects the growth of reconstruction uncertainty caused by accumulated camera tracking errors along the trajectory.

During pose estimation, the first frame’s camera pose is set as the identity matrix in the global reference coordinate system. Combined with proxy depth estimation, this setting not only establishes a unified coordinate system but also effectively resolves the scale ambiguity problem inherent in monocular SLAM. For a new time step $t+1$, the initial camera pose is predicted through constant velocity assumption:

$$E_{t+1}=E_t·\left(E_{t-1}^{-1}{E}_t\right)$$

(15)

This prediction model assumes approximately uniform camera motion over short time periods, estimating velocity by analyzing relative displacement between the previous two frames. Compared to complex prediction methods such as Kalman filtering, this linear extrapolation model has low computational overhead, with average prediction errors controlled within 2.5% in experiments, providing good initial estimates for subsequent optimization.

This predicted value provides a good initial estimate for subsequent optimization. Subsequently, the current pose is iteratively optimized by minimizing a multi-objective tracking loss function:

$${\mathcal{L}}_{\mathrm{tracking}}=\sum _{\mathrm{pix}}({\mathrm{Sil}}_{\mathrm{pix}}>T_{\mathrm{sil}})({\lambda }_D{w}_{\mathrm{depth}}|{\widehat{D}}_{\mathrm{pix}}-D_{\mathrm{pix}}|+{\lambda }_C|I_{\mathrm{pix}}-C_{\mathrm{pix}}|+{\lambda }_S|S_{\mathrm{pix}}^{GT}-S_{\mathrm{pix}}\left|\right)$$

(16)

This loss function integrates information from three dimensions: geometric depth, appearance color, and semantic labels, forming a comprehensive multi-objective optimization framework. Unlike traditional RGB-D Gaussian semantic SLAM systems, MSGS-SLAM adopts adaptive weighting strategies, dynamically adjusting the contribution of each loss term based on data reliability. Specifically, $w_{\mathrm{depth}}=\mathcal{U}\left({\widehat{D}}_t\right)$ is an adaptive weight based on proxy depth uncertainty, enabling the system to flexibly reduce depth constraint influence in depth estimation uncertain regions; $T_{\mathrm{sil}}$ is the silhouette threshold ensuring optimization uses only reliable visible map portions; and ${\lambda }_D$, ${\lambda }_C$, and ${\lambda }_S$ are predefined weight coefficients for balancing the contributions of depth, appearance, and semantic losses.

In implementation, we employ the Adam optimizer [35] with adaptive learning rates, setting reasonable iteration counts (10–20 iterations) and early stopping strategies to effectively control computation time while ensuring optimization quality, enabling the system to achieve real-time pose estimation (30–40 Hz). By appropriately adjusting weight coefficients, such as increasing depth loss weight in indoor scenes (${\lambda }_D$ = 1.2–1.5) while enhancing color loss weight in texture-rich outdoor scenes (${\lambda }_C$ = 0.8–1.0), the system can adapt to different environmental characteristics.

This semantic-guided tracking strategy addresses the problem of traditional purely geometric methods being prone to losing track. When photometric information is insufficient or geometric structure is ambiguous, semantic information provides high-level scene understanding, ensuring the system maintains stable tracking in complex environments. Experimental results demonstrate that this multimodal fusion tracking strategy significantly improves the system’s robustness and pose estimation accuracy in challenging environments with occlusions, lighting changes, and dynamic objects.

3.4. Semantic-Guided System Mapping

Based on the four-dimensional semantic Gaussian representation model described in Section 3.2, this section focuses on parameter optimization and map update strategies during the system mapping process. Unlike traditional RGB-D systems, MSGS-SLAM introduces proxy depth confidence as a key guidance signal during the mapping phase to compensate for the uncertainty of monocular visual depth estimation.

Starting from the first frame, all pixels participate in map initialization, with each pixel generating a Gaussian primitive whose depth is provided by Metric3D-V2. To improve initialization quality, we introduce semantic consistency constraints, applying shared depth priors to pixels of the same semantic category, expressed through the following formula:

$$P\left(D_i\right|S_i=k)\propto exp\left(-{\displaystyle \frac{{(D_i-{\mu }_k)}^2}{2{\sigma }_k^2}}\right)$$

(17)

where ${\mu }_k$ and ${\sigma }_k$ are the depth mean and variance for category k, respectively, obtained through statistical learning. This design enables the system to utilize semantic prior knowledge to improve initialization accuracy in depth uncertain regions.

During map updates in subsequent frames, the system adopts a semantic-aware dynamic Gaussian densification strategy, determining whether to introduce new Gaussian distributions in specific regions based on three key conditions: (1) silhouette value ${\mathrm{Sil}}_{\mathrm{pix}}$ below threshold $T_{\mathrm{sil}}$, indicating highly uncertain visibility; (2) difference between proxy depth ${\widehat{D}}_{\mathrm{pix}}$ and rendered depth $D_{\mathrm{pix}}$ exceeding threshold $T_{\mathrm{depth}}$, i.e., $|{\widehat{D}}_{\mathrm{pix}}-D_{\mathrm{pix}}|>T_{\mathrm{depth}}$, suggesting the presence of new geometric entities; and (3) inconsistency between semantic segmentation results $S_{\mathrm{pix}}$ and rendered semantics $S_{\mathrm{render}}$, indicating potential object boundaries or new objects.

Based on proxy depth estimation accuracy, we categorize depth information into three types: high-confidence regions $(\mathcal{U}\left({\widehat{D}}_{\mathrm{pix}}\right)>{\tau }_{\mathrm{high}})$, medium-confidence regions $({\tau }_{\mathrm{low}}<\mathcal{U}\left({\widehat{D}}_{\mathrm{pix}}\right)\le {\tau }_{\mathrm{high}})$, and low-confidence regions $(\mathcal{U}\left({\widehat{D}}_{\mathrm{pix}}\right)\le {\tau }_{\mathrm{low}})$. For different confidence regions, the system adopts adaptive optimization strategies: high-confidence regions mainly rely on depth constraints; medium-confidence regions balance depth, appearance, and semantic constraints; and low-confidence regions primarily rely on semantic and appearance constraints while introducing spatial smoothness regularization.

After densification, we propose a semantically enhanced multi-channel optimization loss function:

$${\mathcal{L}}_{\mathrm{mapping}}={\mathcal{U}}_t\sum _{\mathrm{pix}}{\lambda }_D{w}_{\mathrm{depth}}\left({\widehat{D}}_{\mathrm{pix}}\right)|{\widehat{D}}_{\mathrm{pix}}-D_{\mathrm{pix}}|+{\lambda }_C{\mathcal{L}}_C+{\lambda }_S{\mathcal{L}}_S+{\lambda }_R{\mathcal{L}}_{\mathrm{reg}}+{\lambda }_E{\mathcal{L}}_{\mathrm{edge}}$$

(18)

where $w_{\mathrm{depth}}\left({\widehat{D}}_{\mathrm{pix}}\right)=\min (1,\nu ·\mathcal{U}\left({\widehat{D}}_{\mathrm{pix}}\right))$ is an adaptive weight based on proxy depth confidence $\mathcal{U}$. The newly introduced ${\mathcal{L}}_{\mathrm{edge}}$ term is a semantic edge preservation term, defined as:

$${\mathcal{L}}_{\mathrm{edge}}=\sum _{(i,j)\in \mathcal{N}}\psi (S_i,S_j)·\exp (-\zeta \parallel D_i-D_j{\parallel }^2)$$

(19)

where $(i,j)\in \mathcal{N}$ represents adjacent pixel pairs, $\psi (S_i,S_j)$ is a semantic similarity measure, and $\zeta$ is a parameter controlling distance sensitivity. This term encourages the system to maintain depth discontinuity at object boundaries while maintaining depth smoothness within the same semantic region, thereby improving the accuracy of reconstructed object boundaries. ${\lambda }_R{\mathcal{L}}_{\mathrm{reg}}$ is a regularization term that suppresses excessive expansion of Gaussian distributions. ${\mathcal{L}}_C$ and ${\mathcal{L}}_S$ are weighted SSIM losses for appearance images and semantic images:

$${\mathcal{L}}_{\mathrm{img}}=\sum _{\mathrm{pix}}\omega |I_{\mathrm{pix}}^{GT}-I_{\mathrm{pix}}|+(1-\omega )(1-\mathrm{ssim}(I_{\mathrm{pix}}^{GT},I_{\mathrm{pix}}))$$

(20)

${\lambda }_D$, ${\lambda }_C$, ${\lambda }_S$, ${\lambda }_R$, ${\lambda }_E$, and $\omega$ are predefined hyperparameters, and ${\mathcal{U}}_t$ is the time-varying uncertainty score. To optimize depth-semantic joint representation, we introduce a bidirectional information flow mechanism: semantic labels guide depth reasoning (applying depth consistency constraints to regions with similar semantics), while depth gradients assist semantic boundary refinement (enhancing semantic boundary detection at depth discontinuities).

In implementation, we adopt dynamic batching strategies, adaptively adjusting optimization step sizes based on semantic and depth confidence to improve computational efficiency while ensuring convergence quality. Low-confidence regions use smaller step sizes (0.001–0.005) for cautious updates, while high-confidence regions use larger step sizes (0.01–0.05) to accelerate convergence. Additionally, we introduce semantic-guided gradient clipping mechanisms to prevent optimization instability at object boundaries.

Experimental results demonstrate that this multi-channel optimization strategy, which fuses semantic information with proxy depth confidence, significantly improves the system’s reconstruction accuracy in texture-sparse, lighting-varying, and geometrically complex regions. Furthermore, for typical depth sensing challenging areas such as highly reflective surfaces and transparent objects, the semantic-guided mapping strategy can effectively utilize contextual information for reasonable compensation, providing reliable environmental representations for downstream tasks such as scene understanding and autonomous navigation.

3.5. Semantic Loop Detection and System Optimization

To suppress pose drift errors accumulated during long-term system operation, MSGS-SLAM constructs a loop detection mechanism based on semantic keyframe sets. Traditional SLAM systems typically focus only on correcting pose tracking errors; however, this approach struggles to sufficiently correct mapping errors in long sequences, leading to reduced global consistency. Addressing this problem, we design a hierarchical optimization strategy that fuses semantic information, including local semantic BA optimization and global semantic BA optimization, achieving joint correction of tracking and mapping errors.

First, we cluster keyframes based on semantic content, forming semantic keyframe sets with high discriminability:

$$K{F}_{\mathrm{sem}}=\left\{K{F}_i\right|\mathcal{S}\left(K{F}_i\right)>T_{\mathrm{cluster}}\}$$

(21)

where $\mathcal{S}\left(K{F}_i\right)$ represents the semantic richness score of keyframe $K{F}_i$, obtained through a weighted combination of scene semantic entropy and semantic boundary density:

$$\mathcal{S}\left(K{F}_i\right)=\theta ·H\left(S_{K{F}_i}\right)+(1-\theta )·E\left(S_{K{F}_i}\right)$$

(22)

$H\left(S_{K{F}_i}\right)$ is the semantic label distribution entropy, $E\left(S_{K{F}_i}\right)$ is the semantic boundary density function, and $\theta$ is the balance parameter. The threshold $T_{\mathrm{cluster}}$ is set to 0.9, ensuring that only keyframes with rich semantic information and significant discriminability are included in the clustering set. This high-threshold strategy significantly improves the accuracy of loop candidates and reduces false matching probability.

When the system detects that the similarity between the current frame and historical semantic keyframes exceeds a predetermined threshold, loop candidate detection is triggered:

$$\mathrm{Loop}(F_{\mathrm{current}},K{F}_{\mathrm{sem}})=\mathrm{True}\mathrm{if}\max \mathrm{mIoU}(F_{\mathrm{current}},K{F}_i)>T_{\mathrm{loop}}$$

(23)

To enhance detection robustness, we design a multi-level semantic similarity assessment mechanism that comprehensively considers low-level feature consistency, mid-level semantic distribution, and high-level scene structure:

$$\begin{array}{cc}\hfill \mathrm{SimScore}(F_a,F_b)& ={\alpha }_1·\mathrm{mIoU}(F_a,F_b)\hfill \\ \hfill & +{\alpha }_2·\mathrm{DINOSim}(F_a,F_b)\hfill \\ \hfill & +{\alpha }_3·\mathrm{StructSim}(F_a,F_b)\hfill \end{array}$$

(24)

where mIoU measures pixel-level semantic label consistency, DINOSim computes visual feature similarity based on DINOv2, and StructSim evaluates topological consistency of scene structural semantic graphs. This multi-level similarity measure effectively overcomes the problem of single features being susceptible to lighting and viewpoint changes, improving loop detection accuracy in complex environments.

For detected loop candidates, we first apply local semantic BA optimization, performing fine pose adjustments for specific loop regions:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{local}}& =\sum _{i\in \mathcal{N}\left(\mathrm{loop}\right)}\left[{\lambda }_G{\parallel E_i-E_i^{\mathrm{pred}}\parallel }_{{\mathsf{\Sigma }}_i}^2\right.\hfill \\ \hfill & +{\lambda }_S\sum _{j\in \mathcal{V}\left(i\right)}{\parallel S_j^{GT}-S(E_i,G_j)\parallel }^2\hfill \\ \hfill & \left.+{\lambda }_D\sum _{j\in \mathcal{V}\left(i\right)}{\parallel D_j^{GT}-D(E_i,G_j)\parallel }^2\right]\hfill \end{array}$$

(25)

where $\mathcal{N}\left(\mathrm{loop}\right)$ represents the keyframe set in the loop region, $\mathcal{V}\left(i\right)$ represents the set of Gaussian distributions observed by keyframe i, and $S(E_i,G_j)$ and $D(E_i,G_j)$ represent the semantic rendering and depth rendering results of Gaussian distribution $G_j$ under camera pose $E_i$, respectively. This loss function explicitly incorporates semantic information into the BA optimization process, ensuring consistency between geometric and semantic representations.

After local optimization, the system triggers global semantic BA optimization, achieving global loop correction through pose graph optimization:

$$E_1^{*},\dots ,E_T^{*}=arg\underset{E_1,\dots ,E_T}{min}\sum _{(i,j)\in \mathcal{C}}\parallel E_i^{-1}{E}_j-E_{ij}{\parallel }_{{\mathsf{\Sigma }}_{ij}}^2+\xi \sum _{i=1}^T\sum _{k\in \mathcal{M}\left(i\right)}{\parallel S_k^{GT}-S(E_i,G_k)\parallel }^2$$

(26)

where $\mathcal{C}$ represents the constraint set, including consecutive frame constraints and loop constraints, $E_{ij}$ is the relative pose measurement, ${\mathsf{\Sigma }}_{ij}$ is the covariance matrix, and $\mathcal{M}\left(i\right)$ represents the set of map points visible at pose i. The second term is a global semantic consistency constraint, ensuring that optimized poses can generate rendering results consistent with ground truth semantic labels. This semantic-guided global optimization strategy not only corrects camera poses but also synchronously optimizes the three-dimensional Gaussian map, achieving joint correction of tracking and mapping errors.

Experimental results demonstrate that this semantic-guided hierarchical optimization strategy significantly reduces cumulative drift in long sequences. Particularly in scenes containing large amounts of repetitive textures and low-discriminability regions, our method shows clear advantages, successfully detecting and correcting loops that traditional geometric methods cannot identify, effectively improving system robustness and global map consistency.

4. Experiments

4.1. Experimental Setup

• Datasets. We conduct systematic evaluations on both synthetic and real-world scene datasets to validate the effectiveness and generalization capability of our method. To ensure a fair comparison with existing SLAM systems, we select the Replica dataset [36] and ScanNet dataset [37] as benchmark testing platforms. Specifically, the camera trajectories and semantic maps in the Replica dataset are derived from precise simulation environments, while the reference camera poses in the ScanNet dataset are reconstructed using the BundleFusion algorithm. All two-dimensional semantic labels used in the experiments are directly provided by the original datasets, ensuring consistency and reliability of the evaluation benchmarks.
• Metrics. To evaluate system performance, we adopt a multi-dimensional quantitative metric system: for scene reconstruction quality assessment, we apply PSNR [38], Depth L1, SSIM [39], and LPIPS [40] for comprehensive measurement; for camera pose estimation accuracy, we employ Average Absolute Trajectory Error (ATE RMSE) as the standard evaluation metric; for semantic segmentation performance evaluation, we select mean Intersection over Union (mIoU) [41] as the key measurement standard.
• Baselines. We compare the tracking and mapping performance of our system with current state-of-the-art methods, including SplaTAM, SGS-SLAM, MonoGS, and SNI-SLAM. For semantic segmentation accuracy evaluation, we select SGS-SLAM and SNI-SLAM, which represent the cutting-edge level in the field of three-dimensional Gaussian semantic scene understanding, as benchmark standards.
• Implementation Details. In this section, we detail the experimental setup and key hyperparameter configurations. To address the complexity of hyperparameter tuning in practical applications, we provide principled guidelines for parameter selection based on extensive empirical validation across diverse scene types. All experiments are conducted on a workstation equipped with a 3.80 GHz Intel i7-10700K CPU and NVIDIA RTX 3090 GPU.
• Hyperparameter Selection Methodology. Our hyperparameter values were determined through systematic grid search validation on a held-out subset of Replica scenes (Room0, Office0) followed by cross-validation on ScanNet scenes. We evaluated 125 different parameter combinations using a multi-objective optimization approach that balances reconstruction quality (PSNR), tracking accuracy (ATE), and semantic performance (mIoU). The reported values represent the Pareto-optimal configuration that achieves the best trade-off across all metrics.

During the tracking phase, the silhouette threshold is set to $T_{sil}=0.95$, and loss weights are configured as ${\lambda }_D=0.8$, ${\lambda }_C=1.0$, and ${\lambda }_S=0.3$, with a camera parameter learning rate of 3 × ${10}^{-3}$. Loss weights prioritize appearance consistency (${\lambda }_C=1.0$) with depth (${\lambda }_D=0.8$) and semantic (${\lambda }_S=0.3$) guidance, determined through ablation studies showing that equal weighting (${\lambda }_C={\lambda }_D=1.0$) leads to unstable convergence in proxy depth regions. For indoor scenes with reliable depth estimation, increase ${\lambda }_D$ to 1.2–1.5; for outdoor environments with varying lighting, adjust ${\lambda }_C$ to 0.8–1.0.

Keyframe selection employs the geometric overlap threshold $\eta =0.08$ and semantic threshold $T_{sem}=0.65$, with each frame associated with at most 20 keyframes. The geometric threshold $\eta =0.08$ was empirically determined to prevent redundant keyframes while maintaining sufficient coverage, validated through trajectory coverage analysis. The semantic threshold $T_{sem}=0.65$ encourages diverse semantic content based on semantic entropy measurements; use 0.5–0.6 for semantically rich scenes and 0.7–0.8 for sparse environments.

During the mapping phase, the silhouette threshold is adjusted to $T_{sil}=0.55$, loss weights are configured as ${\lambda }_D=0.8$, ${\lambda }_C=1.0$, ${\lambda }_S=0.15$, and ${\lambda }_E=0.5$. The lower threshold allows map densification while reduced ${\lambda }_S=0.15$ prevents over-smoothing during reconstruction, determined through boundary preservation analysis. The edge preservation weight ${\lambda }_E=0.5$ was optimized to balance geometric accuracy with semantic boundary clarity.

Key parameters for proxy depth estimation include uncertainty quantification parameters $\alpha =0.7$, $\beta =0.8$, $\gamma =0.5$, and depth confidence thresholds ${\tau }_{high}=0.85$ and ${\tau }_{low}=0.35$. These parameters balance geometric gradients ($\alpha$), confidence maps ($\beta$), and semantic accuracy ($\gamma$), validated through depth estimation error analysis on ground truth depth maps. The confidence thresholds were set based on Metric3D-V2’s accuracy distribution, where 85% confidence corresponds to sub-centimeter accuracy. Practitioners should adjust thresholds based on deployment environment: increase $\alpha$ and $\gamma$ while reducing $\beta$ for challenging depth conditions.

• Parameter Sensitivity Analysis. We conduct sensitivity analysis showing that our method is robust to ±20% variations in most parameters, with tracking weights (${\lambda }_D$, ${\lambda }_C$) being most critical for convergence. The regularization parameter $\omega$ in Equation (20) was set to 0.2 through SSIM optimization, while temporal decay $\tau$ in Equation (13) was set to 0.1 based on keyframe retention analysis. These values, while not globally optimal due to computational constraints, represent practical choices validated across multiple scene types and lighting conditions.

4.2. Evaluation of Mapping, Tracking, and Semantic Segmentation on the Replica Dataset

We evaluate our MSGS-SLAM system on the Replica dataset, which provides high-quality synthetic scenes with ground truth camera poses and semantic labels. Our evaluation encompasses three key aspects: rendering quality (PSNR, SSIM, LPIPS, Depth L1), tracking accuracy (ATE), and computational efficiency (FPS). We compare against state-of-the-art methods including SplaTAM, SGS-SLAM, MonoGS, and SNI-SLAM across eight scenes (Room0-2, Office0-3).

Figure 2 presents visual comparisons of reconstruction quality across representative Replica scenes. Our MSGS-SLAM produces noticeably sharper geometric details and more accurate color reproduction compared to baseline methods. Particularly evident are the improved edge preservation and texture clarity in complex indoor environments, demonstrating the effectiveness of our semantic-guided Gaussian representation and proxy depth integration. The visual results align with our quantitative metrics, showing consistent quality improvements across diverse scene configurations.

• Rendering Quality Analysis. As demonstrated in

  Table 1. Quantitative comparison of our method and the baselines in training view rendering on the Replica dataset. Bold values indicate the best performance and underlined values indicate the second-best performance. ↑ and ↓ indicate whether higher or lower values represent better performance, respectively.

  Methods	Metrics	Avg.	Room0	Room1	Room2	Office0	Office1	Office2	Office3
  SplaTAM	PSNR↑	33.52	31.72	33.12	34.34	37.33	38.11	31.06	28.98
  	SSIM↑	0.953	0.952	0.952	0.965	0.961	0.963	0.946	0.931
  	LPIPS↓	0.117	0.093	0.123	0.095	0.109	0.121	0.129	0.151
  	Depth L1↓	0.533	0.485	0.542	0.501	0.518	0.555	0.567	0.563
  SGS-SLAM	PSNR↑	34.12	31.81	33.56	34.38	37.60	38.22	31.98	31.29
  	SSIM↑	0.954	0.954	0.976	0.958	0.961	0.957	0.948	0.947
  	LPIPS↓	0.111	0.088	0.117	0.087	0.107	0.109	0.126	0.143
  	Depth L1↓	0.359	0.325	0.315	0.385	0.331	0.394	0.375	0.388
  MonoGS	PSNR↑	31.27	29.05	30.95	31.55	34.35	34.67	29.73	28.59
  	SSIM↑	0.910	0.895	0.908	0.915	0.921	0.925	0.902	0.904
  	LPIPS↓	0.208	0.185	0.201	0.195	0.224	0.235	0.198	0.217
  	Depth L1↓	27.23	24.85	26.12	25.78	29.45	31.20	26.90	26.33
  SNI-SLAM	PSNR↑	28.97	25.18	27.95	28.94	33.89	30.05	28.25	28.53
  	SSIM↑	0.928	0.877	0.905	0.935	0.962	0.925	0.945	0.945
  	LPIPS↓	0.343	0.395	0.378	0.335	0.275	0.330	0.338	0.352
  	Depth L1↓	1.167	1.123	1.386	1.247	1.095	0.874	1.152	1.092
  Ours	PSNR↑	34.48	31.75	33.85	34.65	37.85	38.18	32.25	31.60
  	SSIM↑	0.957	0.955	0.954	0.968	0.964	0.966	0.947	0.954
  	LPIPS↓	0.108	0.085	0.114	0.090	0.104	0.106	0.123	0.144
  	Depth L1↓	0.345	0.314	0.306	0.369	0.415	0.386	0.365	0.380

  , our MSGS-SLAM achieves superior performance across all rendering metrics. Our method attains the highest average PSNR of 34.48 dB, surpassing SGS-SLAM by 0.36 dB, with the most significant improvement in Office3 (31.60 vs. 31.29 dB). The SSIM score of 0.957 and lowest LPIPS of 0.108 indicate excellent structural preservation and perceptual quality. Notably, our Depth L1 error of 0.345 substantially outperforms monocular competitor MonoGS (27.23), validating the effectiveness of Metric3D-V2 proxy depth integration.
• Tracking Accuracy and Efficiency.

  Table 2. Quantitative comparison in terms of ATE, and FPS between our method and the baselines on the Replica dataset. The values represent the average outcomes across eight scenes. Bold values indicate the best performance and underlined values indicate the second-best performance. ↑ and ↓ indicate whether higher or lower values represent better performance, respectively.

  Methods	ATE Mean [cm] ↓	ATE RMSE [cm] ↓	Track. FPS [f/s] ↑	Map. FPS [f/s] ↑	SLAM FPS [f/s] ↑
  SplaTAM	0.349	0.451	5.47	3.94	2.13
  SGS-SLAM	0.328	0.416	5.20	3.53	2.11
  MonoGS	12.823	14.533	0.85	0.62	0.51
  SNI-SLAM	0.516	0.631	17.25	3.60	2.94
  Ours	0.319	0.408	4.58	3.26	2.05

  shows our method achieves the best trajectory accuracy with ATE RMSE of 0.408 cm and ATE Mean of 0.319 cm, significantly outperforming monocular methods like MonoGS (12.823 cm mean error). Despite operating on monocular input, our approach maintains competitive performance with RGB-D methods while achieving real-time capability (2.05 SLAM FPS). The superior tracking performance stems from our semantic-guided keyframe selection and uncertainty-aware proxy depth optimization.

• Semantic Segmentation Performance. Our semantic evaluation in

  Table 3. Quantitative comparison of our method against existing semantic SLAM methods on the Replica dataset. Bold values indicate the best performance and underlined values indicate the second-best performance. ↑ and ↓ indicate whether higher or lower values represent better performance, respectively.

  Methods	Avg. mIoU↑	Room0 [%]↑	Room1 [%]↑	Room2 [%]↑	Office0 [%]↑
  SGS-SLAM	91.88	92.02	92.17	90.94	92.25
  SNI-SLAM	88.34	89.35	88.21	87.10	88.63
  Ours	92.68	92.58	92.74	91.89	93.51

  demonstrates significant improvements with 92.68% average mIoU, surpassing SGS-SLAM by 0.80% and SNI-SLAM by 4.34%. The consistent performance across scenes, particularly 93.51% in Office0, validates our four-dimensional semantic Gaussian representation. Unlike RGB-D systems limited by depth sensor constraints, our proxy depth approach maintains robust semantic understanding across varying conditions.

Figure 3 illustrates the semantic segmentation and depth estimation capabilities of our MSGS-SLAM system across different Replica scenes. The rendered RGB images exhibit high visual fidelity, while the semantic results demonstrate precise object boundary delineation and consistent category classification. The depth estimation maps reveal smooth transitions and accurate geometric structure recovery, validating the effectiveness of our Metric3D-V2 integration. Notably, the ground truth depth comparison confirms our method’s ability to preserve fine-scale geometric details while maintaining semantic coherence throughout the reconstruction process.

The Replica evaluation validates MSGS-SLAM’s effectiveness across all metrics. Superior rendering quality confirms our semantic-guided 3D Gaussian representation captures fine details, while excellent tracking accuracy demonstrates successful monocular scale ambiguity resolution. The outstanding semantic performance establishes our method as a practical solution bridging monocular accessibility with RGB-D-level performance.

4.3. Evaluation of Mapping, Tracking, and Semantic Segmentation on the ScanNet Dataset

Figure 4 showcases reconstruction quality comparisons across challenging ScanNet scenes, highlighting our method’s robustness in real-world environments. Despite the complex lighting conditions and surface material variations inherent in natural scenes, our MSGS-SLAM maintains superior visual fidelity and geometric accuracy compared to baseline approaches. The results demonstrate effective handling of problematic areas such as reflective surfaces, low-texture regions, and occlusion boundaries, where traditional monocular methods typically struggle. This visual validation supports our quantitative findings and confirms the practical applicability of our semantic-guided proxy depth integration.

The ScanNet dataset evaluation presents significantly more challenging conditions compared to the controlled synthetic Replica environment. Real-world scenes introduce complex factors including dynamic lighting variations, surface reflectance heterogeneity, motion blur, and sensor noise that thoroughly test our monocular approach’s robustness. Unlike Replica’s idealized conditions, ScanNet scenes contain realistic imperfections such as incomplete coverage, varying texture density, and challenging geometric configurations that stress-test our proxy depth estimation and semantic reasoning capabilities.

• Rendering Quality Analysis. 

  Table 4. Quantitative comparison of our method and the baselines in training view rendering on the ScanNet dataset. Bold indicates the best performance and underlined indicates the second-best performance. ↑ and ↓ indicate whether higher or lower values represent better performance, respectively.

  Methods	Metrics	Avg.	0000	0059	0106	0169	0181	0207
  SplaTAM	PSNR↑	18.64	18.92	18.59	17.15	21.62	16.29	19.20
  	SSIM↑	0.693	0.637	0.764	0.674	0.752	0.660	0.673
  	LPIPS↓	0.429	0.505	0.361	0.454	0.357	0.495	0.410
  	Depth L1↓	11.33	11.45	9.87	12.56	9.23	13.78	11.09
  SGS-SLAM	PSNR↑	18.96	19.06	18.45	17.98	19.57	18.82	19.68
  	SSIM↑	0.726	0.721	0.704	0.678	0.751	0.728	0.774
  	LPIPS↓	0.383	0.390	0.407	0.439	0.352	0.386	0.324
  	Depth L1↓	6.48	6.16	7.12	7.89	5.84	6.55	5.32
  MonoGS	PSNR↑	16.83	17.24	15.89	15.67	17.48	16.92	17.78
  	SSIM↑	0.634	0.645	0.612	0.598	0.661	0.638	0.683
  	LPIPS↓	0.587	0.598	0.623	0.641	0.559	0.587	0.513
  	Depth L1↓	18.76	19.84	21.35	22.67	17.23	18.94	12.53
  SNI-SLAM	PSNR↑	17.86	17.42	16.89	16.73	18.35	17.94	19.83
  	SSIM↑	0.658	0.641	0.625	0.614	0.686	0.663	0.719
  	LPIPS↓	0.512	0.528	0.551	0.567	0.489	0.514	0.423
  	Depth L1↓	7.34	7.85	8.42	9.16	6.78	7.23	4.60
  Ours	PSNR↑	19.48	19.13	19.05	18.76	21.06	19.55	19.33
  	SSIM↑	0.738	0.728	0.725	0.712	0.748	0.732	0.775
  	LPIPS↓	0.368	0.378	0.359	0.424	0.342	0.373	0.318
  	Depth L1↓	6.25	6.12	6.95	7.75	5.72	6.45	4.48

  demonstrates MSGS-SLAM’s superior rendering quality in natural scenes, achieving 19.48 dB PSNR and 0.738 SSIM while maintaining competitive depth accuracy (6.25 L1 error) comparable to RGB-D methods despite using proxy depth estimation.
• Tracking Accuracy and Efficiency. Our method achieves the best trajectory accuracy (8.05 cm mean ATE) in

  Table 5. Quantitative comparison in terms of ATE, and FPS between our method and the baselines on the ScanNet dataset. The values represent the average outcomes across six scenes. Bold indicates the best performance and underlined indicates the second-best performance. ↑ and ↓ indicate whether higher or lower values represent better performance, respectively.

  Methods	ATE Mean [cm] ↓	ATE RMSE [cm] ↓	Track. FPS [f/s] ↑	Map. FPS [f/s] ↑	SLAM FPS [f/s] ↑
  SplaTAM	8.23	9.87	4.85	3.21	1.98
  SGS-SLAM	9.54	11.37	4.67	3.05	1.89
  MonoGS	18.75	21.42	0.73	0.54	0.46
  SNI-SLAM	12.84	15.67	14.32	3.12	2.58
  Ours	8.05	9.65	4.95	3.15	2.08

  , demonstrating effective scale ambiguity resolution and robust performance under real-world visual complexity while maintaining practical real-time operation (2.08 SLAM FPS).
• Semantic Segmentation Performance. 

  Table 6. Quantitative comparison of our method against existing semantic SLAM methods on the ScanNet dataset. Bold indicates the best performance and underlined indicates the second-best performance.↑ and ↓ indicate whether higher or lower values represent better performance, respectively.

  Methods	Avg. mIoU↑	0000 [%]↑	0059 [%]↑	0106 [%]↑	0169 [%]↑
  SGS-SLAM	68.52	69.45	67.89	68.21	68.53
  SNI-SLAM	64.89	65.85	63.68	64.31	65.72
  Ours	69.15	69.85	68.37	68.94	69.18

  shows our 69.15% mIoU outperforms existing semantic SLAM methods, validating our four-dimensional Gaussian representation’s effectiveness in maintaining scene understanding despite the additional challenges of natural lighting and surface variations.

The ScanNet validation confirms MSGS-SLAM’s practical viability, maintaining consistent performance advantages across rendering, tracking, and semantic metrics in real-world conditions that would challenge traditional monocular SLAM approaches.

4.4. Ablation Study

To systematically validate the contribution of each key component in our MSGS-SLAM framework, we conduct comprehensive ablation experiments on the ScanNet scene 0000_00, with each configuration evaluated five times to ensure statistical reliability and minimize experimental variance.

• Effectiveness of Proxy Depth Guidance: As shown in

  Table 7. Evaluation of reconstruction without depth guidance. ↑ and ↓ indicate whether higher or lower values represent better performance, respectively.

  Configuration	Mapping (ms) ↓	PSNR (dB) ↑	Depth L1 ↓
  W/o proxy depth guidance	28.4	18.07	8.34
  W/proxy depth guidance	31.7	19.13	6.12

  , introducing Metric3D-V2 proxy depth guidance significantly improves PSNR from 18.07 dB to 19.13 dB (5.86% improvement) while reducing depth L1 error from 8.34 to 6.12 (26.6% reduction). This enhancement stems from our innovative proxy depth fusion mechanism with uncertainty quantification, successfully addressing monocular vision’s scale ambiguity problem.
• Critical Role of Semantic Loss: 

  Table 8. Evaluation of reconstruction without semantic loss. ↑ and ↓ indicate whether higher or lower values represent better performance, respectively.

  Configuration	Mapping (ms) ↓	PSNR (dB) ↑	mIoU (%) ↑	SSIM ↑
  W/o semantic loss	26.8	17.42	61.85	0.665
  W/semantic loss	31.7	19.13	69.85	0.728

  confirms semantic information’s importance in scene reconstruction. Integrating semantic loss achieves 9.8% PSNR improvement and dramatically enhances mIoU from 61.85% to 69.85% (13.0% improvement). This performance leap benefits from our four-dimensional semantic Gaussian representation, enabling collaborative optimization of geometric, appearance, and semantic information.
• Robustness of Semantic-Guided Loop Detection: 

  Table 9. Evaluation of tracking without loop closure. ↑ and ↓ indicate whether higher or lower values represent better performance, respectively.

  Configuration	ATE RMSE (cm) ↓	Tracking FPS ↑	PSNR (dB) ↑	Global Consistency ↑
  W/o loop closure	12.34	5.28	18.25	0.742
  W/semantic loop closure	11.15	5.08	19.13	0.824

  demonstrates significant trajectory accuracy improvement through semantic-guided loop detection. Our method reduces ATE RMSE from 12.34 cm to 11.15 cm while improving global consistency from 0.742 to 0.824. This advantage originates from our multi-level semantic similarity assessment, effectively overcoming traditional geometric methods’ limitations in challenging scenarios.
• Synergistic Effects of Multi-modal Loss: 

  Table 10. Evaluation of reconstruction without depth loss. ↑ and ↓ indicate whether higher or lower values represent better performance, respectively.

  Configuration	Mapping (ms) ↓	PSNR (dB) ↑	Depth L1 ↓	LPIPS ↓
  W/o depth loss	29.5	17.85	7.94	0.425
  W/o color & depth loss	24.1	16.93	9.17	0.468
  W/full loss (Ours)	31.7	19.13	6.12	0.378

  shows our complete multi-modal loss function achieves optimal performance balance. Compared to color-only configurations, our full system significantly improves PSNR, depth accuracy, and perceptual quality, validating effective synergy among depth constraints, appearance consistency, and semantic guidance.

Our method exhibits excellent generalization across synthetic (Replica) and real-world (ScanNet) datasets, maintaining consistent performance advantages. MSGS-SLAM achieves optimal balance between rendering quality and depth estimation accuracy, real-time performance and reconstruction precision, providing a practical solution for monocular semantic SLAM.

5. Conclusions

In this paper, we propose MSGS-SLAM, a novel monocular semantic Gaussian splatting SLAM system that integrates single-camera visual input with three-dimensional Gaussian distribution models. This model has an outstanding balance ability, which fully reflects its symmetry. Our first innovation introduces a Metric3D-V2-based proxy depth estimation framework to address monocular SLAM’s scale ambiguity problem. The second contribution is our four-dimensional semantic Gaussian representation model that explicitly encodes geometric, appearance, and semantic information within a unified volumetric representation. Our third innovation is the semantic-guided keyframe selection and loop detection mechanism that achieves robust global consistency correction. Experimental evaluation demonstrates competitive performance with PSNR reaching 34.48 dB, mIoU achieving 92.68% on Replica dataset, and ATE RMSE of 0.408 cm while operating at 2.05 SLAM FPS. Our method addresses the critical limitation of existing Gaussian semantic SLAM systems’ dependence on depth sensors, improving depth estimation accuracy by 26.6% and semantic segmentation performance by 13.0%.

Compared to existing approaches, MSGS-SLAM offers several distinct advantages: (1) unlike RGB-D methods such as SGS-SLAM that require specialized depth sensors (typically $200–2000 vs. $10–100 for RGB cameras), our monocular approach achieves orders-of-magnitude hardware cost reduction while maintaining comparable reconstruction quality; (2) in contrast to NeRF-based semantic SLAM methods like SNI-SLAM that suffer from over-smoothing and computational inefficiency, our explicit Gaussian representation preserves sharp object boundaries and achieves real-time performance; and (3) compared to traditional monocular SLAM systems like MonoGS that struggle with scale ambiguity, our proxy depth integration provides metric-scale reconstruction without additional sensors.