Numerical Simulation of 3D Full Hydraulic Jumps Using a GPU-Based SPH Model
Abstract
1. Introduction
2. Numerical Method
2.1. Governing Equations
2.2. Boundary Conditions
3. Validation
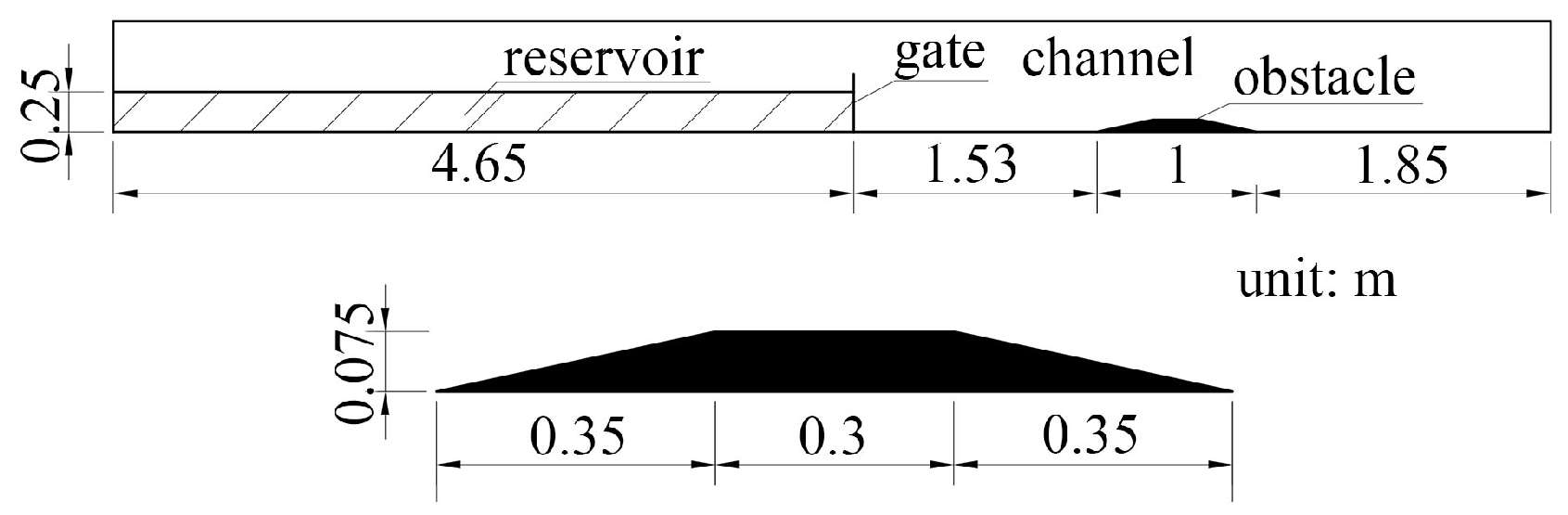
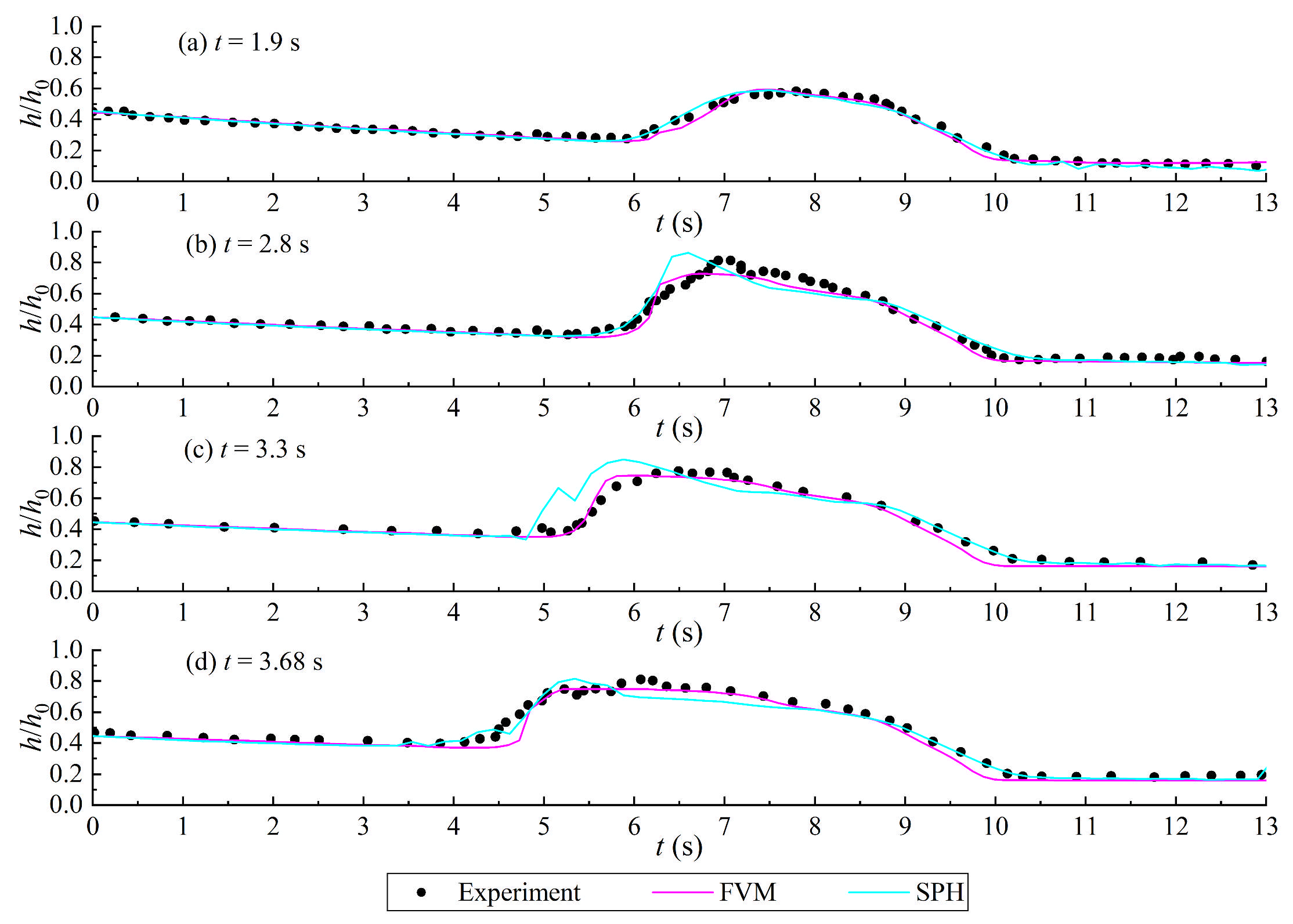
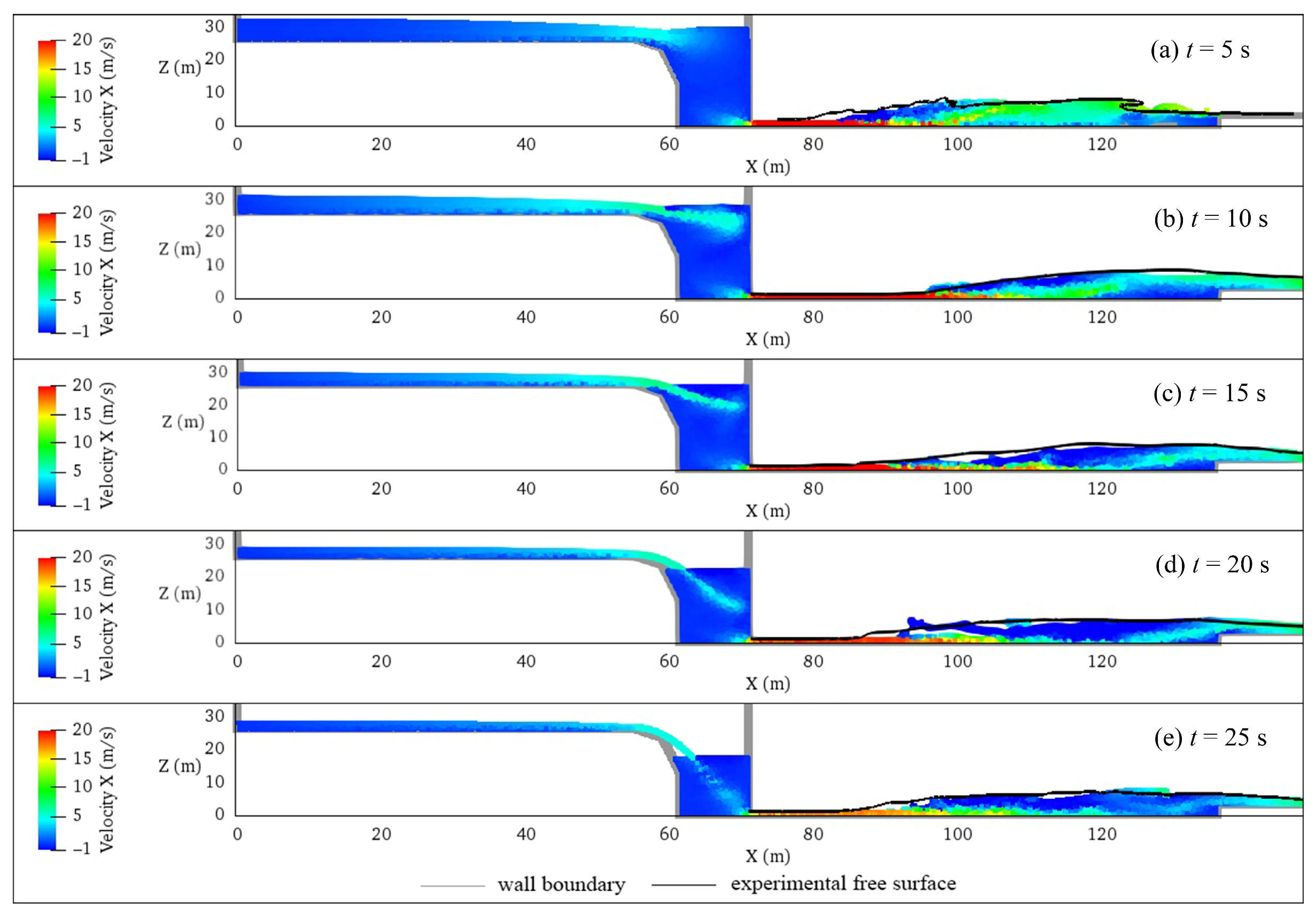
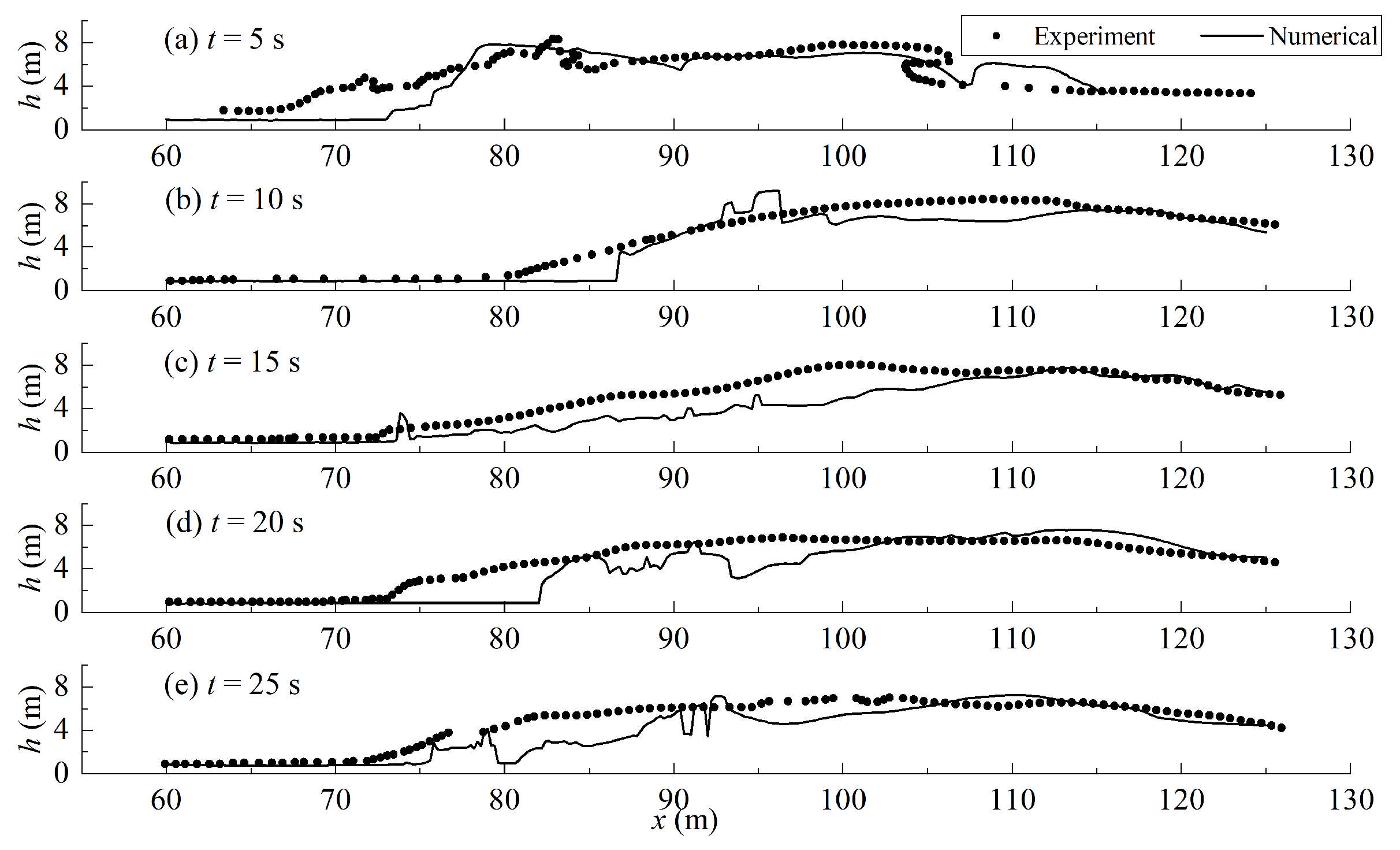
3.1. Dam Break
3.2. Three-Dimensional Hydraulic Jumps
4. Study on Energy Dissipation Process of a Real Gate
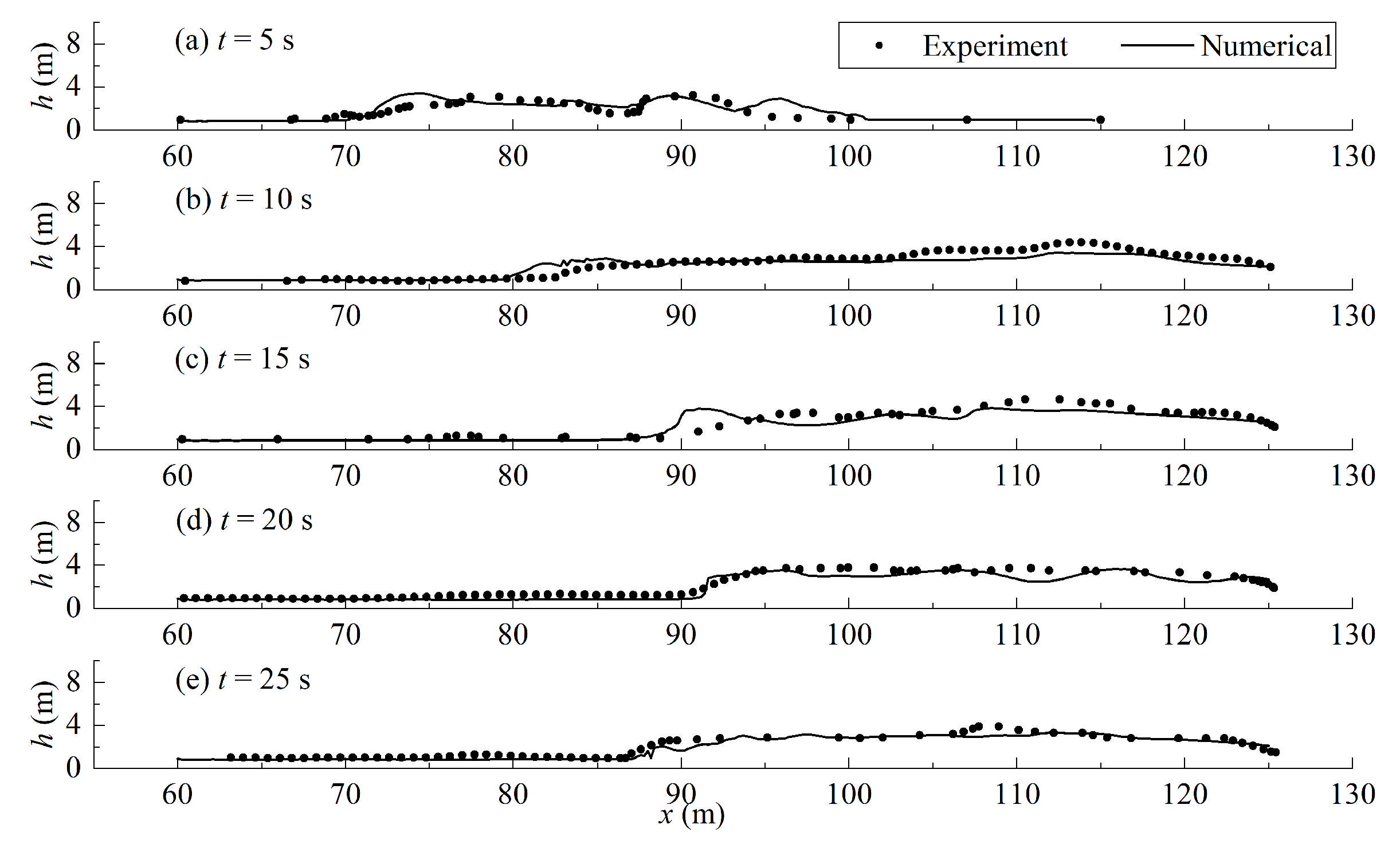
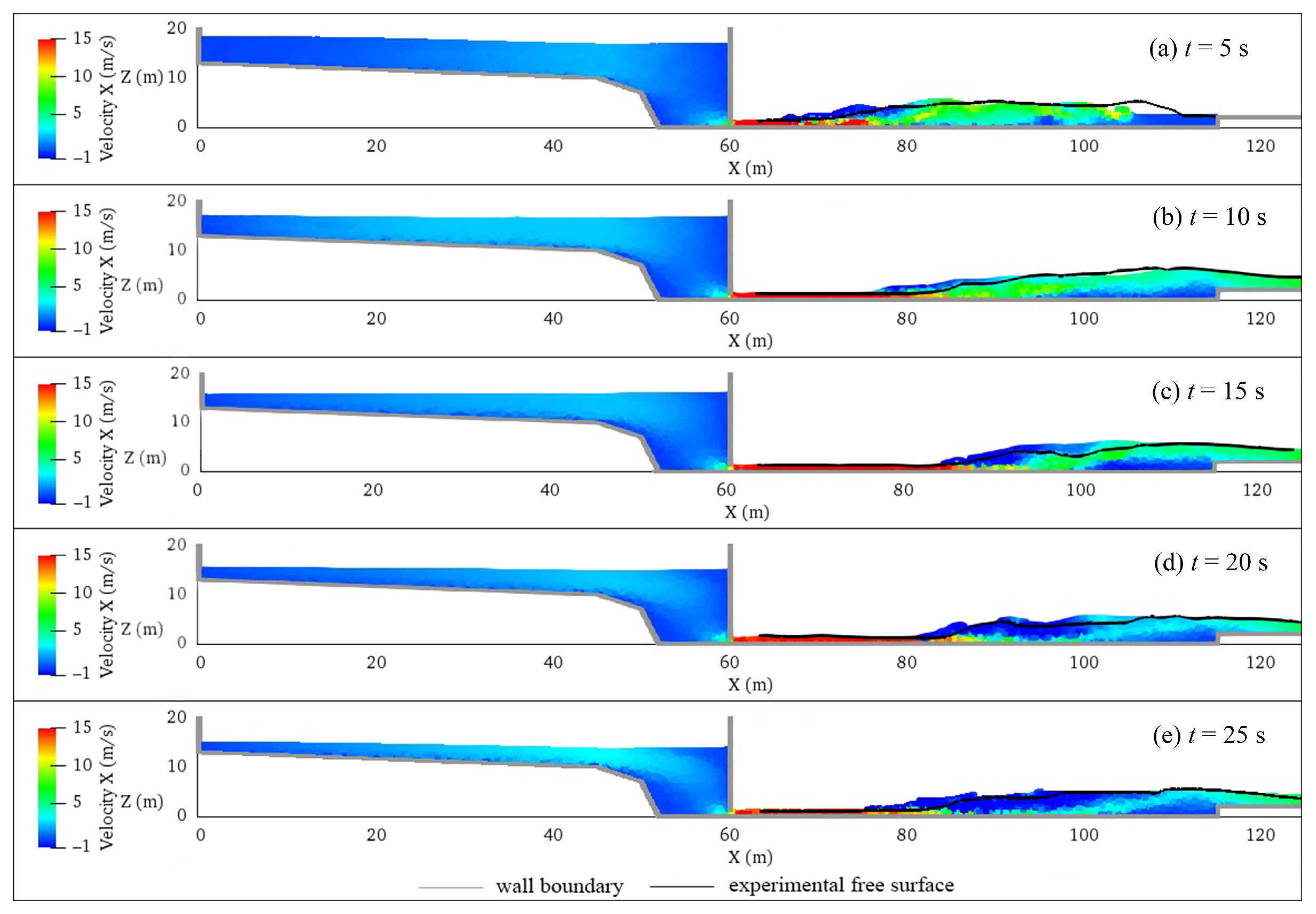
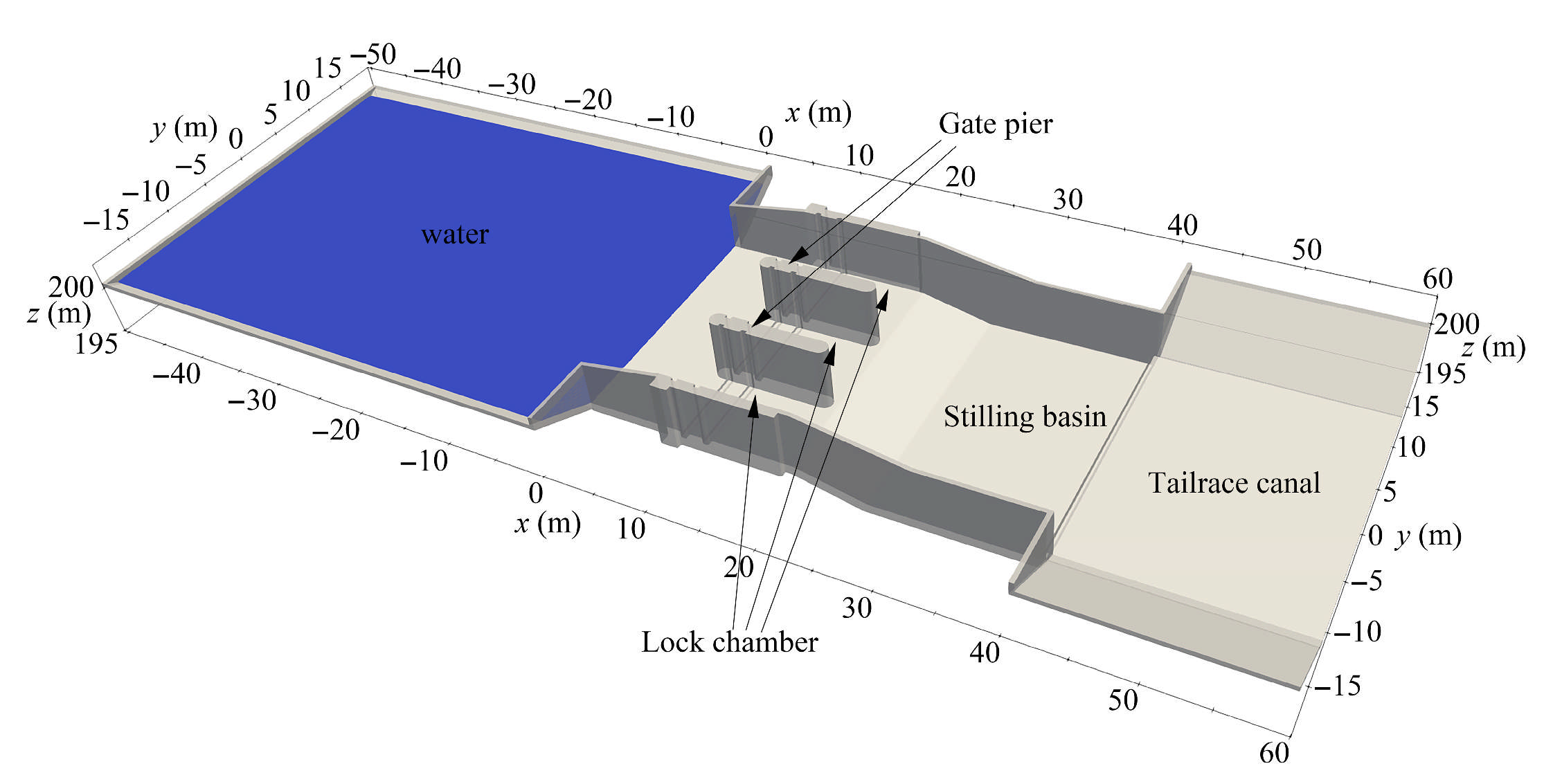
4.1. Model Layout
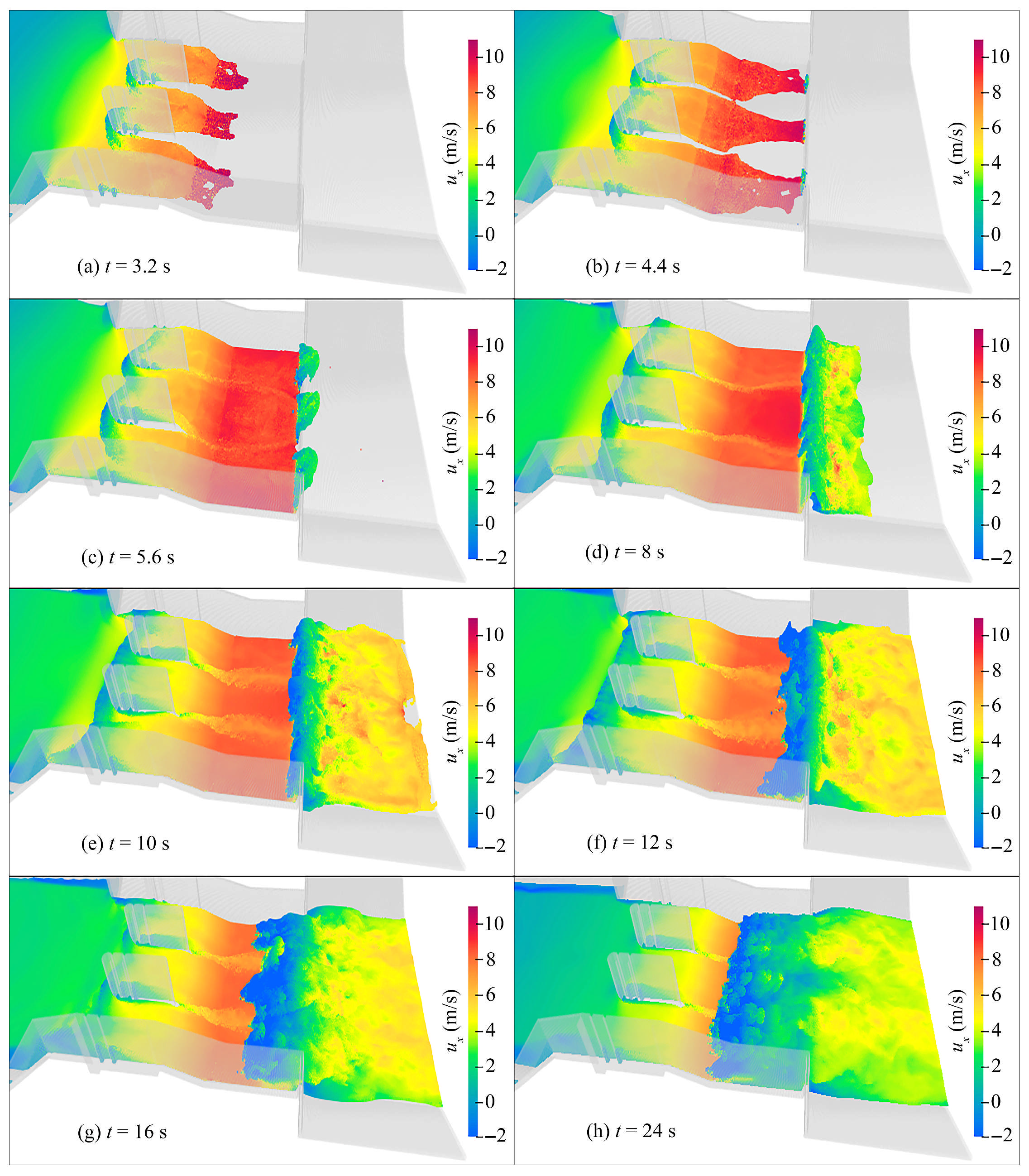
4.2. Stilling Basin Flow Field
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chanson, H. Convective transport of air bubbles in strong hydraulic jumps. Int. J. Multiph. Flow 2010, 36, 798–814. [Google Scholar] [CrossRef]
- Chanson, H. Current knowledge in hydraulic jumps and related phenomena. A survey of experimental results. Eur. J. Mech.-B/Fluids 2009, 28, 191–210. [Google Scholar] [CrossRef]
- Zobeyer, A.T.M.H.; Jahan, N.; Islam, Z.; Singh, G.; Rajaratnam, N. Turbulence characteristics of the transition region from hydraulic jump to open channel flow. J. Hydraul. Res. 2010, 48, 395–399. [Google Scholar] [CrossRef]
- Murzyn, F.; Chanson, H. Free-surface fluctuations in hydraulic jumps: Experimental observations. Exp. Therm. Fluid Sci. 2009, 33, 1055–1064. [Google Scholar] [CrossRef]
- Chippada, S.; Ramaswamy, B.; Wheeler, M.F. Numerical simulation of hydraulic jump. Int. J. Numer. Methods Eng. 1994, 37, 1381–1397. [Google Scholar] [CrossRef]
- Unami, K.; Kawachi, T.; Babar, M.M.; Itagaki, H. Estimation of diffusion and convection coefficients in an aerated hydraulic jump. Adv. Water Resour. 2000, 23, 475–481. [Google Scholar] [CrossRef]
- Gharangik, A.M.; Chaudhry, M.H. Numerical Simulation of Hydraulic Jump. J. Hydraul. Eng. 1991, 117, 1195–1211. [Google Scholar] [CrossRef]
- Zhou, J.G.; Stansby, P.K. 2D shallow water flow model for the hydraulic jump. Int. J. Numer. Methods Fluids 1999, 29, 375–387. [Google Scholar] [CrossRef]
- Shekari, Y.; Javan, M.; Eghbalzadeh, A. Three-dimensional Numerical Study of Submerged Hydraulic Jumps. Arab. J. Sci. Eng. 2014, 39, 6969–6981. [Google Scholar] [CrossRef]
- Babaali, H.; Shamsai, A.; Vosoughifar, H. Computational Modeling of the Hydraulic Jump in the Stilling Basin with Convergence Walls Using CFD Codes. Arab. J. Sci. Eng. 2015, 40, 381–395. [Google Scholar] [CrossRef]
- Gumus, V.; Simsek, O.; Soydan, N.G.; Akoz, M.S.; Kirkgoz, M.S. Numerical Modeling of Submerged Hydraulic Jump from a Sluice Gate. J. Irrig. Drain. Eng. 2016, 142, 04015037. [Google Scholar] [CrossRef]
- Azimi, H.; Shabanlou, S.; Kardar, S. Characteristics of Hydraulic Jump in U-Shaped Channels. Arab. J. Sci. Eng. 2017, 42, 3751–3760. [Google Scholar] [CrossRef]
- Witt, A.; Gulliver, J.S.; Shen, L. Numerical investigation of vorticity and bubble clustering in an air entraining hydraulic jump. Comput. Fluids 2018, 172, 162–180. [Google Scholar] [CrossRef]
- Gu, S.; Ren, L.; Wang, X.; Xie, H.; Huang, Y.; Wei, J.; Shao, S. SPHysics simulation of experimental spillway hydraulics. Water 2017, 9, 973. [Google Scholar] [CrossRef]
- López, D.; Marivela, R.; Garrote, L. Smoothed particle hydrodynamics model applied to hydraulic structures: A hydraulic jump test case. J. Hydraul. Res. 2010, 48, 142–158. [Google Scholar] [CrossRef]
- Federico, I.; Marrone, S.; Colagrossi, A.; Aristodemo, F.; Antuono, M. Simulating 2D open-channel flows through an SPH model. Eur. J. Mech.-B/Fluids 2012, 34, 35–46. [Google Scholar] [CrossRef]
- Chern, M.-J.; Syamsuri, S. Effect of Corrugated Bed on Hydraulic Jump Characteristic Using SPH Method. J. Hydraul. Eng. 2013, 139, 221–232. [Google Scholar] [CrossRef]
- Jonsson, P.; Andreasson, P.; Hellström, J.I.; Jonsén, P.; Lundström, T.S. Smoothed Particle Hydrodynamic simulation of hydraulic jump using periodic open boundaries. Appl. Math. Model. 2016, 40, 8391–8405. [Google Scholar] [CrossRef]
- Jonsson, P.; Jonsén, P.; Andreasson, P.; Lundström, T.S.; Hellström, J.G.I. Smoothed Particle Hydrodynamic Modelling of Hydraulic Jumps: Bulk Parameters and Free Surface Fluctuations. Engineering 2016, 8, 386–402. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S. SPH numerical investigation of characteristics of hydraulic jumps. Environ. Fluid Mech. 2017, 18, 849–870. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S. SPH modelling of hydraulic jump oscillations at an abrupt drop. Water 2017, 9, 790. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S. SPH numerical investigation of the characteristics of an oscillating hydraulic jump at an abrupt drop. J. Hydrodyn. 2018, 30, 106–113. [Google Scholar] [CrossRef]
- Gu, S.; Bo, F.; Luo, M.; Kazemi, E.; Zhang, Y.; Wei, J. SPH Simulation of Hydraulic Jump on Corrugated Riverbeds. Appl. Sci. 2019, 9, 436. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S.; Torti, E. 3D SPH modelling of hydraulic jump in a very large channel. J. Hydraul. Res. 2013, 51, 158–173. [Google Scholar] [CrossRef]
- De Padova, D.; Ben Meftah, M.; Mossa, M.; Sibilla, S. A multi-phase SPH simulation of hydraulic jump oscillations and local scouring processes downstream of bed sills. Adv. Water Resour. 2022, 159, 104097. [Google Scholar] [CrossRef]
- Crespo, A.; Domínguez, J.; Rogers, B.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Altomare, C.; Crespo, A.J.; Domínguez, J.M.; Gómez-Gesteira, M.; Suzuki, T.; Verwaest, T. Applicability of Smoothed Particle Hydrodynamics for estimation of sea wave impact on coastal structures. Coast. Eng. 2015, 96, 1–12. [Google Scholar] [CrossRef]
- Monaghan, J. Simulating Free Surface Flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Pringgana, G.; Cunningham, L.S.; Rogers, B.D. Modelling of tsunami-induced bore and structure interaction. Proc. Inst. Civ. Eng.—Eng. Comput. Mech. 2016, 169, 109–125. [Google Scholar] [CrossRef]
- Barreiro, A.; Crespo, A.J.C.; Dominguez, J.M.; Garcia-Feal, O.; Zabala, I.; Gomez-Gesteira, M. Quasi-static mooring solver implemented in SPH. J. Ocean Eng. Mar. Energy 2016, 2, 381–396. [Google Scholar] [CrossRef]
- Canelas, R.B.; Domínguez, J.M.; Crespo, A.J.; Gómez-Gesteira, M.; Ferreira, R.M. A Smooth Particle Hydrodynamics discretization for the modelling of free surface flows and rigid body dynamics. Int. J. Numer. Methods Fluids 2015, 78, 581–593. [Google Scholar] [CrossRef]
- Marsooli, R.; Wu, W. 3-D finite-volume model of dam-break flow over uneven beds based on VOF method. Adv. Water Resour. 2014, 70, 104–117. [Google Scholar] [CrossRef]





| Time (s) | 5 | 10 | 15 | 20 | 25 | |
|---|---|---|---|---|---|---|
| L2 errors | Case 1 | 0.400 | 0.283 | 0.331 | 0.265 | 0.256 |
| Case 2 | 0.334 | 0.330 | 0.289 | 0.320 | 0.442 | |
| Case 3 | 0.362 | 0.254 | 0.307 | 0.333 | 0.316 | |
| RMSE | Case 1 | 0.614 | 0.582 | 0.752 | 0.506 | 0.539 |
| Case 2 | 1.158 | 0.799 | 0.775 | 0.701 | 0.706 | |
| Case 3 | 1.494 | 1.106 | 1.494 | 1.422 | 1.331 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.; Wu, R.; Ma, Y.; Tian, Z.; He, D.; Zheng, J.; Li, L. Numerical Simulation of 3D Full Hydraulic Jumps Using a GPU-Based SPH Model. Symmetry 2025, 17, 1564. https://doi.org/10.3390/sym17091564
Lin J, Wu R, Ma Y, Tian Z, He D, Zheng J, Li L. Numerical Simulation of 3D Full Hydraulic Jumps Using a GPU-Based SPH Model. Symmetry. 2025; 17(9):1564. https://doi.org/10.3390/sym17091564
Chicago/Turabian StyleLin, Jinbo, Runzhen Wu, Yingchao Ma, Zhenglin Tian, Dongbin He, Jian Zheng, and Lei Li. 2025. "Numerical Simulation of 3D Full Hydraulic Jumps Using a GPU-Based SPH Model" Symmetry 17, no. 9: 1564. https://doi.org/10.3390/sym17091564
APA StyleLin, J., Wu, R., Ma, Y., Tian, Z., He, D., Zheng, J., & Li, L. (2025). Numerical Simulation of 3D Full Hydraulic Jumps Using a GPU-Based SPH Model. Symmetry, 17(9), 1564. https://doi.org/10.3390/sym17091564





