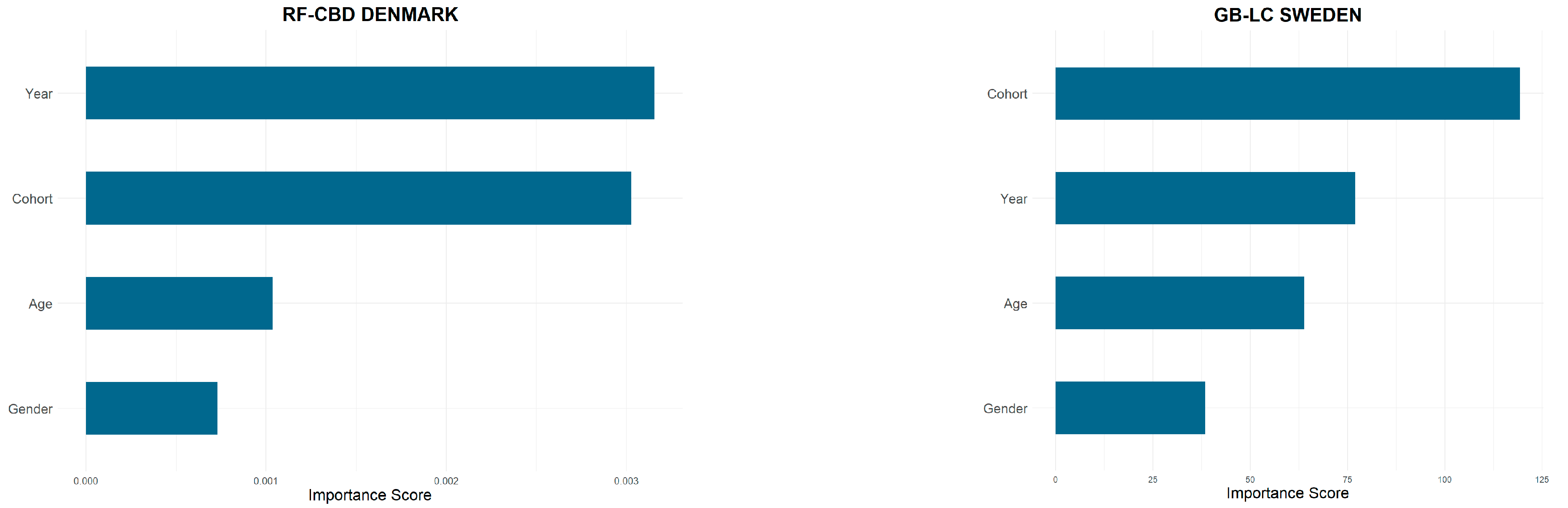Can Tree-Based Models Improve GAPC Mortality Models’ Forecasting Accuracy?

Abstract

Generalized age–period–cohort (GAPC) models are mortality models that incorporate stochasticity, which can be represented in a generalized linear or non-linear context. By fitting the data to either mortality model, one can make forecasts for the future under the extrapolation framework. Previous research indicates that tree-based machine learning (ML) methods are suitable for improving the forecasting ability of such mortality models using different training/testing time periods. However, there is no consensus about generalizing this phenomenon to the improvement of fitted/forecasted mortality rates without depending on a particular mortality model or the model’s training/testing period. Furthermore, GAPC models assume symmetry of the interaction between the features and the mortality rates. Tree-based ML methods can capture asymmetric relationships within demographic data and complement the rigid assumption of symmetry of stochastic mortality models. The objective in our study is to re-estimate the mortality rates obtained from each mortality model by applying tree-based machine learning (ML) methods within a procedure that creates a suitable environment to improve the forecasting accuracy of each GAPC model. By combining mortality models with tree-based methods, both the interpretability of the parameters of mortality models and the features used within machine learning methods can be ensured. In the application carried out in this study for Denmark and Sweden, the results show that all tree-based ML-integrated models reduced the error (root mean squared error) compared to each pure mortality model. This study shows that if the proper procedure is applied, the forecasting ability of each mortality model can be improved.

1. Introduction

Mortality rates form a significant component of actuarial calculations surrounding the valuation and pricing of life insurance. An actuary uses this parameter when modeling annuity products, where the resulting output is extremely sensitive to this particular input. When building the models, stochastic processes are overlaid around the deterministic output to capture the range of expected lifetime uncertainty, and this hybrid output subsequently feeds into both internal economic–capital calculations and the capital frameworks prescribed by regulators [1]. This is crucial as under- or overestimated premiums may even bankrupt companies.

Forecasting mortality rates using mortality laws does not provide uncertainty regarding the advances in mortality, since these models do not include any time component. Ultimately, the lack of information on future mortality improvements may result in a faulty valuation of life insurance products. In addition, according to the Solvency II Framework Directive, a minimum amount of solvency capital should be maintained to prevent financial ruin [2]. The capital is associated with the risk of future mortality being significantly different from that implied by life expectancy and thus should be projected stochastically. Therefore, to quantify the mechanism of mortality progress over the upcoming years and uncertainty in the forecasts, using mortality models that allow stochasticity is crucial [3].

Making accurate forecasts of mortality patterns can inform not only demographers but also researchers, governments, and insurance companies about the future population’s size and longevity. Stochastic mortality modeling has become a pivotal area in current actuarial science and demography, offering valuable tools to predict mortality rates and understand the complex trends and features behind human longevity. The ultimate goal of such models is to provide a more precise forecast of mortality to allow professionals to better manage the longevity risk. This exercise is crucial in the context of a number of applications, including the accurate pricing of insurance policies, construction plans of pension schemes, decision making of social security policies, and risk management in financial firms.

Recently, actuarial and demographic research has begun to benefit from artificial intelligence, specifically machine learning. Humans and animals learn from experience, and that is precisely what machine learning methods do; they copy that concept while teaching computers how to use historical data. These teaching methods include the algorithms that provide information to learn from data that do not need any predetermined equations [4]. Machine learning methods can be advantageous and can learn from computations to make reliable and repeatable decisions and outcomes. It is not new science, but it is newly invigorated. Stochastic mortality models provide a parsimonious mechanism to capture systematic patterns in mortality through the scope of the features they contain. A prominent feature of age–period–cohort mortality models is the enforced smoothness and, as an extension, symmetry across age and over time to achieve model interpretability and tractability. However, mortality dynamics in the real world are often asymmetrical in nature, based on heterogeneous shocks (i.e., pandemics, medical innovation, or region-specific health care reforms) and the non-linear kinds of interactions that these models may not encapsulate [5]. Tree-based machine learning techniques represent an alternative approach since they are able to flexibly detect local deviations, non-monotonicities, and symmetry-breaking effects in mortality data [6].

To be able to model the mortality rates (i.e., age-specific death rates) at the population level, which is a numeric outcome, age, period, cohort, and gender can be used as features. When a response variable (mortality rate) and features as mentioned are available, the problem can be addressed as a regression task aimed at uncovering the underlying pattern of mortality. When it comes to forecasting, mortality models can still produce poor forecasts of mortality rates while fitting almost perfectly on training data. Previous research focused on improving mortality rates under this framework and obtained promising results. In addition to the traditional perspective, tree-based algorithms can be employed for regression tasks. When the dataset comprises multiple predictors and the response variable is continuous, tree-based regression methods provide a suitable modeling framework. From this point of view, in this study, supervised learning methods are used: decision trees (DC), random forest (RF), gradient boosting (GB), and extreme gradient boosting (XGB), which are all tree-based algorithms.

However, research based on the idea of improving the fitting and/or forecasting ability of a mortality model using machine learning techniques heavily depends on the predetermined fitting and testing periods. Changing these periods mostly results in producing more errors than the original (pure) mortality model does. But then, focusing on the improving of fitting ability to rely on making better forecasts of mortality rates may not always be a good idea, especially when the historical mortality pattern that fitted the model is not fully representative of the mortality pattern. The idea behind the out-of-sample tests helps in solving this problem by determining model performance on unseen data while providing unbiased evaluation of how well the model can predict the future.

From this point of view, the target is to increase the forecasting ability of any mortality model using tree-based ML models by focusing on the out-of-sample testing period. To achieve this, we create a trade-off interval which allows the machine learning integrated model to give better forecasted mortality rates as an output without compromising the fitting quality. By doing so, using the procedure proposed in this study will enable us to improve the mortality rates obtained from any mortality model. With this study, one can see the improved rates on the out-of-sample data without abandoning the fitting period of the related mortality model. We contribute to the literature by creating a procedural framework, rather than making specific improvements for limited data and periods or a particular mortality model as used in previous studies. Furthermore, we focus on test data in order to make better forecasts without abandoning the improvement on training data.

In Section 2, previous research on GAPC models and the use of ML methods to improve GAPC models are examined. In Section 3, we examine the GAPC models in detail. In the next section, we outline the four tree-based ML models in a regression setting. In Section 5, we propose the procedure step by step and an application is illustrated. Finally, the discussion and the conclusion parts are given.

2. Literature Review

The Lee–Carter (LC) [7] model, presented by Ronald Lee and Lawrence Carter in 1992, can be considered as leading among stochastic mortality models, becoming a benchmark model in mortality forecasting. Together with the original model, its extensions have also been used by academics, private sector practitioners, and several statistics institutes for nearly three decades [8]. The LC model was the earliest model taking increased life expectancy trends into account, which is related to mortality improvement through time and helped the United States’ public insurance system and federal budget by making better forecasts of mortality [9,10]. Lee and Carter proposed a stochastic method established on age-specific and time-varying components to capture the death rates of the United States population [7]. Despite its simplicity, the LC model has demonstrated excellent results for fitting mortality for several countries.

Building on this work, several important extensions have been implemented to address Lee–Carter model’s limitations and enhance its predictive power. To handle the fundamental assumption of homoscedasticity of errors, Brouhns et al. [11] used the LC model in an embedded Poisson regression framework. The Renshaw–Haberman (RH) model [12] improved the LC model accuracy by capturing the unique mortality experience influenced by the birth year (cohort) of the individuals. Another model is the generalized form of the RH model that is the so-called age–period–cohort (APC) model, first introduced by Hobcraft et al. [13] and Osmond [14], which became visible in the demographic and actuarial literature through Currie [15]. A popular competitor of LC, one stochastic model to appear was the Cairns–Blake–Dowd (CBD) model [16]. Unlike the logarithmic transformation in the LC model, the CBD model applies a logit transformation to the probability of death, which is captured as a linear or quadratic function of age which is also called M7 with an additional cohort effect [17]. Plat [18] combines the LC and CBD models to explain the entire age range. The models mentioned above can be classified as GAPC models that can be written in a generalized linear/non-linear model (GLM/GNM) setting [19]. In mortality modeling, GLMs/GNMs are particularly useful for modeling mortality rates as a function of diverse explanatory variables such as age, sex, and cohort. Popular choices for the distribution of the outcome variable within GLMs/GNMs include the binomial distribution for binary outcomes (e.g., survival vs. death) and the Poisson distribution for count data (e.g., number of deaths). The reason for choosing these mortality models is that these models represent the vast majority of the stochastic mortality models together with being a member of the GAPC family [20,21]. For an extended overview, refer to Hunt and Blake [22], Haberman and Renshaw [23], Booth and Tickle [5], Pitacco et al. [24], Dowd et al. [25], Zamzuri and Hui [26], and Redzwan and Ramli [27]. The framework of the GAPC model is explained in detail in the next section.

Machine learning, on the other hand, has been increasingly used in major fields in science but the demography does not come first. The main reason is probably that researchers find it difficult to interpret the results, since machine learning had still been believed to be a “black box” [28]. This belief came to an end when Deprez et al. [29] showed that using mortality models can produce improved results together with machine learning techniques. Deprez et al. [29] used tree-based machine learning methods in a novel approach and encouraged researchers pondering more about machine learning along with demography. The work was based on improving the stochastic mortality model’s both fitting and forecasting ability by re-estimating the mortality rates using the features age, calendar year, gender, and cohort with the help of machine learning techniques. Soon after, Levantesi and Pizzorusso [28] presented a new approach based on the same idea in Deprez et al. [29] and used three mortality models to re-estimate the mortality rates obtained from the models. For forecasting the mortality rates, they treated the ratio of observed and modeled deaths as mortality rates and used the forecasting procedure of a mortality model. Staying within the context of improving mortality models’ accuracy using a tree-based model, the research has gained momentum. Levantesi and Nigri [30] improved the Lee–Carter predictive accuracy by using random forest and p-splines methods. Bjerre [31] used tree-based methods to improve mortality rates using multi-population data. Gyamerah et al. [32] developed a hybrid LC+ML model where the Lee–Carter time index is forecast using a stack of learners. Qiao et al. [33] applied a complex boosting/ensemble framework to long-term mortality. Across many countries, their method roughly halved the 20-year-forecast mean absolute percentage error compared to classic models. Finally, Levantesi et al. [34] used contrast trees as a diagnostic tool to identify the regions where the model gives higher error and used Friedman’s [35] boosting technique to improve the mortality model accuracy.

This study fills the gaps of the previous literature by using the most common mortality models and tree-based machine learning methods at once, making the “improving” idea more robust by creating a procedure that allows better forecasts of mortality.

3. Generalized Age–Period–Cohort Models

First, we give the demographic notations and assumptions on calculating mortality rates. Second, we present the age, period, and cohort structure of the GAPC models in detail.

3.1. Data and Notation

The human mortality and population data at the population level are often found as the number of deaths and the exposures covering the ages $x_i$ and the calendar year $t_i$ shown in classical demographic and actuarial notation. Exposure is assessed by the person years lived, which means that the contribution of an individual to the life line is given in terms of time. Also, it is generally referred as exposure to risk. When the exposure is not available, the mid-year population is a good approximation. Mortality rates are usually defined as either age-specific death rates, $m_{x,t}$, or probabilities of death, $q_{x,t}$. However, the process underlying the mortality itself is continuous in nature; thus, we first need to make the transition from a continuous state to the discrete one to be able to perform the mortality analysis. In a continuous state, the force of mortality ${\mu }_{x,t}$ shows the instantaneous death rate between t and dt where dt is really small. A single assumption of 0 ≤ s, u < 1, ${\mu }_{x+u,t+s}= {\mu }_{x,t}$, implies that the force of mortality remains constant over each age and calendar year. This assumption results in two important equations:

$$m_{x,t}= {\mu }_{x,t}$$

(1)

$$q_{x,t}=1-e^{-{\mu }_{x,t}}=1-e^{-m_{x,t}}$$

(2)

Let the death counts be $D_{x,t}$ and the exposures $E_{x,t}$. Here $E_{x,t}$ is separated as $E_{x,t}^c$ (central exposed to risk) and $E_{x,t}^0$ (initial exposed to risk). $m_{x,t}$, which is also called the central mortality rate, can be easily calculated by dividing $D_{x,t}$ by $E_{x,t}^c$, while $q_{x,t}$ which is also called the initial mortality rate is calculated the same number of deaths divided by $E_{x,t}^0$. In its absence, initial exposure is approximated by adding half of the death counts to the central exposure. 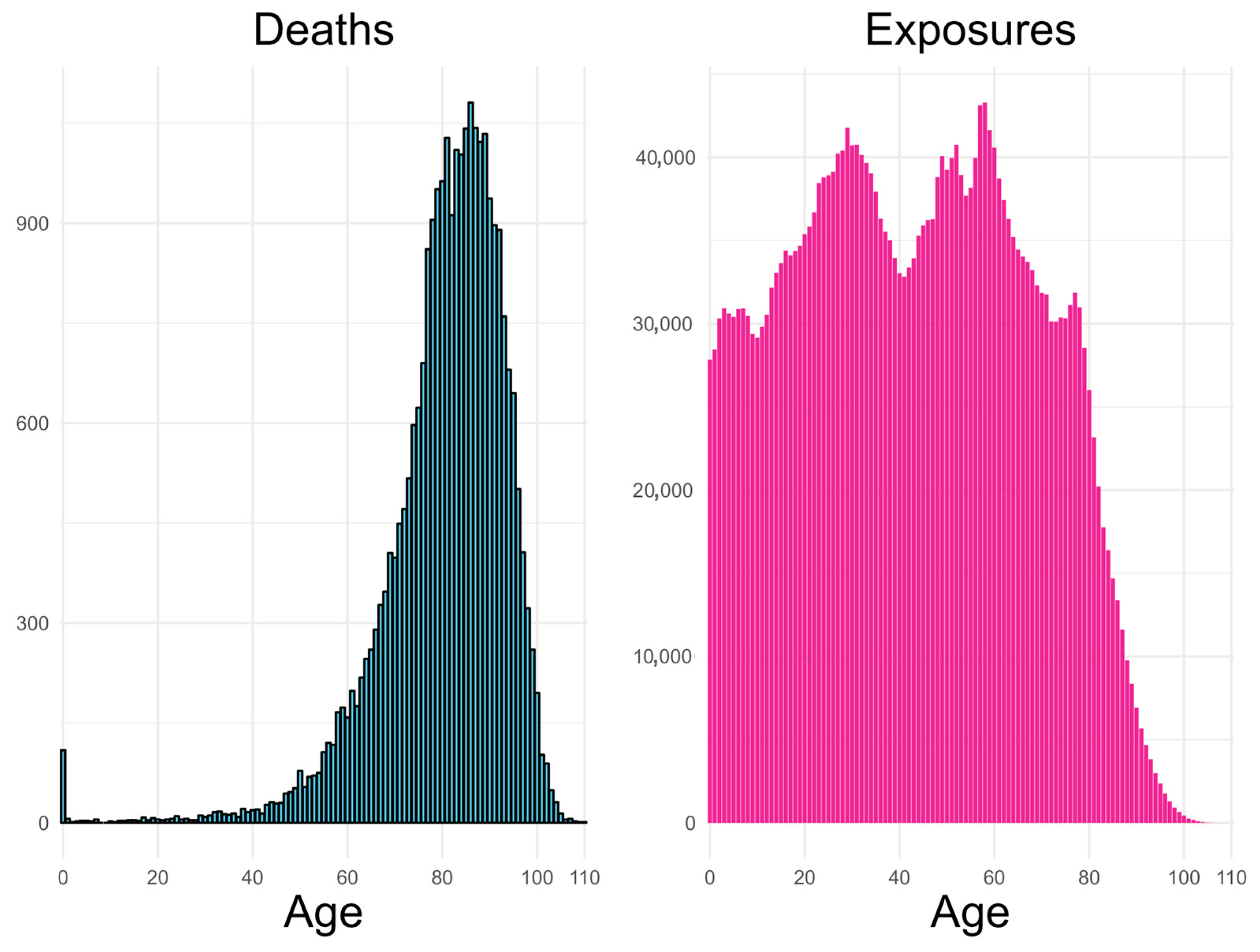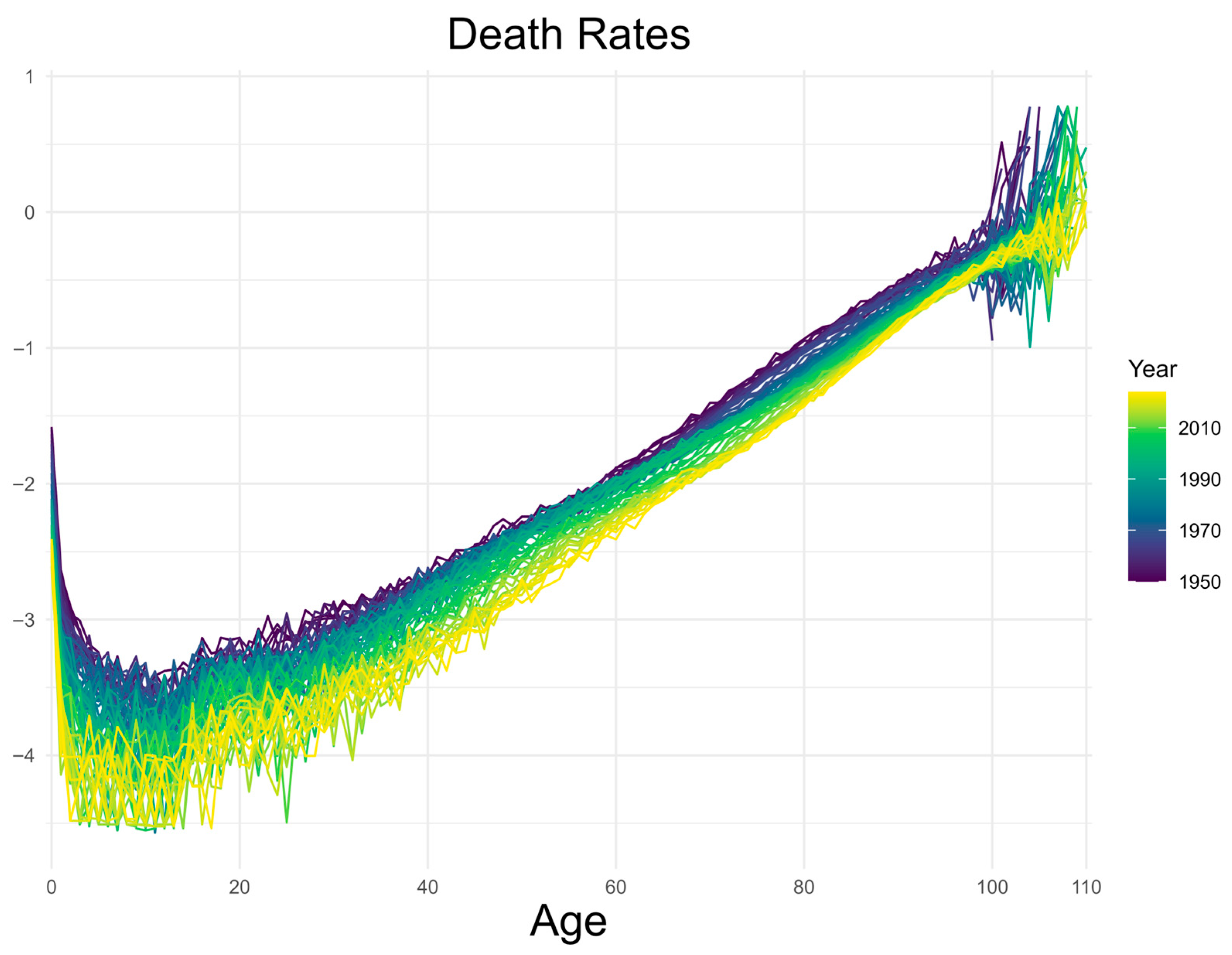For practical purposes, Figure 1 and Figure 2 below show the observed available mortality data for the female population of Denmark.

Figure 2 clearly represents the mortality rate’s reduction over years at almost each age. This phenomenon usually results in increasing life expectancy of the population over the years. The analysis in this study is performed using single age and year intervals.

3.2. Age–Period–Cohort Structure

The GAPC model is a model capable of representing the response variable, a function of any mortality index, using a linear or bilinear predictor structure of the features age, period, and cohort for a population [22]. GAPC models provide a powerful, flexible framework for mortality modeling by systematically incorporating these features’ effects. Their main advantage lies in significantly enhancing the reliability of parameter estimation and contributing to more robust mortality forecasting.

Hunt and Blake [22] discussed that the preponderance of the stochastic mortality models are an expression of an age–period–cohort model. Currie [19] showed the form of a generalized linear or non-linear model with the following components:

$${ƞ}_{x,t}= \underset{\underset{Age}{⏟}}{{\alpha }_x}+ \underset{\underset{Period}{⏟}}{\sum _{i=1}^N{\beta }_x^i{\kappa }_t^i}+ \underset{\underset{Period}{⏟}}{{\beta }_x^{\left(0\right)}{\gamma }_{t-x}}$$

(3)

${ƞ}_{x,t}$ presents the link function of the response variable to the predictor structure. ${\alpha }_x$ is the static age function, representing the general shape of mortality across the age range and fixed over the time period. ${\beta }_x^i{\kappa }_t^i$ is a set of age/period terms where ${\kappa }_t^i$ states the trend of mortality over time and ${\beta }_x^i$ denotes the pattern of mortality change across the ages. ${\gamma }_{t-x}$ determines the effect of the cohorts through their lifetime and ${\beta }_x^{\left(0\right)}$ is the coefficient that modifies ${\gamma }_{t-x}$ [22].

If we treat $D_{x,t}$ as random variables, the assumption can be made as follows: the number of deaths follows either a Poisson or binomial distribution.

$$D_{x,t} ~ Poisson \left(E_{x,t}^c{m}_{x,t}\right)\mathrm{or} D_{x,t} ~ Binomial \left(E_{x,t}^0{q}_{x,t}\right)$$

Then, the link function is shown:

$${ƞ}_{x,t}=g\left(E\left({\displaystyle \frac{D_{x,t}}{E_{x,t}}}\right)\right)$$

(4)

The Poisson distribution can be denoted in the exponential family form by rearranging the probability mass function [37]:

$$P\left(Y=y\right)=\mathrm{e}\mathrm{x}\mathrm{p}(y\mathit{log}\left(\lambda \right)-\lambda -\mathit{log}\left(y!\right)$$

(5)

Here the natural parameter is log(λ), so the canonical link is the log link. If we rearrange the binomial probability mass function, then it can be written in the exponential family form [37]:

$$P\left(Y=y\right)=\mathrm{e}\mathrm{x}\mathrm{p}(\mathrm{y}\log \left({\displaystyle \frac{p}{1-p}}\right)+m\mathit{log}\left(1-p\right)+\mathit{log}\left(\begin{array}{c}m\\ y\end{array}\right))$$

(6)

The natural parameter is $\log \left({\displaystyle \frac{p}{1-p}}\right)$, so the canonical link is logit. The canonical link function is useful not only because it helps in model interpretation, but it also makes maximum likelihood estimation much more straightforward. The likelihood expression for Poisson death counts with the logarithm link function is as follows [22]:

$$\mathcal{L}={\sum }_{x,t}{w}_{x,t}(d_{x,t}\mathit{ln}\left(E_{x,t}^c{m}_{x,t}\right)-E_{x,t}^c{m}_{x,t}-ln(d_{x,t}!))$$

(7)

And for the binomial and the logit link function,

$$\begin{gathered} \mathcal{L}={\sum }_{x,t}{w}_{x,t}(d_{x,t}\mathit{ln}\left(q_{x,t}\right)+\left(E_{x,t}^0-d_{x,t}\right) ln\left(1-q_{x,t}\right)+ln\left(E_{x,t}^0!\right)- \\ ln\left(\left(E_{x,t}^0-d_{x,t}\right)!\right)-ln(d_{x,t}!)) \end{gathered}$$

(8)

where $w_{x,t}$ are (0,1) weights and the symbol “!” means factorial. For details, refer to Villegas et al. [20], Currie [19], and McCullagh and Nelder [38].

The mortality models that can be expressed in GLM/GNM form are available to be fitted to the data by using the StMoMo package in R [20,39]. In this study, tree-based algorithms are applied to each model included in the package StMoMo. These mortality models can be summarized into 3 groups: Lee–Carter [7] and its extensions, Cairns–Blake–Dowd (CBD) [16] and its extensions, and the Plat model [18] which is a hybridized version of the classical age–period–cohort [15], LC [7], and CBD [16].

Table 1. Structure of GAPC models.

Mortality Model	Short Definition	Structure
Lee–Carter (LC)	Static age function, an age–period term, no cohort effect.	$ln\left(m_{x,t}\right)={\alpha }_{x,t}+{\beta }_x{\kappa }_t$
Renshaw-Haberman (RH)	Generalizes LC by adding cohort effect.	$ln\left(m_{x,t}\right)={\alpha }_{x,t}+{\beta }_x{\kappa }_t+{\gamma }_{t-x}$
Age–Period–Cohort (APC)	Basic form of age–period–cohort models.	$ln\left(m_{x,t}\right)={\alpha }_{x,t}+{\kappa }_t+{\gamma }_{t-x}$
Cairns–Blake–Dowd (CBD)	Two age–period terms, no static age function, no cohort effect.	${logit\left(q_{x,t}\right)=\kappa }_t^1+(x-\overline{x}){\kappa }_t^2$
M7	CBD with quadratic age effect and a cohort effect.	${logit\left(q_{x,t}\right)=\kappa }_t^1+\left(x-\overline{x}\right){\kappa }_t^2+{\left[\right(x-\overline{x})}^2-{\sigma }_x^2]{\kappa }_t^3+{\gamma }_{t-x}$
Plat	Hybrid version of LC and CBD.	$ln\left(m_{x,t}\right)={\alpha }_{x,t}+{\kappa }_t^1+\left(\overline{x}-x\right){\kappa }_t^2+{\left(\overline{x}-x\right)}^{+}{\kappa }_t^3+{\gamma }_{t-x}$ where ${\left(\overline{x}-x\right)}^{+}=\mathrm{m}\mathrm{a}\mathrm{x}(0,\overline{x}-x)$

shows the formal structure of GAPC models included in StMoMo.

Since the CBD and M7 models’ response variable is $q_{x,t}$, the transformation is performed to $m_{x,t}$ using Equation (2). In addition to that, forecasting of mortality rates using mortality models is conducted using the “auto.arima” function in R which selects the best Autoregressive Integrated Moving Averages (ARIMA) process of each index.

4. Tree-Based Machine Learning Models

Tree-based models have long been known as a fundamental and successful class of ML algorithms. These models make predictions by applying a hierarchical, tree structure method to the observations that is a unique take on solving problems whether they are classification (predicting categorical values) or regression (predicting numerical values) problems. When it comes to prediction using tree-based methodologies, one basically generates a sequence of if-then rules from an initial root node (at the top) through a sequence of internal decision nodes finalizing in a terminal leaf node. To build this tree-like structure, a set of splitting rules are applied to divide the feature space into smaller groups until the stopping criteria are met. Stopping criteria are based on adjusting the hyperparameters, which are non-learnable parameters (i.e., maximum depth of a tree, minimum samples in a node, etc.) that are defined prior to the commencement of the learning process. They serve to control various aspects of the learning algorithm and can significantly influence the model’s performance and behavior. The careful tuning of these hyperparameters is paramount for achieving improved model performance and, critically, for mitigating the risk of overfitting.

Tree-based models are non-parametric supervised learning algorithms, known as being incredibly flexible for a variety of predictive tasks. These models’ innate ability to capture complex patterns and non-linear interactions in complex datasets is a major advantage over conventional linear models. They are especially effective in real-world applications where relationships between variables are rarely purely linear, in contrast to linear models, which presume a direct, linear relationship between features and outcomes. This ability is useful to use when the mortality itself is considered a non-linear process.

In this study, we used four popular types of tree-based algorithms which are believed to reflect the majority of the methods showing a tree structure, and we can briefly classify them as follows [40]:

• Decision tree model: substructure of tree-based models.
• Random forest model: “ensemble” method constructs more than one decision tree.
• Gradient boosting model: “ensemble” method constructs decision trees sequentially.
• Extreme gradient boosting model: “ensemble” method which is optimized for implementation of a gradient boosting model that enhances the iterative process.

In this study, since the response variable is continuous, the tree-based methods are studied in a regression framework.

4.1. Decision Trees

Decision trees (DT), first introduced by Brieman et al. [41], serve as the foundational element for all tree-based models. Understanding their specific application in regression provides crucial context for more complex ensemble methods.

To build a decision tree, information must be defined for splitting the data. For discrete variables, popular choices would be the Gini information or entropy; however, when the response variable is continuous, an error-based information is needed. Let S represent the total squared error of the tree T; the authors of [42] showed that

$$S={\sum }_{c\in leaves\left(T\right)}{\sum }_{i\in C}{(x_i-f_c)}^2$$

(9)

The final prediction is

$$f_c={\displaystyle \frac{1}{n_c}}{\sum }_{i\in C}{x}_i$$

(10)

The splitting process is stopped by minimizing S with predefined hyperparameters, and the final predictions in each leaf are obtained.

4.2. Random Forest

In 2001, Breiman [43] introduced a powerful tree-based algorithm called random forest (RF). In random forest, a bootstrap sample of the data, or n observations chosen with replacement from the initial n rows, is used to calculate each tree. This method is known as “bagging” which is derived from “bootstrap aggregating” [44]. Predictions are found by pooling the predictions of all trees, mean majority voting for classification problems, and averaging of the predictions from all trees for regression problems.

The progression from single decision trees to ensemble methods like random forests is more than an incremental improvement in accuracy; it represents a fundamental shift in how the bias–variance trade-off is addressed. Single decision tree, by its nature, tends to be a high-variance, low-bias model, meaning it can fit the training data very closely but is sensitive to small variations in that data, leading to poor generalization. Bagging, as implemented in random forests, primarily reduces variance by averaging the predictions of multiple independently trained trees, thereby mitigating the overfitting tendency of individual trees.

$$f_{RF}={\displaystyle \frac{1}{T_c}}{\sum }_{i=1,\in C}^{T_c}{y}_i$$

(11)

The final predictions are simply the averages of each prediction of the individual trees.

4.3. Gradient Boosting

The gradient boosting (GB) algorithm makes accurate predictions with the combination of many decision trees in a single model. It is an algorithmic predictive model invented by Friedman [45] that learns from errors to build up predictive strength. Unlike random forest, gradient boosting combines several weak models of prediction into a single ensemble to improve accuracy. Typically, gradient boosting uses decision trees in an ensemble that are trained sequentially with the idea of minimizing errors [46].

The algorithm fits a decision tree to the residuals of the initial model. In this instance, “fitting a tree based on the current residuals” means that we are fitting a tree, with the residuals as response values rather than the original outcome. This fitted tree now becomes a part of the fitted function and the residuals are updated. By doing so, f is improved bit by bit in the regions in which it is not performing well. The shrinkage parameter λ also slows down the process, leading to more and differently shaped trees applied to the residuals. In general, slow learners lead to a better overall performance [47,48].

The final predictions are shown as

$$f_{GB}\left(x\right)=f_{m-1}\left(x\right)+\lambda T_M\left(x\right)$$

(12)

where $\lambda$ is the learning rate, M represents the total number of trees, $T_M\left(x\right)$ stands for the m regression tree output. Each $T_M\left(x\right)$ is trained on the residuals $r_{im}$, which are shown as

$$r_{im}=-{\displaystyle \frac{\partial L}{\partial f_{m-1}\left(x_i\right)}}=y_i-f_{m-1}\left(x_i\right)$$

(13)

where L is the loss function we aim to minimize.

4.4. Extreme Gradient Boosting

The extreme gradient boosting (XGB) method developed by Chen and Guestrin [49] is an improved implementation of GB basically with the same framework that combines weak learner trees into strong learning by adjusting the residuals. Unlike the gradient boosting method, the trees are grown in parallel, not sequentially. Also, the extreme gradient boosting method has built-in regularization to prevent overfitting by penalizing model complexity.

The final predictions are estimated similarly but with a more regularized objective function [50]:

$$f_c={\displaystyle \frac{1}{n_c}}{\sum }_{i\in C}{x}_i$$

(14)

trying to minimize the function

$$L\left(\varnothing \right)={\sum }_{i}l\left(f_{XGB}\left(x\right),f\left(x\right)\right)+{\sum }_k\Omega \left(f_k\right)$$

(15)

where $l$ presents a differentiable loss function that quantifies the gap involving estimated and response values where $\Omega \left(f_k\right)= \gamma T+{\displaystyle \frac{1}{2}} \lambda {\left|\left|w\right|\right|}^2$ [50,51]. In this formula, w shows the score on the leaves; T, the number of leaves in a tree; $\gamma$, the cost of adding a leaf; and $\lambda$, the regularization term on leaf weights.

5. ML Integrated Model Development

In this study, improvement of the mortality models’ accuracy is performed by integrating the tree-based machine learning methods into the mortality models. Under a regression framework, mortality rates are re-estimated by calibrating the ratio between the estimated and observed number of deaths including the features age, gender, year, and cohort using the most common tree-based ML methods. By combining the two techniques, we neither lose the ability of mortality models to explain the underlying pattern of mortality, nor do we compromise their ability to make better predictions thanks to the data-driven methods.

We support open science practices and have made the entire analysis’ R-codes available at github.com/ozerbakar.

5.1. Improving the Accuracy of a GAPC Model

The idea of improving mortality models’ accuracy is based on approximating the mortality rates of the final model compared to the observed ones. If the total error, which is the difference between the modeled and observed rates, is reduced, then the proposed model would have improved the pure mortality model.

In practice, first the data is fit to each mortality model. Then the number of deaths at age x and year t is able to be extracted from the model (${d_{x,t}}^{mdl}$). Here, “mdl” indicates the mortality model in use. Similarly, when $m_x$ of the model is re-estimated using ML methods, then mortality rate is written as ${m_{x,t}}^{mdl, ML}$. According to Deprez et al. [29] and Levantesi and Pizzorusso [28], improved mortality rates can be estimated as follows:

$${m_{x,t}}^{mdl,ML}= {{\psi }_{x,t}}^{mdl,ML}· {m_{x,t}}^{mdl}$$

(16)

Here, ${{\psi }_{x,t}}^{mdl,ML}$ is a ratio between the estimated and observed death counts. Consider a coefficient ${\psi }_{x,t}$ that can be multiplied by the number of deaths and rewrite the equation:

$$D_{x,t} ~ {\psi }_{x,t} {d_{x,t}}^{mdl}$$

$$\mathrm{where} {\psi }_{x,t}\equiv 1; {d_{x,t}}^{mdl}={m_{x,t}}^{mdl} E_{x,t}$$

(17)

With a perfect model, the coefficient ${\psi }_{x,t}$ would be equal to 1. However, in the real world, there is no model that fits perfectly to any mortality data. Even if such a model existed, it would be useless for forecasting, since it lacks the ability to generalize the mortality pattern and tends to overfit the presented data. Therefore, the idea behind improving the accuracy of a mortality model is to calibrate the coefficient ${\psi }_{x,t}$ by applying the tree-based algorithms under a regression framework with the given features. We can illustrate the model as follows:

$${\displaystyle \frac{D_{x,t}}{{d_{x,t}}^{mdl}}~gender + age + year + cohort}$$

Here, ${\displaystyle \frac{D_{x,t}}{{d_{x,t}}^{mdl}}}$ = ${\psi }_{x,t}$ is found as a solution of the equation above under the regression framework by using four types of tree-based algorithms. After estimating ${{\psi }_{x,t}}^{mdl,ML}$ for each age and year using the machine learning algorithms, it is applied to the mortality rates obtained from the GAPC models to obtain the improved mortality rates.

5.2. Evaluating the Forecasting Performance of a Model

While practicing machine learning techniques, data is split into training and testing parts to fit a particular model to the data and see how it performs. In-sample tests use the same dataset for evaluating the model and measure how well it fits. However, this type of test lacks generalization and accommodates the risk of overfitting. Out-of-sample tests, on the other hand, do not use a part of the data in the training process. The hold-out test is an out-of-sample procedure in which a separate, unseen dataset is reserved for a single final evaluation, yielding a reasonably unbiased estimate of model performance.

The practice in this study is a combination of out-of-sample tests qualifying the forecasting accuracy on unseen data. But the forecasting evaluation is based on mortality rates which is not used in the machine learning process. ${\psi }_{x,t}$ is the only variable calibrated in a regression framework with tree-based methods and multiplied by the mortality rates of the mortality models. These results are then compared with the observed mortality rates. While k-fold cross-validation is used for the calibration of ${\psi }_{x,t}$, a hold-out test is used for qualifying the forecasting accuracy of the tree-based integrated model.

To assess the goodness of fit and forecast of the GAPC and the tree-based improved models, the root mean squared error (RMSE) is used. RMSE is extensively exercised in regression problems as a loss function and in model evaluation, because of its very intuitive interpretation. RMSE is calculated as follows:

$$\sqrt{{\displaystyle \frac{\sum _{i=1}^n{(\overbrace{y_i}-y_i)}^2}{n}}}$$

(18)

where $\overbrace{y_i}$ are predicted values, $y_i$ are observed values, and $n$ is the number of observations. RMSE values are calculated against observed values of mortality rates.

6. A Procedure for Improving the Forecasting Ability

The procedure means applying all methods sequentially to obtain the results without the need for human interaction. Briefly, after fitting a GAPC model to the data and obtaining the mortality rates, ${{\psi }_{x,t}}^{mdl}$ is calculated. Then, the mortality model specific ${{\psi }_{x,t}}^{ML}$ is estimated using tree-based methods for both training and hold-out testing periods including all possible sets of hyperparameters. By multiplying the forecasted (estimated over the hold-out testing period) ${{\psi }_x}^{ML,for}$ with ${m_{x,t}}^{mdl,for}$, which are the mortality rates forecasted using the mortality model, ML-integrated mortality rates (${m_{x,t}}^{mdl,ML,for}$) can easily be estimated. After that, for each hyperparameter set, the RMSE of the ML-integrated mortality rates relative to the observed values is computed, and the configurations yielding a lower RMSE than the baseline mortality models are selected. To mitigate the possibility that this outcome arises merely from randomness, the hyperparameter set that calibrates ${{\psi }_{x,t}}^{mdl}$ and achieves the lowest RMSE in the testing period is further validated by examining whether it also produces a lower RMSE in the training period. Thus, a trade-off interval is created for lowering the error of the original mortality model on both periods. A step-by-step explanation is given below.

• The Procedure

• Reserve a hold-out testing period.
• Fit a mortality model to the training data.
• Extract fitted mortality rates.
• Calculate $\psi$ for each age and year.
• Forecast with same mortality model over the testing period.
• Extract forecasted mortality rates and calculate model RMSE.
• Calibrate $\psi$ with tree-based methods:
  • Determine lower and upper limits of hyperparameters.
  • Extract re-estimated ${\psi }^{ML,fit}$ series calculated with a different set of hyperparameters.
• Obtain each ${\psi }^{ML,for}$ series using tree-based methods.
• Calculate each series of ${m_{x,t}}^{mdl,ML,for}$ over the testing period.
• Identify the ${\psi }^{ML,for,low}$ series that gives less RMSE for the testing period.
• Find ${\psi }^{ML,fit}$ series used to forecast ${\psi }^{ML,for,low}$ and calculate ${m_{x,t}}^{mdl,ML,fit}$ over the training period.
• Search for ${\psi }^{ML,fit,low}$ series that also gives less RMSE for the training period.
• Repeat the steps for each mortality model.

By following through the steps, series of improved mortality rates for both the training and testing periods will be estimated. Under these circumstances, machine learning techniques can improve the mortality models’ forecasting accuracy without relying on the fixed fitting or testing period. At the end, researchers can make robust and reliable forecasts about future mortality.

It is important to remember that mortality rates themselves are not subject to any machine learning process. $\psi$ is the only variable calibrated using tree-based ML methods and multiplied by the mortality rates obtained from the mortality models. With the help of this flexible approach, researchers can adjust the training and testing period of the preferred mortality model and make improved forecasts of future mortality.

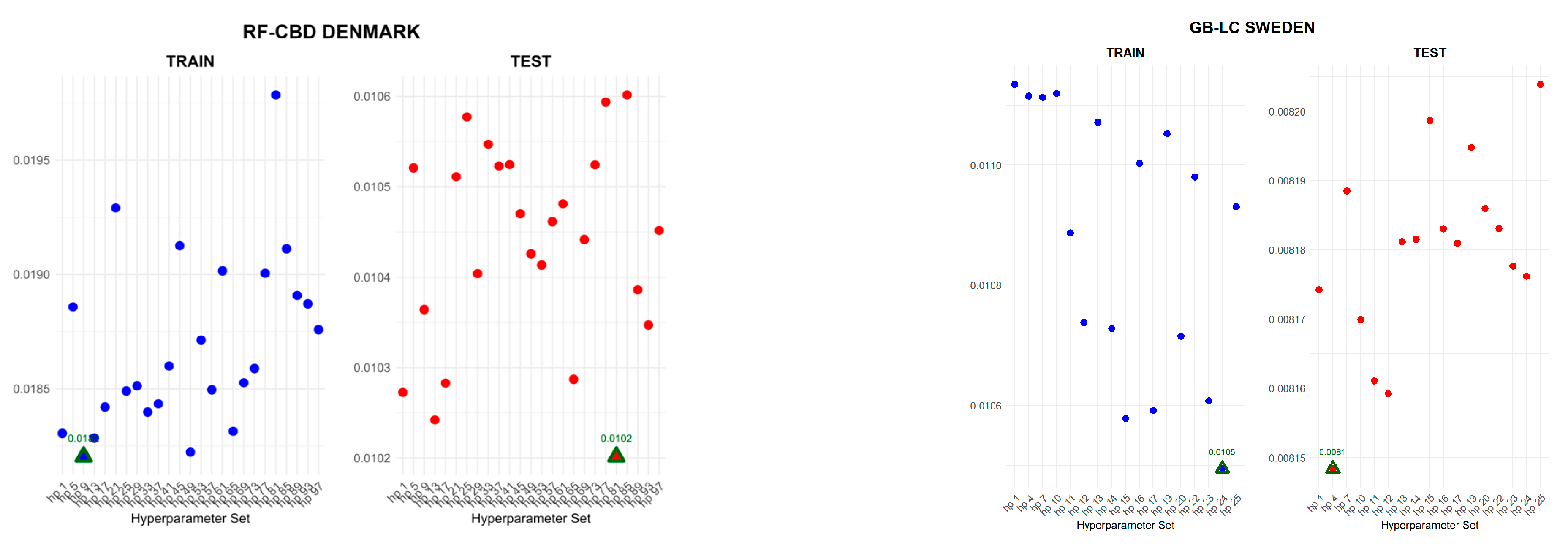
An application is performed for practical representation using female mortality data from Denmark and Sweden; Figure 3 shows the RMSE values of the ML-integrated model, which are lower than those of the pure mortality model. To demonstrate the different outputs of the mechanism used in this study, an RF-integrated CBD model is selected for Denmark and a GB-integrated LC model is selected for Sweden among all improved models (each figure can also be generated using our publicly available R code). For Denmark, the age range is 65–99 and the year range is 1960–2010 for the training period and 2011–2020 for the testing (hold-out) period. For Sweden, the age range is 0–99 and the year range is 1955–2000 for the training period and 2001–2020 for the testing (hold-out) period. The CBD and M7 mortality models are particularly designed for old-age mortality [52]. When they are used for the entire age range, their performance significantly deteriorates; thus, they are not used for Sweden. Here, the RMSE of the pure CBD model for the training period is 0.026751 and for testing period it is 0.010778. The RMSE of the pure LC model for the training period is 0.011144 and for the testing period it is 0.008215.

For the female population of Denmark,

Table 2. Minimum RMSE value of the testing period with corresponding ¹ RMSE of the training period and minimum RMSE value of the training period. * Findings for Danish males and Sweden are given in Appendix B.

	Pure		DT			RF			GB			XGB
	Test	Train	Min Test	Train	Min Train	Min Test	Train	Min Train	Min Test	Train	Min Train	Min Test	Train	Min Train
LC	0.8084	2.1349	0.7615	1.9795	1.2229	0.7635	1.1311	0.8207	0.7668	1.9176	1.8477	0.7547	1.6795	1.3928
CBD	1.0778	2.6752	0.9048	1.9989	1.4155	1.0201	1.9784	1.8203	0.9776	2.0735	1.8669	1.0075	1.7899	1.4575
APC	1.7488	2.4273	1.3095	2.0338	2.0338	1.0152	1.1911	0.8452	1.0411	1.8730	1.8061	0.9701	1.3537	1.3537
RH	1.0053	1.9992	1.0001	1.4051	1.4051	0.8101	1.2610	0.8504	0.9330	1.8479	1.7672	0.7681	1.8907	1.3177
M7	2.7858	1.9877	2.4128	1.9242	1.9198	2.4457	1.2030	0.8489	2.3781	1.7950	1.7824	1.9853	1.8368	1.2736
Plat	2.1286	2.0379	1.8430	1.9432	1.9277	1.9029	1.2281	0.8454	1.8686	1.7536	1.7536	1.5092	1.9064	1.2454

*: Results are multiplied by 10² to make them fit the table. ¹ Training results show the value of the hyperparameter set used over the training period which finds the minimum RMSE over the test period.

shows the RMSE of pure mortality models and the minimum RMSE of their ML-integrated versions over the testing period, as well as the RMSE over the training period when using the same hyperparameter set. The minimum RMSE values over the training period are also provided. Among the mortality models, the LC model showed the best performance for the hold-out testing period. Furthermore, the XGB method performed the greatest improvement of forecasting accuracy as an integration of the LC model among all tree-based models with an approximately 6.64% decrease in terms of error. On the other hand, the RF method showed remarkable improvement for all mortality models for both the testing and training periods with the highest improvement in the APC model’s fitting period around 50.93%. For the female population of Sweden (see

Table A2. Minimum RMSE value of the testing period with corresponding RMSE of the training period and minimum RMSE value of the training period. Data: Denmark’s male population, years between 1960 and 2010 (train), 2011 and 2020 (test), ages between 65 and 99.

	Pure		DT			RF			GB			XGB
	Test	Train	Min Test	Train	Min Train	Min Test	Train	Min Train	Min Test	Train	Min Train	Min Test	Train	Min Train
LC	2.1922	4.0438	2.1244	1.8127	1.7225	2.0977	2.1543	1.5052	2.1233	3.8256	3.3274	2.1167	2.8815	2.1907
CBD	2.0877	3.7642	2.0545	3.5016	2.8520	1.9631	1.7566	1.4695	2.0233	3.4770	3.3159	1.8876	3.6668	2.2994
APC	2.9781	3.9230	2.5461	3.6140	3.6140	2.3023	1.9350	1.4311	2.3170	3.3490	3.1862	2.2897	2.0956	2.0956
RH	2.2360	3.6468	2.2323	3.6204	3.2732	2.2293	3.1565	3.1402	2.2252	3.3834	3.3150	2.2074	2.8230	2.8230
M7	2.1140	3.6614	2.0973	3.5582	3.3742	2.0878	1.9122	1.7146	2.0868	3.5766	3.3615	2.1051	3.5421	2.8256
Plat	2.3274	3.6173	1.9786	3.2534	3.1819	2.0428	2.2212	1.4345	2.1522	3.1389	3.1389	1.8804	3.2549	1.9184

in Appendix B), the lowest error is estimated over the hold-out testing period by the LC model. The improvement of forecasting accuracy is around 11.75% with the integration of the RF method. Moreover, the highest improvement is shown by the RF method combined with the APC model which is approximately 61.51% over the fitting period.

The procedure finds a lower error for the testing period first, then obtains the lower errors for the training period using the same hyperparameter sets against the pure mortality model. As can be seen from Figure 3, the hyperparameter set that gives the minimum error over the test period may not always be the one that produces the minimum error over the training period. In fact, it may even produce higher errors than the pure mortality model. Therefore, while focusing on achieving the lowest error during the testing period, it is also essential to obtain the hyperparameter set that gives a lower error than the pure mortality model over the training period.

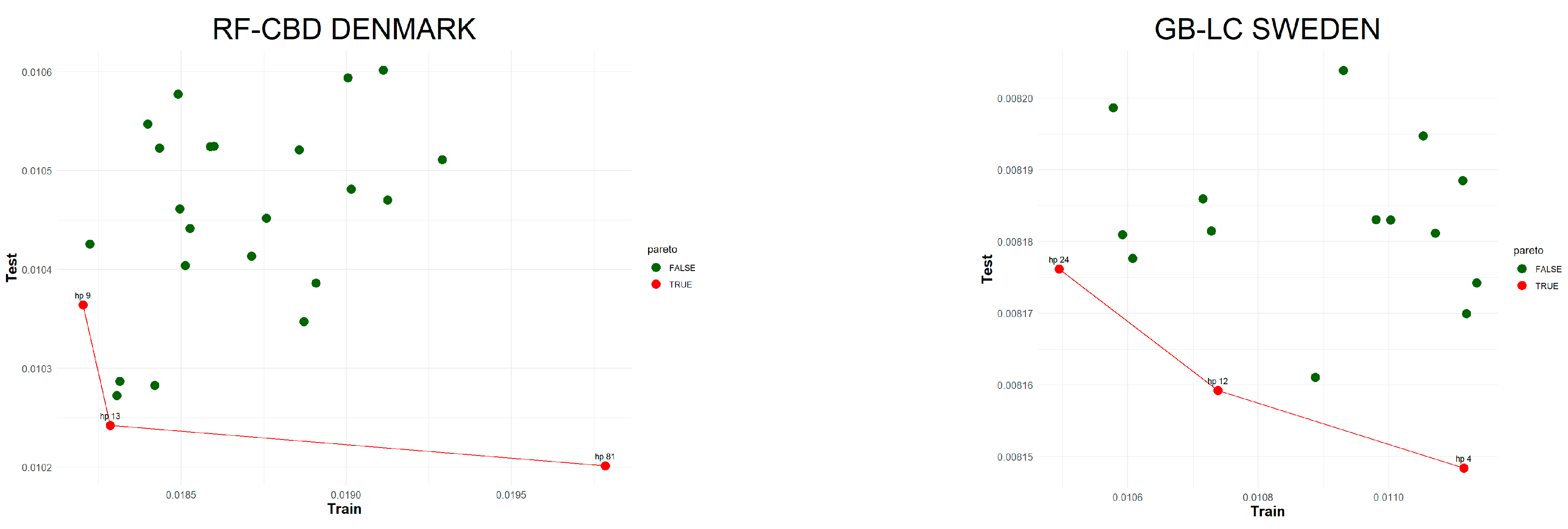
As can be seen from the table, including all ML-integrated methods, using the same hyperparameter set that works best for testing period may produce a higher error for the training period while a different hyperparameter set gives a lower error over the training period. At the same time, the error should not be higher than the pure mortality model’s error. Although the users notice this trade-off mechanism, choosing the best combination can still be confusing. Hence, we use the Pareto [53] optimal method to find the dominant combination of the hyperparameter set. In many instances, it is said there are conflicting objective functions and that there exist Pareto optimal solutions. A susceptible solution is said to be nondominated if none of the objective functions can take on a new value to improve its value without deteriorating some of the other objective functions. These solutions are referred to as Pareto optimal. When no other preference information is supplied, all Pareto optimal solutions are said to be equally good [54]. In this regard, efficient frontier is constructed which shows the Pareto optimal values and connects them together.

Figure 4 visualizes the Pareto optimal values of the hyperparameter set that gives a lower error over both the training and testing periods. The efficient frontier concept guides users in choosing the best balance of testing and training errors.

Machine learning techniques can be considered as “black box” models for most of the researchers especially when the purpose is to increase the predictive performance of the models. However, interpretability can reveal great insights when the outcome is mortality [55]. Indeed, while machine learning algorithms have been found to be highly accurate in mortality prediction, the issue of interpretability, which is intrinsic with such models, has been recognized as an issue. In this study, in an effort to address the issue of interpretability of ML models, variable (feature) importance is explored to extract knowledge about the relationships identified by tree-based models.

Figure 5 presents the significance of variables used in the ML-integrated models (hyperparameter sets 13 and 24 are used, respectively). Feature importance analysis in this study is based on relative influence, which means it measures how much each feature contributes to reducing the model’s prediction error. Higher scores mean that feature is more critical and important for the model. As seen from Figure 5, the year and birth cohort features are the most influential variables when making accurate forecasts over the testing period. In the context of this specific model and dataset, old-age mortality (65–99) is modeled for Denmark. We can interpret that this model tends to capture the long-term effects and unique historical events of mortality that explain why year and cohort are the most important features. On the other hand, when a wider age range including child, adult, and old-age mortality is used for Sweden, the birth cohort feature appears to be the most important feature.

7. Discussion

This study presents a general procedure for improving the forecasting accuracy of mortality models using the most common tree-based machine learning methods, by creating a flexible environment on the training/testing data which is critical for measuring the goodness of fit/forecasting. This will enable researchers to choose the most suitable mortality model for population-specific mortality data and perform the best practices of forecasts for future mortality.

On the other hand, the main challenge of practicing the procedure is the workload of the computer due to the size of the mortality data and the combination of hyperparameters included in the tree-based ML methods. The main working principle of the procedure is to find the sets of hyperparameters that estimate mortality rates while producing less error than the pure mortality model over the testing period by repeatedly testing each psi series on the training data and finding the psi series that estimates mortality rates while producing less error over the training period. Therefore, increasing the number of hyperparameters may cause this mechanism to run for a long time. However, this challenge can be overcome using today’s powerful computers.

In this study, the hold-out testing period plays a significant role. Changing this period will naturally cause the results to change. However, the objective in this paper is enabling the users to select the periods according to the purpose of their own work by easily integrating tree-based ML methods so that they can make better forecasts as a result.

Previous studies mostly aimed to find improved mortality rates based on a specific mortality model or age range and train/test periods. We generalize the improving idea by using common tree-based methods and mortality models. Here, the main constraint is that the user must understand the mortality pattern of the data and should not select an incoherent training/testing period. For example, selecting only a 2-year testing period against a 100-year training period may lead to inaccurate results. The mortality forecasting literature can be examined and appropriate methods for selecting the testing period can be determined.

8. Conclusions

Mortality forecasting does not have a long history in the demographic or actuarial literature. Starting with Lee and Carter [7], mortality forecasting has been gaining momentum, with comprehensive studies being conducted frequently. In recent years, researchers have focused their attention on integrating advanced statistical methods into their studies related to the length of human life. These studies show that when this growing interest is combined with demographic models, more robust and consistent results emerge.

Data for each population has its own unique characteristics. Mortality models aim to explain the mortality pattern and make accurate forecasts based on the historical data. In this context, ML can help to understand the non-linear nature of the mortality rates, which generally tend to decline at almost every age each year. The declining pattern of mortality rates that results in increasing life expectancy poses a significant risk to the sustainability of social security, elderly care, and pension systems, which implies that we need more precise and robust forecasts of mortality.

This study concentrates on facilitating the integration of mortality models into ML methods within a general framework and demonstrating that forecasting accuracy can be improved under specified conditions, rather than taking advantage of analyzing specific periods that increase forecasting accuracy. This study guides researchers in the right direction by offering a flexible structure while choosing the test data, which is one of the most important factors in measuring the quality of the model when using mortality models. We believe researchers will be enabled to make more accurate forecasts for the future.

Our hybrid model can be interpreted as restoring a kind of symmetry between structure and flexibility. While GAPC models add interpretability through parametric descriptions, tree-based methods provide adaptive handling of anomalies in the data. The process introduced produces an interplay of equal balance; mortality models bring theoretical structure and ML brings data-driven refinement, both yielding improved forecasts.

Mortality forecasting at the population level does not include many features in nature. ML techniques can deal with big data and reveal deeper connections within the data. Predicting mortality at the individual level is challenging, since determining the effects of the length of human life is complex. With the help of technology in collecting data at the individual level, future research can be concerned with forecasting mortality at the individual level by using machine learning techniques.