Abstract
As an asymmetric encryption method capable of performing one-to-many encryption, the ciphertext-policy attribute-based encryption (CP-ABE) is widely recognized as an ideal cryptographic tool for cloud-based applications. It can empower data owners to independently and flexibly define and enforce access control policies for cloud-stored data. However, the practical implementation of CP-ABE-based cryptographic access control remains hindered by critical challenges. Firstly, malicious users may engage in key abuse by delegating attribute keys to unauthorized parties or exploiting their keys to construct decryption black-boxes for providing illegal decryption services. Consequently, a secure CP-ABE scheme must incorporate the capability to trace such malicious users who misuse their privileges. Secondly, for resource-constrained IoT devices, the substantial computational overhead of CP-ABE becomes prohibitive, making its deployment in scenarios like IoT-cloud services particularly challenging. In this paper, we propose a new CP-ABE scheme with black-box traceability and computational outsourcing capabilities. Our scheme can improve the tracing efficiency from or (as seen in traditional schemes) to , where N is the number of system users. Furthermore, the proposed scheme features compulsory traceability and maintains outstanding performance in the aspects of encryption, decryption, and tracing operations.
1. Introduction
In recent years, with the continuous integrated development of the Internet of Things (IoT) and cloud computing, research on related security issues has also been constantly updated and iterated. Among these studies, there is emerging research on encryption and decryption algorithms that utilize complex dynamic mechanisms to achieve efficient and secure protection of data in IoT environments—such as the three-dimensional memristive hyperchaotic mapping applicable to image encryption [1,2] and the parallel color image encryption algorithm based on neural mapping [3]. There are also ABE (Attribute-Based Encryption) algorithms used to control data access permissions within systems; these algorithms can play a role in various aspects and solve various security issues emerging in new application scenarios. Due to conflicts of interest or other reasons, a Cloud Service Provider (CSP) sometimes cannot be fully trusted by its customers. Kamara et al. [4] proposed applying cryptographic access control in cloud data management to deal with the problem. The main idea lies in encrypting sensitive data before uploading it to the cloud. By controlling the distribution of keys, the access control policies defined by the data owner can be implemented, so that, under the condition that the CSP is semi-trusted, user-autonomous access control can be realized. A semi-trusted CSP refers to a CSP that will honestly execute all operations but may snoop on users’ data. Kamara proposed leveraging one-to-many encryption mechanisms like Attribute-Based Encryption (ABE) to achieve fine-grained access control, thereby reducing key distribution costs to a manageable level. Among such mechanisms, ABE—with CP-ABE (Ciphertext-Policy Attribute-Based Encryption) in particular—is regarded as an ideal cryptographic tool for data sharing. In a CP-ABE system, each user is associated with a set of attributes. During encryption, an access control policy—defined based on these attributes—is embedded within the ciphertext. Only users whose attributes meet this access control policy can successfully decrypt the ciphertext to retrieve the plaintext. As a result, data owners need not concern themselves with users’ specific identities; instead, they only need to specify the type of individuals authorized to access the data. Thanks to these advantages, since Bethencourt introduced the first CP-ABE scheme [5], the development of CP-ABE schemes has remained a central focus in research on cryptographic access control.
White-box traceability and black-box traceability. However, there are still some obstacles in the practical application of CP-ABE. One of the major issues is privilege abuse, that is, malicious users may abuse their keys and access privileges, leak them to unauthorized users in the form of new keys, or construct a Decryption Black-box (DB) to provide illegal decryption service for profits while hiding their private keys. In traditional CP-ABE schemes, it is almost impossible to track or obtain evidence for these violations. To tackle the issue of privilege misuse, Li et al. [6] pioneered an accountable CP-ABE scheme. In this approach, user-specific information is embedded into the private key during the key generation phase, enabling the identification of malicious users who engage in unauthorized key sharing through analysis of the key itself. However, the challenge of tracing the builder of a database (DB) persisted until Liu et al. [7] introduced the first CP-ABE scheme with black-box traceability. In their work [7], Liu and colleagues defined the concept of traceability explicitly and categorized it into two types: white-box traceability and black-box traceability. Notably, the scheme presented in [6] falls under the category of white-box traceability. However, it is generally believed that only black-box traceable schemes can achieve complete traceability because black-box traceability implies white-box traceability. Although the scheme in [7] achieves black-box traceability, it can only track the key-like black-box and is unable to track the policy-specific black-box. Subsequently, Liu put forward a scheme [8] that can track policy-specific black-box. Nevertheless, both of these schemes exhibit inefficiencies in encryption and decryption. Moreover, the length of the ciphertext is correlated with the number of users. Therefore, Ning et al. [9] proposed a scheme with a fixed ciphertext length to prevent the ciphertext length from expanding with the number of users. Liu proposed a scheme based on prime-order bilinear groups, which greatly reduces the computational cost and makes the application of the black-box tracing algorithm practical.
These schemes, together with subsequent black-box traceable schemes, employ the same tracing algorithm framework. Within this framework, encryption operations must be executed times during a single tracing process, where N denotes the number of users in the system. Encryption itself carries relatively high computational costs, as it requires frequent bilinear pairing operations and exponentiation operations. To address this, Qiao et al. [10] proposed marker tracing to develop an efficient and lightweight tracing algorithm. In their work [10], the number of encryption operations is reduced to or even , and this approach has also been adopted in subsequent studies such as [11,12,13,14] for tracing purposes.
Computation outsourcing capability. Another obstacle faced by CP-ABE in practical applications is the computational overhead of conventional encryption and decryption. This issue is particularly prominent in emerging scenarios such as IoT, smart healthcare, and edge computing, and has also become a core motivation for driving relevant research. From the perspective of these application scenarios, a large number of terminal devices (e.g., sensors and smart wearable devices) are limited by hardware costs and power consumption design, and they generally feature weak computing capabilities and limited storage resources. For instance, the processor frequency of a temperature monitoring sensor is usually lower than 1 GHz, and its memory is only a few MB. However, as a relatively complex asymmetric cryptographic algorithm, CP-ABE involves multiple rounds of bilinear pairing operations and attribute set matching in its encryption and decryption processes. A single device may take hundreds of milliseconds or even seconds to complete the decryption of a single ciphertext, which makes it difficult to meet the requirements of real-time data collection (e.g., industrial equipment status monitoring) and low-latency control (e.g., smart home command response). Green et al. [15] put forward a new approach for secure decryption outsourcing. By adding a blinding factor to generate the transform key for the proxy, the proxy server can perform the majority of decryption computation; meanwhile, it cannot pry into the content of the ciphertext. The user only needs to perform a simple ElGamal-type decryption at last to obtain the plaintext. Most of the later research [16,17,18,19] also adopted similar methods in [15] to transform the major workloads to the proxy server.
To achieve computational outsourcing and black-box traceability simultaneously, Yu et al. [20] proposed an accountable CP-ABE scheme with the ability of computational outsourcing, it is white-box traceable as well as the scheme in [21,22]. As far as we know, only a very few CP-ABE schemes [14,23] can achieve both black-box traceability and computational outsourcing at the same time. Zhang et al. [23] first put forward the scheme that meets the two requirements. They add operations of a subset cover algorithm [24] into encryption and decryption to meet the requirements of revocation and traceability. However, in a subset cover algorithm, encryption operations must be performed for each user subset in every data encryption. In the worst case, the number of user subsets can reach , so that the corresponding ciphertext also contains ciphertext blocks, where N is the number of users. Therefore, it incurs additional costly overhead for the system. Moreover, similarly to the scheme of [7], their tracing algorithm also needs to issue a series of inquiries to gradually locate a certain subset, and then divide this subset to find the traitor within it. The tracing process is rather inefficient. Yin et al. [14] adopt the method of [10] to trace the black-box efficiently. However, in their system, the tracing algorithm can achieve successful tracking only if it obtains both the final decryption result output by the black-box and an intermediate result, which is the partially decrypted ciphertext, output by the Cloud Auxiliary Server. Thus, if the black-box completes all the decryption on its own and only outputs the final decryption result, the system will be unable to track the black-box.
Our contribution. To apply the CP-ABE system securely in scenarios with limited computation resources, such as IoT cloud, it is necessary to realize a practical black-box traceable CP-ABE scheme with outsourcing of computation (OC-BTCP-ABE). So far, in the few existing OC-BTCP-ABE schemes, issues such as low encryption and decryption computational efficiency, poor scalability, or limitations in the tracing algorithm can be observed. This makes it difficult to implement these schemes in reality, especially for those IoT systems with a large number of users. To obtain a secure and efficient scheme, we have proposed a new OC-BTCP-ABE scheme with the following characteristics.
- High practicality: Our scheme is constructed based on prime-order groups rather than composite prime-order groups, and a concise architecture similar to that of [11] is adopted, which makes the scheme highly efficient in computational operations such as encryption and decryption. Moreover, the scheme overcomes the problem that the tracing efficiency drops rapidly with the increase in the number of system users. In our proposed scheme, the computational load of the tracing algorithm is , and its complexity can be further optimized to in efficient tracing mode. Compared with the existing OC-BTCP-ABE schemes, our solution has significant advantages in encryption and tracing efficiency.
- Compulsory traceability: Our scheme possesses the compulsory traceability proposed in [10], which makes it impossible for the adversary to identify the tracing ciphertext, thus unable to counter the tracing. This ensures that the effectiveness of the tracing results cannot be compromised.
2. Background
In this section, we begin by providing background details on Linear Secret Sharing Schemes (LSSSs). Next, we outline the security definitions specific to OC-BTCP-ABE. Lastly, we formulate the formal descriptions of the decisional q-parallel Bilinear Diffie-Hellman Exponent (BDHE) assumption and bilinear groups.
2.1. Access Structure
An access structure refers to a collection composed of sets of attributes. And is a monotone collection, that is, and then . The sets in are authorized sets, and the sets not belonging to are unauthorized sets. The formal definition of access structure is given in [25]. It should be noted that this monotone access structure can also implement a general access structure. In this case, it becomes necessary to create a “not” counterpart for each attribute, which in turn doubles the total number of attributes within the system.
2.2. Linear Secret Sharing Scheme (LSSS)
A LSSS, which is proposed in [25], is applied to implement the access structure of ciphertexts in our scheme.
Definition 1.
(Linear Secret-Sharing Scheme (LSSS)) A secret-sharing scheme Π over a set of parties is called linear (over ) if the following hold:
- 1.
- The shares for each party form a vector over .
- 2.
- There exists a matrix an M with ℓ rows and n columns called the share-generating matrix for Π. For all the function ρ maps the each row of M to an associated attribute . For a vector , where is the secret to be shared, and are randomly chosen, is the vector of ℓ shares of the secret s according to Π. The share belongs to attribute .
It is shown in [25] that a share-generating matrix M can enjoy the linear reconstruction property. Suppose that there is a corresponding share-generating matrix M for an access structure . For an attribute set S, let . For every set , the “target” vector must lie within the span of the rows indexed by . Specifically, for any , there exist constants , that can be computed in polynomial time, such that for any set of shares corresponding to a secret s, the equation holds. Conversely, for any unauthorized set , the target vector does not lie within the span of the rows indexed by .
2.3. Bilinear Map
Assuming denotes a bilinear group generator and taking a security parameter , produces as the output, and are two multiplicative cyclic groups of prime order p, where p is a big prime, and g is a generator of . e denotes a bilinear map , and it has the following properties:
Let represent a bilinear group generator. Given a security parameter , outputs . Here, and are both multiplicative cyclic groups of prime order p, and g serves as a generator of . The symbol e denotes a bilinear map , which possesses the following properties:
- Computability: For any elements , is efficiently computable.
- Non-degeneracy: .
- Bilinearity: For any elements and exponents , the property holds.
The security of our proposed scheme relies on the decisional q-parallel BDHE assumption [26]. Due to space constraints, the formal definition of this assumption is not included herein.
2.4. OC-BTCP-ABE
An OC-BTCP-ABE construction functionality includes five algorithms: Setup, Encrypt, KeyGen, Transform and Decrypt.
- Setup. This algorithm accepts security parameter and the attribute universe U as inputs, and outputs the public parameter and the master secret key .
- KeyGen. The KeyGen algorithm takes the master key as input and generates a transformation key and a private key according to the user’s attribute set S.
- Encrypt. This algorithm encrypts a message M using under a specified access structure . It generates a ciphertext that is decryptable only by users whose attribute sets satisfy the policy of .
- Transform. The Transform algorithm takes as input the ciphertext CT that was encrypted under , the public key and the transformation key according to the attribute set S. It outputs the partially decrypted ciphertext if S satisfies , or it outputs ⊥.
- Decrypt. The Decrypt algorithm decrypts the ciphertext under the user’s secret key and outputs the message M.
2.5. Security Model for OC-BTCP-ABE
Due to differences in structure from ordinary CP-ABE schemes, with the addition of public transformation keys and the requirement of going through two steps (transformation and decryption) during the decryption process, the security model for the OC-BTCP-ABE scheme also differs from that for ordinary CP-ABE schemes. This is typically characterized by a security game played between a challenger and the adversary .
Setup. The challenger performs Setup algorithm and sends the public parameter to .
Phase 1. The challenger creates an empty table T, an empty set and an index . The adversary can adaptively make any of the following queries:
- : The challenger sets , and performs KeyGen algorithms on the attribute set S. It outputs the pair and stores in table T. Then, it returns to .
- : If the j-th entry exists in table T, the challenger gets the entry , updates as , and then returns the private key to . In the absence of such an entry, it returns ⊥ instead.
Challenge. chooses two messages of equal length and gives them to the challenger. In addition, gives an access structure such that none of the attribute sets S of satisfy . The challenger flips a random coin to select . Subsequently, the challenger encrypts the message under the target access structure and provides the resulting ciphertext to the adversary .
Phase 2. Phase 1 is repeated with the restriction that cannot issue a Corrupt query that would result in an attribute sets S which satisfies .
Guess. Ultimately, the adversary outputs a guess . The adversary is deemed to win the game if . Within this game, the advantage of is defined as .
Definition 2.
An OC-BTCP-ABE scheme is CPA secure (secure against chosen-plaintext attacks), if for any polynomial time adversary , the advantage is always negligible in the above game.
Note that a scheme is selectively secure if an Init stage is added before Setup where submits structure in advance. We will prove our construction secure under the selective security model.
2.6. Traceability for CP-ABE
The black-box traceability of CP-ABE refers to the ability to uniquely identify the user who created the black-box by analyzing the black-box’s output results, without being able to view the internal key of the black-box, and it should not incorrectly output a user who is not the creator. In contrast to the decryption black-boxes characterized as probabilistic devices in [7], we adopt a streamlined concept of the decryption black-box, as first proposed in [10]: A decryption black-box linked to an attribute set is capable of decrypting a ciphertext and outputting the correct plaintext M if satisfies the access structure of CT; otherwise, it returns ⊥. This formulation also simplifies the handling of collusion issues. Notably, when two malicious users collude to build a joint decryption black-box, ref. [10] shows that the decryption capability of this collusive device is no stronger than the sum of the individual decryption capabilities of the two separate black-boxes each user would construct independently. Therefore, we mainly consider the black-box independently constructed by a single malicious user.
When tracing, the tracing algorithm always needs to interact with the black-box. Similarly to all existing BT-CP-ABE schemes, in our work, the tracing algorithm functions by sending specific ciphertexts to the black-box and endeavoring to identify the black-box’s creator using the information it returns. To facilitate this, we propose an additional encryption algorithm designed to generate such special ciphertexts, whose decryption results can be leveraged to pinpoint the black-box’s creator. This algorithm is defined as follows:
- Encrypt. This algorithm takes as input the message M, the access structure and the public key . It outputs the tracing ciphertext that can be decrypted under the keys whose corresponding attributes satisfy . When the decryption result is returned, the will be used to search for the private key used in decryption.
2.7. Security Model of Compulsory Traceability
To trace a black-box, it is necessary to analyze the correct decryption results of tracing ciphertexts. However, if the black-box is capable of distinguishing between normal ciphertexts and tracing ciphertexts, it might intentionally output incorrect decryption results for the latter in an attempt to evade tracing while maintaining the ability to correctly decrypt normal ciphertexts. Therefore, it must be ensured that no adversary can distinguish between tracing ciphertexts and normal ciphertexts. When this condition is met, we term it as Compulsory Traceability. The original definition is presented in [10] using a security game between a challenger and an adversary. The main design intuition of this game is that a user, even if his attribute sets satisfy the access policy of the ciphertext, still cannot distinguish whether the ciphertext is a tracing ciphertext or a normal one. Due to the differences from the ordinary CP-ABE structure, we present the security model description of Compulsory Traceability for the OC-BTCP-ABE scheme as follows:
Setup. The challenger executes the Setup algorithm and transmits the public parameter to the adversary .
Phase 1. The challenger initializes an empty set , an empty table T, and sets an index . The adversary is then allowed to adaptively issue any of the following types of queries:
- : The challenger sets , and performs KeyGen algorithms on the attribute set S. It outputs the pair and stores in table T. Then, it returns to .
- : If the j-th entry exists in table T, the challenger gets the entry , updates as , and then returns the private key to . In the absence of such an entry, it returns ⊥ instead.
Challenge. The adversary submits a target access structure to the challenger. The challenger first selects a message uniformly at random and flips a random coin to determine . For , the challenger executes the standard encryption algorithm: , and outputs . For , it runs the tracing encryption algorithm instead: , and outputs . Finally, the challenger sends to .
Phase 2. Phase 1 is repeated.
Guess. outputs a guess of b.
Note that can be satisfied by at least one of the attribute sets in .
If , the adversary wins the game. The advantage of is defined as .
Definition 3.
An OC-BTCP-ABE scheme is compulsorily traceable, if for any polynomial time adversary , the advantage is always negligible in the above game.
3. Our Construction
Our scheme is constructed by modifying the scheme of [11]. Note that U denotes the attribute universe of the system. To prevent collusion among users, we adopt the similar method of [26], assigning each user’s key a random exponent r, which is embedded in the main component D of the key and in the components corresponding to each attribute. This binds together all components of a user’s key, making them incompatible with the key components of other users. During decryption, each share must be computed using the same consistent exponent r to recover the shared secret and thus the plaintext, meaning components from different keys cannot be combined or used together.
3.1. Concrete Construction
- Setup. The algorithm takes the security parameter as input and outputs . It then randomly selects . Furthermore, for each attribute , it randomly chooses . The public key is published as follows:The authority retains the master key in secrecy and initializes an empty table .
- KeyGen. Using the master key , the algorithm generates a private key corresponding to the attribute set S. It randomly selects exponents and obtains the transformation keyIt then sets the private key and the key index . The authority records in table .
- Encrypt. The algorithm takes as input the public key and encrypts the message with an access control structure . Here, M is an LSSS matrix corresponding to the size of the ciphertext access policy, and each row of the matrix can be mapped to an attribute . The algorithm selects a random vector . Then, it randomly selects values for each row of M and performs calculations . It computes and outputs the ciphertext as follows:is published along with . The notation herein represents the set .
- Transform. Using a transformation key and the public key , the algorithm partially decrypts the ciphertext that contains the access structure . If S, where S is the attribute set associated with , does not satisfy the access structure, it outputs ⊥. Suppose a certain subset satisfiesthe access policy of , the algorithm can obtain the set of constants for which . It then proceeds to compute the following:It then outputs the partially decrypted ciphertext .
- Decrypt. The algorithm takes as input the private key . It computes to finish the decryption. Noted that must be the intermediate result generated by decrypting with contained in ; otherwise, the decryption result will be incorrect.
3.2. Tracing the Black-Box
In the process of black-box tracing, one must first send a tracing ciphertext to the black-box and then analyze the output of it to pinpoint the key employed in the decryption process, thereby exposing the identity of the black-box’s creator. In our scheme, the tracing algorithm is described as follows:
- Encrypt. This algorithm encrypts the message with the public key and an access control structure . The steps performed here are basically the same as those of the Encrypt algorithm. The main difference is that it selects two random numbers and uses to construct the vector . Thus, instead of s is distributed in the constants for . The algorithm outputs the tracing ciphertext as follows:It outputs and .
To trace a black-box , the authority selects an access control structure that is satisfiable by the attributes set of , as well as a message randomly selected from the message space . It then runs the algorithm , sends the to , and saves the at the same time. If performs the decryption correctly, it firstly runs Transform and obtains the following:
Then, runs Decrypt as and outputs . When the authority receives the return , it computes . For each entry in , it computes and compares it with E until a match is found. The reveals which private key was used in the construction of the black-box. If the user ID corresponding to is also recorded during the key generation process, the authority can directly use it to expose the identity of the black-box ’s builder.
Efficient tracing. If the parameter is fixed to instead of a randomly selected value, that is, the is set to 1. Therefore, when searching , E can be directly compared with . In this way, the step of performing exponentiation on can be omitted, thereby achieving efficient search and tracking.
4. Performance Analysis
4.1. Theoretical Performance
In general, the overall performance of a CP-ABE scheme can be measured by the cost of encryption and decryption, the length of keys and ciphertexts, and the security model. Thus, we present a brief feature comparison with the only two OC-BTCP-ABE schemes known to us in Table 1.

Table 1.
Theoretical performance analysis and comparison.
In Table 1, N stands for the total number of users in the system, l refers to the number of rows in the LSSS matrix M, is the number of attributes owned by users, and denotes the number of attributes involved in decryption, m is the number of subsets applied in the Subset Cover Method that is adopted in [23]. , , , respectively represent the computational costs required for a pairing operation, an exponentiation operation, a hash operation and a symmetric encryption/decryption operation. , , refer to the size of elements in , , respectively.
Computational outsourcing capability. Similarly to the Green scheme, our scheme primarily focuses on how to securely outsource decryption computations. In our scheme, the Transform operation— which performs a major part of the decryption— can be delegated to a proxy server; this process outputs the transformed ciphertext , and the user only needs to complete the final Decrypt operation on their own to recover the plaintext from . In our scheme, the cost of the transform operation is , while the cost of the decrypting operation is . Tests show that the computational cost of is generally about 10 times that of . Therefore, in our scheme, most of the overhead in decryption computation can be outsourced. For example, if the decryption computation involves 20 attributes (i.e., ), the outsourceable Transform operations account for approximately 94% of the total cost of decryption computation, while users only need to bear about 6% of the computational cost.
Efficiency. By comparison, it can be found that in terms of encryption performance, our scheme is superior to the two existing schemes, but its decryption performance is lower than these two schemes. This is because in the encryption phase, the scheme in [23] actually performs a re-encryption, while the scheme in [14] requires users to interact with the Cloud Encryption Server (CES) using a method similar to the blind signature to complete the relatively complex calculations. The lower decryption efficiency of our scheme is due to that in order to meet the compulsory traceability requirements, the secret parameters must be hidden more deeply. However, the decryption efficiency of this work is the same as that of [11], so its computational efficiency is still sufficient to meet the practical application. Additionally, it is worth noting that both our scheme and the scheme of [14] need to store a list , which is used to compare and search for keys during tracing. This list needs to store each user’s (the mainly contains an element from group ). In our tests, the length is 48 bytes, so the storage overhead during tracing is approximately bytes, where N is the number of users in the system.
Traceability. In our scheme, the tracing algorithm only needs to be executed once, and the computational cost is equivalent to that of an ordinary encryption algorithm Encrypt. Although one has to search through the by running one exponentiation operation for each entry in to find out the key of the malicious user, an exponentiation operation is much lighter than an Encrypt operation, and the number of such operations is at most . Moreover, if efficient tracing is adopted, the exponentiation operations in the searching of can also be omitted, and in this case, the computational cost is , that is almost equivalent to that of a single encryption operation. Compared with our scheme, the two existing schemes have the following defects, respectively.
- Inefficiency of the scheme in [23]. The scheme of [23] is similar to the classic black-box tracing scheme, a series of tracing ciphertexts needs to be sent to gradually find out the secret key of the malicious user. It requires running rounds of tracing algorithms to identify a malicious user. In each round of the tracing algorithm, at most encryptions (or an average of encryptions) need to be executed. Therefore, the total number of encryptions in a tracing process is , while the cost of each encryption is . Since r denotes the number of revoked users in the system, this indicates that when the number of revoked users increases, a rather high computational overhead will be incurred in the tracing process.
- Tracing failure of the scheme in [14]. For the scheme of [14], if the black-box performs the Transform and Decryption on its own instead of relying on the Cloud Auxiliary Server (CAS) to perform the Transform operation, the black-box will only output the final result, and in this case, the tracing will fail.
Finally, compared with the previous two schemes, our scheme further possesses the feature of compulsory traceability.
Security. The security of both existing OC-BTCP-ABE schemes and our scheme is based on the decisional q-parallel BDHE assumption. However, these two schemes are constructed under the random oracle model, whereas our scheme is constructed under the standard model.
4.2. Performance Measurements
For the CP-ABE system, encryption and decryption are the two most frequently executed operations; thus, the computational performance of the system mainly depends on the efficiency of these two operations. We implemented the scheme of [14,23], and our proposed scheme for testing, compared the test results, and presented the specific details in Figure 1.
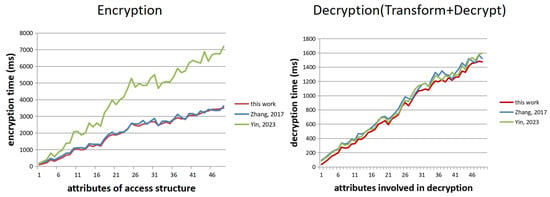
Figure 1.
Performance of encryption and decryption. Zhang states that the scheme is from [23], and Yin states that the scheme is from [14].
All experiments were conducted on a PC equipped with a Core i5-12400 processor and 8 GB RAM. We utilize an elliptic curve group of Type A defined by the equation , where the element representations are 512 bits in length and the group has an order of 160 bits. The scheme is implemented based on the Java Pairing Based Cryptography (JPBC version 2.0.0) library [27].
In the experiment, we set the access control structure in the form , where is an attribute, in order to maintain the consistency of the decryption process and prevent potential differences that may arise when decrypting with different decryption keys. We tested all cases where the number of attributes s ranged from 1 to 50. For each test point, we experimented 100 times and then took the average value.
The experimental results are consistent with the performance expectations from theoretical analysis, and the computational costs of encryption and decryption are proportional to the number of attributes involved in the operations. It should be noted that although more pairing operations are performed in the decryption process of our scheme, the efficiency of decryption operations in our scheme does not show a significant decrease compared with existing schemes. It is because the efficiency of pairing operations is far higher than that of exponentiation operations. Our experimental tests show that the average time for one exponentiation operation in is approximately 12 ms, while the time for one pairing operation is about 1 ms.
As can be seen from Figure 2, the time required for tracing in our scheme is basically independent of the scale of system users. This is because only one tracing ciphertext needs to be generated for each tracing process in our scheme. The scheme of [14] is similar to our scheme. However, the number of tracing ciphertexts generated by the scheme of [23] is , where N represents the number of users in the system and r represents the number of revoked users in the system (r was set to 50 in the test). Therefore, the tracing cost of [23] is much higher than that of our scheme, and it will increase rapidly as the number of users and revoked users increases.
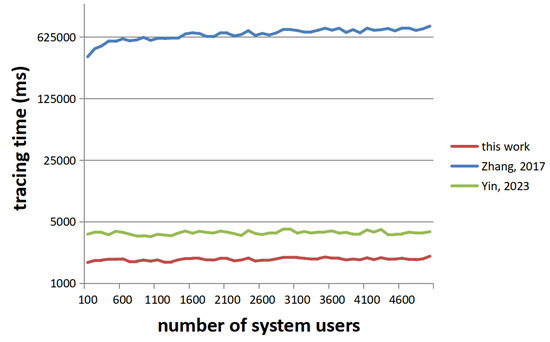
Figure 2.
Performance of tracing. Zhang states that the scheme is from [23], and Yin states that the scheme is from [14].
5. Security Proof
Theorem 1.
Suppose the construction of [11] is a selectively CPA secure scheme. Then our scheme presented above is selectively CPA secure.
Proof of Theorem 1
Suppose there is a polynomial-time adversary that can win with non-negligible advantage in the selective security game against our scheme. Then we show how to build a simulator that can win in the selective security game against the scheme of [11] with the advantage . Since the scheme of [11] is selectively CPA-secure under the decisional q-parallel BDHE assumption, thus, a contradiction arises, and therefore the theorem is proven. The simulator operates as follows.
Init. The simulator invokes the adversary . gives the challenge access structure , where is an LSSS matrix. then sends to the challenger of [11] as the access control structure it intends to challenge.
Setup. The simulator queries the challenger of [11] and obtains the public key It then sends to .
Phase 1. The simulator creates an empty table T, an empty set and an index . It responds to the adversary’s request as follows:
- : sets , and it continues to operate in one of the following two ways according to the situation.
- -
- If S satisfies the access policy contained in , the simulator forms the transformation key as follows. randomly chooses and implicitly sets by generatingIt then sets . Note that is not a well-formed private key, but in the view of adversary , is properly distributed at random.
- -
- Otherwise, calls the key generation oracle of [11] to getIt then randomly chooses and computesthen sets .
The simulator stores in table T and returns to the adversary . - : If there exists an jth entry in table T, the simulator obtains the entry and sets . It then returns the private key to . If no such entry exists, then it returns ⊥. Note that in the selective security game cannot query for any key that satisfies the challenge structure .
Challenge. The adversary chooses two messages of equal length and gives them to . passes them to the challenger of [11] and obtains the returned ciphertext . It then gives to .
Phase 2. Phase 1 is repeated.
Guess. finally outputs a guess of b. Then, the simulator also outputs as its guess. The simulator provides a perfect simulation. If guesses correctly and wins the game, will also win in the security game challenging scheme of [11]. Therefore, wins the selective security game against the scheme of [11] with the non-negligible advantage . So we complete the proof. □
Theorem 2.
Suppose the scheme of [11] is compulsorily traceable. Then our scheme presented above is compulsorily traceable.
Proof of Theorem 2
Suppose there exists a polynomial-time adversary that can play the compulsory traceability security game against our scheme with a non-negligible advantage . Then we show how to build a simulator that can win in the compulsory traceability security game against the scheme proposed in [11] with the same advantage. In [11], the advantage of any adversary is proved to be , where n denotes the total number of group elements that the adversary can obtain from its queries, and p is the group order. This indicates that if the group order p is sufficiently large, the adversary’s advantage is negligible, and in this case, our scheme is compulsorily traceable. The simulator operates as follows.
Setup. The simulator queries the challenger of [11] and obtains the public key It then sends to .
Phase 1. The simulator creates an empty table T, an empty set and an index . It responds to the adversary’s request as follows:
- : sets , and it continues to operate in one of the following two ways according to the situation. calls the key generation oracle of [11] to getIt then randomly chooses and computesthen sets . The simulator stores in table T and returns to the adversary .
- : If there exists an jth entry in table T, the simulator obtains the entry and sets . It then returns the private key to . If no such entry exists, then it returns ⊥.
Challenge. submits an access control structure to . passes to the challenger of [11] and obtains the ciphertext output by this challenger. then sends to .
Phase 2. Phase 1 is repeated.
Guess. outputs a guess of b. also outputs as its guess. The simulator provides a perfect simulation. If guesses correctly and wins the game, will also win. Thus, the advantage of the simulator in its security game against the scheme in [11] is equal to that of the adversary in the game against our scheme. So we complete the proof.
Note that in the same manner, we can prove that when is set to , the adversary is also unable to distinguish whether the ciphertext is a tracing ciphertext or an ordinary ciphertext. Therefore, in the case of efficient tracing, the property of compulsory traceability also holds. □
6. Conclusions
Although CP-ABE is widely recognized as an optimal access control mechanism enabling user-centric autonomy in cloud data services, its practical deployment still necessitates addressing critical challenges related to security and efficiency. From a security perspective, preventing key abuse by users—particularly tracing malicious users who exploit their keys to establish a decryption black-box for providing illegal decryption services for profit—remains a focal point of relevant research. In terms of efficiency, due to the substantial computational overhead inherent in CP-ABE schemes, developing secure computation outsourcing solutions for resource-constrained devices (e.g., IoT devices) has also garnered significant attention. To the best of our knowledge, only a handful of existing CP-ABE schemes [14,23] currently achieve the simultaneous implementation of black-box traceability and computation outsourcing capabilities. However, among these schemes, there are still issues of low computational efficiency or potential failure of tracing. Therefore, we propose a new OC-BTCP-ABE scheme. This scheme not only achieves black-box traceability and secure outsourcing of decryption computations but also features high computational efficiency, with a significant improvement, particularly in the efficiency of the tracing algorithm. Additionally, we prove that the scheme possesses the property of compulsory traceability, which ensures that the tracing algorithm can always function effectively. Our scheme will be particularly suitable for access control applications in scenarios such as the IoT cloud and similar environments.
However, there are still aspects that need improvement for our scheme. For instance, the proposed scheme lacks support for efficient attribute revocation, and this practical barrier needs to be addressed in future research. Similarly, in terms of security, future studies should further consider and handle the following issues: how to defend against key compromise impersonation attacks when the authority issues attribute keys to users; how to realize policy-hiding; and how to assess the threats of quantum computing to the underlying primitives of the scheme.
Author Contributions
Conceptualization, Y.H. and H.Q.; methodology, Y.H.; software, H.Q.; validation, J.L. and P.H.; investigation, J.L. and P.H.; writing—original draft preparation, Y.H.; writing—review and editing, Y.H., H.Q., Z.W., and J.R.; supervision, Z.W. and J.R. All authors have read and agreed to the published version of the manuscript.
Funding
The research is funded in part by the National Natural Science Foundation of China, under grant no. 61303191. It is also supported by the Research Foundation of the Education Bureau of Hunan Province, China (grant no. 22B0735 and no. 24A0532) and the Construct Program of Applied Specialty Disciplines in Hunan Province (Hunan Engineering University), as well as the Hunan Provincial College Students’ Innovation Training Program Project, China (Project Name: “Research and Implementation of an AIoT-based Intelligent Children’s Desk System” and “Research on Key Technologies of Unmanned Mining Locomotives”).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CSP | Cloud Service Provider |
| ABE | Attribute-Based Encryption |
| CP-ABE | Ciphertext-Policy Attribute-Based Encryption |
| OC-BTCP-ABE | Black-Box Traceable CP-ABE with Outsourcing of Computation |
| DB | Decryption Black-box |
| IoT | Internet of Things |
| LSSS | Linear Secret Sharing Scheme |
| BDHE | Bilinear Diffie-Hellman Exponent |
| CES | Cloud Encryption Server |
References
- Gao, S.; Iu, H.H.; Erkan, U.; Simsek, C.; Toktas, A.; Cao, Y. A 3D Memristive Cubic Map With Dual Discrete Memristors: Design, Implementation, and Application in Image Encryption. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 7706–7718. [Google Scholar] [CrossRef]
- Gao, S.; Iu, H.H.; Mou, J.; Erkan, U.; Liu, J.; Wu, R.; Tang, X. Temporal action segmentation for video encryption. Chaos Solitons Fractals 2024, 183, 114958. [Google Scholar] [CrossRef]
- Gao, S.; Liu, J.; Iu, H.H.; Erkan, U.; Zhou, S.; Wu, R.; Tang, X. Development of a video encryption algorithm for critical areas using 2D extended Schaffer function map and neural networks. Appl. Math. Model. 2024, 134, 520–537. [Google Scholar] [CrossRef]
- Kamara, S.; Lauter, K. Cryptographic cloud storage. In International Conference on Financial Cryptography and Data Security; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Bethencourt, J.; Sahai, A.; Waters, B. Ciphertext-policy attribute-based encryption. In Proceedings of the IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 20–23 May 2007. [Google Scholar]
- Li, J.; Ren, K.; Kim, K. A2BE: Accountable Attribute-Based Encryption for Abuse Free Access Control. Cryptol. Eprint Arch. 2009, 1–16. [Google Scholar]
- Liu, Z.; Cao, Z.; Wong, D.S. Blackbox traceable CP-ABE: How to catch people leaking their keys by selling decryption devices on eBay. In Proceedings of the ACM Conference on Computer and Communications Security, Berlin, Germany, 4–8 November 2013; pp. 475–486. [Google Scholar]
- Liu, Z.; Cao, Z.; Wong, D.S. Traceable CP-ABE: How to trace decryption devices found in the wild. IEEE Trans. Inf. Forensics Secur. 2014, 10, 55–68. [Google Scholar] [CrossRef]
- Ning, J.; Cao, Z.; Dong, X.; Gong, J.; Chen, J. Traceable CP-ABE with short ciphertexts: How to catch people selling decryption devices on ebay efficiently. In European Symposium on Research in Computer Security; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9879, pp. 551–569. [Google Scholar]
- Qiao, H.; Ren, J.; Wang, Z.; Ba, H.; Zhou, H. Compulsory traceable ciphertext-policy attribute-based encryption against privilege abuse in fog computing. Future Gener. Comput. Syst. 2018, 88, 107–116. [Google Scholar] [CrossRef]
- Qiao, H.; Ba, H.; Zhou, H.; Wang, Z.; Ren, J.; Hu, Y. Practical, provably secure, and black-box traceable CP-ABE for cryptographic cloud storage. Symmetry 2018, 10, 482. [Google Scholar] [CrossRef]
- He, X.; Li, L.; Peng, H. An enhanced traceable CP-ABE scheme against various types of privilege leakage in cloud storage. J. Syst. Archit. 2023, 136, 102833. [Google Scholar] [CrossRef]
- Liu, Z.; Ding, Y.; Yuan, M.; Wang, B. Black-box accountable authority cp-abe scheme for cloud-assisted e-health system. IEEE Syst. J. 2022, 17, 756–767. [Google Scholar] [CrossRef]
- Yin, Y.; Gan, Q.; Zuo, C.; Liu, N.; Wang, C.; Jiang, Y. A Revocable Outsourced Data Accessing Control Scheme with Black-Box Traceability. In Proceedings of the 18th International Conference on Information Security Practice and Experience, Copenhagen, Denmark, 24–25 August 2023; pp. 380–398. [Google Scholar]
- Green, M.; Hohenberger, S.; Waters, B. Outsourcing the Decryption of ABE Ciphertexts. In Proceedings of the 20th USENIX Security Symposium, San Francisco, CA, USA, 8–12 August 2011. [Google Scholar]
- Li, J.; Huang, X.; Li, J.; Chen, X.; Xiang, Y. Securely outsourcing attribute-based encryption with checkability. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 2201–2210. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Chen, X.; Jia, C.; Lou, W. Identity-based encryption with outsourced revocation in cloud computing. IEEE Trans. Comput. 2015, 64, 425–437. [Google Scholar] [CrossRef]
- Parno, B.; Raykova, M.; Vaikuntanathan, V. How to delegate and verify in public: Verifiable computation from attribute-based encryption. In Proceedings of the 9th Theory of Cryptography Conference, TCC 2012, Taormina, Sicily, Italy, 19–21 March 2012. [Google Scholar]
- Guo, R.; Yang, G.; Shi, H.; Zhang, Y.; Zheng, D. O3-R-CP-ABE: An efficient and revocable attribute-based encryption scheme in the cloud-assisted IoMT system. IEEE Internet Things J. 2021, 8, 8949–8963. [Google Scholar] [CrossRef]
- Yu, G.; Ma, X.; Cao, Z.; Zeng, G.; Han, W. Accountable CP-ABE with public verifiability: How to effectively protect the outsourced data in cloud. Int. J. Found. Comput. Sci. 2017, 28, 705–723. [Google Scholar] [CrossRef]
- Sethi, K.; Pradhan, A.; Bera, P. Practical traceable multi-authority CP-ABE with outsourcing decryption and access policy updation. J. Inf. Secur. Appl. 2020, 51, 102435. [Google Scholar] [CrossRef]
- Ziegler, D.; Marsalek, A.; Palfinger, G. White-box traceable attribute-based encryption with hidden policies and outsourced decryption. In Proceedings of the 20th IEEE International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Shenyang, China, 20–22 October 2021. [Google Scholar]
- Zhang, R.; Hui, L.; Yiu, S.; Yu, X.; Liu, Z.; Jiang, Z.L. A traceable outsourcing cp-abe scheme with attribute revocation. In Proceedings of the 2017 IEEE Trustcom/BigDataSE/ICESS, Sydney, Australia, 11 September 2017. [Google Scholar]
- Naor, D.; Naor, M.; Lotspiech, J. Revocation and tracing schemes for stateless receivers. In Proceedings of the Advances in Cryptology–CRYPTO 2001: 21st Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2001. [Google Scholar]
- Beimel, A. Secure Schemes for Secret Sharing and Key Distribution. Ph.D. Thesis, Israel Institute of Technology, Technion, Haifa, Israel, 1996. [Google Scholar]
- Waters, B. Ciphertext-policy attribute-based encryption: An expressive, efficient, and provably secure realization. Lect. Notes Comput. Sci. 2011, 6571, 53–70. [Google Scholar]
- De Caro, A.; Iovino, V. JPBC: Java pairing based cryptography. In Proceedings of the 16th IEEE Symposium 595 on Computers and Communications, ISCC 2011, Kerkyra, Greece, 28 June–1 July 2011; pp. 850–855. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).