Abstract
Software maintenance is one of the most expensive phases in software development, especially when complex source code is the only available artifact. Clustering software modules and generating a structured architectural model can significantly reduce the effort and cost of maintenance. This study aims to achieve high-quality modularization by maximizing intra-cluster cohesion, minimizing inter-cluster coupling, and optimizing overall modular quality. Since finding optimal clustering is an NP-complete problem, many existing methods suffer from poor modular structures, instability, and inconsistent results. To overcome these limitations, this paper proposes a module clustering method using a discrete bedbug optimizer. In software architecture, symmetry refers to the balanced and structured arrangement of modules. In the proposed method, module clustering aims to identify and group related modules based on structural and behavioral similarities, reflecting symmetrical properties in the source code. Conversely, asymmetries, such as modules with irregular dependencies, can indicate architectural flaws. The method was evaluated on ten widely used real-world software datasets. The experimental results show that the proposed algorithm consistently delivers superior modularization quality, with an average score of 2.806 and a well-balanced trade-off between cohesion and coupling. Overall, this research presents an effective solution for software module clustering and provides better architecture recovery and more maintainable systems.
1. Introduction
Software modification is inevitable as user demands and systems continue to evolve. On average, about 60% of software costs are tied to maintenance activities [1]. A better understanding of software structure can help reduce these maintenance costs. One way to achieve this is by clustering software modules to form a structural model. Modularization quality (MQ) measures the effectiveness of such models. It is based on the number of links within clusters (cohesion) and between clusters (coupling) [2]. MQ helps assess the structural models produced by various algorithms. Models with higher cohesion and lower coupling generally perform better. Software module clustering (SMC) techniques divide the program’s source code into m clusters. These clusters may represent packages, components, or classes. The SMC problem is considered to be NP-complete [2,3].
Several heuristic approaches have been developed to address SMC. However, many suffer from common issues: lower MQ, slow convergence, and poor stability in large-scale and real-world software [4,5]. They also often become stuck in local optima, leading to a low success rate. The main goals of this study are as follows:
- To cluster the most functionally similar modules within the same clusters.
- To improve the modularization quality (MQ) of software module clustering (SMC) methods.
- To enhance the stability of software module clustering (SMC) methods.
- To establish an effective trade-off between cohesion and coupling in software module clustering.
A discrete optimization technique is suggested in this study to address the SMC problem. The Bedbug Optimization Algorithm (BBOA) is the foundation of the suggested approach. A class of tiny parasitic insects known as bedbugs consumes the blood of warm-blooded mammals. Bedbugs possess bloodsucking organs and an alternating cycle of slow transformation, including eggs, nymphs, and adult insects. The bedbug algorithm is used for the best possible clustering of software modules and is inspired by the behavior of bedbug swarms. Every result that the BBOA is able to obtain represents a software module clustering model. The MQ metric is used to assess the quality of the solution. The primary contributions of this work are as follows:
- A unique discrete version of the BBOA was developed to address discrete optimization problems. The developed BBOA can handle most graph-based optimization challenges.
- Clustering the most related software modules using the developed BBOA.
- Achieving a good balance between cohesion and coupling to group functionally similar modules.
- Developing a framework to automatically generate the optimal architectural model of a program’s source code.
Section 2 provides an overview of the major research conducted in the field of software module clustering. Section 3 introduces the proposed framework for SMC using the BBOA. Section 4 describes the experimental platform, tools, and benchmarks, followed by a discussion of the obtained results. Finally, Section 5 concludes the paper and offers suggestions for future research in SMC.
2. Related Works
The Particle Swarm Optimization (PSO) algorithm was adapted to cluster program source code in [3]. In this study, PSO was specifically modified to address the SMC problem. Experimental results indicate that the proposed PSO-based method produces software clusters with higher MQ. However, its main limitation lies in the high probability of being trapped in local optima when applied to large software systems. Conventional approaches often suffer from scalability issues, particularly in the context of large-scale software systems. To address this limitation, a recent study introduced a novel Parallel Hybrid Genetic Algorithm for Architecture Recovery (PHYGAR) [4]. By incorporating parallelism, the proposed method significantly enhances computational efficiency and convergence speed, enabling the analysis of large systems such as Chromium. Empirical evaluations conducted on ten open-source projects show that the parallel versions of the algorithm outperform their sequential counterparts. PHYGAR demonstrated superior performance in seven out of ten systems across all cluster sizes. These results highlight the effectiveness of parallelism in improving the scalability and quality of software architecture recovery (SAR) methods for complex, large-scale software systems.
Detecting semantic similarity between binary code fragments is a critical task in software analysis. In [5], an advanced preprocessing method was proposed for binary code fragments to enhance similarity detection using machine learning. The method centers on the use of Attributed Abstract Syntax Trees (AASTs) derived from decompiled pseudocode of binary functions. It constructs ASTs from code, enriches the nodes with semantic vectors, and employs deep Graph Neural Networks (GNNs) to effectively compare code fragments. Experimental evaluations demonstrate that the proposed method outperforms existing techniques by more accurately capturing the semantic context of code and identifying functionally similar fragments. Additionally, the research provides a comprehensive analysis of binary similarity detection processes and categorizes preprocessing techniques accordingly. Future work in this field will aim to expand the method’s scope to include source-to-binary similarity detection across different platforms. This study significantly contributes to the field by combining syntactic structure with semantic awareness.
In [6], a heuristic algorithm employing a Greedy Randomized Adaptive Search Procedure combined with Variable Neighborhood Descent (GRASP-VND) was proposed to address the SMC challenge. This approach demonstrates superior performance compared to previous Large Neighborhood Search (LNS) methods in terms of both solution quality and computational efficiency. The methodology was rigorously evaluated using 24 real-world benchmark datasets. The GRASP-VND framework capitalizes on domain-specific knowledge to effectively prune the search space and incorporates an enhanced three-fold neighborhood classification scheme. Experimental findings show that algorithmic efficiency and strategic design choices significantly speed up the modularization process. Additionally, the fast computational performance of the proposed method makes it suitable for integration into Integrated Development Environments (IDEs) and real-time applications. The study also emphasizes the versatility of GRASP-VND. It is useful not only as a technique for clustering but also as a tool for evaluating modular design quality.
Arasteh et al. proposed a hybrid PSO-GA to select optimal clusters [7]. This method addresses issues in previous approaches, such as slow convergence, low MQ, poor stability, and low success rates. It combines the advantages of two heuristic techniques. Compared to standalone PSO and GA, the hybrid approach achieves faster convergence and higher MQ. Experiments on ten widely used Modulus Dependency Graphs (MDGs) showed that the PSO-GA method outperforms traditional methods 90% of the time. In [8], the proposed neighborhood tree algorithm built a neighborhood tree from the Artifact Dependency Graph (ADG) and applied it for module clustering; its main merits include the ability to extract meaningful software architecture models more effectively than hierarchical approaches, while also operating within a reasonable time compared to search-based methods. This makes it a practical technique for software engineers in identifying understandable subsystems and supporting system maintenance. However, the algorithm has some limitations: the created architectural models are preliminary and require broader validation on large-scale systems.
In [9], the Shuffled Frog Leaping Algorithm (SFLA) was combined with the GA to develop a method for the SMC problem, referred to as Bölen. This hybrid approach offers a higher MQ, improved stability, and a greater success rate. SFLA-GA outperforms earlier algorithms in 80% of benchmark tests. In 90% of cases, it converges to the optimal solution faster than the GA, Hill Climbing (HC), and PSO. In [10], the Gray Wolf Optimization Algorithm (GWOA) was combined with the GA to create a hybrid single-objective method for the SMC problem. This approach integrates an evolutionary algorithm with a swarm-based technique. Experiments using 14 standard metrics showed that the hybrid GWOA-GA method outperforms the GA, PSO, and PSO-GA in solving the SMC problem. In [11], several chaos-based algorithms were introduced for SMC, including Cuckoo Search, Bat Algorithm, Black Widow Optimization, Teaching–Learning-Based Optimization, and Grasshopper Optimization. The experimental results indicate that using logistic chaos improves the performance of these methods.
A multi-objective homogeneous clustering method, named Savalan, was proposed in [12] to enhance software module clustering using source code. This method aims to simultaneously optimize several conflicting objectives, including cohesion, coupling, MQ, cluster size, and the number of clusters. It utilizes a multi-objective GA to achieve this balance. Savalan demonstrated superior performance on 14 benchmark programs, consistently producing high-quality clusters with strong internal cohesion and weak inter-cluster coupling. However, a key limitation is its increased execution time to reach optimal clustering.
In [13], a framework called E-SC4R was developed to evaluate the effectiveness of software clustering algorithms. It addresses a common software maintenance challenge (understanding software architecture) in the absence of up-to-date documentation. The framework focuses on hierarchical clustering techniques and analyzes the impact of software features on clustering performance using the MoJoFM metric. Evaluated on 30 open-source projects, E-SC4R provides empirical guidance for selecting appropriate clustering methods for specific systems. However, its applicability is limited by the use of only two algorithms and its reliance on relationships derived solely from static analysis. Overall, E-SC4R represents a promising step toward more informed and efficient software remodularization.
Mapping source code to architectural modules is a critical and error-prone task in software maintenance and architecture conformance checking. In [14], a machine learning-based solution using a multinomial naive Bayes classifier was proposed for the SMC problem. The model was trained on both semantic and syntactic dependencies extracted from source code and architectural descriptions. The approach was tested on eight open-source Java projects and consistently outperformed related existing techniques. It also requires less parameter tuning. The study concludes that machine learning offers a promising path toward automating architectural mapping. Future work will focus on improving mapping accuracy and evaluating a broader range of systems.
In [15], the authors introduced a novel method for design pattern detection that integrates both static and dynamic program information. Traditional techniques primarily rely on static analysis of source code. In contrast, the proposed method uses a declarative specification language to define design patterns, which are then automatically translated into SQL queries. These queries run on an augmented call tree to detect pattern instances. The approach was applied to all Gang-of-Four (GoF) design patterns and evaluated on three substantial Java case studies: JHotDraw, JUnit, and QuickUML. The experimental results confirmed the method’s effectiveness in accurately identifying design patterns. Future work in this area will include enhancing the method with UML-based visualizations and progressive diagram exploration to aid comprehension.
In [16], a discretized Sand Cat Swarm Optimization (SCSO) algorithm was developed for SMC. The proposed method addresses limitations of earlier approaches, such as low success rates and poor modularization quality, by minimizing inter-cluster coupling, maximizing intra-cluster cohesion, and enhancing MQ. The method was evaluated on ten real-world benchmark programs. The results showed that the SCSO-based approach outperformed traditional methods such as the GA, PSO, and hybrid PSO-GA in terms of clustering quality, convergence speed, and overall success rate. Key strengths of the method include its effectiveness on both small- and large-scale systems and its adaptability to high-dimensional search spaces. However, the approach also has some limitations. It requires further refinement of the fitness function and currently does not account for global modules. Additionally, its performance is sensitive to software size, which may necessitate calibration for different systems. Table 1 summarizes the main characteristics of the compared methods.

Table 1.
Specification of prior SMC techniques.
3. Proposed Method
One of the challenging optimization problems in software engineering is software module clustering (SMC). Finding an optimal solution involves constructing the most effective structural model. Formally, organizing n modules into m clusters is considered to be a combinatorial problem. In this approach, software modules are initially clustered using the BBOA applied to the Modulus Dependency Graph (MDG) generated from the source code. The workflow of the proposed method is illustrated in Figure 1. The developed model aims to reduce software maintenance costs. This paper presents a modified and discrete version of the BBOA tailored for the SMC problem.
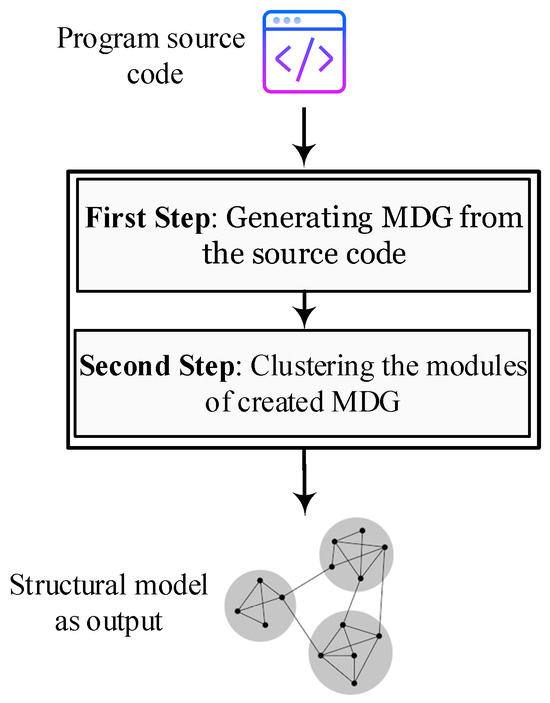
Figure 1.
Workflow of the proposed SMC method.
3.1. MDG Generation
Identifying call instructions and generating the call graph, represented as a Modulus Dependency Graph (MDG), is crucial for capturing inter-procedural relationships between code modules. The proposed BBOA method requires the dependency graph of the source code to produce the clustered design model of the software. Therefore, the MDG must be constructed from the input source code. In the MDG, nodes represent modules, while edges denote relationships such as inheritance and function calls. Static analysis is employed at this stage of the SMC method. This involves examining the source code without executing it to extract call instructions. First, the source code is parsed using language-specific tools to produce an intermediate representation. Each function becomes a node in the graph. Next, the body of each function is traversed to identify call instructions. For each call found, a directed edge is added from the caller node to the callee node. The resulting MDG serves as a high-level abstraction of the system’s runtime behavior.
By converting source code into an MDG structure, functionally related modules can be grouped into logical clusters. Figure 2 illustrates a simple Python program and its corresponding call graph. The main function invokes three modules: load_data, process_data, and save_results. The MDG visually captures the relationships among these functions. In the MDG, load_data calls both read_file and parse_data, while process_data depends on analyze and transform. These edges highlight the internal flow of control and data, making it easier to identify coupled components. In the proposed SMC method, the MDG provides a useful abstraction for software clustering, modularization, and further analyses such as change propagation.
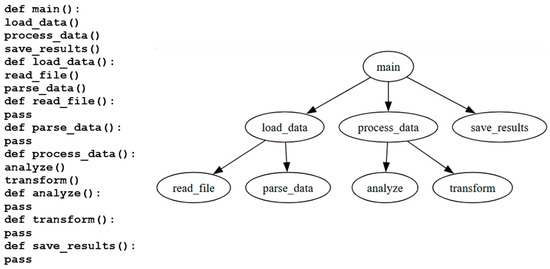
Figure 2.
A source code in Python and the generated call graph, which includes different dependent functions.
To support software module clustering, the structural relationships among functions in the program (shown in Figure 2) are encoded using an adjacency matrix. In the adjacency matrix, each row corresponds to a caller function, and each column corresponds to a callee. A value of 1 at position (i, j) indicates that the function in row i directly calls the function in column j. A value of 0 denotes no direct call between the two functions. This binary encoding enables automated analysis by clustering algorithms.
The structural information captured in the matrix is used by the proposed SMC method to cluster highly interrelated functions. For example, in the program shown in Figure 2, the closely connected group of load_data, read_file, and parse_data may be identified as a data ingestion cluster. Meanwhile, process_data, analyze, and transform may form a data processing cluster. By abstracting program behavior into this graph-based representation, the adjacency matrix supports scalable and structure-aware module analysis. It serves as a foundational input for data-driven software modularization.
3.2. Solution Encoding
In the BBOA, the quality and diversity of the initial population are crucial for effective exploration of the solution space. In the context of software module clustering, each agent in the population is represented as a clustering array. Each element in this array indicates the cluster assignment of a specific software module. The length of the clustering array equals the total number of modules in the system. For example, the MDG created from a program with 100 modules and 120 call instructions consists of 100 nodes and 120 edges. Accordingly, the clustering array for this MDG has a length of 100. Each value in the array corresponds to a cluster identifier, specifying which cluster a module belongs to.
Figure 3 illustrates the structure of a real-world software system, where nodes represent modules and directed edges represent call relationships. In this case study, the system contains 20 modules, so the clustering array length is 20. The array shows that module 1 is assigned to cluster 4, module 2 to cluster 5, and module 3 to cluster 4. The clustering structure is non-uniform, with some clusters being more densely populated. This reflects the natural modularity found in many software systems. Modules within the same cluster are assumed to be strongly interrelated and share functional responsibilities. Each clustering configuration represents a potential solution defining how modules are grouped into cohesive and loosely coupled components. The quality of these solutions is evaluated using the MQ metric.
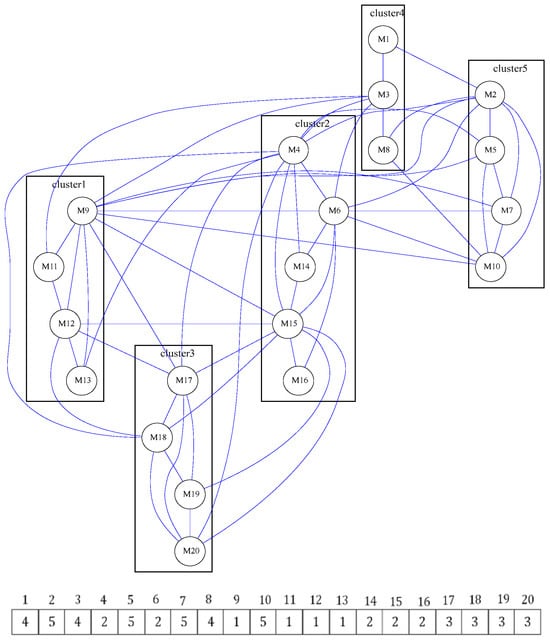
Figure 3.
A clustered MDG and its corresponding agent array.
During initialization, each agent (clustering array) is generated randomly to ensure diverse coverage of possible solutions. The number of initial clusters is selected based on the software size. Identical solutions are avoided to maintain diversity within the population. Over successive iterations, bedbug agents update their positions according to movement rules inspired by bedbug behavior, gradually improving the clustering. This approach combines graph-based representation with bio-inspired search dynamics. It effectively uncovers meaningful modular structures within software systems, enhancing their understandability and maintainability.
3.3. Clustering the Software Modules by BBOA
In the second step of the proposed approach, the BBOA technique is adapted and customized to solve the SMC problem. This adaptation is inspired by the behavioral patterns of bedbugs in nature [17]. Similar to how bedbugs respond to their environment, past experiences, and interactions with others, the BBOA simulates this behavior to explore the search space. Each bedbug agent continuously updates its position based on its own experience, the proximity of other agents, and the quality of nearby solutions. The objective is to guide agents toward optimal clustering solutions by mimicking these natural behaviors. Figure 4 illustrates the key stages of the developed BBOA applied to software module clustering.
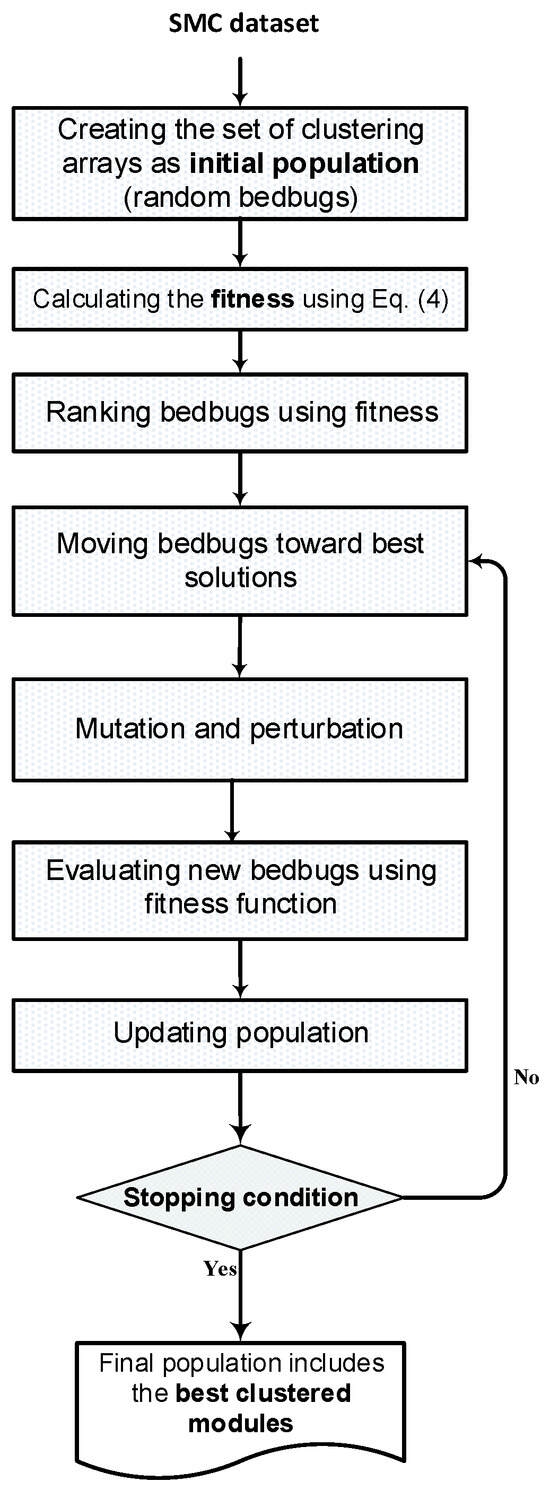
Figure 4.
The flowchart of the suggested BBOA for clustering the software modules.
The proposed method employs the BBOA, a population-based metaheuristic inspired by the propagation behavior of bedbugs. The pseudocode of the BBOA used in this method is presented in Algorithm 1. The algorithm begins by initializing the bedbug population and their velocities (explained in the Solution Encoding subsection). The adapted discrete version of the BBOA was specifically used to deal with the SMC problem in the next step of this research. In this adapted BBOA, each bedbug is symbolized by an array of integers representing its clustering configuration.
| Algorithm 1. Pseudocode of the BBOA [17] |
| 1- Initialize the Bedbug Population X(0) and V(0) |
| 2- Initialize Rc, g, and N |
| 3- Generate a random value between [0.4, 0.9] for w |
| 4- Generate a random value between [0, 1] for rand1, rand2 and rand3 |
| 5- Generate a random value between [0, 2] for c1, c2 and c3 |
| 6- Calculate the fitness function using Equation (4) |
| 7- While (Iter < Max_Iter) do |
| 8- For (each X) do |
| 9- For (each V) do |
| 10- Set LBest equal to the previous position |
| 11- Propagate GBest and SBest |
| 12- Propagate X to new X |
| 13- Update the new value of all variables |
| 14- Calculate the fitness function using Equation (4) |
| 15- end for |
| 16- end for |
| 17- Iter = Iter + 1 |
| 18- end While |
| 19- Return X Best |
In the next stage, the control parameters, including the repulsion coefficient (Rc), gravitational constant (g), equilibrium constant (εg), and the total number of individuals (N), are initialized. Random values are generated for inertia weight (w), acceleration constants (c1, c2, c3), and stochastic terms (rand1, rand2, rand3) to ensure exploration of the search space (lines 3–5). The bedbugs adjust their movement towards these optima, simulating social interaction and adaptation (lines 10–13). The fitness of each updated position is evaluated using a predefined objective function (Equation (4)), which measures clustering quality based on modularization criteria (lines 6 and 14). The iterative process continues until a maximum number of iterations is reached, at which point the best solution found, X Best, is returned (line 19). The core of the algorithm operates within an iterative loop (lines 7–18), where each individual’s position and velocity are updated to reflect the influence of the local best (LBest), global best (GBest), and social best (SBest). The movement of each bedbug in the search space is governed by two main equations that simulate adaptive behavior based on individual and collective experience. Equation (1) updates the velocity Vi(t + 1) of each bedbug_i, which includes four components:
- The inertia of previous velocity;
- Attraction towards its own best-known position (Lbest_i);
- The global best position (Gbest);
- The best social position (Sbest_i).
The parameters ω, α, β, and γ regulate the influence of these components, while r1, r2, and r3 are random values in the range [0, 1], which introduce stochastic behavior. Equation (2) updates the position Xi(t + 1) based on the current position and the best-known position Xi(best), scaled by a random factor r.
The developed BBOA is particularly effective for software module clustering. The BBOA efficiently converges toward optimal or near-optimal modularization schemes; it maximizes cohesion within modules and minimizes inter-module coupling.
3.4. Objective Function
The MQ parameter is used to guide the population based on cohesion and coupling. Arasteh et al. utilized MQ as a metric for clustering quality [7]. High-quality clusters have strong internal cohesion and low inter-cluster coupling. A well-structured cluster is characterized by significant internal connectivity among its modules. The MQ for a specific cluster k is calculated using Equation (3), where i represents the number of internal cohesion links, and j denotes the number of external coupling links. Equation (4) measures the overall MQ across all clusters, with mmm being the total number of clusters. The MQ objective function balances internal cohesion and external coupling by maximizing cohesion while minimizing coupling. Achieving this balance is essential for an optimal design model.
4. Evaluation
4.1. Experimental Platform
A series of extensive experiments were conducted using a unified platform developed in MATLAB (R2023a, 64-bit) and Python 3.13 to evaluate the performance of the proposed SMC method based on the discrete BBOA. All experiments were executed on a system equipped with an Intel Core i7-12700 processor, 32 GB RAM, and Windows 11, to ensure consistency and computational efficiency. For comprehensive benchmarking, the proposed BBOA-based SMC was compared against several well-established metaheuristic algorithms: Genetic Algorithm (GA), Particle Swarm Optimization (PSO), a hybrid PSO-GA approach, Shuffled Frog Leaping Algorithm (SFLA), and Sand Cat Swarm Optimization (SCSO). All algorithms were implemented in MATLAB to maintain a consistent execution environment and minimize external biases.
Each algorithm underwent parameter tuning to achieve optimal performance. Specifically, crossover and mutation probabilities were optimized for GA, inertia weight and acceleration coefficients for PSO, hybridization weights for PSO-GA, and movement control parameters for SCSO. The BBOA was similarly configured with optimized values for inertia weight (ω), acceleration coefficients (α, β, γ), and social interaction terms to enhance convergence speed and clustering quality. Table 2 presents the calibration parameters used for each algorithm. These values were determined through extensive tuning and multiple test runs on benchmark datasets. A consistent population size and iteration limit were applied across all algorithms to ensure reliable evaluation. Each algorithm was independently executed 8 times on a set of benchmark software systems. Key evaluation metrics included MQ, cohesion, coupling, and standard deviation. The unified experimental platform ensured that all methods were tested under identical conditions. The population size affects the performance of heuristic algorithms, and the optimal population size is application-dependent and should be calibrated during experiments. The population size values were adjusted in the conducted experiments, and the selected values for the SMC problem are presented in Table 2.

Table 2.
Calibration parameters and their best values.
4.2. Benchmark Programs
To evaluate the effectiveness and generalizability of the proposed SMC method based on the BBOA, ten real-world and standard benchmark programs were utilized. The data utilized were derived from the module dependencies of real-world software systems (as benchmarks) deployed across various platforms. These benchmarks represent module dependencies in real software across different platforms, and they vary in size, structure, and complexity. Table 3 summarizes the key characteristics of the benchmark programs, which include the number of modules and inter-module connections. Each benchmark consists of source code modules with defined dependencies (call instructions). The goal of the SMC approach is to group highly related modules into the same cluster. Their diversity ensures that the clustering algorithm is tested across various architectures, making the evaluation practical and generalizable.

Table 3.
Features of the utilized benchmarks.
Real-world software systems consist of modules and complex dependencies between them. Table 3 shows that all benchmark programs have more dependencies than modules. For example, mtunis has 20 modules and 57 connections, bison has 37 modules and 179 connections, and grappa has 86 modules and 295 connections. On average, the benchmarks have about 41 modules and 171 connections per program, which shows that dependencies greatly outnumber modules. Understanding these dependencies is crucial for maintenance, evolution, and structural analysis.
On the other hand, in the architectural models (for example, in 4 + 1), connections among software modules are fundamental to capturing the system’s structure and behavior. In the logical view, they define functional relationships and highlight cohesion and coupling. In the development view, they guide the organization of modules into packages and libraries. In the process view, connections indicate runtime interactions, synchronization, and communication patterns. In the physical view, they inform deployment decisions and map modules to hardware nodes. Finally, in the scenarios (use-case) view, module interactions show how use cases traverse the system. Overall, module connections are essential for accurately representing all views of a system.
4.3. Results and Discussion
4.3.1. Analyzing the Created Clusters Using Cohesion and Coupling
Cohesion is a key internal quality metric in SMC. It measures how closely related the elements within a module are. High cohesion typically leads to better modularity, improving maintainability, reusability, and code clarity. To evaluate the performance of the BBOA in generating cohesive clusters, eight independent runs were performed on various benchmark software systems. Figure 5 presents the cohesion values obtained across these runs. The Mtunis project showed moderate variability, with values ranging from 28 to 34. Most of the values clustered between 30 and 33, indicating that the BBOA consistently finds cohesive solutions for this system. The ispell project exhibited more variation, ranging from 31 to 44. A peak cohesion of 44 in one run suggests a well-formed cluster, while lower values may reflect sensitivity to parameters or project complexity. Similarly, the rcs project had a broad range of 44 to 72, with two runs achieving particularly high cohesion.
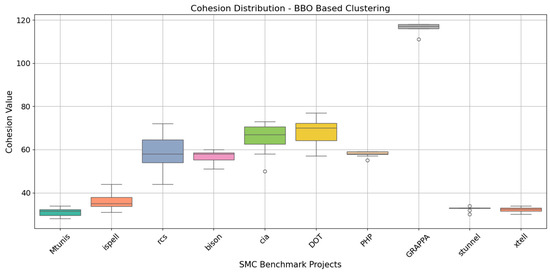
Figure 5.
The cohesion values of the clusters created by the suggested BBOA in 8 runs.
Bison and CIA showed moderate stability. Bison’s cohesion ranged from 51 to 60, while CIA’s varied between 50 and 73. These fluctuations indicate that the BBOA performs reasonably well but can sometimes converge to suboptimal solutions, possibly due to initial population differences or search dynamics. In contrast, the DOT project demonstrated high and stable cohesion between 57 and 77 across all runs. This suggests that the BBOA effectively captures strong modular relationships in this case. The most consistent results came from the PHP and GRAPPA projects. PHP showed a narrow range of 55 to 59, indicating stable clustering performance. GRAPPA had the highest cohesion values, ranging from 111 to 118 in every run. These results highlight the BBOA’s robustness in handling systems with clear structural boundaries.
Finally, both stunnel and xtell showed low variability, with cohesion values between 30 and 34. This reflects stable performance in identifying module boundaries across runs. Overall, the BBOA proves to be a robust and competitive method for SMC. While some benchmarks showed variability due to complexity or stochastic behavior, others consistently benefited from the algorithm’s exploitation capability. These findings underscore the value of repeated runs in metaheuristic clustering to ensure reliable and stable performance.
Coupling is another key metric in SMC that reflects inter-cluster dependencies. An effective clustering method, such as the BBOA, aims to reduce coupling while maximizing cohesion. Lower coupling indicates that modules within each cluster primarily interact internally, which supports modularity, maintainability, and reusability. As illustrated in Figure 6, the coupling values varied across eight independent runs and across different benchmark systems. Mtunis, stunnel, and xtell consistently show low coupling values, typically ranging from 23 to 33. This indicates well-separated clusters with minimal external dependencies. The consistency across runs suggests that the BBOA performs reliably for smaller or well-structured systems.
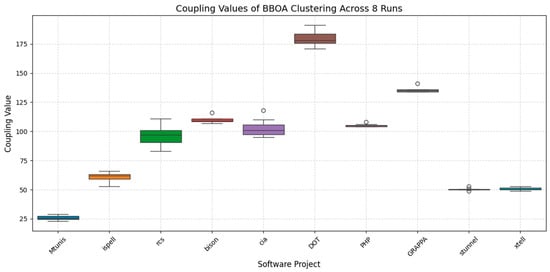
Figure 6.
The coupling values of the clusters created by the suggested BBOA in 8 runs.
In contrast, systems like DOT, bison, and GRAPPA exhibit higher coupling. For example, DOT recorded the highest coupling values, between 171 and 191, indicating significant inter-cluster communication. GRAPPA also shows high but stable coupling in the range of 134 to 141. These results may reflect the intrinsic complexity or tightly integrated architecture of these projects. Intermediate coupling behavior is observed in PHP and rcs, where the values are moderate and stable. This suggests that these systems have a partially modular architecture, and that the BBOA handles them reasonably well, although further improvement is possible.
An important observation is the stability of coupling in some systems across multiple runs. For instance, PHP, GRAPPA, and xtell show consistent values, indicating that the stochastic nature of the BBOA has a limited impact in these cases. However, systems with complex architectures may still experience some variability due to differing initial conditions or search paths. Overall, the BBOA demonstrates a strong capacity to minimize coupling in simpler systems while maintaining stability across runs. This behavior highlights its robustness and suitability for SMC. It also suggests the potential for hybrid or adaptive methods to further improve results on complex software.
Cohesion and coupling are central to evaluating clustering quality. Table 4 presents the mean and standard deviation of cohesion across all benchmark systems. The GRAPPA project achieves the highest mean cohesion (116.4). PHP, bison, and rcs also show good cohesion performance. Simpler systems like Mtunis, ispell, stunnel, and xtell maintain lower but stable cohesion values, likely due to smaller sizes or simpler structures. The relatively low standard deviations across most systems indicate that the BBOA performs consistently. These results affirm the algorithm’s reliability in producing well-formed clusters and underscore the importance of multiple-run evaluations when applying metaheuristic algorithms to SMC.

Table 4.
The mean and STDV of the cohesion within the clusters created by the BBOA.
Table 5 shows the amount of coupling among the clusters created. DOT has the highest coupling (about 180.8), with relatively consistent high values, indicating that the BBOA struggles to separate interdependent components effectively in this large and possibly tightly coupled system. Similarly, GRAPPA and bison show higher coupling, albeit with manageable variance. In contrast, systems like Mtunis, stunnel, and xtell show consistently low coupling, highlighting the BBOA’s effectiveness in these cases. Regarding the results, low coupling and high cohesion are achieved in systems like Mtunis and xtell. Moderate coupling and cohesion are observed in medium-complexity projects like PHP and bison. High coupling with varying cohesion occurs in complex systems like DOT and GRAPPA. The standard deviation values suggest that the results are generally stable across runs, with slightly more variability in systems like rcs, cia, and bison.

Table 5.
The mean and STDV of the coupling among the clusters created by the BBOA.
Figure 7 illustrates the comparative analysis of cohesion and coupling values averaged across eight independent runs for each of the ten software benchmark projects. This comparison underscores the effectiveness of the proposed BBOA-based clustering method in achieving a critical software engineering objective: maximizing cohesion while minimizing coupling. As shown in Figure 7, projects like GRAPPA and DOT exhibit exceptionally high cohesion scores (above 110 and 70, respectively), indicating strong intra-cluster similarity. However, they also demonstrate relatively high coupling values, which implies that some modules maintain dependencies outside their clusters. This suggests that while the BBOA effectively grouped strongly related modules together, the nature or structure of these particular software systems may inherently involve more cross-cluster interactions. In contrast, Mtunis, stunnel, and xtell show a more balanced profile, with moderate cohesion values accompanied by low coupling scores. These systems exhibit a favorable trade-off between cohesion and coupling. With regard to the results, the BBOA was able to form clusters that were both internally coherent and externally independent, which is a desirable metric in software clustering.
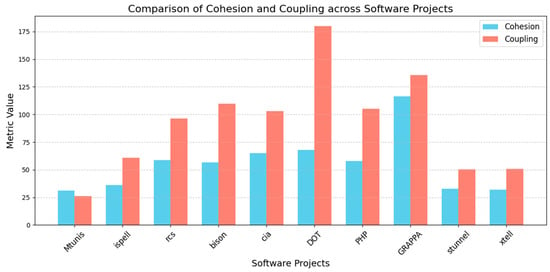
Figure 7.
The average values of cohesion and coupling in the clusters created by the BBOA in different benchmark projects.
PHP and ispell also stand out for maintaining low-to-moderate coupling while achieving consistent cohesion. On the other hand, rcs, bison, and cia show varied patterns, reflecting system-specific complexities that may affect clustering performance. Overall, the results shown in Figure 7 support the core merit of the BBOA approach and its ability to manage the trade-off between cohesion and coupling. By evaluating both metrics side by side, it becomes evident that the BBOA does not simply optimize one metric at the expense of the other; instead, it seeks a balanced modular structure, where tightly bound components are clustered together while inter-module dependencies are minimized. This balance is critical for enhancing the maintainability, scalability, and understandability of software systems.
4.3.2. Analyzing the Created Clusters Using Clustering Quality
Figure 8 presents the boxplot analysis of MQ for ten software benchmark systems across multiple runs. MQ is a comprehensive metric that captures the overall quality of clustering by combining both cohesion and coupling properties. Figure 8 reveals that GRAPPA consistently achieves the highest MQ scores, with median values around 4.9 and narrow interquartile ranges; these results indicate stable and optimal clustering behavior. Similarly, PHP demonstrates robust MQ performance, with values ranging from approximately 3.1 to 3.76. In contrast, systems like ispell and DOT exhibit lower MQ scores, with wider variability in some cases. These fluctuations suggest that the internal structure of these systems may pose challenges to achieving high modularization. Despite this, their MQ scores remain within acceptable bounds, which confirms the general adaptability of the BBOA method. Projects such as bison, rcs, and cia show moderate MQ values with relatively tighter spreads and indicate reliable performance across runs. The stunnel, xtell, and Mtunis systems, while exhibiting slightly lower maximum values, demonstrate consistent MQ scores. The results presented in Figure 8, when interpreted alongside the cohesion and coupling analyses, emphasize the effectiveness of the proposed BBOA-based approach in generating balanced, high-quality clusters. It not only captures high intra-cluster cohesion and low inter-cluster coupling but also translates these into strong overall modularization quality.
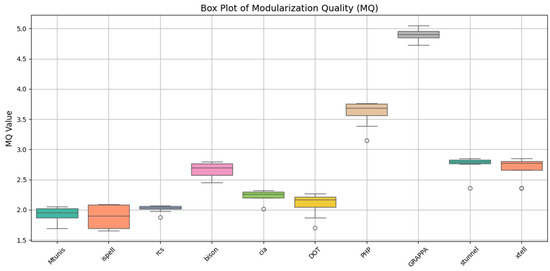
Figure 8.
The MQ values of the clusters created by the suggested BBOA in 8 runs.
Figure 9 shows the two clustering models produced by the proposed BBOA, and they can be compared based on their MQ, cohesion, and coupling. The first clustering model (Clustering 1) has an MQ value of 1.85882, cohesion of 36, and coupling of 21, whereas the second model (Clustering 2) shows a higher MQ of 2.13025, but it has a reduced cohesion of 24 and an increased coupling of 33. These figures highlight a trade-off between achieving higher overall modularization quality and maintaining desirable internal cluster characteristics. In Clustering 1, the higher cohesion value indicates that the modules grouped together within each cluster share stronger internal relationships. This can be observed visually, where core modules such as User, Computer, Memory, and State are placed within the same cluster (Cluster 1). Additionally, coupling is relatively low in this configuration, meaning that inter-cluster dependencies are minimized. This structure is beneficial from a software maintenance perspective, as high cohesion and low coupling typically lead to more understandable, maintainable, and reusable modules.
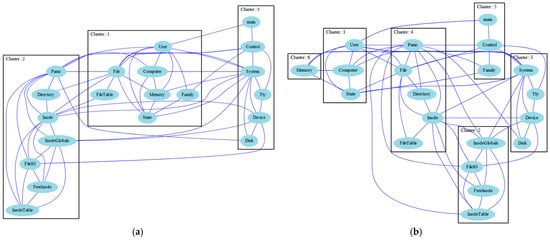
Figure 9.
Two different clustered models for the mtunis software project, which includes 20 modules and 57 edges among the modules. (a) Clustering 1: MQ: 1.85882, cohesion: 36, coupling: 21, number of clusters: 3. (b) Clustering 2: MQ: 2.13025, cohesion: 24, coupling: 33, number of clusters: 6.
On the other hand, Clustering 2 exhibits a higher MQ value, which generally reflects an improved overall balance between cohesion and coupling across all clusters. However, this gain in MQ comes at the expense of both cohesion and coupling individually. The increased number of clusters (from 3 to 6) in Clustering 2 results in the fragmentation of logically related modules across different clusters. For instance, Memory is isolated in its own cluster (Cluster 6), while User, Computer, and State are scattered into separate clusters. This fragmentation likely weakens the internal relationships within clusters and increases the number of cross-cluster interactions. From a modularization perspective, Clustering 2 may be preferable when the primary objective is to maximize MQ. Clustering 2 shows that the BBOA can improve MQ by redistributing modules; further refinements would be necessary to reduce coupling and restore cohesion without compromising overall modular quality. Therefore, the selection of the preferred clustering solution should align with the specific design goals and quality priorities.
The calculated similarity rates for the clusters provide valuable insight into the internal cohesion and external interaction of the modules grouped by the BBOA clustering result. These similarity scores, calculated by Equation (3), quantify the proportion of intra-cluster connectivity relative to inter-cluster communication. Figure 10 shows the similarity rates of the modules located in the same clusters. A higher value suggests that modules within a cluster are more tightly connected to one another and less dependent on modules in other clusters. Among the six clusters, Cluster 5 achieved the highest similarity score of 0.6667, indicating a strong internal structure and minimal external dependency. This cluster includes only three modules (main, Control, and Family), which appears to promote a compact and cohesive module with limited coupling. This configuration reflects a highly modular and maintainable design model. Cluster 3 and Cluster 2 also exhibited relatively high similarity values of 0.6207 and 0.6154, respectively. These values suggest a good balance between internal links and external connections. Their structure implies that while there are some dependencies on other clusters, the modules are generally well grouped and maintain coherent internal relationships.
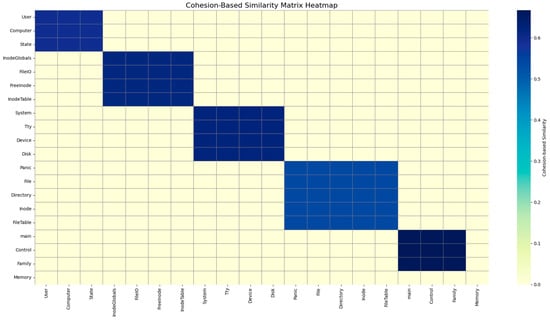
Figure 10.
The similarity rates of the modules located in the same clusters.
Cluster 1 demonstrated a moderate similarity score of 0.5926, which, although lower than that of Clusters 2 and 3, still reflects acceptable modular quality. This result may suggest that, while the internal cohesion is reasonable, there is a slightly higher reliance on other clusters, which could be improved by restructuring the interdependencies. Cluster 4 stands out with a similarity score of 0.5405, the lowest among the multi-module clusters. This lower score results from a relatively high number of inter-cluster links (17), despite having the largest number of internal links (10). The high external interaction suggests that modules in Cluster 4 are heavily coupled with other parts of the system, potentially reducing its modular integrity and maintainability. Such a structure may benefit from a reevaluation of module placement to reduce external dependencies.
Finally, Cluster 6, which includes only the Memory module, has a similarity score of 0.0000. Since there are no intra-cluster links (only one module) and it maintains four links to other clusters, this result emphasizes the module’s complete reliance on external entities. While a single-module cluster is sometimes acceptable, its high degree of coupling suggests that it might be better integrated into a larger, contextually relevant cluster. In conclusion, the similarity analysis supports the overall clustering quality provided by the BBOA, with Clusters 2, 3, and especially 5 reflecting good modular characteristics. However, Clusters 4 and 6 highlight areas for potential improvement in reducing inter-cluster dependency and enhancing cohesion. These metrics can guide future refinement of the clustering strategy to achieve a more modular and maintainable software system architecture.
The suggested SMC method utilizes module clustering to identify structural and behavioral similarities among software modules. By grouping related modules, the approach highlights symmetrical features in the source code, which often indicate well-formed architectural patterns, such as modules that collaborate consistently to achieve a defined functionality. This clustering process improves modularity by exposing natural boundaries within the system. Conversely, the method also uncovers asymmetries. For example, some modules may have excessive dependencies on parts of the system that are not functionally related. Such irregularities often reflect deeper architectural issues, which include poor modularity and understandability. Detecting these asymmetries provides valuable diagnostic insight and enables software architects to refactor problematic modules and strengthen overall architectural quality. In this way, the suggested SMC method functions not only as a tool for system organization but also as a mechanism for identifying and addressing potential architectural weaknesses in large, complex source codes.
4.3.3. Comparison with Previous Works
The comparison of MQ across various clustering methods (implemented under identical software and hardware environments) demonstrates the effectiveness of the proposed BBOA in producing high-quality software modularizations. MQ is a widely accepted metric for evaluating clustering quality, as it reflects the degree of internal cohesion within clusters and the extent of coupling between them; higher MQ values are indicative of more coherent and maintainable module groupings. Figure 11 shows the MQ values obtained by different methods in different benchmark software projects. Among the six evaluated methods (GA, ACO, PSO-GA, SFLA, SCSO) and the proposed BBOA, the BBOA consistently achieved the highest MQ values across the majority of the ten benchmark software systems. Regarding the results, the BBOA outperformed all other techniques. In large-scale systems such as GRAPPA, PHP, and bison, the BBOA demonstrated significant superiority, whereas in smaller systems, like Mtunis and ispell, it remained highly competitive.
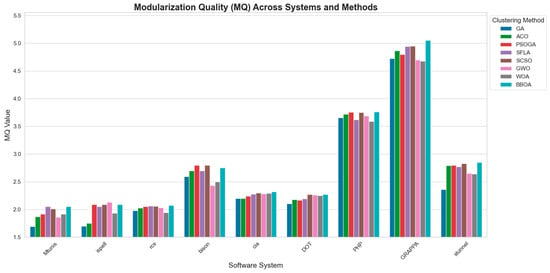
Figure 11.
Comparison of the MQ obtained by different SMC methods implemented in the same software and hardware platform.
Conversely, the GA and ACO reported comparatively lower MQ scores, particularly in complex software systems. Overall, the consistently high MQ values obtained by the BBOA underscore its capability to identify well-defined module boundaries while minimizing inter-module interactions. These results validate the BBOA as a reliable, efficient, and scalable solution for software module clustering and architectural optimization.
Table 6 shows the performance of the proposed SMC method on the Grappa system using different parameter settings. The parameters include population size, êg (reduction percentage), Lm (attraction intensity), and Lf (distance scale). The results are measured with MQ, coupling, and cohesion. The best result is obtained with a population size of 35, êg = 0.185, Lm = 6 mm, and Lf = 5 mm. This setting gives the highest MQ (4.90198), with balanced coupling and cohesion (126, 126). Lower population sizes, such as 20 with êg = 0.155, lead to the lowest MQ (4.56707). Although the cohesion is higher, the clustering quality is weaker. Medium settings (population 25–30, with êg around 0.165–0.185) give stable MQ values with acceptable coupling and cohesion. In summary, larger population sizes and properly tuned êg values (0.180–0.185) improve MQ and keep coupling and cohesion balanced. Parameter selection plays a key role in clustering quality.

Table 6.
Performance of the proposed SMC for the Grappa system with different parameter settings.
The suggested SMC method was further evaluated on another series of real-world software projects of different sizes and complexities. Table 7 presents the results in terms of MQ, cohesion, and coupling. For acqCIGNA (114 nodes, 179 dependencies), the method achieved an MQ of 6.07509, with cohesion of 106 and low coupling (73). In smaller projects such as nos and telnet2, the method also maintained a balance between cohesion and coupling, with acceptable MQ values. In larger projects, the method showed scalability. For Archstudio (583 nodes, 866 dependencies), MQ remained high (6.01205), while cohesion (522) and coupling (340) reflected stable modularization. In the bash project (373 nodes, 901 dependencies), MQ was 3.18053, with high cohesion (767) but also increased coupling (1741) due to system complexity. Overall, the results confirm that the suggested SMC improves modular quality across projects of different scales. It consistently balances cohesion and coupling and ensures more maintainable software structures.

Table 7.
The performance of the suggested method for the new series of real-world software projects.
As shown in Table 8, the paired t-test analysis demonstrates that the proposed BBOA method performs significantly differently from most of the compared algorithms across the evaluated programs. Regarding the results, the BBOA shows statistically significant differences when compared to the GA, ACO, PSOGA, SFLA, GWO, and WOA, with p-values well below the 0.05 threshold. This indicates that the BBOA consistently provides improved performance over these methods. In contrast, the difference between the BBOA and SCSO is not statistically significant (p = 0.1524), suggesting that their performances are comparable. Overall, these results highlight the effectiveness and competitiveness of the BBOA, particularly in scenarios where other methods may struggle to achieve optimal clustered models.

Table 8.
The results of t-test statistical analysis on the results.
4.3.4. Discussion
The proposed BBOA demonstrates significant effectiveness in the domain of software module clustering by consistently yielding high MQ scores and achieving a well-balanced trade-off between cohesion and coupling. MQ serves as an integrated metric that encapsulates both the internal cohesion of modules and the coupling between them. The BBOA’s optimization strategy effectively explores the search space to discover modular boundaries that maximize cohesion (by grouping strongly related modules together) while simultaneously minimizing coupling by reducing unnecessary inter-cluster dependencies. This dual objective is crucial for producing software architectures that are not only logically sound but also easier to maintain, extend, and refactor. The results across multiple benchmark software systems reveal that the BBOA does not merely optimize MQ values in isolation but also ensures that clusters remain semantically meaningful and structurally decoupled. Furthermore, the BBOA maintains a strong global search ability while preserving good local solutions; it is suitable for different software sizes and complexities.
Clustering software modules based on source code and their dependencies (using the proposed method) can reveal the original design and business purpose of a system within the 4 + 1 architectural model. Module dependencies clarify the logical view and show how functionality is distributed. Clusters also reflect the development view by organizing code into coherent subsystems. In the process view, interactions between modules indicate runtime behavior. The physical view can be inferred by mapping clusters to deployment nodes. Finally, use-case scenarios are traced through clustered modules. Dependency-based clustering thus provides a practical way to reconstruct architectural insights and understand the business-driven design of software systems.
The scalability of the proposed SMC method is evidenced by its evaluation across a diverse set of real-world benchmark programs; the benchmark programs vary substantially in size and structural complexity. The results on benchmarks like dot (42 modules, 255 connections) and cia (38 modules, 216 connections) demonstrate that the method can effectively handle highly interconnected graphs where the average module connectivity exceeds five connections per module. Moreover, the successful clustering of a partial subset of PHP with 191 connections further underlines the method’s adaptability to complex and practical codebases. Overall, the benchmarks cover a scaling spectrum from lightweight software systems to larger and more complex systems. This quantitative variation (20–86 modules and 57–295 connections) confirms that the proposed SMC is scalable, generalizable, and applicable in practical software engineering environments.
In software architecture, metrics such as cohesion and coupling are essential for evaluating systems’ quality, maintainability, and scalability [18,19]. High cohesion within the logical and structural models ensures that each component has a clear responsibility, as seen in banking systems, where transaction modules remain focused on financial logic. Low coupling across the process and development models supports concurrency and independent evolution, a necessity in cloud-based microservices such as Netflix or Amazon, where services can be deployed or scaled independently. Recent studies highlight the importance of refined metrics: semantic-based cohesion and coupling measures significantly improve modularization accuracy and adaptability in large-scale architectures [19,20,21]. Thus, cohesion and coupling provide quantitative, objective insights that strengthen the robustness of architectural decisions across all 4 + 1 views.
In the suggested SMC method, the created design model enhances code comprehensibility and reduces maintenance costs by clustering software modules effectively and organizing source code into clear structures. The proposed discrete BBOA-based method improves modularization quality (MQ) by achieving higher cohesion and lower coupling, which are essential metrics of modularity and maintainability. Furthermore, the balanced trade-off between cohesion and coupling directly supports the creation of well-structured software systems, making the software projects easier to understand and evolve. The experimental results, particularly on large and complex systems, demonstrate that the model not only ensures robust modularity but also contributes to improved software architecture recovery; the created clustered models facilitate long-term understandability and maintainability.
The runtime comparison in Figure 12 shows differences among the evaluated SMC methods. Previous approaches such as the GA and PSO require longer execution times due to their iterative search processes. The hybrid PSO-GA achieves better balance but still incurs higher computational cost. In contrast, the proposed method demonstrates reduced runtime and provides higher efficiency in reaching optimal clustering. This reduction highlights the method’s scalability and suitability for larger software systems.
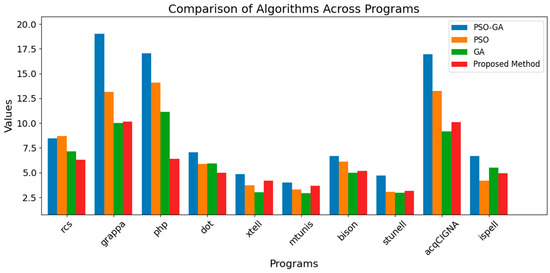
Figure 12.
The average runtime of different methods on different benchmarks.
Despite its strengths, the BBOA has certain limitations. One of the primary drawbacks is its cost when dealing with very large-scale software systems. Additionally, the BBOA, like many metaheuristic algorithms, may require careful parameter tuning to achieve optimal results, and inappropriate settings can lead to premature convergence or suboptimal clustering outcomes. Lastly, the BBOA does not explicitly incorporate domain-specific knowledge or semantic information, which could enhance the quality of clustering in context-sensitive applications. Therefore, while the BBOA proves to be a powerful and general-purpose clustering method, further enhancements could improve both its performance and applicability in practical software engineering environments.
One observed limitation of the proposed method is the occasional formation of single-module clusters that maintain notable coupling with multiple other clusters. While single-module clusters can be valid in certain scenarios (particularly when the module represents a distinct and self-contained functionality), the presence of high inter-cluster coupling suggests that such modules may be more appropriately integrated into a larger, semantically related cluster. This indicates a potential misalignment between structural dependencies and the clustering outcome. As shown in Figure 10, the similarity analysis reinforces the overall effectiveness of the BBOA. However, these observations point to areas where the clustering strategy could be enhanced to yield a more cohesive and maintainable software architecture.
5. Conclusions
Effective clustering of software modules and organizing the source code into well-defined structures significantly enhances code comprehensibility, which, in turn, reduces software maintenance costs. In this study, we developed a discrete version of the bedbug optimizer tailored specifically for the software module clustering problem. The proposed BBOA-based method demonstrates superior performance by generating clusters with higher cohesion and lower coupling. The method improved modularization quality (MQ) compared to several established methods, such as the GA, PSO, hybrid PSO-GA, SCSO, and ACO. Our approach effectively addresses common challenges in SMC, particularly avoiding premature convergence and achieving a well-balanced trade-off between coupling and cohesion (two fundamental metrics of high-quality software modules). The experimental results show that the BBOA maintains robust performance across software systems of varying sizes, with particularly notable advantages in handling larger, more complex codebases. Overall, this research contributes a valuable and effective solution for software module clustering, which leads to high-quality software architecture recovery and maintenance.
For future work, several promising directions emerge. First, developing adaptive or size-independent clustering algorithms could further enhance scalability and applicability across diverse software products. Second, integrating chaotic maps or other nonlinear dynamic strategies into the BBOA framework may improve its exploration capabilities and convergence speed. Third, revisiting the fitness function design to incorporate novel or composite software metrics could better capture nuanced aspects of modular quality.
Author Contributions
Methodology, B.A.; Software, B.A. and S.S.S.; Validation, S.S.S. and H.K.; Formal Analysis, S.S.S.; Investigation, B.A.; Writing—Original Draft, B.A., H.K., and F.K.; Writing—Review and Editing, H.K. and F.K.; Project Administration, B.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BBOA | Bedbug Optimization Algorithm |
| GA | Genetic Algorithm |
| GBest | Global Best |
| LBest | Local Best |
| MDG | Module Dependency Graph |
| MQ | Modularization Quality |
| w | Inertia Weight |
| PSO | Particle Swarm Optimization |
| Rc | Repulsion Coefficient |
| SBest | Social Best |
| SCSO | Sand Cat Swarm Optimization |
| SFLA | Shuffled Frog Leaping Algorithm |
| SMC | Software Module Clustering |
| εg | Equilibrium Constant |
References
- Tan, A.J.J.; Chong, C.Y.; Aleti, A. REARRANGE: Effort estimation approach for software clustering-based remodularisation. Inf. Softw. Technol. 2024, 176, 107567. [Google Scholar] [CrossRef]
- Chhabra, A.J.K. TA-ABC: Two-Archive Artificial Bee Colony for Multi-Objective Software Module Clustering Problem. J. Intell. Syst. 2018, 27, 619–641. [Google Scholar] [CrossRef]
- Prajapati, A.; Chhabra, J.K. A Particle Swarm Optimization-Based Heuristic for Software Module Clustering Problem. Arab. J. Sci. Eng. 2018, 43, 7083–7094. [Google Scholar] [CrossRef]
- Varol, T.; Elyasi, M.; Aktaş, T.H.; Karakaya, M. Parallelization of Genetic Algorithms for Software Architecture Recovery. Autom. Softw. Eng. 2025, 32, 9. [Google Scholar] [CrossRef]
- Gribkov, N.A.; Ovasapyan, T.D.; Moskvin, D.A. Analysis of Decompiled Program Code Using Abstract Syntax Trees. Autom. Control. Comput. Sci. 2023, 57, 958–967. [Google Scholar] [CrossRef]
- Yuste, J.; Duarte, A.; Pardo, E.G. An Efficient Heuristic Algorithm for Software Module Clustering Optimization. J. Syst. Softw. 2022, 190, 111349. [Google Scholar] [CrossRef]
- Arasteh, B.; Sadeghi, R.; Keyvan, A. ARAZ: A Software Modules Clustering Method Using the Combination of Particle Swarm Optimization and Genetic Algorithms. Intell. Decis. Technol. 2020, 14, 449–462. [Google Scholar] [CrossRef]
- Mohammadi, S.; Izadkhah, H. A new algorithm for software clustering considering the knowledge of dependency between artifacts in the source code. Inf. Softw. Technol. 2019, 105, 252–256. [Google Scholar] [CrossRef]
- Arasteh, B.; Sadegi, R.; Arasteh, K. Bölen: Software Module Clustering Method Using the Combination of Shuffled Frog Leaping and Genetic Algorithm. Data Technol. Appl. 2021, 55, 251–279. [Google Scholar] [CrossRef]
- Arasteh, B.; Abdi, M.; Bouyer, A. Program Source Code Comprehension by Module Clustering Using a Combination of Discretized Gray Wolf and Genetic Algorithms. Adv. Eng. Softw. 2022, 173, 103252. [Google Scholar] [CrossRef]
- Arasteh, B. Clustered Design-Model Generation from a Program Source Code Using Chaos-Based Metaheuristic Algorithms. Neural Comput. Appl. 2022, 35, 3283–3305. [Google Scholar] [CrossRef]
- Arasteh, B.; Fatolahzadeh, A.; Kiani, F. Savalan: Multi-Objective and Homogeneous Method for Software Modules Clustering. J. Softw. Evol. Process 2022, 34, e2408. [Google Scholar] [CrossRef]
- Joseph, A.; Yeo, C.; Aleti, A. E-SC4R: Explaining Software Clustering for Remodularisation. J. Syst. Softw. 2022, 186, 111162. [Google Scholar] [CrossRef]
- Olsson, T.; Ericsson, M.; Wingkvist, A. To Automatically Map Source Code Entities to Architectural Modules with Naive Bayes. J. Syst. Softw. 2022, 183, 111095. [Google Scholar] [CrossRef]
- Mohan, A.; Jayaraman, S.; Jayaraman, B. A Declarative Approach to Detecting Design Patterns from Java Execution Traces and Source Code. Inf. Softw. Technol. 2024, 171, 107457. [Google Scholar] [CrossRef]
- Arasteh, B.; Seyyedabbasi, A.; Rasheed, J.; Abu-Mahfouz, A.M. Program Source-Code Re-Modularization Using a Discretized and Modified Sand Cat Swarm Optimization Algorithm. Symmetry 2023, 15, 401. [Google Scholar] [CrossRef]
- Rezvani, K.; Gaffari, A.; Dishabi, M.R.E. The Bedbug Meta-Heuristic Algorithm to Solve Optimization Problems. J. Bionic Eng. 2023, 20, 2465–2485. [Google Scholar] [CrossRef]
- Yang, K.; Wang, J.; Fang, Z.; Wu, P.; Song, Z. Enhancing software modularization via semantic outliers filtration and label propagation. Inf. Softw. Technol. 2022, 145, 106818. [Google Scholar] [CrossRef]
- Alzamil, Z.A. Software Coupling and Cohesion Model for Measuring the Quality of Software Components. Comput. Mater. Contin. 2023, 77, 3139–3161. [Google Scholar] [CrossRef]
- Mohottige, T.I.; Polyvyanyy, A.; Fidge, C.; Buyya, R.; Barros, A. Reengineering software systems into microservices: State-of-the-art and future directions. Inf. Softw. Technol. 2025, 183, 107732. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Y.; Jiao, T.; Bai, L.; Guo, C.; Song, J. Learning code better through structural information of data flow. J. Supercomput. 2025, 81, 882. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).