DSCSRN: Physically Guided Symmetry-Aware Spatial-Spectral Collaborative Network for Single-Image Hyperspectral Super-Resolution

Abstract

Hyperspectral images (HSIs), with their rich spectral information, are widely used in remote sensing; yet the inherent trade-off between spectral and spatial resolution in imaging systems often limits spatial details. Single-image hyperspectral super-resolution (HSI-SR) seeks to recover high-resolution HSIs from a single low-resolution input, but the high dimensionality and spectral redundancy of HSIs make this task challenging. In HSIs, spectral signatures and spatial textures often exhibit intrinsic symmetries, and preserving these symmetries provides additional physical constraints that enhance reconstruction fidelity and robustness. To address these challenges, we propose the Dynamic Spectral Collaborative Super-Resolution Network (DSCSRN), an end-to-end framework that integrates physical modeling with deep learning and explicitly embeds spatial–spectral symmetry priors into the network architecture. DSCSRN processes low-resolution HSIs with a Cascaded Residual Spectral Decomposition Network (CRSDN) to compress redundant channels while preserving spatial structures, generating accurate abundance maps. These maps are refined by two Synergistic Progressive Feature Refinement Modules (SPFRMs), which progressively enhance spatial textures and spectral details via a multi-scale dual-domain collaborative attention mechanism. The Dynamic Endmember Adjustment Module (DEAM) then adaptively updates spectral endmembers according to scene context, overcoming the limitations of fixed-endmember assumptions. Grounded in the Linear Mixture Model (LMM), this unmixing–recovery–reconstruction pipeline restores subtle spectral variations alongside improved spatial resolution. Experiments on the Chikusei, Pavia Center, and CAVE datasets show that DSCSRN outperforms state-of-the-art methods in both perceptual quality and quantitative performance, achieving an average PSNR of 43.42 and a SAM of 1.75 (×4 scale) on Chikusei. The integration of symmetry principles offers a unifying perspective aligned with the intrinsic structure of HSIs, producing reconstructions that are both accurate and structurally consistent.

1. Introduction

Hyperspectral imaging, which integrates spatial and spectral information, has attracted increasing attention in recent years for applications in remote sensing and fine-grained recognition tasks. Hyperspectral images (HSIs) simultaneously capture two-dimensional spatial information along with dozens to hundreds of contiguous, narrow spectral bands. Each pixel in an HSI contains not only spatial location data but also complete spectral features, enabling the identification of subtle spectral differences across various materials. This high-dimensional representation grants HSIs superior material discrimination capabilities compared to multispectral or natural images. Thanks to their rich spectral characteristics, HSIs are widely applied in high-precision sensing tasks such as defect detection [1], mineral exploration [2], agricultural monitoring [3], and environmental protection [4]. However, due to the limited energy reception capacity of imaging sensors, acquiring narrow and continuous spectral bands typically requires lowering the spatial sampling rate within a fixed acquisition time, leading to image blurring and loss of spatial details. This reduction in spatial resolution undermines the image’s ability to represent fine-grained spatial structures and negatively affects performance in practical tasks such as change detection [5], object recognition [6], and classification [7]. Notably, many hyperspectral scenes and their spectral–spatial representations possess inherent symmetries, such as repetitive textures in spatial patterns and balanced reflectance characteristics across certain spectral bands. Exploiting these symmetries can act as an additional prior, reinforcing both the physical and structural consistency of reconstructed HSIs. Motivated by the challenges of low spatial resolution, HSI-SR has emerged as an active research area. HSI-SR enhances the spatial resolution of HSIs through post-processing, without requiring modifications to the imaging hardware. This approach not only improves visual quality but also provides richer spatial–spectral representations for downstream tasks, making it valuable in both theoretical research and practical applications. Current HSI-SR methods can be broadly categorized into two types: fusion-based super-resolution and single-image super-resolution [8]. Fusion-based methods typically integrate low-resolution HSIs with high-resolution multispectral or RGB images to reconstruct high-quality, high-resolution HSIs [9]. In contrast, single-image methods rely solely on a low-resolution HSI for super-resolution, eliminating the need for auxiliary data [10]. This independence simplifies data acquisition and avoids the challenges of image alignment, making single-image approaches more practical and adaptable.

Early single-image HSI-SR methods were primarily based on traditional image processing techniques, such as bicubic interpolation [11], edge-guided reconstruction [12], sparse representation [13], and low-rank tensor recovery [14]. While these methods have achieved certain improvements under predefined priors, they generally suffer from limited modeling capacity and struggle to recover complex textures and details. With the advancement of deep learning, convolutional neural network (CNN)-based methods for HSI-SR have achieved remarkable progress [15]. Mei et al. [16] proposed a method based on a three-dimensional fully convolutional neural network (3D-FCNN) to jointly model spectral and spatial information, capturing spectral–spatial correlations at the voxel level. However, HSIs typically consist of hundreds of spectral bands, resulting in significant computational and storage overhead in practical applications. Moreover, the intrinsic locality of 3D convolutions restricts their ability to capture long-range spectral dependencies. To address these limitations, Li et al. [17] proposed a divide-and-conquer strategy, partitioning the spectral dimension into multiple subgroups for separate modeling. This approach reduced computational complexity and improved network efficiency. However, it failed to fully consider inter-group redundancy and cross-channel correlations, which constrained the overall reconstruction performance. To better capture critical information, Hu et al. [18] introduced a spectral-spatial attention mechanism that assigns explicit weights to features by evaluating the importance of different spectral channels and spatial locations. Although this method improved spectral fidelity and detail restoration, spectral distortions still occurred in complex scenes. Additionally, these attention-based methods heavily rely on feature fusion strategies, which reduce their robustness and generalization ability. Furthermore, Li et al. [19] developed a multi-stage refinement framework, and Yan et al. [20] proposed a recursive residual enhancement method to improve high-frequency detail recovery. However, their increased structural complexity and training costs hinder practical deployment. More recently, Li et al. [21] introduced Transformer-based architectures and frequency-domain modeling to capture long-range dependencies, further enhancing reconstruction quality. Nevertheless, these methods face challenges such as large parameter counts [22], slow training convergence [23], and limited adaptability to small-sample scenarios [24], which restrict their applications. Recent studies have shown that incorporating physical priors, such as abundance modeling, can help alleviate redundancy caused by high spectral dimensionality [25]. In particular, the linear mixture model (LMM) framework [26], which maps low-resolution HSIs to a low-dimensional abundance space and combines endmember information to reconstruct high-resolution images, has proven to be an effective and physically interpretable approach. For example, the aeDPCN framework proposed by Wang et al. [27] employs an autoencoder to extract abundance features and uses dilated convolutional networks to progressively refine reconstruction, achieving high-quality results with low computational cost.

Despite advancements in network design and reconstruction performance, current methods still face three critical challenges. First, most approaches focus solely on feature-level spectral–spatial fusion while overlooking the physical prior that HSIs are formed by a limited number of endmembers through linear mixing, thereby compromising the physical consistency of spectral reconstruction. Second, these methods often struggle to accurately model mixed pixels in low-resolution images, leading to suboptimal recovery of high-frequency details, particularly in complex scenes. Third, the spatial and spectral attention mechanisms in fusion modules are typically designed in isolation, lacking deep interaction and resulting in limited synergy between spatial textures and spectral features. Consequently, there is an urgent need for a method that can incorporate spectral unmixing priors and strengthen the joint modeling of spectral and spatial information, in order to achieve more accurate and physically consistent HSI-SR. Equally important, explicitly modeling spatial–spectral symmetries offers a complementary pathway to reduce redundancy, better handle mixed pixels, and align the reconstruction process with the intrinsic organization of real-world hyperspectral data.

To address these issues, we propose the Dynamic Spectral Collaborative Super-Resolution Network (DSCSRN)—an HSI-SR framework that integrates the strengths of physical priors with deep learning. The core idea is to establish a super-resolution closed-loop process, leveraging abundance maps as intermediaries and grounded in the LMM. This design enables the synergistic enhancement of spatial detail and spectral consistency through a two-stage progressive reconstruction strategy. Unlike prior works that independently adopt spatial–spectral priors, attention mechanisms, or unmixing-based strategies, DSCSRN introduces a collaborative closed-loop framework that unifies these paradigms under the guidance of the LMM. Specifically, (i) CRSDN estimates abundances with residual refinement, (ii) DEAM dynamically adjusts endmember representations to strengthen spectral reconstruction, and (iii) SPFRM progressively enhances spatial–spectral features via the DDSA mechanism. This synergy not only ensures strong physical interpretability but also delivers superior reconstruction accuracy, distinguishing DSCSRN from existing approaches. Our main contributions are summarized as follows:

(1)

Unified Physics–Deep Learning framework: Embedding the LMM into a data-driven architecture bridges the gap between traditional spectral unmixing and modern deep learning, directly addressing the neglect of physical priors and improving the physical interpretability of reconstructed spectra. By incorporating symmetry priors into this framework, the network benefits from balanced dual-domain processing that reflects the natural organization of spectral–spatial information.

(2)

Cascaded Residual Spectral Decomposition Network (CRSDN): By performing residual channel compression and spatial preservation simultaneously, CRSDN enforces the spectral formation prior while reducing spectral redundancy, enabling accurate and efficient abundance estimation—thereby overcoming the challenge of physically inconsistent spectral reconstruction. Its channel–spatial decomposition structure follows a symmetric processing pattern across domains, ensuring balanced feature extraction.

(3)

Two Synergistic Progressive Feature Refinement Modules (SPFRMs): Arranged sequentially, SPFRM employs a two-level upsampling structure with multiple Dual-Domain Synergy Attention (DDSA) blocks to progressively recover spatial textures and spectral details. This design directly mitigates the difficulty of modeling mixed pixels and restores high-frequency details even in complex scenes. The dual-branch DDSA is inherently symmetric in its spatial and spectral pathways, enabling mutual enhancement and avoiding bias toward a single domain.

(4)

Dynamic Endmember Adjustment Module (DEAM): By adaptively updating endmember signatures according to scene context, DEAM overcomes the rigidity of fixed-endmember assumptions and strengthens the synergy between spectral and spatial domains, solving the limitation of isolated attention mechanisms. The DEAM process maintains symmetry in its treatment of spectral endmembers and abundance maps, ensuring consistency in both directions of the reconstruction pipeline.

2. Methods

2.1. Overall Architecture

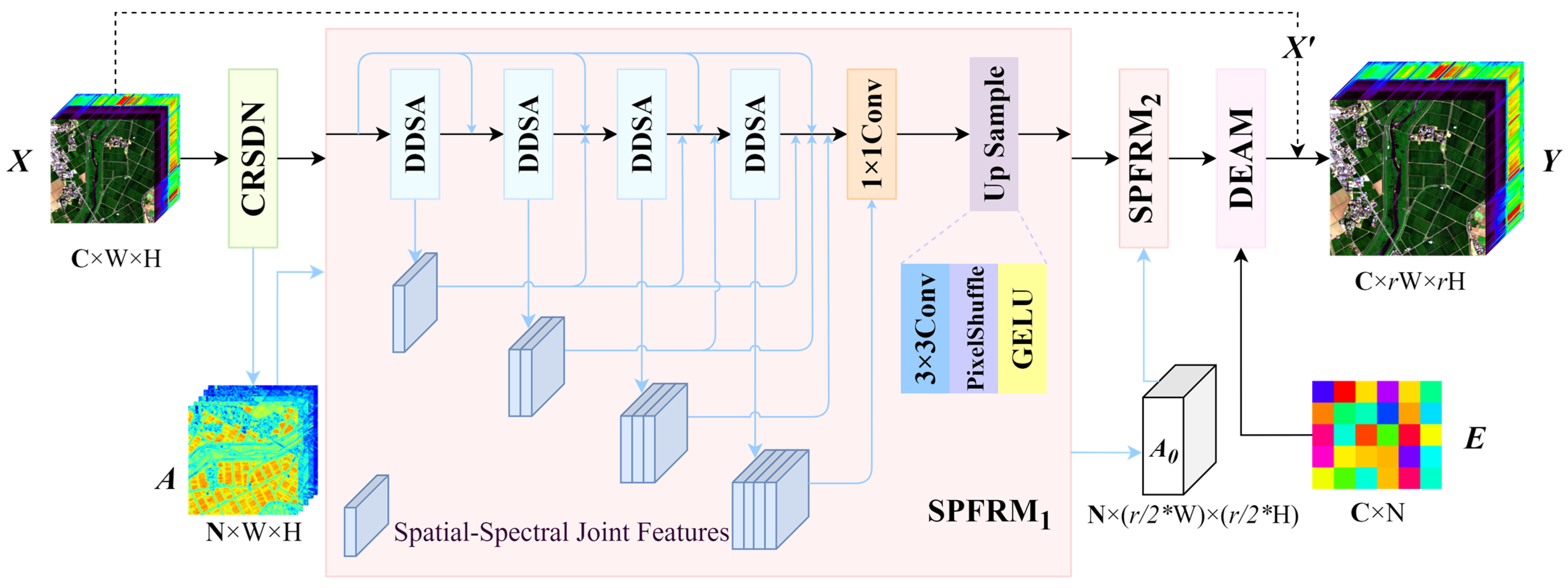
The architecture of the DSCSRN network is illustrated in Figure 1. Based on the LMM, the framework adopts a three-stage process of unmixing–recovery–reconstruction, encompassing spectral unmixing modeling, abundance map recovery, and high-frequency detail reconstruction. This hierarchical design enables collaborative optimization that integrates physical modeling with high-fidelity image reconstruction. Moreover, the architecture is intentionally designed with spatial–spectral symmetry in mind: each processing stage maintains a balanced, dual-path interaction between spatial and spectral domains, ensuring that improvements in one domain are mirrored and reinforced in the other.

Specifically, the input low-resolution hyperspectral image $\mathit{X}\in {\mathbb{R}}^{C\times W\times H}$ is first processed by the CRSDN to generate the initial abundance map $\mathit{A}\in {\mathbb{R}}^{N\times W\times H}$, where C denotes the number of spectral channels, N is the number of endmembers, and W × H represents the spatial resolution. CRSDN preserves both the spatial distribution and the low-dimensional spectral structure of the input, providing a physically meaningful prior for the subsequent super-resolution stages. This initial stage forms a symmetric mapping between spectral signatures and their spatial distributions, acting as the first step of the network’s symmetry-preserving pipeline.

Building on CRSDN’s output, SPFRM enhances the spatial resolution of the abundance map in two stages. Each SPFRM incorporates multiple DDSA modules (see Figure 1) to progressively extract and fuse spatial–spectral features. The first SPFRM upsamples $\mathit{A}$ to an intermediate resolution, yielding ${\mathit{A}}_{\mathbf{0}}\in {\mathbb{R}}^{N\times (r/2\ast W)\times (r/2\ast H)}$, while the second SPFRM further refines it to produce the high-resolution abundance map $\mathit{A}\prime \in {\mathbb{R}}^{N\times rW\times rH}$, where $r$ is the spatial scaling factor. The two-stage SPFRM processing exhibits a scale-symmetric refinement: each upsampling step mirrors the spectral–spatial attention flow, ensuring that feature enhancement is structurally consistent across resolutions.

Subsequently, the DEAM leverages $\mathit{A}\prime$ and a globally shared endmember library $\mathit{E}\in {\mathbb{R}}^{C\times N}$ to adaptively refine endmember representations through context-aware modulation. These adjusted endmembers are linearly combined with $\mathit{A}\prime$ to generate a preliminary high-resolution hyperspectral image ${\mathit{Y}}_{\mathbf{0}}\in {\mathbb{R}}^{C\times rW\times rH}$. This adaptive refinement also follows a symmetry-driven design, treating each endmember–abundance pair as a matched structural unit to maintain balance between spectral precision and spatial coherence.

To enhance texture recovery, a global residual connection incorporates a bicubically upsampled version of the input image, $\mathit{X}\prime \in {\mathbb{R}}^{C\times rW\times rH}$, which is added to ${\mathit{Y}}_{\mathbf{0}}$ to produce the final reconstructed image $\mathit{Y}\in {\mathbb{R}}^{C\times rW\times rH}$. The residual addition completes a symmetry loop, aligning the reconstructed output with both the original low-resolution input and the refined high-resolution prediction.

Unlike a purely sequential design, DSCSRN implements the unmixing–recovery–reconstruction pipeline in a closed-loop, end-to-end manner. Abundance maps estimated by CRSDN are iteratively refined through DEAM, while SPFRMs progressively enforce spatial–spectral consistency. This joint optimization, combined with multi-level supervision, effectively suppresses error propagation across stages and ensures stable, high-fidelity reconstructions.

In summary, DSCSRN’s hierarchical architecture revolves around CRSDN as the cornerstone, with SPFRM and DEAM collaboratively refining its output to achieve high-quality hyperspectral reconstruction. By embedding symmetry principles into the network’s multi-stage pipeline and feature interaction design, DSCSRN achieves a harmonious balance between spatial detail enhancement and spectral fidelity, which is essential for physically consistent reconstruction. This bottom-up process balances physical interpretability with the expressive power of deep neural networks, ensuring robust performance under stringent structural and spectral constraints.

2.2. Cascaded Residual Spectral Decomposition Network

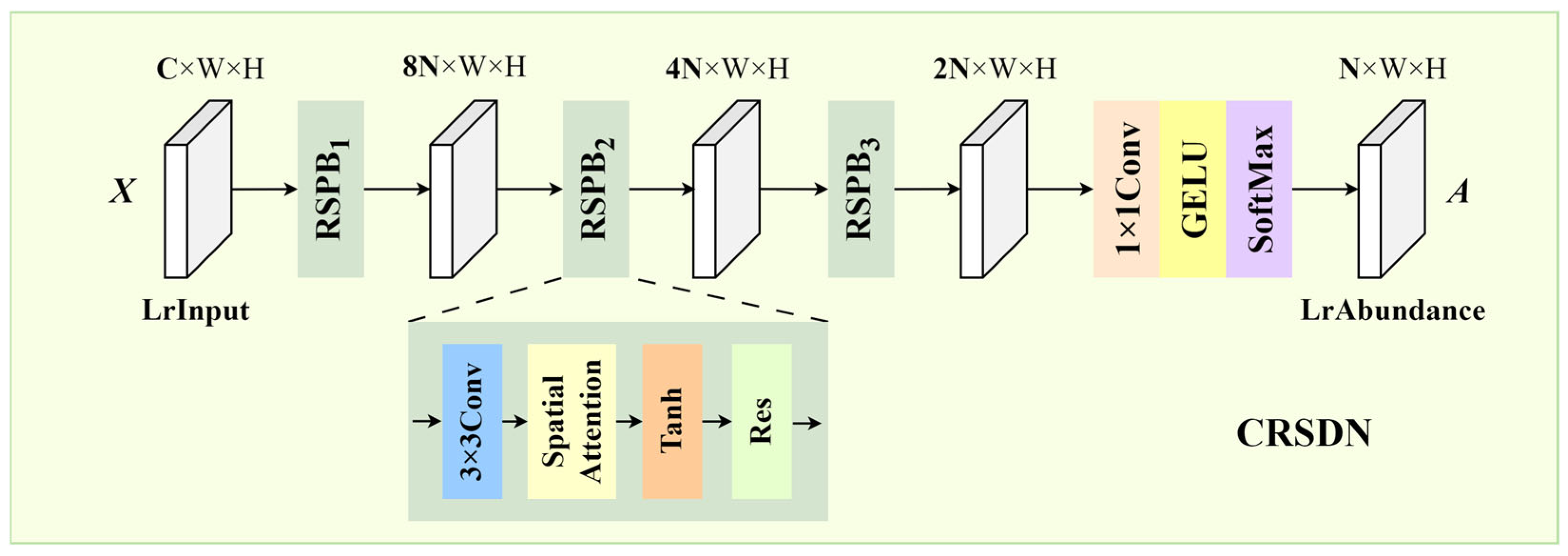
To obtain physically interpretable abundance representations from low-resolution HSIs, we designed the CRSDN as the first-stage core module (Figure 2). Unlike existing single-image HSI-SR methods that directly fuse spectral–spatial features without explicit physical constraints—often leading to physically inconsistent spectra in mixed-pixel-rich scenes—CRSDN embeds the spectral unmixing process, grounded in LMM, into the network architecture. This integration allows the network to compress redundant spectral channels while preserving spatial structures, producing abundance maps that adhere to non-negativity and sum-to-one constraints, and thereby provides a physically meaningful prior for subsequent high-resolution reconstruction.

This module is grounded in the classical LMM, which assumes that the spectral vector of each pixel can be expressed as a linear combination of multiple endmember spectra:

$${\mathit{X}}_{\mathbf{1}}\left(i,j\right)=\sum _{n=1}^N A_{n,i,j}\cdot {\mathit{e}}_n+\epsilon$$

(1)

Here, ${\mathit{X}}_{\mathbf{1}}(i,j)\in {\mathbb{R}}^C$ denotes the observed spectral vector at pixel location $(i,j)$, ${\mathbf{e}}_n\in {\mathbb{R}}^C$ represents the spectral signature of the n-th endmember, $A_{n,i,j}$ is the corresponding abundance coefficient, and $\epsilon$ is a residual error term.

Within the proposed framework, CRSDN takes the low-resolution hyperspectral image $\mathit{X}$ as input and generates the corresponding abundance maps $\mathit{A}$:

$$\mathit{A}=H_{\mathrm{C}\mathrm{R}\mathrm{S}\mathrm{D}\mathrm{N}}\left(\mathit{X}\right)$$

(2)

The architecture of CRSDN follows a layer-wise residual stacking design, consisting of multiple Residual Space Preservation Blocks (RSPBs) arranged in series. As shown in Figure 2, each RSPB contains a 3 × 3 convolutional layer, a Spatial Attention (SA) mechanism [28], a Tanh activation function [29], and a residual connection that directly links the input and output of the block.

The SA layer enhances the model’s capacity to capture fine-grained local features by integrating global spatial context, making it especially effective at delineating edges and structural transitions. The Tanh activation function provides smooth nonlinear mapping while mitigating the gradient saturation problem, maintaining a stable gradient flow during training. Meanwhile, the residual connection facilitates shallow feature reuse and enables better information propagation across layers, effectively mitigating degradation in deep structures.

The channel dimension in the RSPBs is progressively reduced in a cascading fashion as follows:

$$C\stackrel{{\mathrm{R}\mathrm{S}\mathrm{P}\mathrm{B}}_1}{\to }8N\stackrel{{\mathrm{R}\mathrm{S}\mathrm{P}\mathrm{B}}_2}{\to }4N\stackrel{{\mathrm{R}\mathrm{S}\mathrm{P}\mathrm{B}}_3}{\to }2N$$

(3)

This progressive channel compression mechanism aids in aggregating high-dimensional spectral features into a compact representation, mitigating the “curse of dimensionality” [30] while preserving multi-scale spectral information.

After the final RSPB, a 1 × 1 convolutional layer maps the channel dimension to N, corresponding to the number of endmembers. The output is subsequently passed through the GELU activation function [31], which enhances the nonlinearity modeling capacity of the network. To ensure physical interpretability, the model imposes two constraints from the LMM—non-negativity and sum-to-one—on the abundance maps via Softmax normalization [32]:

$$A_{n,i,j}={\displaystyle \frac{\mathit{exp}\left({\mathcal{Z}}_{n,i,j}\right)}{{\sum }_{l=1}^K\mathit{exp}\left({\mathcal{Z}}_{l,i,j}\right)}}$$

(4)

where ${\mathcal{Z}}_{n,i,j}$ denotes the unnormalized abundance response of the n-th endmember at pixel $(i,j)$. This operation ensures that all abundance coefficients are non-negative and sum to one at each pixel, thereby aligning with the physical principles of hyperspectral unmixing. Enforcing these constraints not only enhances the physical realism of the reconstruction process but also improves the model’s generalization across diverse scenes.

Beyond these standard constraints, CRSDN introduces a symmetry prior to enhance physical interpretability. The key intuition is that abundance maps corresponding to spectrally correlated or geometrically symmetric endmembers should exhibit structural consistency. This is formulated as:

$${\mathcal{L}}_{sym}=\sum _{\left(i, j\right)ϵ\mathcal{P}}{‖A_i-\mathcal{S}\left(A_j\right)‖}_2^2$$

(5)

where $A_i$ and $A_j$ denote the abundance maps of an endmember pair $(i,j)$, and $\mathcal{S}(·)$ represents a predefined symmetry transformation. Unlike conventional regularization that penalizes parameter magnitudes, this prior encodes a physically grounded constraint, ensuring consistency across abundance maps of symmetric spectral structures.

Collectively, CRSDN integrates (i) LMM-guided unmixing constraints (non-negativity and sum-to-one), (ii) residual cascaded compression with spatial attention for effective spectral–spatial feature preservation, and (iii) a symmetry prior that enforces structural consistency across abundance maps. This combination yields abundance representations that are both physically interpretable and robust, providing a solid foundation for the subsequent refinement modules in DSCSRN.

2.3. Synergistic Progressive Feature Refinement Module

To bridge the gap between physically interpretable abundance estimation and perceptually faithful high-resolution reconstruction, we propose the SPFRM as the second-stage core component of the DSCSRN framework. Unlike direct single-step upsampling strategies that often amplify noise and blur fine textures, SPFRM adopts a progressive refinement paradigm, gradually enhancing structural integrity and spectral fidelity through coarse-to-fine optimization. By embedding cross-domain feature interactions—explicitly coupling spatial and spectral cues—into each refinement stage, SPFRM not only improves local detail recovery but also enhances robustness to spectral distortions, ensuring that the reconstructed HSI remains consistent with both physical priors and high-frequency scene details.

Within the DSCSRN framework, SPFRM adopts a two-stage stacked structure for coarse recovery and fine enhancement. Given a scaling factor $r\in \left\{\mathrm{4,8}\right\}$, the first stage upsamples the initial abundance map $\mathit{A}\in {\mathbb{R}}^{N\times W\times H}$ by a factor of r/2, producing an intermediate map ${\mathit{A}}_{\mathbf{0}}\in {\mathbb{R}}^{N\times (r/2\ast W)\times (r/2\ast H)}$. The second stage then performs another 2× upsampling, resulting in the final high-resolution abundance map $\mathit{A}\prime \in {\mathbb{R}}^{N\times rW\times rH}$. This progressive design facilitates layer-wise optimization from structural perception to fine-grained detail enhancement:

$${\mathit{A}}_{\mathbf{0}}={\mathrm{S}\mathrm{P}\mathrm{F}\mathrm{R}\mathrm{M}}_1\left(\mathit{A}\right),\hspace{1em}{\mathit{A}}^{\mathit{\prime }}={\mathrm{S}\mathrm{P}\mathrm{F}\mathrm{R}\mathrm{M}}_2\left({\mathit{A}}_{\mathbf{0}}\right)$$

(6)

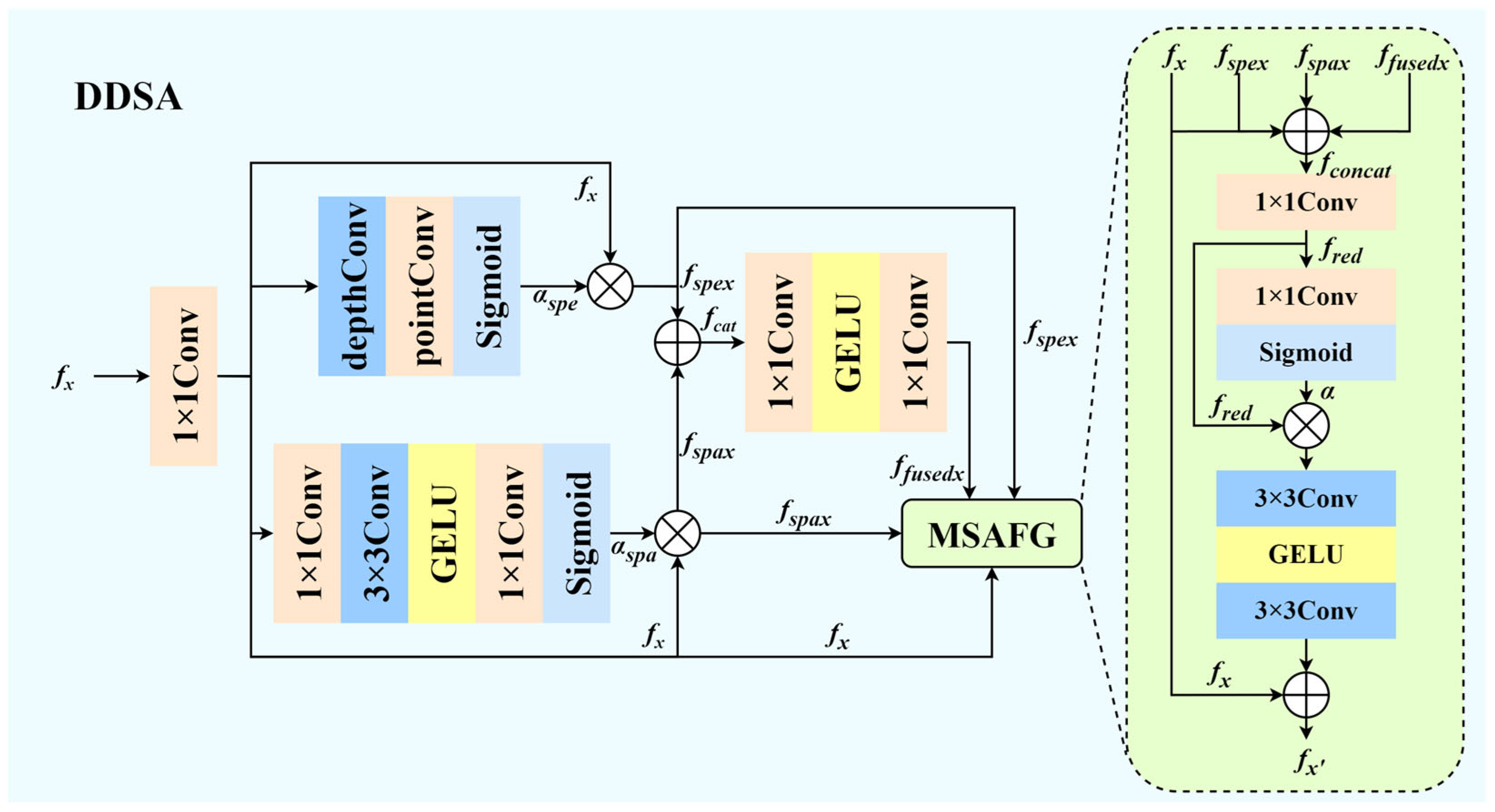
Each SPFRM module incorporates multiple DDSA units, whose detailed structure is illustrated in Figure 3. DDSA is designed to jointly extract spatial and spectral features, achieving effective multi-scale refinement. Given an input feature $f_x\in {\mathbb{R}}^{N\times W\times H}$, DDSA models spectral and spatial interactions through two parallel branches.

In the spectral branch, to capture inter-band relationships and spectral correlations, depthwise convolution [33] is first applied to extract local responses of each band, followed by pointwise convolution [34] to integrate cross-channel information. This yields the spectral attention map:

$${\alpha }_{spe}=\sigma \left({Conv}_{1\times 1}\left({Conv}_{3\times 3}^{dw}\left(f_x\right)\right)\right)$$

(7)

where $\sigma (·)$ is the Sigmoid function. The enhanced spectral features are obtained via element-wise multiplication: $f_{spex}=f_x·{\alpha }_{spe}$.

In parallel, the spatial branch enhances structural sensitivity and texture details. The channel dimension is compressed through a 1 × 1 convolution, producing $f_{red}\in {\mathbb{R}}^{C/2\times W\times H}$, followed by a 3 × 3 convolution with GELU activation and another 1 × 1 convolution to generate the spatial attention map:

$${\alpha }_{spa}=\sigma \left({Conv}_{1\times 1}\left(GELU\left({Conv}_{3\times 3}\left(f_{red}\right)\right)\right)\right)$$

(8)

The spatially enhanced output is $f_{spax}=f_x·{\alpha }_{spa}$.

To fuse spatial and spectral features, the two outputs $f_{spex}$ and $f_{spax}$ are concatenated along the channel dimension, forming $f_{cat}\in {\mathbb{R}}^{2C\times H\times W}$, and then passed through two sequential 1 × 1 convolutions with GELU activation:

$$f_{fusedx}={\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}}_{1\times 1}^{\left(2\right)}\left(GELU\left({Conv}_{1\times 1}^{\left(1\right)}\left(f_{cat}\right)\right)\right)$$

(9)

This process generates high-order features that effectively combine spatial and spectral information with reduced computational complexity.

Finally, to adaptively fuse the original and enhanced features, DDSA employs a Multi-Source Adaptive Fusion Gate (MSAFG). The four feature maps $f_x,{ f}_{spex},f_{spax}, \mathrm{and} f_{fusedx}$ are concatenated and compressed to $f_{red}\in {\mathbb{R}}^{C\times H\times W}$ via a 1 × 1 convolution. A gating map $\alpha \in {\left[\mathrm{0,1}\right]}^{C\times W\times H}$ is generated by another 1 × 1 convolution followed by a Sigmoid function:

$$\alpha =\sigma \left({\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}}_{1\times 1}\left(f_{red}\right)\right)$$

(10)

The final fused feature is obtained through gated multiplication and residual connection:

$$f_x^{\prime }={\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}}_{3\times 3}^{\left(2\right)}\left(\mathrm{G}\mathrm{E}\mathrm{L}\mathrm{U}\left({\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}}_{3\times 3}^{\left(1\right)}\left(f_{red}\cdot \alpha \right)\right)\right)+f_x$$

(11)

Unlike conventional attention that may simply amplify dominant features, our collaborative attention mechanism is explicitly formulated to align spatial–spectral dependencies across multiple scales, ensuring consistent feature refinement throughout the reconstruction pipeline. Moreover, by employing a gating strategy with dynamic weighting, it suppresses redundant feature responses while preserving complementary information, thereby enhancing cross-scale consistency without introducing unnecessary complexity.

Taken together, SPFRM integrates progressive upsampling, dual-branch spatial–spectral attention, and multi-source adaptive fusion into a unified refinement pipeline. This design enables stepwise enhancement from structural perception to fine-grained texture reconstruction, while maintaining spectral consistency through adaptive cross-domain interactions. By jointly leveraging abundance priors and learned high-order features, SPFRM effectively mitigates detail loss, suppresses spectral artifacts, and delivers high-resolution HSIs with both physical plausibility and visual fidelity. Furthermore, the progressive refinement inherently respects a form of structural symmetry, where spatial details and spectral patterns are iteratively balanced and reinforced across scales. This symmetry-driven interaction ensures that enhancement in one domain does not compromise the other, resulting in reconstructions that exhibit both geometrical coherence and spectral integrity.

2.4. Dynamic Endmember Adjustment Module

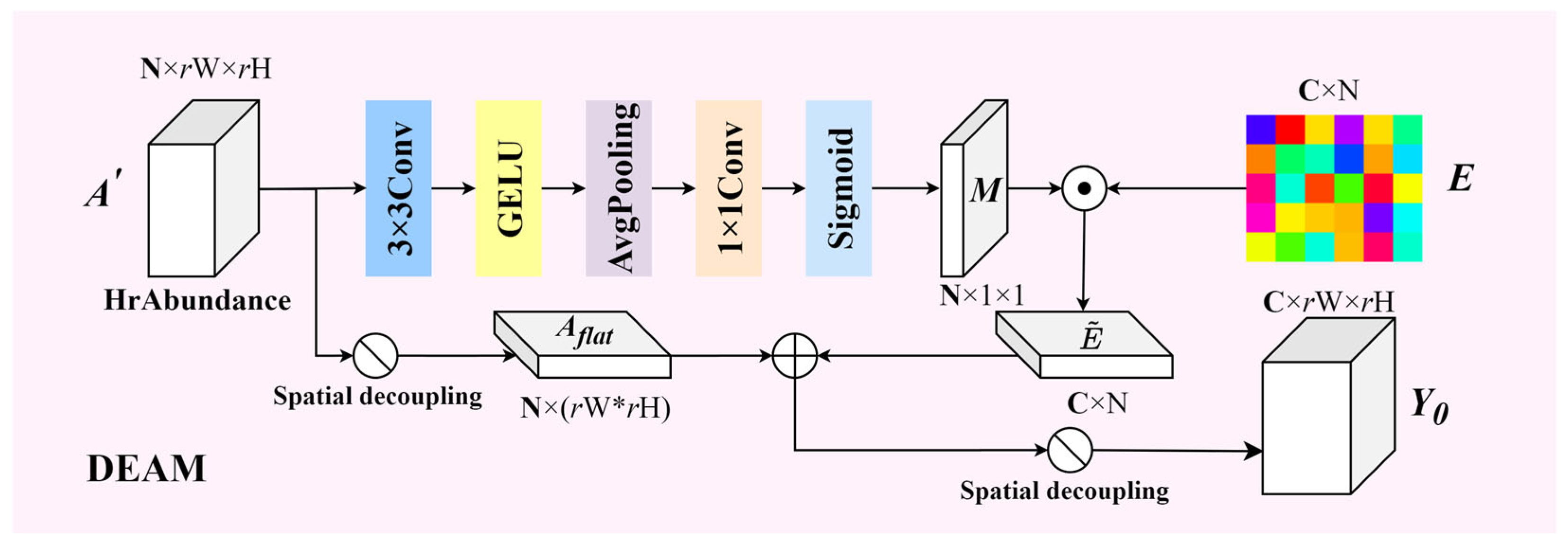
The Dynamic Endmember Adjustment Module (DEAM) is designed to address the challenges of complex and nonlinear spectral mixing by adaptively refining endmember representations and enhancing the fusion between abundances and endmembers, as shown in Figure 4. Through a nonlinear mapping from abundance space to spectral space, DEAM captures intricate spectral dependencies, enabling more accurate reconstruction and improved spectral fidelity.

DEAM begins with an attention generation sub-network, which aggregates spatial features from the input abundance map $\mathit{A}\in {\mathbb{R}}^{N\times W\times H}$. This process extracts importance weights for each endmember across samples by applying convolution, GELU activation, global average pooling, and a Sigmoid function to generate an attention map $\mathit{M}\in {\mathbb{R}}^{N\times 1\times 1}$:

$$\mathit{M}=\sigma \left({\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}}_{1\times 1}\left(\mathrm{A}\mathrm{v}\mathrm{g}\mathrm{P}\mathrm{o}\mathrm{o}\mathrm{l}\left(\mathrm{G}\mathrm{E}\mathrm{L}\mathrm{U}\left({Conv}_{3\times 3}\left(\mathit{A}\right)\right)\right)\right)\right)$$

(12)

Here, $\sigma (\cdot )$ denotes the Sigmoid function, and AvgPool represents adaptive global average pooling, which captures the global spatial context.

The generated attention map is then used to adaptively adjust the globally shared endmember library $\mathit{E}\in {\mathbb{R}}^{C\times N}$, allowing the model to refine endmember representations per sample. For the b-th sample, the adjusted endmember matrix ${\tilde{\mathit{E}}}^{\left(b\right)}\in {\mathbb{R}}^{C\times N}$ is computed as:

$${\tilde{\mathit{E}}}^{\left(b\right)}=\mathit{E}\odot {\mathit{M}}^{\left(b\right)},\hspace{1em}b=1,\dots ,B\alpha =\sigma \left({\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}}_{1\times 1}\left(f_{red}\right)\right)$$

(13)

where $\odot$ denotes element-wise multiplication.

To synthesize the spectral image, DEAM employs a Dynamic Matrix Synthesis (DMS) strategy [35] that fuses the adjusted endmembers and the abundance map. The high-resolution abundance tensor is first flattened into ${\mathit{A}}_{flat}^{\left(b\right)}\in {\mathbb{R}}^{N\times (rW·rH)}$, then linearly combined with ${\tilde{\mathit{E}}}^{\left(b\right)}$ using Einstein summation [36]:

$${\mathit{Y}}^{\left(b\right)}={\tilde{\mathit{E}}}^{\left(b\right)}\times {\mathit{A}}_{flat}^{\left(b\right)}=\sum _{c,n}^N {\tilde{\mathit{E}}}_{c,n}^{\left(b\right)}\cdot {\mathit{A}}_{n,q}^{\left(b\right)},\hspace{1em}{\mathit{Y}}^{\left(\mathit{b}\right)}\in {\mathbb{R}}^{C\times (rW·rH)}$$

(14)

Finally, the spectral output is reshaped into spatial dimensions to produce a preliminary high-resolution hyperspectral image ${\mathit{Y}}_0\in {\mathbb{R}}^{C\times rH\times rW}$. This mechanism enables more accurate estimation of abundances and endmembers, significantly improving the reconstruction quality under complex mixing conditions.

While adaptive endmember models have been explored in traditional unmixing—such as linear perturbation schemes, low-rank constrained adjustments, or adaptive linear mixing models—these methods generally treat endmember refinement as an isolated optimization task.

In contrast, DEAM is seamlessly embedded into the DSCSRN framework, where endmember features are dynamically refined in tandem with abundance estimation and progressive reconstruction. This joint optimization not only captures complex spectral variability but also enforces consistency between the abundance and endmember domains, thereby bridging physical interpretability with deep network adaptability.

Collectively, DEAM tailors endmember spectra to each input scene, mitigating spectral variability and nonlinearity effects. By synergistically integrating refined endmembers with high-resolution abundances, it enhances spectral reconstruction accuracy and improves robustness across diverse hyperspectral scenarios. Moreover, DEAM preserves a functional symmetry between abundance distributions and endmember spectra: adjustments to one are balanced by refinements in the other. This bidirectional symmetry ensures spectral fidelity while maintaining spatial coherence, harmonizing physical interpretability with the flexibility of deep learning.

3. Experiments

3.1. Datasets

To thoroughly evaluate the performance of the proposed method on HSI-SR tasks, three widely used benchmark datasets were selected: Chikusei [37], Pavia Centre (PaviaC) [38], and CAVE [39]. These datasets differ significantly in terms of spectral range, spatial resolution, and scene complexity, offering a comprehensive and diverse testing platform for performance validation. A summary of their basic characteristics is presented in

Table 1. Descriptions of the Chikusei, PaviaC, and CAVE datasets.

Dataset	Spatial Resolution	Spectral Bands	Wavelength Range (nm)	Image Size (C × H × W)	Sensor/Platform
Chikusei	2.5 m	128	363–1018	128 × 2517 × 2335	Headwall Hyperspec VNIR
Pavia Center	1.3 m	102	430–860	102 × 1096 × 1096	ROSIS
CAVE	~0.3 mm/pixel	31	400–700	31 × 512 × 512	Indoor Acquisition

.

For the Chikusei dataset, which contains rich spatial and spectral content, we selected the central region of the image (2048 × 2048 pixels). The top portion was cropped into twelve non-overlapping patches of 512 × 512 pixels to form the training set, while the remaining region was divided into 256 × 256 patches for validation and testing.

For the PaviaC dataset, the original image was partitioned into 24 spatial patches of 120 × 120 pixels. Among these, eighteen were used for training, and the remaining six were used for validation and testing.

The CAVE dataset consists of 32 HSIs of natural indoor scenes. After simulating the corresponding low- and high-resolution image pairs, 22 images were randomly selected for training, and the remaining 10 were used for validation and testing.

These three datasets were deliberately chosen to ensure complementary diversity: Chikusei captures large-scale natural and agricultural areas, Pavia Centre focuses on high-resolution urban environments, and CAVE represents indoor laboratory scenes with controlled spectral variations. This combination covers a broad spectrum of acquisition settings (airborne, urban remote sensing, and indoor imaging), thereby supporting the generalizability of our evaluation and enabling fair benchmarking against existing HSI-SR methods.

3.2. Experimental Setup

In the proposed DSCSRN framework, the number of input channels in the first layer is configured according to the number of spectral bands in the dataset. Following previous work [27], the number of endmembers is set to N = 30, serving as the basis for abundance estimation and subsequent reconstruction.

Super-resolution experiments are conducted using scale factors of ×4 and ×8, and a progressive upsampling strategy is adopted to reduce model complexity. At each upsampling stage, sub-pixel convolution (pixel shuffle) is applied to effectively preserve spatial details.

Model training is conducted using the PyTorch framework on an NVIDIA RTX 4090 GPU. The Adam optimizer is used, with an initial learning rate of $2\times {10}^{-4}$, and training is performed over 1000 epochs. The batch size is set to 16, and automatic mixed precision (AMP) [40] is employed to accelerate training and reduce memory usage. For data augmentation, random rotations and flipping are applied to improve generalization. The model is optimized using L1 Loss [41] to ensure pixel-level reconstruction accuracy.

Table 2. Training and validation efficiency.

Dataset	Phase	Avg Time per Epoch (s)	Total Training Time (min)	GPU Memory Usage
Chikusei	Training	75	1375	5.1 GB
	Validation (per image)	2.76	-	3.5 GB
Pavia Center	Training	45	825	4.9 GB
	Validation (per image)	1.30	-	3.3 GB
CAVE	Training	26	477	4.7 GB
	Validation (per image)	4.95	-	3.8 GB

summarizes the computational efficiency of DSCSRN during training and validation. For the Chikusei dataset at a ×4 scale, each epoch takes approximately 75 s, with a total training time of 1375 min. Validation of a single image requires around 2.76 s. Pavia Center and CAVE exhibit faster per-epoch training times (45 s and 26 s, respectively), reflecting their smaller image sizes and fewer spectral bands. GPU memory consumption remains moderate across all datasets, requiring approximately 5 GB for training and around 3–4 GB for validation, demonstrating that DSCSRN can be trained and evaluated efficiently on a single high-end GPU.

3.3. Experimental Evaluation

To quantitatively assess the quality of the reconstructed high-resolution HSIs, six widely used objective metrics are adopted: Peak Signal-to-Noise Ratio (PSNR) [42], Structural Similarity Index (SSIM) [43], the dimensionless Global Error of Synthesis (ERGAS) [44], Spectral Angle Mapper (SAM) [45], Cross-Correlation (CC) [46], and Root Mean Square Error (RMSE) [47]. Higher values of PSNR, CC, and SSIM indicate better reconstruction performance, while lower values of SAM, RMSE, and ERGAS suggest more accurate results. The ideal values for these metrics are as follows: PSNR → +∞, SAM → 0, CC → 1, RMSE → 0, SSIM → 1, and ERGAS → 0. In practice, a PSNR above 30 dB is generally considered to indicate high-quality reconstruction in HSI tasks. These metrics jointly evaluate signal fidelity (PSNR), global synthesis error (ERGAS), spectral consistency (SAM), and structural similarity (SSIM), providing a comprehensive evaluation framework for assessing the quality of hyperspectral reconstruction.

3.4. Comparative Experiments

To demonstrate the effectiveness of the proposed method, comparative experiments are conducted with several state-of-the-art single-image super-resolution (SISR) methods, including FCNN [16], RFSR [48], DualSR [17], aeDPCN [27], EUNet [49], CST [50], and SNLSR [51]. For each method, the number of channels in the convolutional layers is adjusted to match the spectral dimensionality of the input datasets. Wherever possible, publicly available official implementations are used, and hyperparameters are tuned to achieve optimal performance, ensuring fair and reproducible comparisons across all methods.

3.4.1. Evaluation of the Chikusei Dataset

Table 3. Quantitative performance of the Chikusei dataset. Note: Bold values indicate the best performance, and underlined values denote the second-best. d denotes the upscaling factor.

Methods	d	PSNR↑	SSIM↑	ERGAS↓	SAM↓	CC↑	RMSE↓
Bicubic	4	40.0107	0.9211	5.5602	2.6670	0.9246	0.0129
FCNN [16]	4	41.1959	0.9419	4.9828	2.3463	0.9407	0.0111
RFSR [48]	4	42.7493	0.9568	4.1746	2.0135	0.9565	0.0095
DualSR [17]	4	41.6073	0.9466	5.9922	2.4182	0.9411	0.0105
aeDPCN [27]	4	42.5565	0.9545	4.2307	1.9371	0.9551	0.0098
EUNet [49]	4	42.8889	0.9575	4.0947	1.8648	0.9579	0.0094
CST [50]	4	43.0638	0.9592	4.0290	1.8775	0.9595	0.0093
SNLSR [51]	4	43.1622	0.9601	3.9986	1.8007	0.9600	0.0092
DSCSRN	4	43.4283	0.9618	3.8886	1.7542	0.9618	0.0089
Bicubic	8	36.7340	0.8495	4.0193	4.0013	0.8348	0.0190
FCNN [16]	8	36.8121	0.8511	4.0101	3.8557	0.8487	0.0174
RFSR [48]	8	38.0138	0.8788	3.7709	3.5375	0.8655	0.0168
DualSR [17]	8	37.3567	0.8672	4.0635	3.9346	0.8545	0.0172
aeDPCN [27]	8	38.3404	0.8884	3.3543	3.0587	0.8833	0.0160
EUNet [49]	8	38.3095	0.8882	3.3700	3.0685	0.8828	0.0161
CST [50]	8	38.0569	0.8824	3.4791	3.4218	0.8768	0.0164
SNLSR [51]	8	38.5256	0.8920	3.3036	3.0002	0.8873	0.0157
DSCSRN	8	38.7012	0.8961	3.2526	2.9146	0.8910	0.0154

presents the average results of six evaluation metrics across multiple test samples from the Chikusei dataset. At both 4× and 8× scaling factors, the DSCSRN framework consistently outperforms state-of-the-art methods, achieving superior scores in key metrics such as PSNR, SSIM, and SAM. These results demonstrate its exceptional capability in preserving spatial structures and ensuring spectral consistency. This performance stems from DSCSRN’s three-stage hierarchical design, which integrates the CRSDN, SPFRM, and DEAM. CRSDN generates a physically constrained initial abundance map, SPFRM enhances spatial resolution, and DEAM optimizes endmember representations, collectively ensuring a balance between spatial detail and spectral fidelity.

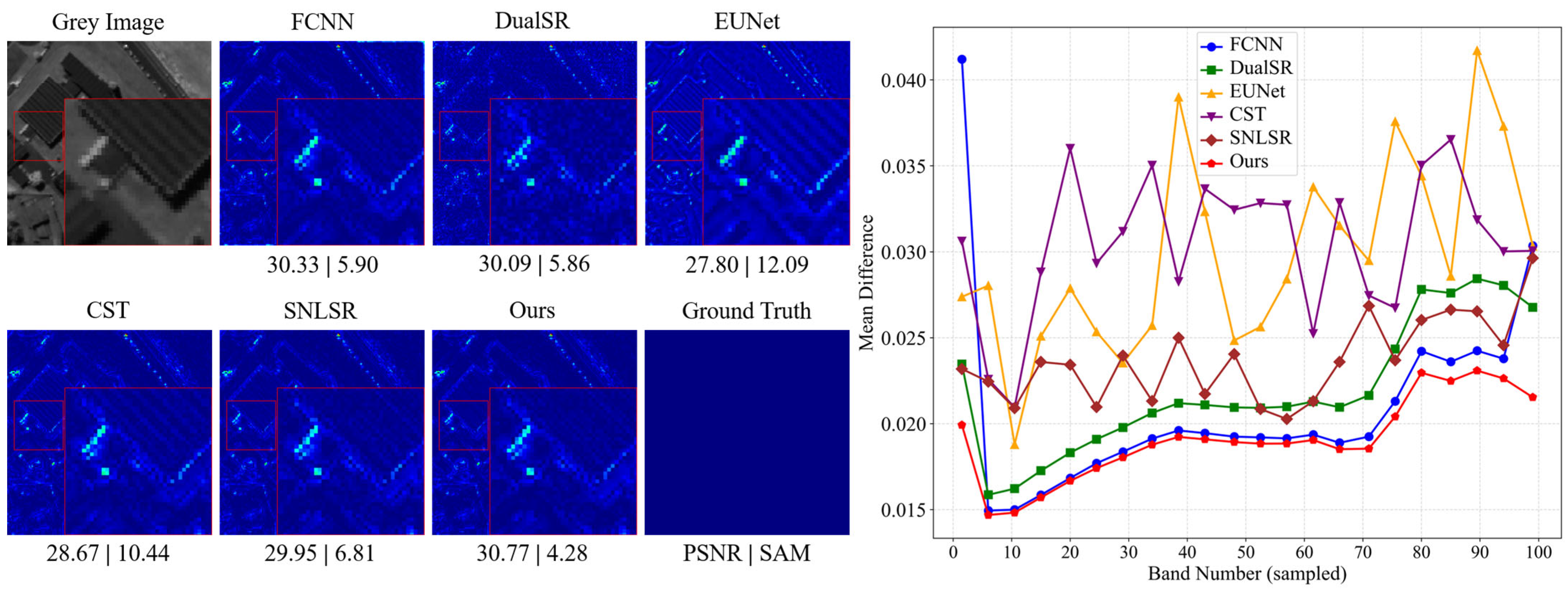
Figure 5 further illustrates DSCSRN’s reconstruction performance through visual comparisons of three representative test samples at a 4× scaling factor, accompanied by their corresponding average spectral difference curves. Pseudo-color images, formed by combining the 70th, 100th, and 36th spectral bands, are annotated with their respective PSNR and SAM values. DSCSRN exhibits higher fidelity in restoring edge structures and texture details, significantly reducing blurring, over-smoothing, and blocky artifacts (highlighted in red boxes). This advantage arises from its multi-stage feature-refinement strategy. The SPFRM’s DDSA modules progressively fuse spatial–spectral features to enhance the spatial resolution of the abundance map, while CRSDN’s initial abundance map ensures physical consistency. The spectral difference curves shown in the right part of Figure 5 further confirm that DSCSRN achieves the lowest spectral distortion across the full wavelength range, validating its superior spectral fidelity.

Other methods, such as FCNN, aeDPCN, DualSR, RFSR, and EUNet, exhibit limitations in spatial integrity or spectral context capture. FCNN produces over-smoothed outputs due to its lack of multi-stage refinement; aeDPCN disrupts spatial integrity by neglecting spectral autocorrelation; DualSR and RFSR show instability under high-bandwidth conditions; and EUNet struggles with edge preservation. In contrast, DSCSRN achieves a robust balance between spatial detail and spectral fidelity through CRSDN’s abundance map generation, SPFRM’s spatial–spectral feature fusion, and DEAM’s dynamic endmember adjustment.

Overall, both quantitative metrics and qualitative visualization results verify that DSCSRN delivers superior reconstruction performance, exhibiting strong generalization abilities, better interpretability, and a balanced preservation of both spatial detail and spectral integrity.

3.4.2. Evaluation of the Pavia Center Dataset

Table 4. Quantitative performance of the Pavia Center dataset. Note: Bold values indicate the best performance, and underlined values denote the second-best. d denotes the upscaling factor.

Methods	d	PSNR↑	SSIM↑	ERGAS↓	SAM↓	CC↑	RMSE↓
Bicubic	4	28.9464	0.7561	6.3584	5.9078	0.8892	0.0380
FCNN [16]	4	29.6709	0.8005	5.8634	6.0106	0.9052	0.0348
RFSR [48]	4	30.4910	0.8335	5.3398	5.4287	0.9214	0.0317
DualSR [17]	4	29.8552	0.8068	5.7609	6.3710	0.9073	0.0343
EUNet [49]	4	30.5021	0.8341	5.3386	5.2527	0.9215	0.0316
CST [50]	4	29.7451	0.8311	5.5829	5.3885	0.9021	0.0337
SNLSR [51]	4	30.4662	0.8362	5.3492	5.0823	0.9211	0.0319
DSCSRN	4	30.6427	0.8405	5.2531	5.0732	0.9238	0.0311
Bicubic	8	26.0420	0.5453	7.9215	7.6157	0.7708	0.0542
FCNN [16]	8	26.2882	0.5524	7.4205	7.5831	0.7759	0.0532
RFSR [48]	8	26.5872	0.5988	7.1662	7.3475	0.7899	0.0511
DualSR [17]	8	25.9474	0.5513	7.4697	9.3803	0.7622	0.0544
EUNet [49]	8	26.5251	0.5970	7.1826	7.3987	0.7948	0.0510
CST [50]	8	26.5282	0.5570	7.1652	7.2988	0.7984	0.0511
SNLSR [51]	8	26.5914	0.6037	7.1566	7.2427	0.7973	0.0505
DSCSRN	8	26.6275	0.6118	7.1365	7.0153	0.7997	0.0504

summarizes the average quantitative performance results for the test images from the PaviaC dataset. Characterized by complex scene structures, pronounced spatial variations, and high spectral noise—along with a relatively limited number of training samples compared to other datasets—PaviaC poses considerable challenges to both reconstruction accuracy and model generalization. Experimental results show that the proposed DSCSRN consistently achieves superior performance across key metrics, including PSNR, SSIM, and SAM, underscoring its strong modeling capability and generalization robustness.

To further assess the visual reconstruction quality, the left part of Figure 6 presents the results for three representative test images at a 4× scaling factor. These include the ground-truth grayscale images, the absolute error maps of the reconstructions, and the corresponding average spectral difference curves. The visualized images are synthesized from the 99th, 46th, and 89th spectral bands. In the absolute error maps, DSCSRN’s reconstructions exhibit consistently darker regions, indicating substantially lower pixel-wise errors compared to the original high-resolution images—especially in edge-dense areas such as building boundaries and heterogeneous land-cover zones—demonstrating its superior error suppression. Moreover, the average spectral difference curves in the right part of Figure 6 further confirm DSCSRN’s high spectral fidelity: its curve remains the lowest across the entire wavelength range, reflecting minimal spectral distortion and strong spectral consistency.

This enhanced performance can be attributed to two key components of the model: DDSA mechanism, which effectively captures complementary spatial and spectral features, and the DEAM, which adaptively refines endmembers to improve both the accuracy and stability of spectral reconstruction.

3.4.3. Evaluation of the CAVE Dataset (Natural Hyperspectral Images)

To further evaluate the generalization ability, adaptability, and robustness of the proposed method on natural-scene hyperspectral images (HSIs), additional experiments were conducted using the CAVE dataset. Unlike remote-sensing hyperspectral data, CAVE images feature more diverse and visually complex indoor scenes. Although the spectral dimensionality of CAVE is relatively lower, slightly reducing the difficulty of high-dimensional feature modeling, the dataset provides a rich variety of structural and textural patterns. This allows the model to demonstrate its capacity to generalize across different domains and effectively learn both spatial structures and spectral characteristics from a broader context.

For these experiments, the number of endmembers was set to N = 8 to match the lower spectral complexity of the CAVE dataset. The quantitative results, presented in

Table 5. Quantitative performance of the CAVE dataset. Note: Bold values indicate the best performance, and underlined values denote the second-best. d denotes the upscaling factor.

Methods	d	PSNR↑	SSIM↑	ERGAS↓	SAM↓	CC↑	RMSE↓
Bicubic	4	35.8303	0.9624	4.3569	3.6099	0.9920	0.0170
FCNN [16]	4	36.4173	0.9573	5.1094	3.2935	0.9928	0.0155
RFSR [48]	4	39.1474	0.9730	2.9552	3.9509	0.9963	0.0116
DualSR [17]	4	38.9682	0.9727	2.9683	3.9888	0.9960	0.0120
aeDPCN [27]	4	37.6579	0.9689	3.5153	3.6876	0.9947	0.0138
EUNet [49]	4	39.1303	0.9748	2.9523	3.4106	0.9962	0.0117
CST [50]	4	40.1006	0.9772	3.3686	2.9119	0.9969	0.0103
SNLSR [51]	4	39.8743	0.9777	2.7004	3.3553	0.9968	0.0107
DSCSRN	4	40.1449	0.9784	2.6792	3.2617	0.9968	0.0105
Bicubic	8	30.9645	0.9114	3.6745	4.6226	0.9766	0.0297
FCNN [16]	8	32.3365	0.9246	2.9752	4.5975	0.9802	0.0247
RFSR [48]	8	34.5322	0.9386	2.5226	4.1501	0.9878	0.0201
DualSR [17]	8	34.2430	0.9347	2.5693	5.1626	0.9868	0.0208
aeDPCN [27]	8	33.3474	0.9317	2.8143	4.5546	0.9859	0.0227
EUNet [49]	8	34.0472	0.9372	2.6358	4.4245	0.9874	0.0208
CST [50]	8	34.6527	0.9212	3.0605	5.6185	0.9898	0.0193
SNLSR [51]	8	34.6181	0.9437	2.4917	4.1639	0.9886	0.0194
DSCSRN	8	34.6935	0.9438	2.4820	4.1458	0.9888	0.0192

, show that in the ×4 magnification task, the proposed DSCSRN method outperforms existing state-of-the-art methods on core metrics such as PSNR, SSIM, and ERGAS, demonstrating its superior ability in structural restoration and detail recovery. Although DSCSRN performs slightly worse than CST in terms of SAM, CC, and RMSE, it still surpasses SNLSR overall, achieving a favorable balance between spectral consistency and spatial clarity.

In the more challenging ×8 magnification task, DSCSRN also demonstrates superior performance, outperforming SNLSR in PSNR, SSIM, ERGAS, and RMSE, and significantly exceeding CST. These results indicate that DSCSRN provides stronger structural reconstruction and spectral stability under the complex-scene content and high scaling of natural images. Notably, although CST achieves better SAM scores, it struggles to maintain spectral accuracy at high magnifications. While SNLSR performs steadily in spectral preservation, it lacks sharpness and structural detail.

To further illustrate the reconstruction quality, three test image sets from the CAVE dataset were selected. The ×4 magnification results of the 18th spectral band are shown in Figure 7, along with the corresponding average spectral difference curves.

The visual comparisons clearly show that DSCSRN excels in structure recovery and texture preservation—especially in terms of edge sharpness, fine details, and transitions between materials. The generated reconstructed images are more natural and visually accurate. In contrast, methods such as RFSR, DualSR, and aeDPCN exhibit noticeable blurring and block artifacts in textured regions, while CST and SNLSR show structural distortions. Analysis of the spectral difference curves further reveals that DSCSRN maintains the lowest deviation across all bands, confirming its superior performance in preserving spectral fidelity.

Overall, DSCSRN demonstrates strong generalization ability and robustness in natural scenes, as evidenced by its performance on the CAVE dataset. Despite the domain gap between CAVE and remote-sensing datasets, the model maintains high reconstruction quality, showcasing its adaptability to diverse environments. This ability to balance spatial detail and spectral fidelity arises from the synergistic interplay among CRSDN’s physically grounded abundance estimation, SPFRM’s progressive feature refinement, and DEAM’s adaptive spectral optimization.

3.4.4. Cross-Dataset Evaluation (Trained on Chikusei, Tested on Pavia)

To further investigate the generalization ability of hyperspectral super-resolution models under domain shifts, we conducted a cross-dataset evaluation by training all models on the Chikusei dataset and testing them on the Pavia dataset. The results are evaluated on an input size of 102 × 40 × 40 at a scale factor of 4. Compared with Chikusei, which contains large agricultural scenes with rich spectral variability, the Pavia dataset primarily captures urban areas with distinct man-made structures, resulting in noticeable differences in both spatial complexity and spectral distributions. This setting introduces significant spectral distribution and spatial content discrepancies between training and testing scenes, making it a challenging benchmark for evaluating model robustness.

Table 6. Quantitative performance of cross-dataset evaluation, where models are trained on the Chikusei dataset and tested on the Pavia dataset. Note: Bold values indicate the best performance, and underlined values denote the second-best.

Methods	PSNR↑	SSIM↑	ERGAS↓	SAM↓	CC↑	RMSE↓
FCNN [16]	28.6269	0.7590	6.8344	7.5196	0.8849	0.0403
DualSR [17]	28.3931	0.7236	6.9560	8.4517	0.8705	0.0410
EUNet [49]	26.6029	0.6994	8.8808	15.0928	0.8812	0.0494
CST [50]	27.2989	0.7155	8.0557	13.3922	0.8811	0.0457
SNLSR [51]	28.3228	0.7307	6.9268	6.1927	0.8869	0.0406
DSCSRN	28.9513	0.7566	6.3550	5.9191	0.8893	0.0381

reports the quantitative metrics under this cross-domain setting. The proposed DSCSRN achieves the best overall performance, with a PSNR of 28.95 dB and SSIM of 0.7566, alongside the lowest ERGAS (6.3550), SAM (5.9191), and RMSE (0.0381). These results clearly demonstrate the model’s superior ability to maintain both spectral fidelity and spatial detail despite significant dataset differences. Among competing methods, FCNN and DualSR exhibit relatively strong performance but remain inferior to DSCSRN, while other approaches such as CST and EUNet show a substantial decline in accuracy, highlighting their sensitivity to distribution shifts.

Figure 8 provides visual comparisons of three representative Pavia test scenes. The left column shows the reconstructed grayscale images and their corresponding absolute error maps. DSCSRN produces consistently darker error regions, particularly around building boundaries and mixed land-cover zones, reflecting its superior reconstruction stability in complex scenes. The mean absolute difference curves (right) further validate this advantage: DSCSRN achieves the lowest spectral error across the entire wavelength range, followed by FCNN and DualSR, indicating its effectiveness in preserving spectral consistency under cross-domain conditions.

This performance gain is primarily attributed to the synergy between DSCSRN’s DDSA mechanism, which extracts complementary spatial–spectral representations, and DEAM, which dynamically refines endmember features to enhance spectral reconstruction robustness across diverse datasets.

3.4.5. Parameter and Complexity Analysis

Beyond reconstruction accuracy, model complexity and parameter size are critical for assessing the practicality of hyperspectral image super-resolution methods. Figure 9 illustrates the trade-off between computational cost (measured in FLOPs) and reconstruction performance (PSNR) for different models, with their parameter sizes annotated alongside each marker. Specifically, blue squares represent existing approaches, while the red circle highlights our proposed DSCSRN. The results are obtained on the Chikusei dataset with a 4× upscaling factor, using input patches of size 128 × 50 × 50. The horizontal axis corresponds to FLOPs (in G), and the vertical axis shows PSNR (in dB).

As shown in Figure 9, DualSR suffers from extremely high computational complexity (1666.9 G FLOPs) despite achieving only moderate accuracy, reflecting the heavy cost of 3D convolutions. CST also involves a large number of parameters (21.3 M) and notable FLOPs (150.8 G), which limits its efficiency in practice. By contrast, lightweight methods such as FCNN (0.84 M, 69.3 G) and EUNet (0.84 M, 69.3 G) exhibit lower complexity but also deliver relatively weaker performance. RFSR strikes a balance with 0.98 M parameters and 60.4 G FLOPs, though its reconstruction quality remains behind the leading methods. Among prior works, SNLSR achieves a strong balance of efficiency and accuracy (1.65 M, 13.7 G FLOPs, 43.16 dB), while aeDPCN further reduces parameters (0.57 M, 14.4 G FLOPs) but with slightly lower accuracy. Most importantly, our proposed DSCSRN (red circle) achieves the best reconstruction quality (43.43 dB) with only 2.13 M parameters and 18.9 G FLOPs, clearly standing out from other methods. This favorable trade-off demonstrates that DSCSRN not only ensures superior image fidelity but also maintains high efficiency, making it well-suited for practical HSI super-resolution tasks.

3.5. Ablation Study

In the proposed DSCSRN, the CRSDN module serves as the core unmixing component, designed to estimate abundance maps under physical constraints. To evaluate its effectiveness, we vectorize the input hyperspectral image into a two-dimensional matrix and replace the spectral constraint decomposition process in CRSDN with a Multilayer Perceptron (MLP) of similar structure. The MLP uses the same activation functions and parameter sizes as CRSDN and directly predicts the initial abundance map from the image pixels. As shown in

Table 7. Ablation study results for the Pavia Center dataset. Note: Bold values indicate the best performance, and underlined values denote the second-best.

Methods	PSNR↑	SSIM↑	SAM↓	RMSE↓
w/o CRSDN	29.7070	0.7961	5.7098	0.0347
w/o DEAM	30.5431	0.8360	5.2438	0.0314
Concatenation	30.5496	0.8364	5.1594	0.0314
Addition	30.5434	0.8377	5.0722	0.0315
DSCSRN	30.6427	0.8405	5.0732	0.0311

, removing CRSDN results in a PSNR drop of 0.94 dB, a decrease of 0.0444 in SSIM, and a significant increase in SAM to 5.7098. These results indicate that removing the physically constrained unmixing modeling introduces more spectral distortion and weakens spatial structure perception, thereby degrading reconstruction accuracy.

The DEAM is designed to dynamically update the endmember library based on high-resolution abundance features to better handle complex mixing scenarios. To evaluate its impact, we replace DEAM with static endmembers, where a fixed set of endmember vectors is used throughout training and inference without adaptive updates. The results show that removing DEAM causes PSNR to drop to 30.5431 (a decrease of 0.10 dB), and SAM increases to 5.2438. This demonstrates that static endmembers limit the model’s capacity to handle nonlinear mixing effects and reduce its ability to capture fine-grained spectral variations.

The MSAFG plays a key role in DSCSRN by integrating spatial, spectral, and cross-domain features with backbone information. To assess its fusion performance, we compared two alternative strategies: (1) concatenating the four feature branches followed by a 3×3 convolution (Concatenation), and (2) performing element-wise addition of the four branches (Addition). The results indicated that compared to MSAFG, the concatenation strategy reduced the PSNR by 0.0931 dB, while the Addition strategy yielded a slightly larger drop of 0.0993 dB. In both cases, the SAM also saw an increase. These findings suggest that such simple fusion mechanisms cannot adequately capture the nonlinear interactions among heterogeneous features. By contrast, MSAFG incorporates a gating mechanism to dynamically control feature flow, enabling more efficient coordination of multi-source features and improved spatial–spectral reconstruction.

To visually compare the impact of different settings, the left part of Figure 10 shows pseudo-color reconstructions and their corresponding absolute error maps under five configurations: the complete DSCSRN model, and four ablation settings (removing CRSDN, removing DEAM, and replacing MSAFG with Concatenation or Addition). It is evident that the DSCSRN-generated images display clearer textures and more precise edge restoration, producing visual results closer to the original image.

In the absolute error maps, DSCSRN outputs appear significantly darker in most regions, indicating lower reconstruction errors. At image boundaries and high-frequency regions in particular, DSCSRN effectively suppresses block artifacts and preserves structural details, whereas the ablated models exhibit noticeable error accumulation in these areas.

To further quantify spectral reconstruction performance, we plot the average spectral difference curves for each ablation variant in the right part of Figure 10. The full DSCSRN achieves the lowest spectral error, while removing CRSDN leads to the highest degradation. Although replacing DEAM or substituting MSAFG with simple concatenation or addition slightly reduces performance, none of these variants outperform the complete DSCSRN.

Together, these visual and quantitative analyses demonstrate the complementary contributions of each module, confirming their indispensable role in enhancing spatial detail and spectral accuracy in DSCSRN.

These ablation results collectively underscore the complementary and synergistic roles of the core modules in DSCSRN. CRSDN provides physically grounded unmixing, forming the basis for accurate abundance estimation. DEAM adaptively refines the spectral bases to better capture complex, scene-specific endmember variations, effectively bridging the gap between low-resolution inputs and high-resolution spectral representations. MSAFG further enhances feature integration by dynamically regulating the flow of information across spatial, spectral, and cross-domain dimensions. Together, these modules construct a coherent “unmix–refine–reconstruct” pipeline: physically interpretable unmixing establishes the foundation, progressive refinement amplifies discriminative features, and adaptive fusion facilitates efficient, context-aware reconstruction. The interplay among modules not only improves reconstruction accuracy across quantitative metrics but also enhances robustness in visually challenging regions, validating the effectiveness of DSCSRN’s design from both theoretical and empirical perspectives.

4. Conclusions

This paper presents a novel HSI-SR method named Dynamic Spectral Collaborative Super-Resolution Network (DSCSRN), which seamlessly integrates physical modeling with deep learning. By formulating a three-stage collaborative pipeline—unmixing, recovery, and reconstruction—the proposed framework effectively models the complex hierarchical relationships between spatial and spectral domains, while preserving physical interpretability. In addition, DSCSRN explicitly leverages the intrinsic symmetries present in hyperspectral data—such as repetitive spatial structures and balanced spectral relationships—using a dual-domain symmetric architecture to ensure consistency between spatial and spectral reconstructions.

The framework jointly exploits CRSDN for abundance estimation, DEAM for adaptive endmember refinement, SPFRM for spatial–spectral feature enhancement, and MSAFG for balanced multi-scale fusion. Collectively, these modules ensure robust reconstruction under diverse scenarios and highlight the unique synergy between physics-inspired priors and deep architectures.

While grounded in the Linear Mixture Model (LMM), we explicitly acknowledge its limitations under nonlinear mixing and illumination variations. DSCSRN addresses these challenges through DEAM, which dynamically refines endmember spectra, and the DDSA mechanism in SPFRM, which enforces spatial–spectral consistency. This hybrid design enhances robustness to practical deviations from LMM, distinguishing DSCSRN from conventional LMM-based methods.

Extensive experiments on three widely used datasets—Chikusei, PaviaC, and CAVE—demonstrate that DSCSRN consistently surpasses state-of-the-art methods across multiple evaluation metrics, exhibiting superior performance in both spatial detail preservation and spectral fidelity. The integration of symmetry principles into both the network architecture and the feature interaction process contributes to this improvement, ensuring that reconstructed HSIs maintain both physical realism and structural balance. The strong performance across diverse datasets further highlights the generalization ability of the proposed model in handling various HSI types and scene domains. Ablation studies also validate the effectiveness and necessity of each proposed module.

Future research will explore cross-modal collaboration mechanisms and endmember uncertainty modeling to further enhance the generalization and robustness of DSCSRN in real-world scenarios. In particular, future work will extend the evaluation to task-driven metrics (e.g., classification accuracy on super-resolved HSIs) and investigate more sophisticated symmetry-aware feature modeling strategies, enabling the network to exploit higher-order geometric and spectral symmetries for improved adaptability. Moreover, the symmetry-driven design principle is not confined to super-resolution; it holds potential for broader inverse imaging problems such as unmixing, fusion, and denoising, where maintaining cross-domain consistency is crucial. We will further pursue optimized symmetry-aware strategies to extend DSCSRN’s applicability across these tasks.