Dynamic Neighborhood Particle Swarm Optimization Algorithm Based on Euclidean Distance for Solving the Nonlinear Equation System

Abstract

Locating all roots of nonlinear equation of systems (NESs) in a single computational procedure remains a fundamental challenge in computational mathematics. The Dynamic Neighborhood Particle Swarm Optimization algorithm based on Euclidean Distance (EDPSO) is proposed to address this issue. First, a dynamic neighborhood strategy based on Euclidean distance is proposed, to facilitate particles within the population with forming appropriate neighborhoods. Secondly, the Levy flight strategy is integrated into the particle velocity-update mechanism to balance the global search capability and local search capability of particles. Furthermore, integrating a discrete crossover strategy into the PSO algorithm enhances its capability in solving high-dimensional nonlinear equations. Finally, to validate the effectiveness and feasibility of the proposed algorithms, the EDPSO algorithm, along with its comparative counterparts, is applied to solve 20 NESs problems and the forward kinematics equations of a 3-RPS parallel mechanism. Experimental results demonstrate that for the 20 NESs, the EDPSO algorithm achieved the highest success rate (SR = 0.992) and root rate (RR = 0.999) among all compared methods, followed by LSTP, NSDE, KSDE, NCDE, HNDE, and DR-JADE. In solving the forward kinematics of the 3-RPS parallel mechanism, the EDPSO algorithm achieved the highest SR of = 0.9975 and RR = 0.9800, followed by LSTP, KSDE, DR-JADE, NCDE, NSDE, and HNDE, based on these metrics.

1. Introduction

Nonlinear equation systems (NESs) play a pivotal role in numerous engineering and scientific domains, with typical application scenarios encompassing the inverse kinematics equations of robotic manipulators [1], the forward kinematics equations of coupled parallel mechanisms [2,3], and the modeling of ill-posed inverse problems in digital image restoration [4]. Conventional numerical calculations can only yield one root of NESs through a single computation. Therefore, localizing multiple roots of NESs within a single computational operation remains a significant challenge.

How to utilize numerical methods to solve all high-precision solutions of NESs under limited computational resources has emerged as a pressing issue demanding urgent resolution by researchers in the relevant field. The classical solution methods for NESs include Newton’s method [5], the homotopy method [6,7], and the gradient descent method [8], etc. Although the aforementioned method has been widely implemented in engineering practice, it still exhibits certain inherent limitations. Newton’s method and the homotopy method exhibit high sensitivity to initial guesses, with the quality of these initial guesses directly dictating the success of the solution process. In summary, most classical algorithms are incapable of solving multiple roots of NESs within a single operation. According to References [9,10], individuals within evolutionary algorithm (EA) populations exhibit multiple distinct characteristics. Leveraging these differential features of intra-population individuals, multiple roots of the NESs problem can be effectively identified.

Compared with traditional methods, evolutionary algorithms (EAs) demonstrate superior robustness in solving NES problems. When addressing complex NES problems, it remains unaffected by challenges such as differentiability, discontinuity, and non-convexity [11]. Currently, the intelligent algorithms employed for solving NES problems include the Differential Evolution (DE) algorithm [2], the Particle Swarm Optimization (PSO) algorithm [3], the Genetic Algorithm (GA) [12], the Simulated Annealing (SA) algorithm [13], and so forth. When solving NES problems using intelligent algorithms, there are primarily two approaches: addressing single-objective optimization problems and multi-objective optimization problems. When solving using single-objective optimization, this method is analogous to multi-modal problem solving [14], involving the transformation of m nonlinear equations into unconstrained optimization equations, followed by their solution [2]. Wang et al. [15] integrated the speciation technique with the neighborhood crowding technique to balance population diversity and convergence. Meanwhile, satisfied solutions were stored in an external repository, and current individuals were reinitialized to conserve computational resources. Liao et al. [16] proposed an archive-guided differential evolution (DE) algorithm. The improvement strategies of this algorithm primarily involve three key components: employing an external archive to store individuals with inferior fitness, reusing historical individuals to select optimal evolutionary candidates, and conducting local searches on distinct subpopulations. The integration of these improved strategies demonstrates effective capability in addressing the problem of multiple roots in nonlinear equation systems. When solving systems of nonlinear equations using multi-objective optimization, the primary challenge primarily lies in how to transform these nonlinear equation systems into a multi-objective optimization model. Grosan et al. [17] proposed a multi-objective optimization model that transforms a system of nonlinear equations into m optimization objectives, and employed evolutionary algorithms to solve it. Suid et al. [18] synergistically combined game theory principles with sinusoidal algorithms to harmonize exploration and exploitation, demonstrating their effectiveness through 13 benchmark functions and real-world engineering applications. To address the local optimum limitation of the marine predators algorithm, Suid et al. [19] incorporated a safety experimental dynamic system algorithm into the update mechanism. Furthermore, an tunable step-size adaptive coefficient was introduced to enhance the algorithm’s searching capability, and the improved algorithm was subsequently applied to the PID control of automatic voltage regulators.

The PSO algorithm, a type of swarm intelligence algorithm, is inspired by the collective collaborative behavior of bird flocks or fish schools. It features a simple structure, is easy to implement, and has few control parameters [20]. To avoid the repeated emergence of solutions and accelerate the convergence speed during the iterative process, El-Shorbahy [21] integrated the chaotic noise method into the particle swarm algorithm and proposed a chaos noise-based particle swarm optimization algorithm (CN-BPSOA). Suganthan et al. [22] first introduced the Niching concept into the PSO algorithm, developed subpopulations using a population-based Euclidean distance approach, and proposed multiple standardized PSO variants. Building on this foundation, Li et al. [23] proposed a ring-topology neighborhood particle swarm optimization (RTN-PSO) algorithm and applied it to address NES problems. Brits et al. [24] employed a domain-based method to partition the population into multiple subpopulations, with each subpopulation evolving independently, to locate multiple optimal solutions. Qu et al. [25] proposed a novel local neighborhood search algorithm, which utilizes particle information within the neighborhood to guide the search direction of other particles.

Substantial research efforts have been devoted to the PSO algorithm. Nevertheless, investigations into its capability to resolve multiple roots of nonlinear equation systems within a single iteration remain conspicuously limited. The capacity to achieve simultaneous root-finding for multiple solutions of nonlinear equation systems through PSO holds significant promise for addressing practical engineering challenges (e.g., real-time control applications in robotic inverse kinematics). Currently, the NichePSO and LIPS algorithms employ a fixed neighborhood size, which may introduce inferior individuals into the neighborhood during the evolutionary process. This scenario affects the balance between population diversity and local search capability in the evolutionary process of the algorithm. Based on this, this paper proposes a PSO algorithm with dynamic domain discrete crossover, aiming to effectively and accurately locate multiple roots of nonlinear equations. The main contributions of this work are as follows:

(1)

A dynamic neighborhood strategy based on Euclidean distance was proposed, where individuals within the population were enabled to form appropriate neighborhoods, according to their own particle characteristics. This mechanism effectively avoids the misleading of the positions of high-quality particles by those with poor fitness values, thereby preventing the algorithm from falling into local optima.

(2)

A dual-strategy velocity-update mechanism based on Levy flight is proposed, which can balance the diversity of particles within the population and local search capability. In the early stage of the algorithm, the global search capability can be enhanced; in the later stage, particles can be enabled to rapidly converge near the optimal solution.

In the research on the solutions to NESs, the root distribution of classical test functions often exhibits distinct spatial symmetry (as shown in Figure 1). Although such symmetry provides an idealized model for algorithm validation, it fundamentally differs from the solution distribution characteristics of nonlinear equations in practical engineering scenarios. Real-world problems, such as the solution of inverse kinematics of robotic manipulators, the calculation of chemical reaction equilibrium equations, and power system load-flow analysis, typically show solutions with irregular and asymmetric topological structures. Therefore, the dependence on the symmetry of the root distribution is deliberately avoided during the design of the EDPSO algorithm.

The remaining sections of this paper are structured as follows: Section 2 presents the basic workflow of the PSO algorithm. Section 3 introduces three improvement strategies for the EDPSO algorithm, along with their detailed implementation processes. Section 4 provides comparative results of the EDPSO algorithm and its benchmarking counterparts in solving 20 classic NES test problems and mechanical optimization case studies, and further discusses the influences of each improvement strategy and control parameters on the algorithm’s performance. Finally, Section 5 concludes the entire study and outlines future research directions.

2. Problem Description and Basic PSO Algorithm

2.1. Problem Description

Without loss of generality, NES can be described as

$$\left\{\begin{array}{c}{f}_1(\mathit{x})=0\\ f_2(\mathit{x})=0\\ ⋮\\ f_m(\mathit{x})=0\end{array}\right.$$

(1)

where x denotes the variable to be solved for, x = [x₁, x₂, …, x_D]^T∈S, and D represents a D-dimensional unknown variable; M represents the number of nonlinear equations; and S denotes the domain of the variable to be solved for. And it can usually be expressed as

S = [L, U]^T

(2)

where L represents the lower bound of the variable to be determined, L = [x_min,1, x_min,2, …, x_min,D], and U denotes the lower bound of the target variable, U = [x_max,1, x_max,2, …, x_max,D].

Figure 1 illustrates the distribution of roots for the NES (i.e., F03 in the Supplementary Materials). This NES, composed of two nonlinear equations, contains six roots in total. In most cases, the nonlinear system of equations in Equation (1) contains multiple roots, with each root being of equal importance. When solving Equation (1) with an intelligent algorithm, one can transform it into the following unconstrained optimization model.

$$\min F(\mathit{x})={\displaystyle \sum _{i=1}^m{f}_i(\mathit{x})}$$

(3)

An intelligent optimization algorithm resolves Equation (3) to derive solutions for NESs.

2.2. Basic PSO Algorithm

The PSO algorithm, a swarm intelligence optimization technique inspired by the collective behavior of bird flocks, is characterized by its simple structure, strong robustness, and outstanding performance across diverse optimization design scenarios. Consequently, it has garnered extensive attention and found widespread application among numerous researchers. Based on distinct neighborhood topologies, PSO algorithms are classified into two primary variants: global best PSO (gbestPSO) and local best PSO (lbestPSO) architectures. In the standard PSO, NP D-dimensional particles are randomly initialized within the solution space, with their position vector denoted as X_NP = (x₁, x₂, …, x_NP). The velocity associated with the i-th particle x_i is denoted as v_i = (v_i,1, v_i,2,…, v_i,D). The extreme position searched by the i-th particle is denoted as p_best,n, and the global optimal position within the entire particle swarm is denoted as p_best,n. The velocity and position-update formulas of the i-th particle in the (t + 1)-th generation are presented as follows:

$${\mathit{v}}_{i,j}^{(t+1)}=\omega {\mathit{v}}_{i,j}^{(t+1)}+c_1{r}_1(p_{best,j}-{\mathit{x}}_n^{(t)})+c_2{r}_2(g_{best,j}-{\mathit{x}}_{i,j}^{(t)})$$

(4)

$${\mathit{x}}_{i,j}^{(t+1)}={\mathit{x}}_{i,j}^{(t)}+{\mathit{v}}_{i,j}^{(t+1)}$$

(5)

where in each iteration, r₁ and r₂ denote independent random numbers generated uniformly on the interval [0, 1]; t denotes the current iteration number of the particle swarm, and T represents the maximum value of t. c₁ and c₂ denote the personal coefficient and social coefficient, respectively, with their values ranging from 0 to 2, and their update manner is presented as follows [26]:

$$\left\{\begin{array}{l}{c}_1={\displaystyle \frac{t(c_{1f}-c_{1i})}{T}}+c_{1i}\hfill \\ c_1={\displaystyle \frac{t(c_{2f}-c_{2i})}{T}}+c_{2i}\hfill \end{array}\right.$$

(6)

c_1f, c_1i, c_2f, and c_2i represent constants.

ω denotes the inertia weight coefficient, and its update manner is presented as follows:

$$\omega ={\omega }_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\displaystyle \frac{t\times ({\omega }_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\omega }_{\mathrm{m}\mathrm{i}\mathrm{n}})}{T}}$$

(7)

Compute and evaluate the fitness value of the objective function based on Equation (3), then update the optimal individual position of particles and the global optimal position, until the stopping criterion is satisfied.

3. Dynamic Neighborhood Particle Swarm Optimization Algorithm Based on Euclidean Distance

In this section, the Dynamic Domain Strategy based on Euclidean distance, the Dual-Strategy Velocity-Update Mechanism based on Levy flight, and the Discrete Intersection are proposed to help the PSO algorithm localize multiple roots of NESs in a single operation.

3.1. Dynamic Domain Strategy Based on Euclidean Distance

In the PSO algorithm, how to generate appropriate neighborhoods around each particle within the population remains a significant challenge [27]. When the fitness values of particles within the neighborhood are suboptimal, they may mislead the positions of high-quality particles, potentially leading the algorithm to fall into a local optimum. By calculating the Euclidean distances between the current particle and other particles within the population, sorting these distances in ascending order, and selecting the m − 1 closest particles to the current particle, we form the neighborhood candidate individuals. To mitigate the adverse impact on algorithm performance caused by the selection of particles at the neighborhood boundary, the sigmoid function is utilized to screen candidate neighborhood individuals.

$$P_j={\displaystyle \frac{1}{1+e^{\left(-\frac{d_j}{\Gamma r}\right)}}}$$

(8)

where P_j denotes the probability that a neighbor candidate individual is selected as a neighboring individual. Specifically, if rand < P_j, the current individual is selected as a neighboring individual; otherwise, it is not selected; rand represents a random number within the interval [0, 1]; d_j denotes the Euclidean distance between the current particle and the j-th particle (where j∈[1, 2, …, NP]); r denotes the neighborhood radius; and Γ represents the weighting coefficient, with specific values detailed in Section 3.3.

Compared with the traditional fixed neighborhood size, the dynamic domain strategy based on Euclidean distance prevents individuals on the neighborhood boundary from being aliased into individuals within the neighborhood. When intra-neighborhood particles converge to one of the roots of NESs, if boundary particles are mistakenly incorporated into the intra-neighborhood set and their convergence rate surpasses that of the currently identified optimal particles, it will drive all intra-neighborhood particles to search in the direction of these boundary particles, potentially resulting in the premature loss of the current root.

3.2. Dual-Strategy Velocity-Update Mechanism Based on Levy Flight

In the process of solving NESs, it is necessary to simultaneously identify multiple optimal solutions. Consequently, maintaining a balance between population diversity and local search capability throughout the iterative procedure becomes crucial. During the initial evolutionary phases, individuals exhibit uniform distribution within the decision space without niche formation. Accordingly, a globally oriented velocity-update mechanism is required to direct particle convergence toward the root proximity. According to the findings reported in [28], Lévy flight demonstrates the capability to extend the search space, thereby improving the global exploration efficiency of the algorithm. The search step size of standard Levy flight is inherently fixed. Larger step sizes exhibit a greater propensity to locate global optimal solutions; however, they often compromise solution accuracy. Conversely, smaller step sizes enhance solution precision but, concurrently, reduce search efficiency. During the later evolutionary stages, as particles have converged in proximity to the optimal region, localized exploitation around the solution vicinity becomes imperative to refine results. Based on the findings in [29], the velocity-update mechanism of particle swarm integrating a contraction factor (Equation (4)) ensures the convergence of particles, thereby effectively enhancing both the convergence velocity and local exploration capacity of the swarm. To summarize, during the early evolutionary phase, current particles execute random movements via Levy flight, with P_best serving as the central reference; in the subsequent algorithmic stages, a local search is conducted using the velocity-update mechanism defined by Equation (3). The specific update protocols are elaborated as follows:

$${\mathit{v}}_{i,j}^{(t+1)}=\left\{\begin{array}{l}\omega {\mathit{v}}_{i,j}^{(t+1)}-{\mathit{x}}_n^{(t)}+P_{best,j}+Lve(g_{best,j}-{\mathit{x}}_{i,j}^{(t)})\hspace{1em}\hspace{1em}\mathrm{rand}>\psi \hfill \\ \omega {\mathit{v}}_{i,j}^{(t+1)}+c_1{r}_1(P_{best,j}-{\mathit{x}}_n^{(t)})+c_2{r}_2(g_{best,j}-{\mathit{x}}_{i,j}^{(t)})\hspace{1em}\mathrm{else}\hfill \end{array}\right.$$

(9)

where in each iteration, r₁ and r₂ denote independent random numbers generated uniformly on the interval [0, 1]; ψ is defined as the ratio of the current population’s evaluation count FES to the maximum allowable evaluation count Max_FES; Lve represents the enhanced adaptive Levy flight strategy, with its explicit mathematical form presented as follows:

$$\left\{\begin{array}{l}Lev=0.05(1-\psi )e^{-\psi }{\displaystyle \frac{uv}{{\left|v\right|}^{1/\beta }}}\hfill \\ u=\mathrm{randn}\cdot \kappa \hfill \\ v={\left({\displaystyle \frac{\kappa (1+\beta )\sin \left(\pi \beta /2\right)}{\kappa \left((1+\beta )/2\right)\beta \cdot 2^{(\beta -1)/2}}}\right)}^{{\displaystyle \frac{1}{\beta }}}\hfill \end{array}\right.$$

(10)

where β designates the control parameter with a defined range of (1, 3], where a value of 1.5 is adopted in this investigation; randn and μ correspond to random variables adhering to a normal distribution; and μ represents the gamma function.

3.3. Discrete Intersection

As reported in [20], when applying the lbestPSO algorithm to solve high-dimensional nonlinear equation systems, this optimization approach exhibits limitations, such as inadequate population diversity and sluggish convergence rate during the optimization process. Based on the investigations in [1], the discrete crossover operator within the DE algorithm exerts control over the proportion of offspring individual characteristics inherited by parent individuals. Therefore, the discrete crossover operation is capable of enhancing population diversity, while concurrently accelerating the convergence velocity of the population. Building on this rationale, to improve the population diversity of the PSO algorithm, the discrete crossover operation is incorporated into the EDDPSO algorithm, with its specific mathematical formulation presented as follows:

$${\mathit{x}}_{n,j}^{t+1}=\left\{\begin{array}{ll}{\mathit{u}}_{n,j}^t\hfill & \mathrm{rand}\le CR\hfill \\ {\mathit{x}}_{n,j}^t\hfill & \mathrm{else}\hfill \end{array}\right.$$

(11)

where ${\mathit{u}}_{n,j}^t$ denotes the experimental individual generated via Equation (4), and j represents the j-th variable of the experimental individual j = 1,2, …, D; ${\mathit{x}}_{n,j}^t$ corresponds to the position of the offspring particle; and CR represents the crossover probability, and its specific value is elaborated in Section 4.3.

3.4. Procedure of EDPSO Algorithm

In the EDPSO algorithm, particles form neighborhoods based on their intrinsic characteristics, through a dynamic neighborhood strategy. Meanwhile, during the evolutionary progression of the algorithm, particles at distinct developmental stages can adopt tailored velocity-update strategies. Furthermore, the incorporation of a discrete crossover operator strengthens the EDDPSO’s ability to address nonlinear equation systems involving high-dimensional variables compared to conventional PSO variants. The pseudocode of the proposed EDPSO algorithm is provided in Algorithm 1 (f_acc represents the acceptable root accuracy).

Algorithm 1: Pseudocode of the EDPSO algorithm

Input: NP; FES; Max_FES; m; Γ; CR

Output: The ultimately obtained roots of the NESs. 1: Initialize population x (x = x1, x2, …, xNP) and velocity parameters v (v = v1, v2, …, vNP). 2: Compute initial fitness values using Equation (2) for all xi∈x. 3: While FES < Max_FES 4: for i = 1 to NP 5: Select neighborhood candidates for xi using Equation (6). 6: If randj < Pj 7: Localize j-th candidate within xn’s neighborhood 8: Endif 9: If randn > ψ 10: Update velocity via adaptive Levy flight (Equation (9)) 11: else 12: Update velocity via adaptive Levy flight (Equation (9)) 13: Endif 14: Construct experimental individual ${\mathit{u}}_{i,j}^t$ using Equation (4) 15: Derive new particle position ${\mathit{x}}_{i,j}^{t+1}$ using Equation (11) 16: Compute fitness of ${\mathit{x}}_{i,j}^{t+1}$ using Equation (2) 17: If f(xn) < facc 18: Add xi to external archive; reset xi’s position and velocity 19: Endif 20: Endfor

Endwhile

4. Simulation Experiments and Analysis of Results

This section assesses the performance of the EDPSO algorithm through two quantitative metrics: the success rate (SR) and success rate ratio (RR), as defined in [8]. The EDPSO, NCDE [20], NSDE [20], DR-JADE [30], LSTP [31], KSDE [32], and HNDE [33] algorithms were applied to solve the positive kinematic equations for 20 NESs test functions and a parallel mechanism. Additionally, the impacts of parameters m, Γ, and CR on EDPSO’s optimization performance and the contributions of its improvement strategies are analyzed.

4.1. Test Functions and Evaluation Metrics

To validate the efficacy of the EDPSO algorithm in root-identification during a single computational run, 20 NESs functions from [16] were selected for experimental verification. To assess the performance of the EDPSO algorithm, two specific evaluation metrics derived from [8], namely Success Rate (SR) and Root Rate (RR), were selected for analysis.

RR: the ratio of the total count of all roots identified across multiple independent algorithm runs to the total number of known roots. The specific computational formulation for RR is provided below:

$$RR={\displaystyle \frac{{\displaystyle \sum _{j=1}^{RN}Ne{s}_j}}{NM\cdot RN}}$$

(12)

where RN denotes the quantity of independent operational trials conducted by the algorithm; Nes_j represents the count of roots successfully identified during the j-th trial; and NM specifies the number of pre-determined known roots within the system of nonlinear equations.

SR: the ratio of the number of independent operational trials where the algorithm successfully identifies all roots of the equation system to the total number of independent operational trials. The specific computational formulation for SR is provided below:

$$SR={\displaystyle \frac{N_{SR}}{RN}}$$

(13)

where N_SR denotes the count of independent executions of the algorithm required to identify all solutions of the equation system.

4.2. Contrastive Algorithms

For the selection of roots in 20 test functions, the acceptable root precision is defined as 1 × 10⁻⁶ when the dimensionality parameter n ≥ 5; in contrast, it is specified as 1 × 10⁻⁴ for scenarios where n < 5. Furthermore, a candidate root is recognized as newly identified only if the spatial separation between this root and any previously detected candidate root exceeds 0.1.

To validate the effectiveness and feasibility of the EDDPSO algorithm, six algorithms—NCDE [30], NSDE [30], DR-JADE [31], LSTP [32], KSDE [33], and HNDE [15]—were employed as the comparative counterparts in this study. To guarantee equity in assessing algorithmic performance, the population size NP and maximum evaluation count parameters for the algorithms under investigation are configured as NP = 100 and Max_FES. (Specifically, the parameter configurations for test functions F1, F8, and F14 are defined as 10,000, 100,000, and 20,000, respectively, while all remaining test functions adopt a parameter value of 50,000.) Other parameters of the algorithms were configured to align with those documented in the original literature, and each algorithm was conducted independently for 50 trials. The mean values of algorithm performance metrics for seven algorithms evaluated on 20 test functions are summarized in

Table 1. Average SR and RR values of seven algorithms for solving 20 test functions.

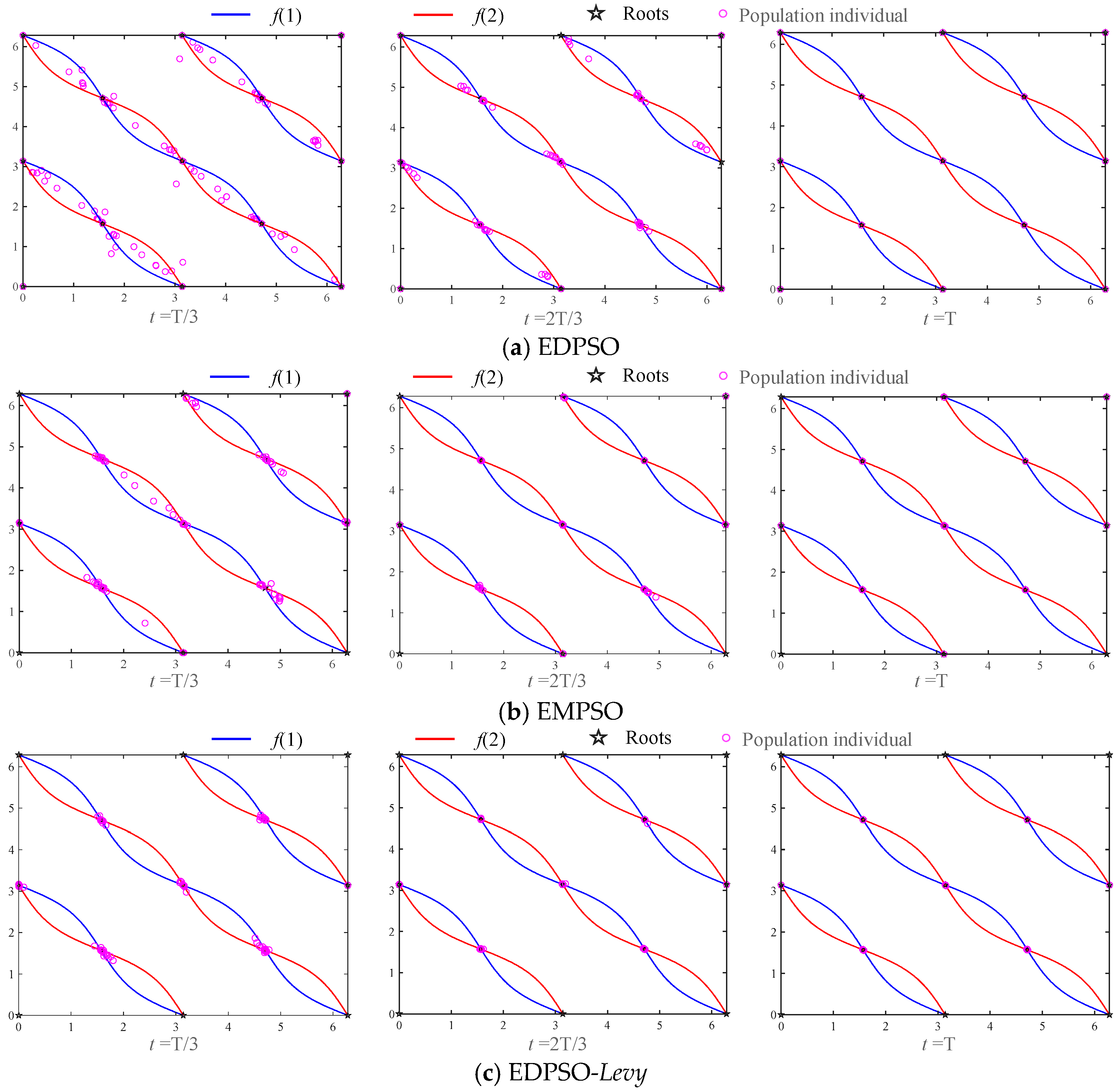
Index	EDPSO	NCDE	NSDE	DR-JADE	LSTP	KSDE	HNDE
RR	0.9989	0.9751	0.9840	0.8957	0.9946	0.9720	0.9626
SR	0.9920	0.9400	0.9660	0.8860	0.9810	0.9550	0.9240

, while comprehensive results for individual test functions are detailed in Supplementary Table S1.

According to the data presented in Table 1, the EDPSO algorithm yields the highest average values for both SR and RR metrics, with subsequent performance rankings occupied by LSTP, NSDE, KSDE, NCDE, HNDE, and DR-JADE algorithms, in that order. Based on the data in Supplementary Table S1, the EDPSO algorithm successfully identified the roots of 20 benchmark functions. In particular, 17 of these test cases displayed both SR and RR values equal to 1, which indicates that the EDPSO algorithm could fully determine all roots of these 17 nonlinear equation systems during 50 independent computational trials. The Wilcoxon signed-rank test was performed on the data from Supplementary S1, with results summarized in

Table 2. Wilcoxon signed-rank test results comparing EDPSO and its counterpart algorithm on SR/RR metrics across 20 NES problems.

EDPSO VS	RR			SR
	R+	R−	p Value	R+	R−	p Value
NCDE	171.0	39.0	0.012622	171.0	39.0	0.012622
NSDE	125.0	85.0	0.444081	125.0	85.0	0.444081
DR-JADE	151.0	39.0	0.022302	142.0	68.0	0.157607
LSTP	137.5	52.5	0.083556	137.5	52.5	0.082006
KSDE	121.5	68.5	0.277241	122.0	68.0	0.266029
HNDE	158.0	52.0	0.044786	158.0	52.0	0.041822

p > 0.05, no significant difference; p < 0.05, statistically significant difference.

.

As shown in Table 2, EDPSO demonstrates significantly superior performance compared with NCDE, DR-JADE, and HNDE (Wilcoxon signed-rank test, p < 0.05). Specifically, EDPSO achieves a significantly higher SR compared to NCDE (R⁺ = 171.0, p = 0.0126) and LSTP (R⁺ = 137.5, p = 0.0126). This result indicates that the dynamic domain strategy based on Euclidean distance effectively avoids boundary individuals being selected as neighbors, thereby preventing the algorithm from losing potential roots near the current optimal individual. Similarly, EDPSO demonstrates faster convergence (higher RR) compared to DR-JADE (R⁺ = 142.0, p = 0.0223), which can be primarily attributed to the differing reinitialization strategies employed by the two algorithms. Specifically, the DR-JADE algorithm triggers a complete reinitialization of all individuals within a subpopulation whenever any individual detects a root of the NESs. In contrast, EDPSO selectively reinitializes only those individuals that have identified a root, thereby facilitating the efficient exploration and rapid discovery of neighboring roots.

4.3. Effect of Parameter Settings on Algorithm Performance

When addressing multiple roots of nonlinear equation systems, the convergence efficiency, SR, and RR of the EDPSO algorithm are influenced by key parameters, including neighborhood size m, weighting factor m, and crossover probability CR.

To investigate the influence of diverse m values on the performance of the EDPSO algorithm, eleven distinct parameter configurations were designed with m spanning from 5 to 15 (inclusive). For each configuration, the algorithm was executed independently 50 times. The statistical outcomes of RR and SR derived from these trials are summarized in

Table 3. Effect of varying m values on the performance of the algorithm.

Index	m = 5	m = 6	m = 7	m = 8	m = 9	m = 10
RR	0.9617	0.9930	0.9942	0.9965	0.9989	0.9961
SR	0.8990	0.9680	0.9750	0.9810	0.9920	0.9810
Index	m = 11	m = 12	m = 13	m = 14	m = 15	-
RR	0.9948	0.9957	0.9951	0.9943	0.9942	-
SR	0.9710	0.9740	0.9740	0.9650	0.9650	-

, while comprehensive detailed data are provided in Supplementary Tables S2 and S3. Based on the data presented in Tables S2 and S3, the RR and SR values exhibit an initial increasing trend followed by a subsequent decrease as the parameter m increases, with their optimal magnitudes achieved specifically at m = 9.

To investigate the influence of varying Γ parameters on the performance of the EDPSO algorithm, ten distinct Γ values (0.1, 0.2, 0.3, …, 1) were selected for experimental validation. For each Γ setting, the algorithm was executed independently over 50 runs. The statistical outcomes of the RR and SR are summarized in

Table 4. Effect of varying Γ values on the performance of the algorithm.

Index	Γ = 0.1	Γ = 0.2	Γ = 0.3	Γ = 0.4	Γ = 0.5	Γ = 0.6	Γ = 0.7	Γ = 0.8	Γ = 0.9	Γ = 1
RR	0.9967	0.9975	0.9978	0.9985	0.9963	0.9964	0.9968	0.9928	0.9943	0.9961
SR	0.9967	0.9975	0.9978	0.9985	0.9963	0.9964	0.9968	0.9928	0.9943	0.9961

, with comprehensive data further detailed in Supplementary Tables S4 and S5. Analysis of Table 4 reveals that with the increase of Γ, both RR and SR values first exhibit an upward trend, followed by a downward trend, reaching their peak values at Γ = 0.4.

To investigate the influence of CR configurations on the performance of the EDPSO algorithm, ten discrete CR values (0.1, 0.2, 0.3, …, 1.0) were selected. For each CR setting, the algorithm was independently executed 50 times, and the statistical outcomes of RR and another key metric SR derived from these trials are summarized in

Table 5. Effect of varying CR values on the performance of the algorithm.

Index	CR = 0.1	CR = 0.2	CR = 0.3	CR = 0.4	CR = 0.5	CR = 0.6	CR = 0.7	CR = 0.8	CR = 0.9	CR = 1
RR	0.3235	0.4246	0.5876	0.7804	0.8562	0.9441	0.9419	0.9469	0.9483	0.9469
SR	0.1730	0.2390	0.3940	0.7050	0.8420	0.9300	0.9230	0.9350	0.9390	0.9340

. Comprehensive details of these results are further provided in Supplementary Tables S6 and S7. Examination of Table 5 demonstrates that as the CR parameter increases, both the RR and SR metrics exhibit an initial upward trend, followed by a subsequent decline, ultimately reaching their peak performance when CR is adjusted to 0.9.

4.4. Impact of Improvement Strategies on the EDPSO Algorithm

To investigate the influence of diverse improvement strategies on the EDPSO algorithm, 20 benchmark test functions were utilized to conduct comparative experiments across its modified variants. The three variants of the EDPSO algorithm can be characterized as follows: (1) EMPSO: this variant omits the neighborhood construction strategy based on the Euclidean distance of the population, while retaining all other modules identical to the original EDPSO algorithm; (2) EDPSO-Levy: here, the velocity-update mechanism associated with Levy flight is removed, and the remaining components maintain consistency with the DEPSO algorithm; (3) EDPSO-CR: a third modified variant in which the discrete crossover strategy is excluded, with all other operational frameworks preserved in line with the EDPSO algorithm. The remaining control parameters of the proposed algorithm maintain consistency with those of the EDPSO algorithm. The average statistical metrics of RR and SR are presented in

Table 6. Impact of Diverse Enhancement Approaches on Algorithm Performance.

Index	EDPSO	EMPSO	EDPSO-Levy	EDPSO-CR
RR	0.9989	0.9644	0.8008	0.6732
SR	0.9920	0.9070	0.7280	0.5830

, while comprehensive details can be found in Supplementary Tables S8 and S9.

As presented in Table 6, during the performance evaluation experiments of the EDPSO algorithm’s multiple improved variants on 20 benchmark test functions, the original EDPSO variant demonstrated optimal average values for both the RR and SR metrics. This outcome effectively validates the efficacy of each proposed improvement strategy. Furthermore, to validate the roles of each improved strategy within the algorithms, we applied EDPSO, EDPSO, EDPSO-Levy, and EDPSO-CR variants to optimize test function F13, respectively. The evolutionary trajectories of these algorithms during the optimization process of this test function at specific time nodes (t = T/3, t = 2T/3, and t = T) were visualized, as illustrated in Figure 2. As shown in Figure 2, during the initial evolutionary stage of the algorithm, the EDPSO-Levy algorithm adopts the lbest-based position-updating mechanism, which induces the aggregation of particles within the swarm around multiple root regions. In contrast, following the incorporation of the Levy flight-based position update formulation, the population individuals demonstrate a uniformly distributed pattern in the vicinity of multiple roots of the objective function. During the mid-stage of algorithm evolution, the population individuals of the EDPSO-Levy algorithm exhibit convergence toward multiple roots previously identified in the early search phase, yet demonstrate a failure to locate the roots that were missed during the initial exploration stages. In contrast, the population individuals of the standard EDPSO algorithm achieve successful convergence around all roots of the target function. In the subsequent stages of algorithm evolution, the EDPSO-Levy variant failed to capture the roots that were overlooked during the initial search phase. Conversely, the standard EDPSO algorithm demonstrated superior root-finding capability by successfully identifying all roots of the target function. To summarize, the integration of Levy flight-based position update mechanism effectively mitigates the drawback of the lbest position-update strategy being susceptible to local stagnation, thereby establishing a two-stage velocity-update framework. In particular, the Levy flight-based position update strategy enables the EDPSO algorithm to sustain robust population diversity in the initial evolutionary phase, while the lbest position-update strategy promotes the convergence of individuals toward distinct roots of the objective function during the later optimization stages.

The performance of the EDPSO algorithm is nearly equivalent to that of the EDPSO-CR algorithm. However, by referring to Supplementary Tables S8 and S9, it is evident that EDPSO-CR yields SR and RR values of 0 during the solution of the high-dimensional system of nonlinear equations F20. In comparison, both the SR and RR metrics of the EDPSO algorithm reach a value of 1. These results indicate that the discrete crossover strategy notably strengthens the EDPSO algorithm’s capability in addressing high-dimensional nonlinear equation systems.

In summary, the developed dynamic domain strategy (anchored in Euclidean distance principles), the dual-strategy velocity-update mechanism (inspired by Levy flight dynamics), and the discrete crossover strategy collectively augment the EDPSO algorithm’s proficiency in identifying multiple roots of multi-peak functions.

4.5. Mechanical Optimization: Example Application

Wen et al. [2] has established that the positive kinematic equations of coupled parallel mechanisms inherently form a system of nonlinear equations. To further validate the practicality of the EDPSO algorithm in mechanical optimization scenarios, this study utilizes the positive kinematic equations of the 3-PRS parallel mechanism proposed in [34] as a representative case for verification.

Existing research [34] indicates that the 3-RPS parallel mechanism exhibits three degrees of freedom, specifically comprising two rotational degrees of freedom and one translational degree of freedom. The three-dimensional model of the 3-RPS parallel mechanism and the top-view schematic of the mechanism are, respectively, illustrated in Figure 3 and Figure 4. The centers of the rotating subunit R1i mounted on the fixed platform are denoted as A_i (i = 1,2,3), and the centers of the spherical subunit S3i attached to the moving platform are defined as B_i (i = 1,2,3). The rotary vise center points A₁A₂A₃ and B₁B₂B₃ are sequentially interconnected to form equilateral triangles, with their respective geometric centers located at P (origin of the dynamic coordinate system) and O (origin of the dynamic coordinate system). The coordinate systems of the fixed and moving platforms are defined as illustrated in Figure 1 and Figure 2. Herein, the coordinate system is defined as follows: the Z-axis and z-axis are, respectively, perpendicular to the fixed platform and east platform of the mechanism; the X-axis and x-axis are each oriented perpendicular to the A₁A₃ link and B₁B₃ link, respectively, while the Y-axis and y-axis adhere to the right-hand rule for their directional determination.

The coordinate representation of point B_i (i = 1,2,3) within the fixed reference frame can be expressed as

$$\left\{\begin{array}{l}{B}_1=(X_{B_1},Y_{B_1},Z_{B_1})={\left({\displaystyle \frac{1}{2}}(R-L_{1}c{\theta }_1),{\displaystyle \frac{\sqrt{3}}{2}}(R-L_{1}c{\theta }_1),L_{1}s{\theta }_1\right)}^T\hfill \\ B_2=(X_{B_2},Y_{B_2},Z_{B_2})={(-R+L_2\mathrm{c}{\theta }_2,0,L_2\mathrm{s}{\theta }_2)}^T\hfill \\ B_3=(X_{B_3},Y_{B_3},Z_{B_3})={\left({\displaystyle \frac{1}{2}}(R-L_3\mathrm{c}{\theta }_3),-{\displaystyle \frac{\sqrt{3}}{2}}(R-L_3\mathrm{c}{\theta }_3),L_3\mathrm{s}{\theta }_3\right)}^T\hfill \end{array}\right.$$

(14)

where, cθ = cosθ, sθ = sinθ.

Once the geometric dimensions of the mechanism are finalized, the inter-center spacing of the spherical components within the ball joint associated with the moving platform will maintain a constant value. Consequently, utilizing the distance between the sub-center points of two neighboring spherical structures as a rod-length constraint leads to

$$\left\{\begin{array}{c}{(B_1-B_2)}^T(B_1-B_2)=\overline{{B_1{B}_2}^2}\\ {(B_2-B_3)}^T(B_2-B_3)=\overline{{B_2{B}_3}^2}\\ {(B_1-B_3)}^T(B_1-B_3)=\overline{{B_1{B}_3}^2}\end{array}\right.$$

(15)

Equation (15) can be simplified to the following form:

$$\left\{\begin{array}{c}{(X_{B_1}-X_{B_2})}^2+{(Y_{B_1}-Y_{B_2})}^2+{(Z_{B_1}-Z_{B_2})}^2=3r^2\\ {(X_{B_2}-X_{B_3})}^2+{(Y_{B_2}-Y_{B_3})}^2+{(Z_{B_2}-Z_{B_3})}^2=3r^2\\ {(X_{B_1}-X_{B_3})}^2+{(Y_{B_1}-Y_{B_3})}^2+{(Z_{B_1}-Z_{B_3})}^2=3r^2\end{array}\right.$$

(16)

Given that x = (x₁,x₂,x₃)^T = (θ₁,θ₂,θ₃)^T, Equation (16) can be re-expressed through the following transformation:

$$\left\{\begin{array}{l}f(1)={\left({\displaystyle \frac{3}{2}}R-{\displaystyle \frac{1}{2}}{L}_1\mathrm{c}{x}_1-L_2\mathrm{c}{x}_2\right)}^2+{\displaystyle \frac{3}{4}}{\left(R-L_1\mathrm{c}{x}_1\right)}^2+{\left(L_1\mathrm{s}{x}_1-L_2\mathrm{s}{x}_2\right)}^2-3r^2\hfill \\ f(2)={\left(-{\displaystyle \frac{3}{2}}R+L_2\mathrm{c}{x}_2-L_3\mathrm{c}{x}_3\right)}^2+{\displaystyle \frac{3}{4}}{\left(R-L_3\mathrm{c}{x}_3\right)}^2+{\left(L_2\mathrm{s}{x}_2-L_3\mathrm{s}{x}_3\right)}^2-3r^2\hfill \\ f(3)={\left({\displaystyle \frac{1}{2}}{L}_1\mathrm{c}{x}_1+L_3\mathrm{c}{x}_3\right)}^2+{\left(\sqrt{3}R-{\displaystyle \frac{\sqrt{3}}{2}}{L}_1\mathrm{c}{x}_1-{\displaystyle \frac{\sqrt{3}}{2}}{L}_3\mathrm{c}{x}_3\right)}^2+{\left(L_1\mathrm{s}{x}_1-L_3\mathrm{s}{x}_3\right)}^2-3r^2\hfill \end{array}\right.$$

(17)

The scale parameters of the 3-RPS parallel mechanism are defined as follows: R = 160 mm, r = 100 mm, and (L₁, L₂, L₃)^T = (132, 152, 132)^T mm. The algorithm’s search space is explicitly defined through the configuration x_max = [π,π,π] and x_min = −x_max. With respect to other control parameters, this implementation maintains consistency with the specifications detailed in Section 4.2. The positive kinematic equations of the 3-RPS parallel mechanism were independently solved 50 times, via each of the following optimization algorithms: EDPSO, NCDE, NSDE, DR-JADE, LSTP, KSDE, and HNDE. The roots derived from these equations are systematically presented in

Table 7. Positive solutions for the position of the 3-RPS parallel mechanism.

Num.	θ1	θ2
1	−1.63631461687421	63.5147256862694
2	63.3314584255204	−6.02190524082467
3	−64.4626549032305	−62.7136209043545
4	1.63613571288348	−63.5147650619382
5	−62.4277287170268	−64.5135098221173
6	64.4626615445065	62.7134310018056
7	−63.3312267809634	6.02209000699150
8	62.4281274010519	64.5133664633938

, with detailed values of the SR and RR provided in

Table 8. RR and SR values of EDPSO algorithm and its comparative algorithms for solving 3-RPS parallel mechanism.

Index	EDPSO	NCDE	NSDE	DR-JADE	LSTP	KSDE	HNDE
RR	0.9800	0.8800	0.8600	0.9000	0.9400	0.9200	0.8600
SR	0.9975	0.9750	0.9800	0.9875	0.9925	0.9900	0.9826

.

Based on the data presented in Table 8, the EDPSO algorithm continues to exhibit superior performance in terms of SR and RR metrics when addressing the forward kinematic problem of the 3-RPS parallel manipulator. The ranking of subsequent algorithms, from highest to lowest performance, is as follows: LSTP, KSDE, DR-JADE, NCDE, NSDE, and HNDE. The validity of the EDPSO algorithm in the context of mechanical optimization problems has been experimentally validated.

5. Conclusions

To enable the identification of multiple roots for nonlinear equation systems within a single numerical iteration, this study integrates three specialized enhancement strategies into the standard PSO framework: a Euclidean distance-based dynamic neighborhood strategy, a dual-strategy velocity-update mechanism inspired by Levy flight dynamics, and a discrete crossover operator. This integration ultimately leads to the development of a novel EDPSO algorithm. To validate the finiteness and generalizability of the proposed algorithm, 20 benchmark test functions combined with mechanical case studies were employed as evaluation subjects. Empirical validation through experimental investigations demonstrates that the EDPSO algorithm exhibits superior performance characteristics relative to its competing peer algorithms. Finally, the influences of each proposed enhancement approach, in conjunction with the control parameters m, Γ, and CR, on the optimization performance of the EDPSO algorithm, are systematically examined.

Although the EDPSO algorithm shows potential in solving NSEs with diverse characteristics, the approach suffers from a significant limitation: its control parameters (e.g., m, Γ, and CR) rely on empirical presets, making adaptive tuning to problem-specific features challenging. Furthermore, algorithm robustness remains incompletely validated under demanding engineering constraints. To overcome these limitations, future work will develop adaptive control parameter strategies for the EDPSO algorithm to handle diverse NSE problems and validate its effectiveness in practical engineering scenarios (e.g., robotic-arm inverse kinematics and real-time trajectory planning).