Statistical Evaluation of Alpha-Powering Exponential Generalized Progressive Hybrid Censoring and Its Modeling for Medical and Engineering Sciences with Optimization Plans
Abstract
1. Introduction
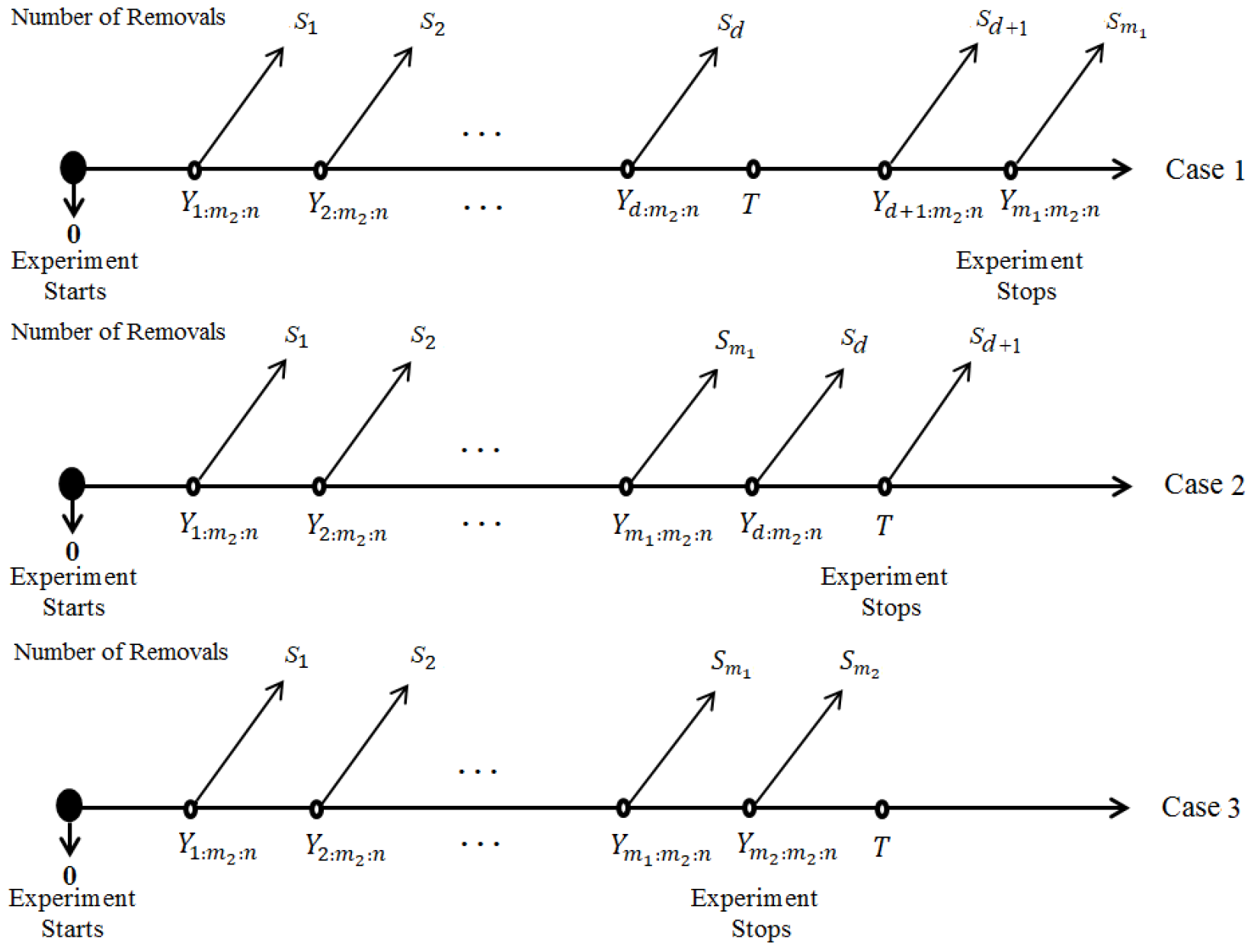
- Case 1: If , end the test at ;
- Case 2: If , end the test at T. Let d denote the number of failures observed up to time T;
- Case 3: If , end the test at .
- , , , and (Case 1);
- , , , and (Case 2);
- , , , and (Case 3).
- (i)
- Unlike existing works that treat the APE distribution and the G-PH censoring scheme separately, this study provides the first comprehensive statistical evaluation of the APE distribution under the G-PH framework;
- (ii)
- We develop the complete likelihood-based and Bayesian inferential framework, deriving asymptotic properties and assessing bootstrap performance under severe censoring conditions;
- (iii)
- We design optimized censoring and test plans that minimize experimental cost subject to precision constraints, a novel contribution for this class of models; and
- (iv)
- We validate the proposed methodology through applications in both medical and engineering sciences, offering concrete guidelines for practical test design.
- Driving maximum likelihood and Bayesian estimations for the APE parameters and , and associated reliability measures and .
- Employing independent gamma priors, the Bayesian estimation is implemented using the Metropolis-Hastings algorithm under a squared-error loss (SEL) function.
- Two asymptotic confidence intervals alongside two Bayesian credible intervals for all model parameters are created.
- Extensive Monte Carlo simulations are conducted to assess the accuracy and precision of the developed estimators across various thresholds, sample sizes, censoring levels, and prior choices. The proposed methodology is validated on two real datasets (breast cancer and oil reserve data) to illustrate the practical utility and flexibility of the examined model.
- The study performs a comparative evaluation of different progressive censoring patterns, revealing distinct strengths of each plan depending on the parameter of interest.
2. Likelihood Inference
2.1. Point Estimators
2.2. Interval Estimators
3. Bayesian Inference
- Case 1: .
- Case 2: .
- Case 3: .
| Algorithm 1 The M-H Sampling: |
|
4. Numerical Evaluations
4.1. Simulation Design
| Algorithm 2 Generation Procedure of G-PH censoring plan: |
|
- ,
- ,
- , or after a maximum of 200 iterations.
- (i)
- Reparameterizing as and to automatically enforce and ;
- (ii)
- Evaluating terms using numerically stable primitives (e.g., and ) to avoid cancellation when is close to zero;
- (iii)
- Scaling the data by to keep in a moderate range and clipping away from exact 0 or 1.
- For Pop-1:APE(0.5, 1.5):
- –
- Prior I: and ;
- –
- Prior II: and ,
- For Pop-2:APE(1.5, 2.5):
- –
- Prior I: and ;
- –
- Prior II: and .
- Root Mean Squared Error:
- Mean Relative Absolute Bias:
- Average Interval Length:
- Coverage Percentage:where is the calculated point estimate of at ith sample, is the indicator function, is two-sided of ACI-NA/ACI-NL (or BCI/HPD) of .
4.2. Simulation Results and Discussions
- The overall estimation procedures yield satisfactory outcomes for the parameters and , as well as for and , across all simulation settings.
- Estimation accuracy, in both point and interval terms, improves with increasing sample size n, and likewise when the total number of censoring units is reduced, highlighting the sensitivity of the inferential results to test size and censoring intensity.
- As grow, all estimation findings of , , , and perform well.
- As T grows, the RMSE, MRAB, and AIL results of , , , and decreased while their CPs increased.
- When APE() grows, we noticed that:
- –
- The RMSEs and MRABs of APE model parameters and increased except for APE reliability parameters and decreased;
- –
- The AILs of , , and increased while those of decreased;
- –
- The CPs of , , and decreased while those of increased.
- The incorporation of prior knowledge through informative gamma priors substantially enhances the Bayesian estimates compared to the MLEs for all parameters under consideration, yielding narrower and more reliable HPD intervals.
- Bayesian inference, facilitated by prior information, consistently outperforms classical counterparts in estimating , , , and , particularly under informative prior settings.
- Given that Prior-II exhibits lower variance compared to Prior-I, the MCMC-based Bayesian estimation under Prior-II yields more precise posterior estimates of , , , and for both populations (Pop-i for ), outperforming the results obtained under alternative prior specifications.
- Comparing the proposed interval estimations of , , , and , it is observed that:
- –
- All credible interval estimates of , , , and produced by BCI/HPD methods outperformed the asymptotic interval estimates produced by ACI-NA/ACI-NL methods;
- –
- The ACI-NA method is the best choice compared to the ACI-NL method for estimating the interval estimates of , , and . The opposite comment is also noted for .
- –
- The HPD interval method is the best choice compared to the BCI method for estimating the interval estimates of all unknown subjects.
- Comparing the proposed censoring schemes PCP[i] (for ) reveals that the PCP[3] is most effective for estimating and , the PCP[2] excels for , and the PCP[1] is preferable for .
- To ensure high-quality estimation of lifetime characteristics under complex censoring, experimental designs should aim to maximize test duration within the constraints of cost and logistical feasibility.
- Overall, for data arising from the generalized progressive hybrid censoring framework, the Bayesian methodology, specifically employing the Metropolis-Hastings algorithm, proves to be a stable and reliable approach for inference on both model parameters and associated reliability functions.
- Algorithm 1: Generating an MCMC sample via the M–H sampler with 12,000 iterations and a burn-in of 2000 required approximately 3 s. The computational cost scales linearly with the number of iterations and sample size but remains highly manageable across all simulation settings.
- Algorithm 2: Generating censored samples required less than 0.1 s, which is negligible compared to the iterative M–H sampling.
5. Real Data Applications
5.1. Breast Data
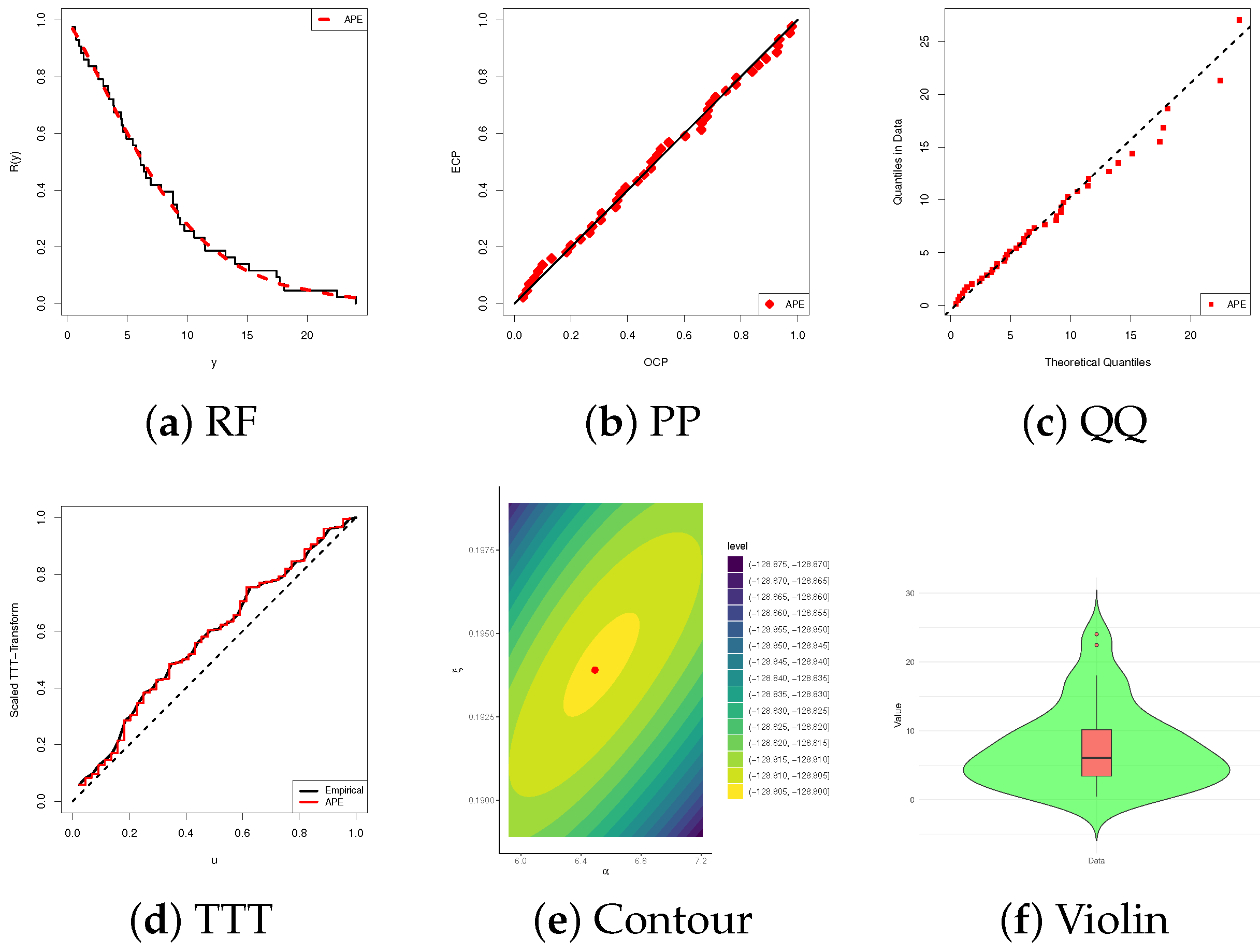
- Figure 5a demonstrates close agreement between the empirical estimates and the fitted APE reliability function.
- Figure 5b shows alignment of fitted and empirical probabilities along the 45° line.
- Figure 5c confirms that the model adequately captures the distributional shape of the data, as most points follow the diagonal.
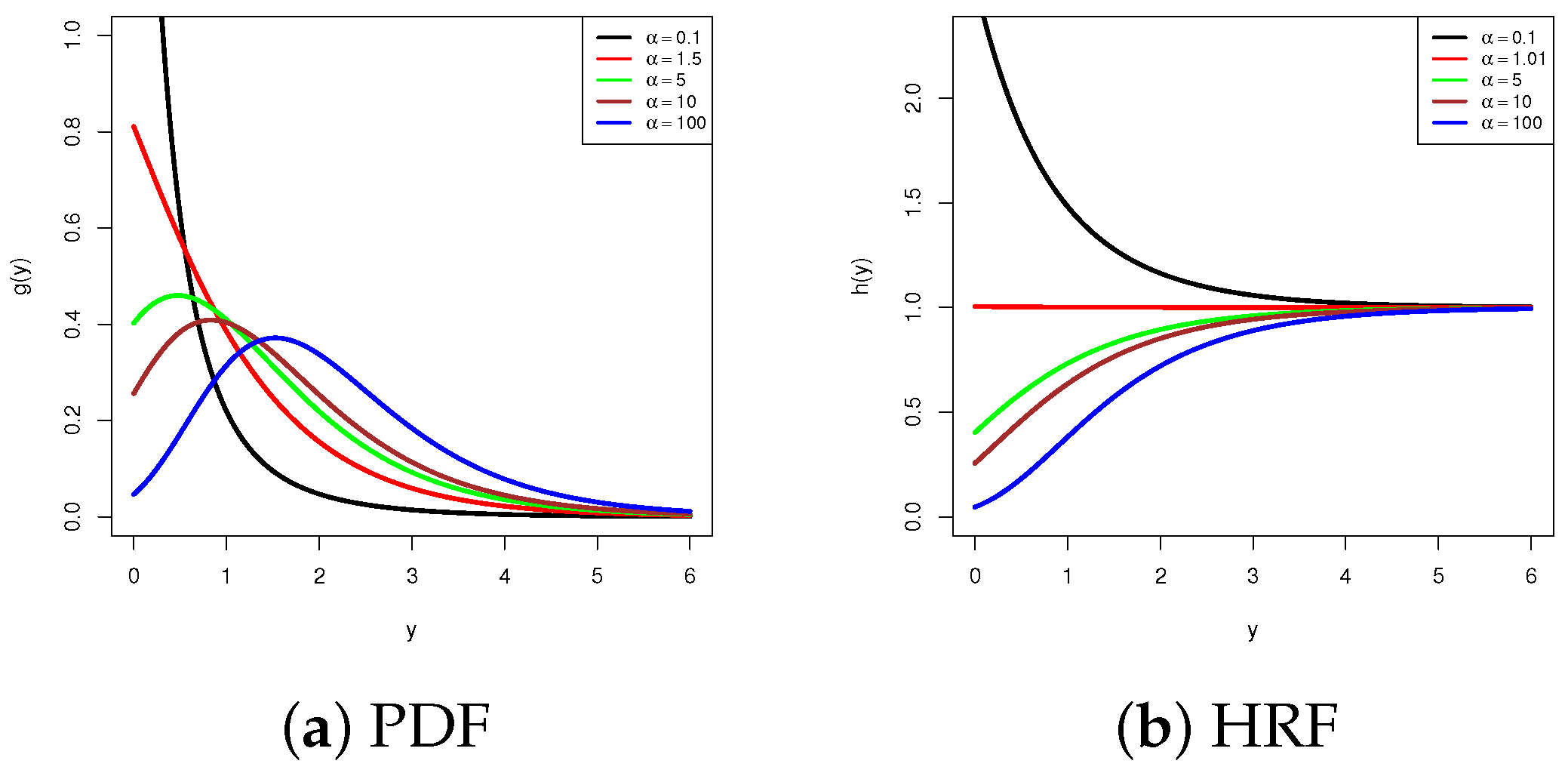
- Figure 5d reveals that the BC data exhibit an increasing failure rate, consistent with one of the theoretical forms predicted by the APE model.
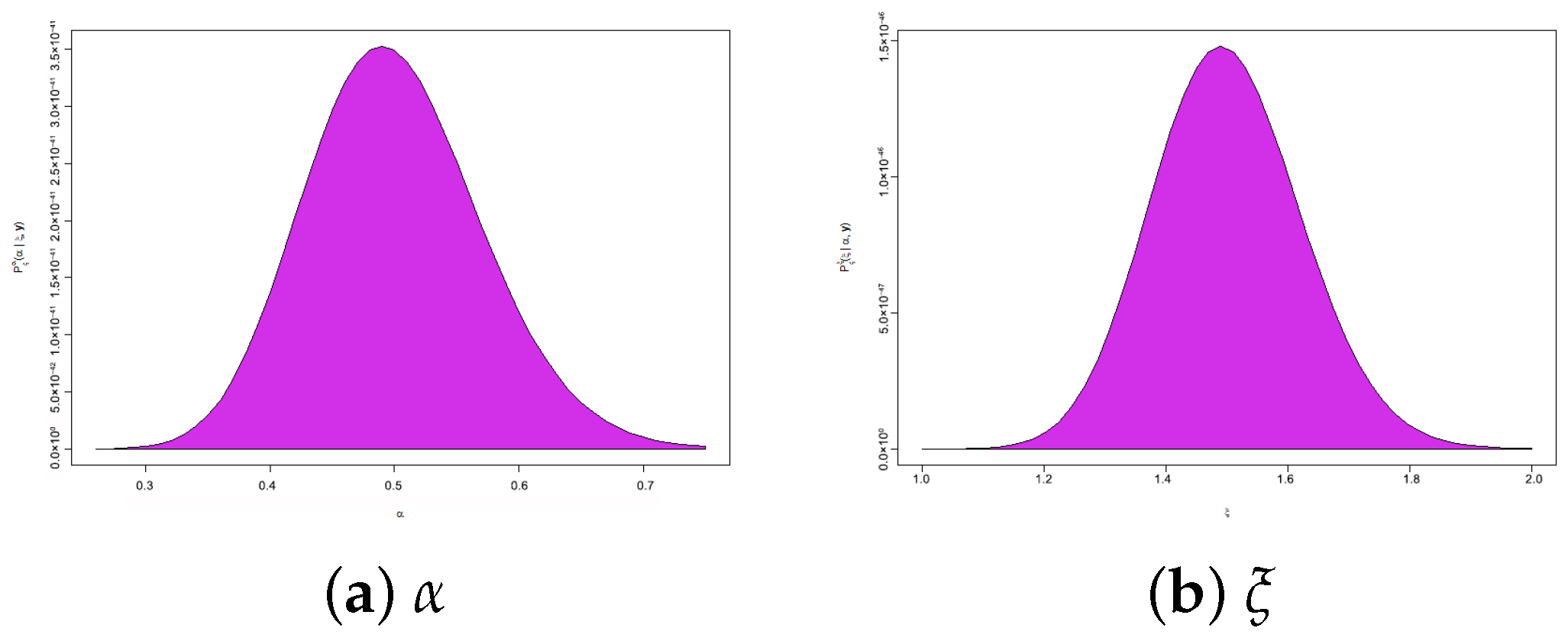
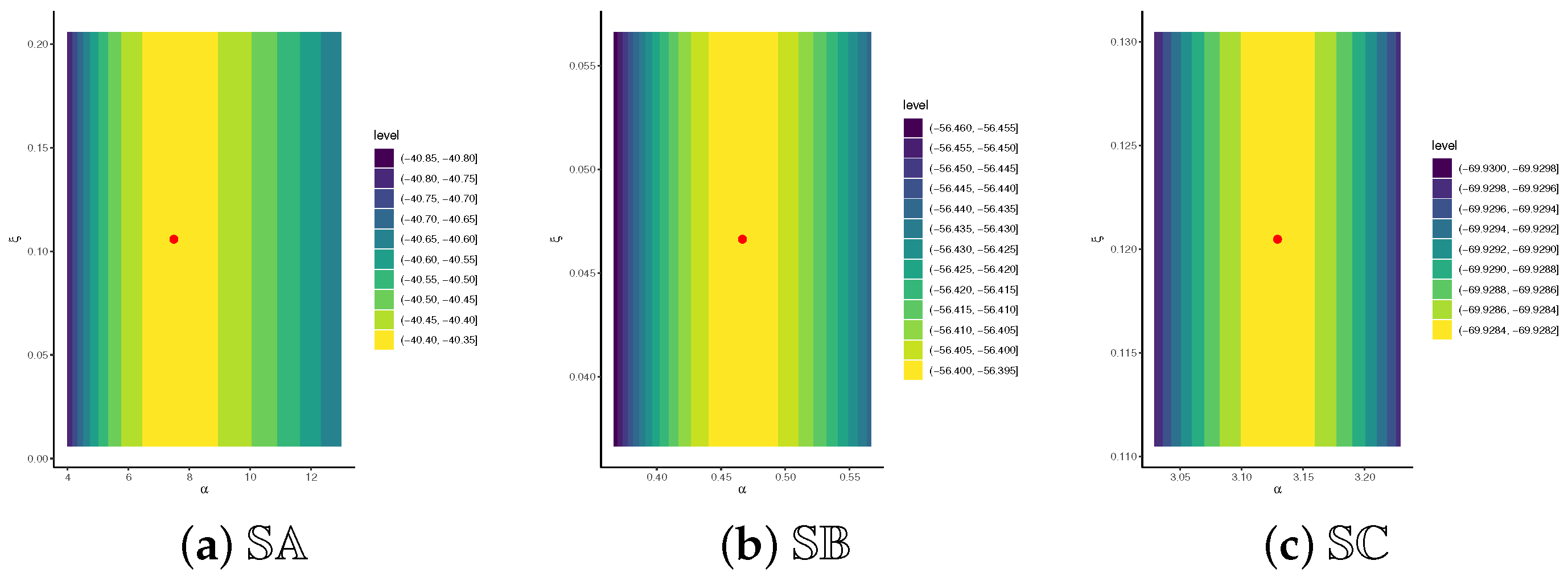
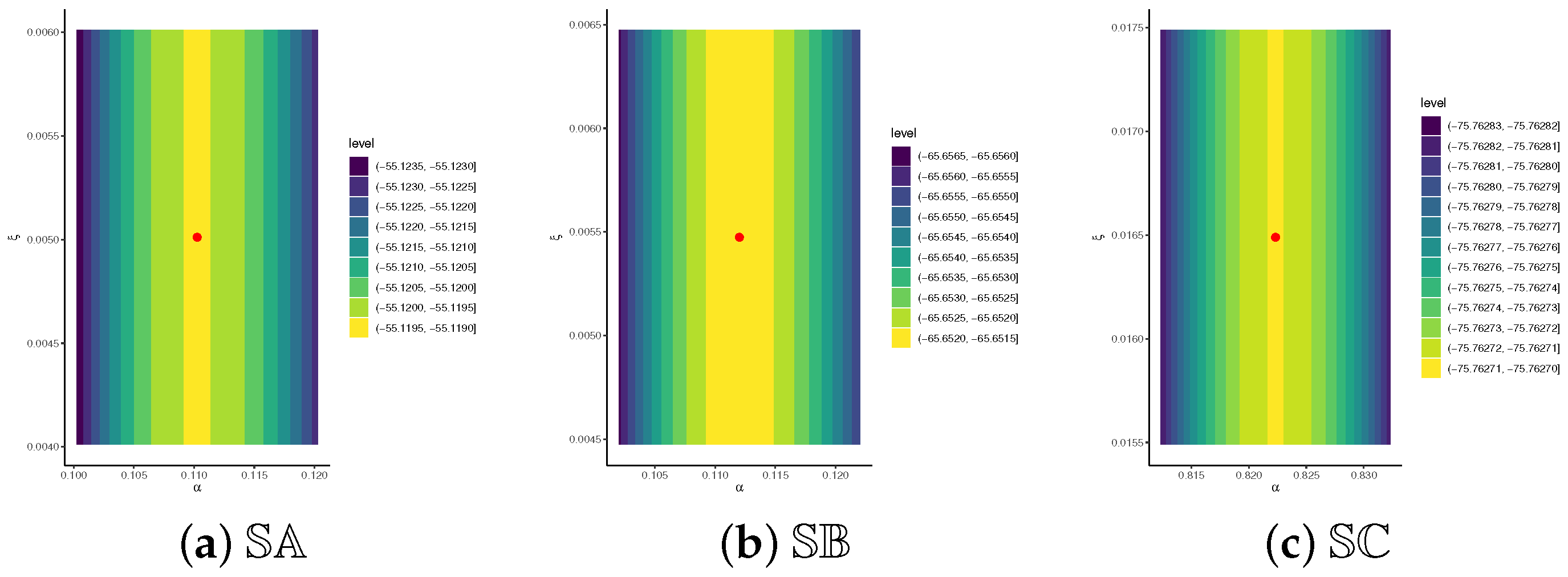
- Figure 5e highlights the parameter region of highest support, with the red dot marking the global maximum, and further confirms the existence and uniqueness of the MLEs and .
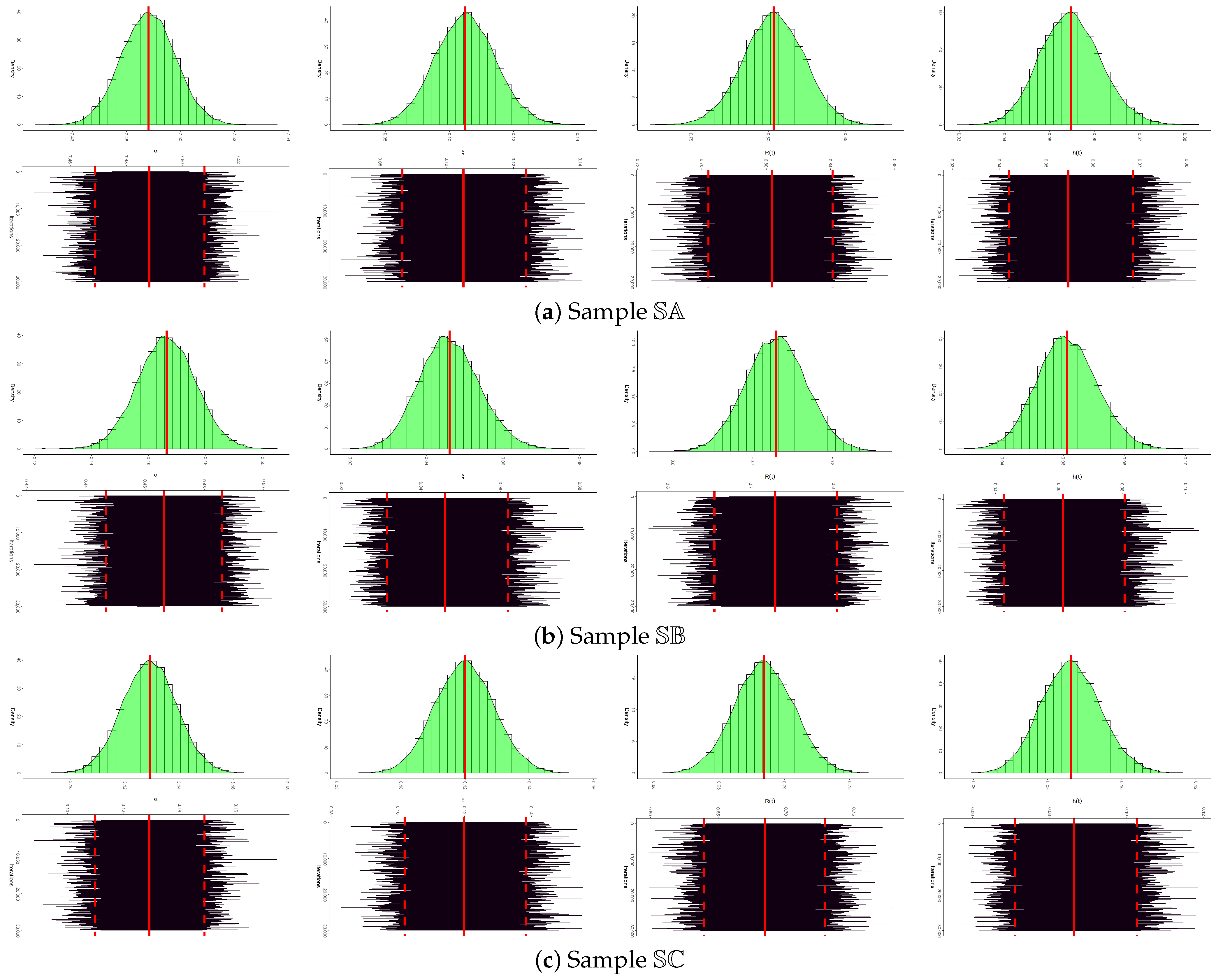
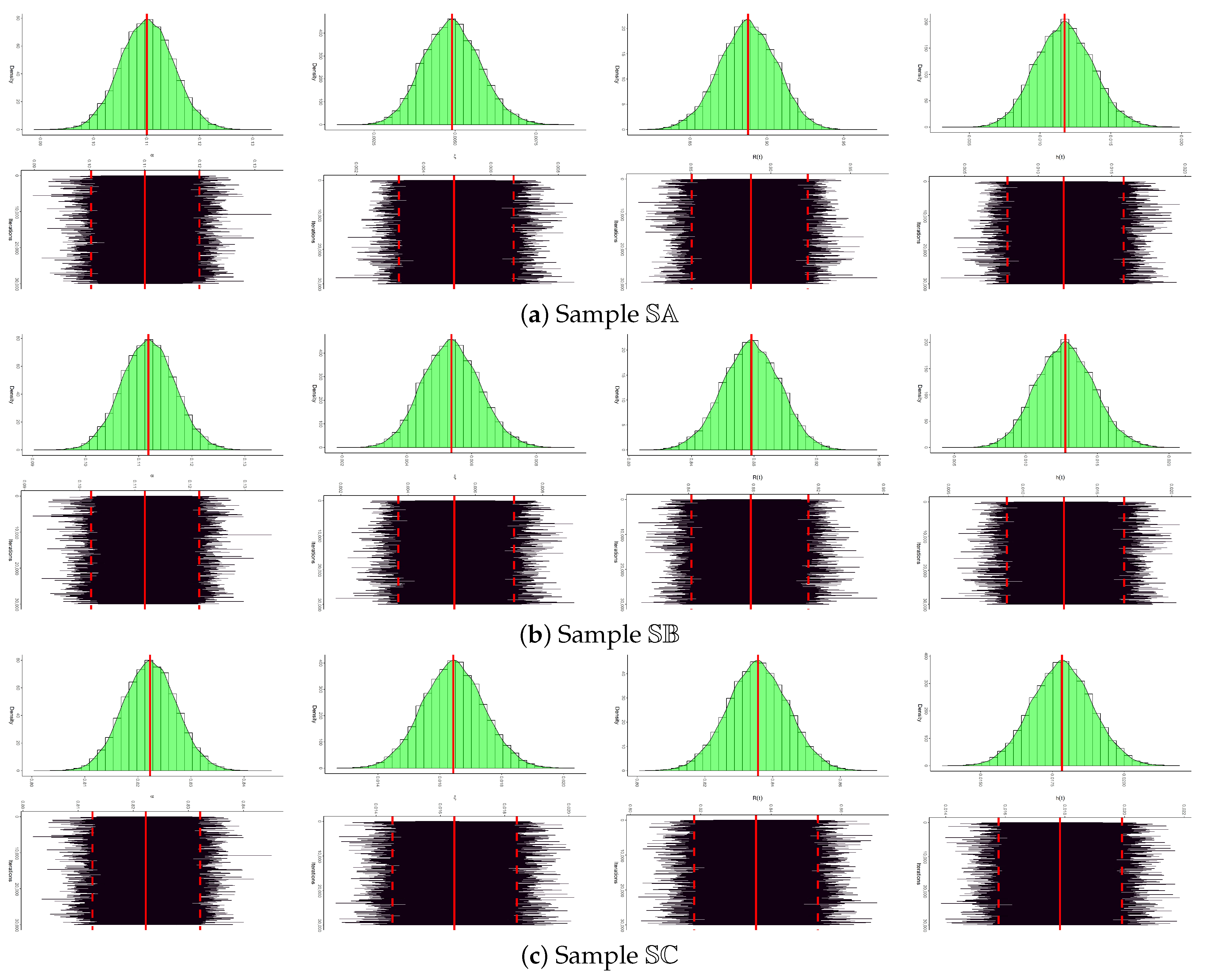
- Figure 5f summarizes the posterior sample distribution, including density shape and central tendency, indicating that the data exhibit moderate right skewness with the central tendency clustered around the median.
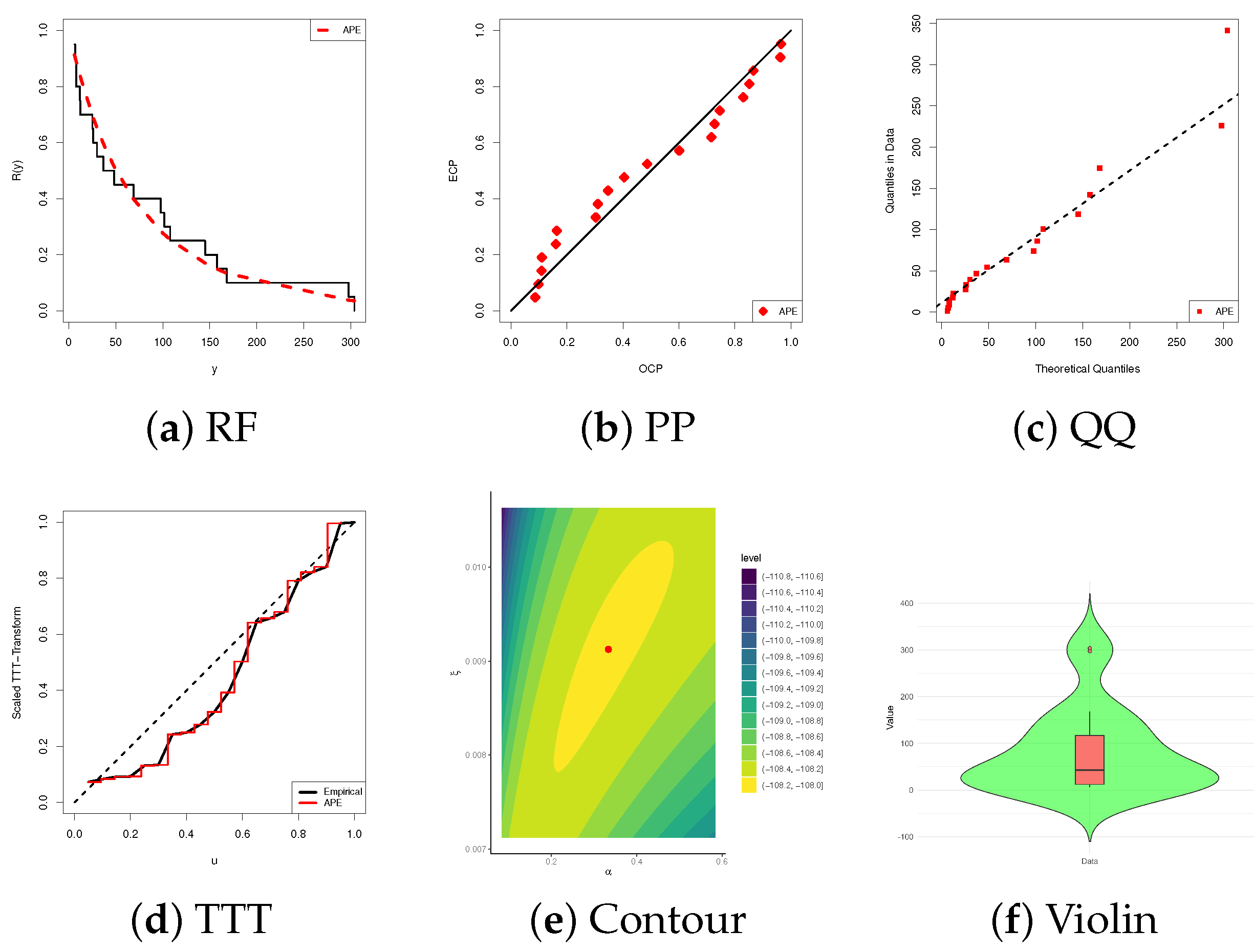
5.2. Oil Data
6. Optimal PCP
- Criterion : Maximizing the trace of ;
- Criterion : Minimizing the trace of ;
- Criterion : Minimizing the determinant of ;
- Criterion : Minimizing the variance of the MLE of the logarithm of th APE quantile (for ), where , aswithand
- For the BC data:
- –
- Using , the optimal PCP design corresponds to Sample ‘’ (i.e., left-censoring);
- –
- Using , the optimal PCP design corresponds to Sample ‘’ (i.e., middle-censoring);
- –
- Using , the optimal PCP design corresponds to Sample ‘’ (i.e., right-censoring),
- For the oil data:
- –
- Using , the optimal PCP design corresponds to Sample ‘’ (i.e., right-censoring);
- –
- Using , the optimal PCP design corresponds to Sample ‘’ (i.e., middle-censoring).
7. Conclusions and Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The FI Components
- ,
- ,
- ,
- .
References
- Balakrishnan, N.; Cramer, E. The Art of Progressive Censoring; Springer: Birkhäuser, NY, USA, 2014. [Google Scholar]
- Kundu, D.; Joarder, A. Analysis of Type-II progressively hybrid censored data. Comput. Stat. Data Anal. 2006, 50, 2509–2528. [Google Scholar] [CrossRef]
- Cho, Y.; Sun, H.; Lee, K. Exact likelihood inference for an exponential parameter under generalized progressive hybrid censoring scheme. Stat. Methodol. 2015, 23, 18–34. [Google Scholar] [CrossRef]
- Koley, A.; Kundu, D. On generalized progressive hybrid censoring in presence of competing risks. Metrika 2017, 80, 401–426. [Google Scholar] [CrossRef]
- Wang, L. Inference for Weibull competing risks data under generalized progressive hybrid censoring. IEEE Trans. Reliab. 2018, 67, 998–1007. [Google Scholar] [CrossRef]
- Lee, S.O.; Kang, S.B. Estimation for the half-logistic distribution based on generalized progressive hybrid censoring. J. Korean Data Inf. Sci. Soc. 2018, 29, 1049–1059. [Google Scholar] [CrossRef]
- Lee, K. Bayesian and maximum likelihood estimation of entropy of the inverse Weibull distribution under generalized type I progressive hybrid censoring. Commun. Stat. Appl. Methods 2020, 27, 469–486. [Google Scholar] [CrossRef]
- Zhu, T. Statistical inference of Weibull distribution based on generalized progressively hybrid censored data. J. Comput. Appl. Math. 2020, 371, 112705. [Google Scholar] [CrossRef]
- Singh, D.P.; Lodhi, C.; Tripathi, Y.M.; Wang, L. Inference for two-parameter Rayleigh competing risks data under generalized progressive hybrid censoring. Qual. Reliab. Eng. Int. 2021, 37, 1210–1231. [Google Scholar] [CrossRef]
- Elshahhat, A.; Abu El Azm, W.S. Statistical reliability analysis of electronic devices using generalized progressively hybrid censoring plan. Qual. Reliab. Eng. Int. 2022, 38, 1112–1130. [Google Scholar] [CrossRef]
- Maswadah, M. Improved maximum likelihood estimation of the shape-scale family based on the generalized progressive hybrid censoring scheme. J. Appl. Stat. 2022, 49, 2825–2844. [Google Scholar] [CrossRef]
- Alotaibi, R.; Elshahhat, A.; Nassar, M. Analysis of Muth parameters using generalized progressive hybrid censoring with application to sodium sulfur battery. J. Radiat. Res. Appl. Sci. 2023, 16, 100624. [Google Scholar] [CrossRef]
- Mahdavi, A.; Kundu, D. A new method for generating distributions with an application to exponential distribution. Commun.-Stat.-Theory Methods 2017, 46, 6543–6557. [Google Scholar] [CrossRef]
- Salah, M.M. On Progressive Type-II Censored Samples from Alpha Power Exponential Distribution. J. Math. 2020, 2020, 2584184. [Google Scholar] [CrossRef]
- Salah, M.M.; Ahmed, E.A.; Alhussain, Z.A.; Ahmed, H.H.; El-Morshedy, M.; Eliwa, M.S. Statistical inferences for type-II hybrid censoring data from the alpha power exponential distribution. PLoS ONE 2021, 16, e0244316. [Google Scholar] [CrossRef]
- Elsherpieny, E.A.; Abdel-Hakim, A. Statistical analysis of Alpha-Power exponential distribution using unified Hybrid censored data and its applications. Computational J. Math. Stat. Sci. 2025, 4, 283–315. [Google Scholar] [CrossRef]
- Henningsen, A.; Toomet, O. maxLik: A package for maximum likelihood estimation in R. Comput. Stat. 2011, 26, 443–458. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley and Sons: New York, NY, USA, 2011. [Google Scholar]
- Greene, W.H. Econometric Analysis, 4th ed.; Prentice-Hall: New York, NY, USA, 2000. [Google Scholar]
- Meeker, W.Q.; Escobar, L.A. Statistical Methods for Reliability Data; John Wiley and Sons: New York, NY, USA, 1998. [Google Scholar]
- Kundu, D. Bayesian inference and life testing plan for the Weibull distribution in presence of progressive censoring. Technometrics 2008, 50, 144–154. [Google Scholar] [CrossRef]
- Plummer, M.; Best, N.; Cowles, K.; Vines, K. CODA: Convergence diagnosis and output analysis for MCMC. R News 2006, 6, 7–11. [Google Scholar]
- Royston, P.; Altman, D.G. External validation of a Cox prognostic model: Principles and methods. BMC Med. Res. Methodol. 2013, 13, 33. [Google Scholar] [CrossRef] [PubMed]
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring Theory, Methods and Applications; Birkhäuser: Boston, MA, USA, 2000. [Google Scholar]
- Wang, B.X.; Yu, K. Optimum plan for step-stress model with progressive type-II censoring. Test 2009, 18, 115–135. [Google Scholar] [CrossRef]
- Pradhan, B.; Kundu, D. Inference and optimal censoring schemes for progressively censored Birnbaum–Saunders distribution. J. Stat. Plan. Inference 2013, 143, 1098–1108. [Google Scholar] [CrossRef]
| S | ||
|---|---|---|
| (10, 15) | (15, 20) | |
| 30 | PCP[1]: | PCP[1]: |
| PCP[2]: | PCP[2]: | |
| PCP[3]: | PCP[3]: | |
| (20, 30) | (40, 30) | |
| 50 | PCP[1]: | PCP[1]: |
| PCP[2]: | PCP[2]: | |
| PCP[3]: | PCP[3]: | |
| (50, 40) | (50, 60) | |
| 80 | PCP[1]: | PCP[1]: |
| PCP[2]: | PCP[2]: | |
| PCP[3]: | PCP[3]: | |
| PCP | MLE | MCMC | MLE | MCMC | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior→ | I | II | I | II | ||||||||||
| Pop-1 | ||||||||||||||
| (30,15,10) | PCP[1] | 4.1354 | 1.2642 | 0.2444 | 0.2063 | 0.1980 | 0.1698 | 3.4061 | 1.1304 | 0.2283 | 0.2012 | 0.1794 | 0.1692 | |
| PCP[2] | 4.2151 | 1.3430 | 0.2906 | 0.2388 | 0.2039 | 0.1707 | 3.9360 | 1.2081 | 0.2414 | 0.2088 | 0.1805 | 0.1692 | ||
| PCP[3] | 3.5341 | 1.2394 | 0.2301 | 0.2058 | 0.1879 | 0.1691 | 3.3023 | 1.0223 | 0.2258 | 0.1983 | 0.1794 | 0.1689 | ||
| (30,20,15) | PCP[1] | 2.9043 | 0.8034 | 0.2216 | 0.1909 | 0.1789 | 0.1636 | 2.0837 | 0.7586 | 0.2160 | 0.1877 | 0.1769 | 0.1630 | |
| PCP[2] | 3.2644 | 1.1335 | 0.2256 | 0.1974 | 0.1833 | 0.1670 | 3.0338 | 0.9289 | 0.2214 | 0.1928 | 0.1794 | 0.1645 | ||
| PCP[3] | 3.1648 | 0.8997 | 0.2219 | 0.1917 | 0.1793 | 0.1636 | 2.4519 | 0.8977 | 0.2168 | 0.1889 | 0.1791 | 0.1636 | ||
| (50,30,20) | PCP[1] | 2.5234 | 0.5811 | 0.2187 | 0.1877 | 0.1721 | 0.1489 | 1.3066 | 0.5681 | 0.2121 | 0.1800 | 0.1602 | 0.1373 | |
| PCP[2] | 2.6603 | 0.5932 | 0.2201 | 0.1903 | 0.1752 | 0.1600 | 1.5488 | 0.5922 | 0.2144 | 0.1854 | 0.1614 | 0.1385 | ||
| PCP[3] | 2.4101 | 0.5214 | 0.2178 | 0.1835 | 0.1691 | 0.1382 | 1.2482 | 0.4363 | 0.2102 | 0.1780 | 0.1560 | 0.1372 | ||
| (50,40,30) | PCP[1] | 2.2283 | 0.4199 | 0.2112 | 0.1827 | 0.1660 | 0.1372 | 1.1561 | 0.3559 | 0.2078 | 0.1771 | 0.1433 | 0.1332 | |
| PCP[2] | 2.1762 | 0.3889 | 0.2107 | 0.1806 | 0.1625 | 0.1332 | 1.0838 | 0.3184 | 0.2063 | 0.1769 | 0.1433 | 0.1315 | ||
| PCP[3] | 2.0457 | 0.3740 | 0.2037 | 0.1763 | 0.1554 | 0.1315 | 1.0486 | 0.3094 | 0.2026 | 0.1741 | 0.1421 | 0.1302 | ||
| (80,50,40) | PCP[1] | 1.5479 | 0.3563 | 0.1910 | 0.1630 | 0.1474 | 0.1283 | 0.8735 | 0.2868 | 0.1907 | 0.1623 | 0.1407 | 0.1281 | |
| PCP[2] | 1.6581 | 0.3613 | 0.2008 | 0.1739 | 0.1514 | 0.1299 | 0.9731 | 0.2979 | 0.1964 | 0.1676 | 0.1409 | 0.1284 | ||
| PCP[3] | 1.5431 | 0.3487 | 0.1896 | 0.1614 | 0.1428 | 0.1278 | 0.8599 | 0.2779 | 0.1896 | 0.1614 | 0.1401 | 0.1274 | ||
| (80,60,50) | PCP[1] | 1.4439 | 0.3147 | 0.1840 | 0.1556 | 0.1393 | 0.1184 | 0.8181 | 0.2381 | 0.1805 | 0.1555 | 0.1392 | 0.1217 | |
| PCP[2] | 1.4667 | 0.3418 | 0.1894 | 0.1609 | 0.1403 | 0.1195 | 0.8544 | 0.2742 | 0.1861 | 0.1580 | 0.1397 | 0.1171 | ||
| PCP[3] | 1.3399 | 0.3090 | 0.1828 | 0.1531 | 0.1379 | 0.1160 | 0.6979 | 0.2267 | 0.1678 | 0.1384 | 0.1379 | 0.1150 | ||
| Pop-2 | ||||||||||||||
| (30,15,10) | PCP[1] | 6.2369 | 1.3162 | 0.5490 | 0.5147 | 0.2084 | 0.1956 | 3.7562 | 1.2906 | 0.5208 | 0.4864 | 0.2012 | 0.1880 | |
| PCP[2] | 6.5361 | 1.4431 | 0.5606 | 0.5258 | 0.2106 | 0.2019 | 3.8960 | 1.3227 | 0.5344 | 0.4979 | 0.2020 | 0.1898 | ||
| PCP[3] | 5.8117 | 1.2879 | 0.5447 | 0.5102 | 0.2020 | 0.1896 | 3.5386 | 1.2243 | 0.5108 | 0.4758 | 0.2002 | 0.1856 | ||
| (30,20,15) | PCP[1] | 5.3495 | 1.0840 | 0.4746 | 0.4129 | 0.1976 | 0.1799 | 3.1078 | 1.0510 | 0.4537 | 0.3886 | 0.1906 | 0.1720 | |
| PCP[2] | 5.6283 | 1.2259 | 0.4857 | 0.4509 | 0.1995 | 0.1842 | 3.3892 | 1.1610 | 0.4726 | 0.4419 | 0.1976 | 0.1816 | ||
| PCP[3] | 5.4979 | 1.1732 | 0.4848 | 0.4153 | 0.1991 | 0.1803 | 3.2430 | 1.1101 | 0.4560 | 0.4008 | 0.1936 | 0.1799 | ||
| (50,30,20) | PCP[1] | 4.9242 | 0.8761 | 0.4439 | 0.3889 | 0.1827 | 0.1517 | 2.7762 | 0.6965 | 0.4346 | 0.3806 | 0.1748 | 0.1492 | |
| PCP[2] | 5.1598 | 0.9775 | 0.4477 | 0.4071 | 0.1848 | 0.1541 | 2.9746 | 0.9560 | 0.4439 | 0.3877 | 0.1765 | 0.1507 | ||
| PCP[3] | 4.4894 | 0.7993 | 0.4262 | 0.3806 | 0.1807 | 0.1478 | 2.5543 | 0.6451 | 0.4173 | 0.3805 | 0.1736 | 0.1478 | ||
| (50,40,30) | PCP[1] | 4.1980 | 0.6539 | 0.4145 | 0.3794 | 0.1776 | 0.1458 | 2.1952 | 0.5341 | 0.4139 | 0.3777 | 0.1573 | 0.1445 | |
| PCP[2] | 3.9823 | 0.6482 | 0.4081 | 0.3759 | 0.1706 | 0.1451 | 2.1079 | 0.5279 | 0.4040 | 0.3704 | 0.1565 | 0.1445 | ||
| PCP[3] | 3.8817 | 0.6162 | 0.3988 | 0.3668 | 0.1655 | 0.1441 | 2.0042 | 0.4883 | 0.3988 | 0.3598 | 0.1553 | 0.1434 | ||
| (80,50,40) | PCP[1] | 3.0194 | 0.5558 | 0.3843 | 0.3521 | 0.1584 | 0.1383 | 1.7741 | 0.4422 | 0.3740 | 0.3391 | 0.1540 | 0.1382 | |
| PCP[2] | 3.8142 | 0.5706 | 0.3935 | 0.3598 | 0.1615 | 0.1392 | 2.0022 | 0.4551 | 0.3773 | 0.3404 | 0.1541 | 0.1390 | ||
| PCP[3] | 2.7186 | 0.5529 | 0.3773 | 0.3404 | 0.1541 | 0.1374 | 1.5914 | 0.3974 | 0.3637 | 0.3306 | 0.1533 | 0.1338 | ||
| (80,60,50) | PCP[1] | 2.6114 | 0.5272 | 0.3186 | 0.2748 | 0.1520 | 0.1294 | 1.5606 | 0.3795 | 0.3124 | 0.2690 | 0.1512 | 0.1293 | |
| PCP[2] | 2.7064 | 0.5420 | 0.3345 | 0.2895 | 0.1530 | 0.1302 | 1.5673 | 0.3945 | 0.3136 | 0.2706 | 0.1525 | 0.1294 | ||
| PCP[3] | 2.5171 | 0.4764 | 0.3120 | 0.2702 | 0.1509 | 0.1283 | 1.5254 | 0.3219 | 0.2982 | 0.2576 | 0.1452 | 0.1219 | ||
| PCP | MLE | MCMC | MLE | MCMC | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior→ | I | II | I | II | ||||||||||
| Pop-1 | ||||||||||||||
| (30,15,10) | PCP[1] | 2.1662 | 1.5862 | 0.5873 | 0.3845 | 0.2078 | 0.1955 | 2.1632 | 1.5716 | 0.5572 | 0.3436 | 0.2032 | 0.1915 | |
| PCP[2] | 1.5848 | 1.2360 | 0.3693 | 0.3220 | 0.2004 | 0.1888 | 1.4199 | 1.1365 | 0.3608 | 0.3108 | 0.1928 | 0.1817 | ||
| PCP[3] | 1.9363 | 1.4477 | 0.4637 | 0.3667 | 0.2034 | 0.1917 | 1.5359 | 1.2505 | 0.4162 | 0.3165 | 0.1983 | 0.1868 | ||
| (30,20,15) | PCP[1] | 1.4278 | 1.1526 | 0.3610 | 0.3174 | 0.1921 | 0.1688 | 1.3751 | 1.0943 | 0.3433 | 0.3038 | 0.1890 | 0.1659 | |
| PCP[2] | 1.2913 | 1.0173 | 0.3586 | 0.3117 | 0.1879 | 0.1650 | 1.2407 | 0.9667 | 0.3315 | 0.3034 | 0.1785 | 0.1626 | ||
| PCP[3] | 1.4071 | 1.0759 | 0.3601 | 0.3155 | 0.1890 | 0.1659 | 1.3271 | 1.0546 | 0.3350 | 0.3036 | 0.1890 | 0.1659 | ||
| (50,30,20) | PCP[1] | 1.2637 | 0.9878 | 0.3556 | 0.3084 | 0.1685 | 0.1593 | 1.2021 | 0.9383 | 0.3239 | 0.2776 | 0.1685 | 0.1593 | |
| PCP[2] | 1.1368 | 0.8846 | 0.3439 | 0.3012 | 0.1623 | 0.1538 | 1.0077 | 0.7982 | 0.3171 | 0.2718 | 0.1587 | 0.1299 | ||
| PCP[3] | 1.2258 | 0.9142 | 0.3497 | 0.3022 | 0.1685 | 0.1570 | 1.0435 | 0.8370 | 0.3179 | 0.2754 | 0.1659 | 0.1564 | ||
| (50,40,30) | PCP[1] | 1.0632 | 0.8722 | 0.3362 | 0.2849 | 0.1587 | 0.1299 | 0.9068 | 0.7247 | 0.2965 | 0.2413 | 0.1553 | 0.1295 | |
| PCP[2] | 0.9991 | 0.8148 | 0.3120 | 0.2589 | 0.1571 | 0.1283 | 0.8150 | 0.6612 | 0.2743 | 0.2276 | 0.1370 | 0.1193 | ||
| PCP[3] | 1.0257 | 0.8219 | 0.3230 | 0.2769 | 0.1575 | 0.1287 | 0.8393 | 0.6741 | 0.2897 | 0.2352 | 0.1471 | 0.1268 | ||
| (80,50,40) | PCP[1] | 0.9716 | 0.7807 | 0.3010 | 0.2496 | 0.1327 | 0.1033 | 0.8018 | 0.6465 | 0.2594 | 0.2124 | 0.1277 | 0.0993 | |
| PCP[2] | 0.9504 | 0.7654 | 0.2648 | 0.2162 | 0.1254 | 0.0989 | 0.7679 | 0.6292 | 0.2553 | 0.2076 | 0.1243 | 0.0986 | ||
| PCP[3] | 0.9540 | 0.7711 | 0.2711 | 0.2241 | 0.1290 | 0.1007 | 0.7812 | 0.6453 | 0.2592 | 0.2084 | 0.1263 | 0.0990 | ||
| (80,60,50) | PCP[1] | 0.9345 | 0.7432 | 0.2541 | 0.2076 | 0.1162 | 0.0983 | 0.7629 | 0.6287 | 0.2541 | 0.2035 | 0.1155 | 0.0979 | |
| PCP[2] | 0.8864 | 0.6833 | 0.2534 | 0.2016 | 0.1146 | 0.0970 | 0.7285 | 0.5751 | 0.2533 | 0.2009 | 0.1138 | 0.0964 | ||
| PCP[3] | 0.8892 | 0.7014 | 0.2540 | 0.2030 | 0.1160 | 0.0979 | 0.7486 | 0.5910 | 0.2537 | 0.2021 | 0.1152 | 0.0971 | ||
| Pop-2 | ||||||||||||||
| (30,15,10) | PCP[1] | 2.2653 | 1.6760 | 0.5963 | 0.5020 | 0.2214 | 0.2008 | 2.1998 | 1.6499 | 0.5628 | 0.4373 | 0.2132 | 0.2004 | |
| PCP[2] | 1.7048 | 1.3757 | 0.4723 | 0.4155 | 0.2132 | 0.2004 | 1.4601 | 1.1621 | 0.4495 | 0.3923 | 0.2064 | 0.1942 | ||
| PCP[3] | 1.9937 | 1.6234 | 0.5262 | 0.4560 | 0.2132 | 0.2004 | 1.7551 | 1.3828 | 0.4715 | 0.4102 | 0.2065 | 0.1942 | ||
| (30,20,15) | PCP[1] | 1.5423 | 1.2700 | 0.4652 | 0.4083 | 0.1971 | 0.1728 | 1.4497 | 1.1360 | 0.4451 | 0.3761 | 0.1971 | 0.1728 | |
| PCP[2] | 1.4278 | 1.1817 | 0.4521 | 0.3890 | 0.1964 | 0.1721 | 1.3404 | 1.0665 | 0.3942 | 0.3487 | 0.1851 | 0.1618 | ||
| PCP[3] | 1.5326 | 1.2360 | 0.4625 | 0.4070 | 0.1971 | 0.1728 | 1.3556 | 1.0787 | 0.4376 | 0.3660 | 0.1971 | 0.1728 | ||
| (50,30,20) | PCP[1] | 1.3738 | 1.1209 | 0.4116 | 0.3741 | 0.1680 | 0.1590 | 1.2091 | 0.9612 | 0.3758 | 0.3469 | 0.1664 | 0.1565 | |
| PCP[2] | 1.2915 | 1.0264 | 0.3711 | 0.3281 | 0.1664 | 0.1574 | 1.0320 | 0.8096 | 0.3655 | 0.3025 | 0.1655 | 0.1552 | ||
| PCP[3] | 1.3055 | 1.0928 | 0.3824 | 0.3387 | 0.1678 | 0.1589 | 1.1552 | 0.9093 | 0.3718 | 0.3152 | 0.1664 | 0.1558 | ||
| (50,40,30) | PCP[1] | 1.1751 | 0.9877 | 0.3655 | 0.3185 | 0.1664 | 0.1359 | 1.0020 | 0.8054 | 0.3561 | 0.2952 | 0.1648 | 0.1359 | |
| PCP[2] | 1.1442 | 0.9015 | 0.3625 | 0.3025 | 0.1632 | 0.1330 | 0.9425 | 0.7094 | 0.3331 | 0.2833 | 0.1511 | 0.1222 | ||
| PCP[3] | 1.1464 | 0.9362 | 0.3629 | 0.3125 | 0.1640 | 0.1359 | 0.9600 | 0.7356 | 0.3342 | 0.2882 | 0.1618 | 0.1320 | ||
| (80,50,40) | PCP[1] | 1.1304 | 0.9011 | 0.3342 | 0.2805 | 0.1333 | 0.1035 | 0.9420 | 0.6965 | 0.3323 | 0.2787 | 0.1306 | 0.1017 | |
| PCP[2] | 1.0616 | 0.8262 | 0.3228 | 0.2657 | 0.1311 | 0.1021 | 0.8799 | 0.6556 | 0.2992 | 0.2448 | 0.1302 | 0.1014 | ||
| PCP[3] | 1.1280 | 0.8927 | 0.3266 | 0.2787 | 0.1314 | 0.1022 | 0.9418 | 0.6927 | 0.3034 | 0.2490 | 0.1306 | 0.1017 | ||
| (80,60,50) | PCP[1] | 1.0571 | 0.8165 | 0.3143 | 0.2577 | 0.1175 | 0.0998 | 0.8610 | 0.6405 | 0.2599 | 0.2133 | 0.1173 | 0.0997 | |
| PCP[2] | 0.9820 | 0.7688 | 0.2505 | 0.2088 | 0.1170 | 0.0995 | 0.8052 | 0.5962 | 0.2480 | 0.2058 | 0.1159 | 0.0987 | ||
| PCP[3] | 1.0436 | 0.8132 | 0.2982 | 0.2460 | 0.1170 | 0.0995 | 0.8473 | 0.6315 | 0.2505 | 0.2088 | 0.1167 | 0.0993 | ||
| PCP | MLE | MCMC | MLE | MCMC | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior→ | I | II | I | II | ||||||||||
| Pop-1 | ||||||||||||||
| (30,15,10) | PCP[1] | 0.7525 | 0.5831 | 0.4565 | 0.3838 | 0.0651 | 0.0550 | 0.7602 | 0.4782 | 0.4016 | 0.2783 | 0.0586 | 0.0476 | |
| PCP[2] | 0.8790 | 0.6101 | 0.5254 | 0.3877 | 0.0660 | 0.0570 | 0.7995 | 0.5609 | 0.5004 | 0.3219 | 0.0613 | 0.0525 | ||
| PCP[3] | 0.9817 | 0.6453 | 0.5626 | 0.4094 | 0.0700 | 0.0605 | 0.8346 | 0.6232 | 0.5305 | 0.3467 | 0.0637 | 0.0555 | ||
| (30,20,15) | PCP[1] | 0.5561 | 0.4539 | 0.3619 | 0.2783 | 0.0557 | 0.0480 | 0.5527 | 0.4435 | 0.3618 | 0.2572 | 0.0495 | 0.0390 | |
| PCP[2] | 0.6088 | 0.5089 | 0.4068 | 0.2965 | 0.0621 | 0.0524 | 0.5782 | 0.4660 | 0.3782 | 0.2738 | 0.0540 | 0.0445 | ||
| PCP[3] | 0.6054 | 0.4867 | 0.3684 | 0.2867 | 0.0616 | 0.0499 | 0.5635 | 0.4536 | 0.3648 | 0.2663 | 0.0534 | 0.0410 | ||
| (50,30,20) | PCP[1] | 0.4525 | 0.3694 | 0.3373 | 0.2424 | 0.0506 | 0.0420 | 0.4354 | 0.3488 | 0.2940 | 0.2336 | 0.0461 | 0.0370 | |
| PCP[2] | 0.5495 | 0.4406 | 0.3437 | 0.2572 | 0.0516 | 0.0437 | 0.4704 | 0.3806 | 0.3140 | 0.2392 | 0.0475 | 0.0377 | ||
| PCP[3] | 0.5551 | 0.4466 | 0.3499 | 0.2614 | 0.0548 | 0.0449 | 0.4841 | 0.3939 | 0.3499 | 0.2565 | 0.0486 | 0.0379 | ||
| (50,40,30) | PCP[1] | 0.4111 | 0.3262 | 0.2667 | 0.2157 | 0.0437 | 0.0350 | 0.3816 | 0.3026 | 0.2649 | 0.2090 | 0.0420 | 0.0337 | |
| PCP[2] | 0.4479 | 0.3693 | 0.3234 | 0.2352 | 0.0504 | 0.0397 | 0.4140 | 0.3299 | 0.2887 | 0.2254 | 0.0450 | 0.0361 | ||
| PCP[3] | 0.4151 | 0.3285 | 0.2958 | 0.2290 | 0.0475 | 0.0370 | 0.4001 | 0.3163 | 0.2810 | 0.2097 | 0.0437 | 0.0350 | ||
| (80,50,40) | PCP[1] | 0.3822 | 0.3087 | 0.2323 | 0.1961 | 0.0352 | 0.0281 | 0.3307 | 0.2634 | 0.2017 | 0.1701 | 0.0352 | 0.0280 | |
| PCP[2] | 0.3832 | 0.3129 | 0.2383 | 0.1967 | 0.0368 | 0.0289 | 0.3431 | 0.2711 | 0.2073 | 0.1735 | 0.0365 | 0.0288 | ||
| PCP[3] | 0.3984 | 0.3136 | 0.2403 | 0.2024 | 0.0437 | 0.0350 | 0.3592 | 0.2866 | 0.2342 | 0.1969 | 0.0368 | 0.0289 | ||
| (80,60,50) | PCP[1] | 0.3305 | 0.2626 | 0.2152 | 0.1612 | 0.0331 | 0.0269 | 0.3131 | 0.2478 | 0.1795 | 0.1321 | 0.0331 | 0.0236 | |
| PCP[2] | 0.3527 | 0.2789 | 0.2294 | 0.1936 | 0.0342 | 0.0278 | 0.3292 | 0.2622 | 0.1974 | 0.1653 | 0.0340 | 0.0269 | ||
| PCP[3] | 0.3401 | 0.2656 | 0.2167 | 0.1811 | 0.0337 | 0.0269 | 0.3150 | 0.2504 | 0.1874 | 0.1561 | 0.0331 | 0.0264 | ||
| Pop-2 | ||||||||||||||
| (30,15,10) | PCP[1] | 0.6090 | 0.4887 | 0.4131 | 0.3048 | 0.0485 | 0.0428 | 0.5858 | 0.4718 | 0.3884 | 0.2887 | 0.0447 | 0.0390 | |
| PCP[2] | 0.6350 | 0.5068 | 0.4161 | 0.3064 | 0.0485 | 0.0436 | 0.6198 | 0.5005 | 0.3976 | 0.2973 | 0.0468 | 0.0398 | ||
| PCP[3] | 0.6747 | 0.5518 | 0.4420 | 0.3915 | 0.0494 | 0.0455 | 0.6368 | 0.5249 | 0.4131 | 0.3048 | 0.0485 | 0.0447 | ||
| (30,20,15) | PCP[1] | 0.5716 | 0.4570 | 0.3623 | 0.2678 | 0.0394 | 0.0346 | 0.5699 | 0.4552 | 0.3217 | 0.2607 | 0.0387 | 0.0334 | |
| PCP[2] | 0.5908 | 0.4756 | 0.4115 | 0.2978 | 0.0396 | 0.0414 | 0.5804 | 0.4689 | 0.3731 | 0.2678 | 0.0424 | 0.0381 | ||
| PCP[3] | 0.5787 | 0.4700 | 0.3871 | 0.2783 | 0.0396 | 0.0380 | 0.5725 | 0.4648 | 0.3470 | 0.2637 | 0.0391 | 0.0337 | ||
| (50,30,20) | PCP[1] | 0.4583 | 0.3689 | 0.3112 | 0.2584 | 0.0364 | 0.0322 | 0.4479 | 0.3569 | 0.3088 | 0.2473 | 0.0329 | 0.0273 | |
| PCP[2] | 0.4651 | 0.3722 | 0.3217 | 0.2589 | 0.0390 | 0.0341 | 0.4555 | 0.3622 | 0.3102 | 0.2512 | 0.0377 | 0.0303 | ||
| PCP[3] | 0.5341 | 0.4401 | 0.3391 | 0.2652 | 0.0393 | 0.0341 | 0.4971 | 0.3978 | 0.3160 | 0.2599 | 0.0377 | 0.0313 | ||
| (50,40,30) | PCP[1] | 0.4350 | 0.3465 | 0.2875 | 0.2263 | 0.0306 | 0.0253 | 0.4268 | 0.3400 | 0.2795 | 0.2236 | 0.0256 | 0.0207 | |
| PCP[2] | 0.4503 | 0.3635 | 0.3085 | 0.2493 | 0.0329 | 0.0273 | 0.4394 | 0.3482 | 0.3067 | 0.2374 | 0.0311 | 0.0264 | ||
| PCP[3] | 0.4473 | 0.3571 | 0.2886 | 0.2333 | 0.0326 | 0.0270 | 0.4271 | 0.3419 | 0.2875 | 0.2263 | 0.0299 | 0.0245 | ||
| (80,50,40) | PCP[1] | 0.3805 | 0.3049 | 0.2033 | 0.1659 | 0.0222 | 0.0181 | 0.3647 | 0.2940 | 0.1882 | 0.1507 | 0.0217 | 0.0172 | |
| PCP[2] | 0.4246 | 0.3447 | 0.2387 | 0.1933 | 0.0223 | 0.0182 | 0.3847 | 0.3073 | 0.2115 | 0.1694 | 0.0220 | 0.0180 | ||
| PCP[3] | 0.4345 | 0.3458 | 0.2415 | 0.1934 | 0.0234 | 0.0189 | 0.4097 | 0.3311 | 0.2139 | 0.1697 | 0.0220 | 0.0180 | ||
| (80,60,50) | PCP[1] | 0.3546 | 0.2810 | 0.1662 | 0.1404 | 0.0204 | 0.0153 | 0.3499 | 0.2781 | 0.1555 | 0.1325 | 0.0204 | 0.0143 | |
| PCP[2] | 0.3674 | 0.2946 | 0.1948 | 0.1565 | 0.0210 | 0.0164 | 0.3606 | 0.2890 | 0.1630 | 0.1342 | 0.0205 | 0.0164 | ||
| PCP[3] | 0.3578 | 0.2877 | 0.1932 | 0.1555 | 0.0205 | 0.0154 | 0.3526 | 0.2819 | 0.1562 | 0.1333 | 0.0204 | 0.0154 | ||
| PCP | MLE | MCMC | MLE | MCMC | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior→ | I | II | I | II | ||||||||||
| Pop-1 | ||||||||||||||
| (30,15,10) | PCP[1] | 0.7630 | 0.6900 | 0.6028 | 0.4539 | 0.0675 | 0.0574 | 0.6922 | 0.6416 | 0.5538 | 0.3666 | 0.0654 | 0.0552 | |
| PCP[2] | 0.7421 | 0.7095 | 0.6337 | 0.4651 | 0.0708 | 0.0605 | 0.7188 | 0.7013 | 0.5732 | 0.3938 | 0.0660 | 0.0558 | ||
| PCP[3] | 0.6992 | 0.5547 | 0.4958 | 0.4470 | 0.0673 | 0.0548 | 0.6288 | 0.5167 | 0.4543 | 0.3230 | 0.0650 | 0.0542 | ||
| (30,20,15) | PCP[1] | 0.6753 | 0.5295 | 0.4818 | 0.3408 | 0.0642 | 0.0539 | 0.6227 | 0.4958 | 0.4415 | 0.3196 | 0.0541 | 0.0443 | |
| PCP[2] | 0.6706 | 0.5231 | 0.4347 | 0.3381 | 0.0638 | 0.0512 | 0.6204 | 0.4848 | 0.4291 | 0.3141 | 0.0535 | 0.0405 | ||
| PCP[3] | 0.6232 | 0.4934 | 0.4233 | 0.3196 | 0.0572 | 0.0479 | 0.6081 | 0.4839 | 0.4232 | 0.3005 | 0.0507 | 0.0401 | ||
| (50,30,20) | PCP[1] | 0.6165 | 0.4837 | 0.3942 | 0.2984 | 0.0529 | 0.0432 | 0.5183 | 0.4188 | 0.3658 | 0.2785 | 0.0489 | 0.0384 | |
| PCP[2] | 0.6127 | 0.4855 | 0.4015 | 0.3075 | 0.0548 | 0.0441 | 0.5213 | 0.4242 | 0.4015 | 0.2979 | 0.0500 | 0.0393 | ||
| PCP[3] | 0.4838 | 0.3953 | 0.3788 | 0.2807 | 0.0518 | 0.0417 | 0.4736 | 0.3936 | 0.3422 | 0.2720 | 0.0474 | 0.0381 | ||
| (50,40,30) | PCP[1] | 0.4824 | 0.3938 | 0.3573 | 0.2734 | 0.0518 | 0.0405 | 0.4497 | 0.3782 | 0.3355 | 0.2611 | 0.0468 | 0.0373 | |
| PCP[2] | 0.4359 | 0.3462 | 0.3424 | 0.2663 | 0.0489 | 0.0384 | 0.4319 | 0.3444 | 0.3264 | 0.2430 | 0.0460 | 0.0371 | ||
| PCP[3] | 0.4342 | 0.3438 | 0.3096 | 0.2507 | 0.0460 | 0.0373 | 0.4055 | 0.3239 | 0.3071 | 0.2419 | 0.0450 | 0.0365 | ||
| (80,50,40) | PCP[1] | 0.4045 | 0.3282 | 0.2771 | 0.2305 | 0.0420 | 0.0357 | 0.3650 | 0.2888 | 0.2416 | 0.2029 | 0.0430 | 0.0335 | |
| PCP[2] | 0.4154 | 0.3299 | 0.2806 | 0.2353 | 0.0460 | 0.0373 | 0.3910 | 0.3120 | 0.2734 | 0.2308 | 0.0420 | 0.0342 | ||
| PCP[3] | 0.3964 | 0.3205 | 0.2714 | 0.2297 | 0.0406 | 0.0342 | 0.3565 | 0.2847 | 0.2354 | 0.1990 | 0.0410 | 0.0322 | ||
| (80,60,50) | PCP[1] | 0.3768 | 0.2981 | 0.2681 | 0.2270 | 0.0405 | 0.0342 | 0.3421 | 0.2715 | 0.2300 | 0.1924 | 0.0399 | 0.0300 | |
| PCP[2] | 0.3477 | 0.2731 | 0.2527 | 0.2110 | 0.0399 | 0.0338 | 0.3344 | 0.2658 | 0.2182 | 0.1816 | 0.0390 | 0.0272 | ||
| PCP[3] | 0.3428 | 0.2716 | 0.2508 | 0.1894 | 0.0380 | 0.0333 | 0.3249 | 0.2572 | 0.2092 | 0.1563 | 0.0383 | 0.0244 | ||
| Pop-2 | ||||||||||||||
| (30,15,10) | PCP[1] | 0.7088 | 0.5571 | 0.5011 | 0.3736 | 0.0804 | 0.0738 | 0.7046 | 0.5535 | 0.4779 | 0.3602 | 0.0750 | 0.0688 | |
| PCP[2] | 0.7707 | 0.6268 | 0.5356 | 0.4760 | 0.0814 | 0.0760 | 0.7108 | 0.5657 | 0.5011 | 0.3736 | 0.0803 | 0.0750 | ||
| PCP[3] | 0.6760 | 0.5356 | 0.4958 | 0.3725 | 0.0803 | 0.0728 | 0.6695 | 0.5187 | 0.4666 | 0.3500 | 0.0725 | 0.0678 | ||
| (30,20,15) | PCP[1] | 0.6673 | 0.5350 | 0.4892 | 0.3478 | 0.0676 | 0.0685 | 0.6653 | 0.5123 | 0.4351 | 0.3140 | 0.0676 | 0.0582 | |
| PCP[2] | 0.6647 | 0.5121 | 0.4560 | 0.3271 | 0.0676 | 0.0658 | 0.6472 | 0.5121 | 0.4053 | 0.3080 | 0.0669 | 0.0577 | ||
| PCP[3] | 0.6379 | 0.5008 | 0.4241 | 0.3202 | 0.0665 | 0.0621 | 0.6239 | 0.4915 | 0.3787 | 0.3060 | 0.0641 | 0.0573 | ||
| (50,30,20) | PCP[1] | 0.5156 | 0.4091 | 0.3787 | 0.3104 | 0.0634 | 0.0578 | 0.4853 | 0.3856 | 0.3673 | 0.3028 | 0.0602 | 0.0561 | |
| PCP[2] | 0.5965 | 0.4923 | 0.4006 | 0.3140 | 0.0640 | 0.0601 | 0.5355 | 0.4262 | 0.3677 | 0.3048 | 0.0618 | 0.0561 | ||
| PCP[3] | 0.4915 | 0.3905 | 0.3688 | 0.3075 | 0.0601 | 0.0545 | 0.4852 | 0.3820 | 0.3657 | 0.2905 | 0.0557 | 0.0480 | ||
| (50,40,30) | PCP[1] | 0.4870 | 0.3859 | 0.3620 | 0.3016 | 0.0557 | 0.0461 | 0.4625 | 0.3625 | 0.3611 | 0.2902 | 0.0552 | 0.0461 | |
| PCP[2] | 0.4734 | 0.3806 | 0.3455 | 0.2775 | 0.0552 | 0.0458 | 0.4541 | 0.3612 | 0.3402 | 0.2731 | 0.0509 | 0.0423 | ||
| PCP[3] | 0.4700 | 0.3747 | 0.3402 | 0.2703 | 0.0522 | 0.0428 | 0.4462 | 0.3564 | 0.3319 | 0.2632 | 0.0435 | 0.0357 | ||
| (80,50,40) | PCP[1] | 0.4537 | 0.3607 | 0.2990 | 0.2439 | 0.0376 | 0.0305 | 0.4008 | 0.3167 | 0.2661 | 0.2139 | 0.0370 | 0.0300 | |
| PCP[2] | 0.4603 | 0.3653 | 0.3071 | 0.2545 | 0.0396 | 0.0319 | 0.4361 | 0.3490 | 0.2728 | 0.2237 | 0.0370 | 0.0300 | ||
| PCP[3] | 0.3972 | 0.3120 | 0.2697 | 0.2246 | 0.0374 | 0.0303 | 0.3868 | 0.3081 | 0.2414 | 0.1979 | 0.0364 | 0.0295 | ||
| (80,60,50) | PCP[1] | 0.3890 | 0.3090 | 0.2598 | 0.2095 | 0.0304 | 0.0269 | 0.3661 | 0.2909 | 0.2213 | 0.1803 | 0.0340 | 0.0282 | |
| PCP[2] | 0.3654 | 0.2910 | 0.2482 | 0.2044 | 0.0304 | 0.0249 | 0.3641 | 0.2881 | 0.2177 | 0.1776 | 0.0330 | 0.0268 | ||
| PCP[3] | 0.3578 | 0.2828 | 0.2231 | 0.1906 | 0.0303 | 0.0222 | 0.3562 | 0.2823 | 0.2106 | 0.1760 | 0.0302 | 0.0248 | ||
| PCP | ACI-NA | ACI-NL | BCI | HPD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior→ | I | II | I | II | |||||||||
| Pop-1 () | |||||||||||||
| (30,15,10) | PCP[1] | 0.981 | 0.960 | 1.226 | 0.956 | 0.809 | 0.962 | 0.781 | 0.963 | 0.270 | 0.967 | 0.267 | 0.968 |
| PCP[2] | 1.200 | 0.957 | 1.290 | 0.955 | 0.859 | 0.962 | 0.832 | 0.962 | 0.281 | 0.967 | 0.271 | 0.967 | |
| PCP[3] | 0.920 | 0.961 | 1.150 | 0.957 | 0.762 | 0.963 | 0.728 | 0.964 | 0.269 | 0.968 | 0.266 | 0.968 | |
| (30,20,15) | PCP[1] | 0.793 | 0.963 | 0.991 | 0.960 | 0.710 | 0.964 | 0.689 | 0.964 | 0.239 | 0.969 | 0.238 | 0.969 |
| PCP[2] | 0.865 | 0.962 | 1.081 | 0.958 | 0.748 | 0.963 | 0.723 | 0.964 | 0.250 | 0.968 | 0.246 | 0.969 | |
| PCP[3] | 0.817 | 0.962 | 1.022 | 0.959 | 0.715 | 0.964 | 0.702 | 0.964 | 0.239 | 0.969 | 0.238 | 0.969 | |
| (50,30,20) | PCP[1] | 0.774 | 0.963 | 0.967 | 0.960 | 0.670 | 0.965 | 0.650 | 0.965 | 0.229 | 0.970 | 0.226 | 0.970 |
| PCP[2] | 0.780 | 0.963 | 0.975 | 0.960 | 0.675 | 0.964 | 0.668 | 0.965 | 0.231 | 0.969 | 0.228 | 0.970 | |
| PCP[3] | 0.761 | 0.963 | 0.952 | 0.960 | 0.645 | 0.965 | 0.625 | 0.965 | 0.228 | 0.970 | 0.221 | 0.970 | |
| (50,40,30) | PCP[1] | 0.715 | 0.964 | 0.893 | 0.961 | 0.560 | 0.966 | 0.545 | 0.966 | 0.224 | 0.971 | 0.210 | 0.971 |
| PCP[2] | 0.708 | 0.964 | 0.885 | 0.961 | 0.554 | 0.966 | 0.534 | 0.967 | 0.206 | 0.971 | 0.207 | 0.972 | |
| PCP[3] | 0.703 | 0.964 | 0.879 | 0.961 | 0.521 | 0.967 | 0.504 | 0.967 | 0.203 | 0.972 | 0.204 | 0.972 | |
| (80,50,40) | PCP[1] | 0.580 | 0.966 | 0.844 | 0.962 | 0.458 | 0.968 | 0.445 | 0.968 | 0.198 | 0.973 | 0.192 | 0.973 |
| PCP[2] | 0.621 | 0.965 | 0.856 | 0.962 | 0.495 | 0.967 | 0.461 | 0.968 | 0.199 | 0.972 | 0.197 | 0.973 | |
| PCP[3] | 0.562 | 0.966 | 0.780 | 0.963 | 0.450 | 0.968 | 0.442 | 0.968 | 0.195 | 0.973 | 0.186 | 0.973 | |
| (80,60,50) | PCP[1] | 0.531 | 0.967 | 0.664 | 0.965 | 0.445 | 0.968 | 0.436 | 0.968 | 0.194 | 0.973 | 0.179 | 0.973 |
| PCP[2] | 0.558 | 0.966 | 0.763 | 0.963 | 0.448 | 0.968 | 0.441 | 0.968 | 0.194 | 0.973 | 0.183 | 0.973 | |
| PCP[3] | 0.448 | 0.968 | 0.657 | 0.965 | 0.439 | 0.968 | 0.259 | 0.971 | 0.192 | 0.973 | 0.172 | 0.974 | |
| Pop-1 () | |||||||||||||
| (30,15,10) | PCP[1] | 0.937 | 0.961 | 1.171 | 0.957 | 0.799 | 0.966 | 0.767 | 0.967 | 0.270 | 0.971 | 0.262 | 0.972 |
| PCP[2] | 0.976 | 0.960 | 1.220 | 0.956 | 0.852 | 0.965 | 0.813 | 0.966 | 0.277 | 0.970 | 0.268 | 0.971 | |
| PCP[3] | 0.887 | 0.961 | 1.108 | 0.958 | 0.754 | 0.966 | 0.715 | 0.968 | 0.269 | 0.971 | 0.260 | 0.972 | |
| (30,20,15) | PCP[1] | 0.759 | 0.963 | 0.949 | 0.960 | 0.699 | 0.967 | 0.668 | 0.969 | 0.239 | 0.972 | 0.232 | 0.973 |
| PCP[2] | 0.824 | 0.962 | 1.030 | 0.959 | 0.745 | 0.966 | 0.710 | 0.968 | 0.249 | 0.971 | 0.240 | 0.973 | |
| PCP[3] | 0.813 | 0.962 | 1.017 | 0.959 | 0.711 | 0.967 | 0.701 | 0.968 | 0.239 | 0.972 | 0.238 | 0.973 | |
| (50,30,20) | PCP[1] | 0.681 | 0.964 | 0.851 | 0.962 | 0.662 | 0.968 | 0.642 | 0.969 | 0.228 | 0.973 | 0.221 | 0.974 |
| PCP[2] | 0.720 | 0.964 | 0.899 | 0.961 | 0.675 | 0.967 | 0.667 | 0.969 | 0.229 | 0.972 | 0.223 | 0.974 | |
| PCP[3] | 0.645 | 0.965 | 0.807 | 0.962 | 0.640 | 0.968 | 0.621 | 0.970 | 0.226 | 0.973 | 0.212 | 0.975 | |
| (50,40,30) | PCP[1] | 0.606 | 0.965 | 0.757 | 0.963 | 0.557 | 0.969 | 0.544 | 0.970 | 0.219 | 0.974 | 0.208 | 0.975 |
| PCP[2] | 0.596 | 0.966 | 0.746 | 0.963 | 0.547 | 0.969 | 0.531 | 0.971 | 0.205 | 0.974 | 0.202 | 0.976 | |
| PCP[3] | 0.590 | 0.966 | 0.737 | 0.964 | 0.507 | 0.970 | 0.492 | 0.971 | 0.202 | 0.975 | 0.201 | 0.976 | |
| (80,50,40) | PCP[1] | 0.464 | 0.968 | 0.676 | 0.964 | 0.454 | 0.971 | 0.437 | 0.972 | 0.195 | 0.975 | 0.190 | 0.977 |
| PCP[2] | 0.497 | 0.967 | 0.685 | 0.964 | 0.479 | 0.970 | 0.446 | 0.972 | 0.198 | 0.975 | 0.193 | 0.977 | |
| PCP[3] | 0.455 | 0.968 | 0.624 | 0.965 | 0.449 | 0.971 | 0.437 | 0.972 | 0.195 | 0.976 | 0.182 | 0.977 | |
| (80,60,50) | PCP[1] | 0.449 | 0.968 | 0.545 | 0.966 | 0.440 | 0.971 | 0.436 | 0.972 | 0.191 | 0.976 | 0.174 | 0.977 |
| PCP[2] | 0.449 | 0.968 | 0.610 | 0.965 | 0.447 | 0.971 | 0.436 | 0.972 | 0.192 | 0.976 | 0.181 | 0.977 | |
| PCP[3] | 0.442 | 0.968 | 0.526 | 0.967 | 0.432 | 0.971 | 0.207 | 0.973 | 0.189 | 0.976 | 0.167 | 0.978 | |
| Pop-2 () | |||||||||||||
| (30,15,10) | PCP[1] | 1.886 | 0.946 | 2.811 | 0.933 | 1.195 | 0.957 | 1.181 | 0.957 | 0.298 | 0.962 | 0.295 | 0.962 |
| PCP[2] | 2.954 | 0.931 | 3.192 | 0.927 | 1.201 | 0.957 | 1.194 | 0.957 | 0.299 | 0.962 | 0.296 | 0.962 | |
| PCP[3] | 1.791 | 0.948 | 2.521 | 0.937 | 1.176 | 0.957 | 1.168 | 0.957 | 0.294 | 0.963 | 0.291 | 0.962 | |
| (30,20,15) | PCP[1] | 1.397 | 0.954 | 1.926 | 0.946 | 1.158 | 0.957 | 1.125 | 0.958 | 0.271 | 0.964 | 0.270 | 0.963 |
| PCP[2] | 1.549 | 0.951 | 2.257 | 0.941 | 1.168 | 0.957 | 1.160 | 0.957 | 0.279 | 0.963 | 0.274 | 0.962 | |
| PCP[3] | 1.543 | 0.952 | 2.144 | 0.943 | 1.166 | 0.957 | 1.147 | 0.957 | 0.271 | 0.964 | 0.270 | 0.962 | |
| (50,30,20) | PCP[1] | 1.376 | 0.954 | 1.751 | 0.948 | 0.960 | 0.960 | 0.922 | 0.961 | 0.250 | 0.965 | 0.247 | 0.966 |
| PCP[2] | 1.392 | 0.954 | 1.908 | 0.946 | 0.966 | 0.960 | 0.948 | 0.960 | 0.252 | 0.965 | 0.249 | 0.965 | |
| PCP[3] | 1.139 | 0.958 | 1.490 | 0.952 | 0.931 | 0.961 | 0.911 | 0.961 | 0.250 | 0.966 | 0.247 | 0.966 | |
| (50,40,30) | PCP[1] | 1.108 | 0.958 | 1.489 | 0.952 | 0.917 | 0.961 | 0.885 | 0.961 | 0.227 | 0.966 | 0.226 | 0.966 |
| PCP[2] | 1.028 | 0.959 | 1.468 | 0.953 | 0.916 | 0.961 | 0.865 | 0.962 | 0.224 | 0.966 | 0.223 | 0.967 | |
| PCP[3] | 1.027 | 0.959 | 1.466 | 0.953 | 0.883 | 0.961 | 0.863 | 0.962 | 0.224 | 0.966 | 0.222 | 0.967 | |
| (80,50,40) | PCP[1] | 0.987 | 0.960 | 1.233 | 0.956 | 0.792 | 0.963 | 0.785 | 0.963 | 0.217 | 0.968 | 0.215 | 0.968 |
| PCP[2] | 1.022 | 0.959 | 1.390 | 0.954 | 0.818 | 0.962 | 0.810 | 0.962 | 0.219 | 0.967 | 0.218 | 0.967 | |
| PCP[3] | 0.885 | 0.961 | 1.106 | 0.958 | 0.785 | 0.963 | 0.780 | 0.963 | 0.216 | 0.968 | 0.212 | 0.968 | |
| (80,60,50) | PCP[1] | 0.684 | 0.964 | 0.908 | 0.961 | 0.667 | 0.965 | 0.659 | 0.965 | 0.211 | 0.970 | 0.209 | 0.970 |
| PCP[2] | 0.777 | 0.963 | 1.082 | 0.958 | 0.702 | 0.964 | 0.695 | 0.964 | 0.212 | 0.969 | 0.210 | 0.969 | |
| PCP[3] | 0.665 | 0.965 | 0.681 | 0.964 | 0.559 | 0.966 | 0.447 | 0.968 | 0.210 | 0.971 | 0.208 | 0.970 | |
| Pop-2 () | |||||||||||||
| (30,15,10) | PCP[1] | 1.509 | 0.952 | 2.617 | 0.936 | 1.184 | 0.960 | 1.180 | 0.961 | 0.295 | 0.965 | 0.292 | 0.966 |
| PCP[2] | 2.925 | 0.931 | 3.085 | 0.929 | 1.194 | 0.960 | 1.189 | 0.961 | 0.297 | 0.965 | 0.294 | 0.965 | |
| PCP[3] | 1.433 | 0.953 | 2.257 | 0.941 | 1.172 | 0.960 | 1.160 | 0.961 | 0.294 | 0.965 | 0.291 | 0.966 | |
| (30,20,15) | PCP[1] | 1.160 | 0.957 | 1.541 | 0.952 | 1.126 | 0.961 | 1.117 | 0.962 | 0.271 | 0.966 | 0.270 | 0.967 |
| PCP[2] | 1.239 | 0.956 | 2.059 | 0.944 | 1.164 | 0.960 | 1.158 | 0.961 | 0.278 | 0.965 | 0.273 | 0.966 | |
| PCP[3] | 1.235 | 0.956 | 1.948 | 0.946 | 1.160 | 0.960 | 1.145 | 0.961 | 0.271 | 0.965 | 0.270 | 0.966 | |
| (50,30,20) | PCP[1] | 1.101 | 0.958 | 1.401 | 0.954 | 0.951 | 0.963 | 0.914 | 0.965 | 0.250 | 0.968 | 0.247 | 0.970 |
| PCP[2] | 1.114 | 0.958 | 1.527 | 0.952 | 0.958 | 0.963 | 0.937 | 0.965 | 0.250 | 0.968 | 0.247 | 0.970 | |
| PCP[3] | 0.940 | 0.961 | 1.192 | 0.957 | 0.912 | 0.964 | 0.905 | 0.965 | 0.247 | 0.969 | 0.244 | 0.970 | |
| (50,40,30) | PCP[1] | 0.927 | 0.961 | 1.191 | 0.957 | 0.887 | 0.964 | 0.883 | 0.965 | 0.226 | 0.969 | 0.224 | 0.970 |
| PCP[2] | 0.925 | 0.961 | 1.174 | 0.957 | 0.876 | 0.964 | 0.822 | 0.966 | 0.224 | 0.969 | 0.222 | 0.971 | |
| PCP[3] | 0.885 | 0.961 | 1.173 | 0.957 | 0.873 | 0.965 | 0.822 | 0.966 | 0.223 | 0.970 | 0.220 | 0.971 | |
| (80,50,40) | PCP[1] | 0.805 | 0.963 | 1.006 | 0.960 | 0.786 | 0.966 | 0.777 | 0.967 | 0.215 | 0.971 | 0.211 | 0.972 |
| PCP[2] | 0.824 | 0.962 | 1.112 | 0.958 | 0.816 | 0.965 | 0.804 | 0.967 | 0.216 | 0.970 | 0.212 | 0.972 | |
| PCP[3] | 0.787 | 0.963 | 0.977 | 0.960 | 0.782 | 0.966 | 0.776 | 0.967 | 0.213 | 0.971 | 0.210 | 0.972 | |
| (80,60,50) | PCP[1] | 0.682 | 0.964 | 0.726 | 0.964 | 0.666 | 0.968 | 0.534 | 0.971 | 0.210 | 0.973 | 0.205 | 0.975 |
| PCP[2] | 0.714 | 0.964 | 0.865 | 0.962 | 0.701 | 0.967 | 0.622 | 0.969 | 0.210 | 0.972 | 0.208 | 0.974 | |
| PCP[3] | 0.658 | 0.965 | 0.678 | 0.964 | 0.552 | 0.969 | 0.442 | 0.972 | 0.209 | 0.973 | 0.205 | 0.975 | |
| PCP | ACI-NA | ACI-NL | BCI | HPD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior→ | I | II | I | II | |||||||||
| Pop-1 () | |||||||||||||
| (30,15,10) | PCP[1] | 1.060 | 0.944 | 1.458 | 0.926 | 1.031 | 0.945 | 0.822 | 0.955 | 0.275 | 0.981 | 0.268 | 0.981 |
| PCP[2] | 0.987 | 0.947 | 1.357 | 0.930 | 0.962 | 0.949 | 0.695 | 0.961 | 0.267 | 0.981 | 0.262 | 0.981 | |
| PCP[3] | 0.994 | 0.947 | 1.367 | 0.930 | 0.979 | 0.948 | 0.798 | 0.956 | 0.268 | 0.981 | 0.263 | 0.981 | |
| (30,20,15) | PCP[1] | 0.977 | 0.948 | 1.343 | 0.931 | 0.956 | 0.949 | 0.645 | 0.963 | 0.256 | 0.981 | 0.254 | 0.982 |
| PCP[2] | 0.927 | 0.950 | 1.274 | 0.934 | 0.903 | 0.951 | 0.616 | 0.965 | 0.255 | 0.981 | 0.252 | 0.982 | |
| PCP[3] | 0.956 | 0.949 | 1.314 | 0.932 | 0.937 | 0.950 | 0.616 | 0.965 | 0.255 | 0.981 | 0.252 | 0.982 | |
| (50,30,20) | PCP[1] | 0.895 | 0.952 | 1.231 | 0.936 | 0.893 | 0.952 | 0.570 | 0.967 | 0.255 | 0.982 | 0.252 | 0.982 |
| PCP[2] | 0.866 | 0.953 | 1.191 | 0.938 | 0.857 | 0.954 | 0.542 | 0.968 | 0.252 | 0.982 | 0.244 | 0.982 | |
| PCP[3] | 0.874 | 0.953 | 1.202 | 0.937 | 0.866 | 0.953 | 0.549 | 0.968 | 0.252 | 0.982 | 0.249 | 0.982 | |
| (50,40,30) | PCP[1] | 0.844 | 0.954 | 1.161 | 0.939 | 0.826 | 0.955 | 0.538 | 0.968 | 0.243 | 0.982 | 0.238 | 0.982 |
| PCP[2] | 0.809 | 0.956 | 1.112 | 0.942 | 0.787 | 0.957 | 0.497 | 0.970 | 0.241 | 0.982 | 0.233 | 0.982 | |
| PCP[3] | 0.841 | 0.954 | 1.156 | 0.940 | 0.813 | 0.956 | 0.500 | 0.970 | 0.242 | 0.982 | 0.236 | 0.982 | |
| (80,50,40) | PCP[1] | 0.773 | 0.957 | 1.062 | 0.944 | 0.753 | 0.958 | 0.478 | 0.971 | 0.215 | 0.983 | 0.211 | 0.984 |
| PCP[2] | 0.738 | 0.959 | 1.015 | 0.946 | 0.730 | 0.959 | 0.471 | 0.971 | 0.205 | 0.984 | 0.194 | 0.984 | |
| PCP[3] | 0.762 | 0.958 | 1.048 | 0.945 | 0.738 | 0.959 | 0.475 | 0.971 | 0.215 | 0.983 | 0.210 | 0.984 | |
| (80,60,50) | PCP[1] | 0.711 | 0.960 | 0.978 | 0.948 | 0.698 | 0.961 | 0.440 | 0.973 | 0.194 | 0.984 | 0.190 | 0.984 |
| PCP[2] | 0.639 | 0.964 | 0.878 | 0.953 | 0.624 | 0.964 | 0.418 | 0.974 | 0.187 | 0.985 | 0.173 | 0.985 | |
| PCP[3] | 0.688 | 0.961 | 0.945 | 0.949 | 0.656 | 0.963 | 0.422 | 0.974 | 0.192 | 0.984 | 0.188 | 0.985 | |
| Pop-1 () | |||||||||||||
| (30,15,10) | PCP[1] | 1.054 | 0.944 | 1.246 | 0.935 | 1.018 | 0.946 | 0.821 | 0.955 | 0.270 | 0.981 | 0.263 | 0.981 |
| PCP[2] | 0.981 | 0.948 | 1.159 | 0.939 | 0.950 | 0.949 | 0.533 | 0.969 | 0.264 | 0.981 | 0.259 | 0.981 | |
| PCP[3] | 0.982 | 0.948 | 1.168 | 0.939 | 0.968 | 0.948 | 0.580 | 0.966 | 0.267 | 0.981 | 0.262 | 0.981 | |
| (30,20,15) | PCP[1] | 0.961 | 0.949 | 1.147 | 0.940 | 0.945 | 0.949 | 0.506 | 0.970 | 0.256 | 0.981 | 0.254 | 0.982 |
| PCP[2] | 0.923 | 0.950 | 1.089 | 0.943 | 0.897 | 0.952 | 0.439 | 0.973 | 0.253 | 0.982 | 0.249 | 0.982 | |
| PCP[3] | 0.944 | 0.949 | 1.123 | 0.941 | 0.933 | 0.950 | 0.477 | 0.971 | 0.253 | 0.982 | 0.250 | 0.982 | |
| (50,30,20) | PCP[1] | 0.895 | 0.952 | 1.052 | 0.944 | 0.893 | 0.952 | 0.429 | 0.973 | 0.252 | 0.982 | 0.249 | 0.982 |
| PCP[2] | 0.863 | 0.953 | 1.018 | 0.946 | 0.852 | 0.954 | 0.375 | 0.976 | 0.248 | 0.982 | 0.242 | 0.982 | |
| PCP[3] | 0.869 | 0.953 | 1.027 | 0.946 | 0.866 | 0.953 | 0.418 | 0.974 | 0.251 | 0.982 | 0.244 | 0.982 | |
| (50,40,30) | PCP[1] | 0.840 | 0.954 | 0.992 | 0.947 | 0.819 | 0.955 | 0.356 | 0.977 | 0.242 | 0.982 | 0.236 | 0.982 |
| PCP[2] | 0.802 | 0.956 | 0.950 | 0.949 | 0.783 | 0.957 | 0.348 | 0.977 | 0.239 | 0.982 | 0.232 | 0.983 | |
| PCP[3] | 0.837 | 0.954 | 0.988 | 0.947 | 0.807 | 0.956 | 0.355 | 0.977 | 0.239 | 0.982 | 0.232 | 0.983 | |
| (80,50,40) | PCP[1] | 0.763 | 0.958 | 0.908 | 0.951 | 0.737 | 0.959 | 0.327 | 0.978 | 0.215 | 0.983 | 0.211 | 0.984 |
| PCP[2] | 0.736 | 0.959 | 0.868 | 0.953 | 0.717 | 0.960 | 0.320 | 0.978 | 0.202 | 0.984 | 0.191 | 0.984 | |
| PCP[3] | 0.744 | 0.959 | 0.895 | 0.952 | 0.729 | 0.959 | 0.324 | 0.978 | 0.211 | 0.984 | 0.207 | 0.984 | |
| (80,60,50) | PCP[1] | 0.703 | 0.961 | 0.836 | 0.954 | 0.690 | 0.961 | 0.304 | 0.979 | 0.193 | 0.984 | 0.189 | 0.985 |
| PCP[2] | 0.632 | 0.964 | 0.750 | 0.958 | 0.624 | 0.964 | 0.190 | 0.985 | 0.177 | 0.985 | 0.115 | 0.988 | |
| PCP[3] | 0.678 | 0.962 | 0.808 | 0.956 | 0.642 | 0.964 | 0.253 | 0.982 | 0.191 | 0.984 | 0.187 | 0.985 | |
| Pop-2 () | |||||||||||||
| (30,15,10) | PCP[1] | 1.132 | 0.941 | 1.556 | 0.921 | 1.085 | 0.943 | 0.880 | 0.952 | 0.277 | 0.980 | 0.271 | 0.981 |
| PCP[2] | 1.077 | 0.943 | 1.481 | 0.924 | 1.061 | 0.944 | 0.747 | 0.959 | 0.272 | 0.981 | 0.267 | 0.981 | |
| PCP[3] | 1.084 | 0.943 | 1.491 | 0.924 | 1.077 | 0.943 | 0.861 | 0.953 | 0.273 | 0.981 | 0.268 | 0.981 | |
| (30,20,15) | PCP[1] | 1.073 | 0.943 | 1.475 | 0.925 | 1.015 | 0.946 | 0.697 | 0.961 | 0.265 | 0.981 | 0.264 | 0.981 |
| PCP[2] | 1.069 | 0.944 | 1.470 | 0.925 | 1.004 | 0.947 | 0.647 | 0.963 | 0.261 | 0.981 | 0.260 | 0.981 | |
| PCP[3] | 1.069 | 0.944 | 1.470 | 0.925 | 1.009 | 0.946 | 0.651 | 0.963 | 0.265 | 0.981 | 0.260 | 0.981 | |
| (50,30,20) | PCP[1] | 1.039 | 0.945 | 1.429 | 0.927 | 1.002 | 0.947 | 0.615 | 0.965 | 0.260 | 0.981 | 0.259 | 0.981 |
| PCP[2] | 1.011 | 0.946 | 1.389 | 0.929 | 0.982 | 0.948 | 0.578 | 0.966 | 0.260 | 0.981 | 0.258 | 0.981 | |
| PCP[3] | 1.038 | 0.945 | 1.428 | 0.927 | 0.986 | 0.947 | 0.589 | 0.966 | 0.260 | 0.981 | 0.258 | 0.981 | |
| (50,40,30) | PCP[1] | 1.003 | 0.947 | 1.379 | 0.929 | 0.972 | 0.948 | 0.532 | 0.969 | 0.258 | 0.981 | 0.251 | 0.982 |
| PCP[2] | 0.985 | 0.948 | 1.354 | 0.930 | 0.963 | 0.949 | 0.500 | 0.970 | 0.250 | 0.982 | 0.247 | 0.982 | |
| PCP[3] | 0.986 | 0.947 | 1.356 | 0.930 | 0.971 | 0.948 | 0.512 | 0.970 | 0.251 | 0.982 | 0.247 | 0.982 | |
| (80,50,40) | PCP[1] | 0.982 | 0.948 | 1.350 | 0.931 | 0.959 | 0.949 | 0.486 | 0.971 | 0.213 | 0.983 | 0.209 | 0.984 |
| PCP[2] | 0.935 | 0.950 | 1.285 | 0.934 | 0.918 | 0.951 | 0.460 | 0.972 | 0.213 | 0.983 | 0.209 | 0.984 | |
| PCP[3] | 0.975 | 0.948 | 1.340 | 0.931 | 0.935 | 0.950 | 0.467 | 0.972 | 0.213 | 0.983 | 0.209 | 0.984 | |
| (80,60,50) | PCP[1] | 0.908 | 0.951 | 1.249 | 0.935 | 0.888 | 0.952 | 0.454 | 0.972 | 0.198 | 0.984 | 0.195 | 0.984 |
| PCP[2] | 0.867 | 0.953 | 1.193 | 0.938 | 0.846 | 0.954 | 0.414 | 0.974 | 0.197 | 0.984 | 0.193 | 0.984 | |
| PCP[3] | 0.888 | 0.952 | 1.221 | 0.937 | 0.876 | 0.953 | 0.436 | 0.973 | 0.197 | 0.984 | 0.193 | 0.984 | |
| Pop-2 () | |||||||||||||
| (30,15,10) | PCP[1] | 1.126 | 0.941 | 1.330 | 0.932 | 1.079 | 0.943 | 0.880 | 0.952 | 0.271 | 0.981 | 0.266 | 0.981 |
| PCP[2] | 1.064 | 0.944 | 1.266 | 0.935 | 1.055 | 0.944 | 0.606 | 0.965 | 0.270 | 0.981 | 0.265 | 0.981 | |
| PCP[3] | 1.082 | 0.943 | 1.274 | 0.934 | 1.069 | 0.944 | 0.621 | 0.964 | 0.271 | 0.981 | 0.266 | 0.981 | |
| (30,20,15) | PCP[1] | 1.059 | 0.944 | 1.260 | 0.935 | 1.008 | 0.946 | 0.563 | 0.967 | 0.265 | 0.981 | 0.264 | 0.981 |
| PCP[2] | 1.054 | 0.944 | 1.256 | 0.935 | 0.993 | 0.947 | 0.518 | 0.969 | 0.260 | 0.981 | 0.259 | 0.981 | |
| PCP[3] | 1.056 | 0.944 | 1.256 | 0.935 | 1.006 | 0.947 | 0.547 | 0.968 | 0.264 | 0.981 | 0.259 | 0.981 | |
| (50,30,20) | PCP[1] | 1.014 | 0.946 | 1.221 | 0.937 | 0.991 | 0.947 | 0.471 | 0.971 | 0.260 | 0.981 | 0.259 | 0.981 |
| PCP[2] | 0.997 | 0.947 | 1.187 | 0.938 | 0.963 | 0.949 | 0.441 | 0.973 | 0.259 | 0.981 | 0.251 | 0.982 | |
| PCP[3] | 1.010 | 0.946 | 1.220 | 0.937 | 0.978 | 0.948 | 0.442 | 0.973 | 0.259 | 0.981 | 0.251 | 0.982 | |
| (50,40,30) | PCP[1] | 0.982 | 0.948 | 1.179 | 0.939 | 0.950 | 0.949 | 0.395 | 0.975 | 0.258 | 0.981 | 0.251 | 0.982 |
| PCP[2] | 0.967 | 0.948 | 1.157 | 0.940 | 0.945 | 0.949 | 0.367 | 0.976 | 0.248 | 0.982 | 0.243 | 0.982 | |
| PCP[3] | 0.980 | 0.948 | 1.159 | 0.939 | 0.947 | 0.949 | 0.370 | 0.976 | 0.248 | 0.982 | 0.243 | 0.982 | |
| (80,50,40) | PCP[1] | 0.960 | 0.949 | 1.153 | 0.940 | 0.938 | 0.950 | 0.347 | 0.977 | 0.212 | 0.983 | 0.208 | 0.984 |
| PCP[2] | 0.934 | 0.950 | 1.098 | 0.942 | 0.918 | 0.951 | 0.326 | 0.978 | 0.210 | 0.984 | 0.206 | 0.984 | |
| PCP[3] | 0.955 | 0.949 | 1.145 | 0.940 | 0.918 | 0.951 | 0.344 | 0.977 | 0.212 | 0.984 | 0.208 | 0.984 | |
| (80,60,50) | PCP[1] | 0.888 | 0.952 | 1.067 | 0.944 | 0.876 | 0.953 | 0.309 | 0.979 | 0.197 | 0.984 | 0.194 | 0.984 |
| PCP[2] | 0.852 | 0.954 | 1.019 | 0.946 | 0.829 | 0.955 | 0.279 | 0.980 | 0.195 | 0.984 | 0.191 | 0.984 | |
| PCP[3] | 0.882 | 0.952 | 1.043 | 0.945 | 0.871 | 0.953 | 0.300 | 0.979 | 0.196 | 0.984 | 0.193 | 0.984 | |
| PCP | ACI-NA | ACI-NL | BCI | HPD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior→ | I | II | I | II | |||||||||
| Pop-1 () | |||||||||||||
| (30,15,10) | PCP[1] | 0.217 | 0.958 | 0.213 | 0.958 | 0.139 | 0.977 | 0.138 | 0.977 | 0.137 | 0.977 | 0.137 | 0.977 |
| PCP[2] | 0.233 | 0.954 | 0.227 | 0.955 | 0.143 | 0.976 | 0.141 | 0.976 | 0.140 | 0.977 | 0.139 | 0.977 | |
| PCP[3] | 0.243 | 0.951 | 0.236 | 0.953 | 0.146 | 0.975 | 0.143 | 0.976 | 0.142 | 0.976 | 0.141 | 0.976 | |
| (30,20,15) | PCP[1] | 0.196 | 0.963 | 0.191 | 0.964 | 0.133 | 0.978 | 0.129 | 0.979 | 0.118 | 0.982 | 0.114 | 0.983 |
| PCP[2] | 0.211 | 0.959 | 0.210 | 0.959 | 0.138 | 0.977 | 0.134 | 0.978 | 0.132 | 0.978 | 0.129 | 0.979 | |
| PCP[3] | 0.201 | 0.961 | 0.199 | 0.962 | 0.134 | 0.978 | 0.131 | 0.979 | 0.121 | 0.981 | 0.115 | 0.983 | |
| (50,30,20) | PCP[1] | 0.162 | 0.971 | 0.150 | 0.974 | 0.113 | 0.983 | 0.111 | 0.984 | 0.110 | 0.984 | 0.105 | 0.985 |
| PCP[2] | 0.168 | 0.969 | 0.157 | 0.972 | 0.114 | 0.983 | 0.111 | 0.984 | 0.110 | 0.984 | 0.105 | 0.985 | |
| PCP[3] | 0.183 | 0.966 | 0.161 | 0.971 | 0.117 | 0.982 | 0.115 | 0.983 | 0.114 | 0.983 | 0.111 | 0.984 | |
| (50,40,30) | PCP[1] | 0.149 | 0.974 | 0.133 | 0.978 | 0.102 | 0.986 | 0.097 | 0.987 | 0.091 | 0.989 | 0.087 | 0.989 |
| PCP[2] | 0.159 | 0.972 | 0.149 | 0.974 | 0.112 | 0.983 | 0.109 | 0.984 | 0.107 | 0.985 | 0.101 | 0.986 | |
| PCP[3] | 0.154 | 0.973 | 0.142 | 0.976 | 0.108 | 0.984 | 0.103 | 0.986 | 0.101 | 0.986 | 0.096 | 0.987 | |
| (80,50,40) | PCP[1] | 0.132 | 0.978 | 0.122 | 0.981 | 0.071 | 0.994 | 0.070 | 0.994 | 0.069 | 0.994 | 0.069 | 0.994 |
| PCP[2] | 0.135 | 0.978 | 0.125 | 0.980 | 0.076 | 0.992 | 0.075 | 0.993 | 0.074 | 0.993 | 0.073 | 0.993 | |
| PCP[3] | 0.142 | 0.976 | 0.127 | 0.980 | 0.084 | 0.990 | 0.082 | 0.991 | 0.082 | 0.991 | 0.081 | 0.991 | |
| (80,60,50) | PCP[1] | 0.124 | 0.980 | 0.066 | 0.995 | 0.063 | 0.996 | 0.060 | 0.996 | 0.055 | 0.997 | 0.054 | 0.998 |
| PCP[2] | 0.126 | 0.980 | 0.121 | 0.981 | 0.069 | 0.994 | 0.068 | 0.994 | 0.066 | 0.995 | 0.065 | 0.995 | |
| PCP[3] | 0.125 | 0.980 | 0.077 | 0.992 | 0.068 | 0.994 | 0.067 | 0.994 | 0.062 | 0.996 | 0.062 | 0.996 | |
| Pop-1 () | |||||||||||||
| (30,15,10) | PCP[1] | 0.215 | 0.958 | 0.210 | 0.959 | 0.138 | 0.977 | 0.138 | 0.977 | 0.137 | 0.977 | 0.136 | 0.977 |
| PCP[2] | 0.229 | 0.954 | 0.215 | 0.958 | 0.142 | 0.976 | 0.141 | 0.976 | 0.140 | 0.977 | 0.138 | 0.977 | |
| PCP[3] | 0.239 | 0.952 | 0.230 | 0.954 | 0.145 | 0.975 | 0.142 | 0.976 | 0.141 | 0.976 | 0.140 | 0.976 | |
| (30,20,15) | PCP[1] | 0.194 | 0.963 | 0.189 | 0.964 | 0.132 | 0.978 | 0.128 | 0.979 | 0.117 | 0.982 | 0.113 | 0.983 |
| PCP[2] | 0.211 | 0.959 | 0.208 | 0.960 | 0.137 | 0.977 | 0.133 | 0.978 | 0.131 | 0.979 | 0.128 | 0.980 | |
| PCP[3] | 0.199 | 0.962 | 0.197 | 0.962 | 0.133 | 0.978 | 0.130 | 0.979 | 0.120 | 0.981 | 0.115 | 0.983 | |
| (50,30,20) | PCP[1] | 0.161 | 0.971 | 0.148 | 0.974 | 0.112 | 0.983 | 0.110 | 0.984 | 0.109 | 0.984 | 0.104 | 0.985 |
| PCP[2] | 0.164 | 0.970 | 0.156 | 0.973 | 0.113 | 0.983 | 0.111 | 0.984 | 0.110 | 0.984 | 0.104 | 0.985 | |
| PCP[3] | 0.178 | 0.967 | 0.159 | 0.972 | 0.116 | 0.982 | 0.115 | 0.983 | 0.114 | 0.983 | 0.110 | 0.984 | |
| (50,40,30) | PCP[1] | 0.148 | 0.975 | 0.132 | 0.978 | 0.101 | 0.986 | 0.096 | 0.987 | 0.090 | 0.989 | 0.087 | 0.990 |
| PCP[2] | 0.158 | 0.972 | 0.148 | 0.975 | 0.111 | 0.984 | 0.108 | 0.984 | 0.106 | 0.985 | 0.100 | 0.986 | |
| PCP[3] | 0.153 | 0.973 | 0.140 | 0.976 | 0.105 | 0.985 | 0.101 | 0.986 | 0.100 | 0.986 | 0.096 | 0.987 | |
| (80,50,40) | PCP[1] | 0.131 | 0.979 | 0.121 | 0.981 | 0.070 | 0.994 | 0.069 | 0.994 | 0.069 | 0.994 | 0.068 | 0.994 |
| PCP[2] | 0.134 | 0.978 | 0.124 | 0.980 | 0.076 | 0.992 | 0.075 | 0.993 | 0.074 | 0.993 | 0.072 | 0.993 | |
| PCP[3] | 0.141 | 0.976 | 0.126 | 0.980 | 0.083 | 0.990 | 0.082 | 0.991 | 0.081 | 0.991 | 0.080 | 0.991 | |
| (80,60,50) | PCP[1] | 0.123 | 0.981 | 0.064 | 0.995 | 0.060 | 0.996 | 0.059 | 0.996 | 0.055 | 0.998 | 0.054 | 0.998 |
| PCP[2] | 0.125 | 0.980 | 0.120 | 0.981 | 0.069 | 0.994 | 0.068 | 0.994 | 0.065 | 0.995 | 0.064 | 0.995 | |
| PCP[3] | 0.124 | 0.980 | 0.076 | 0.992 | 0.068 | 0.994 | 0.067 | 0.995 | 0.062 | 0.996 | 0.061 | 0.996 | |
| Pop-2 () | |||||||||||||
| (30,15,10) | PCP[1] | 0.230 | 0.954 | 0.229 | 0.954 | 0.119 | 0.982 | 0.117 | 0.982 | 0.116 | 0.982 | 0.115 | 0.983 |
| PCP[2] | 0.242 | 0.951 | 0.237 | 0.952 | 0.121 | 0.981 | 0.119 | 0.982 | 0.118 | 0.982 | 0.117 | 0.982 | |
| PCP[3] | 0.263 | 0.946 | 0.253 | 0.949 | 0.122 | 0.981 | 0.121 | 0.981 | 0.120 | 0.981 | 0.119 | 0.982 | |
| (30,20,15) | PCP[1] | 0.216 | 0.958 | 0.213 | 0.959 | 0.112 | 0.983 | 0.111 | 0.984 | 0.110 | 0.984 | 0.108 | 0.984 |
| PCP[2] | 0.223 | 0.956 | 0.221 | 0.956 | 0.117 | 0.982 | 0.116 | 0.982 | 0.116 | 0.982 | 0.114 | 0.983 | |
| PCP[3] | 0.219 | 0.957 | 0.215 | 0.958 | 0.114 | 0.983 | 0.113 | 0.983 | 0.112 | 0.983 | 0.110 | 0.984 | |
| (50,30,20) | PCP[1] | 0.176 | 0.968 | 0.175 | 0.968 | 0.110 | 0.984 | 0.107 | 0.985 | 0.105 | 0.985 | 0.103 | 0.985 |
| PCP[2] | 0.182 | 0.966 | 0.181 | 0.966 | 0.110 | 0.984 | 0.107 | 0.984 | 0.107 | 0.985 | 0.105 | 0.985 | |
| PCP[3] | 0.199 | 0.962 | 0.192 | 0.964 | 0.111 | 0.984 | 0.110 | 0.984 | 0.108 | 0.984 | 0.105 | 0.985 | |
| (50,40,30) | PCP[1] | 0.169 | 0.969 | 0.166 | 0.970 | 0.101 | 0.986 | 0.098 | 0.987 | 0.091 | 0.989 | 0.086 | 0.990 |
| PCP[2] | 0.172 | 0.969 | 0.171 | 0.969 | 0.103 | 0.986 | 0.101 | 0.986 | 0.100 | 0.986 | 0.098 | 0.987 | |
| PCP[3] | 0.169 | 0.969 | 0.167 | 0.970 | 0.103 | 0.986 | 0.100 | 0.986 | 0.099 | 0.987 | 0.097 | 0.987 | |
| (80,50,40) | PCP[1] | 0.141 | 0.976 | 0.139 | 0.977 | 0.073 | 0.993 | 0.071 | 0.993 | 0.069 | 0.994 | 0.068 | 0.994 |
| PCP[2] | 0.149 | 0.974 | 0.147 | 0.975 | 0.085 | 0.990 | 0.081 | 0.991 | 0.078 | 0.992 | 0.074 | 0.993 | |
| PCP[3] | 0.159 | 0.972 | 0.158 | 0.972 | 0.085 | 0.990 | 0.084 | 0.990 | 0.082 | 0.991 | 0.076 | 0.992 | |
| (80,60,50) | PCP[1] | 0.137 | 0.977 | 0.134 | 0.978 | 0.056 | 0.997 | 0.055 | 0.997 | 0.055 | 0.998 | 0.053 | 0.998 |
| PCP[2] | 0.139 | 0.977 | 0.138 | 0.977 | 0.064 | 0.995 | 0.063 | 0.996 | 0.055 | 0.997 | 0.054 | 0.998 | |
| PCP[3] | 0.137 | 0.977 | 0.136 | 0.977 | 0.060 | 0.996 | 0.059 | 0.996 | 0.055 | 0.997 | 0.054 | 0.998 | |
| Pop-2 () | |||||||||||||
| (30,15,10) | PCP[1] | 0.230 | 0.954 | 0.227 | 0.955 | 0.119 | 0.982 | 0.116 | 0.982 | 0.115 | 0.983 | 0.115 | 0.983 |
| PCP[2] | 0.239 | 0.952 | 0.234 | 0.953 | 0.120 | 0.981 | 0.119 | 0.982 | 0.118 | 0.982 | 0.117 | 0.982 | |
| PCP[3] | 0.261 | 0.947 | 0.250 | 0.949 | 0.121 | 0.981 | 0.120 | 0.981 | 0.119 | 0.982 | 0.118 | 0.982 | |
| (30,20,15) | PCP[1] | 0.215 | 0.958 | 0.210 | 0.959 | 0.111 | 0.984 | 0.110 | 0.984 | 0.109 | 0.984 | 0.107 | 0.985 |
| PCP[2] | 0.222 | 0.956 | 0.220 | 0.957 | 0.117 | 0.982 | 0.116 | 0.982 | 0.115 | 0.983 | 0.113 | 0.983 | |
| PCP[3] | 0.217 | 0.957 | 0.212 | 0.959 | 0.113 | 0.983 | 0.112 | 0.983 | 0.111 | 0.984 | 0.110 | 0.984 | |
| (50,30,20) | PCP[1] | 0.175 | 0.968 | 0.173 | 0.968 | 0.109 | 0.984 | 0.106 | 0.985 | 0.104 | 0.985 | 0.103 | 0.986 |
| PCP[2] | 0.181 | 0.966 | 0.179 | 0.967 | 0.109 | 0.984 | 0.107 | 0.985 | 0.106 | 0.985 | 0.104 | 0.985 | |
| PCP[3] | 0.197 | 0.962 | 0.190 | 0.964 | 0.110 | 0.984 | 0.109 | 0.984 | 0.107 | 0.985 | 0.104 | 0.985 | |
| (50,40,30) | PCP[1] | 0.167 | 0.970 | 0.165 | 0.970 | 0.100 | 0.986 | 0.097 | 0.987 | 0.090 | 0.989 | 0.085 | 0.990 |
| PCP[2] | 0.172 | 0.969 | 0.170 | 0.969 | 0.102 | 0.986 | 0.100 | 0.986 | 0.099 | 0.987 | 0.097 | 0.987 | |
| PCP[3] | 0.167 | 0.970 | 0.165 | 0.970 | 0.102 | 0.986 | 0.100 | 0.986 | 0.099 | 0.987 | 0.096 | 0.987 | |
| (80,50,40) | PCP[1] | 0.141 | 0.976 | 0.138 | 0.977 | 0.072 | 0.993 | 0.071 | 0.994 | 0.069 | 0.994 | 0.067 | 0.994 |
| PCP[2] | 0.148 | 0.974 | 0.146 | 0.975 | 0.084 | 0.990 | 0.081 | 0.991 | 0.078 | 0.992 | 0.073 | 0.993 | |
| PCP[3] | 0.158 | 0.972 | 0.157 | 0.972 | 0.085 | 0.990 | 0.083 | 0.990 | 0.081 | 0.991 | 0.076 | 0.992 | |
| (80,60,50) | PCP[1] | 0.136 | 0.978 | 0.134 | 0.978 | 0.056 | 0.997 | 0.055 | 0.998 | 0.054 | 0.998 | 0.053 | 0.998 |
| PCP[2] | 0.138 | 0.977 | 0.137 | 0.977 | 0.064 | 0.995 | 0.062 | 0.996 | 0.055 | 0.998 | 0.054 | 0.998 | |
| PCP[3] | 0.136 | 0.977 | 0.135 | 0.978 | 0.060 | 0.996 | 0.058 | 0.997 | 0.055 | 0.998 | 0.053 | 0.998 | |
| PCP | ACI-NA | ACI-NL | BCI | HPD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior→ | I | II | I | II | |||||||||
| Pop-1 () | |||||||||||||
| (30,15,10) | PCP[1] | 1.634 | 0.929 | 2.553 | 0.900 | 0.166 | 0.970 | 2.401 | 0.905 | 1.595 | 0.931 | 0.159 | 0.971 |
| PCP[2] | 1.721 | 0.927 | 2.842 | 0.891 | 0.169 | 0.969 | 2.629 | 0.898 | 1.635 | 0.929 | 0.165 | 0.970 | |
| PCP[3] | 1.618 | 0.930 | 2.514 | 0.902 | 0.157 | 0.970 | 2.347 | 0.907 | 1.588 | 0.931 | 0.153 | 0.971 | |
| (30,20,15) | PCP[1] | 1.594 | 0.931 | 2.373 | 0.906 | 0.152 | 0.971 | 2.249 | 0.910 | 1.560 | 0.932 | 0.149 | 0.972 |
| PCP[2] | 1.579 | 0.931 | 2.261 | 0.910 | 0.150 | 0.971 | 2.145 | 0.913 | 1.425 | 0.936 | 0.148 | 0.972 | |
| PCP[3] | 1.564 | 0.932 | 2.142 | 0.913 | 0.149 | 0.971 | 2.034 | 0.917 | 1.398 | 0.937 | 0.148 | 0.972 | |
| (50,30,20) | PCP[1] | 1.336 | 0.939 | 1.791 | 0.924 | 0.147 | 0.972 | 1.728 | 0.926 | 1.304 | 0.940 | 0.146 | 0.973 |
| PCP[2] | 1.372 | 0.938 | 1.962 | 0.919 | 0.148 | 0.972 | 1.791 | 0.924 | 1.325 | 0.939 | 0.147 | 0.973 | |
| PCP[3] | 1.335 | 0.939 | 1.779 | 0.925 | 0.146 | 0.972 | 1.649 | 0.929 | 1.273 | 0.941 | 0.145 | 0.973 | |
| (50,40,30) | PCP[1] | 1.241 | 0.942 | 1.681 | 0.928 | 0.145 | 0.973 | 1.618 | 0.930 | 1.235 | 0.942 | 0.143 | 0.974 |
| PCP[2] | 1.222 | 0.942 | 1.644 | 0.929 | 0.144 | 0.973 | 1.560 | 0.932 | 1.175 | 0.944 | 0.141 | 0.974 | |
| PCP[3] | 1.188 | 0.943 | 1.580 | 0.931 | 0.141 | 0.973 | 1.448 | 0.935 | 1.053 | 0.948 | 0.141 | 0.974 | |
| (80,50,40) | PCP[1] | 0.870 | 0.953 | 1.426 | 0.936 | 0.139 | 0.974 | 1.322 | 0.939 | 0.852 | 0.954 | 0.137 | 0.975 |
| PCP[2] | 0.971 | 0.950 | 1.529 | 0.933 | 0.140 | 0.974 | 1.385 | 0.937 | 0.946 | 0.951 | 0.138 | 0.975 | |
| PCP[3] | 0.814 | 0.955 | 1.408 | 0.937 | 0.136 | 0.974 | 1.308 | 0.940 | 0.803 | 0.956 | 0.137 | 0.975 | |
| (80,60,50) | PCP[1] | 0.801 | 0.956 | 1.311 | 0.940 | 0.127 | 0.975 | 1.283 | 0.940 | 0.761 | 0.957 | 0.124 | 0.976 |
| PCP[2] | 0.788 | 0.956 | 1.302 | 0.940 | 0.125 | 0.975 | 0.809 | 0.955 | 0.723 | 0.958 | 0.122 | 0.976 | |
| PCP[3] | 0.703 | 0.959 | 1.293 | 0.940 | 0.122 | 0.975 | 0.706 | 0.959 | 0.619 | 0.961 | 0.121 | 0.976 | |
| Pop-1 () | |||||||||||||
| (30,15,10) | PCP[1] | 1.623 | 0.930 | 2.544 | 0.901 | 0.161 | 0.971 | 2.397 | 0.905 | 1.592 | 0.931 | 0.153 | 0.973 |
| PCP[2] | 1.681 | 0.928 | 2.764 | 0.894 | 0.168 | 0.970 | 2.549 | 0.901 | 1.629 | 0.930 | 0.154 | 0.972 | |
| PCP[3] | 1.594 | 0.931 | 2.453 | 0.904 | 0.153 | 0.971 | 2.295 | 0.909 | 1.583 | 0.931 | 0.152 | 0.973 | |
| (30,20,15) | PCP[1] | 1.583 | 0.931 | 2.373 | 0.906 | 0.151 | 0.972 | 2.249 | 0.910 | 1.522 | 0.933 | 0.148 | 0.974 |
| PCP[2] | 1.556 | 0.932 | 2.233 | 0.911 | 0.149 | 0.972 | 2.114 | 0.914 | 1.361 | 0.938 | 0.148 | 0.974 | |
| PCP[3] | 1.534 | 0.933 | 2.089 | 0.915 | 0.148 | 0.972 | 1.985 | 0.918 | 1.359 | 0.938 | 0.147 | 0.974 | |
| (50,30,20) | PCP[1] | 1.305 | 0.940 | 1.742 | 0.926 | 0.147 | 0.973 | 1.683 | 0.928 | 1.246 | 0.942 | 0.145 | 0.975 |
| PCP[2] | 1.347 | 0.938 | 1.878 | 0.922 | 0.147 | 0.973 | 1.733 | 0.926 | 1.308 | 0.940 | 0.146 | 0.975 | |
| PCP[3] | 1.294 | 0.940 | 1.721 | 0.927 | 0.145 | 0.973 | 1.601 | 0.930 | 1.230 | 0.942 | 0.144 | 0.975 | |
| (50,40,30) | PCP[1] | 1.237 | 0.942 | 1.630 | 0.929 | 0.144 | 0.973 | 1.572 | 0.931 | 1.180 | 0.944 | 0.141 | 0.976 |
| PCP[2] | 1.190 | 0.943 | 1.595 | 0.931 | 0.144 | 0.974 | 1.521 | 0.933 | 1.120 | 0.946 | 0.140 | 0.976 | |
| PCP[3] | 1.132 | 0.945 | 1.534 | 0.933 | 0.141 | 0.974 | 1.415 | 0.936 | 1.024 | 0.949 | 0.138 | 0.976 | |
| (80,50,40) | PCP[1] | 0.854 | 0.954 | 1.392 | 0.937 | 0.139 | 0.976 | 1.297 | 0.940 | 0.844 | 0.954 | 0.135 | 0.977 |
| PCP[2] | 0.962 | 0.951 | 1.488 | 0.934 | 0.139 | 0.974 | 1.358 | 0.938 | 0.944 | 0.951 | 0.137 | 0.977 | |
| PCP[3] | 0.813 | 0.955 | 1.379 | 0.937 | 0.139 | 0.976 | 1.284 | 0.940 | 0.800 | 0.956 | 0.133 | 0.977 | |
| (80,60,50) | PCP[1] | 0.796 | 0.956 | 1.287 | 0.940 | 0.125 | 0.977 | 1.260 | 0.941 | 0.754 | 0.957 | 0.123 | 0.978 |
| PCP[2] | 0.785 | 0.956 | 1.277 | 0.941 | 0.123 | 0.977 | 0.791 | 0.956 | 0.719 | 0.958 | 0.121 | 0.978 | |
| PCP[3] | 0.700 | 0.959 | 1.269 | 0.941 | 0.121 | 0.977 | 0.704 | 0.959 | 0.593 | 0.962 | 0.120 | 0.978 | |
| Pop-2 () | |||||||||||||
| (30,15,10) | PCP[1] | 1.457 | 0.935 | 2.775 | 0.893 | 0.136 | 0.973 | 2.597 | 0.899 | 1.437 | 0.936 | 0.133 | 0.974 |
| PCP[2] | 1.472 | 0.934 | 2.916 | 0.889 | 0.140 | 0.972 | 2.888 | 0.890 | 1.455 | 0.935 | 0.136 | 0.973 | |
| PCP[3] | 1.435 | 0.936 | 2.734 | 0.895 | 0.135 | 0.973 | 2.581 | 0.900 | 1.415 | 0.936 | 0.138 | 0.974 | |
| (30,20,15) | PCP[1] | 1.388 | 0.937 | 2.560 | 0.900 | 0.133 | 0.974 | 2.430 | 0.904 | 1.384 | 0.937 | 0.134 | 0.975 |
| PCP[2] | 1.383 | 0.937 | 2.478 | 0.903 | 0.131 | 0.974 | 2.353 | 0.907 | 1.357 | 0.938 | 0.132 | 0.975 | |
| PCP[3] | 1.360 | 0.938 | 2.361 | 0.906 | 0.131 | 0.974 | 2.247 | 0.910 | 1.336 | 0.939 | 0.130 | 0.975 | |
| (50,30,20) | PCP[1] | 1.322 | 0.939 | 1.976 | 0.919 | 0.130 | 0.975 | 1.908 | 0.921 | 1.282 | 0.940 | 0.126 | 0.976 |
| PCP[2] | 1.339 | 0.939 | 2.210 | 0.911 | 0.130 | 0.975 | 2.103 | 0.915 | 1.314 | 0.939 | 0.129 | 0.976 | |
| PCP[3] | 1.298 | 0.940 | 1.928 | 0.920 | 0.129 | 0.975 | 1.867 | 0.922 | 1.232 | 0.942 | 0.122 | 0.976 | |
| (50,40,30) | PCP[1] | 1.251 | 0.941 | 1.817 | 0.924 | 0.128 | 0.976 | 1.764 | 0.925 | 1.205 | 0.943 | 0.120 | 0.977 |
| PCP[2] | 1.219 | 0.942 | 1.806 | 0.924 | 0.126 | 0.976 | 1.752 | 0.926 | 1.174 | 0.944 | 0.118 | 0.977 | |
| PCP[3] | 1.205 | 0.943 | 1.782 | 0.925 | 0.124 | 0.976 | 1.731 | 0.926 | 1.107 | 0.946 | 0.123 | 0.977 | |
| (80,50,40) | PCP[1] | 0.978 | 0.950 | 1.588 | 0.931 | 0.113 | 0.977 | 1.533 | 0.933 | 0.966 | 0.950 | 0.111 | 0.978 |
| PCP[2] | 1.050 | 0.948 | 1.716 | 0.927 | 0.116 | 0.977 | 1.672 | 0.928 | 1.004 | 0.949 | 0.119 | 0.978 | |
| PCP[3] | 0.905 | 0.952 | 1.492 | 0.934 | 0.110 | 0.977 | 1.463 | 0.935 | 0.864 | 0.954 | 0.109 | 0.978 | |
| (80,60,50) | PCP[1] | 0.815 | 0.955 | 1.434 | 0.936 | 0.109 | 0.978 | 1.407 | 0.937 | 0.723 | 0.957 | 0.105 | 0.979 |
| PCP[2] | 0.763 | 0.957 | 1.413 | 0.936 | 0.106 | 0.978 | 1.387 | 0.937 | 0.713 | 0.958 | 0.102 | 0.979 | |
| PCP[3] | 0.727 | 0.958 | 1.403 | 0.937 | 0.103 | 0.978 | 1.378 | 0.937 | 0.703 | 0.958 | 0.100 | 0.980 | |
| Pop-2 () | |||||||||||||
| (30,15,10) | PCP[1] | 1.445 | 0.935 | 2.748 | 0.894 | 0.136 | 0.974 | 2.589 | 0.899 | 1.425 | 0.936 | 0.136 | 0.976 |
| PCP[2] | 1.457 | 0.935 | 2.801 | 0.893 | 0.139 | 0.973 | 2.758 | 0.894 | 1.437 | 0.936 | 0.140 | 0.975 | |
| PCP[3] | 1.432 | 0.936 | 2.678 | 0.896 | 0.134 | 0.974 | 2.503 | 0.902 | 1.404 | 0.937 | 0.131 | 0.976 | |
| (30,20,15) | PCP[1] | 1.388 | 0.937 | 2.559 | 0.900 | 0.132 | 0.975 | 2.429 | 0.904 | 1.384 | 0.937 | 0.129 | 0.977 |
| PCP[2] | 1.362 | 0.938 | 2.375 | 0.906 | 0.131 | 0.975 | 2.253 | 0.910 | 1.338 | 0.939 | 0.128 | 0.977 | |
| PCP[3] | 1.339 | 0.939 | 2.343 | 0.907 | 0.131 | 0.975 | 2.230 | 0.911 | 1.335 | 0.939 | 0.127 | 0.977 | |
| (50,30,20) | PCP[1] | 1.316 | 0.939 | 1.928 | 0.920 | 0.128 | 0.976 | 1.861 | 0.922 | 1.262 | 0.941 | 0.125 | 0.978 |
| PCP[2] | 1.318 | 0.939 | 2.119 | 0.914 | 0.129 | 0.976 | 2.016 | 0.917 | 1.293 | 0.940 | 0.126 | 0.978 | |
| PCP[3] | 1.276 | 0.941 | 1.922 | 0.920 | 0.127 | 0.976 | 1.861 | 0.922 | 1.226 | 0.942 | 0.124 | 0.978 | |
| (50,40,30) | PCP[1] | 1.230 | 0.942 | 1.808 | 0.924 | 0.125 | 0.976 | 1.755 | 0.926 | 1.181 | 0.944 | 0.122 | 0.979 |
| PCP[2] | 1.194 | 0.943 | 1.754 | 0.926 | 0.125 | 0.977 | 1.701 | 0.927 | 1.164 | 0.944 | 0.120 | 0.979 | |
| PCP[3] | 1.181 | 0.944 | 1.739 | 0.926 | 0.121 | 0.977 | 1.689 | 0.928 | 1.069 | 0.947 | 0.119 | 0.979 | |
| (80,50,40) | PCP[1] | 0.975 | 0.950 | 1.552 | 0.932 | 0.110 | 0.979 | 1.498 | 0.934 | 0.919 | 0.952 | 0.109 | 0.980 |
| PCP[2] | 1.006 | 0.949 | 1.675 | 0.928 | 0.115 | 0.977 | 1.632 | 0.929 | 0.947 | 0.951 | 0.113 | 0.980 | |
| PCP[3] | 0.891 | 0.953 | 1.490 | 0.934 | 0.110 | 0.979 | 1.461 | 0.935 | 0.854 | 0.954 | 0.109 | 0.980 | |
| (80,60,50) | PCP[1] | 0.808 | 0.955 | 1.415 | 0.936 | 0.108 | 0.980 | 1.388 | 0.937 | 0.712 | 0.958 | 0.099 | 0.981 |
| PCP[2] | 0.755 | 0.957 | 1.410 | 0.936 | 0.104 | 0.980 | 1.384 | 0.937 | 0.705 | 0.959 | 0.093 | 0.981 | |
| PCP[3] | 0.717 | 0.958 | 1.399 | 0.937 | 0.100 | 0.980 | 1.373 | 0.938 | 0.705 | 0.959 | 0.091 | 0.981 | |
| 0.45 | 0.64 | 0.75 | 1.01 | 1.17 | 1.37 | 1.77 | 2.42 | 2.60 | 3.01 | 3.38 | 3.49 |
| 3.85 | 3.89 | 4.49 | 4.55 | 4.68 | 4.91 | 5.46 | 5.75 | 6.08 | 6.11 | 6.38 | 6.56 |
| 6.96 | 7.84 | 8.81 | 8.82 | 9.17 | 9.24 | 9.40 | 9.77 | 10.57 | 11.43 | 11.49 | 13.19 |
| 13.98 | 15.15 | 17.43 | 17.72 | 18.06 | 22.48 | 24.05 |
| Par. | MLE | 95% ACI-NA | 95% ACI-NL | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Est. | Std.Er | Low. | Upp. | IL | Low. | Upp. | IL | Statistic | p-Value | |
| 6.4938 | 5.8447 | 0.0000 | 17.949 | 17.949 | 1.1127 | 37.899 | 36.786 | 0.0555 | 0.9984 | |
| 0.1939 | 0.0364 | 0.1226 | 0.2652 | 0.1426 | 0.1342 | 0.2801 | 0.1459 | |||
| Sample | PCP | Data | |||
|---|---|---|---|---|---|
| 2.5 (3) | 13 | 7.84 | 0.45, 1.01, 1.37, 2.60, 3.01, 3.89, 4.68, 5.75, 6.38, 7.84 | ||
| 5.5 (11) | 8 | 10 | 0.45, 0.64, 0.75, 1.01, 1.17, 1.37, 2.42, 3.01, 3.89, 4.55 | ||
| 4.91, 5.75, 6.56, 8.81, 9.77 | |||||
| 11.5 (20) | 0 | 11.43 | 0.45, 0.64, 0.75, 1.01, 1.17, 1.37, 1.77, 2.42, 2.60, 3.01, | ||
| 3.89, 4.55, 4.68, 5.75, 6.96, 7.84, 8.82, 9.24, 10.57, 11.43 |
| Sample | Par. | MLE | ACI-NA | BCI | |||||
|---|---|---|---|---|---|---|---|---|---|
| MCMC | ACI-NL | HPD | |||||||
| Est. | Std.Er | Lower | Upper | IL | Lower | Upper | IL | ||
| 7.4882 | 15.426 | 0.0000 | 37.722 | 37.722 | 7.4688 | 7.5078 | 0.0390 | ||
| 7.4882 | 0.0099 | 0.1321 | 14.496 | 14.364 | 7.4689 | 7.5079 | 0.0390 | ||
| 0.1058 | 0.0754 | 0.0021 | 0.2537 | 0.2916 | 0.0866 | 0.1237 | 0.0371 | ||
| 0.1050 | 0.0094 | 0.0262 | 0.4280 | 0.4018 | 0.0871 | 0.1241 | 0.0370 | ||
| 0.8017 | 0.0598 | 0.6845 | 0.9189 | 0.2344 | 0.7639 | 0.8413 | 0.0774 | ||
| 0.8034 | 0.0197 | 0.6927 | 0.9279 | 0.2352 | 0.7632 | 0.8404 | 0.0772 | ||
| 0.0552 | 0.0215 | 0.0130 | 0.0973 | 0.0843 | 0.0420 | 0.0685 | 0.0265 | ||
| 0.0547 | 0.0067 | 0.0257 | 0.1185 | 0.0928 | 0.0412 | 0.0675 | 0.0263 | ||
| 0.4666 | 3.1792 | 0.0000 | 6.6977 | 6.6977 | 0.4469 | 0.4860 | 0.0391 | ||
| 0.4663 | 0.0100 | 0.0018 | 16.235 | 16.233 | 0.4474 | 0.4864 | 0.0390 | ||
| 0.0466 | 0.1269 | 0.0011 | 0.2953 | 0.2942 | 0.0314 | 0.0618 | 0.0305 | ||
| 0.0460 | 0.0078 | 0.0002 | 9.6464 | 9.6461 | 0.0311 | 0.0614 | 0.0304 | ||
| 0.7252 | 0.0639 | 0.6000 | 0.8503 | 0.2504 | 0.6559 | 0.8036 | 0.1477 | ||
| 0.7293 | 0.0380 | 0.6102 | 0.8618 | 0.2516 | 0.6552 | 0.8026 | 0.1475 | ||
| 0.0621 | 0.0171 | 0.0286 | 0.0956 | 0.0670 | 0.0427 | 0.0807 | 0.0380 | ||
| 0.0613 | 0.0098 | 0.0362 | 0.1065 | 0.0703 | 0.0425 | 0.0805 | 0.0380 | ||
| 3.1291 | 4.3336 | 0.0000 | 11.623 | 11.623 | 3.1097 | 3.1488 | 0.0390 | ||
| 3.1291 | 0.0099 | 0.2073 | 17.235 | 17.028 | 3.1100 | 3.1490 | 0.0390 | ||
| 0.1205 | 0.0548 | 0.0131 | 0.2279 | 0.2148 | 0.1020 | 0.1383 | 0.0364 | ||
| 0.1199 | 0.0092 | 0.0494 | 0.2939 | 0.2445 | 0.1017 | 0.1379 | 0.0363 | ||
| 0.6826 | 0.0646 | 0.5560 | 0.8093 | 0.2532 | 0.6395 | 0.7290 | 0.0894 | ||
| 0.6844 | 0.0227 | 0.5671 | 0.8218 | 0.2547 | 0.6402 | 0.7294 | 0.0892 | ||
| 0.0868 | 0.0213 | 0.0450 | 0.1285 | 0.0834 | 0.0710 | 0.1026 | 0.0316 | ||
| 0.0863 | 0.0080 | 0.0536 | 0.1403 | 0.0867 | 0.0708 | 0.1023 | 0.0315 | ||
| Sample | Par. | Mean | Mode | Std.D | Sk. | |||
|---|---|---|---|---|---|---|---|---|
| 7.48816 | 7.47713 | 7.48140 | 7.48814 | 7.49483 | 0.00994 | 0.01162 | ||
| 0.10495 | 0.09175 | 0.09855 | 0.10493 | 0.11128 | 0.00939 | 0.03441 | ||
| 0.80337 | 0.78946 | 0.79019 | 0.80351 | 0.81678 | 0.01959 | −0.06067 | ||
| 0.05471 | 0.04546 | 0.05007 | 0.05455 | 0.05916 | 0.00670 | 0.16136 | ||
| 0.46634 | 0.45892 | 0.45950 | 0.46628 | 0.47311 | 0.01002 | −0.00075 | ||
| 0.04601 | 0.04545 | 0.04064 | 0.04573 | 0.05116 | 0.00779 | 0.16086 | ||
| 0.72925 | 0.72938 | 0.70356 | 0.72945 | 0.75481 | 0.03778 | 0.01932 | ||
| 0.06127 | 0.06100 | 0.05458 | 0.06101 | 0.06775 | 0.00973 | 0.10517 | ||
| 3.12912 | 3.11684 | 3.12236 | 3.12911 | 3.13578 | 0.00994 | 0.01114 | ||
| 0.11985 | 0.10643 | 0.11355 | 0.11980 | 0.12608 | 0.00922 | 0.04243 | ||
| 0.68440 | 0.66837 | 0.66899 | 0.68429 | 0.69977 | 0.02268 | 0.00864 | ||
| 0.08629 | 0.07482 | 0.08078 | 0.08617 | 0.09163 | 0.00801 | 0.10262 |
| 6.1 | 7.0 | 7.8 | 7.9 | 11.9 | 12.2 | 25.2 | 26 | 30 | 36.9 |
| 48.4 | 68.8 | 97.8 | 101.5 | 107.8 | 145 | 157.8 | 168.1 | 297.5 | 303.8 |
| Par. | MLE | 95% ACI-NA | 95% ACI-NL | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Est. | Std.Er | Low. | Upp. | IL | Low. | Upp. | IL | Statistic | p -Value | |
| 0.3337 | 0.5481 | 0.0000 | 1.4078 | 1.4078 | 0.0133 | 8.3450 | 8.3317 | 0.1361 | 0.8052 | |
| 0.0091 | 0.0047 | 0.0000 | 0.0183 | 0.0183 | 0.0033 | 0.0250 | 0.0217 | |||
| Sample | PCP | Data | |||
|---|---|---|---|---|---|
| 12(3) | 5 | 101.5 | 6.1, 7.8, 11.9, 12.2, 26, 30, 36.9, 48.4, 68.8, 101.5 | ||
| 150(12) | 3 | 150 | 6.1, 7.0, 7.8, 7.9, 11.9, 12.2, 26, 30, 36.9, 68.8, 107.8, 145 | ||
| 170(15) | 0 | 168.1 | 6.1, 7.0, 7.8, 7.9, 11.9, 12.2, 25.2, 26, 30, 36.9, 48.4, 97.8, 101.5, 145, 168.1 |
| Sample | Par. | MLE | ACI-NA | BCI | |||||
|---|---|---|---|---|---|---|---|---|---|
| MCMC | ACI-NL | HPD | |||||||
| Est. | Std.Er | Lower | Upper | IL | Lower | Upper | IL | ||
| 0.1103 | 0.9196 | 0.0000 | 1.9126 | 1.9126 | 0.1003 | 0.1199 | 0.0196 | ||
| 0.1100 | 0.0050 | 0.0008 | 5.2424 | 5.2416 | 0.1006 | 0.1201 | 0.0196 | ||
| 0.0050 | 0.0140 | 0.0000 | 0.0324 | 0.0324 | 0.0033 | 0.0067 | 0.0034 | ||
| 0.0049 | 0.0009 | 0.0002 | 1.1891 | 1.1891 | 0.0032 | 0.0067 | 0.0034 | ||
| 0.8852 | 0.0376 | 0.8114 | 0.9589 | 0.1475 | 0.8505 | 0.9231 | 0.0727 | ||
| 0.8876 | 0.0187 | 0.8144 | 0.9621 | 0.1476 | 0.8506 | 0.9232 | 0.0726 | ||
| 0.0120 | 0.0041 | 0.0039 | 0.0200 | 0.0161 | 0.0079 | 0.0158 | 0.0079 | ||
| 0.0117 | 0.0020 | 0.0061 | 0.0234 | 0.0173 | 0.0079 | 0.0158 | 0.0079 | ||
| 0.1120 | 0.3872 | 0.0000 | 0.8709 | 0.8709 | 0.1021 | 0.1217 | 0.0196 | ||
| 0.1118 | 0.0050 | 0.0003 | 98.050 | 98.050 | 0.1023 | 0.1219 | 0.0195 | ||
| 0.0055 | 0.0064 | 0.0000 | 0.0181 | 0.0181 | 0.0037 | 0.0071 | 0.0034 | ||
| 0.0054 | 0.0009 | 0.0005 | 0.0549 | 0.0543 | 0.0037 | 0.0071 | 0.0034 | ||
| 0.8760 | 0.0380 | 0.8015 | 0.9505 | 0.1490 | 0.8417 | 0.9136 | 0.0719 | ||
| 0.8783 | 0.0184 | 0.8046 | 0.9538 | 0.1492 | 0.8415 | 0.9132 | 0.0717 | ||
| 0.0130 | 0.0042 | 0.0048 | 0.0212 | 0.0164 | 0.0089 | 0.0168 | 0.0079 | ||
| 0.0127 | 0.0020 | 0.0069 | 0.0244 | 0.0175 | 0.0090 | 0.0168 | 0.0079 | ||
| 0.8223 | 1.4073 | 0.0000 | 3.5807 | 3.5807 | 0.8126 | 0.8321 | 0.0195 | ||
| 0.8223 | 0.0050 | 0.0287 | 23.541 | 23.512 | 0.8128 | 0.8323 | 0.0195 | ||
| 0.0165 | 0.0090 | 0.0000 | 0.0342 | 0.0342 | 0.0145 | 0.0184 | 0.0039 | ||
| 0.0164 | 0.0010 | 0.0056 | 0.0483 | 0.0426 | 0.0145 | 0.0183 | 0.0039 | ||
| 0.8351 | 0.0587 | 0.7201 | 0.9501 | 0.2300 | 0.8181 | 0.8533 | 0.0351 | ||
| 0.8357 | 0.0089 | 0.7277 | 0.9584 | 0.2307 | 0.8188 | 0.8538 | 0.0351 | ||
| 0.0179 | 0.0062 | 0.0057 | 0.0301 | 0.0245 | 0.0158 | 0.0199 | 0.0041 | ||
| 0.0178 | 0.0011 | 0.0090 | 0.0354 | 0.0264 | 0.0157 | 0.0198 | 0.0041 | ||
| Sample | Par. | Mean | Mode | Std.D | Sk. | |||
|---|---|---|---|---|---|---|---|---|
| 0.11004 | 0.11043 | 0.10664 | 0.11004 | 0.11339 | 0.00499 | 0.01525 | ||
| 0.00490 | 0.00435 | 0.00430 | 0.00489 | 0.00549 | 0.00087 | 0.12879 | ||
| 0.88760 | 0.89931 | 0.87505 | 0.88768 | 0.90031 | 0.01851 | −0.05361 | ||
| 0.01173 | 0.01045 | 0.01034 | 0.01171 | 0.01309 | 0.00201 | 0.09596 | ||
| 0.11180 | 0.09655 | 0.10840 | 0.11180 | 0.11515 | 0.00498 | 0.01223 | ||
| 0.00537 | 0.00465 | 0.00476 | 0.00536 | 0.00597 | 0.00088 | 0.10814 | ||
| 0.87828 | 0.87104 | 0.86583 | 0.87831 | 0.89084 | 0.01831 | −0.03389 | ||
| 0.01275 | 0.01131 | 0.01136 | 0.01273 | 0.01410 | 0.00201 | 0.07644 | ||
| S3 | 0.82228 | 0.83506 | 0.81890 | 0.82228 | 0.82562 | 0.00498 | 0.01779 | |
| 0.01643 | 0.01548 | 0.01576 | 0.01643 | 0.01709 | 0.00098 | 0.03125 | ||
| 0.83566 | 0.84524 | 0.82965 | 0.83563 | 0.84170 | 0.00892 | 0.00265 | ||
| 0.01783 | 0.01671 | 0.01712 | 0.01783 | 0.01854 | 0.00105 | 0.02685 |
| Sample | ||||||
|---|---|---|---|---|---|---|
| 0.3 | 0.6 | 0.9 | ||||
| 6297.789 | 237.9618 | 0.160199 | 3.204534 | 28.21442 | 222.9919 | |
| 1485.411 | 10.12321 | 0.001607 | 2.396828 | 35.74682 | 2187.111 | |
| 1865.942 | 18.78300 | 0.010066 | 1.114359 | 4.582958 | 45.16951 | |
| Sample | ||||||
|---|---|---|---|---|---|---|
| 0.3 | 0.6 | 0.9 | ||||
| 316,665.1 | 0.845848 | 0.000003 | 115.4766 | 905.6239 | 1548.539 | |
| 299,664.8 | 0.149952 | 0.000001 | 87.04930 | 682.4630 | 6981.514 | |
| 52,748.25 | 1.980712 | 0.000038 | 50.21496 | 214.3330 | 13,502.72 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, H.S.; Abo-Kasem, O.E.; Elshahhat, A. Statistical Evaluation of Alpha-Powering Exponential Generalized Progressive Hybrid Censoring and Its Modeling for Medical and Engineering Sciences with Optimization Plans. Symmetry 2025, 17, 1473. https://doi.org/10.3390/sym17091473
Mohammed HS, Abo-Kasem OE, Elshahhat A. Statistical Evaluation of Alpha-Powering Exponential Generalized Progressive Hybrid Censoring and Its Modeling for Medical and Engineering Sciences with Optimization Plans. Symmetry. 2025; 17(9):1473. https://doi.org/10.3390/sym17091473
Chicago/Turabian StyleMohammed, Heba S., Osama E. Abo-Kasem, and Ahmed Elshahhat. 2025. "Statistical Evaluation of Alpha-Powering Exponential Generalized Progressive Hybrid Censoring and Its Modeling for Medical and Engineering Sciences with Optimization Plans" Symmetry 17, no. 9: 1473. https://doi.org/10.3390/sym17091473
APA StyleMohammed, H. S., Abo-Kasem, O. E., & Elshahhat, A. (2025). Statistical Evaluation of Alpha-Powering Exponential Generalized Progressive Hybrid Censoring and Its Modeling for Medical and Engineering Sciences with Optimization Plans. Symmetry, 17(9), 1473. https://doi.org/10.3390/sym17091473








