Abstract
The present paper treats the problem of steady laminar MHD flow of an incompressible viscous fluid for mixed convection stagnation-point flow over a vertical stretching sheet in the presence of an externally magnetic field. By means of the Optimal Auxiliary Functions Method (OAFM), the resulting nonlinear ODEs are semi-analytically solved. The impact of various physical parameters, such as the velocity ratio parameter A, the Prandtl number , and the Hartmann number , on the behavior of velocity and temperature profiles is analyzed. Both assisting () and opposing () flows are considered. The influence of these parameters is tabulated and graphically presented. The originality of this work lies in the development of effective semi-analytical solutions and in the excellent agreement between these solutions and the corresponding numerical solutions. This highlights the accuracy of the proposed method applied to steady laminar MHD flow. A comparative analysis underlines the advantages of the OAFM compared to the iterative method. The obtained results confirm that the OAFM represents a competitive mathematical tool to explore a large class of nonlinear problems with applications in engineering.
1. Introduction
Boundary layer flow and heat transfer over a stretched sheet have been studied over time by many researchers. Many metallurgical processes involve cooling continuous strips or filaments by drawing them through a latent fluid. By drawing these strips in an electrically conductive fluid subjected to a magnetic field, the cooling rate can be controlled and a final product of desired quality can be obtained, which can be used in copper drawing, annealing, and hot tinning. In these cases, a mixed convection MHD flow is used on a vertical surface stretched in the presence of a magnetic field [1]. MHD flow and heat transfer of viscous fluids on a continuously stretched surface also have engineering applications in geothermal energy extraction, metal purification from non-metallic enclosures, plasma studies, and aerodynamic extrusion of plastic sheets. Kumari and Nath [2] studied unsteady magnetohydrodynamic (MHD) mixed convection flow on a vertical permeable stretched impulsively in the presence of a transverse uniform magnetic field. Prasad et al. [3] studied mixed convection boundary layer flow on a heated vertical sheet with variable fluid properties. Ali et al. [4] investigated MHD boundary layer flow on a stretched sheet with the effect of an induced magnetic field. Ali et al. [1] studied the problem of point stagnation flow using mixed convection MHD and heat transfer on a stretched vertical sheet with an external magnetic field. Another important application of hydromagnetism in metallurgy is the purification of molten metals from non-metallic inclusions by applying a magnetic field. The flow of fluid near a stagnation point is relevant for bodies in high-speed flow. It is used to reduce the drag in the design of thrust bearings and cooling of nuclear reactors and hydrodynamic processes. This flow was first analyzed by Hiemanz [5], who used the similarity transformation to reduce the Navier–Stokes equation to third-order ordinary differential equations, subject to two-point boundary conditions. Eckert [6] also considered the energy equation. Subsequently, many studies have considered the magnetic field, heat source/sink, and suction/injection to improve the properties of fluids in point stagnation flow. Mixed convection in stagnation flows adjacent to vertical surfaces was analyzed by Ramchandran et al. [7]. Andersson [8] obtained an exact solution for the MHD flow of a viscoelastic fluid past a spreading sheet in the presence of a transverse magnetic field. Ishak et al. [9] considered the MHD flow of a micropolar fluid toward a stagnation point on a vertical surface. Gupta et al. [10] investigated the MHD boundary layer flow and heat transfer over a spreading sheet with Hall effects. Abel et al. [11] discussed the effects of buoyancy force and thermal radiation in the MHD boundary layer flow over a continuously moving spreading surface. Ishak et al. [12] considered hydromagnetic flow and heat transfer adjacent to a vertical spreading sheet. Sharma et al. [13] investigated the effects of heat generation/absorption on the point stagnation flow of mixed convective MHD along a vertical stretching sheet in the presence of an external magnetic field, the effects of which were highlighted on some physical parameters such as the velocity ratio parameter, mixed convection parameter, Hartmann number, Prandtl number, and heat source/sink on the velocity and temperature distributions. Many researchers have been attracted to convective heat transfer using nanofluids, mixtures of base fluids and nanometer-sized particles, with complex applications in medical applications, the petroleum industry, and food processing. The temperature of the base fluid increases due to nanoparticles, which are the main source in the heat transfer performance. Zainal et al. [14] investigated the mixed convective MHD stagnation flow of a hybrid nanofluids past a vertical flat plate under convective boundary conditions. Double stratification of nanofluids over a vertical plate was studied by Ibrahim and Makinde [15], while Kandasamy et al. [16] investigated the effect of thermal and solute stratification on MHD nanofluids over a porous vertical plate. Later, Khashi’ie et al. [17] applied the non-Fourier energy model to solve the double-stratified nanofluid flow and heat transfer over a permeable stretching/contracting sheet. Abdal et al. [18] investigated the multislip effects on the unsteady magnetohydrodynamic (MHD) mixed convection flow of micropolar nanofluids over a stretching/contracting sheet, along with radiation, in the presence of a heat source. Murtaza et al. [19] studied the effects of diffusion on the mixed convective peristaltic flow of a bi-viscous Bingham nanofluid through a porous medium in a vertical channel, with convective boundary conditions, using Fick’s and Fourier’s ordering laws for the generalized mathematical model. Choudhary et al. [20] showed that different shapes of nanoparticles influence the heat transfer performance of radiative magnetohydrodynamic tetra-hybrid nanofluids flowing past a stretching surface in a porous medium, allowing the fluid to be tailored to specific industrial needs. The initially formulated governing flow equations are nonlinear partial differential equations, which are transformed into a set of linear ordinary differential equations, adopting relevant similarity transformations. Ajithkumar et al. [21] studied the impact of Hall current, thermal radiation, and cross-diffusion on mixed convection peristaltic pumping of a bi-viscous Bingham nanofluid in a porous medium. Nisar et al. [22] dealt with the peristaltic magnetohydrodynamic (MHD) flow of Bingham nanofluids in a channel with symmetric and elastic walls. Velocity slip, thermal convection, and mass flow conditions were imposed on the channel walls. Dissipation, Joule heating, and mixed convection aspects were analyzed. Akbar et al. [23] investigated the thermal and flow characteristics of mixed convective peristaltic transport of nanofluids by considering the induced magnetic field, variable viscosity, buoyancy force, viscosity dissipation, and effects of porous media. Jagadesh et al. [24] studied the peristaltic flow of a Jeffrey nanofluid through a vertically diverging channel, subjected to the impact of thermal radiation, heat generation, activation energy, and an angular magnetic field. Neelav et al. [25] studied the complex magnetohydrodynamic (MHD) flow dynamics of a Jeffrey hybrid nanofluid cascading over an exponentially stretching porous surface. They considered a complex interplay of factors, including aligned magnetic fields, radiation effects, non-uniform heat fluxes, and the influence of the Arrhenius activation energy. Ajithkumar et al. [26] conducted a comparative study of free convective peristaltic flow of non-Newtonian fluids (Casson and Jeffrey) in a symmetrical conical porous pipe with Hall current and viscosity dissipation effects. Sahar et al. [27] studied the impact of viscous dissipation and ohmic heating on the heat plume generated by a linear heat source under the impact of an aligned magnetic field. Ajithkumar et al. [28] studied the flow of a Casson fluid for free convective peristaltic pumping in the presence of a uniform magnetic field in the transverse direction through an inclined porous corrugated channel. Later, Khashi’ie et al. [29] studied the problem of MHD point stagnation flow toward a saturated stretching/contracting surface in a porous medium, also considering the combined effects of double stratification and convection. Alarifi et al. [30] analyzed the steady laminar flow over a stretched vertical sheet, with the existence of viscous dissipation, heat source/sink, and magnetic fields. Thus, they numerically analyzed the governing equation and the boundary-layer balance using a shooting scheme based on the Runge–Kutta–Fehlberg integration algorithm and obtained a nonlinear normal system of differential equations using appropriate transformations. They followed the impact of physical parameters on the dimensionless velocity, temperature, local Nusselt coefficient, and skin friction coefficient.
These studies contributed to our motivation to build semi-analytical solutions for steady laminar MHD flow of an incompressible viscous fluid using the OAFM. At the same time, this work is based on our preliminary results for thermal analysis of the fluid flow [31,32]. Recently, Farooq et al. [33] investigated the mechanical problem of the steady flow of couple stress fluid between two infinitely parallel inclined plates under the impact of MHD by comparative analysis of the HAM method versus the OAFM. The performance of the OAFM was highlighted by the residual error of the OAFM and HAM solutions for velocity. Zada et al. [34] used the OAFM to solve the nonlinear differential equation of the Blasius problem, showing that it is extremely efficient and provides the means to control the convergence of the approximate solution, using only a single iteration. Recently, using the OAFM, Khan et al. [35] solved the Falkner–Skan heat transfer equation. The constitutive equations obtained from the Navier–Stokes equations were converted into a set of nonlinear ordinary differential equations (ODEs) using a similarity transformation. The OAFM was used in this case to find accurate solutions and to study the effects of various physical parameters, such as the Falkner–Skan power law parameter, thermal conductivity, and slip conditions, on the fluid velocity and temperature profiles. The advantage of the OAFM compared to other known methods, such as the HPM (Homotopy Perturbation Method), VIM (Variational Iteration Method), or ADM (Adomian Decomposition Method), is the reduced number of iterations (just two) for control of convergence of the approximate solutions [36]. There are some strongly nonlinear differential equations for which the HPM method requires more than two iterations. In the OAFM, the deformed equations (for the first approximation, the second approximation, and so on) are easily constructed, and the initial guess is freely selected and could be applied to the study of 3D flows, unsteady regimes, inclusion of nanoparticle effects, and so on. A limitation of the OAFM is its application to nonlinear problems with discontinuities, where the implementation of the OAFM and its modifications becomes complex and computationally demanding.
Our paper is organized as follows: Section 1 is followed by Section 2 describing equations of motion for steady two-dimensional flow of a viscous fluid and providing a brief description of the theoretical approach of the OAFM. Section 3 is dedicated to the results and discussion about the effects of physical parameters on the flow and heat transfer. Conclusions are summarized in the last section, Section 4.
2. Methodology
2.1. Equation of Motion
The problem of steady two-dimensional flow of a viscous fluid near the stagnation point on a vertical stretching flat plate is considered for analysis in the present section. The physical model is shown in [1], with the flat plate coinciding with the plane and the x-axis measured along the sheet oriented in the upward direction, while the y-axis is normal. The temperature of the plate is proposed to be , where is the temperature of the ambient fluid, while c is a constant with for a heated surface (assisting flow) and for a cooled surface (opposing flow).
The steady two-dimensional flow of a viscous and electrically conducting fluid, taking into account the effect of the external magnetic field with constant magnetic intensity and neglecting the viscous dissipation effect, is modeled by the following equations [1]:
where u and v are the velocity components along the x- and y-axes, respectively; is the fluid density; p is the pressure; T is the fluid temperature; g is the gravitation acceleration; is the thermal diffusivity; is the kinematic viscosity; is the thermal expansion coefficient; is the electrical conductivity; and is the magnetic permeability.
For Equations (1)–(3), the boundary conditions are
where is the velocity of the stretching surface, and is the velocity of the flat surface, with a and b as the positive constants.
In this study, the induced magnetic field was ignored. For the most general model of practical importance, the forces due to the hydrostatic and magnetic pressure gradient would be in equilibrium (see Sutton and Sherman [37]), namely,
because in the inviscid (outer boundary layer) flow. From Equations (5) and (2), the boundary layer equation has the form
The stream function defined by means u and v: and , leads to the following similarity transformation:
where describes the mass transfer, and models the heat transfer.
Equations (6) and (3) are reduced to the nonlinear ordinary differential equations for the f and functions:
and Equation (4) becomes
with describing the velocity function of the flow.
The parameter is the velocity ratio parameter, and parameter is the Prandtl number. The Hartmann number is
It quantifies the relative strength of the magnetic force compared to the viscous forces in the fluid. A higher Hartmann number suggests that the magnetic forces significantly influence the flow properties, suppressing the turbulence in the fluid and making the flow more streamlined and stable.
The parameter is the constant mixed convection or buoyancy parameter, which is defined as
where is the local Grashof number, and is the local Reynolds number. A positive value of corresponds to assisting flow, a negative one corresponds to opposing flow, and corresponds to forced convection flow.
2.2. Semi-Analytical Solutions via the Optimal Auxiliary Functions Method (OAFM)
Linear operator and nonlinear operator satisfy the second-order nonlinear differential equation [38]:
where g is a known function, t is the independent variable, and unknown function has two components:
where the initial approximation satisfies
From Equation (13), the first approximation verifies
The nonlinear operator can be expanded in the form
Using Equations (16) and (17), the first approximation is the solution to the following problem:
where and are two arbitrary auxiliary functions depending on the initial approximation and several unknown parameters and , , .
Finally, the approximate analytic solution from Equation (14) is obtained, with and solutions for Equations (15) and (18), respectively.
Remark 1.
The nonlinear operator from Equation (17) has the form
where is a positive integer, refers to linearly independent functions, and are known functions that depend on . This justifies the form of Equation (18) as
with , , , … arbitrary auxiliary functions depending on the unknown parameters , , , … being optimally computed via the various methods, such as the least squares method and the weighted residual method.
Definition 1.
The OAFM functions satisfying the conditions
are called ε-approximate OAFM solutions of Equation (13), with .
Definition 2.
The OAFM functions satisfying the conditions
are called weak ε-approximate OAFM solutions of Equation (13) on the real interval .
The existence of weak -approximate OAFM solutions is built by the theorem presented above.
Theorem 1.
Equation (13) admits a sequence of weak ε-approximate OAFM solutions.
Proof.
It is similar to the theorem from [39]. □
Here, we apply the OAFM procedure to obtain approximate solutions for Equations (8) and (9) with the initial/boundary conditions in Equation (10).
First, it is clear from Equation (8) that
To obtain semi-analytical solution , in the case of the nonlinear Equations (8) and (9), we choose the linear operators of the form
where the given arbitrary function and K, , and are some unknown positive parameters and are determined at the end.
The initial approximations and result from the problems
whose solutions are
where and depend on parameters and , K, , and .
The nonlinear operator , from Equation (8), is defined as
This expression is a linear combination of the following functions set:
Let be a nonempty finite subset of real numbers.
The first approximation could be obtained from Equation (21), which becomes
where .
We have freedom to choose numerous possibilities for the convergence of control functions , as follows (see Marinca and Herisanu [38]):
or
- orand so on, with , , , , , , , , , , , , , , , and arbitrary parameters at this moment depending on , , K, , and .
The first-order approximate solution provided by Equation (14) is obtained from Equations (27) and (33):
The unknown constants , , , , , , , , , , , , , , , and from Equation (34) depend on parameters , , K, , and and will be optimally identified.
In this way, we can find other semi-analytical solutions as well.
By means of the OAFM procedure, the semi-analytical solutions for unknown function could be obtained from Equation (24) as
where is defined in Equation (34).
Remark 2.
The initial conditions and for are equivalent to , . The optimal parameters are obtained using the least square method, taking into account of the numerical values of the unknown functions , for domain , with .
3. Numerical Results and Discussion
In this section, the advantages of the OAFM and its accuracy are proved by comparison of our semi-analytical solutions with numerical results obtained via the fourth-order Runge–Kutta method for velocity and temperature profiles, considering representative values of physical parameters: , , . The effects of these different parameters are discussed for both assisting and opposing flows. The precision of the semi-analytic solutions is shown in Table 1, Table 2 and Table 3 by the calculus for absolute values displayed in the last column for each table.

Table 1.
Numerical results versus OAFM solutions from Equation (A1) for the values , (assisting flow), , and , respectively, (absolute values: ).

Table 2.
Numerical results versus OAFM solutions from Equation (A12) for the values , (opposing flow), , and , respectively, (absolute values: ).

Table 3.
Numerical results versus OAFM solutions from Equation (A13) for the values , (opposing flow), , and , respectively, (absolute values: ).
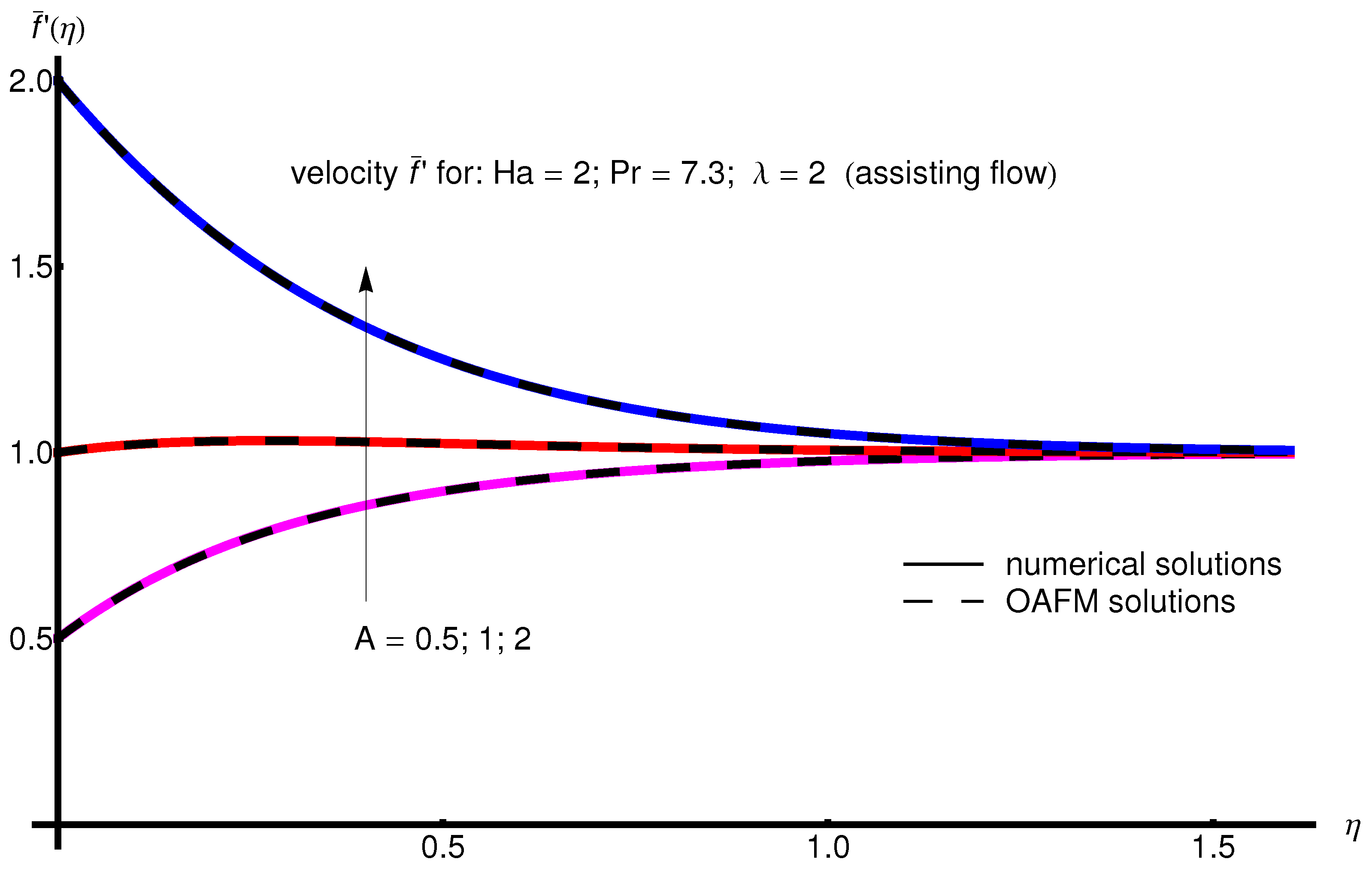
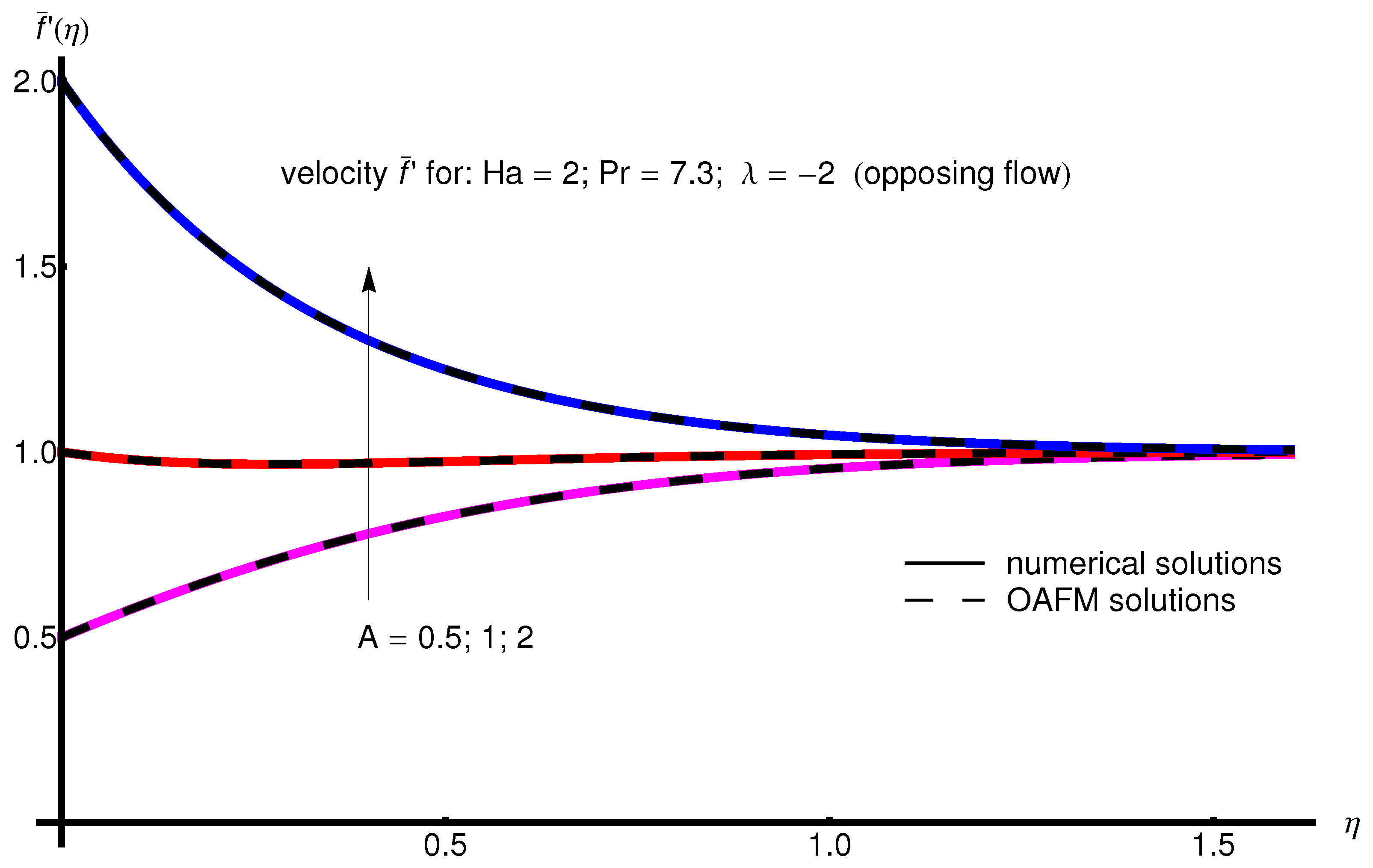
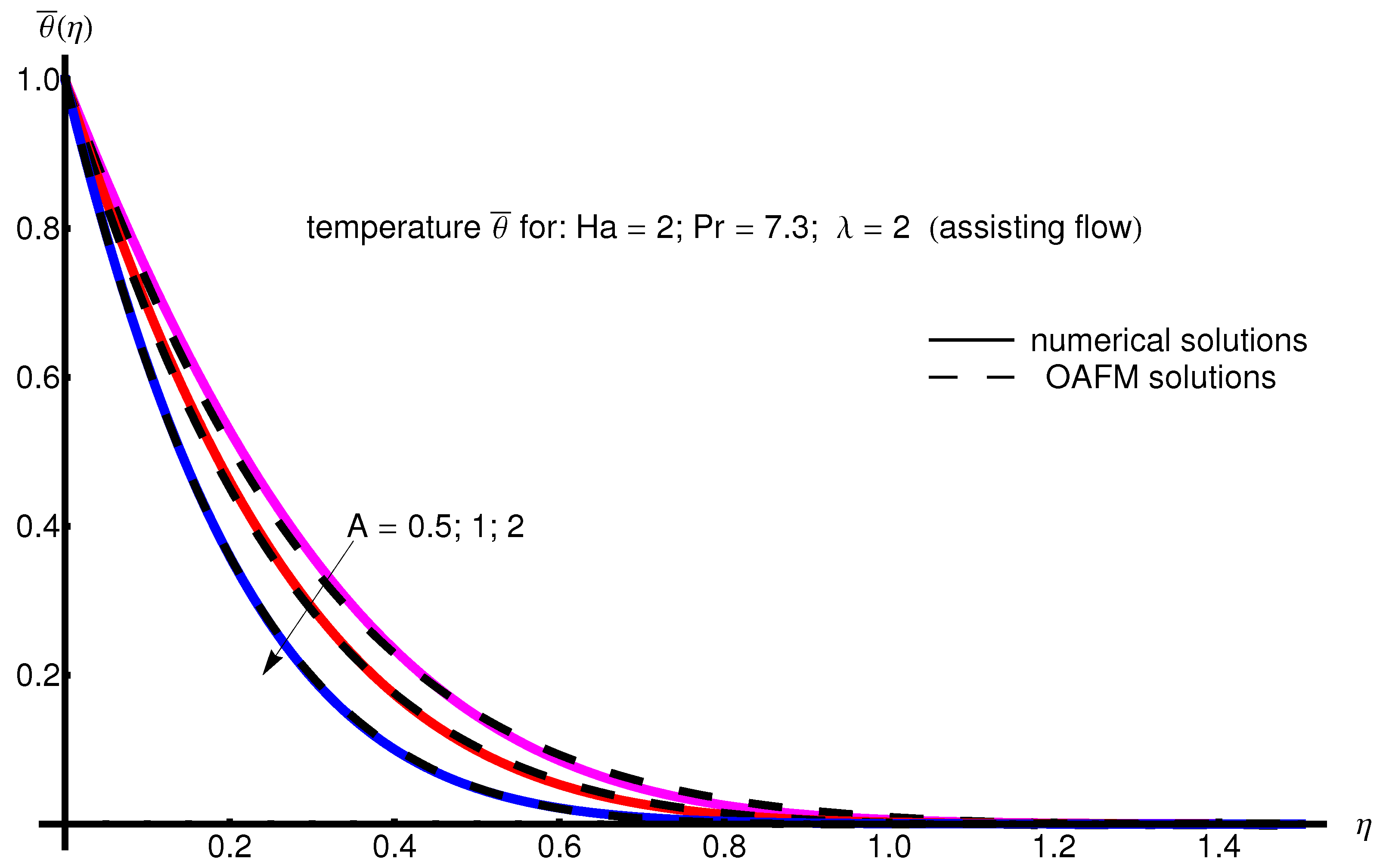
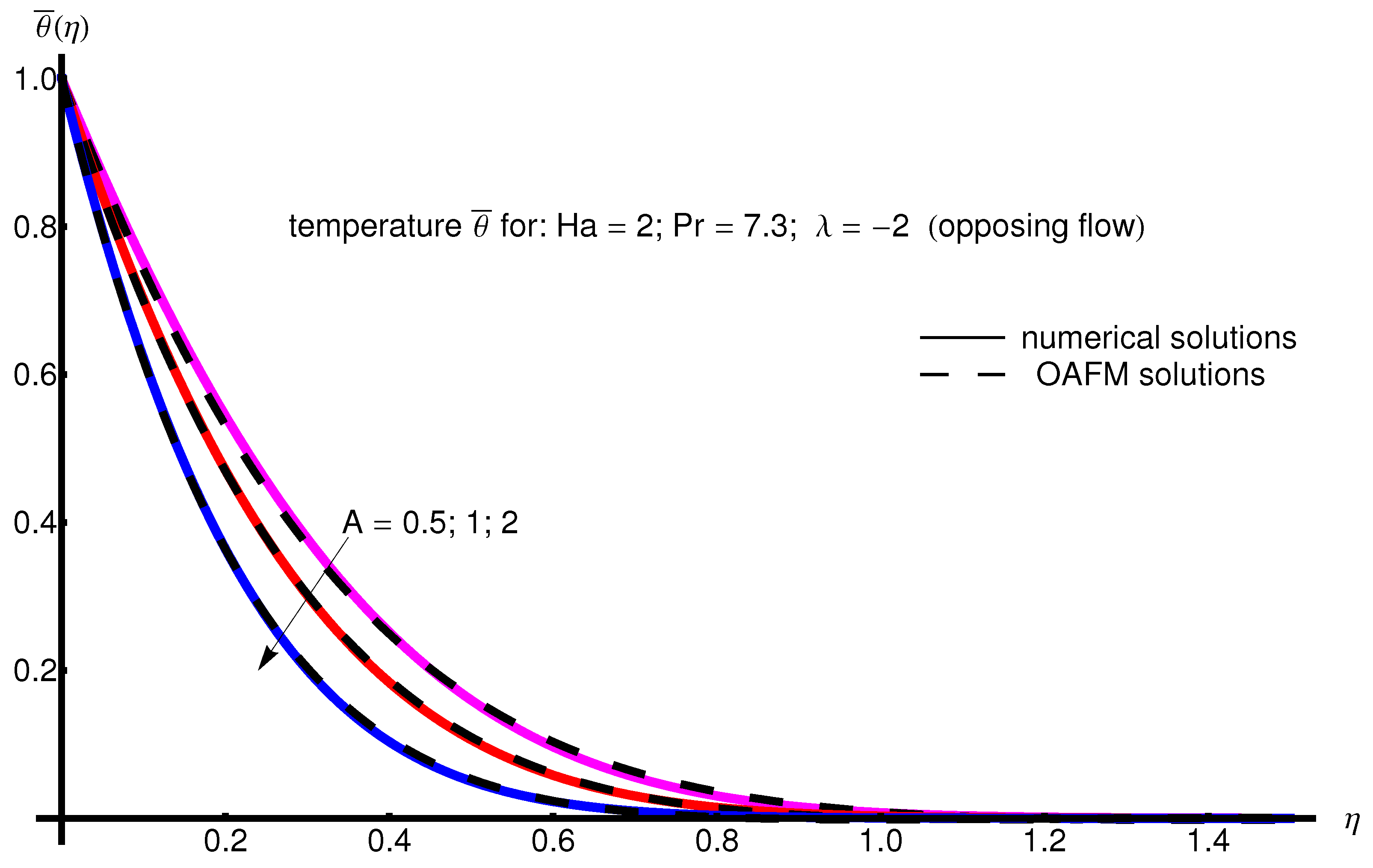
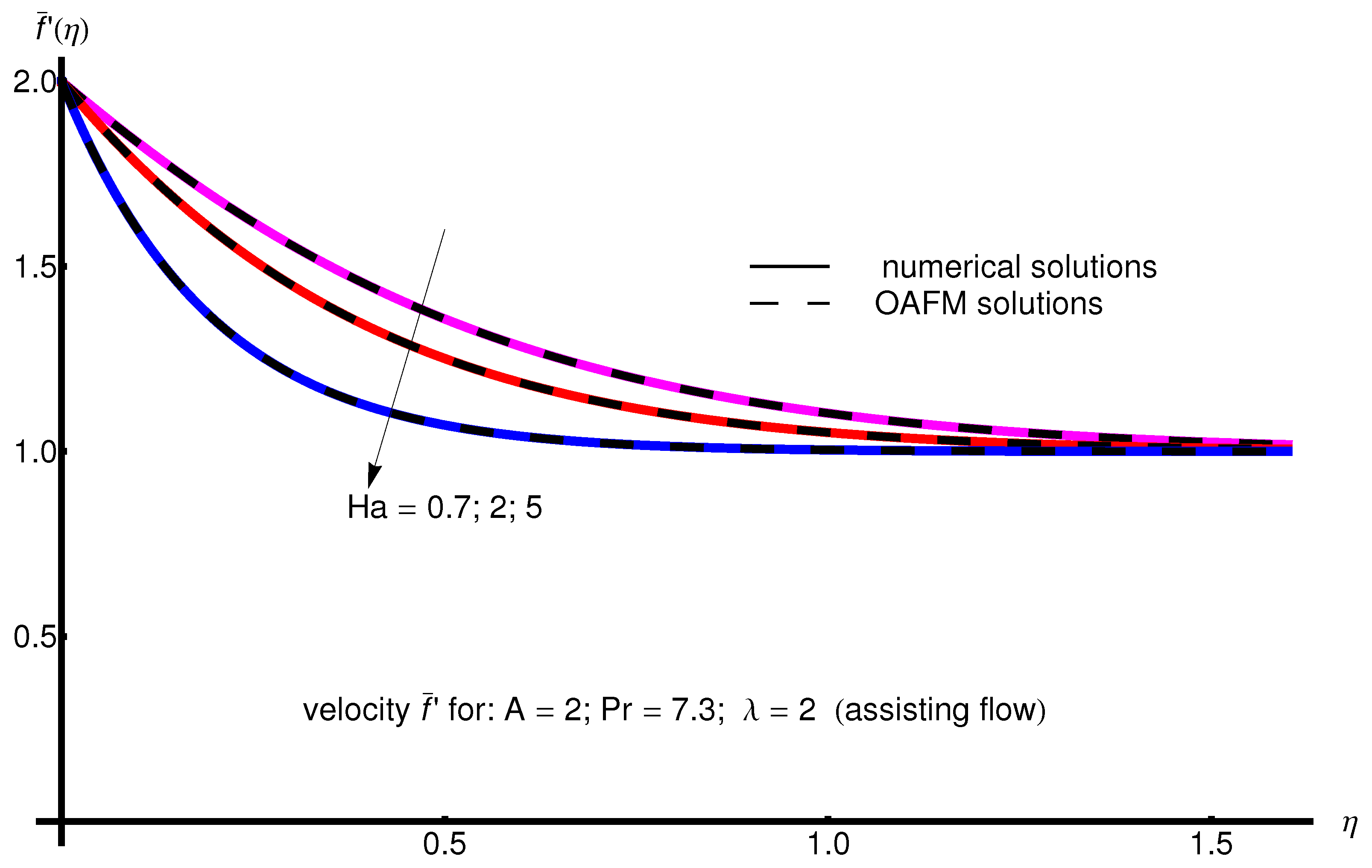
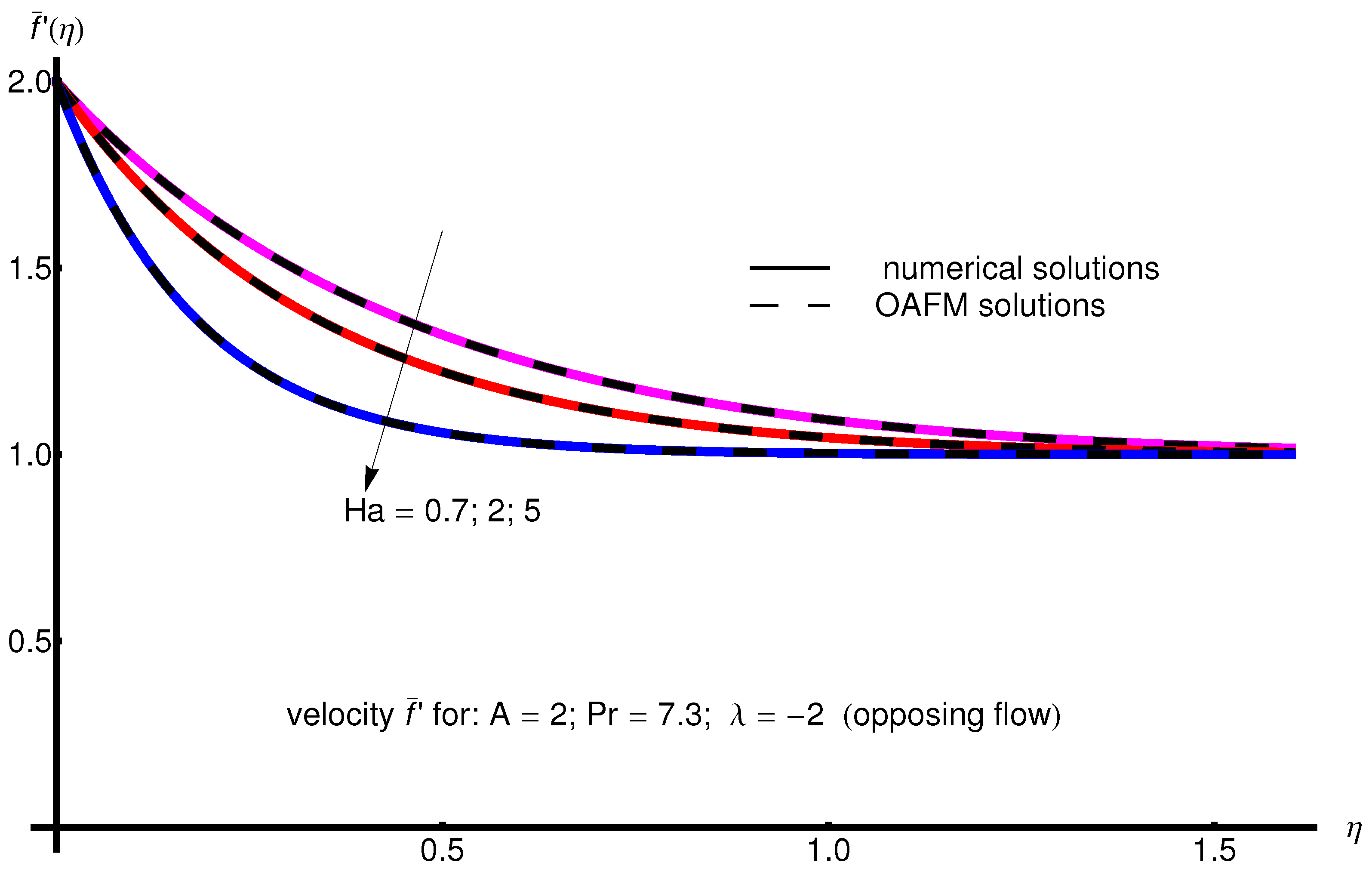
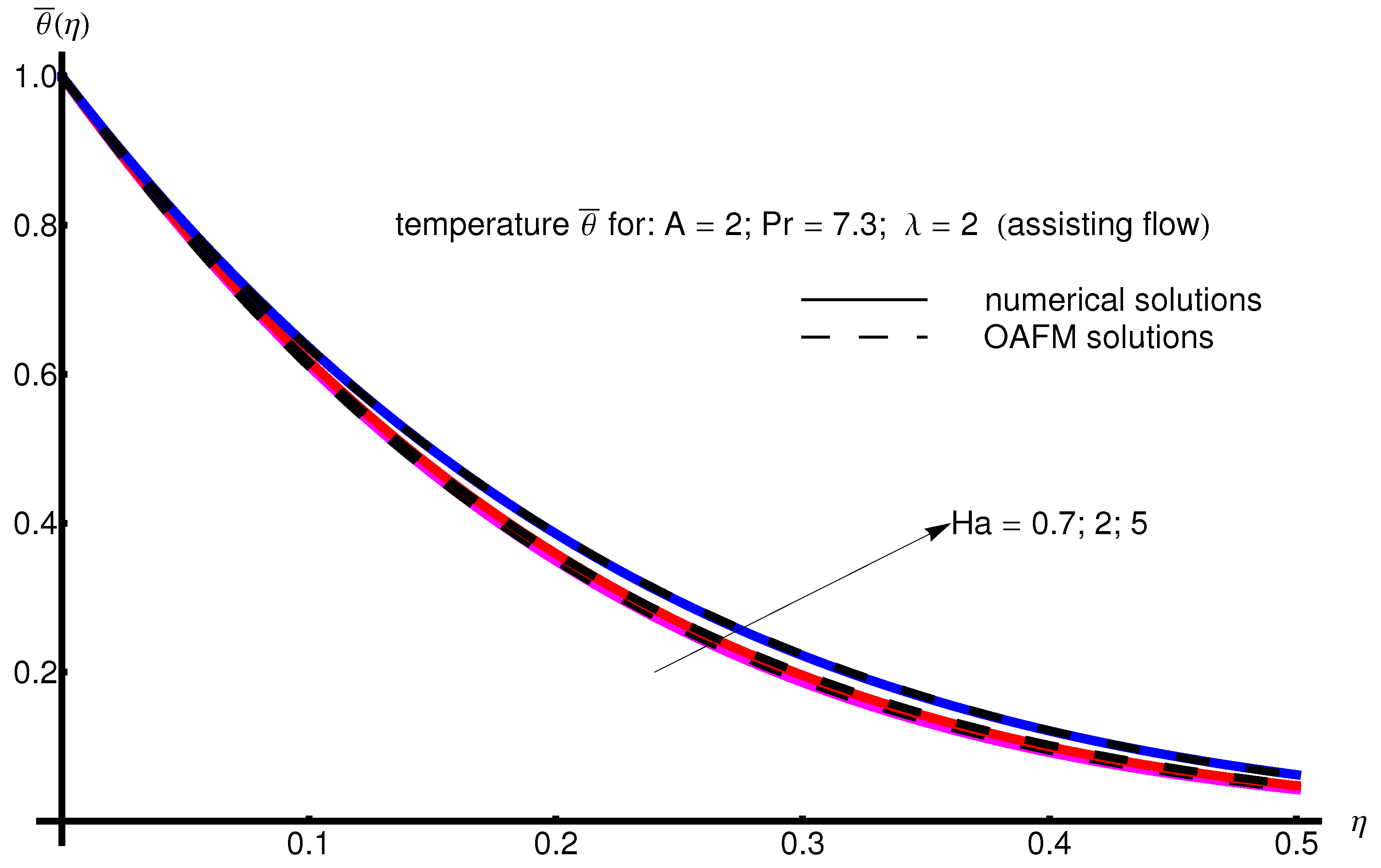
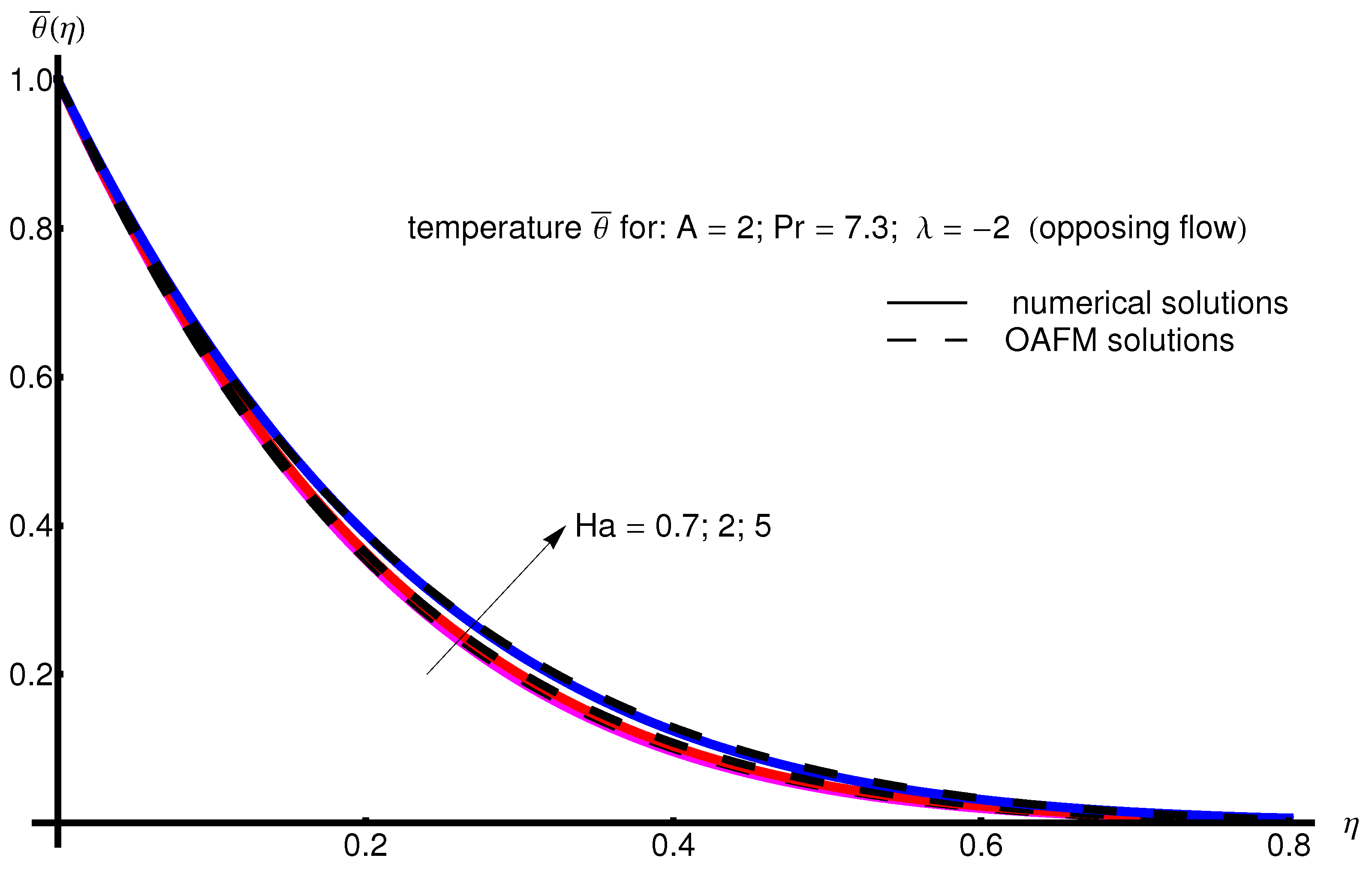
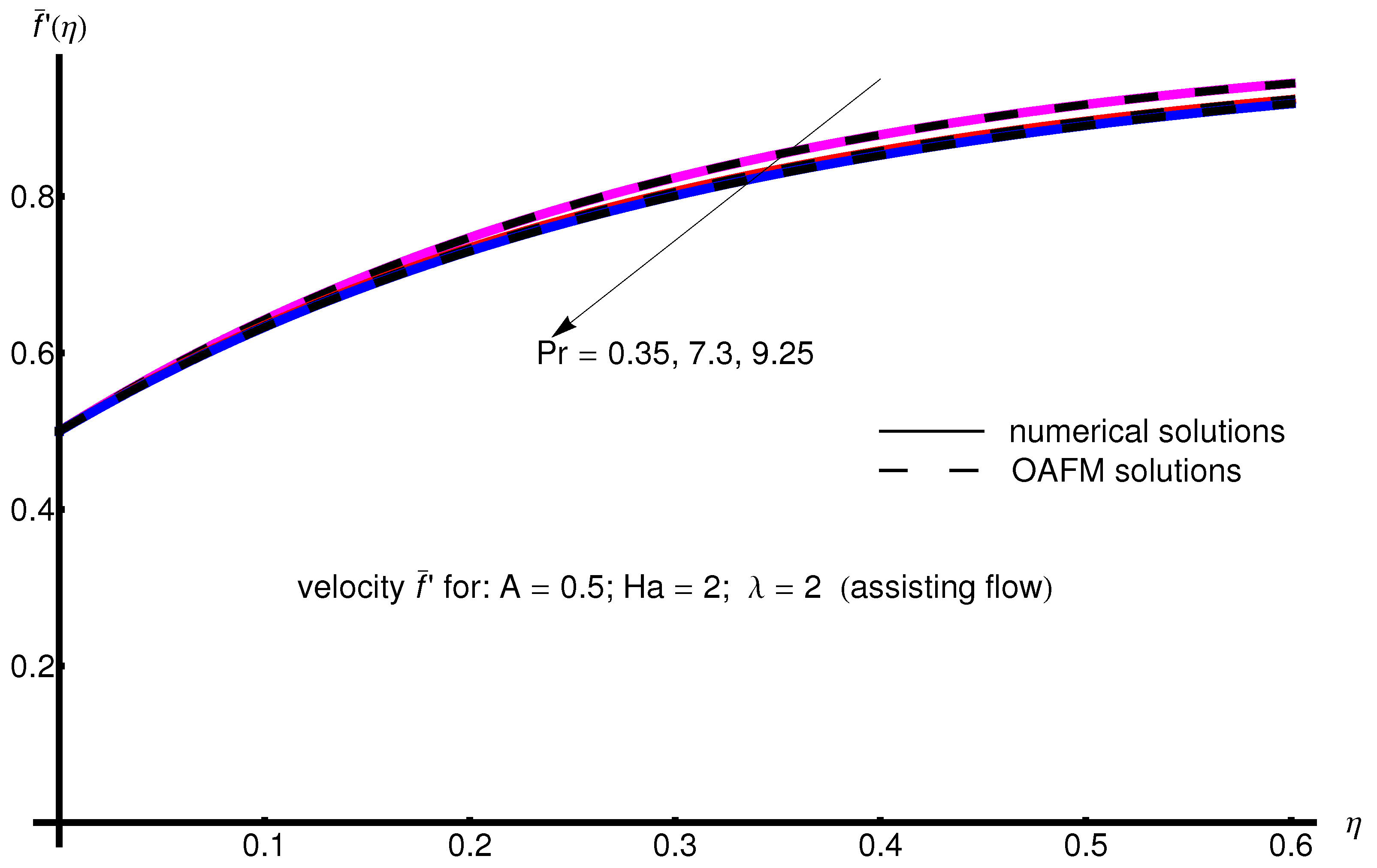
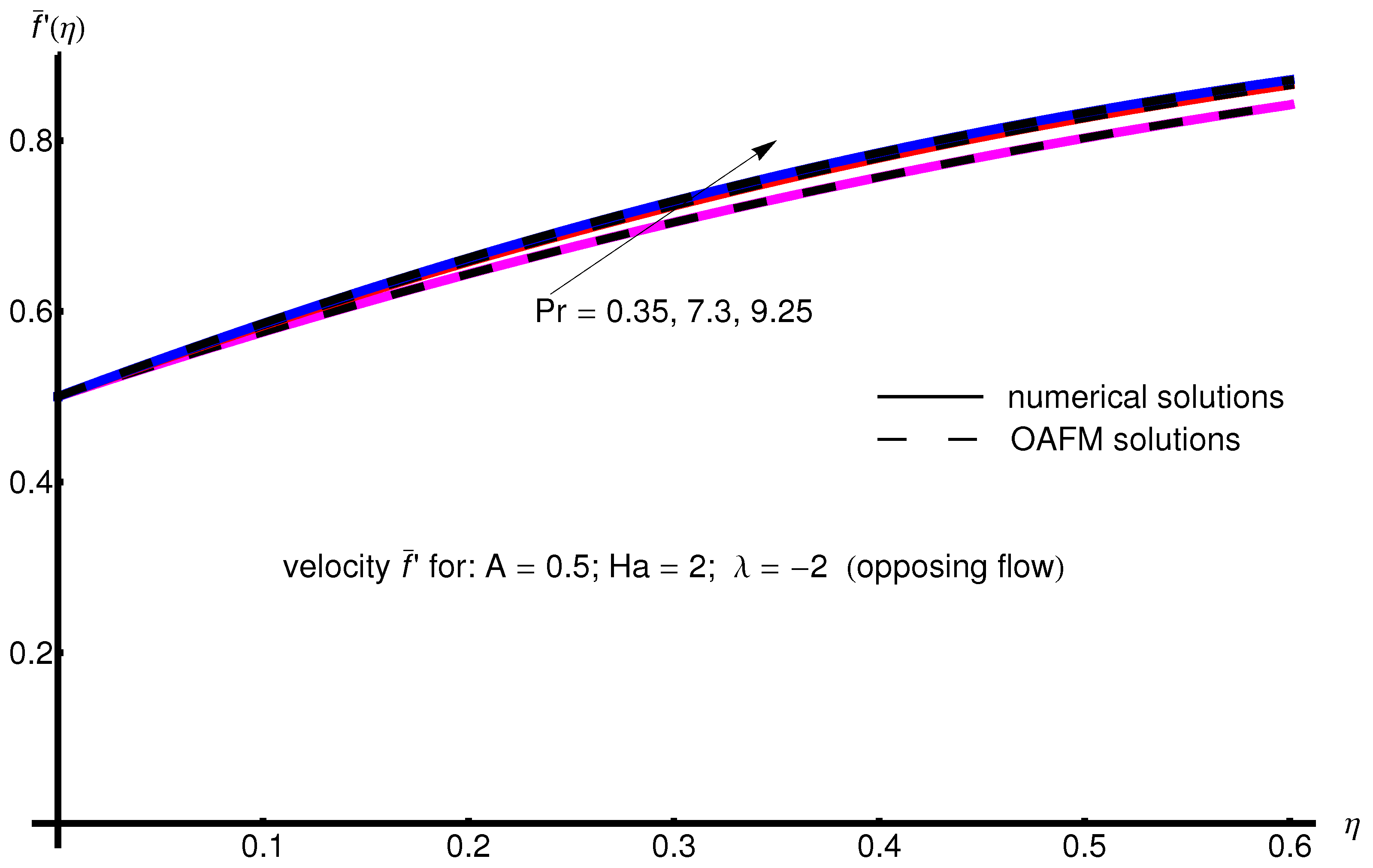
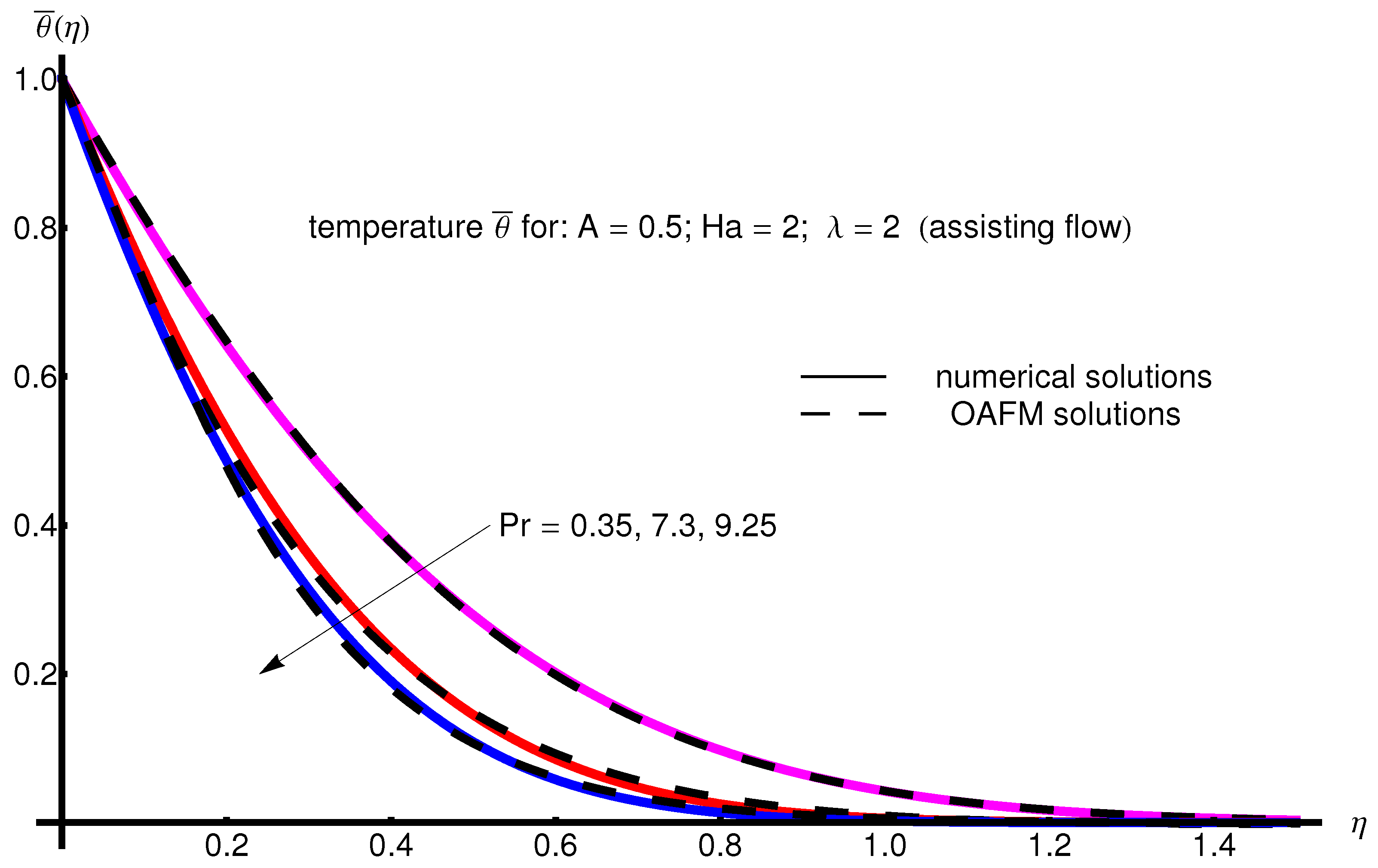
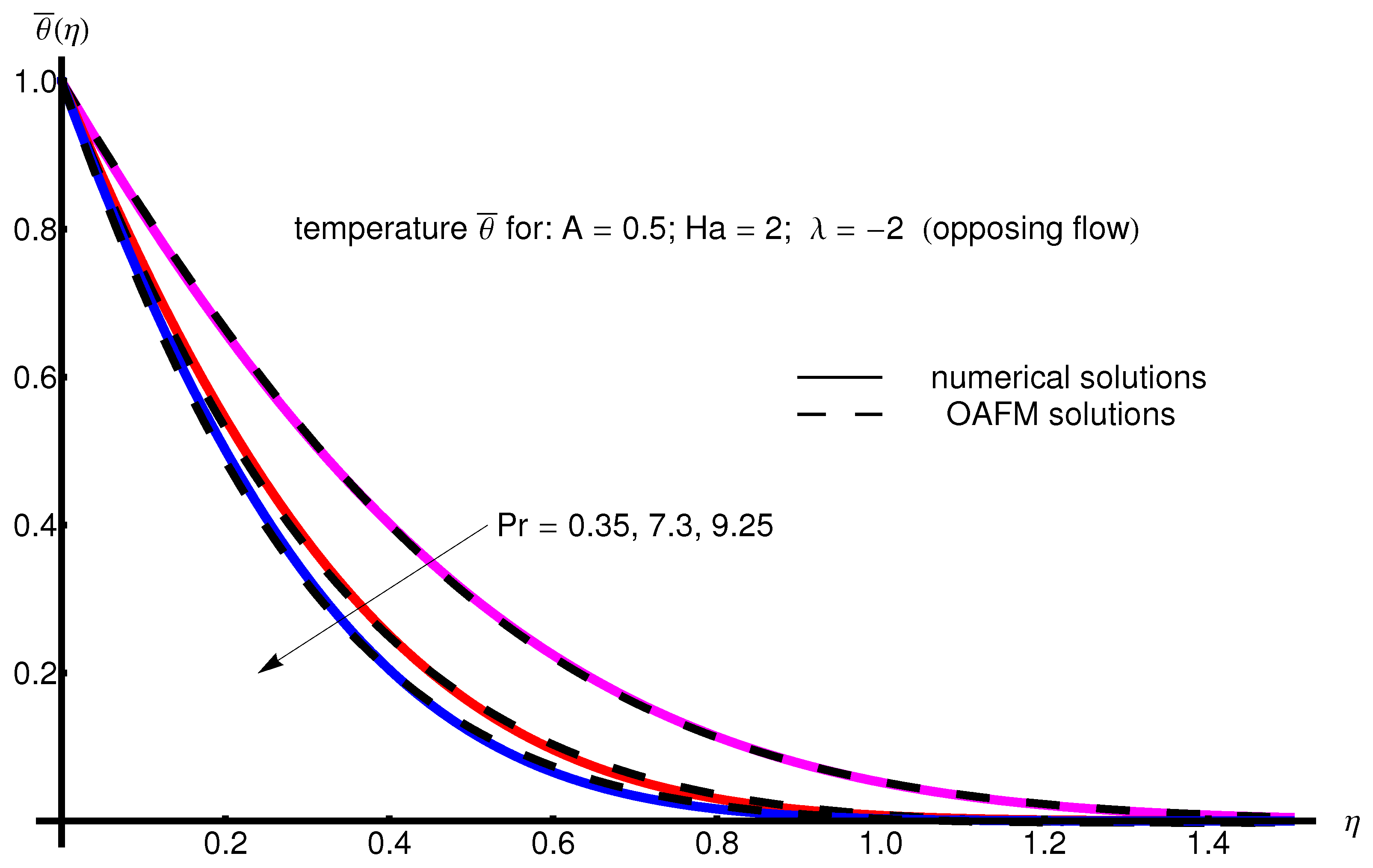
The profile of velocity obtained from Equation (34) by increasing the parameter A for , is depicted in Figure 1 for assisting flow () and in Figure 2 for opposing flow (). If the stretching velocity of the surface is greater than the velocity of the free stream, then the flow shows an inverted boundary layer structure for in the same manner as in [1]. The temperature profiles are displayed in Figure 3 (assisting flow) and Figure 4 (opposing flow) for same values of the physical parameters mentioned above. These figures show a fast decrease in the temperature profile with increasing parameter A. Dependence of the Hartmann number on the velocity profile is presented in Figure 5 (assisting flow), and Figure 6 (opposing flow). While the velocity profiles decrease with Hartmann number for and , the temperature profiles increase with this parameter for the same values A and , as observed in Figure 7 and Figure 8. The profile of velocity with increasing parameter for , decreases for assisting flow () and increases for opposing flow (), as illustrated in Figure 9 and Figure 10. The decrease in the temperature profiles with an increasing number for both flows is presented in Figure 11 and Figure 12 under the same conditions.
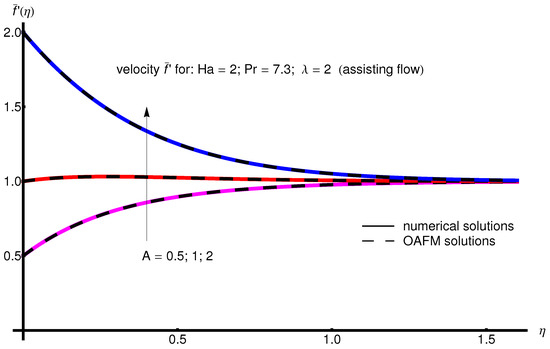
Figure 1.
Profile of velocity obtained from Equation (34) with increasing parameter A for , , and (assisting flow).
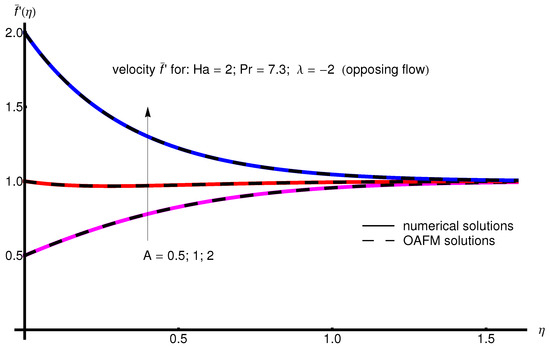
Figure 2.
Profile of velocity obtained from Equation (34) with increasing parameter A for , , and (opposing flow).
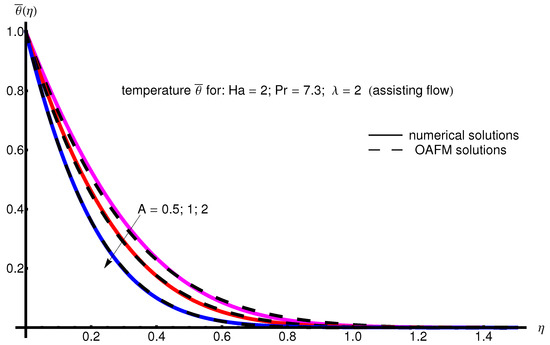
Figure 3.
Profile of temperature obtained from Equation (35) with increasing parameter A for , , and (assisting flow).
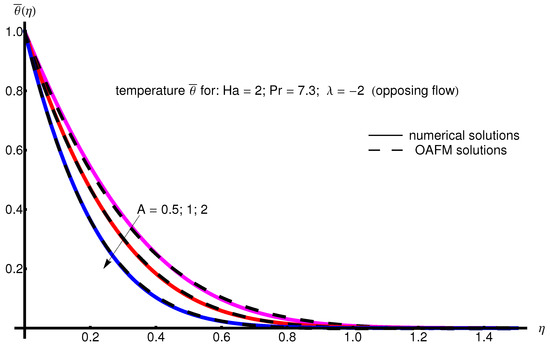
Figure 4.
Profile of temperature obtained from Equation (35) with increasing parameter A for , , and (opposing flow).

Figure 5.
Profile of velocity obtained from Equation (34) with increasing parameter for , , and (assisting flow).
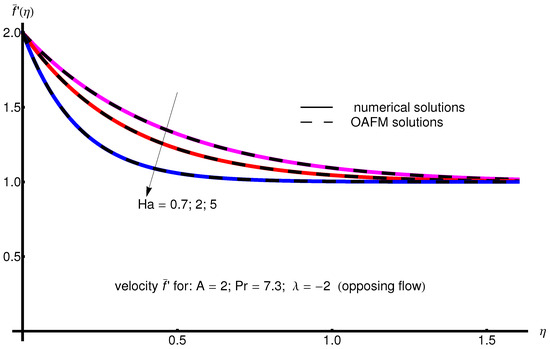
Figure 6.
Profile of velocity obtained from Equation (34) with increasing parameter for , , and (opposing flow).
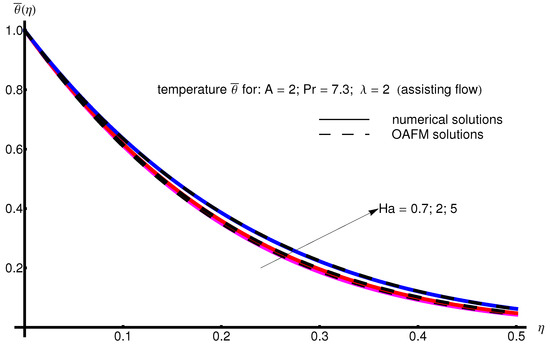
Figure 7.
Profile of temperature obtained from Equation (35) with increasing parameter for , , and (assisting flow).
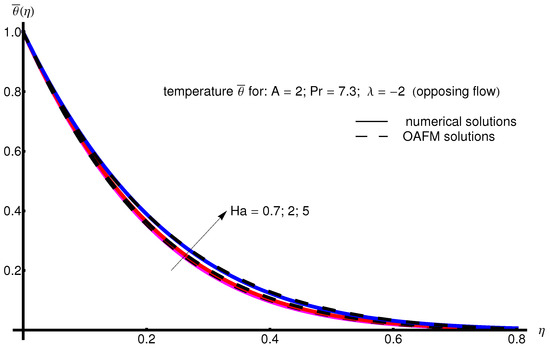
Figure 8.
Profile of temperature obtained from Equation (35) with increasing parameter for , , and (opposing flow).
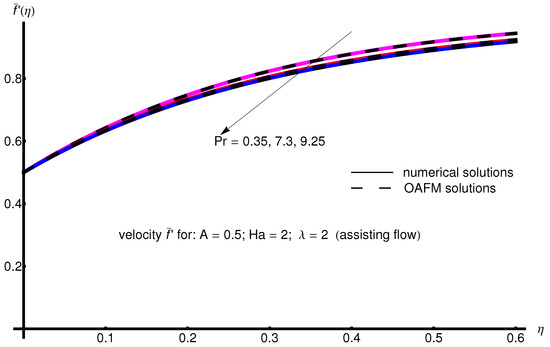
Figure 9.
Profile of velocity obtained from Equation (34) with increasing parameter for , , and (assisting flow).
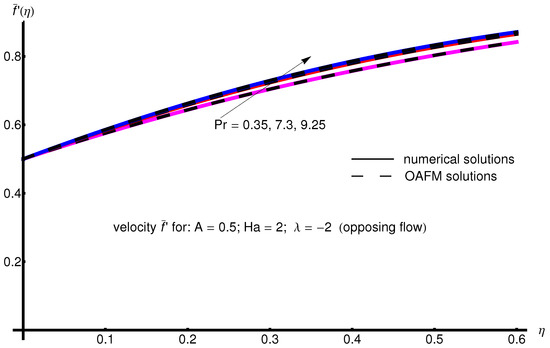
Figure 10.
Profile of velocity obtained from Equation (34) with increasing parameter for , , and (opposing flow).
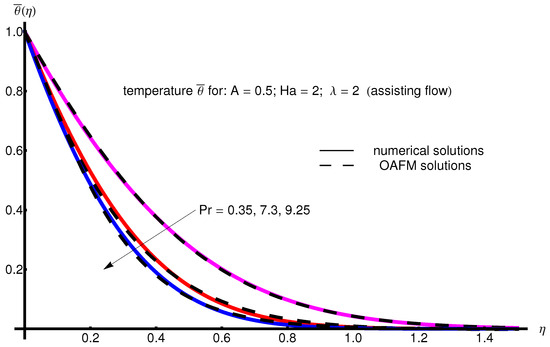
Figure 11.
Profile of temperature obtained from Equation (35) with increasing parameter for , , and (assisting flow).
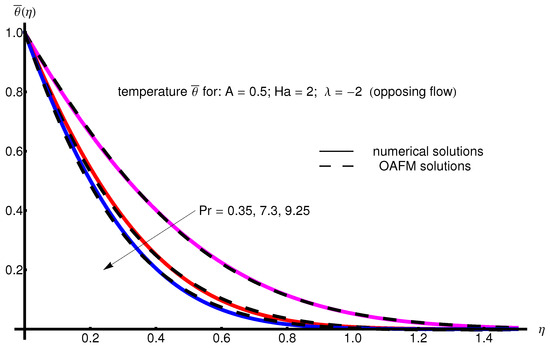
Figure 12.
Profile of temperature obtained from Equation (35) with increasing parameter for , , and (opposing flow).
The accuracy of these graphical solutions is quantitatively presented in Table 1 (for , (assisting flow), , and ), Table 2 (for , (opposing flow), , and ), and Table 3 (for , (opposing flow), , and ), together with the corresponding absolute differences for velocity function. The corresponding OAFM solutions are described in effective form in Appendix A and Appendix B, respectively.
Remark 3.
Dual solutions. If there are dual solutions, then the first solution is physically realizable (stable solution) [1], while the corresponding dual solution is unstable (not realizable physically). Appendix C presents the displacement function obtained from Equation (34) for physical constants , (opposing flow), , and : The first solution (stable solution).
Remark 4.
In the case of , Equation (8) depends on the unknown function , describing the mass transfer in fluid flow. It can be semi-analytically solved by means of the OAFM procedure for given values of physical parameters. Using this OAFM solution for function , Equation (9) can be solved following the same technique for temperature function .
A comparison between the OAFM results and corresponding iterative solutions, via the iterative method [40] after 7 iterations, is presented in Appendix D, for the initial conditions , , , , and and the physical constants , , , and .
4. Conclusions
The semi-analitycal solutions for the problem of MHD mixed convection stagnation-point flow of an incompressible viscous fluid in the presence of an externally magnetic field were built using the OAFM. A good agreement between the OAFM results and the corresponding numerical ones were highlighted in this work. The comparative analysis reflected the accuracy of the method; the obtained solutions approached the exact solution. The advantages of the OAFM procedure were highlighted by comparison with the iterative method.
The impact of various parameters, such as the velocity ratio parameter A, the Prandtl number , and the Hartmann number , on the behaviors of the velocity and temperature profiles for assisting flow () and opposing flow () were highlighted qualitatively in the figures and quantitatively in the tables.
MHD flow and heat transfer of viscous fluids on a continuously stretched surface also have engineering applications in geothermal energy extraction, metal purification from non-metallic enclosures, plasma studies, and aerodynamic extrusion of plastic sheets.
The applicability of the OAFM in these research directions, such as 3D flows, unsteady regimes, and inclusion of nanoparticle effects, using the present results, can be the subject of future work.
Author Contributions
Conceptualization, N.P.; data curation, R.-D.E. and N.P.; formal analysis, N.P.; investigation, R.-D.E. and R.B.; methodology, R.-D.E., R.B. and N.P.; software, R.-D.E. and R.B.; supervision, N.P.; validation, R.-D.E., R.B. and N.P.; visualization, R.-D.E., R.B. and N.P.; writing—original draft, R.-D.E., R.B. and N.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Assisting Flow
- Example 1. Displacement functions obtained from Equation (34) for different values of the velocity ratio parameter A in the case of (assisting flow), , an .
- Example 2. Displacement functions obtained from Equation (34) for different values of the Hartmann number in the case of (assisting flow), , and .
- Example 3. Displacement functions obtained from Equation (34) for different values of the Prandtl number in the case of (assisting flow), , and .
Appendix B. Opposing Flow
- Example 4. Displacement functions obtained from Equation (34) for different values of the velocity ratio parameter A in the case of (opposing flow), , and .
- Example 5. Displacement functions obtained from Equation (34) for different values of the Hartmann number in the case of (opposing flow), , and .
- Example 6. Displacement functions obtained from Equation (34) for different values of the Prandtl number in the case of (opposing flow), , and .
Appendix C. Dual Solutions
- Example 7. Displacement functions obtained from Equation (34) for physical parameters , (opposing flow), , and : The first solution and corresponding dual solution, respectively.
The first solution is stable (physically realizable [1]):
Appendix D. Comparison with the Iterative Method
The proposed iterative procedure was developed by Daftardar-Gejji et al. [40] for solving nonlinear functional equations. This technique is validated just for a special class of nonlinear functional equations with known exact solutions.
This system does not admit symmetries.
If the system (A16) is integrated over the interval , it results in the following:
The iterative procedure leads to
The iterative solutions, after seven iterations and considering the initial conditions , , , , and (presented in Table 1 and Table 2) and the physical constants , , , and , taking into account of algorithm (A18), become
Figure A1 and Figure A2 and in Table A1 respectively present a parallel between the OAFM solutions and and the corresponding iterative solutions and provided in Equation (A19) for the initial data and physical constants mentioned above. This comparative analysis highlights the efficiency, precision, and accuracy of the OAFM using only one iteration, not seven iterations as in the case of the iterative method.
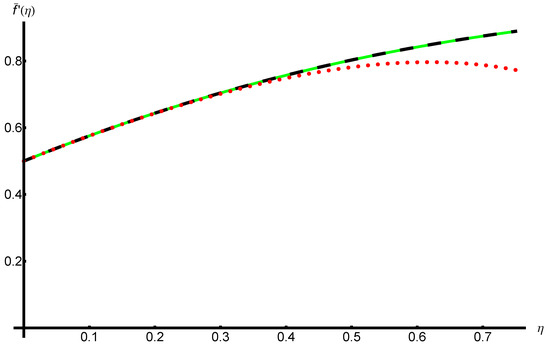
Figure A1.
Profile of the velocity of Equation (8) provided by Equation (A8), the iterative solution obtained from Equation (A19), and the corresponding numerical solution for , , , and : numerical solution (withgreen line), OAFM solution (dashed black line), and iterative solution (dotted red curve), respectively.
Figure A1.
Profile of the velocity of Equation (8) provided by Equation (A8), the iterative solution obtained from Equation (A19), and the corresponding numerical solution for , , , and : numerical solution (withgreen line), OAFM solution (dashed black line), and iterative solution (dotted red curve), respectively.
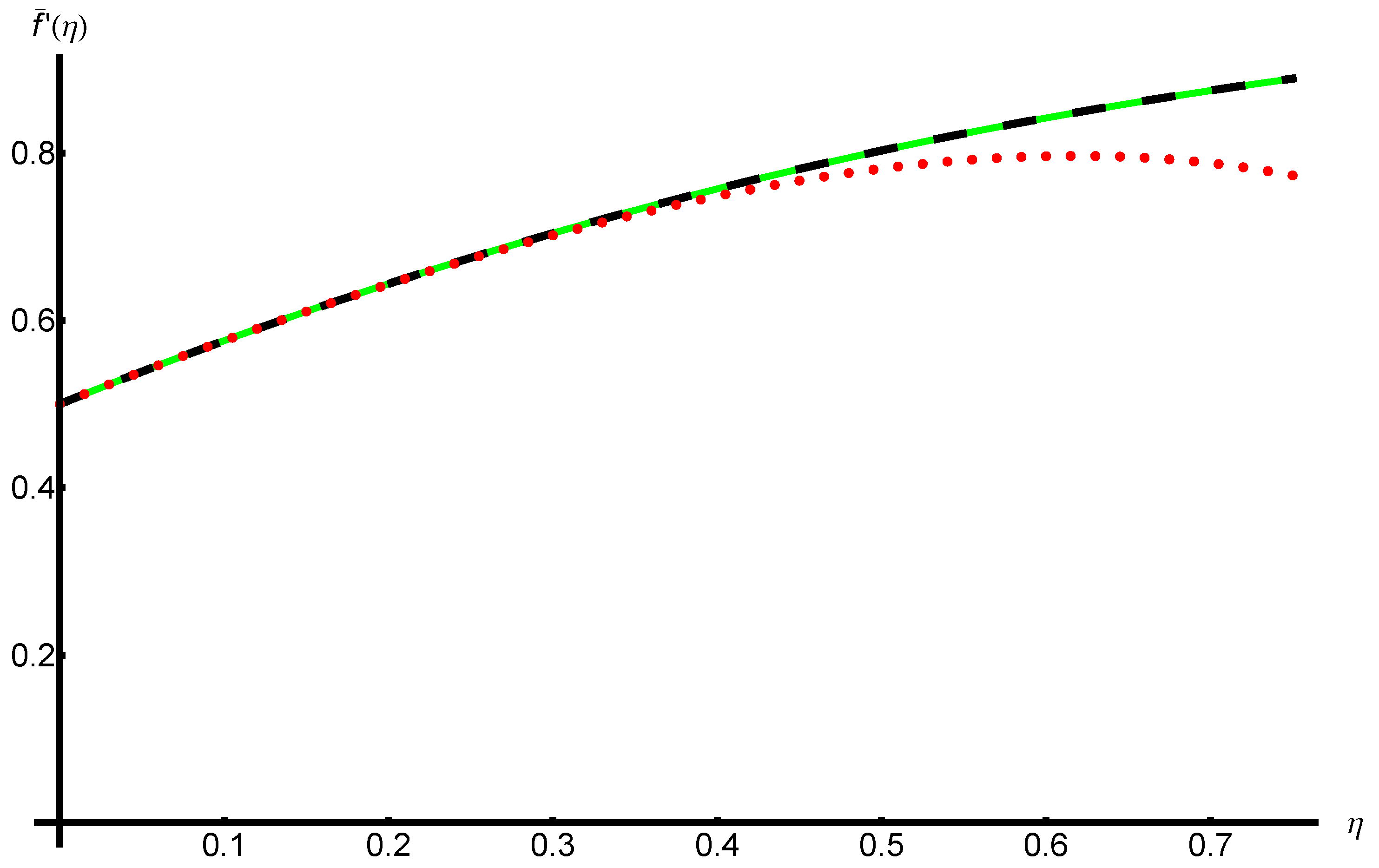
Figure A2.
Profile of the temperature of Equation (9) obtained from Equation (A8), the corresponding numerical solution, and the iterative solution provided by Equation (A19) for , , , and : numerical solution (green line), OAFM solution (dashed black line), and iterative solution (dotted red curve), respectively.
Figure A2.
Profile of the temperature of Equation (9) obtained from Equation (A8), the corresponding numerical solution, and the iterative solution provided by Equation (A19) for , , , and : numerical solution (green line), OAFM solution (dashed black line), and iterative solution (dotted red curve), respectively.
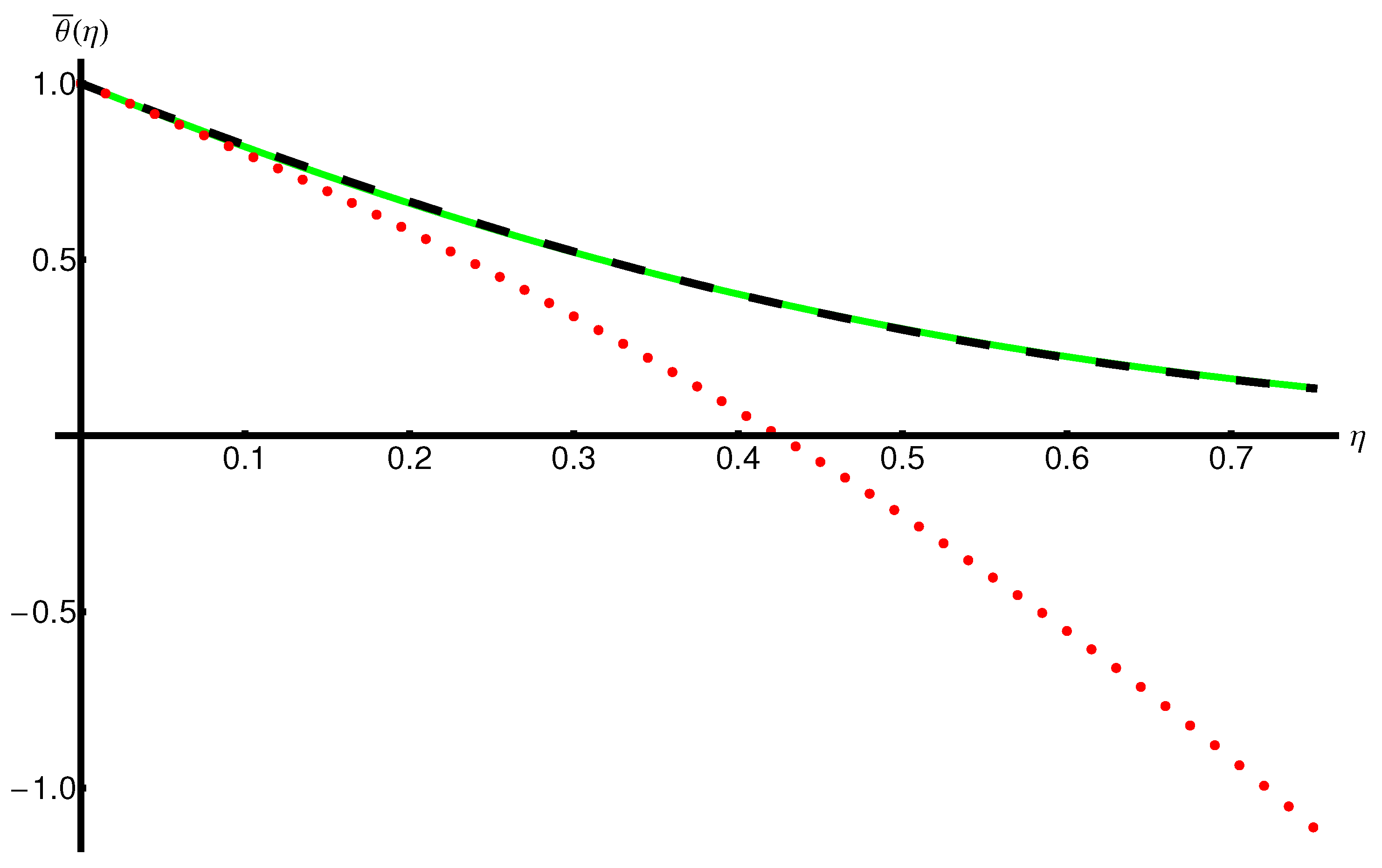

Table A1.
Comparison between the approximate analytical solution provided by Equation (A8), the iterative solution provided by Equation (A19), and the corresponding numerical solution.
| 0 | 0.5 | 0.5000000000000004 | 0.5 |
| 1/10 | 0.5756672164 | 0.5755589774 | 0.5756360967 |
| 1/5 | 0.6437024937 | 0.6435682607 | 0.6431918691 |
| 3/10 | 0.7041027770 | 0.7040298059 | 0.7014524785 |
| 2/5 | 0.7570149426 | 0.7570421789 | 0.7484293304 |
| 1/2 | 0.8027327943 | 0.8028453714 | 0.7812520446 |
| 3/5 | 0.8416816830 | 0.8418330275 | 0.7960406675 |
| 7/10 | 0.8743938092 | 0.8745327430 | 0.7877586448 |
| 4/5 | 0.9014776556 | 0.9015675201 | 0.7500482070 |
| 9/10 | 0.9235851162 | 0.9236113433 | 0.6750525517 |
| 1 | 0.9413796329 | 0.9413478685 | 0.5532342414 |
References
- Ali, F.M.; Nazar, R.; Arifin, N.M.; Pop, I. Mixed convection stagnation-point flow on vertical stretching sheet with external magnetic field. Appl. Math. Mech.-Engl. Ed. 2014, 35, 155–166. [Google Scholar] [CrossRef]
- Kumari, M.; Nath, G. Unsteady MHD mixed convection flow over an impulsively stretched permeable vertical surface in a quiescent fluid. Int. J. Non-Linear Mech. 2010, 45, 310–319. [Google Scholar] [CrossRef]
- Prasad, K.V.; Vajravelu, K.; Datti, P.S. Mixed convection heat transfer over a non-linear stretching surface with variable fluid properties. Int. J. Non-Linear Mech. 2010, 45, 320–330. [Google Scholar] [CrossRef]
- Ali, F.M.; Nazar, R.; Arifin, N.M.; Pop, I. MHD boundary layer flow and heat transfer over a stretching sheet with induced magnetic field. Heat Mass Transf. 2011, 47, 155–162. [Google Scholar] [CrossRef]
- Hiemenz, K. Die Grenzschicht an einem in den gleichformigen Flussigkeitsstrom eingetauchten geraden Kreiszylinder. Dingler’s Polytech. J. 1911, 326, 321–324. [Google Scholar]
- Eckert, E.R.G. Die Berechnung des Warmeubergangs in der laminaren Grenzschicht umstromter Korpe. VDI Forschungsheft. 1942, 416, 1–23. [Google Scholar]
- Ramachandran, N.; Chen, T.S.; Armaly, B.F. Mixed convection in stagnation flows adjacent to vertical surfaces. J. Heat Transf. 1988, 110, 373–377. [Google Scholar] [CrossRef]
- Andersson, H.I. MHD flow of a viscoelastic fluid past a stretching surface. Acta Mech. 1922, 95, 227–230. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Magnetohydrodynamic (MHD) flow of a micropolar fluid towards a stagnation point on a vertical surface. Comput. Math. Appl. 2008, 56, 3188–3194. [Google Scholar] [CrossRef]
- Gupta, A.S.; Pal, A.; Pal, B.; Takhar, H.S. Hall effects on MHD flow and heat transfer over a stretching surface. Int. J. Appl. Mech. Eng. 2003, 8, 219–232. [Google Scholar]
- Abel, S.; Prasad, K.V.; Mahaboob, A. Buoyancy force and thermal radiation effects in MHD boundary layer visco-elastic fluid flow over continuously moving stretching surface. Int. J. Ther. Sci. 2005, 44, 465–476. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Hydromagnetic flow and heat transfer adjacent to a stretching vertical sheet. Heat Mass Transf. 2008, 44, 921–927. [Google Scholar] [CrossRef]
- Sharma, P.R.; Sinha, S.; Yadav, R.S.; Filippov, A.N. MHD mixed convective stagnation point flow along a vertical stretching sheet with heat source/sink. Int. J. Heat Mass Transf. 2018, 117, 780–786. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD mixed convection stagnation point flow of a hybrid nanofluid past a vertical flat plate with convective boundary condition. Chin. J. Phys. 2020, 66, 630–644. [Google Scholar] [CrossRef]
- Ibrahim, W.; Makinde, O.D. The effect of double stratification on boundary-layer flow and heat transfer of nanofluid over a vertical plate. Comput. Fluids 2013, 86, 433–441. [Google Scholar] [CrossRef]
- Kandasamy, R.; Dharmalingam, R.; Prabhu, K.K. Thermal and solutal stratification on MHD nanofluid flow over a porous vertical plate. Alex. Eng. J. 2018, 57, 121–130. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Hafidzuddin, E.H.; Wahi, N. Dual stratified nanofluid flow past a permeable shrinking/stretching sheetusing a non-Fourier energy model. Appl. Sci. 2019, 9, 2124. [Google Scholar] [CrossRef]
- Abdal, S.; Ali, B.; Younas, S.; Ali, L.; Mariam, A. Thermo-Diffusion and Multislip Effects on MHD Mixed Convection Unsteady Flow of Micropolar Nanofluid over a Shrinking/Stretching Sheet with Radiation in the Presence of Heat Source. Symmetry 2020, 12, 49. [Google Scholar] [CrossRef]
- Murtaza, S.; Kumam, P.; Ahmad, Z.; Sitthithakerngkiet, K.; Sutthibutpong, T. Fractional Model of Brinkman-Type Nanofluid Flow with Fractional Order Fourier’s and Fick’s Laws. Fractals 2023, 31, 2340199. [Google Scholar] [CrossRef]
- Choudhary, P.; Loganathan, K.; Jat, K.; Arunachalam, K.P.; Eswaramoorthi, S. Thermal and velocity slip impacts on MHD tetra-hybrid nanofluids flow over a porous stretching surface. Discov. Appl. Sci. 2025, 7, 720. [Google Scholar] [CrossRef]
- Ajithkumar, M.; Lakshminarayana, P.; Vajravelu, K. Diffusion effects on mixed convective peristaltic flow of a bi-viscous Bingham nanofluid through a flexible porous channel with convective boundary conditions. Phys. Fluids 2023, 35, 032008. [Google Scholar] [CrossRef]
- Nisar, Z.; Ahmed, B.; Ghoneim, M.E.; Elkotb, M.A. Thermal performance of mixed convective radiative peristaltic flow of Bingham nanofluid. Sens. Actuators A Phys. 2024, 373, 115399. [Google Scholar] [CrossRef]
- Akbar, Y.; Huang, S.; Magesh, A.; Ji, J.; Alam, M.M. Thermal analysis of mixed convective peristaltic pumping of nanofluids in the occurrence of an induced magnetic field and variable viscosity. J. Taibah Univ. Sci. 2024, 18, 2319890. [Google Scholar] [CrossRef]
- Jagadesh, V.; Sreenadh, S.; Ajithkumar, M.; Lakshminarayana, P.; Sucharitha, G. Numerical exploration of the peristaltic flow of MHD Jeffrey nanofluid through a non-uniform porous channel with Arrhenius activation energy. Numer. Heat Transf. Part A Appl. 2024, 86, 5542–5556. [Google Scholar] [CrossRef]
- Neelav, S.; Ashish, P.; Bhagyashri, P. Computational study of Jeffrey Hybrid nanofluid flow over on a non-uniformly heated permeable exponentially stretching surface with Arrhenius activation energy and inclined magnetic field. Hybrid Adv. 2024, 6, 100194. [Google Scholar] [CrossRef]
- Ajithkumar, M.; Lakshminarayana, P.; Sucharitha, G.; Vajravelu, K. Investigation of convective peristaltic flow of non-Newtonian fluids through a non-uniform tapered porous conduit with Ohmic heating and viscous dissipation. Int. Model. Simul. 2024, 1–14. [Google Scholar] [CrossRef]
- Sahar, A.; Ghulam, R.; Muhammad, A.; Uzma, A.; Tao, S. Impact of Viscous Dissipation and Ohmic Heating on Natural Convection Heat Transfer in Thermo-Magneto Generated Plume. Front. Heat Mass Transf. 2024, 22, 1323–1341. [Google Scholar] [CrossRef]
- Ajithkumar, M.; Lakshminarayana, P.; Sucharitha, G.; Sreenadh, S.; Jagadesh, V. Investigation of dissipative heat transfer and peristaltic pumping on MHD Casson fluid flow in an inclined channel filled with porous medium. Numer. Heat Transf. Fundam. 2023, 85, 1654–1672. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Rashidi, M.M. Magnetohydrodynamics (MHD) stagnation point flow past a shrinking/stretching surface with double stratification effect in a porous medium. J. Therm. Anal. Calorim. 2020, 139, 3635–3648. [Google Scholar] [CrossRef]
- Alarifi, I.M.; Abokhalil, A.G.; Osman, M.; Lund, L.A.; Ayed, M.B.; Belmabrouk, H.; Tlili, I. MHD Flow and Heat Transfer over Vertical Stretching Sheet with Heat Sink or Source Effect. Symmetry 2019, 11, 297. [Google Scholar] [CrossRef]
- Ene, R.-D.; Pop, N.; Badarau, R. Heat and Mass Transfer Analysis for the Viscous Fluid Flow: Dual Approximate Solutions. Mathematics 2023, 11, 1648. [Google Scholar] [CrossRef]
- Ene, R.-D.; Pop, N.; Badarau, R. Partial Slip Effects for Thermally Radiative Convective Nanofluid Flow. Mathematics 2023, 11, 2199. [Google Scholar] [CrossRef]
- Farooq, M.; Rahman, A.U.; Khan, A.; Ozsahin, I.; Uzun, B.; Ahmad, H. Comparative analysis of magnetohydrodynamic inclined Poiseulle flow of couple stress fluids. J. Comput. Appl. Mech. 2025, 56, 536–560. [Google Scholar]
- Zada, L.; Nawaz, R.; Nisar, K.S.; Tahir, M.; Yavuz, M.; Kaabar, M.K.A.; Martínez, F. New approximate-analytical solutions to partial differential equations via auxiliary function method. Partial Differ. Equ. Appl. Math. 2021, 4, 100045. [Google Scholar] [CrossRef]
- Khan, I.; Ullah, H.; Fiza, M.; Islam, S.; Kuman, P.; Sitthithakerngkiet, P. Falkner-Skan equation with Heat Transfer: A new Optimal approach. Authorea 2024. [Google Scholar] [CrossRef]
- Ene, R.-D.; Pop, N.; Badarau, R. Symmetries and Closed-Form Solutions for Some Classes of Dynamical Systems. Symmetry 2025, 17, 546. [Google Scholar] [CrossRef]
- Sutton, G.W.; Sherman, A. Engineering Magnetohydrodynamics; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Marinca, V.; Herisanu, N. Approximate analytical solutions to Jerk equation. In Springer Proceedings in Mathematics & Statistics: Proceedings of the Dynamical Systems: Theoretical and Experimental Analysis, Lodz, Poland, 7–10 December 2015; Springer: Cham, Switzerland, 2016; Volume 182, pp. 169–176. [Google Scholar]
- Ene, R.-D.; Pop, N.; Lapadat, M.; Dungan, L. Approximate closed-form solutions for the Maxwell-Bloch equations via the Optimal Homotopy Asymptotic Method. Mathematics 2022, 10, 4118. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).