Numerical Treatment of the Time Fractional Diffusion Wave Problem Using Chebyshev Polynomials
Abstract
1. Introduction
- Proposing new basis functions in terms of to treat this type of FDE.
- Developing some new theoretical results of , such as their definite integral formulas.
- Designing a new PGA for treating the based on the theoretical background of these polynomials.
2. Some Fundamentals
2.1. Caputo Fractional Derivative
2.2. An Overview of
3. Treatment for the with Homogeneous Conditions
3.1. Basis Functions
3.2. for the with Homogeneous Conditions
- Assume that
3.3. Transformation to the
4. Error Bound
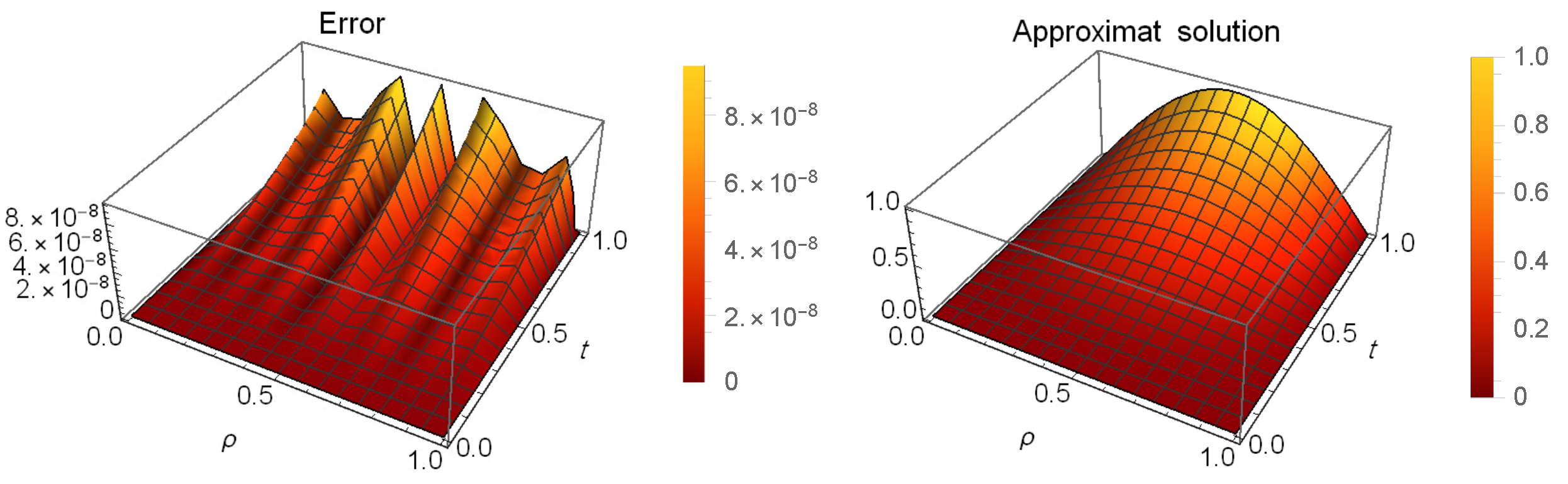
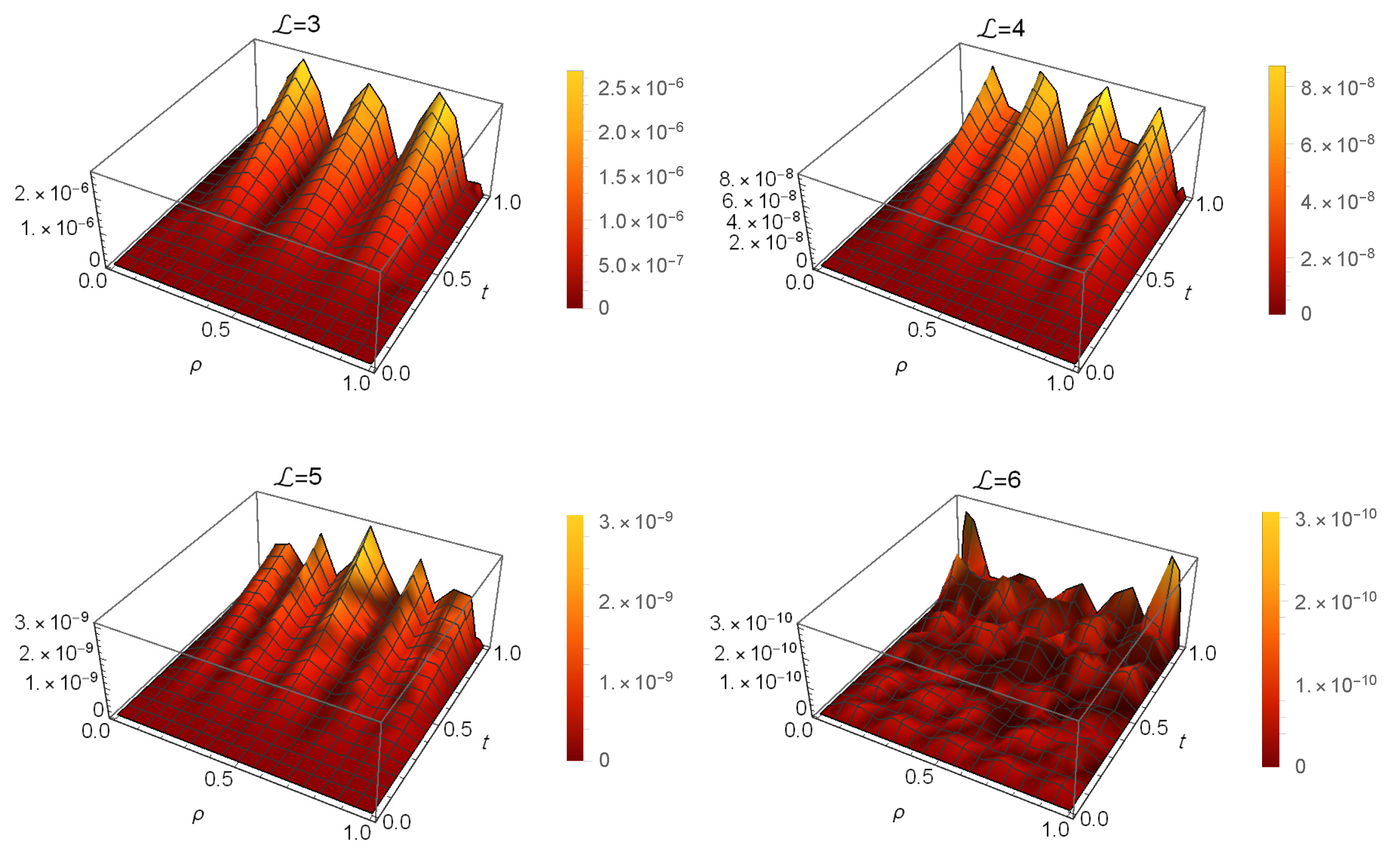
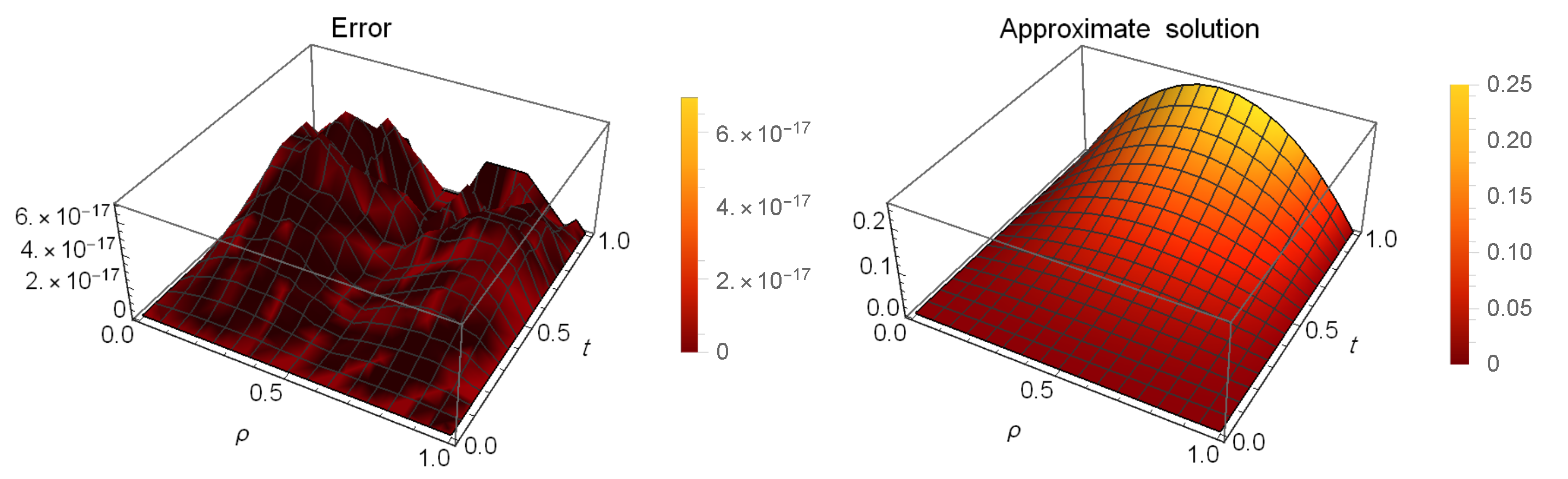
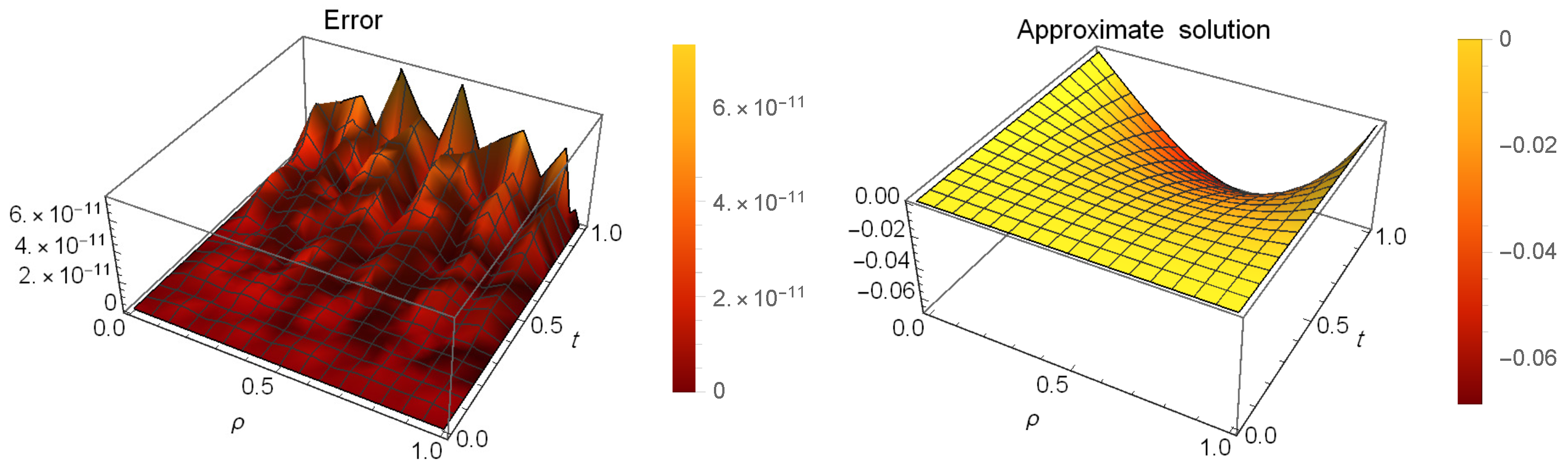
5. Examples
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ordokhani, Y.; Sabermahani, S.; Rahimkhani, P. Application of Chelyshkov Wavelets and Least Squares Support Vector Regression to Solve Fractional Differential Equations Arising in Optics and Engineering. Math. Methods Appl. Sci. 2025, 48, 1996–2010. [Google Scholar] [CrossRef]
- Dehestani, H. Performance of Ritz-Piecewise Gegenbauer Approach for Two Types of Fractional Pantograph Equations Including Piecewise Fractional Derivative. Math. Methods Appl. Sci. 2025, 48, 6889–6903. [Google Scholar] [CrossRef]
- Jassim, H.; Hussein, G. Analytical Solutions to Fractional Differential Equations: A Comparative Study with the Natural Homotopy Perturbation Method. In Proceedings of the 3rd International Conference on Mathematics, AI, Information and Communication Technologies (ICMAICT 2023), Erbil, Iraq, 27–28 April 2025; AIP Conference Proceedings. AIP Publishing: Melville, NY, USA, 2025; Volume 3264, p. 050048. [Google Scholar]
- Sayed, S.; Mohamed, A.; Abo El-Dahab, E.; Youssri, Y. Alleviated Shifted Gegenbauer Spectral Method for Ordinary and Fractional Differential Equations. Contemp. Math. 2024, 1344–1370. [Google Scholar] [CrossRef]
- Ramadan, M.; Mansour, M.; El-Shazly, N.; Osheba, H. The Double Ramadan Group Accelerated Adomian Decomposition Method for Solving Nonlinear Partial Differential Equations. Comput. Methods Differ. Equ. 2025. [Google Scholar] [CrossRef]
- Vargas, A. Finite Difference Method for Solving Fractional Differential Equations at Irregular Meshes. Math. Comput. Simul. 2022, 193, 204–216. [Google Scholar] [CrossRef]
- Nedaiasl, K.; Dehbozorgi, R. Galerkin Finite Element Method for Nonlinear Fractional Differential Equations. Numer. Algorithms 2021, 88, 113–141. [Google Scholar] [CrossRef]
- Maayaha, B.; Bushnaq, S.; Moussaoui, A. Numerical solution of fractional order SIR model of dengue fever disease via Laplace optimized decomposition method. J. Math. Comput. Sci. 2024, 32, 86–93. [Google Scholar] [CrossRef]
- Samy, H.; Adel, W.; Hanafy, I.; Ramadan, M. A Petrov–Galerkin approach for the numerical analysis of soliton and multi-soliton solutions of the Kudryashov–Sinelshchikov equation. Iran. J. Numer. Anal. Optim. 2024, 14, 1309–1334. [Google Scholar]
- Yassin, N.; Atta, A.; Aly, E. Numerical Solutions for Nonlinear Ordinary and Fractional Newell–Whitehead–Segel Equation Using Shifted Schröder Polynomials. Bound. Value Probl. 2025, 2025, 57. [Google Scholar] [CrossRef]
- Atta, A. Approximate Petrov–Galerkin Solution for the Time Fractional Diffusion Wave Equation. Math. Methods Appl. Sci. 2025, 48, 11670–11685. [Google Scholar] [CrossRef]
- Hafez, R.; Ahmed, H.; Alqubori, O.; Amin, A.; Abd-Elhameed, W. Efficient Spectral Galerkin and Collocation Approaches Using Telephone Polynomials for Solving Some Models of Differential Equations with Convergence Analysis. Mathematics 2025, 13, 918. [Google Scholar] [CrossRef]
- Taema, M.; Dagher, M.; Youssri, Y. Spectral Collocation Method via Fermat Polynomials for Fredholm–Volterra Integral Equations with Singular Kernels and Fractional Differential Equations. J. Math. 2025, 14, 481–492. [Google Scholar]
- Salamaa, M.H.; Zedan, H.A.; Abd-Elhameed, W.M.; Youssri, Y.H. Galerkin Method with Modified Shifted Lucas Polynomials for Solving the 2D Poisson Equation. J. Comput. Appl. Mech. 2025, 56, 737–775. [Google Scholar]
- Abdelhakem, M.; Abdelhamied, D.; El-Kady, M.; Youssri, Y. Two Modified Shifted Chebyshev–Galerkin Operational Matrix Methods for Even-Order Partial Boundary Value Problems. Bound. Value Probl. 2025, 2025, 34. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Alkhamisi, S.O.; Amin, A.K.; Youssri, Y.H. Numerical contrivance for Kawahara-type differential equations based on fifth-kind Chebyshev polynomials. Symmetry 2023, 15, 138. [Google Scholar] [CrossRef]
- Yağmurlu, N.M.; Karakaş, A.S. A novel perspective for simulations of the MEW equation by trigonometric cubic B-spline collocation method based on Rubin-Graves type linearization. Comput. Methods Differ. Equ. 2022, 10, 1046–1058. [Google Scholar]
- Kutluay, S.; Yağmurlu, N.M.; Karakaş, A.S. A novel perspective for simulations of the Modified Equal-Width Wave equation by cubic Hermite B-spline collocation method. Wave Motion 2024, 129, 103342. [Google Scholar] [CrossRef]
- Kutluay, S.; Yağmurlu, N.M.; Karakaş, A.S. A robust septic Hermite collocation technique for Dirichlet boundary condition heat conduction equation. Int. J. Math. Comput. Eng. 2025, 3, 253–266. [Google Scholar] [CrossRef]
- Luo, M.; Qiu, W.; Nikan, O.; Avazzadeh, Z. Second-order accurate, robust and efficient ADI Galerkin technique for the three-dimensional nonlocal heat model arising in viscoelasticity. Appl. Math. Comput. 2023, 440, 127655. [Google Scholar] [CrossRef]
- Gottlieb, D.; Orszag, S. Numerical Analysis of Spectral Methods: Theory and Applications; SIAM: Philadelphia, PA, USA, 1977. [Google Scholar]
- Brezinski, C. Padé-Type Approximation and General Orthogonal Polynomials; Springer: Berlin/Heidelberg, Germany, 1980; Volume 50. [Google Scholar]
- Funaro, D. Polynomial Approximation of Differential Equations; Springer: Berlin/Heidelberg, Germany, 2008; Volume 8. [Google Scholar]
- Gautschi, W. Orthogonal Polynomials: Computation and Approximation; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Gamal, M.; Zaky, M.; El-Kady, M.; Abdelhakem, M. Chebyshev Polynomial Derivative-Based Spectral Tau Approach for Solving High-Order Differential Equations. Comput. Appl. Math. 2024, 43, 412. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.; Youssri, Y. New Formulas of the High-Order Derivatives of Fifth-Kind Chebyshev Polynomials: Spectral Solution of the Convection–Diffusion Equation. Numer. Methods Partial Differ. Equ. 2024, 40, e22756. [Google Scholar] [CrossRef]
- Sadiq, S.; ur Rehman, M. Numerical Technique Based on Generalized Laguerre and Shifted Chebyshev Polynomials. J. Appl. Anal. Comput. 2024, 14, 1977–2001. [Google Scholar] [CrossRef]
- Brahim, M.S.T.; Youssri, Y.H.; Alburaikan, A.; Khalifa, H.; Radwn, T. A Refined Galerkin Approach for Solving Higher-Order Differential Equations via Bernoulli Polynomials. Fractals 2025, 2540183, 14. [Google Scholar]
- Adebisi, A.; Uwaheren, O.; Oseni, W.; Ishola, C.; Peter, O. Numerical Solution of Fractional Order Differential Equations by Chebyshev Least Squares Approximation Method. Euler J. Ilm. Mat. Sains Teknol. 2025, 13, 38–44. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.; Ahmed, H. Spectral Solutions for the Time-Fractional Heat Differential Equation Through a Novel Unified Sequence of Chebyshev Polynomials. AIMS Math. 2024, 9, 2137–2166. [Google Scholar] [CrossRef]
- Ahmed, H.; Hafez, R.; Abd-Elhameed, W. A Computational Strategy for Nonlinear Time-Fractional Generalized Kawahara Equation Using New Eighth-Kind Chebyshev Operational Matrices. Phys. Scr. 2024, 99, 045250. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Abd-Elhameed, W.; Youssri, Y. Explicit Shifted Second-Kind Chebyshev Spectral Treatment for Fractional Riccati Differential Equation. Comput. Model. Eng. Sci. 2019, 121, 1029–1049. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.; Al-Sady, A.; Alqubori, O.; Atta, A. Numerical Treatment of the Fractional Rayleigh-Stokes Problem Using Some Orthogonal Combinations of Chebyshev Polynomials. AIMS Math. 2024, 9, 25457–25481. [Google Scholar] [CrossRef]
- Shafiq, M.; Abbas, M.; El-Shewy, E.; Abdelrahman, M.; Abdo, N.; El-Rahman, A. Numerical Investigation of the Fractional Diffusion Wave Equation with the Mittag–Leffler Function. Fractal Fract. 2023, 8, 18. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, L.L.; Xie, Z. Sharp Error Bounds for Jacobi Expansions and Gegenbauer–Gauss Quadrature of Analytic Functions. SIAM J. Numer. Anal. 2013, 51, 1443–1469. [Google Scholar] [CrossRef]

| x | Method in [35] | Our Method |
|---|---|---|
| 0.1 | ||
| 0.2 | ||
| 0.3 | ||
| 0.4 | ||
| 0.5 | ||
| 0.6 | ||
| 0.7 | ||
| 0.8 | ||
| 0.9 |
| Method in [35] | Our Method at | |||
|---|---|---|---|---|
| Error at | Error at | Error | Error | |
| 0.2 | ||||
| 0.4 | ||||
| 0.6 | ||||
| 0.8 | ||||
| 1 | ||||
| 7 | |
| Error in Theorem 4 |
| 0.1 | |||
| 0.2 | |||
| 0.3 | |||
| 0.4 | |||
| 0.5 | |||
| 0.6 | |||
| 0.7 | |||
| 0.8 | |||
| 0.9 | |||
| CPU time | 6.907 | 6.907 | 6.907 |
| 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|
| CPU time | 1.922 | 2.203 | 2.829 | 4. | 6.986 |
| CPU time | 1.845 | 2.173 | 2.829 | 4.094 | 6.907 |
| Method in [35] at , | Our Method | |||
|---|---|---|---|---|
| 0.1 | ||||
| 0.2 | ||||
| 0.3 | 0 | |||
| 0.4 | 0 | |||
| 0.5 | 0 | 0 | ||
| 0.6 | 0 | |||
| 0.7 | 0 | |||
| 0.8 | ||||
| 0.9 | ||||
| Method in [35] at , | Our Method at | |||
|---|---|---|---|---|
| Errors | Errors | Errors | Errors | |
| 0.2 | ||||
| 0.4 | ||||
| 0.6 | ||||
| 0.8 | ||||
| 1 | ||||
| Method in [35] | Our Method at | |||
|---|---|---|---|---|
| 0.1 | ||||
| 0.2 | ||||
| 0.3 | ||||
| 0.4 | ||||
| 0.5 | ||||
| 0.6 | ||||
| 0.7 | ||||
| 0.8 | ||||
| 0.9 | ||||
| Method in [35] | Our Method at | |||||
|---|---|---|---|---|---|---|
| Error | Error | Error | CPU Time | Error | CPU Time | |
| 0.2 | 9.986 | 8.017 | ||||
| 0.4 | 11.954 | 8.017 | ||||
| 0.6 | 14.376 | 8.017 | ||||
| 0.8 | 16.704 | 8.032 | ||||
| 1 | 16.704 | 8.032 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzahrani, S.S.; Alanazi, A.A.; Atta, A.G. Numerical Treatment of the Time Fractional Diffusion Wave Problem Using Chebyshev Polynomials. Symmetry 2025, 17, 1451. https://doi.org/10.3390/sym17091451
Alzahrani SS, Alanazi AA, Atta AG. Numerical Treatment of the Time Fractional Diffusion Wave Problem Using Chebyshev Polynomials. Symmetry. 2025; 17(9):1451. https://doi.org/10.3390/sym17091451
Chicago/Turabian StyleAlzahrani, S. S., Abeer A. Alanazi, and Ahmed Gamal Atta. 2025. "Numerical Treatment of the Time Fractional Diffusion Wave Problem Using Chebyshev Polynomials" Symmetry 17, no. 9: 1451. https://doi.org/10.3390/sym17091451
APA StyleAlzahrani, S. S., Alanazi, A. A., & Atta, A. G. (2025). Numerical Treatment of the Time Fractional Diffusion Wave Problem Using Chebyshev Polynomials. Symmetry, 17(9), 1451. https://doi.org/10.3390/sym17091451






