Abstract
The High-Energy Ray Observatory (HERO) is a space-based experiment designed to measure the spectrum and composition of cosmic rays using an ionization calorimeter. The instrument’s effective geometric factor is at least 12 m2·sr for protons and 16 m2·sr or more for nuclei and electrons. Over an exposure period of approximately 5 to 7 years, the mission will enable high-resolution, element-by-element measurements of cosmic ray spectra in the energy range of 1012 to 1016 eV per particle. A Monte Carlo simulation of the calorimeter—based on a scintillation detector with and without boron additives—was carried out using the GEANT4 software package. In this study, we examine the impact of boron additives in scintillator materials on energy resolution and their potential for discriminating between electromagnetic and hadronic components of cosmic rays. The primary objectives are to demonstrate that boron does not degrade detector characteristics and that it enables an additional timing-based method for cosmic-ray component rejection. The planned launch of the orbital experiment is scheduled for no earlier than 2029.
1. Introduction
Cosmic rays (CRs) are composed of elementary particles, photons, and atomic nuclei that travel through space at high energies. CRs consist of two main components: hadronic and electromagnetic.
The hadronic component includes Galactic Cosmic Rays (GCRs), which are nuclei of various chemical elements entering our solar system isotropically from the interstellar medium. The most widely accepted origin of GCRs is supernova explosions [1]. Supernova astrophysics is of considerable interest for several reasons. Supernovae are the primary source of heavy elements that form the Earth and other terrestrial planets. Past nearby supernova explosions may have significantly influenced the course of biological evolution on Earth and may continue to do so in the future. These events also represent one of the most critical stages in the life cycle of massive stars, often resulting in the formation of relativistic objects such as neutron stars and black holes. These compact objects are of particular scientific interest because they are linked to unresolved questions in modern physics concerning space, time, and matter. Therefore, understanding the types of supernovae, the consequences of their explosions, and the potential risks or influences from our stellar neighborhood is essential from both theoretical and practical perspectives.
Since supernova explosions are the primary source of cosmic rays, they not only provide extensive information about cosmic ray origins but also offer valuable insights into supernova physics. In recent years, research has increasingly focused on the fine structure of the energy spectra of cosmic ray nuclei and their chemical composition. The CREAM experiment [2] was the first to observe evidence of a spectral break in the proton and helium spectra near a magnetic rigidity of 10 TV. This feature was subsequently confirmed at a significance level of four standard deviations by the NUCLEON experiment [3]. The presence of this “knee” in the proton and helium spectra has also been corroborated by the DAMPE [4] and CALET [5] missions.
Studying this spectral feature provides crucial insights into the detailed mechanisms of supernova explosions and cosmic ray acceleration, potentially revealing differences among supernova types, their respective energy thresholds for particle acceleration, and the composition of their source material.
As a result, two key objectives have emerged in high-energy cosmic ray physics:
- Precise measurement of the cosmic ray energy spectrum below the Kulikov–Christiansen knee (~3 PeV) [6].
- Element-resolved charge spectra in this energy range.
Finally, the electromagnetic component of cosmic rays includes electrons, positrons, and gamma rays. There are numerous compelling research directions in cosmic gamma-ray studies for several reasons. While the primary sources of gamma rays are regions where ordinary charged cosmic rays are accelerated, other significant sources may also exist, such as the decay or annihilation of dark matter particles. Therefore, studying cosmic gamma radiation offers deeper insights into the nature of cosmic ray sources and their underlying physical mechanisms, as well as valuable information about dark matter.
A key distinction between gamma rays and charged cosmic rays is that gamma rays travel almost in a straight line, except for slight deflections caused by gravitational lensing due to space curvature. Consequently, the direction of their arrival can be used to accurately identify their origin.
Measuring the cosmic gamma-ray spectrum with the highest possible energy resolution is particularly important, as a narrow peak in this spectrum may indicate gamma rays produced by dark matter annihilation, thereby providing direct information about the mass of dark matter particles. If the arrival directions of gamma rays contributing to such a peak predominantly point toward the Galactic center [7,8,9], where a steep cusp in the dark matter density distribution is expected, then the likelihood of interpreting the signal as evidence of dark matter annihilation becomes significantly stronger.
To address these problems, the High-Energy Ray Observatory (HERO) experiment was proposed.
To directly detect cosmic ray (CR) particles, the scientific payload must include at least two detection systems: one for energy measurement and another for charge detection. Only the ionization calorimeter technique is capable of functioning as a spectrometer across such an unprecedentedly wide range of high and ultra-high energies. The HERO space observatory utilizes a heavy-ionization imaging calorimeter (weighing 10 tons or more), which incorporates a polystyrene scintillator to measure particle energy, reconstruct their trajectories, and distinguish between the electromagnetic and hadronic components of CR [10]. The charge measurement system is implemented as a multilayer silicon pad detectors matrix—a technique successfully used in several space missions, including the NUCLEON experiment [11]. A core principle of the HERO project is the necessity of achieving a high exposure factor, one that exceeds those of all previous and currently planned experiments by 1.5 to 2 orders of magnitude. This high exposure must be matched with exceptional measurement precision, which is critical for constructing the spectra of rare components and for identifying fine structures in various cosmic ray energy spectra.
2. Materials and Methods
It is well established that hadronic interactions in calorimeter materials produce significantly more secondary neutrons than purely electromagnetic cascades. To detect these neutrons, a boron-based compound (4–5% by weight) was introduced into the scintillating plastic. Boron-10 has a large thermal neutron capture cross-section (755 barns), and the reaction (1) produces an α-particle carrying most of the released energy. Because α-particles have a very short mean free path, they are detected essentially at the site of neutron capture, providing a clear signal. Neutron detection is further advantageous because it occurs with a delay relative to the prompt cascade, making it separable from background.
A primary particle with an energy of ~1 GeV or higher initiates a cascade of secondaries, leaving nuclei in an excited state. These nuclei de-excite through evaporation of neutrons, protons, and gamma rays. The evaporated neutrons have typical energies of 4–5 MeV and become thermalized in the detector material within 2.5–3 µs. Once thermalized, they can be captured on Boron-10. Thus, in addition to the prompt cascade signal, the detector response includes a delayed component from neutron captures. For each simulated event, the total α-yield from these captures is integrated within a microsecond-scale window. This delayed signal provides a distinctive signature of hadronic cascades, since electromagnetic showers produce only negligible numbers of evaporation neutrons. In the analysis, the delayed neutron component is treated as an independent parameter that complements the prompt energy deposition and enables more reliable separation between hadronic and electromagnetic events.
To study the moderation of evaporated neutrons to thermal energies (~0.025 eV), a prototype of the HERO detector [12] was developed in 2018 and tested at the SPS accelerator at CERN.
Monte Carlo simulations were conducted for two calorimeter geometries:
- (1)
- A simplified 23.5 ton model designed to study the impact of boron on the calorimetric energy resolution, as well as on the characteristics of the background signal from cosmic protons, including its mean level and standard deviation.
- (2)
- A calorimeter prototype was developed to investigate the influence of boron on the delayed-neutron signals from hadronic and electromagnetic cascades, focusing on their differences in amplitude and time profile. Time distributions of detected scintillation photons for various primary particles are presented.
This study evaluates the energy loss of alpha particles generated by reaction (1), the time profiles of scintillation photon emissions, the average calorimetric response, and the energy resolution of the HERO detector utilizing a borated scintillator. Additionally, the background signal level from cosmic protons was estimated using a simplified detector model.
Simulations were carried out using the Geant4 version 11.2.0 software package [13,14]. The QGSP_BERT_HP physics list [15], which incorporates neutron interactions, was employed to model cascade development. Simulations included electrons, protons, and helium, carbon, and iron nuclei. Each secondary shower particle was tracked in GEANT4 down to the energy threshold, allowing for the formation of excited nuclei (the sources of evaporative neutrons), their subsequent thermalization, and either the production of α-particles or the escape of secondary particles from the detector.
3. Results
3.1. Monte Carlo Simulation of a Simplified Model of the HERO Detector
A simplified Monte Carlo model of the HERO detector was implemented as a 2.5 m diameter sphere, consisting of 125 alternating spherical layers: 0.1 cm thick tungsten and 0.9 cm thick borated scintillator (see left panel of Figure 1). This configuration corresponds to approximately 38 radiation lengths and 2.8 nuclear interaction lengths. The model was designed to simulate the background signal from cosmic protons.
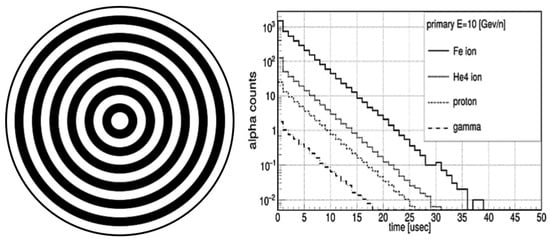
Figure 1.
On the left, a schematic representation of the simplified HERO calorimeter model, implemented as a solid sphere of 2.5 m diameter, consisting of alternating concentric layers: 0.9 cm boron-loaded scintillator (white) and 0.1 cm tungsten (black). On the right, the α-particle yields due to different initial particles. (Reproduced with permission from Kh. Karatash et al., Physics of Particles and Nuclei, published by Springer Nature, 2025 [16]).
The right panel of Figure 1 shows the time dependence of the alpha particle yield for 10-GeV gamma quanta, as well as for protons, helium nuclei (He), and iron nuclei (Fe) at 10 GeV/nucleon. A clear difference in the alpha particle yield is observed among these particles. This displacement originates from the different numbers of evaporation neutrons produced in the cascades: hadronic primaries (protons, He, Fe) generate substantially more secondary neutrons than electromagnetic primaries (gamma quanta). In addition, heavier nuclei produce higher neutron multiplicities, which explains the larger α-yields for He and Fe compared to protons. Gamma-induced cascades produce very few neutrons, resulting in the lowest yield. This fundamental difference in delayed α-signals underlies the method’s ability to discriminate between hadronic and electromagnetic components in the HERO calorimeter.
The cosmic proton flux data from the PAMELA experiment [17] was used to simulate the background proton signal. In this work, the proton flux’s energy dependence was employed to model the energy distribution of background protons. The arrival directions of cosmic protons were assumed to be isotropic and uniformly distributed, meaning protons could enter the detector from any direction with equal probability. Due to the spherical symmetry of the detector, all points on its surface are equivalent. Therefore, it was sufficient to select a single point on the sphere’s surface and generate all possible proton incidence angles that resulted in trajectories intersecting at least one layer of the detector.
Figure 2 illustrates how the background signal depends on the width of the integration window for detectors of different radii. For each chosen window, the time axis was divided into bins of the corresponding width, and the total energy deposited in the detector by all secondary particles was summed within each bin. From the resulting distribution, both the mean background signal and its standard deviation were determined and are shown as functions of the integration time.
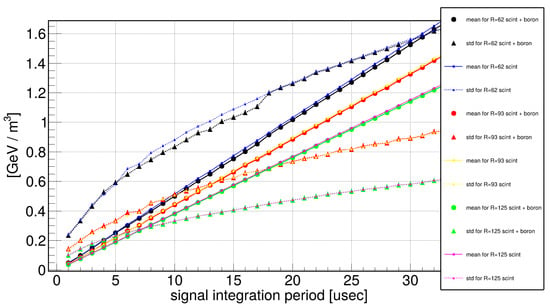
Figure 2.
Dependence of the mean background count (in GeV) and the standard deviation of the background count on the integration step of the background signal for detectors with different radii, shown both with and without boron admixture in the scintillator.
The results demonstrate that the average background signal increases linearly with the width of the integration window, while the standard deviation grows more slowly, approximately following a square root dependence. As a consequence, relative fluctuations decrease with longer windows. The point where the mean value becomes comparable to its spread can be used as a practical criterion for stable background counting: for a detector with a radius of 125 cm this occurs at about 7 µs, corresponding to an average of three to four background protons within the integration window. Similar behavior is observed for other detector sizes, showing that the stability threshold is mainly determined by the expected number of protons in the window.
Importantly, the simulations show that adding boron to the scintillator does not alter the level of the background signal from cosmic protons. The absolute background increases with detector size, but when normalized per unit volume it decreases, since the number of incoming protons scales with the detector’s cross-sectional area, while normalization is by its volume. Therefore, larger detectors exhibit lower background intensity per unit volume.
As shown in Figure 3, proton-related uncertainties exceed electron uncertainties by two orders of magnitude. Furthermore, proton energy loss fluctuations are several orders of magnitude greater than the mean background level. As a result, the background signal does not affect the detector’s energy resolution for protons with energies above 1 TeV.
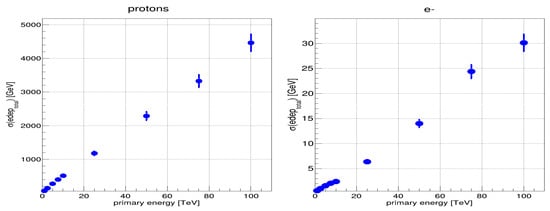
Figure 3.
Standard deviation of the total energy deposited in the detector by all cascade particles, calculated over many simulated events, vs. incident particle energy for protons (left) and electrons (right). Data points are shown with error bars corresponding to the statistical uncertainty of the calculated standard deviation, obtained from event-to-event fluctuations. Detector radius: 125 cm.
Electrons show a very different behavior. With a long integration window of 16 microseconds, the fluctuations in the total deposited energy stay at or below about 5 GeV for electron energies up to 20 TeV. This level of variation is comparable to the average background signal of roughly 5 GeV collected over the same period. As a result, background noise has a significant impact on the detector’s ability to measure electron energies in this regime. Reducing the integration window to 3 microseconds—a timescale that matches the average thermalization time of evaporated neutrons—lowers the mean background to about 0.93 GeV (for a detector with a 125 cm radius). Under these conditions, the fluctuations for 2.5 TeV electrons are still around 1 GeV (see Figure 3). This means that for electron energies below about 2.5 TeV, the resolution is still limited by the background signal, even when shorter integration times are used.
Figure 4 illustrates the fundamental physical difference between electromagnetic and hadronic cascades: electron-induced showers, governed by bremsstrahlung and pair production, are practically instantaneous, with almost all energy deposited in an extremely short time interval. In contrast, proton-induced showers involve nuclear interactions, producing numerous evaporation neutrons and other secondaries whose thermalization and capture generate delayed signals extending over microseconds. This distinction in temporal structure explains why short integration windows can effectively mitigate the background limitation for electrons, while for protons the long-lived hadronic component is an intrinsic part of the signal.
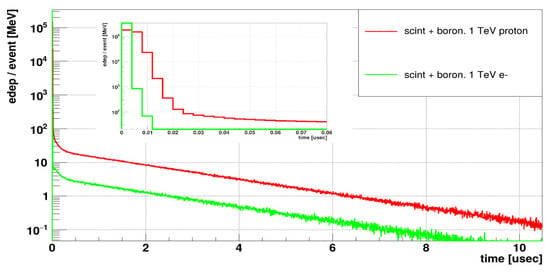
Figure 4.
Energy deposition in the detector as a function of time for protons and electrons.
Figure 5 (left panel) displays the mean detector response versus primary proton energy, demonstrating a linear relationship across the entire energy range. The right panel presents the calorimeter’s energy resolution when using borated scintillator, achieving 15–16% for 100 TeV protons. For comparison, the dashed line shows the resolution without boron. Similar analyses were conducted for electrons, comparing both scintillator configurations (with and without boron). Monte Carlo simulations for protons (Figure 5) and electrons (Figure 6) revealed that boron loading had negligible impact on either detector response or energy resolution.
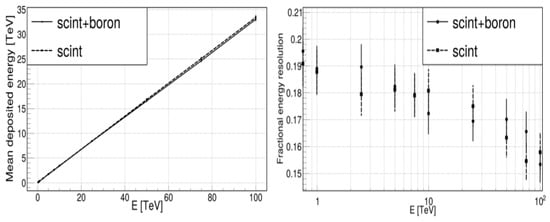
Figure 5.
Average detector response as a function of primary proton energy and the energy resolution of the calorimeter using borated and non-borated scintillator.
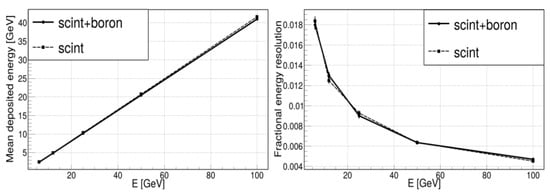
Figure 6.
Average detector response as a function of primary electron energy and the energy resolution of the calorimeter when using borated and non-borated scintillator.
3.2. Monte Carlo Simulation of the HERO Detector Prototype
For high-energy accelerator beam tests, we developed an upgraded prototype of the HERO detector calorimeter (Figure 7). The design enables reconstruction of primary particle trajectories through signals from borated scintillator plates. The calorimeter consists of 30 orthogonal detection planes, each containing 16 strips (200 × 12.5 × 7 mm3 per strip). Alternating absorber layers of 2 mm copper and 3 mm lead provide approximately 20 radiation lengths and ~1.15 nuclear interaction lengths—sufficient for secondary shower development. To enhance interaction probability, we incorporated a 120 mm plastic target upstream of the calorimeter.
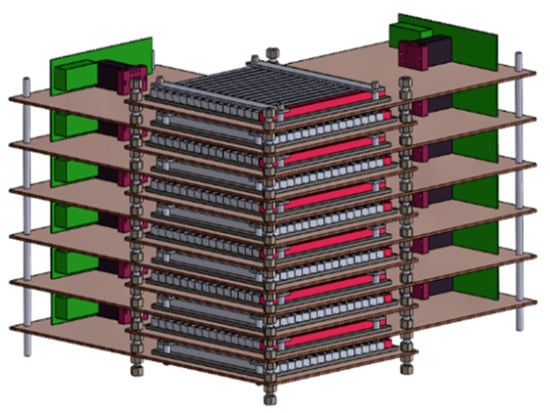
Figure 7.
Schematic view of the assembly of the HERO detector prototype. (Reproduced with permission from Kh. Karatash et al., Physics of Particles and Nuclei, published by Springer Nature, 2025 [16]).
Tests of the prototype are scheduled to be conducted at the WWR-K reactor in Almaty, Kazakhstan, and the SPS accelerator at CERN. A test was previously conducted in 2018 using lead fragmentation nuclei (13 GeV/nucleon, A/Z = 2.1–2.2) [12].
We performed Monte Carlo simulations of a 100-layer prototype to study secondary cascade development in greater detail. The simulation included primary particles (electrons, protons, and helium, carbon, and iron nuclei) with identical energies of 13 GeV/nucleon.
Figure 8 (right panel) shows the layer-by-layer alpha particle energy losses for each primary particle type, revealing significant variations in alpha particle yield. Notably, electron-induced events produced detector responses 5–10 times lower than proton-initiated events throughout all calorimeter layers.
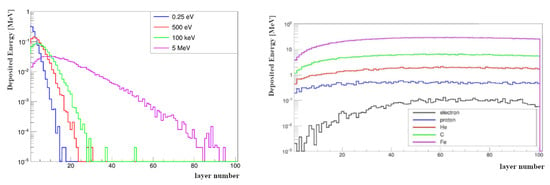
Figure 8.
On the left, the energy losses of α-particles from neutrons of varying energies are shown. On the right, the energy losses of α-particles from electrons, protons (p), helium (He), carbon (C), and iron (Fe) with energies of 13 GeV/nucleon are displayed. The histograms are normalized to one event. (Reproduced with permission from Kh. Karatash et al., Physics of Particles and Nuclei, published by Springer Nature, 2025 [16]).
We subsequently simulated incident neutrons with energies of 0.25 eV, 500 eV, 100 keV, and 5 MeV in the same model. The left panel of Figure 8 illustrates the energy losses of alpha particles for neutrons of varying energies. Figure 8 (left panel) displays the alpha particle energy losses for these neutron energies. Given the extremely short range of produced alpha particles in the scintillator material, we determined neutron absorption locations by identifying complete alpha particle stopping points. The results reveal that detection efficiency decreases sharply with depth—only the highest-energy neutron component (>100 keV) penetrates beyond the 30th layer. These conclusions will be verified during upcoming prototype tests at the WWR-K reactor channel (Almaty, Kazakhstan), which provides an ideal neutron spectrum (0.25–5 MeV) for validation.
As previously noted, boron’s key discriminating parameter is its characteristic timing signature. Figure 9 compares time distributions between prototypes with pure scintillator (left panel) and boron-loaded scintillator (right panel). The data reveal that following cascade decay (~2.5 μs), the boron-doped prototype demonstrates a prolonged signal corresponding to alpha particles from neutron capture reactions. This observation aligns with results obtained during 2018 prototype testing [9].
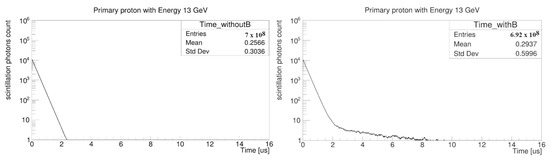
Figure 9.
Time distribution of scintillation photons detected in the fiber for the prototype without boron (left) and the prototype with boron (right). The bin size is 4 ns, and the histograms are normalized to the number of events.
Figure 10 presents a comparative analysis of time distributions for equal-energy electrons, gamma rays, protons, and alpha particles. The results demonstrate a striking difference in light yield: the hadronic component is two orders of magnitude greater light output than the electromagnetic component (electrons/gamma rays).
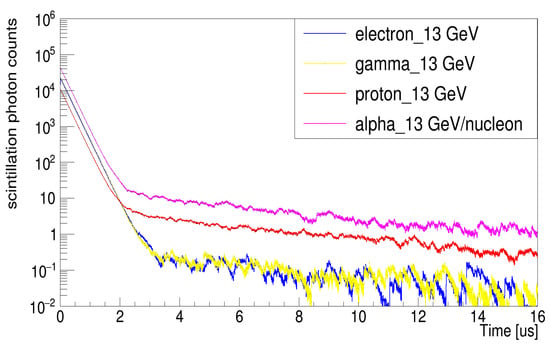
Figure 10.
Comparison of time distributions for electrons, gamma rays, and protons with an energy of 13 GeV, as well as alpha particles with an energy of 13 GeV per nucleon. The bin size is 4 ns, and histograms are normalized to the number of events.
Figure 11 (left panel) displays the mean detector response versus incident proton energy, showing excellent linearity across the measured range. The right panel reveals the energy resolution, which degrades by approximately a factor of two compared to the simplified full-scale detector model. This performance reduction stems from two factors: (1) the prototype’s limited nuclear interaction length, and (2) increasing secondary cascade leakage at higher proton energies.
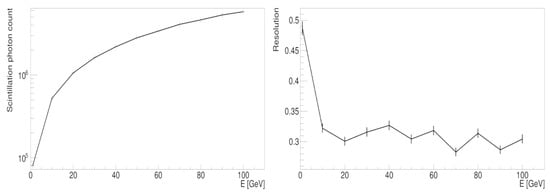
Figure 11.
Left: Average detector response as a function of the incident proton energy. Right: Energy resolution as a function of the incident proton energy.
4. Conclusions
We performed preliminary Monte Carlo simulations of both the full-scale HERO detector calorimeter and its prototype featuring a borated scintillator. The simulations characterized the following:
- Alpha particle energy losses;
- Energy resolution performance;
- Time distributions of fiber-detected scintillation photons.
Key findings include the following:
- (1)
- Strong dependence of alpha particle yield on primary particle type;
- (2)
- Negligible impact of boron doping on energy resolution for protons and electrons across the studied energy range;
- (3)
- Effective discrimination capability between electromagnetic and hadronic components via boron-induced timing signatures.
These results will be experimentally validated through upcoming beam tests at accelerator facilities and at the WWR-K reactor (Almaty, Kazakhstan).
Author Contributions
Conceptualization, O.K. and K.K.; Methodology, Y.M. and I.S.; Formal analysis, N.S. and A.P.; Data curation, Y.S. and A.B.; Writing—original draft, O.K. and I.S.; Writing—review & editing, O.K. and I.S.; Visualization, K.K.; Project administration, O.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Committee of Science of the Ministry of Science and Higher Education of the Republic of Kazakhstan, Grant No. IRN AP19678699.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ginzburg, V.; Syrovatskii, S. The Origin of Cosmic Rays; Pergamon Press: Oxford, UK, 1964. [Google Scholar]
- Ahn, H.S.; Allison, P.; Bagliesi, M.G.; Beatty, J.J.; Bigongiari, G.; Childers, J.T.; Conklin, N.B.; Coutu, S.; DuVernois, M.A.; Ganel, O.; et al. Discrepant hardening observed in cosmic-ray elemental spectra. Astrophys. J. Lett. 2010, 714, L89–L93. [Google Scholar] [CrossRef]
- Atkin, E.; Bulatov, V.; Dorokhov, V.; Gorbunov, N.; Filippov, S.; Grebenyuk, V.; Karmanov, D.; Kovalev, I.; Kudryashov, I.; Kurganov, A.; et al. New universal cosmic-ray knee near a magnetic rigidity of 10 TV with the NUCLEON space observatory. JETP Lett. 2018, 108, 5–12. [Google Scholar] [CrossRef]
- DAMPE Collaboration; An, Q.; Asfandiyarov, R.; Azzarello, P.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Chang, J.; Chen, D.Y.; Chen, H.F.; et al. Measurement of the cosmic ray proton spectrum from 40 GeV to 100 TeV with the DAMPE satellite. Sci. Adv. 2019, 5, eaax3793. [Google Scholar] [CrossRef]
- CALET Collaboration; Marrocchesi, P.S. CALET results after 5 years on the ISS. PoS 2021, 10, 1–16. [Google Scholar] [CrossRef]
- Kulikov, G.V.; Christiansen, G.B. On the spectrum of extensive air showers by the number of particles. JETP 1958, 35, 635–640. [Google Scholar]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; et al. The Fermi Galactic Center GeV Excess and Implications for Dark Matter. Astrophys. J. 2017, 840, 43. [Google Scholar] [CrossRef]
- Daylan, T.; Finkbeiner, D.P.; Hooper, D.; Linden, T.; Portillo, S.K.N.; Rodd, N.L.; Slatyer, T.R. The characterization of the gamma-ray signal from the central Milky Way: A case for annihilating dark matter. Phys. Dark Univ. 2016, 12, 1–23. [Google Scholar] [CrossRef]
- Prosin, V.V.; Astapov, I.I.; Bezyazeekov, P.A.; Boreyko, V.; Borodin, A.N.; Brueckner, M.; Budnev, N.M.; Wischnewski, R.; Garmash, A.Y.; Gafarov, A.R.; et al. Energy spectrum of primary cosmic rays, according to TUNKA-133 and TAI-GA-HiSCORE EAS Cherenkov light data. Bull. Russ. Acad. Sci. Phys. 2019, 83, 1016–1019. [Google Scholar] [CrossRef]
- Voronin, G.; Grebenyuk, V.M.; Karmanov, D.E.; Korotkova, N.A.; Krumshtein, Z.V.; Merkin, M.M.; Pakhomov, A.Y.; Podorozhnyi, D.M.; Sadovskii, A.B.; Sveshnikova, L.G.; et al. Testing a prototype of the charge-measuring system for the NUCLEON setup. Instrum. Exp. Tech. 2007, 50, 187–195. [Google Scholar] [CrossRef]
- Pan, A.; Grebenyuk, V.M.; Karmanov, D.M.; Krasnoperov, A.V.; Podorozhny, D.M.; Porokhovoy, S.Y.; Rogov, A.D.; Sadovsky, A.B.; Satyshev, I.; Slunecka, M.; et al. Tests of the OLVE-HERO calorimeter prototype at heavy-ion beams at SPS CERN. Phys. At. Nucl. 2019, 82, 788–794. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Dubois, P.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Recent developments in Geant4. Nucl. Instrum. Meth. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Dubois, P.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Dubois, P.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; et al. Geant4—A simulation toolkit. Nucl. Instrum. Meth. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Karatash, K.; Satyshev, I.; Tkachev, L.G. Monte Carlo Simulation of the OLVE-HERO Orbital Experiment. Phys. Part. Nucl. 2025, 56, 113–117. [Google Scholar] [CrossRef]
- Martucci, M.; Munini, R.; Boezio, M.; Di Felice, V.; Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Bongi, M.; Bonvicini, V.; et al. Proton fluxes measured by the PAMELA experiment from the minimum to the maximum solar activity for solar cycle 24. Astrophys. J. Lett. 2018, 854, L2. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).