The Jacobi Elliptic Function and Incomplete Elliptic Integral of Second Kind Solutions of the Wazwaz Negative Order Korteweg–de Vries Equation
Abstract
1. Introduction
2. Description of the Jacobi Elliptic Function Scheme
3. Mathematical Analysis of Wazwaz Negative-Order KdV Equation Using Jacobi Elliptic Function Scheme
| Algorithm 1 Description of proposed scheme |
|
4. The Jacobi Elliptic Solutions of the Wazwaz Negative-Order KDV Equation
- Solution Equation (17) is undefined due to division by zero; hence, the existence condition of is .
- Solution Equation (43) is undefined due to division by zero; hence, in exists.
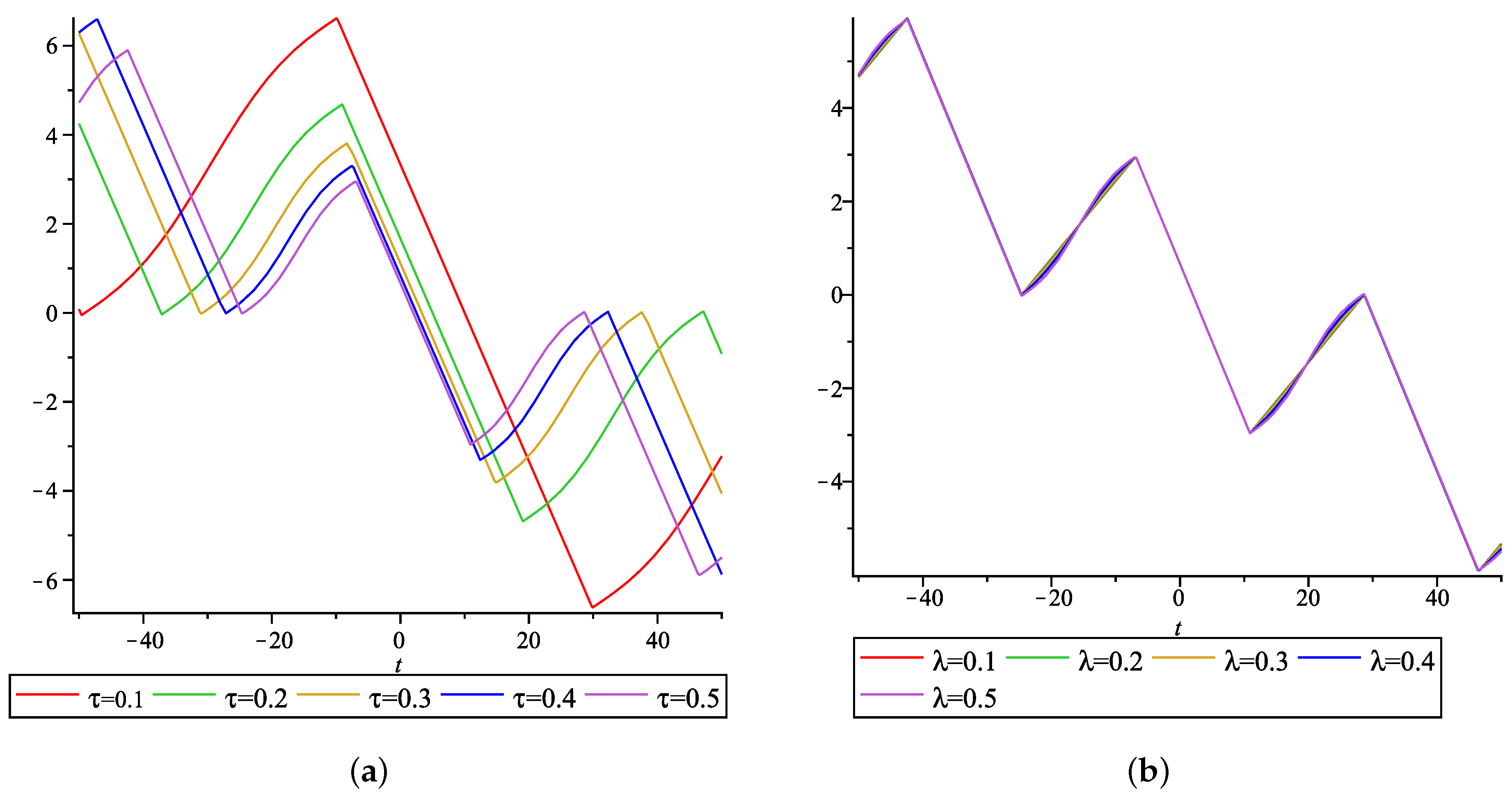
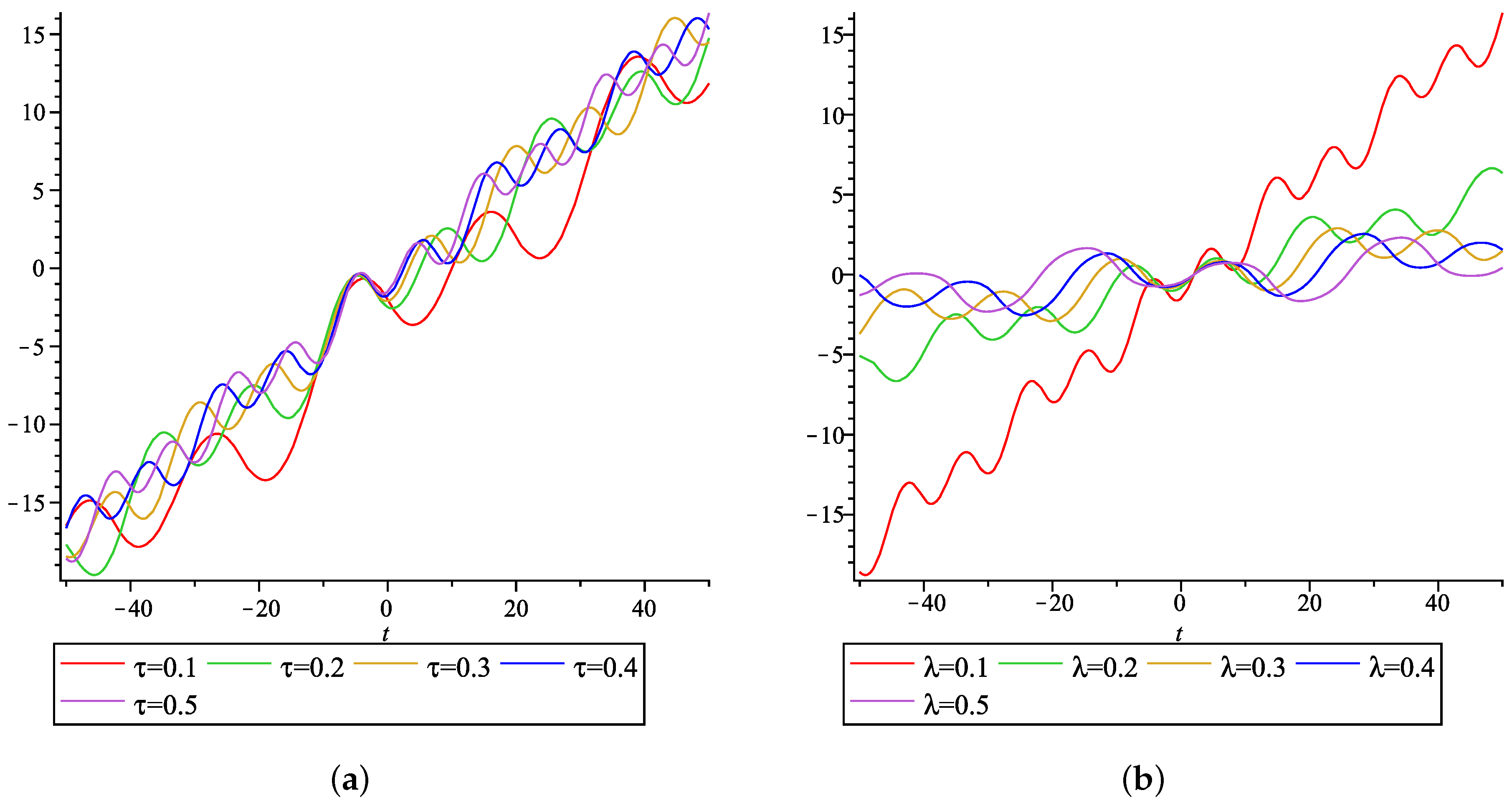
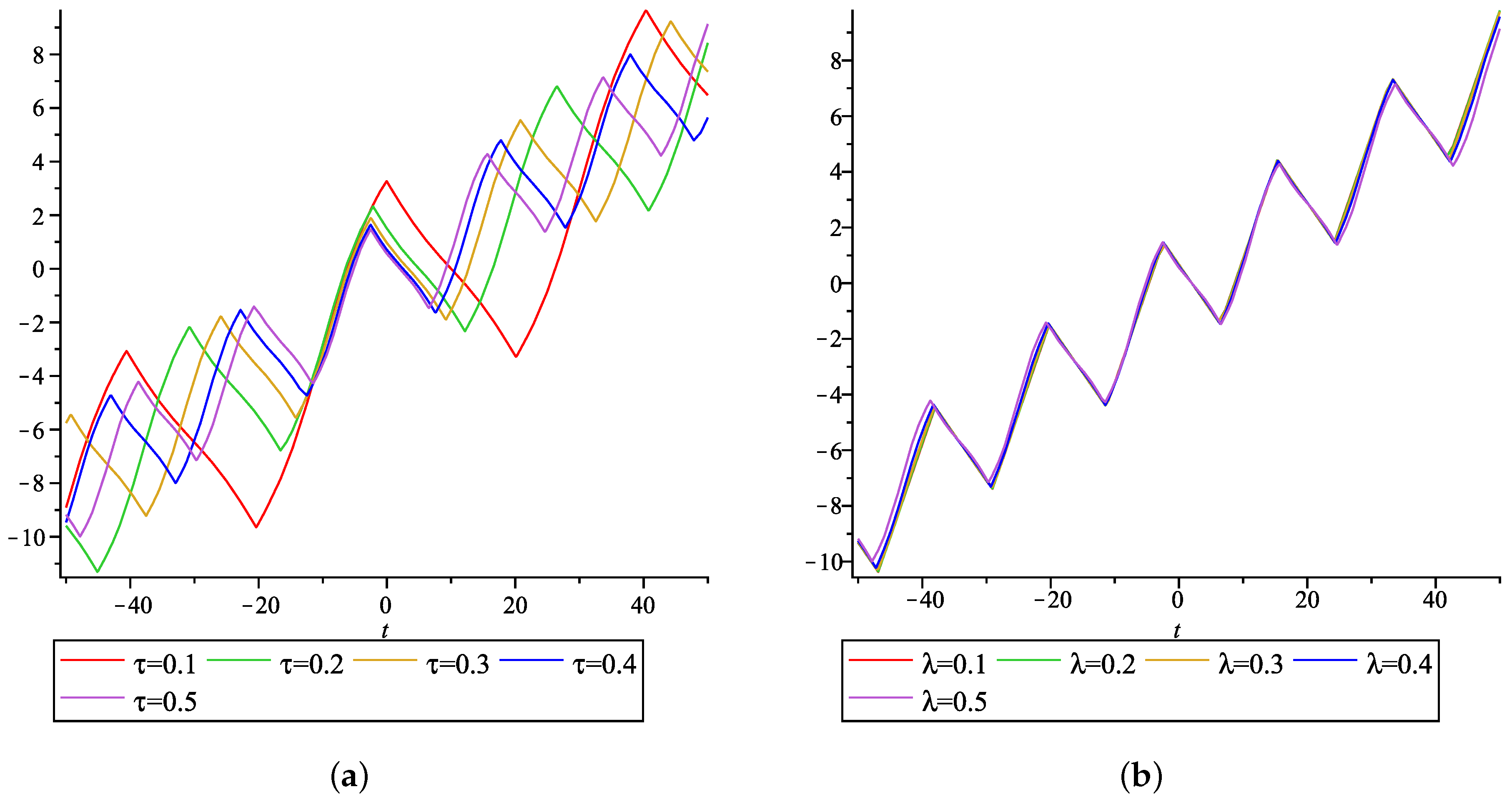
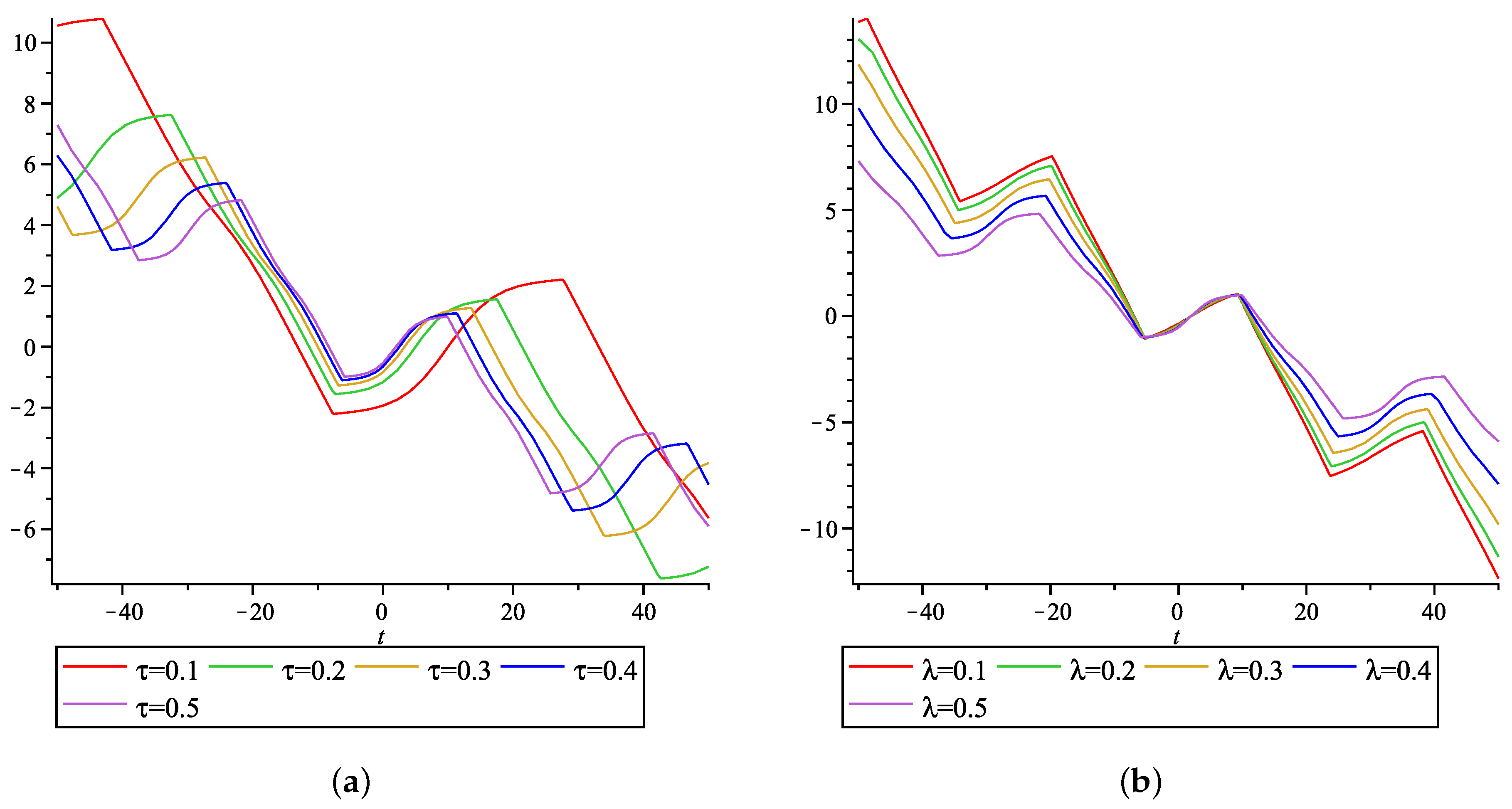
5. Interpretation of Results and Discussion
- For the modulus when the velocity increases, the wave propogation and decreases.
- For the modulus when the velocity increases, the wave propogation and positive part of increases.
- For the velocity when the modulus increases, the wave propogation and do not have much variation.
- For the velocity when the modulus increases, the wave propogation and positive part of increases.
- For the velocity when the modulus increases, the wave propogation decreases.
- For , and , .
- For , and , .
- For , and , .
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wazwaz, A.M. Multiple complex soliton solutions for integrable negative-order KdV and integrable nega-tive-order modified KdV equations. Appl. Math. Lett. 2019, 88, 1–7. [Google Scholar] [CrossRef]
- Oliver, P.J. Evolution equations possessing infinitely many symmetries. J. Math. Phys. 1977, 18, 1212–1215. [Google Scholar] [CrossRef]
- Verosky, J.M. Negative powers of Olver recursion operators. J. Math. Phys. 1991, 32, 1733–1736. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Negative-Order KdV and Negative-Order KP Equations: Multiple Soliton Solutions. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2017, 87, 291–296. [Google Scholar] [CrossRef]
- Cheng, W.; Xu, T. N-th Bäcklund transformation and soliton-cnoidal wave interaction solution to the combined KdV-negative-order KdV equation. Appl. Math. Lett. 2019, 94, 21–29. [Google Scholar] [CrossRef]
- Sil, S.; Guha, P. Symmetry reductions and exact solutions of two new generalized negative KdV type equa-tions. J. Geom. Phys. 2022, 178, 104558. [Google Scholar] [CrossRef]
- Yuan, S.; Xu, J. On a Riemann-Hilbert problem for the negative-order KdV equation. Appl. Math-Ematics Lett. 2022, 132, 108106. [Google Scholar] [CrossRef]
- Cai, N.; Qiao, Z.; Zhou, Y. Wave solutions to an integrable negative order KdV equation. Wave Motion 2023, 116, 103072. [Google Scholar] [CrossRef]
- Qiao, Z.; Li, J. Negative-order KdV equation with both solitons and kink wave solutions. A Lett. J. Explor. Front. Phys. 2011, 94, 5. [Google Scholar] [CrossRef]
- Qiao, Z.; Fan, E. Negative-order Korteweg-de Vries equations. Phys. Rev. E 2011, 86, 016601. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, M.; Li, J.; Qiao, Z. Negative Order KdV Equation with No Solitary Traveling Waves. Mathematics 2022, 10, 48. [Google Scholar] [CrossRef]
- Rabie, W.B.; Ahmed, H.M. Cubic-quartic solitons perturbation with couplers in optical metamaterials having tri-ple-power law nonlinearity using extended F-expansion method. Opt.-Int. J. Light Electron Opt. 2022, 262, 169255. [Google Scholar] [CrossRef]
- Rabie, W.B.; Ahmed, H.M. Construction cubic-quartic solitons in optical metamaterials for the perturbed twin-core couplers with Kudryashov’s sextic power law using extended F-expansion method. Chaos Solitons Fractals 2022, 160, 112289. [Google Scholar] [CrossRef]
- Borg, M.; Badra, N.M.; Ahmed, H.M.; Rabie, W.B. Solitons behavior of Sasa-Satsuma equation in birefrin-gent fibers with Kerr law nonlinearity using extended F-expansion method. Ain Shams Eng. J. 2024, 15, 102290. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alngar, M.E.M. Optical solitons in birefringent fibers with Biswas-Arshed model by gener-alized Jacobi elliptic function expansion method. Optik 2020, 203, 163922. [Google Scholar] [CrossRef]
- Zhang, J.; Hao, H.-Q. Soliton solutions of the AB system via the Jacobi elliptic function expansion method. Opt.-Int. J. Light Electron Opt. 2021, 244, 167541. [Google Scholar] [CrossRef]
- Khalil, T.A.; Badra, N.; Ahmed, H.M.; Rabie, W.B. Optical solitons and other solutions for coupled system of nonlinear Biswas-Milovic equation with Kudryashov’s law of refractive index by Jacobi elliptic function expansion method. Opt.-Int. J. Light Electron Opt. 2022, 253, 168540. [Google Scholar] [CrossRef]
- Khalil, T.A.; Badra, N.; Ahmed, H.M.; Rabie, W.B. Bright solitons for twin-core couplers and multiple-core couplers having polynomial law of nonlinearity using Jacobi elliptic function expansion method. Alex. Eng. J. 2022, 61, 11925–11934. [Google Scholar] [CrossRef]
- Hussain, A.; Chahlaoui, Y.; Zaman, F.D.; Parveen, T.; Hassan, A.M. The Jacobi elliptic function method and its application for the stochastic NNV system. Alex. Eng. J. 2023, 81, 347–359. [Google Scholar] [CrossRef]
- Silambarasan, R.; Nisar, K.S. Doubly periodic solutions and non-topological solitons of (2+1)—dimen-sion Wazwaz Kaur Boussinesq equation employing Jacobi elliptic function method. Chaos Solitons Fractals 2023, 175, 113997. [Google Scholar] [CrossRef]
- Ali, K.K.; Yokus, A.; Seadawy, A.R.; Yilmazer, R. The ion sound and Langmuir waves dynamical system via computational modified generalized exponential rational function. Chaos Solitons Fractals 2022, 161, 112381. [Google Scholar] [CrossRef]
- Iqbal, M.S.; Seadawy, A.R.; Baber, M.Z.; Qasim, M. Application of modified exponential rational function method to Jaulent-Miodek system leading to exact classical solutions. Chaos Solitons Fractals 2022, 164, 112600. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Xu, G.Q. Variety of optical solitons for perturbed Fokas-Lenells equation through modified exponential rational function method and other distinct schemes. Opt. Int. J. Light Electron Opt. 2023, 287, 171011. [Google Scholar] [CrossRef]
- Kilicman, A.; Silambarasan, R. Modified Kudryashov Method to Solve Generalized Kuramoto-Sivashinsky Equation. Symmetry 2018, 10, 527. [Google Scholar] [CrossRef]
- Akbulut, A.; Arnous, A.H.; Hashemi, M.S.; Mirzazadeh, M. Solitary waves for the generalized nonlinear wave equation in (3+1) dimensions with gas bubbles using the Nnucci’s reduction, enhanced and modified Kudryashov algorithms. J. Ocean. Eng. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Silambarasan, R.; Kilicman, A. Solitons of dispersive wave steered from Navier-Bernoulli and Love’s hy-pothesis in cylindrical elastic rod with compressible Murnaghan’s materials. Math. Comput. Simul. 2023, 203, 699–720. [Google Scholar] [CrossRef]
- Nisar, K.S.; Silambarasan, R. Jacobi elliptic solutions, bright, compound bright-complex singular solitons of (3+1)—dimensional Wazwaz Kaur Boussinesq equation. Opt. Quantum Electron. 2024, 56, 1301. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathe-Matical Tables; Dover Publ, Inc.: New York, NY, USA, 1972. [Google Scholar] [CrossRef]


| S.No | ||||
|---|---|---|---|---|
| 1 | 1 | |||
| 2 | ||||
| 3 | 1 | |||
| 4 | 1 | |||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | 1 | 1 | ||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 |
| Set | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | |||||
| 2 | 0 | 0 | 0 | ||||
| 3 | 0 | 0 | 0 |
| i | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
| i | |
|---|---|
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silambarasan, R.; Kilicman, A.; Jyotheeswari, P. The Jacobi Elliptic Function and Incomplete Elliptic Integral of Second Kind Solutions of the Wazwaz Negative Order Korteweg–de Vries Equation. Symmetry 2025, 17, 1447. https://doi.org/10.3390/sym17091447
Silambarasan R, Kilicman A, Jyotheeswari P. The Jacobi Elliptic Function and Incomplete Elliptic Integral of Second Kind Solutions of the Wazwaz Negative Order Korteweg–de Vries Equation. Symmetry. 2025; 17(9):1447. https://doi.org/10.3390/sym17091447
Chicago/Turabian StyleSilambarasan, Rathinavel, Adem Kilicman, and Purushotham Jyotheeswari. 2025. "The Jacobi Elliptic Function and Incomplete Elliptic Integral of Second Kind Solutions of the Wazwaz Negative Order Korteweg–de Vries Equation" Symmetry 17, no. 9: 1447. https://doi.org/10.3390/sym17091447
APA StyleSilambarasan, R., Kilicman, A., & Jyotheeswari, P. (2025). The Jacobi Elliptic Function and Incomplete Elliptic Integral of Second Kind Solutions of the Wazwaz Negative Order Korteweg–de Vries Equation. Symmetry, 17(9), 1447. https://doi.org/10.3390/sym17091447







