Aerodynamic Shape Optimization Analysis of Axisymmetric Bullet Based on Response Surface NSGA-II Algorithm

Abstract

The aerodynamic characteristics of the axisymmetric bullet determine the effectiveness of the final damage purpose. To solve the contradiction problem between the aerodynamic drag coefficient and the objective volume in the design and selection of oval head bullet, four design parameters, namely, head length, body length, and tail length and tail angle, are selected as response factors. They have significant impacts on the aerodynamic performance and volume of the rotating stable axisymmetric bullet. The optimization boundary for these four parameters is established, and the sample space of 30 optimization groups is created by using the response surface method. Through the finite volume simulation of these 30 groups of samples, the corresponding drag coefficient and bullet volume are obtained. The function between the drag coefficient, bullet volume and sample parameters is fitted. Then, the NSGA-II algorithm is combined to conduct optimization analysis on the fitting function, and four response factor combinations on the Pareto boundary are obtained, where the drag coefficient is decreased and the bullet volume is increased. The second derivative of the solution set is analyzed to determine the optimal shape of the oval head axisymmetric bullet. The comparison shows that the drag coefficient of the optimized bullet shape is 13.1% lower than the average drag coefficient of 30 original samples, and the volume is increased by 39.5%. The method, combined the response surface method with NSGA-II algorithm, effectively improves the design efficiency of oval head axisymmetric bullet optimization design.

1. Introduction

The development of aviation technology has promoted the effective and deep application of bullets. Oval head axisymmetric bullet is a new type of bullet that relies on the kinetic energy to penetrate the incoming target and continuously destroy the target. They have strong practical significance in the face of incoming targets that can maintain sufficient kinetic energy [1].

To improve the hit rate of incoming targets, oval head bullets need to have a low drag shape to maintain stable high-speed flight. At the same time, it is necessary to maximize the bullet volume to achieve a higher explosive charge capacity and improve the explosive damage effectiveness after penetrating the target. Therefore, under the conditions of determined initial velocity, caliber, and configuration of the oval head bullet, it is necessary to conduct aerodynamic shape optimization analysis and auxiliary design selection for the oval head bullet to seek the relatively optimal solution between the drag coefficient and the bullet volume. And it enables the bullet to increase the charge capacity while maintaining its initial velocity as much as possible. With the advantages of simple structure and low cost, the rotating stabilized oval head bullet has become one of the main alternative optimized bullet types for various oval head cores [2]. Considering that the oval-shaped truncated cone head structure is most conducive to the realization of post-target energy release for the explosive charge [3], this paper would focus on the aerodynamic shape optimization of a 14.5 mm caliber, oval-head, rotationally stable bullet type, as shown in Figure 1 for its physical prototype.

The theoretical characteristics and optimization research of the aerodynamic shape of rotationally stable bullets have been conducted for more than half a century. With the wide application of the mathematical and physical model of the aerodynamic shape of the rotating stable bullet and modern information technology, the optimization research of the aerodynamic shape can be roughly divided into the optimization research based on the mathematical and physical model and simulation optimization method and the optimization research based on intelligent algorithm.

In the 1980s, Miao Ruisheng and Wu Jiasheng comprehensively presented a physical theoretical model and systematic exposition of the aerodynamics of rotationally stable bullets [4]. Subsequently, research directions emerged that focused on aerodynamic parameter measurements, aerodynamic similarity of bullets, and aerodynamic expert systems for rotationally stable bullets based on mathematical models. For instance, Yao Yongxing et al. [5] and Shen Zhongshu et al. [6] described and applied numerical engineering methods to calculate aerodynamic parameters. However, due to human factors, it was necessary to repeatedly measure the aerodynamic parameters of the mathematical model and use the average values in engineering calculation models. This would result in high preparation costs for the early stages of aerodynamic calculations for bullet shapes, and significant human-induced errors in precision. To reduce the cost of aerodynamic measurements for bullets and support rapid and repeated predictions, Wang Zhijie et al. [7] and Wessam Mahfouz Elnaggar [8] preselected different bullet types and size combinations, calculated the corresponding aerodynamic parameters based on finite volume methods, and optimized them accordingly. However, the optimization results were greatly influenced and limited by the preselected bullet types and size combinations, and the finite volume calculation time was costly. Therefore, Wang Liangming [9] and Wang Zhongyuan [10] proposed and effectively applied a theory for deriving aerodynamic parameters between different caliber similar bullets. Additionally, to further improve the optimization efficiency of the aerodynamic shape of bullets, Yuan Zihuai et al. [11] developed an aerodynamic shape optimization expert system for bullets using software and database technology, realizing a full-process optimization design from aerodynamic engineering estimation to ballistic integration calculation. The current research has made significant progress in the control of high-speed aircraft and projectiles, as well as in aerodynamic characteristics and protective structures. Wang et al. [12] proposed a combined control method of aerodynamic force and lateral thrust based on regional pole configuration, achieving rapid attitude response for hypersonic skimming missiles. Cheng et al. [13] revealed the destruction mechanism of explosive-formed projectiles penetrating multiple layers of steel targets through experiments and numerical simulations. Jiao et al. [14] established an aerodynamic characteristic analysis model for small cylindrical projectiles, and determined the main influencing factors using global sensitivity analysis. Yin et al. [15] simulated the aerodynamic response of rotating-cone swing coupled projectiles, revealing the significant influence of cone swing motion on the flight stability.

Due to the limitations of mathematical models, it is usually necessary for personnel with sufficient experience in aerodynamic shape design to create models for different application scenarios. The optimization work conducted in this manner is not easily scalable or transferable. Additionally, various simulation systems often require significant computational resources, making it challenging to support extensive aerodynamic parameter optimization searches. In the late 1990s, the industry began introducing intelligent optimization algorithms, leveraging existing aerodynamic samples to search for optimal aerodynamic shapes. This approach effectively expanded the scope and efficiency of optimization searches. For instance, Wang Xiaopeng et al. [16] and Li Kejing et al. [17] combined genetic algorithms with maximum likelihood and niche-based optimal preservation strategies to predict aerodynamic parameters and optimize bullet structures. However, these methods can sometimes get trapped in local optimal solutions. To avoid falling into local optima during the optimization process, Deb K et al. [18], LIU Lin et al. [19], and Chen Liang et al. [20] further improved the efficiency and search range of bullet shape optimization by utilizing various modified genetic algorithms, particle swarm optimization [21], and topological optimization [22]. In recent years, genetic algorithms have also been effectively applied in the multi-objective optimization of aerodynamic shapes for vehicles flying near the speed of sound [23]. Simultaneously, to enhance the global accuracy of multi-objective optimization, Zhao Qiang et al. [24], Qiang Zhao et al. [25], and Tianbao Ma et al. [26] achieved good results by combining approximation models such as Kriging with optimization algorithms. Nevertheless, due to the high cost of acquiring and accurately measuring aerodynamic optimization samples for bullet shapes, as well as the complexity of multi-response factor combinations in multi-objective optimization scenarios, the above optimization models cannot provide clear optimization directions. Therefore, they are not suitable for situations where multiple response factors and multi-objective optimization occur simultaneously.

In recent years, the combination of response surface methodology (RSM) and intelligent optimization algorithms has been widely applied in scenarios where multiple response factors and multi-objective optimization need to be optimized simultaneously [27,28]. Response Surface Method (RSM) is a fitting design approach that uses approximate functional relationships to represent the connections between variables and the objective function [29]. By establishing a continuous response variable surface model, it can significantly reduce the number of experimental tests, thus achieving a cost-effective product design optimization method that saves manpower, material, and financial resources [30]. Additionally, RSM can provide effective optimization directions for product design. Typically, after obtaining a certain amount of simulation data through reasonable experiments, RSM employs multivariate quadratic regression equations to fit the functional relationships between response factors and response values. The variance analysis of the regression equation is then used to seek optimal parameters for the quadratic regression equation. Sensitivity analysis is also conducted to investigate the sensitivity of changes in various response factors to the response value. The traditional methods for aerodynamic optimization of bullet shapes at supersonic speeds are numerical simulation, empirical formula derivation, and wind tunnel tests. Their disadvantages are high computational cost, low accuracy, and high test cost, respectively. By using the multi-objective optimization method proposed in this paper, the optimal solution in the optimization space can be quickly found based on high-quality simulation calculation data, ensuring good prediction accuracy while avoiding high test and computational costs.

The aim of this study is to seek a rapid optimization design method for the bullet structure design of multi-objective conflicts. Based on the theory and experience of aerodynamic shape design for spin-stabilized bullets, fixed simulation boundary conditions such as flow field properties and attack angles of the bullet are selected. Using the classical aerodynamic design theory and geometric conditions of volume size for spin-stabilized bullets, the main optimization parameters for the shape of oval head bullets are chosen. According to the response surface method, these parameter objects are combined to design the optimization space. Initial optimization data is obtained by calculating these optimized shape combinations using the finite volume simulation method. Then, traditional optimization algorithms are employed to conduct optimization analysis for two objectives: the drag coefficient of the bullet and the volume of the oval head bullet. This provides a reference for selecting the optimal geometric structure parameters of oval head bullets under different working conditions. The optimization process is illustrated in Figure 2. This study effectively enhances the design efficiency by combining the response surface method with the NSGA-II algorithm in the optimization design of the shape selection for bullets. It successfully resolves the conflict between the aerodynamic drag coefficient and the volume of the bullet.

2. Optimization Data Design and Simulation

2.1. Physical Geometric Model

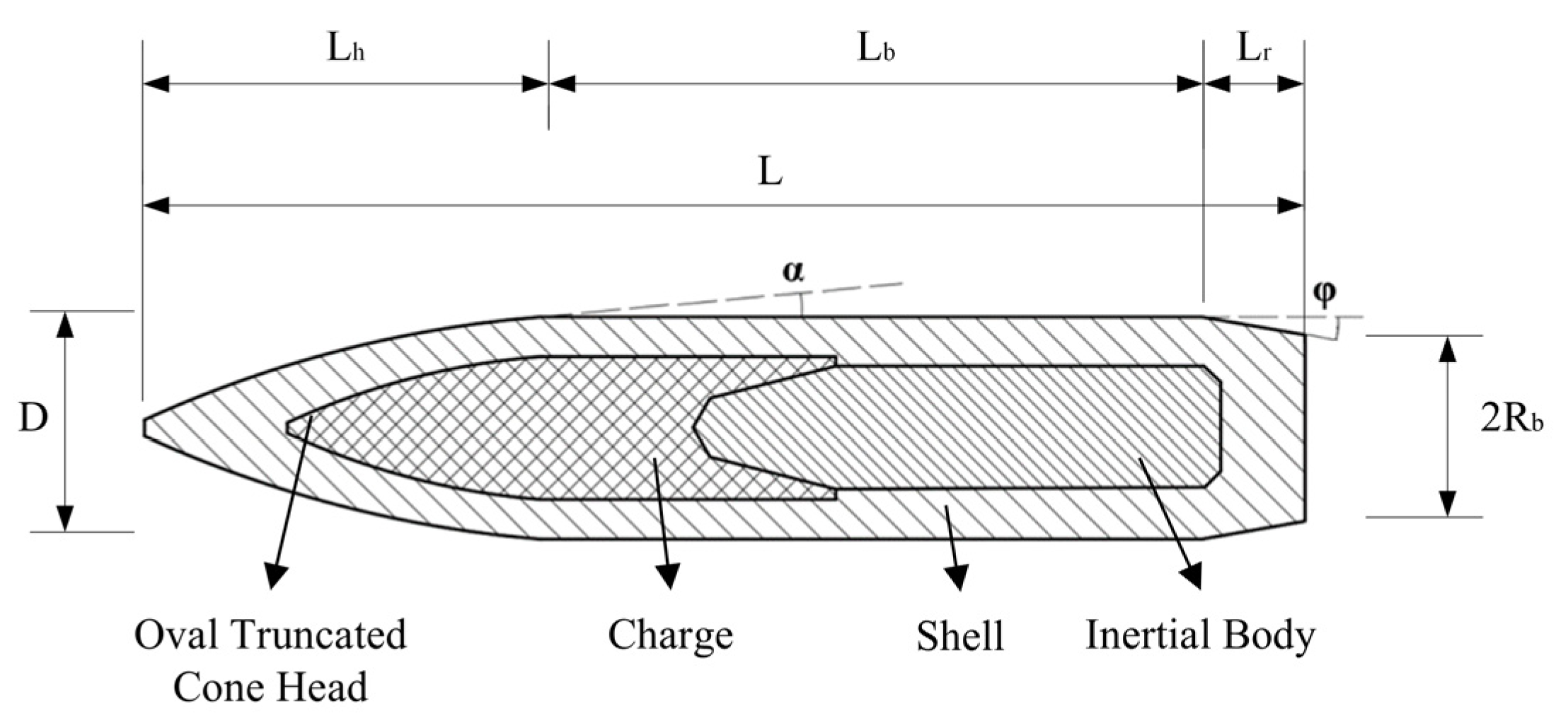
The initial two-dimensional geometric selection for the spin-stabilized oval head bullet is shown in Figure 3. In the figure, $D$ represents the diameter of the bullet. The length of the bullet head is $L_h$, the length of the bullet body is $L_b$, the length of the bullet tail is $L_r$, the radius of the bullet base is $R_b$, the tail angle is $\phi$, the total length of the bullet is $L$, and the included angle between the tangent line of the front edge of the bullet and the bullet body is $\alpha$.

2.2. Finite Volume Simulation Mathematical Model

Taking into account the near-field defense of oval head bullets under near-ground conditions, the external flow field fluid can be approximated as an ideal gas. The numerical solution employs the integral Navier–Stokes (N-S) equations to establish a mathematical fluid dynamics model for the external flow field of the bullet [31].

The continuity equation is:

$${\displaystyle \frac{\partial }{\partial \mathrm{t}}}{\displaystyle \underset{\Omega }{\iiint }\rho }\mathrm{d}\Omega +{\displaystyle \underset{s}{∯}\rho V•}n\mathrm{d}S=0$$

(1)

Here, $\mathsf{\Omega }$ represents the control volume of the integral equation $\mathrm{d}\mathsf{\Omega }=\mathrm{dxdydz}$; $\mathrm{S}=\partial \mathsf{\Omega }$ is the surface of the control volume; $\rho$ is the density; and $V$ is the velocity vector of the fluid motion.

The energy equation is:

$${\displaystyle \frac{\partial }{\partial \mathrm{t}}}{\displaystyle \underset{\Omega }{\iiint }\rho E\mathrm{d}\Omega }+{\displaystyle \underset{S}{∯}\rho EV•n\mathrm{d}S={\displaystyle \underset{\Omega }{\iiint }\rho F•V\mathrm{d}\Omega +{\displaystyle \underset{S}{∯}({\overleftrightarrow{\tau }}^{\ast }•V-q)}}}•n\mathrm{d}S$$

(2)

Here, $\rho E=\rho e+{\displaystyle \frac{\rho }{2}}V$, $E$ represents the total energy, and e represents the internal energy. $q=-k\nabla T$, $q$ is the heat flux, and k is the thermal conductivity coefficient. n is the unit normal vector, $\tau$ is the surface stress, and F is the volume force.

According to the experiments reported in ref. [2], the detonation threshold velocity of oval head bullets is generally above Mach 1.1 [3]. The flight speed covers the transonic and supersonic ranges, and the flow field around the bullet is a turbulent field with a high Reynolds number. Taking into account the respective advantages of model $\mathit{k-}\omega$ in near-wall calculations and model $\mathit{k-}\omega$ in far-field calculations, this article selects the SST $\mathit{k-}\omega$ turbulence model. This model adds a lateral dissipation derivative term and modifies the turbulence viscosity, making it better suited for the flow field around bullets experiencing transonic and supersonic shock wave phenomena [32]. The SST $\mathit{k-}\omega$ turbulence model equation is as follows:

$$\left\{\begin{array}{l}{\displaystyle \frac{\partial k}{\partial t}}+\overline{u_i}{\displaystyle \frac{\partial k}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left[\left(u+{\displaystyle \frac{u_t}{{\sigma }_k}}\right){\displaystyle \frac{\partial k}{\partial x_j}}\right]+G_k-{\beta }^{\prime }k\omega \\ G_k=-{\displaystyle \frac{\overline{u_i^{\prime }{u}_j^{\prime }}\partial u_j}{\partial x_j}}\\ {\displaystyle \frac{\partial \omega }{\partial t}}+\overline{u_i}{\displaystyle \frac{\partial \omega }{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left[\left(u+{\displaystyle \frac{u_t}{{\sigma }_{\omega }}}\right){\displaystyle \frac{\partial \omega }{\partial x_j}}\right]+G_{\omega }-{\beta }^{ȃ}{\omega }^2+D_{\omega }\\ G_{\omega }=\xi {\displaystyle \frac{\omega }{k}}{G}_k\end{array}\right.$$

(3)

Here, t represents time, $\overline{u_i}$ represents the time-averaged velocity in the direction, $x_i$ and $x_j$ represent the position coordinates in the $\mathrm{i}$ direction and $\mathrm{j}$ direction, respectively, $u$ represents the dynamic viscosity of the fluid, $u_t$ represents the turbulent viscosity, ${\sigma }_k$ and ${\sigma }_w$ are the turbulent Prandtl constants for turbulent kinetic energy $k$ and dissipation rate $\omega$, respectively. $G_k$ represents the generation term of turbulent kinetic energy caused by the mean velocity gradient, $G_{\omega }$ represents the generation term of turbulent kinetic energy influenced by buoyancy, $\xi$ is the turbulent viscosity coefficient, its value depends on the magnitude of the Reynolds number, ${\beta }^{\prime }$ and ${\beta }^{″}$ are model constants, and $D_{\omega }$ represents the orthogonal divergence term.

2.3. Aerodynamic Finite Volume Analysis and Optimal Parameter Selection for Bullet Shape

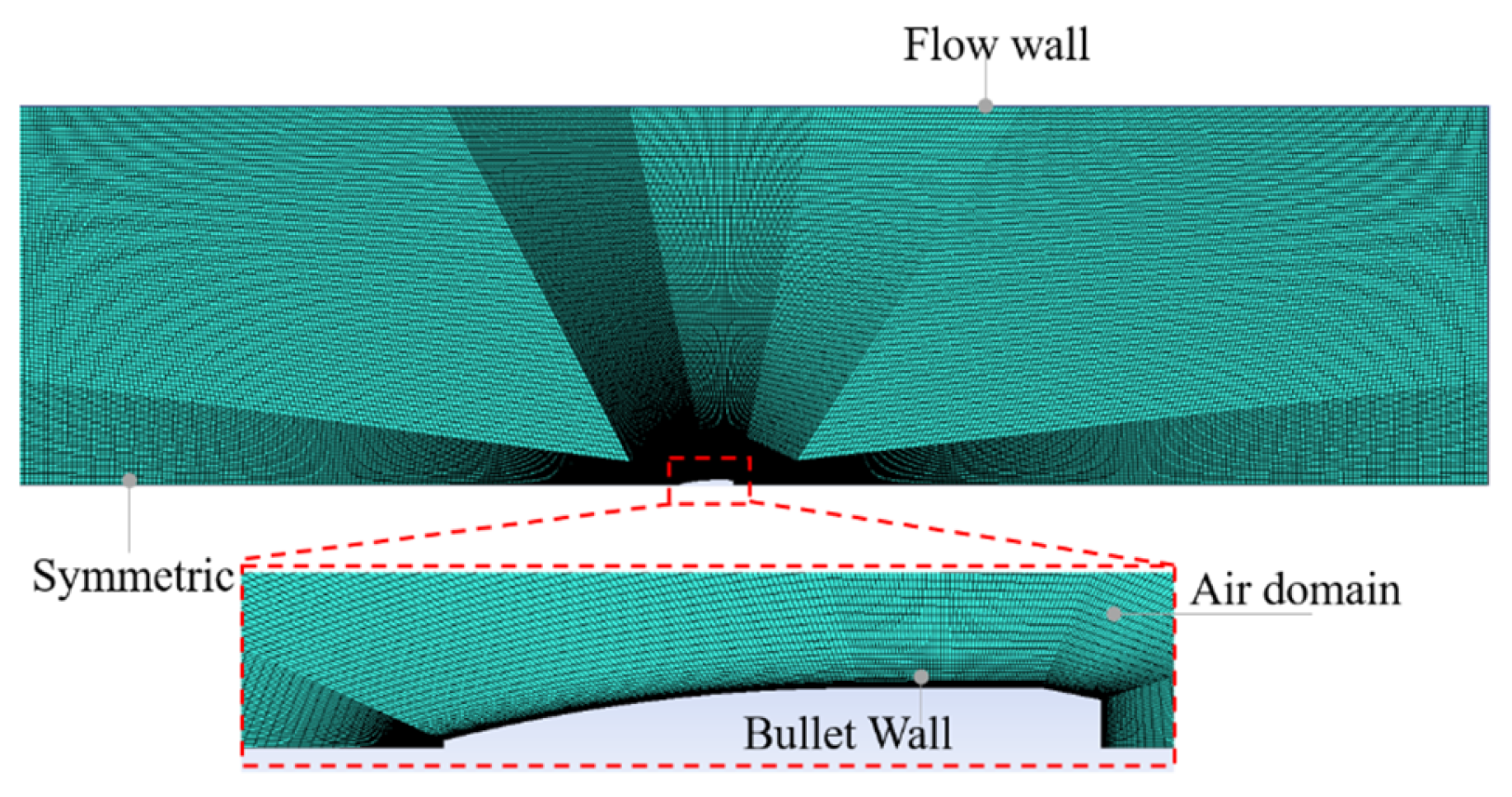
In the Fluent software, the flow field calculation conditions are set to near-ground meteorological conditions, with the incoming gas treated as an ideal gas with a Mach number of 2, and Sutherland viscosity employed. The attack angle is set to horizontal. The bullet surface adopts a no-slip adiabatic solid wall boundary condition, while the outer boundary of the flow field employs a pressure far-field boundary condition. The lengths of the flow fields in the front and rear areas of the bullet in the far-field region are set to 13 times the length of the bullet, and the width of the side flow field of the bullet body is set to 38 times the diameter of the bullet. To improve the capture accuracy of the laminar flow influence on the bullet surface, the mesh area is encrypted near the body wall boundary layer of the bullet, with the first layer height set to less than 2.4 × 10⁻⁷ m. The boundary layer is extended in 20 layers with a growth factor of 1.2. In Figure 4, it shows the position of the bullet in the computational domain and the size ratio of the domain. It clearly marks the settings of boundary conditions such as inlet (velocity inlet), outlet (pressure outlet), wall (no-slip wall), and symmetry plane.

The grid independence analysis is as shown in

Table 1. Grid independence analysis.

Mesh Size (×104 Cells)	Drag Coefficient	Deviation (%)
3.4	0.255	13.6
4.5	0.27	8.5
5.6	0.278	5.7
6.8	0.282	4.4
8.6	0.295	/

. Deviations are calculated between different grid quantities and the standard value based on the maximum grid quantity. When the grid quantity is 68,000, the deviation of the calculated drag coefficient is 4.4%, which is the smallest compared with other deviation results. Therefore, the grid quantity is set as 68,000 for simulation calculations.

When selecting the SST model for the finite volume calculation, the solver is chosen to be Pressure-Based finite volume, and the discretization method is set to second-order upwind scheme. The Roe-FDS flux difference method is employed for convective fluxes. To verify the accuracy of the simulation calculation for the supersonic flow field of the bullet, it is simulated based on the AD report [33] in this study. Through calculation, the pressure cloud diagram of the flow field is shown in Figure 5. At a Mach number of 2, the drag coefficient is 0.27135, which differs from the drag coefficient of 0.26 reported in ref. [33] by 4.36% deviation, approximately less than 5%. This indicates that the simulation calculation model for the supersonic flow field of the bullet designed in this paper is accurate and applicable. It can be seen from Figure 5 that there are distinct shock wave fronts in the supersonic flow field at the head and the front lateral edge of the bullet, as well as at the junction between the head and the body of the bullet, and at the tail section of the bullet. The shock wave front area from the head to the junction between the head and the body is a high-pressure area, while the body and tail sections of the bullet are negative pressure turbulent areas. According to the design theory of rotating stable bullet shapes [34] and experimental experience, the drag of the bullet at zero angle of attack is mainly composed of the head shock wave drag, the rotational friction drag on the surface of the bullet body, the tail drag, and the hull vortex drag. Obviously, the high and negative pressure areas in Figure 5 are one of the important factors causing the flight drag of the bullet. Therefore, the shape of the bullet head, the angle between the front lateral edge and the body, the length of the body, and the shape of the tail are directly related to the generation of flight drag in the bullet.

According to experimental analysis in ref. [3] and the theory in ref. [34], when the side edge of the rotating stable bullet’s head is designed as a circular arc oval shape, it can effectively reduce the generation of shock waves and vortices on the side edge of the head under supersonic conditions, resulting in a lower drag coefficient. Additionally, considering the ease of processing during the generation of the circular arc side edge generatrix, the side edge of the oval head bullet’s head is set as a circular arc shape in this study. At this point, when the diameter of the oval head bullet is fixed, the shape of the head and the angle of the front side edge are mainly directly related to the length of the head. Meanwhile, with a fixed bullet diameter, the size of the negative pressure region at the tail is obviously related to the length and angle of the tail. Therefore, based on the above considerations, the oval head bullet is selected based on the classic rotating stable bullet shape, taking into account the design objectives of minimizing the drag coefficient and maximizing the internal volume of the bullet. In this study, the length of the head, the length of the body, the length of the tail, and the tail angle are chosen as the optimization parameters.

2.4. Optimization Parameter Boundary Setting

According to ref. [34], the optimal angle α between the tangent of the generatrix of the side edge of the bullet’s head and the body is generally controlled within $1–3°$ range. Based on the geometric derivation from Figure 3, it can be obtained:

$$\theta =90-\left(\arcsin \left({\displaystyle \frac{\sqrt{L_h^2+{\left(\frac{D}{2}\right)}^2}}{2E}}\right)-\arcsin \left({\displaystyle \frac{L_h}{\sqrt{L_h^2+{\left(\frac{D}{2}\right)}^2}}}\right)\right)\times {\displaystyle \frac{180}{\pi }}$$

(4)

Here, $E$ represents the radius of the head’s leading edge. According to the calculation using formula (1), when $E=1.5D$, selecting a value within the range of $2.5D\le L_{\mathrm{h}}\le 3.5D$ can satisfy the condition of $1°\le \alpha \le 3°$. Therefore, the optimization of the angle α between the generatrix of the side edge of the bullet’s head and the body can be transformed into the optimization of $L_{\mathrm{h}}$ the length of the bullet’s head under a fixed circular arc curvature.

Although an excessively long bullet body can increase the side rotational friction drag, a too-short body can also lead to an increase in induced drag [34]. Moreover, the length of the bullet body has significant geometric implications for the size of the oval head bullet charge volume. In this paper, the length of the bullet body is taken as $1.5D\le L_b\le 2.5D$ from ref. [35]. At the supersonic speed, the hull and keel vortex drag of the bullet increases rapidly. To effectively reduce this drag, without affecting the volume of the oval head bullet, the tail of the bullet is typically designed as a short truncated cone, allowing the airflow lines at the tail boundary layer to align with the edges of the hull. Based on optimization experience from ref. [35], the hull angle $\phi$ in Figure 3 is controlled within 3°~12° range to keep the hull and keel vortex drag within certain limits. Geometric derivations from Figure 3 yield:

$$\phi =\arctan \left({\displaystyle \frac{D-2R_b}{2L_r}}\right)\times {\displaystyle \frac{180}{\pi }}$$

(5)

At the same time, according to ref. [31], the length of rotationally stabilized bullets cannot be too long due to certain limitations on their rotational speed, and generally speaking, it should be within $L\le 5.5D$ range. Therefore, based on the derived values of $2.5D\le L_h\le 3.5D$ and $1.5D\le L_b\le 2.5D$, the value of $0.5D\le L_r\le 1.5D$ can be determined. As can be seen from Equation (5), once the hull angle $\phi$ and hull length $L_r$ are determined, the radius of the bullet base $R_b$ is also simultaneously determined. Therefore, only $\phi$ and $L_r$ need to be optimized.

In summary, for the optimization of the oval head bullet’s shape, considering both the correlation between the optimization objectives and the geometric shape, as well as the ease of obtaining optimization data, the length of the bullet’s head $L_h$, the length of the bullet’s body $L_b$, the length of the hull $L_r$, and the hull angle $\phi$ are selected as the main influencing factors that affect the aerodynamic shape and volume of the oval head bullet (where influencing factors refer to the parameters that affect the test results [36]). Based on the two-level approach of the response surface method [37], the optimization boundary conditions for these four influencing factors are set as shown in

Table 2. Levels of influencing factors for shape optimization.

Symbol	Factor Name	Lower Limit	Upper Limit
Lh	Head Length	2.5D	3.5D
Lb	Body Length	1.5D	2.5D
Lr	Tail Length	0.5D	2D
ψ	Tail Angle	3°	12°

.

Given the optimization background of this paper, which focuses on assisting in the selection of bullet shapes, it is assumed in the sample simulations that the overall density of the bullet is uniform and that the moment of inertia about the center of gravity is not considered.

2.5. Sample Simulation Based on Response Surface Methodology

To obtain accurate experimental results with fewer simulation experiments, this paper adopts the Box–Behnken design method [38] to obtain the level combinations of the four influencing factors for the shape of the oval head bullet, as shown in Table 2. The table contains 30 complete level combinations of the shape parameters for the oval head bullet, among which 24 are analysis factors and 6 are zero-point factors, meaning that the parameter level combinations are identical and used for estimating experimental errors. Based on the finite volume analysis model described in Section 2.2, simulations are performed on these 30 sets of parameter level combinations. After the simulation analysis, the drag coefficients and volumes of the bullets corresponding to the 30 level combinations are obtained, as shown in the last two columns of

Table 3. Response surface combinations and simulation results for shape of oval head axisymmetric bullet.

Combination No.	Simulation Experiment Impact Factor Combination (D = 14.5 mm)				Simulation Results
	${\mathit{L}}_{\mathit{h}}$/D	${\mathit{L}}_{\mathit{b}}$/D	${\mathit{L}}_{\mathit{r}}$/D	$\mathit{\phi }$/°	Drag Coefficient	Bullet Volume/mm3
1	3.00	2.00	1.00	0.00	0.282	10,622.55
2	2.50	2.50	1.50	3.75	0.2524	11,593.53
3	3.00	2.00	1.00	7.50	0.2457	10,046.87
4	3.50	1.50	0.50	11.25	0.22026	9357.41
5	3.00	2.00	2.00	7.50	0.224	10,938.84
6	4.00	2.00	1.00	7.50	0.2374	12,034.65
7	3.00	2.00	0.00	7.50	0.2712	8228.16
8	2.00	2.00	1.00	7.50	0.301	8629.51
9	2.50	1.50	0.50	3.75	0.27503	7387.80
10	2.50	2.50	0.50	11.25	0.27699	9636.57
11	2.50	1.50	1.50	11.25	0.2677	8142.83
12	3.50	2.50	1.50	11.25	0.2403	12,205.30
13	2.50	2.50	0.50	3.75	0.2816	9782.20
14	3.50	1.50	1.50	11.25	0.23626	9810.90
15	3.50	2.50	1.50	3.75	0.23104	13,261.86
16	2.50	1.50	1.50	3.75	0.25527	9199.14
17	3.00	2.00	1.00	7.50	0.24028	10,047.66
18	3.00	2.00	1.00	15.00	0.272	9569.15
19	3.00	2.00	1.00	7.50	0.24574	10,047.66
20	3.50	1.50	0.50	3.75	0.24828	9055.87
21	3.50	2.50	0.50	3.75	0.2564	11,450.27
22	3.00	2.00	1.00	7.50	0.23408	10,047.66
23	3.00	2.00	1.00	7.50	0.23517	10,047.66
24	2.50	2.50	1.50	11.25	0.27091	10,537.23
25	3.50	1.50	1.50	3.75	0.22875	10,867.47
26	3.00	2.00	1.00	7.50	0.24505	10,047.66
27	3.00	1.00	1.00	7.50	0.24321	7653.26
28	3.50	2.50	0.50	11.25	0.25847	11,304.90
29	3.00	3.00	1.00	7.50	0.24924	12,442.05
30	2.50	1.50	0.50	11.25	0.28707	7242.17

.

3. Optimization Based on Response Surface and NSGA-II Algorithm

As can be seen from the finite volume simulation data, there exists an uncertain correlation between the aerodynamic drag coefficient and the bullet volume distribution under different structural parameters of the oval head bullet shape (as shown in Figure 6). To find the optimal combination of the minimum drag coefficient and the maximum bullet volume within a certain range of oval head bullet dimensions and structures, as well as to establish the relationship between the four main parameters of the oval head bullet shape and the drag coefficient and bullet volume, this paper adopts a response surface method in conjunction with the Non-dominated Sorting Genetic Algorithm II (NSGA-II) to design the following optimization process. NSGA-II is one of the mainstream algorithms in the field of multi-objective optimization. It reduces the complexity of the non-dominated sorting genetic algorithm, and has the advantages of fast optimization speed, good robustness, and good convergence of the solution set [18], which meets the precision requirements of the optimization objectives in this paper.

3.1. Establishment of Dual-Objective Response Surface Model

There are various mathematical models that can be selected for RSM, including unary linear regression models, multivariate linear regression models, and polynomial regression models. Based on the theory in calculus that any function can be approximated by a piecewise polynomial of several terms, this paper adopts a second-order polynomial model derived from the Taylor expansion:

$$Y=a_0+{\displaystyle \sum _{i=1}^n{a}_i{x}_j}+{\displaystyle \sum _{i=1}^n{a}_{ii}{x}_j^2+}{\displaystyle \sum _{i=1}^{n-1}{\displaystyle \sum _{j=2}^n{a}_{ij}{x}_i{x}_j+\epsilon }}$$

(6)

In Equation (6), $Y$ represents the target value, $a_0$ is the constant term, $a_i$ is the linear coefficient, $a_{ii}$ is the quadratic coefficient, $a_{ij}$ is the cross-term coefficient, $\varepsilon$ is the random error, and $n$ is the number of variables. By performing a quadratic multiple regression fit on the experimental factor combinations and their results in Table 2, we obtain the quadratic polynomial regression equations for the drag coefficient cd and the bullet volume V, respectively.

$$\begin{array}{r}cd=0.690677-0.204903*L_h-0.007552*\phi -0.041682*L_b\\ -0.044063*L_r-0.001585*L_h*B+0.013958*L_h*L_b\\ +0.006838*L_h*L_r+0.000709*\phi *L_b+0.002208*\phi *L_r\\ -0.009037*L_b*L_r+0.02514*L_h^2+0.000586*{\phi }^2\\ +0.002165*L_b^2+0.00354*L_r^2\end{array}$$

(7)

$$\begin{array}{r}V=-(87000+32000*L_h+11000*\phi +984000*L_b\\ +1265000*L_r+5656.67*L_h*\phi -42000*L_h*L_b\\ -42000*L_h*L_r-565.667*\phi *L_b-52000*\phi *L_r\\ +42000*L_b*L_r+118000*L_h^2+494.741*{\phi }^2\\ +9529.17*L_b^2-167000*L_r^2);\end{array}$$

(8)

3.2. Dual-Objective Optimization Based on NSGA-II

By combining Equations (7) and (8) with the NSGA-II algorithm, the parameter optimization is conducted for the four external dimension parameters of the oval head bullet, namely, the head length $L_h$, body length $L_b$, tail length $L_r$, and tail angle $\phi$, with the assistance of the MATLAB (R2020a Campus version) genetic algorithm toolbox. This algorithm is simultaneously used to obtain the predicted values of the bullet’s drag coefficient and volume. The parameter settings for the NSGA-II algorithm are presented in

Table 4. NSGA-II algorithm parameter settings.

Parameter Name	Parameter Value	Description and Remarks
fitnessfcn	@Myfun	Objective function (including the fitting functions of Equations (7) and (8))
Number of Variables	4	Total number of optimization variables
Lower	[2, 0, 1, 0]	Lower limits for all optimization parameters (derived from Table 2)
Upper	[4, 15, 3, 2]	Upper limits for all optimization parameters (derived from Table 2)
PopulationSize	200	Size of the population
ParetoFraction	0.5	Crossover proportion
Generations	200	Number of iterations
TolFun	1 × 10−100	Optimization tolerance
PlotFcns	@gaplotpareto	Plotting function is a 2D scatter plot

.

After configuring the corresponding parameters, running the edited program in MATLAB yields the Pareto Front between the drag coefficient and volume of the oval head bullet as shown in Figure 7. This represents the distribution of 100 sets of Pareto Front optimized solutions (non-dominated solutions) obtained after solving with the gamultiobj function. As can be seen from the figure, the 100 optimized solutions are distributed smoothly and uniformly, and the optimized solutions are significantly closer to the Pareto Front compared to the original sample distribution. This indicates that the optimized solutions have significantly improved relative to the response surface sample data.

During the bi-objective optimization process of reducing the drag coefficient and increasing the volume of the oval head bullet, the goal is to simultaneously minimize the drag coefficient of the bullet shape while maximizing its volume, as a smaller drag coefficient and a larger volume would result in a greater payload capacity. The optimal solution set is obtained through multi-objective genetic algorithm optimization. However, the optimal solution needs to be selected based on the actual engineering application requirements. For example, the weight decision algorithm [39] can be used based on the weight coefficients of engineering requirements.

3.3. Analysis of Distribution of Optimized Solution Sets

A further analysis of the distribution of the 100 optimized solution sets in Figure 7 reveals the following patterns:

(a)

The leftmost point among the 100 optimized solutions represents the minimum drag coefficient, with the smallest volume. Conversely, the rightmost point represents the maximum drag coefficient, with the largest volume.

(b)

As the drag coefficient increases from a smaller value, the points to the left of the blue boxed region exhibit a relatively small increase in drag coefficient, but a relatively rapid increase in volume.

(c)

To the right of the points in the blue boxed region, as the drag coefficient continues to increase, the increase in volume becomes significantly smaller.

From the perspective of the design objectives for the oval head bullet shape in this study, it is evident that the leftmost and rightmost points among the 100 optimized solutions only satisfy one of the two optimization objectives while sacrificing the other. Therefore, it is necessary to find the most suitable solution among the 100 optimized solutions that offers a sufficiently small drag coefficient and a sufficiently large bullet volume. Obviously, the set of points (solution set) within the blue boxed region in Figure 7 represents the situation where the volume increases to its maximum with the smallest increase in drag coefficient as the set of points changes from left to right. Further to the right, the increase in volume becomes less significant. Consequently, it is necessary to identify the most suitable inflection point within the blue boxed region as the optimal solution among the 100 optimized solutions.

Using the software Origin, the set of 100 optimized solution points in Figure 7 is sorted according to the drag coefficient to generate a curve, as shown in Figure 8. First-order derivative filtering is applied to this curve, followed by the calculation of the second-order derivative. It can be observed that the second-order derivative curve exhibits a minimum value in Figure 8. This value geometrically signifies the point where the distribution of optimized solutions begins to change direction, indicating a shift in the distribution inflection point. At this point, the increase in drag coefficient starts to significantly outpace the increase in volume. In Origin, the drag coefficient value at this inflection point is determined to be 0.22053, with a corresponding bullet volume of 14,005.21 mm³. The four optimized parameters for the oval head bullet shape corresponding to this point in the optimized solution set are: L_h = 47.21 mm, L_b = 40.36 mm, L_r = 29 mm, ψ = 5.14°.

4. Verification of the Optimal Parameter Set for the Shape Optimization of Oval Head Bullets

Based on the optimal combination of the main parameters for the shape of the oval head bullet obtained through the response surface method and NSGA-II algorithm in Section 3.3, a new analysis model is established for simulation analysis under the condition of maintaining other variables unchanged. The new model is set with a head length of 47.12 mm, a body length of 40.36 mm, a tail length of 29 mm, and a tail angle of 5.14°. Under near-ground meteorological conditions, the incoming gas flow is considered as an ideal gas with a Mach number of $Ma=2$, and the attack angle is set to horizontal 0°. The simulation results indicate a drag coefficient of 0.2312 for the oval head bullet. The pressure contour of the supersonic external flow field for the bullet is shown in Figure 9. It can be observed that under the optimal dimensions for the oval head bullet shape, the drag coefficient obtained from the simulation differs from the predicted value of the NSGA-II algorithm by approximately 4.84%. This suggests that the optimization predictions made by the NSGA-II algorithm are relatively accurate and effective, demonstrating their practical value. Some reasons are considered to cause this deviation. The local fitting accuracy of the response surface model decreases under supersonic conditions. Systematic errors are introduced by mesh division and turbulence model assumptions in the CFD numerical simulation process. There is a deviation between the excessively high precision of the optimization results and the CFD calculation results.

Furthermore, a comparison with other horizontal schemes presented in Table 3 reveals that the optimized optimal solution set achieves an optimal balance between the drag coefficient and the volume of the oval head bullet. When comparing the optimal solution with Group 4 in Table 3, it can be seen that while the drag coefficient only increases by 0.122%, the volume increases by 49.7%. Similarly, comparing the optimal solution with Group 15 in Table 3 shows that when the volume increases by 5.61%, the drag coefficient decreases by 4.55%. This demonstrates the significant optimization effect of the NSGA-II algorithm on the optimization space designed by the response surface method. It is evident that the combination of the response surface method and NSGA-II algorithm successfully achieves the design objectives of minimizing the drag coefficient and maximizing the volume of the oval head bullet during the selection of its shape. The original bullet has concentrated high pressure at the head, with sharp shock waves and greater head pressure. It also features a large flow separation area at the tail, a pressure recovery area far from the tail, and a more extensive distribution of low-pressure areas. The optimized oval head makes the high-pressure distribution gentle, “softens” the shock waves, reduces the head pressure, achieves uniform tail pressure recovery, and minimizes the low-pressure area. The original bullet, with strong shock waves and a large flow separation area, has high wave resistance and separation resistance (base resistance). After optimization, the wave resistance decreases due to the dispersed intensity of shock waves. The delayed or weakened separation reduces frictional resistance and separation resistance, leading to a significant drop in the total drag coefficient. The oval head increases the internal volume, enables gradual airflow compression and a uniform pressure field, thereby reducing resistance and increasing range. This facilitates stable detonation of energetic bullet, improves damage consistency, and achieves “structure-pneumatic” collaborative optimization.

5. Conclusions

A dual-objective optimization study is conducted to simultaneously minimize the drag coefficient and maximize the volume of an oval-head bullet’s geometric shape, aiming to identify an optimal set of dimensional parameters. Compared to the average drag coefficient of 0.25376 among the 30 optimization samples before optimization, the optimal solution obtained after optimization achieves a 13.1% reduction in drag coefficient. Furthermore, the optimized bullet exhibits a 39.5% increase in volume compared to the average volume of 10,041.29 mm³ among the 30 response surface space combinations before the optimization. This demonstrates the practical feasibility of combining the response surface method with the NSGA-II algorithm in the optimization design of the oval head bullet’s shape selection. This approach has significant practical value in improving the simulation design of the bullet, reducing experimental costs, and enhancing design efficiency.