On the Sets of Stability to Perturbations of Some Continued Fraction with Applications

Abstract

This paper investigates the stability of continued fractions with complex partial denominators and numerators equal to one. Such fractions are an important tool for function approximation and have wide application in physics, engineering, and mathematics. A formula is derived for the relative error of the approximant of a continued fraction, which depends on both the relative errors of the fraction’s elements and the elements themselves. Based on this formula, using the methodology of element sets and their corresponding value sets, conditions are established under which the approximants of continued fractions are stable to perturbations of their elements. Stability sets are constructed, which are sets of admissible values for the fraction’s elements that guarantee bounded errors in the approximants. For each of these sets, an estimate of the relative error that arises from the perturbation of the continued fraction’s elements is obtained. The results are illustrated with an example of a continued fraction that is an expansion of the ratio of Bessel functions of the first kind. A numerical experiment is conducted, comparing two methods for calculating the approximants of a continued fraction: the backward and forward algorithms. The computational stability of the backward algorithm is demonstrated, which corresponds to the theoretical research results. The errors in calculating approximants with this algorithm are close to the unit round-off, regardless of the order of approximation, which demonstrates the advantages of continued fractions in high-precision computation tasks. Another example is a comparative analysis of the accuracy and stability to perturbations of second-order polynomial model and so-called second-order continued fraction model in the problem of wood drying modeling. Experimental studies have shown that the continued fraction model shows better results both in terms of approximation accuracy and stability to perturbations, which makes it more suitable for modeling processes with pronounced asymptotic behavior.

1. Introduction

Let $b_0\left(z\right),$ $a_k\left(z\right),$ $b_k\left(z\right),$ $k\in \mathbb{N},$ be certain polynomials, $z\in \mathbb{C}$, and let $N\in \mathbb{N},$ $i\left(k\right)=(i_1,i_2,\dots ,i_k)$ be a multiindex,

$$\mathcal{I}=\{i\left(k\right):1\le i_r\le N,1\le r\le k,k\ge 1\}$$

be set of multiindices, $d_0\left(\mathbf{z}\right),$ $c_{i\left(k\right)}\left(\mathbf{z}\right),$ $d_{i\left(k\right)}\left(\mathbf{z}\right),$ $i\left(k\right)\in \mathcal{I},$ be certain polynomials, $\mathbf{z}=(z_1,z_2,\dots ,z_N)\in {\mathbb{C}}^N$.

Continued fractions (see, [1])

$$b_0\left(\mathbf{z}\right)+{\displaystyle \frac{a_1\left(\mathbf{z}\right)}{{\displaystyle b_1\left(\mathbf{z}\right)+\frac{a_2\left(\mathbf{z}\right)}{{\displaystyle b_2\left(\mathbf{z}\right)+\frac{a_3\left(\mathbf{z}\right)}{{\displaystyle b_3\left(\mathbf{z}\right){+}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}}$$

and branched continued fractions (see, [2])

$$d_0\left(\mathbf{z}\right)+\sum _{i_1=1}^N{\displaystyle \frac{c_{i\left(1\right)}\left(\mathbf{z}\right)}{{\displaystyle d_{i\left(1\right)}\left(\mathbf{z}\right)+\sum _{i_2=1}^N\frac{c_{i\left(2\right)}\left(\mathbf{z}\right)}{{\displaystyle d_{i\left(2\right)}\left(\mathbf{z}\right)+\sum _{i_3=1}^N\frac{c_{i\left(3\right)}\left(\mathbf{z}\right)}{{\displaystyle d_{i\left(3\right)}\left(\mathbf{z}\right){+}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}}$$

are finding increasingly wide application in various fields of fundamental and applied sciences. The spectrum of their use covers computational mathematics, applied mathematics, theoretical and applied physics, quantum mechanics, as well as the rapidly growing field of computer science [1,3,4]. Continued fractions are used in the latest research areas such as artificial intelligence [5,6,7], cryptography [8,9,10], and signal and image processing [11,12], difference equations [13], demonstrating their effectiveness, universality, and adaptability. Continued fractions are also effectively used to solve problems in the theory of complex variable [1,14] and the theory of functions of several complex variables, in particular to construct algorithms for the expansion of formal multiple power series into corresponding branched continued fractions, such as multidimensional g-fractions with independent variables [15,16], multidimensional S-fractions with independent variables [17], multidimensional regular C-fractions with independent variables [18,19], multidimensional regular A- and J-fractions with independent variables [20,21,22]. The basis of these algorithms are the corresponding classical algorithms for constructing classes of functional continued fractions [1]. Note that the branched continued fractions of the above classes are natural expansions into branched continued fractions for hypergeometric functions Horn $H_4$ [23,24,25], Horn ${\mathrm{H}}_7$ [26,27], Appel $F_2$ [28,29,30], and Lauricella–Saran $F_K$ [31,32].

In addition to the accuracy of the approximation, a key characteristic of continued fractions and branched continued fractions are their stability to perturbations. Stability to perturbations is a fundamental property that studies how perturbations of the elements of a continued fraction (or branched continued fraction) affect the values of its approximants. When computing approximants of continued fractions, this property guarantees that rounding errors that arise during the computation will not lead to significant deviations in the results, making them a promising tool for high-precision computations. This problem is addressed in [33,34,35,36,37]. The numerical stability of some continued fractions and branched continued fraction expansions of some special functions was also considered in [38,39,40]. In particular, in [40] numerical stability conditions were established for continued fraction expansions of the Horn hypergeometric function ${\mathrm{H}}_7$ ratios using a new method of estimating relative errors in computing their approximants using the backward recurrence algorithm. Similarly, they are established for branched continued fraction expansions of the ratios of the Horn hypergeometric functions $H_4$ [38] and ${\mathrm{H}}_6$ [39]. These studies show that their result depends on the structure of branched continued fractions. More information about these structures can be found in [41].

The concept of stability to perturbations was studied in the context of branched continued fractions (see [42,43]) and played an important role in the analysis of approximation of special functions of several variables. For continued fractions, this problem, as the authors know, is being studied for the first time. The study of stability sets is not only of theoretical importance, but also opens up promising directions for practical application. The results obtained can contribute to the development of reliable algorithms for computing approximants of continued fractions and find application in various problems of physics, engineering and applied mathematics, where continued fraction expansions are used.

Thus, in the analytical theory of continued fractions, the problem of stability to perturbations of various classes of continued fractions remains relevant. Of particular interest are fractions with complex partial denominators and numerators equal to unity, which are the object of study of this work. The purpose of this work is to establish the conditions for the stability of elements of the above-mentioned continued fractions to perturbations, construct sets of stability to perturbations, and obtain estimates for the errors of their approximants.

The paper is organized as follows. Section 3 presents the main results (Theorems 1–7) and their Corollaries 1–6, while Section 2 provides the necessary definitions. Section 4 presents the application of the obtained results to the numerical stability of algorithms for computing approximants of the continued fraction expansion for Bessel functions (Theorem 8) and to polynomial and continued fraction models in the problem of wood drying modeling. Finally, Section 5 summarizes the important conclusions.

2. Preliminaries

Let us consider the continued fraction

$$b_0+\underset{k=1}{\overset{\infty }{\mathrm{K}}}{\displaystyle \frac{1}{b_k}}=b_0+{\displaystyle \frac{1}{b_1+\frac{1}{b_2+\genfrac{}{}{0pt}{}{}{\ddots }}}},$$

(1)

where $b_k\in \mathbb{C}$, $k\ge 0$.

The finite continued fractions

$$f_n=b_0+\underset{k=1}{\overset{n}{\mathrm{K}}}{\displaystyle \frac{1}{b_k}}=b_0+{\displaystyle \frac{1}{b_1+\frac{1}{b_2+\genfrac{}{}{0pt}{}{}{{\displaystyle \ddots +\frac{1}{b_n}}}}}},n\ge 1,$$

are called the nth approximants of the continued fraction (1). The quantities

$$Q_k^{\left(n\right)}=b_k+\underset{m=k+1}{\overset{n}{\mathrm{K}}}{\displaystyle \frac{1}{b_m}},0\le k\le n,n\ge 1,$$

are called the tails of the nth approximant. From the definition of the tail of the nth approximant, it follows that $f_n=Q_0^{\left(n\right)}$, $n\ge 1$. For the tails $Q_k^{\left(n\right)}$, $0\le k\le n,$ $n\ge 1,$ the following recurrence relations hold

$$Q_k^{\left(n\right)}=b_k+{\displaystyle \frac{1}{Q_{k+1}^{\left(n\right)}}},0\le k\le n,n\ge 1,$$

(2)

with the initial condition $Q_n^{\left(n\right)}=b_n$, $n\ge 1$.

Let ${\widehat{b}}_k,k\ge 0$, be the perturbed values of the elements $b_k$ of the continued fraction (1). The continued fraction

$${\widehat{b}}_0+\underset{k=1}{\overset{\infty }{\mathrm{K}}}{\displaystyle \frac{1}{{\widehat{b}}_k}}$$

(3)

is called the perturbed continued fraction corresponding to the continued fraction (1).

Let $\left\{G_k\right\}$, $\varnothing \ne G_k\subset \mathbb{C}$, $k\ge 0$, be a sequence of element sets of the continued fraction (1) and its perturbed counterpart (3):

$$b_k\in G_k,{\widehat{b}}_k\in G_k,k\ge 0.$$

If for all $k\ge 0$, $G_k=G$, the set G is called a simple element set. If for all $k\ge 0$, $G_{2k+1}=G_1$, $G_{2k}=G_2$, the sets $G_1,G_2$ are called twin element sets.

Definition 1. 

A sequence $\left\{V_k\right\}$, $\varnothing \ne V_k\subset \mathbb{C}$, $k\ge 0$, is called a sequence of value sets for the tails of the approximants of the continued fraction (1), corresponding to the sequence of element sets $\left\{G_k\right\}$, if for every $b_k\in G_k$, $k\ge 0$,

$$b_k\in V_k,$$

(4)

and for every $v\in V_{k+1}$ and every $b_k\in G_k$, $k\ge 0$,

$$b_k+{\displaystyle \frac{1}{v}}\in V_k.$$

(5)

From this definition, it follows that $Q_k^{\left(n\right)}\in V_k$, $0\le k\le n,$ $n\ge 1$.

Definition 2. 

A sequence of element sets $\left\{G_k\right\}$, $k\ge 0$, is called a sequence sets of stability to perturbations for the continued fraction (1) if for any $\epsilon >0$ there exists a $\delta >0$ such that for any $b_k\in G_k$, $b_k\ne 0$, $k\ge 0$, and any ${\widehat{b}}_k\in G_k$, $k\ge 0$, such that

$$\left|{\displaystyle \frac{{\widehat{b}}_k-b_k}{b_k}}\right|<\delta ,$$

the following inequality holds

$$\left|{\displaystyle \frac{{\widehat{f}}_n-f_n}{f_n}}\right|<\epsilon ,$$

where $f_n$ and ${\widehat{f}}_n$ are the approximants of the continued fractions (1) and (3), respectively, herewith $f_n\ne 0$, $n\ge 1$.

Let us denote by ${\beta }_k$, $k\ge 0,$ ${ϵ}^{\left(n\right)}$, $n\ge 1,$ and ${ϵ}_k^{\left(n\right)},$ $0\le k\le n,$ $n\ge 1$ the relative errors of the elements $b_k$, the approximant $f_n$, and the tails $Q_k^{\left(n\right)}$ of the continued fraction (1), respectively, namely,

$$\begin{array}{c}{\widehat{b}}_k=b_k(1+{\beta }_k),k\ge 0,\\ {\widehat{f}}_n=f_n(1+{ϵ}^{\left(n\right)}),n\ge 1,\\ {\widehat{Q}}_k^{\left(n\right)}=Q_k^{\left(n\right)}(1+{ϵ}_k^{\left(n\right)}),0\le k\le n,n\ge 1.\end{array}$$

Since $f_n=Q_0^{\left(n\right)}$ and ${\widehat{f}}_n={\widehat{Q}}_0^{\left(n\right)}$, $n\ge 1,$ then ${ϵ}^{\left(n\right)}={ϵ}_0^{\left(n\right)}$, $n\ge 1$.

Let us consider the relative errors ${\widehat{ϵ}}_k^{\left(n\right)}$, $0\le k\le n$, $n\ge 1$, defined by the relations

$$Q_k^{\left(n\right)}={\widehat{Q}}_k^{\left(n\right)}(1+{\widehat{ϵ}}_k^{\left(n\right)}),0\le k\le n,n\ge 1.$$

Assuming that $b_k\ne 0,{\widehat{b}}_k\ne 0,k\ge 0$, and $Q_k^{\left(n\right)}\ne 0,{\widehat{Q}}_k^{\left(n\right)}\ne 0,0\le k\le n$, $n\ge 1,$ we will prove that the following recurrence formulas hold

$$\begin{array}{c}{ϵ}_k^{\left(n\right)}={\beta }_k+g_{k+1}^{\left(n\right)}({\widehat{ϵ}}_{k+1}^{\left(n\right)}-{\beta }_k),0\le k\le n-1,n\ge 1,\end{array}$$

(6)

and

$$\begin{array}{c}{\widehat{ϵ}}_k^{\left(n\right)}=-{\displaystyle \frac{{\beta }_k}{1+{\beta }_k}}+{\widehat{g}}_{k+1}^{\left(n\right)}\left({ϵ}_{k+1}^{\left(n\right)}+{\displaystyle \frac{{\beta }_k}{1+{\beta }_k}}\right),0\le k\le n-1,n\ge 1,\end{array}$$

(7)

with the initial conditions

$${ϵ}_n^{\left(n\right)}={\beta }_n,{\widehat{ϵ}}_n^{\left(n\right)}=-{\displaystyle \frac{{\beta }_n}{1+{\beta }_n}},n\ge 1,$$

(8)

where

$$\begin{array}{c}{g}_k^{\left(n\right)}={\displaystyle \frac{1}{Q_{k-1}^{\left(n\right)}{Q}_k^{\left(n\right)}}},1\le k\le n,n\ge 1,\end{array}$$

(9)

and

$$\begin{array}{c}{\widehat{g}}_k^{\left(n\right)}={\displaystyle \frac{1}{{\widehat{Q}}_{k-1}^{\left(n\right)}{\widehat{Q}}_k^{\left(n\right)}}},1\le k\le n,n\ge 1.\end{array}$$

(10)

Let n be a fixed natural number. Since $Q_n^{\left(n\right)}=b_n$, ${\widehat{Q}}_n^{\left(n\right)}={\widehat{b}}_n$, then

$${ϵ}_n^{\left(n\right)}={\beta }_n,{\widehat{ϵ}}_n^{\left(n\right)}={\widehat{\beta }}_n=-{\displaystyle \frac{{\beta }_n}{1+{\beta }_n}}.$$

For arbitrary $k,$ $0\le k\le n-1,$ we have

$$\begin{array}{cc}\hfill {ϵ}_k^{\left(n\right)}& ={\displaystyle \frac{{\widehat{Q}}_k^{\left(n\right)}-Q_k^{\left(n\right)}}{Q_k^{\left(n\right)}}}\hfill \\ & ={\displaystyle \frac{1}{Q_k^{\left(n\right)}}}\left(b_k(1+{\beta }_k)+{\displaystyle \frac{1}{Q_{k+1}^{\left(n\right)}(1+{ϵ}_{k+1}^{\left(n\right)})}}\right)-1\hfill \\ \hfill & ={\displaystyle \frac{b_k}{Q_k^{\left(n\right)}}}(1+{\beta }_k)+{\displaystyle \frac{1+{\widehat{ϵ}}_{k+1}^{\left(n\right)}}{Q_k^{\left(n\right)}{Q}_{k+1}^{\left(n\right)}}}-1\hfill \\ & =(1-g_{k+1}^{\left(n\right)})(1+{\beta }_k)+g_{k+1}^{\left(n\right)}(1+{\widehat{ϵ}}_{k+1}^{\left(n\right)})-1\hfill \\ \hfill & ={\beta }_k+g_{k+1}^{\left(n\right)}({\widehat{ϵ}}_{k+1}^{\left(s\right)}-{\beta }_k)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\widehat{ϵ}}_k^{\left(n\right)}& ={\displaystyle \frac{{\widehat{Q}}_k^{\left(n\right)}-Q_k^{\left(n\right)}}{{\widehat{Q}}_k^{\left(n\right)}}}\hfill \\ & ={\displaystyle \frac{1}{{\widehat{Q}}_k^{\left(n\right)}}}\left({\widehat{b}}_k(1+{\widehat{\beta }}_k)+{\displaystyle \frac{1}{{\widehat{Q}}_{k+1}^{\left(n\right)}(1+{\widehat{ϵ}}_{k+1}^{\left(n\right)})}}\right)-1\hfill \\ \hfill & ={\displaystyle \frac{{\widehat{b}}_k}{{\widehat{Q}}_k^{\left(n\right)}}}(1+{\widehat{\beta }}_k)+{\displaystyle \frac{1+{ϵ}_{k+1}^{\left(n\right)}}{{\widehat{Q}}_k^{\left(n\right)}{\widehat{Q}}_{k+1}^{\left(n\right)}}}-1\hfill \\ & =(1-{\widehat{g}}_{k+1}^{\left(n\right)})(1+{\widehat{\beta }}_k)+{\widehat{g}}_{k+1}^{\left(n\right)}(1+{ϵ}_{k+1}^{\left(n\right)})-1\hfill \\ \hfill & ={\widehat{\beta }}_k+{\widehat{g}}_{k+1}^{\left(n\right)}({ϵ}_{k+1}^{\left(s\right)}-{\widehat{\beta }}_k)\hfill \\ & =-{\displaystyle \frac{{\beta }_k}{1+{\beta }_k}}+{\widehat{g}}_{k+1}^{\left(n\right)}\left({ϵ}_{k+1}^{\left(s\right)}+{\displaystyle \frac{{\beta }_k}{1+{\beta }_k}}\right).\hfill \end{array}$$

Thus, from (6)–(8) it follows

$${\epsilon }^{\left(n\right)}={\tilde{\beta }}_0+\sum _{k=1}^n({\tilde{\beta }}_k-{\tilde{\beta }}_{k-1})\prod _{m=1}^k{\tilde{g}}_m^{\left(n\right)},n\ge 1,$$

(11)

where

$${\tilde{g}}_k^{\left(n\right)}=\left\{\begin{array}{c}{g}_k^{\left(n\right)},k=2m+1,\hfill \\ {\widehat{g}}_k^{\left(n\right)},k=2m,\hfill \end{array}\right.\mathrm{a}\mathrm{n}\mathrm{d}{\tilde{\beta }}_k=\left\{\begin{array}{c}{\beta }_k,k=2m,\hfill \\ -{\displaystyle \frac{{\beta }_k}{1+{\beta }_k}},k=2m+1.\hfill \end{array}\right.$$

(12)

3. Main Results

The following result holds.

Theorem 1. 

Let there exist a constant β, $0<\beta <1$, such that for the relative errors of the elements of the continued fraction (1), the following inequality holds

$$|{\beta }_k|\le \beta ,k\ge 0.$$

(13)

The simple element set

$$G=(0,+\infty )$$

(14)

is a set of stability to perturbations for the continued fraction (1). In addition, the following estimate holds

$$|{ϵ}^{\left(n\right)}|\le {\displaystyle \frac{\beta }{1-\beta }},n\ge 1.$$

(15)

Proof. 

Since $b_k\in G$, ${\widehat{b}}_k\in G$, $k\ge 0$, where G is defined by (14), then $Q_k^{\left(n\right)}>0$ and ${\widehat{Q}}_k^{\left(n\right)}>0$, $0\le k\le n,$ $n\ge 1$, and for $1\le k\le n,$ $n\ge 1,$ we have

$$\begin{array}{c}0<g_k^{\left(n\right)}={\displaystyle \frac{1}{Q_{k-1}^{\left(n\right)}{Q}_k^{\left(n\right)}}}={\displaystyle \frac{1/Q_k^{\left(n\right)}}{b_{k-1}+1/Q_k^{\left(n\right)}}}<1\end{array}$$

(16)

and

$$\begin{array}{c}0<{\widehat{g}}_k^{\left(n\right)}={\displaystyle \frac{1}{{\widehat{Q}}_{k-1}^{\left(n\right)}{\widehat{Q}}_k^{\left(n\right)}}}={\displaystyle \frac{1/{\widehat{Q}}_k^{\left(n\right)}}{{\widehat{b}}_{k-1}+1/{\widehat{Q}}_k^{\left(n\right)}}}<1.\end{array}$$

(17)

Let us rewrite the formula (11) as follows

$$\begin{array}{cc}\hfill {\epsilon }^{\left(n\right)}& ={\tilde{\beta }}_0+\sum _{k=1}^n({\tilde{\beta }}_k-{\tilde{\beta }}_{k-1})\prod _{m=1}^k{\tilde{g}}_m^{\left(n\right)}\hfill \\ \hfill & ={\tilde{\beta }}_0+\sum _{k=1}^n{\tilde{\beta }}_k\prod _{m=1}^k{\tilde{g}}_m^{\left(n\right)}-\sum _{k=0}^{n-1}{\tilde{\beta }}_k\prod _{m=1}^{k+1}{\tilde{g}}_m^{\left(n\right)}\hfill \\ \hfill & ={\tilde{\beta }}_0-{\tilde{\beta }}_0{\tilde{g}}_1^{\left(n\right)}+\sum _{k=1}^{n-1}{\tilde{\beta }}_k\left(\prod _{m=1}^k{\tilde{g}}_m^{\left(n\right)}-\prod _{m=1}^{k+1}{\tilde{g}}_m^{\left(n\right)}\right)+{\tilde{\beta }}_n\prod _{m=1}^n{\tilde{g}}_m^{\left(n\right)}\hfill \\ \hfill & ={\tilde{\beta }}_0(1-{\tilde{g}}_1^{\left(n\right)})+\sum _{k=1}^{n-1}{\tilde{\beta }}_k(1-{\tilde{g}}_{k+1}^{\left(n\right)})\prod _{m=1}^k{\tilde{g}}_m^{\left(n\right)}+{\tilde{\beta }}_n\prod _{m=1}^n{\tilde{g}}_m^{\left(n\right)}\hfill \\ \hfill & =\sum _{k=0}^{n-1}{\tilde{\beta }}_k(1-{\tilde{g}}_{k+1}^{\left(n\right)})\prod _{m=1}^k{\tilde{g}}_m^{\left(n\right)}+{\tilde{\beta }}_n\prod _{m=1}^n{\tilde{g}}_m^{\left(n\right)}.\hfill \end{array}$$

Then, taking into account the inequalities (13), (16), and (17), we have

$$\begin{array}{cc}\hfill |{\epsilon }^{\left(n\right)}|& =\left|\sum _{k=0}^{n-1}{\tilde{\beta }}_k(1-{\tilde{g}}_{k+1}^{\left(n\right)})\prod _{m=1}^k{\tilde{g}}_m^{\left(n\right)}+{\tilde{\beta }}_n\prod _{m=1}^n{\tilde{g}}_m^{\left(n\right)}\right|\hfill \\ \hfill & \le \sum _{k=0}^{n-1}|{\tilde{\beta }}_k|(1-{\tilde{g}}_{k+1}^{\left(n\right)})\prod _{m=1}^k{\tilde{g}}_m^{\left(n\right)}+\left|{\tilde{\beta }}_n\right|\prod _{m=1}^n{\tilde{g}}_m^{\left(n\right)}\hfill \\ \hfill & \le {\displaystyle \frac{\beta }{1-\beta }}\left(\sum _{k=0}^{n-1}(1-{\tilde{g}}_{k+1}^{\left(n\right)})\prod _{m=1}^k{\tilde{g}}_m^{\left(n\right)}+\prod _{m=1}^n{\tilde{g}}_m^{\left(n\right)}\right)\hfill \\ \hfill & ={\displaystyle \frac{\beta }{1-\beta }}.\hfill \end{array}$$

This proves the estimate (15).

Let us consider the function

$$\begin{array}{c}\hfill \psi \left(\beta \right)={\displaystyle \frac{\beta }{1-\beta }}.\end{array}$$

Since

$$\underset{\beta \to 0^{+}}{lim}\psi \left(\beta \right)=0,$$

for any $\epsilon >0$ there exists ${\delta }_{\epsilon }=\epsilon /(1+\epsilon )$ such that for any $0<\beta <{\delta }_{\epsilon }$ the inequality $\psi \left(\beta \right)<\epsilon$ holds.

Thus, if $|{\beta }_k|\le \beta <{\delta }_{\epsilon }$, $k\ge 0$, then $|{\epsilon }^{\left(n\right)}|\le \psi \left(\beta \right)<\epsilon$, $n\ge 1$, which proves the stability to perturbations of the continued fraction (1) in the set G. □

The following result concerns symmetric sets of stability to perturbations of the continued fraction (1).

Theorem 2. 

Let the relative errors of the elements of the continued fraction (1) satisfy conditions (13). The sequence of element sets

$$G_k{=\{z\in \mathbb{C}:argz=(-1)}^k\phi ,\left|z\right|\ge {\rho }_k\},k\ge 0,$$

(18)

is a sequence of sets of stability to perturbations for the continued fraction (1) if the series

$$\sum _{k=1}^{\infty }\prod _{m=1}^k{\displaystyle \frac{1}{1+{\rho }_{m-1}{\rho }_m}}$$

(19)

converges, where $0\le \phi <2\pi$, ${\rho }_k>0$, $k\ge 0$, are real constants. In addition, the following estimate holds

$$|{ϵ}^{\left(n\right)}|\le {\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta )\sum _{k=1}^n\prod _{m=1}^k{\displaystyle \frac{1}{1+{\rho }_{m-1}{\rho }_m}}\right),n\ge 1.$$

(20)

Proof. 

Let us prove that the sequence $\left\{G_k\right\}$, where $G_k,$ $k\ge 0$, are defined by (18), is a sequence of value sets for the tails of the approximants of the continued fraction (1).

Let n be an arbitrary natural number and k be an arbitrary integer such that $k\ge 0.$ Then, the function $t\left(z\right)=1/z$ maps the set

$$G_{k+1}{=\{z\in \mathbb{C}:argz=(-1)}^{k+1}\phi ,\left|z\right|\ge {\rho }_{k+1}\}$$

into the set

$$G_{k+1}^{\prime }{=\{z\in \mathbb{C}:argz=(-1)}^k\phi ,\left|z\right|\le 1/{\rho }_{k+1}\}.$$

For all $z\in G_{k+1}^{\prime }$ we have

$$\begin{array}{cc}\hfill b_k+z& =|b_k|exp({(-1)}^{k}i\phi )+|z|exp({(-1)}^{k}i\phi )\hfill \\ & =(|b_k|+|z|)exp({(-1)}^{k}i\phi ).\hfill \end{array}$$

It follows that

$$\begin{array}{c}\hfill arg(b_k+z)={(-1)}^k\phi ,|b_k+z|=|b_k|+|z|\ge {\rho }_k.\end{array}$$

This proves that condition (5) is satisfied. Therefore, the element sets $G_k$ are the value sets for the tails $Q_k^{\left(n\right)}$.

Let us estimate the quantities $g_k^{\left(n\right)}$, $1\le k\le n$. For $1\le k\le n,$ we write the quantities $g_k^{\left(n\right)}$ as

$$\begin{array}{cc}\hfill g_k^{\left(n\right)}& ={\displaystyle \frac{1}{Q_{k-1}^{\left(n\right)}{Q}_k^{\left(n\right)}}}\hfill \\ & ={\displaystyle \frac{1}{(b_{k-1}+1/Q_k^{\left(n\right)})Q_k^{\left(n\right)}}}\hfill \\ & ={\displaystyle \frac{1}{1+b_{k-1}{Q}_k^{\left(n\right)}}}.\hfill \end{array}$$

Let us denote

$$b_{k-1}=|b_{k-1}|exp({(-1)}^{k-1}i\phi ),Q_k^{(n)}=\left|Q_k^{(n)}\right|exp({(-1)}^{k}i\phi ).$$

Then,

$$\begin{array}{cc}\hfill |1+b_{k-1}{Q}_k^{\left(n\right)}|& =\sqrt{1+|b_{k-1}{|}^2|Q_k^{\left(n\right)}{|}^2+2|b_{k-1}\left|\right|Q_k^{\left(n\right)}|}\hfill \\ & =1+|b_{k-1}\left|\right|Q_k^{\left(n\right)}|\hfill \\ & \ge 1+{\rho }_{k-1}{\rho }_k.\hfill \end{array}$$

Therefore,

$$|g_k^{\left(n\right)}| \le {\displaystyle \frac{1}{1+{\rho }_{k-1}{\rho }_k}},1\le k\le n.$$

(21)

Since ${\widehat{b}}_k\in G_k$, $k\ge 0$, then

$$|{\widehat{g}}_k^{\left(n\right)}| \le {\displaystyle \frac{1}{1+{\rho }_{k-1}{\rho }_k}},1\le k\le n.$$

(22)

If the inequalities (17), (21), and (22) are satisfied, then from the Formula (11) for the relative error of the nth approximant of the continued fraction (1), we obtain

$$\begin{array}{cc}\hfill |{\epsilon }^{\left(n\right)}|& \le |{\tilde{\beta }}_0|+\sum _{k=1}^n\left(|{\tilde{\beta }}_k|+|{\tilde{\beta }}_{k-1}|\right)\prod _{m=1}^k\left|{\tilde{g}}_m^{\left(n\right)}\right|\hfill \\ & \le {\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta )\sum _{k=1}^n\prod _{m=1}^k{\displaystyle \frac{1}{1+{\rho }_{m-1}{\rho }_m}}\right).\hfill \end{array}$$

If the series (19) converges, then there exists a positive constant C such that

$$\begin{array}{c}\hfill \sum _{k=1}^n\prod _{m=1}^k{\displaystyle \frac{1}{1+{\rho }_{m-1}{\rho }_m}}\le C,n\ge 1.\end{array}$$

Then

$$|{\epsilon }^{\left(n\right)}|\le {\displaystyle \frac{\beta }{1-\beta }}(1+(2-\beta )C),n\ge 1.$$

Let us consider the function

$$\begin{array}{c}\hfill \psi \left(\beta \right)={\displaystyle \frac{\beta }{1-\beta }}(1+(2-\beta )C).\end{array}$$

Since

$$\underset{\beta \to 0^{+}}{lim}\psi \left(\beta \right)=0,$$

then for any $\epsilon >0$ there exists

$${\delta }_{\epsilon }={\displaystyle \frac{1+\epsilon +2C-\sqrt{{(1+\epsilon +2C)}^2-4\epsilon C}}{2C}}$$

such that for any $0<\beta <{\delta }_{\epsilon }$, the inequality $\psi \left(\beta \right)<\epsilon$ holds. Therefore, if $|{\beta }_k|\le \beta <{\delta }_{\epsilon }$, $k\ge 0$, then $|{\epsilon }^{\left(n\right)}|\le \psi \left(\beta \right)<\epsilon$, which proves that the conditions for determining the sets of stability to perturbations of the continued fraction (1) are satisfied. □

Setting ${\rho }_{2k+1}={\rho }_1,$ ${\rho }_{2k}={\rho }_2$, $k\ge 0$, ${\rho }_1>0$, and ${\rho }_2>0$ in Theorem 2, we obtain the following corollary.

Corollary 1.

Let the relative errors of the elements of the continued fraction (1) satisfy conditions (13). The twin element sets

$$G_1=\{z\in \mathbb{C}:argz=-\phi ,|z|\ge {\rho }_1\},G_2=\{z\in \mathbb{C}:argz=\phi ,|z|\ge {\rho }_2\}$$

are sets of stability to perturbations of the continued fraction (1), where $0\le \phi <2\pi$, ${\rho }_1>$0, ${\rho }_2>0$ are real constants. In addition, the following estimate holds

$$|{\epsilon }^{\left(n\right)}|\le {\displaystyle \frac{\beta }{1-\beta }}\left(1+{\displaystyle \frac{2-\beta }{{\rho }_1{\rho }_2}}\left(1-{\displaystyle \frac{1}{{(1+{\rho }_1{\rho }_2)}^n}}\right)\right),n\ge 1.$$

Theorem 3.

Let the relative errors of the elements of the continued fraction (1) satisfy conditions (13). The sequence of element sets

$$G_k=\{z\in \mathbb{C}:|argz|\le \pi /4,\left|z\right|\ge {\rho }_k\},k\ge 0,$$

(23)

is a sequence of sets of stability to perturbations of the continued fraction (1), if the series

$$\sum _{k=1}^{\infty }\prod _{m=1}^k{\displaystyle \frac{1}{\sqrt{1+{\rho }_{m-1}^2{\rho }_m^2}}}$$

(24)

converges, where ${\rho }_k,$ $k\ge 0,$ are positive real constants. For the relative errors of the approximants, the following estimate

$$|{\epsilon }^{\left(n\right)}|\le {\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta )\sum _{k=1}^n\prod _{m=1}^k{\displaystyle \frac{1}{\sqrt{1+{\rho }_{m-1}^2{\rho }_m^2}}}\right),n\ge 1,$$

(25)

is valid.

Proof. 

Let us prove that the sequence $\left\{G_k\right\}$, where the sets $G_k,k\ge 0$, are defined by (23), is a sequence of value sets for the tails of the approximants of the continued fraction (1).

Let n be an arbitrary natural number and k be an arbitrary integer such that $k\ge 0.$ The function $t\left(z\right)=1/z$ maps the set

$$G_{k+1}=\{z\in \mathbb{C}:|argz|\le \pi /4,\left|z\right|\ge {\rho }_{k+1}\}$$

into the set

$$G_{k+1}^{\prime }=\{z\in \mathbb{C}:|argz|\le \pi /4,\left|z\right|\ge 1/{\rho }_{k+1}\}.$$

Then, condition (5) is satisfied if for all $z\in G_{k+1}^{\prime }$

$$\begin{array}{c}|arg(b_k+z)|\le {\displaystyle \frac{\pi }{4}},\end{array}$$

(26)

and

$$\begin{array}{c}|b_k+z|\ge {\rho }_k.\end{array}$$

(27)

Let us denote $b_k=Re{b}_k+iIm{b}_k$, $z=Rez+iImz$. Since

$$|arg{b}_k| \le \pi /4,|argz|\le \pi /4,$$

then

$$|Im{b}_k| \le Re{b}_k,|Imz|\le Rez.$$

Taking into account that $Re{b}_k>0$, $Rez\ge 0$, we have

$$\begin{array}{cc}\hfill \left|{\displaystyle \frac{Im(b_k+z)}{Re(b_k+z)}}\right|& ={\displaystyle \frac{|Im{b}_k+Imz|}{Re{b}_k+Rez}}\hfill \\ & \le {\displaystyle \frac{|Im{b}_k|+|Imz|}{Re{b}_k+Rez}}\hfill \\ & \le 1.\hfill \end{array}$$

This proves that the inequality (26) holds for all $z\in G_{k+1}^{\prime }$.

To prove inequality (27), we denote $b_k=\left|b_k\right|exp\left(i{\phi }_k\right)$, $z=\left|z\right|exp\left(i\phi \right)$. Then,

$$|b_k+z|=\sqrt{|b_k{|}^2+{\left|z\right|}^2+2|b_k\left|\right|z|cos({\phi }_k-\phi )}.$$

Since $|{\phi }_k-\phi |\le \pi /2$, then

$$|b_k+z|\ge |b_k| \ge {\rho }_k.$$

Therefore, the element sets $G_k$ are the value sets for the tails $Q_k^{\left(n\right)}$.

Let us estimate the quantities $|1+b_{k-1}{Q}_k^{\left(n\right)}|$ from below, for $1\le k\le n$. Let us denote

$$b_{k-1}=|b_{k-1}|exp\left(i{\phi }_{k-1}\right),Q_k^{\left(n\right)}=\left|Q_k^{\left(n\right)}\right|exp\left(i{\phi }_k^{\left(n\right)}\right).$$

Then

$$|1+b_{k-1}{Q}_k^{\left(n\right)}|=\sqrt{1+|b_{k-1}{|}^2|Q_k^{\left(n\right)}{|}^2+2|b_{k-1}\left|\right|Q_k^{\left(n\right)}|cos({\phi }_{k-1}+{\phi }_k^{\left(n\right)})}.$$

Since $|{\phi }_{k-1}+{\phi }_k^{\left(n\right)}|\le \pi /2$, then

$$\begin{array}{cc}\hfill |1+b_{k-1}{Q}_k^{\left(n\right)}|& \ge \sqrt{1+|b_{k-1}{|}^2{\left|Q_k^{\left(n\right)}\right|}^2}\hfill \\ & \ge \sqrt{1+{\rho }_{k-1}^2{\rho }_k^2}.\hfill \end{array}$$

Therefore, for $1\le k\le n$

$$|g_k^{\left(n\right)}|={\displaystyle \frac{1}{|1+b_{k-1}{Q}_k^{\left(n\right)}|}}\le {\displaystyle \frac{1}{\sqrt{1+{\rho }_{k-1}^2{\rho }_k^2}}}.$$

(28)

Since ${\widehat{b}}_k\in G_k$, $k\ge 0$, then

$$|{\widehat{g}}_k^{\left(n\right)}|\le {\displaystyle \frac{1}{\sqrt{1+{\rho }_{k-1}^2{\rho }_k^2}}},1\le k\le n.$$

(29)

If inequalities (13), (28) and (29) hold, then from Formula (11) for the relative error of the nth approximant of the continued fraction (1), we have

$$\begin{array}{cc}\hfill |{\epsilon }^{\left(n\right)}|& \le |{\tilde{\beta }}_0|+\sum _{k=1}^n\left(\right|{\tilde{\beta }}_k|+|{\tilde{\beta }}_{k-1}\left|\right)\prod _{m=1}^k\left|{\tilde{g}}_m^{\left(n\right)}\right|\hfill \\ \hfill & \le {\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta )\sum _{k=1}^n\prod _{m=1}^k{\displaystyle \frac{1}{\sqrt{1+{\rho }_{m-1}^2{\rho }_m^2}}}\right).\hfill \end{array}$$

If the series (24) converges, then there exists a positive constant C such that

$$\sum _{k=1}^n\prod _{m=1}^k{\displaystyle \frac{1}{\sqrt{1+{\rho }_{m-1}^2{\rho }_m^2}}}\le C,n\ge 1.$$

Then, for the errors of the nth approximant of the continued fraction (1), the estimate

$$|{\epsilon }^{\left(n\right)}|\le {\displaystyle \frac{\beta }{1-\beta }}(1+(2-\beta )C),n\ge 1,$$

is valid, from which, as in the Theorem 2, it follows that the conditions for determining the sets of stability to perturbations are satisfied. □

Setting ${\rho }_k=\rho$, $k\ge 0$, $\rho >0$ in Theorem 3, we obtain the following corollary.

Corollary 2. 

Let the relative errors of the elements of the continued fraction (1) satisfy conditions (13). The simple element set

$$G=\{z\in \mathbb{C}:|argz|\le \pi /4,|z|\ge \rho \}$$

is a set of stability to perturbations of the continued fraction (1), where ρ is a positive real constant. For the relative errors of the approximants, the following estimate

$$|{\epsilon }^{\left(n\right)}|\le {\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta ){\displaystyle \frac{1-{\sqrt{(1+{\rho }^4)}}^{-n}}{\sqrt{1+{\rho }^4}-1}}\right),n\ge 1,$$

(30)

is valid.

Theorem 4. 

Let the relative errors of the elements of the continued fraction (1) satisfy conditions (13). The sequence of element sets

$$G_k\left(\phi \right)={\{z\in \mathbb{C}:|argz+(-1)}^{k+1}\phi |\le \pi /4,|z|\ge {\rho }_k\},k\ge 0,$$

(31)

is a sequence of stability sets to perturbations of the continued fraction (1), if the series (24) converges, where $0\le \phi <2\pi$, ${\rho }_k>0$, $k\ge 0$, are real constants. For the relative errors of the approximants, the estimate (25) holds.

Proof. 

Let us consider the continued fractions

$$\begin{array}{c}{r}_0{b}_0+\underset{k=1}{\overset{\infty }{\mathrm{K}}}{\displaystyle \frac{r_{k-1}{r}_k}{r_k{b}_k}}\end{array}$$

(32)

and

$$\begin{array}{c}{r}_0{\widehat{b}}_0+\underset{k=1}{\overset{\infty }{\mathrm{K}}}{\displaystyle \frac{r_{k-1}{r}_k}{r_k{\widehat{b}}_k}},\end{array}$$

(33)

where $r_k=exp\left({(-1)}^{k}i\phi \right)$, $k\ge 0$, $0\le \phi <2\pi$, $b_k\in G_k,{\widehat{b}}_k\in G_k$, $k\ge 0$, and the sets $G_k,$ $k\ge 0,$ are defined by (23). Then, $b_{k}exp\left({(-1)}^{k}i\phi \right)\in G_k\left(\phi \right)$, ${\widehat{b}}_{k}exp\left({(-1)}^{k}i\phi \right)\in G_k\left(\phi \right)$, where the sets $G_k\left(\phi \right),$ $k\ge 0,$ are defined by (31).

Let us denote by

$$f_n^{*}=r_0{b}_0+\underset{k=1}{\overset{n}{\mathrm{K}}}{\displaystyle \frac{r_{k-1}{r}_k}{r_k{b}_k}},{\widehat{f}}_n^{*}=r_0{\widehat{b}}_0+\underset{k=1}{\overset{n}{\mathrm{K}}}{\displaystyle \frac{r_{k-1}{r}_k}{r_k{\widehat{b}}_k}},n\ge 1,$$

the approximants of the continued fractions (32) and (33), respectively, and

$$\begin{array}{c}\hfill Q_k^{*\left(n\right)}=r_k{b}_k+\underset{m=k+1}{\overset{n}{\mathrm{K}}}{\displaystyle \frac{r_{m-1}{r}_m}{r_m{b}_m}},{\widehat{Q}}_k^{*\left(n\right)}=r_k{\widehat{b}}_k+\underset{m=k+1}{\overset{n}{\mathrm{K}}}{\displaystyle \frac{r_{m-1}{r}_m}{r_m{\widehat{b}}_m}},0\le k\le n,\end{array}$$

the tails of the approximants $f_n^{*},$ ${\widehat{f}}_n^{*}$, respectively.

It is known that $g_k^{*\left(n\right)}=g_k^{\left(n\right)}$, ${\widehat{g}}_k^{*\left(n\right)}={\widehat{g}}_k^{\left(n\right)}$, $1\le k\le n$, [36], where

$$g_k^{*\left(n\right)}={\displaystyle \frac{1}{Q_{k-1}^{*\left(n\right)}{Q}_k^{*\left(n\right)}}},{\widehat{g}}_k^{*\left(n\right)}={\displaystyle \frac{1}{{\widehat{Q}}_{k-1}^{*\left(n\right)}{\widehat{Q}}_k^{*\left(n\right)}}},1\le k\le n,$$

and the quantities $g_k^{\left(n\right)}$, ${\widehat{g}}_k^{\left(n\right)},$ $1\le k\le n,$ are defined by (9) and (10), respectively. Then, if $b_k\in G_k,{\widehat{b}}_k\in G_k$, $k\ge 0$, then for the quantities $g_k^{*\left(n\right)},{\widehat{g}}_k^{*\left(n\right)},$ $1\le k\le n,$ the following estimates hold

$$|g_k^{*\left(n\right)}| \le {\displaystyle \frac{1}{\sqrt{1+{\rho }_{k-1}^2{\rho }_k^2}}},\left|{\widehat{g}}_k^{*\left(n\right)}\right|\le {\displaystyle \frac{1}{\sqrt{1+{\rho }_{k-1}^2{\rho }_k^2}}},1\le k\le n.$$

(34)

Therefore, if condition (13) and inequalities (34) are satisfied, then for the relative error of the nth approximant, the estimate (25) holds. Then, according to Theorem 3, if the series (24) converges, the sequence of sets (31) is a sequence sets of stability to perturbations of the continued fraction (1). □

Setting ${\rho }_{2k+1}={\rho }_1$, ${\rho }_{2k}={\rho }_2$, $k\ge 0$, ${\rho }_1>0$, ${\rho }_2>0$ in Theorem 4, we obtain the following corollary.

Corollary 3. 

Let the relative errors of the elements of the continued fraction (1) satisfy conditions (13). The paired element sets

$$\begin{array}{c}{G}_1\left(\phi \right)=\left\{z\in \mathbb{C}:|argz+\phi |\le \pi /4,\left|z\right|\ge {\rho }_1\right\},\\ G_2\left(\phi \right)=\left\{z\in \mathbb{C}:|argz-\phi |\le \pi /4,\left|z\right|\ge {\rho }_2\right\}\end{array}$$

are sets of stability to perturbations of the continued fraction (1), where $0\le \phi <2\pi$, ${\rho }_1>0$, ${\rho }_2>0$ are real constants. For the relative errors of the approximants, the estimate (30) holds.

Theorem 5. 

Let the relative errors of the elements of the continued fraction (1) satisfy conditions (13). The sequence of element sets

$$G_k=\{z\in \mathbb{C}:|z|\ge {\rho }_k+1/{\rho }_{k+1}\},k\ge 0,$$

(35)

is a sequence sets of stability to perturbations of the continued fraction (1), if the series

$$\sum _{k=1}^{\infty }\prod _{m=1}^k{\displaystyle \frac{1}{{\rho }_{m-1}{\rho }_m}}$$

(36)

converges, where ${\rho }_k$, $k\ge 0,$ are positive real constants. For the relative errors of the approximants, the following estimate holds

$$|{\epsilon }^{\left(n\right)}|\le {\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta )\sum _{k=1}^n\prod _{m=1}^k{\displaystyle \frac{1}{{\rho }_{m-1}{\rho }_m}}\right),n\ge 1,$$

is valid.

Proof. 

Let us consider the sequence of sets $\left\{V_k\right\}$, where

$$V_k=\{z\in \mathbb{C}:|z|\ge {\rho }_k\},k\ge 0.$$

Then, $G_k\subset V_k$, $k\ge 0$, where the sets $G_k$, $k\ge 0$, are defined by (35), which ensures that condition (4) is satisfied.

Let k be an arbitrary nonnegative integer number. The function $t\left(z\right)=1/z$ maps $V_{k+1}$ to the set $V_{k+1}^{\prime }=\{z\in \mathbb{C}:|z|\le 1/{\rho }_{k+1}\}$. Then, condition (5) is satisfied if inequality (27) holds for all $z\in V_{k+1}^{\prime }$.

Let us denote $b_k=\left|b_k\right|exp\left(i{\phi }_k\right)$, $z=\left|z\right|exp\left(i\phi \right)$. Then,

$$\begin{array}{cc}\hfill |b_k+z|& =\sqrt{|b_k{|}^2+{\left|z\right|}^2+2|b_k\left|\right|z|cos({\phi }_k-\phi )}\hfill \\ \hfill & \ge \sqrt{|b_k{|}^2+{\left|z\right|}^2-2|b_k\left|\right|z|}\hfill \\ \hfill & =\left|\right|b_k|-|z\left|\right|\ge {\rho }_k+1/{\rho }_{k+1}-1/{\rho }_{k+1}\hfill \\ & ={\rho }_k.\hfill \end{array}$$

This proves that condition (5) is satisfied. Therefore, the sequence of sets $\left\{V_k\right\}$ is a sequence of value sets for the tails $Q_k^{\left(n\right)},$ $k\ge 0.$

Let us denote $b_{k-1}=\left|b_{k-1}\right|exp\left(i{\phi }_{k-1}\right)$, $Q_k^{\left(n\right)}=\left|Q_k^{\left(n\right)}\right|exp\left(i{\phi }_k^{\left(n\right)}\right)$. Then,

$$\begin{array}{cc}\hfill |1+b_{k-1}{Q}_k^{\left(n\right)}|& =\sqrt{1+|b_{k-1}{|}^2|Q_k^{\left(n\right)}{|}^2+2|b_{k-1}\left|\right|Q_k^{\left(n\right)}|cos({\phi }_{k-1}+{\phi }_k^{\left(n\right)})}\hfill \\ \hfill & \ge \sqrt{1+|b_{k-1}{|}^2|Q_k^{\left(n\right)}{|}^2-2|b_{k-1}\left|\right|Q_k^{\left(n\right)}|}=\left|\right|b_{k-1}\left|\right|Q_k^{\left(n\right)}|-1|\hfill \\ \hfill & \ge \left({\rho }_{k-1}+{\displaystyle \frac{1}{{\rho }_k}}\right){\rho }_k-1\hfill \\ & ={\rho }_{k-1}{\rho }_k.\hfill \end{array}$$

Thus,

$$|g_k^{\left(n\right)}|={\displaystyle \frac{1}{|1+b_{k-1}{Q}_k^{\left(n\right)}|}}\le {\displaystyle \frac{1}{{\rho }_{k-1}{\rho }_k}},1\le k\le n.$$

(37)

Since ${\widehat{b}}_k\in G_k$, $k\ge 0$, then

$$|{\widehat{g}}_k^{\left(n\right)}|\le {\displaystyle \frac{1}{{\rho }_{k-1}{\rho }_k}},1\le k\le n.$$

(38)

Taking into account the fulfillment of inequalities (13), (37), (38), from Formula (11) for the relative error of the nth approximant of the continued fraction (1), we have

$$\begin{array}{cc}\hfill |{\epsilon }^{\left(n\right)}|& \le |{\tilde{\beta }}_0|+\sum _{k=1}^n\left(\right|{\tilde{\beta }}_k|+|{\tilde{\beta }}_{k-1}\left|\right)\prod _{m=1}^k\left|{\tilde{g}}_m^{\left(n\right)}\right|\hfill \\ \hfill & \le {\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta )\sum _{k=1}^n\prod _{m=1}^k{\displaystyle \frac{1}{{\rho }_{m-1}{\rho }_m}}\right).\hfill \end{array}$$

As in the proof of Theorem 2, we conclude that the convergence of the series (36) ensures the fulfillment of the conditions of the definition sets of stability to perturbations of the continued fraction (1). □

Setting ${\rho }_k=\rho$, $k\ge 0$ herewith $\rho >1$ in Theorem 5, we obtain the following result.

Corollary 4. 

Let the relative errors of the elements of the continued fraction (1) satisfy conditions (13). The simple element set

$$G=\{z\in \mathbb{C}:|z|\ge \rho +1/\rho \}$$

is a set of stability to perturbations of the continued fraction (1), where $\rho >1$ is a real constant. In addition, the following estimate holds

$$|{\epsilon }^{\left(n\right)}|\le {\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta ){\displaystyle \frac{1-{\rho }^{-2n}}{{\rho }^2-1}}\right),n\ge 1.$$

Theorem 6. 

Let there exist a constant β, $0<\beta <1$, such that the relative errors of the elements of the continued fraction (1) satisfy conditions (13). The sequence of sets

$$G_k=\{z\in \mathbb{C}:Rez\ge {\rho }_k\},k\ge 0,$$

(39)

is a sequence sets of stability to perturbations of the continued fraction (1), if the series

$$\sum _{k=1}^{\infty }\prod _{m=1}^k{\eta }_m,$$

(40)

converges, where ${\rho }_k$, $k\ge 0$, are positive real constants,

$${\eta }_k=\left\{\begin{array}{c}{\displaystyle \frac{1}{1+{\rho }_{k-1}{\rho }_k}},{\rho }_{k-1}{\rho }_k\ge 1,\hfill \\ {\displaystyle \frac{1}{2\sqrt{{\rho }_{k-1}{\rho }_k}}},0<{\rho }_{k-1}{\rho }_k<1,\hfill \end{array}\right.k\ge 1.$$

(41)

For the relative errors of the approximants, the following estimate

$$|{\epsilon }^{\left(n\right)}|\le {\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta )\sum _{k=1}^n\prod _{m=1}^k{\eta }_m\right),n\ge 1,$$

(42)

is valid.

Proof. 

Let us prove that the sequence $\left\{G_k\right\}$, where the sets $G_k$, $k\ge 0$, are defined by (39), is a sequence of value sets for the tails of the approximants of the continued fraction (1).

Let k be an arbitrary nonnegative integer number. Since $0\notin G_k$, the function $t\left(z\right)=1/z$ maps the set $G_{k+1}$ to a circle with center at the point $1/\left(2{\rho }_{k+1}\right)$ and radius $1/\left(2{\rho }_{k+1}\right)$. Then,

$$b_k+{\displaystyle \frac{1}{G_{k+1}}}=\{z:|z-q_k|\le r_k\},$$

where $r_k=1/\left(2{\rho }_{k+1}\right)$, $q_k=b_k+1/\left(2{\rho }_{k+1}\right)\in G_k$. Condition (5) is satisfied if $q_k\in V_k$ and $Re\left(q_k\right)-{\rho }_k\ge r_k$. The last inequality is equivalent to the inequality by which the sets (39) are defined. Thus, the sets (39) are the value sets for the tails of the approximants of the continued fraction (1).

Let n be an arbitrary natural number and k be an arbitrary positive integer number. Let us denote $b_{k-1}=x_1+i{y}_1$, $Q_k^{\left(n\right)}=x_2+i{y}_2$. Then,

$$|g_k^{\left(n\right)}|={\displaystyle \frac{1}{|1+b_{k-1}{Q}_k^{\left(n\right)}|}}={\displaystyle \frac{1}{\sqrt{{(1+x_1{x}_2-y_1{y}_2)}^2+{(x_1{y}_2+x_2{y}_1)}^2}}}.$$

Since

$$\underset{\begin{array}{c}{x}_1\ge {\rho }_{k-1},x_2\ge {\rho }_k,\\ y_1,y_2\in \mathbb{R}\end{array}}{min}\sqrt{{(1+x_1{x}_2-y_1{y}_2)}^2+{(x_1{y}_2+x_2{y}_1)}^2}=\left\{\begin{array}{c}1+{\rho }_{k-1}{\rho }_k,{\rho }_{k-1}{\rho }_k\ge 1,\hfill \\ 2\sqrt{{\rho }_{k-1}{\rho }_k},0<{\rho }_{k-1}{\rho }_k<1,\hfill \end{array}\right.$$

then

$$|g_k^{\left(n\right)}|\le {\eta }_k,$$

(43)

where ${\eta }_k$ is defined by (41).

In addition, since ${\widehat{b}}_k\in G_k$, then

$$|{\widehat{g}}_k^{\left(n\right)}|\le {\eta }_k.$$

(44)

Therefore, if inequalities (13), (43) and (44) hold, then for the relative error of the nth approximant of the continued fraction (1), the estimate (42) holds. Then, if the series (38) converges, the sets (39) are sets of stability to perturbations of the continued fraction (1). □

Setting ${\rho }_k=\rho$, $k\ge 0$, herewith $\rho >1/2$ in Theorem 6, we obtain the following corollary.

Corollary 5. 

Let the relative errors of the elements of the continued fraction (1) satisfy conditions (13). The simple element set

$$G_k=\{z\in \mathbb{C}:Rez\ge \rho \}$$

is a set of stability to perturbations of the continued fraction (1), where $\rho >1/2$ is a real constant. The following estimate holds

$$|{\epsilon }^{\left(n\right)}|\le {\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta ){\displaystyle \frac{\eta (1-{\eta }^n)}{1-\eta }}\right),n\ge 1,$$

(45)

where

$$\eta =\left\{\begin{array}{c}{\displaystyle \frac{1}{1+{\rho }^2}},\rho \ge 1,\hfill \\ {\displaystyle \frac{1}{2\rho }},1/2<\rho <1.\hfill \end{array}\right.$$

Finally, by the same way of proving Theorem 4, we obtain the following result.

Theorem 7. 

Let the relative errors of the elements of the continued fraction (1) satisfy conditions (13). The sequence of sets

$$G_k=\{z\in \mathbb{C}:Re(zexp\left({(-1)}^{k+1}i\phi \right))\ge {\rho }_k\},k\ge 0,$$

is a sequence sets of stability to perturbations of the continued fraction (1), if the series (40) converges, where ${\rho }_k>0$, $k\ge 0$, $0\le \phi <2\pi$ are real constants. For the relative errors of the approximants, the estimate (42) holds.

Setting ${\rho }_{2k+1}={\rho }_1$, ${\rho }_{2k}={\rho }_2$, $k\ge 0$, herewith ${\rho }_1>0$, ${\rho }_2>0$, and ${\rho }_1{\rho }_2>1/2$ in Theorem 7, we obtain the following corollary.

Corollary 6. 

Let the relative errors of the elements of the continued fraction (1) satisfy conditions (13). The paired element sets

$$G_1=\left\{z\in \mathbb{C}:Re(zexp\left(i\phi \right))\ge {\rho }_1\right\},G_2=\left\{z\in \mathbb{C}:Re(zexp(-i\phi ))\ge {\rho }_2\right\}$$

are sets of stability to perturbations of the continued fraction (1), where $0\le \phi <2\pi$, ${\rho }_1>0$, ${\rho }_2>0$, ${\rho }_1{\rho }_2>1/2$, are real constants. For the relative errors of the approximants, the estimate (45) holds, where

$$\eta =\left\{\begin{array}{c}{\displaystyle \frac{1}{1+{\rho }_1{\rho }_2}},{\rho }_1{\rho }_2\ge 1,\hfill \\ {\displaystyle \frac{1}{2\sqrt{{\rho }_1{\rho }_2}}},1/2<{\rho }_1{\rho }_2<1.\hfill \end{array}\right.$$

4. Applications

4.1. Numerical Stability of Algorithms for Computing Approximants of Continued Fraction

The theoretical results presented in the previous sections describe the conditions under which continued fractions with partial numerators equal to one are stable to perturbations of their elements. The purpose of this experiment is to numerically verify and visualize these properties using the example of Bessel functions of the first kind, which are used in physics and engineering, signal processing, and mathematics [44,45,46,47,48,49,50].

The Bessel function of the first kind is defined as (see [51,52])

$$J_{\nu }\left(z\right)={\left({\displaystyle \frac{z}{2}}\right)}^{\nu }\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k}{k!\Gamma (\nu +k+1)}}{\left({\displaystyle \frac{z}{2}}\right)}^{2k},|argz|<\pi ,$$

where $\nu \in \mathbb{C}$ is the order of the Bessel function, and $\Gamma \left(z\right)$ is the gamma function.

For our investigation, we consider the continued fraction expansion for the ratio of Bessel functions (see [14])

$${\displaystyle \frac{J_{\nu +1}\left(z\right)}{J_{\nu }\left(z\right)}}={\displaystyle \frac{z/\left(2\right(\nu +1\left)\right)}{1-\frac{z^2/\left(4(\nu +1)(\nu +2)\right)}{1-\frac{z^2/\left(4(\nu +2)(\nu +3)\right)}{1-\genfrac{}{}{0pt}{}{}{\ddots }}}}}.$$

By an equivalence transformation, this continued fraction can be converted to a continued fraction with partial denominators $b_k\left(z\right)={(-1)}^{k-1}2(\nu +k)/z$ and unit partial numerators:

$$\underset{k=1}{\overset{\infty }{\mathrm{K}}}{\displaystyle \frac{1}{b_k\left(z\right)}}={\displaystyle \frac{1}{2(\nu +1)/z+\frac{1}{-2(\nu +2)/z+\frac{1}{2(\nu +3)/z-\genfrac{}{}{0pt}{}{}{\ddots }}}}}.$$

(46)

For (46), consider the perturbed continued fraction

$${\displaystyle \frac{1}{2(\widehat{\nu }+1)/\widehat{z}+\frac{1}{-2(\widehat{\nu }+2)/\widehat{z}+\frac{1}{2(\widehat{\nu }+3)/\widehat{z}-\genfrac{}{}{0pt}{}{}{\ddots }}}}},$$

(47)

Let $z,\widehat{z}\in G_M$, where

$$G_M=\{z\in \mathbb{C}:|z|\le M\}.$$

(48)

where M is a positive real constant.

Theorem 8. 

Let there exist a constant β, $0<\beta <1$, such that the relative errors of the elements $b_k\left(z\right)={(-1)}^{k-1}2(\nu +k)/z$ of the continued fraction (46) satisfy conditions (13). The set (48) is a set of stability for the continued fraction (46) if $M<(1+\vartheta )$, where $\vartheta =min\{\nu ,\widehat{\nu }\}$. The following estimate holds

$$|{ϵ}^{\left(n\right)}|\le {\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta ){\displaystyle \frac{1-{\rho }^{-2(n-1)}}{{\rho }^2-1}}\right),n\ge 1,$$

where $\rho =(a+\sqrt{a^2-4})/2>1$, $a=2(\vartheta +1)/M$.

Proof. 

Since $b_0\left(z\right)={\widehat{b}}_0\left(z\right)=0$, then ${\beta }_0=0$ and

$$g_1^{\left(n\right)}={\displaystyle \frac{1}{1+b_0{Q}_1^{\left(n\right)}}}=1.$$

Then, the formula for the relative error of the nth approximant takes the form

$${\epsilon }^{\left(n\right)}={\tilde{\beta }}_1+\sum _{k=2}^n({\tilde{\beta }}_k-{\tilde{\beta }}_{k-1})\prod _{m=2}^k{\tilde{g}}_m^{\left(n\right)},$$

(49)

where the quantities ${\tilde{\beta }}_k$, $k\ge 1$, ${\tilde{g}}_k^{\left(n\right)}$, $k\ge 2$, are defined by (12).

Since $z,\widehat{z}\in G_M$, where the set $G_M$ is defined by (48), then for the elements of the continued fraction (46) and its perturbed continued fraction (47) for $k\ge 1$, the following estimates hold

$$\begin{array}{cc}\hfill |b_k\left(z\right)|& {=|(-1)}^{k-1}2(\nu +k)/z|\hfill \\ & =2(\nu +k)/\left|z\right|\hfill \\ & \ge 2(\vartheta +1)/M,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill |{\widehat{b}}_k\left(\widehat{z}\right)|& {=|(-1)}^{k-1}2(\widehat{\nu }+k)/\widehat{z}|\hfill \\ & =2(\widehat{\nu }+k)/\left|\widehat{z}\right|\hfill \\ & \ge 2(\vartheta +1)/M,\hfill \end{array}$$

If $M<(1+\vartheta )$, then the quantity $a=2(\vartheta +1)/M$ can be written as $a=\rho +1/\rho$, where $\rho =(a+\sqrt{a^2-4})/2>1$. Then, $|b_k\left(z\right)|\ge \rho +1/\rho$, $|{\widehat{b}}_k\left(\widehat{z}\right)|\ge \rho +1/\rho$, $k\ge 1$, and according to Corollary 4, the set (48) is a set of stability to perturbations of the continued fraction (46). In addition,

$$|g_k^{\left(n\right)}\left(z\right)|\le {\rho }^{-2},\left|{\widehat{g}}_k^{\left(n\right)}\left(\widehat{z}\right)\right|\le {\rho }^{-2},k\ge 2.$$

and from Formula (49) we have

$$\begin{array}{cc}\hfill |{\epsilon }^{\left(n\right)}|& \le |{\tilde{\beta }}_1|+\sum _{k=2}^n\left(\right|{\tilde{\beta }}_k|-|{\tilde{\beta }}_{k-1}\left|\right)\prod _{m=2}^k\left|{\tilde{g}}_m^{\left(n\right)}\right|\hfill \\ & \le {\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta )\sum _{k=2}^n{\rho }^{-2(k-1)}\right)\hfill \\ \hfill & ={\displaystyle \frac{\beta }{1-\beta }}\left(1+(2-\beta ){\displaystyle \frac{1-{\rho }^{-2(n-1)}}{{\rho }^2-1}}\right)\hfill \end{array}$$

for $n\ge 1.$ □

To compute the approximants of the continued fraction (46), two fundamental algorithms were used: the backward recurrence algorithm (BR-algorithm), where the computation of the approximant is performed from the “tail” of the fraction to its “head” using the recurrence relations (2), and the forward recurrence algorithm (FR-algorithm), according to which $f_n=A_n/B_n$, where $A_n,B_n$ are the numerator and denominator of the nth approximant, respectively, determined by the recurrence relations

$$\begin{array}{c}{A}_n=b_n{A}_{n-1}+A_{n-2},B_n=b_n{B}_{n-1}+B_{n-2},n\ge 1,\end{array}$$

with initial conditions $A_{-1}=1,$ $A_0=0,$ $B_{-1}=0,$ $B_0=1.$

The computation of the approximants of the continued fraction (46) for different values of the order $\nu$ and the variable z was performed in the Maple 2024.0 computer algebra system using double-precision floating-point numbers [53,54]. Below are the results for two representative cases: (1) $\nu =1.0,z=1.5$; (2) $\nu =4.1,z=3.0+4.0i$.

In the first case, the elements of the continued fraction (46) are real numbers and satisfy the conditions of Theorem 8. The relative errors in the calculation of the approximants are shown in

Table 1. Relative errors for (46) using the BR-algorithm and FR-algorithm at the point $z=1.5$ and order $\nu =1.0$.

n	$({\mathit{f}}_{\mathit{n}}^{\left(\mathit{BR}\right)}-{\mathit{f}}_{\mathit{n}})/{\mathit{f}}_{\mathit{n}}$	$({\mathit{f}}_{\mathit{n}}^{\left(\mathit{FR}\right)}-{\mathit{f}}_{\mathit{n}})/{\mathit{f}}_{\mathit{n}}$
1	0	0
2	$2.083333333333333\times {10}^{-15}$	$4.5\times {10}^{-15}$
3	$2.185792349726776\times {10}^{-15}$	$4.590163934426230\times {10}^{-15}$
4	$1.461711711711712\times {10}^{-15}$	$6.269707207207207\times {10}^{-15}$
5	$8.353967057810313\times {10}^{-16}$	$3.239387088671188\times {10}^{-15}$
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14	$2.783898469841665\times {10}^{-15}$	$7.591879029562294\times {10}^{-15}$
15	$2.783898469841700\times {10}^{-15}$	$5.187888749702014\times {10}^{-15}$
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
99	$2.783898469841700\times {10}^{-15}$	$4.365173322746704\times {10}^{-14}$
100	$2.783898469841700\times {10}^{-15}$	$4.365173322746704\times {10}^{-14}$
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2099	$2.783898469841700\times {10}^{-15}$	$1.630914308405200\times {10}^{-13}$
2100	$2.783898469841700\times {10}^{-15}$	$1.630914308405200\times {10}^{-13}$
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9999	$2.783898469841700\times {10}^{-15}$	$1.404403348918050\times {10}^{-14}$
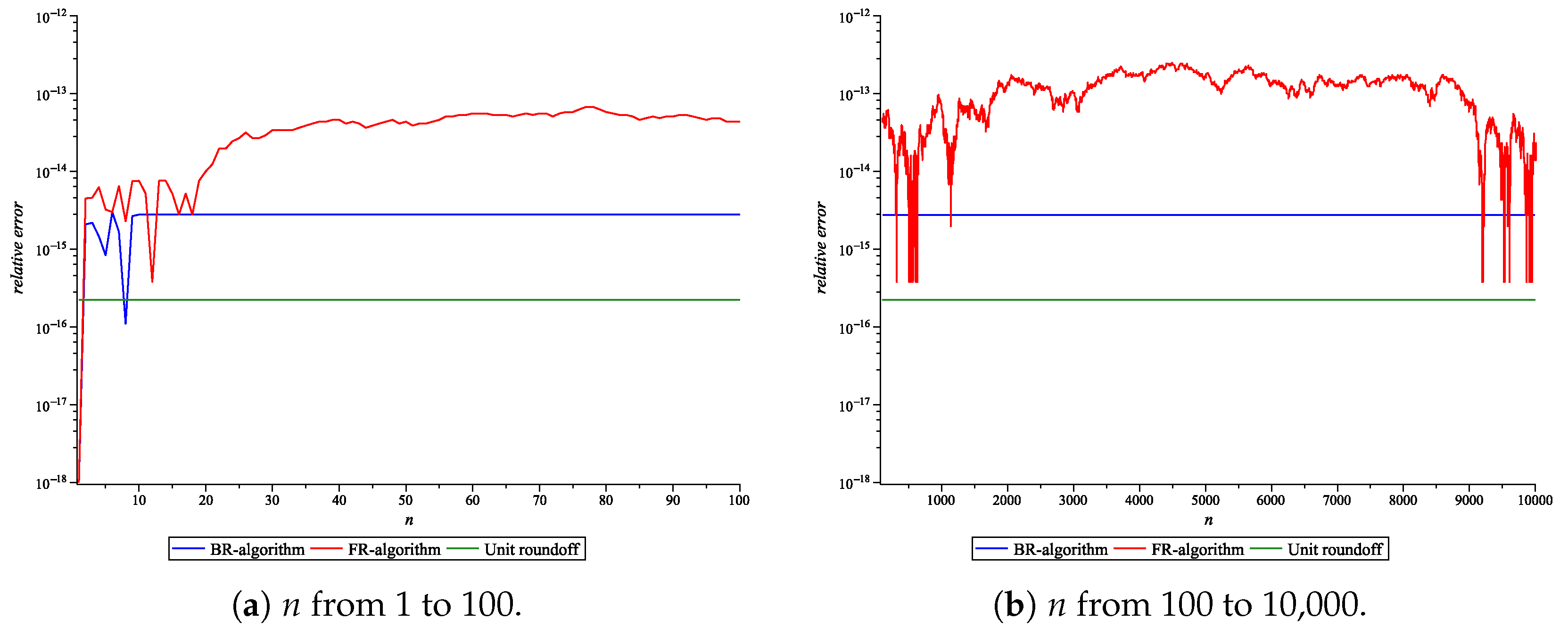
10,000	$2.783898469841700\times {10}^{-15}$	$1.64480237690408\times {10}^{-14}$

and visualized in Figure 1.

As can be seen from Table 1 and Figure 1a,b, the BR-algorithm demonstrates numerical stability. Relative errors are close to the unit round-off (machine epsilon), and, starting from the 15th approximant, do not change their value. In contrast, when computing the approximants using the FR-algorithm, their relative values significantly exceed the unit round-off but remain bounded.

In the second case (see,

Table 2. Relative errors for (46) using the BR-algorithm and FR-algorithm at the point $z=3.0+4.0i$ and order $\nu =4.1$.

n	$({\mathit{f}}_{\mathit{n}}^{\left(\mathit{BR}\right)}-{\mathit{f}}_{\mathit{n}})/{\mathit{f}}_{\mathit{n}}$	$({\mathit{f}}_{\mathit{n}}^{\left(\mathit{FR}\right)}-{\mathit{f}}_{\mathit{n}})/{\mathit{f}}_{\mathit{n}}$
1	$9.633275663033836\times {10}^{-16}$	$9.633275663033836\times {10}^{-16}$
2	$1.832435286958924\times {10}^{-15}$	$1.211310665610329\times {10}^{-15}$
3	$2.231005996753781\times {10}^{-15}$	$9.113913504252372\times {10}^{-17}$
4	$1.163235854061239\times {10}^{-15}$	$1.163235854061239\times {10}^{-15}$
5	$6.902425771685029\times {10}^{-16}$	$6.902425771685029\times {10}^{-16}$
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14	$3.961931945697510\times {10}^{-16}$	$4.714179043370162\times {10}^{-15}$
15	$3.963094932223096\times {10}^{-16}$	$5.336629962010334\times {10}^{-15}$
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
99	$3.963060131680243\times {10}^{-16}$	$3.214063110145439\times {10}^{-14}$
100	$3.963060131680243\times {10}^{-16}$	$3.030197672227112\times {10}^{-14}$
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2099	$3.963060131680243\times {10}^{-16}$	$2.089370349182762\times {10}^{-13}$
2100	$3.963060131680243\times {10}^{-16}$	$2.113726461511491\times {10}^{-13}$
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9999	$3.963060131680243\times {10}^{-16}$	$2.604540504957798\times {10}^{-13}$
10,000	$3.963060131680243\times {10}^{-16}$	$2.61406512503510\times {10}^{-13}$

and Figure 2a,b), the elements of the continued fraction are complex numbers and also satisfy the conditions of Theorem 8.

The results for the complex value of the variable z illustrate the stability of the BR-algorithm. The behavior of the errors in the FR-algorithm demonstrates their slow accumulation.

Thus, the BR-algorithm is numerically stable, which corresponds to the property of limited error accumulation, one of the key advantages of continued fractions. The error of this method remains at the level of the unit round-off. The calculation of approximants of a continued fraction using the FR-algorithm can lead to the accumulation of errors and loss of accuracy, especially when calculating high-order approximants. The results highlight the importance of choosing the right algorithm. For practical problems requiring high-precision results, preference should be given to the BR-algorithm.

4.2. Polynomial and Continued Fraction Models in the Problem of Wood Drying Modeling

One of the key stages of mathematical modeling of physical and technological processes, such as the drying of moisture in wood, is the construction of an analytical dependence that reflects the change in humidity over time. This study compares two approaches to approximating experimental data: approximation by the second-order polynomial model

$$p_2\left(x\right)=a_0+a_{1}x+a_2{x}^2$$

and the so-called second-order continued fraction model

$$f_2\left(x\right)=b_0+{\displaystyle \frac{1}{b_{1}x+\frac{1}{b_{2}x}}}.$$

Here, the second-order continued fraction is the 2nd approximant of the continued fraction. The purpose of the analysis is not only to assess the accuracy of the approximation, but also to study the stability of the models to parameter perturbations.

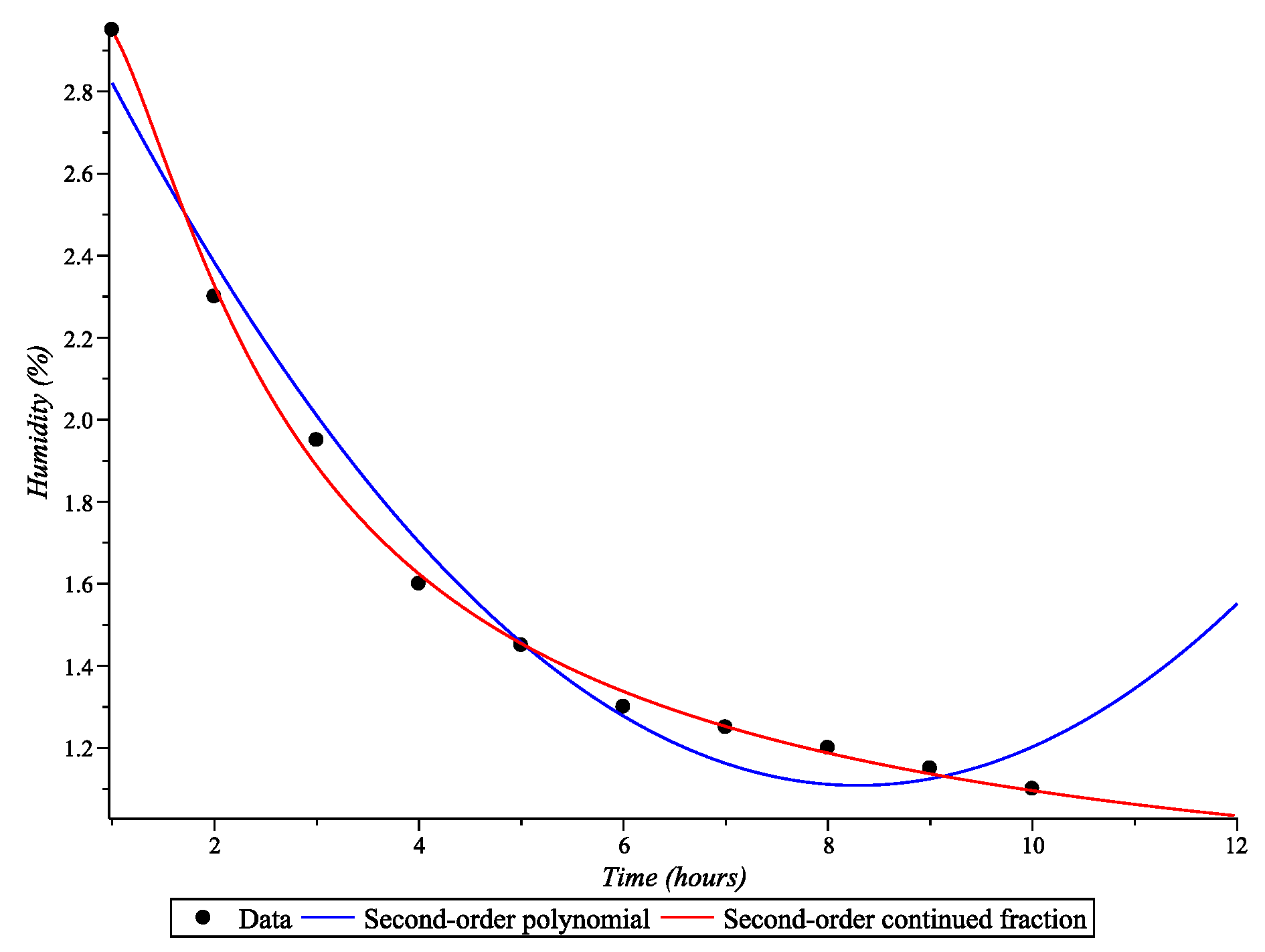
For the exact data $(x_i,y_i)$ describing the decrease in wood moisture content over time, the second-order polynomial model and the second-order continued fraction model was constructed. The quality of the approximation was assessed using the following criteria: standard deviation $RMSE$ and coefficient of determination $R^2$. The approximation results indicate a significant advantage of the continued fraction model according to these criteria (see

Table 3. Values of $RMSE$ and $R^2$ for polynomial and continued fraction models.

Model	RMSE	${\mathit{R}}^2$
Second-order polynomial	0.08056	0.98019
Second-order continued fraction	0.02651	0.99786

).

Figure 3 shows the exact data, second-order polynomial model, and second-order continued fraction model of the moisture reduction process in wood.

From Table 3 and Figure 3 it is seen that the continued model allows to reduce the error by almost three times, while maintaining a high correlation with the experimental data. This is due to the fact that such a model is able to naturally take into account the asymptotic behavior of the function, inherent in drying processes, where the humidity decreases nonlinearly and asymptotically approaches the limiting value.

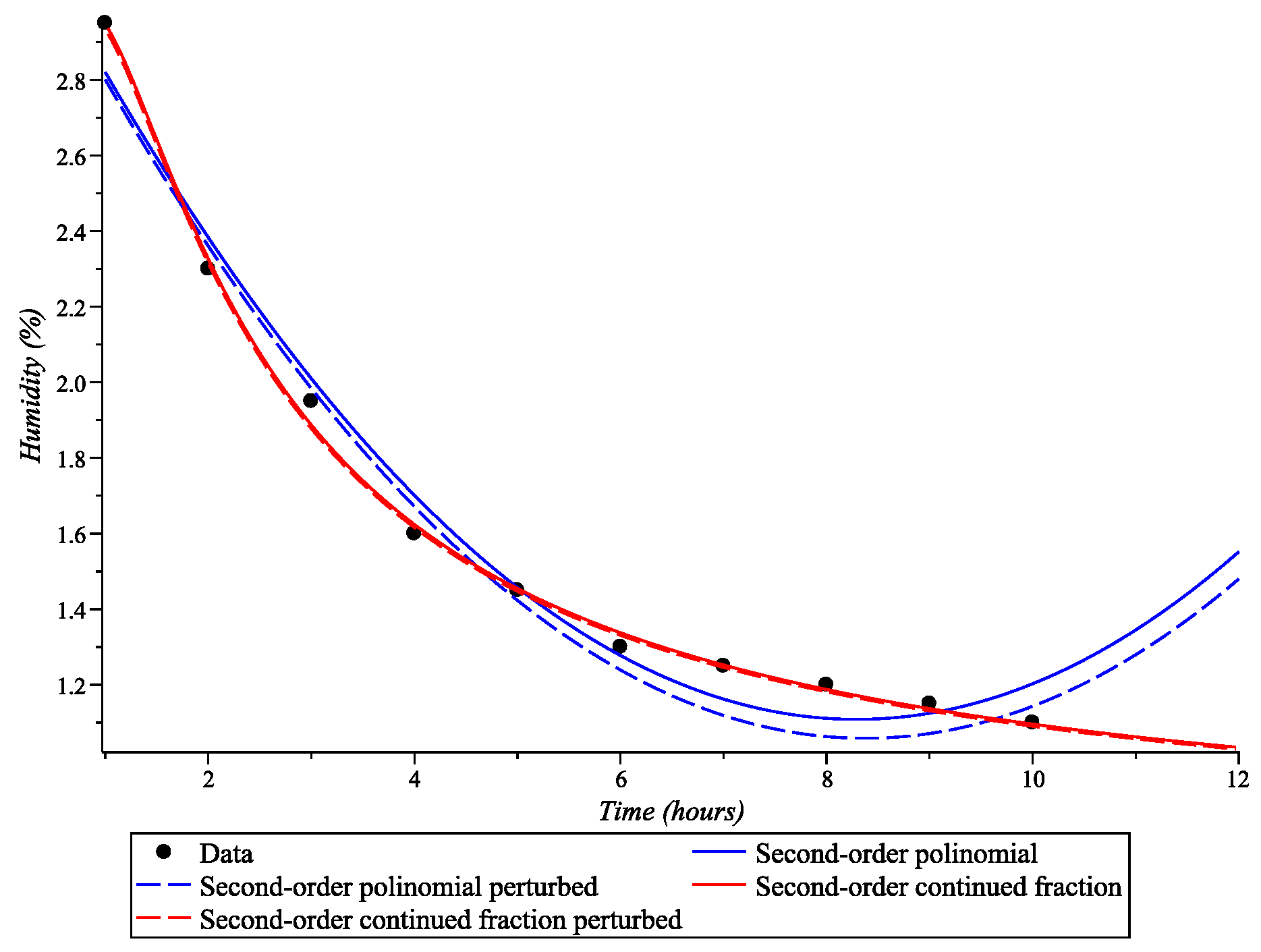
An experiment was also conducted in which the coefficients of each model were perturbed to random values within a given maximum. The values of and when perturbing the coefficients of both models are given in

Table 4. Values of $RMSE$ when perturbing the coefficients of polynomial and continued fraction models.

Model	RMSE
Second-order polynomial	0.08977
Second-order continued fraction	0.02787

.

Figure 4 shows the exact data, unperturbed and perturbed to the maximum value polynomial and continued fraction models of the moisture reduction process in wood.

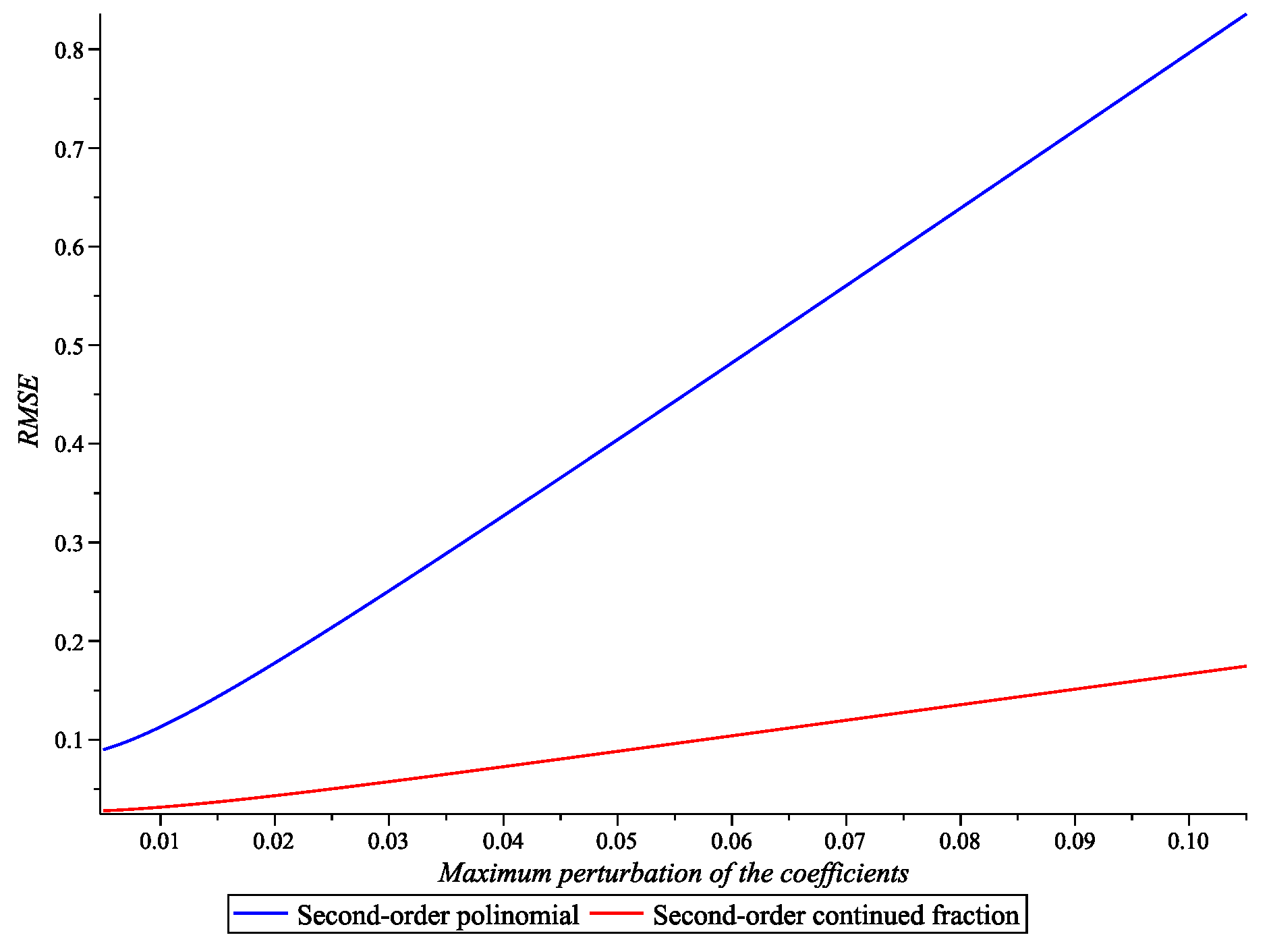
To assess the stability of the models to errors in the coefficients, a simulation of coefficient perturbations in the range from 0.5% to 10.5% with a step of 0.001 was performed. For each level of perturbation, values were calculated for both models.

Table 5. Values due to perturbation of coefficients of polynomial and continued fraction models.

Maximum Perturbation of Coefficients	RMSE (Polynomial)	RMSE (Continued Fraction)
0.00500	0.08977	0.02787
0.00600	0.09354	0.02844
0.00700	0.09780	0.02911
0.00800	0.10250	0.02985
0.00900	0.10758	0.03068
0.01000	0.11299	0.03157
0.01100	0.11868	0.03253
0.01200	0.12461	0.03354
0.01300	0.13076	0.03461
0.01400	0.13709	0.03573
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
0.10000	0.79638	0.16679
0.10100	0.80426	0.16835
0.10200	0.81215	0.16990
0.10300	0.82003	0.17146
0.10400	0.82792	0.17302
0.10500	0.83580	0.17457

shows the results of this experiment.

Figure 5 shows a plot of the dependence of $RMSE$ on the magnitude of the disturbance for both models.

The polynomial model shows a significant increase in $RMSE$ even with small perturbations. On the contrary, the continued fraction model is characterized by a gradual and slow increase in error, which confirms its lower sensitivity to perturbations of its coefficients. It is significantly more reliable compared with the polynomial model, which is important when working with experimental or approximate data.

Therefore, the continued fraction model shows better results both in terms of approximation accuracy and stability to perturbations, which makes it more suitable for modeling processes with pronounced asymptotic behavior. Polynomial models, despite their simplicity, are more sensitive to changes in the data.

5. Conclusions

In this paper, a formula for the relative error of the nth approximant of a continued fraction has been established, which describes the dependence of this error on the relative errors of the fraction’s elements and on quantities that depend on the elements of the fraction. This formula is the basis for further analysis of stability under perturbations and for the construction of sequences of stability sets. For each sequence of stability sets, estimates for the relative error of the nth approximant have been obtained. These estimates allow the evaluation of the maximum possible perturbation error of the approximant, provided that the elements of the fraction and their perturbations belong to the corresponding stability sets. The research results complement and extend existing results in the theory of stability of continued fractions.

The results of this work provide a toolkit for analyzing the numerical stability of algorithms that use continued fractions of the type under investigation. The error estimates can be used to select computation parameters, control accuracy, and ensure the reliability of results in applied problems that use continued fractions.

A promising direction is the extension of the obtained results to more general classes of continued fractions and their generalizations, as well as the application of stability criteria to special functions that are expanded into continued fractions, for the analysis of the errors in their computation.