Application of the GM(1,1) Model in Predicting the Cohesion of Laterite Soil Under Dry–Wet Cycles with Temporal Translational Symmetry

Abstract

To investigate cohesion degradation in laterite soil under dry–wet cycles—a process exhibiting intrinsic asymmetric evolution in natural systems—direct shear tests were conducted on natural and stabilized soils (guar gum/coconut fiber composites) under simulated cycles. A cohesion prediction model was developed using the gray system GM(1,1) framework, with validation confirming its applicability and reliability. Results indicate the following: (1) Stabilized soils showed significantly increased cohesion and reduced cohesion degradation rates. (2) Compared to coconut fiber-stabilized soil, guar gum-stabilized soil exhibited smaller cohesion decay magnitude and more stable internal structure. (3) Cohesion degradation in both natural and stabilized soils conformed to the GM(1,1) model, achieving >95% fitting accuracy across all groups (peak: 99.84% for natural soil). This model effectively characterizes the strength degradation process under dry–wet cycles, establishing a novel methodology for predicting cohesion in natural/stabilized laterite soils.

1. Introduction

Laterite soil, a distinctive pedological formation developed in carbonate rock regions [1], is extensively distributed across warm–humid climatic zones south of the Yangtze River in China. It covers over 2 million km² in provinces including Guangxi, Guizhou, and Yunnan. As a primary soil category in regional engineering projects, it exhibits marked environmental susceptibility and physical degradability—characterized by humidity sensitivity, strong swell–shrink behavior, multi-cracking tendency, and strength degradation [2].

In warm–humid environments, these characteristics exhibit synergistic interactions, further accelerating the deterioration of geotechnical performance and inducing progressive geotechnical hazards [3]. Typical failures include weathering, spalling, collapse, erosion, and slope instability in laterite soil highway embankments in Guizhou [4], Jiangxi [5], and Yunnan [6], as well as shallow instability and landslides in road foundations/subgrades in Hunan [7] and Guangxi [8]. These issues severely impede construction progress, compromise operational safety, and incur substantial economic and social losses. Consequently, research addressing performance deterioration in laterite soil engineering is crucial for ensuring structural integrity and long-term operational safety of constructions, carrying significant theoretical and practical value.

Existing studies indicate that the shear strength of laterite soil is influenced by multiple factors, including moisture content [9], crack propagation [10], compaction density [11], and temperature [12]. The interactions among these factors result in exceptionally complex shear strength behavior under dry–wet cycles. Consequently, stability assessments based on shear strength necessitate comprehensive integration of multifactorial influences, resulting in intricate procedures and substantial workloads. This poses significant challenges for engineering stability evaluations.

The gray theory GM(1,1) model constructs a dynamically evolving model through differential equations based on raw data, revealing developmental trajectories and predicting future behavioral patterns [13]. Among shear strength parameters, cohesion primarily originates from molecular attraction and cementation bonds, exhibiting significant water sensitivity characteristics. In contrast, the angle of internal friction depends on interparticle friction effects, influenced by mineral hardness and compaction density [14], with minimal sensitivity to moisture fluctuations. During dry–wet cycling tests on laterite soil, the dominant factor in shear strength degradation is typically the attenuation of cohesion, while changes in the angle of internal friction remain minor or irregular [9]. Introducing this model into stability assessment for laterite soil enables cohesion prediction under dry–wet cycles, thereby providing a novel theoretical framework for evaluating the stability of laterite soil subjected to cyclic moisture fluctuations.

This study investigates the influence of dry–wet cycles—a natural process characterized by temporal translational symmetry—on the asymmetric degradation of cohesion in natural and stabilized laterite soils. Direct shear tests were conducted on laterite soil specimens (natural and guar gum-/coconut fiber-stabilized) after five dry–wet cycles. A GM(1,1) prediction model for cohesion under moisture fluctuations was established using gray theory. The model’s application to predict cohesion in both soil types demonstrated high accuracy and reliability when validated against experimental data. This work establishes a theoretical foundation for stability assessment of laterite soils in engineering practice.

2. Sample Preparation and Testing Program

2.1. Sample Preparation

The test soil specimens, retrieved from Guilin, Guangxi Province, exhibited reddish-brown coloration, homogeneous texture, and moderately compact structure. Following China’s Standard for Geotechnical Testing Methods (GB/T 50123-2019) [15], laboratory testing determined basic physical properties as summarized in Table 1.

Both natural and stabilized laterite soils were investigated to enhance applicability across scenarios. Guar gum and coconut fiber were selected as eco-friendly stabilizers due to their negligible environmental impact [16,17], commercial accessibility, and low industrial processing requirements. The improvement efficacy of low-dosage guar gum and coconut fiber has been confirmed. However, higher dosages induce agglomeration of cementitious materials, forming large particles that create macro-pores [16], leading to strength reduction. Similarly, the reinforcement effect of coconut fiber exhibits a saturation threshold; excessive fibers cause entanglement, generating weak zones [17] that compromise overall strength. Consequently, gradient dosage tests were conducted for both materials, identifying 0.3% as the optimal dosage (yielding peak cohesion) [18].

Table 1. Basic physical properties of laterite soil [18].

Specimen	Liquid Limit	Plastic Limit	Optimum Moisture Content	Maximum Dry Density
laterite soil	55.22%	30.24%	26.70%	1.50 g/cm3

Table 1. Basic physical properties of laterite soil [18].

Specimen	Liquid Limit	Plastic Limit	Optimum Moisture Content	Maximum Dry Density
laterite soil	55.22%	30.24%	26.70%	1.50 g/cm3

Thus, modified specimens were prepared by incorporating 0.3% guar gum and 0.3% coconut fiber separately. To align with high-moisture conditions during rainy seasons—when laterite soil disasters frequently occur—and validate improvement effects under the least favorable conditions (minimal cohesion), modifications were exclusively applied to Sample A3. Specimen preparation details are summarized in

Table 2. Sample preparation details.

Specimen Type		Key Parameters		Specimen ID	Dimensions	Quantity
natural specimens		Moisture content	18.7%	A1	Standard ring-knife specimens (Φ61.8 × 20 mm)	Tested in groups of 24 specimens per group, totaling 120 specimens
			26.7%	A2
			34.7%	A3
stabilized specimens (modified from A3)		Guar gum dosage	0.3%	B1
		Coconut fiber dosage	0.3%	B2

.

2.2. Testing Procedure

2.2.1. Dry–Wet Cycling Test

The prepared ring-knife specimens were dried in a constant-temperature oven at 60 °C. Mass was recorded at 2 h intervals until stabilization (≤0.1% difference between consecutive measurements). The dried specimens were then saturated in a stacking saturator and vacuum-pumped for 3 h followed by 10 h water immersion. This sequence constituted one dry–wet cycle. The procedure was repeated for five full cycles. The dry–wet cycle testing protocol is shown in Figure 1. Comparative specimen states before and after cycling are presented in Figure 2.

2.2.2. Direct Shear Test

Ring-knife specimens subjected to 0, 1, 2, 3, 4, and 5 dry–wet cycles were sheared using a ZJ-type quad strain-controlled direct shear apparatus (manufactured by Nanjing Soil Instrument Factory Co., Ltd., Nanjing, China, as shown in Figure 3). Quick shear tests were conducted at a shear rate of 0.8 mm/min with a shear displacement of 6 mm under vertical stresses of 100, 200, 300, and 400 kPa.

2.2.3. Microscopic Observation Test

Field emission scanning electron microscopy (FESEM) was conducted using an S-4800 instrument (Hitachi, Tokyo, Japan). Specimens before and after dry–wet cycles were prepared as FESEM-compatible samples (2–3 mm fragments) to examine pore structure and morphological evolution.

3. Results and Analysis of Direct Shear Tests Under Dry–Wet Cycles

Based on direct shear test results, shear strength failure envelopes for each specimen group under varying cycle counts were derived. Using Specimen A1 as an example, this envelope is illustrated in Figure 4. Cohesion and internal friction angle values across different cycle counts for all groups were further determined, as detailed in

Table 3. Variations in cohesion and internal friction angle under dry–wet cycles [18].

Specimen ID	Parameters	Cycles
		0	1	2	3	4	5
A1 (18.7%)	c (kPa)	235.45	217.76	212.83	187.61	173.99	152.46
	ϕ (°)	30.83	30.28	29.10	29.80	30.05	30.70
A2 (26.7%)	c (kPa)	210.90	204.98	188.54	169.35	157.64	140.59
	ϕ (°)	29.18	26.05	26.68	26.40	25.85	26.42
A3 (34.7%)	c (kPa)	161.14	125.83	103.04	84.00	71.15	57.82
	ϕ (°)	28.93	30.57	31.04	31.71	32.26	31.48
B1 (guar gum-stabilized)	c (kPa)	290.41	268.59	251.68	236.17	196.18	168.81
	ϕ (°)	29.02	29.92	29.55	27.74	29.12	29.00
B2 (coconut fiber-stabilized)	c (kPa)	317.28	286.16	228.04	197.15	175.24	159.58
	ϕ (°)	30.44	29.38	27.63	29.11	29.95	29.40

and Figure 5.

Analysis of Table 3 and Figure 5a reveals the following: (1) For natural specimens, cohesion exhibited a significant reduction with increasing moisture content under identical dry–wet cycles. As cycle count increased, c progressively declined, with Specimens A1, A2, and A3 exhibiting reductions of 35.25%, 33.34%, and 64.12%, respectively, after five cycles. (2) For stabilized specimens, guar gum-stabilized ones (B1) and coconut fiber-stabilized ones (B2) showed pre-cycle c increases of 129.27 kPa (80.22%) and 156.14 kPa (96.90%), respectively, versus A3. After five cycles, B1 and B2 maintained c increases of 110.99 kPa (191.96%) and 101.76 kPa (175.99%) relative to A3. Coconut fiber demonstrated more pronounced cohesion improvement, whereas guar gum exhibited enhanced stability retention under moisture fluctuations.

Analysis of Table 3 and Figure 5b indicates the following: The internal friction angle φ is governed by multiple factors (e.g., particle shape characteristics, size distribution, and external stress conditions), resulting in significant measurement uncertainty under laboratory settings. Consequently, (1) for natural specimens, φ exhibited no significant correlation with dry–wet cycle count, and no clear pattern emerged under moisture content variations, and (2) both guar gum-stabilized (B1) and coconut fiber-stabilized (B2) specimens showed irregular fluctuations in φ. Therefore, only cohesion will be discussed as the primary shear strength parameter in subsequent analyses.

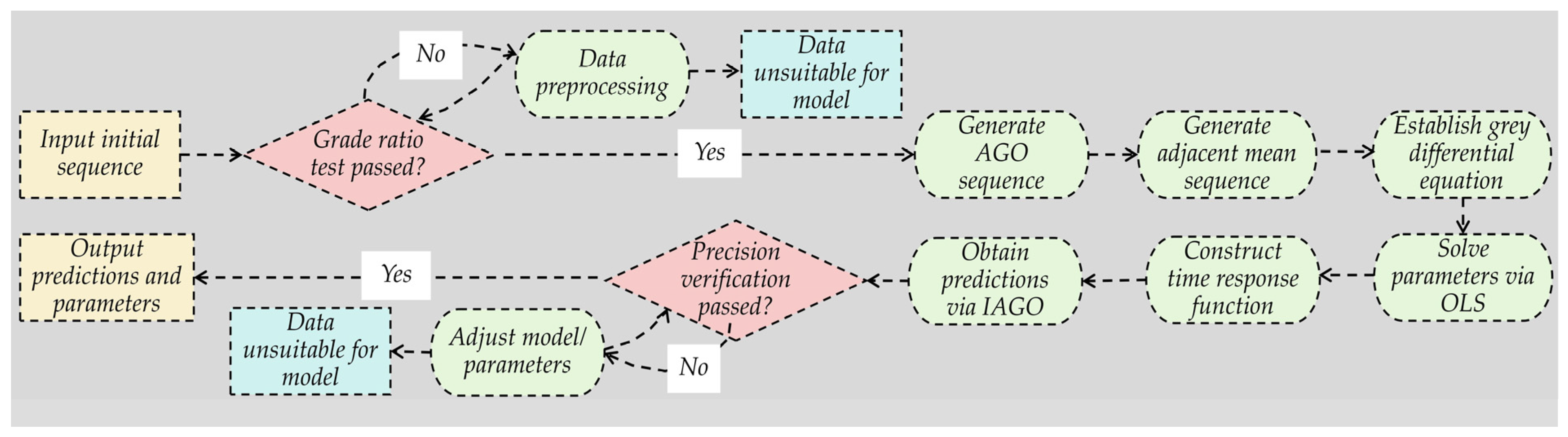
4. Construction of Gray Theory-Based GM(1,1) Cohesion Model for Laterite Soil Under Dry–Wet Cycles

4.1. Applicability Arguments of the Gray System Theory GM(1,1) Model

Gray system theory was proposed by Deng Julong in the early 1980s to address uncertain problems [19]. The Gray Model (GM), also known as the Gray Dynamic Model and abbreviated as the GM(1,1) model, reveals developmental processes of systems and predicts their future patterns.

The core hypotheses of GM(1,1) modeling are reflected in three aspects:

• Small-sample applicability: Given the long monitoring cycles and heavy workloads in geotechnical engineering, data samples are limited. This model uses Accumulating Generation Operation (AGO) to process raw discrete data, excavating underlying patterns to effectively overcome small-sample constraints. This study conducted only five cyclic tests, with the data volume (n = 5) satisfying the minimum requirement (n > 4) [20].
• Uncertainty handling mechanism: Addressing the uncertainty of laterite soil cohesion under multi-factor coupling, gray theory dynamically incorporates these influences through gray parameters and residual modification. The modeling process relies solely on inherent data patterns, avoiding interference from extraneous complex factors [21].
• Geotechnical data compatibility: GM(1,1) modeling requires no specific data distribution, only non-negative values whose accumulated sequence follows an exponential pattern (confirmed by level ratio tests) [22]. Soil degradation is intrinsically a gray system—partially known (e.g., cohesion attenuation) and partially unknown (e.g., cementation evolution, fiber distribution, crack propagation)—with experimental data fully aligning with model prerequisites.

As evidenced by the analysis of

Table 4. Applicability comparison table between GM(1,1) model and other prediction models.

Methods	Sample Requirements	Geotechnical Engineering Applicability Validation	Case Study Compatibility in This Research
GM(1,1) Model	≥4	Exhibits strong applicability for small-sample prediction	✓
Machine Learning (ANN)	large sample size	Requires substantial training data	✗
Random Forest	≥50	Suitable for multi-feature datasets	✗
Neural Networks (LSTM)	large sample size	Demands extensive training data	✗
Multiple Regression	≥tenfold variables	Needs quantification of multiple influencing parameters	✗
Time Series (ARIMA)	≥30	Requires strictly equally spaced data collection	✗
Bayesian Networks	≥tenfold variables	Precise conditional probability distributions of variables must be provided as prior inputs	✗

, captioned Applicability comparison table between GM(1,1) model and other prediction models, the GM(1,1) model aligns with this study’s requirements—namely limited sample size, susceptibility to multi-factor influences, and inherent data-model compatibility. Consequently, this research employed the GM(1,1) model to predict the cohesion of laterite soil under dry–wet cycles.

4.2. GM(1,1) Model of Gray System Theory

The initial data sequence is denoted as

$$c^{\left(0\right)}(t)=\left(c^{(0)}(1),c^{(0)}(2){,c}^{(0)}(3),\cdots {,c}^{(0)}(n)\right)$$

(1)

$n$ is the number of initial data points.

Applying a first-order Accumulating Generation Operation (1-AGO) to the initial data sequence generates the accumulated sequence $c^{(1)}(k)$, with elements defined as

$$c^{(1)}(t)=\sum _{i=1}^t{c}^{\left(0\right)}(i)$$

(2)

To prevent data anomalies, the accumulated sequence $c^{\left(1\right)}\left(k\right)$ undergoes adjacent-averaging generation during preprocessing, producing a new sequence $L^{(1)}(t)$ defined as

$$L^{(1)}(t)={\displaystyle \frac{1}{2}}\left(c^{(1)}(t)+c^{(1)}(t-1)\right)t=\mathrm{2,3},\cdots ,n$$

(3)

Based on gray system theory, construct the first-order ordinary differential equation with respect to $t$:

$${\displaystyle \frac{d{L}^{(1)}}{dt}}+a{L}^{(1)}=u$$

(4)

By constructing and solving the system matrix, we obtain $Y=BU$, and

$$Y=\left[\begin{array}{c}{c}^{(0)}(2)\\ c^{(0)}(3)\\ \begin{array}{c}⋮\\ c^{(0)}(n)\end{array}\end{array}\right],B=\left[\begin{array}{c}\begin{array}{cc}-L^{(1)}(2)& 1\\ -L^{(1)}(3)& 1\\ ⋮& ⋮\end{array}\\ \begin{array}{cc}-L^{(1)}(n)& 1\end{array}\end{array}\right],U={\left[a,u\right]}^T$$

(5)

In the equation, $a$ and $u$ are undetermined coefficients representing the development coefficient and gray action quantity, respectively. In the GM(1,1) equation, the coefficients $a$ and $u$ are to-be-determined parameters representing the development coefficient and gray action quantity, respectively. Using the least-squares method, we minimize the sum of squared errors to match the optimal function, yielding

$$U={(B^{T}B)}^{-1}(B^{T}Y)$$

(6)

After solving for the gray parameters $a$ and $u$, they are substituted into Equation (4) to yield

$${\widehat{c}}^{(1)}(t)=(c^{(0)}(1)-{\displaystyle \frac{u}{a}})e^{-a(t-1)}+{\displaystyle \frac{u}{a}}t=\mathrm{2,3},\cdots ,n$$

(7)

Applying a single inverse Accumulating Generation Operation (1-IAGO) to the sequence ${\widehat{c}}^{(1)}(t)$ generates the restored sequence ${\widehat{c}}^{(0)}(t)$, defined as

$${\widehat{c}}^{(0)}(t)={\widehat{c}}^{(1)}(t)-{\widehat{c}}^{(1)}(t-1)t=\mathrm{2,3},\cdots ,n$$

(8)

By integrating Equations (7) and (8), the GM(1,1) model is formally established as

$${\widehat{c}}^{(0)}(t)=(c^{(0)}(1)-{\displaystyle \frac{u}{a}})(1-e^a)e^{-a(\mathrm{t}-1)}t=\mathrm{2,3},\cdots ,n,{\widehat{c}}^{(0)}(1)=c^{\left(0\right)}(1)$$

(9)

4.3. Construction of GM(1,1)-Based Cohesion Model for Laterite Soil Under Dry–Wet Cycles

To ensure the applicability of the GM(1,1) model for predicting the cohesion of laterite soil under dry–wet cycles, the cohesion of specimens A1, A2, A3, B1, and B2 after 0–4 cycles served as the foundational dataset. Following the GM(1,1) formulation in Equation (12) (Section 4.2), sequential cohesion prediction models were developed for each specimen, as illustrated in Figure 6.

Taking specimen A3 as an example, the initial data sequence is input, yielding

$${c^{\left(0\right)}}_{A3}=\left(161.14,125.83,103.04,84.00,71.15\right)$$

(10)

Level ratio testing of the initial data sequence yields

$${ϵ}_{A3}(t)={\displaystyle \frac{c^{\left(0\right)}(t-1)}{c^{\left(0\right)}(t)}},t=\mathrm{2,3},\cdots ,n$$

(11)

Then,

$${ϵ}_{A3}=(1.28,1.22,1.23,1.18)$$

(12)

The validity of the level value ${ϵ}_{A3}(t)$ is determined by its inclusion within the feasible interval $(e^{-{\displaystyle \frac{2}{\mathrm{n}+1}}},e^{{\displaystyle \frac{2}{\mathrm{n}+1}}})$, specifically $(e^{-{\displaystyle \frac{1}{3}}},e^{{\displaystyle \frac{1}{3}}})$. If ${ϵ}_{A3}(t)$ falls within this interval, the test is passed; otherwise, data preprocessing must be performed to eliminate outliers. Should the test remain unpassed after preprocessing, the data is deemed incompatible with this model. In this study, all specimen datasets successfully satisfied the level ratio test criteria, indicating full compliance with GM(1,1) modeling prerequisites for all specimens.

The accumulated sequence is generated according to Equation (2), yielding

$${c^{\left(1\right)}}_{\mathrm{A}3}=(161.14,286.97,390.01,474.01,545.16)$$

(13)

The adjacent-average sequence is generated according to Equation (3), yielding

$${L^{(1)}}_{A3}=(224.06,338.49,432.01,509.59)$$

(14)

The gray differential equation is established based on Equations above (4) and (5), and solved via matrix operations to yield

$$Y_{A3}=\left[\begin{array}{c}125.83\\ 103.04\\ \begin{array}{c}84.00\\ 71.15\end{array}\end{array}\right],B_{A3}=\left[\begin{array}{c}\begin{array}{cc}-224.06& 1\\ -338.49& 1\\ -432.01& 1\end{array}\\ \begin{array}{cc}-509.59& 1\end{array}\end{array}\right]$$

(15)

The parameters $a$ and $u$ were obtained via the least-squares method based on Equation (6), yielding the following values:

$${\left[a_{A3},u_{A3}\right]}^T={\left[0.1933,168.6757\right]}^T$$

(16)

Substituting the gray parameters $a_{A3}$ and $u_{A3}$ into Equation (4) to construct the time response function, and combining with Equation (7), yields

$${{\widehat{c}}^{(1)}}_{A3}(t)=-711.6540e^{-0.1933(t-1)}+872.7940$$

(17)

The cohesion prediction model for laterite soil under dry–wet cycles is derived for specimen A3 via inverse accumulation operation according to Equation (8):

$${{\widehat{c}}^{(0)}}_{A3}(t)=-711.6540\left(1-e^{0.1933}\right)e^{-0.1933(t-1)}$$

(18)

Ultimately, the GM(1,1) prediction model for cohesion of laterite soil under dry–wet cycles is established:

$${\widehat{c}}^{(0)}(t)=m\left(1-e^b\right)e^{-b(t-1)}$$

(19)

where c denotes the predicted cohesion value (primary shear strength indicator), $t$ represents the number of dry–wet cycles, and $m$ and $b$ are model parameters tabulated in

Table 5. Specimen identification codes.

Parameters	Specimen ID
	A1	A2	A3	B1	B2
$\mathrm{m}$	−2947.2819	$-2385.9346$	$-711.6540$	$-2994.0340$	$-1802.9327$
$\mathrm{b}$	7.8230 × 10−2	8.9815 × 10−2	1.9326 × 10−1	9.5697 × 10−2	1.6866 × 10−1

.

5. Accuracy and Analysis of GM(1,1) Cohesion Model for Laterite Soil Under Dry–Wet Cycles

5.1. Goodness-of-Fit Validation for Prediction Model

Model validity is verified through accuracy assessment, evaluated via the Relative Error Test and Posterior Variance Test [23].

The percentage error test is as follows (20).

$$(t)={\widehat{c}}^{(0)}(t)-c^{\left(0\right)}(t)d,\epsilon (t)=\left|{\displaystyle \frac{\delta (t)}{c^{\left(0\right)}(t)}}\right|$$

(20)

where $\mathrm{\delta }$—error; $\mathrm{\epsilon }$—absolute percentage error; $t$—the number of dry–wet cycles.

Classification of model precision into four grades based on the $\epsilon$-value is formalized in

Table 6. Reference table for precision grading by percentage error test.

Grade	I (Excellent)	II (Qualified)	III (Marginal)	IV (Invalid)
$\epsilon$$-\mathrm{value}$	$\epsilon \le 5\%$	$5\%<\epsilon \le 10\%$	$10\%<\epsilon \le 20\%$	$\epsilon >20\%$

.

The posterior variance test is as follows (21)–(24).

$$\overline{c}={\displaystyle \frac{1}{n}}{\sum }_{i=1}^t{C}^{\left(0\right)}(i),S_1=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^t{\left[c^{\left(0\right)}(i)-\overline{c}\right]}^2}$$

(21)

$$\overline{\epsilon }={\displaystyle \frac{1}{n}}{\sum }_{i=1}^t\epsilon (t),S_2=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^t{\left[\epsilon (t)-\overline{\epsilon }\right]}^2}$$

(22)

$$C={\displaystyle \frac{S_1}{S_2}}$$

(23)

$$p=P\left\{\left|\epsilon (t)-\overline{\epsilon }\right|<0.6745S_1\right\}$$

(24)

where $\overline{c}$—the mean of the initial data; $S_1$—the variance of the raw data; $\overline{\epsilon }$—the mean absolute percentage error (MAPE); $S_2$—the variance of absolute percentage errors; $C$—the posterior discrepancy ratio; $p$—the small-error probability.

The $\mathrm{C}$-value quantifies prediction-data dispersion, where higher values indicate greater divergence. The $p$-value represents the proportion of residuals satisfying $\left|\epsilon (t)-\overline{\epsilon }\right|<0.6745S_1$, with larger values denoting superior distribution uniformity. These validation metrics collectively assess the accuracy of the GM(1,1) model, as quantitatively detailed in

Table 7. Reference table for precision grading by posterior variance test.

Grade	I (Excellent)	II (Qualified)	III (Marginal)	IV (Invalid)
$C$-value	$C\le 0.35$	$0.35<C\le 0.50$	$0.50<C\le 0.65$	$C>0.65$
$p$-value	$p\ge 0.95$	$0.80\le p<0.95$	$0.70\le p<0.80$	$p<0.70$

.

Dual-validation classifies GM(1,1) models into four precision grades: Grade I enables high-reliability predictions; Grade II is acceptable for most engineering applications; Grade III requires cautious implementation; and Grade IV indicates validation failure, necessitating model reconfiguration or incompatible dataset replacement.

The validation results in

Table 8. Goodness-of-fit metrics.

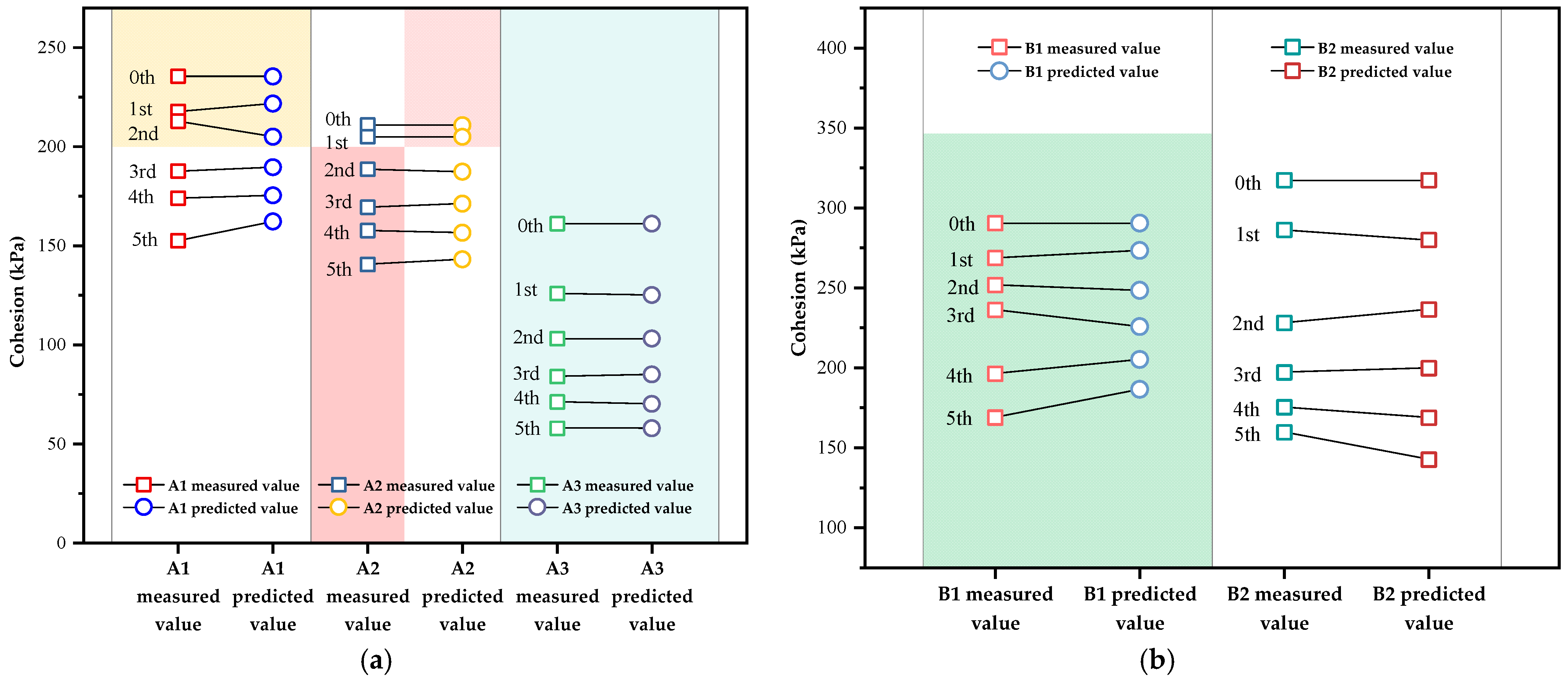
Specimen	Cycles	Measured Value (kPa)	Fitted Value (kPa)	Error (kPa)	Absolute Percentage Error	$\mathbf{C}$-Value	$\mathit{p}$-Value	Grade
A1	0	235.45	235.45	0.00	0.00%	0.185	1.00	I
	1	217.76	221.78	4.02	1.84%
	2	212.83	205.09	−7.74	3.64%
	3	187.61	189.66	2.05	1.09%
	4	173.99	175.38	1.39	0.80%
A2	0	210.9	210.90	0.00	0.00%	0.055	1.00	I
	1	204.98	204.95	−0.03	0.01%
	2	188.54	187.35	−1.19	0.63%
	3	169.35	171.25	1.90	1.12%
	4	157.64	156.54	−1.10	0.70%
A3	0	161.14	161.14	0.00	0.00%	0.023	1.00	I
	1	125.83	125.06	−0.77	0.61%
	2	103.04	103.08	0.04	0.04%
	3	84.00	84.97	0.97	1.16%
	4	71.15	70.04	−1.11	1.56%
B1	0	290.41	290.41	0.00	0.00%	0.209	1.00	I
	1	268.59	273.24	4.65	1.73%
	2	251.68	248.3	−3.38	1.34%
	3	236.17	225.64	−10.53	4.46%
	4	196.18	205.05	8.87	4.52%
B2	0	317.28	317.28	0.00	0.00%	0.105	1.00	I
	1	286.16	279.82	−6.34	2.22%
	2	228.04	236.39	8.35	3.66%
	3	197.15	199.7	2.55	1.29%
	4	175.24	168.71	−6.53	3.73%

demonstrate Grade I precision for all specimens: the posterior discrepancy ratios ($C$) < 0.35 and small-error probabilities ($p$) = 1.00. The natural specimens (A1–A3) achieved superior fitting accuracy compared to stabilized specimens (B1, B2), with the maximum absolute percentage error = 4.46% and minimum R² = 95.48%. This demonstrates the efficacy of the GM(1,1) model in simulating cohesion degradation for both natural and stabilized laterite soils under dry–wet cycles across varying moisture conditions.

5.2. Predictive Accuracy Verification of Forecasting Model

Per the prediction model in Equation (19), the cohesion of specimens after five dry–wet cycles was forecasted and compared with experimental results to verify model reliability. As shown in

Table 9. Predictive accuracy metrics.

Specimen	Cohesion c After the 5th Drying–Wetting Cycle
	Measured Value (kPa)	Predicted Value (kPa)	Error (kPa)	Absolute Percentage Error
A1	152.46	162.19	9.73	6.38%
A2	140.59	143.10	2.51	1.78%
A3	57.82	57.73	−0.09	−0.16%
B1	168.81	186.34	17.53	10.38%
B2	159.58	142.52	−17.06	−10.69%

and Figure 7, natural specimens (A1–A3) exhibit close agreement between predicted and measured cohesion values. Predictions align with experimental trends: cohesion decreases with increasing cycles and inversely correlates with moisture content. Deviation rates are ≤ 6.38% (A1: 6.38%; A2: 1.92%; A3: 0.89%), with A3 showing near-perfect overlap between predicted and measured values. This confirms the GM(1,1) model’s robust applicability for predicting cohesion of unmodified laterite across varying moisture contents. For stabilized specimens, B1 and B2 display inverse cohesion-cycle relationships with values significantly exceeding those of A3 at equivalent cycles. The guar gum-stabilized specimen (B1) shows slower degradation than coconut coir fiber-stabilized specimen (B2), consistent with direct shear test analyses. Though predictive accuracy for stabilized specimens is slightly lower (B1: 10.38%; B2: −10.69% deviation), results remain within permissible error limits.

In summary, the GM(1,1) model demonstrates robust applicability and reliability for predicting cohesion degradation in laterite soil under dry–wet cycles. This study reveals a continuous decrease in cohesion with increasing cycle counts when modeled via GM(1,1). Using specimen group B1 as a representative case, microstructural evolution under cyclic conditions was analyzed through SEM imaging (Figure 8), validating the macroscopic degradation trends. In the uncycled state (Figure 8a), soil particles primarily exhibited face-to-face contacts with horizontal sheet-stacking structures. Particles were densely arranged, and guar gum colloids were visibly attached to particle surfaces. Filamentous cementation formed by guar gum adsorbed fine particles in soil pores, enhancing interparticle cohesion and thereby improving soil cohesion. After the first dry–wet cycle (Figure 8b), particles gradually loosened with increased surface roughness, reducing cohesion. Nevertheless, abundant guar gum cementation persisted, maintaining significantly higher cohesion than specimen group A3 at equivalent cycles. Following the second cycle (Figure 8c), fine clay particles and guar gum cementation progressively eroded. Pores expanded noticeably, structures weakened, and initial fissures developed, further deteriorating cohesion. After the third cycle (Figure 8d), repeated hydraulic action substantially diminished observable guar gum cementation on soil surfaces. Interparticle interactions and guar gum cementation weakened while microcracks progressively deepened and expanded, intensifying cohesion deterioration. Post-fourth cycle (Figure 8e), continuous flushing caused significant fine-particle loss, increased porosity, and partial particle collapse. The original sheet-stacking structure disintegrated, severely compromising structural integrity and reducing cohesion to levels far below the uncycled state. After the fifth cycle (Figure 8f), interconnected fissures widened considerably, causing severe structural damage and exacerbated cohesion deterioration.

This microstructural degradation trend quantitatively aligns with the cohesion decline predicted by the GM(1,1) model, providing microscopic validation of the model’s efficacy in predicting the behavior of laterite soil under dry–wet cycles.

5.3. Analysis of Generalizability and Limitations of the GM(1,1) Model Based on This Study

Generalizability:

Regional Applicability: Laterite soils are widely distributed across southern China, sharing common characteristics including high liquid limits, strong swell–shrink potential, and pronounced cracking behavior. Their degradation patterns under dry–wet cycles align with Guilin samples [4,5,6,7]. Model parameters can be rapidly calibrated with a small amount of local data, confirming the GM(1,1) model’s applicability to other regions. Soil-Type Variability: For distinct soil types (e.g., silty or sandy laterite), significant differences in clay content and permeability lead to divergent dry–wet degradation mechanisms. Model applicability to these variants requires further validation. Component Adaptability: The model’s tolerance for compositional changes has been indirectly verified through stabilized soil samples (B1, B2) in this study. Complex Environments: In scenarios involving crack development, crack evolution is a critical factor driving cohesion decay during dry–wet cycles. The GM(1,1) model indirectly captures this influence through cohesion attenuation, successfully predicting decay trends. This demonstrates its strong noise resistance and suitability for complex environments.

Limitations:

Sample Size Limitations: Although the GM(1,1) model accommodates small samples, insufficient data may cause excessive sensitivity to stochastic fluctuations, leading to significant prediction deviations. Increasing sample size enhances model stability. For larger datasets (n > 15), alternative models or metabolic models [22] are recommended. Long-Term Prediction Uncertainty: This study’s limited dry–wet cycles prevent validation of long-term prediction accuracy. While exponential cohesion decay aligns with GM(1,1) modeling prerequisites, excessive cycles induce material fatigue failure (Figure 8f). Subsequent experiments must obtain extrapolation parameters and incorporate fatigue modification mechanisms. Single-Output Constraint: The model exclusively uses cohesion sequences as input/output, omitting direct incorporation of other factors (e.g., crack propagation). Consequently, it cannot quantify individual contributions of distinct factors to soil degradation.

6. Conclusions

This study investigates the symmetry-driven natural process of “dry–wet cycles”—characterized by temporal translational symmetry—and explores its asymmetric degradation effects on the cohesion of laterite soil. A novel GM(1,1)-based cohesion prediction method is proposed, establishing a theoretical framework for stability assessment in laterite soil engineering. Principal conclusions are summarized as follows:

(1)

The cohesion (shear strength indicator) of laterite soil decreases with increasing drying–wetting cycles; cementation products from guar gum–laterite reactions and reinforcement effects of coconut fibers significantly enhance soil cohesion.

(2)

The GM(1,1) model for predicting cohesion under drying–wetting cycles, constructed based on gray theory, demonstrates small deviation rates and Grade I accuracy. It reliably predicts cohesion for both stabilized and natural specimens with wide applicability.

(3)

Gray system models enable precise predictions with minimal data in complex environments, demonstrating significant advantages for short-to-medium-term forecasting. However, their long-term predictive capability requires dynamic updating and correction mechanisms to ensure stability. Given that the monitoring of mechanical properties in laterite soil-related engineering often involves low sampling frequency and large sampling ranges, gray theory models hold substantial application potential in geotechnical engineering.