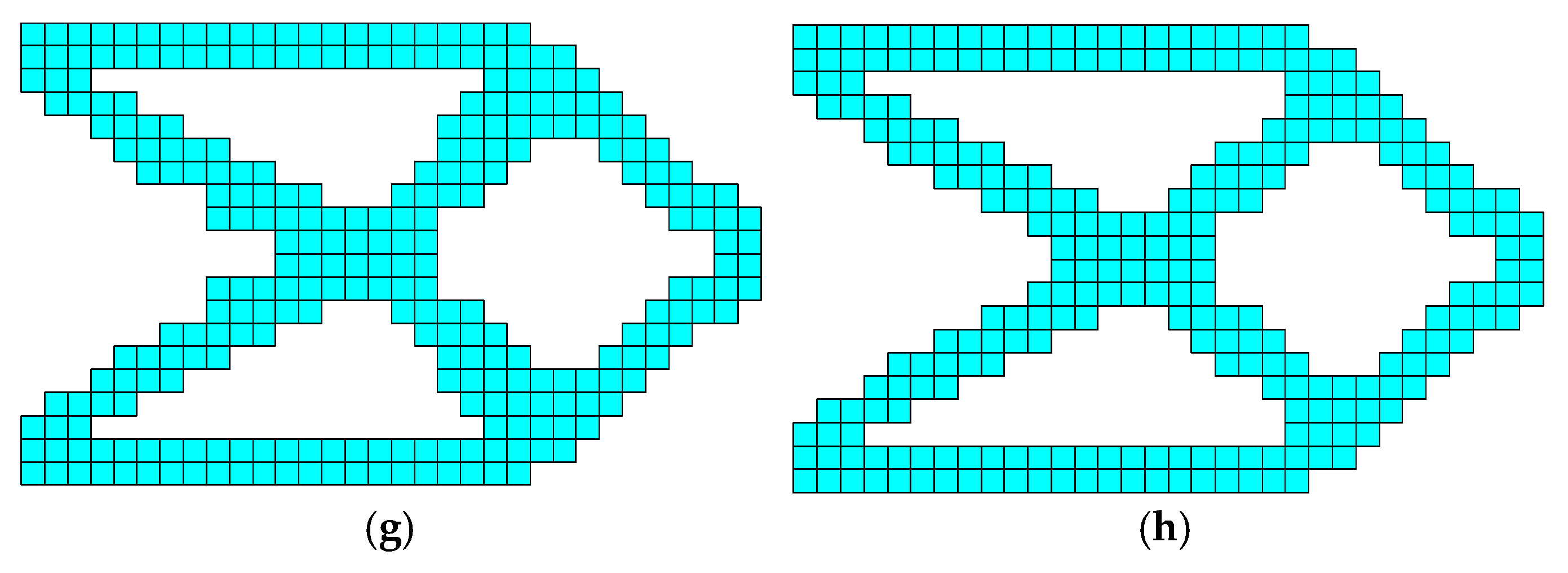Figure 1.
Cantilever slab force transfer path. (a) Cantilever slab structure; (b) visualization of force transfer path.
Figure 1.
Cantilever slab force transfer path. (a) Cantilever slab structure; (b) visualization of force transfer path.
Figure 2.
Schematic diagram of the structural force transfer path.
Figure 2.
Schematic diagram of the structural force transfer path.
Figure 3.
Schematic diagram of a continuum structure.
Figure 3.
Schematic diagram of a continuum structure.
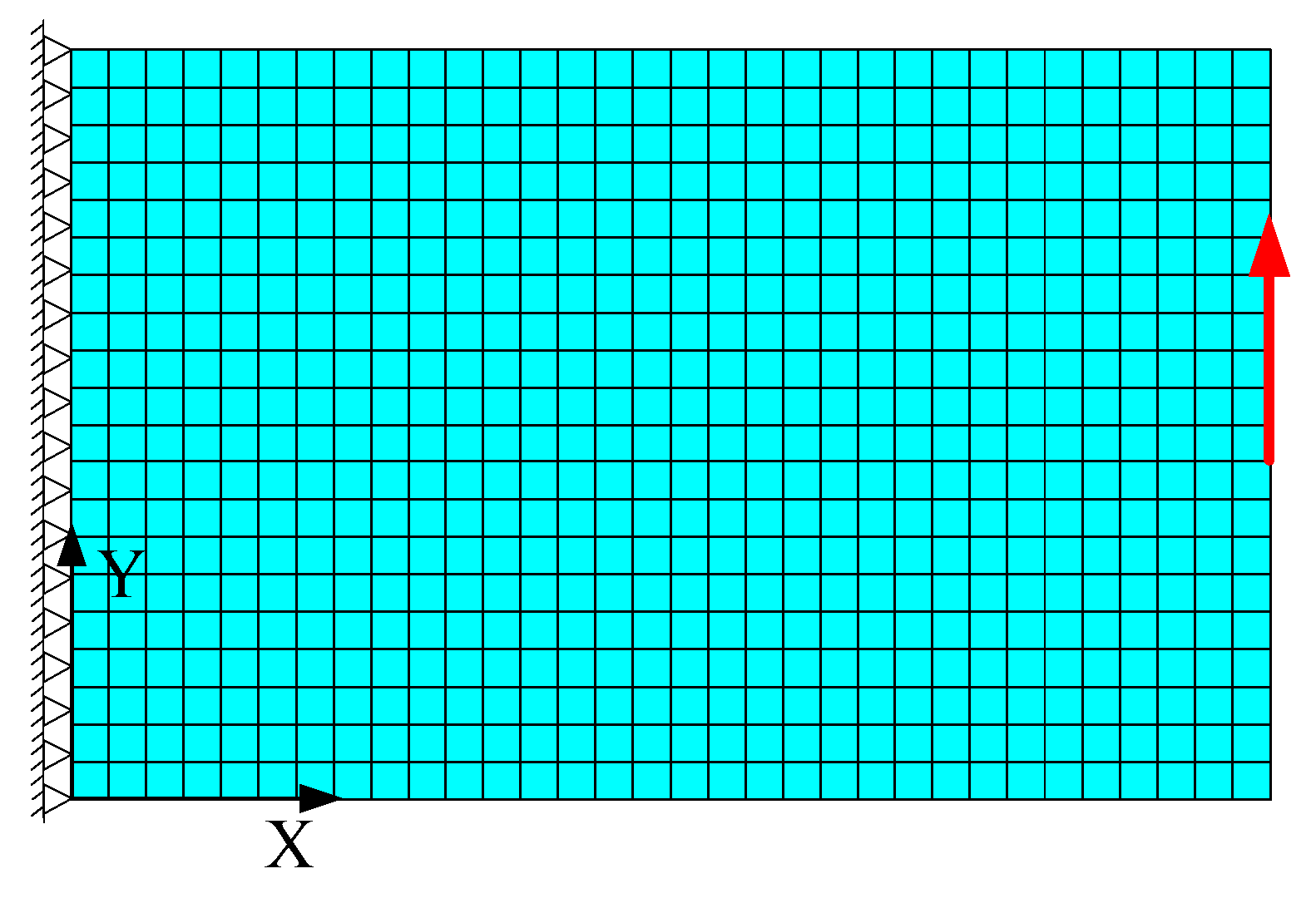
Figure 4.
Finite element model of a rectangular cantilever structure.
Figure 4.
Finite element model of a rectangular cantilever structure.
Figure 5.
Cantilever plate subjected to a unidirectional force.
Figure 5.
Cantilever plate subjected to a unidirectional force.
Figure 6.
Sensitivity allocation coefficient. (a) First-order sensitivity allocation ratio, ; (b) second-order sensitivity allocation ratio, .
Figure 6.
Sensitivity allocation coefficient. (a) First-order sensitivity allocation ratio, ; (b) second-order sensitivity allocation ratio, .
Figure 7.
Schematic diagram of sensitivity allocation.
Figure 7.
Schematic diagram of sensitivity allocation.
Figure 8.
Flow chart of the topology optimization model based on element bearing capacity.
Figure 8.
Flow chart of the topology optimization model based on element bearing capacity.
Figure 9.
Visualization results of the load-bearing capacity of one-bay five-bar truss. (a) Structural schematic; (b) element load-bearing force diagram; (c) axial contour map.
Figure 9.
Visualization results of the load-bearing capacity of one-bay five-bar truss. (a) Structural schematic; (b) element load-bearing force diagram; (c) axial contour map.
Figure 10.
Visualization results of the load-bearing capacity of a rectangular thin plate. (a) Structural schematic; (b) element load-bearing force diagram; (c) stress contour map; (d) topology optimization density contour map.
Figure 10.
Visualization results of the load-bearing capacity of a rectangular thin plate. (a) Structural schematic; (b) element load-bearing force diagram; (c) stress contour map; (d) topology optimization density contour map.
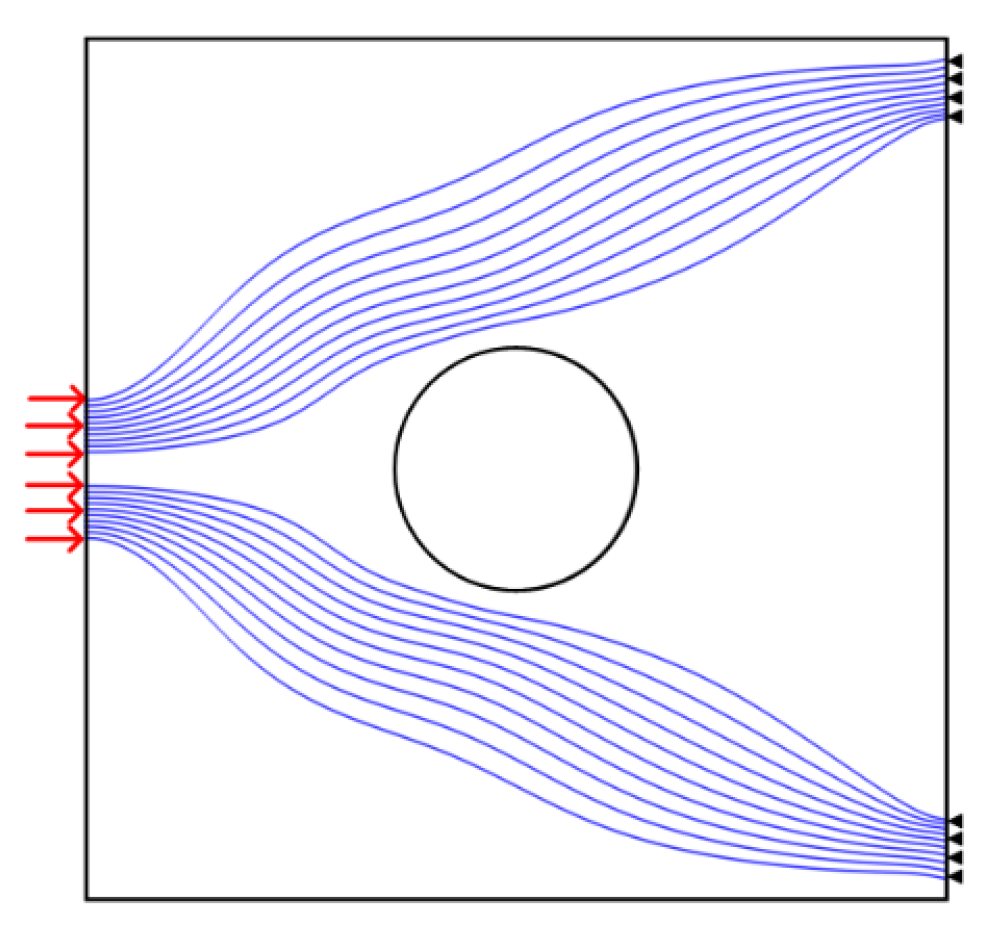
Figure 11.
Visualization results of the load-bearing capacity of a rectangular cantilever structure with a central circular hole. (a) Structural schematic; (b) element load-bearing force diagram; (c) stress contour map; (d) topology optimization density contour map.
Figure 11.
Visualization results of the load-bearing capacity of a rectangular cantilever structure with a central circular hole. (a) Structural schematic; (b) element load-bearing force diagram; (c) stress contour map; (d) topology optimization density contour map.
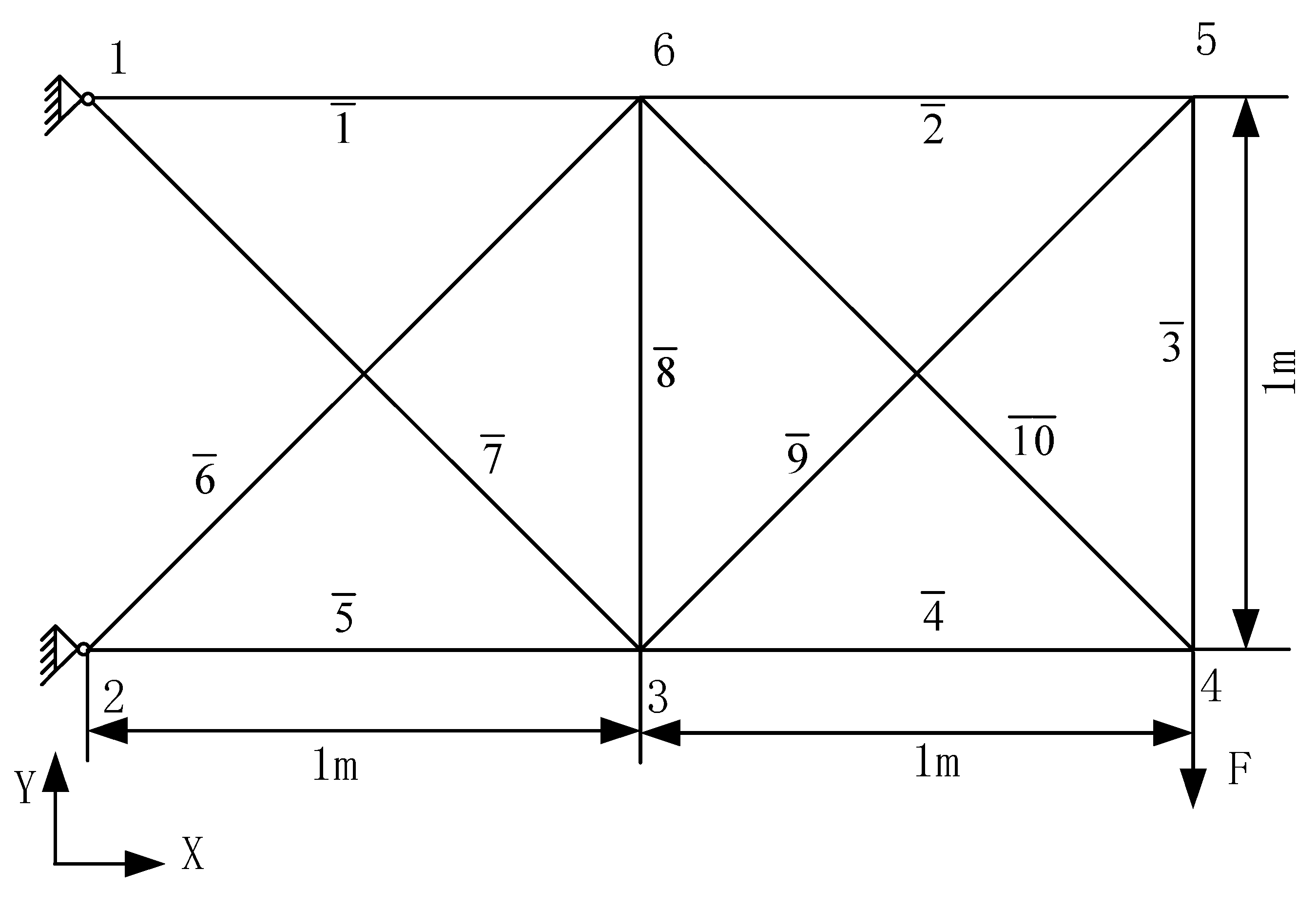
Figure 12.
Two-bay ten-bar truss. Number denotes node number, number denotes member number.
Figure 12.
Two-bay ten-bar truss. Number denotes node number, number denotes member number.
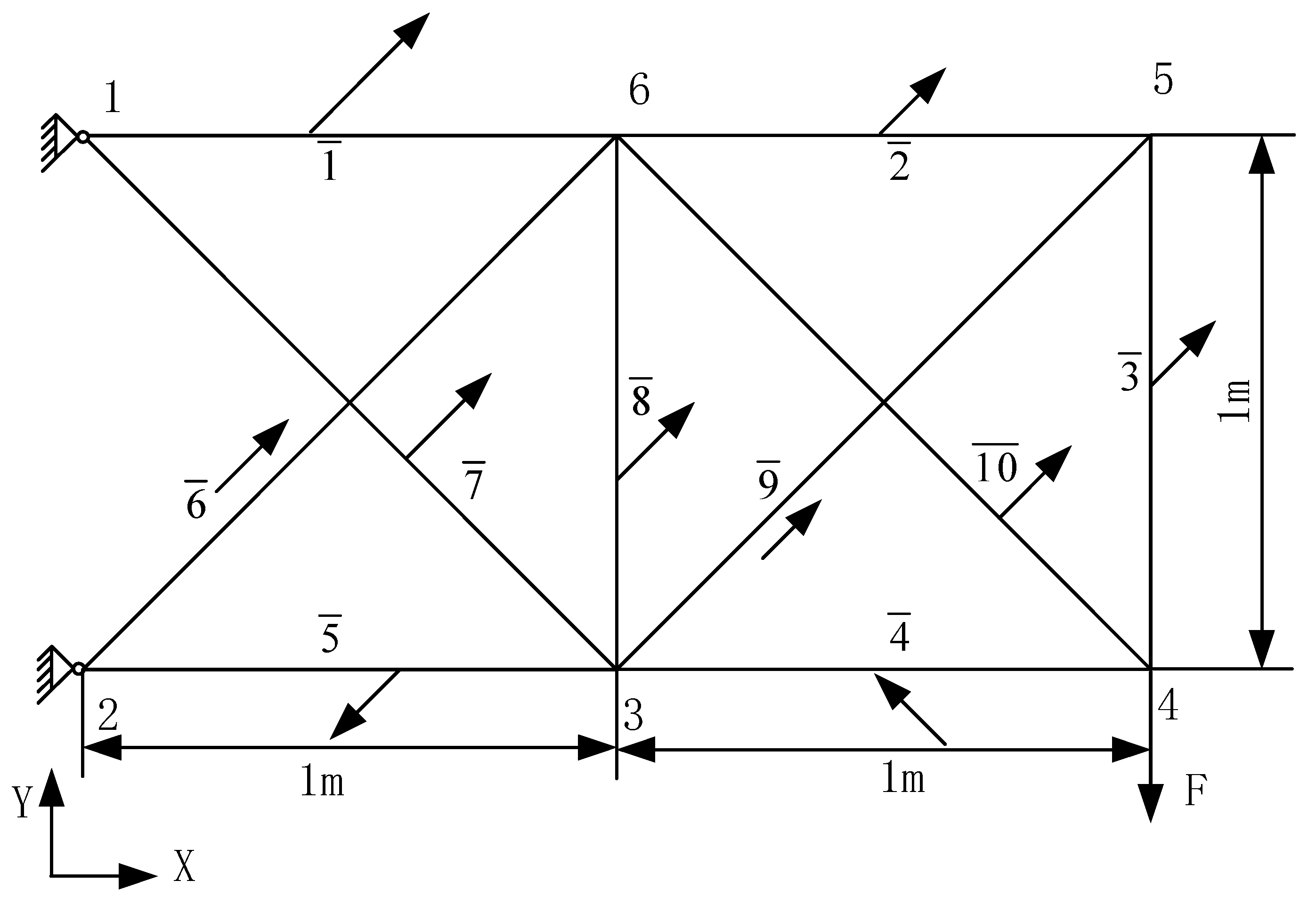
Figure 13.
Element load-bearing force diagram for two-bay ten-bar truss.
Figure 13.
Element load-bearing force diagram for two-bay ten-bar truss.
Figure 14.
Optimum design for two-bay ten-bar truss.
Figure 14.
Optimum design for two-bay ten-bar truss.
Figure 15.
Cantilever plate model.
Figure 15.
Cantilever plate model.
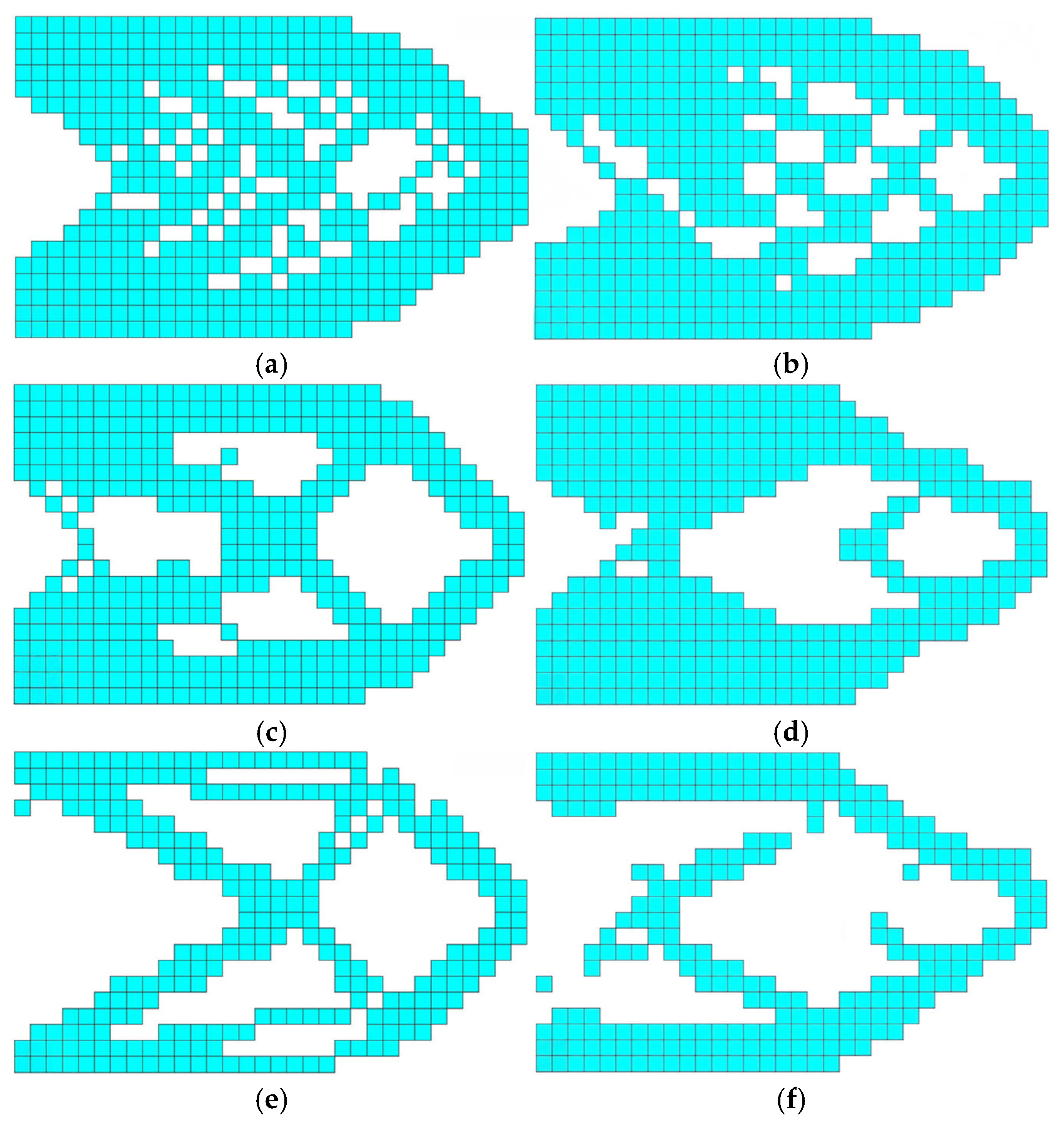
Figure 16.
The checkerboard patterns, disconnected elements, and loss of symmetry are iterative diagrams based on element load-bearing capacity. (a) = 90%; (b) = 80%; (c) = 70%; (d) = 60%; (e) = 50%; (f) = 40%; (g) = 30%.
Figure 16.
The checkerboard patterns, disconnected elements, and loss of symmetry are iterative diagrams based on element load-bearing capacity. (a) = 90%; (b) = 80%; (c) = 70%; (d) = 60%; (e) = 50%; (f) = 40%; (g) = 30%.
Figure 17.
The checkerboard patterns, disconnected elements, and loss of symmetry in the final iterative diagram are based on element load-bearing capacity. (a) = 16, = 70%; (b) = 32, = 70%; (c) = 64, = 50%; (d) = 128, = 60%; (e) = 64, = 40%; (f) = 128, = 40%.
Figure 17.
The checkerboard patterns, disconnected elements, and loss of symmetry in the final iterative diagram are based on element load-bearing capacity. (a) = 16, = 70%; (b) = 32, = 70%; (c) = 64, = 50%; (d) = 128, = 60%; (e) = 64, = 40%; (f) = 128, = 40%.
Figure 18.
Topology iteration diagrams with the checkerboard suppression algorithm applied: (a) 1st iteration; (b) 2nd iteration; (c) 3rd iteration; (d) 4th iteration; (e) 5th iteration; (f) 6th iteration; (g) 7th iteration; (h) 8th iteration.
Figure 18.
Topology iteration diagrams with the checkerboard suppression algorithm applied: (a) 1st iteration; (b) 2nd iteration; (c) 3rd iteration; (d) 4th iteration; (e) 5th iteration; (f) 6th iteration; (g) 7th iteration; (h) 8th iteration.
Figure 19.
Topology optimization diagrams before and after mesh dependency elimination: (a) 160 elements, unoptimized; (b) 160 elements, optimized; (c) 640 elements, unoptimized; (d) 640 elements, optimized; (e) 2560 elements, unoptimized; (f) 2560 elements, optimized.
Figure 19.
Topology optimization diagrams before and after mesh dependency elimination: (a) 160 elements, unoptimized; (b) 160 elements, optimized; (c) 640 elements, unoptimized; (d) 640 elements, optimized; (e) 2560 elements, unoptimized; (f) 2560 elements, optimized.
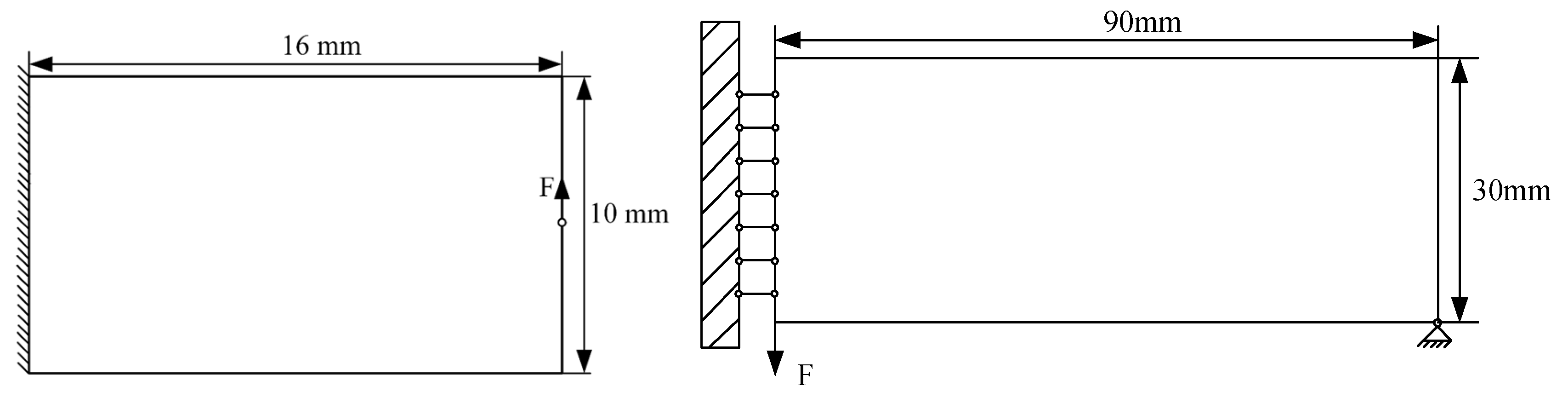
Figure 20.
The dimensions and boundary conditions of the cantilever beam and MBB beam structure.
Figure 20.
The dimensions and boundary conditions of the cantilever beam and MBB beam structure.
Figure 21.
The finite element analysis results of the cantilever beam and MBB beam using the BESO method and the proposed topology optimization method. (a) Topology element density of the cantilever beam obtained with the BESO method (element threshold = 0.5); (b) topology element density of the MBB beam obtained with the BESO method (element threshold = 0.5); (c) topology element density of the cantilever beam obtained with the proposed method (element threshold = 0.5); (d) topology element density of the MBB beam obtained with the proposed method (element threshold = 0.5).
Figure 21.
The finite element analysis results of the cantilever beam and MBB beam using the BESO method and the proposed topology optimization method. (a) Topology element density of the cantilever beam obtained with the BESO method (element threshold = 0.5); (b) topology element density of the MBB beam obtained with the BESO method (element threshold = 0.5); (c) topology element density of the cantilever beam obtained with the proposed method (element threshold = 0.5); (d) topology element density of the MBB beam obtained with the proposed method (element threshold = 0.5).
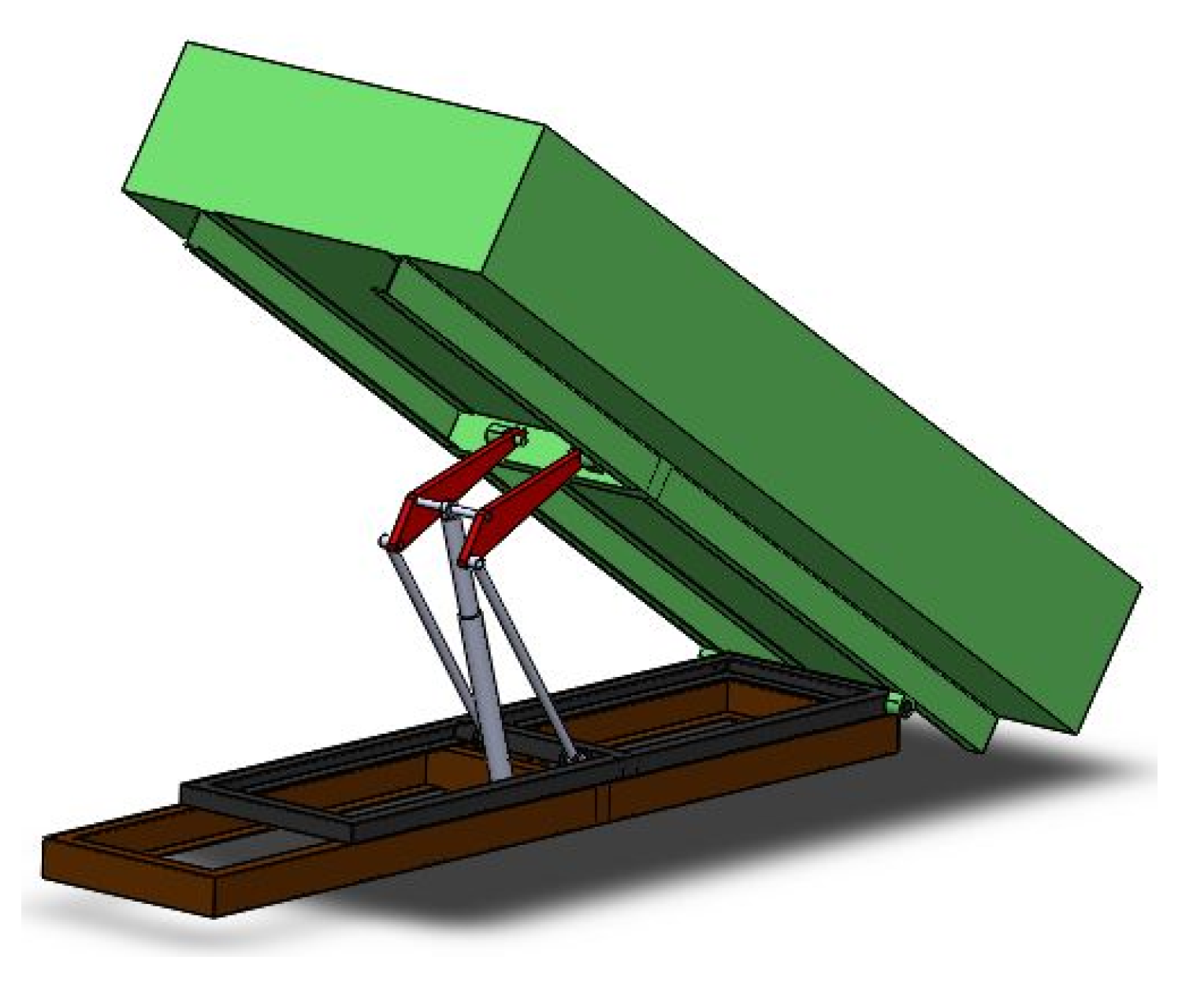
Figure 22.
The triangular arm of a dump truck before optimization. (a) Dump truck lifting mechanism diagram; (b) dump truck.
Figure 22.
The triangular arm of a dump truck before optimization. (a) Dump truck lifting mechanism diagram; (b) dump truck.
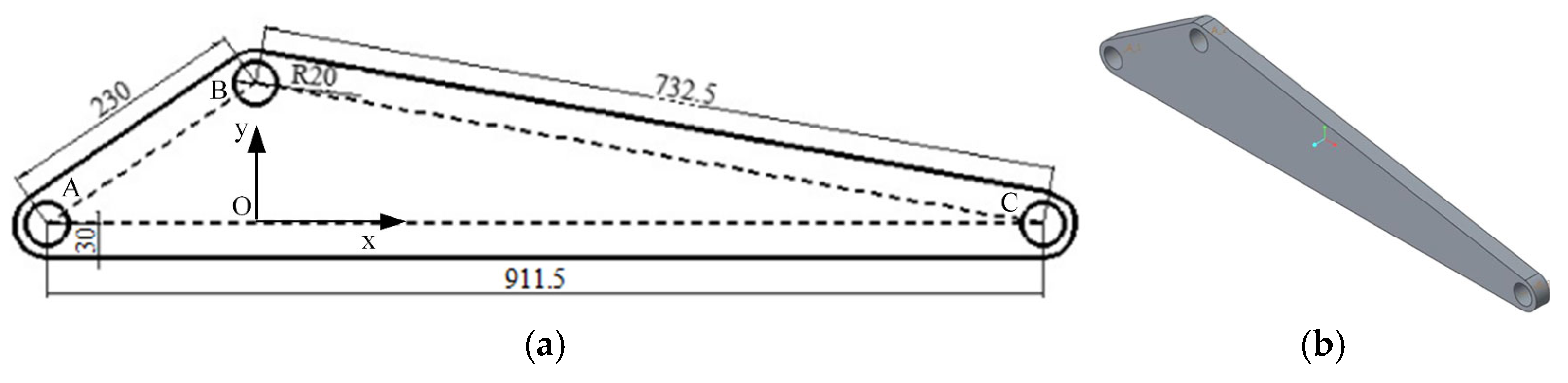
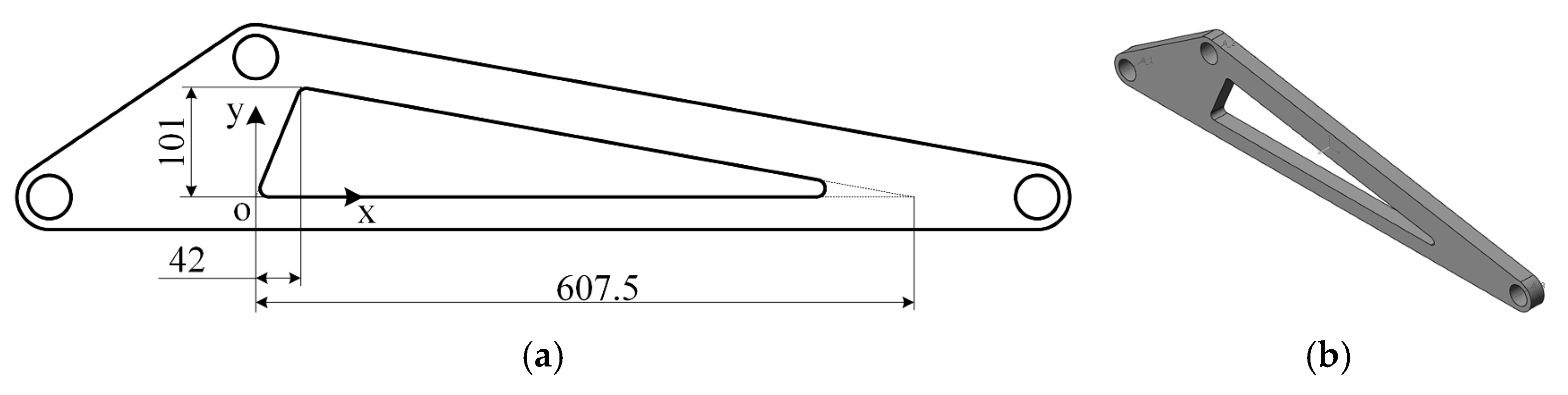
Figure 23.
The triangular arm of a dump truck before optimization. (a) Dimensional schematic; (b) 3D model.
Figure 23.
The triangular arm of a dump truck before optimization. (a) Dimensional schematic; (b) 3D model.
Figure 24.
Dump truck lifting mechanism assembly [
38].
Figure 24.
Dump truck lifting mechanism assembly [
38].
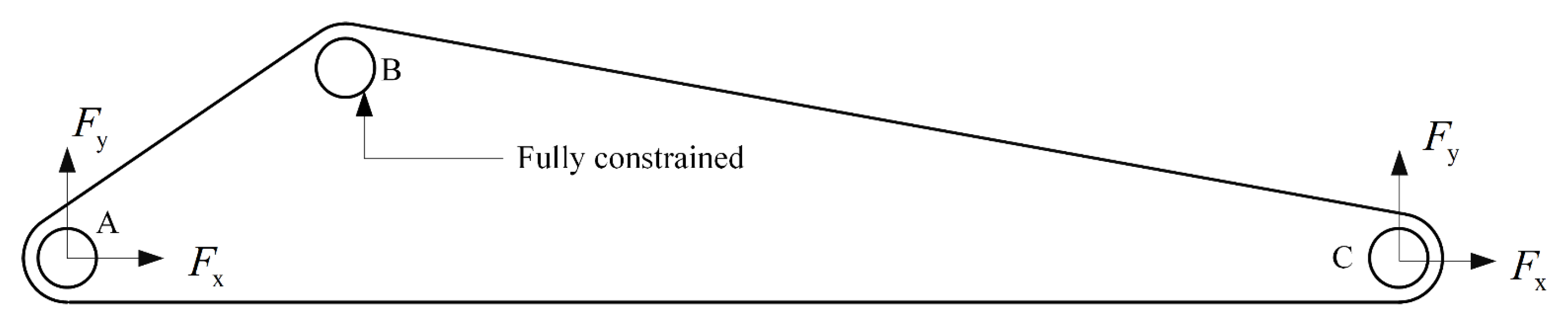
Figure 25.
Schematic diagram of loads and constraints on the triangular arm.
Figure 25.
Schematic diagram of loads and constraints on the triangular arm.
Figure 26.
Implementation of loads and constraints on the triangular arm in ANSYS APDL 2024 R1.
Figure 26.
Implementation of loads and constraints on the triangular arm in ANSYS APDL 2024 R1.
Figure 27.
Two types of finite elements for the triangular arm. (a) Three-dimensional solid element SOLID185; (b) plane element PLANE42.
Figure 27.
Two types of finite elements for the triangular arm. (a) Three-dimensional solid element SOLID185; (b) plane element PLANE42.
Figure 28.
Analysis results of 3D solid elements. (a) Stress diagram; (b) displacement diagram.
Figure 28.
Analysis results of 3D solid elements. (a) Stress diagram; (b) displacement diagram.
Figure 29.
Analysis results of 2D plane elements. (a) Stress diagram; (b) displacement diagram.
Figure 29.
Analysis results of 2D plane elements. (a) Stress diagram; (b) displacement diagram.
Figure 30.
Stress contour maps of the triangular arm under various working conditions. (a) T = 1; (b) T = 2; (c) T = 3; (d) T = 4.
Figure 30.
Stress contour maps of the triangular arm under various working conditions. (a) T = 1; (b) T = 2; (c) T = 3; (d) T = 4.
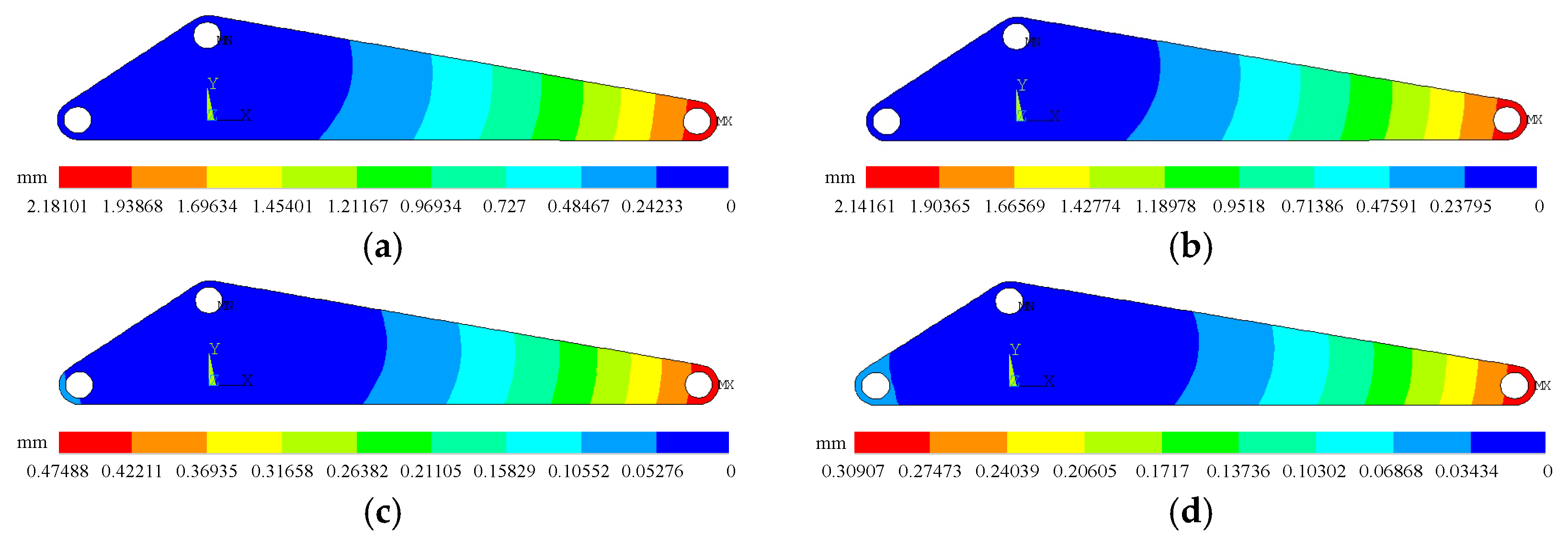
Figure 31.
Displacement diagrams of the triangular arm under various working conditions. (a) T = 1; (b) T = 2; (c) T = 3; (d) T = 4.
Figure 31.
Displacement diagrams of the triangular arm under various working conditions. (a) T = 1; (b) T = 2; (c) T = 3; (d) T = 4.
Figure 32.
The topological results of the triangular arm based on the element load-bearing capacity under four working conditions. (a) T = 1; (b) T = 2; (c) T = 3; (d) T = 4.
Figure 32.
The topological results of the triangular arm based on the element load-bearing capacity under four working conditions. (a) T = 1; (b) T = 2; (c) T = 3; (d) T = 4.
Figure 33.
The triangular arm density color maps under four working conditions. (a) T = 1; (b) T = 2; (c) T = 3; (d) T = 4.
Figure 33.
The triangular arm density color maps under four working conditions. (a) T = 1; (b) T = 2; (c) T = 3; (d) T = 4.
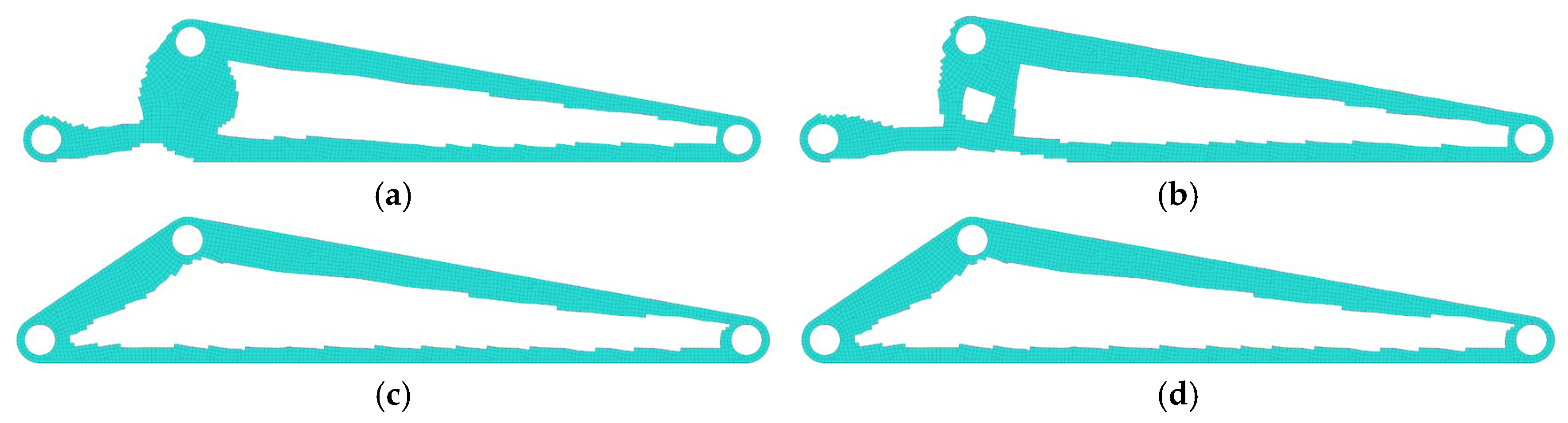
Figure 34.
Optimized triangular arm. (a) Dimensional schematic; (b) 3D model.
Figure 34.
Optimized triangular arm. (a) Dimensional schematic; (b) 3D model.
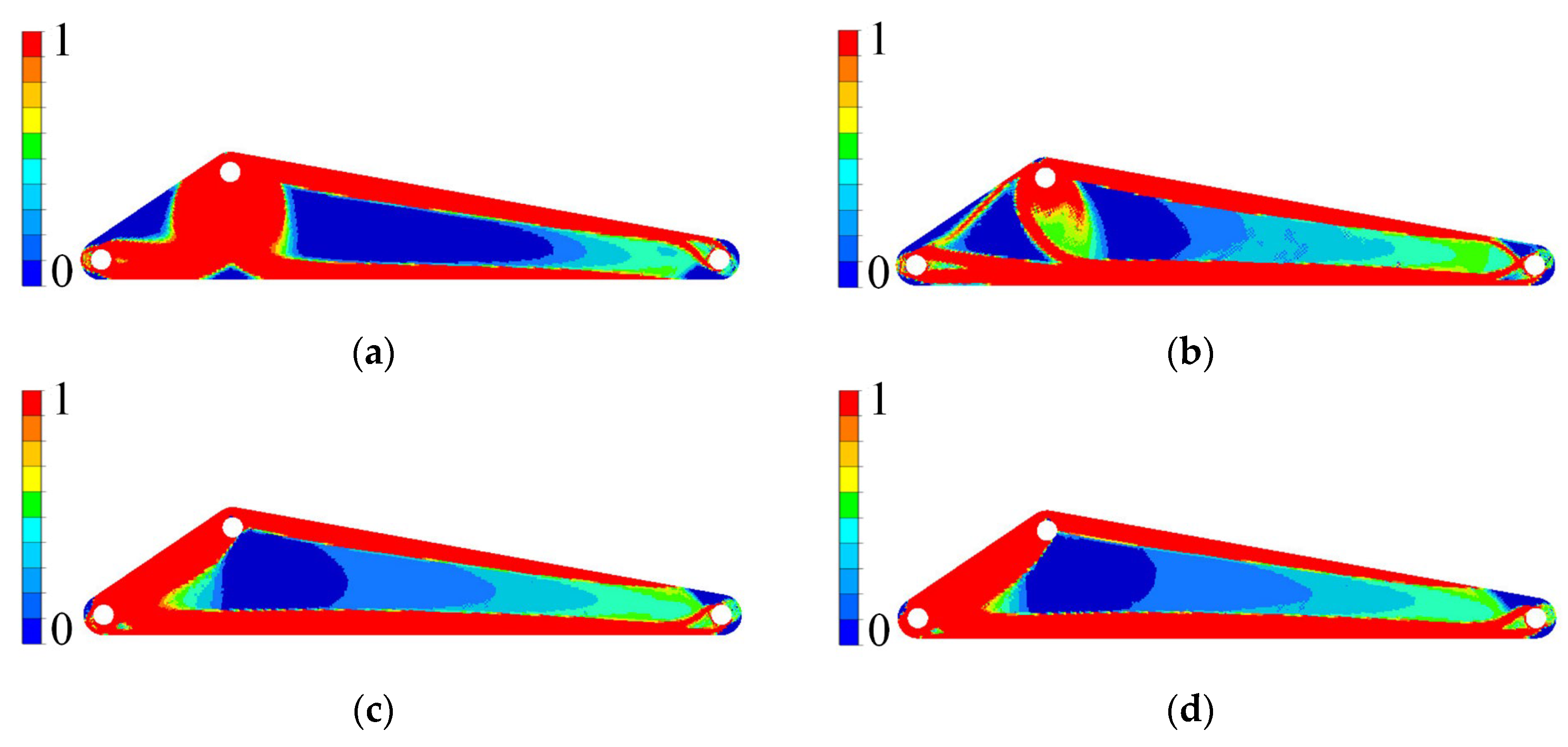
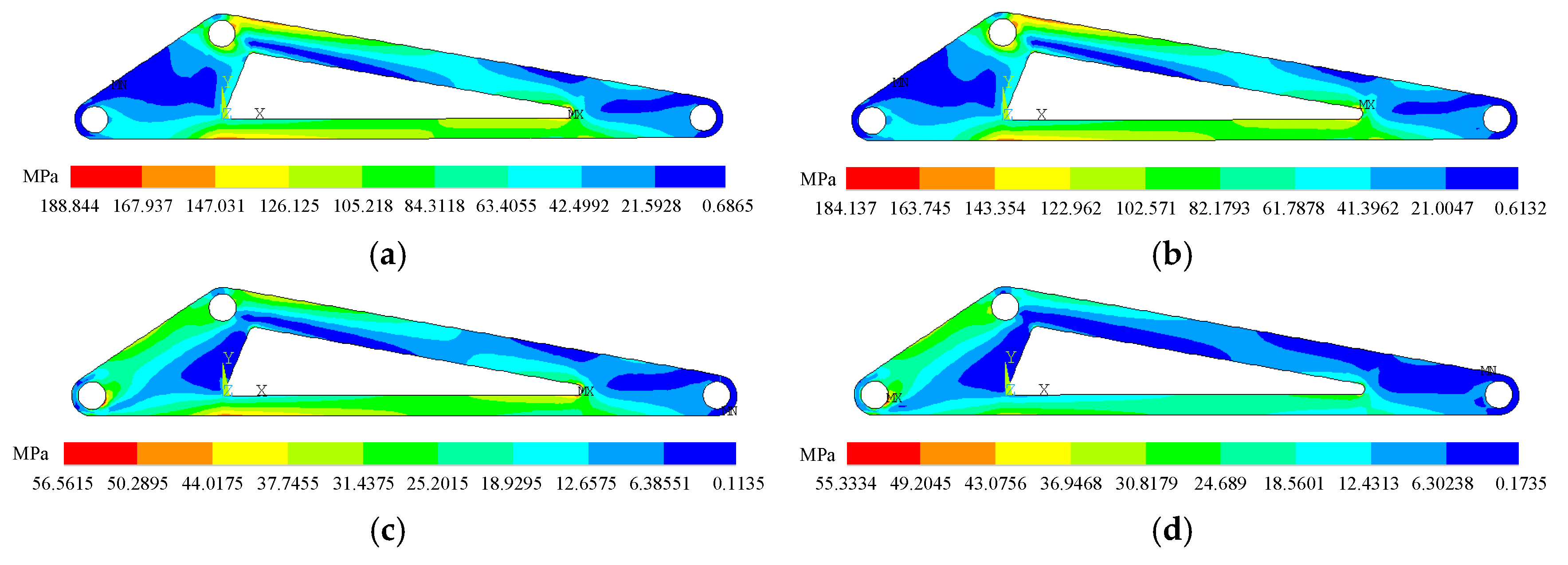
Figure 35.
Stress contour map of the optimized triangular arm. (a) T = 1; (b) T = 2; (c) T = 3; (d) T = 4.
Figure 35.
Stress contour map of the optimized triangular arm. (a) T = 1; (b) T = 2; (c) T = 3; (d) T = 4.
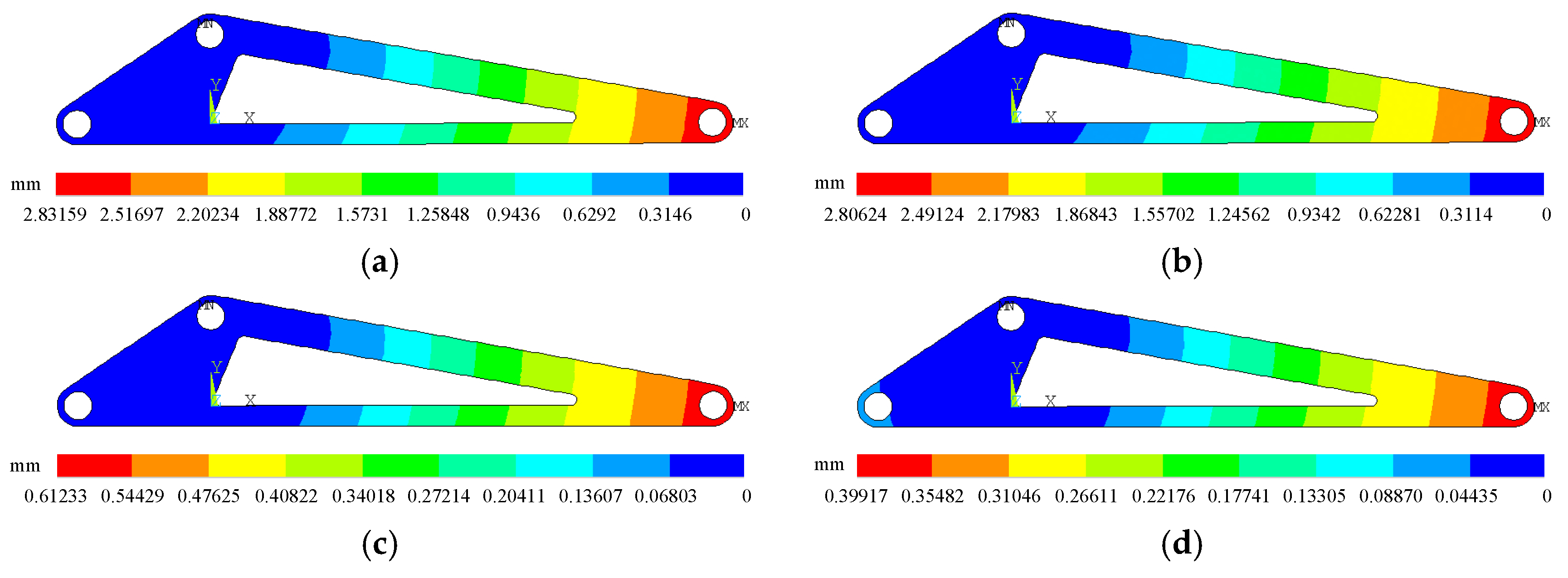
Figure 36.
Displacement contour map of the optimized triangular arm. (a) T = 1; (b) T = 2; (c) T = 3; (d) T = 4.
Figure 36.
Displacement contour map of the optimized triangular arm. (a) T = 1; (b) T = 2; (c) T = 3; (d) T = 4.
Table 1.
Thin plate model and associated parameters.
Table 1.
Thin plate model and associated parameters.
| Property | Young’s Modulus/MPa | Poisson’s Ratio | Element Type | Thickness/m | Width/m | Height/m | Load/N |
|---|
| Value | 2.1 × 105 | 0.3 | Quadrilateral elements | 0.002 | 0.2 | 0.1 | −50 |
Table 2.
Normalized element bearing capacity and subjected forces for the two-bay ten-bar truss.
Table 2.
Normalized element bearing capacity and subjected forces for the two-bay ten-bar truss.
Member
No. | Normalized Element Bearing Capacity (N/m2) | Subjected Force (N) |
|---|
| Node 1 | Node 2 |
|---|
| 1 | | | |
| 2 | | | |
| 3 | | | |
| 4 | | | |
| 5 | | | |
| 6 | | | |
| 7 | | | |
| 8 | | | |
| 9 | | | |
| 10 | | | |
Table 3.
Normalized element bearing capacity to the support for two bay ten-bar truss.
Table 3.
Normalized element bearing capacity to the support for two bay ten-bar truss.
Member
No. | Normalized Element Bearing Capacity (N/m2) | Subjected Force (N) |
|---|
| Vector | Norm |
|---|
| 1 | | | |
| 2 | | | |
| 3 | | | |
| 4 | | | |
| 5 | | | |
| 6 | | | |
| 7 | | | |
| 8 | | | |
| 9 | | | |
| 10 | | | |
Table 4.
Normalized element bearing capacity and subjected forces for redesigned two-bay ten-bar truss.
Table 4.
Normalized element bearing capacity and subjected forces for redesigned two-bay ten-bar truss.
Member
No. | Normalized Element Bearing Capacity (N/m2) | Difference in Norm (%) | Subjected Force (N) |
|---|
| Vector | Norm |
|---|
| 1 | | | 34.3 | |
| 4 | | | 80.3 | |
| 5 | | | 38.7 | |
| 6 | | | 495 | |
| 10 | | | 120 | |
Table 5.
Cantilever plate model and associated parameters.
Table 5.
Cantilever plate model and associated parameters.
| Property | Young’s Modulus/MPa | Poisson’s Ratio | Element Type | | Width/mm | Height/mm | Load/N |
|---|
| Value | 2.07 × 105 | 0.3 | Quadrilateral elements | 1.0 | 16.0 | 10.0 | 300 |
Table 6.
Time record of structural optimization.
Table 6.
Time record of structural optimization.
| Volume Removal Rate/% | 90 | 80 | 70 | 60 | 50 | 40 | 30 |
|---|
| CPU time/s | 573 | 1090 | 1545 | 1948 | 2291 | 2581 | 2817 |
Table 7.
Variation in volume removal rate and element load-bearing capacity.
Table 7.
Variation in volume removal rate and element load-bearing capacity.
| Volume Constraint /% | Element Load-Bearing Capacity TF | Difference Rate/% |
|---|
| Initial | 4.2440 × 10−3 | 0 |
| 90 | 4.7415 × 10−3 | 11.7 |
| 80 | 5.7526 × 10−3 | 35.5 |
| 70 | 7.1891 × 10−3 | 69.4 |
| 60 | 9.5599 × 10−3 | 125.3 |
| 50 | 1.3532 × 10−2 | 218.8 |
| 40 | 4.1118 × 10−3 | 868.9 |
| 30 | 0.8827 | 20,698.77 |
Table 8.
Time consumption for the number of different elements deleted.
Table 8.
Time consumption for the number of different elements deleted.
| Number of Different Elements Deleted/RR | 16 | 32 | 64 | 128 |
|---|
| CPU time/s | 9803 | 4998 | 1948 | 1377 |
Table 9.
Comparison table of strain energy and computational efficiency.
Table 9.
Comparison table of strain energy and computational efficiency.
| Method | Case | Strain Energy (mJ) | Time/s |
|---|
| BESO | The cantilever beam | 1.18 | 117.35 |
| MBB beam | 4041 | 164 |
| Element Bearing Capacity | The cantilever beam | 0.956 | 139.21 |
| MBB beam | 3915 | 198 |
Table 10.
Material parameter information for the triangular arm of a dump truck.
Table 10.
Material parameter information for the triangular arm of a dump truck.
| Property | Type | Density/kg/m3 | Young’s Modulus/MPa | Poisson’s Ratio | Allowable Stress/MPa |
|---|
| Value | Q235 | 7.8 × 103 | 2.1 × 10−5 | 0.3 | 235 |
Table 11.
Force magnitudes under four typical working conditions.
Table 11.
Force magnitudes under four typical working conditions.
| Working Conditions | A (Tie Rod and Triangular Arm) | B (Hydraulic Cylinder and Triangular Arm) | C (Truck Bed and Triangular Arm) |
|---|
| Fx/N | Fy/N | Fx/N | Fy/N | Fx/N | Fy/N |
|---|
| T = 1 | −81,091.21 | −1597.29 | 54,770.83 | 16,239.501 | 26,320.38 | 17,703.81 |
| T = 2 | −76,817.49 | −2652.94 | 55,955.94 | 16,592.86 | 22,161.57 | 17,678.02 |
| T = 3 | 7945.82 | 28,150.84 | −35,377.21 | −10,544.15 | 8881.45 | 4556.58 |
| T = 4 | 15,082.74 | 27,489.86 | −36,914.45 | −11,015.70 | 8463.93 | 2831.41 |
Table 12.
Maximum and minimum stress under four working conditions.
Table 12.
Maximum and minimum stress under four working conditions.
| Working Conditions | T = 1 | T = 2 | T = 3 | T = 4 |
|---|
| Stress distribution | Minimum stress/MPa | 1.04372 | 0.859471 | 0.353 | 0.303 |
| Maximum stress/MPa | 157.912 | 158.264 | 59.791 | 59.703 |
| Stress in the intermediate region/MPa | 70.763 | 70.8169 | 26.7697 | 26.703 |
Table 13.
Minimum and maximum stresses under four working conditions before and after optimization.
Table 13.
Minimum and maximum stresses under four working conditions before and after optimization.
| Working Conditions | T = 1 | T = 2 | T = 3 | T = 4 |
|---|
| Minimum stresses/MPa | Before optimization | 1.04372 | 0.859471 | 0.353 | 0.303 |
| After optimization | 0.68649 | 0.613186 | 0.113512 | 0.173505 |
| Maximum stresses/MPa | Before optimization | 157.912 | 158.264 | 59.791 | 59.703 |
| After optimization | 188.844 | 184.137 | 56.5615 | 55.334 |
Table 14.
Maximum and minimum displacements before and after optimization.
Table 14.
Maximum and minimum displacements before and after optimization.
| Working Conditions | T = 1 | T = 2 | T = 3 | T = 4 |
|---|
| Minimum displacements/mm | Before optimization | 0.242335 | 0.237956 | 0.52765 | 0.034342 |
| After optimization | 0.314621 | 0.311405 | 0.068037 | 0.044353 |
| Maximum displacements/mm | Before optimization | 2.18101 | 2.14161 | 0.474882 | 0.309076 |
| After optimization | 2.83159 | 2.80264 | 0.612332 | 0.399173 |