Research on the Prediction Model of Sudden Death Risk in Coronary Heart Disease Based on XGBoost and Random Forest
Abstract
Featured Application
Abstract
1. Introduction
- It is the first to apply the XGBoost–random forest ensemble model to SCD risk prediction, verifying the feasibility and superiority of the ensemble model in SCD prediction tasks and providing a method reference for the intelligent prediction of related diseases in the future.
- It innovatively introduces the fuzzy comprehensive evaluation method into the SCD prediction process for the first time. In view of the common characteristics of clinical data such as information fuzziness and incompleteness, the fuzzy comprehensive evaluation method, with its advantages in uncertainty modeling, can perform fuzzification processing and normalized weight integration on the original data in the early stage of the prediction process.
- It combines the fuzzy comprehensive evaluation method with XGBoost and random forest algorithms to construct an ensemble model. By organically integrating the strengths of the fuzzy comprehensive evaluation method in handling fuzziness and the advantages of XGBoost and random forest algorithms in mining nonlinear relationships in data, this ensemble model demonstrates outstanding capabilities in handling the fuzziness and nonlinear relationships of clinical data in the overall process covering feature weighting, model training, and integrated prediction, significantly improving the accuracy and stability of SCD prediction.
2. Materials and Methods
2.1. Related Work
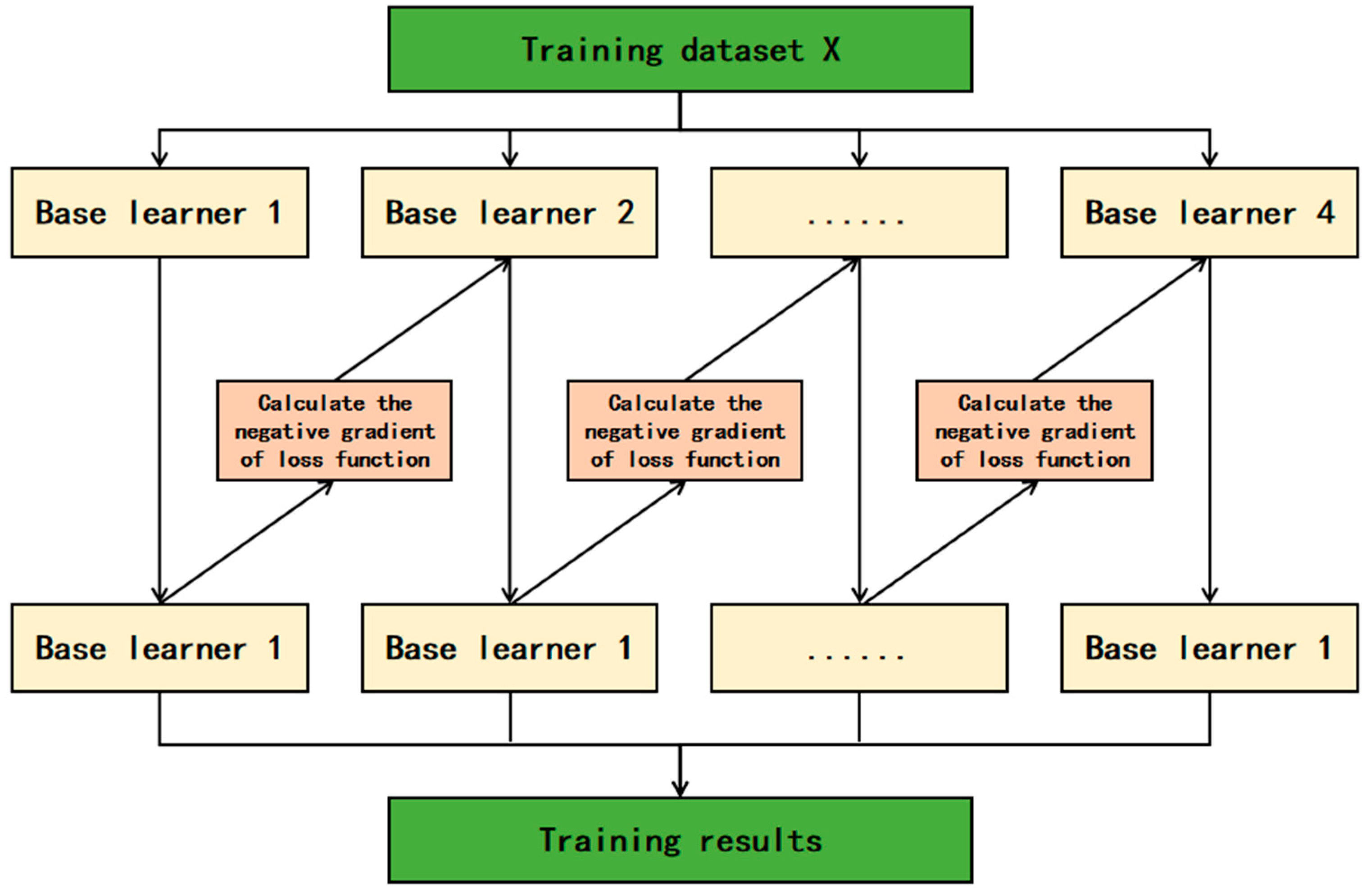
2.1.1. XGBoost Model
- The objective function
- Tree-Building
- Diversity Gain
2.1.2. XGBoost with Fuzzy Synthetic Evaluation Features
2.1.3. Random Forest Model
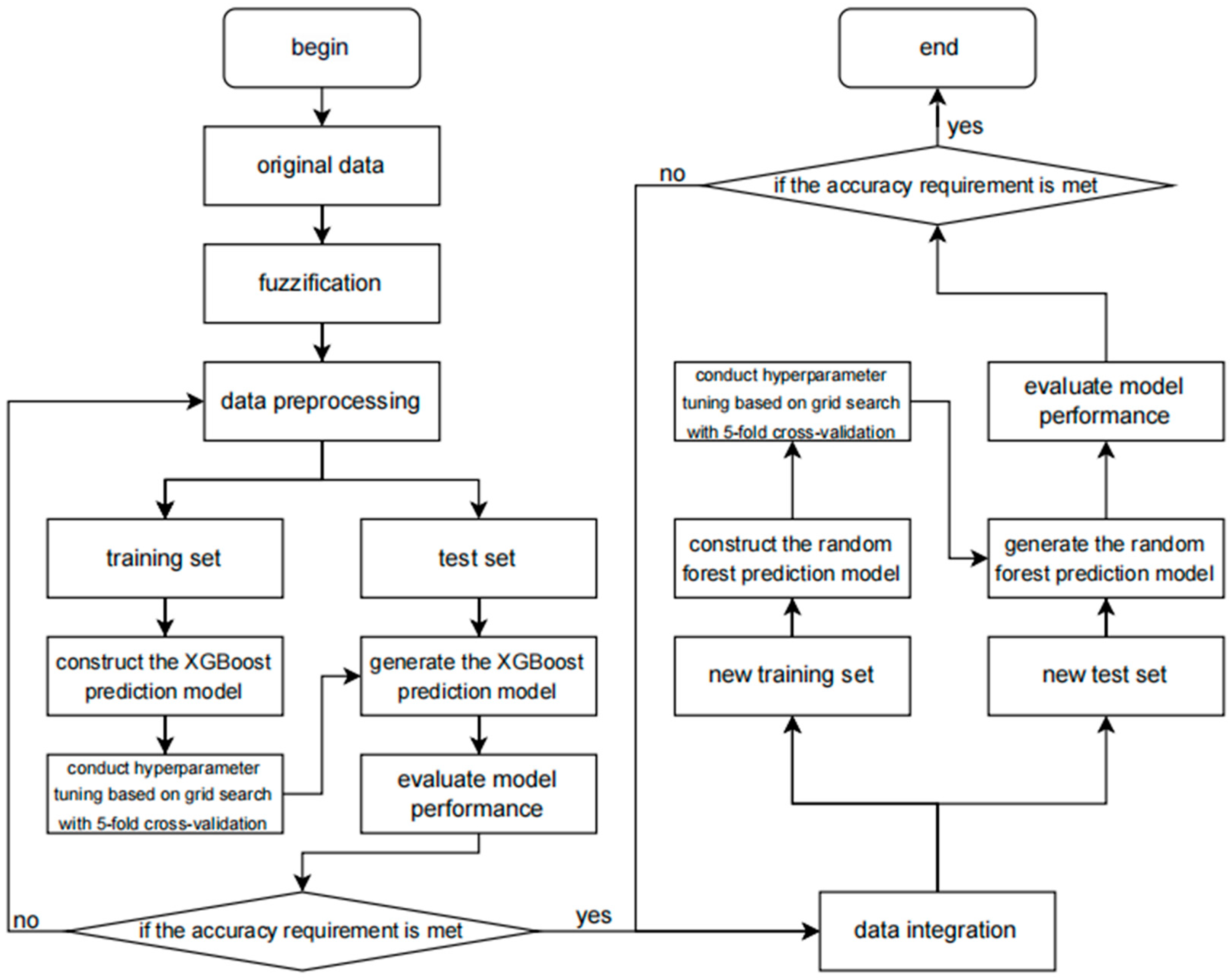
2.2. Methodology
2.2.1. Model Introduction
2.2.2. Fuzzification
2.2.3. Construct Feature Matrix
2.2.4. Model Training and Data Processing
3. Results
3.1. Experimental Results and Analysis
3.2. Predictive Value Assessment
4. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- National Center for Cardiovascular Diseases. Report on Cardiovascular Health and Diseases in China 2023 (Section on Coronary Heart Disease). J. Cardiovasc. Pulm. Dis. 2024, 43, 1015–1024. [Google Scholar]
- Liu, M.B.; He, X.Y.; Yang, X.H.; Wang, Z.W. Interpretation of Key Points in “Report on Cardiovascular Health and Diseases in China 2023”. Chin. Gen. Pract. 2025, 28, 20–38. [Google Scholar]
- Kaur, B.; Kaur, G. Heart Disease Prediction Using Modified Machine Learning Algorithm. In International Conference on Innovative Computing and Communications. Lecture Notes in Networks and Systems; Gupta, D., Khanna, A., Bhattacharyya, S., Hassanien, A.E., Anand, S., Jaiswal, A., Eds.; Springer: Singapore, 2023; Volume 473. [Google Scholar] [CrossRef]
- Dai, J.; Xiao, Y.; Sheng, Q.; Zhou, J.; Zhang, Z.; Zhu, F. Epidemiology and SARIMA model of deaths in a tertiary comprehensive hospital in Hangzhou from 2015 to 2022. BMC Public Health 2024, 24, 2549. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD′16), New York, NY, USA, 13 August 2016; pp. 785–794. [Google Scholar]
- Li, J.; An, X.; Li, Q.; Wang, C.; Yu, H.; Zhou, X.; Geng, Y.-A. Application of XGBoost algorithm in the optimization of pollutant concentration. Atmos. Res. 2022, 276, 106238. [Google Scholar] [CrossRef]
- Thomas, N.S.; Kaliraj, S. An Improved and Optimized Random Forest Based Approach to Predict the Software Faults. SN Comput. Sci. 2024, 5, 530. [Google Scholar] [CrossRef]
- Liao, K.-M.; Cheng, K.-C.; Sung, M.-I.; Shen, Y.-T.; Chiu, C.-C.; Liu, C.-F.; Ko, S.-C. Machine learning approaches for practical predicting outpatient near-future AECOPD based on nationwide electronic medical records. iScience 2024, 27, 109542. [Google Scholar] [CrossRef]
- Ma, Y.; Kong, D.L.; Ye, X.Y.; Ding, Y.L. Application and Comparison of Classification and Prediction Models for Type 2 Diabetes Mellitus Complicated with Hypertension Based on Random Forest and XGBoost Algorithms. J. Guangdong Med. Univ. 2024, 42, 523–534. [Google Scholar]
- Li, T.Y.; Xu, X.C.; Yang, X.; Cui, B.; Chen, H.A.; Zhao, X.Y.; Yuan, N.; Meng, F.Q. Prediction of Nitrogen Leaching in Winter Wheat Production in North China Using Random Forest and XGBoost. China Environ. Sci. 2025, 1, 343–354. [Google Scholar]
- Pritika; Shanmugam, B.; Azam, S. Risk Evaluation and Attack Detection in Heterogeneous IoMT Devices Using Hybrid Fuzzy Logic Analytical Approach. Sensors 2024, 24, 3223. [Google Scholar] [CrossRef]
- Yalcinkaya, F.; Erbas, A. Convolutional neural network and fuzzy logic-based hybrid melanoma diagnosis system. Elektron. Ir Elektrotechnika 2021, 27, 69–77. [Google Scholar] [CrossRef]
- Huang, L.; Alhulwah, K.H.; Hanif, M.F.; Siddiqui, M.K.; Ikram, A.S. On QSPR analysis of glaucoma drugs using machine learning with XGBoost and regression models. Comput. Biol. Med. 2025, 187, 109731. [Google Scholar] [CrossRef]
- Mitchell, R.; Frank, E. Accelerating the XGBoost algorithm using GPU computing. PeerJ Comput. Sci. 2017, 3, e127. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Approximating XGBoost with an interpretable decision tree. Inf. Sci. 2021, 572, 522–542. [Google Scholar] [CrossRef]
- Ye, L.Z.; Zheng, D.H.; Liu, Y.H.; Niu, S. Unbalanced Data Classification Based on Whale Swarm Optimized Random Forest Algorithm. J. Nanjing Univ. Posts Telecommun. 2022, 42, 99–105. [Google Scholar]
- Zhang, Z.W.; Zhang, Y.Y.; Wen, Y.T.; Ren, Y.X. Prediction Method of Performance Parameters of Multi-Defect Lattice Structures Based on XGBoost Model. Acta Metrol. Sin. 2024, 45, 559–564. [Google Scholar]
- Sun, L.K.; Lou, K. Fault Diagnosis of Hydraulic System Test Bench for Controllable Pitch Propeller Based on XGBoost Method. Ship Eng. 2024, 46, 190–196. [Google Scholar]
- Zheng, H.; Jia, Z.F.; Zhou, L.T.; Wang, Z. Defect Classification Algorithm for Wind Turbine Blades Based on PSO-XGBoost. Acta Energiae Solaris Sin. 2024, 45, 127–133. [Google Scholar]
- Han, Z.Z.; Zhou, S.R.; Fang, C. Fuzzy statistic and comprehensive evaluating study for activity characterization of the active region. Sci. China Ser. A-Math. 2001, 44, 662–668. [Google Scholar] [CrossRef]
- Yang, L.; Wang, P.C. A Useful Mathematical Evaluation Method in Medicine. J. Math. Med. 2010, 23, 509–510. [Google Scholar]
- Li, G.; Tong, J.Y.; Zhu, J.; Li, D.; Hao, S.B. Application of Fuzzy Comprehensive Evaluation Method in Risk Prediction of Sudden Coronary Death. J. Southeast Univ. 2014, 33, 300–303. [Google Scholar]
- Wang, L.C.; Liu, S.S. Research on Improved Random Forest Algorithm Based on Hybrid Sampling and Feature Selection. J. Nanjing Univ. Posts Telecommun. 2022, 42, 81–89. [Google Scholar]
- Yang, M.J.; Wang, C.F.; Wu, C.H. Research on Multi-Factor Stock Selection Model Based on Random Forest Algorithm (English). Pure Appl. Math. 2023, 39, 506–519. [Google Scholar]
- Lu, R.; Li, L.Y.; Sun, Y.Y. A Suspicious Transaction Detection Method Based on Random Forest. J. Liaoning Tech. Univ. 2021, 40, 82–89. [Google Scholar]
- Lü, H.Y.; Feng, Q. A Review of Research on Random Forest Algorithm. J. Hebei Acad. Sci. 2019, 36, 37–41. [Google Scholar]
- Imani, M.; Beikmohammadi, A.; Arabnia, H.R. Comprehensive Analysis of Random Forest and XGBoost Performance with SMOTE, ADASYN, and GNUS Under Varying Imbalance Levels. Technologies 2025, 13, 88. [Google Scholar] [CrossRef]
- Lu, Y.; Song, J.X.; Zhu, J.; Bian, Y.P.; Tong, J.Y.; Feng, Y. Analysis of Related Risk Factors for 104 Cases of Sudden Cardiac Death. J. Southeast Univ. 2012, 31, 397–399. [Google Scholar]
- Han, X.J.; Mao, J.Y. Investigation and Analysis of Knowledge, Attitude and Practice about Related Risk Factors in Coronary Heart Disease Patients. Health Med. Res. Pract. 2008, 3, 51–53. [Google Scholar]
- Zhang, F.J.; Liu, S.M. Fuzzy Comprehensive Evaluation of Disease Risk among Rural Residents in China. Shandong Soc. Sci. 2012, 7, 31–35. [Google Scholar] [CrossRef]
- Xu, H.; Wu, Q.Y. Discussion on the Application of Fuzzy Mathematics in Medicine. J. Math. Med. 2000, 6, 564–565. [Google Scholar]
- Yu, J.; Yi, F.; Ma, G.S. Clinical Observation of Coronary Intervention in Elderly Patients with Coronary Heart Disease Complicated with Diabetes Mellitus. Mod. Med. 2012, 40, 671–674. [Google Scholar]
- Tian, F. Application of Fuzzy Comprehensive Evaluation Method in Risk Analysis. Syst. Eng. Electron. 2003, 2, 174–176. [Google Scholar]
- Panjaitan, F.; Nurmaini, S.; Partan, R.U. Accurate Prediction of Sudden Cardiac Death Based on Heart Rate Variability Analysis Using Convolutional Neural Network. Medicina 2023, 59, 1394. [Google Scholar] [CrossRef]
- Sherpa, M.D.; Sonkawade, S.D.; Jonnala, V.; Pokharel, S.; Khazaeli, M.; Yatsynovich, Y.; Kalot, M.A.; Weil, B.R.; Canty, J.M., Jr.; Sharma, U.C. Galectin-3 Is Associated with Cardiac Fibrosis and an Increased Risk of Sudden Death. Cells 2023, 12, 1218. [Google Scholar] [CrossRef]
- Franczyk, B.; Rysz, J.; Olszewski, R.; Gluba-Sagr, A. Do Implantable Cardioverter-Defibrillators Prevent Sudden Cardiac Death in End-Stage Renal Disease Patients on Dialysis? J. Clin. Med. 2024, 13, 1176. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Liao, J. Sudden Cardiac Death Risk Prediction Based on Noise Interfered Single-Lead ECG Signals. Electronics 2024, 13, 4274. [Google Scholar] [CrossRef]
- Salzillo, C.; La Verde, M.; Imparato, A.; Molitierno, R.; Lucà, S.; Pagliuca, F.; Marzullo, A. Cardiovascular Diseases in Public Health: Chromosomal Abnormalities in Congenital Heart Disease Causing Sudden Cardiac Death in Children. Medicina 2024, 60, 1976. [Google Scholar] [CrossRef] [PubMed]



| Challenge | Mechanism of FSE + XGBoost | Empirical Results (SCD Dataset) |
|---|---|---|
| Sparsity | Probabilistic smoothing of membership vectors transforms sparse samples into continuous signals. Gradient boosting iteratively upweights sparse regions. | 30% sparsity: 7.6% AUC gain over hard encoding; 40% overfitting reduction. |
| Nonlinearity | Combinatorial explosion of semantic intervals acts as implicit kernels. XGBoost learns optimal nonlinear paths via enumerating membership combinations. | 20% shallower trees; 63% higher H-statistic for nonlinearity. |
| Missing Values | Dynamic weighting allows split nodes to avoid missing-sensitive features. Gradient boosting regularization suppresses noise from missingness. | 10% missingness: Stable test AUC at 0.85 (RF drops to 0.81). |
| Feature | XGBoost + Fuzzification | RF + Fuzzification |
|---|---|---|
| Sparsity | Optimizes splits in sparse regions via gradient smoothing | Relies on random subsampling, leading to unstable sparsity exploitation |
| Nonlinearity | Explicitly combines semantic intervals with shallower tree depths | Implicitly combines features, requiring deeper trees and increasing overfitting risk |
| Missing Values | Dynamically allocates weights with gradient boosting-based regularization | Uses static proxy value imputation, prone to introducing bias |
| Step | Key Operations | Explanation | Examples |
|---|---|---|---|
| Indicator System | Divide into primary/secondary indicators; assign local weights. | 3 primary indicators (e.g., medical history, physiology, family history) with 15 secondary variables. | Primary: myocardial infarction history; Secondary: heart rate, family sudden death history. |
| Risk Levels | Define 4 risk levels (V1 to V4) and preset standard vectors. | Levels: extremely high, high, medium, low risk. | Extremely high-risk vector: (0.5,0.3,0.2,0.1). |
| Fuzzification | Calculate membership degrees for each risk level based on variable type. | Categorical: Direct assignment (e.g., family history: (0.6,0.4,0.2,0.1)). Ordinal: Clinical risk classification (e.g., myocardial infarction: none/acute/old). Continuous: Boundary-based functions (e.g., heart rate threshold at 60 bpm). | Heart rate > 60 bpm → higher membership in “extremely high risk.” |
| Fuzzy Matrix | Combine secondary indicators′ memberships into matrix Ri. | Each row represents a secondary indicator′s membership across 4 levels. | If heart rate membership is (0.1,0.3,0.5,0.1), it fills one row of Ri. |
| Primary Synthesis | Synthesize local weights (Ai) with Ri to get primary output Bi. | Weighted average of secondary indicators′ memberships (refer to Formula (9)). | If Ai = (0.4,0.3,0.3), Bi aggregates three secondary indicators. |
| Secondary Synthesis | Combine primary outputs (Bi) using global weights (W) to get final B. | Weighted average of primary indicators (refer to Formula (10)). | If W = (0.5,0.3,0.2), B aggregates three primary indicators. |
| Defuzzification | Select risk level with the smallest Euclidean distance to B. | Compare B with ideal vectors of each level (refer to Formula (11)). | If B = (0.2,0.4,0.3,0.1), choose the closest risk level (e.g., V2). |
| Output | Use fuzzy result B as input for XGBoost model training/prediction. | Convert B into a clear risk label (e.g., “high risk” = V2). | Sample classified as V2 becomes the model′s target label. |
| The Outcome/Risk Assessment Level | Extremely High Risk | High Risk | Moderate Risk | Low Risk |
|---|---|---|---|---|
| Extremely high risk: Five-year risk of sudden death > 50% | 0.5 | 0.3 | 0.2 | 0.2 |
| High risk: Five-year risk of sudden death 25–50% | 0.4 | 0.3 | 0.3 | 0.2 |
| Moderate risk: Five-year risk of sudden death 5–25% | 0.2 | 0.3 | 0.4 | 0.3 |
| Low risk: Five-year risk of sudden death < 5% | 0.1 | 0.2 | 0.3 | 0.5 |
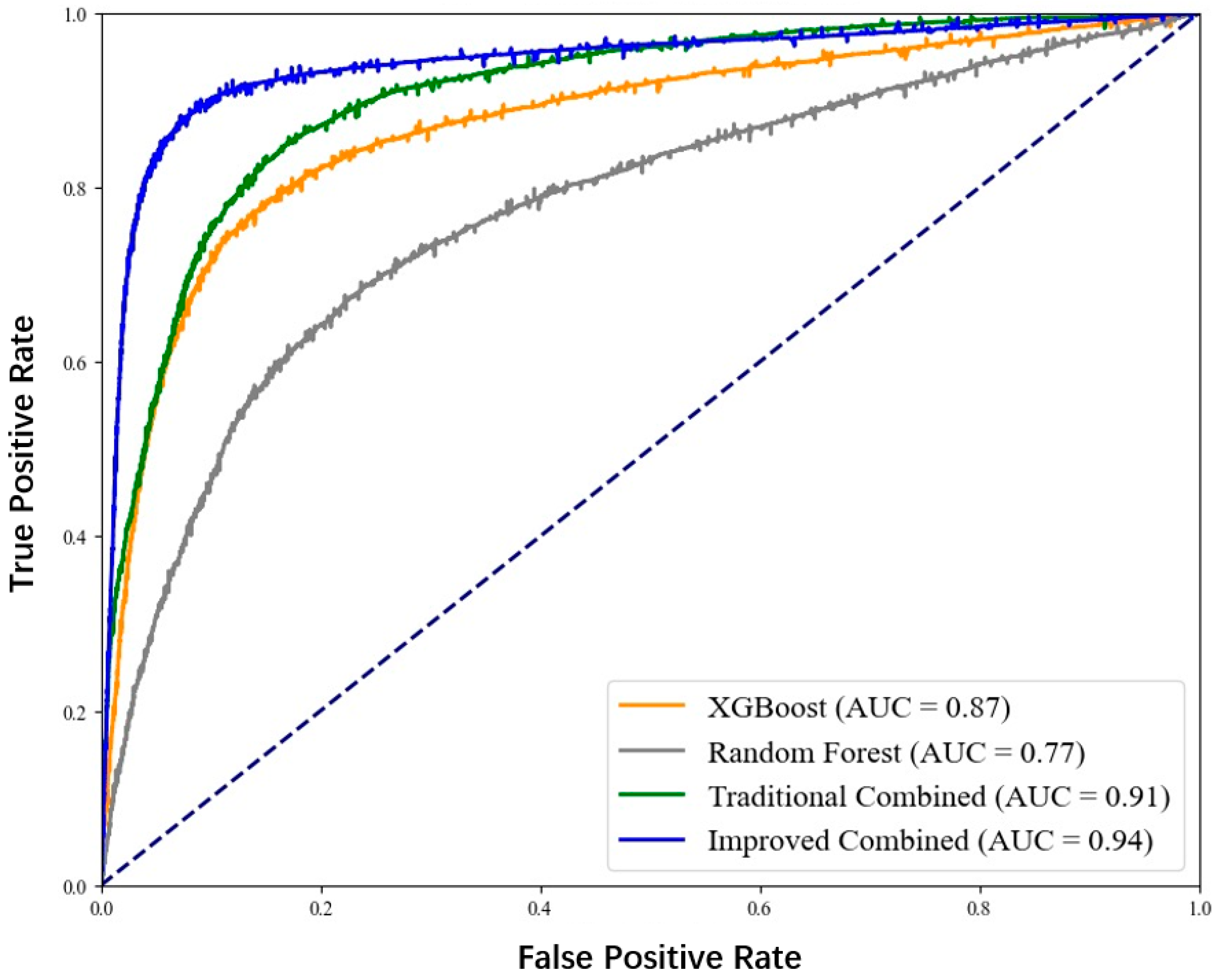
| Model | Accuracy | Precision | Recall | F1-Score | AUC |
|---|---|---|---|---|---|
| XGBoost | 0.85 | 0.82 | 0.78 | 0.85 | 0.87 |
| Random Forest | 0.83 | 0.80 | 0.83 | 0.83 | 0.77 |
| Traditional Combined (XGBoost + Random Forest) | 0.87 | 0.84 | 0.89 | 0.86 | 0.91 |
| Improved Combined (Improved XGBoost + Random Forest) | 0.89 | 0.87 | 0.91 | 0.89 | 0.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, D.; Xu, Y. Research on the Prediction Model of Sudden Death Risk in Coronary Heart Disease Based on XGBoost and Random Forest. Symmetry 2025, 17, 1421. https://doi.org/10.3390/sym17091421
Li Y, Li D, Xu Y. Research on the Prediction Model of Sudden Death Risk in Coronary Heart Disease Based on XGBoost and Random Forest. Symmetry. 2025; 17(9):1421. https://doi.org/10.3390/sym17091421
Chicago/Turabian StyleLi, Yong, Dubai Li, and Yushi Xu. 2025. "Research on the Prediction Model of Sudden Death Risk in Coronary Heart Disease Based on XGBoost and Random Forest" Symmetry 17, no. 9: 1421. https://doi.org/10.3390/sym17091421
APA StyleLi, Y., Li, D., & Xu, Y. (2025). Research on the Prediction Model of Sudden Death Risk in Coronary Heart Disease Based on XGBoost and Random Forest. Symmetry, 17(9), 1421. https://doi.org/10.3390/sym17091421






