Generalized Planck–Einstein Relation in Curved Spacetimes: Implications for Light Propagation Near Black Holes

Abstract

By applying Maxwell’s equations to curved spacetimes, the Planck–Einstein energy–frequency relation for photons, originally formulated in Minkowski space, is generalized for application in Riemann space. According to this relation, photon energy depends not only on the photon frequency but also on the physical speed of photons, which may vary when locally measured in non-inertial static frames. In Minkowski space, the energy of free photons is conserved as neither frequency shifts nor changes in photon speed are observed. In Riemann space, energy of free photons also remains conserved as gravitational redshift is compensated by a corresponding variation in photon speed. The generalized Planck–Einstein relation may have significant astrophysical implications, particularly for gravitational lensing, observations of neutron star mergers, supernovae and quasars, the propagation of light near black holes, and expanding cosmologies.

1. Introduction

In general relativity (GR), static gravitational fields affect the geometry of rays of electromagnetic waves or photons and change their angular frequency $\omega$. This effect, known as the gravitational redshift, was first described by Einstein in 1907 [1,2]. The gravitational redshift is one of the fundamental classical tests of GR, with the first experimental evidence for Earth’s gravity reported by Pound and Rebka [3] and Pound and Snider [4]. The authors detected the frequency shift of gamma-ray photons from ${}^{57}\mathrm{Fe}$ at different altitudes. Since the effect was tiny, they utilized the Mössbauer effect to produce a narrow resonance line to improve the measurement accuracy. Later experiments measured, for example, spectral lines in the Sun’s gravitational field, the redshift of light from galaxies in clusters, and the change in the rate of atomic clocks or optical lattice clocks in ground-based measurements or space measurements with clocks transported on aircrafts, rockets, or satellites [5,6,7,8,9,10,11].

Since the gravitational redshift predicts a change in the frequency of photons, it should also affect their energy. According to the Planck–Einstein relation, the change in photon energy $\Delta E$ is related to the change in angular frequency $\Delta \omega$ as follows [12]:

$$\Delta E=\hslash \Delta \omega ,$$

(1)

where ℏ is the reduced Planck constant. The energy change of photons is commonly interpreted as a loss (or gain) of energy due to interaction with the gravitational field. If a photon propagates against the gravitational acceleration (to higher potential), it expends work and its kinetic energy decreases. Conversely, if the photon propagates with the gravitational acceleration, its kinetic energy increases. The energy change $\Delta E$ is calculated from the difference in gravitational potential $\Delta \Phi$ between two observers. For Earth’s gravitational field, expressed as

$${\displaystyle \frac{\Delta E}{E}}={\displaystyle \frac{\Delta \omega }{\omega }}={\displaystyle \frac{\Delta \Phi }{c^2}}={\displaystyle \frac{gz}{c^2}},$$

(2)

where g is the gravitational acceleration, c is the speed of light, and z is the height difference between the observers. Thus, the sum of kinetic energy and gravitational potential energy of photons is conserved, similarly to a massive particle moving in a gravitational field [13,14]. This holds in the classical geometric-optics treatment, where vacuum (zero-point) energy is not included.

However, this explanation of the gravitational redshift as the effect of energy change of photons or light due to gravity is intuitive and simplistic, interpreting GR effects in terms of the Newtonian gravity developed for massive particles. On closer examination, the problem is more complex [15,16,17,18]. The idea of the gravitational redshift as a transformation between potential and kinetic energy cannot apply to photons for several reasons [13,19]. First, gravitational potential energy for photons as massless particles is not defined in GR; as Weinberg states ([13], p. 85), ‘the concept of gravitational potential energy for a photon is otherwise without foundation’. Second, no energy transfer between photons and static gravity is allowed in the standard GR. Photon in free space is massless and transient, so its stress–energy tensor is dynamic with no static component. Therefore, photons cannot contribute to the curvature of static spacetime as photons and static gravity are treated separately in the Einstein–Maxwell equations [20,21]. Obviously, if photons did couple with static gravity (and spacetime), defining rays as the null geodesics of spacetime would be meaningless because the presence of photons would distort spacetime.

Thus, a proper interpretation of the gravitational redshift requires GR and follows this procedure [13,14,21,22,23]:

• The Maxwell equations are expressed in a generally covariant form to be valid in both Minkowski spacetime and curved Riemannian manifolds.
• The curvature of Riemann spacetime is calculated from the distribution of mass and other static physical fields.
• Using Einstein’s principle of equivalence, assume that photon energy and frequency are unaffected by gravitational fields in free-falling frames, so there is no redshift in a free-falling frame.
• The gravitational redshift of light is calculated as a Doppler effect caused by relative motion between a free-falling frame and a non-inertial stationary frame fixed with respect to the gravity field. This shows that clocks in a static gravitational field at low potential run slower than clocks at higher potential.
• The same results are obtained if the shift in photon frequency is considered as an effect of the time dilation of Riemann spacetime curved by gravity. Since the time rate defined by the time-time component $g_{tt}$ of the metric tensor $g_{\alpha \beta }$ differs for the emitter e and receiver r, the photon frequency must vary:

  $${\displaystyle \frac{\omega \left(e\right)}{\omega \left(r\right)}}=\sqrt{{\displaystyle \frac{g_{tt}\left(r\right)}{g_{tt}\left(e\right)}}}.$$

  (3)

Nevertheless, the problem of energy of light in gravity remains unclear, posing several questions:

• The energy of photons is conserved in the free-falling frame but apparently not in the non-inertial static frame. Since the frequency of photons changes for observers at rest, the photon energy should also change according to the Planck–Einstein relation. If so, where does the energy go, or how is energy conservation understood in GR?
• How does light energy behave in different frames? Is there a difference when evaluated in free-falling (inertial) frames versus static (non-inertial) frames?
• The frequency of light changes due to spacetime deformation, but the coordinate speed of light also changes in non-inertial static frames. How does this affect the light energy?
• Adopting the geometric-optics treatment and setting aside quantum-field effects, we consider the locally measured energy and momentum of a photon to satisfy $E=pc$ (equivalently $E=\hslash \omega$ and $p=\hslash k$). This raises questions about photon momentum in a gravitational field. Is photon momentum conserved in GR, and how does it depend on the frame in which it is evaluated? This problem has an analogue in dielectric media, known as the Abraham–Minkowski controversy, where competing theories predict different photon-momentum formulas [24,25,26,27,28,29,30].

This paper addresses these questions by studying photon energy and momentum through the Einstein–Maxwell equations for electromagnetic waves propagating in curved spacetimes with static gravity. Using covariant coordinate transformations in static (non-inertial) frames in Riemann spacetime, we derive expressions for the speed, energy, and momentum of photons in gravitational fields. These expressions are further specified for the Schwarzschild metric describing a local gravitational field around a black hole. It is shown that photon energy is conserved in both free-falling and static frames. Finally, we modify the Planck–Einstein relation for photon energy from Special Relativity to a form valid in GR. We then discuss potential applications to astrophysical systems with strong gravitational fields, such as neutron star mergers, core-collapse supernovae, white dwarfs, and accretion disks around compact objects, and to expanding cosmologies.

2. Maxwell’s Equations in Static Riemann Space

Considering curved spacetime with coordinates $x^{\alpha }=(ct,x,y,z)$, we can introduce [20,22]

• The electromagnetic four-potential $A^{\alpha }$

  $$A^{\alpha }=\left({\displaystyle \frac{\varphi }{c}},\mathbf{A}\right),\alpha =0,1,2,3,$$

  (4)
• The electromagnetic (Faraday) tensor $F^{\alpha \beta }$

  $$F^{\alpha \beta }={\partial }^{\alpha }{A}^{\beta }-{\partial }^{\beta }{A}^{\alpha },$$

  (5)
• The electromagnetic stress–energy tensor $T^{\alpha \beta }$

  $$T^{\alpha \beta }={\displaystyle \frac{1}{{\mu }_0}}\left(F^{\alpha \mu }{F^{\beta }}_{\mu }-{\displaystyle \frac{1}{4}}{g}^{\alpha \beta }{F}_{\mu \nu }{F}^{\mu \nu }\right),$$

  (6)
• The four-momentum density vector $p^{\alpha }$, represented by the zeroth column of $T^{\alpha \beta }$,

  $$p^{\alpha }=T^{\alpha 0},$$

  (7)

  where $\varphi$ is the scalar electric potential, $\mathbf{A}$ is the vector three-potential, and c is the speed of light in vacuum undistorted by gravity.

The derivatives ${\partial }_{\alpha }$ and ${\partial }^{\alpha }$ in Equation (5) are defined as

$${\partial }_{\alpha }=\partial /\partial x^{\alpha },\mathrm{and}{\partial }^{\alpha }=g^{\alpha \beta }\partial /\partial x^{\beta },$$

(8)

where $g^{\alpha \beta }$ is the contravariant metric tensor of Riemann spacetime. Note that since the electromagnetic tensor $F^{\alpha \beta }$ is antisymmetric, the covariant derivatives used in curved spacetimes reduce to partial derivatives as shown in Equation (5).

Formulating Maxwell’s equations for electromagnetic waves in empty curved spacetime, we obtain the wave equation for electromagnetic potential [22,31]

$$\square A^{\alpha }={\nabla }_{\beta }{\nabla }^{\beta }{A}^{\alpha }=0,$$

(9)

where $\square \equiv {\nabla }_{\beta }{\nabla }^{\beta }$ is the wave operator (i.e., the covariant d’Alambert operator), ${\nabla }_{\alpha }$ is the covariant derivative, and the vector potential $A^{\alpha }$ should satisfy also the Lorenz gauge condition

$${\nabla }_{\alpha }{A}^{\alpha }=0.$$

(10)

Additionally, Maxwell’s equations imply the energy–momentum conservation law for electromagnetic waves in the following form:

$${\nabla }_{\alpha }{T}^{\alpha \beta }=0.$$

(11)

3. Speed of Light in Static (Non-Inertial) Frames

The above equations hold within general relativity (GR) for electromagnetic waves (light) propagating in spacetimes curved by a static gravitational field [13,20,32]. Most differences between electromagnetic phenomena in GR and SR arise from a fundamentally different understanding of the speed of light in curved (Riemann) versus flat (Minkowski) spacetime. In Minkowski spacetime, the speed of light is supposed to be constant. However, in Riemann spacetime, the speed of light may vary depending on the frame considered. Consequently, GR distinguishes between free-falling (locally inertial) and static (non-inertial) frames.

According to Einstein’s equivalence principle, physical quantities in free-falling frames are unaffected by gravity and behave similarly as in inertial frames in Minkowski space [20]. By contrast, the behavior of physical quantities in static frames fixed relative to the gravitational field is more complex. Since all frames at rest with respect to the gravitational field are non-inertial, they are influenced by gravity. Gravity affects not only the geometry of rays but also the coordinate and physical speeds of waves propagating along the rays [2,33,34,35,36,37,38]. As Einstein wrote [36], ‘the law of constancy of the velocity of light in vacuo, which constitutes one of the fundamental assumptions in the special theory of relativity and to which we have already frequently referred, cannot claim an unlimited validity… its results hold only so long as we are able to disregards the influences of gravitational fields on the phenomena (e.g., of light)’.

Hence, there are solutions within GR, in which the speed of light varies in non-inertial (static) frames without contradicting the local constancy of c in free-fall. An illustrative example is gravitational lensing, where ‘a curvature of rays of light can only take place when the velocity of propagation of light varies with position’, see Einstein [36].

Note that the possibility of a varying speed of light (VSL) has also been discussed in broader context. Dicke [39] and Dirac [40,41] considered that physical laws and fundamental constants might vary over cosmological time. Subsequently, VSL theories were proposed [42,43,44,45,46,47]. However, these models often involve departures from standard GR (e.g., breaking local Lorentz invariance or modifying conservation laws) and remain the subject of ongoing debate. By contrast, the present work stays strictly within standard GR: by ‘varying speed of light’, we mean the frame-dependent speed in non-inertial static spacetimes not a fundamental variation of the locally measured c in free-fall.

3.1. Coordinate Speed of Light

Let us assume Riemann spacetime described by metric tensor $g_{\alpha \beta }$. Since any symmetric tensor can be diagonalized using a coordinate transformation, we can write the metric tensor with no loss of generality in the following form:

$$d{s}^2=-g_{tt}{c}^{2}d{t}^2+g_{ii}d{x}^{i}d{x}^i,$$

(12)

where $g_{tt}$ and $g_{ii}$ mean the time dilation and space deformation due to the gravity, and summation is over $i=1,2,3$. The propagation of the electromagnetic waves obeys the equation of the null spacetime distance, $d{s}^2=0$. Hence,

$$g_{tt}{c}^{2}d{t}^2=g_{ii}d{x}^{i}d{x}^i,$$

(13)

and the contravariant speed of light ${c_g}^i$ along the $x^i$-axis reads

$$\begin{array}{c}\hfill c_g^i={\displaystyle \frac{\sqrt{d{x}^{i}d{x}^i}}{dt}}=\sqrt{{\displaystyle \frac{g_{tt}}{g_{ii}}}}c\\ \hfill (\mathrm{no}\mathrm{summation}\mathrm{over}i),\end{array}$$

(14)

where the coordinate time t is used as a parameter along the ray.

Equation (14) expresses the coordinate (contravariant) speed of light, which is coordinate-dependent because it relies on the specific choice of coordinates. In addition, it is unphysical because it is expressed in terms of generally non-unit coordinate base vectors.

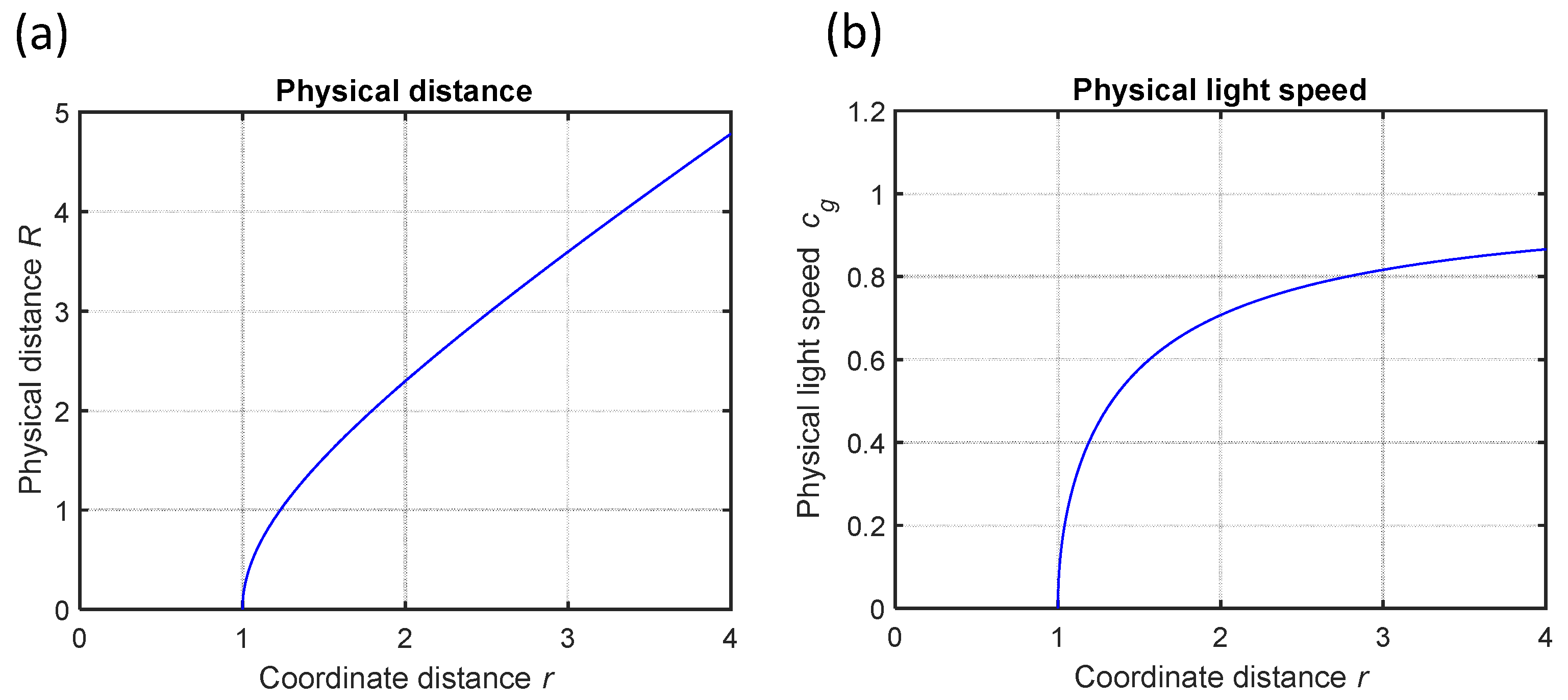
3.2. Physical Speed of Light

The physical speed of light must be coordinate-invariant to be physically meaningful as it is calculated using the physical distance and physical time measured, for example, by rigid rods and atomic clocks in the given frame (see [21], pp. 153–154, or [48]). Unlike to flat spacetime described by Cartesian coordinates, where coordinates t and r have direct physical meaning, in curved spacetime described by curvilinear coordinates, t and r are not invariant but rather artificial parameters with no direct physical interpretation. To eliminate the dependence on the choice of coordinates and express these quantities in terms of physical time and distance, we adopt an orthonormal coordinate basis by rescaling the original non-orthonormal base vectors (for details, see Appendix A).

In the static frame, the i-th component of the physical speed of light is given by ([22], p. 252)

$$c_{g\left(i\right)}=\sqrt{c_{gi}{c}_g^i}=\sqrt{g_{ii}}{c}_g^i=\sqrt{g_{tt}}c(\mathrm{no}\mathrm{summation}\mathrm{over}i),$$

(15)

where $X_{\left(i\right)}$ denotes the i-th physical component of three-vector $\mathbf{X}$ (see Appendix A). Since the physical light speed has the same magnitude in all directions, we can write ([37], p. 309; [49], Equation (27))

$$c_g={\displaystyle \frac{\sqrt{d{x}_{i}d{x}^i}}{dt}}=\sqrt{g_{tt}}c.$$

(16)

The physical speed of light $c_g$ is a quantity measured in a frame at rest relative to the sources of the gravitational field. This speed of light is not constant but varies with the distance between the observer and the source of gravity.

It is important to note that the variation of $c_g$ in non-inertial (static) frames does not contradict the common assumption of the constancy of the proper speed of light c in free-falling frames. In free-falling frames, the proper time $\tau$ is related to the coordinate time t by $d\tau =\sqrt{g_{tt}}dt$, which implies fundamentally different properties of the speed of light compared to static frames.

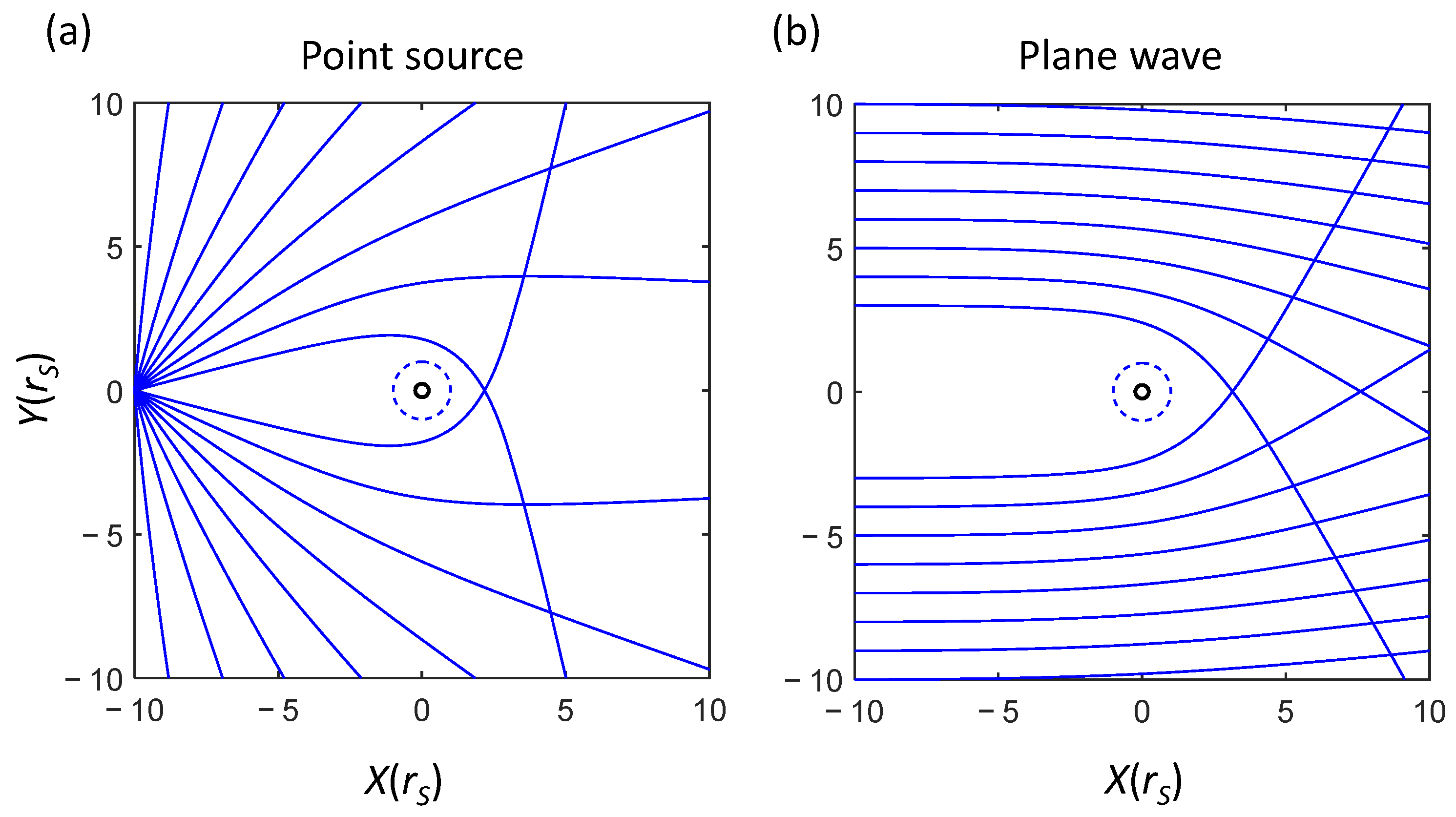
3.3. High-Frequency Electromagnetic Waves

Let us consider light as high-frequency electromagnetic waves propagating locally as plane waves through a smoothly curved spacetime. The electromagnetic four-potential $A^{\alpha }$ is then expressed as [20] (§22.5)

$$A^{\alpha }=\mathrm{Re}\left(a^{\alpha }{e}^{\mathrm{i}\theta }\right),$$

(17)

where $a^{\alpha }$ is the slowly varying complex amplitude, and $\theta$ is the rapidly varying phase.

The electromagnetic tensor $F^{\alpha \beta }$ (see Equation (5)) and the electromagnetic stress–energy tensor $T^{\alpha \beta }$ (see Equation (6)) are given by ([20], Box 22.4E)

$$F^{\alpha \beta }=\mathrm{i}\left(k^{\alpha }{a}^{\beta }-k^{\beta }{a}^{\alpha }\right),$$

(18)

$$T^{\alpha \beta }={\displaystyle \frac{1}{{\mu }_0}}{a}^2{k}^{\alpha }{k}^{\beta },$$

(19)

where $k^{\alpha }={\partial }^{\alpha }\theta$ is the four-wave vector ([20], Equation (22.26d)), which defines the ray direction, perpendicular to the wavefront, $a=\sqrt{a^{\mu }{a}_{\mu }^{*}}$ is the scalar amplitude, and $a_{\mu }^{*}$ is the complex-conjugate value of $a_{\mu }$. In deriving Equations (18) and (19), derivatives of the amplitude $a^{\alpha }$ are neglected because the phase $\theta$ varies with time more rapidly than $a^{\alpha }$.

The four-wave vector $k^{\alpha }$ satisfies the eikonal equation, i.e., the Hamilton–Jacobi equation for the rapidly varying phase $\theta$ in the geometric-optics (WKB) limit:

$$g_{\alpha \beta }{k}^{\alpha }{k}^{\beta }=0,$$

(20)

which follows directly from the null geodesic Equation (13) and indicates that rays are null geodesics of the curved spacetime.

Finally, for high-frequency waves in curved spacetime, the energy conservation law in Equation (11) takes the form ([20], Box 22.4D):

$${\nabla }_{\alpha }\left(a^2{k}^{\alpha }{k}^{\beta }\right)=0,$$

(21)

where ${\nabla }_{\alpha }$ denotes the covariant derivative, meaning the derivative along a ray path.

Equation (21) is called the transport equation for radiation energy and states that the energy flux of light is conserved along rays when measured in a fixed frame.

3.4. Four-Wave Vector of High-Frequency Electromagnetic Waves

Similarly as for the speed of light, we have to distinguish between the coordinate (covariant or contravariant) components and the physical components of the four-wave vector $k_{\alpha }$. The zeroth covariant component of the four-wave vector $k_0$ is expressed as

$$k_0={\displaystyle \frac{1}{c}}{\displaystyle \frac{\partial \theta }{\partial t}}={\displaystyle \frac{\omega }{c}},$$

(22)

where $\omega =\partial \theta /\partial t$ is the standard angular frequency defined in flat Minkowski space.

By contrast, the zeroth physical component of the four-wave vector $k_{\left(0\right)}$ is

$$k_{\left(0\right)}=\sqrt{|k_0{k}^0|}=\sqrt{g^{tt}}{\displaystyle \frac{1}{c}}{\displaystyle \frac{\partial \theta }{\partial t}}={\displaystyle \frac{{\omega }_g}{c}},$$

(23)

where ${\omega }_g={\displaystyle \frac{1}{\sqrt{g_{tt}}}}{\displaystyle \frac{\partial \theta }{\partial t}}={\displaystyle \frac{\omega }{\sqrt{g_{tt}}}}$ is the angular frequency measured in Riemann space, and the absolute value is used to avoid the imaginary unit.

Taking into account Equation (16), we readily obtain a relation between angular frequencies ${\omega }_g$ and $\omega$ of photons in curved Riemann space and flat Minkowski space

$${\omega }_g={\displaystyle \frac{c}{c_g}}\omega ,$$

(24)

which is a formula for the gravitational redshift for photons in gravitational fields.

Since the magnitude of the four-wave vector is zero, $K=\sqrt{k_{\alpha }{k}^{\alpha }}=0$, we readily obtain that the spatial physical components of the wave vector $k_{\left(i\right)}$ in Riemann space are scaled similarly as the zeroth component $k_{\left(0\right)}$. Consequently, we write

$$k_{\left(\alpha \right)}={\displaystyle \frac{c}{c_g}}{k}_{\alpha }.$$

(25)

3.5. Planck–Einstein Relation for Energy of Photons

Now, we adopt a quantum mechanical concept of light and treat light as a beam of photons that are massless particles propagating at the speed of light. The energy and momentum densities of light will be transformed into the photon energy and photon momentum. The relationship between components of the four-wave vector $k_{\alpha }$ and the four-momentum $p_{\alpha }$ of photons is well known ([20], Box 22.4E):

$$p_{\alpha }=\hslash k_{\alpha },p_{\left(\alpha \right)}=\hslash k_{\left(\alpha \right)},$$

(26)

where ℏ is the reduced Planck constant, and $p_{\alpha }$ and $p_{\left(\alpha \right)}$ are null vectors satisfying the null geodesic equation. Consequently, the zeroth components of the four-momentum vectors $p_{\alpha }$ and $p_{\left(\alpha \right)}$ are given by

$$p_0=\hslash k_0=\hslash {\displaystyle \frac{\omega }{c}},p_{\left(0\right)}=\hslash k_{\left(0\right)}=\hslash {\displaystyle \frac{{\omega }_g}{c}}.$$

(27)

Since the photon energy in Riemann space is obtained as

$$E=p_g{c}_g,$$

(28)

where

$$p_g=\sqrt{p_i{p}^i}=\hslash {\displaystyle \frac{{\omega }_g}{c}}$$

(29)

is the three-momentum, and $c_g$ is the physical speed of light in a vacuum distorted by gravity. We finally obtain the energy–frequency relation for photons in Riemann space

$$E_g=\hslash {\omega }_g{\displaystyle \frac{c_g}{c}}=\widehat{\hslash }{\omega }_g{c}_g,$$

(30)

where $\widehat{\hslash }=\hslash /c$ is the reduced Planck constant ℏ normalized to the speed of light c in vacuum with no gravity.

For Minkowski space $(g_{tt}=1)$, we obtain ${\omega }_g=\omega$ and $c_g=c$, and Equation (30) transforms to the standard Planck–Einstein relation [12,20]

$$E=\hslash \omega .$$

(31)

In fact, Equation (30) represents the energy conservation law for photons propagating in curved spacetime. Since ${\omega }_g=\omega /\sqrt{g_{tt}}$ and $c_g=c\sqrt{g_{tt}}$, their product is invariant irrespective of the spacetime curvature. The validity of the photon energy conservation is not surprising. The energy conservation for freely propagating (non-interacting) photons in a static gravitational field is reported by Misner et al. [20] (p. 579 and Figure 22.2), Hartle [21] (p. 177), and others. However, the authors usually consider energy conservation for photons in free-falling frames. Here, this law is derived for non-inertial static frames.

4. Light Speed, Gravitational Redshift, and Photon Energy in the Schwarzschild Metric

The Schwarzschild metric describing the gravitational field of a body with mass M situated at the origin of coordinates is defined as follows [20]:

$$d{s}^2=-\left(1-{\displaystyle \frac{r_s}{r}}\right)c^{2}d{t}^2+{\left(1-{\displaystyle \frac{r_s}{r}}\right)}^{-1}d{r}^2+r^{2}d{\Omega }^2,$$

(32)

$$d{\Omega }^2=d{\vartheta }^2+{sin}^2\vartheta d{\phi }^2,$$

(33)

where $r_s=2GM/c^2$ is the Schwarzschild radius, G is the gravitational constant, r and t are the coordinate distance and time, $\vartheta$ and $\phi$ are the Schwarzschild angles, and c is the speed of light far from the source of gravity.

Using Equation (32), the gravitational redshift at distance r expressed as the relative change of the photon angular frequency ${\omega }_g$ with respect to the photon angular frequency $\omega$ at $r\to \infty$ reads

$${\displaystyle \frac{{\omega }_g}{\omega }}=\sqrt{{\displaystyle \frac{g_{tt}(\infty )}{g_{tt}\left(r\right)}}}={\left(1-{\displaystyle \frac{r_s}{r}}\right)}^{-{\displaystyle \frac{1}{2}}}.$$

(34)

Furthermore, we can express the physical distance R and the physical speed of light $c_g$ as ([49], Equation (31))

$$R={\int }_{r_s}^r{\displaystyle \frac{1}{\sqrt{1-\frac{r_s}{r}}}}dr,c_g=\sqrt{1-{\displaystyle \frac{r_s}{r}}}c.$$

(35)

It follows from Equation (35) that the physical speed of light $c_g$ depends on the distance from the black hole: it is zero for $r=r_s$ (corresponding to $R=0$) and becomes c for $r\to \infty$ (see Figure 1). In the far-field approximation

$${\displaystyle \frac{r_s}{r}}={\displaystyle \frac{GM}{r{c}^2}}\ll 1,$$

(36)

the formulas read for the gravitational redshift

$$g_{tt}=1+{\displaystyle \frac{2\Phi }{c^2}},{\omega }_g=\left(1-{\displaystyle \frac{\Phi }{c^2}}\right)\omega ,{\displaystyle \frac{\Delta \omega }{\omega }}=-{\displaystyle \frac{\Phi }{c^2}},$$

(37)

and for the light speed $c_g$ and the photon energy $E_g$

$$c_g=\left(1+{\displaystyle \frac{\Phi }{c^2}}\right)c,$$

(38)

$$E_g=\widehat{\hslash }{\omega }_g{c}_g=\widehat{\hslash }\omega c=\hslash \omega =E,$$

(39)

where $\Phi =-GM/r$ is the Newtonian gravitational potential, and $\Delta \omega ={\omega }_g-\omega$ is the frequency change between the angular frequency ${\omega }_g$ observed at finite r (affected by gravity) and the angular frequency $\omega$ observed at $r\to \infty$ (no gravity).

Note that Equation (38) was originally derived by Einstein himself, who stated in his 1911 paper [2] that gravitation affects the propagation speed of light, causing it to vary with the gravitational potential. However, owing to a confusion between free-falling and non-inertial (static) frames, this interpretation was later abandoned by the relativistic community and replaced by the postulate of a constant speed of light, overlooking the essential difference between free-falling and static frames.

5. Discussion

5.1. Energy Transfer Between Light and Static Gravitational Field

The intuitive interpretation of gravitational redshift as an exchange of energy between light and the gravitational field in the form of gravitational potential energy is misleading. A careful application of the Einstein–Maxwell equations reveals that the energy of high-frequency electromagnetic waves and free photons propagating in a vacuum distorted by a static gravitational field is conserved. Their energy changes only through interactions with matter (massive particles) via absorption, reflection, or scattering. Free photons in a vacuum do not supply static pressure that would modify a static spacetime geometry.

Because the Lagrangian is time-independent in a static spacetime, the energy of free, non-interacting, collisionless photons is invariant in a vacuum with a static gravitational field. This point is standard in the relativity literature [20,21], but it is often overlooked when discussing the photon energy measured by observers in non-inertial (static) frames. A closely related statement holds in stationary (time-independent but not static) spacetimes produced, for example, by rotating black holes. Similarly, the photon energy is conserved for time-dependent backgrounds (e.g., expanding cosmologies) if metric variations are slow compared with the photon’s period.

5.2. Modified Planck–Einstein Relation

Consequently, the idea that the energy of photons depends only on their frequency must be corrected because the energy is conserved even for redshifted photons observed in static frames. The standard energy–frequency relation is valid only in SR, where the light speed c is considered constant. In GR, the energy of photons depends not only on the frequency of photons but also on the physical speed of photons $c_g$. The original Planck–Einstein relation $E=\hslash \omega$ must be modified to the new relation

$$E=\widehat{\hslash }{\omega }_g{c}_g,$$

(40)

where $\widehat{\hslash }=\hslash /c$ is the reduced Planck constant normalized to the speed of light c in a vacuum with no gravity, and ${\omega }_g$ and $c_g$ denote the angular photon frequency and physical speed of light measured in a non-inertial static frame experiencing gravity. If the frequency of photons is changed due to the gravitational redshift, the physical speed of light $c_g$ is also changed, and both effects are compensated.

5.3. Gravitational Field as an Analogue of a Dielectric Medium

In classical electromagnetism, a dielectric medium is a material that does not conduct electricity but can store electrical energy in an electric field. Here, we do not claim that the vacuum in a gravitational field is a material dielectric; rather, we use a standard optical analogy: Maxwell’s equations in curved spacetime can be rewritten as Maxwell’s equations in flat spacetime filled with an equivalent medium whose permittivity and permeability encode the spacetime metric. This ‘effective-medium’ description goes back to Gordon and Plebanski and is widely used in gravitational optics [22,50,51,52,53].

Within this geometric-optics limit, the relation between photon energy and momentum

$$E=p_g{c}_g$$

(41)

remains valid, and from Equation (40), the photon momentum is

$$p_g=\widehat{\hslash }{\omega }_g,$$

(42)

where the subscript ‘g’ denotes a quantity affected by gravity and measured in a static frame.

Hence, the physical (locally measured) photon momentum is not invariant when gravity is present because the measured photon frequency changes for static observers.

For static spacetimes, the effective-medium model reduces to a scalar refractive index n, and the photon momentum transforms as in Minkowski’s theory of dielectrics [25,26,27,28,29,50,53]

$$p_g=np,$$

(43)

with

$$n={\displaystyle \frac{c}{c_g}}={\displaystyle \frac{1}{\sqrt{g_{tt}}}},$$

(44)

where $c_g$ is the speed of light measured by static observers in the gravitational field, and c is the speed of light in the absence of gravity (see [37], Chapter X, Equation (94) or [22], pp. 247–248). In more general stationary (rotating) spacetimes, the equivalent medium becomes anisotropic and exhibits magneto-electric terms; the simple scalar n is then replaced by tensorial constitutive relations [52,53].

Note that this effective-medium approach is routinely employed together with Fermat’s principle to study light trajectories (e.g., gravitational lensing) using methods of geometrical optics in media [54,55,56,57,58,59,60,61,62].

5.4. Astrophysical Implications

The modified Planck–Einstein relation presented in Equation (40) has significant astrophysical implications for interpreting redshift in gravitational fields, such as those around black holes and neutron stars [63,64,65]. In these environments, spacetime is intensely curved, which leads to a substantial reduction in the physical speed of light in the reference frame fixed to these massive objects, resulting in observable gravitational redshift. Additionally, the geometry of light rays becomes highly nontrivial as they are strongly deflected by the gravitational field (Figure 2).

Gravitational redshift is also expected to be significant in a number of other astrophysical contexts. For instance,

• Neutron star mergers, which are the confirmed origin of short-duration gamma-ray bursts (GRBs), produce extremely intense and dynamic gravitational fields. These conditions give rise to significant gravitational redshift, affecting both the prompt gamma-ray emission and subsequent afterglow spectra [66,67].
• Core-collapse supernovae, particularly during the formation of proto-neutron stars, exhibit strong gravitational gradients affecting neutrino and photon propagation [68,69].
• White dwarfs, though less compact than neutron stars, show measurable gravitational redshift, as confirmed through high-precision spectroscopy of systems like Sirius B [70,71].
• Accretion disks around compact objects, such as those in X-ray binaries and quasars, exhibit spectral line shifts and broadening due to gravitational redshift and relativistic effects [72].

The same reasoning applies to active galactic nuclei [73,74], as well as galaxy clusters [75], where intense gravitational fields and spacetime distortions strongly influence radiation behavior. In all these cases, the varying local speed of light (Figure 1) and the complex geometry of rays (Figure 2) must be considered to understand gravitational lensing phenomena (e.g., Einstein rings and lensing near black holes), black hole shadows, relativistic beaming and magnification in jets, pulsar timing and Shapiro delay, caustics in gamma-ray bursts, and gravitational time delay, all of which affect the energy transport and budget of electromagnetic waves, which are crucial for accurate interpretation of observational data [76,77,78,79].

5.5. Cosmological Implications

At cosmological scales, the derived results could improve our understanding of the energy budget of redshifted light caused by the expansion of the universe. In the early universe, the gravitational field was extremely strong due to the very high mass density. As the universe expanded, the mass density decreased and the gravitational field weakened. This weakening is manifested in observations of cosmic time dilation [80], as observed in the time-stretching of Type Ia supernova light curves [81,82,83,84,85,86].

Another key observational manifestation is the cosmological redshift [87,88]. It is commonly interpreted as the stretching of photon wavelengths during their propagation through an expanding universe and described by the Friedmann–Lemaître–Robertson–Walker (FLRW) metric [13,89,90]. Since the speed of light is constant during cosmic evolution in the FLRW metric, the frequency change of redshifted photons projects into declining the photon energy during space expansion. However, there is no physical mechanism to explain this energy loss. Since Einstein’s field equations do not permit any interaction between freely moving photons and a gravitational field, this raises a critical issue for the ΛCDM model based on the FLRW metric.

By contrast, if the FLRW metric is substituted by a more general framework such as the Conformal Cosmology (CC) metric [33,35,80,91], the physical speed of light in earlier cosmic epochs would differ from the value measured today. Consequently, the energy of light propagating through the expanding universe remains conserved. In addition, the varying speed of light predicted by the CC metric explains flat galaxy rotation curves without invoking dark matter [34] and the dimming of Type Ia supernovae [92,93] without requiring the concept of dark energy [33]. These results challenge the necessity of both dark matter and dark energy in explaining fundamental cosmological observations.