Model Research on the Influence of the Biological Clock Network Structure on Function Under Light Stimulation
Abstract
1. Introduction
2. Model Comparison
2.1. Goodwin Model
2.2. Kuramoto Model
2.3. Poincaré Model
2.4. Simulation Details
3. Results
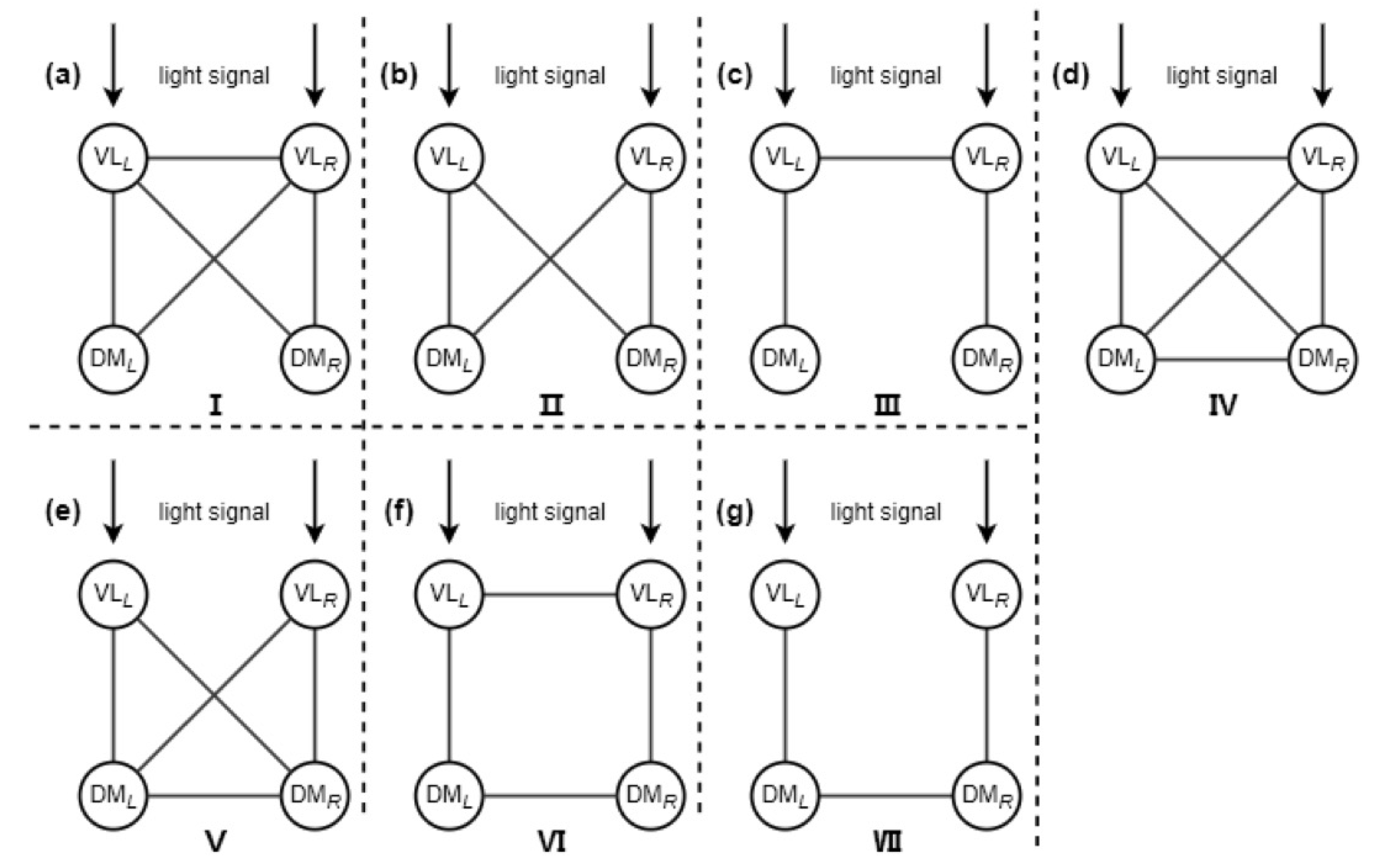
3.1. Motif Structure
3.2. All-to-All Network
3.2.1. Light Sensitivity Heterogeneity
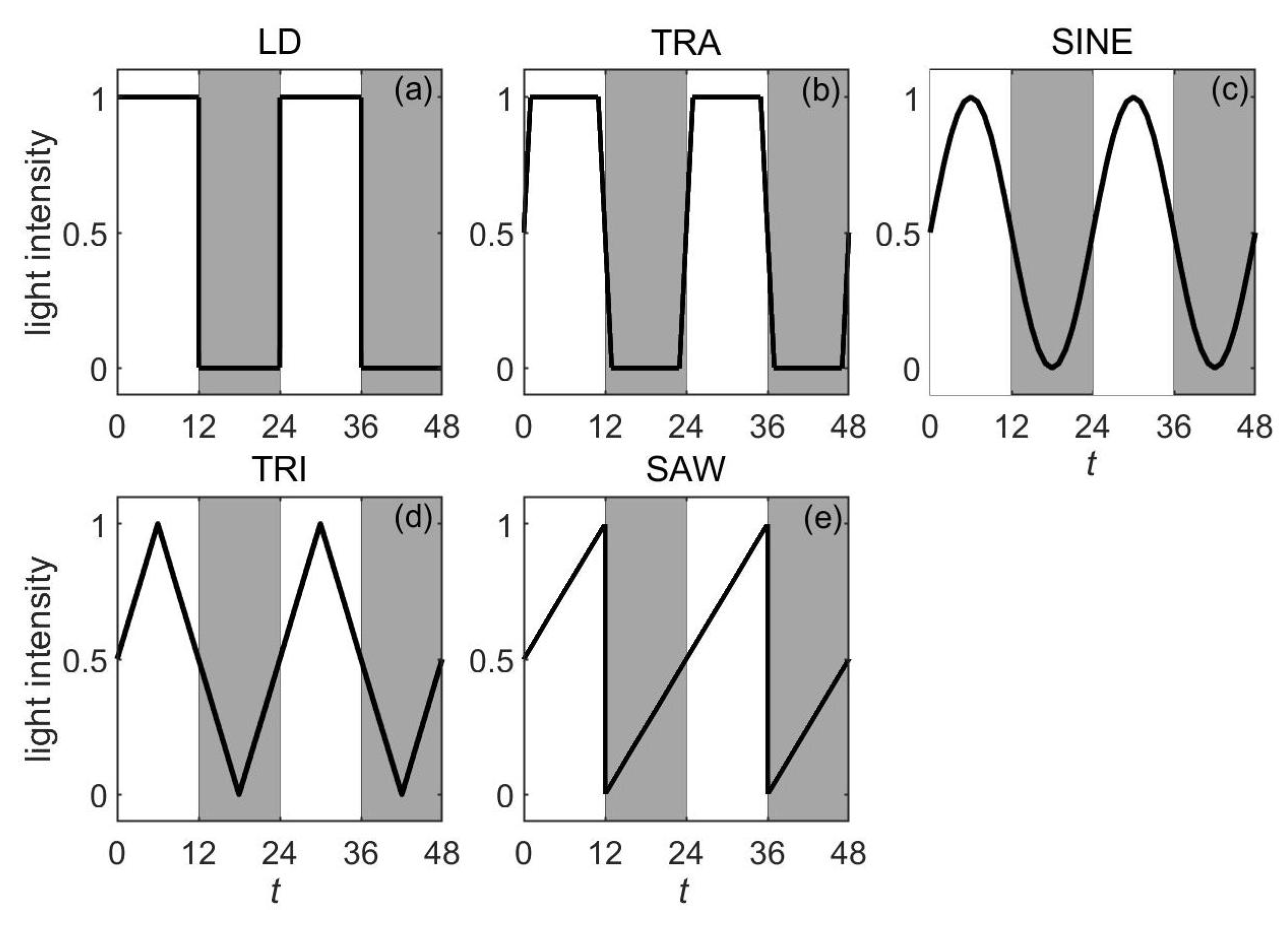
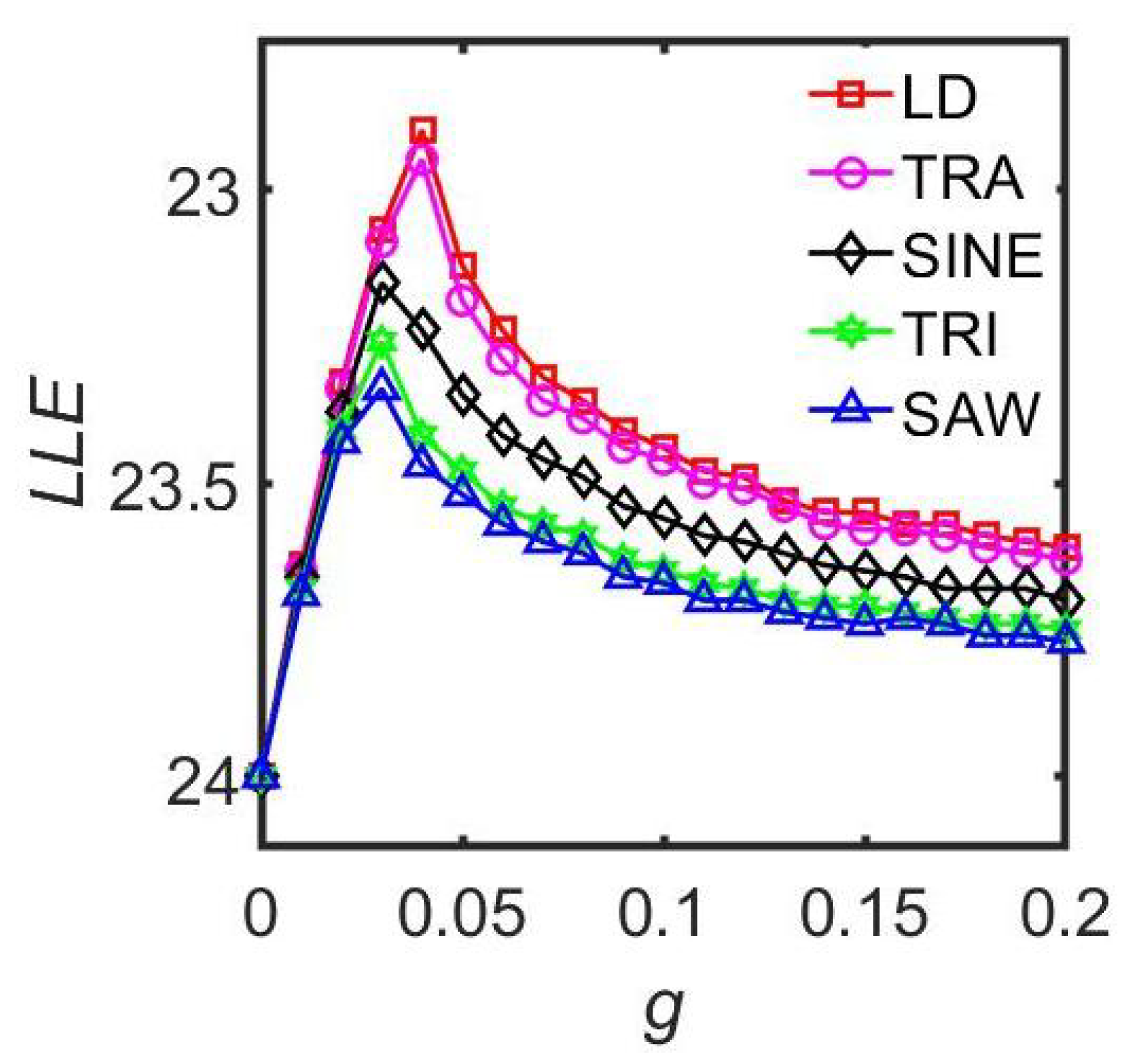
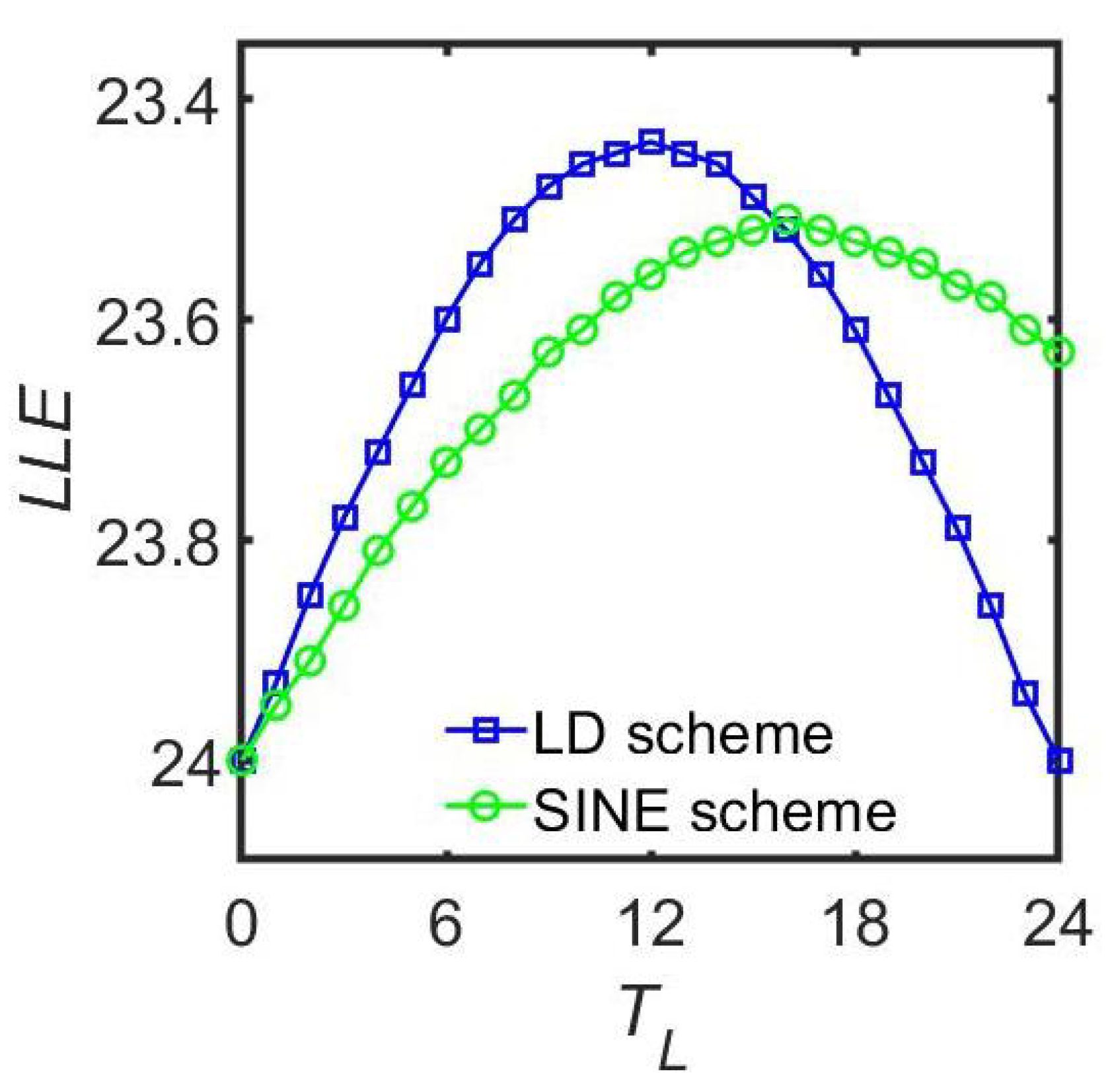
3.2.2. The Light Waveforms
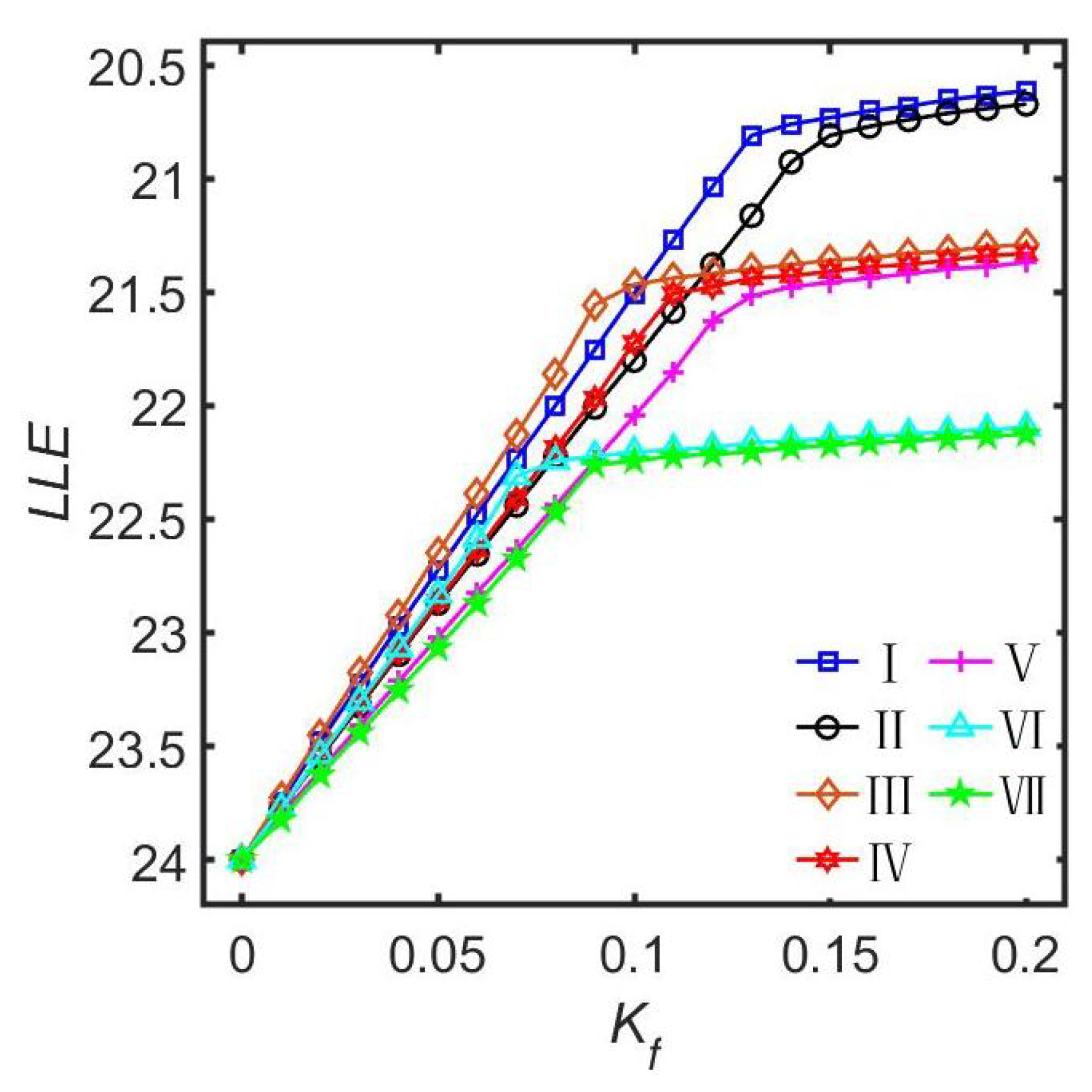
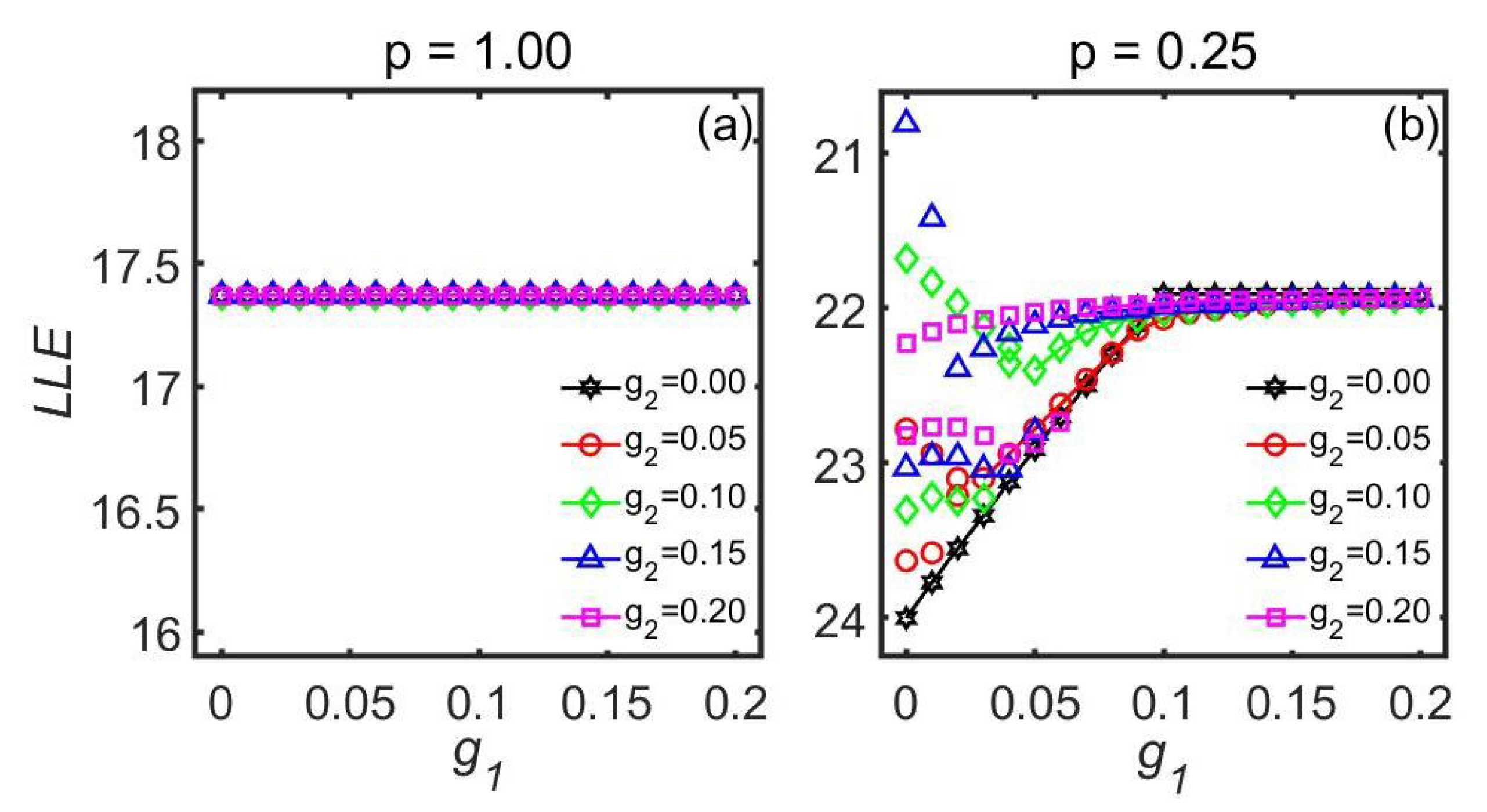
3.2.3. The Coupling Strength
3.2.4. The Adaptive Coupling
3.3. Small-World Network
3.4. Scale-Free Network
3.5. Higher-Order Interaction Network
4. Critical Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SCN | suprachiasmatic nucleus |
| FRP | free-running period |
| LLE | lower limit of entrainment |
| ULE | upper limit of entrainment |
| VL | ventrolateral |
| DM | dorsomedial |
| VIP | vasoactive intestinal peptide |
| AVP | arginine vasopressin |
| GABA | gamma-aminobutyric acid |
| NW | Newman–Watts |
| BA | Barabási–Albert |
| LP | long photoperiod |
| SP | short photoperiod |
| DD | constant darkness |
| LL | constant light |
| ER | Erdős–Rényi |
References
- Hastings, M.H.; Reddy, A.B.; Maywood, E.S. A clockwork web: Circadian timing in brain and periphery, in health and disease. Nat. Rev. Neurosci. 2003, 4, 649–661. [Google Scholar] [CrossRef]
- Meléndez-Fernández, O.H.; Liu, J.A.; Nelson, R.J. Circadian rhythms disrupted by light at night and mistimed food intake alter hormonal rhythms and metabolism. Int. J. Mol. Sci. 2023, 24, 3392. [Google Scholar] [CrossRef]
- Evans, J.A.; Gorman, M.R. In Synch but Not in Step: Circadian Clock Circuits Regulating Plasticity in Daily Rhythms. Neuroscience 2016, 320, 259–280. [Google Scholar] [CrossRef]
- Finger, A.M.; Kramer, A. Mammalian circadian systems: Organization and modern life challenges. Acta Physiol. 2021, 231, e13548. [Google Scholar] [CrossRef]
- Czeisler, C.A.; Duffy, J.F.; Shanahan, T.L.; Brown, E.N.; Mitchell, J.F.; Rimmer, D.W.; Ronda, J.M.; Silva, E.J.; Allan, J.S.; Emens, J.S.; et al. Stability, Precision, and Near-24-Hour Period of the Human Circadian Pacemaker. Science 1999, 284, 2177. [Google Scholar] [CrossRef]
- Srivastava, M.; Varma, V.; Abhilash, L.; Sharma, V.K.; Sheeba, V. Circadian Clock Properties and Their Relationships as a Function of Free-Running Period in Drosophila melanogaster. J. Biol. Rhythm. 2019, 34, 231. [Google Scholar] [CrossRef] [PubMed]
- Flanagan, A.; Bechtold, D.A.; Pot, G.K.; Johnston, J.D. Chrono-nutrition: From molecular and neuronal mechanisms to human epidemiology and timed feeding patterns. J. Neurochem. 2021, 157, 53–72. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.A.; Leise, T.L.; Castanon-Cervantes, O.; Davidson, A.J. Dynamic interactions mediated by nonredundant signaling mechanisms couple circadian clock neurons. Neuron 2013, 80, 973–983. [Google Scholar] [CrossRef] [PubMed]
- Ashton, A.; Jagannath, A. Disrupted sleep and circadian rhythms in schizophrenia and their interaction with dopamine signaling. Front. Neurosci. 2020, 14, 636. [Google Scholar] [CrossRef]
- Gu, C.G.; Li, J.H.; Zhou, J.; Yang, H.J.; Wang, M. Strengthen the circadian rhythms by the mathematical model of the SCN. Eur. Phys. J. Spec. Top. 2022, 231, 827–832. [Google Scholar] [CrossRef]
- Yamaguchi, S.; Isejima, H.; Matsuo, T. Synchronization of cellular clocks in the suprachiasmatic nucleus. Science 2003, 302, 1408–1412. [Google Scholar] [CrossRef]
- Daido, H. Why circadian rhythms are circadian: Competitive population dynamics of biological oscillators. Phys. Rev. Lett. 2001, 87, 048101. [Google Scholar] [CrossRef] [PubMed]
- Zhu, B.; Zhou, J.; Jia, M.T.; Yang, H.J.; Gu, C.G. Entrainment range affected by the difference in sensitivity to light-information between two groups of SCN neurons. Chin. Phys. B 2020, 29, 068702. [Google Scholar] [CrossRef]
- Maywood, E.S.; Chesham, J.E.; Winsky-Sommerer, R.; Smyllie, N.J.; Hastings, M.H. Circadian chimeric mice reveal an interplay between the suprachiasmatic nucleus and local brain clocks in the control of sleep and memory. Front. Neurosci. 2021, 15, 639281. [Google Scholar] [PubMed]
- Abraham, U.; Granada, A.E.; Westermark, P.O.; Heine, M.; Kramer, A.; Herzel, H. Coupling governs entrainment range of circadian clocks. Mol. Syst. Biol. 2010, 6, 438. [Google Scholar] [CrossRef]
- Usui, S.; Takahashi, Y.; Okazaki, T. Range of entrainment of rat circadian rhythms to sinusoidal light-intensity cycles. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 2000, 278, R1148–R1156. [Google Scholar] [CrossRef]
- Li, Y.N.; Androulakis, I.P. Light entrainment of the SCN circadian clock and implications for personalized alterations of corticosterone rhythms in shift work and jet lag. Sci. Rep. 2021, 11, 17929. [Google Scholar] [CrossRef]
- Gu, C.G.; Yang, H.J.; Wang, M. Ratio between sensitive strength to light information and coupling strength affects entrainment range of suprachiasmatic nucleus. Commun. Theor. Phys. 2018, 70, 771–776. [Google Scholar] [CrossRef]
- Weinert, D.; Gubin, D. The impact of physical activity on the circadian system: Benefits for health, performance and wellbeing. Appl. Sci. 2022, 12, 9220. [Google Scholar] [CrossRef]
- Ono, D.; Honma, K.; Honma, S. Roles of neuropeptides, VIP and AVP, in the mammalian central circadian clock. Front. Neurosci. 2021, 15, 650154. [Google Scholar]
- Welsh, D.K.; Takahashi, J.S.; Kay, S.A. Suprachiasmatic Nucleus: Cell Autonomy and Network Properties. Annu. Rev. Physiol. 2010, 72, 551–577. [Google Scholar] [CrossRef]
- Schlaeger, L.; Olejniczak, I.; Lehmann, M.; Schmidt, C.X.; Astiz, M.; Oster, H.; Pilorz, V. Estrogen-mediated coupling via gap junctions in the suprachiasmatic nucleus. Eur. J. Neurosci. 2024, 59, 1723–1742. [Google Scholar] [CrossRef] [PubMed]
- Gonze, D.; Bernard, S.; Waltermann, C.; Kramer, A.; Herzel, H. Spontaneous synchronization of coupled circadian oscillators. Biophys. J. 2005, 89, 120–129. [Google Scholar] [CrossRef] [PubMed]
- Rohling, J.H.T.; Vanderleest, H.T.; Michel, S.; Vansteensel, M.J.; Meijer, J.H. Phase resetting of the mammalian circadian clock relies on a rapid shift of a small population of pacemaker neurons. PLoS ONE 2011, 6, e25437. [Google Scholar] [CrossRef] [PubMed]
- Gu, C.G.; Ramkisoensing, A.; Liu, Z.H.; Meijer, J.H.; Rohling, J.H.T. The proportion of light-responsive neurons determines the limit cycle properties of the suprachiasmatic nucleus. J. Biol. Rhythm. 2014, 29, 16–27. [Google Scholar] [CrossRef]
- Schwartz, M.D.; Cambras, T.; Díez-Noguera, A.; Campuzano, A.; Oda, G.A.; Yamazaki, S.; de la Iglesia, H.O. Coupling between subregional oscillators within the suprachiasmatic nucleus determines free-running period in the rat. J. Biol. Rhythm. 2022, 37, 620–630. [Google Scholar] [CrossRef]
- Myung, J.; Pauls, S.D. Encoding seasonal information in a two-oscillator model of the multi-oscillator circadian clock. Eur. J. Neurosci. 2018, 48, 2718–2727. [Google Scholar] [CrossRef]
- De la Iglesia, H.O.; Cambras, T.; Schwartz, W.J.; Díez-Noguera, A. Forced desynchronization of dual circadian oscillators within the rat suprachiasmatic nucleus. Curr. Biol. 2004, 14, 796–800. [Google Scholar] [CrossRef]
- Tsuno, Y.; Peng, Y.B.; Horike, S.I.; Wang, M.; Matsui, A.; Yamagata, K.; Sugiyama, M.; Nakamura, T.J.; Daikoku, T.; Maejima, T. In vivo recording of suprachiasmatic nucleus dynamics reveals a dominant role of arginine vasopressin neurons in circadian pacesetting. PLoS Biol. 2023, 21, e3002281. [Google Scholar] [CrossRef]
- Schwartz, M.D.; Wotus, C.; Liu, T.C.; Friesen, W.O.; Borjigin, J.; Oda, G.A.; de la Iglesia, H.O. Dissociation of circadian and light inhibition of melatonin release through forced desynchronization in the rat. Proc. Natl. Acad. Sci. USA 2009, 106, 17540–17545. [Google Scholar] [CrossRef]
- Lee, H.S.; Nelms, J.L.; Nguyen, M.; Silver, R.; Lehman, M.N. The eye is necessary for a circadian rhythm in the suprachiasmatic nucleus. Nat. Neurosci. 2003, 6, 111–112. [Google Scholar] [CrossRef]
- VanderLeest, H.T.; Rohling, J.H.T.; Michel, S.; Meijer, J.H. Phase Shifting Capacity of the Circadian Pacemaker Determined by the SCN Neuronal Network Organization. PLoS ONE 2009, 4, e4976. [Google Scholar] [CrossRef] [PubMed]
- Nagano, M.; Ikegami, K.; Minami, Y.; Kanazawa, Y.; Koinuma, S.; Sujino, M.; Shigeyoshi, Y. Slow shift of dead zone after an abrupt shift of the light-dark cycle. Brain Res. 2019, 1714, 73–80. [Google Scholar] [CrossRef] [PubMed]
- Boulos, Z.; Macchi, M.; Terman, M. Twilight transitions promote circadian entrainment to lengthening light-dark cycles. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 1996, 271, R813–R818. [Google Scholar] [CrossRef] [PubMed]
- Boulos, Z.; Macchi, M.M.; Terman, M. Twilights widen the range of photic entrainment in hamsters. J. Biol. Rhythm. 2002, 17, 353–363. [Google Scholar] [CrossRef]
- Fonken, L.K.; Nelson, R.J. The effects of light at night on circadian clocks and metabolism. Endocr. Rev. 2014, 35, 648–670. [Google Scholar] [CrossRef]
- Zheng, W.X.; Gu, C.G.; Yang, H.J.; Rohling, J.H.T. A modeling approach shows the effects of different light-dark schemes on the entrainment ability of the suprachiasmaticnucleus. Nonlinear Dyn. 2023, 111, 12625–12638. [Google Scholar] [CrossRef]
- Madahi, P.G.; Ivan, O.; Adriana, B.; Diana, O.; Carolina, E. Constant light during lactation programs circadian and metabolic systems. Chronobiol. Int. 2018, 35, 1153–1167. [Google Scholar] [CrossRef]
- De la Iglesia, H.O.; Meyer, J.; Carpino, A.; Schwartz, W.J. Antiphase oscillation of the left and right suprachiasmatic nuclei. Science 2000, 290, 799–801. [Google Scholar] [CrossRef]
- Ohta, H.; Yamazaki, S.; McMahon, D.G. Constant light desynchronizes mammalian clock neurons. Nat. Neurosci. 2005, 8, 267–269. [Google Scholar] [CrossRef]
- Leise, T.L.; Goldberg, A.; Michael, J.; Montoya, G.; Solow, S.; Molyneux, P.; Vetrivelan, R.; Harrington, M.E. Recurring circadian disruption alters circadian clock sensitivity to resetting. Eur. J. Neurosci. 2020, 51, 2343–2354. [Google Scholar] [CrossRef] [PubMed]
- Gu, C.G.; Li, J.H.; Zhou, J.; Yang, H.J.; Rohling, J.H.T. Network structure of the master clock is important for its primary function. Front. Physiol. 2021, 12, 678391. [Google Scholar] [CrossRef]
- Pittendrigh, C.S.; Daan, S. A functional analysis of circadian pacemakers in nocturnal rodents. J. Comp. Physiol. 1976, 106, 223. [Google Scholar] [CrossRef]
- Moriya, T.; Yoshinobu, Y.; Kouzu, Y.; Katoh, A.; Gomi, H.; Ikeda, M.; Yoshioka, T.; Itohara, S.; Shibata, S. Involvement of glial fibrillary acidic protein (GFAP) expressed in astroglial cells in circadian rhythm under constant lighting conditions in mice. J. Neurosci. Res. 2000, 60, 212–218. [Google Scholar] [CrossRef]
- Hughes, A.T.L.; Croft, C.L.; Samuels, R.E.; Takumi, T.; Piggins, H.D. Constant light enhances synchrony among circadian clock cells and promotes behavioral rhythms in VPAC2-signaling deficient mice. Sci. Rep. 2015, 5, 14044. [Google Scholar] [CrossRef]
- Abel, J.H.; Meeker, K.; Granados-Fuentes, D.; St John, P.C.; Wang, T.J.; Bales, B.B.; Doyle, F.J.; Herzog, E.D.; Petzold, L.R. Functional network inference ofthe suprachiasmatic nucleus. Proc. Natl. Acad. Sci. USA 2017, 113, 4512–4517. [Google Scholar] [CrossRef]
- McBride, D.; Petzold, L. Model-based inference of a directed network of circadian neurons. J. Biol. Rhythm. 2018, 33, 515–522. [Google Scholar] [CrossRef]
- Gu, C.G.; Gu, X.W.; Wang, P.; Ren, H.G.; Weng, T.F.; Yang, H.J.; Rohling, J.H.T. Disassortative network structure improves the synchronization between neurons in the suprachiasmatic nucleus. J. Biol. Rhythm. 2019, 34, 515–524. [Google Scholar] [CrossRef]
- Vasalou, C.; Herzog, E.D.; Henson, M.A. Small-world network models of intercellular coupling predict enhanced synchronization in the suprachiasmatic nucleus. J. Biol. Rhythm. 2009, 24, 243–254. [Google Scholar] [CrossRef]
- Zheng, W.X.; Gu, C.G.; Yang, H.J.; Rohling, J.H.T. Motif structure for the four subgroups within the suprachiasmatic nuclei affects its entrainment ability. Phys. Rev. E 2022, 105, 014314. [Google Scholar] [CrossRef]
- Zhou, J.; Gu, C.G.; Song, Y.X.; Xu, Y. Free running period affected by network structures of suprachiasmatic nucleus neurons exposed to constant light. Chin. Phys. B 2023, 32, 098701. [Google Scholar] [CrossRef]
- Zheng, W.X.; Gu, C.G.; Xu, Y.; Yang, H.J. Entrainment range affected by the second-order interactions between coupled neuron oscillators in the suprachiasmatic nucleus. Chaos Solitons Fractals 2023, 172, 114051. [Google Scholar] [CrossRef]
- Liu, C.; Weaver, D.R.; Strogatz, S.H.; Reppert, S.M. Cellular Construction of a Circadian Clock: Period Determination in the Suprachiasmatic Nuclei. Cell 1997, 91, 855–860. [Google Scholar] [CrossRef] [PubMed]
- Locke, J.C.W.; Westermark, P.O.; Kramer, A.; Herzel, H. Global parameter search reveals design principles of the mammalian circadian clock. BMC Syst. Biol. 2008, 2, 22. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.B.; Xu, C.; Zheng, Z.G. Phase transition and scaling in Kuramoto model with high-order coupling. Nonlinear Dyn. 2021, 103, 2721–2732. [Google Scholar] [CrossRef]
- Skardal, P.S.; Arenas, A. Higher order interactions in complex networks of phase oscillators promote abrupt synchronization switching. Commun. Phys. 2020, 3, 218. [Google Scholar] [CrossRef]
- Schmal, C.; Myung, J.; Herzel, H.; Bordyugov, G. A theoretical study on seasonality. Front. Neurol. 2015, 6, 94. [Google Scholar] [CrossRef]
- Xu, Y.; Gu, C.G.; Qu, D.Q.; Wang, H.Y.; Rohling, J.H.T. Light-induced synchronization modulation: Enhanced in weak coupling and attenuated in strong coupling among suprachiasmatic nucleus neurons. Phys. Rev. E 2025, 111, 014401. [Google Scholar] [CrossRef]
- Gonze, D. Modeling circadian clocks: From equations to oscillations. Cent. Eur. J. Biol. 2011, 6, 699–711. [Google Scholar] [CrossRef]
- Michel, S.; Marek, R.; vanderLeest, H.T.; vanSteensel, M.J.; Schwartz, W.J.; Colwell, C.S.; Meijer, J.H. Mechanism of bilateral communication in the suprachiasmatic nucleus. J. Neurosci. 2013, 37, 964–971. [Google Scholar] [CrossRef]
- Fernandez, D.C.; Chang, Y.T.; Hattar, S.; Chen, S.K. Architecture of retinal projections to the central circadian pacemaker. Proc. Natl. Acad. Sci. USA 2016, 113, 6047–6052. [Google Scholar] [CrossRef]
- Zhou, J.; Gu, C.G.; Zhu, B.; Yang, H.J.; Rohling, J.H.T. Poincaré model shows how heterogeneity in light sensitivity can alter circadian clock function. Commun. Nonlinear Sci. Numer. Simul. 2022, 111, 106462. [Google Scholar] [CrossRef]
- Rumanova, V.S.; Okuliarova, M.; Zeman, M. Differential Effects of Constant Light and Dim Light at Night on the Circadian Control of Metabolism and Behavior. Int. J. Mol. Sci. 2020, 21, 5478. [Google Scholar] [CrossRef] [PubMed]
- VanderLeest, H.T.; Houben, T.; Michel, S.; Deboer, T.; Albus, H.; Vansteensel, M.J.; Block, G.D.; Meijer, J.H. Seasonal encoding by the circadian pacemaker of the SCN. Curr. Biol. 2007, 17, 468–473. [Google Scholar] [CrossRef] [PubMed]
- Meijer, J.H.; Michel, S.; vanderLeest, H.T.; Rohling, J.H.T. Daily and seasonal adaptation of the circadian clock requires plasticity of the SCN neuronal network. Eur. J. Neurosci. 2010, 32, 2143–2151. [Google Scholar] [CrossRef]
- Ramkisoensing, A.; Gu, C.G.; Gastelaars, H.M.D.V.; Michel, S.; Deboer, T.; Rohling, J.H.T.; Meijer, J.H. Enhanced Phase Resetting in the Synchronized Suprachiasmatic Nucleus Network. J. Biol. Rhythm. 2014, 29, 4–15. [Google Scholar] [CrossRef]
- Gu, C.G.; Tang, M.; Yang, H.J. The synchronization of neuronal oscillators determined by the directed network structure of the suprachiasmatic nucleus under different photoperiods. Sci. Rep. 2016, 6, 28878. [Google Scholar] [CrossRef]
- Colwell, C.S.; Michel, S.; Itri, J.; Rodriguez, W.; Tam, J.; Lelievre, V.; Hu, Z.; Liu, X.; Waschek, J.A. Disrupted circadian rhythms in VIP- and PHI-deficient mice. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 2003, 285, R939–R949. [Google Scholar] [CrossRef]
- Freeman, G.M.; Krock, R.M.; Aton, S.J.; Thaben, P.; Herzog, E.D. GABA networks destabilize genetic oscillations in the circadian pacemaker. Neuron 2013, 78, 799–806. [Google Scholar] [CrossRef]
- Zhou, J.X.; Wang, H.L.; Ouyang, Q. Network rewiring and plasticity promotes synchronization of suprachiasmatic nucleus neurons. Chaos 2022, 32, 023101. [Google Scholar] [CrossRef]
- Zheng, W.X.; Gu, C.G.; Yang, H.J.; Wang, H.Y.; Rohling, J.H.T. Adaptive coupling between neurons widens the entrainment range of the suprachiasmatic nucleus. Phys. Rev. E 2024, 110, 034212. [Google Scholar] [CrossRef]
- Hafner, M.; Koeppl, H.; Gonze, D. Effect of Network Architecture on Synchronization and Entrainment Properties of the Circadian Oscillations in the Suprachiasmatic Nucleus. PLoS Comput. Biol. 2012, 8, e1002419. [Google Scholar] [CrossRef]
- Bodenstein, C.; Gosak, M.; Schuster, S.; Marhl, M.; Perc, M. Modeling the seasonal adaptation of circadian clocks by changes in the network structure of the suprachiasmatic nucleus. PLoS Comput. Biol. 2012, 8, e1002697. [Google Scholar] [CrossRef] [PubMed]
- Šimonka, V.; Fras, M.; Gosaka, M. Stochastic simulation of the circadian rhythmicity in the SCN neuronal network. Physica A 2015, 424, 1–10. [Google Scholar] [CrossRef]
- Ohta, H.; Mitchell, A.C.; McMahon, D.G. Constant light disrupts the developing mouse biological clock. Pediatr. Res. 2006, 60, 304–308. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Aschoff, J. Exogenous and Endogenous Components in Circadianrhythms. Cold Spring Harb. Symp. Quant. Biol. 1960, 25, 11–28. [Google Scholar] [CrossRef] [PubMed]

| Goodwin Model | Kuramoto Model | Poincaré Model | ||
|---|---|---|---|---|
| Motif structure | NA | [50] | [50] | |
| light sensitivity heterogeneity | NA | NA | [13,62] | |
| light waveforms | [37] | [67] | [37] | |
| All-to-all network | coupling strength | [25] | NA | [25,58] |
| adaptive coupling | NA | [71] | NA | |
| NW network | NA | NA | [51] | |
| ER network | NA | NA | [51] | |
| Higher-order interaction network | NA | [52] | NA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Zheng, W.; Gu, C. Model Research on the Influence of the Biological Clock Network Structure on Function Under Light Stimulation. Symmetry 2025, 17, 1418. https://doi.org/10.3390/sym17091418
Feng J, Zheng W, Gu C. Model Research on the Influence of the Biological Clock Network Structure on Function Under Light Stimulation. Symmetry. 2025; 17(9):1418. https://doi.org/10.3390/sym17091418
Chicago/Turabian StyleFeng, Jing, Wenxin Zheng, and Changgui Gu. 2025. "Model Research on the Influence of the Biological Clock Network Structure on Function Under Light Stimulation" Symmetry 17, no. 9: 1418. https://doi.org/10.3390/sym17091418
APA StyleFeng, J., Zheng, W., & Gu, C. (2025). Model Research on the Influence of the Biological Clock Network Structure on Function Under Light Stimulation. Symmetry, 17(9), 1418. https://doi.org/10.3390/sym17091418





