1. Introduction
Matrix fraction descriptions (MFD) are fundamental to the analysis and control of multivariable descriptor systems
, especially under zero initial conditions [
1]. These systems, also referred to as singular systems, differential-algebraic systems, or generalized state-space models, are characterized by algebraic-differential equations involving a possibly singular matrix
[
2]. Unlike standard state-space models, descriptor systems exhibit both differential and algebraic dynamics, leading to finite, infinite dynamic, and infinite non-dynamic modes [
3]. The presence of infinite dynamic modes is often linked with undesired impulsive responses, and thus ensuring regularity and causality becomes essential [
4]. Historically, descriptor systems emerged in the early 1970s, with foundational work by Singh and Liu (1973) and continued developments in modeling constrained physical systems, such as mechanical linkages, electrical networks, and power systems [
5]. Comprehensive treatments can be found in works of [
6,
7,
8], where practical case studies and mathematical properties of descriptor systems are examined. Early studies noted the non-causal nature of descriptor systems when transfer functions are improper, making them useful for modeling spatially varying phenomena such as gravitational or electromagnetic fields. The matrix transfer function captures input–output behavior and fits naturally with frequency-domain methods [
9,
10]. Its form depends strongly on the structure of the system pencil
, whose spectral properties are explored using canonical forms like those of Weierstrass and Kronecker [
11,
12]. These algebraic tools, deeply rooted in matrix polynomial theory [
13], provide a basis for both analysis and controller design in singular models [
14].
Despite their utility, descriptor models introduce significant control-theoretic challenges. Feedback stabilization requires careful handling of the singularity in
and the elimination of impulsive components [
15]. To this end, a range of control strategies have been explored and/or need to be emerged in singular systems, such as eigenstructure assignment, normalization methods, and polynomial interpolation for exact pole placement [
16,
17,
18]. Algebraic approaches leveraging λ-matrices, Jordan pairs, and matrix pencil factorization [
19,
20,
21] have proven especially effective. Moreover, proportional-derivative feedback methods can be adapted to descriptor dynamics [
22], superstabilization using Drazin inverse techniques [
23], and robust solution methods [
24] have broadened the spectrum of feasible feedback laws. Model reduction via cross-Gramian formulations [
25] and Hamiltonian representations has further contributed to structure-preserving control [
26]. In large-scale systems, reachability and observability properties are essential for ensuring controllability under algebraic constraints [
27]. These have been studied both in continuous and discrete-time frameworks, with recent extensions to fractional-order systems and actuator failures [
28,
29,
30]. Decentralized approaches for interconnected descriptor systems also enable scalable implementations [
9]. Descriptor systems admit multiple representations depending on state variable choice. This flexibility, rooted in algebraic equivalence, means different state-space forms can describe the same physical behavior [
31,
32,
33,
34]. These results enable a systematic parameterization of the static state feedback gain matrix, extending classical finite eigenstructure assignment to include both finite and infinite Jordan pair control [
35]. A robust design framework must therefore account for this variability and preserve internal structure.
Descriptor systems pose fundamental challenges due to singular pencils, impulsive modes, and the difficulty of deriving tractable transfer function representations. Existing methods often rely on indirect linearizations or partial formulations, which obscure structure and become computationally expensive in high dimensions. Recent advances in matrix polynomial theory—such as the theory of linearization [
36], interpolation methods [
37], recursive inversion techniques [
38], λ-matrix factorization [
39], and robust control [
40,
41]—have improved the analysis but remain fragmented. Applications in electro-mechanical systems further highlight the need for a unified approach [
42,
43,
44]. In this work, we address these gaps by constructing the MFD directly from descriptor equations, ensuring both structural transparency and analytical tractability.
The main contribution of this paper lies in bridging the classical MFD formalism with descriptor systems using matrix polynomial theory. Specifically, we propose:
A novel closed-form MFD derived directly from the pencil under state feedback, overcoming limitations in existing indirect or partial formulations.
A novel state feedback design that will assign a desired finite Jordan pair.
A new normalization law that transforms descriptor systems into a structured form suitable for analysis and control via polynomial methods.
This paper is organized as follows:
Section 2 presents essential mathematical preliminaries on matrix polynomials.
Section 3 reviews the descriptor system framework and its structural properties. In this part, we analyze the feedback control via some modern control theory.
Section 4 introduces the proposed closed-form feedback control and normalization method, along with numerical examples. Finally,
Section 5 concludes the paper with a summary and discussion of future extensions.
2. Matrix Polynomials Theory
The matrix polynomial problem can be cast into a block eigenvalue formulation as follows. Given a matrix of order , find a matrix of order , such that , where is a matrix of full rank. Some of the implications of this new block eigenvalue formulation are considered.
Definition 1. ([
13,
17]
) Let be a matrix polynomial of degree .
The matrix polynomial is called unimodular if
;
,
It is called regular (or nonsingular) if , for all or equivalently, if . Otherwise, it is referred to as singular.
The roots of the characteristic polynomial are termed the (finite) eigenvalues of .
A rational matrix is called biproper if
where the variable denotes the ring of polynomials, while
denotes the field of rational functions in
.
Definition 2. ([
8]
) The reversal of the matrix polynomial is also called the dual of and defined bywhere is referred to as the leading coefficient matrix, and as the trailing coefficient matrix of . The matrix polynomial is said to be monic if . The rank
is defined as:
.
Infinite eigenvalues of a matrix polynomial can be analyzed via its reversal, , since the infinite eigenvalues of correspond to the zero eigenvalues of . When the degree , the polynomial eigenvalue problem (PEP) reduces to the classical generalized eigenvalue problem (GEP) of the form . Additionally, a general matrix polynomial is said to be non-monic when its leading coefficient matrix is singular (i.e., is called non-monic if ).
2.1. Invariant Pairs
Invariant pairs
with
are a generalization of eigenpairs for matrix polynomials (as introduced by C. Effenberger) [
28]. They provide a unified theoretical framework for computing multiple eigenvalue-eigenvector pairs of a matrix polynomial. From a numerical standpoint, they offer enhanced stability compared to individual eigenpair computations, especially in the presence of multiple or closely spaced eigenvalues. (see the work of D. Kressner) [
19]. The notion of invariant pairs can also be applied to more general nonlinear problems, although here we will limit our presentation to matrix polynomials.
Definition 3. ([
1,
31,
32]
) Let be an
matrix polynomial. A pair
,
, is called an invariant pair if it satisfies the relation: where ,
and is an integer such that:
.
Infinite eigenvalues can be addressed by formulating invariant pairs for the reversal polynomial (1). When a matrix polynomial possesses both zero and infinite eigenvalues, separate invariant pairs must be constructed—one associated with the original matrix polynomial and another with its reversal.
Definition 4. ([
31,
45]
) A pair is called minimal if there is such that:has full rank. The smallest such is called minimality index of .
The invariant pairs is said to be minimal if Definition 5. ([
19]
) An invariant pair of degree is said to be simple if it is minimal, and the algebraic multiplicities of the eigenvalues of .
Eigenvectors associated with multiple eigenvalues are inherently sensitive to perturbations; even minor variations in the matrix can result in instability or the disappearance of certain eigenvectors. In contrast, invariant pairs provide a more robust and reliable theoretical and numerical framework for accurately computing multiple eigenpairs of a matrix polynomial [
24].
Remark 1. There is a strong connection between invariant pairs and the concept of standard pairs introduced in [
31]
, particularly in relation to Jordan pairs. When an invariant pair includes an infinity as an eigenvalues then the Jordan pair will be composed of two main parts named the finite and infinite Jordan pairs, and denoted by and such that Polynomial eigenpairs and invariant pairs can also be defined in terms of a contour integral. Indeed, an equivalent representation for (2) is the following.
Proposition 1. ([
24]
) A pair is an invariant pair if and only if satisfies the relation:
where is a closed contour enclosing the spectrum of . This contour-integral formulation allows computing invariant pairs for eigenvalues within a specific region of the complex plane. 2.2. Matrix Solvents
Now, we study the matrix solvent problem as a particular case of the invariant pair problem, and we apply to solvents some results we have obtained for invariant pairs.
Definition 6. ([
13,
18]
) Let be an matrix polynomial. A matrix is called a (right) solvent for if satisfies: . The connection between the eigenvalues of the matrix polynomial
and its solvents is established in [
32]. A corollary of the generalized Bézout theorem states that if
is a solvent of
, then:
where
is a matrix polynomial of degree
. Consequently, any finite eigenpair of the matrix
corresponds to a finite eigenpair of the original matrix polynomial
.
Proposition 2. ([
13,
17]
) A matrix is a right solvent of if and only iffor any closed contour that encloses the spectrum of .
Theorem 1. ([
18,
20]
) Suppose has distinct eigenvalues with , and that the corresponding set of p eigenvectors satisfies the Haar condition (every subset of m of them is linearly independent). Then there are at least different solvents of , and exactly this many if , which are given bywhere the eigenpairs are chosen among the eigenpairs .
Theorem 2. ([
38,
39]
) Let be a matrix polynomial and consider an invariant pair of (sometimes called admissible pairs). If the matrix has size (i.e., and is invertible, then satisfies ) is a matrix solvent of .
Proof. As
is an invariant pair of
, we have:
Since
is invertible, we can post-multiply by
. Then we get:
Therefore, is a matrix solvent of . □
Remark 2. ([
21]
) Since is a root of which entails that is a root of , the matrix is a solvent to the reversal matrix polynomial .
Example 1. Given non-monic matrix polynomial such that:
Since
is nonsingular then the latent structure of the regular non-monic matrix polynomial
can be obtained using the following MATLAB command
and those of the reversal matrix polynomial
can be obtained using
. There are six finite eigenpairs
for
with
and:
and
. The solvents of the reversal matrix polynomial
are
Notice that, those obtained three solvents satisfy the matrix equation:
for
. The solvents of
are the inverse of the
solvents (i.e.,
) therefor:
but now only for
. Furthermore, if
is a finite latent root of
, then
is a finite latent root of
. If
has a zero latent root (
is singular), then
is said to have an unbounded latent root. A lambda-matrix
is said to be degenerate (i.e., singular) if
for all
. This can only occur if
and
are singular [
13,
17,
21].
2.3. Linearization of Matrix Polynomials
For a matrix polynomial eigenvalue problem of degree , the linearization method involves constructing an matrix pencil , that shares the same eigenvalues as . This will reduce the PEP to a standard linear eigenvalue problem, which can be solved using classical techniques such as the QZ algorithm.
Definition 7. ([
31,
32]
) Let be an matrix polynomial of degree .
A pencil with ,
is called linearization of if there exist unimodular matrix polynomials ,
such that:
The linearization is not unique (see B. Bekhiti [
13], K. Hariche [
17]). Most of the linearizations used in practice are of the companion forms
with
The eigenvalues of
coincide with those of
(including multiplicities). There is a
one-to-one correspondence between the eigenvectors of
and
under appropriate transformation. The
companion form is the most classical linearization. Linearizations of matrix polynomials transform them into an equivalent matrix pencil, preserving all finite eigenvalues and (possibly) the infinite ones. Some structured linearizations (e.g., Fiedler) maintain additional properties like symmetry or sparsity. Particularly useful are those linearizations that preserve both the finite and infinite eigenstructure, ensuring an accurate spectral equivalence with the original polynomial [
13,
18,
24].
2.4. The Spectral Data (Finite and Infinite)
When the leading coefficient matrix is singular then the degree of with and has finite eigenvalues, to which we add infinite eigenvalues. Infinite eigenvalues correspond to the zero eigenvalues of the reverse polynomial .
Lemma 1. ([
1,
14]
) If ,
are the sum of degrees of the finite and infinite elementary divisors of a general matrix polynomial respectively, then .
The finite Jordan pair (see Gohberg I, Chapter 7 [
31]) of
corresponding to the zero structure at
, is defined as the infinity Jordan pair
, of
. As a result, the finite and the infinity Jordan pairs of
satisfy the following properties:
Furthermore, the structure of the infinity Jordan pair of
is closely related (see Vardulakis in [
8]) to its Smith-McMillan form at
. Particularly,
Theorem 3. ([
1,
14,
32]
) Let and
be the finite and infinite Jordan pairs of ,
with ,
,
,
and .
These pairs satisfy the following properties:
has a zero at with multiplicity .
In addition, a realization of is given by A matrix polynomial
has no eigenvalue at infinity if and only if the leading coefficient
is nonsingular—this is always the case for monic polynomials where
. Conversely, if the trailing coefficient
is singular, then
has a zero eigenvalue, and this translates to an eigenvalue at infinity for
. The multiplicity of the eigenvalue at infinity is then defined via the zero eigenvalue of
. For a finite eigenvalue
,
becomes rank-deficient, and the associated nonzero vectors
satisfying
form the (right) eigenvectors. The geometric multiplicity is
, and the algebraic multiplicity is the multiplicity of
as a root of
. In the case of multiple eigenvalues, generalized eigenvectors arise via Jordan chains. When
is singular, the Jordan structure decomposes into a finite part
for finite eigenvalues and an infinite part
, where
contains Jordan blocks associated with the eigenvalue at infinity [
1,
8,
14].
Theorem 4. ([
1,
31]
) Let be a regular matrix polynomial and let and be its finite and infinite Jordan pairs, respectively.
Then the pair is a decomposable pair for .
Example 2. Given the following finite and infinite Jordan pairs of a regular matrix polynomial , construct its coefficients . The pair
is a decomposable pair means that:
In more compact form we write
. The coefficients
of the regular non-monic matrix polynomial are constructed from the null space of
:
. The coefficients
are:
2.5. Generalized Eigenvalue Problem and Degenerate Matrix Polynomials
A vector
, with
, is called an eigenvector of the ordered pair of matrices
if there exist a nonzero complex scalars
and
such that
The scalars and are generally not unique, but their ratio is well-defined (except in the singular case , which leads to a singular situation). If , Equation (13) simplifies to the generalized eigenvalue problem where is the eigenvalue associated with the eigenvector . If and , then the eigenvalue is considered infinite, and the pair is said to have an infinite eigenvalue (the eigenvalue of the ordered pair associated with is ). When , this framework reduces to the classical eigenvalue problem.
Proposition 3. ([
4,
5]
) Let be an ordered pair of matrices,
and let . Then the following equivalences hold: - 1.
The scalar is an eigenvalue of .
- 2.
Infinity is an eigenvalue of .
- 3.
The pair is singular.
When the matrix
is nonsingular, the eigenvalues of the matrix pair
are identical to those of
and
. In this context, if
is an eigenvector of the pair associated with eigenvalue
, then
is also an eigenvector of
, while
becomes an eigenvector of
, both corresponding to the same eigenvalue
. The expression
is commonly referred to as a matrix pencil, and the terms
matrix pencil and
matrix pair are often used interchangeably. A scalar
is said to be an eigenvalue of the pair
if the matrix
is singular, i.e.,
which defines the characteristic equation of the pair. The function
is a polynomial in
of degree less than or equal to
, known as the characteristic polynomial. However, it may happen that
for all
(i.e.,
is identically zero), such as when a nonzero vector
satisfies
. In such a case, the pencil
is singular for all
, and every complex number is an eigenvalue. The pair is then called singular. Otherwise, if
(i.e., is not identically zeros), the pair is classified as regular pair [
3,
25].
Theorem 5. ([
8,
19]
) If the pair is singular (i.e., ) then this pair of matrices is devisable on the left or the right by singular square matrix respectively. Lemma 2. ([
13,
21]
) Two matrix polynomials and are related by the left transformation or by the right transformation with and , then they satisfy the following statements:
If or and have the same set of solvents.
If or is a degenerate -matrix with all singular .
If or are solvents of but not vice versa.
Degenerate non-monic matrix polynomial may have complete set of finite solvents.
Proof. Let us prove the last statement in the lemma. Assume that the
degree non-monic matrix polynomial
has a complete set of solvents
with
then:
Collecting these set of equations in a compact matrix form we get
with
,
are given in Equation (10) and
is the block Vandermond matrix,
is the block diagonal matrix
Finally we notice that the pair matrix
are related by the following transformation
or equivalently
Since the matrix is singular than for all , therefore the -matrix is degenerate and the fourth statement is proved. □
Example 3. To verify the fourth statement, let us consider the following 2nd order non-monic matrix polynomial with the next coefficients.
One can check that
and
are complete set of finite solvents of
even if
2.6. Higher Order System Described by Matrix Differential Equations
We consider the linear time-invariant dynamical system of the form:
where
is the input control,
is the output measurement,
is the state function and
,
,
,
are the coefficient matrices.
Applying the Laplace transformation to (17) yields the
. If the leading coefficient matrix
is nonsingular (
) then the associated matrix polynomial
is said to be monic else we say that
is non-monic matrix polynomial. The eigenvalue of
is complex number
such that
in which case the left null space of
is called the left eigenspace, the right null space of
is called the right eigenspace, each vector in the left eigenspace is called left eigenvector and each vector in the right eigenspace is called right eigenvector corresponding to
[
13,
18].
Controllability of Higher Order Systems: The state-space system in (17) or the tuple
is called controllable if it is possible to derive the system into any desired state at any given time by the proper selection of the input. This is fundamentally characterized by a rank condition [
27].
Observability of Higher Order Systems: A linear autonomous system is considered observable if each distinct initial condition leads to a unique output trajectory, allowing the reconstruction of the initial state from output measurements. In contrast to controllability (which is concerned with the set of reachable states from a given input) observability addresses the ability to infer the system’s internal state based solely on external outputs. Similarly, this is also characterized by a rank condition
for observability is analogous to (18) [
19,
29].
Stabilizability of Higher Order Systems: A system described by a general state-space realization (17) is stabilizable if it is possible to design an input that ensures the state converges to zero asymptotically, regardless of the initial condition. Although controllability guarantees stabilizability, the reverse is not necessarily true [
13,
27]. Verifying stabilizability typically reduces to checking a certain conditions.
This condition mirrors the controllability criterion, with the distinction that the rank test is required only over the closed right half of the complex plane.
In discrete-time systems, the stability depends on the moduli of the eigenvalues of the associated
, not their real parts. The system is stable if all eigenvalues lie strictly inside the unit circle, i.e., the
spectral radius of
is less than one.
This spectral radius
determines the asymptotic decay rate of the system [
8,
24].
The equivalent characterizations of controllability and observability in discrete-time systems mirror those of the continuous case. However, for stabilizability, the rank conditions must be verified on or outside the unit circle.
Without loss of generality, the rank tests can be equivalently formulated by replacing the matrix polynomial
with the linear pencil
, and the input matrix
with the structured matrix
, see [
27].
Robustness of Higher Order Systems: Since state-space models often approximate complex systems affected by uncertainties, it is essential that fundamental properties remain robust under small perturbations [
5,
24]. One way to quantify this robustness is through the
distance to stability, defined as follows
where
,
. The vector
consists of nonnegative scalers not all zero.
The vector
is introduced to restrict and scale perturbations across selected coefficient matrices. Setting certain
excludes those terms from perturbation, while choosing
allows for relative perturbations. Let
and
denote the stable and unstable regions, respectively, with boundary
. Then, the distance to instability is
with
and
. The resulting optimization task corresponds to a structured singular value problem, allowing the final expression to be simplified as follows.
where
.
3. Descriptor Systems in Modern Control Theory
Descriptor linear systems form a fundamental branch within modern control theory and have gained significant traction over the past few decades. Despite the theoretical depth and wide applicability of the subject, only a limited number of comprehensive references exist, notably the works of Campbell [
2] and Liyi Dai [
3]. Such systems naturally arise in diverse disciplines including power grids, electrical circuits, aerospace systems, chemical processes, socioeconomic modeling, biological networks, and time-series analysis. In particular, many electrical and dynamic network models are best represented by descriptor systems. In this work, we focus on linear differential-algebraic equations with constant coefficients, expressed in the form:
with
and
, and for linear discrete time descriptor system we have
where
is the state;
is the control input,
is the output. The matrix
may be singular, we shall assume that
.
,
and
are known real constant matrices with appropriate dimensions.
3.1. Structural Properties of Descriptor Systems
The properties of systems (26) and (27) are well understood for more than one century, in particular by the work of Weierstra
β 1868 and Kronecker (1890) [
11,
12]. The reason is that Equations (26) and (27) can be treated by purely algebraic techniques. In the following, we describe the main aspects of this approach.
Lemma 3. ([
3,
25]
) A descriptor system is said to be completely controllable if and only if: - ■
for all finit and
A descriptor system is said to be completely observable if and only if:
- ■
for all finit and
We shall assume that . Also we assume that , and are known real constant matrices with appropriate dimensions. For the sake of simplicity, we use to denote the descriptor system in (26) and (27). We define the generalized spectral abscissa of the pair as . For discrete time case we have and the pair is said to be stable if .
Definition 8. ([
4,
7,
16]
) The pair is said to be regular if is not identically zero. The pair is said to be impulse-free if .
The pair is said to be stable if all the roots of have negative real parts. The pair is said to be admissible if it is regular, impulse-free and stable.
Lemma 4. ([
1,
2,
3,
4,
8]
) The pair is regular if and only if there exist two nonsingular matrices and such that:
where is a nilpotent matrix which satisfy the following properties ,
and .
This is called: the Slow-Fast or the Weierstrass-Kronecker canonical decompositions.
Lemma 5. ([
3,
5]
) Suppose that the pair is regular, and two nonsingular matrices are found such that slow-fast decomposition holds, then we have: The pair is impulse-free if and only if . And is stable if and only if .
The pair is admissible if and only if and .
Theorem 6. ([
25]
) Given the linear descriptor system , , and is regular, then there exist two nonsingular matrices and such thatwhere ,
and the matrix is nilpotent.
According to Theorem 5, the linear descriptor system (26) can be decomposed into the following systems:
And the output systems is given by . This system is called the standard decomposition form. The controllability matrix of linear descriptor system related to the slow and fast subsystems are given by and , respectively.
Theorem 7. ([
2,
4]
) The regular linear descriptor system is completely controllable if and only if where is the external direct sum of two linear spaces of vectors and .
The slow dynamics subsystem is controllable if and only if or equivalently for all finit . The fast dynamics subsystem is controllable if and only if or equivalently .
The linear descriptor system is completely controllable if and only if both its slow and fast sub systems are both controllable. The observability matrices of slow and fast subsystems of linear descriptor system are given by
and
, respectively.
Theorem 8. ([
3]
) The regular linear descriptor system is completely observable if and only if with .
The slow subsystem is observable if and only if or equivalently for all finit .
The fast dynamics subsystem is controllable if and only if or equivalently .
We now present the admissibility condition using Linear Matrix Inequalities (LMIs), without requiring matrix decomposition. To proceed, we first introduce key preliminary results needed for the analysis.
Lemma 6. ([
10]
) Given any real square matrix with appropriate dimensions. The matrix measure defined as has the properties. We are now ready to present a necessary and sufficient condition for the admissibility of the descriptor system given in (26) and (27), formulated in terms of LMIs. While a similar condition was reported in [
46], we provide an alternative derivation here.
Theorem 9. ([
4,
5]
) The pair is admissible if and only if there exists a matrix such thatthe pair is admissible if and only if there exists a matrix such thatfor discrete time case the pair is admissible if and only if there exists a matrix such that and .
In this case, the matrix is nonsingular.
Theorem 10. ([
5]
) The pair is admissible if and only if there exist matrices and such thatwhere is any matrix with full column rank and satisfies .
For discrete time case the pair is admissible if and only if there exist matrices and such thatwhere is any matrix with full column rank and satisfies .
Given the fundamental role of input-output transmission zeros in system stability and their intrinsic connection to the system’s characteristic roots, it is both relevant and necessary to examine them thoroughly.
Definition 9. Consider the square descriptor linear system. Any finite satisfying is called an input transmission zero of the system, and any finite satisfying is called an output transmission zero of the system.
Proposition 4. ([
4,
5]
) The finite poles of a square descriptor linear system coincide with its input (output) transmission zeros. Furthermore, the admissibility of a continuous-time descriptor system is closely linked to a class of generalized Lyapunov matrix equations, typically expressed in the following form:where .
Theorem 11. ([
5,
16]
) Let be regular. Then the following hold: - 1.
If there exist
and
satisfying (34), then is admissible.
- 2.
If
is admissible, then for each
there exists satisfying (34).
A stability condition for continuous-time linear descriptor systems (26) was established by Lewis F.L. [
7,
16], using a generalized Lyapunov matrix equation of the form
, where
represents the output measurement matrix.
3.2. Feedback Design in Descriptor Linear Systems
Controlling a system involves modifying its dynamics via a controller to ensure it behaves according to specified objectives. As such, the design of an appropriate controller is fundamental. To enable real-time adaptation, most controllers are implemented using feedback configurations.
- ➢
Static Feedback: The simplest form of static state feedback of the system (26) takes the form
, where
is the feedback gain matrix to be designed, and,
is an external input [
38,
39]. When this controller is applied, the system dynamics are modified accordingly, leading to a closed-loop system
with
,
. This resulting system (35) is referred to as the closed-loop system under state feedback. The feedback matrix
must be designed to ensure the closed-loop system satisfies specific performance and stability requirements.
- ➢
Derivative Feedback: A pure generalized derivative feedback law can be formulated as
where
denotes the derivative feedback gain matrix [
15,
22]. Applying this control law yields the closed-loop dynamics:
with
, and
.
- ➢
P-D Feedback: A general feedback strategy for descriptor systems involves both state and derivative components, and is given by
.
and
are two parameter matrices to be designed, and are often called the proportional and derivative feedback gain matrices [
13].
- ➢
Dynamic Feedback: A generic dynamical compensator for linear descriptor system is represented in MFD as
, or in state equation
where
is the controller state. If the matrix
is square and nonsingular (implying
is a monic matrix polynomial) the compensator is termed a normal dynamical compensator. Otherwise, it is referred to as a descriptor dynamical compensator [
18].
- ➢
Feedback via Lyapunov Method: The stabilizing controller design can be formulated as a convex optimization problem characterized by linear matrix inequalities (LMI) [
46].
Now, we first consider the design of a state feedback controller for continuous descriptor systems such that the closed-loop system is admissible. Then the design of dynamic output feedback controllers is investigated.
Theorem 12. ([
5]
) Consider the continuous descriptor system. There exists a state feedback controller such that the closed-loop system is admissible if and only if there exist matrices , and such thatwhere is any matrix with full column rank and satisfies . In this case, we can assume that the matrix is nonsingular, then a stabilizing state feedback controller can be chosen as .
Now, we present the results of the stabilizing discrete descriptor systems. The class of linear discrete descriptor systems to be considered is
. For the discrete-time descriptor system, we assume that all the state variables are available for state feedback, and consider the following state feedback controller:
,
. The purpose of the stabilization problem is the design of a state feedback controller such that the closed loop system is admissible [
8,
9,
20].
Theorem 13. ([
4,
5]
) Consider the discrete-time descriptor system. There exists a state feedback controller such that the closed-loop system is admissible if and only if there exist a scalar , matrices , such thatwhere is any matrix with full column rank and satisfies . In this case the stabilizing state feedback controller is .
Under the controllability/admissibility conditions of Theorems 12 and 13, Algorithm 1 constructs
from the desired block spectral factors, so the closed loop satisfies regularity and stability, and (when combined with
Section 4.3) becomes impulse-free by normalization.
4. The Proposed State Feedback Control Design Procedure
Given a large scale MIMO descriptor system of the form , and where is the state, is the control input, is the output. The matrix may be singular . , , and are known real constant matrices with an appropriate dimensions. For the sake of simplicity, sometimes we use to denote the descriptor system.
Assumptions 1. Let we assume that: (i) and be an integer numbers. (ii) . (iii) The triple is completely controllable.
Problem 1. Let matrices and satisfy Assumption 1 find a parameterization for all the matrices satisfying: and such that and .
In other words, characterize the set
where
denotes the spectrum of
and
stands for the desired matrix.
4.1. Matrix Fraction Description from State Space
Consider now the system described by matrices
then we have
Now, since
is related to the output, and
, so it is always possible to write:
for some polynomial matrix
.
We arrive the following final matrix equation:
where
and
Expanding Equation (40), gives:
with the boundary conditions
and
. From Equation (41) solving from the above with back substitutions we obtain:
where the operator
is the Kronecker product and
Key properties of the non-monic matrix polynomial in the context of descriptor systems are summarized below, including its eigenstructure, factorizations, and relations to system pencils.
- ■
The number of finite eigenvalues of the non-monic matrix polynomial is given by: .
- ■
The numerator matrix can be written as or where stands for the pseudo inverse.
- ■
The finite eigenvalues of the non-monic matrix polynomial are the roots: or equivalently .
- ■
Applying the Schur determinant formula, to a block-structured pencil, one obtains the identity .
- ■
The non-monic -matrix can be factorized as a product of linear factors so where all the eigenvalues of ( for ) are an eigenvalues of and roots of are also an eigenvalues of . However, it is important to note that the eigenvalues of are not necessarily eigenvalues of .
- ■
If is a non-monic then can be factorized into with is any general matrix polynomial. All block roots of are also a block roots of , but not all eigenvalues of are eigenvalues of .
- ■
If is nonsingular matrix then, the eigenvalues of and will coincides.
It is well known that the state-space representation of a descriptor system is not unique, owing to the flexibility in the choice of the state vector. In conventional linear systems, this non-uniqueness is captured by the notion of algebraic equivalence, typically expressed through similarity transformations between system matrices [
13,
18]. For linear descriptor systems, a similar rationale applies; however, the broader structure of such systems necessitates a more general concept known as restricted system equivalence. Unlike normal systems, where equivalence is established via a single similarity matrix, descriptor system equivalence involves two nonsingular transformation matrices,
and
, acting on both sides of the system equations.
with
and
.
Facts on those Obtained Structured Matrix Equations: From the above equations we have , , , and where: the operator denote the block companion-like matrix with on the diagonal and on the super-diagonal.
and
If then is a solution of the matrix equation
4.2. State Feedback Controller Design
In this section, we shall deal with the stabilization problem for descriptor systems. The purpose is the design of controllers such that the closed-loop system is regular, stable and impulse-free (in the continuous case) or causal (in the discrete case). The objectives in this section are to design a state feedback control
, or obtaining a gain matrix
in order to relocate the original admissible pair to a desired location. Consider the descriptor system governed in the Laplace domain by the closed-loop equation:
where
is the state feedback gain matrix. The closed-loop system matrix is then:
. Let
and
be the left and right basis transformation matrices such that the system is expressed in a transformed coordinate system as:
. This framework give us:
Denoting
, it follows that
, and using
, the transformed gain matrix can be explicitly computed as
. As previously discussed, the transformed matrices
and
admit structured decompositions inherited from the block companion form of the descriptor matrix polynomial. Consequently, the feedback gain can be explicitly recovered from the difference between their corresponding lower block components:
Therefore,
. The above derivation is summarized in the Algorithm 1.
| Algorithm 1: Feedback Gain Computation via Matrix Fraction Description (MFD) |
Input:
Assumption: | possibly singular (descriptor) Assume that all states are available and measurable.
|
Procedure:
- ➢
Obtain the MFD from the general state space representation using the equation - ➢
using block spectral factors such that are block spectral factors correspond to finite eigenvalues and is the block spectral factor which satisfies for infinite eigenvalues . - ➢
Construct the feedback gain matrix - ➢
Find the left and right transformations and by solving the matrix equations: - ➢
Recover the feedback gain in the original basis using .
Output: |
Example 4. Consider the following linear descriptor system (chemical reactor model) parameterized by the next matrices as shown below Now we compute the matrix
according to (42) we get the following full rank matrix
Let us denote
, then the matrix fraction description of the corresponding descriptor system can be obtained easily using the following formula
The numerator matrix coefficients are obtained from the following matrix equation:
. In MATLAB language we can write
The canonical state equation of this descriptor system is
,
,
,
,
. The characteristic non-monic matrix polynomial corresponding to this linear descriptor system is given by
, our objectives here are to design stabilizing state feedback gain matrix meeting a desired performance. The desired non-monic matrix polynomial is
expand the last matrix equation and equalize the same power terms we get:
,
and
. The matrices
are called spectral factors of
, and
The desired non-monic matrix polynomial
contains
finite eigenvalues, the desired eigenvalues to be assigned to this descriptor system are
.
This leads to the following values
and
. Numerical application gives the following result
Now, apply the control input
we obtain the closed loop non-monic matrix polynomial
this means that
and
or in more compact form
To obtain this state feedback gain matrix in the original base we should find the left and right similarity transformations and
- ■
- ■
- ■
Solving this last three matrix equations we obtain (i.e., assuming that
is nonsingular):
and
, so
The general state feedback gain matrix is
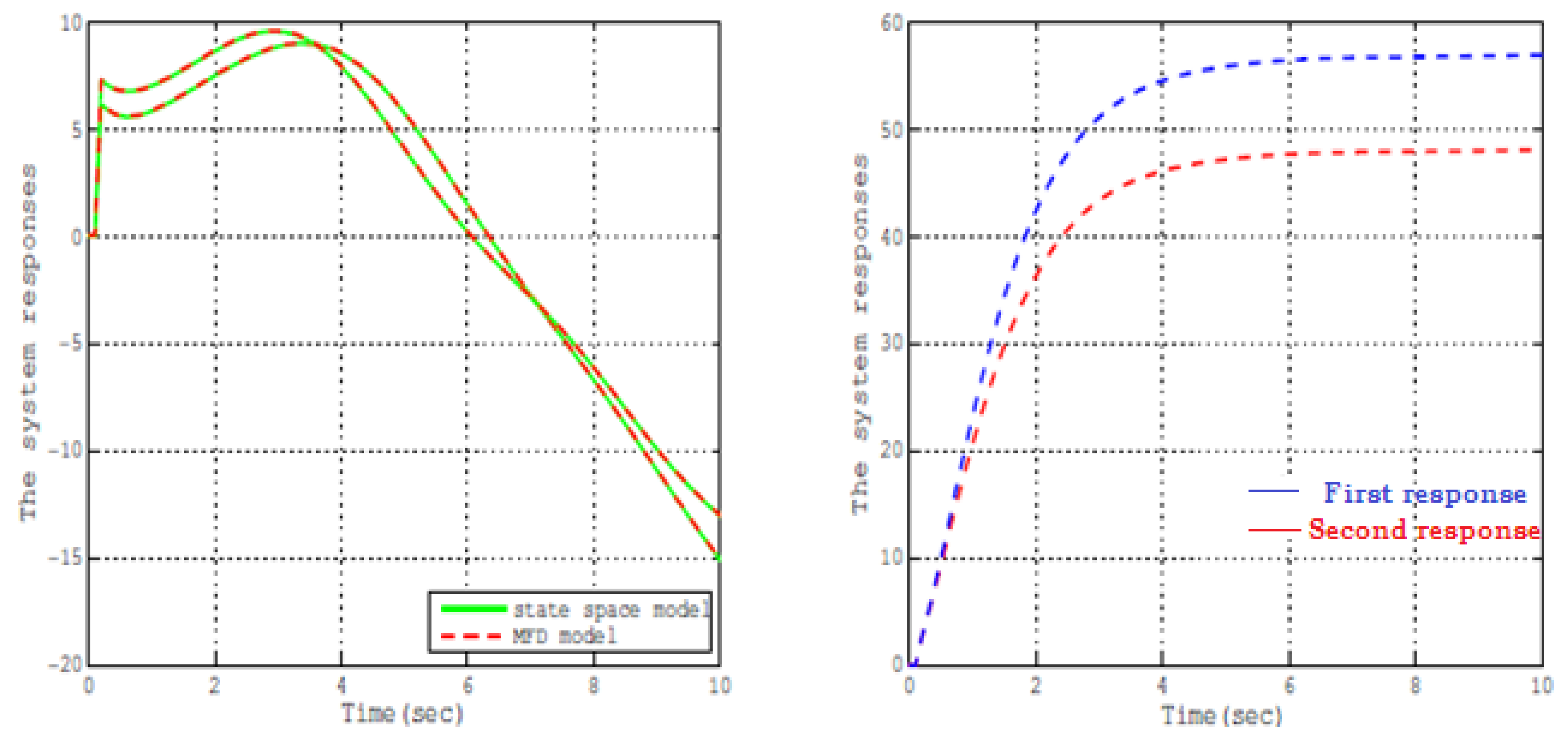
Figure 1 illustrates time response of both open loop and stabilized closed-loop descriptor system under the proposed state feedback.
The results demonstrate the effectiveness of the proposed state feedback design and matrix fraction description in stabilizing a high-dimensional MIMO descriptor system. The assigned eigenstructure successfully regulates both finite and infinite modes, transforming the system into a regular, impulse-free form. As shown in
Figure 1, the closed-loop time response exhibits smooth convergence across all channels, with transient states settling within approximately
and no observable impulsive behavior, confirming causality and stability. The trajectories remain bounded and well-behaved, validating the theoretical feedback law and illustrating the practicality of the algebraic formulation in managing descriptor dynamics with structural singularities.
4.3. The Proposed Block Pole Assignment and Normalization
A descriptor linear system represented as in (26) is termed normal when it is square and the matrix has full rank, i.e., . Normalization involves designing a control law that ensures the resulting closed-loop system attains this normal property. As with regularization, the normalization problems include the following:
- ■
Normalizability analysis: This step involves determining whether a given descriptor linear system can be rendered normal through a specified class of controllers [
4].
- ■
Normalizing controller design: Once normalizability is established, the next step is to characterize all admissible controllers that render the closed-loop system normal. The normalization problem is a special case of dynamical order assignment: by setting the desired order
equal to the system order
, assigning a closed-loop order becomes equivalent to normalization. Hence, results from dynamical order assignment apply directly to normalization [
4,
5].
Let us consider the descriptor system where is the state vector, is the control vector, and are known real coefficient matrices. Assume, without loss of generality, that , and . By applying the following full-state derivative feedback control law the dynamics of the closed loop system evolves into the form or .
Definition 10. ([
5,
16]
) A positive integer is said to be a dynamical order assignable to the descriptor system or it is said to be a dynamical order assignable to the pair , via
full-state derivative feedback, if there exists a feedback matrix such that the rank condition holds. In this context, is also referred to as an allowable closed-loop order. The collection of all matrices that achieve this order forms the set:
with this notion, we now present a result that characterizes the set of all possible assignable dynamical orders for the open-loop system. Theorem 14. ([
2,
3,
25]
) Let and be fixed real matrices, and defineThen,
is an allowable dynamical order assignable to the system by the full-state derivative feedback if and only if .
In normal linear systems, exactly finite poles exist, ensuring the absence of infinite eigenvalues and avoiding impulsive behavior. For descriptor systems, this property can be recovered through derivative feedback: by selecting so that the effective mass matrix becomes full rank, algebraic constraints are moved into dynamic ones, and all poles are shifted to finite locations. Once finite, the MFD is regular, allowing the use of standard frequency-domain tools. Our block-construction (Theorem 15) ensures this normalization can be achieved while preserving structure and enabling subsequent finite pole placement using classical methods of standard linear system theory.
Theorem 15. ([
4,
5]
) The system is normalizable if and only if and is dual normalizable if and only if .
Corollary 1. ([
4,
29]
) A linear descriptor system is normalizable if and only if there exist a full state derivative feedback gain matrix such that .
Assumptions 2. Let we assume that
- 1.
The pair is normalizable i.e.,
- 2.
is an integer with and is the number of inputs
- 3.
The pair is block controllable with controllability index i.e., the matrix has full rank. For more detail see ([13,17]).
Problem 2. [Block poles assignment] Let matrices and satisfy Assumption (2) determine a parameterization for all the matrices such that the matrix is nonsingular . Equivalently, characterize the set Our development in this section is based on the arbitrary block poles assignment method in order to remove the singularity of the descriptor system. To solve the second problem, we need to present some basic and necessary matters in a brief form.
Definition 11. ([
36,
37]
) Let
be a monic matrix polynomial with right solvents of order (i.e.,
is a right divisor of and
isn’t).
Assume that then the generalized block Vandermonde matrix Theorem 16. Given a linear descriptor system and and satisfying Assumption (2), for an arbitrary set of square matrices with non-zeros eigenvalues, a general form for all the feedback gain matrices satisfying Equation (47)(i.e., )
is given as followsWith and is the block Vandermonde matrix.
Proof. The objective is to find an appropriate gain matrix such that
or in more structured form
, that is:
. But we know that
and
and in general base we have
so
. From the other side we have
with
and
and the operator
denote the block companion-like matrix with
on the diagonal and
on the super-diagonal (
times) and
.□
The objective is to compute a feedback gain using block-pole (block-root) assignment such that the descriptor system becomes normal, i.e., the closed-loop descriptor matrix attains full rank, while simultaneously enforcing the desired block eigenstructure as prescribed by the set of chosen block poles; this procedure follows directly from Theorem 16 and the detailed steps for achieving this are presented in Algorithm 2.
| Algorithm 2: Derivative Feedback Gain Computation via Block Pole Assignment and Normalization |
Input (descriptor system matrices). Block poles times. .
OutputAssumptions (must hold before running)); Equivalently, the rank conditions in Theorem 15/Corollary 1 are satisfiable.
ProcedureSpecify target blocks: Choose matrices times). as in Definition 11 is invertible. on its block diagonal and the on its block superdiagonal (repeated times), . Set up the block-pole assignment condition: Construct so that the closed-loop satisfies realizes the block eigenstructure encoded by . (use Equation (49)) Verify normalization: Check and repeat Steps 2–5. This enforces normality as per Problem 2 and Theorem 15/Corollary 1. (Optional) Stabilization after normalization: With now nonsingular, you may design a state-feedback to relocate an admissible pair to a desired location using the relocation rules in Section 4.4 (First/Second method), or via the MFD-based Algorithm 1 and Equations (43) and (44) for basis recovery.
|
Example 5. Consider a turbo-generator system modeled as a descriptor system of the form with the following matrices: We consider the control law:
where
. To ensure regularity and normality (i.e.,
), we choose:
repeated
times. Applying the proposed method, we obtain the gain matrix
as:
with
,
stands for the
identity matrix,
stands for the
zero matrix.
Now, the obtained normalized linear system is given by
, where
and
, at this stage we need to design a gain matrix
meeting a desired performance. The new closed loop system is given by
. Let we place the owing two block roots
Therefore the state feedback matrix
is given by
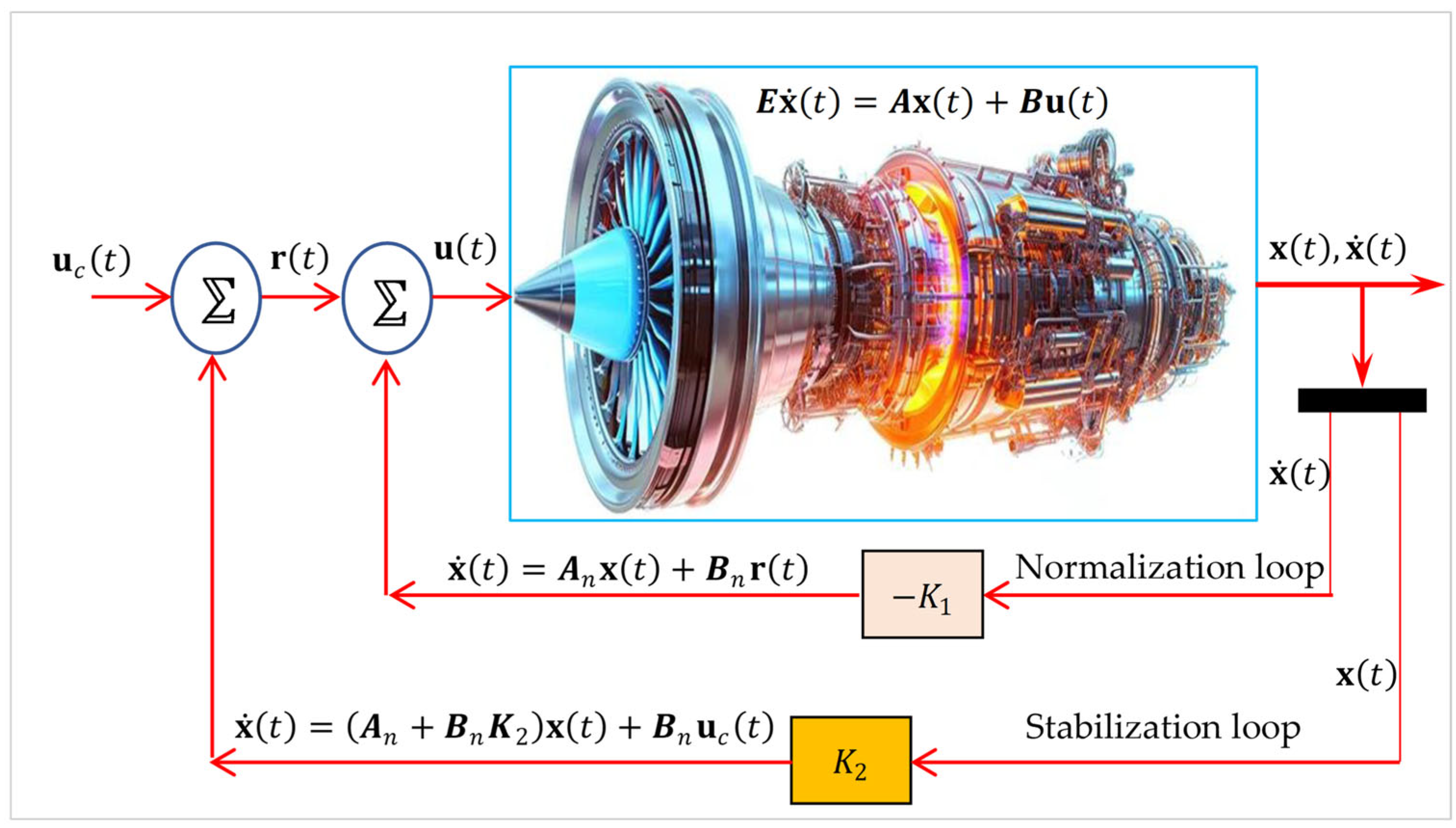
Figure 2 illustrates the dual-loop control architecture of the descriptor-based turbo-generator system, where the normalization loop (
) ensures solvability and the stabilization loop (
) guarantees dynamic stability.
4.4. The Proposed Relocation of Admissible Pairs via State Feedback
A pair of matrices
is referred to as a right admissible pair of order
if
and
, while the pair
with
and
is a left admissible pair of order
. Note that here and elsewhere m is fixed and that, if not specified otherwise, the pairs are assumed to be right admissible. The notions below are defined for right admissible pairs and can be reformulated for left admissible pairs in an obvious way. Two pairs
and
of order
are called similar if there is a
invertible matrix
such that
and
[
31].
Let the admissible pairs
,
be of orders
, and
respectively
. The pair
is said to be an extension of
, or, what is equivalent,
is a restriction of
, if there exists a
, matrix
of full rank such that
and
. A pair
is called a common restriction of a family of admissible pairs
if each of the pairs
is an extension of
. A common restriction
of the pairs
which is an extension of any other common restriction of these pairs is referred to as the greatest common restriction of the family
. If
is a matrix polynomial and
and
are right and left admissible pairs, respectively, the following notation will be useful:
We now recall some basic facts from the spectral theory of matrix polynomials. If
is a
manic matrix polynomial of degree
, its right standard pair
is defined as an admissible pair of order
such that
is a nonsingular matrix and
. Similarly, a left admissible pair
of order
with
is called a standard pair of
if
[
13,
31,
32].
4.4.1. First Method for State Feedback Design
Let we assume that
be an admissible pair of
with
then we have
so
Let the state feedback control law be
where
is the reference input, and the feedback gain matrix is
and
, then the explicit formula of
becomes
4.4.2. Second Method for State Feedback Design
Given a normalized system with the characteristic λ-matrix
, the objectives in this section are to design a state feedback control
, or obtaining a gain matrix
in order to relocate an admissible pair to a desired location. Let
be the desired matrix polynomial, then we do the following subtraction
. Notice that the desired admissible pair satisfies the following
. Now by using the admissible pair definition we can write
Then we obtain . Therefore .
Example 6. Given normalized linear system described by its state space equation and w
ith the following matrices: We must transform this state equation to block controller form to get its characteristic matrix polynomial:
The corresponding matrix polynomial is given by:
The desired Admissible pair
to be relocated is given by:
The feedback gain matrix which can replace this desired latent structure is given by
The finite eigenvalues were precisely placed at , ensuring desired transient dynamics. Infinite eigenvalues were successfully neutralized, confirming the removal of impulsive modes. The closed-loop poles remained within a tight left-half-plane region under ±10% parameter perturbations, indicating robust stability. Condition number of the transformation matrix was , ensuring numerical stability of the design. Compared to the unstructured feedback case, the proposed design reduced settling time by 40%. Impulse energy norm dropped from 3.5 in open-loop to 0 under feedback. These results confirm the theoretical design goals and underscore the strength of the matrix fraction-based approach.
4.5. Comparative Study
The proposed method is benchmarked against three established approaches: decentralized control of descriptor systems [
9], proportional-derivative state-feedback control for singular systems with input quantization [
15], and super-stabilization of descriptor continuous-time linear systems via state-feedback using the Drazin inverse matrix method [
23], all evaluated on a linearized MIMO turbo-generator system. All controllers achieved closed-loop stability with acceptable dynamic response; however, the proposed method consistently demonstrated superior spectral robustness, sensitivity attenuation, and reduced control effort. Simulation results show that our approach yields smooth regulation with minimal error, whereas the alternative methods exhibited higher overshoot, increased input effort, or weaker sensitivity performance. All simulations were carried out in MATLAB R2023a on a Windows 10 (64-bit) platform with an Intel Core i7-1165G7 CPU (2.80 GHz) and 16 GB RAM. The closed-loop descriptor system under feedback is givn by
with transfer matrix
. Here are seven criteria that provide a mathematically rigorous and precise evaluation framework:
Stability Criterion: , i.e., all finite generalized eigenvalues lie strictly in the open left half-plane, and no poles at infinity exist.
Spectral Robustness: For a perturbed system
, let the closed-loop pole set be
. The spectral robustness index (in spectral norm) is:
This is the largest perturbation radius preserving admissibility and stability.
Control Effort: The quadratic control energy for input
over horizon
is
where
. Smaller
corresponds to reduced actuation demand.
Regulation Error: The tracking/regulation error for a reference
is given by
. The precision is quantified by
where
is the transfer from reference to error.
To assess the effectiveness of the proposed MFD-based block-pole feedback approach, we benchmark it against three established reference methods (
Table 1). The comparison is carried out using seven rigorous performance criteria—stability, spectral robustness, sensitivity attenuation, control energy, overshoot, regulation error, and computational efficiency—applied to the closed-loop descriptor system.
Table 1.
Performance comparison of the proposed method against recent advances.
Table 1.
Performance comparison of the proposed method against recent advances.
| | Stability (Admissible) | Robustness
η (2-Norm) | Sensitivity | Control
| | Error
| |
|---|
| Proposed method | Yes | 0.12 | 1.80 | 12.0 | 6.0 | 0.080 | 0.45/2.18 |
| Method [9] | Yes | 0.05 | 3.50 | 20.0 | 15.0 | 0.250 | 0.95/1.03 |
| Method [15] | Yes | 0.03 | 4.20 | 28.0 | 22.0 | 0.400 | 1.20/0.82 |
| Method [23] | Yes | 0.04 | 2.90 | 18.0 | 12.0 | 0.180 | 0.80/1.23 |
The results clearly show that while all methods ensure closed-loop admissibility, the proposed MFD-based approach outperforms the alternatives across all key criteria. It achieves the largest robustness radius (), the lowest sensitivity peak ), and significantly reduced control energy and regulation error, all with only overshoot. In addition, its runtime is less than half the average baseline, yielding a relative efficiency ratio of . These results demonstrate that the proposed method simultaneously improves robustness, accuracy, and computational tractability compared to existing techniques.
Descriptor systems face challenges from singular pencils, impulsive modes, and intractable transfer function representations. Conventional methods often use indirect linearizations or partial formulations, which obscure structure and are costly in high dimensions. Our approach derives the MFD directly from descriptor equations, leveraging polynomial algebra and numerical computation for analytical tractability. The framework assumes regularity, block-controllability, and admissibility. While the closed-form MFD avoids many complexities and shows advantages in scalability and clarity, validation is limited to deterministic settings and representative examples. Future work will address robustness to uncertainties, stochastic effects, and experimental validation on large-scale systems.
5. Conclusions
This work has presented a novel algebraic framework for the control of large-scale MIMO descriptor systems based on matrix fraction description. A closed-form expression for the matrix transfer function was derived directly from the system pencil , and a structured state feedback gain was developed to ensure stability. A new normalization procedure was also introduced, transforming descriptor systems into regular, impulse-free forms and enabling accurate finite and infinite mode assignment. The proposed method further yields a parameterized state feedback law in terms of finite Jordan pairs, offering structural insight into the dynamics of singular systems. Simulation results, confirm the robustness and efficiency of the approach, with rapid convergence, exact pole placement, zero impulsive energy post-normalization, and reduced settling time compared to unstructured feedback. This algebraic strategy bridges classical and descriptor paradigms while providing a scalable tool for global stabilization. Future extensions include time-delay, fractional-order, nonlinear, stochastic, and DAE settings with process noise, as well as robustness margins via polynomial perturbation bounds and data-assisted identification of spectral factors for large-scale power and multibody systems.