Abstract
The Lorentzian structure of space-time limits velocities, preventing the universe from achieving the thermal equilibrium suggested by the cosmic microwave background (CMB). However, if one follows Hawking’s idea of an initial Euclidean metric—where no such velocity limit exists—thermalization become possible without invoking an arbitrary new field. A mathematical framework describing how today’s Lorentzian space-time could evolve from an early Euclidean phase has been proposed, resolving issues like the initial singularity and CMB uniformity. Still, the model’s stability has not yet been examined, nor has a mathematical condition for the Euclidean–Lorentzian transition been established; these aspects are partially addressed in this work. We show that the collapse of the Euclidean sector is an inevitable result of matter moving into thermodynamical equilibrium.
1. Introduction
The universe of the current epoch is obviously Lorentzian. We know this because particle accelerators cannot accelerate a massive particle to the speed of light or above. It is also obvious that the cosmic microwave background is extremely homogeneous. One cannot achieve such homogeneity in a Lorentzian universe unless it went through an epoch of cosmic inflation. However, to achieve such inflation, one needs to postulate one or more scalar fields [1], with no purpose in nature except causing cosmological inflation. This is in contradiction to the principle of Occam’s razor. The only other possibility is to assume, as Hawking [2] suggested, that the universe was initially Euclidean. In this case the speed-of-light limitation does not apply. A Euclidean space-time allows superluminal motion and thus can reach thermodynamic equilibrium in time. An additional advantage is that if the universe is initially Euclidean, it does not suffer from an initial unphysical singularity. Thus general relativity does not lose its validity at the Big Bang. The singularity can also be avoided if matter was initially in a “dark energy” form [3] but this option is unlikely. If the universe was initially Euclidean and now it is Lorentzian, the only logical possibility is that the universe went through a transition. This should be denoted as the Euclidean–Lorentzian transition.
The Euclidean–Lorentzian universe is a universe which contains a (short) epoch of a Euclidean metric, which later becomes the universe that we know, which possesses a Lorentz metric. In the Euclidean regime the scale factor reaches a minimal value, with a finite scalar curvature, and not zero with an infinite scalar curvature. Matter can move superluminally and thus reach thermal equilibrium, in accordance with the observed cosmic microwave background characteristics. Later it becomes the universe that we know today, with speed-of-light limitations related to velocity. The model validity is based on a metric which satisfies the Einstein equations of general relativity, and the Friedman equations of cosmology.
We do not consider the reverse Lorentzian–Euclidean transition for the following reasons: It is obvious that the universe today is not Euclidean because massive particles cannot travel at a speed which is equal to or greater than the speed of light. Moreover, Maxwell’s electromagnetic field equations are symmetric under Lorentz transformations but not under Euclidean rotations. Hence it is clear that the current universe is not Euclidean but Lorentzian. Thus, it is not necessary from an observational point of view to consider the Lorentzian–Euclidean transition because there is no evidence that such a transition occurred. However, there is considerable evidence that a Euclidean–Lorentzian transition occurred in the primordial universe as previously explained.
The current analysis is relevant to the recent universe as follows: What is left from the primordial state of the universe is the extremely uniform cosmic microwave background with its spectrum of perturbations. We also witness the result of cosmological baryonic acoustic oscillations, namely galaxy and galaxy cluster distributions. All those features may be affected by the Euclidean epoch. Other indicators are the distribution of light nuclei, the results of the Big Bang nucleosynthesis phase. Those include the relative percentage of hydrogen, deuterium, tritium, helium, and lithium. However, those were created probably after the transition to the Lorentzian phase.
In [4], an extensive introduction to the subject of Euclidean and Lorentzian space-times was given. Certainly, the idea of a primordial Euclidean universe is not new. Leading physicists such as Sakharov [5,6], Hawking [2], Ellis [7], and Davidson [8] have considered the possibility that near its inception, the metric of the universe had a Euclidean signature. Notice that a change in metric is not related only to cosmology but also to black-hole physics (see, for example, [9]). It was shown [10] that such a metric cannot be sustained for a long time because for an expanding universe, the density of the universe diminishes. The reason is that for (nearly) empty universes, only a Lorentzian metric is stable. So naturally all other metric signatures must be confined to a limited portion of space-time. This of course is also true for the Euclidean signature which is confined, as suggested here, to a tiny duration after the universe was created. This coupled with the radical dynamics of particles in this primordial Euclidean universe, with no upper velocity limit and bizarre physical statistics that favor high velocities [4], suggests an alternative for scalar-field-driven cosmic inflation [1]. A mathematical model for a hybrid Euclidean–Lorentzian universe is described in [11]. This is achieved by transforming Einstein’s equations while taking into account the homogeneity and isotropy of space into a generalized form of the Friedmann–Lemaître–Robertson–Walker (FLRW) equations, which are valid in both the Euclidean and Lorentzian sectors. Of course a transition hypersurface separates the Euclidean part of space-time from the Lorentzian part of space-time. Both the Euclidean part and the Lorentzian part are four-dimensional hypervolumes while the transition hypersurface is of zero measure and is three dimensional.
It was shown that within the framework of the hybrid Euclidean–Lorentzian universe, problems such as the initial singularity and the homogeneity of the CMB are solved [11]. However, stability properties of the hybrid model were not discussed yet, and these aspects will be partially addressed below.
The structure of the current paper is as follows: We start with a general geometry and apply the standard restrictions that are implied by homogeneity and isotropy. However, we do not restrict our metric to be either Lorentzian or Euclidean. This will result in a metric with reduced degrees of freedom. Next we use Einstein’s equations and obtain the generalized FLRW equations which are valid for both the Lorentzian and Euclidean signatures. This is followed by some discussions of the equation of state and the relation between pressure and energy in the Euclidean era. Finally we discuss the stability of the solutions of those equations, in which we shall attempt to obtain some insight regarding the transition from the Euclidean epoch to the Lorentzian epoch.
2. The Metric
The metric of a four-dimensional space is connected to the infinitesimal square interval by the following well-known equation:
in which represents the coordinates describing the location of some point P in this space, and we use the Einstein summation convention. We shall single out one coordinate and refer to it as “temporal”. This can be easily understood in a Lorentzian space-time in which the diagonalized form of will have a different sign for this coordinate with respect to the other coordinates. For the Euclidean case the choice seems arbitrary; however, if one bears in mind that any Euclidean portion of space-time will turn into a Lorentzian epoch, then the direction of “symmetry breaking” allows us to define a temporal direction. Thus we may write the following:
Next we invoke isotropy in the usual spatial sense, which is assumed in standard cosmological models to claim that there cannot be a preferred direction in our space at any given time. As the vector whose components are points to such a direction, it follows that we must have , and thus
The next step [12] is to look at a “comoving observer”, which is an observer that does not feel himself moving in the coordinate system. Such an observer will report that and thus will be displaced by the following interval:
As the observer is not displaced in space, he will interpret the change he is feeling as a change in time; this is denoted as “proper time” . Till now we have measured all dimensions in the same units (say meters); however, it is customary to measure time using a different set of units (seconds). To convert between the units, we introduce the conversion factor × m/s (which appears later in the theory as the velocity of gravitational and electromagnetic waves in a vacuum). Thus
There are two alternatives:
So we obtain the following:
Now consider an observer who inspects his surroundings in a given instant of time; since space is assumed to be isotropic, he may choose spherical coordinates (), in which case [12]
As we do not specify in advance the signature of the metric, it follows that
Thus we may write the line interval square as follows:
It follows that there are two equivalent Euclidean choices ( and ) and two equivalent Lorentzian choices ( and ). Hence without loss of generality, we choose a positive sign for the spatial component, leaving the metric type to be determined by the temporal part.
Following [12], we shall choose from now on units in which and use the following notation:
So
This means that for the Euclidean regions of space-time, we use an imaginary time coordinate, while for the Lorentzian regions, the time coordinate is real, where
The spatial scalar curvature (which is different from the four-dimensional scalar curvature) is
If we assume that space must be homogeneous, it follows that the spatial scalar curvature of space cannot depend on r, but it can depend on t. It follows that
since is by assumption independent of t. To avoid a singular expression, we may choose and thus obtain
It is now customary to redefine r such that for the cases that , which will lead to the following customary form:
For the case , we take . Finally we drop the bars for convenience and write the following:
3. The FLRW Equations
In the previous section we have went as far as is possible to determine the metric from symmetry considerations (isotropy and homogeneity). However, in order to gain more information, one must solve Einstein’s equations. This will lead to the following FLRW model equations:
It is assumed that the pressure p and the energy density are connected through an equation of state, and thus, given appropriate initial conditions, those equations can be integrated. Let us combine Equations (20) and (21), this will lead to
In [11] (Section 4), we have shown that the above equation implies singularity for a completely Lorentzian universe, while it implies a well-behaved solution for a hybrid Euclidean–Lorentzian universe.
4. A General Discussion Regarding Pressure–Energy Relations
Let us discuss the possible pressure–energy relations defined as w for an ideal gas. It thus follows that
According to Weinberg [13] (Equation 2.10.20), the energy–momentum tensor of an ideal gas of N point particles is as follows:
where is the four-momentum of particle I, is the energy of particle I, and is its location. is a three-dimensional Dirac delta function. (Weinberg takes ; however, we do not make this assumption in order to retain dimensional clarity.) He then defines the energy density as follows:
And the pressure (assuming isotropy) is defined as follows:
Notice that none of the above definitions require the system of particles to be in thermodynamic equilibrium. Now according to Equations (31) and (39) of [4], free particles, whether Euclidean or subluminal Lorentzian, satisfy the relations as follows:
in which is the rest mass of particle I and is the velocity of particle I. The factor differs for the various sectors, where
It follows that the following energy–momentum relations hold:
Plugging this into Equation (26), we obtain the following:
For subluminal Lorentzian particles, we always have , and thus
The Lorentzian sector contains ordinary free matter or radiation that does not admit , so it does not admit “stiff” matter with . For the Euclidean sector, , and thus
Notice, however, that those values do not assume thermodynamic equilibrium and may be restricted in the case where the thermodynamic equilibrium requirement is applied, as will be shown in Section 5.
5. The Value of w for a Euclidean Ideal Gas in Thermodynamic Equilibrium
In this section we follow the approach suggested by Bloch [14]. Let us first consider a free particle in a box of volume V. Physically this means that particle dynamics is described by the Hamiltonian equation, where
such that
The value of depends on the sector in which the particle is in, that is, whether it is Euclidean or Lorentzian (Equation (50) of [4]):
in which m is the particle rest mass and p is the particles momentum. The partition function of a single particle is (see Equations (13.8) and (13.10) of [14])
Here , in which is the Boltzmann constant () and T is the temperature measured in degrees Kelvin. The partition function of a system of N particles is as follows:
in which we assume for simplicity that the particles are identical. The pressure in the system can be calculated as follows (Equations (13.30) and (13.31) of [14]):
where n is the particle density. This equation does not depend on the specific form of the kinetic Hamiltonian and thus is valid also for classical non-relativistic ideal gases as well as for gases in Euclidean space-times. Introducing the dimensionless temperature, where
it follows that
The total energy of the non-interacting (ideal) particles is as follows:
This can be averaged such that
in which we assume that the average energy of each particle is the same. It follows that the energy density inside the box is as follows:
in which is the normalized averaged single particle energy. We are now in a position to calculate w using Equation (23), where
The value of is essentially independent of temperature for high temperatures, as can be seen from Figure 1.
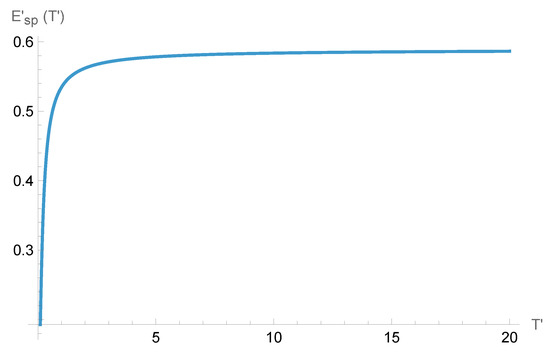
Figure 1.
The value of as a function of for high temperatures. At values of , it is approximately a constant with the asymptotic value .
We notice that there is the relation between the parameter defined in [4] and the dimensionless temperature defined here. Thus infinite temperature is equivalent to , and we obtain using Equations (75) and (76) of [4], the result
This means that for high temperatures, w is a linear function of temperature (see also Figure 2), where
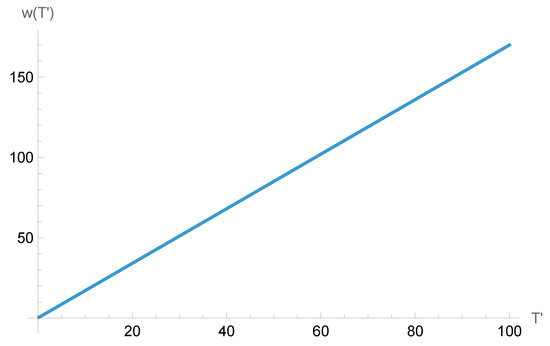
Figure 2.
The value of w as function of for high temperatures basically indicates a linear dependence.
Thus w can grow without limit provided that the temperature is high enough. For low temperatures the energy behavior is depicted in Figure 3, and w is depicted in Figure 4, from which it can be seen that w cannot be lower than in the Euclidean sector.
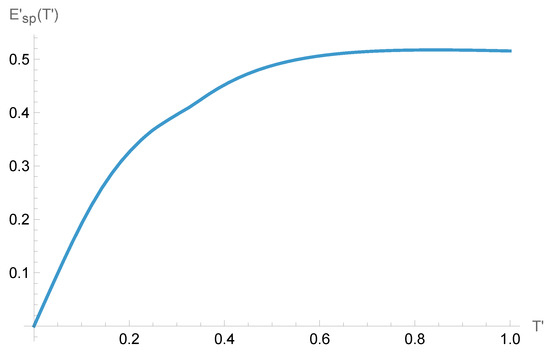
Figure 3.
The value of as a function of for low temperatures.
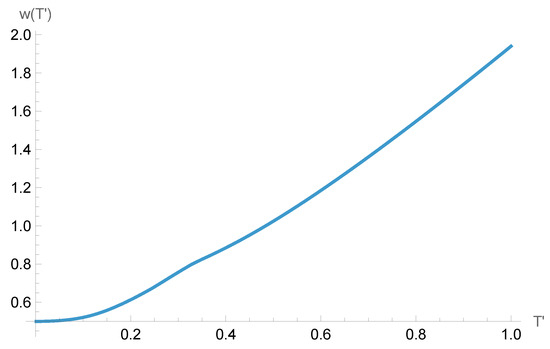
Figure 4.
The value of w as a function of for low temperatures.
To understand this result, we look again at Equation (74) of [4], where
so we shall investigate more closely the limit , which is equivalent to . Let us make a change in integration variables such that , so in terms of the new variable,
and as only a small q will contribute to the above integral; thus
and in the above equation, we neglected exponential decreasing terms which are surely negligible at . This allows us to calculate the asymptotic value of the single-particle average energy using Equation (76) of [4], where
Thus the asymptotic value of w for low temperatures, which is also the lowest possible value for w in the Euclidean sector for matter in thermal equilibrium is as follows:
6. Stability Analysis
It is interesting to look at the stability properties of the hybrid Lorentzian–Euclidean universe. In this case, one needs to look at the new metric
in which is the FLRW metric defined in Equation (19) and is a small perturbation. Inserting this metric into Einstein’s equations and keeping only the linear terms will result in an equation of the following form:
in which the operator is a second-order differential operator that depends on the FLRW metric, and has ten degrees of freedom. Following Padmanabhan [12] (p. 562), we introduce a conformal time, where
and this time coordinate is real in the Lorentzian sector and imaginary in the Euclidean sector of the universe. Equation (19) can now be written in the following form:
If the above form simplifies to
Following Padmanabhan [12], we shall assume for the sake of simplicity that ; presumably the value of k will not have a significant effect on the early universe (see Section 7 for further details). Padmanabhan [12] also suggests partitioning the perturbation to the following spatial and temporal components:
where and are scalar, vector, and tensor perturbations. Furthermore, and are partitioned into curl-free and divergence-free parts:
where is a Kronecker delta, is divergence-free and thus has two degrees of freedom, and is traceless, has zero divergence, and thus also has two degrees of freedom. Padmanabhan [12] shows that is also gauge-independent. Furthermore, it is shown in [12] that, by a proper choice of gauge, one can set . The terms is decoupled from the rest of the perturbation terms by using the following ansatz:
in which is a constant. By virtue of Equation (54), one obtains the following equation for ([12] p. 566 Equation 13.26):
This implies that there is a critical wavenumber, where
(using Equations (20) and (21) and assuming to obtain it). It thus follows that generically speaking, we have an equation of the following form:
The above equation seems to show that neither a Euclidean state nor a Lorentzian state would be generically stable. In fact for and thus for (short) wavelengths such that , the Lorentzian metric will prevail, while the Euclidean metric will destabilize, and for (long) wavelengths, the Lorentzian metric will destabilize, and the Euclidean metric will prevail. However, this is not so because according to Equation (61), the relevant quantity is , and thus even if v grows, it may be counter balanced by a growing a. Thus, for example, for an infinite wave length , we obtain
This equation has two solutions ([12] page 568):
in which and are constants. Thus Equation (61) takes the following form:
If a increases, the perturbation does not destabilize the cosmological solution; however, for a decreasing a as occurs in a closed universe with at its later stages, this may indeed seem to cause instability. Notice, however, that this universe has a limited scale factor (see Equation (41) of [11]), and thus if the universe has a finite radius, the discussion of a perturbation with infinite wavelength does not make sense physically. However, if the universe has infinite size, the solution will destabilize as a decreases, leading perhaps to a Euclidean metric that is not susceptible to long wavelength instabilities.
There are of course special circumstances in which v is bounded, for example, for times for which . Moreover, even at times in which and the maximal size of the universe is smaller than , one will not be able to destabilize the Lorentzian universe with long wavelength perturbations. On the other hand, let us suppose that is smaller than the smallest possible scale in which a continuous model is applicable. One can take the case where as an example. This implies that one cannot consider a short wavelength perturbation of the form , so there is no way to destabilize a Euclidean sector.
To evaluate we use Equation (23) such that
It follows that in the radiation era, or any other era in which matter is relativistic and thus , the universe is purely Lorentzian, and any Euclidean submanifold destabilizes. In this situation, and . In the literature, various types of matter for which also exist; for example Padmanabhan [12] discussed “stiff” matter in which the velocity of sound propagation is equal to the velocity of light in a vacuum; in this case, . Notice, however, that the existence of such types of matter is not verified, and in fact they are not possible for ordinary matter and radiation (see Section 4). Nevertheless, they arise naturally in scalar field theories, for which kinetic energy is much larger than potential energy ([12] page 469). As we have shown in Section 4, a Lorentzian sector with ordinary matter and radiation must have (see Equation (32)); this limitation is much less restrictive in the Euclidean section for which (see Equation (33)). A discussion of the possible values of w for an ideal gas in a state of thermal equilibrium in the Euclidean sector is given in Section 5; it is shown there that once matter reaches thermal equilibrium (as is required by cosmic microwave background observations), it follows that (see Equation (52)). Thus, the Euclidean sector violently collapses as , leading plausibly to the next Lorentzian era.
Let us estimate the size of . According to Equations (35) of [11],
Thus
will decrease as a grows for every , but the most dramatic effect will occur when w increases as matter reaches thermal equilibrium and changes sign from positive to negative. We shall now assume for simplicity that ; this will allow us to estimate in the Euclidean sector. Thus
Now if is still positive, stability means that
Thus as the wavenumber decreases, a point will be reached at which the Euclidean sector destabilizes; this will occur for some . A typical growing time of such instability is expressed as
If we assume Planck density at (the time of a minimal scale factor, see [11] Equation (60)), it follows that
This time is many magnitudes shorter than time scales suggested by current inflation models, typically assumed in standard cosmological models, which are between to s. However, to understand the true dynamics of matter in the Euclidean sector, one needs to understand how matter reaches thermal equilibrium, and this will require a full kinetic treatment, which is out of the scope of the current work.
This is presumably followed by a stable Lorentzian solution, which requires the thermalization of matter into a relativistic form with . As discussed in [4], an Euclidean metric does not restrict matter to move at subluminal speeds, and thus despite the rapid destabilization of the Euclidean space-time, thermalization is indeed achievable.
7. The Effect of Finite k
In the current paper we follow Padmanabhan [12] and assume that . Although a full perturbation analysis with finite k remains a task for the future, it is worthwhile to study the effect of a finite k for a simple perturbation; for this we use the equation derived for in [15]. This analysis leads to the following stability condition (Equation (30) of [15]):
in which we replaced the previous paper’s scale notation with the current paper’s notation , and is the Hubble function. By defining the curvature density, we obtain
This quantity is obviously null when and can be positive or negative for other values of k. However, according to Equations (52) and (53) of [11], the Euclidean sector only allows ; hence this quantity is positive in that sector. Using Equation (77) we can now write Equation (76) in the following form:
Hence stability is controlled by an effective density, where
To estimate we invert Equation (69) and obtain the following:
Inserting the above equation into Equation (77) results in the following expression:
As the highest density is , this quantity is bounded by
in which we used Equation (58) of [11]. This in turn allows us to write the following:
Taking into account that in the Euclidean sector, and , it follows that the effective density is as follows:
Hence a non-zero curvature will change the density by about a factor of two; thus for a preliminary study, one may ignore the curvature effect without risking a significant error.
8. Conclusions
We have shown that completely Lorentzian cosmology described in many textbooks [12,13,16,17] cannot describe the entire history of the universe, as it must break down at some time and lead to unphysical divergences. However, the cosmology of the Euclidean and Lorentzian sectors does not contain unphysical singularities and provides sufficient time [4] to the CMB to achieve thermal equilibrium. Indeed black-hole singularities can also be avoided in a similar fashion [9,18,19]. As matter achieves thermal equilibrium in the Euclidean epoch, we deduce that this sector must collapse naturally. Thus the need to introduce cosmological inflation using ad hoc (and redundant anywhere else in physics) scalar fields [1] is avoided. We mention that the scale factor at the end of the Euclidean epoch serves as an initial condition for the scale factor in the Lorentzian epoch. That may have some bearing on the apparent scale factor acceleration, as evident in the red shift in distant super novae [20]. However, some authors suggest keeping the cosmological constant to show how a signature change may affect its value [21].
The current work of course does not deal with all issues related to the Euclidean–Lorentzian transition. Major concerns are related to the neglect of the curvature effect () for the cosmological model, as well as other types of perturbations. Other concerns are related to the dynamics of particles moving from the Euclidean sector to the Lorentzian sector, as well as the kinetics of matter in the Euclidean sector leading to thermodynamic equilibrium. Those subjects will be dealt with in future works.
The study of the evolution of in both the Lorentzian and Euclidean sectors may benefit from modern mathematical approximation techniques of time-dependent scaling factors, as suggested by [22]. Also notice [23] connects invariant means to cosmological homogeneity. The current work assume only ideal gases; however, in the future more realistic equations of state may be used, such as those described by General-Appell polynomials [24]. Finally we mention [25], which introduced q-calculus frameworks that are relevant to conformal-time () statistics.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Acknowledgments
The author would like to thank Ido Ben-Dayan for discussion and for making important comments. Additional thanks are given to the anonymous reviewers that have suggested important corrections.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. 1981, D23, 347–356. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W. Wave function of the Universe. Phys. Rev. D 1983, 28, 2960–2975. [Google Scholar] [CrossRef]
- Ling, E. Remarks on the cosmological constant appearing as an initial condition for Milne-like spacetimes. Gen. Relativ. Gravit. 2022, 54, 68. [Google Scholar] [CrossRef]
- Yahalom, A. The Primordial Particle Accelerator of the Cosmos. Universe 2022, 8, 594. [Google Scholar] [CrossRef]
- Sakharov, A.D. Cosmological transitions with changes in the signature of the metric. Sov. Phys. JETP 1984, 60, 214–218. [Google Scholar]
- Shestakova, T.P. The Birth of the Universe as a Result of the Change of the Metric Signature. Physics 2022, 4, 160–171. [Google Scholar] [CrossRef]
- Ellis, G.; Sumeruk, A.; Coule, D.; Hellaby, C. Change of signature in classical relativity. Class. Quantum Grav. 1992, 9, 1535–1554. [Google Scholar] [CrossRef]
- Davidson, A.; Yellin, B. Is spacetime absolutely or just most probably Lorentzian? Class. Quantum Grav. 2016, 33, 165009. [Google Scholar] [CrossRef][Green Version]
- Capozziello, S.; De Bianchi, S.; Battista, E. Avoiding singularities in Lorentzian-Euclidean black holes: The role of atemporality. Phys. Rev. D 2024, 109, 104060. [Google Scholar] [CrossRef]
- Yahalom, A. The Geometrical Meaning of Time. Found. Phys. 2008, 38, 489–497. [Google Scholar] [CrossRef]
- Yahalom, A. A Hybrid Euclidean-Lorentzian Universe. Int. J. Geom. Methods Mod. Phys. 2024, 21, 2440034. [Google Scholar] [CrossRef]
- Padmanabhan, T. Gravitation: Foundations and Frontiers; Cambridge U. Press: Cambridge, UK, 2010. [Google Scholar]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1972. [Google Scholar]
- Bloch, F.; Walecka, J.D. Fundamental Statistical Mechanics, Manuscript and Notes of Felix Bloch; Imperial College Press & World Scientific: London, UK, 2000. [Google Scholar]
- Yahalom, A. Preliminary stability analysis of a Friedman-Lemaitre-Robertson-Walker universe. J. Phys. Conf. Ser. 2017, 845, 012009. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W.H. Freeman & Company: New York, NY, USA, 1973. [Google Scholar]
- Narlikar, J.V. Introduction to Cosmology; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Battista, E.; Esposito, G. Geodesic motion in Euclidean Schwarzschild geometry. Eur. Phys. J. C 2022, 82, 1088. [Google Scholar] [CrossRef] [PubMed]
- Garnier, A. Particle dynamics in spherically symmetric electro-vacuum instantons. Eur. Phys. J. C 2024, 84, 374. [Google Scholar] [CrossRef]
- Yahalom, A. Gravity, Stability and Cosmological Models. Int. J. Mod. Phys. D 2017, 26, 1743026. [Google Scholar] [CrossRef]
- Alexandre, B.; Gielen, S.; Magueijo, J. Overall signature of the metric and the cosmological constant. J. Cosmol. Astropart. Phys. 2024, 2, 036. [Google Scholar] [CrossRef]
- Özger, F.; Aslan, R.; Ersoy, M. Some Approximation Results on a Class of Szász-Mirakjan-Kantorovich Operators Including Non-negative parameter α. Numer. Funct. Anal. Optim. 2025, 46, 481–484. [Google Scholar] [CrossRef]
- Ayman-Mursaleen, M.; Nasiruzzaman, M.; Sharma, S.; Cai, Q. Invariant means and lacunary sequence spaces of order (α, β). Demonstr. Math. 2024, 57, 20240003. [Google Scholar] [CrossRef]
- Rao, N.; Farid, M.; Jha, N.K. Szász-integral operators linking general-Appell polynomials and approximation. AIMS Math. 2025, 10, 13836–13854. [Google Scholar] [CrossRef]
- Ayman Mursaleen, M.; Serra-Capizzano, S. Statistical Convergence via q-Calculus and a Korovkin’s Type Approximation Theorem. Axioms 2022, 11, 70. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).