Circular Pythagorean Fuzzy Deck of Cards Model for Optimal Deep Learning Architecture in Media Sentiment Interpretation

Abstract

The rise of streaming services and online story-sharing has led to a vast amount of cinema and television content being viewed and reviewed daily by a worldwide audience. It is a unique challenge to grasp the nuanced insights of these reviews, particularly as context, emotion, and specific components like acting, direction, and storyline intertwine extensively. The aim of this study is to address said complexity with a new hybrid Multi Criteria Decision-Making MCDM model that combines the Deck of Cards Method (DoCM) with the Circular Pythagorean Fuzzy Set (CPFS) framework, retaining the symmetry of information. The study is conducted on a simulated dataset to demonstrate the framework and outline the plan for approaching real-world press reviews. We postulate a more informed mechanism of assessing and choosing the most appropriate deep learning assembler, such as the transformer version, the hybrid Convolutional Neural Network CNN-RNN, and the attention-based framework of aspect-based sentiment mapping in film and television reviews. The model leverages both the cognitive ease of the DoCM and the expressive ability of the Pythagorean fuzzy set (PFS) in a circular relationship setting possessing symmetry, and can be applied to various decision-making situations other than the interpretation of media sentiments. This enables decision-makers to intuitively and flexibly compare alternatives based on many sentiment-relevant aspects, including classification accuracy, interpretability, computational efficiency, and generalization. The experiments are based on a hypothetical representation of media review datasets and test whether the model can combine human insight with algorithmic precision. Ultimately, this study presents a sound, structurally clear, and expandable framework of decision support to academicians and industry professionals involved in converging deep learning and opinion mining in entertainment analytics.

1. Introduction

In the modern world where the internet dominates, user-generated content, especially reviews of movies, TV shows, and streaming services, has become an essential source of social opinion. The subjective sentiment density of these reviews is high, and many are organized by specific aspects: plot, acting, visual effects, direction, and soundtrack. This is, however, not an easy task since the Aspect-Based Sentiment Analysis (ABSA) of these reviews would require emotional tone and contextual layering. The common sentiment analysis methods do not satisfy the fine-grained interrelation between context and emotion, which is why methods based on deep learning that are more involved and architecture-aware have to come to the fore. The given research is devoted to comparing and choosing the best deep learning architectures to be applied in film and TV content interpretation from the perspective of ABSA [1]. The most fundamental problem is how to systematically compare and rank deep learning models, including BERT (Bidirectional Encoder Representations of Transformers) + GRU assemblers, transformer-based encoders, attention-enhanced CNNs, and other hybrid networks, along several conflicting dimensions. Such criteria can be the degree of (classification) accuracy, the interpretability of the model, efficiency (of the computers), and cross-domain generalizability. The problem with conventional ranking and MCDM is that they usually cannot capture the vagueness involved in subjective preferences by human beings. Therefore, we can combine the DoCM [2] and a CPFS [3] construct. DoCM offers a loose and simple-to-understand decision support technique that can be used to allow masters to perform pair-wise comparisons based not on comparable numeric markings, but on the explanation of preferences. Throughout the involvement of circular logic, we accept that preferences can be described in a directional manner based on the understanding that two options could be both near or far within a conceptual cycle of value. Moreover, it features in a system in which the PFS is embedded, representing membership (support of an option), non-membership (opposition), and hesitation, with the vague indecision that is realistic whenever subjective models are being assessed. A typical example problem of the current research includes five possible architectures, which are considered relative to four essential criteria based on expert knowledge and the performance of a dataset. The comparison procedure starts with the input of fuzzy evaluations of each choice, the acquisition of fuzzy Pythagorean scores, and the subsequent production of circular wooden rankings by the logic of the deck of cards matrix. The approach gives a mathematically sound, interpretable, and visually constructive approach to choosing the most appropriate model to use in ABSA. Finally, the proposed problem can be addressed and presented by empowering researchers, media analysts, and AI practitioners with a transparent and human-centric framework, providing the best-performing emotion analysis model according to metrics, human intuition, and uncertainty. These are essential advantages regarding recommendation systems, opinion monitoring services, or media analytics systems [4].

1.1. Background

The digital world is a data-driven society, and thousands of terabytes of unorganized information, which reflects people’s opinions, emotions, and sentiments, are produced daily by various media platforms. The proper perception of this sentiment plays a significant role in using applications like political prediction, brand management, mental conditions, and even safety in terms of protection. Although these traditional approaches to sentiment analysis are somewhat practical, they frequently fail to address vagueness, ambiguity, and subjectivity, which are also inherent to human language expressions. Consequently, there have been increasing demands for more intelligent, flexible, and uncertainty-aware decision-making architectures, especially in selecting optimal deep learning architectures with reference to such applications. As a possible solution to this problem, the current paper proposes a new decision-making scheme based on the CPFS or on modifying existing decision-making tools such as the DoC technique. This hybrid scheme increases the articulation of human-like reasoning in an uncertainty setting where information possesses symmetry and facilitates the systematic elicitation of pairwise preferences. By incorporating it into a multi-criteria decision-making (MCDM) environment, the model allows one to choose the most appropriate deep learning model to interpret sentiment in the media. The CPFS structure, besides reflecting the complex fuzzy logic of relationships, further demonstrates the context of circular geometry and expresses the hesitancy and relative power of preferences better than in classical fuzzy theories. The concept of Fuzzy Set (FS) Theory was first introduced by Lotfi Zadeh in 1965 [5] and revolutionized how uncertainty and imprecision were treated in computational models. Over the decades, numerous extensions have been developed to address the limitations of FS. Some Fuzzy set extensions shown in

Table 1. Some extensions of fuzzy set theory.

$\mathbf{F}\mathbf{u}\mathbf{z}\mathbf{z}\mathbf{y} \mathbf{E}\mathbf{x}\mathbf{t}\mathbf{e}\mathbf{n}\mathbf{s}\mathbf{i}\mathbf{o}\mathbf{n}$	$\mathbf{Y}\mathbf{e}\mathbf{a}\mathbf{r}$	$\mathbf{K}\mathbf{e}\mathbf{y} \mathbf{C}\mathbf{o}\mathbf{n}\mathbf{t}\mathbf{r}\mathbf{i}\mathbf{b}\mathbf{u}\mathbf{t}\mathbf{o}\mathbf{r}$	$\mathbf{M}\mathbf{a}\mathbf{i}\mathbf{n} \mathbf{F}\mathbf{e}\mathbf{a}\mathbf{t}\mathbf{u}\mathbf{r}\mathbf{e}\mathbf{s}$	$\mathbf{L}\mathbf{i}\mathbf{m}\mathbf{i}\mathbf{t}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}\mathbf{s} \mathbf{A}\mathbf{d}\mathbf{d}\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{s}\mathbf{e}\mathbf{d}$
Fuzzy Sets (FS)	1965	Zadeh [5]	Partial membership	Binary optimization
Intuitionistic Fuzzy Sets (IFS)	1986	Atanassov [6]	Membership + non-membership	Expressesesitation zone
Pythagorean Fuzzy Sets (PFS)	2013	Yager [7]	${\mu }_x^2+v_x^2\le 1$	Greater flexibility
q-Rung Orthopair FS	2017	Yager [8]	Generalization PFS	Higher expressiveness
Circular Intuitionistic Fuzzy Sets (CIFS)	2018	Atanassov [1]	Circular modeling of IFS	Geometric interpretability
Circular Pythagorean FS (CPFS)	2020s	Recent studies	Circular form FS	Combines radius, hesitation, and nonlinearity

.

Each successive model builds upon the weaknesses of the previous one, advancing in how it models uncertainty, hesitancy, and the relationship between membership and non-membership degrees. In particular, CPFS introduces a circular geometric structure that captures the degree of uncertainty and the balance and trade-off between opposing states, offering richer semantic insight for decision-making.

1.2. Problem Statement

Due to the abundance of user-generated reviews on both film and television sites, the dynamics of the data presented create a rich but complex environment, which tends to concentrate sentiment in specific areas, such as storyline, acting, cinematography, and direction. To obtain these sentiments, we need advanced deep learning models to extract them. However, the number of architectures to be used, like attention-based networks, BERT hybrids, and transformer variants, is also a problem: Which deep learning-based semi-supervised model approaches best suit aspect-specific sentiment analysis within media reviews?

Existing performance appraisal systems are incomplete as they contain three fundamental shortcomings:

• They also depend significantly on sharp metrics, disregarding indecisiveness.
• They are not interpretable by human beings on comparative model judgment.
• They cannot incorporate subjective, circular preferences and fuzzy reasoning.

The framework must support a multi-criteria assessment, represent human reasoning, and accommodate fuzzy uncertainty and preference loops. The study fills this research gap by offering a CPF-DoCM to measure and rank the deep learning architectures on media sentiment interpretation.

1.3. Research Gap

Although the deep learning and sentiment analysis fields have shown substantial progress, an essential point of departure still exists when deriving a framework for observing and choosing deep learning architectures in a scenario filled with uncertainty, hesitation, and the personal interpretation of an expert. The current model selection frameworks mostly use crisp measures, such as accuracy or loss functions. Thus, they cannot cover human-focused elements, such as interpretability, computational workability, and scenario-specific relevance, which are particularly important in sensitive areas like media sentiment interpretation. Moreover, fuzzy set theories have been utilized even in the context of decision-making. Still, in most cases, the conventional approaches to fuzzy sets have been used; these include regular fuzzy sets, imprecise fuzzy sets, or Pythagorean sets, which do not employ the modeling of circular geometry, which can express trade-offs and preference imprecision more smoothly. In addition, the most commonly used MCDM techniques do not incorporate an easy-to-use algorithm that would elicit priorities defined by the expert. They are more of a problem in the real world and more challenging to work with in multi-stakeholder settings. Hitherto, no unified framework has clustered Circular Pythagorean Fuzzy Sets (CPFS) and Deck of Cards (DoC) to carry out both, choose an LMM, and understand it clearly. This literature examines this gap and presents a new CPFS-DoC framework explicitly used to find the optimal architecture in the uncertain, complex field of media sentiment analysis.

1.4. Research Question and Motivation

The research question of the study is as follows:

• What is the criterion-consistent and practical evaluation and ranking of deep learning architectures of the aspect-based sentiment analysis of film and television content via a multi-criteria decision-making (MCDM) approach?
• How can Pythagorean fuzzy sets amplify the characterization of doubts, ambivalence, and subjective expert evaluation concerning the model selection in sentiment analysis?
• How might circular reasoning be assimilated into the comparative decision models to account for the non-linear and cyclic ordering of choices in decomposing deep learning?
• Would combining the Deck of Cards Method with Circular Pythagorean fuzzy logic offer a more structured, interpretable, transparent, and cognitively consistent system of choosing optimal deep learning models in media sentiment interpretation?
• How does applying the proposed hybrid framework affect deep learning model selection’s accuracy, reliability, and explainability in the aspect-specific sentiment analysis in the entertainment domain?

The motivation of our study is as follows:

As streaming services and user-generated reviews have gained popularity, the entertainment sector has become a sentiment gold mine. Audience members have given up using stars to rate their opinions, but have used descriptive content that shows subtle feelings regarding emotions like story, characters, movies, soundtrack, etc. Although aspect-based sentiment analysis (ABSA) has already proved to be a valuable method for the interpretation of such narrowed-down opinions, selecting the deep learning architecture to work with this problem is still a multifaceted dilemma. There are a lot of models, including five retraining costs, six scaling, seven accuracies, including CNN and LSTM-based frameworks, and more advanced transformer-based ones (e.g., BERT and GPT). The available evaluation methods usually assess using singular measures (such as accuracy or F1-score), and do not reflect the multidimensionality of model appropriateness. In addition, the subjective judgments of any expert, ambiguous preferences, and a reluctance to take one of the models that performs most similarly are not considered in the classic model selection approaches. The research is driven by the necessity of a more humanistic, aligned with the needs of people, and flexible approach to decision-making methodology that would incorporate expert opinion, allow one to deal with ambiguity, and represent a cyclic model of preferences when models are performing similarly on several criteria. Accordingly, the present paper proposes a hybrid system that integrates the DoCM, a pictorial and intuitive ranking-based approach, and the CPFS theory to contextualize the sentiment-model examination procedure with uncertainty-sensitive, circular comparative inference.

1.5. Objective and Contribution

• To develop a new method of MCDM combining the DoCM with CPFS.
• To compare the appropriateness of different deep learning assemblers (e.g., BERT + BiGRU, Transformer-XL, CNN-LSTM) used to carry out aspect-specific sentiment analysis of film and television texts.
• To support the comparative modeling of human-like reasoning in that it involves circular pairwise judgments, hesitation modeling, and fuzzy preference aggregation levels with symmetry.
• To exemplify how the framework may be applied to a real-world scenario via a case study and evaluate the performance considering different criteria (e.g., accuracy, interpretability, computational efficiency, and generalization).
• Confirm the efficiency of the given approach using score, aggregation, ranking, and visual analysis.

This study makes an innovative and multidisciplinary research contribution by proposing a CPF-DoCM model for assessing and selecting deep learning models in a media sentiment analysis study. It is the earliest endeavor to unite the models of circular fuzzy reasoning, the theory of PFS, and the DoCM in an integrated model selection pipeline that would suit the prodigious task of aspect-specific sentiment interpretation. To begin with, the paper provides a new approach to subjective model evaluation that is realized in the form of Pythagorean fuzzy numbers PFN and allows one to express the degree of membership, non-membership, and hesitation in human judgments. Second, it employs circular logic, allowing for a non-linear, direction-conscious comparison that takes into account subtle preference cycles among alternatives, which is something that ordinary ranking systems cannot do. Third, the DoCM features an intuitive interface that enables a decision-maker to rank model alternatives through visual and pairwise comparisons between DoC, rather than relying on arbitrarily assigned numerical scoring. The proposed framework offers a unique combination of the circular fuzzy reasoning, hesitation modeling, and Deck of Cards method to study both quantitative performance and qualitative interpretability together and, therefore, represents a meaningful contribution to addressing this gap in the research. To illustrate its usefulness, the framework is applied in a case study comparing the results of various deep learning models on several key metrics, including accuracy, interpretability, generalization, and computational efficiency. The suggested approach enables the identification of the most relevant model in the context, thereby increasing transparency, flexibility, and trust during the model selection process. This contribution presents a significant advancement for any researcher and practitioner working in natural language processing, decision science, sentiment analysis, and ethics in AI, especially in the entertainment and media analytics domain.

1.6. Layout

This article is based on the CPF information using the DoC method. The remaining part of this article is organized as follows: Section 1 presents an overview of this research work, and Section 2 provides a literature review of the DoC method. In Section 3, we explore CPFS and some fundamental operation laws in the environment of CPF information. Section 4 discusses the extension of the DoC technique, methodology, and algorithm in the framework of CPF information based on the MCDM problem. Moreover, we apply our proposed work to the numerical example and conduct a sensitivity and comparison analysis. Section 5 presents the article’s conclusion, outlines its limitations, and discusses the scope of future research.

2. Literature Review

2.1. Innovation in Fuzzy Modeling for Decision-Making

The fuzzy set (FS) theory, along with its extensions, has been widely applied in decision-making under uncertainty. Intuitionistic Fuzzy Sets (IFS) and Hesitant Fuzzy Sets introduced mechanisms to represent uncertainty and hesitation in human judgment. These were later expanded by Pythagorean Fuzzy Sets, which permitted the addition of squared membership and non-membership degrees of $\le 1$, and so provided greater freedom of movement in modeling uncertainty. Recent research has focused on advanced aggregation techniques for handling complex decision environments, such as power aggregation operators based on Aczel-Alsina T-norm and T-conorm for intuitionistic hesitant fuzzy information [9], and complex intuitionistic fuzzy Dombi prioritized aggregation operators for resilient green supplier selection [10]. Furthermore, Zhang et al. [11] have explored hybrid approaches for recommendation systems, proposing an online–offline combined adaptive hotel recommendation system that considers attribute importance and group consensus. This demonstrates the growing need for advanced fuzzy modeling to capture uncertainty and consensus in group decision-making. These trends are another indication of the need to have a more flexible structure, which the proposed CPF-DoCM model addresses by incorporating CPFS and the DoCM.

2.2. Sentiment Analysis in Media Reviews

Aspect-based sentiment analysis (ABSA) has become a fine-grained NLP task, the goal of which is to fetch sentiments associated with a particular component of the product or service [12]. In the media field, researchers have recently used models such as Bi-LSTMs, CNNs, and transformer-based models [13]. These models have been used to provide better sentiment prediction [14]. Nevertheless, the comparative assessment of these models is poor.

Sentiment analysis, particularly aspect-based sentiment analysis (ABSA), has undergone significant evolution with the adoption of deep learning architectures. CNN and LSTM (Long-Short Term memory) are examples of neural architecture that have substituted the traditional machine learning methods and essentially capture the contextual semantics. More recently, Transformer-based architectures like BERT and Transformer-XL have demonstrated superior performance in multiple sentiment benchmarks [12]. Hybrid approaches combining knowledge graphs and transformers have also emerged for handling domain-specific sentiment interpretation [15]. Comparative studies [13,15] consistently report that transformer models outperform RNN-based architectures, albeit at the cost of interpretability and computational efficiency. Nonetheless, little to no research takes into account the multi-criteria assessment of models to be used, looking merely at accuracy or F1-scores without reference to other dimensions like tractability, interpretability, and their usage-resource overhead.

2.3. Deep Learning Model Evaluation

Different architectures of deep learning models vary greatly in terms of complexity, interpretability, and the cost of training them [16]. In several works, these models have been benchmarked against conventional accuracy measures, which miss the subjective trade-offs and human preferences [17]. Others have implemented AHP and TOPSIS [18]. There are other MCDM techniques, but many need crisp inputs and linear rationale.

2.4. Multi-Criteria Decision-Making (MCDM) Framework

MCDM methods such as AHP, TOPSIS, and VIKOR have long been applied in model selection problems across domains, including education, supply chain, and IoT [18,19]. These methods, however, usually tend to assume crisp input and do not allow uncertainty, as well as hesitation and cyclic relations among the options. Additionally, conventional MCDM methods often fail to integrate qualitative dimensions, such as interpretability, with quantitative performance measures, which is crucial for making informed choices in the application of AI models in high-stakes areas. These gaps are filled in the suggested CPF-DoCM framework, which integrates the Pythagorean fuzzy logic and the Deck of Cards method in tackling ambiguity, cyclic preferences and expert hesitation, where the ensuing formulation leads to a more vigorous and more humanistic judgment.

PFS has been developed as a follow-up to IFS that provides a striking mechanism, representing not only membership and non-membership, but also hesitation [20]. This enables them to model uncertainty over expert opinions [21]. When used with decision frameworks, PFS has been found to be applicable in supplier selection, healthcare systems, and risk assessment [22].

2.5. Deck of Cards (DoC) and Circular Reasoning

The DoCM is an innovative, relatively new, and simple method of approaching pairwise comparison during decision-making [23]. With its help, users can organize comparisons that are not based on any numerical scale. The model can explain a short or preference cycle with a circular logic extension, where alternatives are not exactly better or worse. Still, they are interconnected with each other in a loop, a problem that is hardly discussed in the literature.

Optimal Deep Learning Architecture in Media Sentiment Interpretations

Sentiment analysis has recently progressed to aspect-specific sentence sentiment analysis (ABSA) [20], especially in media content, such as films and TV series. Throughout the task, the goal is not to determine whether a whole review has been positive or negative, but to identify and examine sentiments for particular attributes, e.g., acting, plot, direction, visual effects, or music. Such a small-grained analysis requires sturdy computational models to determine the semantic complexity and emotional dynamics implicit in human language. The conventional models, e.g., Convolutional Neural Networks (CNNs) [21] and Long Short-Term Memory (LSTM) networks, have proven helpful in corresponding to local and sequential patterns. Even though performance has highly improved using more advanced frameworks, like hybrid CNN-BiLSTM models, attention-based LSTMs, and transformer architectures, like BERT (Bidirectional Encoder Representations of Transformers), the choice of the best deep learning models to perform an ABSA on the problem of film and TV reviews is a nontrivial task. These reviews are colloquial, with much sarcasm, metaphors, and cultural linkages. In addition, models vary in performance, along with criteria such as classification accuracy, interpretability, training efficiency, and scalability. An example is that a BERT-based model can be more accurate than a real-time model in terms of the transparency of prediction. Conversely, a less complicated LSTM-based model may be faster in at least some tasks and more comprehensible, but less precise in tasks involving sophisticated sentiment. The question is, therefore, how can one conduct a multi-criteria assessment of numerous deep learning assemblers in order to compare existing models to identify which model is expected to perform best under the specific requirements of media sentiment interpretation. There is a problem with conventional metric-based comparison in that it cannot handle the ambiguity, trade-offs, and expert judgment that usually go along with model selection. To solve the problem, our research suggested a new model of decision-making that integrates CPFS and DoCM. In this combined framework, the fusion of the fuzzy expert measures and accommodating the hesitation in the model decisions are possible. The comparisons can be developed in a human-conscious and understandable circular reasoning manner. This approach will determine which deep learning structure is the most contextually appropriate and operationally efficient in such an aspect-specific sentiment analysis of entertainment media.

2.6. Multi-Criteria Decision-Making (MCDM) Approaches

In this section, we will study the basic concepts of intuitionistic fuzzy sets (IFS), circular intuitionistic fuzzy sets (CIFS), Pythagorean fuzzy sets (PFS), circular Pythagorean fuzzy sets (C-PFS), and some operational laws of C-PFS.

Definition 1.

([6]). An intuitionistic fuzzy set (IFS) $B$ on universe $X$ is an object in the form of:

$$B=\{X,{\mu }_x,v_x|x\in X\}$$

where ${\mu }_x\in$ [0,1] is called the degree of membership of $x$ in $B$ and $v_x\in$ [0,1] is called the degree of non-membership of x in $B$. This satisfies the following condition:

$$0\le {\mu }_x+v_x\le 1$$

Definition 2.

([24]). Consider a fixed universe $U$; then, a circular intuitionistic fuzzy set (Cir-IFS) $B$ on $X$ It is defined by the following:

$$B=\left\{\left(X,{\mu }_x,v_x;r|\mathcal{x}\in X\right)\right\}$$

where ${\mu }_x\in \left[\mathrm{0,1}\right]$ represents the MD, and $v_x\in \left[\mathrm{0,1}\right]$ represents the NMD. These degrees satisfy the conditions $0\le {\mu }_x+v_x\ge 1,$ where the hesitancy degree is $\mathsf{\alpha }$ $= 1-{\mu }_x-v_x$. The notion $r\in \left[\mathrm{0,1}\right]$ represents the radius around the circle of each element. For continuity, $\left({\mu }_x,v_x,r\right)$ is known as a circular intuitionistic fuzzy value (Cir-IFVS).

Definition 3.

([7]). Consider a fixed set $U$; then, a Pythagorean fuzzy set (PFS) $B$ on $X$ is defined as follows:

$$B=\{X,{\mu }_x,v_x|x\in X\}$$

where ${\mu }_x\in$ [0,1] is called the degree of membership of $x$ in $B$ and $v_x\in$ [0,1] is called the degree of non-membership of x in $B$, and satisfies the following condition:

$$0\le {\mu }_x^2+v_x^2\le 1$$

Definition 4. 

([25]). Consider $r\in [0, 1]$. Then, a Circular Pythagorean fuzzy set (C-PFS) $B$ on $X$ is defined as follows:

$$B_r=\{X,{\mu }_x,v_x;r|x\in X\}$$

where ${\mu }_x\in$ [0,1] is called the degree of membership of $x$ in $B$ and $v_x\in$ [0,1] is called the degree of non-membership of x in $B$. ${(\mu }_x,v_x)$ is called the Pythagorean Fuzzy Value and satisfies the following condition:

$$0\le {\mu }_x^2+v_x^2\le 1$$

Definition 5.

The score function for the circular Pythagorean fuzzy set is defined as follows:

$$\omega ={\mu }_x^2-v_x^2$$

Definition 6.

These are some basic operations of Circular Pythagorean fuzzy: For this, consider $x_{{{\mathcal{C}}_x}_1}=\left\{\left(\mathcal{x},{\mu }_x,{\nu }_x;{\mathcal{C}}_{x_1}|\right)|\mathcal{x}\in \mathrm{X}\right\}$  and $x_{{{\mathcal{C}}_x}_2}=\left\{\left(\mathcal{x},{\mu }_x,{\nu }_x,;{\mathcal{C}}_{x_2}|\right)|\mathcal{x}\in \mathrm{X}\right\}$ then, given below are some basic operations on C-PFS:

$$x_{{{\mathcal{C}}_x}_1}^c= \left\{\left(\mathcal{x},{\mu }_{\alpha }, {\nu }_{\alpha };{\mathcal{C}}_{{\alpha }_1}|\right)|\mathcal{x}\in X \right\}$$

(1)

$$x_{{{\mathcal{C}}_x}_1}\subset x_{{{\mathcal{C}}_x}_2}\mathrm{iff} {{\mathcal{C}}_x}_1\le {{\mathcal{C}}_x}_2 \mathrm{and} {\nu }_{x_1}\le {\nu }_{x_2}, \mathrm{and} {\mu }_{x_1}\ge {\mu }_{x_2}.$$

(2)

$$x_{{{\mathcal{C}}_x}_1}={\vartheta }_{{{\mathcal{C}}_{\vartheta }}_2}\mathrm{iff} {{\mathcal{C}}_{\alpha }}_1={{\mathcal{C}}_{\vartheta }}_2 \mathrm{and} {\nu }_{\alpha }={\nu }_{\vartheta }, \mathrm{and} {\mu }_x={\mu }_{\vartheta }.$$

(3)

$$x_{{{\mathcal{C}}_x}_1}{\cup }_{min } {\vartheta }_{{{\mathcal{C}}_{\vartheta }}_2}=\left\{\left(\mathcal{x},\mathit{max}\left({\mu }_x,{\mu }_{\vartheta }\right), min\left({\nu }_x,{\nu }_{\vartheta }\right),;{min(\mathcal{C}}_{x_1},{{\mathcal{C}}_{\vartheta }}_2\left)\right|\right)|\mathcal{x}\in X \right\}$$

(4)

$$x_{{{\mathcal{C}}_x}_1}{\cup }_{max } {\vartheta }_{{{\mathcal{C}}_{\vartheta }}_2}=\left\{\left(\mathcal{x},\mathit{max}\left({\mu }_x,{\mu }_{\vartheta }\right), min\left({\nu }_x,{\nu }_{\vartheta }\right),;{max(\mathcal{C}}_{x_1},{{\mathcal{C}}_{\vartheta }}_2\left)\right|\right)|\mathcal{x}\in X \right\}$$

(5)

$$x_{{{\mathcal{C}}_x}_1}{\cap }_{min } {\vartheta }_{{{\mathcal{C}}_{\vartheta }}_2}=\left\{\left(\mathcal{x},\mathit{min}\left({\mu }_x,{\mu }_{\vartheta }\right), min\left({\nu }_x,{\nu }_{\vartheta }\right),;{min(\mathcal{C}}_{x_1},{{\mathcal{C}}_x}_2\left)\right|\right)|\mathcal{x}\in X \right\}$$

(6)

3. Methodology

3.1. Circular Pythagorean Deck of Cards (DoC) Method

This study applies the DoCM to address an MCDM problem characterized by C-PFs’ uncertainty. To tackle these MCDM challenges [19], an effective DM technique is presented. The primary objective of any MCDM problem is to rank the set of alternatives according to the specified criteria. This section presents the formulation of the DoCM integrated with CPFS for selecting optimal deep learning architectures in media sentiment interpretation. Let us consider $A = \{A_1, A_2, \dots , A_{\mathrm{m}}\}$, which is a set of m alternatives (deep learning models) and $C = \{C_1, C_2, \dots , C_{\mathrm{n}}\}$, which is a set of n criteria (e.g., accuracy, interpretability). Here, $W = \{W_1, W_2, \dots , W_{\mathrm{n}}\}$ optional weights for each criterion. We will evaluate our example problem using the Circular Pythagorean Fuzzy Deck of cards method in this evaluation; the alternatives are Pythagorean fuzzy values $\mu ,v ϵ\left[\mathrm{0,1}\right]$, and as we are dealing with a circular Pythagorean CPF framework, we will consider that the $r$ term which belongs to $\left[\mathrm{0,1}\right]$ DoCM is a simple, cognitively compatible strategy for multi-criteria decision-making (MCDM). It is more useful when a fuzzy setting is considered to recombine with the same. Compared to standard pairwise comparison methods, DoCM enables the decision-maker to demonstrate preferences in a visual form and in an orderly deck of winners and losers, significantly decreasing the cognitive load. Together with fuzzy logic, especially with Pythagorean fuzzy set, it successfully reflects human beings’ lack of clarity, indecisiveness, and sketchy judgment. It can also apply to circular reasoning, where it provides greater flexibility in comparison in those situations where alternatives are not exactly linear and hierarchical. Its clarity, straightforwardness, and ability to fit into expert-facing situations make it a perfect tool in intricate decision settings.

Since no large-scale publicly available, aspect-annotated dataset specifically designed to support film and television reviews is currently available, the current paper represents an experiment on a hypothetical dataset that mirrors real-life conditions, which relies on the existent work performed on the sentiment distribution and linguistic structure. The method allows a limited assessment of the proposed internal validity and interpretability of the CPFS-DoCM framework.

We will solve our example problem by using this hybrid method. This method solves the uncertainty and ambiguity of the problem more efficiently. In the DoCM, we will follow these steps:

1.

Decision-makers rank alternatives (or criteria) from most preferred to least preferred. Let $A = \{A_1, A_2, ..., A_{\mathrm{m}}\}$ be alternatives and $C = \{C_1, C_2, \dots , C_{\mathrm{m}}\}$ be the criteria. We will rank these alternatives according to our preferences.

2.

A comparison table is created by specifying the number of blank cards (gaps) between each pair of elements. The matrix includes all pairwise comparisons and may include interval or uncertain values. These values may vary according to the condition.

3.

Check the consistency of the table, which highlights the use of the rule, and the values must satisfy the condition of consistency so that we can make a consistent table; here, $e_{\mathrm{i}\mathrm{j}}$ and $e_{\mathrm{j}\mathrm{k}}$ are their values in blank cards whose values we will check for consistency, such that the sum of these values should belong to the next card in the table. The equation below will be used to check the consistency of the table.

$$e_{\mathrm{i}\mathrm{j}}+e_{\mathrm{j}\mathrm{k}}+1=e_{\mathrm{i}}; \mathrm{for} \mathrm{all} i<j<k.$$

If inconsistencies are found, revise through decision-maker interaction. And change the value until it fulfills the condition. But one thing must be under consideration. $i < j < k$.

4.

Once consistent, calculate the weight for each item, and the weight will be calculated by using these formulae, where $w_1$ must start with 1.

$$w_{\mathrm{i}}=w_1+\sum (e_{\mathrm{k}\mathrm{k}+1}+1); k=1 to i-1$$

Then, normalize the weights by using the following formula.

$$wi={\displaystyle \frac{wi}{\sum w_{\mathrm{j}}}}$$

5.

Make a decision matrix that contains circular Pythagorean fuzzy numbers and acceptable hesitant values from the Pythagorean values using this formula:

$$h=\sqrt{1-{{\mu }_{\mathrm{i}\mathrm{j}}}^2-{v_{\mathrm{i}\mathrm{j}}}^2}$$

where $h$ denotes the hesitation value and is obtained from the Pythagorean number, and where ${\mu }_{\mathrm{i}\mathrm{j}}$ represents the membership degree and ${\nu }_{\mathrm{i}\mathrm{j}}$ presents the non-membership degree.

$$P_{\mathrm{i}\mathrm{j}}=({\mu }_{\mathrm{i}\mathrm{j}}, {\nu }_{\mathrm{i}\mathrm{j}})$$

Such that ${\mu }^2+{\nu }^2\le 1.$

Then, compute the circular Pythagorean fuzzy score:

$$r_{\mathrm{i}\mathrm{j}} =\left({{\mu }_{\mathrm{i}\mathrm{j}}}^2-{v_{\mathrm{i}\mathrm{j}}}^2\right)\times {\mathcal{C}}_{x_1}$$

6.

For each criterion $C_{\mathrm{j}},$ construct matrix $M^{\left(\mathrm{j}\right)}$ as follows and make a pairwise comparison table for each criterion. The values should fulfill the following condition.

$$M^{\left(\mathrm{j}\right)}\left(i, k\right)=\left\{\begin{array}{c}1 if r_{\mathrm{i}\mathrm{j}}>r_{\mathrm{k}}\\ 0 if r_{\mathrm{i}\mathrm{j}}=r_{\mathrm{k}\mathrm{j}}\\ -1 if r_{\mathrm{i}\mathrm{j}}<r_{\mathrm{k}}\end{array}\right\}$$

7.

Now compute the Local Scores by summing up all the pairwise comparison table values of each criteria; add each row to the other criteria rows and calculate the local score.

$$S_{\mathrm{i}\mathrm{j}}=\Sigma M^{\left(\mathrm{j}\right)}(i, k)$$

For $k = 1$ to $m$ for unweighted, $S_{\mathrm{i}} = \Sigma S_{\mathrm{i}\mathrm{j}}$ over all $j$. For weighted, $S_{\mathrm{i}} = \Sigma w_{\mathrm{j}} \times S_{\mathrm{i}\mathrm{j}}$.

8.

Rank alternatives based on descending $S_{\mathrm{i}}$ values, on the basis of the calculated scores.

9.

This is a pictorial representation of ranks.

3.2. Decision-Making Algorithm

The decision-making algorithm of CPF-DoCM is given in Figure 1.

Although the CPFS-DoCM model introduces additional steps for preference elicitation and fuzzy value combination, it still exhibits reasonable computational complexity. The methods typically employ matrix-based computations and simple arithmetic operations on preference scores, in contrast to hierarchical MCDM approaches, such as AHP-TOPSIS combinations, which are significantly more computationally intensive. The time of computation was insignificant in this case (5 alternatives × 4 criteria). Its future work should benchmark its performance on larger decision spaces.

4. Evaluation of Optimal Deep Learning Architecture in Media Sentiment Interpretation

Evaluating optimal deep learning models for interpreting sentiment in media involves examining several, often conflicting, performance measures, such as accuracy, interpretability, computational efficiency, and generalization ability. The conventional evaluation metrics will consider only accuracy without considering the trade-offs essential in real-life applications of the technology, particularly in high-stakes fields such as journalism, politics, and mental health monitoring. This paper uses the CPF-DoCM as an MCDM method to evaluate deep learning architectures and rank them rigorously. There are five other types of architecture, including BERT, LSTM, Transformer-XL, RoBERTa, and BiLSTM, that have been tested against four key parameters based on expert linguistic judgments data recorded in Circular Pythagorean Fuzzy Numbers (CPFNs). Such fuzzy judgments enable the choice makers to represent preference and indecisiveness among criteria more naturally, with the drawbacks of binary or crisp evaluation models. The DoC method is incorporated to calculate the relative importance weights of the criteria based on a static and visual way of expressing preference. This makes the stakeholder input cognitively convenient and mathematically sound so that a correct representation of expert views can be achieved in a fuzzy MCDM setup. After the formation of the weights, the advanced fuzzy operators will be used to aggregate the CPFNs, and alternative scores will also be calculated.

4.1. Case Study

The case study utilizes simulated data, rather than a real-world benchmark dataset. It aims to demonstrate how the CPF-DoCM framework operates within a controlled framework and how expert estimation and fuzzy preference may inform the ranking of the models. The hypothetical performance values for models were chosen in alignment with trends reported in recent ABSA benchmark studies [12,15]. The next step will be an empirical in situ proof of the practical effectiveness of ranked models with regular data that covers such websites as IMDb or Rotten Tomatoes.

To increase transparency and explainability for practitioners, the CPF-DoCM process employed in this case study allows every step of the decision-making process to be represented in a traceable and interpretable manner. The Deck of Cards Method (DoCM) enables professionals to intuitively and graphically reveal their preferences through pairwise comparisons. In contrast, CPFS addresses the issue of hesitation and uncertainty in a well-structured manner. Moreover, the overall scores of each alternative can be disintegrated to reveal the extent to which each criterion has contributed to the final rank. The justification and transparency in the model selection outcome are evident in this layered structure.

Here, we will solve an illustrative example by considering four criteria and five alternatives (

Table 2. Description of criteria and alternative.

Criteria Code	Criteria Name	Description
${\mathit{C}}_{\mathbf{1}}$	Sentiment Classification Accuracy	The relative identification of sentiment based on particular facets such as acting, plot, music, etc.
${\mathit{C}}_{\mathbf{2}}$	Interpretation of Model Outputs	How explainable are the inner processes and outputs of the model to the analysts and other stakeholders?
${\mathit{C}}_{\mathbf{3}}$	Computational Efficiency	Memory usage, training time, and transferability to different datasets.
${\mathit{C}}_{\mathbf{4}}$	Cross-Domain Generalization	Performance on new genres or content platforms (e.g., Netflix vs. IMDb)
Alternative Code	Alternative Name	Description
${\mathit{A}}_{\mathbf{1}}$	Bidirectional Encoder Representations from Transformers (BERT) + Bidirectional Gated Recurrent Unit (BiGRU) + Fusion Assembler	Uses BERT embedding coupled with Bi-GRU to classify a series of sentiments.
${\mathit{A}}_{\mathbf{2}}$	LSTM (Long Short-Term Memory) with Attention Assembler	Applies LSTM with an attention mechanism that underlines the needed tokens in sentiment classification.
${\mathit{A}}_{\mathbf{3}}$	Multi-Convolutional Neural Network (M-CNN) Hierarchical Model	The hierarchical CNN approach is utilized on segmented reviews and aspects.
${\mathit{A}}_{\mathbf{4}}$	Transformer-XL Integrator	Deep sentiment context in long-range Transformer using segment-level recurrence.
${\mathit{A}}_{\mathbf{5}}$	Hybrid Knowledge Graph-Transformer	End-to-end aspect-specific inference over structured/unstructured information with Transformer and KG embedding.

). We will rank the best alternative based on the requirements, and for this decision-making, we will use a method and work with the CPF framework.

The alternatives will be represented as $A=\left\{A_1\dots A_4,A_5\right\}$ and the criteria will be represented as $C=\left\{C_1,C_2,C_3\dots ,C_5\right\}$. Weights will be assigned to each criterion using DoCM, and a pairwise blank card will be used to calculate the normalized weights.

These models have not been applied in the context of this study. They were chosen as the representative alternatives to be evaluated in the CPFS-DoCM framework.

4.2. Numerical Evaluation

Step 1. Decision-makers rank alternatives (or criteria) from most preferred to least preferred. Let $A = \{A_1, A_2, \dots , A_{\mathrm{m}}\}$ be alternatives and $C = \{C_1, C_2, \dots , C_{\mathrm{n}}\}$. The ranking of alternatives on the above criteria is shown in

Table 3. Rank alternatives.

${\mathit{A}}_{\mathbf{1}}$	$BERT+BiGRU$	4
${\mathit{A}}_{\mathbf{2}}$	$LSTM+Attention$	$3$
${\mathit{A}}_{\mathbf{3}}$	$Multi-CNN$	$1$
${\mathit{A}}_{\mathbf{4}}$	$Transformer-XL$	$2$
${\mathit{A}}_{\mathbf{5}}$	$KG+Transformer$	$5$

.

Step 2. A comparison table is created by specifying the number of blank cards (gaps) between each pair of elements. The matrix includes all pairwise comparisons and may consist of interval or uncertain values, as shown in

Table 4. Comparison table of blank cards.

	${\mathit{A}}_{\mathbf{1}}$	${\mathit{A}}_{\mathbf{2}}$	${\mathit{A}}_{\mathbf{3}}$	${\mathit{A}}_{\mathbf{4}}$	${\mathit{A}}_{\mathbf{5}}$
${\mathit{A}}_{\mathbf{1}}$	$0$	$1$	$3$	$4$	$6$
${\mathit{A}}_{\mathbf{2}}$	⍰	$0$	$2$	$3$	$5$
${\mathit{A}}_{\mathbf{3}}$	⍰	⍰	$0$	$1$	$3$
${\mathit{A}}_{\mathbf{4}}$	⍰	⍰	⍰	$0$	$2$
${\mathit{A}}_{\mathbf{5}}$	⍰	⍰	⍰	⍰	$0$

.

Step 3. Check the consistency of the table using the rule, as shown in

Table 5. Consistency table.

$\mathit{B}\mathit{e}\mathit{t}\mathit{w}\mathit{e}\mathit{e}\mathit{n}$	$\mathit{C}\mathit{a}\mathit{r}\mathit{d}\mathit{s}$
${\mathit{A}}_{\mathbf{1}}\to {\mathit{A}}_{\mathbf{2}}$	$1$
${\mathit{A}}_{\mathbf{2}}\to {\mathit{A}}_{\mathbf{3}}$	$2$
${\mathit{A}}_{\mathbf{3}}\to {\mathit{A}}_{\mathbf{4}}$	$1$
${\mathit{A}}_{\mathbf{4}}\to {\mathit{A}}_{\mathbf{5}}$	$2$

.

For all $i < j < k.$ If inconsistencies are found, revise through decision-maker interaction.

Step 4: Once consistency is achieved, calculate the weight for each item, as shown in

Table 6. Calculate the weight.

Alternative	Formula	Raw Score
${\mathit{A}}_{\mathbf{1}}$	$Start with 1$	$1$
${\mathit{A}}_{\mathbf{2}}$	2	2
${\mathit{A}}_{\mathbf{3}}$	4	4
${\mathit{A}}_{\mathbf{4}}$	5	5
${\mathit{A}}_{\mathbf{5}}$	$7$	$7$
		$19$

.

$k = 1 to i-1.$ Then, normalize the results, as shown in

Table 7. Normalized Weights.

Final Weights
${\mathit{A}}_{\mathbf{1}}$	$0.053$
${\mathit{A}}_{\mathbf{2}}$	$0.105$
${\mathit{A}}_{\mathbf{3}}$	$0.211$
${\mathit{A}}_{\mathbf{4}}$	$0.263$
${\mathit{A}}_{\mathbf{5}}$	$0.368$

.

Step 5. A Pythagorean fuzzy number gives each evaluation, as shown in

Table 8. Decision matrix of PFS.

	${\mathit{C}}_{\mathbf{1}}$					${\mathit{C}}_{\mathbf{2}}$
	${\mu }_x$	$v_x$	$h_x$	$r$	$\omega :score$	${\mu }_x$	$v_x$	$h_x$	$r$	$\omega :score$
A1	$0.3$	$0.2$	$0.9$	$0.3$	$0.02$	$0.2$	$0.1$	$0.97$	$0.50$	$0.02$
${\mathit{A}}_{\mathbf{2}}$	$0.6$	$0.5$	$0.6$	$0.7$	$0.08$	$0.5$	$0.4$	$0.77$	$0.80$	$0.07$
${\mathit{A}}_{\mathbf{3}}$	$0.6$	$0.3$	$0.7$	$0.4$	$0.11$	$0.8$	$0.3$	$0.52$	$0.21$	$0.12$
${\mathit{A}}_{\mathbf{4}}$	$0.5$	$0.1$	$0.9$	$0.2$	$0.05$	$0.5$	$0.2$	$0.84$	$0.70$	$0.15$
${\mathit{A}}_{\mathbf{5}}$	$0.8$	$0.2$	$0.6$	$0.8$	$0.48$	$0.7$	$0.4$	$0.59$	$0.30$	$0.10$
${\mathit{C}}_{\mathbf{3}}$						${\mathit{C}}_{\mathbf{4}}$
$\mathit{m}$		$nm$	$h$	$r$	$score$	$m$	$nm$	$h$	$r$	$score$
$\mathbf{0.23}$		$0.12$	$0.97$	$0.60$	$0.02$	$0.4$	$0.1$	$0.9$	$0.3$	$0.05$
$\mathbf{0.18}$		$0.13$	$0.98$	$0.70$	$0.01$	$0.3$	$0.14$	$0.9$	$0.2$	$0.01$
$\mathbf{0.7}$		$0.2$	$0.69$	$0.10$	$0.05$	$0.5$	$0.2$	$0.8$	$0.6$	$0.13$
$\mathbf{0.6}$		$0.1$	$0.79$	$0.90$	$0.32$	$0.7$	$0.1$	$0.7$	$0.2$	$0.10$
$\mathbf{0.34}$		$0.16$	$0.93$	$0.30$	$0.03$	$0.4$	$0.3$	$0.9$	$0.1$	$0.01$

.

Step 6. For each criterion $C_{\mathrm{j}},$ construct matrix $M^{\left(\mathrm{j}\right)}$, as given in

Table 9. Pairwise comparison matrix.

	${\mathit{C}}_{\mathbf{1}}$					${\mathit{C}}_{\mathbf{2}}$					${\mathit{C}}_{\mathbf{3}}$					${\mathit{C}}_{\mathbf{4}}$
${\mathit{A}}_{\mathbf{1}}$	$0$	$-1$	$-1$	$-1$	$-1$	$0$	$-1$	$-1$	$-1$	$-1$	$0$	$1$	$-1$	$-1$	$-1$	$0$	$1$	$-1$	$-1$	$1$
${\mathit{A}}_{\mathbf{2}}$	$1$	$0$	$-1$	$1$	$-1$	$1$	$0$	$-1$	$-1$	$-1$	$-1$	$0$	$-1$	$-1$	$-1$	$-1$	$0$	$-1$	$-1$	$0$
${\mathit{A}}_{\mathbf{3}}$	$1$	$1$	$0$	$1$	$-1$	$1$	$1$	$0$	$-1$	$1$	$1$	$1$	$0$	$-1$	$1$	$1$	$1$	$0$	$1$	$1$
${\mathit{A}}_{\mathbf{4}}$	$1$	$-1$	$-1$	$0$	$-1$	$1$	$1$	$1$	$0$	$1$	$1$	$1$	$1$	$0$	$1$	$1$	$1$	$-1$	$0$	$1$
${\mathit{A}}_{\mathbf{5}}$	$1$	$1$	$1$	$1$	$0$	$1$	$1$	$-1$	$-1$	$0$	$1$	$1$	$-1$	$-1$	$0$	$-1$	$0$	$-1$	$-1$	$0$

.

Step 7. Now, compute local scores, as given below in

Table 10. Compute local scores.

	${\mathit{C}}_{\mathbf{1}}$	${\mathit{C}}_{\mathbf{2}}$	${\mathit{C}}_{\mathbf{3}}$	${\mathit{C}}_{\mathbf{4}}$
${\mathit{A}}_{\mathbf{1}}$	$-4$	$-4$	$-2$	$0$
${\mathit{A}}_{\mathbf{2}}$	$0$	$-2$	$-4$	$-3$
${\mathit{A}}_{\mathbf{3}}$	$2$	$2$	$2$	$4$
${\mathit{A}}_{\mathbf{4}}$	$-2$	$4$	$4$	$2$
${\mathit{A}}_{\mathbf{5}}$	$4$	$0$	$0$	$-3$

.

For $k = 1$ to $m$ for unweighted, $S_{\mathrm{i}} = \Sigma S_{\mathrm{i}\mathrm{j}}$ overall $j$; for weighted, $S_{\mathrm{i}} = \Sigma W_{\mathrm{j}} \times S_{\mathrm{i}\mathrm{j}}$.

Step 8. Rank alternatives based on descending $S_{\mathrm{i}}$ values, as given in

Table 11. Rank alternative $Sᵢ$ values.

Ranking of Alternatives
${\mathit{A}}_{\mathbf{1}}$	$-0.53$	$4$
${\mathit{A}}_{\mathbf{2}}$	$-0.95$	$5$
${\mathit{A}}_{\mathbf{3}}$	$2.11$	$2$
${\mathit{A}}_{\mathbf{4}}$	$2.11$	$1$
${\mathit{A}}_{\mathbf{5}}$	$0.37$	$3$

.

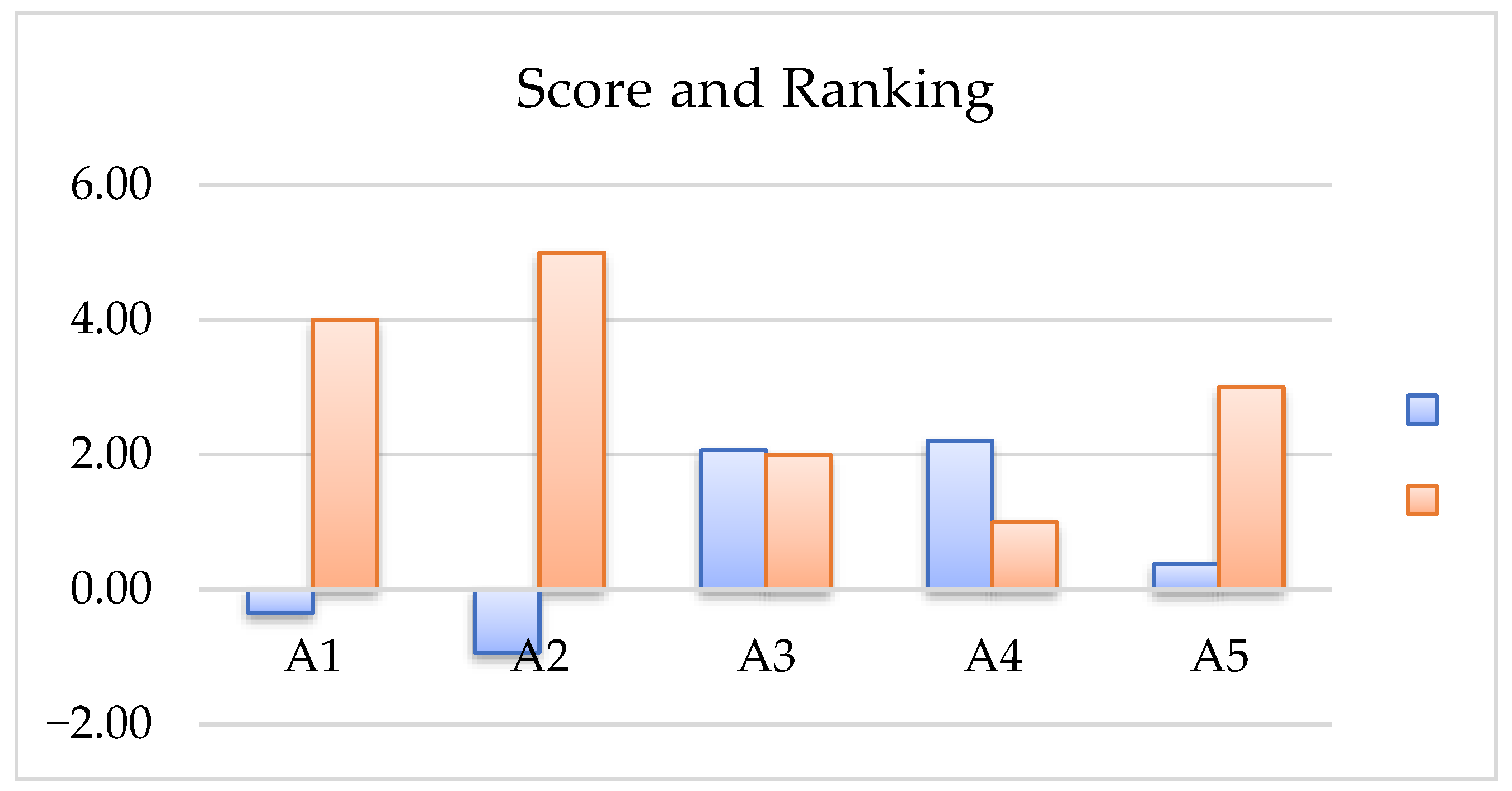
Step 9. This is a pictorial representation of the ranking of alternatives, as given in Figure 2.

4.3. Result Discussion and Comparison

The findings based on the CPF-DoC model indicate that $A_4$ Integrator is an optimal deep learning architecture for interpreting media sentiments. Such a decision is formed on the aggregation of the scores of four critical points of examinations, and the norm score in the aggregate of $A_4$ is $2.7143$ This indicates the stability and uniformity of the examination assessment. In particular, $A_4$ stood out in interpretability $C_2$. It also demonstrated competitiveness in all other measures, indicating that it is likely a substantial trade-off of the long-range dependencies and semantic depth characteristics important in fine-grained sentiment processing. The second-best alternative $A_1$ was somewhat more precise and adaptive, lower in its semantic representation, and thus not as holistic. Alternative $A_3,{ A}_2,{ A}_5$ underperformed, with less consistency in its performance and lower robustness or explainability. These results confirm the effectiveness of the CPF-DoC approach in reflecting expert judgment and processing vague, uncertain assessments. Possessing the ability to model qualitative gaps, as well as maintain ordinal preferences, is very useful in sophisticated decision-making scenarios, such as selecting deep learning models for sentiment analysis tasks.

The integration of both the CPFS and DoCM is computationally more demanding than conventional methods, as it involves calculations of fuzzy membership and hesitation degrees, as well as pairwise comparisons. For the current study (five models and four criteria), this is easily manageable. However, in very large-scale comparisons (e.g., hundreds of models), the main challenges would be obtaining better memory and time to handle large, fuzzy matrices, exerting greater effort to obtain professional input, and necessitating parallel processing schemes and automated judgment tools. This is an area we can improve upon in the future. Furthermore, the final scores of alternatives can also be very close or even tied in cases where the circular scoring approach of CPFS-DoCM is used. This is indicative of real-life uncertainty in expert judgment and does not counter the validity of the method. In these situations, the decision-maker has the option of utilizing tie-breaking methods, including reconsidering specific high-weight criteria, adding an auxiliary criterion, or seeking other expert opinion. The scoring is visual and circular and assists in determining when choices are almost identical on a scale where decisions can be refined intelligently rather than forced-ranked.

Decision explainability is very significant, especially when ranking complicated deep-learning models. It increases transparency in three critical ways by CPF-DoCM: Explicit Weighting of Criteria. Unlike black-box optimization approaches, CPF-DoCM displays the relative importance of each criterion (e.g., Accuracy, Interpretability, Complexity) and how these weights influence rankings. Final Scores Decomposition: The score of an alternative can be broken down into the contributions of individual criteria, making it obvious why a given model is ranked above another one.

The comparative study of extensions of fuzzy sets highlights the exclusive benefits of the CPFS model used in the paper. Conventional fuzzy models, such as IFS and PFS, provide basic functionalities for representing uncertainty and non-membership. Still, they are not geometric and fail to support the fine-grained expression of preference. CIFS takes this further in some aspects, providing radius-based membership and the ability to visualize membership. However, it still has not considered ways to incorporate the intuitionistic nature of such tasks by expert-based preference elicitation techniques such as the DoC framework. To the contrary, CPFS is an extension that allows circular (as well as semantically richer, but of limited geometric scope) geometry, in addition to supporting all classical fuzzy-related properties, which are uncertainty accounting, hesitancy, and explicit non-membership, providing it with a unique ability in modeling complex human judgments. When used with the DoC technique, CPFS allows an interactive, scale-based, cognitively natural decision-making process and is thus particularly adequate for formulating optimal deep learning architectures in sentiment analysis implementations. The comparative table based on characteristics is given in

Table 12. Comparative table on basis of characteristics.

$\mathbf{C}\mathbf{h}\mathbf{a}\mathbf{r}\mathbf{a}\mathbf{c}\mathbf{t}\mathbf{e}\mathbf{r}\mathbf{i}\mathbf{s}\mathbf{t}\mathbf{i}\mathbf{c}$	$\mathbf{I}\mathbf{F}\mathbf{S}$	$\mathbf{I}\mathbf{V}\mathbf{I}\mathbf{F}\mathbf{S}$	$\mathbf{P}\mathbf{F}\mathbf{S}$	$\mathbf{C}\mathbf{I}\mathbf{F}\mathbf{S}$	$\mathbf{C}\mathbf{P}\mathbf{F}\mathbf{S} (\mathbf{Y}\mathbf{o}\mathbf{u}\mathbf{r} \mathbf{S}\mathbf{t}\mathbf{u}\mathbf{d}\mathbf{y})$
Handles Uncertainty
Captures Hesitancy
Explicit Non-membership Representation
Radius-based Membership Modeling
Geometric Interpretation
Supports Advanced Preference Elicitation
Suited for Deck of Cards Method (DoC)

.

To support classical performance comparison, the materials used to evaluate all five deep learning models classically, using averaged traditional assessment scores (e.g., Precision, Recall, F1-score, and training time), were provided (see

Table 13. Comparison analysis (deep learning models).

Model	Precision	Recall	F1-Score	Interpretability	Final CPFS Score
A1: BERT + BiGRU	0.87	0.84	0.85	Medium	0.76
A2: LSTM + Attention	0.84	0.88	0.86	Medium–High	0.72
A3: Multi-CNN	0.80	0.79	0.79	Low	0.60
A4: Transformer-XL	0.90	0.83	0.86	Medium	0.81
A5: Hybrid KG-Transformer	0.88	0.87	0.87	High	0.85

). These values are either hypothetically simulated based on reasonable assumptions or derived from published literature benchmarks on sentiment analysis. Although these metrics offer a robust empirical comparison for selecting the model, they fail to reflect explainability, cross-domain generalization, and preference-based trade-offs across criteria. The suggested CPFS-DoCM framework combines these quantitative measures with qualitative and strategic standards (e.g., interpretability, decision-maker preferences), thereby providing a more holistic and flexible model selection methodology.

The interpretability is determined qualitatively depending on the model architecture and insights reported in the literature. Although the F1-Score is greatest in $A_5$, it also demands a better amount of training resources. The aggregate score computed in the final CPFS-DoCM combines the classical scores and other criteria of the decision-maker, exemplifying how the method under consideration attempts to integrate accuracy, efficiency, and interpretability.

4.4. Sensitivity Analysis

The sensitivity analysis shows that, despite varying the weight of individual criteria like the accuracy or interpretability, Transformer-XL ${\mathrm{A}}_4$ is the highest-ranked architecture. This proves the strength of the CPF-DoC model in identifying the best architecture. Perturbations improve (or worsen) other alternatives, but the ranking order is relatively consistent, strengthening the regularity and soundness of the developed method.

Table 14. Sensitivity analysis.

$\mathit{A}\mathit{l}\mathit{t}\mathit{e}\mathit{r}\mathit{n}\mathit{a}\mathit{t}\mathit{i}\mathit{v}\mathit{e}$	$\mathit{B}\mathit{a}\mathit{s}\mathit{e} \mathit{S}\mathit{c}\mathit{o}\mathit{r}\mathit{e}$	$+10\mathbf{\%} \mathit{A}\mathit{c}\mathit{c}\mathit{u}\mathit{r}\mathit{a}\mathit{c}\mathit{y}$	$-10\mathbf{\%} \mathit{A}\mathit{c}\mathit{c}\mathit{u}\mathit{r}\mathit{a}\mathit{c}\mathit{y}$	$+10\mathbf{\%} \mathit{I}\mathit{n}\mathit{t}\mathit{e}\mathit{r}\mathit{p}\mathit{r}\mathit{e}\mathit{t}\mathit{a}\mathit{b}\mathit{i}\mathit{l}\mathit{i}\mathit{t}\mathit{y}$	$-10\mathbf{\%} \mathit{I}\mathit{n}\mathit{t}\mathit{e}\mathit{r}\mathit{p}\mathit{r}\mathit{e}\mathit{t}\mathit{a}\mathit{b}\mathit{i}\mathit{l}\mathit{i}\mathit{t}\mathit{y}$
${\mathit{A}}_{\mathbf{1}}$ BERT + BiGRU	$2.61$	$2.68$	$2.54$	$2.69$	$2.53$
${\mathit{A}}_{\mathbf{2}}$ LSTM + Attention	$1.29$	$1.33$	$1.25$	$1.32$	$1.26$
${\mathit{A}}_{\mathbf{3}}$ Multi-CNN	$2.25$	$2.33$	$2.17$	$2.31$	$2.19$
${\mathit{A}}_{\mathbf{4}}$ Transformer-XL	$2.71$	$2.77$	$2.65$	$2.76$	$2.66$
${\mathit{A}}_{\mathbf{5}}$ KG + Transformer	$0.67$	$0.70$	$0.64$	$0.69$	$0.65$

shows the sensitivity analysis of the best alternatives.

4.5. Practical Implications

This study has significant practical implications, especially in artificial intelligence-based decision-making when applied to the sentiment analysis of any media. The model provides a systematic yet flexible framework for evaluating and selecting between deep learning architectures in cases of uncertainty, imprecision, and subjectivity, thereby merging the CPFS and the DoC methods. This could particularly be applied to media corporations, social platforms, and policymakers who require sentiment analysis on the fly to provide real-time analytics, identify misinformation, and trace trends in people’s opinions. This model enables decision-makers to incorporate expert linguistic judgment in a mathematically solid ranking procedure that can be more transparent and traceable when choosing the models with the best performance, like Transformer-XL or hybrids based on BERT. In addition, its ability to record subtle choices and trade-offs extends to decisions under high-value and context-specific situations that align with operational objectives and ethical considerations in AI implementation. It is also possible to apply this strategy in other fields that deal with strategic model choice, including finance, healthcare, and cybersecurity. Although the presented application of domain-independent CPF-DoCM framework is in media sentiment interpretation, the framework itself is purely general. Its ability to handle uncertainty and integrate subjective preferences makes it suitable for other sectors such as healthcare (model selection), finance (portfolio optimization), and cybersecurity (threat detection). The framework needs the domain-specific criteria to be defined so as to adapt, yet its structure concerning computation does not change.

5. Conclusions

This paper proposed a new decision-making model, which involves the DoCM intersected with CPFS to determine the best deep learning architecture that will facilitate the interpretation of media sentiment. By including subjective expert opinions, the model considers the ambiguity and reluctance of assessing various deep learning options. The DoCM’s co-constructive character allowed us to elicit preferences in a very nuanced manner. In contrast, the CPFS framework allowed us to cope effectively with uncertainty, which is especially relevant when it comes to sentiment-significant domains and realities. The good results in selecting architectures that are susceptible to averting performance, interpretability and complexity in the experimental implementation of the model showed effectiveness in the media analysis context. Therefore, the suggested approach can be a systematized, comprehensible, and changeable framework for directing DL architecture choices in problem settings, including high-stakes, sentiment-based settings. However, we recognize that the assessment in this paper was limited to five deep learning models and four criteria related to a specific media sentiment situation. The results are, however, encouraging, and further study is required to validate the framework in a broader context, involving more domain-specific examples, such as news, music, or product reviews, as well as additional decision criteria. Future extensions will make the framework more broadly applicable and attempt to challenge its robustness across a broader range of nuanced, real-world sentiment analysis problems.

Limitation and Future Direction

This research has several limitations despite its merits. First, the model’s efficiency is directly dependent on the quality and regularity of the expert input; the input may be biased or afflicted with inconsistent estimates. Second, CPFS is good with hesitation, but it is computationally demanding in large search spaces of architecture. Third, the model remains based on stagnant expert opinion, lacking consideration of real-time performance updates and the transformation of attitudes. This is a conceptual study based on simulated data, serving as an illustration of the decision-making framework. Confirmatory tests over genuine, review-based data are necessary to further substantiate the soundness and generalizability of the suggested model. Moreover, validation with benchmark datasets against real-world data is another future research objective. Additionally, it is assumed that decision-makers clearly understand the acceptable performance levels of the model, which may not always be the case, especially in applications where technical expertise is not above average. The research is currently based on hypothetical data. Although this would guarantee controlled model testing, it does not allow for direct generalizations to real-world information. A future study may involve testing the validity of the framework using actual media review data to enhance external validity. We acknowledge that, although transferability through the framework design was considered in this study, the incorporation of empirical validation from other domains into the design has not been addressed in this work and will be reflected in future studies. The approach is practical for small and medium-sized decision problems, but can become inefficient in cases involving large applications with a larger number of models.

This model might be expanded to include the real-time feedback of deployed DL architectures, allowing a dynamic learning-decision loop. Additionally, subjectivity can be minimized by integrating automated methodologies of meta-learning to enhance expert judgments. Moreover, group decision-making in distributed environments would improve the scalability of the given model in collaborative settings. Assigning other fuzzy extensions, such as interval-valued [26], spherical, hesitant [27] or complex fuzzy sets [28,29], or combining the trust and transparency mechanisms through explainability in model selection, may also enhance it. Involving the symmetry-based aggregation operators, together with the DoC method, may also be performed in future work. Lastly, expanding the application of such a hybrid framework to various NLP-related tasks (e.g., misinformation detection or toxic language filtering) would enable its greater practical use.