Abstract
In biochemical reaction control loops, the fast response and accuracy of the system are often at odds with stability. Especially when the system faces external changes in different situations, the control system needs to be more robust. To address this problem, a novel ultrasensitive quasi-fuzzy proportional integral (QFPI) molecular controller using a covalent modification cycle is designed. The quasi-fuzzy control performance is achieved through a symmetric dual-rail covalent modification cycle structure. It can effectively suppress the impact of external changes on the controlled process and overcome the limitation of finite-time regulation caused by substrate consumption. At the same time, the time performance of the controller is significantly improved by utilizing the fast response characteristics of the ultrasensitive response. Subsequently, a single-rail optimization of the chemical reaction network (CRN) of the QFPI controller is performed to design a modified ultrasensitive quasi-fuzzy PI (M-QFPI) molecular controller. The M-QFPI controller not only significantly reduces the number of chemical reactions required to implement the controller, but also effectively improves the temporal performance and robustness of the controller. Finally, the effectiveness of the ultrasensitive quasi-fuzzy PI molecular controller for the control of the phosphorylation reaction process is verified. The results show that the ultrasensitive quasi-fuzzy PI control strategy provides an effective solution for the co-optimization of response speed, robustness and stability.
1. Introduction
Control theory originated from the effort to conceptualize and generalize design strategies aimed at enhancing the stability and robustness of various systems. These systems encompass mechanical equipment, electrical systems, space systems, and chemical molecular processes [1]. Feedback mechanisms are a central strategy in the operation of biochemical molecular controllers, and they are widely used in synthetic biology to construct chemical reaction loops in biochemical systems [2]. CRN is a programming language based on chemical reaction networks [3], which can be compiled into an abstract control system using the theory of mass action dynamics [4]. However, the internal complexity of biochemical systems and the uncertainty of external changes make it necessary for biochemical molecular controllers to be robust in the face of disturbances such as external changes [5,6]. In biochemical molecular circuits, the impact of perturbations within the network can be represented by a cascading failure mechanism. This approach is used to simulate the robustness of the biochemical molecular network [7]. Robustness is a key attribute to ensure that biochemical molecular controllers maintain stability and performance in a variety of environments [8,9]. It is therefore challenging to design molecular controllers with robust robustness to ensure their effectiveness and reliability in complex biochemical environments.
In 2010, Oishi et al. explored the integration of control theory with biochemical reactions with the help of ideal chemical reactions [10]. Sawlekar et al. introduced a highly modular nonlinear quasi-sliding mode controller, expanding the implementation possibilities for biochemical molecular feedback systems [11]. In addition, Paulino et al. proposed proportional integral derivative (PID) and state feedback controllers based on chemical reaction networks and validated them at the molecular level using chemical reaction network mechanisms [12]. The above studies have demonstrated the feasibility of nonlinear controllers based on biochemical reactions. However, their regulation times are usually in the range of hundreds or even tens of thousands of seconds, which cannot meet the requirement of fast response. Therefore, there is a need to think about control strategies to achieve shorter regulation times using biochemical reaction networks.
In the context of molecular control, a “reverse-engineered” biochemical network, ultrasensitivity is a key feature for perfect adaptation [13]. The ultrasensitive response could be used as a paradigm to simplify controller design and improve the response speed. The ultrasensitive response is often found in biology, and it could occur naturally through the interconnection of different modules without laborious tuning, making it an attractive design specification [14,15]. Geobrl et al. found that when one or more converting enzymes operated in the “zero-level” region, it could generate sensitivity equivalent to that of co-enzymes with high Hill coefficients. They also found that this hypersensitivity could be exploited to dramatically shorten the reaction time of chemical reaction networks [16]. Foo et al. developed a nonlinear covalent modification cycle controller using chemical reaction networks (CRNs) by leveraging the dynamic properties of covalent modification cycles. Their findings demonstrated that biochemical molecular circuits utilizing covalent modification cycles need fewer nonlinear operators compared to purely theoretical designs based on chemical reaction network theory [17]. Samaniego et al. constructed an ultrasensitive quasi-integral Brink controller using a modular design strategy and applied it to regulate the expression of target RNAs or proteins, utilizing covalent modification cycles to achieve an ultrasensitive response and reduce the controller regulation time. This ultrasensitive response is important for the rapid regulation of complex dynamic processes in biochemical reaction systems [18]. In addition, Xiao et al. constructed a new nonlinear biomolecular controller using an abstract set of chemical reactions with fewer substrates and shorter response times to achieve a Brink controller with direct positive autoregulation (i.e., BC-DPAR controller) [19]. Previous studies have shown that it is feasible to design molecular controllers with ultrasensitive responses, while further research is needed to design biochemical molecular controllers with higher control efficiency using ultrasensitive responses.
In covalent modification cycles with ultrasensitive responses, the limitations of finite-time regulation are exposed as the substrate is consumed. Takashi et al. introduced the novel concept of “finite-time regulatory properties” for analyzing the regulatory properties over a finite time in biochemical molecular systems [20]. Rong et al. successfully implemented the concept of finite-time modulation properties in a biomolecular PI control system, achieving a quasi-steady state with an output signal that closely matches the target level [21]. Xiao et al. developed a BC-DPAR controller utilizing a covalent modification cycle and demonstrated through simulation experiments that covalent modification cycles with ultrasensitive responses have limitations in finite-time regulation [19]. The question that needs to be pondered at the moment is how to solve the stability challenges posed by limited time regulation to ensure continuous and stable operation of the system.
Implementing biochemical molecular feedback in a modular design paradigm is an important goal of synthetic biology [22,23,24,25]. Modular PID feedback controllers are the most commonly used controllers in the industry [26,27]. PID controllers and similar solutions are binary devices with only two states (0 or 1), making them not always suitable for nonlinear complex systems [28]. Fuzzy control, as an empirically based control method, is suitable for some complex control systems that are difficult to model [29,30]. Fuzzy control is unique in that its simplicity makes it more flexible in dealing with real biochemical molecular systems and provides a more natural way to achieve process control at the molecular level [31,32]. Fuzzy control is a control method based on fuzzy logic, which can deal with complex disturbances and problems caused by external changes [33,34]. Fuzzy control theory, with its ability to map linguistic rules into control actions, has been applied to describe complex regulatory processes [35]. In a seminal study by Basu et al., the authors constructed an intercellular communication system that achieved fuzzy pattern recognition, laying the groundwork for applying fuzzy control to cellular behavior regulation [36]. Subsequent studies proposed enzyme-based fuzzy-like adders and multipliers, demonstrating how cascaded biochemical reactions can emulate the response characteristics of fuzzy controllers [37,38]. Additionally, Qian et al. designed tunable chemical logic systems using DNA strand displacement reactions, providing both theoretical foundations and experimental validation for building programmable fuzzy control modules [39]. Especially in complex biochemical molecular systems, fuzzy control will be one of the methods for achieving process control. What needs to be explored is how to design modular fuzzy molecular controllers to control complex biochemical molecular processes so that the molecular controllers can achieve faster response time as well as greater robustness and stability.
In this paper, an ultrasensitive quasi-fuzzy PI molecular controller with ultrasensitive response is designed and modified. Firstly, a dual-rail covalent modification cycle is designed and embedded into the PI control system, successfully realizing the QFPI controller. The design method of the dual-rail covalent modification cycle allows for continuous reaction. Subsequently, a single-rail optimization of the QFPI controller is carried out, and the M-QFPI controller is designed to further enhance control efficiency by reducing substrate dosage and lowering system complexity. Additionally, a chemical reaction network (CRN)-based model of the phosphorylation reaction process is developed. Given that biochemical reactions in the system are susceptible to external changes such as temperature and pressure, complex external changes are considered as perturbations, and the effects of these changes on the control system are simulated in different scenarios. The experimental results show that this method not only significantly reduces the rise time and regulation time of the biochemical molecular controller and suppresses the influence of perturbations on the control process but also overcomes the limitation of finite-time regulation in the covalent modification cycle. This provides an effective optimization path for the design of biochemical molecular control systems.
In this study, an ultrasensitive quasi-fuzzy PI molecular control strategy based on a dual-rail covalent modification cycle is proposed, and its main contributions are as follows:
- (1)
- The ultrasensitive quasi-fuzzy PI molecular controller is designed using covalent modification cycles, and the quasi-fuzzy PI molecular control system is made to obtain fast response characteristics by covalent modification cycles. Compared with previous studies on biochemical molecular controllers [10,18,19], the controller’s rising time and adjusting time are reduced considerably.
- (2)
- A dual-rail covalent modification cycle structure is designed and utilized to implement quasi-fuzzy control rules using its physical structure similar to fuzzy control rules. Compared with the traditional nonlinear controllers [18,19], the effects of external perturbations on the controlled system are effectively suppressed, which significantly improves the robustness of the biochemical molecular controller.
- (3)
- The QFPI and M-QFPI controllers continuously stabilize the system using a dual-rail covalent modification cycle, which overcomes the limitation of finite-time regulation by covalent modification cycles [18,19]. Furthermore, the M-QFPI control scheme employs a single-rail representation to overcome the limitations associated with dual-rail representation. This approach notably simplifies the complexity of the ultrasensitive quasi-fuzzy PI molecular control strategy.
2. Materials and Methods
The purpose of this section is to design and improve a quasi-fuzzy PI molecular controller with an ultrasensitive response. Firstly, the chemical reaction network of the phosphorylation reaction is constructed and used as the controlled object. Then, the dual-rail ultrasensitive response mechanism is used to design ultrasensitive quasi-fuzzy PI molecular control strategies to cope with the effects of perturbations on the system through dual-rail covalent modification cycles and to overcome the limitation of finite-time regulation of covalent modification cycles. Finally, the optimization mechanism using a single-rail approach reduces the number of chemical reactions required to implement the controller, thereby lowering the complexity of the control strategy.
2.1. Phosphorylation Reaction
Abstract chemical reaction networks serve as a framework for describing the intricate behaviors observed in specific biochemical systems. Specific biochemical systems are susceptible to changes in external conditions such as temperature and pressure. These complex external changes are considered perturbations, and a model of the phosphorylation reaction process with perturbations is constructed through a chemical reaction network. The phosphorylation reaction process of CRNs can be expressed as
where , , and denote the reaction rates of the phosphorylation process, respectively. In addition, U denotes the intermediate species, which serves as the output of the controller; B, D and F denote the substrates, respectively; S denotes the activating enzyme; and V and Y denote the enzyme–substrate complex and the product, respectively. From a molecular point of view, the modeling of the robustness of the control system can be achieved using a cascade failure mechanism influenced by perturbations in the biochemical network. Thus, the cascade reaction corresponds to a process that uses the substrate F to cascade with the control process and generates the activating enzyme S through an autocatalytic reaction, which in turn affects its concentration and ultimately the concentration of the product Y of the phosphorylation reaction. As shown in Figure 1, the controller output species U and F are converted into the activator S and combined with the substrate B to produce the complex V. Subsequently, the substrate V is decomposed into the corresponding product Y and the substrate B.
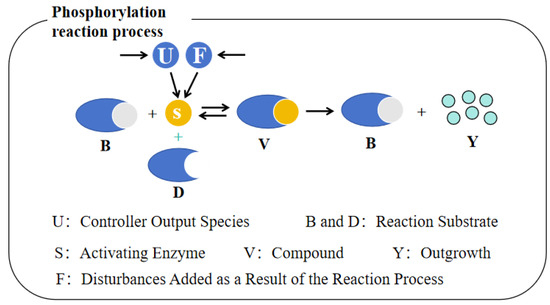
Figure 1.
Schematic representation of the phosphorylation reaction with disturbances.
Next, the phosphorylation reaction with perturbations is used as the controlled object of the control system and applied to a closed-loop network to implement an ultrasensitive quasi-fuzzy control strategy.
2.2. QFPI: Ultrasensitive Quasi-Fuzzy PI Molecular Controller
For a given precise controlled object, PI control is an ideal and reliable control solution. However, fuzzy controllers are more robust against perturbations caused by complex external changes in biochemical systems because fuzzy control mechanisms can better suppress the effects of external perturbations on the system. To achieve the synergistic design of biochemical molecular controllers in terms of temporal performance, robustness and stability, in this section, the dual-rail covalent modification cycle structure will be utilized to achieve a dual-rail ultrasensitive response for designing quasi-fuzzy PI molecular controllers with ultrasensitive responses.
Definition 1.
Dual-rail ultrasensitive response is an effect of positive synergistic bonding coupled to a substrate response mechanism, whereby a dual-rail covalent modification cycle of the chemical reaction network of a cycle structure is employed so that the molecular pathway achieves a rapid increase in output when the input exceeds a certain threshold.
Next, the QFPI control strategy is realized by a dual-rail (four-chain) covalent modification cycle, i.e., a dual-rail ultrasensitive response. A two-dimensional quasi-fuzzy molecular controller with a fuzzy language is realized by an activation–deactivation cycle using the proportional gain E of the error signal and the result of the integral process, , as inputs to the fuzzy control strategy. In this case, the general form of fuzzy language is presented below.
Remark 1.
Obtaining fuzzy rules in biological interactions usually involves abstracting the complex dynamic behavior of a biological system into a fuzzy logic model, an approach that can help to capture the uncertainty and complexity in the system. Fuzzy control rules can be understood as logical abstractions of molecular interactions in biological systems, reflecting the inhibitory effect of inhibitors on enzyme activity, consistent with the inhibition mechanism in enzyme dynamics. The modules of fuzzy controllers can be analogized to negative feedback mechanisms in biological systems, e.g., in metabolic pathways, when the concentration of a product is too high, the production of the product is reduced by feedback inhibition. In biological systems, the regulatory mechanism of biochemical processes is often multi-level, involving multiple feedback loops and regulatory factors, and the fuzzy control rules can simulate this complex regulatory network through hierarchical fuzzy rules and control modules, similar to the synergistic work of different functional modules in biological systems, and the synergistic action of the different modules in the fuzzy controller, to achieve the dynamic equilibrium of the overall system.
where E and ΔE denote the proportional gain signal and integral signal, respectively, and i and j denote the components of the signal, respectively.
As shown in Figure 2, the ultrasensitive quasi-fuzzy controller utilizes the structure of a near-switch with an ultrasensitive response to implement the quasi-fuzzy control logic through an activation–deactivation cycle: (1) When the error component E is positive, the concentration of the controller’s output is increased; conversely, the concentration of the output is decreased. (2) When the error transformation component is positive, the concentration of the controller’s output is decreased; conversely, the concentration of the output is increased. Here is the chemical reaction network:
where , , and are the inputs to the controller and and are the catalytic reaction rates. is the output of the controller, is the substrate and is waste. + represents the positive component and − represents the negative component of the signal, while denotes the output of the controller.
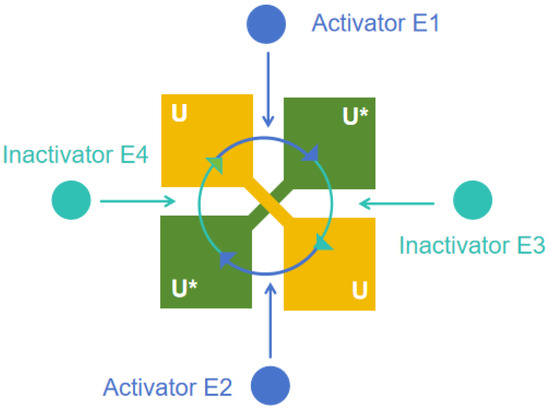
Figure 2.
Ultrasensitive quasi-fuzzy molecular controller.
An ultrasensitive quasi-fuzzy PI molecular controller is cascaded with the phosphorylation reaction as shown in Figure 3. According to mass action dynamics, the constant derivative equation describing the QFPI control strategy can be formulated as follows:
where is the concentration of the reference species, is the concentration of the output species, and and denote the products of and , respectively, produced by the autocatalytic reaction. , , , , , , and denote the rate of the reaction.
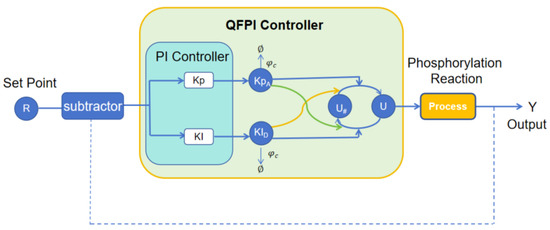
Figure 3.
Block diagram of QFPI controller.
Remark 2.
In this paper, a quasi-fuzzy PI molecular controller with ultrasensitive response is constructed using a dual-rail covalent modification cycle structure. The method realizes a quasi-fuzzy control process using a covalent modification cycle strategy, and the physical structure of the covalent modification cycle approximating the fuzzy control rules gives the QFPI both ultrasensitive and quasi-fuzzy control characteristics.
Definition 2.
Quasi-fuzzy control is a control method based on biological molecular networks and feedback mechanisms. It simulates fuzzy control rules through specific molecular reaction networks (such as dual-rail covalent modification cycles), thereby achieving complex nonlinear regulation at the molecular level. This method can handle the uncertainty and fuzziness within a system and performs tasks similar to fuzzy logic control through the dynamic behavior of biochemical reactions. Specifically, the network uses dual-rail covalent modification cycles to implement the general form of the fuzzy control rules expressed in Equation (2).
Theorem 1.
Assuming that the parameters satisfy , the QFPI controller (4) exhibits characteristics similar to fuzzy control, enabling it to flexibly and intelligently regulate complex systems at the molecular level by simulating fuzzy logic.
Proof.
The QFPI controller uses a dual-rail representation, when the QFPI control system reaches steady-state output. Setting the left-hand side of Equation (4) to 0 yields the following results:
The expression for the steady-state output of the QFPI controller is
The output of the control process is obtained in a steady state:
where and .
From Equation (7), when the QFPI control system achieves the desired steady-state output, i.e., when the condition is satisfied, the following outcomes can be observed:
Assuming that the process reaches a steady-state output, the conditions to be satisfied can be determined from Equation (8), including . When the steady-state output is reached, then the concentration of both and in the equation is 0, so .
When the actual parameters satisfy the above conditions, the QFPI controller (4) can work as a quasi-fuzzy controller and realize the quasi-fuzzy control rule shown in Equation (2), which is expressed as follows:
where , , and are the outputs of the QFPI controller (4), , of the error and the result of the integration, , in the different positive and negative components, respectively. This can be expressed as follows:
This completes the proof. □
This section is concerned with a modular strategy in quasi-fuzzy PI molecular controllers, namely the QFPI control strategy. The QFPI controller (4) achieves quasi-fuzzy control performance through the fast response characteristics of the ultrasensitive response and the use of a dual-rail covalent modification cycle structure, resulting in a significant reduction in the regulation time and rise time compared to the PI controller [10]. However, the QFPI control scheme involves a large number of chemical reactions. Next, The QFPI controller (4) will be streamlined into a single-rail configuration to enhance the control efficiency of the biochemical molecular controller and simplify its implementation.
2.3. M-QFPI: Modified Ultrasensitive Quasi-Fuzzy Controller
The design of the M-QFPI controller is achieved by single-rail optimization of the chemical reaction based on the QFPI controller (4). The M-QFPI control strategy implements a dual-rail covalent modification cycle structure through a single-rail chemical reaction, thereby significantly reducing the complexity of its implementation.
As shown in Figure 4, by cascading the dual-rail covalent modification cycle with the phosphorylation reaction process, an M-QFPI control strategy that enables quasi-fuzzy control rules has been designed, which can be described by the following chemical reactions:
where , , and are the inputs to the PI controller, is the concentration of the reference species, is the concentration of the output species, and and denote the products of and , respectively, produced by the autocatalytic reaction. , , , , , , and denote the rate of the reaction.
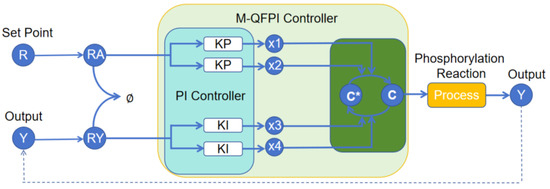
Figure 4.
Block diagram of M-QFPI controller.
With the help of the kinetic theory of mass action, based on the chemical reaction network shown in Equation (11), M-QFPI can be expressed as
The M-QFPI control strategy uses a single-rail representation to realize a dual-rail ultrasensitive response mechanism, i.e., a single-rail representation is used to design a dual-rail metric valence modification loop so that the M-QFPI obtains a quasi-fuzzy control characteristic with an ultrasensitive response.
Theorem 2.
Assuming that the parameters satisfy , , the M-QFPI controller (12) exhibits characteristics similar to fuzzy control, enabling it to flexibly and intelligently regulate complex systems at the molecular level by simulating fuzzy logic.
Proof.
Assuming that the M-QFPI control system has attained steady-state output, and setting the left hand of Equation (12) to 0,
Assuming that the reference input of the M-QFPI controller (12) is constant and remains unchanged during regulation, Equation (13) implies that Equation (14) can be derived:
The output of the control process is then obtained in steady state:
where , .
From Equation (15), when the M-QFPI control system achieves the desired steady-state output, meaning that the condition is met, the following outcomes can be observed:
Assuming that the process reaches steady-state output, the conditions that need to be met can be identified based on expression (16), including , (because ). Assuming that the process reaches steady-state output, the equations have both and concentrations at 0, so that .
The M-QFPI controller (12) is an optimization of the chemical reaction network of the QFPI controller (4) by applying the single-rail representation. Therefore, the M-QFPI controller has quasi-fuzzy control rules similar to those of QFPI when the actual parameters satisfy the above conditions. It is specifically represented as
where , , and are the error and the integration result of the output of the M-QFPI controller, , which can be expressed as
This completes the proof. □
Remark 3.

This section aims to implement a quasi-fuzzy PI molecular control strategy using fewer chemical reactions. Table 1 provides a comparison of the chemical reaction requirements for implementing M-QFPI controllers (12) and QFPI controllers (4). Since no dual-rail representation is involved, the M-QFPI controller is an optimization of the chemical reaction network of the QFPI controller by applying a single-rail representation to cascade the QFPI controller and the M-QPFI controller with the phosphorylation reaction, respectively, and the QFPI control strategy requires a network of 30 abstract chemical reactions to achieve the process control. In contrast, the M-QFPI control strategy necessitates 17 abstract chemical reactions. The M-QFPI control strategy reduces the amount of chemistry required to implement the ultrasensitive quasi-fuzzy PI molecular control strategy by 43%, thereby effectively reducing the complexity of the CRN implementation of the QFPI control strategy.

Table 1.
Required number of CRN reactions to implement the M-QFPI controller and QFPI controller.
3. Results
In this section, the objective is to apply process control to the phosphorylation reaction under perturbations using the QFPI controller (4) and the M-QFPI (12) controller, and the time performance, robustness and stability of the ultrasensitive quasi-fuzzy PI molecular controllers are sequentially verified by comparing four sets of simulation experiments.
3.1. QFPI Controller Performance Verification
In this section, the regulatory scheme of the QFPI controller (4) for phosphorylation reactions with perturbations is implemented using chemical reaction networks. In contrast to the conventional PI controller [10], the QFPI controller implements a quasi-fuzzy control function through an approximate switching structure with an ultrasensitive response. Next, the numerical comparison of closed-loop dynamic responses between the PI controller [10] and the QFPI controller is conducted. The parameter definitions for the CRN-based QFPI control strategy are provided in Table 2.

Table 2.
Parametric representation of QFPI.
Figure 5 displays the response curves of the PI controller [10], while Figure 6 illustrates those of the QFPI controller (4) for achieving process control of the phosphorylation reaction. With the same parameters, the QFPI controller significantly improves the temporal performance of the biochemical molecular controller compared to the the PI controller by decreasing the rise time from 234,727.2 s to 5984.4 s, compared to 97.5%, and the regulation time from 345,373.7 s to 7038 s, compared to 97.9% [10]. With the fast response characteristic of the ultrasensitive response, the overshoot is reduced by 78.5%, and the specific control performance comparison is demonstrated in Table 3.
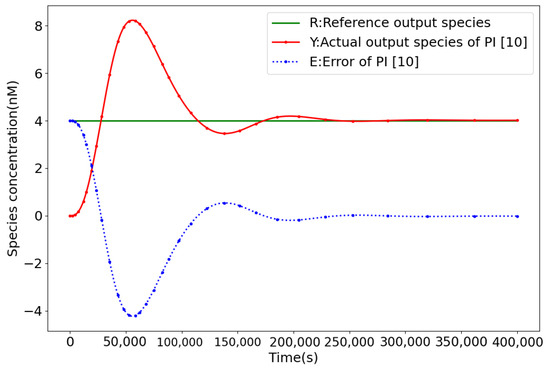
Figure 5.
PI controller closed-loop response curve.
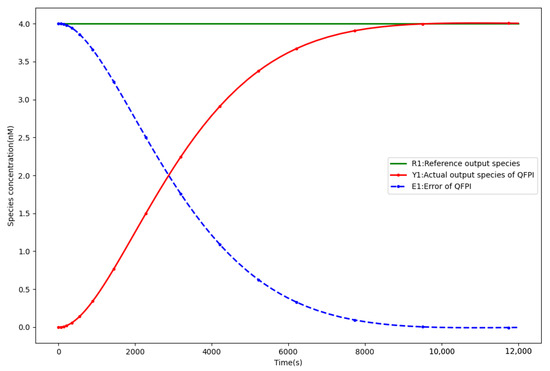
Figure 6.
QFPI controller closed-loop response curve.

Table 3.
Control performance comparison of QFPI and PI [10].
The QFPI controller (4) combines the advantages of fuzzy control and conventional PI control and uses a dual-rail ultrasensitive response design method to implement a quasi-fuzzy control rule. The QFPI control strategy achieves significant reductions in both regulation time and rise time due to its fast response characteristics and ultrasensitive nature.
3.2. M-QFPI Controller Performance Verification
In this section, the M-QFPI controller (12), the Brink controller [18] and the BC-DPAR controller [19] are cascaded with the phosphorylation reaction process to verify the performance of the M-QFPI controller. Table 4 presents all the reaction rates and total substrate values associated with the CRN-based M-QFPI strategies.

Table 4.
Parametric representation of M-QFPI.
As shown in Figure 7, the M-QFPI controller (12) has excellent timing performance, with its rise time and regulation time dropping to 46.6 s and 72.2 s, respectively. Compared to the QFPI controller (4), the rise time is reduced by 99.2%, the regulation time is reduced by 98%, and overshooting is avoided. Compared to the PI controller [10], the rise time is reduced by 99.6%, the regulation time is reduced by 99.8%, and the generation of overshoot is suppressed. Compared to the Brink controller [18], the rise time is reduced by 88.8% and the regulation time is reduced by 86.8%, and neither of them produces overshooting. Compared to the BC-DPAR controller [19], the rise time is reduced by 81.2% and the regulation time is reduced by 79%, and both are free of overshoot. The details are demonstrated in Table 5.
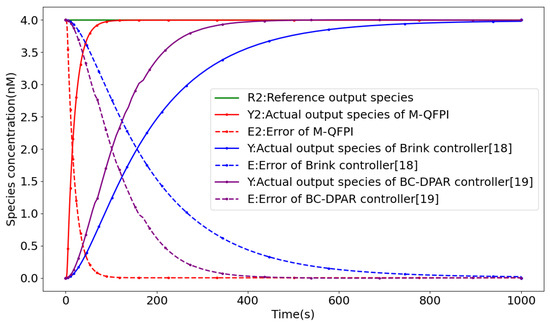
Figure 7.
Closed-loop response curves of M-QFPI controller, Brinker controller and BC-DPAR controller.

Table 5.
Control performance comparison of M-QFPI and other controllers.
The optimal design of the dual-rail covalent modification cycle of the QFPI controller (4) (i.e., the dual-rail covalent modification cycle is implemented through a single-rail representation) reduces the number of reactions by 43%, thus significantly reducing the control strategy complexity. The M-QFPI controller (12) responds quickly to changes in biochemical molecular systems and reduces the time needed to achieve a steady state.
3.3. M-QFPI Controller Disturbance Test
In this section, simulation experiments are performed on the perturbed signals in two cases. In Case 1, a constant value function signal is set as the perturbation to simulate a single linear external variation. In Case 2, a nonlinear repeating sequence stair signal is set as the perturbation signal to simulate complex nonlinear external variations to verify the robustness of the controller. (Since the PI controller [10] and the BC-DPAR controller [19] are not perturbation-resistant, their data will not be shown in this section.)
- Case 1: The molecular control system disturbance signal nM/s; the closed-loop response curve of the M-QFPI controller (12) is shown in Figure 8. The M-QFPI controller adopts the dual-rail covalent modification cycle design method, which enables it to better adapt to the system changes, suppress the perturbation, achieve fast response to the complex controlled system and avoid the generation of overshoots, thus demonstrating strong robustness.
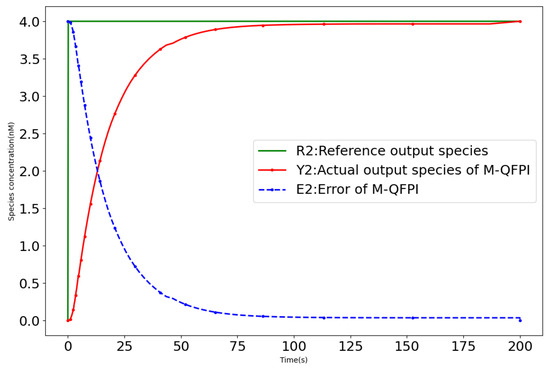 Figure 8. Closed-loop response curve of M-QFPI controller with disturbances (Case 1).
Figure 8. Closed-loop response curve of M-QFPI controller with disturbances (Case 1).
As shown in Figure 9, when the Brink control system disturbance signal nM/s, the closed-loop response curve of the Brink controller [18] produces an overshooting amount of 13.5% and its regulation time increases by 9278.5 s from 549 s to 9827.5 s, which makes it unable to meet the biochemical response control strategy’s controller time performance and robustness requirements in the biochemical reaction control strategy. Specific data are presented in Table 6.
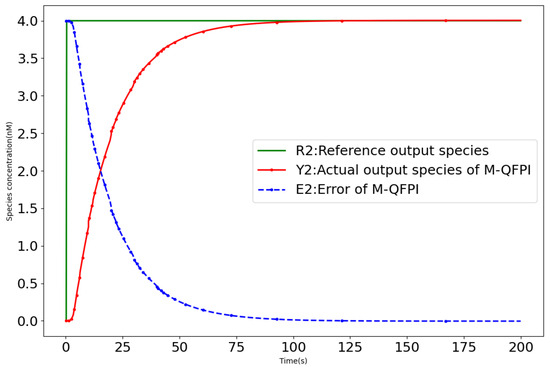
Figure 9.
Closed-loop response curve of M-QFPI controller (12) with disturbances (Case 2).

Table 6.
Comparison of control performance of QFPI and M-QFPI with others under linear perturbation.
- Case 2: In this case, the M-QFPI molecular control system perturbation is expressed aswhere … denotes that the signal undergoes step changes with a period of 10 s and subsequently continues to cycle according to this rule. The M-QFPI controller (12) demonstrates strong robustness, as shown in Figure 10. In contrast, when the same disturbance signal is introduced into the control process of the Brink controller [18] with the same disturbance signal, the output of the Brink controller and moves away from the setpoint and loses control performance in setpoint tracking.
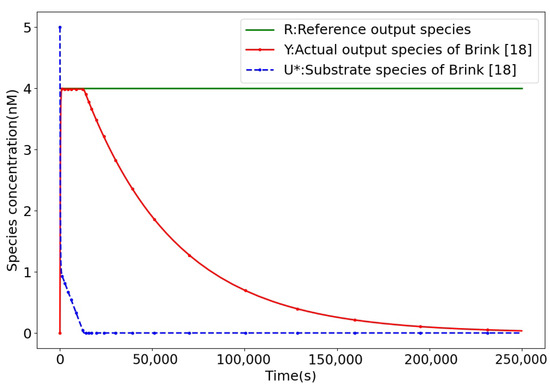 Figure 10. Brink controller quantitative representation of substrate concentration.
Figure 10. Brink controller quantitative representation of substrate concentration.
Table 7 gives a comparison of the control performance of the QFPI and M-QFPI controllers (12) with other controllers under nonlinear perturbations. In Case 1, compared to the Brink controller [18], the M-QFPI controller reduces the rise time, overshoot and regulation time by 71.7%, 13.5% and 99.4%, respectively. In Case 2, the M-QFPI still maintains excellent control performance, while the Brink controller loses setpoint tracking performance. This shows that the M-QFPI controller exhibits strong temporal performance and robustness in dealing with biochemical molecular controlled systems with perturbations.

Table 7.
Comparison of control performance of QFPI and M-QFPI with others under nonlinear perturbations.
Remark 4.
Biochemical reaction systems face many perturbations in practice, and the controller needs to suppress their negative impact on the system and achieve the desired control effect. However, The Brink controller [18] and the BC-DPAR controller [19] fail under nonlinear disturbances because they rely on linear assumptions, fixed gain and simplified disturbance models, lacking the capability to model, observe and compensate for strong nonlinear behaviors. To overcome this limitation, in this paper, the M-QFPI controller is designed using a dual-rail covalent modification cycle, which utilizes the ultrasensitive response and fuzzy rules to achieve the regulation of the system, which enhances the resistance to perturbations, shortens the regulation time and effectively suppresses the influence of perturbations on the control system while achieving a fast response. The M-QFPI controller can better adapt to a variety of environmental changes and maintain good control performance without the need for frequent parameter adjustments to achieve the desired control effect.
3.4. M-QFPI Controller Stability Test
Stable biochemical molecular controllers are essential for maintaining the accuracy of the steady state in biochemical reaction processes. They ensure the consistent stability required for biochemical reactions to proceed accurately, which puts higher requirements on the stability of the controllers. The M-QFPI controller (12) achieves ultrasensitive quasi-fuzzy control functionality through a covalent modification cycle. By employing the design method of a dual-rail covalent modification cycle, the M-QFPI controller overcomes the limitation of finite-time regulation. (Because the Brink controller [18] has the same covalent modification cycle structure as the BC-DPAR controller [19], only a quantitative representation of the substrate concentration of the Brink controller is shown in this section.)
As shown in Figure 11, in the CRNs of the Brink controller [18], when the system reaches equilibrium, the covalent modification cycle structure stops carrying out cycle reactions and evolves into a unidirectional reaction, where the substrate decreases as the reaction proceeds, and the control system eventually collapses due to substrate depletion. It is impossible to meet the requirement of continuous and stable control.
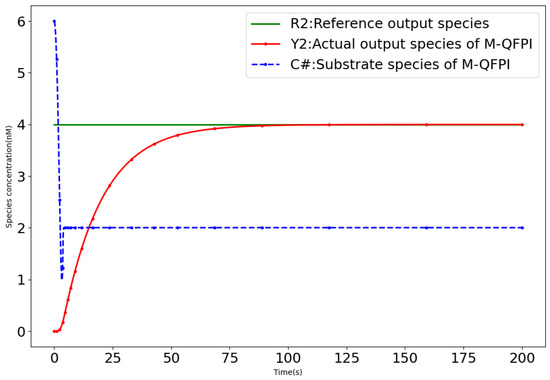
Figure 11.
Quantitative expression of substrate concentration for the M-QFPI controller.
Remark 5.
The M-QFPI controller (12) is designed using a single-rail representation within a dual-rail covalent modification cycle, which ensures that, upon reaching equilibrium, the system continues to maintain the covalent modification cycle. Consequently, the M-QFPI controller overcomes the limitation of finite-time regulation. The above results show that the M-QFPI controller with an ultrasensitive response can exhibit strong temporal performance, robustness and stability in response to complex and variable external changes.
3.5. Comparison of Ultrasensitive Quasi-Fuzzy Controller Functions with Other Controllers
This paper aims to design ultrasensitive quasi-fuzzy PI molecular controllers with ultrasensitive responses using covalent modification cycle structures. Table 8 provides a functional comparison of the five controllers. Compared with the PI controller [10], the QFPI controller (4) and the M-QFPI controller (12) use different covalent modification cycle design methods, respectively, to obtain an ultrasensitive response and achieve quasi-fuzzy control performance. Although the PI controller [10] can overcome the limitations of finite-time regulation, its performance in terms of response time and robustness is not satisfactory, especially when facing nonlinear disturbances. In contrast to the Brink controller [18] and BC-DPAR controller [19], both the QFPI and M-QFPI controllers surpassed the finite-time regulation constraint in the covalent modification cycle. They notably decreased the regulation time and rise time of the biochemical molecular controller due to their quasi-fuzzy control attributes. The M-QFPI controller demonstrates even better control performance when the system is perturbed. Compared to the QFPI controller (4), the M-QFPI (12) uses fewer chemical reactions, making it possible for the M-QFPI to provide better control effects even though both have the same functionality. (Note: ✓ indicates the presence of performance, and × indicates the absence of performance.)

Table 8.
Comparison of the functions of the five controllers.
Remark 6.
Ultrasensitive QFPI controllers (4) and M-QFPI controllers (12) utilize a covalent modification cycle structure to obtain an ultrasensitive response that significantly reduces the rise time and regulation time of the biochemical molecular controllers, adopt a dual-rail ultrasensitive response design approach to achieve quasi-fuzzy control performance, and efficiently suppress perturbations due to external variations, thereby significantly improving the robustness of the biochemical molecular controller and overcoming the limitation of effective time regulation. In addition, the M-QFPI control strategy, which realizes a dual-rail covalent modification cycle structure through a single-rail representation method, significantly reduces the complexity of the ultrasensitive quasi-fuzzy PI molecular control strategy. The above studies show that the quasi-fuzzy PI molecular controller proposed in this paper is more flexible compared with the traditional linear and nonlinear controllers, and can adapt to different control requirements and environmental changes.
4. Conclusions
In this paper, we propose a quasi-fuzzy PI molecular controller with an ultrasensitive response using a dual-rail covalent modification cycle. The phosphorylation process under perturbations is modeled via abstract chemical reactions, and disturbance effects are simulated through a cascade failure mechanism. Based on covalent modification cycles, ultrasensitive QFPI and M-QFPI controllers are designed to achieve fast response and reduced regulation and rise times. Quasi-fuzzy control rules effectively suppress perturbation effects. The M-QFPI controller optimizes the QFPI structure by replacing its dual-rail design with a single-rail implementation, reducing chemical reaction network (CRN) components by about 43%. Simulations show that M-QFPI improves closed-loop speed, eliminates overshoot, suppresses disturbances and overcomes finite-time regulation limits, providing a balanced solution for speed, robustness and stability in biochemical molecular control.
This work is based on theoretical modeling and simulations, supported by prior experimental validations of similar molecular logic modules. The framework is compatible with DNA strand displacement techniques and shows strong experimental potential. Future work will focus on experimental implementation to bridge theory and practice in molecular-level intelligent control.
Author Contributions
Y.L. and L.P. made equal contributions to this work. They are co-first authors and are responsible for conceptualization, investigation, and writing—original draft preparation of the entire manuscript. B.F. and J.Y. are responsible for writing—review and revision. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (No. 62203064).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| R1 and R2 | Setpoint (input) |
| Y1 and Y2 | Output |
| U and C | Substrate of covalent modification cycle |
| U* and C* | Product of covalent modification cycle |
| E1, E2, E3, E4 | PI component |
| X1, X2, X3, X4 | PI component |
| Ra and RA | Setpoint component |
| Ry and RY | Output component |
References
- Del Vecchio, D.; Dy, A.J.; Qian, Y. Control theory meets synthetic biology. J. R. Soc. 2016, 12, 0380. [Google Scholar] [CrossRef] [PubMed]
- Filo, M.; Chang, C.H.; Khammash, M. Biomolecular feedback controllers: From theory to applications. Curr. Opin. Biotechnol. 2023, 79, 102882. [Google Scholar] [CrossRef] [PubMed]
- Haney, S.; Bardwell, L.; Nie, Q. Ultrasensitive responses and specificity in cell signaling. BMC Syst. Biol. 2010, 4, 119. [Google Scholar] [CrossRef] [PubMed]
- Badelt, S.; Shin, S.W.; Johnson, R.F. A general-purpose CRN-to-DSD compiler with formal verification, optimization, and simulation capabilities. Comput. Sci. 2017, 10467, 232–248. [Google Scholar]
- Gupta, A.; Khammash, M. Universal structural requirements for maximal robust perfect adaptation in bi-omolecular networks. Proc. Natl. Acad. Sci. USA 2022, 119, e2207802119. [Google Scholar] [CrossRef]
- Anastassov, S.; Filo, M.; Chang, C.H. A cybergenetic framework for engineering intein-mediated integral feedback control systems. Nat. Commun. 2023, 14, 1337. [Google Scholar] [CrossRef]
- Vijayakumar, J.; Mathew, L.; Nagar, A.K. A new class of graph grammars and modelling of certain bio-logical structures. Symmetry 2023, 15, 349. [Google Scholar] [CrossRef]
- Kell, B.; Ripsman, R.; Hilfinger, A. Noise properties of adaptation-conferring biochemical control modules. Proc. Natl. Acad. Sci. USA 2023, 120, e2302016120. [Google Scholar] [CrossRef]
- Aoki, S.K.; Lillacci, G.; Gupta, A.; Baumschlager, A.; Schweingruber, D.; Khammash, M. A universal biomolecular integral feedback controller for robust perfect adaptation. Nature 2019, 570, 533–537. [Google Scholar] [CrossRef]
- Oishi, K.; Klavins, E. Biomolecular implementation of linear I/O systems. IET Syst. Biol. 2011, 5, 252–260. [Google Scholar] [CrossRef]
- Sawlekar, R.; Montefusco, F.; Kulkarni, V.V. Implementing nonlinear feedback controllers using DNA strand displacement reactions. IEEE Trans. Nanobiosci. 2016, 15, 443–454. [Google Scholar] [CrossRef]
- Jiang, K. A Neural Network Training Method Based on Distributed PID Control. Symmetry 2025, 17, 1129. [Google Scholar] [CrossRef]
- Poole, W.; Pandey, A.; Shur, A. BioCRNpyler: Compiling chemical reaction networks from biomolecular parts in diverse contexts. PLoS Comput. Biol. 2022, 18, e1009987. [Google Scholar] [CrossRef] [PubMed]
- Samaniego, C.C.; Qian, Y.; Carleton, K. Building subtraction operators and controllers via molecular se-questration. IEEE Trans. Autom. Control 2023, 7, 3361–3366. [Google Scholar]
- Ullah, A.; Zulfiqar, M.H.; Khan, M.A. Fast response facile fabricated IDE-based ultra-sensitive humidity sensor for medical applications. Trends Biochem. Sci. 2023, 8, 16842–16850. [Google Scholar] [CrossRef] [PubMed]
- Goldbeter, A.; Koshland, D.E., Jr. An amplified sensitivity arising from covalent modification in biological systems. Proc. Natl. Acad. Sci. USA 1981, 78, 6840–6844. [Google Scholar] [CrossRef]
- Ignatov, I.; Marinov, Y.G.; Vassileva, P.; Gluhchev, G.; Pesotskaya, L.A.; Jordanov, I.P.; Iliev, M.T. Nonlinear Hydrogen Bond Network in Small Water Clusters: Combining NMR, DFT, FT-IR, and EIS Research. Symmetry 2025, 17, 1062. [Google Scholar] [CrossRef]
- Samaniego, C.C.; Franco, E. Ultrasensitive molecular controllers for quasi-integral feedback. Cell Syst. 2021, 12, 272–288. [Google Scholar] [CrossRef]
- Xiao, Y.; Lv, H. Implementation of an ultrasensitive biomolecular controller for enzymatic reaction pro-cesses with delay using DNA strand displacement. IEEE Trans. NanoBiosci. 2023, 22, 967–977. [Google Scholar] [CrossRef]
- Nakakuki, T.; Imura, J. Finite-time regulation property of DNA feedback regulator. Automatica 2020, 114, 108826. [Google Scholar] [CrossRef]
- Rong, P.; Nakakuki, T. Analysis of finite-time regulation property of biomolecular PI controller. Control Theory Technol. 2020, 18, 135–142. [Google Scholar] [CrossRef]
- Araujo, R.P.; Liotta, L.A. Universal structures for adaptation in biochemical reaction networks. Nat. Commun. 2023, 14, 2251. [Google Scholar] [CrossRef] [PubMed]
- Stephenson, A.; Lastra, L.; Nguyen, B. Physical laboratory automation in synthetic biology. ACS Synth. Biol. 2023, 12, 3156–3169. [Google Scholar] [CrossRef] [PubMed]
- Alexis, E.; Schulte, C.C.M.; Cardelli, L. Regulation strategies for two-output biomolecular networks. J. R. Soc. Interface 2023, 20, 20230174. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Liu, H.; Li, X. Modularized synthetic biology enabled intelligent biosensors. Trends Biotechnol. 2023, 41, 1055–1065. [Google Scholar] [CrossRef]
- Feng, G. A survey on analysis and design of model-based fuzzy control systems. IEEE Trans. Fuzzy Syst. 2006, 14, 676–697. [Google Scholar] [CrossRef]
- Borase, R.P.; Maghade, D.K.; Sondkar, S.Y. A review of PID control, tuning methods and applications. Int. J. Dyn. Control 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Filo, M.; Kumar, S.; Khammash, M. A hierarchy of biomolecular proportional-integral-derivative feedback controllers for robust perfect adaptation and dynamic performance. Nat. Commun. 2022, 13, 2119. [Google Scholar] [CrossRef]
- Liu, J.; Gong, E.; Zha, L. Observer-based security fuzzy control for nonlinear networked systems under weighted try-once-discard protocol. IEEE Trans. Fuzzy Syst. 2023, 31, 3853–3865. [Google Scholar] [CrossRef]
- Lamamra, K.; Batat, F.; Mokhtari, F. A new technique with improved control quality of nonlinear systems using an optimized fuzzy logic controller. Expert Syst. Appl. 2020, 145, 113148. [Google Scholar] [CrossRef]
- Alsharaiah, M.A.; Samarasinghe, S.; Kulasiri, D. Proteins as fuzzy controllers: Auto tuning a biological fuzzy inference system to predict protein dynamics in complex biological networks. Biosystems 2023, 224, 104826. [Google Scholar] [CrossRef]
- Ding, Y.; Tiwari, P.; Guo, F. Multi-correntropy fusion based fuzzy system for predicting DNA N4-methylcytosine sites. Inf. Fusion 2023, 100, 101911. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, J.; Zhao, H. Composite-disturbances-observer-based finite-time fuzzy adaptive dynamic surface control of nonlinear systems with preassigned performance. IEEE Trans. Fuzzy Syst. 2023, 31, 3710–3720. [Google Scholar] [CrossRef]
- Sun, Y.; Feng, G.; Cao, J. A new approach to dynamic fuzzy modeling of genetic regulatory networks. IEEE Trans. NanoBiosci. 2010, 9, 263–272. [Google Scholar]
- Yager, R.R.; Zadeh, L.A. An Introduction to Fuzzy Logic Applications in Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Basu, S.; Gerchman, Y.; Collins, C.H.; Arnold, F.H.; Weiss, R. A synthetic multicellular system for programmed pattern formation. Nature 2005, 434, 1130–1134. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Sun, W.; Heiner, M.; Gilbert, D. Hybrid modelling of biological systems using fuzzy continuous Petri nets. Briefings Bioinform. 2021, 22, 438–450. [Google Scholar] [CrossRef]
- Kondo, T.; Bourassa, F.X.; Achar, S.; DuSold, J.; Céspedes, P.F.; Ando, M.; Dwivedi, A.; Moraly, J.; Chien, C.; Majdoul, S.; et al. Engineering TCR-controlled fuzzy logic into CAR T cells en-hances therapeutic specificity. Cell 2025, 188, 2372–2389. [Google Scholar] [CrossRef]
- Qian, L.; Winfree, E.; Bruck, J. Neural network computation with DNA strand displacement cascades. Nature 2011, 475, 368–372. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).