Research on a Multi-Agent Job Shop Scheduling Method Based on Improved Game Evolution
Abstract
1. Introduction
- The independent optimization of the machine allocation and AGV path will lead to an increase in AGV waiting time and an idling rate of more than 30% [12];
- The equipment starts and stops frequently, and the idle energy consumption accounts for more than 25% of the total energy consumption [13];
- When dynamic orders are inserted, the fixed scheduling rules make it difficult to quickly reconstruct the production schedule, and the order delivery delay rate increases by 40% [14].
2. Related Work, Problems, and Challenges
2.1. Existing Scheduling Methods for Manufacturing Workshops
2.2. Core Challenges in Current Scheduling
- A single game is prone to conflict in resource allocation due to insufficient negotiation [22];
- There is a lack of refined modeling of AGV charging scheduling, machine energy consumption differences, and other practical constraints [23];
- The population diversity declines during evolution, and it is difficult to approach the Pareto front stably [24].
3. Materials and Methods
3.1. Problem Description
3.2. Mathematical Model
3.2.1. Objective Function
3.2.2. Constraint Condition
- Precedence Constraint of OperationsOperations of the same job must be processed in sequence such that a subsequent operation can only start after the completion of its preceding operation:where denotes the completion time of operation , and denotes the start time of operation .
- Machine Exclusivity ConstraintAt any given time, a single machine can process at most one operation:where indicates that machine is processing operation at time t (0 otherwise).
- Transportation Constraints
- (a)
- Single-Task ExclusivityA mobile robot can transport at most one job at a time:where indicates that mobile robot is transporting operation at time t (0 otherwise).
- (b)
- Conflict-Free PathAt any time, a single path node can be occupied by at most one mobile robot:where represents a path node (e.g., workstation, warehouse, charging station).
- Charging Trigger ConstraintWhen the battery level of a mobile robot drops below a threshold, transportation must be interrupted for charging:where − is the battery level of mobile robot at time t; − is the battery threshold; is the rated battery capacity; and − denotes the charging duration.
- Warehouse Exclusivity ConstraintAt any time, a single warehouse can be accessed by at most one mobile robot:where indicates that mobile robot is accessing warehouse at time t (0 otherwise).
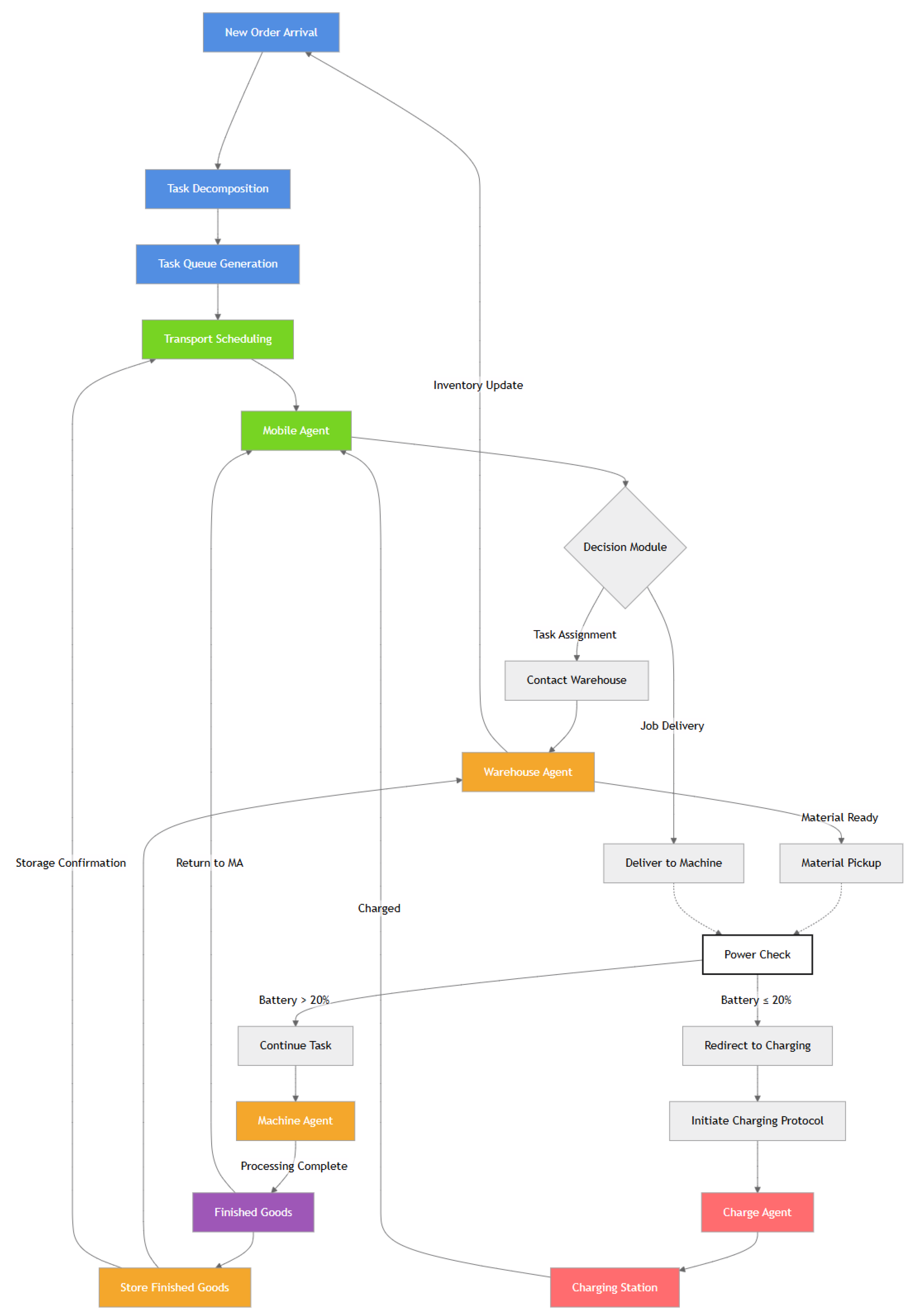
3.3. Multi-Agent System Architecture Design
3.4. An Algorithmic Framework Based on a Hybrid Game–Genetic Algorithm
3.4.1. The Decision-Makers in the Game
| Algorithm 1 Enhanced Best-Response Dynamic Algorithm | |
| Require: , , Jobs, , , , | |
| Ensure: , , | |
| 1: Initialization: | |
| 2: for each do | |
| 3: Initialize (queue), (idle time) | ▹ Section 3.4.1 |
| 4: end for | |
| 5: for each do | |
| 6: Initialize position, (energy), current task | ▹ Equation (8) |
| 7: end for | |
| 8: repeat | ▹ Dual-stage symmetric game |
| 9: Stage 1: Machine Competition | |
| 10: for each operation do | |
| 11: Calculate utility : | |
| ▹ Equation (10) | |
| 12: Assign to | |
| 13: | ▹ Update queue |
| 14: end for | |
| 15: Stage 2: AGV Competition | |
| 16: for each do | |
| 17: Generate paths with ST-A* satisfying: | |
| 18: | ▹ Single-task exclusivity (Equation (6)) |
| 19: | ▹ Path conflict-free (Equation (7)) |
| 20: | ▹ Warehouse exclusivity (Equation (9)) |
| 21: Check charging: if enforce | ▹ Equation (8) |
| 22: Select path maximizing: | |
| ▹ Equation (11) | |
| 23: end for | |
| 24: Symmetric Update: | |
| 25: for each do | |
| 26: if then | |
| 27: | ▹ Update idle time |
| 28: end if | |
| 29: end for | |
| 30: Update AGV selection probabilities via Softmax() | ▹ Nash refinement |
| 31: until or | ▹ Convergence condition |
| 32: Output: , , | |
3.4.2. Layer of Genetic Optimization
| Algorithm 2 Integrated Competition-Driven Genetic Optimization | |
| Require: : Current population, | |
| 1: : Nash equilibrium solutions, | |
| 2: : Machine bid counts, | |
| 3: : Path conflict counts | |
| Ensure: : Optimized population | |
| 4: Phase 1: Adaptive Genetic Operations | |
| 5: for each parent pair do | |
| 6: Initialize offspring | ▹ Competition-aware crossover |
| 7: for each gene do | |
| 8: if Machine selection gene then | |
| 9: Compute | ▹ Equation (14) |
| 10: Adjust based on | |
| 11: if then | |
| 12: Apply restricted crossover | ▹ High-competition zone |
| 13: end if | |
| 14: else if Path gene then | |
| 15: Compute | ▹ Equation (15) |
| 16: Adjust based on | |
| 17: if then | |
| 18: Verify energy: if enforce charging | ▹ Equation (8) |
| 19: Recombine paths with ST-A* verification | ▹ Equation (9) |
| 20: end if | |
| 21: end if | |
| 22: end for | |
| ▹ Strategy-guided mutation | |
| 23: for each gene do | |
| 24: if Machine gene then | |
| 25: Replace with low-competition machine | |
| 26: else if Machine gene then | |
| 27: Explore underutilized machines | |
| 28: else if Path gene then | |
| 29: Reroute using conflict-aware planning | |
| 30: else if Path gene then | |
| 31: Explore adjacent nodes | |
| 32: end if | |
| 33: end for | |
| 34: Add to | |
| 35: end for | |
| 36: Phase 2: Elite Selection | |
| 37: Normalize objectives: | |
| 38: Select: | |
| 39: Top 10% by | ▹ Global fitness |
| 40: Top 5% per objective | ▹ Single-objective excellence |
| 41: Nash solutions with Stability Contribution | ▹ Section 3.4.2 constraint |
| 42: Aggregate elite pool | |
| 43: Phase 3: Dynamic Adaptation | |
| 44: | |
| 45: Update | ▹ Equation (14) |
| 46: if then | |
| 47: Refresh competition metrics | |
| 48: Adjust via gradient ascent on | ▹ Section 3.4.2 mechanism |
| 49: end if | |
3.4.3. Coordinated Pivot Level
| Algorithm 3 Real-Time Coordination Mechanism | |
| Require: : Real-time monitoring data (equipment status, energy, paths), | |
| 1: : Current population of genetic optimization layer, | |
| 2: : Nash equilibrium solutions from game layer, | |
| 3: : Machine competition factors (Equation (13)), | |
| 4: : Path conflict factors (Equation (14)) | |
| Ensure: : Updated constraints for scheduling, | |
| 5: : Feasibility flag (True if all constraints are satisfied) | |
| 6: Step 1: Update energy constraints (Equation (8)) | |
| 7: for all do | ▹ AGV set as defined in Chapter 3 |
| 8: if then | ▹ Battery threshold |
| 9: | ▹ Add charging task to constraints |
| 10: end if | |
| 11: end for | |
| 12: Step 2: Update path conflict constraints (Equation (9)) | |
| 13: Calculate path node occupancy: | |
| ▹ Ensure no concurrent occupancy of path nodes | |
| 14: Step 3: Update competition factors (Equations (13) and (14)) | |
| 15: Machine competition factors: | |
| ▹ Exponential smoothing for dynamic adaptation | |
| 16: Path conflict factors: | |
| ▹ Normalize by maximum conflict count | |
| 17: Step 4: Verify feasibility against core constraints | |
| 18: Check operation precedence constraint (Equation (4)): | |
| 19: Verify machine exclusivity constraint (Equation (5)): | |
| 20: Validate transportation-charging exclusivity (Equation (8)): | |
| 21: Step 5: Set feasibility flag | |
| 22: if all constraints in are satisfied, else False | |
| 23: return | |
4. Simulation Evaluation
4.1. Simulation Setup
4.2. Comparative Analysis of Simulation Results
4.2.1. Algorithm Analysis in Simple Scenarios
4.2.2. Algorithm Analysis in Complex Scenarios
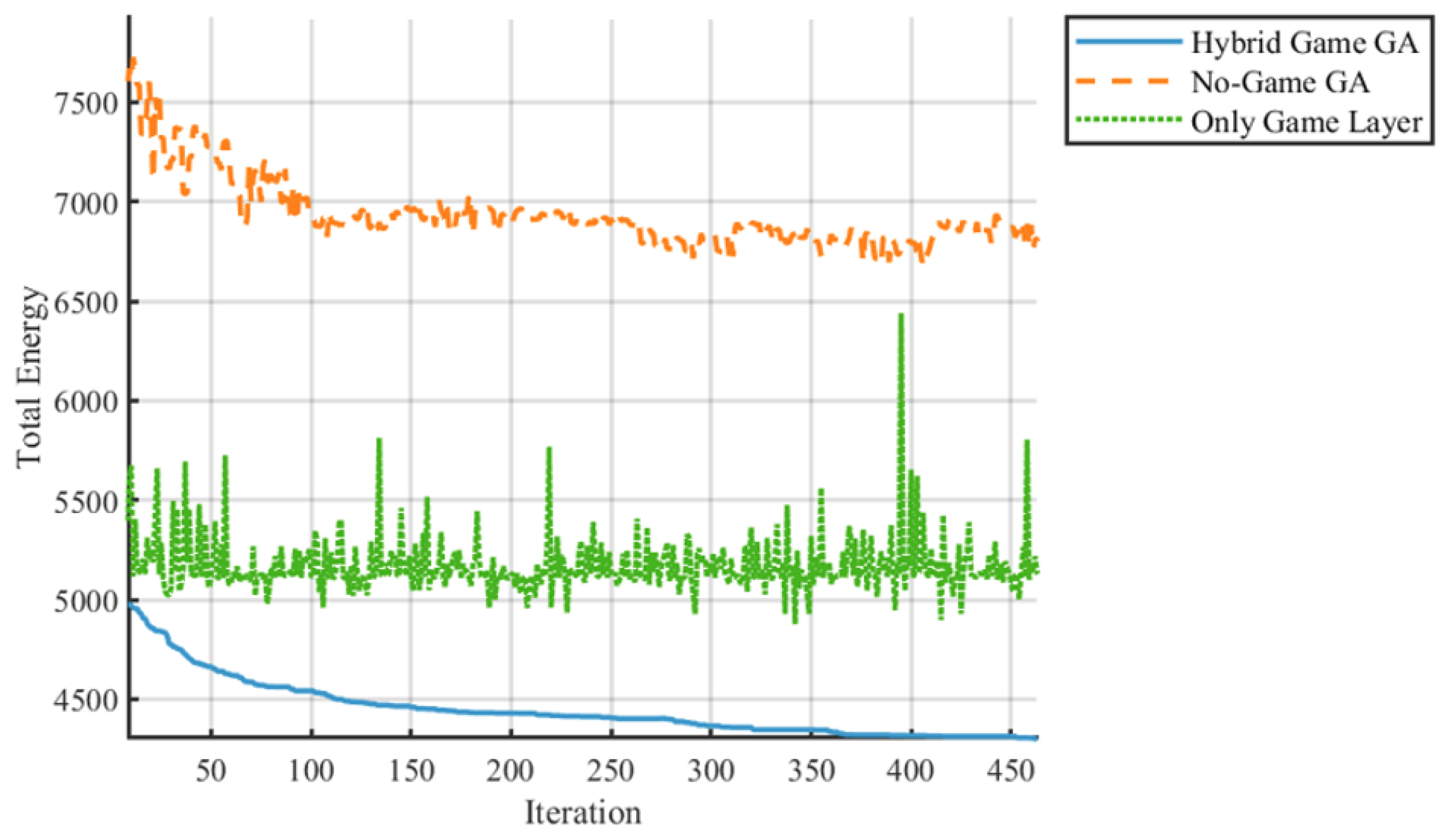
4.2.3. Component Contribution Analysis Through Ablation Studies
5. Conclusions and Discussion
5.1. Core Contributions and Performance Validation
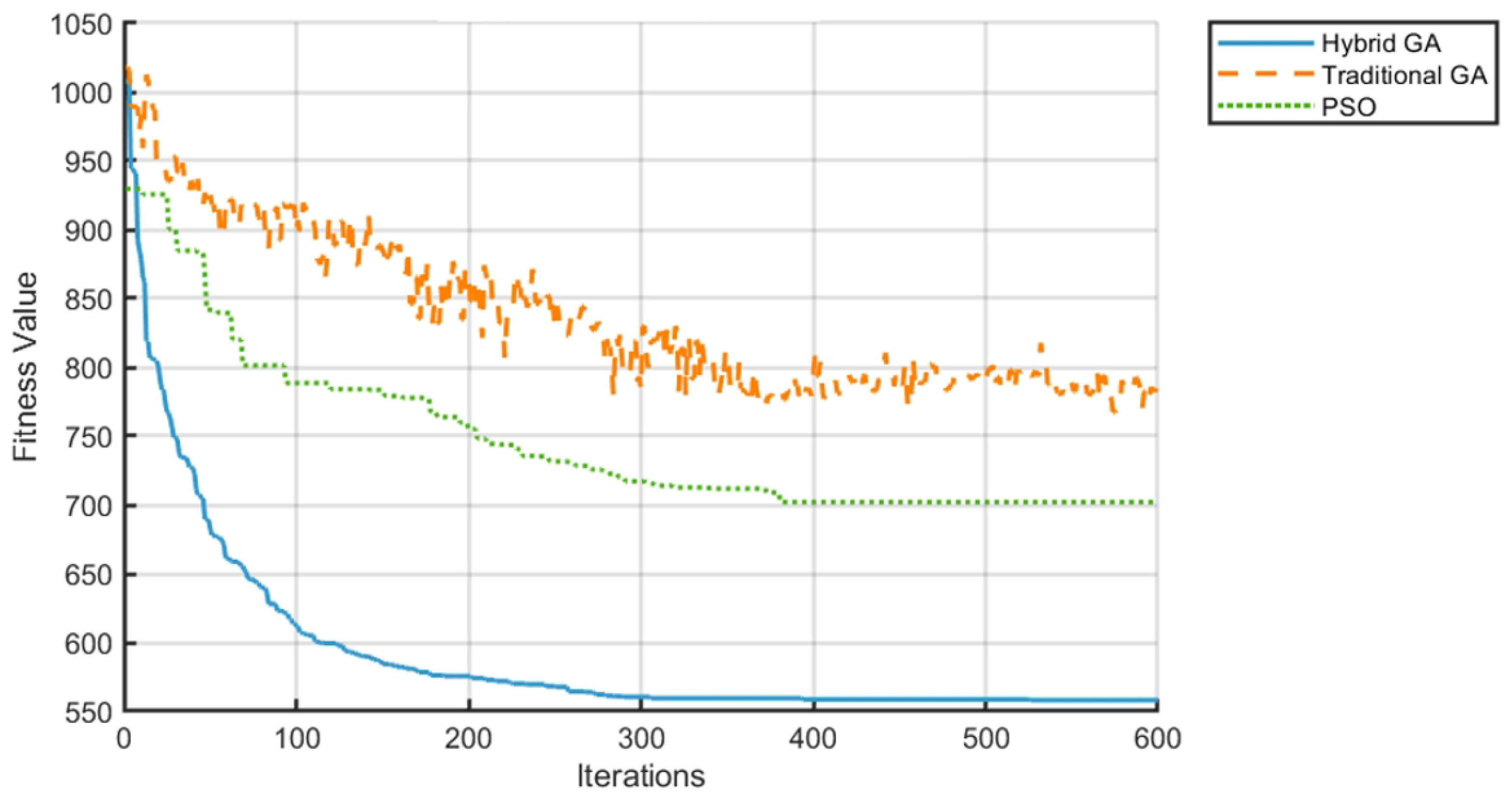
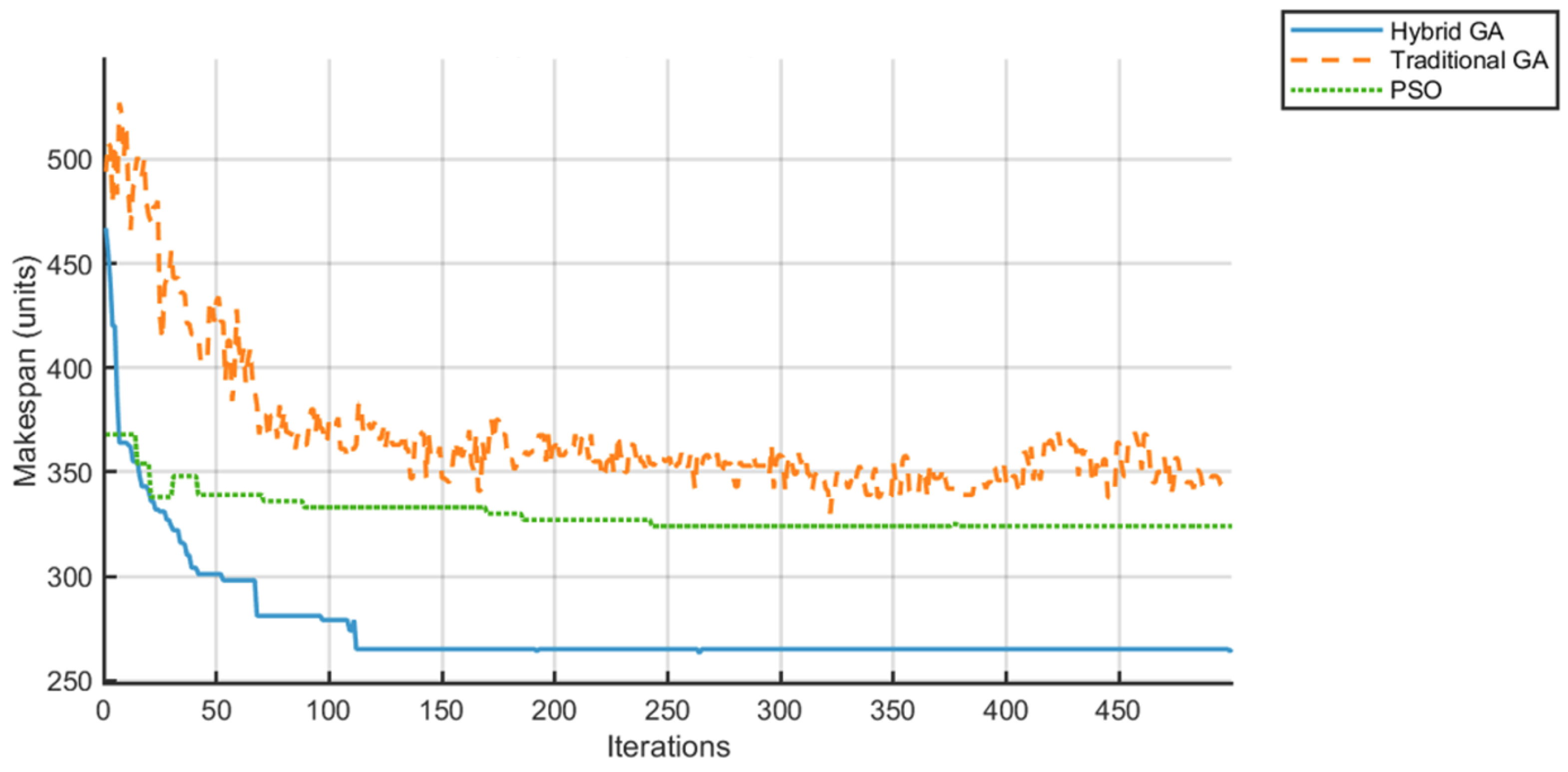
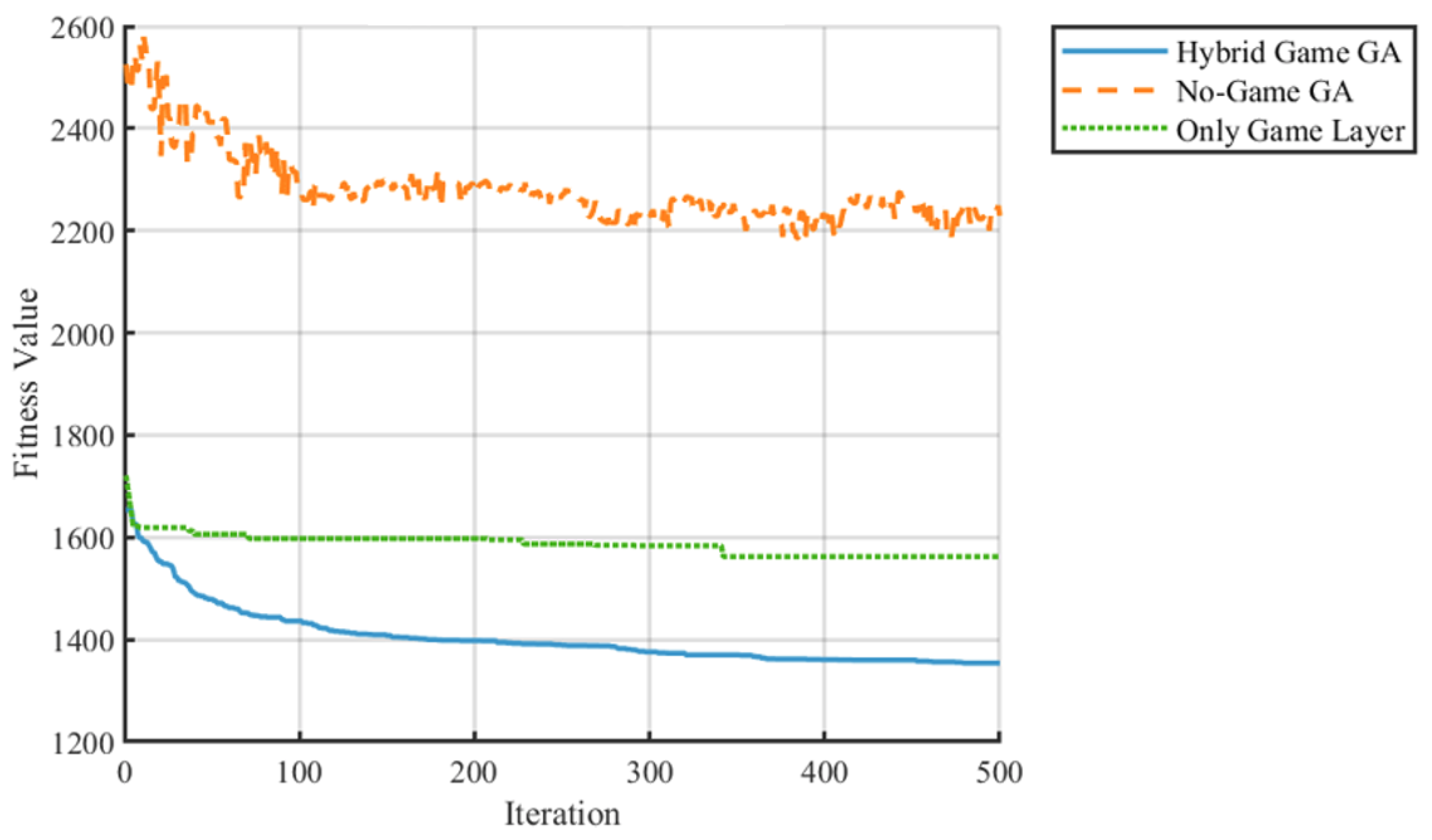
- The fitness value converges rapidly from an initial 330 to a stable 250, representing a 20.6% improvement over the TGA (315) and a 7.4% improvement over PSO (270).
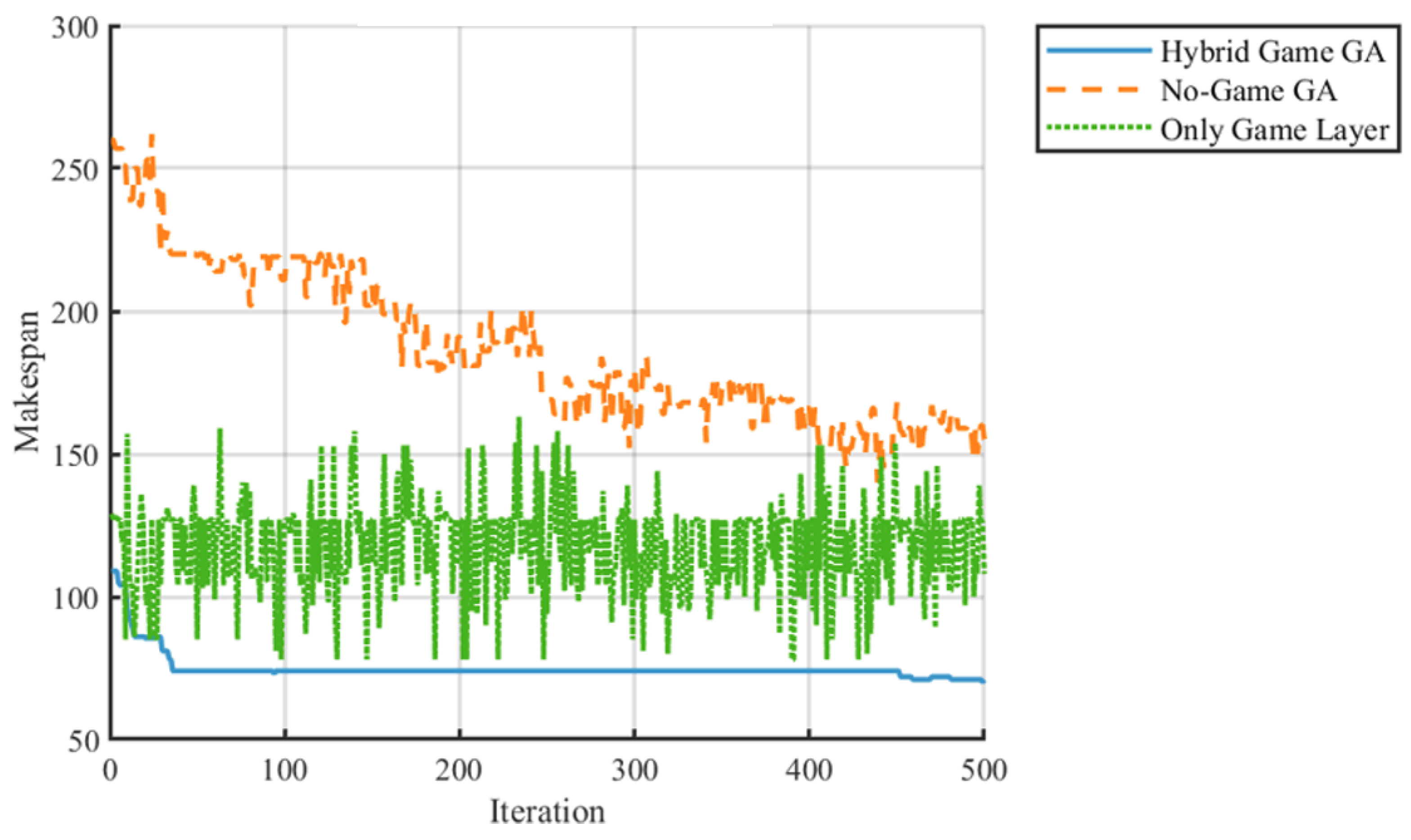
- The maximum completion time is shortened to 50 units, a 54.5% reduction compared to the TGA (110 units) and a 44.4% reduction compared to PSO (90 units), highlighting its ability to streamline production cycles.
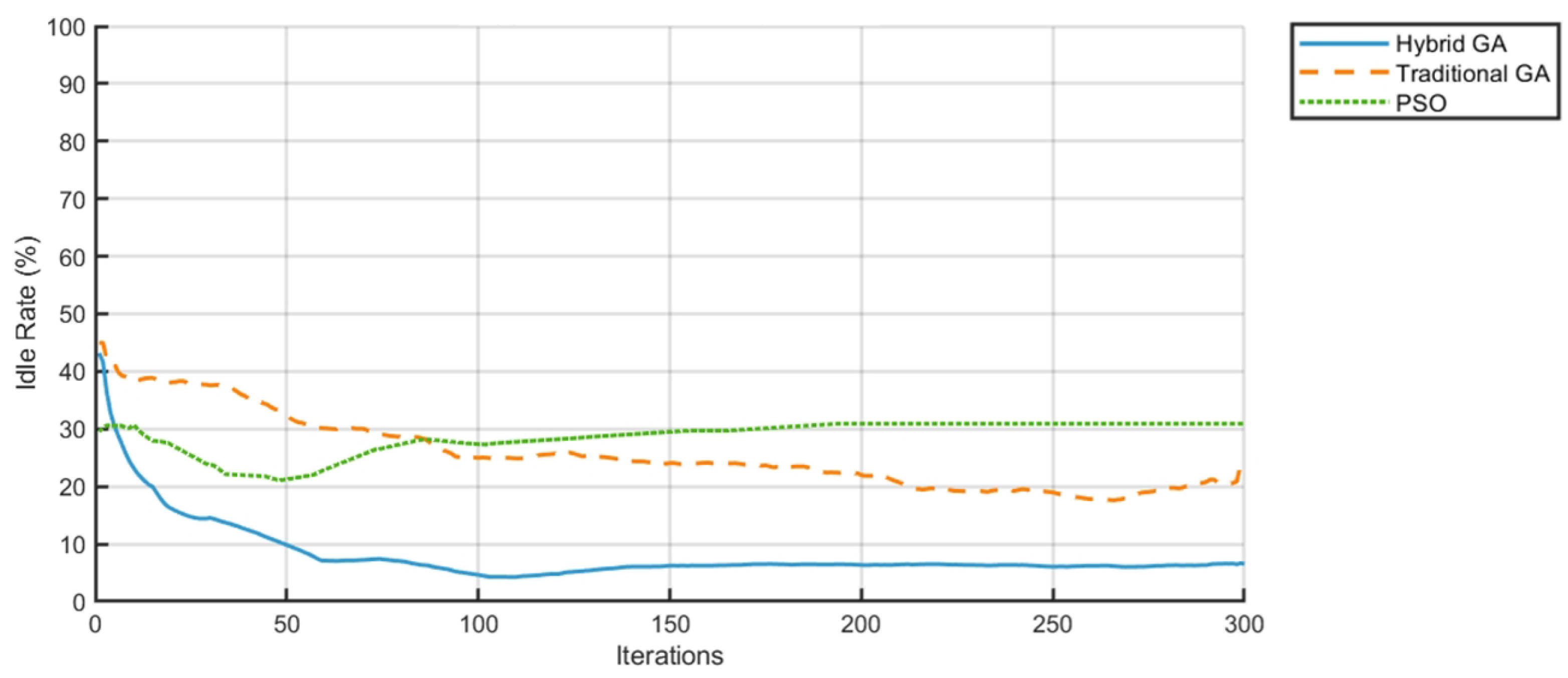
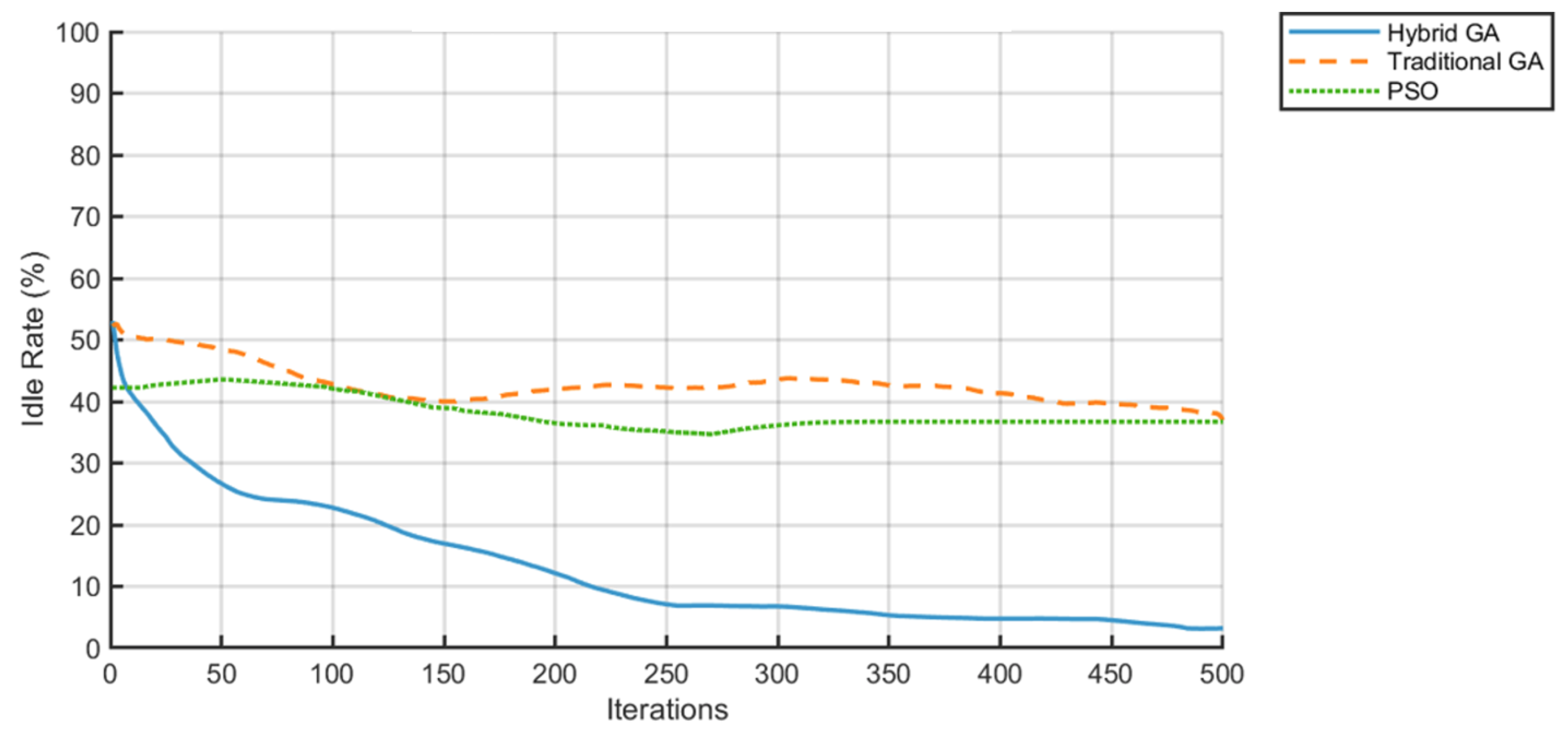
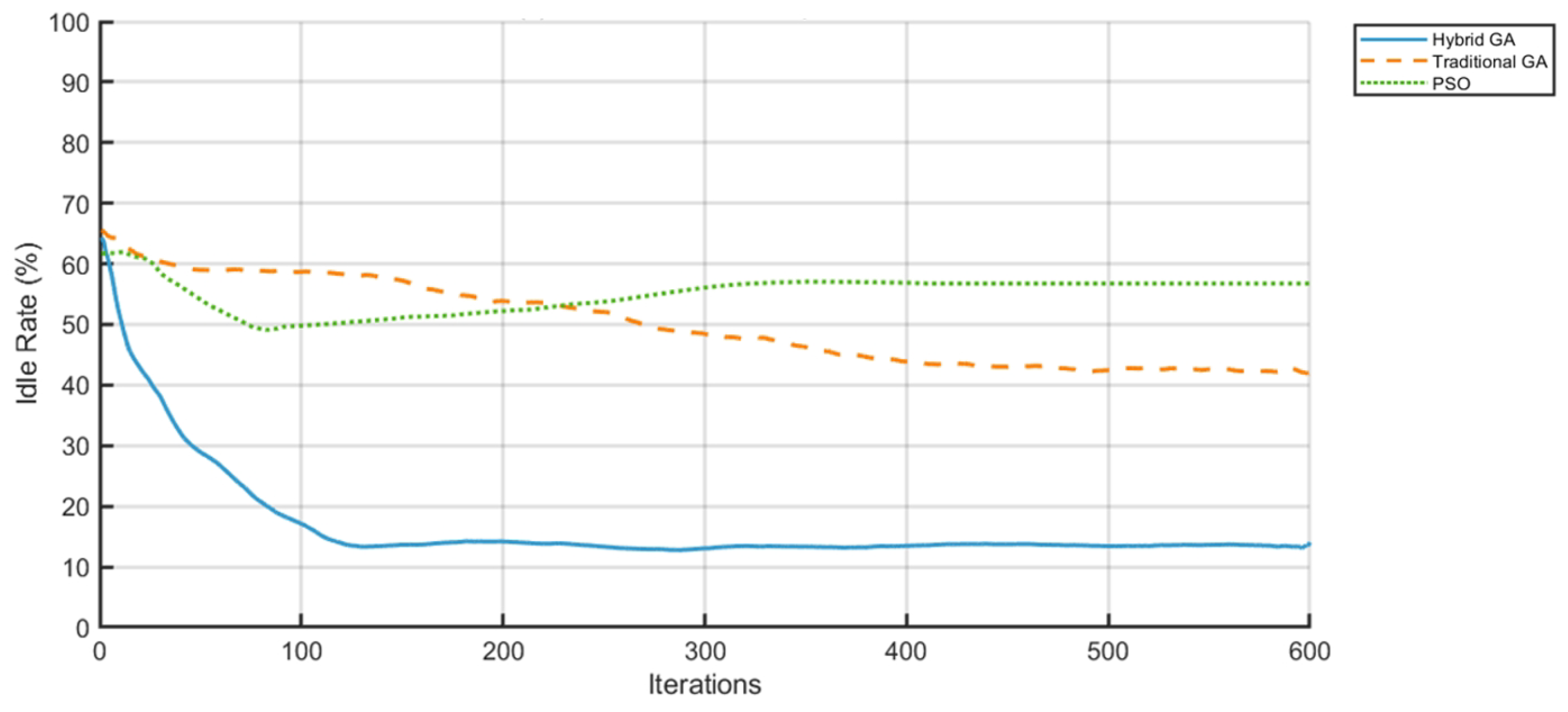
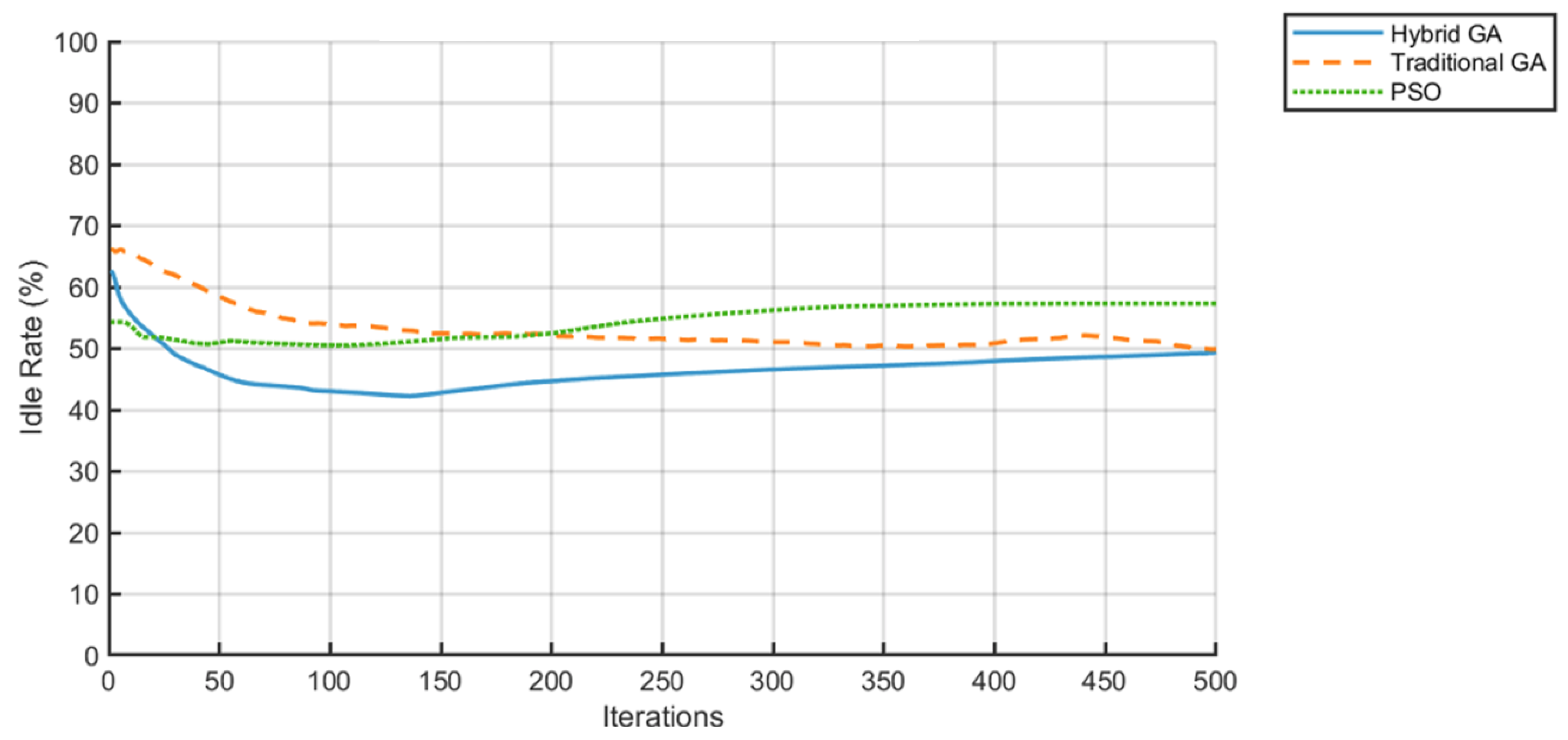
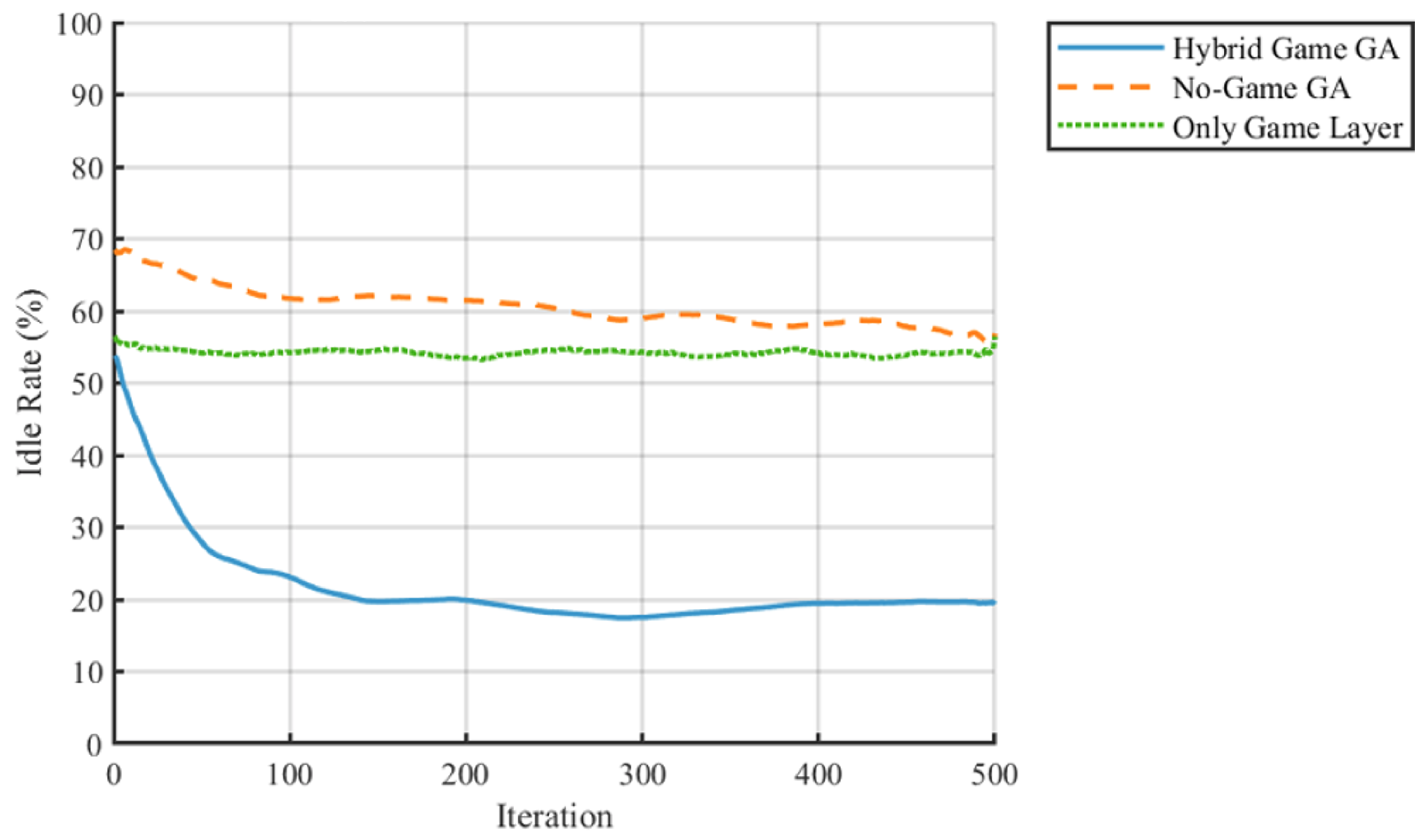
- The AGV idle rate is reduced from 40% to 9.5%, achieving a 68.3% optimization over both the TGA and PSO (30% each), effectively mitigating resource waste.
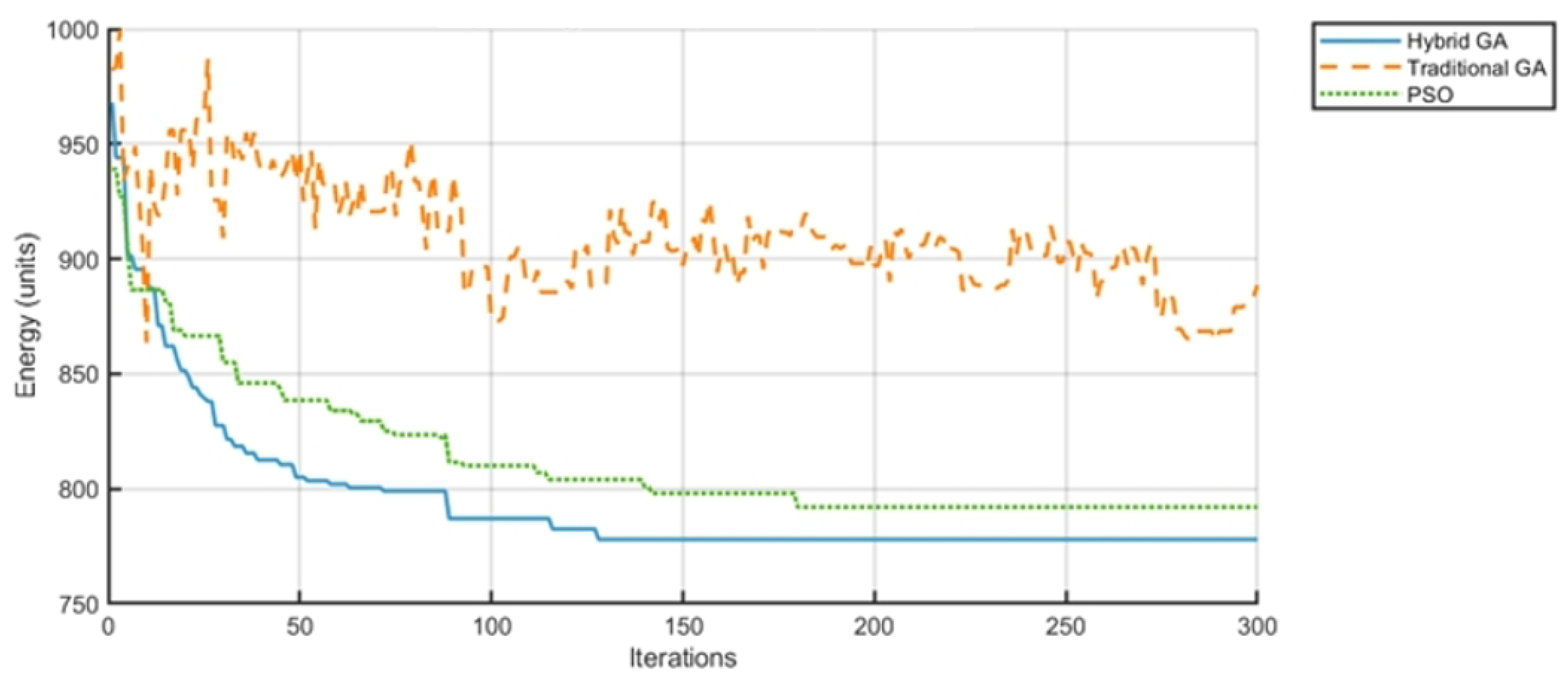
- Total energy consumption drops from 1000 units to 780 units, with 15.7% lower consumption than the TGA (925 units) and 10.9% lower consumption than PSO (875 units), demonstrating its energy-saving potential.
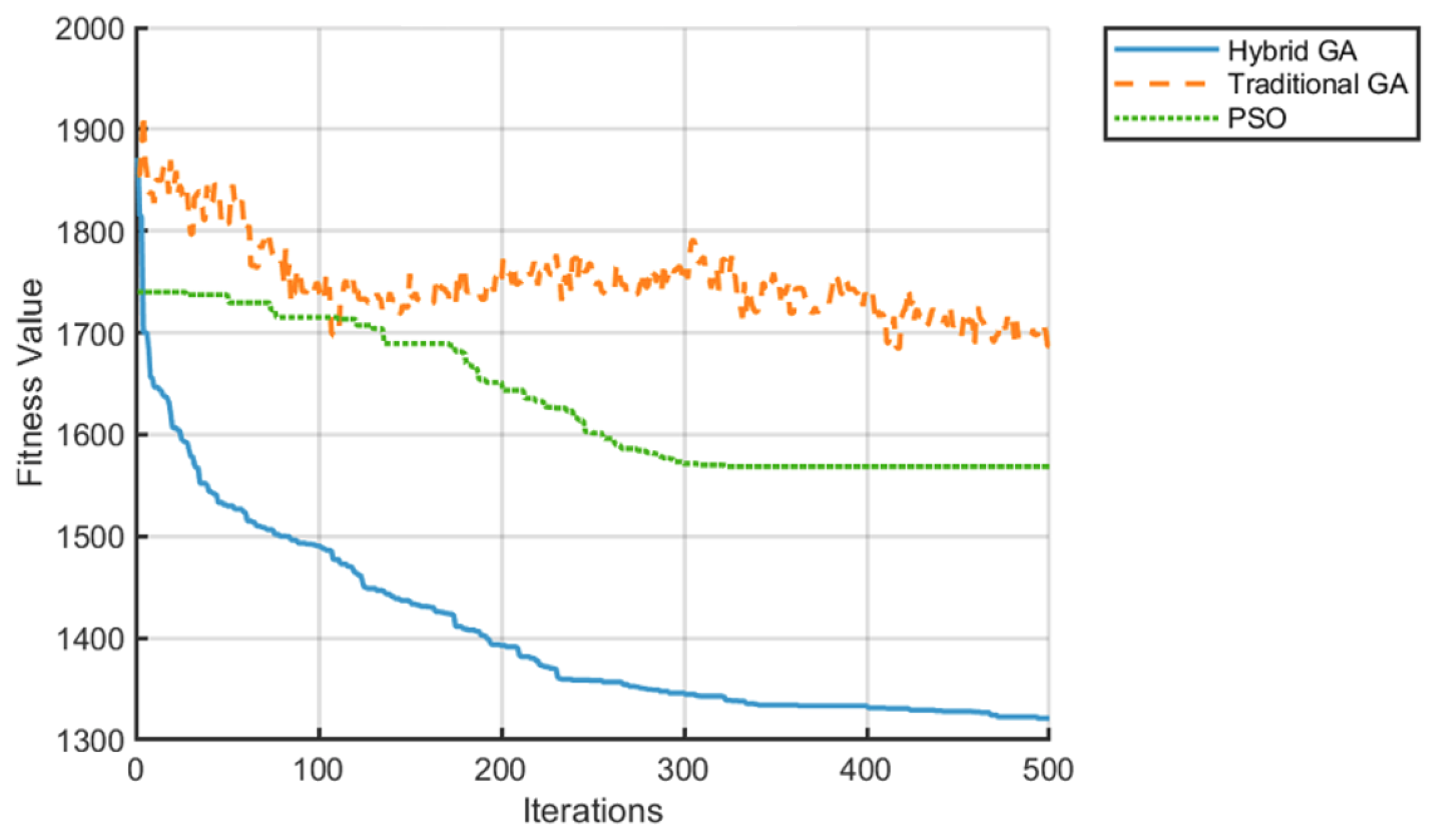
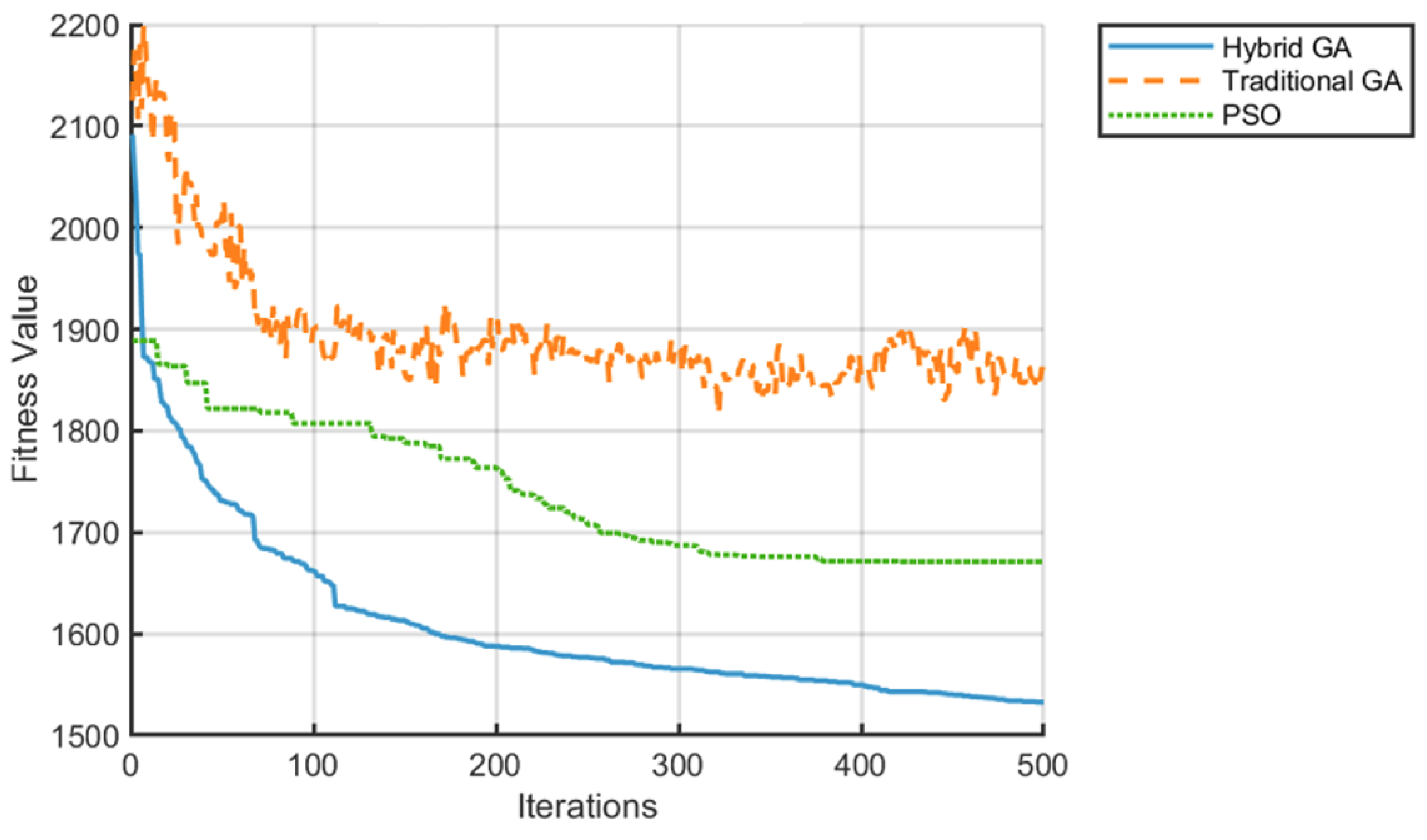
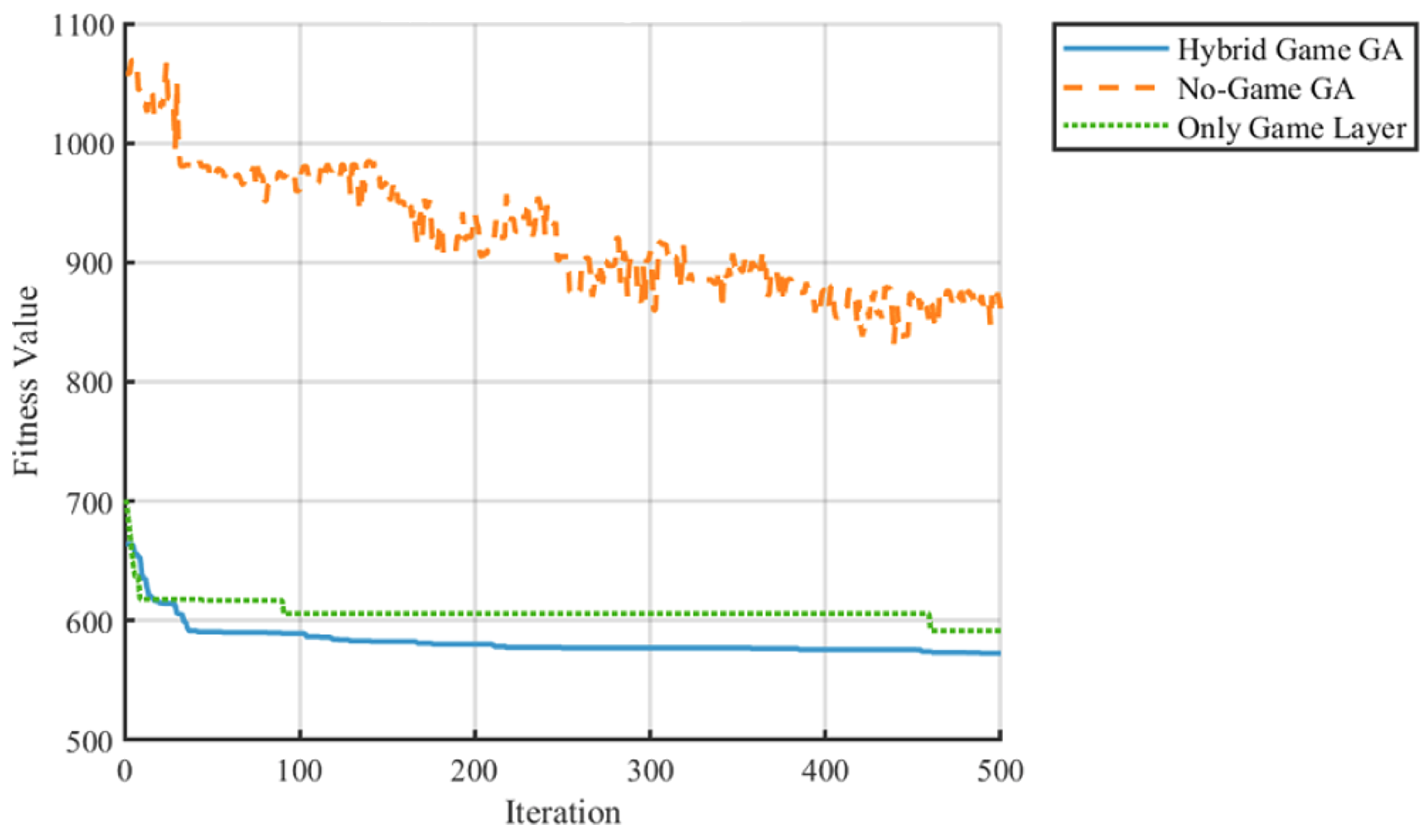
- The fitness value stabilizes at 550, a 29.5% improvement over the TGA (780) and a 21.4% improvement over PSO (700), reflecting stronger adaptability to high-complexity tasks.
- The maximum completion time is reduced to 60 units, a 57.1% reduction compared to both the TGA and PSO (140 units), underscoring its efficiency in coordinating multi-resource interactions.
- The AGV idle rate is optimized to 13%, a 67.5% reduction compared to the TGA (40%) and a 77.6% reduction compared to PSO (58%), indicating superior dynamic load balancing.
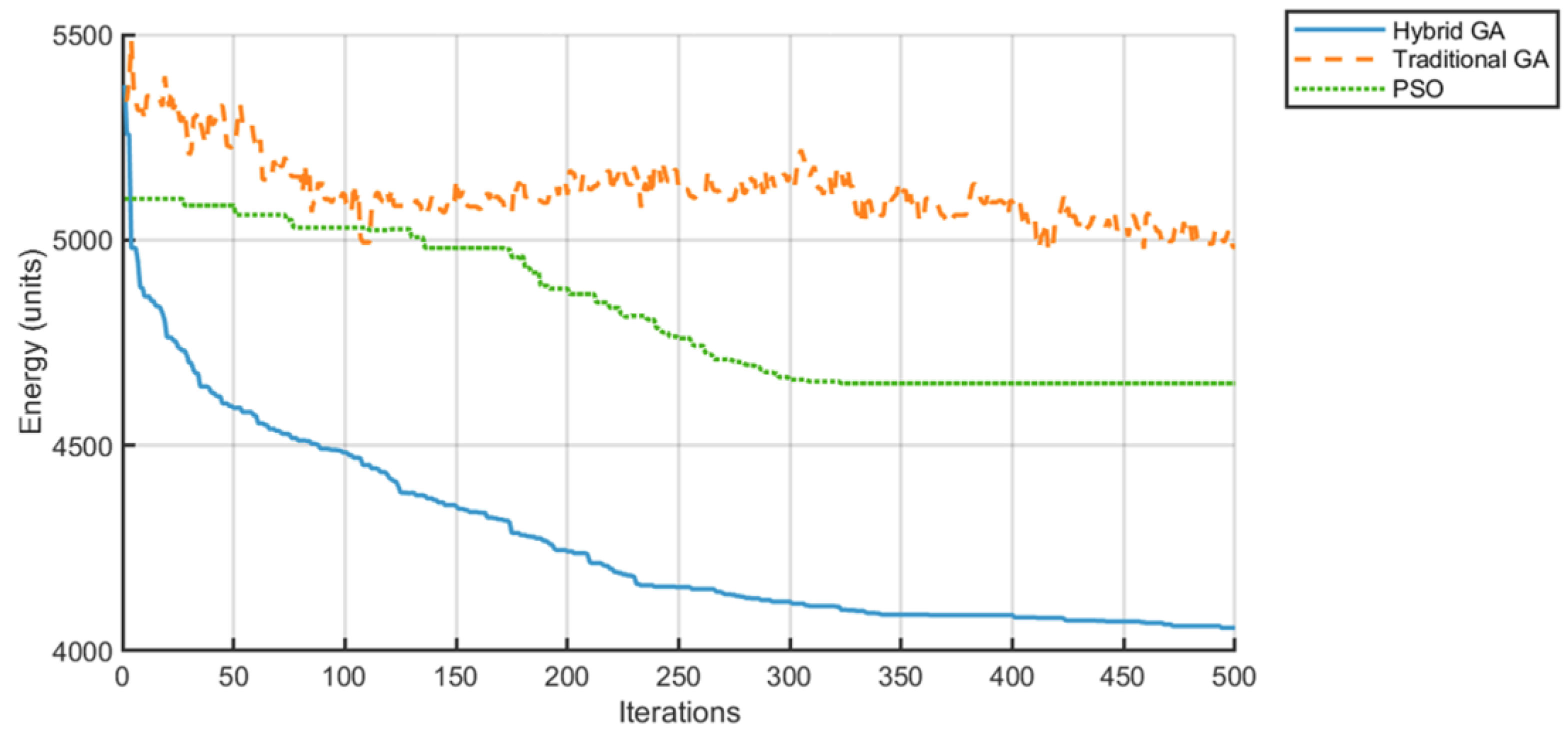
- Total energy consumption is lowered to 1800 units, 25% less than the TGA (2400 units) and 18.2% less than PSO (2200 units), validating its effectiveness in integrating processing and transportation energy optimization.
5.2. Theoretical Innovations and Mechanism Analysis
5.2.1. Hybrid Game–Genetic Synergy
5.2.2. Symmetric Multi-Agent Framework
5.2.3. Real-Time Coordination Mechanism
5.3. Practical Implications and Industry Relevance
5.3.1. Efficiency and Resource Utilization
5.3.2. Energy Conservation and Low-Carbon Development
5.3.3. Adaptability to Dynamic Scenarios
5.3.4. Industrial Implementation and Validation
5.4. Limitations and Future Work
5.4.1. Current Limitations
5.4.2. Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Yao, Y.; Li, X. Integrated Scheduling of Flexible Job-Shop Considering Heterogeneous AGVs. Comput. Integr. Manuf. Syst. 2024, 31, 1539–1554. [Google Scholar] [CrossRef]
- Tian, Z.; Jiang, X.; Liu, W.; Zhao, B.; Liu, S.; Tan, Q.; Tian, G. Lot-Streaming Workshop Scheduling with Operation Flexibility: Review and Extension. Systems 2025, 13, 271. [Google Scholar] [CrossRef]
- Destouet, C.; Tlahig, H.; Bettayeb, B.; Mazari, B. Flexible job shop scheduling problem under Industry 5.0: A survey on human reintegration, environmental consideration and resilience improvement. J. Manuf. Syst. 2023, 67, 155–173. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Gao, L.; Li, P. Research Review of Distributed Workshop Scheduling. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2022, 50, 1–10. [Google Scholar] [CrossRef]
- Dauzère-Pérés, S.; Ding, J.; Shen, L.; Tamsaaouet, K. The flexible job shop scheduling problem: A review. Eur. J. Oper. Res. 2024, 314, 409–432. [Google Scholar] [CrossRef]
- Jiang, B.; Ma, Y.; Chen, L.; Huang, B.; Huang, Y.; Guan, L. A Review on Intelligent Scheduling and Optimization for Flexible Job Shop. Int. J. Control. Autom. Syst. 2023, 21, 3127–3150. [Google Scholar] [CrossRef]
- Yu, B. Review of Flexible Flow Shop Scheduling. Mod. Manuf. Eng. 2022, 41, 154–162+71. [Google Scholar] [CrossRef]
- He, C.; Song, Y.; Lei, Q.; Lü, X.; Liu, R.; Chen, J. Integrated scheduling of multiple automated guided vehicles and machines in flexible job-shop. China Mech. Eng. 2019, 30, 438–447. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Wu, Y.; Li, S.; Zong, W. Improved NSGA-II Algorithm for Energy-Saving Flexible Job-Shop Scheduling Considering Transportation Constraints. Comput. Integr. Manuf. Syst. 2023, 29, 3028–3040. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, M.; Zhang, G. Research on Path Planning for Automated Guided Vehicles Based on Improved A* Algorithm. Fire Control Command Control 2021, 46, 130–138+144. [Google Scholar] [CrossRef]
- Zhao, X.; Ye, H.; Jia, W.; Sun, Z. Research review of agv path planning and obstacle avoidance algorithms. J. Chin. Comput. Syst. 2024, 45, 529–541. [Google Scholar] [CrossRef]
- Guo, C.; Chen, X.; Guo, P.; Wang, Q.; Wang, S. Conflict-Free Path Planning for Multiple AGVs Based on Spatiotemporal Astar Algorithm. Comput. Syst. Appl. 2022, 31, 360–368. [Google Scholar] [CrossRef]
- Huang, X.; Chen, S.; Zhou, T.; Sun, Y. Review of Genetic Algorithms for Flexible Job-Shop Scheduling. Comput. Integr. Manuf. Syst. 2022, 28, 536–551. [Google Scholar] [CrossRef]
- Yu, N.; Li, T.; Wang, B.; Yuan, S. Multi-AGV Scheduling and Path Planning in Automated Sorting Warehouses. Comput. Integr. Manuf. Syst. 2020, 26, 171–180. [Google Scholar] [CrossRef]
- Chen, K.; Bi, L.; Wang, W. Research on Integrated Scheduling of AGV and Machines in Flexible Job-Shop. J. Syst. Simul. 2022, 34, 461–469. [Google Scholar] [CrossRef]
- Homayouni, S.; Fontes, D. Production and transport scheduling in flexible job shop manufacturing systems. J. Glob. Optim. 2021, 79, 463–502. [Google Scholar] [CrossRef]
- Song, C. Improved NSGA-II for Multi-Objective Hybrid Flow Shop Scheduling. Comput. Integr. Manuf. Syst. 2022, 28, 1777–1789. [Google Scholar] [CrossRef]
- Zhang, W.; Hu, M.; Li, J.; Zhang, J. Machine-AGV Collaborative Scheduling in Flexible Job-Shop Based on Multi-Agent Non-Cooperative-Evolutionary Game. Comput. Integr. Manuf. Syst. 2024, 1–19. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J. An Improved Particle Swarm Optimization Algorithm for Integrated Scheduling Model in AGV-Served Manufacturing Systems. J. Adv. Manuf. Syst. 2018, 17, 375–390. [Google Scholar] [CrossRef]
- Xiao, Z.; Cheng, S.; Zheng, D.; Yan, J.; Lou, P.; Wang, X. Digital Twin-Driven Path Planning for AGVs in Workshops. Comput. Integr. Manuf. Syst. 2023, 29, 1905–1915. [Google Scholar] [CrossRef]
- Luo, X.; Qian, Q.; Fu, Y. Application Review of Genetic Algorithms for Flexible Job-Shop Scheduling. Comput. Eng. Appl. 2019, 55, 15–21+34. [Google Scholar] [CrossRef]
- Li, X.; Nan, K.; Zhao, Z.; Wang, X.; Jing, J. Task Allocation of Handling Robots in Textile Workshops Based on Multi-Agent Game. J. Text. Res. 2020, 41, 78–87. [Google Scholar] [CrossRef]
- Yu, H.; Bai, H.; Li, C. Path Planning Research and Simulation for Warehouse-Type Multi-AGV Systems. Comput. Eng. Appl. 2020, 56, 233–241. [Google Scholar] [CrossRef]
- Chen, X.; Hou, Z.; Guo, L.; Luo, W. Improved Multi-Objective Genetic Algorithm Based on NSGA-II. Comput. Appl. 2006, 26, 2453–2456. [Google Scholar]
- Yu, H.; Wang, Y.; Huang, Y. Research on path planning and task scheduling for multiple agvs. J. Shanghai Univ. Electr. Power 2022, 38, 89–93+97. [Google Scholar] [CrossRef]
- Wang, H.; Yin, P.; Zheng, W.; Wang, H.; Zuo, J. Path planning for mobile robots based on improved a* algorithm and dynamic window approach. Robot 2020, 42, 346–353. [Google Scholar] [CrossRef]
- Li, S.; Song, Q.; Li, Z.; Zhang, X.; Zhe, L. Research Review of Genetic Algorithms in Robot Path Planning. Sci. Technol. Eng. 2020, 20, 423–431. [Google Scholar] [CrossRef]
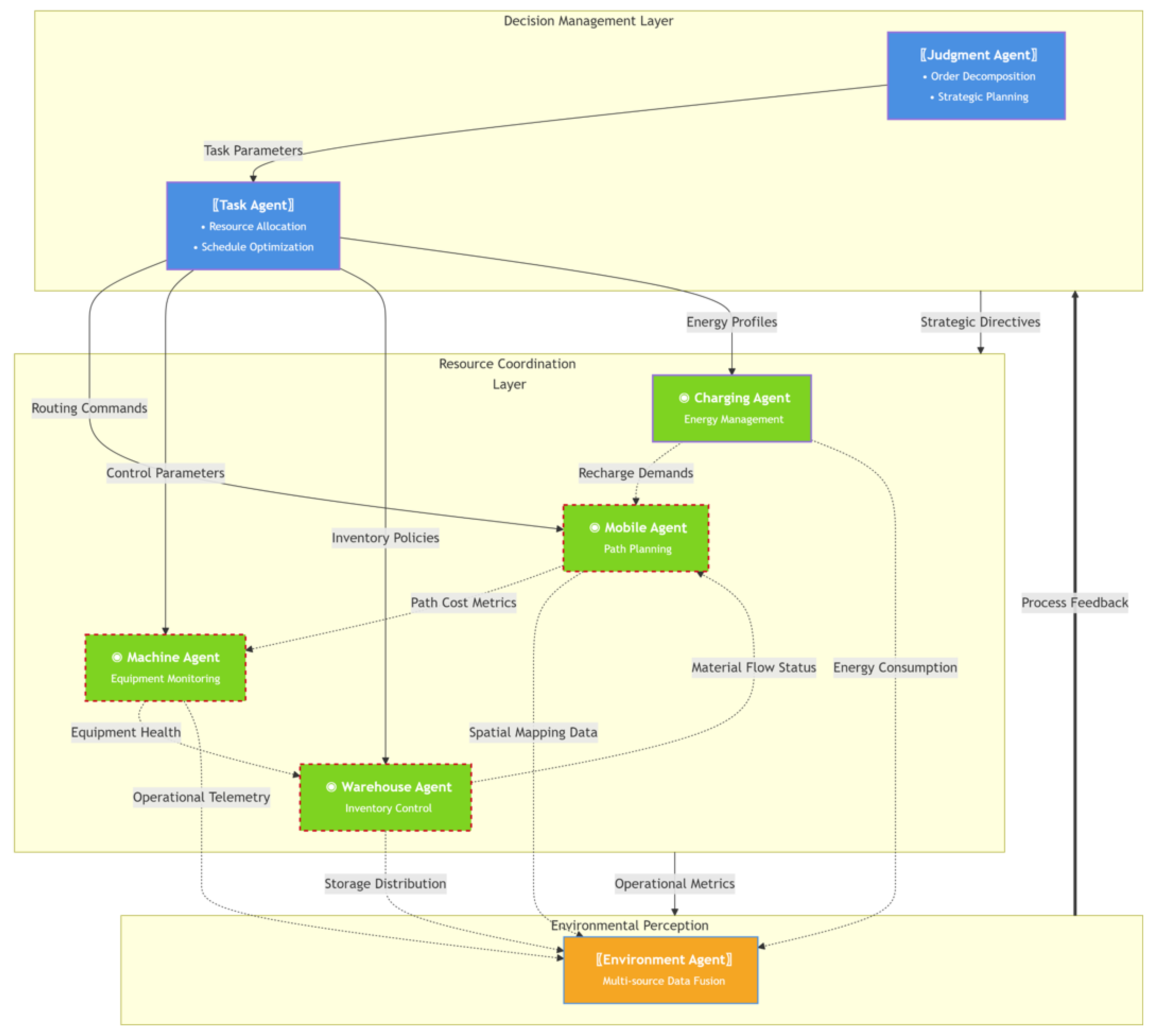









| Agent Type | Strategy Space | Key State Variables |
|---|---|---|
| Machine Agent | Whether to accept the current workpiece | Queue length , idle time |
| AGV Agent | Transportation path selection | Remaining power , current position |
| Workpiece | Select processing equipment and transportation path | Current position , process constraint |
| Scenario | Workpieces | Metric | Algorithm Performance | Improvement (%) | |||
|---|---|---|---|---|---|---|---|
| HG-GA | TGA | PSO | vs. TGA | vs. PSO | |||
| Simple | 20 | Fitness | 250.0 | 315.0 | 270.0 | 20.6 | 7.4 |
| Makespan (min) | 50.0 | 110.0 | 90.0 | 54.5 | 44.4 | ||
| AGV Idle Rate (%) | 9.5 | 30.0 | 30.0 | 68.3 | 68.3 | ||
| Energy (kWh) | 780.0 | 925.0 | 875.0 | 15.7 | 10.9 | ||
| 100 | Fitness | 295.0 | 385.0 | 320.0 | 23.4 | 7.8 | |
| Makespan (min) | 300.0 | 500.0 | 480.0 | 40.0 | 37.5 | ||
| AGV Idle Rate (%) | 13.0 | 30.0 | 35.0 | 56.7 | 62.9 | ||
| Energy (kWh) | 4000.0 | 5000.0 | 4800.0 | 20.0 | 16.7 | ||
| Complex | 40 | Fitness | 550.0 | 780.0 | 700.0 | 29.5 | 21.4 |
| Makespan (min) | 60.0 | 140.0 | 140.0 | 57.1 | 57.1 | ||
| AGV Idle Rate (%) | 13.0 | 40.0 | 58.0 | 67.5 | 77.6 | ||
| Energy (kWh) | 1800.0 | 2400.0 | 2200.0 | 25.0 | 18.2 | ||
| 100 | Fitness | 1500.0 | 1900.0 | 1700.0 | 21.1 | 11.8 | |
| Makespan (min) | 300.0 | 450.0 | 450.0 | 33.3 | 33.3 | ||
| AGV Idle Rate (%) | 13.0 | 40.0 | 58.0 | 67.5 | 77.6 | ||
| Energy (kWh) | 4500.0 | 6500.0 | 5500.0 | 30.8 | 18.2 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, W.; Du, B.; Ma, J.; Chen, J.; Zheng, X. Research on a Multi-Agent Job Shop Scheduling Method Based on Improved Game Evolution. Symmetry 2025, 17, 1368. https://doi.org/10.3390/sym17081368
Xie W, Du B, Ma J, Chen J, Zheng X. Research on a Multi-Agent Job Shop Scheduling Method Based on Improved Game Evolution. Symmetry. 2025; 17(8):1368. https://doi.org/10.3390/sym17081368
Chicago/Turabian StyleXie, Wei, Bin Du, Jiachen Ma, Jun Chen, and Xiangle Zheng. 2025. "Research on a Multi-Agent Job Shop Scheduling Method Based on Improved Game Evolution" Symmetry 17, no. 8: 1368. https://doi.org/10.3390/sym17081368
APA StyleXie, W., Du, B., Ma, J., Chen, J., & Zheng, X. (2025). Research on a Multi-Agent Job Shop Scheduling Method Based on Improved Game Evolution. Symmetry, 17(8), 1368. https://doi.org/10.3390/sym17081368





