More Diagonal Distributions of Coexisting Attractors
Abstract
1. Introduction
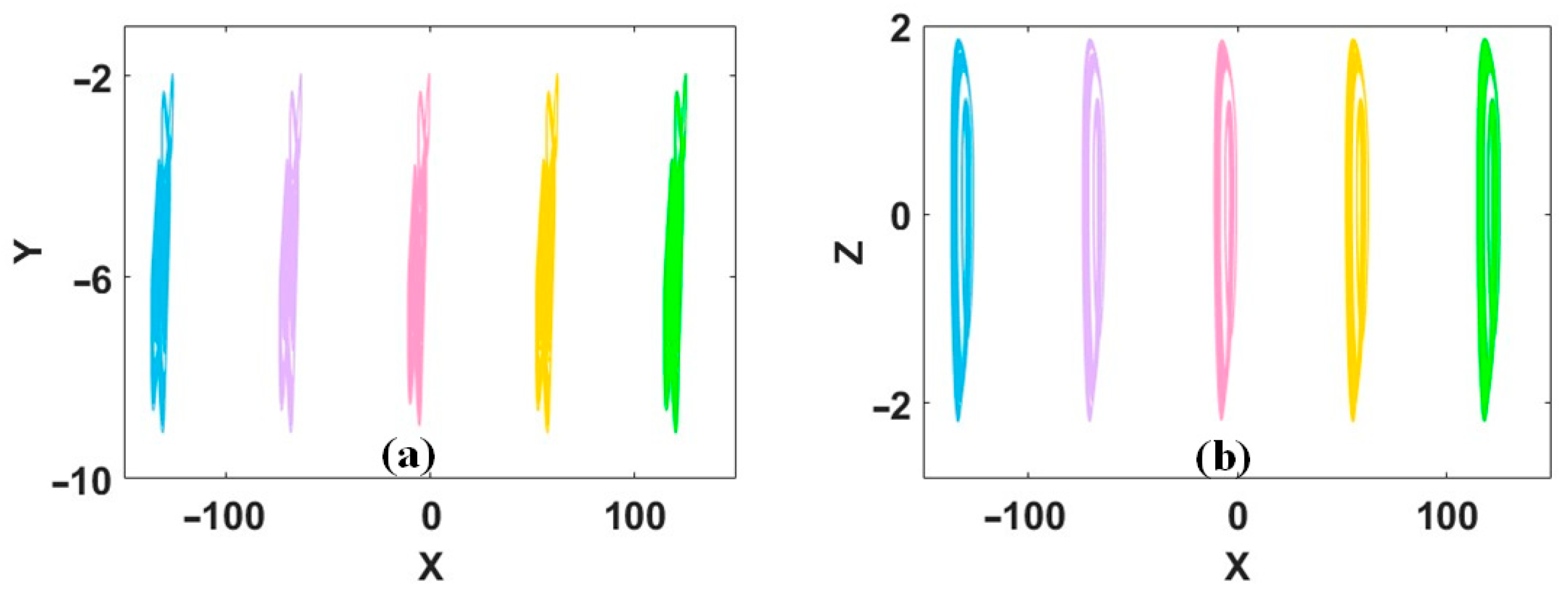
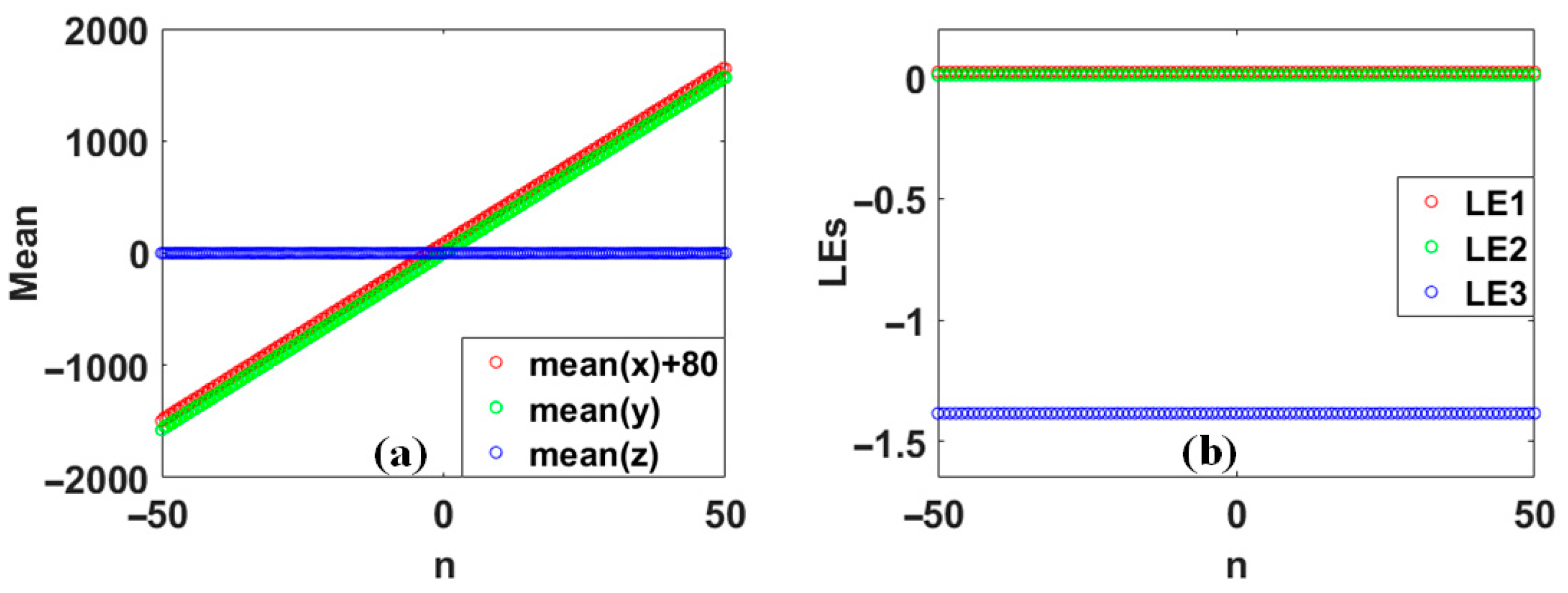
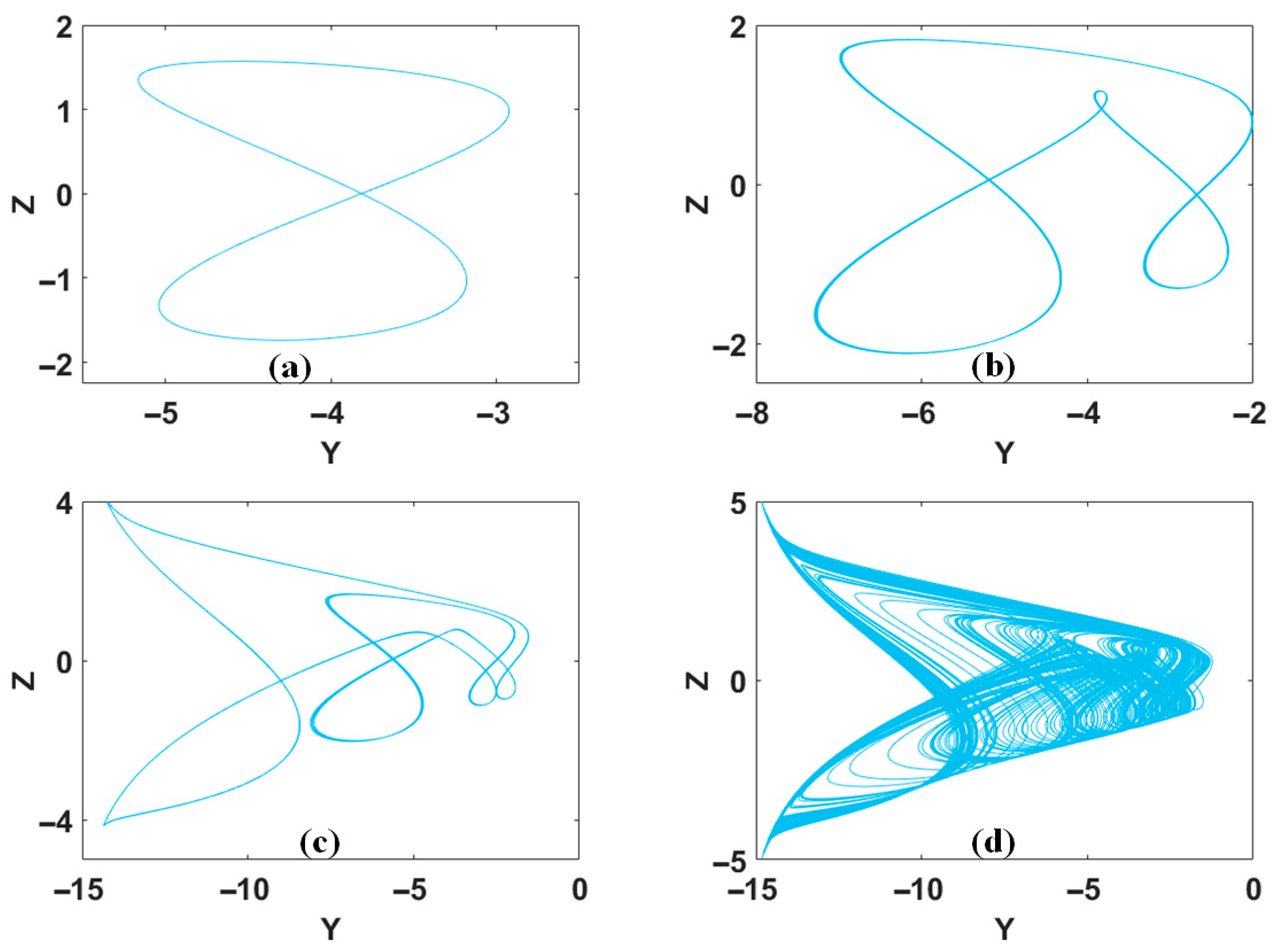
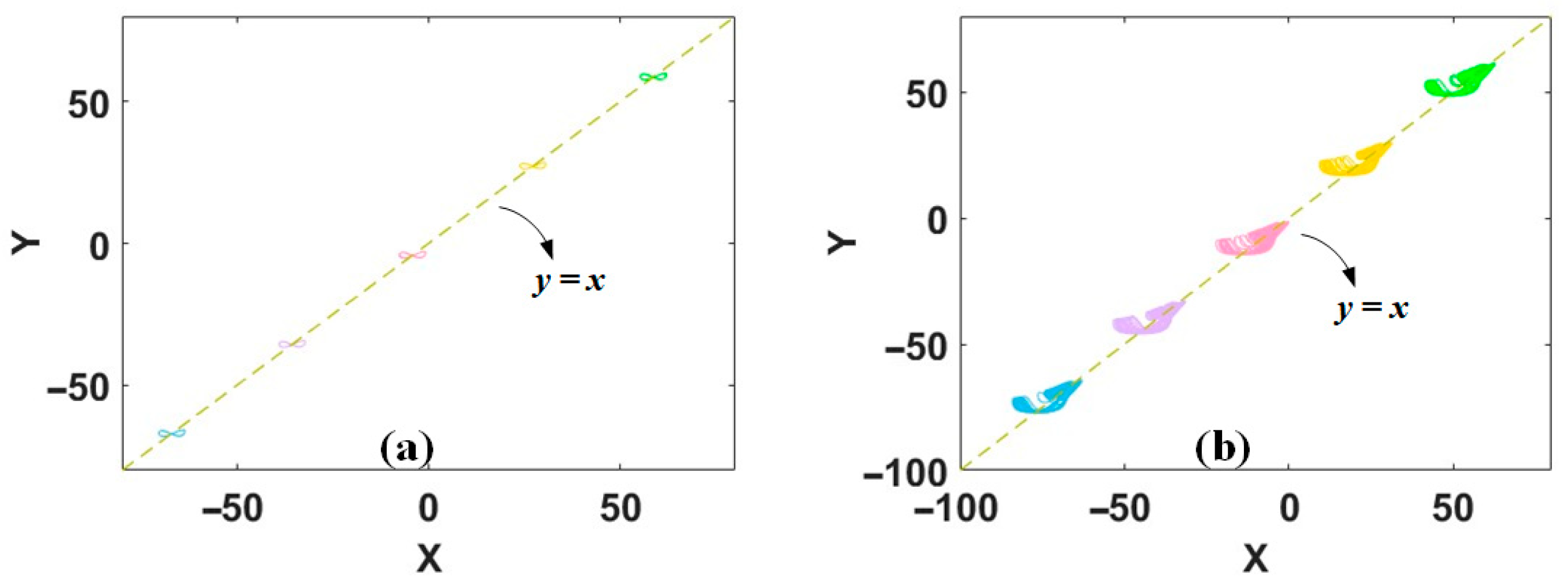
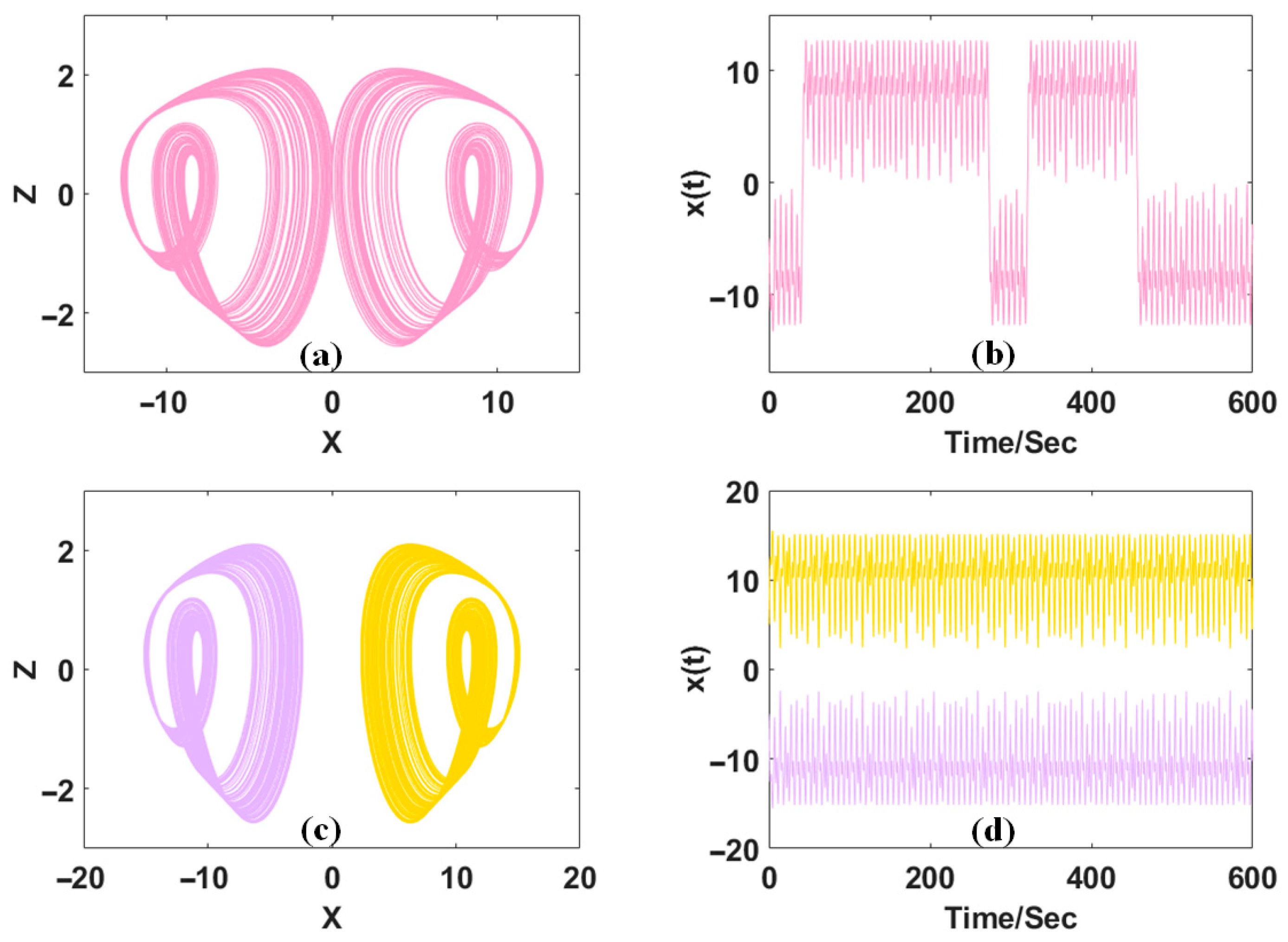
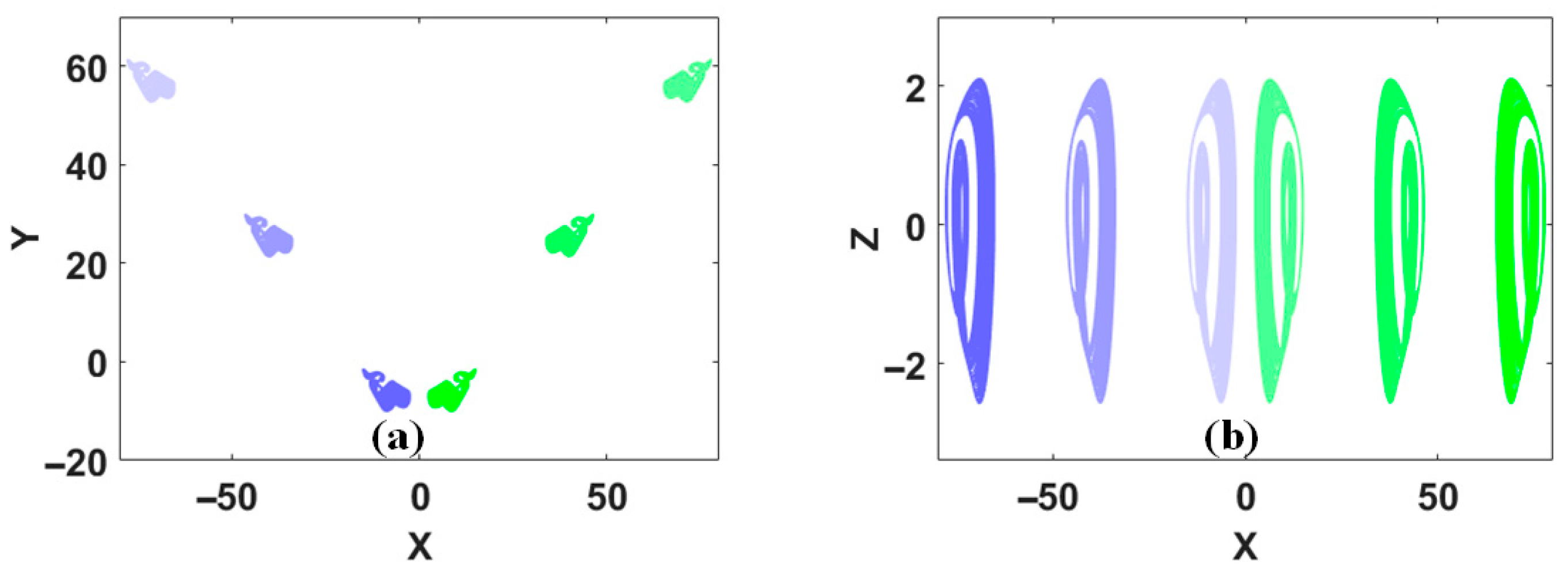
2. Single-Line Distributed Coexisting Attractors
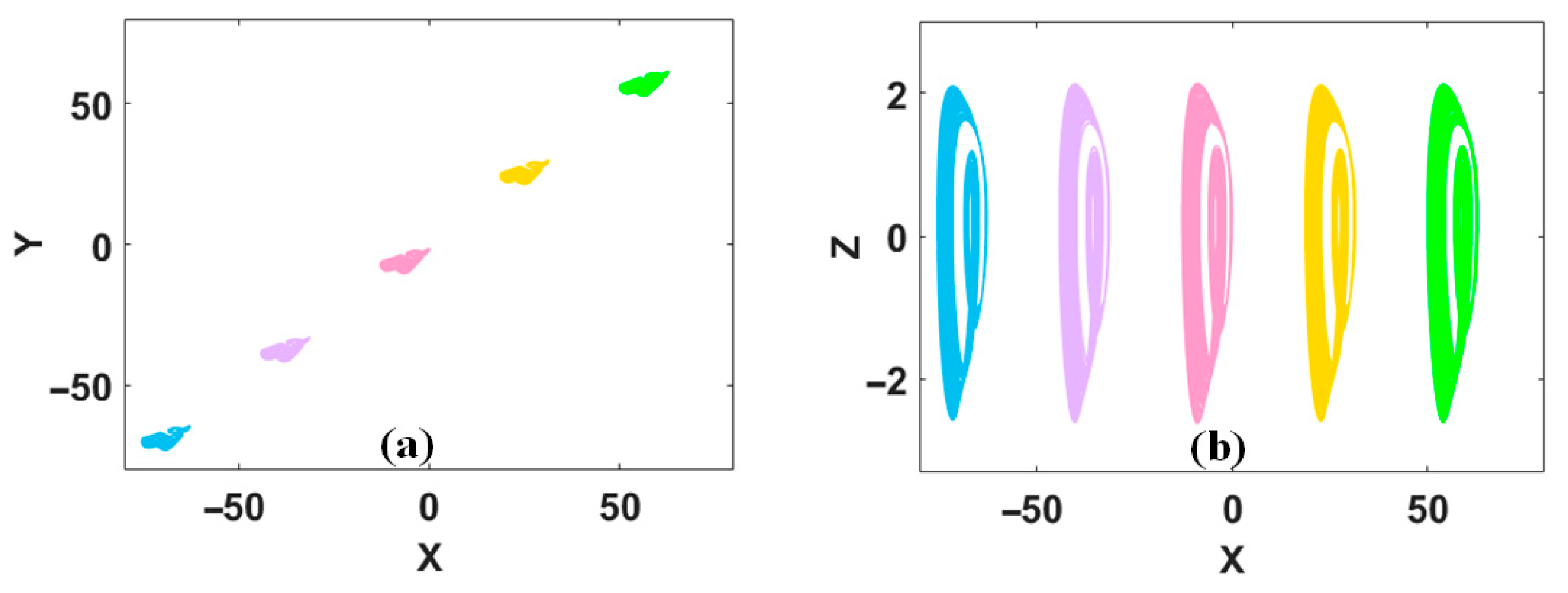
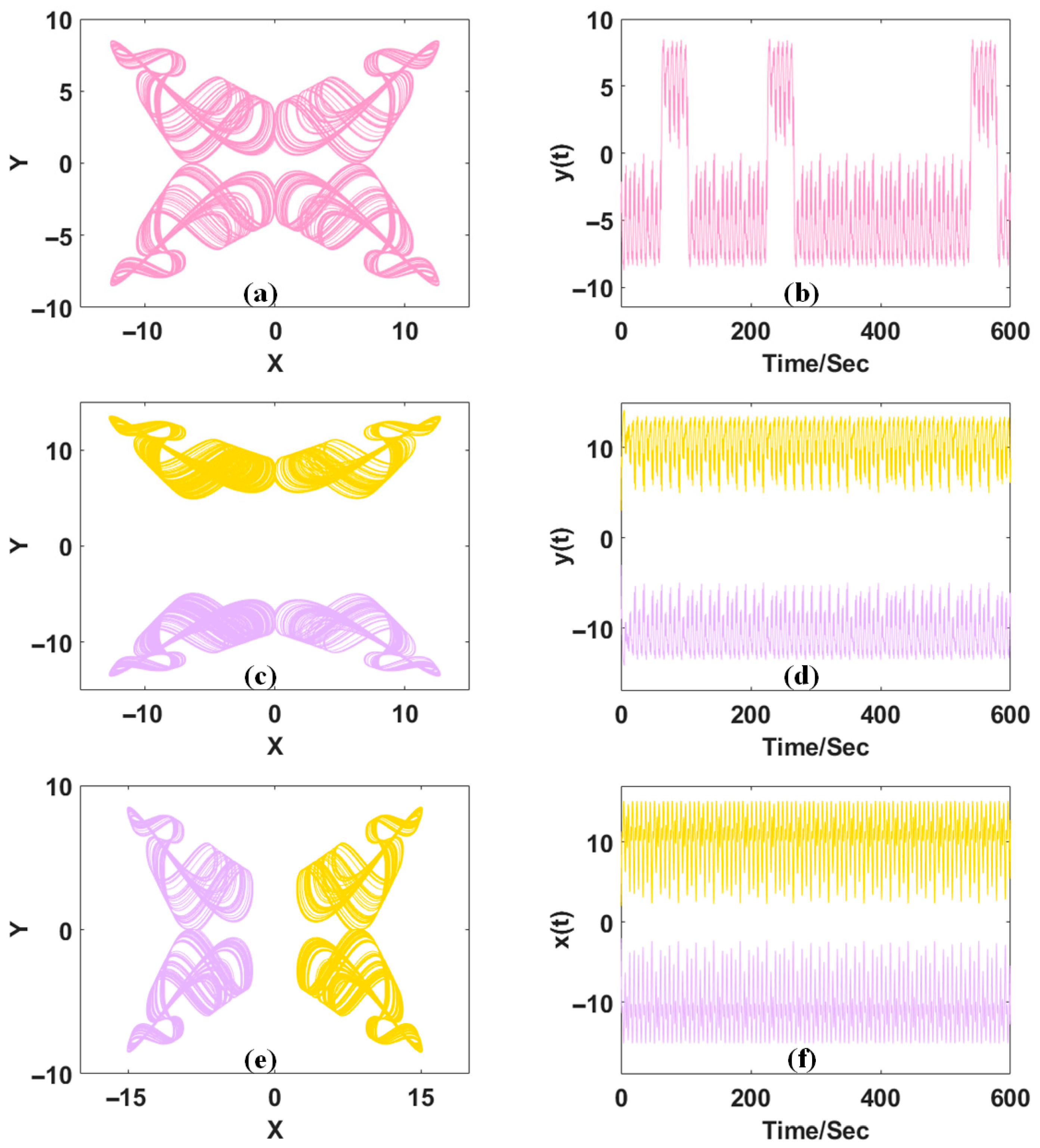
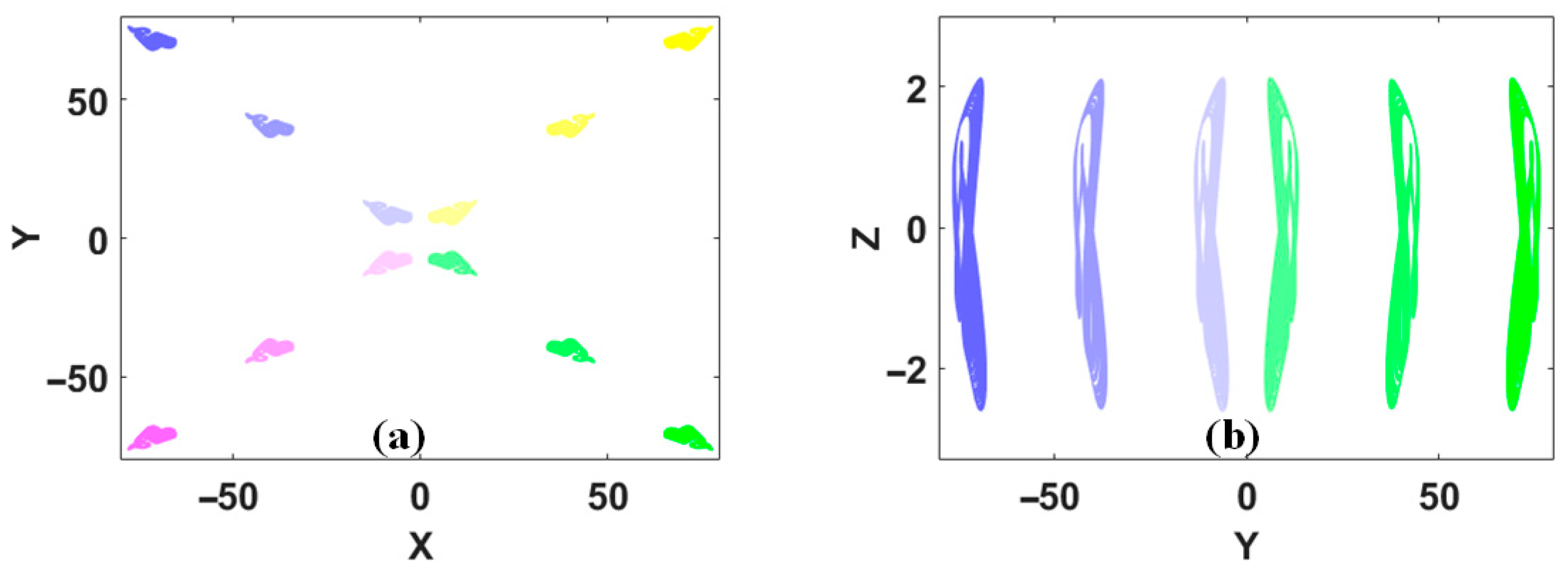
3. V-Shaped and X-Shaped Coexisting Attractors
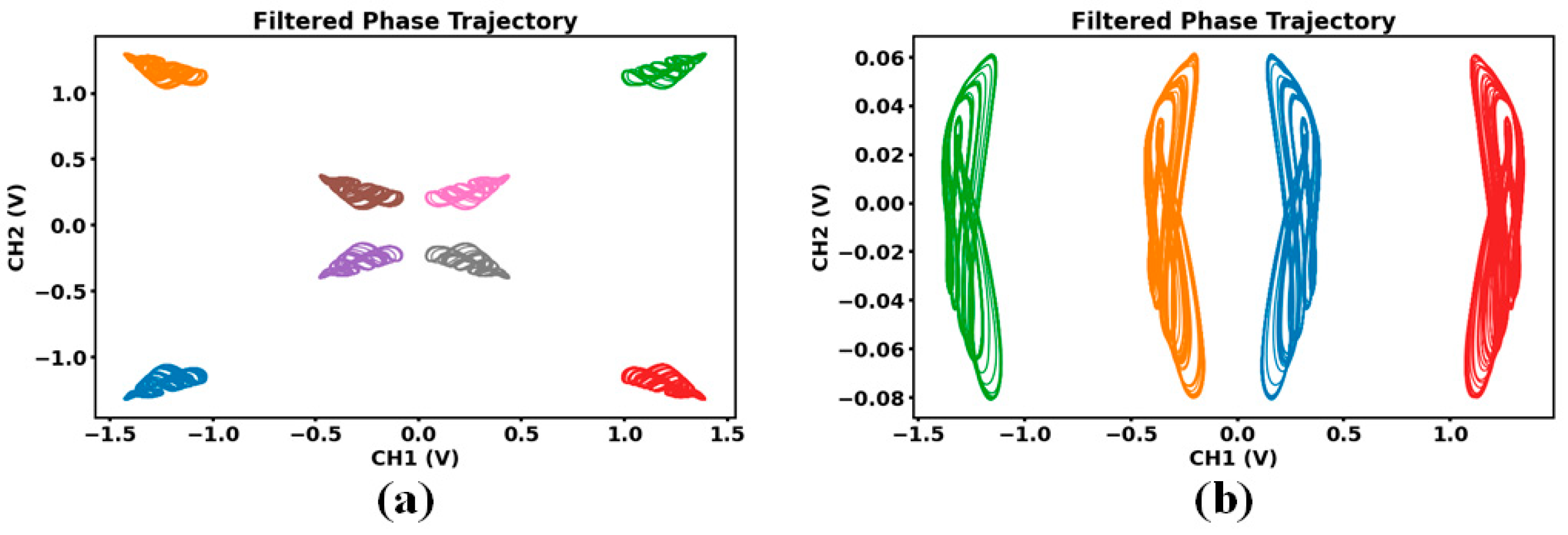
4. FPGA-Based Implementation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tsonis, A.A. Chaos: From Theory to Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar][Green Version]
- Karimov, T.; Rybin, V.; Kolev, G.; Rodionova, E.; Butusov, D. Chaotic communication system with symmetry-based modulation. Appl. Sci. 2021, 11, 3698. [Google Scholar] [CrossRef]
- Baptista, M.S. Chaos for communication. Nonlinear Dyn. 2021, 105, 1821–1841. [Google Scholar] [CrossRef]
- Zhang, G.; Shao, S.; Huang, T. A high-data-rate hybrid index communication system based on quadrature chaos shift keying. Chaos Solitons Fractals 2024, 185, 115117. [Google Scholar] [CrossRef]
- Wang, X.; Chen, S.; Zhang, Y. A chaotic image encryption algorithm based on random dynamic mixing. Opt. Laser Technol. 2021, 138, 106837. [Google Scholar] [CrossRef]
- Alawida, M. A novel DNA tree-based chaotic image encryption algorithm. J. Inf. Secur. Appl. 2024, 83, 103791. [Google Scholar] [CrossRef]
- Li, L. A novel chaotic map application in image encryption algorithm. Expert Syst. Appl. 2024, 252, 124316. [Google Scholar] [CrossRef]
- Skinner, J.E.; Molnar, M.; Vybiral, T.; Mitra, M. Application of chaos theory to biology and medicine. Integr. Physiol. Behav. Sci. 1992, 27, 39–53. [Google Scholar] [CrossRef] [PubMed]
- Chirumbolo, S.; Franzini, M.; Tirelli, U.; Ricevuti, G.; Loprete, F.; Richelmi, T.; Vaiano, F.; Galoforo, A.C.; Chierchia, M.; Valdenassi, L. Harnessing Adaptive Chaos: Exploring the role of oxygen-ozone therapy in modulating complexity and repair in spine disorders via a bio-informatic model. bioRxiv 2025. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Sun, J.; Sun, Y.; Jiang, J.; Lin, H.; Deng, Z. Nonvolatile CMOS memristor, reconfigurable array, and its application in power load forecasting. IEEE Trans. Ind. Inform. 2023, 20, 6130–6141. [Google Scholar] [CrossRef]
- Wang, M.; Gu, L. Multiple mixed state variable incremental integration for reconstructing extreme multistability in a novel memristive hyperchaotic jerk system with multiple cubic nonlinearity. Chin. Phys. B 2024, 33, 020504. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, Y. Switchable memristive HR neurons with hidden firing patterns and offset boosting dynamics. Eur. Phys. J. Spec. Top. 2025, 34, 1–18. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Xiong, L.; Banerjee, S.; Liu, T.; Han, X. Dynamical analysis of a new chaotic system: Asymmetric multistability, offset boosting control and circuit realization. Nonlinear Dyn. 2021, 103, 2867–2880. [Google Scholar] [CrossRef]
- Xin, Z.J.; Lai, Q. Dynamical investigation and encryption application of a new multiscroll memristive chaotic system with rich offset boosting features. Chaos Solitons Fractals 2024, 181, 114696. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, P.; Wang, X.; Cheng, N. The design, circuit realization and applications of chaotic system with offset-boosting and multistability. Phys. Scr. 2024, 99, 085206. [Google Scholar] [CrossRef]
- Leng, X.; Wang, X.; Zeng, Z. Memristive Hopfield neural network with multiple controllable nonlinear offset behaviors and its medical encryption application. Chaos Solitons Fractals 2024, 183, 114944. [Google Scholar] [CrossRef]
- Feudel, U.; Grebogi, C. Multistability and the control of complexity. Chaos Interdiscip. J. Nonlinear Sci. 1997, 7, 597–604. [Google Scholar] [CrossRef]
- Liu, J.; Sun, K.; Wang, H. Mechanism of multistability in chaotic maps. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 083102. [Google Scholar] [CrossRef] [PubMed]
- Tang, D.; Wang, C.; Lin, H.; Yu, F. Dynamics analysis and hardware implementation of multi-scroll hyperchaotic hidden attractors based on locally active memristive Hopfield neural network. Nonlinear Dyn. 2024, 112, 1511–1527. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Mei, Y. An infinite 2-D lattice of strange attractors. Nonlinear Dyn. 2017, 89, 2629–2639. [Google Scholar] [CrossRef]
- Muthuswamy, B.; Banerjee, S. A Route to Chaos Using FPGAs; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Moreira Bezerra, J.I.; Machado, G.; Iankowski Soares, R.; Valduga de Almeida Camargo, V.; Molter, A. FPGA implementation of low cost and low power chaotic encryption scheme based on a discrete-space chaotic map. Multimed. Tools Appl. 2025, 84, 33331–33352. [Google Scholar] [CrossRef]
- Li, C.; Gao, Y.; Lei, T.; Li, R.Y.M.; Xu, Y. Two independent offset controllers in a three-dimensional chaotic system. Int. J. Bifurc. Chaos 2024, 34, 2450008. [Google Scholar] [CrossRef]
- Li, C.; Shen, M.; Wang, L.; Xue, Y.; Qi, X. Diagonal attractor self-reproducing via a single periodic function. Nonlinear Dyn. 2025, 1–13. [Google Scholar] [CrossRef]
- Kahan, W. IEEE standard 754 for binary floating—Point arithmetic. Lect. Notes Status IEEE 1996, 754, 11. [Google Scholar]











| Distribution Type | 1-Shaped Distribution | Tilted-1-Shaped Distribution | V-Shaped Distribution | X-Shaped Distribution |
|---|---|---|---|---|
| Trigonometric function | 1 | 1 | 1 | 1 |
| Absolute value function | 0 | 0 | 1 | 3 |
| Signum function | 0 | 0 | 1 | 2 |
| Number of offset operations | 0 | 0 | 1 | 1 |
| x | y | z | |
| xs1 | 3F800000 | 3F800000 | 3F800000 |
| xs2 | BB7F9724 | BB656041 | BA83126E |
| xs3 | 0 | 3DCCCCCC | 0 |
| cs1 | x | y | z |
| cs2 | 3F800000 | 3F800000 | 3F800000 |
| cs3 | 3F800000 | z | 3F800000 |
| cs4 | z | z | y |
| cs5 | 0 | 0 | 0 |
| cs6 | 0 | y | 0 |
| cs7 | 3F800000 | 0 | x |
| cs8 | 0 | 0 | 0 |
| cs9 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, M.; Li, C.; Wang, L.; Xue, Y.; Qi, X. More Diagonal Distributions of Coexisting Attractors. Symmetry 2025, 17, 1331. https://doi.org/10.3390/sym17081331
Shen M, Li C, Wang L, Xue Y, Qi X. More Diagonal Distributions of Coexisting Attractors. Symmetry. 2025; 17(8):1331. https://doi.org/10.3390/sym17081331
Chicago/Turabian StyleShen, Menghui, Chunbiao Li, Lili Wang, Yishi Xue, and Xiaolong Qi. 2025. "More Diagonal Distributions of Coexisting Attractors" Symmetry 17, no. 8: 1331. https://doi.org/10.3390/sym17081331
APA StyleShen, M., Li, C., Wang, L., Xue, Y., & Qi, X. (2025). More Diagonal Distributions of Coexisting Attractors. Symmetry, 17(8), 1331. https://doi.org/10.3390/sym17081331






