TS-SMOTE: An Improved SMOTE Method Based on Symmetric Triangle Scoring Mechanism for Solving Class-Imbalanced Problems
Abstract
1. Introduction
2. Related Works
- Determine the minority class sample set . For each sample in it, calculate and find its k nearest neighbors through methods such as the Euclidean distance.
- For each minority class sample , randomly select a nearest neighbor sample from its k nearest neighbors.
- Synthesize a new sample through the formula , where is a random number.
- Repeat the above steps to generate a sufficient number of minority class samples, so as to balance the class distribution of the dataset and solve the problem of data imbalance.
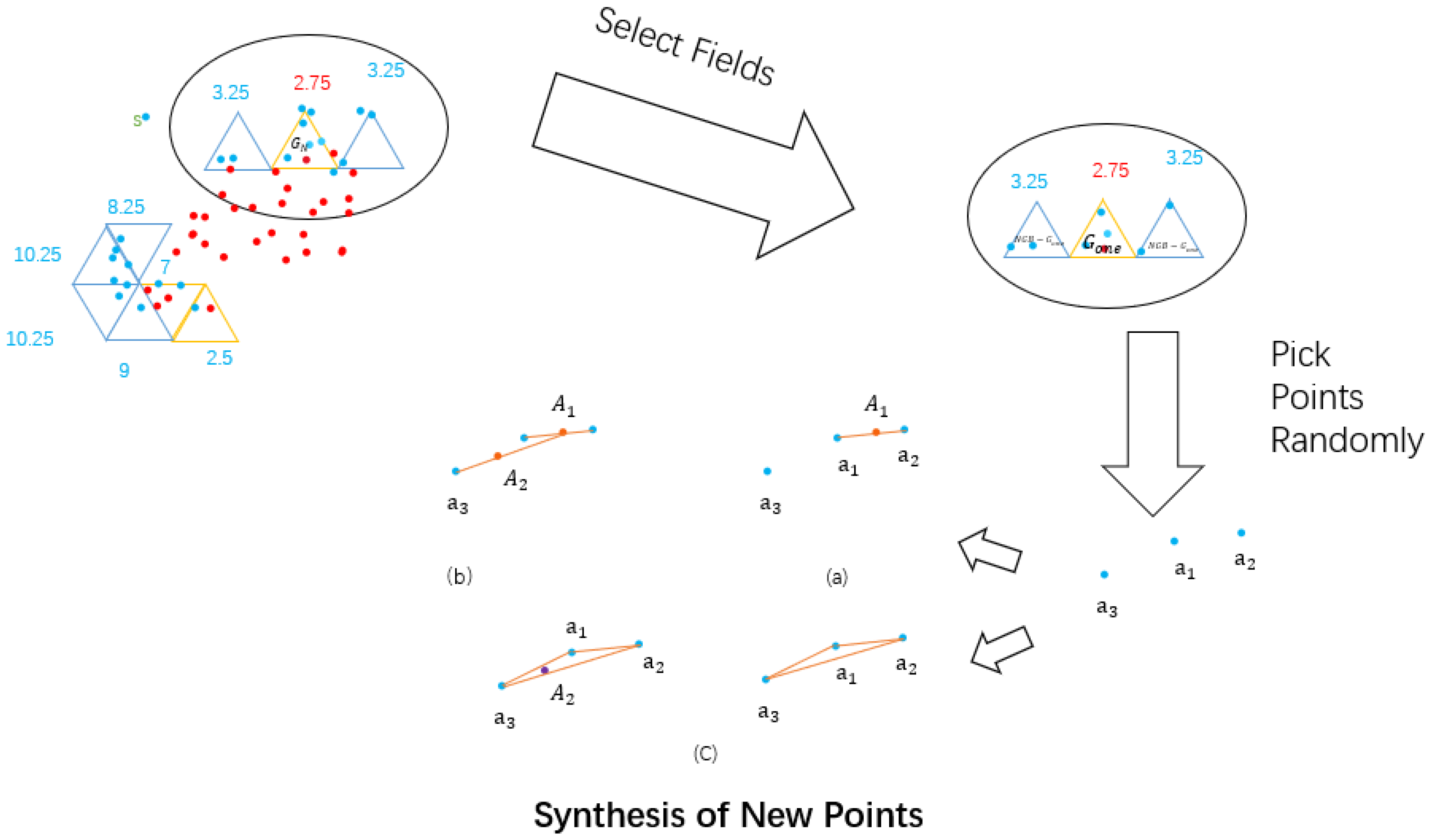
3. Specific Methods of the Improved Symmetric Triangle Scoring Mechanism
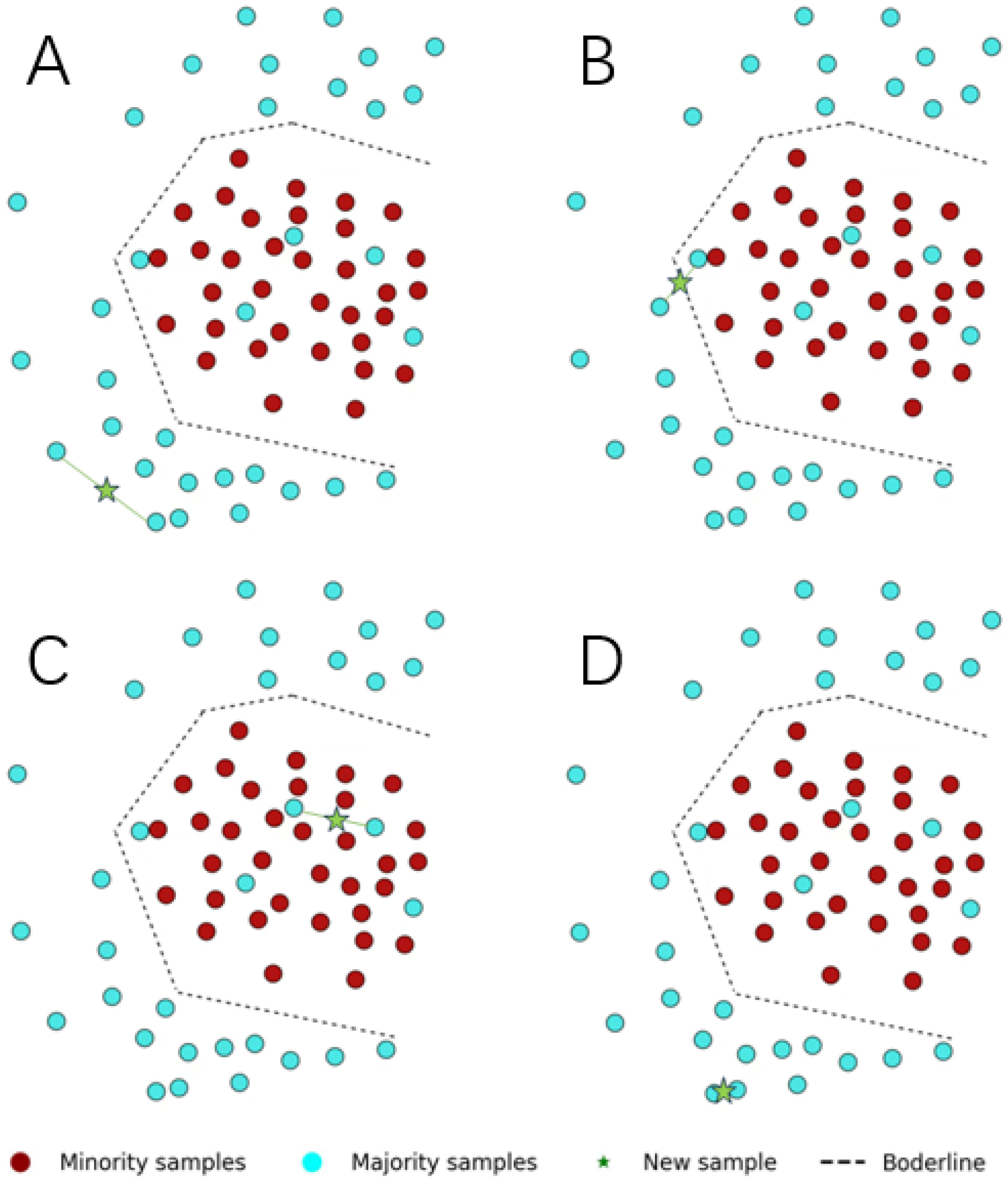
3.1. Detailed Introduction of Methods
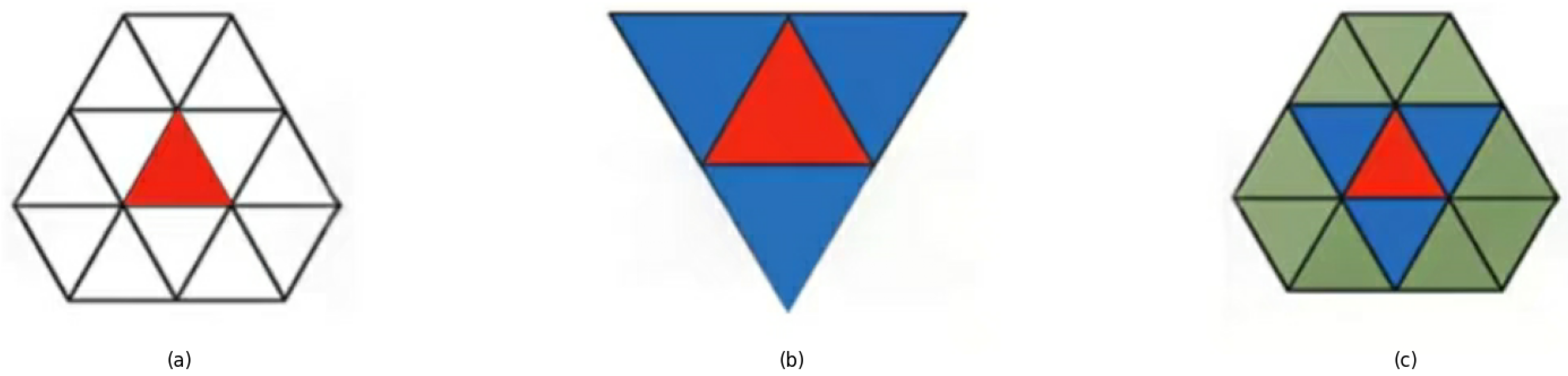
- Step 1. Multidimensional data is projected onto a 2D plane via PCA.
- Step 2. Pave the entire two-dimensional plane with regular triangles.
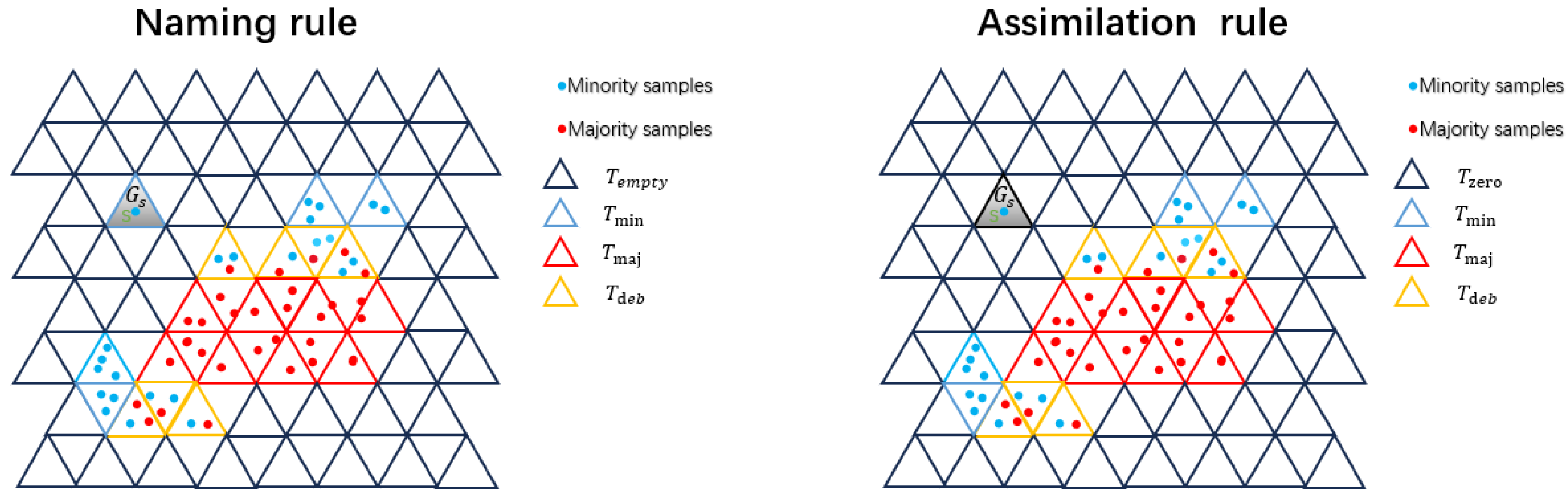
- Step 3. Rules for naming and assimilation.
- Rules for naming.
- T: Each regular triangles is recorded as a field T.
- : The remaining 12 regular triangles adjacent to field T are called neighbors of field T and recorded as . They include three triangles with connected sides and nine triangles with adjacent vertices.
- : Triangles connected to a regular triangle by their sides.
- : Triangles connected to a regular triangle by their vertices.
- : A triangle containing only minority samples.
- : A triangle containing only majority samples.
- : A triangle that does not contain any samples.
- : A triangle that contains both majority and minority samples, which requires further debate.
- Rules for Assimilation.
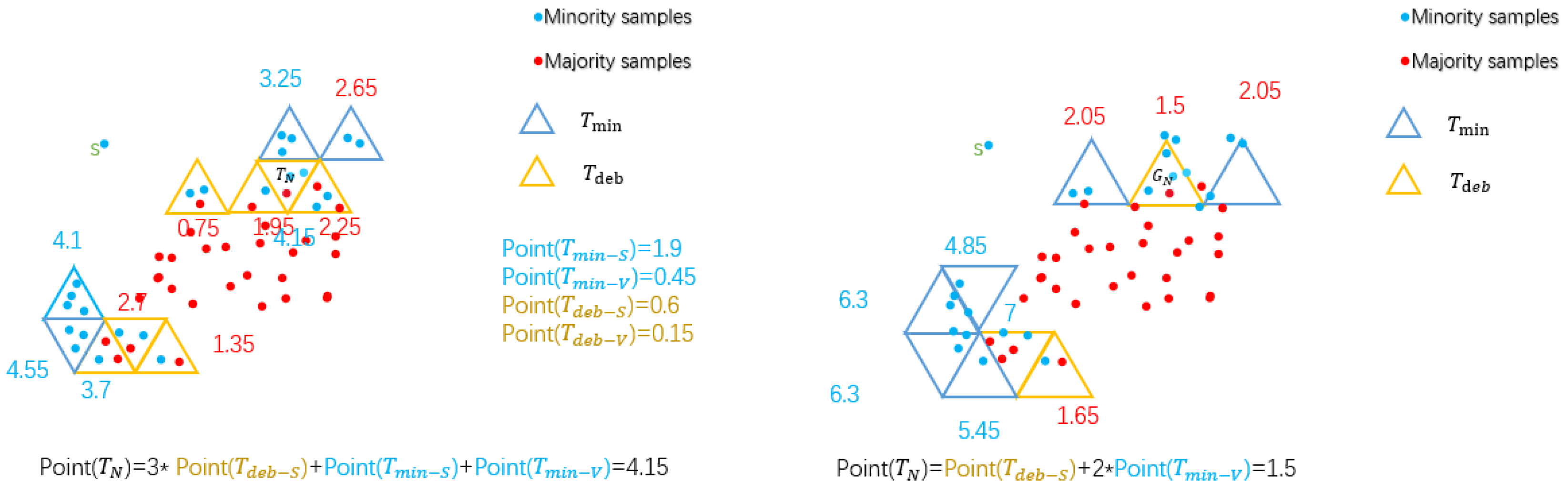
- Step 4. Obtain marking mechanism.
- (1)
- The overall score is 18 points, and the score assigned to is represented as .
- (2)
- If and they are connected by side, called , then .
- (3)
- If and they are connected by vertex, called , then .
- (4)
- If and they are connected by side, called , then .
- (5)
- If and they are connected by vertex, called , then .
- (6)
- For itself, it is calculated according to the highest score.
- (7)
- If then .
- Step 5. Sampling and synthesizing new samples.
- TS-SMOTE algorithm
| Algorithm 1 TS-SMOTE |
|
3.2. Discussion of Parameters
3.2.1. Discussion on Factor a
3.2.2. Discussion on Factor b
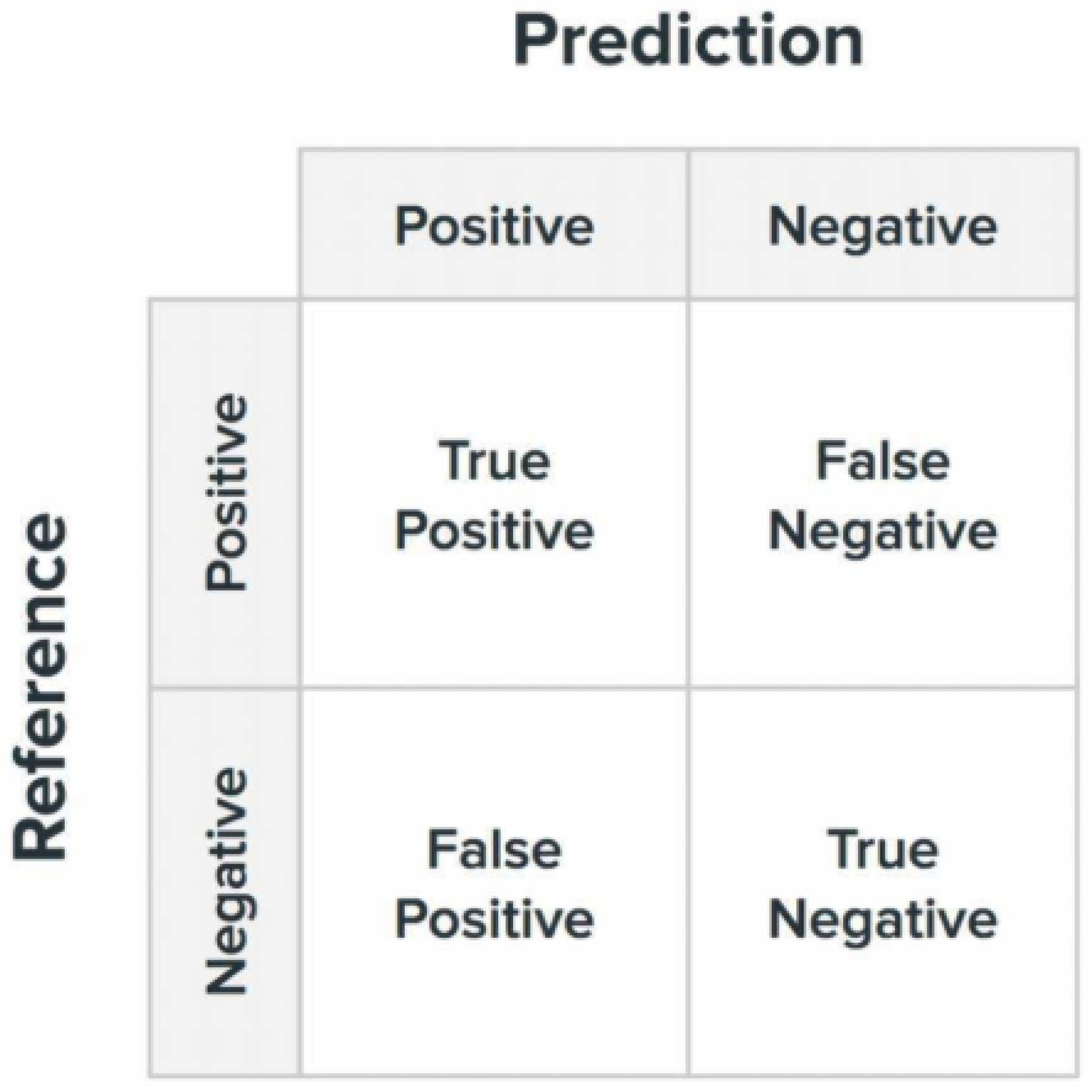
4. Specific Settings of the Experiment and Comparative Analysis
4.1. Related Methods and Experimental Settings
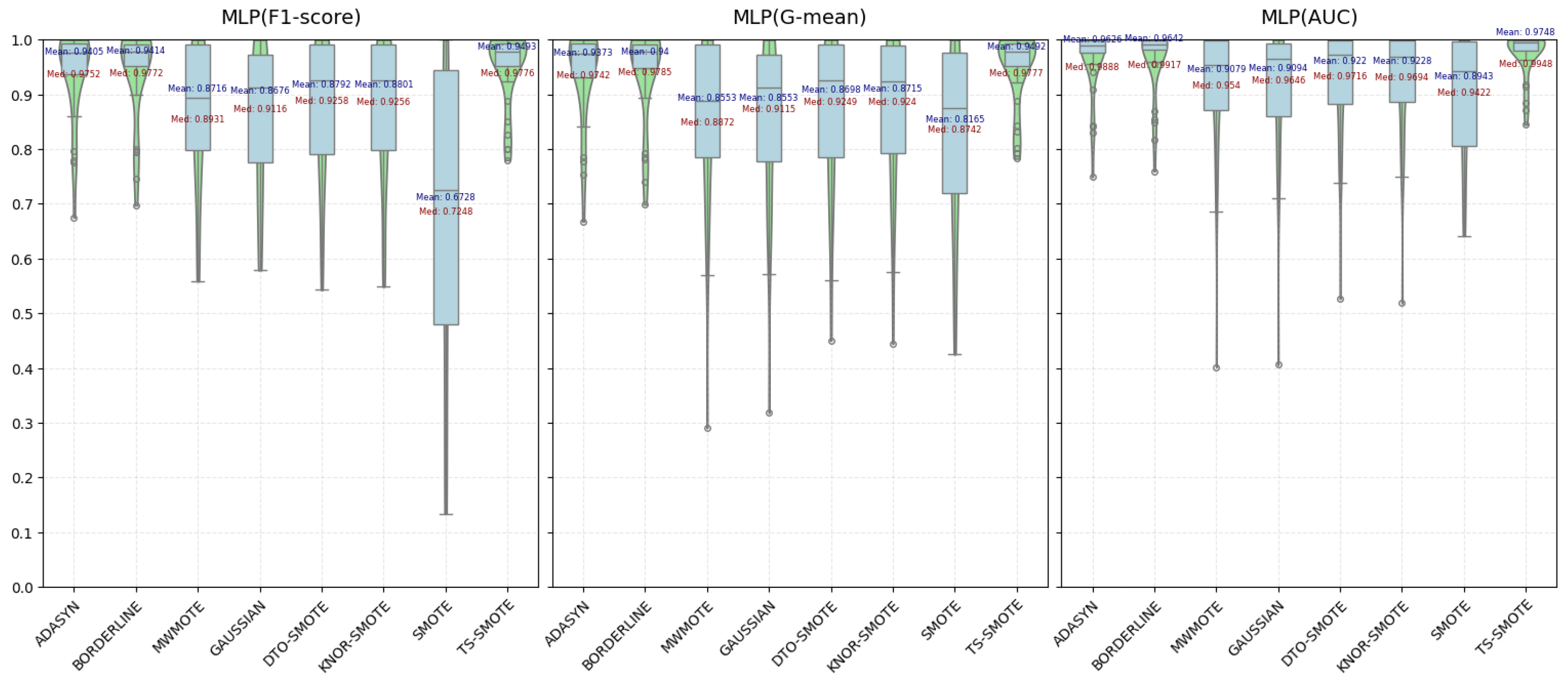
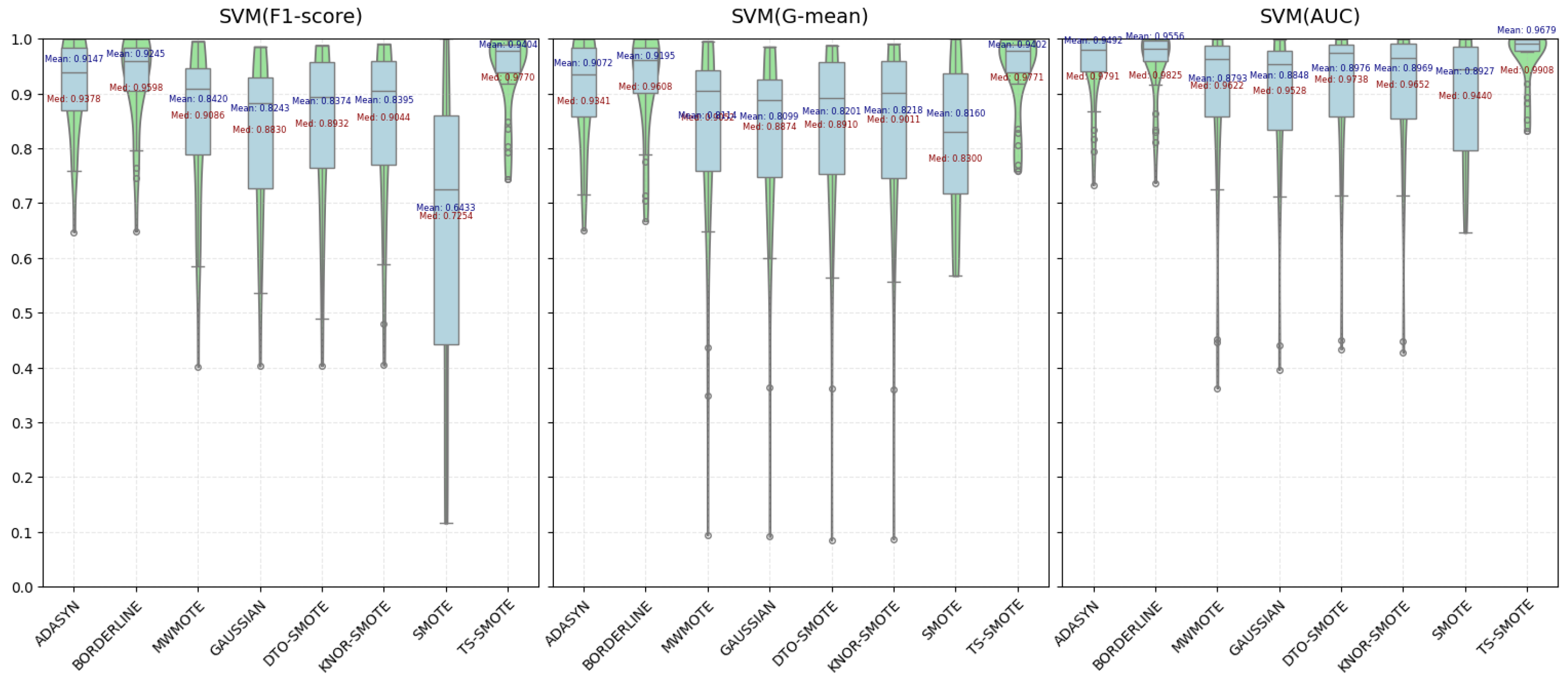
4.2. Experimental Results and Comparative Analysis
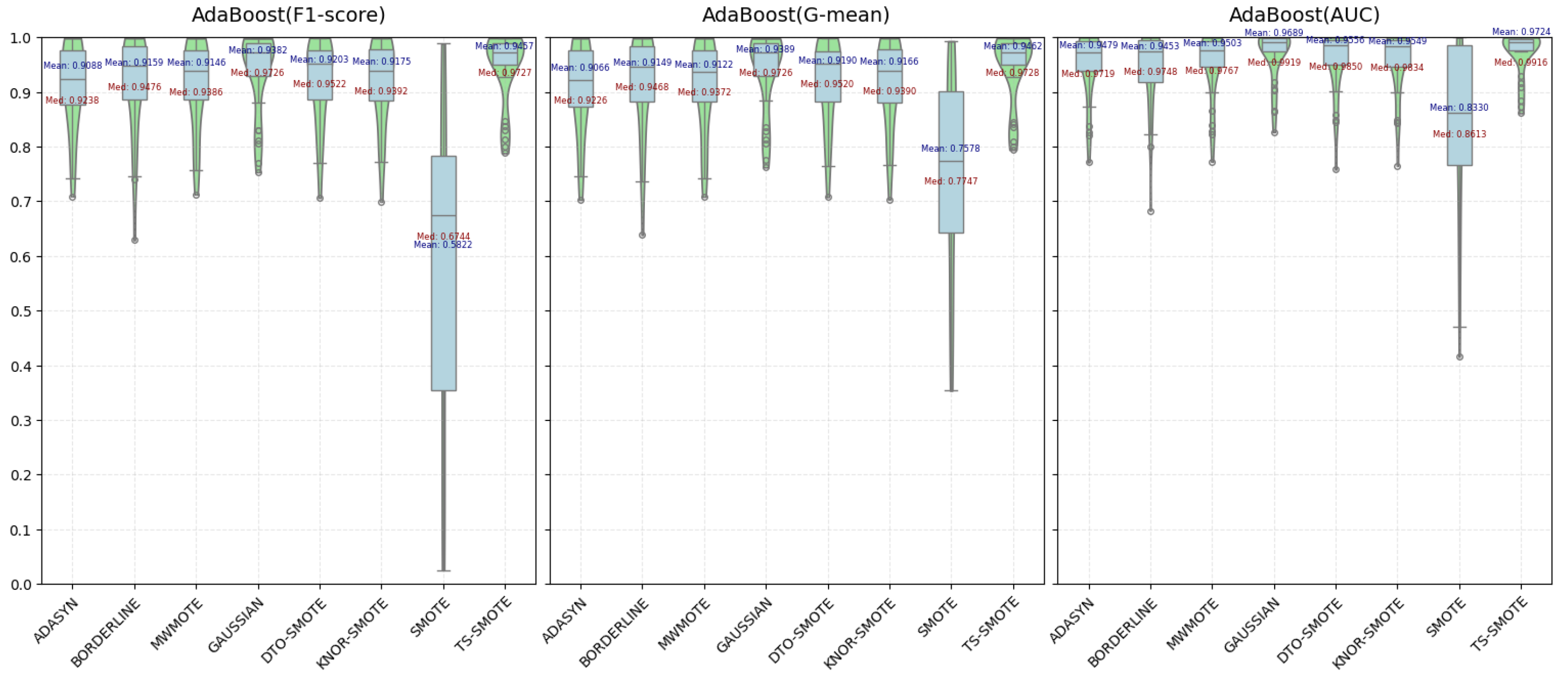
4.2.1. Comparison and Analysis of Various Metric Evaluations
4.2.2. Data Visualization of Some Characteristic Datasets
4.2.3. Friedman Test and Wilcoxon Signed Rank Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Lee, A.; Taylor, P.; Kalpathy-Cramer, J.; Tufail, A. Machine learning has arrived! Ophthalmology 2017, 124, 1726–1728. [Google Scholar] [CrossRef]
- Mukhamediev, R.I.; Popova, Y.; Kuchin, Y.; Zaitseva, E.; Kalimoldayev, A.; Symagulov, A.; Levashenko, V.; Abdoldina, F.; Gopejenko, V.; Yakunin, K.; et al. Review of artificial intelligence and machine learning technologies: Classification, restrictions, opportunities and challenges. Mathematics 2022, 10, 2552. [Google Scholar] [CrossRef]
- Tarekegn, A.N.; Giacobini, M.; Michalak, K. A review of methods for imbalanced multi-label classification. Pattern Recognit. 2021, 118, 107965. [Google Scholar] [CrossRef]
- Yang, P.; Yu, J. Challenges in Binary Classification. arXiv 2024, arXiv:2406.13665. [Google Scholar] [CrossRef]
- Singh, S.; Khim, J.T. Optimal binary classification beyond accuracy. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; Volume 35, pp. 18226–18240. [Google Scholar]
- Casebolt, M.K. Gender Diversity In Aviation: What Is It Like To Be In The Female Minority? J. Aviat. Educ. Res. 2023, 32, 4. [Google Scholar] [CrossRef]
- Guo, L.Z.; Li, Y.F. Class-imbalanced semi-supervised learning with adaptive thresholding. In Proceedings of the International Conference on Machine Learning (PMLR), Baltimore, MD, USA, 17–23 July 2022; pp. 8082–8094. [Google Scholar]
- Fan, J.; Yuan, B.; Chen, Y. Improved dimension dependence of a proximal algorithm for sampling. In Proceedings of the 36th Annual Conference on Learning Theory (PMLR), Bangalore, India, 12–15 July 2023; pp. 1473–1521. [Google Scholar]
- Ding, S.; Li, C.; Xu, X.; Ding, L.; Zhang, J.; Guo, L.; Shi, T. A sampling-based density peaks clustering algorithm for large-scale data. Pattern Recognit. 2023, 136, 109238. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Z.; Wang, D. RFCL: A new under-sampling method of reducing the degree of imbalance and overlap. Pattern Anal. Appl. 2021, 24, 641–654. [Google Scholar] [CrossRef]
- Goyal, S. Handling class-imbalance with KNN (neighbourhood) under-sampling for software defect prediction. Artif. Intell. Rev. 2022, 55, 2023–2064. [Google Scholar] [CrossRef]
- Islam, A.; Belhaouari, S.B.; Rehman, A.U.; Bensmail, H. KNNOR: An oversampling technique for imbalanced datasets. Appl. Soft Comput. 2022, 115, 108288. [Google Scholar] [CrossRef]
- Feng, S.; Keung, J.; Yu, X.; Xiao, Y.; Zhang, M. Investigation on the stability of SMOTE-based oversampling techniques in software defect prediction. Inf. Softw. Technol. 2021, 139, 106662. [Google Scholar] [CrossRef]
- Jiang, Z.; Pan, T.; Zhang, C.; Yang, J. A new oversampling method based on the classification contribution degree. Symmetry 2021, 13, 194. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Fernández, A.; Garcia, S.; Herrera, F.; Chawla, N.V. SMOTE for learning from imbalanced data: Progress and challenges, marking the 15-year anniversary. J. Artif. Intell. Res. 2018, 61, 863–905. [Google Scholar] [CrossRef]
- Blagus, R.; Lusa, L. SMOTE for high-dimensional class-imbalanced data. BMC Bioinform. 2013, 14, 106. [Google Scholar] [CrossRef]
- Camacho, L.; Douzas, G.; Bacao, F. Geometric SMOTE for regression. Expert Syst. Appl. 2022, 193, 116387. [Google Scholar] [CrossRef]
- Zha, D.; Lai, K.H.; Tan, Q.; Ding, S.; Zou, N.; Hu, X.B. Towards automated imbalanced learning with deep hierarchical reinforcement learning. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 2476–2485. [Google Scholar]
- Sharma, A.; Singh, P.K.; Chandra, R. SMOTified-GAN for class imbalanced pattern classification problems. IEEE Access 2022, 10, 30655–30665. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Q. SMOTE oversampling algorithm based on generative adversarial network. Clust. Comput. 2025, 28, 271. [Google Scholar] [CrossRef]
- Puri, A.; Kumar Gupta, M. Improved hybrid bag-boost ensemble with K-means-SMOTE–ENN technique for handling noisy class imbalanced data. Comput. J. 2022, 65, 124–138. [Google Scholar] [CrossRef]
- Chawla, N.V.; Lazarevic, A.; Hall, L.O.; Bowyer, K.W. SMOTEBoost: Improving prediction of the minority class in boosting. In Proceedings of the European Conference on Principles of Data Mining and Knowledge Discovery, Dubrovnik, Croatia, 22–26 September 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 107–119. [Google Scholar]
- Law, T.J.; Ting, C.Y.; Ng, H.; Goh, H.N.; Quek, A. Ensemble-SMOTE: Mitigating class imbalance in graduate on time detection. J. Inform. Web Eng. 2024, 3, 229–250. [Google Scholar] [CrossRef]
- Fan, W.; Stolfo, S.J.; Zhang, J.; Chan, P.K. AdaCost: Misclassification cost-sensitive boosting. In Proceedings of the International Conference on Machine Learning, Bled, Slovenia, 27–30 June 1999; Volume 99, pp. 97–105. [Google Scholar]
- Wang, J.B.; Zou, C.A.; Fu, G.H. AWSMOTE: An SVM-Based Adaptive Weighted SMOTE for Class-Imbalance Learning. Sci. Program. 2021, 2021, 9947621. [Google Scholar] [CrossRef]
- Turlapati, V.P.K.; Prusty, M.R. Outlier-SMOTE: A refined oversampling technique for improved detection of COVID-19. Intell.-Based Med. 2020, 3, 100023. [Google Scholar] [CrossRef]
- Li, J.; Zhu, Q.; Wu, Q.; Zhang, Z.; Gong, Y.; He, Z.; Zhu, F. SMOTE-NaN-DE: Addressing the noisy and borderline examples problem in imbalanced classification by natural neighbors and differential evolution. Knowl.-Based Syst. 2021, 223, 107056. [Google Scholar] [CrossRef]
- Meng, D.; Li, Y. An imbalanced learning method by combining SMOTE with Center Offset Factor. Appl. Soft Comput. 2022, 120, 108618. [Google Scholar] [CrossRef]
- Pinkus, A. Approximation theory of the MLP model in neural networks. Acta Numer. 1999, 8, 143–195. [Google Scholar] [CrossRef]
- Jakkula, V. Tutorial on Support Vector Machine (SVM); School of EECS, Washington State University: Pullman, WA, USA, 2006; Volume 37, p. 3. [Google Scholar]
- Schapire, R.E. Explaining adaboost. In Empirical Inference: Festschrift in Honor of Vladimir N. Vapnik; Springer: Berlin/Heidelberg, Germany, 2013; pp. 37–52. [Google Scholar]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In Proceedings of the International Conference on Intelligent Computing, Hefei, China, 23–26 August 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 878–887. [Google Scholar]
- Barua, S.; Islam, M.M.; Yao, X.; Murase, K. MWMOTE—Majority weighted minority oversampling technique for imbalanced data set learning. IEEE Trans. Knowl. Data Eng. 2012, 26, 405–425. [Google Scholar] [CrossRef]
- de Carvalho, A.M.; Prati, R.C. DTO-SMOTE: Delaunay tessellation oversampling for imbalanced data sets. Information 2020, 11, 557. [Google Scholar] [CrossRef]
- Bunkhumpornpat, C.; Sinapiromsaran, K.; Lursinsap, C. Safe-level-smote: Safe-level-synthetic minority over-sampling technique for handling the class imbalanced problem. In Proceedings of the 13th Pacific-Asia conference of the Advances in Knowledge Discovery and Data Mining (PAKDD), Bangkok, Thailand, 27–30 April 2009; Proceedings 13. Springer: Berlin/Heidelberg, Germany, 2009; pp. 475–482. [Google Scholar]
- Viadinugroho, R.A.A. Imbalanced Classification in Python: SMOTE-Tomek Links Method; Medium: San Francisco, CA, USA, 2021. [Google Scholar]
- Kosolwattana, T.; Liu, C.; Hu, R.; Han, S.; Chen, H.; Lin, Y. A self-inspected adaptive SMOTE algorithm (SASMOTE) for highly imbalanced data classification in healthcare. BioData Min. 2023, 16, 15. [Google Scholar] [CrossRef]
- Muntasir Nishat, M.; Faisal, F.; Jahan Ratul, I.; Al-Monsur, A.; Ar-Rafi, A.M.; Nasrullah, S.M.; Reza, M.T.; Khan, M.R.H. A Comprehensive Investigation of the Performances of Different Machine Learning Classifiers with SMOTE-ENN Oversampling Technique and Hyperparameter Optimization for Imbalanced Heart Failure Dataset. Sci. Program. 2022, 2022, 3649406. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; IEEE: New York, NY, USA, 2008; pp. 1322–1328. [Google Scholar]
- Lee, H.; Kim, J.; Kim, S. Gaussian-based SMOTE algorithm for solving skewed class distributions. Int. J. Fuzzy Log. Intell. Syst. 2017, 17, 229–234. [Google Scholar] [CrossRef]
- Douzas, G.; Bacao, F. Geometric SMOTE a geometrically enhanced drop-in replacement for SMOTE. Inf. Sci. 2019, 501, 118–135. [Google Scholar] [CrossRef]
- Santos, M.S.; Abreu, P.H.; García-Laencina, P.J.; Simão, A.; Carvalho, A. A new cluster-based oversampling method for improving survival prediction of hepatocellular carcinoma patients. J. Biomed. Inform. 2015, 58, 49–59. [Google Scholar] [CrossRef]
- Ren, J.; Wang, Y.; Cheung, Y.m.; Gao, X.Z.; Guo, X. Grouping-based oversampling in kernel space for imbalanced data classification. Pattern Recognit. 2023, 133, 108992. [Google Scholar] [CrossRef]
- Feng, F.; Li, K.C.; Yang, E.; Zhou, Q.; Han, L.; Hussain, A.; Cai, M. A novel oversampling and feature selection hybrid algorithm for imbalanced data classification. Multimed. Tools Appl. 2023, 82, 3231–3267. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Liberti, L.; Lavor, C.; Maculan, N.; Mucherino, A. Euclidean distance geometry and applications. SIAM Rev. 2014, 56, 3–69. [Google Scholar] [CrossRef]
- Demmel, J.W. Matrix computations (gene h. golub and charles f. van loan). SIAM Rev. 1986, 28, 252–255. [Google Scholar] [CrossRef]
- Popescu, M.C.; Balas, V.E.; Perescu-Popescu, L.; Mastorakis, N. Multilayer perceptron and neural networks. WSEAS Trans. Circuits Syst. 2009, 8, 579–588. [Google Scholar]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- He, H.; Garcia, E. Learning from Imbalanced Data IEEE Transactions on Knowledge and Data Engineering; IEEE: New York, NY, USA, 2009. [Google Scholar]
- Douzas, G.; Rauch, R.; Bacao, F. G-SOMO: An oversampling approach based on self-organized maps and geometric SMOTE. Expert Syst. Appl. 2021, 183, 115230. [Google Scholar] [CrossRef]
- Sheldon, M.R.; Fillyaw, M.J.; Thompson, W.D. The use and interpretation of the Friedman test in the analysis of ordinal-scale data in repeated measures designs. Physiother. Res. Int. 1996, 1, 221–228. [Google Scholar] [CrossRef] [PubMed]
- Woolson, R.F. Wilcoxon signed-rank test. In Encyclopedia of Biostatistics; Wiley: Hoboken, NJ, USA, 2005; Volume 8. [Google Scholar]

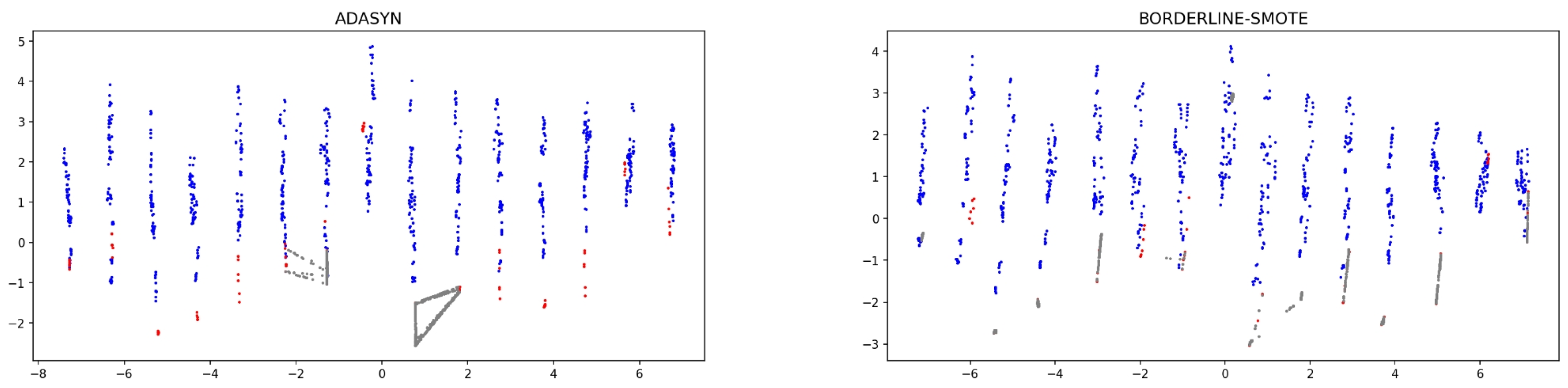
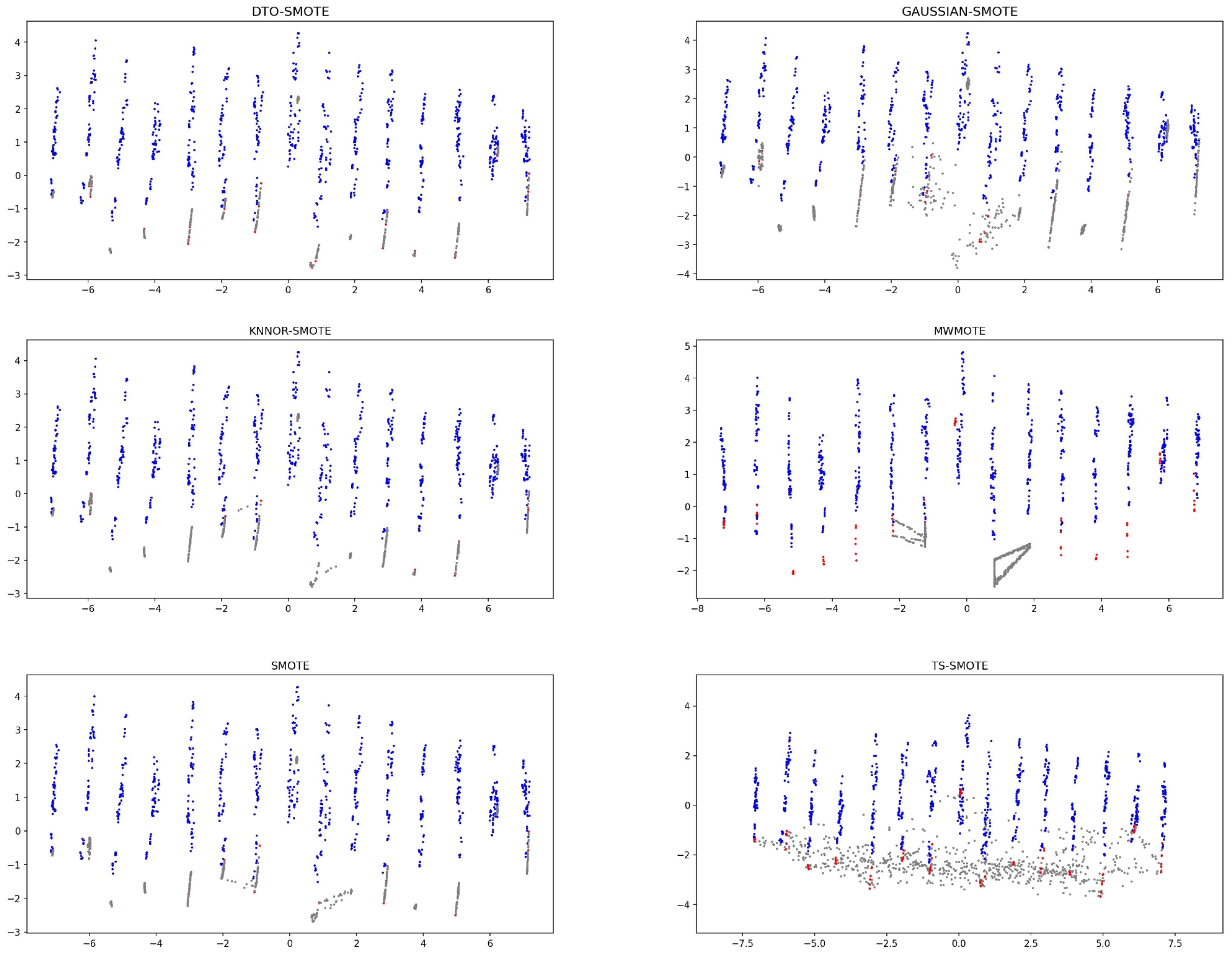
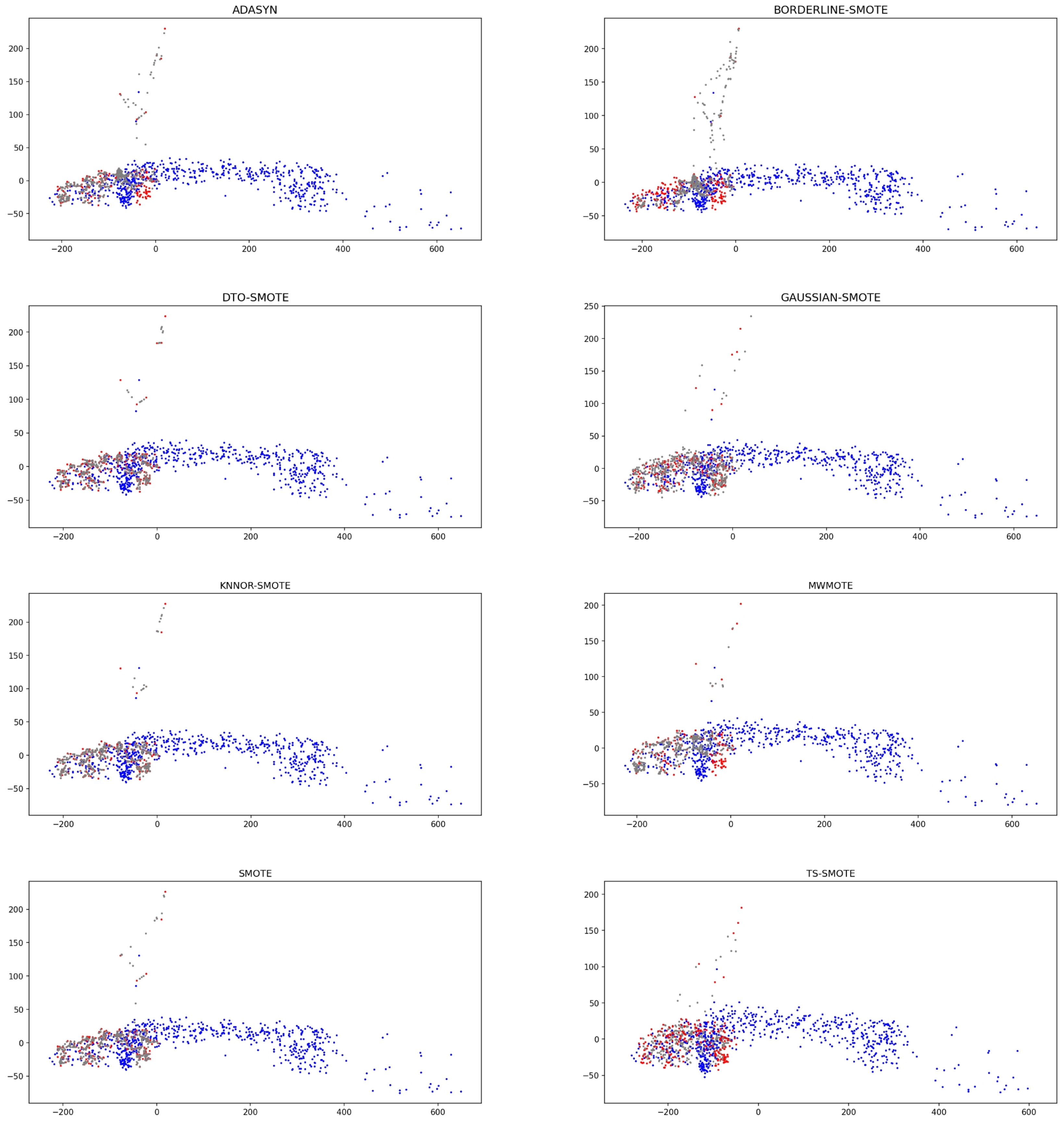
| Datesets | Samples | Minority Samples | Majority Samples | IR |
|---|---|---|---|---|
| glass1 | 214 | 76 | 138 | 1.82 |
| wisconsin | 683 | 238 | 444 | 1.86 |
| pima | 768 | 268 | 500 | 1.87 |
| glass0 | 214 | 70 | 144 | 2.06 |
| yeast1 | 1484 | 429 | 1055 | 2.46 |
| haberman | 306 | 81 | 225 | 2.78 |
| vehicle3 | 846 | 212 | 634 | 2.99 |
| vehicle0 | 846 | 199 | 647 | 3.25 |
| ecoli1 | 336 | 77 | 259 | 3.36 |
| new-thyroid2 | 215 | 35 | 180 | 5.14 |
| ecoli2 | 336 | 52 | 284 | 5.46 |
| segment0 | 2308 | 329 | 1979 | 6.02 |
| yeast3 | 1484 | 163 | 1321 | 8.10 |
| yeast-2_vs_4 | 514 | 51 | 463 | 9.08 |
| yeast-0-2-5-7-9_vs_3-6-8 | 1004 | 99 | 905 | 9.14 |
| yeast-0-5-6-7-9_vs_4 | 528 | 51 | 477 | 9.35 |
| vowel0 | 988 | 90 | 898 | 9.98 |
| yeast-1_vs_7 | 459 | 30 | 429 | 14.30 |
| ecoli4 | 336 | 20 | 316 | 15.80 |
| page-blocks-1-3_vs_4 | 472 | 28 | 444 | 15.86 |
| dermatology-6 | 358 | 20 | 338 | 16.9 |
| yeast-1-4-5-8_vs_7 | 693 | 30 | 663 | 22.10 |
| yeast4 | 1484 | 51 | 1433 | 28.1 |
| winequality-red-4 | 1599 | 53 | 1546 | 29.17 |
| yeast-1-2-8-9_vs_7 | 947 | 30 | 917 | 30.57 |
| yeast5 | 1484 | 44 | 1440 | 32.73 |
| yeast6 | 1484 | 35 | 1449 | 41.4 |
| poker-8-9_vs_5 | 1485 | 25 | 1460 | 58.4 |
| poker-8-9_vs_6 | 2075 | 25 | 2050 | 82 |
| poker-8_vs_6 | 1477 | 17 | 1460 | 85.88 |
| Datasets | Estimators | IR | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | M | G | D | K | S | T | |||
| glass1 | F1-score | 0.7962 | 0.7969 | 0.5584 | 0.5786 | 0.5425 | 0.5485 | 0.6309 | 0.7994 | 1.82 |
| G-mean | 0.7853 | 0.7816 | 0.2905 | 0.3182 | 0.4503 | 0.4444 | 0.7050 | 0.7924 | 1.82 | |
| AUC | 0.8439 | 0.8538 | 0.4016 | 0.4058 | 0.5265 | 0.5183 | 0.8008 | 0.8708 | 1.82 | |
| wisconsin | F1-score | 0.9791 | 0.9727 | 0.9793 | 0.9671 | 0.9740 | 0.9752 | 0.9554 | 0.9741 | 1.86 |
| G-mean | 0.9786 | 0.9720 | 0.9788 | 0.9669 | 0.9738 | 0.9749 | 0.9690 | 0.9739 | 1.86 | |
| AUC | 0.9894 | 0.9885 | 0.9918 | 0.9945 | 0.9947 | 0.9944 | 0.9953 | 0.9953 | 1.86 | |
| pima | F1-score | 0.7800 | 0.7949 | 0.6934 | 0.6950 | 0.7095 | 0.7177 | 0.6665 | 0.8002 | 1.87 |
| G-mean | 0.7770 | 0.7857 | 0.6748 | 0.6763 | 0.6848 | 0.6965 | 0.7409 | 0.8019 | 1.87 | |
| AUC | 0.8410 | 0.8478 | 0.7539 | 0.7571 | 0.7750 | 0.7839 | 0.8208 | 0.8843 | 1.87 | |
| glass0 | F1-score | 0.8591 | 0.8000 | 0.7466 | 0.7388 | 0.7744 | 0.7753 | 0.7201 | 0.8513 | 2.06 |
| G-mean | 0.8416 | 0.7928 | 0.6809 | 0.6811 | 0.7042 | 0.7028 | 0.7949 | 0.8430 | 2.06 | |
| AUC | 0.9078 | 0.8693 | 0.8083 | 0.8106 | 0.8217 | 0.8203 | 0.8597 | 0.9183 | 2.06 | |
| yeast1 | F1-score | 0.7765 | 0.7461 | 0.7379 | 0.7116 | 0.7476 | 0.7471 | 0.5981 | 0.8262 | 2.46 |
| G-mean | 0.7525 | 0.7408 | 0.7077 | 0.7092 | 0.7376 | 0.7359 | 0.7195 | 0.8321 | 2.46 | |
| AUC | 0.8292 | 0.8171 | 0.7899 | 0.7930 | 0.8154 | 0.8172 | 0.7929 | 0.9143 | 2.46 | |
| haberman | F1-score | 0.6750 | 0.6972 | 0.6434 | 0.6070 | 0.6266 | 0.6114 | 0.4723 | 0.7797 | 2.78 |
| G-mean | 0.6676 | 0.6988 | 0.6272 | 0.6402 | 0.6569 | 0.6464 | 0.6255 | 0.7826 | 2.78 | |
| AUC | 0.7493 | 0.7597 | 0.6858 | 0.7097 | 0.7389 | 0.7490 | 0.6949 | 0.8447 | 2.78 | |
| vehicle3 | F1-score | 0.8911 | 0.8984 | 0.5827 | 0.6056 | 0.6285 | 0.6128 | 0.6732 | 0.8873 | 2.99 |
| G-mean | 0.8848 | 0.8933 | 0.5689 | 0.5719 | 0.5597 | 0.5749 | 0.7916 | 0.8872 | 2.99 | |
| AUC | 0.9400 | 0.9551 | 0.7365 | 0.7550 | 0.7660 | 0.7656 | 0.8952 | 0.9621 | 2.99 | |
| vehicle0 | F1-score | 0.9885 | 0.9888 | 0.9364 | 0.9178 | 0.9347 | 0.9352 | 0.9550 | 0.9863 | 3.25 |
| G-mean | 0.9885 | 0.9886 | 0.9334 | 0.9123 | 0.9326 | 0.9319 | 0.9787 | 0.9862 | 3.25 | |
| AUC | 0.9981 | 0.9984 | 0.9799 | 0.9811 | 0.9851 | 0.9855 | 0.9978 | 0.9988 | 3.25 | |
| ecoli1 | F1-score | 0.8999 | 0.9114 | 0.9063 | 0.8732 | 0.8953 | 0.8919 | 0.7864 | 0.9238 | 3.36 |
| G-mean | 0.8952 | 0.9114 | 0.8977 | 0.8704 | 0.8911 | 0.8879 | 0.8862 | 0.9223 | 3.36 | |
| AUC | 0.9558 | 0.9595 | 0.9413 | 0.9516 | 0.9633 | 0.9647 | 0.9546 | 0.9758 | 3.36 | |
| new-thyroid2 | F1-score | 0.9935 | 0.9937 | 0.9973 | 0.9911 | 0.9973 | 0.9973 | 0.9746 | 0.9961 | 5.14 |
| G-mean | 0.9933 | 0.9936 | 0.9972 | 0.9911 | 0.9972 | 0.9972 | 0.9923 | 0.9961 | 5.14 | |
| AUC | 0.9998 | 1.0000 | 0.9999 | 0.9992 | 0.9997 | 0.9996 | 0.9996 | 0.9997 | 5.14 | |
| ecoli2 | F1-score | 0.9667 | 0.9875 | 0.8671 | 0.9130 | 0.9403 | 0.9365 | 0.8480 | 0.9605 | 5.46 |
| G-mean | 0.9654 | 0.9883 | 0.8669 | 0.9113 | 0.9384 | 0.9345 | 0.9194 | 0.9605 | 5.46 | |
| AUC | 0.9841 | 0.9963 | 0.9497 | 0.9525 | 0.9753 | 0.9717 | 0.9671 | 0.9883 | 5.46 | |
| segment0 | F1-score | 0.9988 | 0.9989 | 0.9986 | 0.9974 | 0.9986 | 0.9986 | 0.9922 | 0.9982 | 6.02 |
| G-mean | 0.9988 | 0.9989 | 0.9986 | 0.9974 | 0.9986 | 0.9986 | 0.9951 | 0.9982 | 6.02 | |
| AUC | 0.9998 | 0.9999 | 0.9998 | 0.9997 | 0.9998 | 0.9998 | 0.9997 | 0.9994 | 6.02 | |
| yeast3 | F1-score | 0.9665 | 0.9678 | 0.9431 | 0.9065 | 0.9528 | 0.9513 | 0.7544 | 0.9682 | 8.10 |
| G-mean | 0.9656 | 0.9670 | 0.9415 | 0.9070 | 0.9521 | 0.9506 | 0.8938 | 0.9684 | 8.10 | |
| AUC | 0.9828 | 0.9894 | 0.9765 | 0.9700 | 0.9846 | 0.9848 | 0.9652 | 0.9948 | 8.10 | |
| yeast-2_vs_4 | F1-score | 0.9787 | 0.9773 | 0.8711 | 0.9205 | 0.9168 | 0.9159 | 0.7294 | 0.9742 | 9.08 |
| G-mean | 0.9781 | 0.9797 | 0.8729 | 0.9167 | 0.9172 | 0.9160 | 0.8662 | 0.9742 | 9.08 | |
| AUC | 0.9890 | 0.9914 | 0.9579 | 0.9621 | 0.9679 | 0.9671 | 0.9506 | 0.9949 | 9.08 | |
| yeast-0-2-5-7-9_vs_3-6-8 | F1-score | 0.9741 | 0.9783 | 0.8218 | 0.9089 | 0.9063 | 0.9086 | 0.7648 | 0.9792 | 9.14 |
| G-mean | 0.9730 | 0.9777 | 0.8187 | 0.9117 | 0.9071 | 0.9097 | 0.8822 | 0.9793 | 9.14 | |
| AUC | 0.9887 | 0.9935 | 0.9046 | 0.9565 | 0.9519 | 0.9560 | 0.9337 | 0.9925 | 9.14 | |
| yeast-0-5-6-7-9_vs_4 | F1-score | 0.9526 | 0.9562 | 0.8114 | 0.9490 | 0.8224 | 0.8227 | 0.5053 | 0.9494 | 9.35 |
| G-mean | 0.9505 | 0.9546 | 0.8061 | 0.9498 | 0.8219 | 0.8249 | 0.7432 | 0.9499 | 9.35 | |
| AUC | 0.9808 | 0.9810 | 0.9002 | 0.9785 | 0.9123 | 0.9091 | 0.8635 | 0.9821 | 9.35 | |
| vowel0 | F1-score | 0.9990 | 0.9986 | 0.9984 | 0.9977 | 0.9983 | 0.9984 | 0.9893 | 0.9992 | 9.98 |
| G-mean | 0.9990 | 0.9986 | 0.9984 | 0.9977 | 0.9983 | 0.9984 | 0.9989 | 0.9992 | 9.98 | |
| AUC | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 9.98 | |
| yeast-1_vs_7 | F1-score | 0.9342 | 0.9621 | 0.8262 | 0.7903 | 0.8040 | 0.8220 | 0.3021 | 0.9612 | 14.3 |
| G-mean | 0.9288 | 0.9614 | 0.8136 | 0.7886 | 0.7995 | 0.8163 | 0.6579 | 0.9615 | 14.3 | |
| AUC | 0.9754 | 0.9857 | 0.8803 | 0.8722 | 0.8926 | 0.8998 | 0.7690 | 0.9796 | 14.3 | |
| ecoli4 | F1-score | 0.9874 | 0.9765 | 0.9856 | 0.9741 | 0.9856 | 0.9871 | 0.7984 | 0.9845 | 15.8 |
| G-mean | 0.9870 | 0.9811 | 0.9851 | 0.9738 | 0.9854 | 0.9870 | 0.9003 | 0.9843 | 15.8 | |
| AUC | 0.9955 | 0.9985 | 0.9980 | 0.9964 | 0.9990 | 0.9993 | 0.9863 | 0.9963 | 15.8 | |
| page-blocks-1-3_vs_4 | F1-score | 0.9970 | 0.9965 | 0.9959 | 0.9764 | 0.9943 | 0.9950 | 0.9107 | 0.9935 | 15.86 |
| G-mean | 0.9969 | 0.9965 | 0.9958 | 0.9761 | 0.9942 | 0.9949 | 0.9918 | 0.9935 | 15.86 | |
| AUC | 0.9973 | 0.9971 | 0.9970 | 0.9806 | 0.9959 | 0.9961 | 0.9982 | 0.9978 | 15.86 | |
| dermatology-6 | F1-score | 1.0000 | 1.0000 | 1.0000 | 0.9997 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 16.9 |
| G-mean | 1.0000 | 1.0000 | 1.0000 | 0.9997 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 16.9 | |
| AUC | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 16.9 | |
| yeast-1-4-5-8_vs_7 | F1-score | 0.9409 | 0.9490 | 0.7908 | 0.7248 | 0.7853 | 0.7905 | 0.1399 | 0.9739 | 22.1 |
| G-mean | 0.9362 | 0.9467 | 0.7745 | 0.7103 | 0.7675 | 0.7707 | 0.5011 | 0.9742 | 22.1 | |
| AUC | 0.9769 | 0.9824 | 0.8677 | 0.8068 | 0.8598 | 0.8523 | 0.6412 | 0.9854 | 22.1 | |
| yeast4 | F1-score | 0.9747 | 0.9797 | 0.8799 | 0.8553 | 0.8857 | 0.8905 | 0.3594 | 0.9812 | 28.1 |
| G-mean | 0.9738 | 0.9793 | 0.8766 | 0.8558 | 0.8833 | 0.8885 | 0.7187 | 0.9813 | 28.1 | |
| AUC | 0.9874 | 0.9907 | 0.9502 | 0.9280 | 0.9514 | 0.9554 | 0.8627 | 0.9948 | 28.1 | |
| winequality-red-4 | F1-score | 0.9757 | 0.9771 | 0.8702 | 0.8628 | 0.8586 | 0.8726 | 0.1336 | 0.9760 | 29.17 |
| G-mean | 0.9747 | 0.9768 | 0.8654 | 0.8620 | 0.8522 | 0.8677 | 0.4250 | 0.9762 | 29.17 | |
| AUC | 0.9906 | 0.9887 | 0.9336 | 0.9350 | 0.9286 | 0.9365 | 0.6719 | 0.9890 | 29.17 | |
| yeast-1-2-8-9_vs_7 | F1-score | 0.9588 | 0.9637 | 0.7935 | 0.7716 | 0.7860 | 0.7907 | 0.1529 | 0.9837 | 30.57 |
| G-mean | 0.9571 | 0.9633 | 0.7771 | 0.7727 | 0.7796 | 0.7852 | 0.5071 | 0.9838 | 30.57 | |
| AUC | 0.9862 | 0.9920 | 0.8623 | 0.8552 | 0.8790 | 0.8821 | 0.7009 | 0.9907 | 30.57 | |
| yeast5 | F1-score | 0.9922 | 0.9920 | 0.9814 | 0.9642 | 0.9819 | 0.9824 | 0.6945 | 0.9886 | 32.73 |
| G-mean | 0.9922 | 0.9919 | 0.9808 | 0.9630 | 0.9813 | 0.9818 | 0.9118 | 0.9887 | 32.73 | |
| AUC | 0.9964 | 0.9972 | 0.9903 | 0.9868 | 0.9925 | 0.9923 | 0.9874 | 0.9995 | 32.73 | |
| yeast6 | F1-score | 0.9861 | 0.9883 | 0.9396 | 0.9102 | 0.9366 | 0.9373 | 0.4551 | 0.9910 | 41.4 |
| G-mean | 0.9857 | 0.9882 | 0.9370 | 0.9098 | 0.9356 | 0.9363 | 0.7965 | 0.9910 | 41.4 | |
| AUC | 0.9939 | 0.9958 | 0.9798 | 0.9670 | 0.9845 | 0.9844 | 0.9226 | 0.9982 | 41.4 | |
| poker-8-9_vs_5 | F1-score | 0.9931 | 0.9913 | 0.9920 | 0.9190 | 0.9927 | 0.9913 | 0.2277 | 0.9928 | 58.4 |
| G-mean | 0.9930 | 0.9912 | 0.9919 | 0.9182 | 0.9926 | 0.9911 | 0.5858 | 0.9929 | 58.4 | |
| AUC | 0.9992 | 0.9979 | 0.9990 | 0.9771 | 0.9993 | 0.9990 | 0.7983 | 0.9967 | 58.4 | |
| poker-8-9_vs_6 | F1-score | 0.9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9999 | 1.0000 | 1.0000 | 82 |
| G-mean | 0.9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9999 | 1.0000 | 1.0000 | 82 | |
| AUC | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 82 | |
| poker-8_vs_6 | F1-score | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9999 | 1.0000 | 0.9938 | 1.0000 | 85.88 |
| G-mean | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9999 | 1.0000 | 0.9963 | 1.0000 | 85.88 | |
| AUC | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 85.88 | |
| Datasets | Estimators | IR | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | M | G | D | K | S | T | |||
| glass1 | F1-score | 0.7705 | 0.7639 | 0.4011 | 0.4027 | 0.4031 | 0.4041 | 0.626 | 0.7918 | 1.82 |
| G-mean | 0.7303 | 0.7046 | 0.094 | 0.0912 | 0.0845 | 0.0866 | 0.6985 | 0.7709 | 1.82 | |
| AUC | 0.8176 | 0.8293 | 0.3623 | 0.3961 | 0.4334 | 0.4271 | 0.7819 | 0.8519 | 1.82 | |
| wisconsin | F1-score | 0.9772 | 0.9703 | 0.9778 | 0.9734 | 0.977 | 0.9783 | 0.9575 | 0.9775 | 1.86 |
| G-mean | 0.9766 | 0.9691 | 0.9769 | 0.973 | 0.9764 | 0.9778 | 0.9723 | 0.9771 | 1.86 | |
| AUC | 0.9852 | 0.9765 | 0.9843 | 0.9891 | 0.986 | 0.9869 | 0.9864 | 0.991 | 1.86 | |
| pima | F1-score | 0.7712 | 0.7963 | 0.6935 | 0.7038 | 0.7114 | 0.717 | 0.6657 | 0.8042 | 1.87 |
| G-mean | 0.7647 | 0.7759 | 0.6885 | 0.7085 | 0.7208 | 0.7251 | 0.7402 | 0.8063 | 1.87 | |
| AUC | 0.8338 | 0.8339 | 0.7717 | 0.8051 | 0.8152 | 0.8192 | 0.8248 | 0.894 | 1.87 | |
| glass0 | F1-score | 0.8334 | 0.8085 | 0.584 | 0.5887 | 0.5883 | 0.5877 | 0.7157 | 0.8478 | 2.06 |
| G-mean | 0.7875 | 0.7895 | 0.3491 | 0.3634 | 0.3621 | 0.3602 | 0.7913 | 0.8284 | 2.06 | |
| AUC | 0.8677 | 0.8635 | 0.452 | 0.4408 | 0.4493 | 0.4476 | 0.8523 | 0.8831 | 2.06 | |
| yeast1 | F1-score | 0.7586 | 0.7461 | 0.7477 | 0.7179 | 0.7366 | 0.7395 | 0.5859 | 0.744 | 2.46 |
| G-mean | 0.7156 | 0.7134 | 0.6968 | 0.7134 | 0.7236 | 0.7253 | 0.7091 | 0.7582 | 2.46 | |
| AUC | 0.795 | 0.8117 | 0.7798 | 0.8004 | 0.811 | 0.8145 | 0.7857 | 0.8321 | 2.46 | |
| haberman | F1-score | 0.6473 | 0.6483 | 0.5939 | 0.5362 | 0.4895 | 0.4803 | 0.4323 | 0.744 | 2.78 |
| G-mean | 0.6502 | 0.6672 | 0.437 | 0.6001 | 0.5637 | 0.5571 | 0.589 | 0.7582 | 2.78 | |
| AUC | 0.7331 | 0.7372 | 0.4458 | 0.7164 | 0.7166 | 0.7184 | 0.68 | 0.8321 | 2.78 | |
| vehicle3 | F1-score | 0.8606 | 0.8679 | 0.6265 | 0.6445 | 0.645 | 0.6458 | 0.6537 | 0.8347 | 2.99 |
| G-mean | 0.835 | 0.8474 | 0.6486 | 0.661 | 0.6642 | 0.664 | 0.7951 | 0.8356 | 2.99 | |
| AUC | 0.8976 | 0.9168 | 0.7244 | 0.7351 | 0.7388 | 0.7396 | 0.8713 | 0.9185 | 2.99 | |
| vehicle0 | F1-score | 0.9742 | 0.9736 | 0.8515 | 0.8414 | 0.8419 | 0.8426 | 0.9248 | 0.9679 | 3.25 |
| G-mean | 0.9737 | 0.9725 | 0.8066 | 0.7884 | 0.7893 | 0.7905 | 0.9699 | 0.9677 | 3.25 | |
| AUC | 0.998 | 0.9948 | 0.9479 | 0.9552 | 0.9619 | 0.9624 | 0.9942 | 0.9972 | 3.25 | |
| ecoli1 | F1-score | 0.9106 | 0.9057 | 0.9171 | 0.9099 | 0.9096 | 0.9133 | 0.7707 | 0.9188 | 3.36 |
| G-mean | 0.9046 | 0.9048 | 0.9087 | 0.9024 | 0.9031 | 0.9072 | 0.8824 | 0.9185 | 3.36 | |
| AUC | 0.952 | 0.9511 | 0.9569 | 0.9504 | 0.9676 | 0.9679 | 0.9469 | 0.976 | 3.36 | |
| new-thyroid2 | F1-score | 0.9945 | 0.9945 | 0.9138 | 0.8922 | 0.8652 | 0.8649 | 0.9671 | 0.9882 | 5.14 |
| G-mean | 0.9944 | 0.9944 | 0.9082 | 0.8979 | 0.8737 | 0.8735 | 0.9872 | 0.9882 | 5.14 | |
| AUC | 1 | 1 | 0.9786 | 0.9913 | 0.9817 | 0.9916 | 0.9994 | 0.9993 | 5.14 | |
| ecoli2 | F1-score | 0.9153 | 0.9814 | 0.9127 | 0.9328 | 0.9588 | 0.9595 | 0.8794 | 0.9618 | 5.46 |
| G-mean | 0.9166 | 0.9827 | 0.9108 | 0.9335 | 0.9588 | 0.9597 | 0.9414 | 0.9622 | 5.46 | |
| AUC | 0.9781 | 0.9891 | 0.9776 | 0.9716 | 0.9864 | 0.986 | 0.9597 | 0.9893 | 5.46 | |
| segment0 | F1-score | 0.9943 | 0.9964 | 0.948 | 0.9851 | 0.9882 | 0.9871 | 0.9892 | 0.9968 | 6.02 |
| G-mean | 0.9943 | 0.9964 | 0.9435 | 0.9851 | 0.9881 | 0.9871 | 0.9911 | 0.9968 | 6.02 | |
| AUC | 0.9998 | 0.9999 | 0.9986 | 0.9977 | 0.9989 | 0.9988 | 0.9998 | 0.9999 | 6.02 | |
| yeast3 | F1-score | 0.9471 | 0.937 | 0.9416 | 0.9086 | 0.9559 | 0.956 | 0.7352 | 0.9577 | 8.1 |
| G-mean | 0.9447 | 0.9335 | 0.9389 | 0.9095 | 0.9548 | 0.955 | 0.8988 | 0.9576 | 8.1 | |
| AUC | 0.9801 | 0.9792 | 0.9764 | 0.9722 | 0.9851 | 0.9852 | 0.9688 | 0.9861 | 8.1 | |
| yeast-2_vs_4 | F1-score | 0.966 | 0.9663 | 0.9476 | 0.9328 | 0.9211 | 0.931 | 0.7452 | 0.9768 | 9.08 |
| G-mean | 0.9643 | 0.9693 | 0.9429 | 0.9279 | 0.9229 | 0.932 | 0.882 | 0.9771 | 9.08 | |
| AUC | 0.9918 | 0.9871 | 0.9842 | 0.9698 | 0.9885 | 0.9895 | 0.9696 | 0.9961 | 9.08 | |
| yeast-0-2-5-7-9_vs_3-6-8 | F1-score | 0.8978 | 0.9078 | 0.8118 | 0.9127 | 0.9211 | 0.924 | 0.7904 | 0.9656 | 9.14 |
| G-mean | 0.8926 | 0.9005 | 0.7969 | 0.9155 | 0.9229 | 0.9261 | 0.8825 | 0.9661 | 9.14 | |
| AUC | 0.9602 | 0.9758 | 0.8975 | 0.9454 | 0.9885 | 0.9559 | 0.941 | 0.9907 | 9.14 | |
| yeast-0-5-6-7-9_vs_4 | F1-score | 0.9062 | 0.9051 | 0.8388 | 0.8078 | 0.8336 | 0.8506 | 0.4727 | 0.934 | 9.35 |
| G-mean | 0.9008 | 0.9046 | 0.8321 | 0.8123 | 0.8389 | 0.8543 | 0.7433 | 0.9355 | 9.35 | |
| AUC | 0.9584 | 0.9693 | 0.9138 | 0.9015 | 0.9264 | 0.9298 | 0.8778 | 0.9828 | 9.35 | |
| vowel0 | F1-score | 0.9991 | 0.9997 | 0.9841 | 0.9787 | 0.9819 | 0.9819 | 0.9968 | 0.9994 | 9.98 |
| G-mean | 0.9991 | 0.9997 | 0.9841 | 0.978 | 0.9813 | 0.9814 | 0.9997 | 0.9994 | 9.98 | |
| AUC | 1 | 1 | 0.9975 | 0.9991 | 0.9992 | 0.9994 | 1 | 1 | 9.98 | |
| yeast-1_vs_7 | F1-score | 0.8699 | 0.9354 | 0.8445 | 0.8201 | 0.8329 | 0.8511 | 0.275 | 0.9486 | 14.3 |
| G-mean | 0.8594 | 0.9344 | 0.8259 | 0.817 | 0.8264 | 0.8418 | 0.6656 | 0.9489 | 14.3 | |
| AUC | 0.9398 | 0.9747 | 0.9116 | 0.8975 | 0.9179 | 0.9254 | 0.7682 | 0.9777 | 14.3 | |
| ecoli4 | F1-score | 0.9875 | 0.9765 | 0.9871 | 0.9854 | 0.9878 | 0.9903 | 0.7748 | 0.99 | 15.8 |
| G-mean | 0.9872 | 0.9811 | 0.9867 | 0.985 | 0.9878 | 0.9901 | 0.8831 | 0.99 | 15.8 | |
| AUC | 0.9982 | 0.9961 | 0.9991 | 0.9974 | 0.9995 | 0.9997 | 0.9909 | 0.9994 | 15.8 | |
| page-blocks-1-3_vs_4 | F1-score | 0.9824 | 0.9976 | 0.9201 | 0.7186 | 0.7595 | 0.7869 | 0.8741 | 0.9882 | 15.86 |
| G-mean | 0.9824 | 0.9976 | 0.9199 | 0.747 | 0.7813 | 0.8036 | 0.968 | 0.9882 | 15.86 | |
| AUC | 0.9994 | 1 | 0.9675 | 0.9064 | 0.9281 | 0.9169 | 0.9981 | 0.9995 | 15.86 | |
| dermatology-6 | F1-score | 1 | 1 | 0.9956 | 0.9845 | 0.9876 | 0.9839 | 1 | 0.9981 | 16.9 |
| G-mean | 1 | 1 | 0.9955 | 0.9842 | 0.9873 | 0.9837 | 1 | 0.9981 | 16.9 | |
| AUC | 1 | 1 | 1 | 0.9986 | 0.9995 | 0.9995 | 1 | 1 | 16.9 | |
| yeast-1-4-5-8_vs_7 | F1-score | 0.8697 | 0.8939 | 0.7847 | 0.7495 | 0.7766 | 0.7656 | 0.1377 | 0.9742 | 22.1 |
| G-mean | 0.8573 | 0.8863 | 0.7556 | 0.7471 | 0.7446 | 0.7321 | 0.5672 | 0.9745 | 22.1 | |
| AUC | 0.9339 | 0.9556 | 0.8611 | 0.8243 | 0.8501 | 0.8448 | 0.6461 | 0.9808 | 22.1 | |
| yeast4 | F1-score | 0.9286 | 0.9532 | 0.884 | 0.8739 | 0.8769 | 0.8955 | 0.2942 | 0.9786 | 28.1 |
| G-mean | 0.9235 | 0.9528 | 0.8789 | 0.8741 | 0.879 | 0.895 | 0.7475 | 0.9789 | 28.1 | |
| AUC | 0.9753 | 0.9857 | 0.9485 | 0.9365 | 0.9524 | 0.9577 | 0.8831 | 0.9932 | 28.1 | |
| winequality-red-4 | F1-score | 0.9173 | 0.9472 | 0.6572 | 0.6032 | 0.6261 | 0.6241 | 0.1719 | 0.9772 | 29.17 |
| G-mean | 0.9115 | 0.9462 | 0.6777 | 0.6387 | 0.6462 | 0.6481 | 0.614 | 0.9774 | 29.17 | |
| AUC | 0.9636 | 0.9793 | 0.7517 | 0.7123 | 0.7147 | 0.7145 | 0.7163 | 0.987 | 29.17 | |
| yeast-1-2-8-9_vs_7 | F1-score | 0.8548 | 0.9284 | 0.8037 | 0.7655 | 0.8016 | 0.7974 | 0.1156 | 0.9823 | 30.57 |
| G-mean | 0.8463 | 0.9273 | 0.7715 | 0.7773 | 0.7878 | 0.7854 | 0.5731 | 0.9825 | 30.57 | |
| AUC | 0.9426 | 0.9782 | 0.857 | 0.8638 | 0.8804 | 0.8818 | 0.6894 | 0.9879 | 30.57 | |
| yeast5 | F1-score | 0.985 | 0.9852 | 0.9741 | 0.9647 | 0.9749 | 0.9748 | 0.6332 | 0.9885 | 32.73 |
| G-mean | 0.9847 | 0.9849 | 0.973 | 0.963 | 0.9739 | 0.9737 | 0.9191 | 0.9885 | 32.73 | |
| AUC | 0.9937 | 0.9935 | 0.9886 | 0.9879 | 0.9908 | 0.9906 | 0.9854 | 0.9991 | 32.73 | |
| yeast6 | F1-score | 0.9494 | 0.9806 | 0.9046 | 0.9154 | 0.9247 | 0.9266 | 0.394 | 0.989 | 41.4 |
| G-mean | 0.9476 | 0.9802 | 0.9022 | 0.9156 | 0.9253 | 0.9271 | 0.815 | 0.9891 | 41.4 | |
| AUC | 0.9863 | 0.9937 | 0.9689 | 0.9666 | 0.9799 | 0.9802 | 0.9242 | 0.9976 | 41.4 | |
| poker-8-9_vs_5 | F1-score | 0.9714 | 0.97 | 0.9633 | 0.909 | 0.9656 | 0.9632 | 0.12 | 0.9939 | 58.4 |
| G-mean | 0.97 | 0.9688 | 0.9614 | 0.9069 | 0.9641 | 0.9612 | 0.5999 | 0.9939 | 58.4 | |
| AUC | 0.9957 | 0.9952 | 0.9914 | 0.9683 | 0.9941 | 0.9909 | 0.7749 | 0.9946 | 58.4 | |
| poker-8-9_vs_6 | F1-score | 1 | 0.9993 | 0.9186 | 0.8697 | 0.9408 | 0.9331 | 0.821 | 0.9947 | 82 |
| G-mean | 1 | 0.9993 | 0.9102 | 0.877 | 0.9383 | 0.9273 | 0.8449 | 0.9947 | 82 | |
| AUC | 1 | 0.9999 | 0.9881 | 0.9677 | 0.9898 | 0.9904 | 0.9805 | 0.9998 | 82 | |
| poker-8_vs_6 | F1-score | 1 | 0.9997 | 0.9297 | 0.8997 | 0.9382 | 0.9292 | 0.7803 | 0.997 | 85.88 |
| G-mean | 1 | 0.9997 | 0.9212 | 0.9037 | 0.9316 | 0.9205 | 0.8093 | 0.997 | 85.88 | |
| AUC | 1 | 1 | 0.9953 | 0.9791 | 0.9967 | 0.995 | 0.9854 | 0.9997 | 85.88 | |
| Datasets | Estimators | IR | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | M | G | D | K | S | T | |||
| glass1 | F1-score | 0.7914 | 0.8175 | 0.7906 | 0.805 | 0.8216 | 0.7987 | 0.6742 | 0.8128 | 1.82 |
| G-mean | 0.7897 | 0.8144 | 0.7858 | 0.8053 | 0.8153 | 0.7943 | 0.7407 | 0.8101 | 1.82 | |
| AUC | 0.8376 | 0.8465 | 0.8396 | 0.8662 | 0.8574 | 0.8453 | 0.7975 | 0.8722 | 1.82 | |
| wisconsin | F1-score | 0.9695 | 0.9637 | 0.9727 | 0.969 | 0.9697 | 0.9702 | 0.943 | 0.9671 | 1.86 |
| G-mean | 0.9695 | 0.9632 | 0.9726 | 0.969 | 0.9696 | 0.97 | 0.9575 | 0.9671 | 1.86 | |
| AUC | 0.9897 | 0.984 | 0.9907 | 0.9948 | 0.9937 | 0.9939 | 0.991 | 0.9928 | 1.86 | |
| pima | F1-score | 0.7426 | 0.746 | 0.7581 | 0.7707 | 0.7742 | 0.7773 | 0.6539 | 0.8003 | 1.87 |
| G-mean | 0.7459 | 0.7358 | 0.7547 | 0.7747 | 0.7721 | 0.7757 | 0.7301 | 0.8007 | 1.87 | |
| AUC | 0.8197 | 0.7994 | 0.8279 | 0.8633 | 0.8488 | 0.8492 | 0.8106 | 0.884 | 1.87 | |
| glass0 | F1-score | 0.8259 | 0.8764 | 0.8115 | 0.8299 | 0.8525 | 0.8669 | 0.7101 | 0.8471 | 2.06 |
| G-mean | 0.8128 | 0.8738 | 0.8012 | 0.8282 | 0.8445 | 0.8622 | 0.7818 | 0.8452 | 2.06 | |
| AUC | 0.8725 | 0.8952 | 0.8656 | 0.9038 | 0.9046 | 0.9087 | 0.847 | 0.909 | 2.06 | |
| yeast1 | F1-score | 0.7694 | 0.7395 | 0.7571 | 0.8301 | 0.7693 | 0.7721 | 0.5913 | 0.8297 | 2.46 |
| G-mean | 0.7509 | 0.7363 | 0.7427 | 0.8356 | 0.7641 | 0.7668 | 0.7126 | 0.8354 | 2.46 | |
| AUC | 0.8267 | 0.8221 | 0.8226 | 0.9176 | 0.8444 | 0.8439 | 0.7891 | 0.9157 | 2.46 | |
| haberman | F1-score | 0.7091 | 0.6288 | 0.7126 | 0.7532 | 0.7063 | 0.6993 | 0.3879 | 0.788 | 2.78 |
| G-mean | 0.7028 | 0.6385 | 0.7083 | 0.7621 | 0.7077 | 0.7034 | 0.5505 | 0.794 | 2.78 | |
| AUC | 0.7713 | 0.6829 | 0.7724 | 0.8265 | 0.7581 | 0.7648 | 0.6057 | 0.8612 | 2.78 | |
| vehicle3 | F1-score | 0.8312 | 0.8429 | 0.8287 | 0.8117 | 0.824 | 0.8233 | 0.5901 | 0.8375 | 2.99 |
| G-mean | 0.83 | 0.8371 | 0.8241 | 0.8129 | 0.8211 | 0.8209 | 0.7286 | 0.8417 | 2.99 | |
| AUC | 0.9034 | 0.9078 | 0.8998 | 0.9047 | 0.9008 | 0.9001 | 0.8348 | 0.9283 | 2.99 | |
| vehicle0 | F1-score | 0.9791 | 0.9791 | 0.9771 | 0.9743 | 0.9769 | 0.9799 | 0.9171 | 0.9709 | 3.25 |
| G-mean | 0.9791 | 0.9787 | 0.9766 | 0.974 | 0.9765 | 0.9796 | 0.9577 | 0.9707 | 3.25 | |
| AUC | 0.9959 | 0.9954 | 0.9955 | 0.9934 | 0.9959 | 0.9966 | 0.9871 | 0.9938 | 3.25 | |
| ecoli1 | F1-score | 0.8855 | 0.915 | 0.8991 | 0.9237 | 0.9153 | 0.9103 | 0.7575 | 0.9282 | 3.36 |
| G-mean | 0.8845 | 0.9177 | 0.8949 | 0.9227 | 0.9136 | 0.9087 | 0.8591 | 0.9272 | 3.36 | |
| AUC | 0.9382 | 0.9509 | 0.9444 | 0.9731 | 0.9565 | 0.9548 | 0.9218 | 0.9741 | 3.36 | |
| new-thyroid2 | F1-score | 0.994 | 0.9904 | 0.9928 | 0.9842 | 0.9909 | 0.9906 | 0.9286 | 0.981 | 5.14 |
| G-mean | 0.9938 | 0.9902 | 0.9927 | 0.984 | 0.9907 | 0.9905 | 0.9521 | 0.9809 | 5.14 | |
| AUC | 0.9997 | 0.9996 | 0.9997 | 0.999 | 0.9998 | 0.9997 | 0.9971 | 0.999 | 5.14 | |
| ecoli2 | F1-score | 0.9363 | 0.9686 | 0.929 | 0.9636 | 0.9576 | 0.9492 | 0.7802 | 0.9618 | 5.46 |
| G-mean | 0.9357 | 0.9702 | 0.9271 | 0.9639 | 0.9575 | 0.9492 | 0.874 | 0.962 | 5.46 | |
| AUC | 0.9723 | 0.9738 | 0.967 | 0.9906 | 0.9819 | 0.9802 | 0.9337 | 0.9867 | 5.46 | |
| segment0 | F1-score | 0.9982 | 0.9983 | 0.9982 | 0.9977 | 0.9982 | 0.9985 | 0.9884 | 0.9975 | 6.02 |
| G-mean | 0.9982 | 0.9983 | 0.9982 | 0.9977 | 0.9982 | 0.9985 | 0.9927 | 0.9975 | 6.02 | |
| AUC | 1 | 1 | 0.9999 | 0.9999 | 0.9998 | 0.9999 | 0.9995 | 0.9998 | 6.02 | |
| yeast3 | F1-score | 0.953 | 0.9468 | 0.9504 | 0.9697 | 0.9586 | 0.9585 | 0.7709 | 0.971 | 8.1 |
| G-mean | 0.9523 | 0.9456 | 0.9498 | 0.9696 | 0.9583 | 0.9582 | 0.9028 | 0.9711 | 8.1 | |
| AUC | 0.9807 | 0.9828 | 0.9817 | 0.996 | 0.9873 | 0.9873 | 0.9684 | 0.9925 | 8.1 | |
| yeast-2_vs_4 | F1-score | 0.9683 | 0.9655 | 0.9699 | 0.9452 | 0.9699 | 0.967 | 0.7365 | 0.9744 | 9.08 |
| G-mean | 0.9679 | 0.9682 | 0.9692 | 0.9454 | 0.9694 | 0.9667 | 0.8511 | 0.9745 | 9.08 | |
| AUC | 0.9867 | 0.9743 | 0.9855 | 0.9872 | 0.9874 | 0.9888 | 0.9097 | 0.9893 | 9.08 | |
| yeast-0-2-5-7-9_vs_3-6-8 | F1-score | 0.9224 | 0.9362 | 0.9339 | 0.9772 | 0.9421 | 0.9317 | 0.7188 | 0.9781 | 9.14 |
| G-mean | 0.9218 | 0.9355 | 0.9319 | 0.9774 | 0.9427 | 0.9326 | 0.8746 | 0.9782 | 9.14 | |
| AUC | 0.9712 | 0.9753 | 0.9701 | 0.9934 | 0.9827 | 0.9821 | 0.9324 | 0.992 | 9.14 | |
| yeast-0-5-6-7-9_vs_4 | F1-score | 0.8899 | 0.9263 | 0.9037 | 0.949 | 0.9093 | 0.9025 | 0.4829 | 0.9475 | 9.35 |
| G-mean | 0.8892 | 0.9244 | 0.901 | 0.9498 | 0.9083 | 0.902 | 0.7392 | 0.9482 | 9.35 | |
| AUC | 0.949 | 0.9634 | 0.9509 | 0.9785 | 0.9589 | 0.9586 | 0.8072 | 0.9754 | 9.35 | |
| vowel0 | F1-score | 0.9964 | 0.9966 | 0.9959 | 0.9964 | 0.9963 | 0.9971 | 0.9628 | 0.9908 | 9.98 |
| G-mean | 0.9964 | 0.9966 | 0.9959 | 0.9964 | 0.9963 | 0.997 | 0.984 | 0.9909 | 9.98 | |
| AUC | 0.9996 | 0.9996 | 0.9998 | 0.9997 | 0.9997 | 0.9998 | 0.9982 | 0.9976 | 9.98 | |
| yeast-1_vs_7 | F1-score | 0.886 | 0.9333 | 0.8976 | 0.9557 | 0.8966 | 0.8993 | 0.294 | 0.9546 | 14.3 |
| G-mean | 0.8823 | 0.9295 | 0.8946 | 0.9561 | 0.8944 | 0.897 | 0.6198 | 0.9548 | 14.3 | |
| AUC | 0.9459 | 0.9609 | 0.9488 | 0.9823 | 0.9523 | 0.9538 | 0.7581 | 0.9795 | 14.3 | |
| ecoli4 | F1-score | 0.9873 | 0.9926 | 0.9888 | 0.9864 | 0.9882 | 0.9885 | 0.7837 | 0.9838 | 15.8 |
| G-mean | 0.9872 | 0.9925 | 0.9887 | 0.9863 | 0.9881 | 0.9884 | 0.8826 | 0.9838 | 15.8 | |
| AUC | 0.9984 | 0.9975 | 0.999 | 0.9992 | 0.9992 | 0.9992 | 0.9878 | 0.9992 | 15.8 | |
| page-blocks-1-3_vs_4 | F1-score | 0.9981 | 0.9969 | 0.9979 | 0.9911 | 0.9989 | 0.9984 | 0.9551 | 0.9964 | 15.86 |
| G-mean | 0.9981 | 0.997 | 0.9979 | 0.9911 | 0.9989 | 0.9984 | 0.972 | 0.9964 | 15.86 | |
| AUC | 1 | 0.9988 | 0.9989 | 0.9982 | 0.9989 | 0.9989 | 0.9989 | 0.9998 | 15.86 | |
| dermatology-6 | F1-score | 0.9972 | 0.9984 | 0.9979 | 0.9964 | 0.9982 | 0.9985 | 0.9378 | 0.9985 | 16.9 |
| G-mean | 0.9972 | 0.9984 | 0.9979 | 0.9964 | 0.9982 | 0.9985 | 0.9634 | 0.9985 | 16.9 | |
| AUC | 0.9985 | 0.9985 | 0.9985 | 0.9994 | 0.9985 | 0.9985 | 0.9985 | 0.9985 | 16.9 | |
| yeast-1-4-5-8_vs_7 | F1-score | 0.8747 | 0.9243 | 0.883 | 0.9708 | 0.8827 | 0.8811 | 0.1419 | 0.9702 | 22.1 |
| G-mean | 0.8694 | 0.9222 | 0.8792 | 0.9712 | 0.8787 | 0.8765 | 0.4893 | 0.9705 | 22.1 | |
| AUC | 0.9419 | 0.969 | 0.9494 | 0.9865 | 0.9485 | 0.9433 | 0.6543 | 0.9857 | 22.1 | |
| yeast4 | F1-score | 0.932 | 0.9625 | 0.9322 | 0.9787 | 0.9407 | 0.932 | 0.3462 | 0.9789 | 28.1 |
| G-mean | 0.9313 | 0.962 | 0.9312 | 0.9788 | 0.9401 | 0.9318 | 0.7409 | 0.9791 | 28.1 | |
| AUC | 0.9724 | 0.9844 | 0.9717 | 0.9937 | 0.977 | 0.976 | 0.8392 | 0.9923 | 28.1 | |
| winequality-red-4 | F1-score | 0.8446 | 0.9531 | 0.8633 | 0.881 | 0.848 | 0.8449 | 0.1227 | 0.9675 | 29.17 |
| G-mean | 0.8419 | 0.9525 | 0.8617 | 0.8839 | 0.8454 | 0.8434 | 0.538 | 0.9676 | 29.17 | |
| AUC | 0.9191 | 0.9827 | 0.9331 | 0.9549 | 0.9193 | 0.9197 | 0.6305 | 0.9863 | 29.17 | |
| yeast-1-2-8-9_vs_7 | F1-score | 0.8895 | 0.9484 | 0.8945 | 0.9813 | 0.9025 | 0.8969 | 0.1496 | 0.9803 | 30.57 |
| G-mean | 0.8863 | 0.9481 | 0.8908 | 0.9814 | 0.9009 | 0.8949 | 0.5398 | 0.9804 | 30.57 | |
| AUC | 0.9534 | 0.9827 | 0.9561 | 0.9907 | 0.9635 | 0.9588 | 0.695 | 0.9895 | 30.57 | |
| yeast5 | F1-score | 0.9863 | 0.9881 | 0.9863 | 0.9892 | 0.989 | 0.9883 | 0.6745 | 0.9902 | 32.73 |
| G-mean | 0.9862 | 0.9879 | 0.9861 | 0.9892 | 0.9889 | 0.9882 | 0.8938 | 0.9902 | 32.73 | |
| AUC | 0.9937 | 0.9947 | 0.9939 | 0.9996 | 0.9955 | 0.9954 | 0.9835 | 0.9994 | 32.73 | |
| yeast6 | F1-score | 0.9578 | 0.9842 | 0.9586 | 0.9881 | 0.9595 | 0.9623 | 0.3768 | 0.9894 | 41.4 |
| G-mean | 0.9573 | 0.984 | 0.9579 | 0.9881 | 0.9592 | 0.9621 | 0.7675 | 0.9894 | 41.4 | |
| AUC | 0.9852 | 0.9934 | 0.9855 | 0.9982 | 0.9889 | 0.9887 | 0.8756 | 0.9975 | 41.4 | |
| poker-8-9_vs_5 | F1-score | 0.9229 | 0.851 | 0.9434 | 0.9932 | 0.9467 | 0.9363 | 0.0251 | 0.9939 | 58.4 |
| G-mean | 0.919 | 0.8431 | 0.9425 | 0.9932 | 0.9466 | 0.9354 | 0.3727 | 0.9939 | 58.4 | |
| AUC | 0.9714 | 0.902 | 0.985 | 0.9931 | 0.9885 | 0.9848 | 0.471 | 0.994 | 58.4 | |
| poker-8-9_vs_6 | F1-score | 0.9004 | 0.7933 | 0.9461 | 0.9896 | 0.9584 | 0.9421 | 0.0279 | 0.9913 | 82 |
| G-mean | 0.8985 | 0.7934 | 0.9465 | 0.9897 | 0.9587 | 0.9427 | 0.3535 | 0.9913 | 82 | |
| AUC | 0.9624 | 0.8755 | 0.9838 | 0.9889 | 0.9875 | 0.9858 | 0.4155 | 0.9912 | 82 | |
| poker-8_vs_6 | F1-score | 0.9247 | 0.9145 | 0.9659 | 0.9931 | 0.9669 | 0.9635 | 0.0361 | 0.9933 | 85.88 |
| G-mean | 0.9234 | 0.9108 | 0.9657 | 0.9932 | 0.9668 | 0.9631 | 0.4112 | 0.9934 | 85.88 | |
| AUC | 0.9816 | 0.9649 | 0.9922 | 0.9944 | 0.9928 | 0.9917 | 0.5509 | 0.9951 | 85.88 | |
| Classifier | MLP | SVM | AdaBoost | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimators | F1-Score | G-Mean | AUC | F1-Score | G-Mean | AUC | F1-Score | G-Mean | AUC |
| ADASYN | 2.47 | 2.53 | 2.93 | 2.77 | 3.10 | 2.90 | 5.27 | 5.37 | 5.40 |
| BORDERLINE | 2.30 | 2.53 | 2.93 | 2.70 | 3.10 | 2.90 | 3.97 | 3.37 | 4.87 |
| MWMOTE | 4.47 | 5.00 | 5.53 | 5.23 | 5.83 | 6.13 | 4.60 | 4.80 | 5.00 |
| GAUSSIAN-SMOTE | 6.20 | 6.47 | 5.73 | 6.50 | 6.43 | 6.83 | 3.43 | 3.40 | 3.00 |
| DTO-SMOTE | 4.80 | 4.47 | 4.03 | 5.27 | 5.20 | 4.77 | 3.67 | 3.70 | 3.00 |
| KNNOR-SMOTE | 4.40 | 4.43 | 4.00 | 4.90 | 4.87 | 4.57 | 4.00 | 3.90 | 3.00 |
| SMOTE | 7.13 | 6.37 | 5.53 | 6.73 | 6.07 | 6.00 | 8.00 | 8.00 | 8.00 |
| TS-SMOTE | 2.20 | 2.10 | 1.87 | 1.73 | 1.63 | 1.43 | 2.77 | 2.70 | 2.00 |
| Classifier | ADASYN | BORDERLINE | MWMOTE | GAUSSIAN | DTO-SMOTE | KNNOR-SMOTE | SMOTE | TS-SMOTE |
|---|---|---|---|---|---|---|---|---|
| MLP | 2.64 | 2.30 | 4.90 | 6.13 | 4.43 | 4.28 | 6.34 | 2.06 |
| SVM | 2.92 | 2.68 | 5.73 | 6.59 | 5.08 | 4.78 | 6.27 | 1.60 |
| AdaBoost | 5.34 | 4.27 | 4.80 | 3.04 | 3.61 | 3.86 | 7.82 | 2.58 |
| Classifier | MLP | SVM | AdaBoost | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimators | F1-Score | G-Mean | AUC | F1-Score | G-Mean | AUC | F1-Score | G-Mean | AUC |
| ADASYN | 0.9405 | 0.9373 | 0.9666 | 0.9147 | 0.9072 | 0.9492 | 0.9088 | 0.9066 | 0.9479 |
| BORDERLINE | 0.9414 | 0.9400 | 0.9642 | 0.9245 | 0.9195 | 0.9556 | 0.9159 | 0.9149 | 0.9453 |
| MWMOTE | 0.8716 | 0.8553 | 0.9079 | 0.8420 | 0.8114 | 0.8793 | 0.9146 | 0.9122 | 0.9503 |
| GAUSSIAN-SMOTE | 0.8676 | 0.8553 | 0.9094 | 0.8243 | 0.8099 | 0.8848 | 0.9382 | 0.9389 | 0.9689 |
| DTO-SMOTE | 0.8792 | 0.8698 | 0.9220 | 0.8374 | 0.8201 | 0.8976 | 0.9203 | 0.9190 | 0.9556 |
| KNNOR-SMOTE | 0.8801 | 0.8715 | 0.9228 | 0.8395 | 0.8218 | 0.8969 | 0.9175 | 0.9166 | 0.9549 |
| SMOTE | 0.6728 | 0.8165 | 0.8943 | 0.6433 | 0.8160 | 0.8927 | 0.5822 | 0.7578 | 0.8330 |
| TS-SMOTE | 0.9493 | 0.9492 | 0.9748 | 0.9404 | 0.9402 | 0.9679 | 0.9457 | 0.9462 | 0.9724 |
| Classifier | MLP | SVM | AdaBoost | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimators | F1-Score | G-Mean | AUC | F1-Score | G-Mean | AUC | F1-Score | G-Mean | AUC |
| ADASYN | 0.93% | 1.25% | 0.85% | 2.77% | 3.58% | 1.95% | 3.98% | 4.27% | 2.55% |
| BORDERLINE | 0.84% | 0.97% | 1.09% | 1.70% | 2.23% | 1.28% | 3.20% | 3.36% | 2.83% |
| MWMOTE | 8.54% | 10.41% | 7.11% | 11.04% | 14.70% | 9.59% | 3.35% | 3.65% | 2.30% |
| GAUSSIAN | 9.00% | 10.40% | 6.94% | 13.16% | 14.89% | 8.97% | 0.80% | 0.77% | 0.36% |
| DTO-SMOTE | 7.67% | 8.73% | 5.57% | 11.59% | 13.65% | 7.53% | 2.73% | 2.91% | 1.74% |
| KNNOR-SMOTE | 7.57% | 8.53% | 5.48% | 11.33% | 13.44% | 7.61% | 3.03% | 3.18% | 1.81% |
| SMOTE | 34.09% | 15.03% | 8.61% | 37.51% | 14.14% | 8.08% | 47.59% | 22.11% | 15.44% |
| Classifier | MLP | SVM | AdaBoost | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimators | F1-Score | G-Mean | AUC | F1-Score | G-Mean | AUC | F1-Score | G-Mean | AUC |
| p-value | 2.968 × | 5.305 × | 6.116 × | 6.467 × | 9.582 × | 9.465 × | 6.864 × | 1.808 × | 1.197 × |
| Classifier | ADASYN | BORDERLINE | MWMOTE | GAUSSIAN | DTO-SMOTE | KNNOR-SMOTE | SMOTE |
|---|---|---|---|---|---|---|---|
| MLP | 8.691 × | 9.346 × | 2.041 × | 4.654 × | 1.310 × | 1.540 × | 6.963 × |
| SVM | 7.957 × | 1.683 × | 4.169 × | 1.743 × | 1.802 × | 3.293 × | 8.920 × |
| AdaBoost | 1.934 × | 6.107 × | 5.350 × | 2.586 × | 1.068 × | 3.023 × | 2.730 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Yang, S. TS-SMOTE: An Improved SMOTE Method Based on Symmetric Triangle Scoring Mechanism for Solving Class-Imbalanced Problems. Symmetry 2025, 17, 1326. https://doi.org/10.3390/sym17081326
Song S, Yang S. TS-SMOTE: An Improved SMOTE Method Based on Symmetric Triangle Scoring Mechanism for Solving Class-Imbalanced Problems. Symmetry. 2025; 17(8):1326. https://doi.org/10.3390/sym17081326
Chicago/Turabian StyleSong, Shihao, and Sibo Yang. 2025. "TS-SMOTE: An Improved SMOTE Method Based on Symmetric Triangle Scoring Mechanism for Solving Class-Imbalanced Problems" Symmetry 17, no. 8: 1326. https://doi.org/10.3390/sym17081326
APA StyleSong, S., & Yang, S. (2025). TS-SMOTE: An Improved SMOTE Method Based on Symmetric Triangle Scoring Mechanism for Solving Class-Imbalanced Problems. Symmetry, 17(8), 1326. https://doi.org/10.3390/sym17081326






