Symmetric Versus Asymmetric Transformer Architectures for Spatio-Temporal Modeling in Effluent Wastewater Quality Prediction
Abstract
1. Introduction
- (1)
- The integration of the MSSA mechanism, which utilizes varying dilation rates to capture short-term, medium-term, and long-term temporal dependencies in wastewater datasets, leveraging a multi-head attention structure to process different temporal scales in parallel;
- (2)
- The incorporation of SGCN to explicitly model spatial relationships between monitoring locations, enhancing the model’s ability to handle spatial variations and interactions;
- (3)
- The introduction of a symmetric architecture that processes spatial and temporal features in parallel, ensuring equal importance to both aspects and enabling more effective feature fusion;
- (4)
- The validation of the DMST-Transformer framework using a full-process wastewater treatment dataset, demonstrating superior performance in prediction accuracy and robustness compared to traditional deep learning models.
2. Materials and Methods
2.1. Data Structure and Temporal Encoding
2.1.1. Spatio-Temporal Data Structure
2.1.2. Temporal Encoding
2.2. Spatial Representation Methods
2.2.1. Traditional Embedding-Based Representation
2.2.2. Graph-Based Representation with SGCN
2.3. Multi-Scale Self-Attention and Dynamic Self-Tuning
2.4. Benchmark Architecture: Asymmetric ST-Transformer Architecture
2.5. Proposed Architecture: Symmetric DMST-Transformer Architecture
3. Results and Discussion
3.1. Data Description
3.2. Model Architecture and Hyperparameter Setup
3.2.1. Asymmetric ST-Transformer
3.2.2. Symmetric DMST-Transformer
3.2.3. Baseline and Ablation Model Configurations
- (1)
- Linear regression (LR): As a basic regression method, LR comprises 32 trainable parameters, including 31 weight coefficients corresponding to input features and one bias term. The model is fitted using ordinary least squares minimization.
- (2)
- The number of latent components was determined through cross-validation. A total of 6 latent variables were selected to balance complexity and performance. This configuration maximized the cumulative explained variance of the input matrix X, while achieving a response variable Y explained variance of 51.53%.
- (3)
- Spatial graph convolutional network (SGCN): The GCN model employs a 31-dimensional embedding layer aligned with the feature dimension. A fixed identity adjacency matrix is used to represent pairwise feature connectivity. The hidden layer dimension is set to 128, and global average pooling is applied to generate the final output.
- (4)
- Transformer: The model adopts a sequence-to-one structure with 2 encoder and 2 decoder blocks, each employing 2 attention heads. The input embedding dimension is 31, consistent with the number of features, and the feed-forward network uses a hidden layer of size 128.
- (5)
- T-SGCN-Transformer: Removes the multi-scale attention and DST modules, retaining only the spatial modeling branch with SGCN. This model follows an asymmetric sequential structure.
- (6)
- T-MSSA-DST-Transformer: Removes the SGCN branch and retains the multi-scale self-attention with dynamic self-tuning in the temporal pathway. It also follows an asymmetric sequential structure.
- (7)
- T-SGCN-MSSA-Transformer: Removes the DST module while retaining both the spatial and multi-scale attention branches, to evaluate the standalone effect of MSSA. This model follows a symmetric parallel structure.
3.3. Modeling Evaluation Metrics
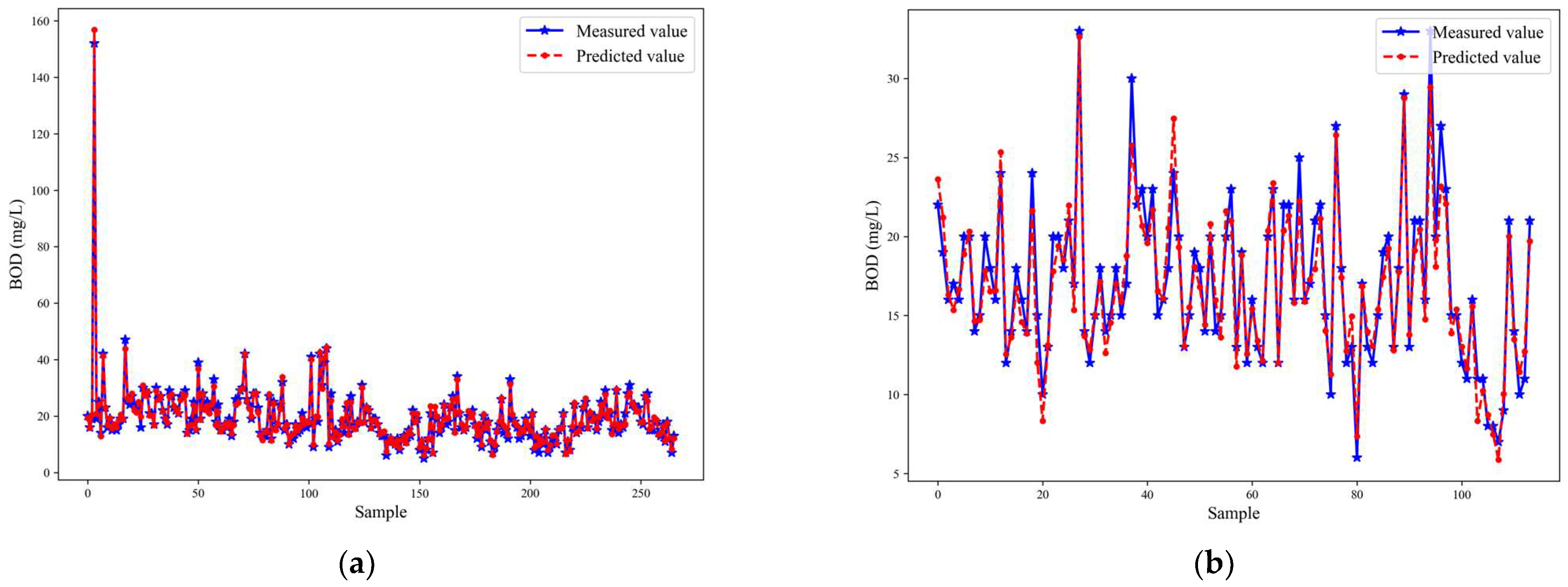
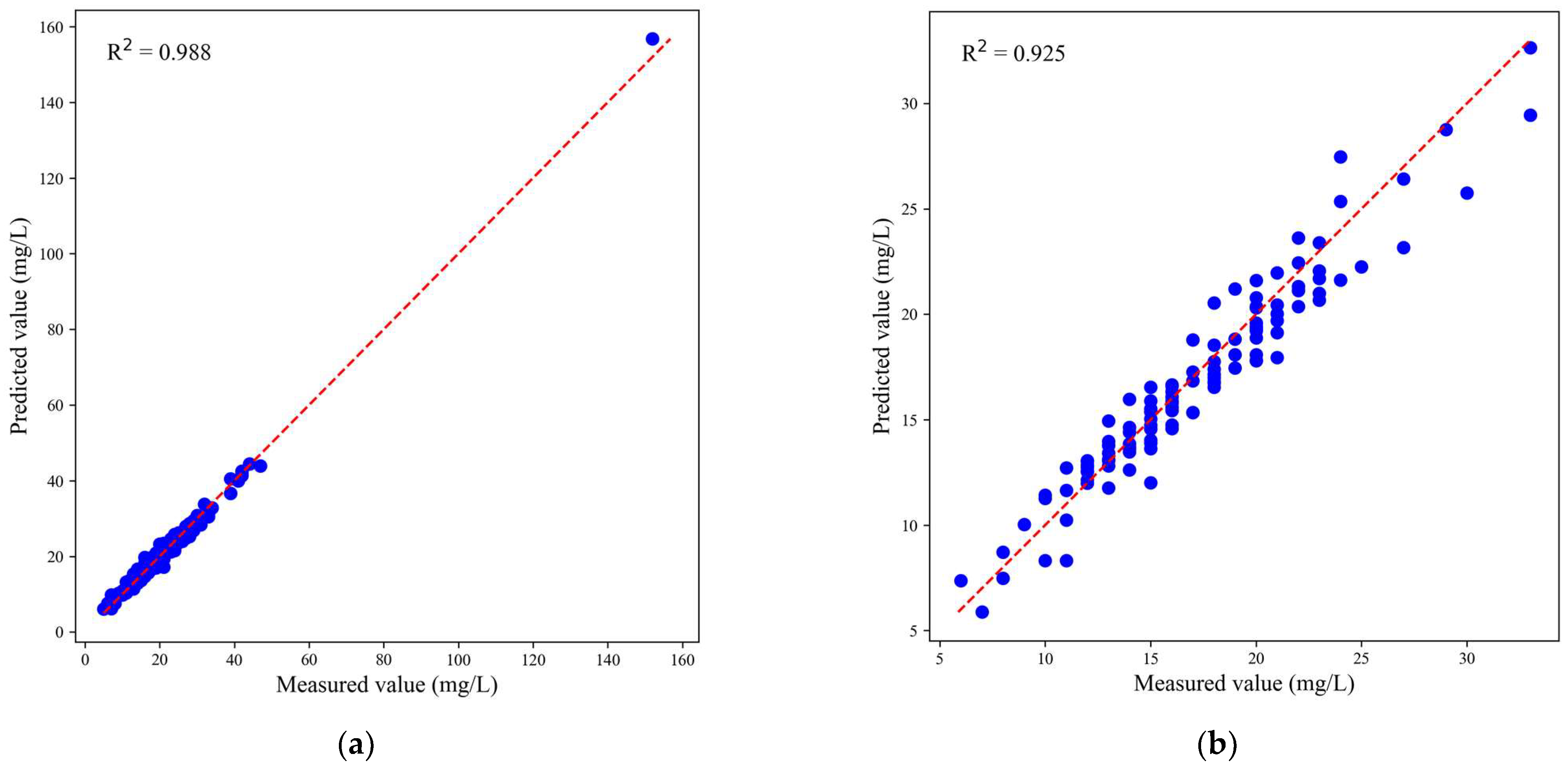
3.4. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, G.; Li, J.; Zeng, G. Recent development in the treatment of oily sludge from petroleum industry: A review. J. Hazard. Mater. 2013, 261, 470–490. [Google Scholar] [CrossRef]
- Li, J.; Du, Q.; Peng, H.; Zhang, Y.; Bi, Y.; Shi, Y.; Xu, Y.; Liu, T. Optimization of biochemical oxygen demand to total nitrogen ratio for treating landfill leachate in a single-stage partial nitrification-denitrification system. J. Clean. Prod. 2020, 266, 121809. [Google Scholar] [CrossRef]
- Ma, J.; Ding, Y.; Cheng, J.C.P.; Jiang, F.; Xu, Z. Soft detection of 5-day BOD with sparse matrix in city harbor water using deep learning techniques. Water Res. 2020, 170, 115350. [Google Scholar] [CrossRef] [PubMed]
- Song, P.; Huang, G.; An, C.; Shen, J.; Zhang, P.; Chen, X.; Shen, J.; Yao, Y.; Zheng, R.; Sun, C. Treatment of rural domestic wastewater using multi-soil-layering systems: Performance evaluation, factorial analysis and numerical modeling. Sci. Total Environ. 2018, 644, 536–546. [Google Scholar] [CrossRef] [PubMed]
- Solgi, A.; Pourhaghi, A.; Bahmani, R.; Zarei, H. Improving SVR and ANFIS performance using wavelet transform and PCA algorithm for modeling and predicting biochemical oxygen demand (BOD). Ecohydrol. Hydrobiol. 2017, 17, 164–175. [Google Scholar] [CrossRef]
- Del Rio-Chanona, E.A.; Cong, X.; Bradford, E.; Zhang, D.; Jing, K. Review of advanced physical and data-driven models for dynamic bioprocess simulation: Case study of algae–Bacteria consortium wastewater treatment. Biotechnol. Bioeng. 2019, 116, 342–353. [Google Scholar] [CrossRef]
- Huang, R.; Ma, C.; Ma, J.; Huangfu, X.; He, Q. Machine learning in natural and engineered water systems. Water Res. 2021, 205, 117666. [Google Scholar] [CrossRef]
- Zaghloul, M.S.; Hamza, R.A.; Iorhemen, O.T.; Tay, J.H. Comparison of adaptive neuro-fuzzy inference systems (ANFIS) and support vector regression (SVR) for data-driven modelling of aerobic granular sludge reactors. J. Environ. Chem. Eng. 2020, 8, 103742. [Google Scholar] [CrossRef]
- Yu, H.; Song, Y.; Liu, R.; Pan, H.; Xiang, L.; Qian, F. Identifying changes in dissolved organic matter content and characteristics by fluorescence spectroscopy coupled with self-organizing map and classification and regression tree analysis during wastewater treatment. Chemosphere 2014, 113, 79–86. [Google Scholar] [CrossRef]
- Harrou, F.; Cheng, T.; Sun, Y.; Leiknes, T.; Ghaffour, N. A Data-Driven Soft Sensor to Forecast Energy Consumption in Wastewater Treatment Plants: A Case Study. IEEE Sens. J. 2021, 21, 4908–4917. [Google Scholar] [CrossRef]
- Li, Z.; Ma, X.; Xin, H. Feature engineering of machine-learning chemisorption models for catalyst design. Catal. Today 2017, 280, 232–238. [Google Scholar] [CrossRef]
- Dittrich, I.; Gertz, M.; Maassen-Francke, B.; Krudewig, K.H.; Junge, W.; Krieter, J. Combining multivariate cumulative sum control charts with principal component analysis and partial least squares model to detect sickness behaviour in dairy cattle. Comput. Electron. Agric. 2021, 186, 106209. [Google Scholar] [CrossRef]
- Liu, H.; Yang, J.; Zhang, Y.; Yang, C. Monitoring of wastewater treatment processes using dynamic concurrent kernel partial least squares. Process Saf. Environ. Prot. 2021, 147, 274–282. [Google Scholar] [CrossRef]
- Alvi, M.; Batstone, D.; Mbamba, C.K.; Keymer, P.; French, T.; Ward, A.; Dwyer, J.; Cardell-Oliver, R. Deep learning in wastewater treatment: A critical review. Water Res. 2023, 245, 120518. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.; Wang, P.; Abbas, K. A survey on deep learning and its applications. Comput. Sci. Rev. 2021, 40, 100379. [Google Scholar] [CrossRef]
- Pouyanfar, S.; Sadiq, S.; Yan, Y.; Tian, H.; Tao, Y.; Reyes, M.P.; Shyu, M.-L.; Chen, S.-C.; Iyengar, S.S. A Survey on Deep Learning: Algorithms, Techniques, and Applications. ACM Comput. Surv. 2018, 51, 1–36. [Google Scholar] [CrossRef]
- Li, X.; Yi, X.; Liu, Z.; Liu, H.; Chen, T.; Niu, G.; Yan, B.; Chen, C.; Huang, M.; Ying, G. Application of novel hybrid deep leaning model for cleaner production in a paper industrial wastewater treatment system. J. Clean. Prod. 2021, 294, 126343. [Google Scholar] [CrossRef]
- Xie, W.; Wang, J.; Xing, C.; Guo, S.; Guo, M.; Zhu, L. Variational Autoencoder Bidirectional Long and Short-Term Memory Neural Network Soft-Sensor Model Based on Batch Training Strategy. IEEE Trans. Ind. Inform. 2021, 17, 5325–5334. [Google Scholar] [CrossRef]
- Chen, H.; Chen, A.; Xu, L.; Xie, H.; Qiao, H.; Lin, Q.; Cai, K. A deep learning CNN architecture applied in smart near-infrared analysis of water pollution for agricultural irrigation resources. Agric. Water Manag. 2020, 240, 106303. [Google Scholar] [CrossRef]
- Yu, M.; Huang, Q.; Li, Z. Deep learning for spatiotemporal forecasting in Earth system science: A review. Int. J. Digit. Earth 2024, 17, 2391952. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Chang, P.; Zhang, S.; Wang, Z. Soft sensor of the key effluent index in the municipal wastewater treatment process based on transformer. IEEE Trans. Ind. Inform. 2023, 20, 4021–4028. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, X.; Xu, A.; Sun, Q.; Peng, X. A hybrid CNN-Transformer model for ozone concentration prediction. Air Qual. Atmos. Health 2022, 15, 1533–1546. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, S. Modeling air quality PM2. 5 forecasting using deep sparse attention-based transformer networks. Int. J. Environ. Sci. Technol. 2023, 20, 13535–13550. [Google Scholar] [CrossRef]
- Tang, S.; Li, C.; Zhang, P.; Tang, R. Swinlstm: Improving spatiotemporal prediction accuracy using swin transformer and lstm. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 13470–13479. [Google Scholar]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in time series: A survey. arXiv 2022, arXiv:2202.07125. [Google Scholar]
- Rahali, A.; Akhloufi, M.A. End-to-end transformer-based models in textual-based NLP. AI 2023, 4, 54–110. [Google Scholar] [CrossRef]
- Yu, M.; Masrur, A.; Blaszczak-Boxe, C. Predicting hourly PM2. 5 concentrations in wildfire-prone areas using a SpatioTemporal Transformer model. Sci. Total Environ. 2023, 860, 160446. [Google Scholar] [CrossRef]
- Geng, Y.; Zhang, F.; Liu, H. Multi-scale temporal convolutional networks for effluent cod prediction in industrial wastewater. Appl. Sci. 2024, 14, 5824. [Google Scholar] [CrossRef]
- Wang, P.; Wang, K.; Song, Y.; Wang, X. AutoLDT: A lightweight spatio-temporal decoupling transformer framework with AutoML method for time series classification. Sci. Rep. 2024, 14, 29801. [Google Scholar] [CrossRef]
- Naghashi, V.; Boukadoum, M.; Diallo, A.B. A multiscale model for multivariate time series forecasting. Sci. Rep. 2025, 15, 1565. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Huang, D.; Li, Y. Development of interval soft sensors using enhanced just-in-time learning and inductive confidence predictor. Ind. Eng. Chem. Res. 2012, 51, 3356–3367. [Google Scholar] [CrossRef]
- Luo, L.; Bao, S.; Mao, J. Adaptive Selection of Latent Variables for Process Monitoring. Ind. Eng. Chem. Res. 2019, 58, 9075–9086. [Google Scholar] [CrossRef]
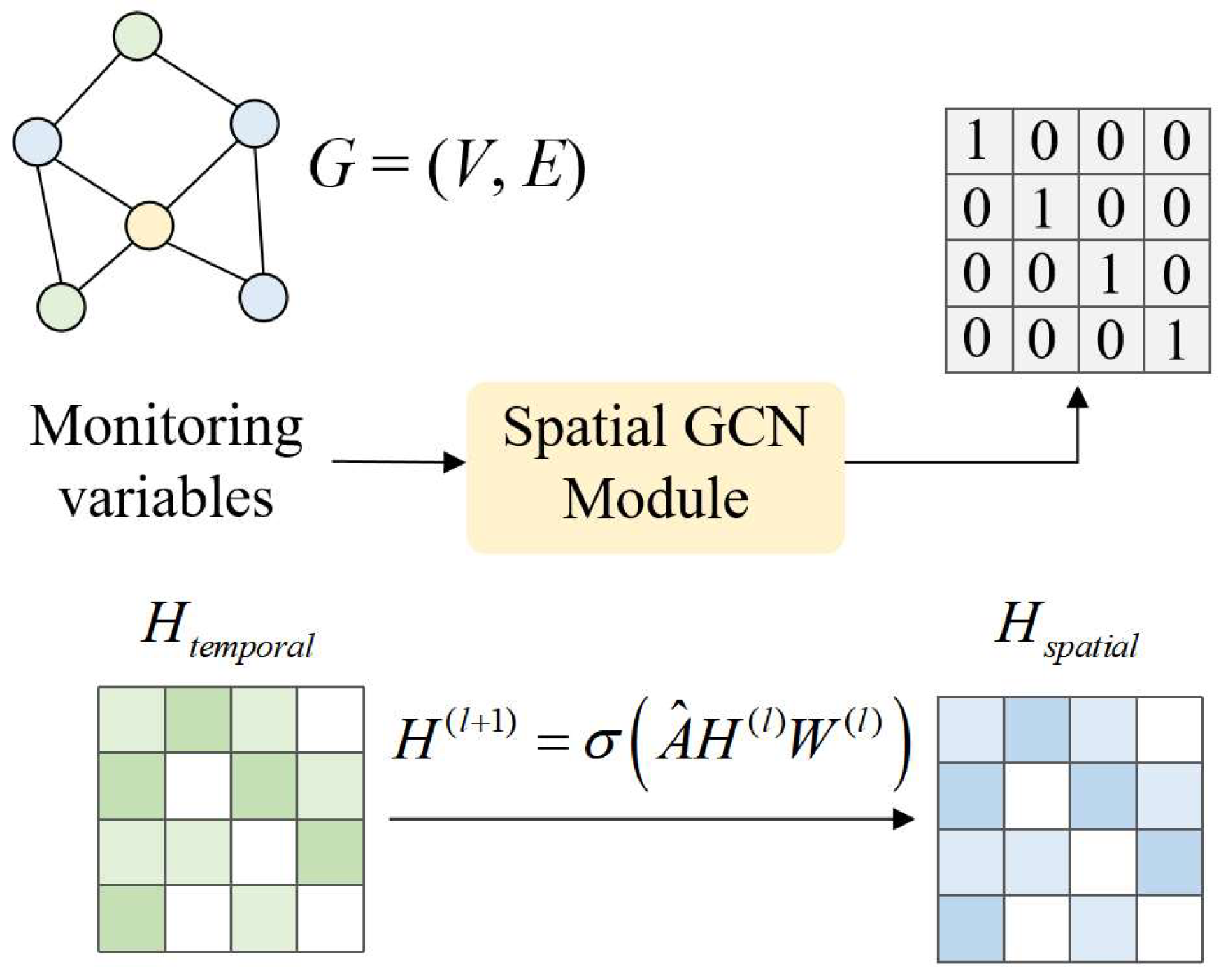






| Position | Variables |
|---|---|
| Influent to WWTP | Flow (Q-E), Zinc (Zn-E), pH (pH-E), Biological oxygen demand (BOD-E), chemical oxygen demand (COD-E), suspended solids (SS-E), volatile suspended solids (VSS-E), sediments (SED-E), conductivity (COND-E) |
| Primary settlers | pH (pH-P), Biological oxygen demand (BOD-P), suspended solids (SS-P), volatile suspended solids (VSS-P), sediments (SED-P), conductivity (COND-P) |
| Secondary settlers | pH (pH-D), Biological oxygen demand (BOD-D), chemical oxygen demand (COD-D), suspended solids (SS-D), volatile suspended solids (VSS-D), sediments (SED-D), conductivity (COND-D) |
| Returned sludge | Biological oxygen demand (RD-BOD-P), suspended solids (RD-SS-P), sediments (RD-SED-P) |
| Wasted sludge | Biological oxygen demand (RD-BOD-S), chemical oxygen demand (RD-COD-S) |
| Aeration tanks | Biological oxygen demand (RD-BOD-G), chemical oxygen demand (RD-COD-G), suspended solids (RD-SS-G), sediments (RD-SED-G) |
| Effluent | pH (pH-S), Biological oxygen demand (BOD-S), chemical oxygen demand (COD-S), suspended solids (SS-S), volatile suspended solids (VSS-S), sediments (SED-S), conductivity (COND-S) |
| Layer | Output Size |
|---|---|
| Input | [batch, 10, 31] |
| Temporal Encoding | [batch, 10, 64] |
| Spatial Embedding | [batch, 10, 64] |
| Spatio-Temporal Fusion | [batch, 10, 64] |
| Transformer Block-1 | [batch, 10, 31] |
| Multi-Head Attention | [batch, 10, 31] |
| LayerNorm | [batch, 10, 31] |
| Dropout (0.3) | [batch, 10, 31] |
| Feed-Forward | [batch, 10, 31] |
| Transformer Encoder-2 | [batch, 10, 31] |
| Average Pooling | [batch, 31] |
| Dense | [batch, 1] |
| Layer | Output Size |
|---|---|
| Input | [batch, 10, 31] |
| Positional Encoding | [batch, 10, 31] |
| Adjacency Matrix | [31, 31] |
| GraphConv-1 | [batch, 10, 64] |
| GraphConv-2 | [batch, 10, 31] |
| Multi-Scale Attention (D = 1) | [batch, 10, 31] |
| Multi-Scale Attention (D = 2) | [batch, 10, 31] |
| Multi-Scale Attention (D = 4) | [batch, 10, 31] |
| Dynamic Self-Tuning (DST) | [batch, 10, 31] |
| Transformer Block-1 | [batch, 10, 31] |
| Multi-Head Attention | [batch, 10, 31] |
| LayerNorm | [batch, 10, 31] |
| Dropout (0.1) | [batch, 10, 31] |
| Feed-Forward | [batch, 10, 31] |
| Transformer Block-2 | [batch, 10, 31] |
| Average Pooling | [batch, 31] |
| Dense | [batch, 1] |
| Models | BOD | ||||
|---|---|---|---|---|---|
| R2 | RMSE (mg/L) | MAPE (%) | Times (s) | ||
| LR | Training set | 0.71 | 5.82 | 25.12 | 0.01 |
| Test set | 0.65 | 2.97 | 15.07 | ||
| PLS | Training set | 0.89 | 3.57 | 14.09 | 0.01 |
| Test set | 0.68 | 3.11 | 13.63 | ||
| GCN | Training set | 0.75 | 5.48 | 28.74 | 0.21 |
| Test set | 0.51 | 4.66 | 24.58 | ||
| Transformer (Asymmetric) | Training set | 0.91 | 3.35 | 13.53 | 0.5 |
| Test set | 0.72 | 2.72 | 13.22 | ||
| ST-Transformer (Asymmetric) | Training set | 0.94 | 2.67 | 11.83 | 0.86 |
| Test set | 0.77 | 2.44 | 12.89 | ||
| DMST-Transformer (Symmetric) | Training set | 0.99 | 1.19 | 5.47 | 0.66 |
| Test set | 0.93 | 1.40 | 6.61 | ||
| T-SGCN-Transformer (Asymmetric) | Training set | 0.91 | 2.56 | 10.35 | 0.92 |
| Test set | 0.85 | 2.29 | 10.92 | ||
| T-MSSA-DST-Transformer (Asymmetric) | Training set | 0.89 | 2.63 | 10.77 | 0.75 |
| Test set | 0.81 | 2.34 | 11.13 | ||
| T-SGCN-MSSA-Transformer (Symmetric) | Training set | 0.95 | 1.67 | 8.42 | 0.68 |
| Test set | 0.89 | 1.72 | 8.89 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, T.; Chen, Z.; Song, J.; Liu, H. Symmetric Versus Asymmetric Transformer Architectures for Spatio-Temporal Modeling in Effluent Wastewater Quality Prediction. Symmetry 2025, 17, 1322. https://doi.org/10.3390/sym17081322
Hu T, Chen Z, Song J, Liu H. Symmetric Versus Asymmetric Transformer Architectures for Spatio-Temporal Modeling in Effluent Wastewater Quality Prediction. Symmetry. 2025; 17(8):1322. https://doi.org/10.3390/sym17081322
Chicago/Turabian StyleHu, Tong, Zikang Chen, Jun Song, and Hongbin Liu. 2025. "Symmetric Versus Asymmetric Transformer Architectures for Spatio-Temporal Modeling in Effluent Wastewater Quality Prediction" Symmetry 17, no. 8: 1322. https://doi.org/10.3390/sym17081322
APA StyleHu, T., Chen, Z., Song, J., & Liu, H. (2025). Symmetric Versus Asymmetric Transformer Architectures for Spatio-Temporal Modeling in Effluent Wastewater Quality Prediction. Symmetry, 17(8), 1322. https://doi.org/10.3390/sym17081322





