An Improved Self-Organizing Map (SOM) Based on Virtual Winning Neurons
Abstract
1. Introduction
1.1. Motivation and Incitement
1.2. A Review of Related Literature
1.3. Contribution and Paper Organization
2. Related Technology
Principles of SOM
3. Principles of vwSOM
3.1. Initialize the Weight Matrix Using the PCA Algorithm
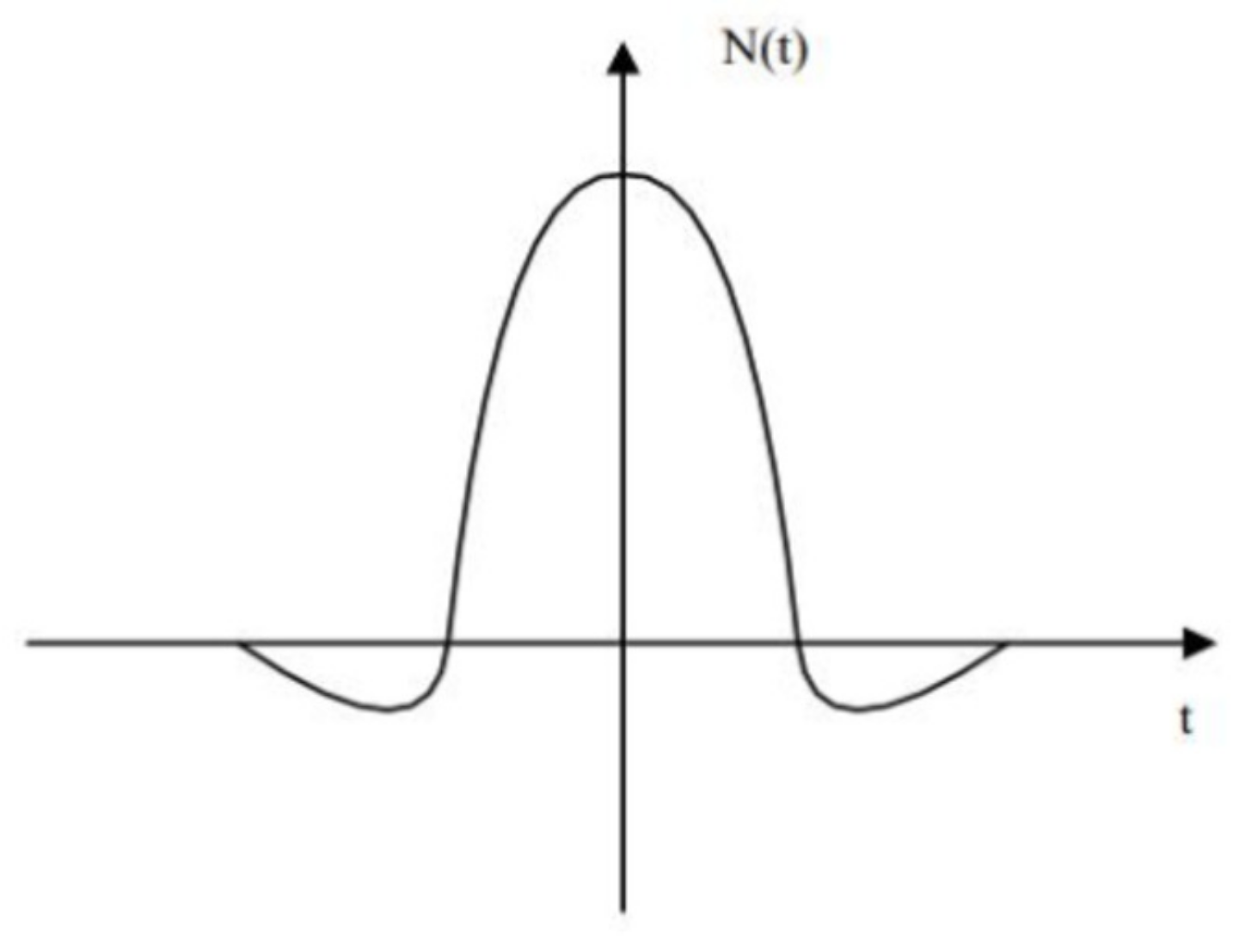
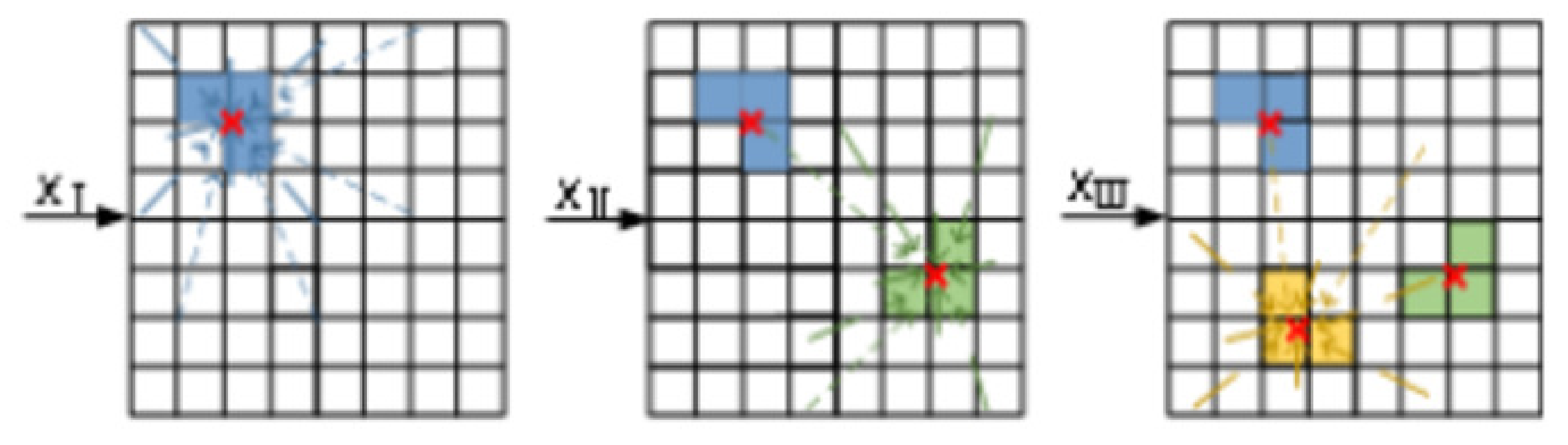
3.2. The Virtual Winning Neuron
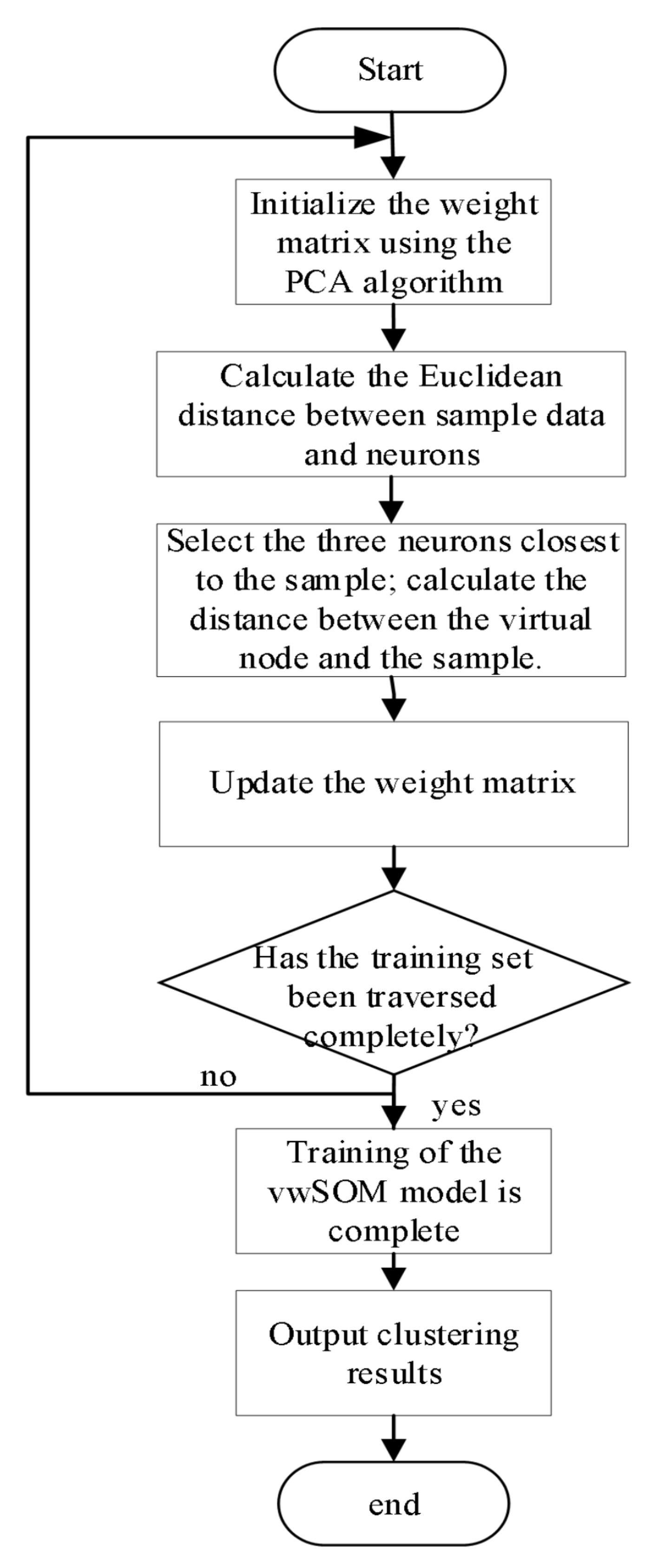
3.3. The vwSOM Algorithm
4. Experimental Results and Analysis
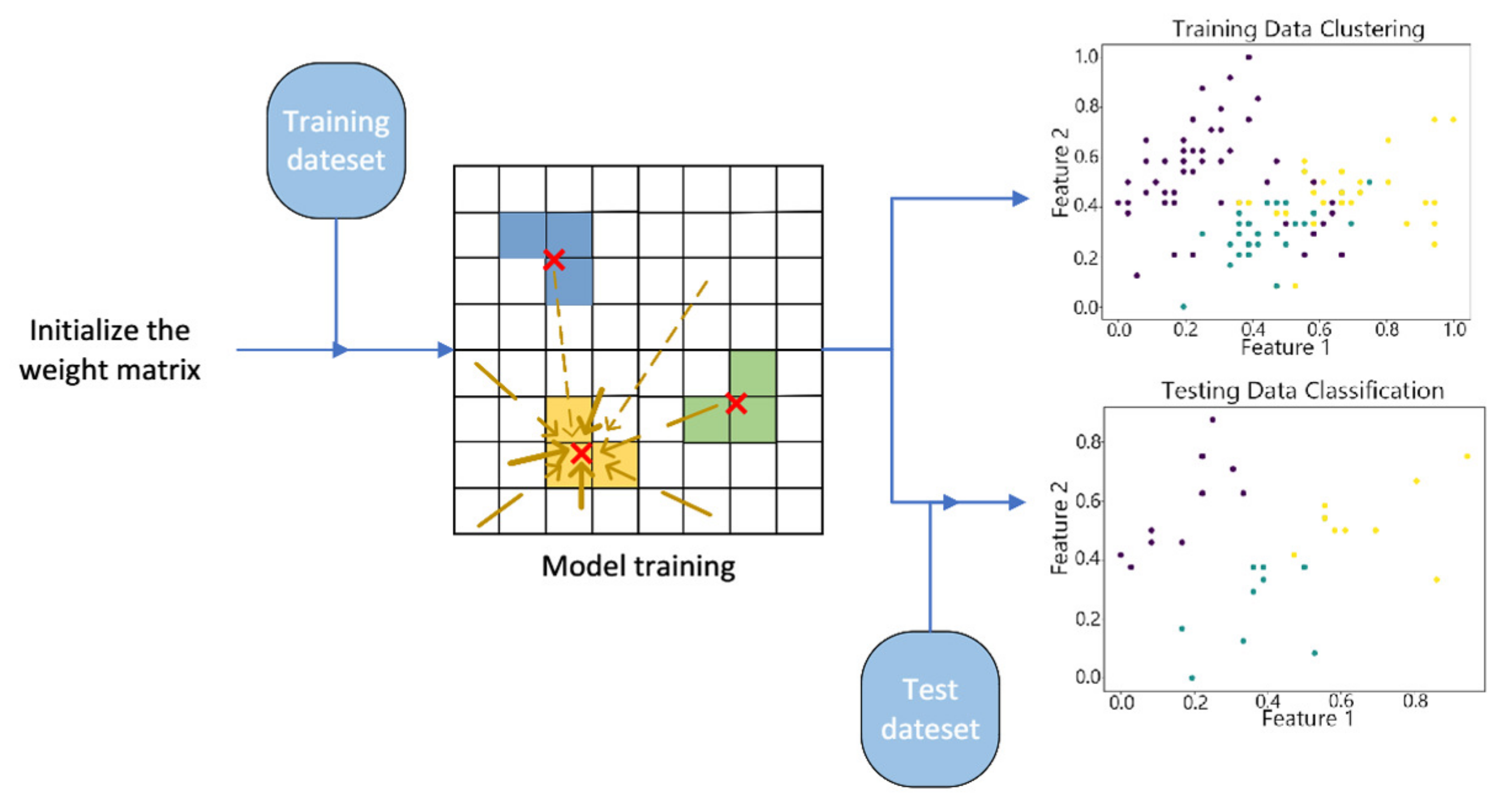
4.1. Experimental Setup
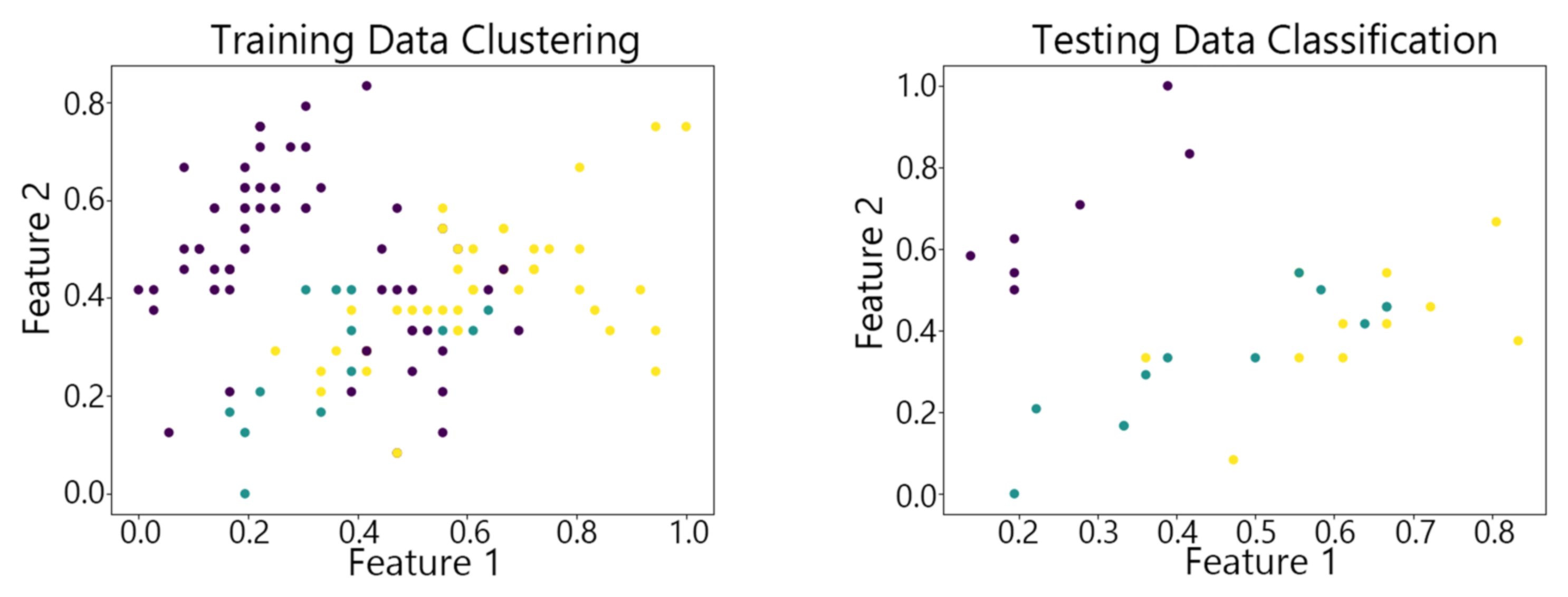
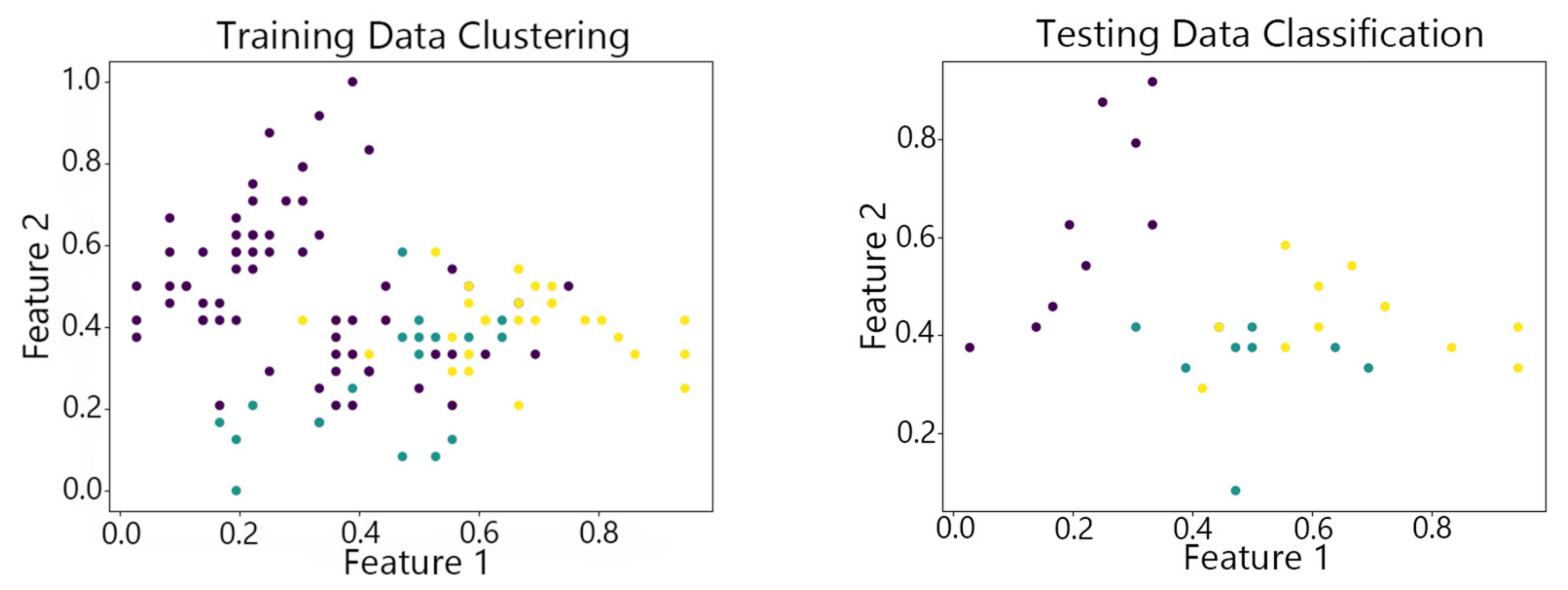
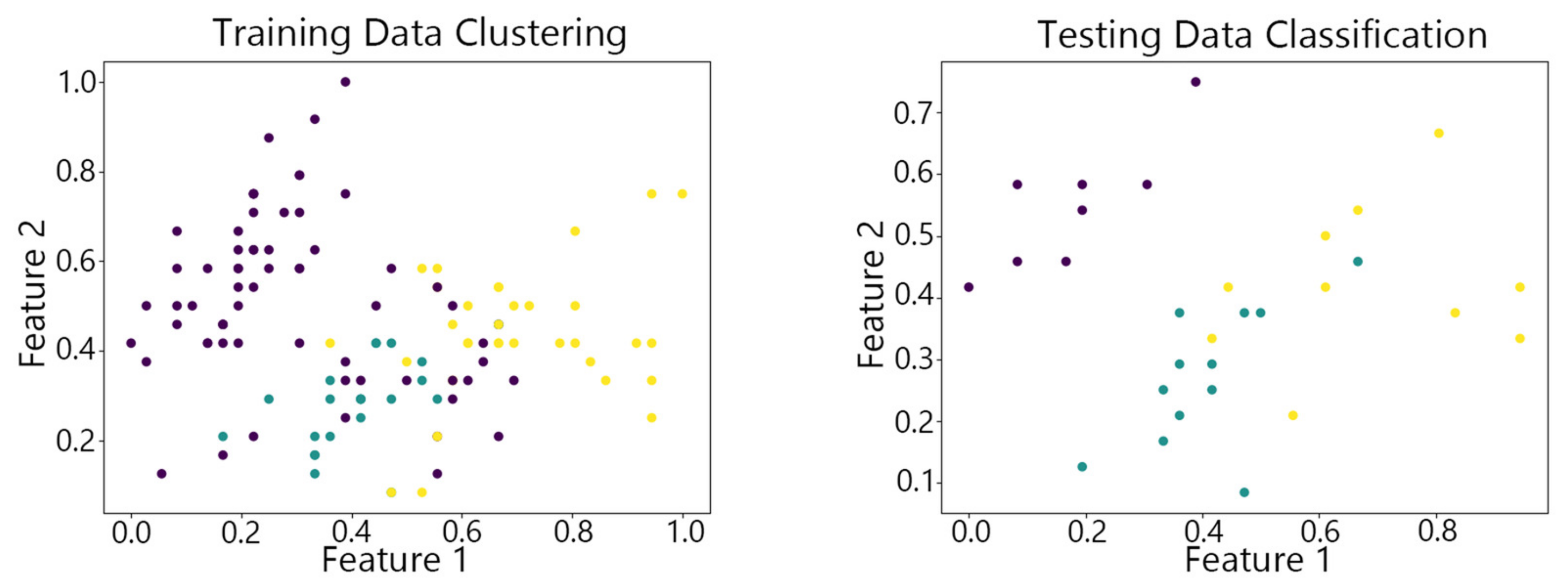
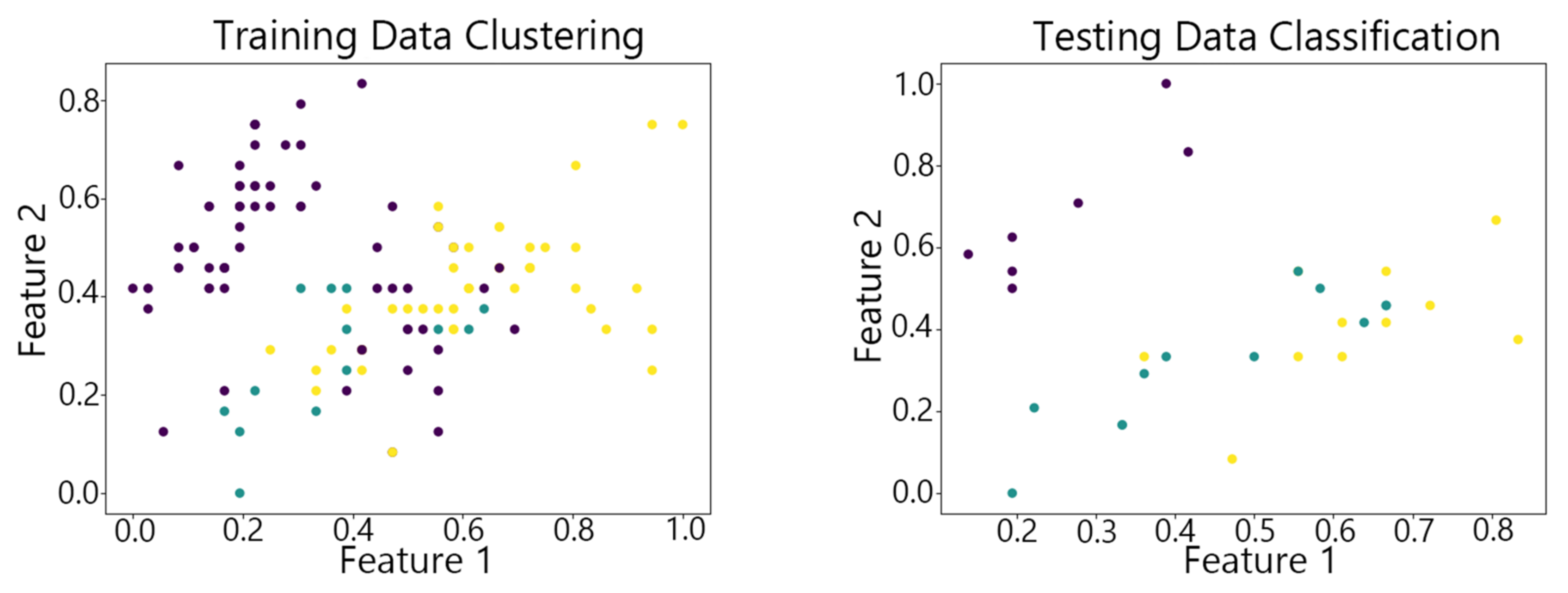
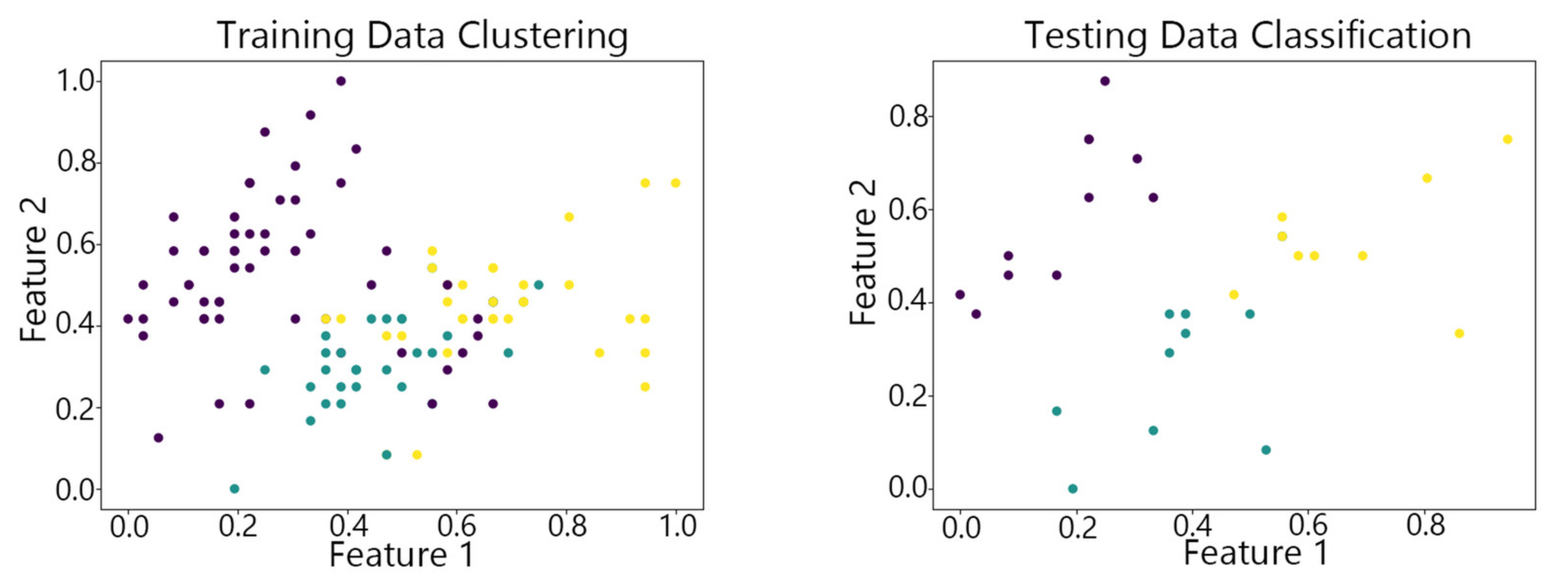
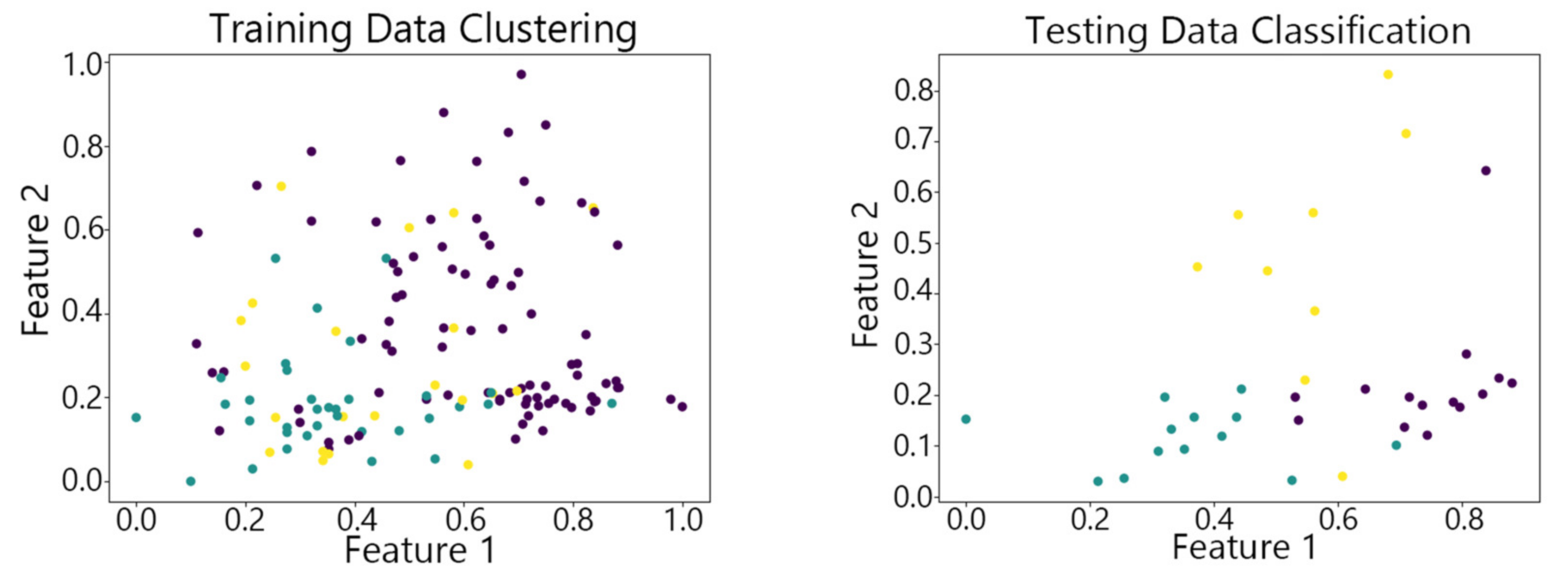
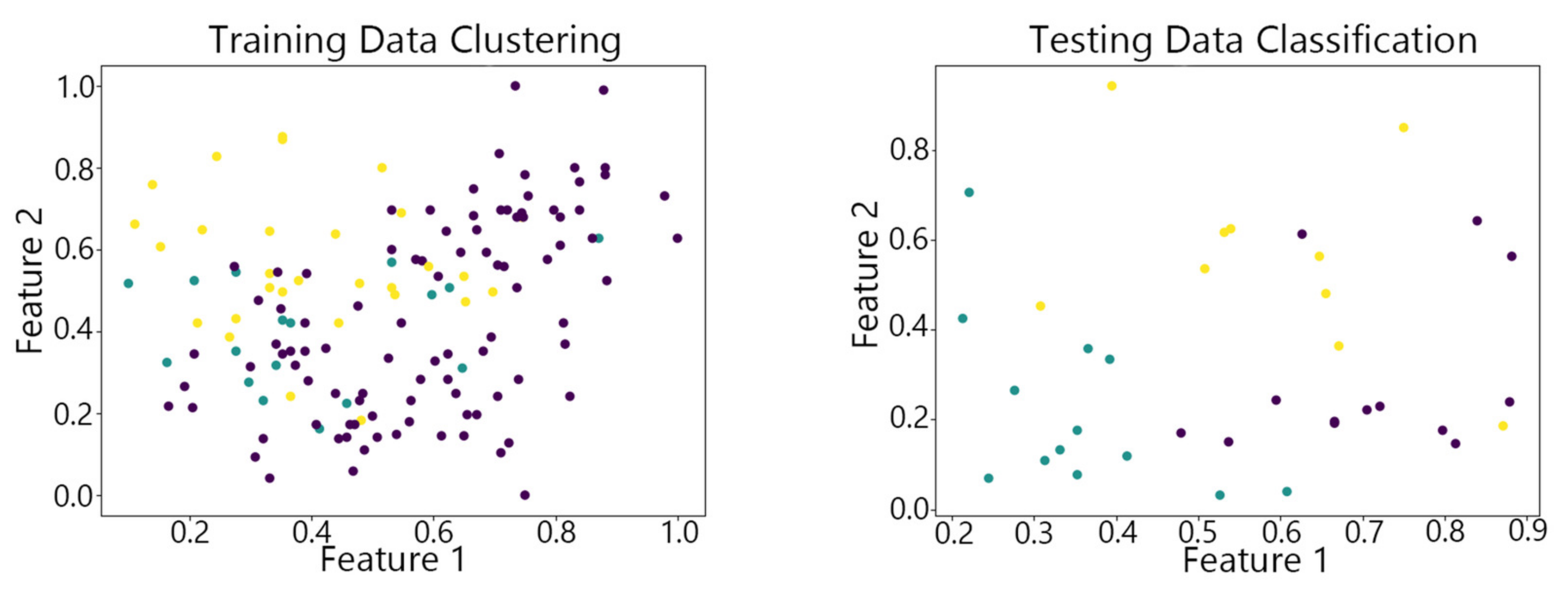
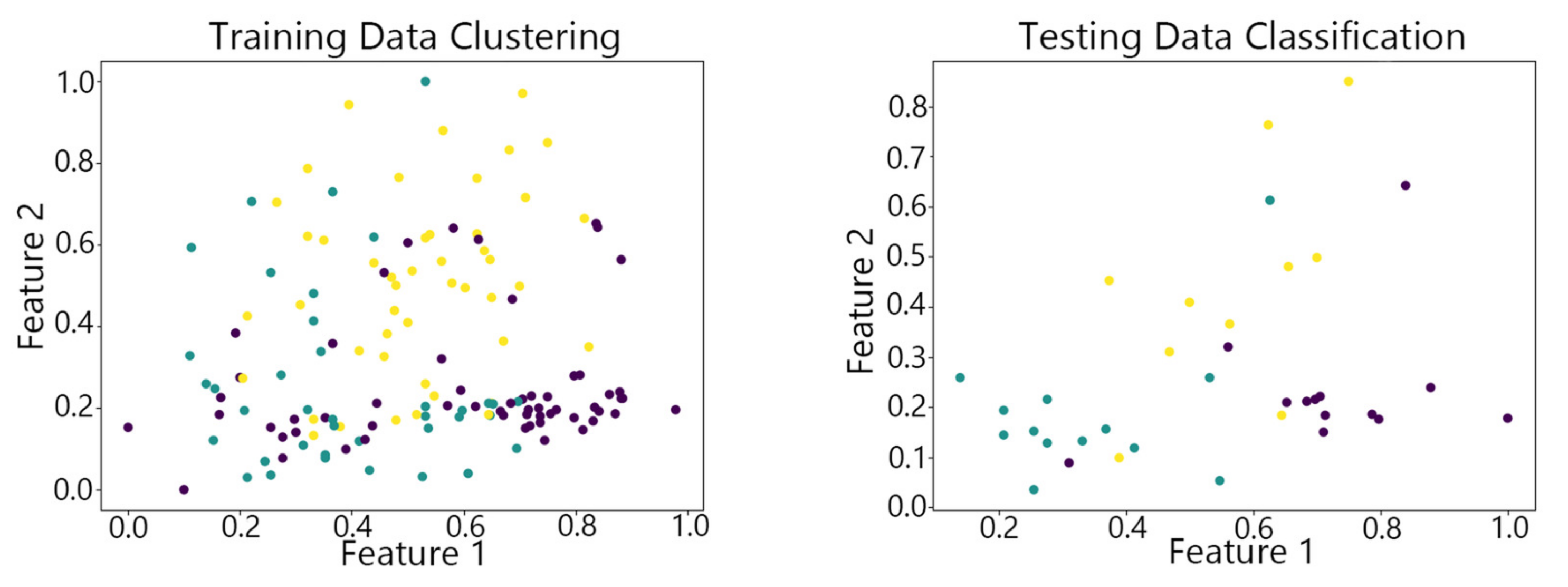
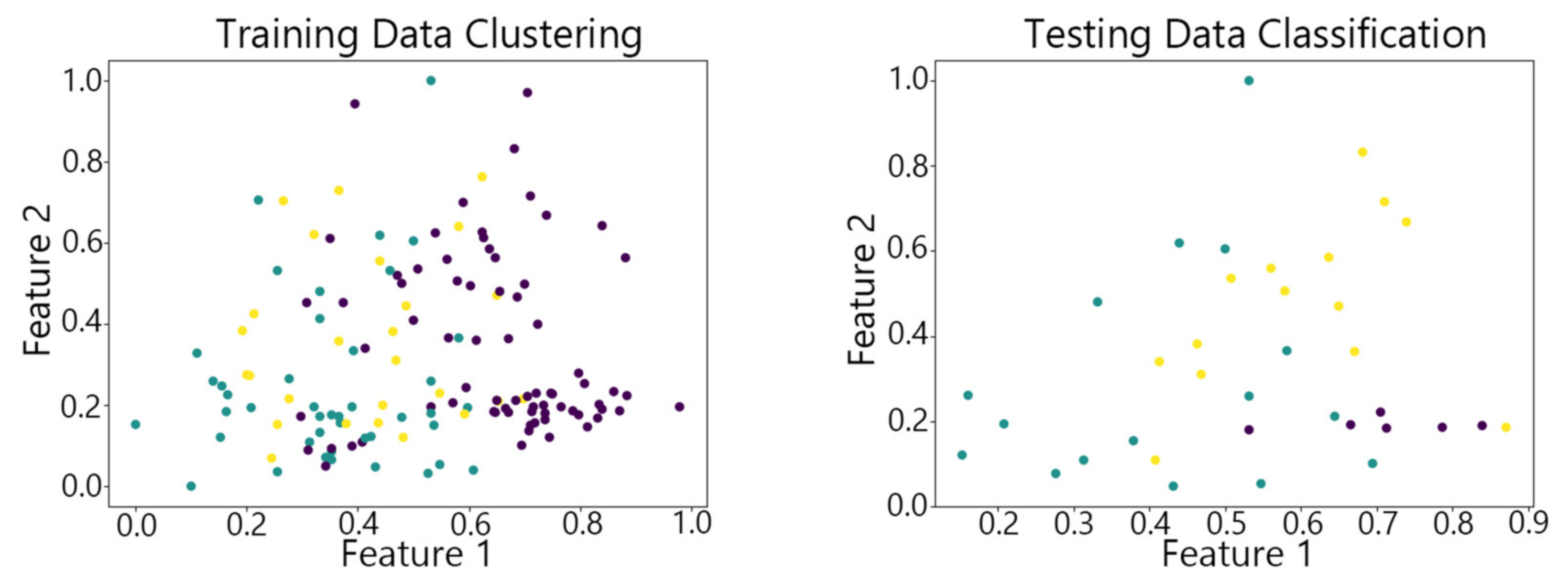
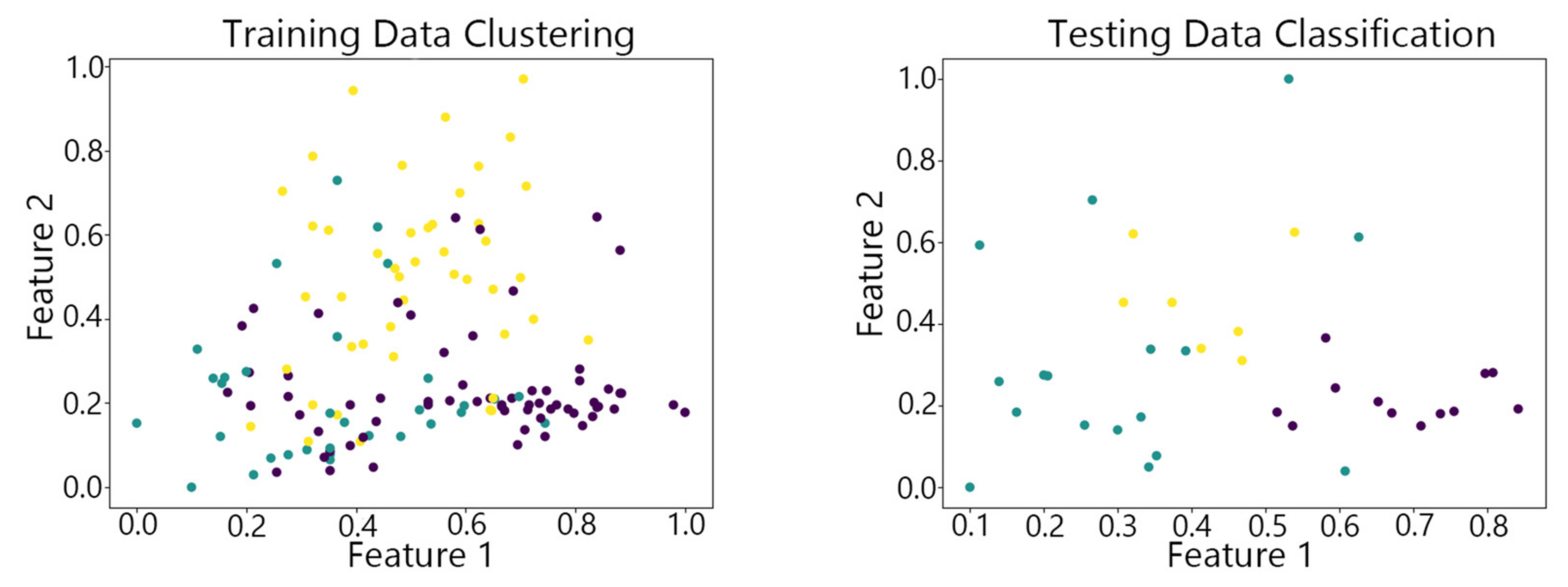
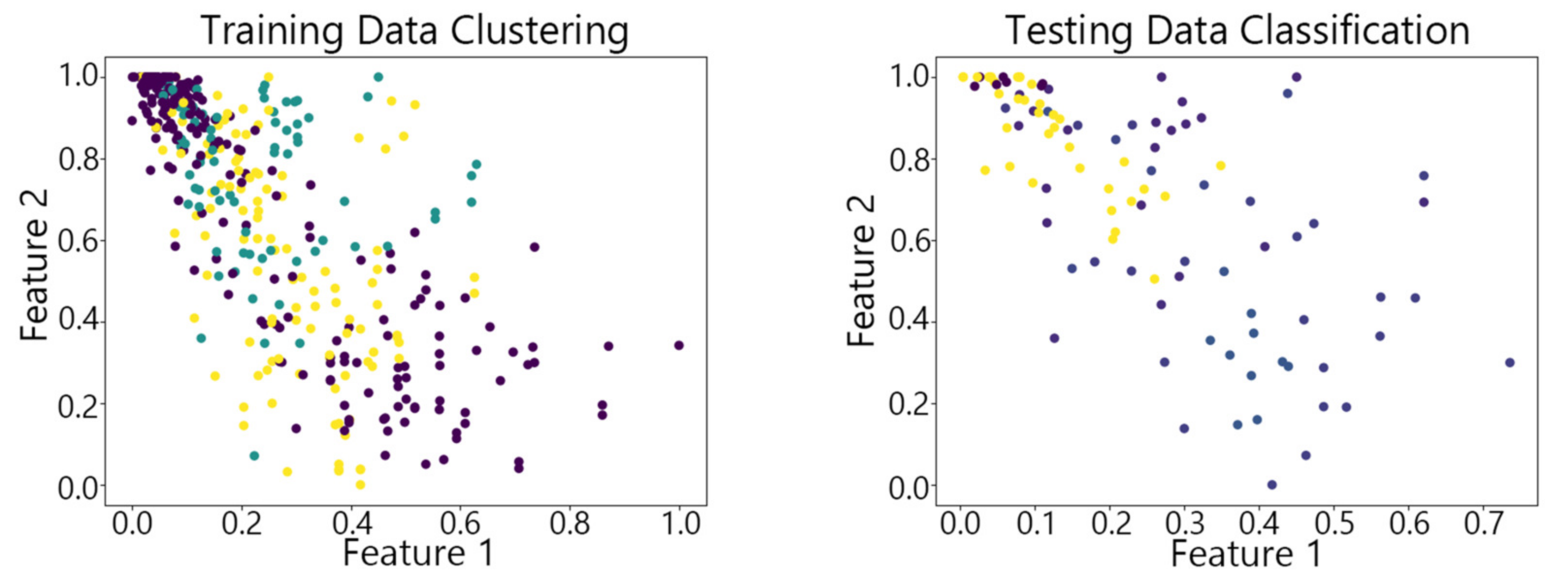
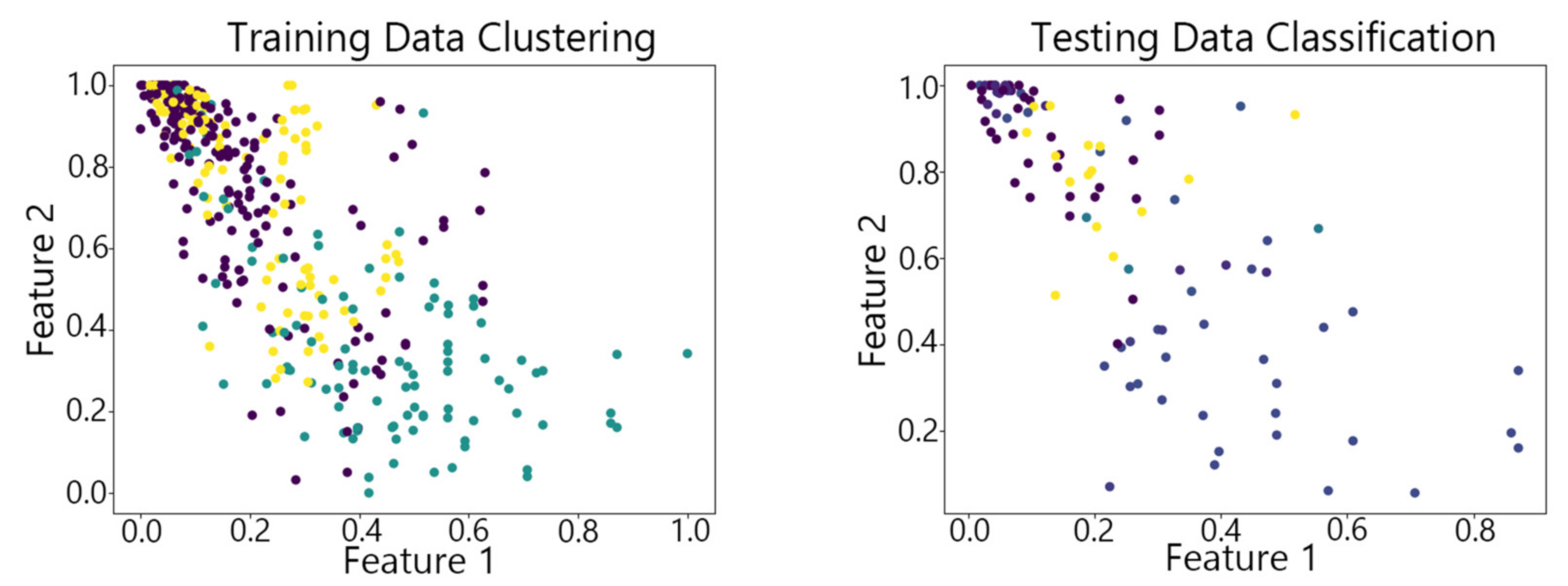
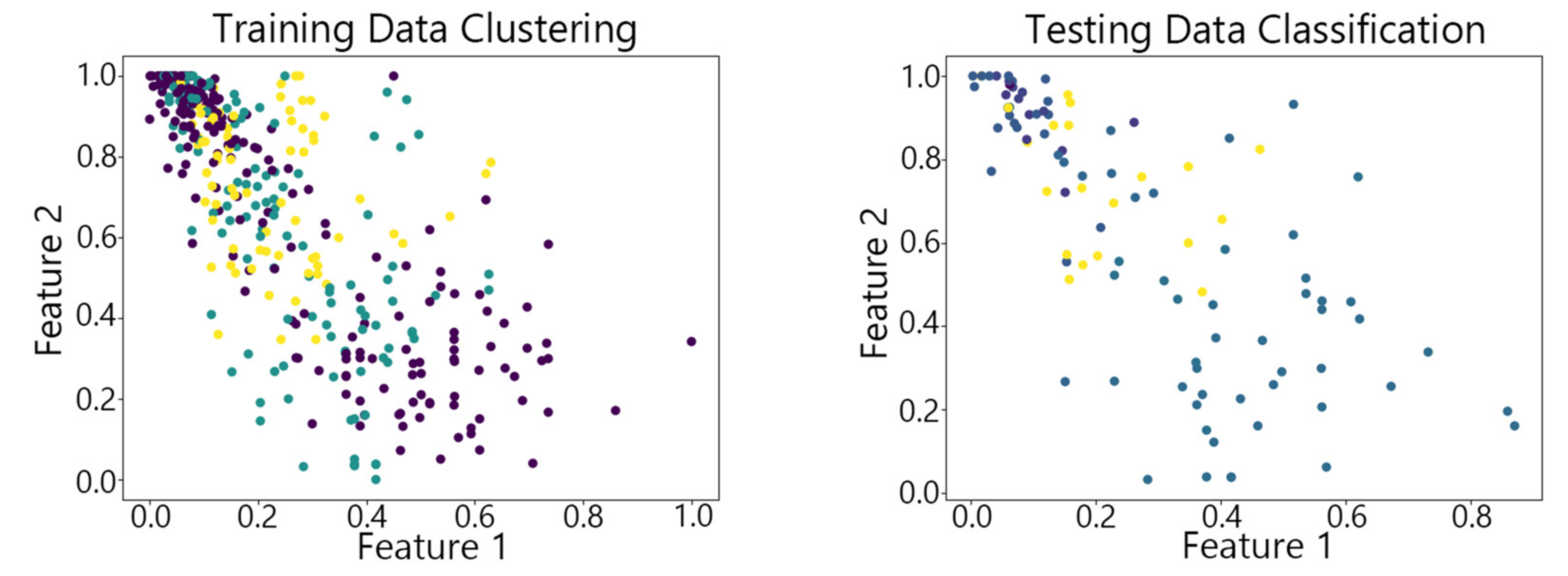
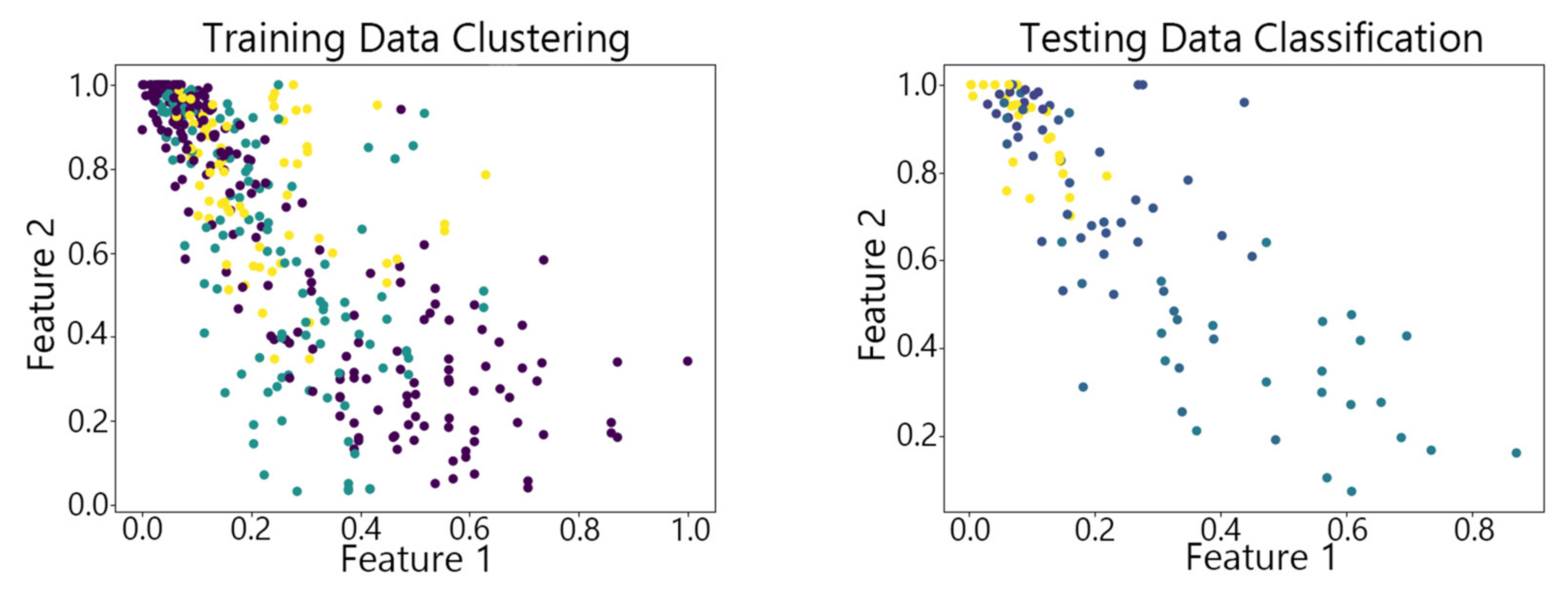
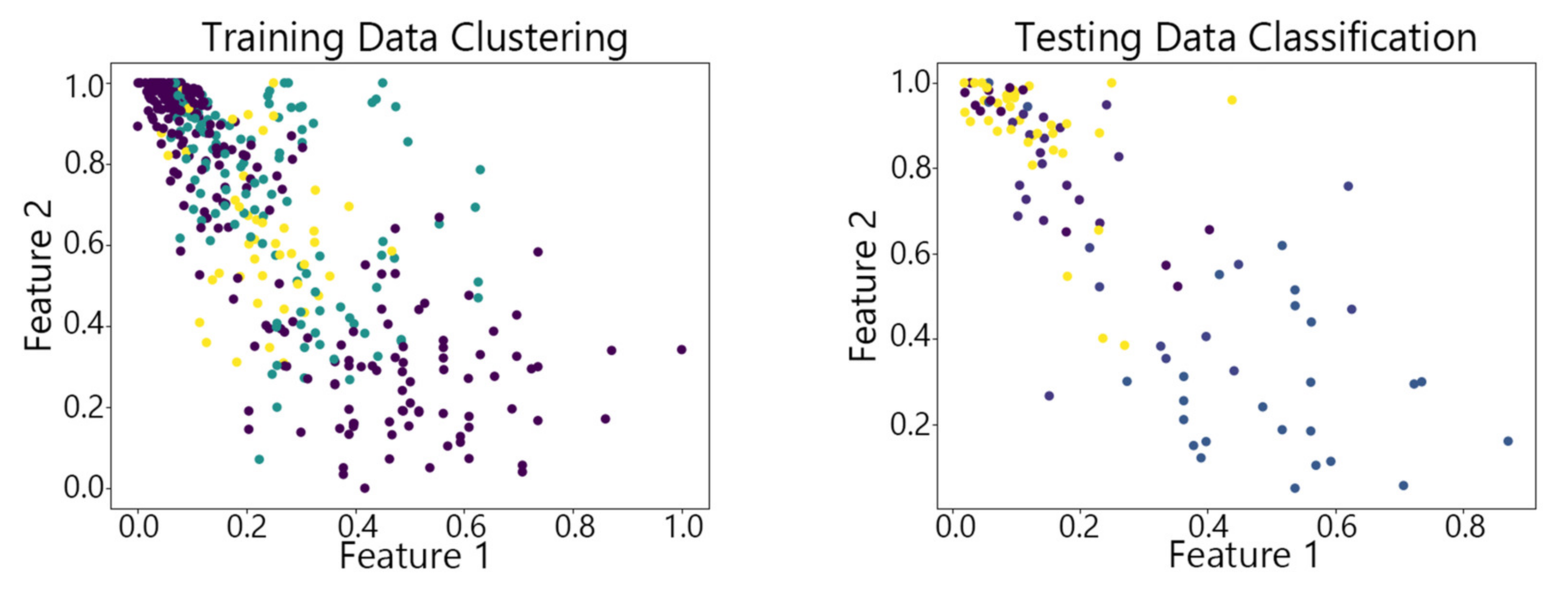
4.2. Visualization of Clustering Results
4.3. Clustering Results of Different Algorithms
4.4. Ablation Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Z. Machine Learning; Tsinghua University Press: Beijing, China, 2016. [Google Scholar]
- Li, Y.; Li, H.; Qian, X.; Zhu, Y. A review and analysis of outlier detection algorithms. Comput. Eng. 2002, 28, 5–6+32. [Google Scholar]
- Xu, X.; Liu, H.; Yao, M. Recent Progress of Anomaly Detection. Complexity 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Omar, S.; Ngadi, A.; Jebur, H.H. Machine Learning Techniques for Anomaly Detection: An Overview. Int. J. Comput. Appl. 2013, 79, 3–41. [Google Scholar] [CrossRef]
- Nassif, A.B.; Talib, M.A.; Nasir, Q.; Dakalbab, F.M. Machine Learning for Anomaly Detection: A Systematic Review. IEEE Access 2021, 9, 78658–78700. [Google Scholar] [CrossRef]
- Bzdok, D.; Krzywinski, M.; Altman, N. Machine learning: Supervised methods. Nat. Methods 2018, 15, 5–6. [Google Scholar] [CrossRef] [PubMed]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD’96), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Goldstein, M.; Uchida, S. A comparative evaluation of unsupervised anomaly detection algorithms for multivariate data. PLoS ONE 2016, 11, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Gadal, S.; Mokhtar, R.; Abdelhaq, M.; Alsaqour, R.; Ali, E.S.; Saeed, R. Machine Learning-Based Anomaly Detection Using K-Mean Array and Sequential Minimal Optimization. Electronics 2022, 11, 2158. [Google Scholar] [CrossRef]
- Jain, M.; Kaur, G.; Saxena, V. A K-Means clustering and SVM based hybrid concept drift detection technique for network anomaly detection. Expert Syst. Appl. 2022, 193, 116510. [Google Scholar] [CrossRef]
- Dai, Y.; Sun, S.; Che, L. Improved DBSCAN-based Data Anomaly Detection Approach for Battery Energy Storage Stations. J. Phys. Conf. Ser. 2022, 2351, 012025. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, L. Data anomaly detection based on isolation forest algorithm. In Proceedings of the 2022 International Conference on Computation, Big-Data and Engineering (ICCBE), Yunlin, Taiwan, 27–29 May 2022; pp. 87–89. [Google Scholar]
- Kohonen, T. The Self-Organizing Map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Kohonen, T. Things you haven’t heard about the Self-Organizing Map. In Proceedings of the IEEE international Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; pp. 1147–1156. [Google Scholar]
- Kohonen, T. Exploration of very large databases by Self-Organizing Maps. In Proceedings of International Conference on Neural Networks (icnn’97), Houston, TX, USA, 12 June 1997; pp. PL1–PL6. [Google Scholar]
- Kohonen, T. Essentials of the Self-Organizing Map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef] [PubMed]
- Sandoval-Lara, Z.; Gómez-Gil, P.; Moreno-Rodríguez, J.C.; Ramírez-Cortés, M. Self-Organizing Clustering by Growing-SOM for EEG-Based Biometrics. In Proceedings of the 2023 International Conference on Artificial Intelligence and Applications (ICAIA) Alliance Technology Conference (ATCON-1), Bangalore, India, 21–22 April 2023; pp. 1–4. [Google Scholar]
- Cui, W.; Xue, W.; Li, L.; Shi, J. A Method for Intermittent Fault Diagnosis of Electronic Equipment Based on Labeled SOM. In In Proceedings of the 2020 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Beijing, China, 5–7 August 2020; pp. 149–154. [Google Scholar]
- Zhang, X.; Xu, J.; Zhang, H. Fault Diagnosis of Levitation Controller of Medium-Speed Maglev Train Based on SOM-BP Neural Network. In Proceedings of the 2023 35th Chinese Control and Decision Conference (CCDC), Yichang, China, 20–22 May 2023; pp. 4162–4167. [Google Scholar]
- Chen, S.; Liu, Z.; Zhou, H.; Wen, X.; Xue, Y. Seismic Facies Visualization Analysis Method of SOM Corrected by Uniform Manifold Approximation and Projection. IEEE Geosci. Remote. Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Faithfull, W.J. PCA Feature Extraction for Change Detection in Multidimensional Unlabeled Data. IEEE Trans. Neural Networks Learn. Syst. 2014, 25, 69–80. [Google Scholar] [CrossRef] [PubMed]
- Anderson, E. The Irises of the Gaspe Peninsula. Bull. Am. Iris Soc. 1935, 59, 2–5. [Google Scholar]
- Aeberhard, S.; Coomans, D.; de Vel, O. Comparison of Classifiers in High Dimensional Settings; Technical Report; Department of Mathematics and Statistics, James Cook University: North Queensland, Australia, 1992; Volume 92. [Google Scholar]
- Aha, D.W.; Kibler, D. Instance-based learning algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef]
- Khan, S.; Mailewa, A.B. Discover botnets in IoT sensor networks: A lightweight deep learning framework with hybrid Self-Organizing Maps. Microprocess. Microsystems 2023, 97, 104753. [Google Scholar] [CrossRef]
- Manikant, M.N. Improved Classification of Cyber-Bullying Tweets in Social Media Using SVM-MaxEnt Based Dynamic Programming Based Self Organizing Maps. In Proceedings of the 2024 13th International Conference on System Modeling & Advancement in Research Trends (SMART), Moradabad, India, 6–7 December 2024; pp. 99–106. [Google Scholar]


| Methods | Strengths | Weaknesses |
|---|---|---|
| K-means + SMO | addresses the issues of accuracy and low false positive rates | its complexity is relatively high |
| K-means+data capture and drift analysis | improve accuracy and FAP | its accuracy is unstable when facing different traffic patterns and large datasets |
| self-selecting DBSCAN | solves the problem of parameter selection in DBSCAN and can effectively cluster multi-dimensional data | it faces the issue of over-dispersed clustering, so it is ranked after reference |
| PCA+isolation forest | improves computational efficiency | low detection accuracy and poor generalization ability |
| Methods | Strengths | Weaknesses |
|---|---|---|
| GSOM | can dynamically adjust the network size to adapt to different data shapes, offering strong adaptability | it performs poorly in handling noise |
| SOM+SVM | uses a secondary anomaly detection approach to improve fault diagnosis accuracy | it increases complexity and the possibility of errors |
| SOM+BP | addresses the issue of directly judging the accuracy of SOM clustering results and enhances the stability and accuracy of the detection results | needs repeated experimentation to select parameters |
| SOM+UMAP | handles high-dimensional data and better represent the topological structure of the data | constructs high-dimensional graphs may lead to the loss of distance and meaning between clusters |
| Dataset Name | Sample Size | Number of Classes | Number of Features | Feature Description | Common Use |
|---|---|---|---|---|---|
| IRIS Dataset | 150 | 3 | 4 | Sepal length, sepal width, petal length, petal width | Studying classification algorithms, commonly used in machine learning and data mining |
| Wine Dataset | 178 | 3 | 13 | Chemical components such as alcohol content, malic acid, ash, etc. | Studying the performance of classification and regression algorithms |
| Waveform Dataset | 5000 | 3 | 21 | Features representing signals from three different waveform types | Testing the classification and clustering performance of machine learning models |
| Hyperparameter Name | Description | Common Optimization Methods |
|---|---|---|
| Learning Rate | Controls the step size for updating the weights of the network | Decreases over training epochs |
| Neighborhood Radius | Affects the range of neighboring nodes, determining how many nodes are updated at each step | Decreases over time |
| Epochs | Controls the number of iterations during training | Set appropriately to avoid overtraining; selected through experimentation |
| Grid Size | Determines the structure of the SOM network | Adjust the grid size based on data complexity |
| Initialization Method | The method used to initialize the weights | Using the PCA algorithm |
| Training Sequence | The order in which data are presented during training, affecting the final results of SOM | Shuffle data order randomly or use mini-batch training |
| S | P | R | F1 | ACC | VA | AOT/ms | |
|---|---|---|---|---|---|---|---|
| SOM | 0.5109 | 0.88 | 0.85 | 0.86 | 0.8986 | 0.0026 | 0.0318 |
| DBSCAN | 0.5054 | 0.85 | 0.84 | 0.84 | 0.8800 | 0.0025 | 0.0244 |
| HybridSOM | 0.5235 | 0.93 | 0.90 | 0.91 | 0.9395 | 0.0013 | 0.0675 |
| DP-SOM | 0.5211 | 0.92 | 0.93 | 0.92 | 0.9381 | 0.0019 | 0.0594 |
| vwSOM | 0.5262 | 0.94 | 0.93 | 0.93 | 0.9412 | 0.0012 | 0.2221 |
| S | P | R | F1 | ACC | VA | AOT/ms | |
|---|---|---|---|---|---|---|---|
| SOM | 0.5032 | 0.82 | 0.84 | 0.83 | 0.8630 | 0.0040 | 0.0326 |
| DBSCAN | 0.5062 | 0.85 | 0.84 | 0.84 | 0.8700 | 0.0038 | 0.0251 |
| HybridSOM | 0.5184 | 0.92 | 0.91 | 0.91 | 0.9268 | 0.0019 | 0.0679 |
| DP-SOM | 0.5189 | 0.92 | 0.90 | 0.91 | 0.9279 | 0.0017 | 0.0603 |
| vwSOM | 0.5255 | 0.94 | 0.92 | 0.93 | 0.9401 | 0.0014 | 0.2263 |
| S | P | R | F1 | ACC | VA | AOT/ms | |
|---|---|---|---|---|---|---|---|
| SOM | 0.4553 | 0.68 | 0.72 | 0.70 | 0.7900 | 0.0125 | 0.0624 |
| DBSCAN | 0.4713 | 0.72 | 0.75 | 0.73 | 0.8200 | 0.0107 | 0.0375 |
| HybridSOM | 0.5079 | 0.88 | 0.87 | 0.87 | 0.8667 | 0.0049 | 0.1007 |
| DP-SOM | 0.5089 | 0.88 | 0.88 | 0.89 | 0.8904 | 0.0038 | 0.0944 |
| vwSOM | 0.5101 | 0.88 | 0.89 | 0.88 | 0.8931 | 0.0033 | 0.3981 |
| S | P | R | F1 | ACC | VA | |
|---|---|---|---|---|---|---|
| SOM | 0.5109 | 0.88 | 0.85 | 0.86 | 0.8986 | 0.0026 |
| SOM + PCA | 0.5127 | 0.91 | 0.88 | 0.89 | 0.8999 | 0.0017 |
| SOM + virtual winner | 0.5205 | 0.94 | 0.92 | 0.93 | 0.9385 | 0.0020 |
| vwSOM | 0.5262 | 0.94 | 0.93 | 0.93 | 0.9412 | 0.0012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Zhang, S.; Xue, X.; Jiang, R.; Fan, S.; Kou, H. An Improved Self-Organizing Map (SOM) Based on Virtual Winning Neurons. Symmetry 2025, 17, 449. https://doi.org/10.3390/sym17030449
Fan X, Zhang S, Xue X, Jiang R, Fan S, Kou H. An Improved Self-Organizing Map (SOM) Based on Virtual Winning Neurons. Symmetry. 2025; 17(3):449. https://doi.org/10.3390/sym17030449
Chicago/Turabian StyleFan, Xiaoliang, Shaodong Zhang, Xuefeng Xue, Rui Jiang, Shuwen Fan, and Hanliang Kou. 2025. "An Improved Self-Organizing Map (SOM) Based on Virtual Winning Neurons" Symmetry 17, no. 3: 449. https://doi.org/10.3390/sym17030449
APA StyleFan, X., Zhang, S., Xue, X., Jiang, R., Fan, S., & Kou, H. (2025). An Improved Self-Organizing Map (SOM) Based on Virtual Winning Neurons. Symmetry, 17(3), 449. https://doi.org/10.3390/sym17030449





