1. Introduction
The support function of a convex hypersurface measures the (signed) distance of the supporting hyperplanes of the surface to the origin. It is also possible to parameterize strictly convex hypersurfaces by means of their support function. This representation has led to major advances in convex geometry, geometric analysis, and geometric computing (see, e.g., [
1,
2,
3,
4]). More recently, generalizations of a classical theorem by Blaschke [
5] have grown in interest and relevance. In [
6], this problem is addressed for k-convex hypersurfaces in Hadamard manifolds, and in [
7], the same authors study a discrete version of the Blaschke problem for convex polygons when the ambient space is a two-dimensional space form.
The support function has been extensively used in the development of new computational methods and algorithms for the reconstruction of shapes [
8,
9,
10] using only a finite number of measurements of the values, allowing some error terms (noisy measurements). This has many applications, particularly within computer vision software.
In [
11], Pedro R. S. Antunes and Beniamin Bogosel present a numerical framework for the optimization of geometric functionals of convex shapes. In this case, the support function is used to approximate solutions to various optimization problems. Among these, they study the famous open problem of Blaschke–Lebesgue, that is, the minimization of the volume of a strictly convex surface subject to a given constant width (see also [
12] for a more geometric approach). The conjectured optimizers are the shapes called Meissner’s bodies. Related problems discussed in [
11] include minimizing Dirichlet–Laplace eigenvalues under a convexity constraint and finding rotors of minimal volume.
In this work, we recall the geometry of hypersurfaces and the geometry of convex hypersurfaces in the Euclidean space . Our approach is to obtain explicit formulae in local coordinates in terms of the support function and its derivatives. It is worth remarking that even though we restricted ourselves to the case of strictly convex hypersurfaces, many of these identities will still hold in the case that one requires only convexity.
Our main contributions can be found in
Section 4 and
Section 6. We obtain an explicit expression for a differential equation satisfied by the support function when it is restricted to a curve on the sphere, providing a more general form than the one utilized in [
13,
14], where the curves are geodesics on the unit sphere. In the last section, we also provide the parameterization by support functions of ellipsoids, where symmetry plays an important role and allows us to derive the recurrence relations for the angles needed for such a representation. These advances will help us understand how the geometry of curves on the sphere changes when it is mapped to a convex surface by means of its support function.
2. Geometry of Hypersurfaces in
In this section, we recall some formulae in the geometry of the hypersurfaces in in local coordinates.
Let be a hypersurface. Then, . For any point , parameterized as , we denote the usual tangent frame , for . We also write for the usual inner product in . The induced metric in M is the restriction of to the tangent spaces . It is referred to as the induced metric on M, is denoted by g, and is determined by the values . The inverse of g is denoted by upper indices: . We denote by D the usual derivative on and ∇ the covariant derivative of M. Throughout this document, we use the Einstein summation convention for repeated indices.
The Christoffel symbols of
M, defined by
, can be obtained in terms of the derivatives of the metric
The Riemann curvature in local coordinates is
and the curvature tensor is
For every
, the Gauss formula relates
D to ∇ by the identity
where
h is the second fundamental form and
is a unit vector normal to
M. In coordinates, we have
The Gauss map is defined as
, with
. Note that there are two possible choices for
in terms of
; we use
.
The shape operator
A is obtained by contracting the second fundamental form with respect to the metric
The eigenvalues of the shape operator are called the principal curvatures of
M. The mean curvature is the trace of the second fundamental form in the sense that
The Gauss curvature is the determinant of the shape operator
The Gauss equation relates the Riemann curvature to the second fundamental form
This allows for the definition of other notions of intrinsic curvatures. The Ricci curvature arises as the contraction of the Riemann tensor with the metric as
and the scalar curvature as
Let
be a smooth function, and let ∇ be the covariant derivative. The gradient of
u is the vector field
and the Hessian of
u is defined by
One can easily see that the Hessian is commutative:
. Using the notation
, we have the following expressions for higher-order derivatives:
On the other hand, the Hessian of the parameterization
X is
and by the Gauss formula, we get the identity
After some lengthy computations, one can also show the following identities:
.
.
We finish this section by writing some identities for the case of the round sphere , with an induced metric . In this case, we write . It is clear that the antipode of the position vector is the inward unit normal vector , that the second fundamental form yields , and that we still use to denote the Christoffel symbols of .
The Gauss formula for the sphere then reads
The Gauss equation is written as
the Ricci curvature is written as
and the scalar curvature of the unit sphere is written as
In an orthonormal frame, we have
yielding the following identity:
If we sum over
k, we obtain the following useful identity:
Remark 1. A natural question is that of finding solutions to . One can see that, by the maximum principle, if is harmonic, then u must be a constant valued function.
3. Geometry of the Support Function
A strictly convex hypersurface
is diffeomorphic to the sphere
by means of the Gauss map
. Denote by
the inverse of the Gauss map. The support function
is defined for every
by
Hence, we identify
with the outward normal direction of
M, and
is referred to as the inward normal direction of
M. The following proposition shows how to parameterize the strictly convex hypersurface
M by means of its support function.
Proposition 1. Let be the support function of a strictly convex hypersurface . Then, the inverse of the Gauss map is given bywhere ∇
is the covariant derivative of the usual round sphere . Proof. We aim to find the coefficients in the following equality:
Taking the inner product with
, we get
. Now note that
Thus, we may write
Since we also have that for every
, it holds that
, and we see that
Then, the gradient of the support function is
and its norm is
Finally, we conclude that the parameterization of the strictly convex hypersurface
M is
□
Proposition 2. Let M be a strictly convex hypersurface in parameterized by its support function as in (
21)
. Then, the induced metric g of M is given by Proof. The derivative of the inverse of a matrix yields
Using (
16), we can also compute the following:
This implies that
Then, we can get an expression for the induced metric
□
Proposition 3. Let M be a strictly convex hypersurface in parameterized by its support function as in (
21)
. Then, the second fundamental form h of M is given by Proof. In order to obtain an expression for the second fundamental form, we use the identity
, where we use the notation
. The sign convention here guarantees that we are measuring convexity with respect to the inward normal vector. Then, differentiating Equation (
32), we only expand the terms with the normal component:
From this, it follows that
□
Proposition 4. Let M be a strictly convex hypersurface in parameterized by its support function as in (
21)
. The shape operator is defined as . Then, the inverse of the shape operator is given by Proof. Using (
29) and (
33), we have
From this identity, it follows that the inverse of the shape operator is
Denote by
B the inverse of the shape operator. Then, we have proven the identity
as we claimed. □
The eigenvalues of B are , where , , are the principal curvatures of the strictly convex hypersurface.
Now we are able to give an expression for the Christoffel symbols
of the hypersurface
M in terms of the Christoffel symbols
of the sphere and the inverse of the shape operator.
Proposition 5. Let M be a strictly convex hypersurface in parameterized by its support function as in (
21)
. Let denote the shape operator of M. Then, it holds that Proof. By the Gauss formula and our sign convention for
h, we have
Note that
from Equation (
32) can also be written in terms of
B as
where we use
. Similarly, we can rewrite (
34) as
Note that in the last identity, we have interchanged the indices
r and
s, as both are summing. Finally, Equation (
39) is obtained by equating Equations (
42) and (
40). □
4. Curves on Convex Hypersurfaces
Let
be a smooth curve on the sphere. Recall that we write
. We use the dot notation for differentiation with respect to
t.
Theorem 1. Let be a strictly convex hypersurface parameterized by its support function as in (
21)
, and let be a smooth curve on the sphere. Then, the support function satisfies the equationwhere B is the inverse of the shape operator (
36)
and . Proof. The following identities hold:
From our parameterization,
is the corresponding curve on the convex hypersurface
M. Equations (
32) and (
36) imply that
Restricting the support function
u to the curve,
, and differentiating, we have
since clearly
. Differentiating again, we get
On the other hand,
Recalling that
, we can get the general expression
□
Remark 2. If is a unit speed geodesic on , then it satisfiesand in this particular case, we have . Equations (
44), (
45), and (
47) imply the following proposition.
Proposition 6 ([
13])
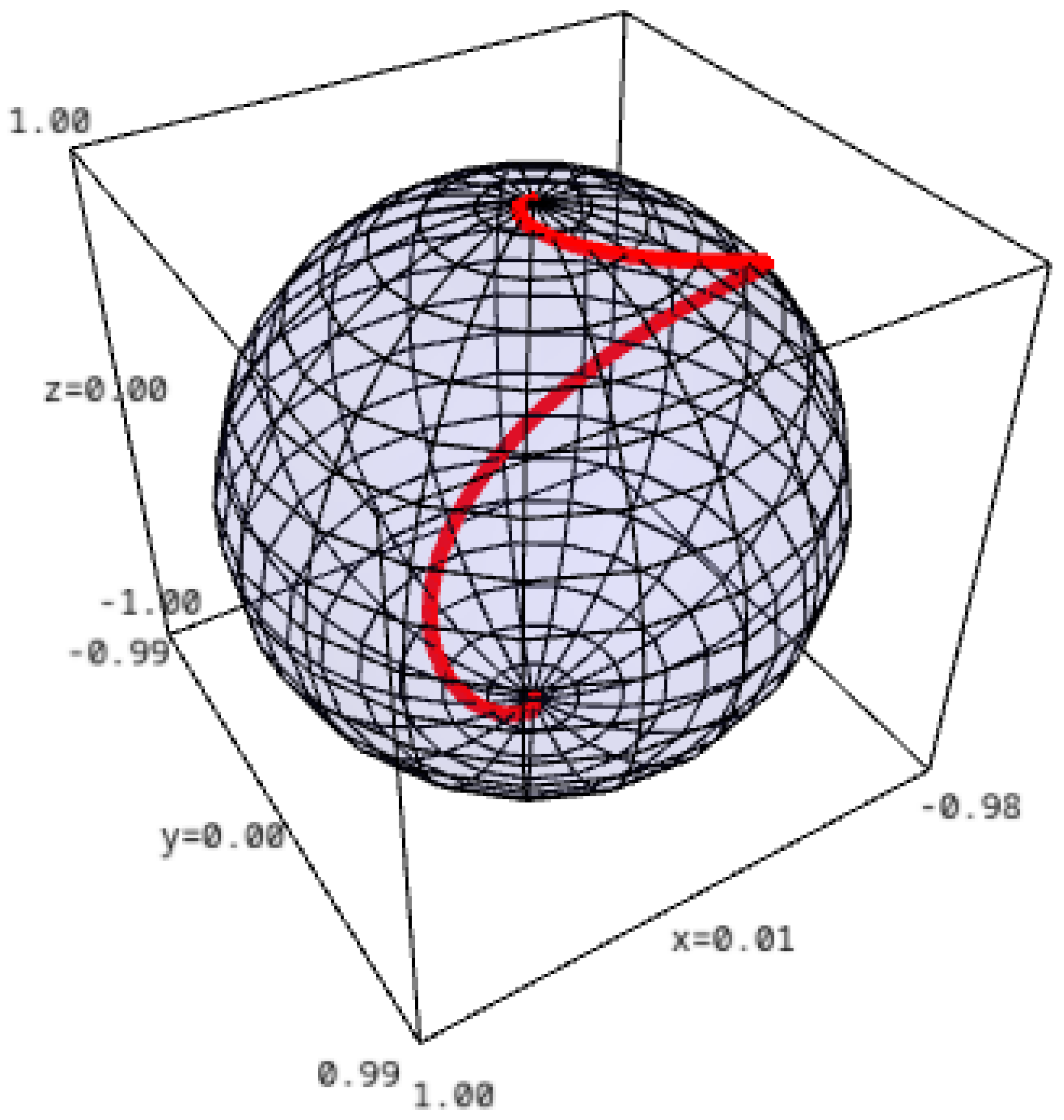
. Let be a geodesic on . Then, the support function u of a closed convex hypersurface M in , restricted to , satisfies the following differential equation: The following example gives the parameterization of a curve on the sphere called a loxodrome. From the identities described in this and the previous section, one can get explicit formulas of curves on the sphere transformed into curves on a strictly convex surface in terms of the support function
u and geometric quantities on the sphere. In [
15], the authors point out the importance of such curves in maritime surface navigation. Let
. For
, consider the curve
. We say that the curve
is a loxodrome on the 2-sphere if
makes an angle
with
. Then, we have
where
and
which leads to the following equation:
Its solution is then
Then, the equation for a loxodrome (see
Figure 1) is given by
An interesting matter is then to understand how the geometry of such curves changes in terms of the support function when it is mapped to an ellipsoid by means of the mappings described in
Section 6.
5. The Area Element and Curvatures for Convex Surfaces
The surface area element of the surface parameterized by the support function is given by
For the rest of this section, we restrict our analysis to the case of dimension
. The following useful identity holds:
In the last identity, we put
. Then, the area element of the surface,
, can be written in terms of the area element of the round unit sphere,
,
Denote by
the shape operator with eigenvalues
. From the expression of the inverse of the shape operator, we have
Let , , be the eigenvalues of B.
The determinant of
B is then
Note that the characteristic polynomial is
so the roots are precisely
From this, it follows that the principal curvatures of the surface are
Proposition 7 ([
12])
. Let M be a strictly convex surface in the three-dimensional Euclidean space . If is the support function of M, then the following identities hold: As an example, if
M is the sphere of radius
R, then its support function is the constant
. Then,
and
, and from (
59) and (
60), we get the known values
and
, respectively.
6. Identities for Ellipsoids in
In this section, we develop explicit expressions for the parameterization of ellipsoids by means of their support functions. It is worth noting that by the symmetry of the ellipsoids, it is always possible, after a translation and rotation, to assume that these are centered at the origin and use the standard polar coordinates to represent them.
Lemma 1. Let . Let be a vector in the ellipse in polar coordinates. The field ξ is normal to the ellipse at Y if it holds that Proof. By symmetry arguments, it is enough to show the identity for
. In polar coordinates, the tangent vector to
is given by
and the normal vector is
If
and
N have the same direction, then it must hold that
From this, (
61) follows. □
As a consequence of the previous lemma, we obtain the parameterization of an ellipse in terms of its support function.
Proposition 8. Consider the ellipse on the plane given by the equationThen, for any , with , the ellipse can be parameterized as In this case, ξ is the outer unit normal vector to the ellipse at the point , and the support function of the ellipse is given by Proof. The claim follows from the previous lemma, after making
□
Proposition 9. Consider the ellipsoid in three-dimensional Euclidean space given by the equationThen, for any , with , the ellipsoid can be parameterized aswithand In this case, ξ is the outer unit normal vector to the ellipsoid at the point , and the support function of the ellipsoid is given by Proof. Proceeding as in the previous proposition, let , and let be a parameterization of the ellipsoid in polar coordinates.
The tangent vectors are
The outer normal vector is
If
N and
have the same direction, we have
which is equivalent to
From
we obtain
Then, the proposition is established. □
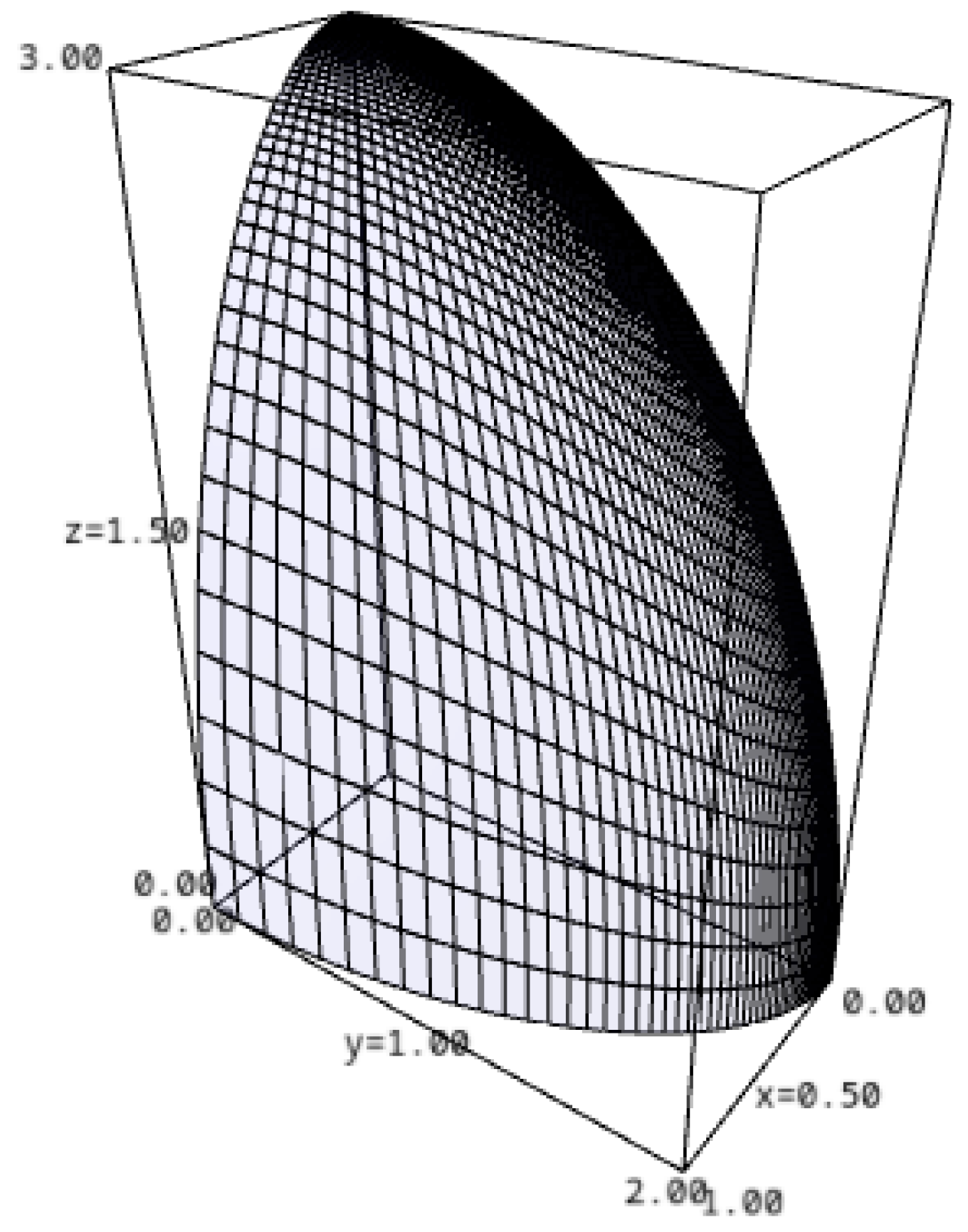
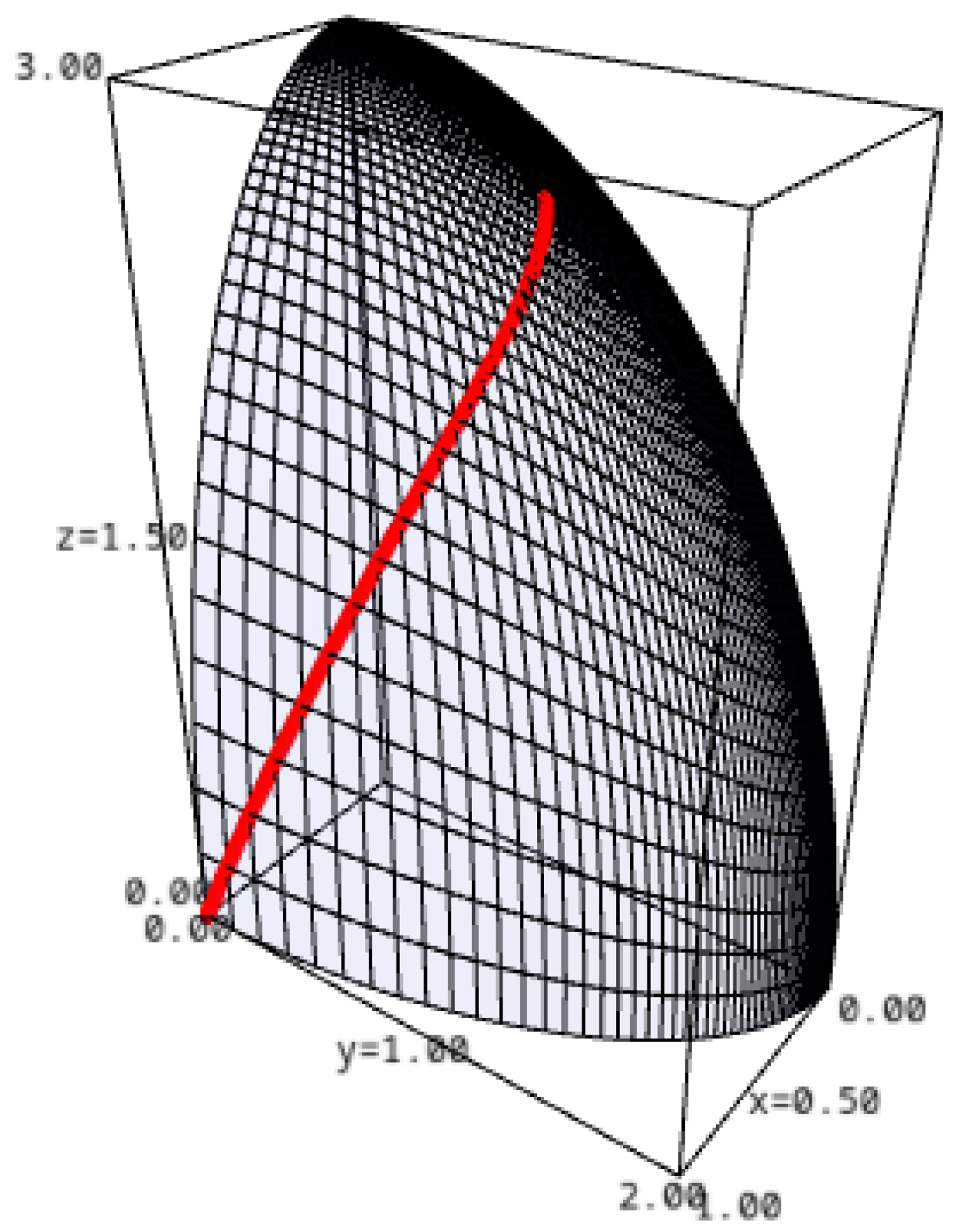
We consider, as an example, the ellipsoid
, in
(see
Figure 2). Using (
49), (
66), and (
69), we show in
Figure 3 the image of a loxodrome on the sphere mapped into the ellipsoid.
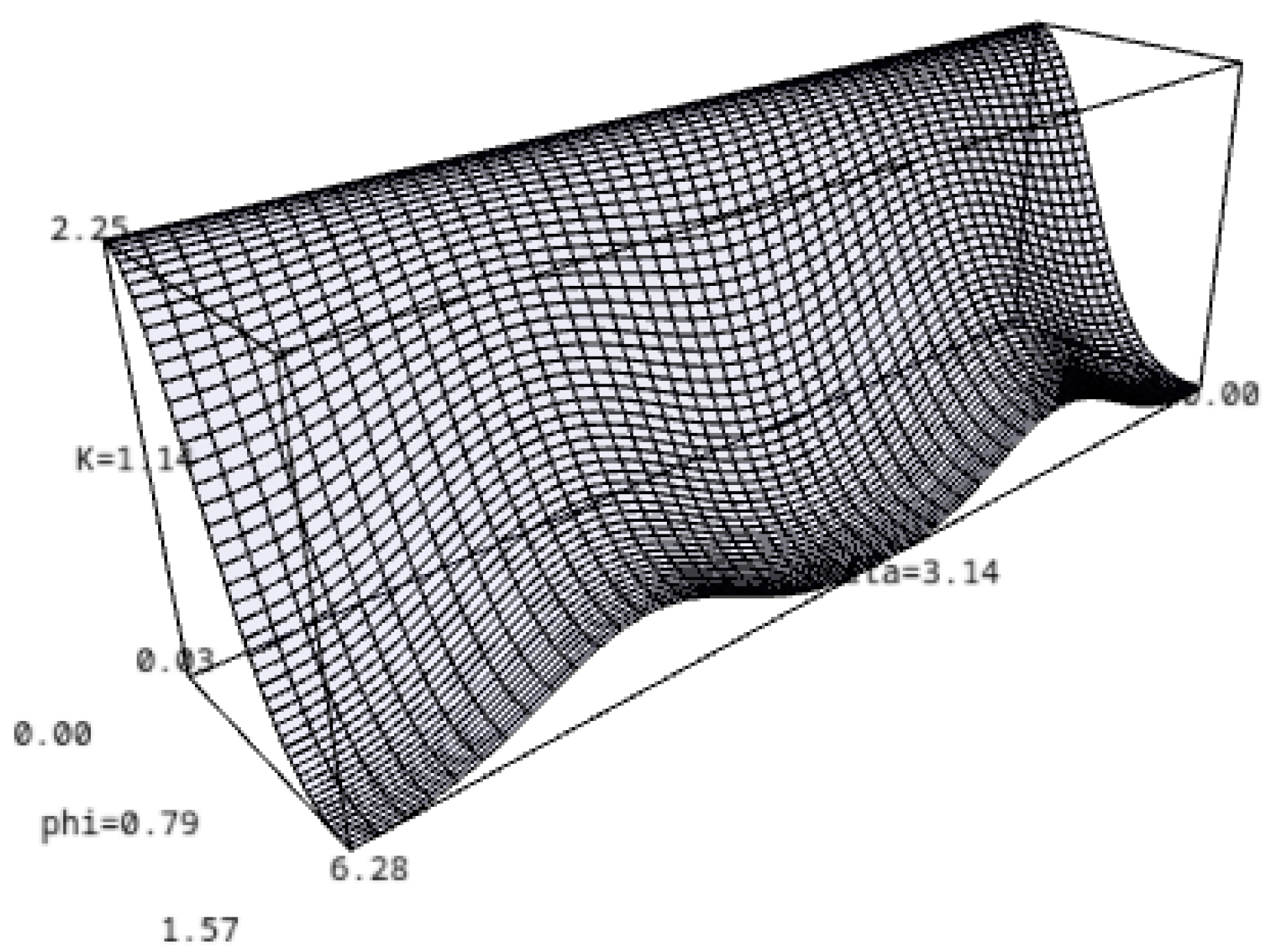
Continuing with this example, we give an expression for the Gauss curvature. First, note that the non-vanishing Christoffel symbols of the sphere are
For any smooth function
, the Hessian is given explicitly as
Then, the Hessian matrix with respect to the round metric is
Now we can give explicitly the identities
and
Using these last two expressions together with (
60), we can obtain the graph of the Gaussian curvature
(see
Figure 4) over the parameter space.
Now we conclude this section with a general formula for the parameterization of ellipsoids over the sphere as the inverse of their Gauss map in any dimension.
Proposition 10. Consider the ellipsoid in and suppose it is parameterized in polar coordinates with angles by . Let . If the s satisfy the following identities:the parameterization is the inverse of its Gauss map with normal ξ, and its support function is given by Proof. Using spherical coordinates for
, we have
Note the following relations with the angles
Recall that for any ellipsoid given by the equation
a normal vector field is given by the gradient
, where
Then,
If the ellipsoid is parameterized in polar coordinates,
Then, we must have
The result now follows after rearranging each equation for
,
. □
7. Discussion
In this work, a detailed description of the geometry of surfaces parameterized by a support function is given. A presentation in local coordinates is rare in the literature, and our approach provides explicit formulas for ease of manipulation and computational implementation.
Theorem 1 gives a differential equation for the support function restricted to any smooth curve on the sphere. With this result, one can study how the geometry of curves on the sphere changes when it is mapped to a strictly convex hypersurface.
A method to parameterize ellipsoids using the inverse of the Gauss map is provided. These formulas work in any dimension n.
These theoretical tools provide a foundation that may prove instrumental in extending classical results such as Blaschke’s inclusion theorems. In particular, the availability of explicit and generalizable identities allows for new approaches to problems involving curvature, inclusion, and comparison of convex bodies.